Last updated: 2018-05-12

workflowr checks: (Click a bullet for more information)

  • ✔ R Markdown file: up-to-date

    Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

  • ✔ Environment: empty

    Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

  • ✔ Seed: set.seed(12345)

    The command set.seed(12345) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

  • ✔ Session information: recorded

    Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

  • ✔ Repository version: 140be7f

    Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

    Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 
    
Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store
    Ignored:    analysis/BH_robustness_cache/
    Ignored:    analysis/FDR_Null_cache/
    Ignored:    analysis/FDR_null_betahat_cache/
    Ignored:    analysis/Rmosek_cache/
    Ignored:    analysis/StepDown_cache/
    Ignored:    analysis/alternative2_cache/
    Ignored:    analysis/alternative_cache/
    Ignored:    analysis/ash_gd_cache/
    Ignored:    analysis/average_cor_gtex_2_cache/
    Ignored:    analysis/average_cor_gtex_cache/
    Ignored:    analysis/brca_cache/
    Ignored:    analysis/cash_deconv_cache/
    Ignored:    analysis/cash_fdr_1_cache/
    Ignored:    analysis/cash_fdr_2_cache/
    Ignored:    analysis/cash_fdr_3_cache/
    Ignored:    analysis/cash_fdr_4_cache/
    Ignored:    analysis/cash_fdr_5_cache/
    Ignored:    analysis/cash_fdr_6_cache/
    Ignored:    analysis/cash_plots_cache/
    Ignored:    analysis/cash_sim_1_cache/
    Ignored:    analysis/cash_sim_2_cache/
    Ignored:    analysis/cash_sim_3_cache/
    Ignored:    analysis/cash_sim_4_cache/
    Ignored:    analysis/cash_sim_5_cache/
    Ignored:    analysis/cash_sim_6_cache/
    Ignored:    analysis/cash_sim_7_cache/
    Ignored:    analysis/correlated_z_2_cache/
    Ignored:    analysis/correlated_z_3_cache/
    Ignored:    analysis/correlated_z_cache/
    Ignored:    analysis/create_null_cache/
    Ignored:    analysis/cutoff_null_cache/
    Ignored:    analysis/design_matrix_2_cache/
    Ignored:    analysis/design_matrix_cache/
    Ignored:    analysis/diagnostic_ash_cache/
    Ignored:    analysis/diagnostic_correlated_z_2_cache/
    Ignored:    analysis/diagnostic_correlated_z_3_cache/
    Ignored:    analysis/diagnostic_correlated_z_cache/
    Ignored:    analysis/diagnostic_plot_2_cache/
    Ignored:    analysis/diagnostic_plot_cache/
    Ignored:    analysis/efron_leukemia_cache/
    Ignored:    analysis/fitting_normal_cache/
    Ignored:    analysis/gaussian_derivatives_2_cache/
    Ignored:    analysis/gaussian_derivatives_3_cache/
    Ignored:    analysis/gaussian_derivatives_4_cache/
    Ignored:    analysis/gaussian_derivatives_5_cache/
    Ignored:    analysis/gaussian_derivatives_cache/
    Ignored:    analysis/gd-ash_cache/
    Ignored:    analysis/gd_delta_cache/
    Ignored:    analysis/gd_lik_2_cache/
    Ignored:    analysis/gd_lik_cache/
    Ignored:    analysis/gd_w_cache/
    Ignored:    analysis/knockoff_10_cache/
    Ignored:    analysis/knockoff_2_cache/
    Ignored:    analysis/knockoff_3_cache/
    Ignored:    analysis/knockoff_4_cache/
    Ignored:    analysis/knockoff_5_cache/
    Ignored:    analysis/knockoff_6_cache/
    Ignored:    analysis/knockoff_7_cache/
    Ignored:    analysis/knockoff_8_cache/
    Ignored:    analysis/knockoff_9_cache/
    Ignored:    analysis/knockoff_cache/
    Ignored:    analysis/knockoff_var_cache/
    Ignored:    analysis/marginal_z_alternative_cache/
    Ignored:    analysis/marginal_z_cache/
    Ignored:    analysis/mosek_reg_2_cache/
    Ignored:    analysis/mosek_reg_4_cache/
    Ignored:    analysis/mosek_reg_5_cache/
    Ignored:    analysis/mosek_reg_6_cache/
    Ignored:    analysis/mosek_reg_cache/
    Ignored:    analysis/pihat0_null_cache/
    Ignored:    analysis/plot_diagnostic_cache/
    Ignored:    analysis/poster_obayes17_cache/
    Ignored:    analysis/real_data_simulation_2_cache/
    Ignored:    analysis/real_data_simulation_3_cache/
    Ignored:    analysis/real_data_simulation_4_cache/
    Ignored:    analysis/real_data_simulation_5_cache/
    Ignored:    analysis/real_data_simulation_cache/
    Ignored:    analysis/rmosek_primal_dual_2_cache/
    Ignored:    analysis/rmosek_primal_dual_cache/
    Ignored:    analysis/seqgendiff_cache/
    Ignored:    analysis/simulated_correlated_null_2_cache/
    Ignored:    analysis/simulated_correlated_null_3_cache/
    Ignored:    analysis/simulated_correlated_null_cache/
    Ignored:    analysis/simulation_real_se_2_cache/
    Ignored:    analysis/simulation_real_se_cache/
    Ignored:    analysis/smemo_2_cache/
    Ignored:    data/LSI/
    Ignored:    docs/.DS_Store
    Ignored:    docs/figure/.DS_Store
    Ignored:    output/fig/

Untracked files:
    Untracked:  docs/figure/smemo.rmd/

Unstaged changes:
    Modified:   analysis/smemo.rmd
    Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
Expand here to see past versions:
    File Version Author Date Message
    Rmd cc0ab83 Lei Sun 2018-05-11 update
    html 0f36d99 LSun 2017-12-21 Build site.
    html 853a484 LSun 2017-11-07 Build site.
    html 1ea081a LSun 2017-07-03 sites
    html 7693edf LSun 2017-02-14 pipeline
    Rmd 681085c LSun 2017-02-10 fdr
    html 681085c LSun 2017-02-10 fdr
    html 81d84f5 LSun 2017-02-10 FDR
    Rmd 2696cb2 LSun 2017-02-10 fwer
    html 2696cb2 LSun 2017-02-10 fwer
    html 066c544 LSun 2017-02-03 StepDown
    Rmd 4afbe4e LSun 2017-02-03 StepDown
    html 59fd661 LSun 2017-02-03 Build site.
    Rmd c4165dc LSun 2017-02-03 simulation
    html c4165dc LSun 2017-02-03 simulation
    Rmd 313897f LSun 2017-02-03 details
    html 313897f LSun 2017-02-03 details
    html 36c1e4c LSun 2017-02-03 Build site.
    Rmd d25a6e3 LSun 2017-02-03 step-down
    html d25a6e3 LSun 2017-02-03 step-down

Last updated: 2018-05-12

Code version: 140be7f

Introduction

In order to understand the behavior of \(p\)-values of top expressed, correlated genes under the global null, simulated from GTEx data, we apply two FWER-controlling multiple comparison procedures, Holm’s “step-down” (Holm 1979) and Hochberg’s “step-up.” (Hochberg 1988)

Holm’s step-down procedure: start from the smallest \(p\)-value

It can be shown that Holm’s procedure conservatively controls the FWER in the strong sense, under arbitrary correlation among \(p\)-values.

First, order the \(p\)-values

\[ p_{(1)} \leq p_{(2)} \leq \cdots \leq p_{(n)} \]

and let \(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\) be the corresponding hypotheses. Then examine the \(p\)-values in order.

Step 1: If \(p_{(1)} \leq \alpha/n\) reject \(H_{(1)}\) and go to Step 2. Otherwise, accept \(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\) and stop.

……

Step \(i\): If \(p_{(i)} \leq \alpha / (n − i + 1)\) reject \(H_{(i)}\) and go to step \(i + 1\). Otherwise, accept \(H_{(i)}, H_{(i + 1)}, \ldots, H_{(n)}\) and stop.

……

Step \(n\): If \(p_{(n)} \leq \alpha\), reject \(H_{(n)}\). Otherwise, accept \(H_{(n)}\).

Hence the procedure starts with the most extreme (smallest) \(p\)-value and stops the first time \(p_{(i)}\) exceeds the critical value \(\alpha_i = \alpha/(n − i + 1)\).

It can be shown that Holm’s procedure conservatively controls the FWER in the strong sense, under arbitrary correlation among \(p\)-values.

Hochberg’s step-up procedure: start from the largest \(p\)-value

It can be shown that Hochberg’s procedure conservatively controls the FWER in the strong sense, when \(p\)-values are independent.

First, order the \(p\)-values

\[ p_{(1)} \leq p_{(2)} \leq \cdots \leq p_{(n)} \]

and let \(H_{(1)}, H_{(2)}, \ldots, H_{(n)}\) be the corresponding hypotheses. Then examine the \(p\)-values in order.

Step 1: If \(p_{(n)} \leq \alpha\) reject \(H_{(1)}, \ldots, H_{(n)}\) and stop. Otherwise, accept \(H_{(n)}\) and go to step 2.

……

Step \(i\): If \(p_{(n - i + 1)} \leq \alpha / i\) reject \(H_{(1)}, \ldots, H_{(n - i + 1)}\) and stop. Otherwise, accept \(H_{(n - i + 1)}\) and go to step \(i + 1\).

……

Step \(n\): If \(p_{(1)} \leq \alpha / n\), reject \(H_{(1)}\). Otherwise, accept \(H_{(1)}\).

Hence the procedure starts with the least extreme (largest) \(p\)-value and stops the first time \(p_{(i)}\) falls below the critical value \(\alpha_i = \alpha/(n − i + 1)\).

It can be shown that Hochberg’s procedure conservatively controls the FWER in the strong sense, when \(p\)-values are independent.

Sarkar 1998 also pointed out that Hochberg’s procedure can control the FWER strongly under certain dependency among the test statistics, such as a multivariate normal with a common marginal distribution and positive correlations.

Holm’s procedure is based on Bonferroni correction, whereas Hochberg’s on Sime’s inequality. Both use exactly the same thresholds, comparing \(p_{(i)}\) with \(\alpha/(n − i + 1)\), yet Holm’s starts from the smallest \(p\)-value, and Hochberg’s from the largest. Hochberg’s is thus strictly more powerful than Holm’s.

Result

Now we apply the two procedures to the simulated, correlated null data.

p1 = read.table("../output/p_null_liver.txt")
p2 = read.table("../output/p_null_liver_777.txt")
p = rbind(p1, p2)
m = nrow(p)
holm = hochberg = matrix(nrow = m, ncol = ncol(p))

for(i in 1:m){
  holm[i, ] = p.adjust(p[i, ], method = "holm") # p-values adjusted by Holm (1979)
  hochberg[i, ] = p.adjust(p[i, ], method = "hochberg") # p_values adjusted by Hochberg (1988)
}
## calculate empirical FWER at 100 nominal FWER's

alpha = seq(0, 0.15, length = 100)
fwer_holm = fwer_hochberg = c()
for (i in 1:length(alpha)) {
  fwer_holm[i] = mean(apply(holm, 1, function(x) {min(x) <= alpha[i]}))
  fwer_hochberg[i] = mean(apply(hochberg, 1, function(x) {min(x) <= alpha[i]}))
}

fwer_holm_se = sqrt(fwer_holm * (1 - fwer_holm) / m)
fwer_hochberg_se = sqrt(fwer_hochberg * (1 - fwer_hochberg) / m)

Here at each nominal FWER from \(0\) to \(0.15\), we plot the empirical FWER, calculated from \(m = 2000\) independent simulation trials. Dotted lines indicate one standard error computed from binomial model \(= \sqrt{\hat{\text{FWER}}(1 - \hat{\text{FWER}}) / m}\).

plot(alpha, fwer_holm, pch = 1, xlab = "nominal FWER", ylab = "empirical FWER", xlim = c(0, max(alpha)), ylim = c(0, max(alpha)), cex = 0.75)
points(alpha, fwer_hochberg, col = "blue", pch = 19, cex = 0.25)
lines(alpha, fwer_holm - fwer_holm_se, lty = 3)
lines(alpha, fwer_holm + fwer_holm_se, lty = 3)
lines(alpha, fwer_hochberg + fwer_hochberg_se, lty = 3, col = "blue")
lines(alpha, fwer_hochberg - fwer_hochberg_se, lty = 3, col = "blue")

abline(0, 1, lty = 3, col = "red")
legend("topleft", c("Holm", "Hochberg"), col = c(1, "blue"), pch = c(1, 19))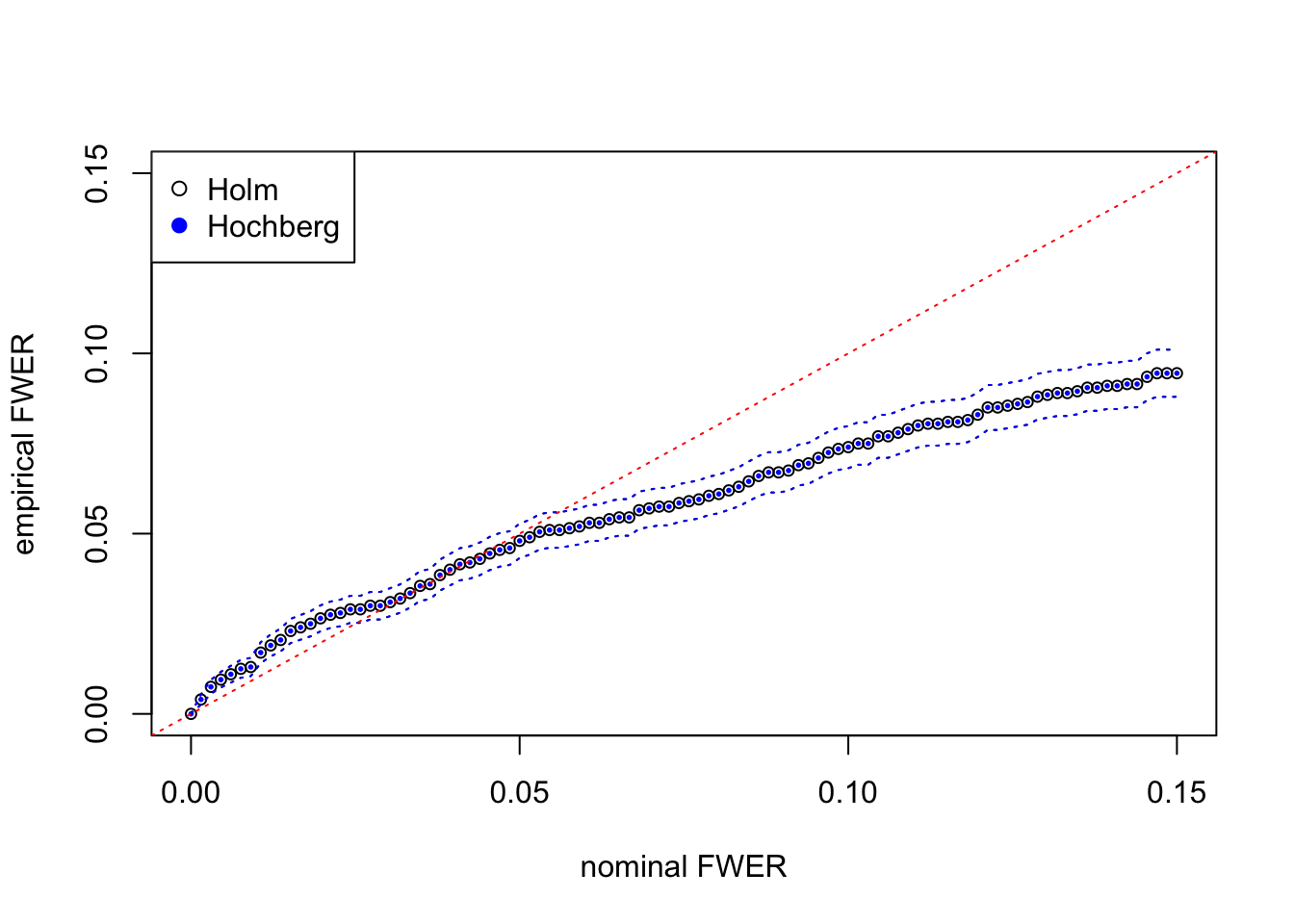

Expand here to see past versions of unnamed-chunk-3-1.png:
Version Author Date
0f36d99 LSun 2017-12-21
2696cb2 LSun 2017-02-10

The results from Holm’s step-down and Hochberg’s step-up are almost the same for this simulated data set. They both give almost the same discoveries, although in theory Hochberg’s should be strictly more powerful than Holm’s. The agreement of both procedures may indicate that test statistics are indeed inflated for moderate observations but not extreme observations.

Session Information

Session information

sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] workflowr_1.0.1   Rcpp_0.12.16      digest_0.6.15    
 [4] rprojroot_1.3-2   R.methodsS3_1.7.1 backports_1.1.2  
 [7] git2r_0.21.0      magrittr_1.5      evaluate_0.10.1  
[10] stringi_1.1.6     whisker_0.3-2     R.oo_1.21.0      
[13] R.utils_2.6.0     rmarkdown_1.9     tools_3.4.3      
[16] stringr_1.3.0     yaml_2.1.18       compiler_3.4.3   
[19] htmltools_0.3.6   knitr_1.20

This reproducible R Markdown analysis was created with workflowr 1.0.1