Last updated: 2019-02-10

workflowr checks: (Click a bullet for more information)

✔ R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
✔ Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
✔ Seed: set.seed(20180501)

The command set.seed(20180501) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
✔ Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
✔ Repository version: d255e06
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
```
Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    data/.DS_Store

Untracked files:
    Untracked:  analysis/chipexoeg.Rmd
    Untracked:  analysis/efsd.Rmd
    Untracked:  analysis/talk1011.Rmd
    Untracked:  data/chipexo_examples/
    Untracked:  data/chipseq_examples/
    Untracked:  talk.Rmd
    Untracked:  talk.pdf

Unstaged changes:
    Modified:   analysis/binomial.Rmd
    Modified:   analysis/fda.Rmd
    Modified:   analysis/index.Rmd
    Modified:   analysis/r2.Rmd
    Modified:   analysis/sigma.Rmd
```
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

Expand here to see past versions:

File	Version	Author	Date	Message
Rmd	d255e06	Dongyue Xie	2019-02-10	wflow_publish(“analysis/r2b.Rmd”)
html	c6f9a91	Dongyue Xie	2019-02-10	Build site.
Rmd	7e08c59	Dongyue Xie	2019-02-10	wflow_publish(“analysis/r2b.Rmd”)
html	c7f4704	Dongyue Xie	2019-01-27	Build site.
Rmd	a1a64c5	Dongyue Xie	2019-01-27	wflow_publish(“analysis/r2b.Rmd”)
html	9ce257c	Dongyue Xie	2019-01-27	Build site.
Rmd	d6bcb1a	Dongyue Xie	2019-01-27	wflow_publish(“analysis/r2b.Rmd”)
html	97b73fc	Dongyue Xie	2019-01-22	Build site.
Rmd	b5029e2	Dongyue Xie	2019-01-22	wflow_publish(“analysis/r2b.Rmd”)
html	ad12c40	Dongyue Xie	2019-01-22	Build site.
Rmd	11f83fb	Dongyue Xie	2019-01-22	wflow_publish(“analysis/r2b.Rmd”)

For the method used in these examples, see here

True \(R^2\) is defined as \(R^2=\frac{var(X\beta)}{var(y)}=\frac{var(y)-\sigma^2}{var(y)}=1-\frac{\sigma^2}{var(y)}=1-\frac{\sigma^2}{\sigma^2+var(X\beta)}\)
Ajusted R^2: \(1-\frac{\sum(y_i-\hat y_i)^2/(n-p-1)}{\sum(y_i-\bar y)^2/(n-1)}\)
Shrunk adjusted R^2: use fash shrinking \(fash.output=\log(\frac{\sum(y_i-\hat y_i)^2/(n-p-1)}{\sum(y_i-\bar y)^2/(n-1)})\) then shrunk adjusted R^2 is \(1-\exp(fash.output)\)
Shrunk R^2: use fash shrinking \(fash.output=\log(\frac{\sum(y_i-\hat y_i)^2/(n-1)}{\sum(y_i-\bar y)^2/(n-1)})\) then shrunk adjusted R^2 is \(1-\exp(fash.output)\)
Another Shrunk R^2: shrink all \(\betas\) using ash, obtain posterior means then calculate \(\hat\sigma^2\) then obtain \(\frac{var(X\hat\beta)}{var(\hat\beta)+\hat\sigma^2}\).

(note: this is the old idea which introduces bias to R^2 when multiplying \(\frac{n-p-1}{n-1}\) so I discard this method.)(Shrunk R^2 = \(1 - \exp(fash.output)*\frac{n-p-1}{n-1}\), because \(R^2=1-\frac{\sum(y_i-\hat y_i)^2}{\sum(y_i-\bar y)^2}=1-\frac{\sum(y_i-\hat y_i)^2/(n-p-1)}{\sum(y_i-\bar y)^2/(n-1)}*\frac{n-p-1}{n-1}=1-(1-adjR^2)*\frac{n-p-1}{n-1}\))

R Function

R function for shrinking adjusted R/ R squared:

library(ashr)
#'@param R2: R squared from linear regression model fit
#'@param n: sample size
#'@param p: the number of covariates
#'@output shrunk R squared.

ash_ar2=function(R2,n,p){
  df1=n-p-1
  df2=n-1
  log.ratio=log((1-R2)/(df1)*(df2))
  shrink.log.ratio=ash(log.ratio,1,lik=lik_logF(df1=df1,df2=df2))$result$PosteriorMean
  ar2=1-exp(shrink.log.ratio)
  return(ar2)
}


ash_r2=function(R2,n,p){
  df1=n-1
  df2=n-1
  log.ratio=log(1-R2)
  shrink.log.ratio=ash(log.ratio,1,lik=lik_logF(df1=df1,df2=df2))$result$PosteriorMean
  r2=1-exp(shrink.log.ratio)
  return(r2)
}

Compare Shrunk \(R^2\) with True \(R2\).

Assume linear model \(y=X\beta+\epsilon\) where \(\epsilon\sim N(0,\sigma^2I)\)

n=100, p=5. Each cordinate of \(\beta\) ranges from 0 to 1, for example \(\beta=(0,0,0,0,0)\),…,\(\beta=(0.1,0.1,0.1,0.1,0.1)\),…, \(\beta=(1,1,1,1,1)\) etc.

If I generate X from Uniform(0,1), then fash shirnks all \(R^2\) to 0. If generate X from Uniform(0,2), then it does not

Uniform(0,1):

set.seed(1234)

n=100
p=5
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=var(X%*%beta)/(1+var(X%*%beta))
}
R2s=ash_r2(R2,n,p)
R2as=ash_ar2(R2,n,p)
plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
lines(beta.list,R2as,col=3)
lines(beta.list,R2s,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))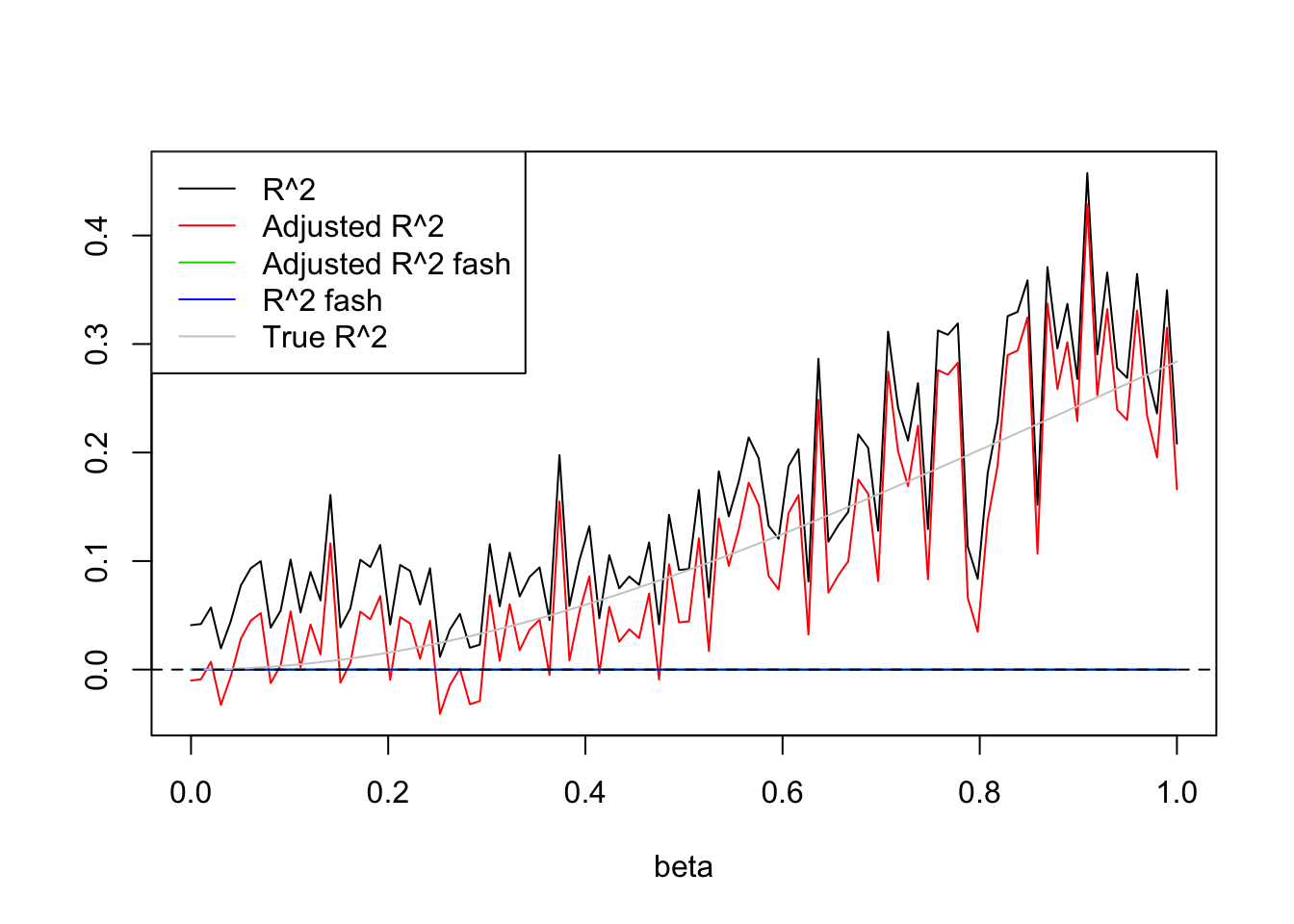

Expand here to see past versions of unnamed-chunk-2-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2as,col=3)
lines(trueR2,R2s,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash'),lty=c(1,1,1,1),col=c(1,2,3,4))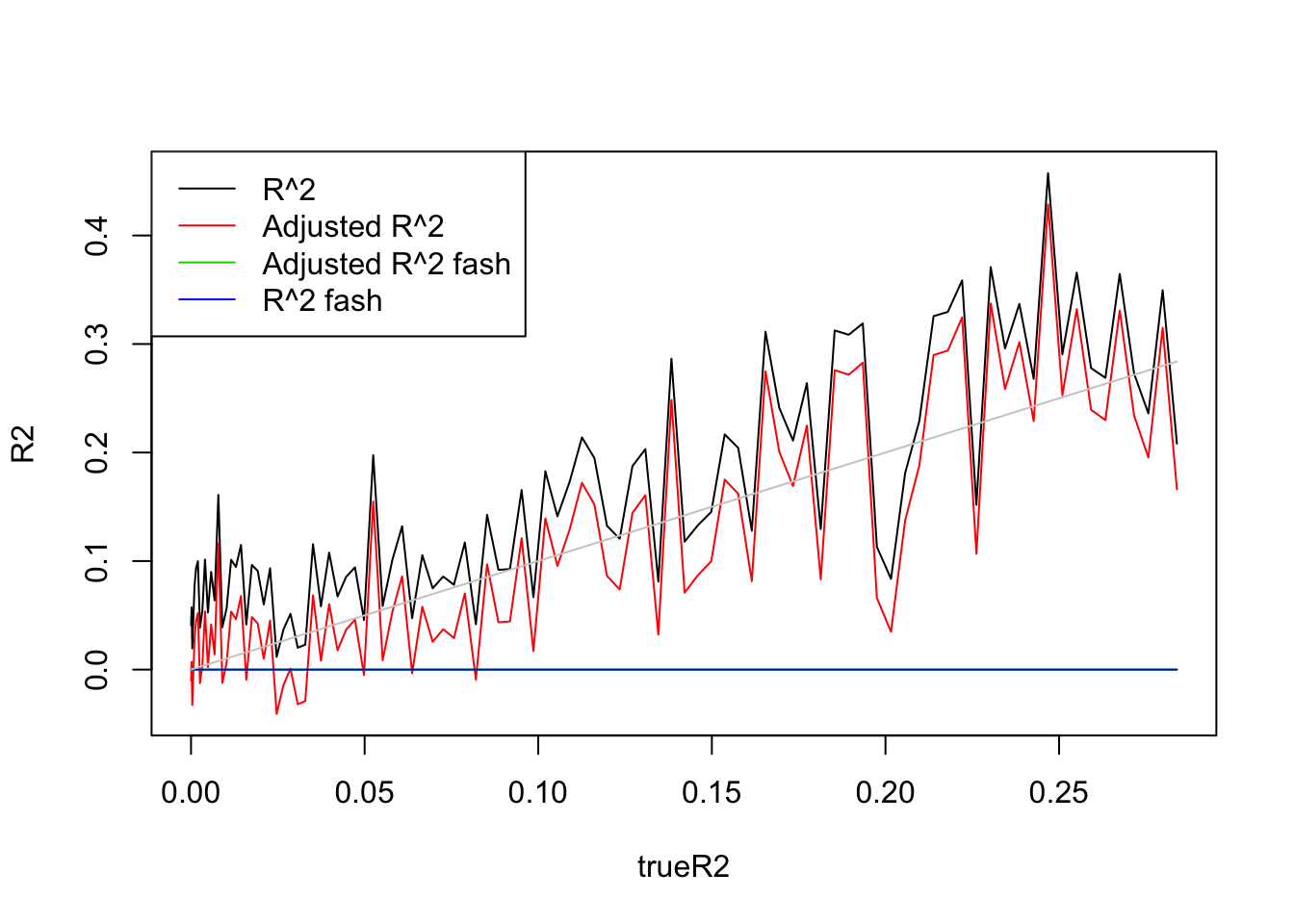

Expand here to see past versions of unnamed-chunk-2-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

Uniform(0,3):

set.seed(1234)

n=100
p=5
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,3),n,p)
for (i in 1:length(beta.list)) {
  
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=var(X%*%beta)/(1+var(X%*%beta))
}
R2s=ash_r2(R2,n,p)
R2as=ash_ar2(R2,n,p)
plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
lines(beta.list,R2as,col=3)
lines(beta.list,R2s,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))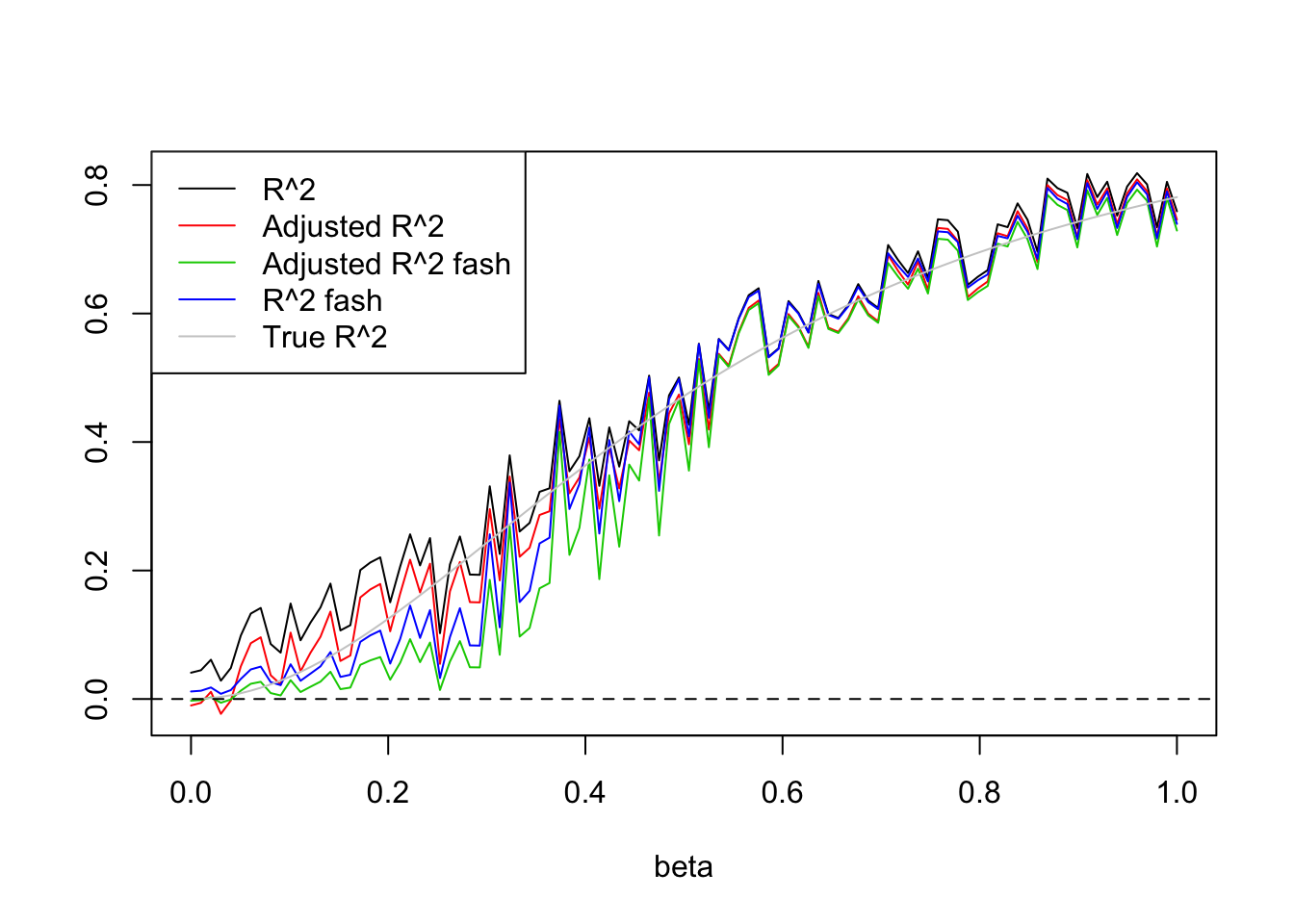

Expand here to see past versions of unnamed-chunk-3-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2as,col=3)
lines(trueR2,R2s,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash'),lty=c(1,1,1,1),col=c(1,2,3,4))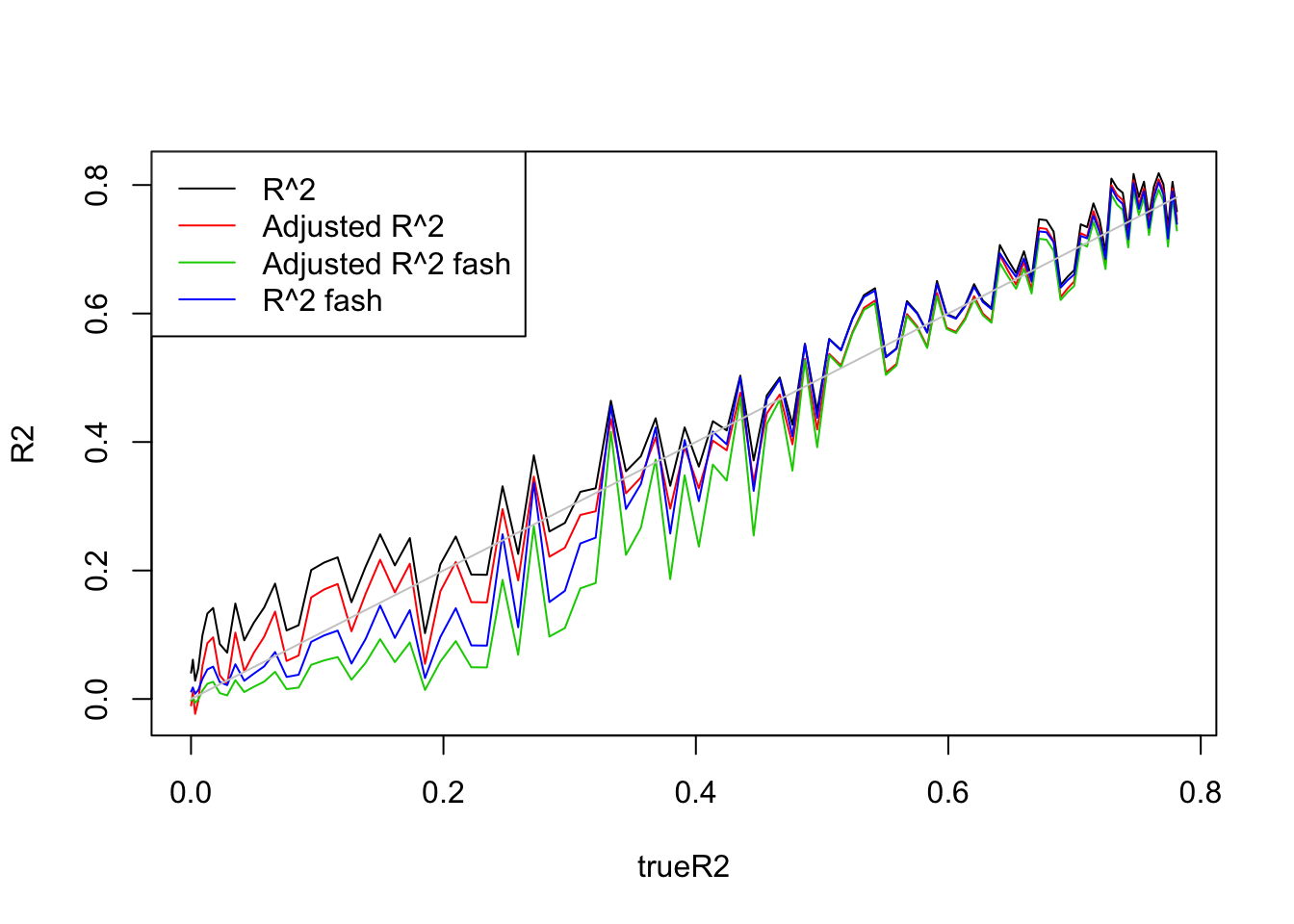

Expand here to see past versions of unnamed-chunk-3-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

Uniform(0,5):

set.seed(1234)

n=100
p=5
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=var(X%*%beta)/(1+var(X%*%beta))
}
R2s=ash_r2(R2,n,p)
R2as=ash_ar2(R2,n,p)
plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
lines(beta.list,R2as,col=3)
lines(beta.list,R2s,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))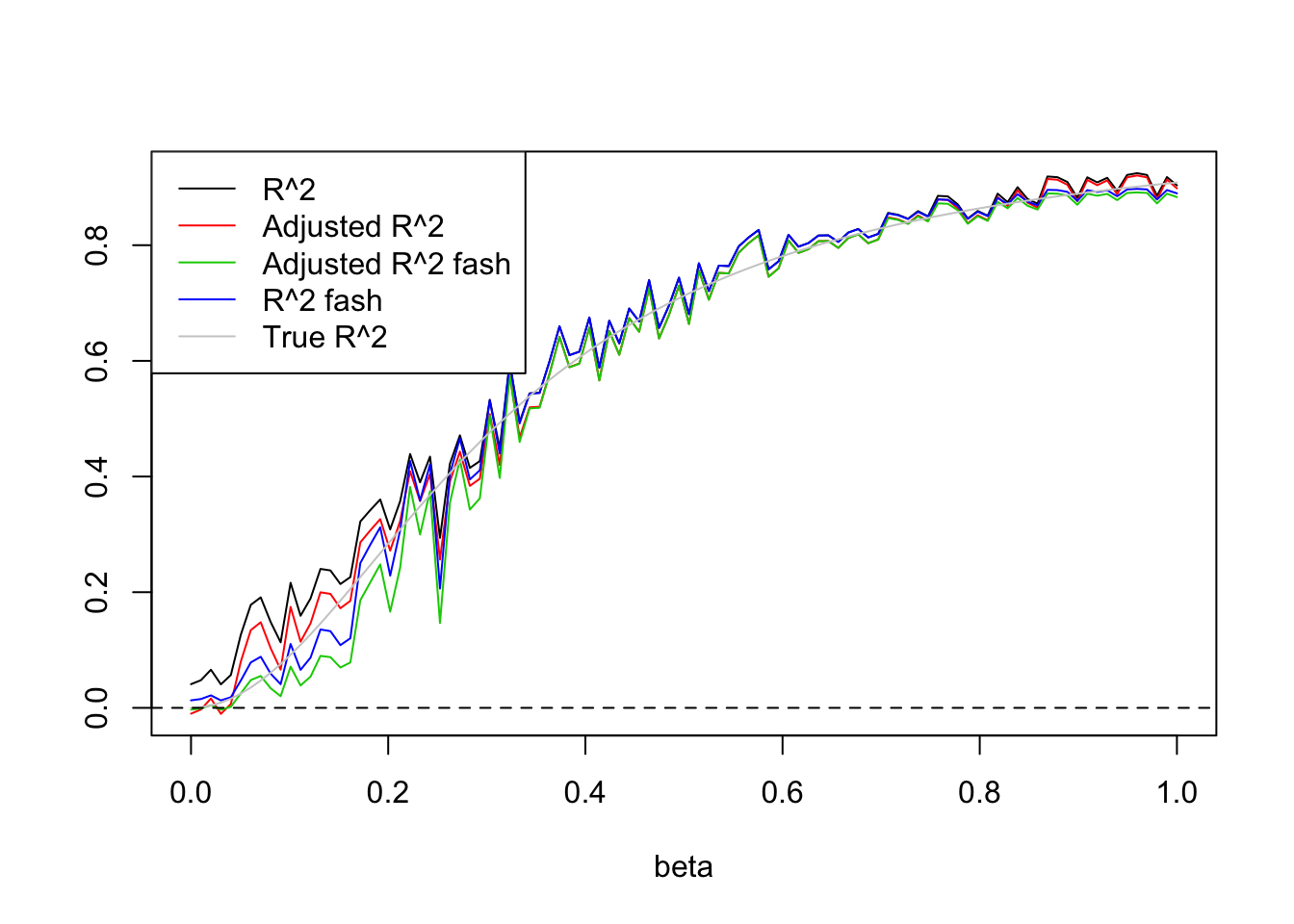

Expand here to see past versions of unnamed-chunk-4-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2as,col=3)
lines(trueR2,R2s,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash'),lty=c(1,1,1,1),col=c(1,2,3,4))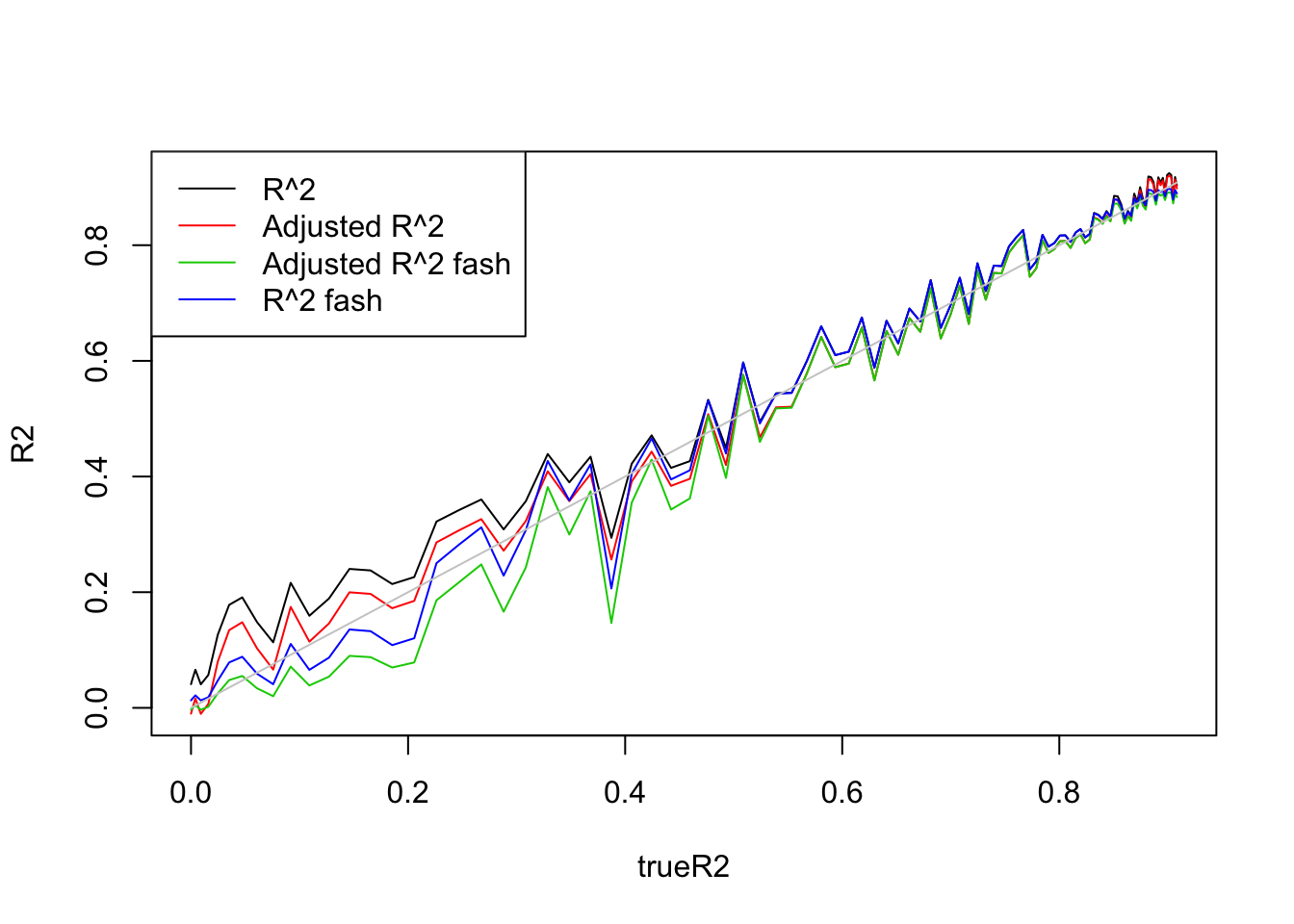

Expand here to see past versions of unnamed-chunk-4-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
9ce257c	Dongyue Xie	2019-01-27

Increase \(p\) to 20.

This time, if I generate X from Uniform(0,1), then fash does not shirnk all \(R^2\) to 0.

Uniform(0,1):

set.seed(1234)

n=100
p=20
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=var(X%*%beta)/(1+var(X%*%beta))
}
R2s=ash_r2(R2,n,p)
R2as=ash_ar2(R2,n,p)
plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
lines(beta.list,R2as,col=3)
lines(beta.list,R2s,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))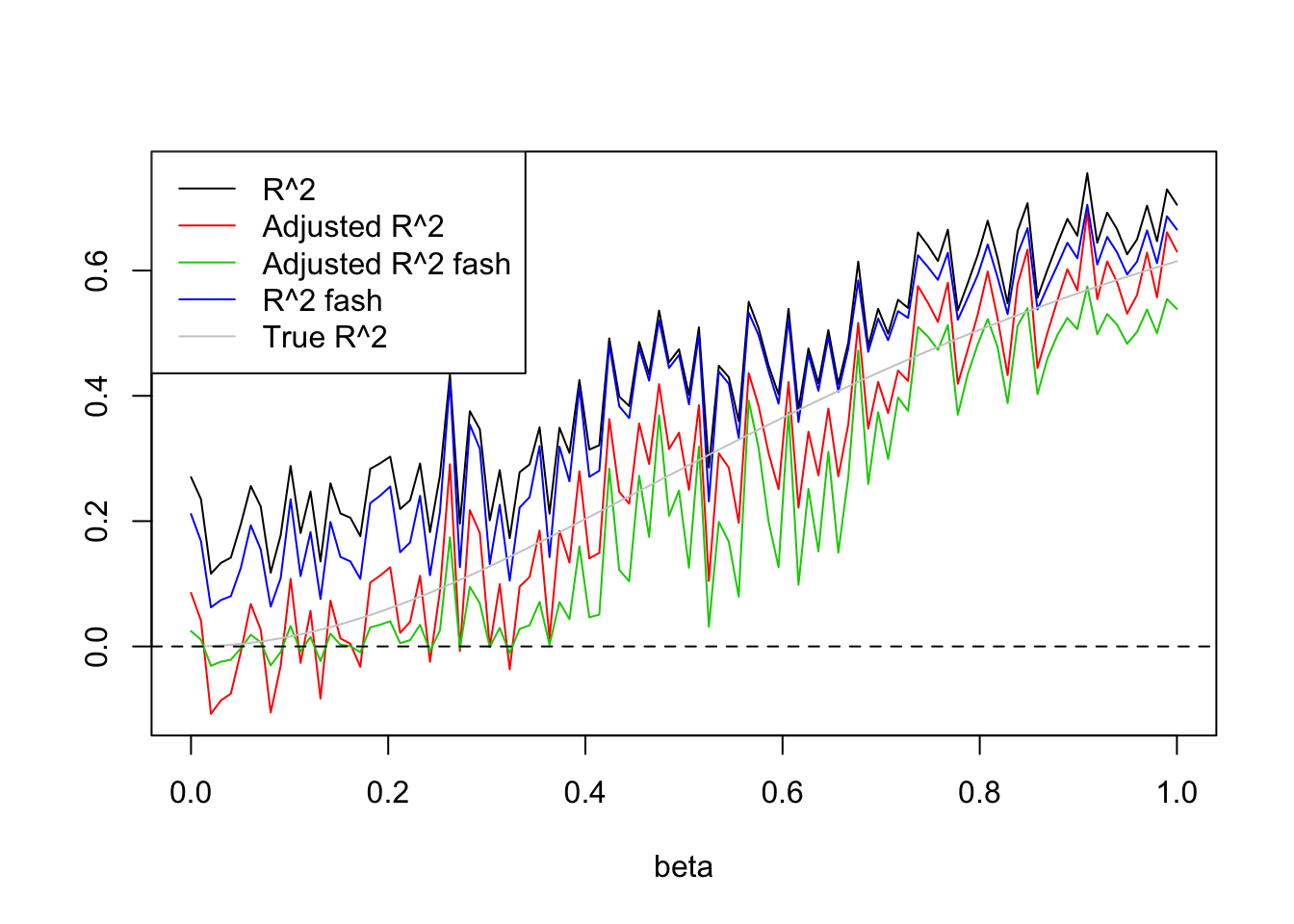

Expand here to see past versions of unnamed-chunk-5-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27
9ce257c	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2as,col=3)
lines(trueR2,R2s,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash'),lty=c(1,1,1,1),col=c(1,2,3,4))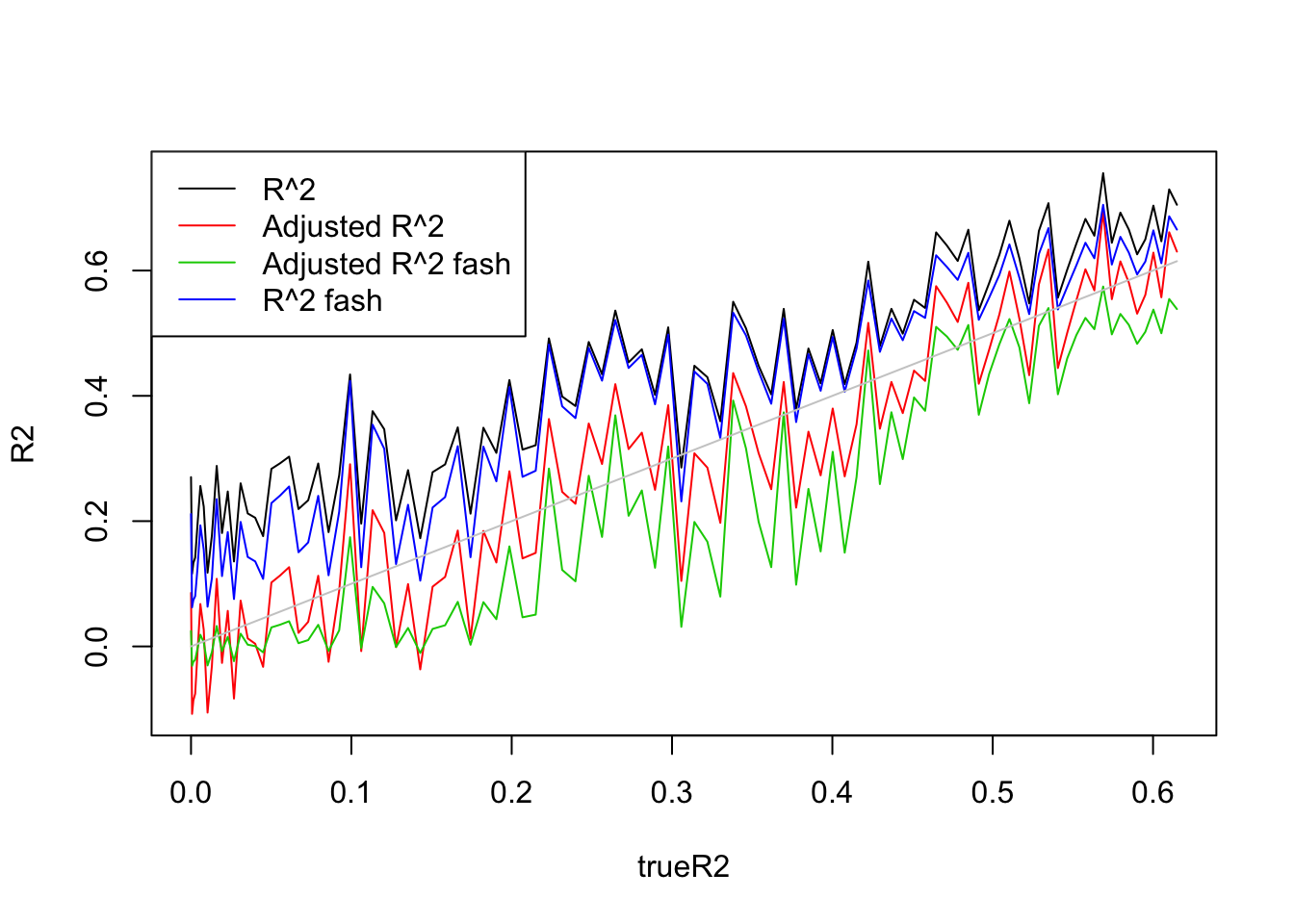

Expand here to see past versions of unnamed-chunk-5-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27
9ce257c	Dongyue Xie	2019-01-27

\(n=30, p=3\).

This time, I have to generate X from at least Uniform(0,3) to avoid over-shrinkage of fash. Here, I tried Uniform(0,5)

Uniform(0,5):

set.seed(1234)

n=30
p=3
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=var(X%*%beta)/(1+var(X%*%beta))
}
R2s=ash_r2(R2,n,p)
R2as=ash_ar2(R2,n,p)
plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
lines(beta.list,R2as,col=3)
lines(beta.list,R2s,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))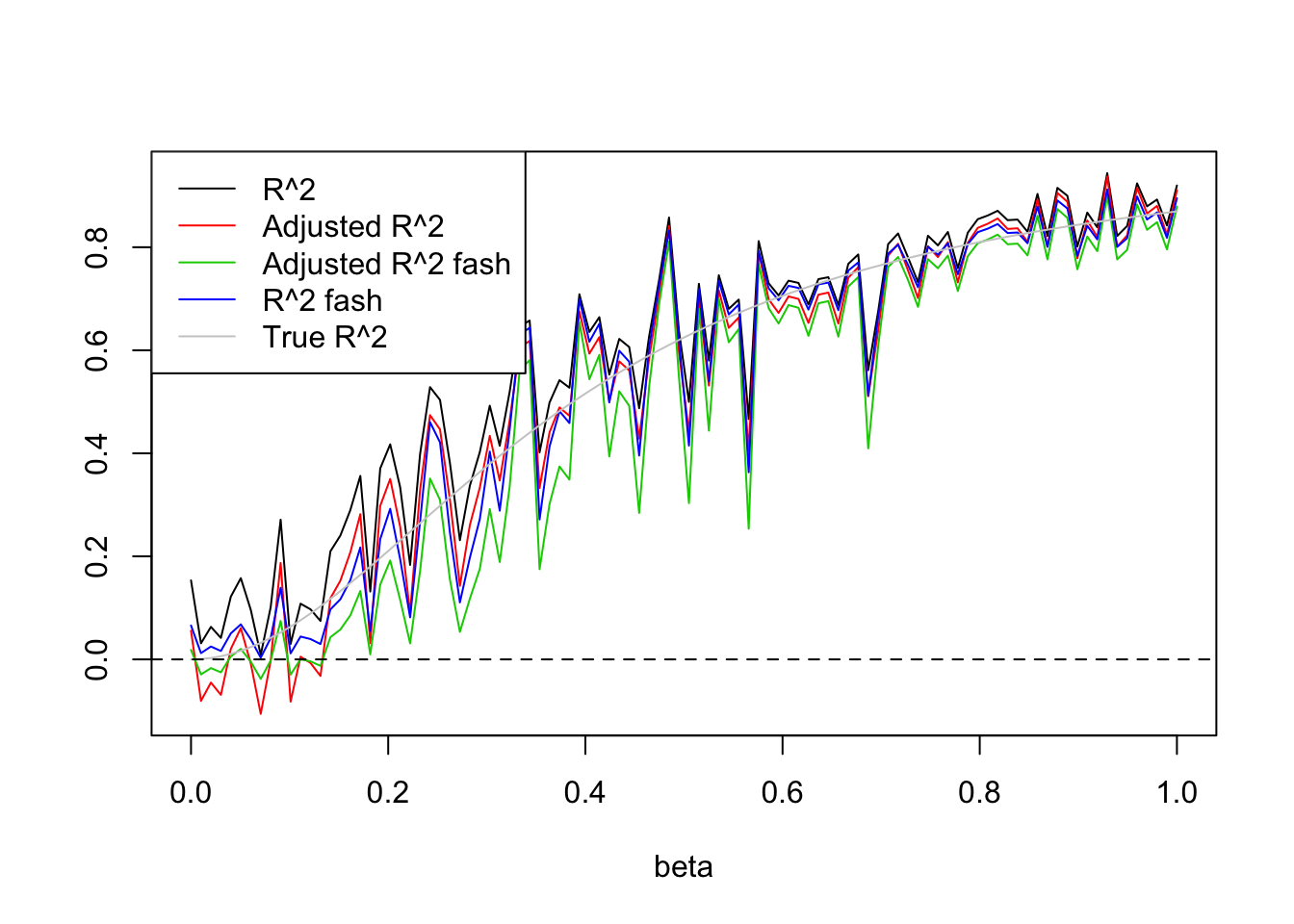

Expand here to see past versions of unnamed-chunk-6-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27
9ce257c	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2as,col=3)
lines(trueR2,R2s,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','Adjusted R^2 fash','R^2 fash'),lty=c(1,1,1,1),col=c(1,2,3,4))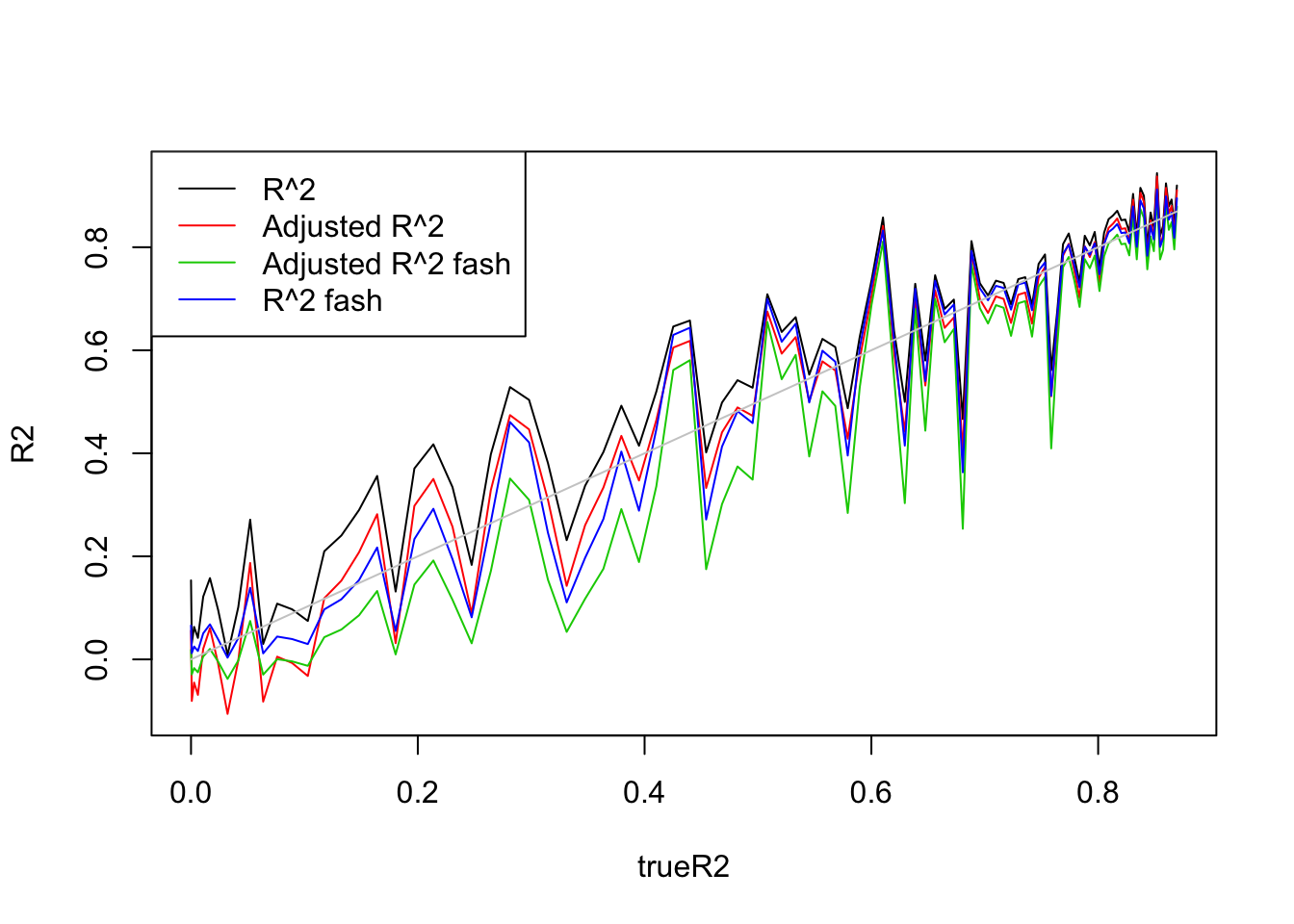

Expand here to see past versions of unnamed-chunk-6-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27
9ce257c	Dongyue Xie	2019-01-27

Compare fash and corshrink

1-d case

\(n=100,p=1\)

Uniform(0,5):

library(CorShrink)
set.seed(1234)

n=100
p=1
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X*beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))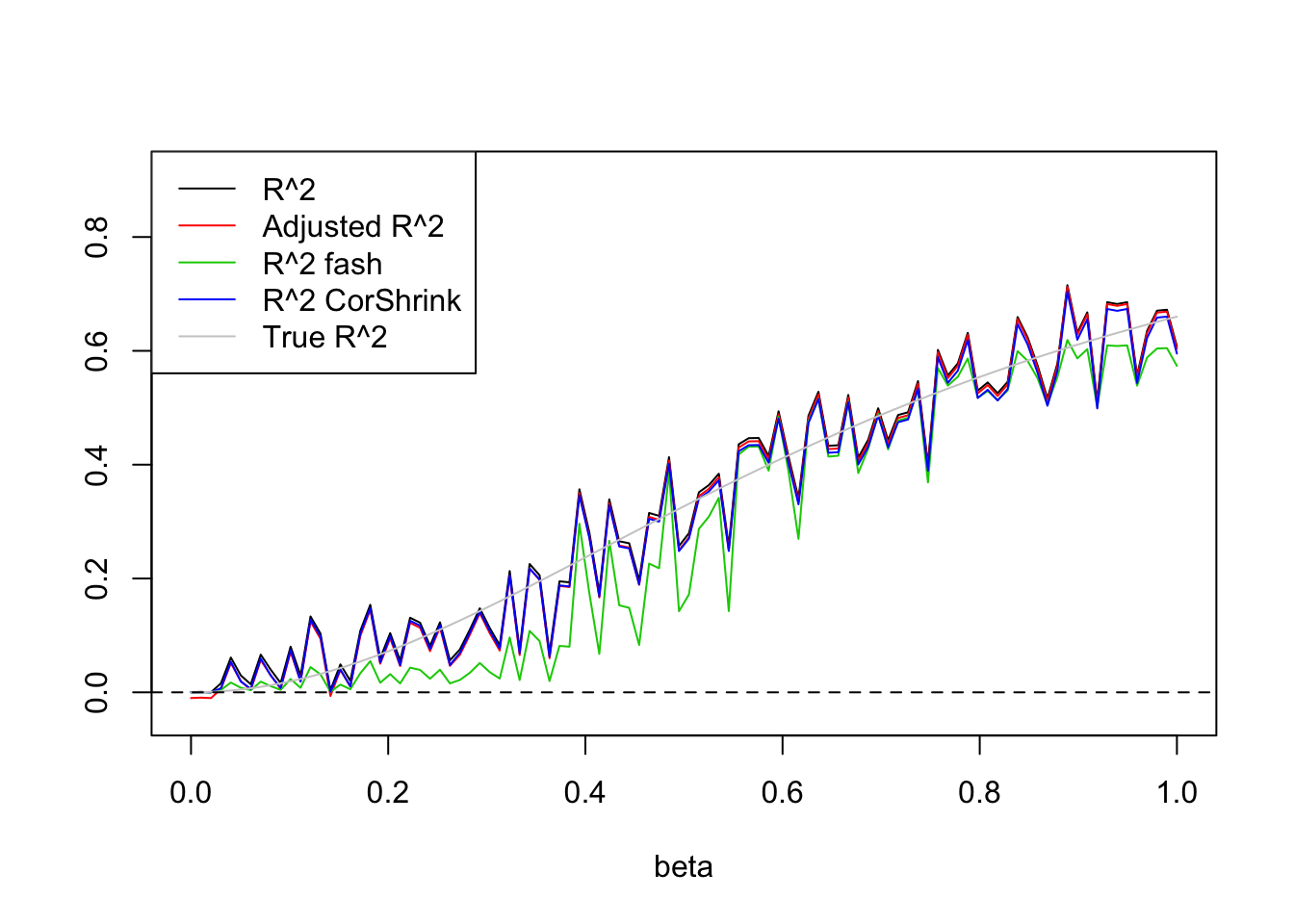

Expand here to see past versions of unnamed-chunk-7-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))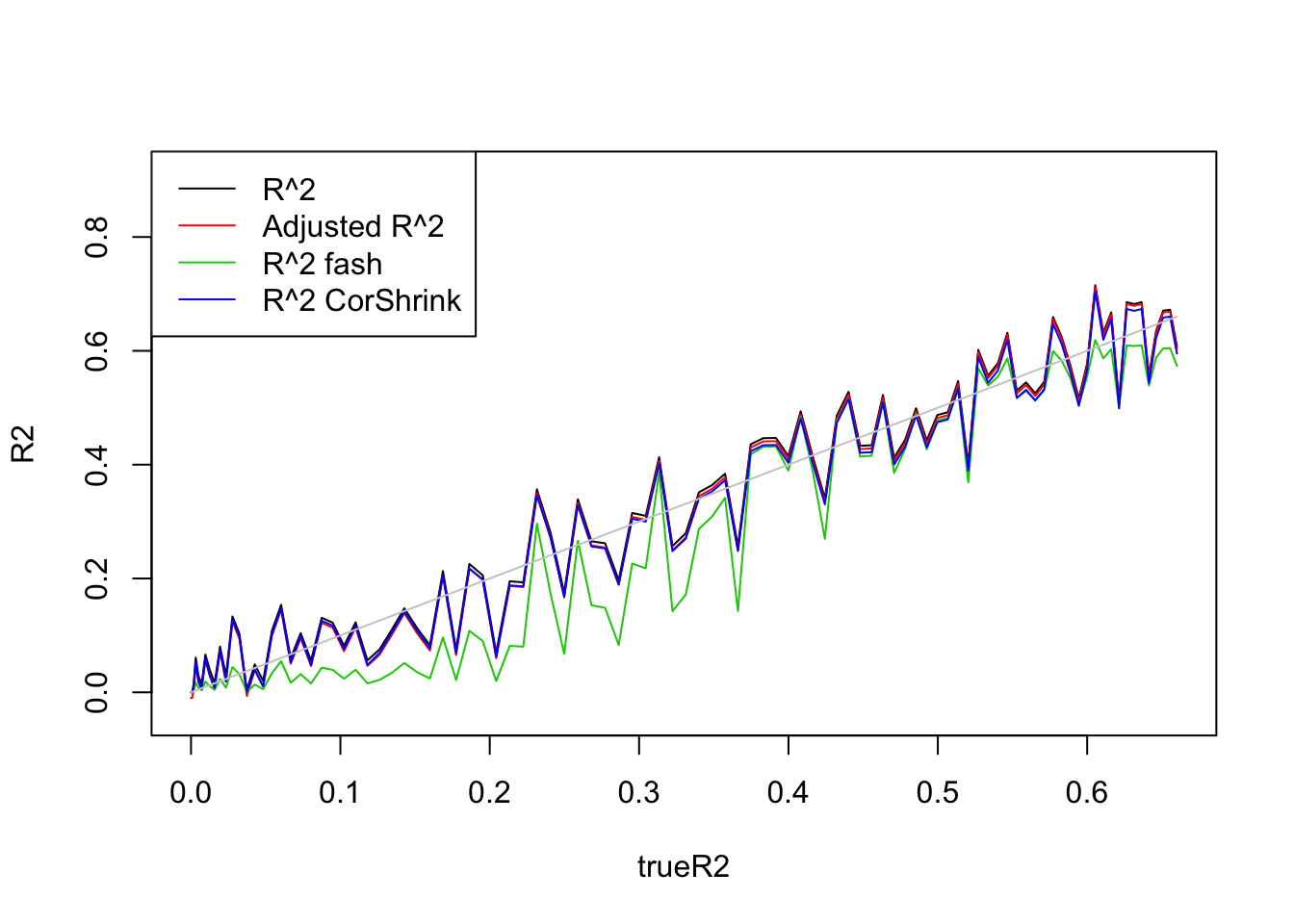

Expand here to see past versions of unnamed-chunk-7-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27

\(n=30,p=1\)

Uniform(0,5):

set.seed(1234)

n=30
p=1
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X*beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))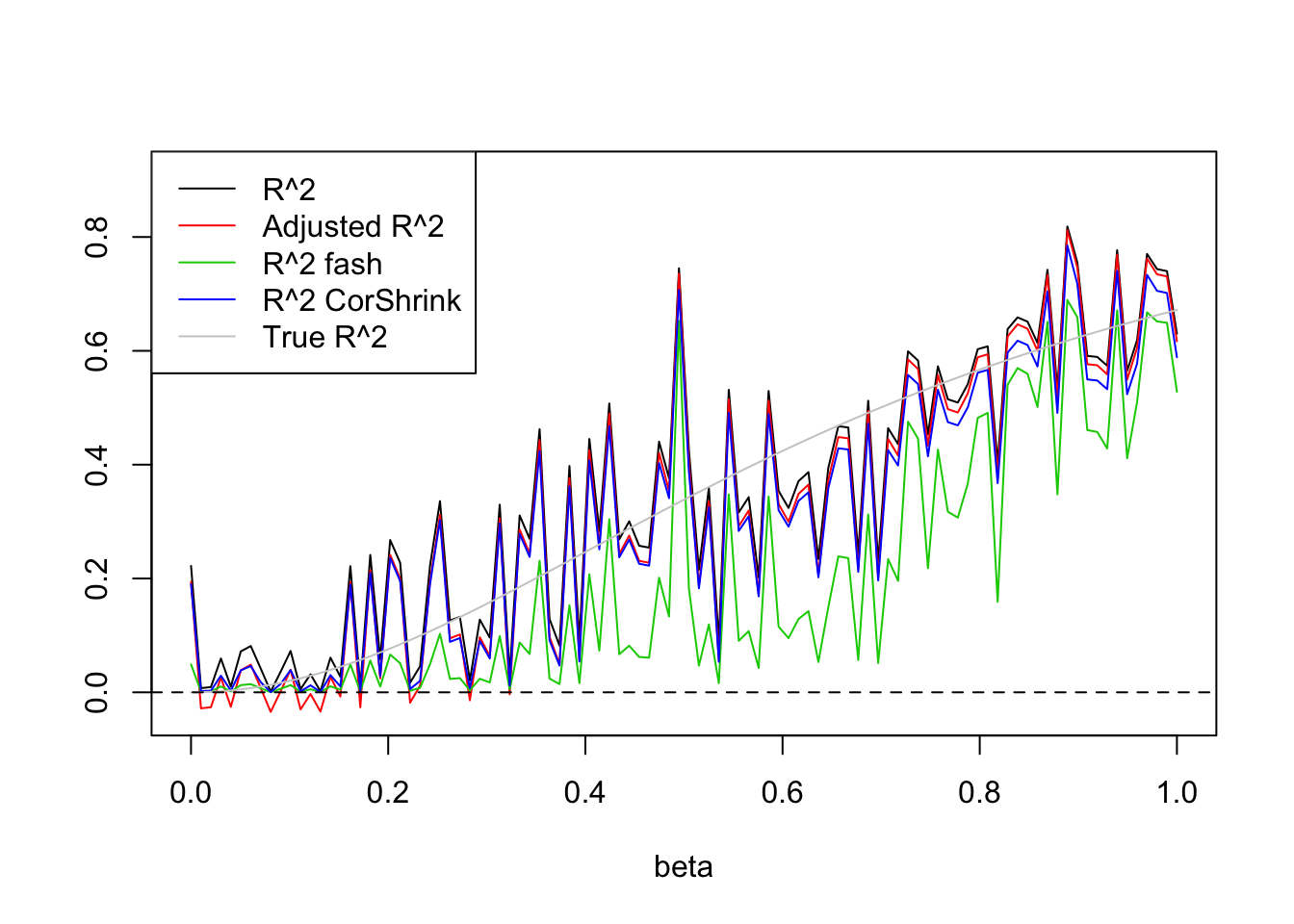

Expand here to see past versions of unnamed-chunk-8-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))

Expand here to see past versions of unnamed-chunk-8-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10
c7f4704	Dongyue Xie	2019-01-27

Multiple regression

\(n=100, p=5\)

Uniform(0,2):

set.seed(1234)

n=100
p=5
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,2),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))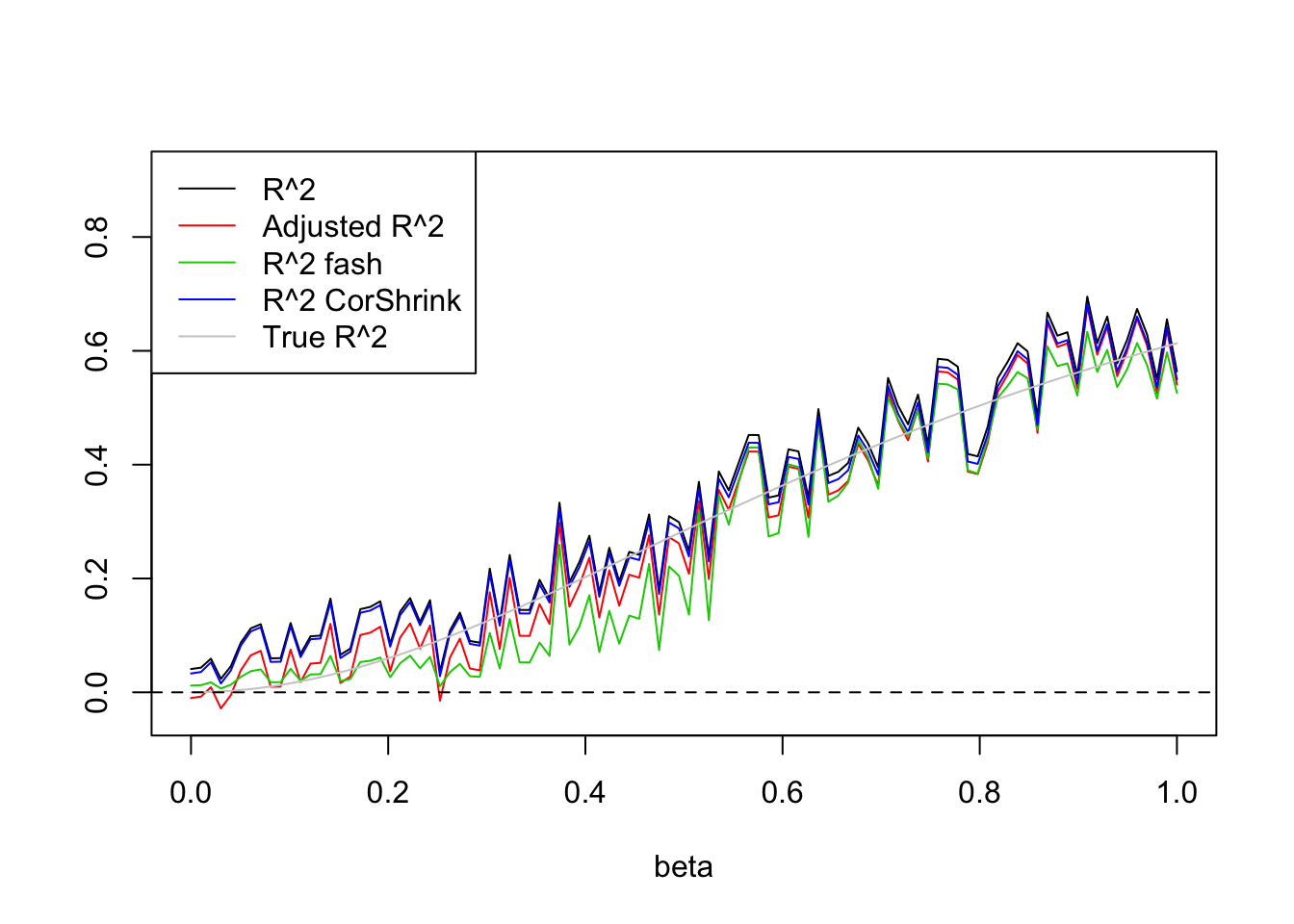

Expand here to see past versions of unnamed-chunk-9-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))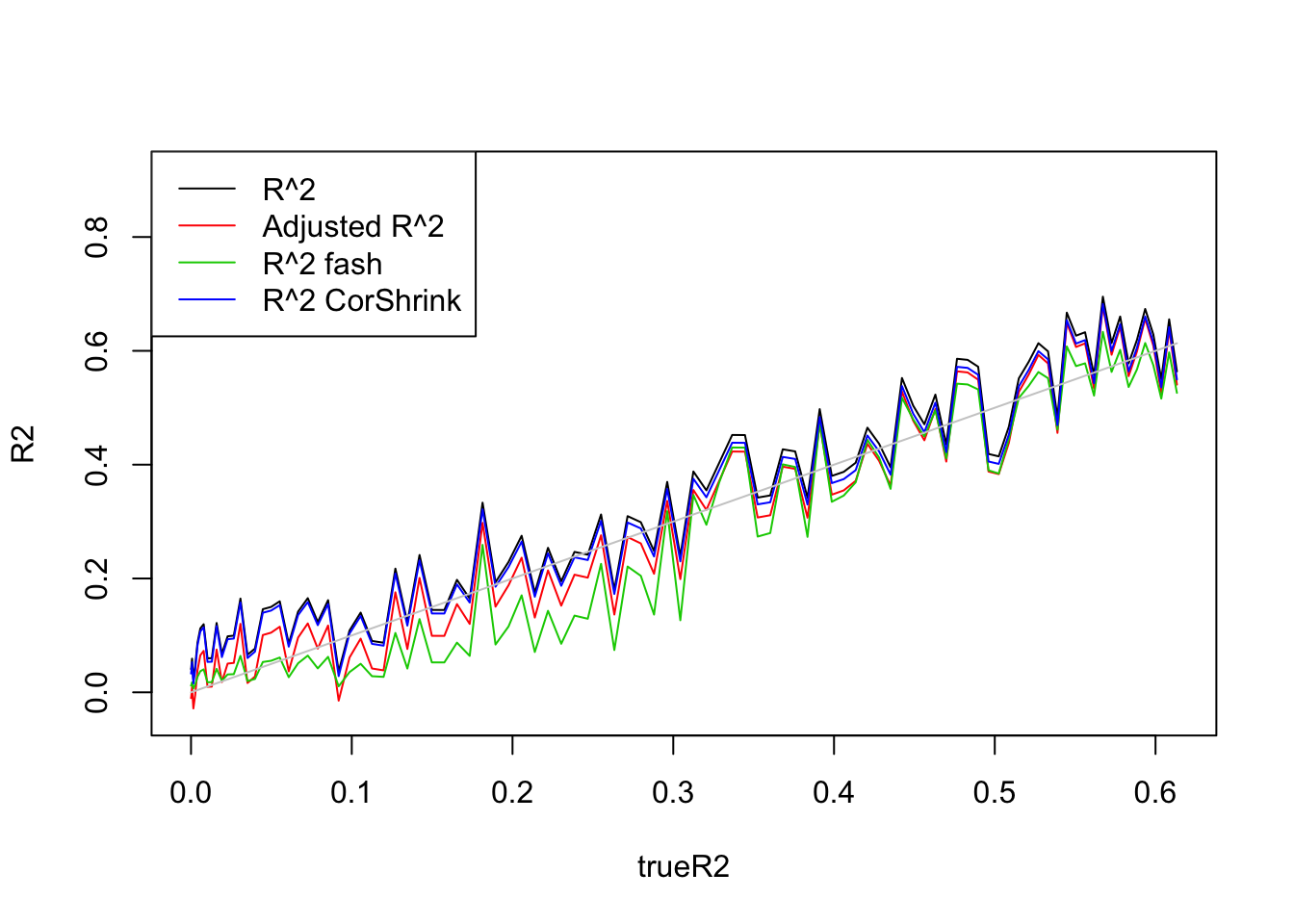

Expand here to see past versions of unnamed-chunk-9-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

\(n=100,p=20\)

Uniform(0,1):

set.seed(1234)

n=100
p=20
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))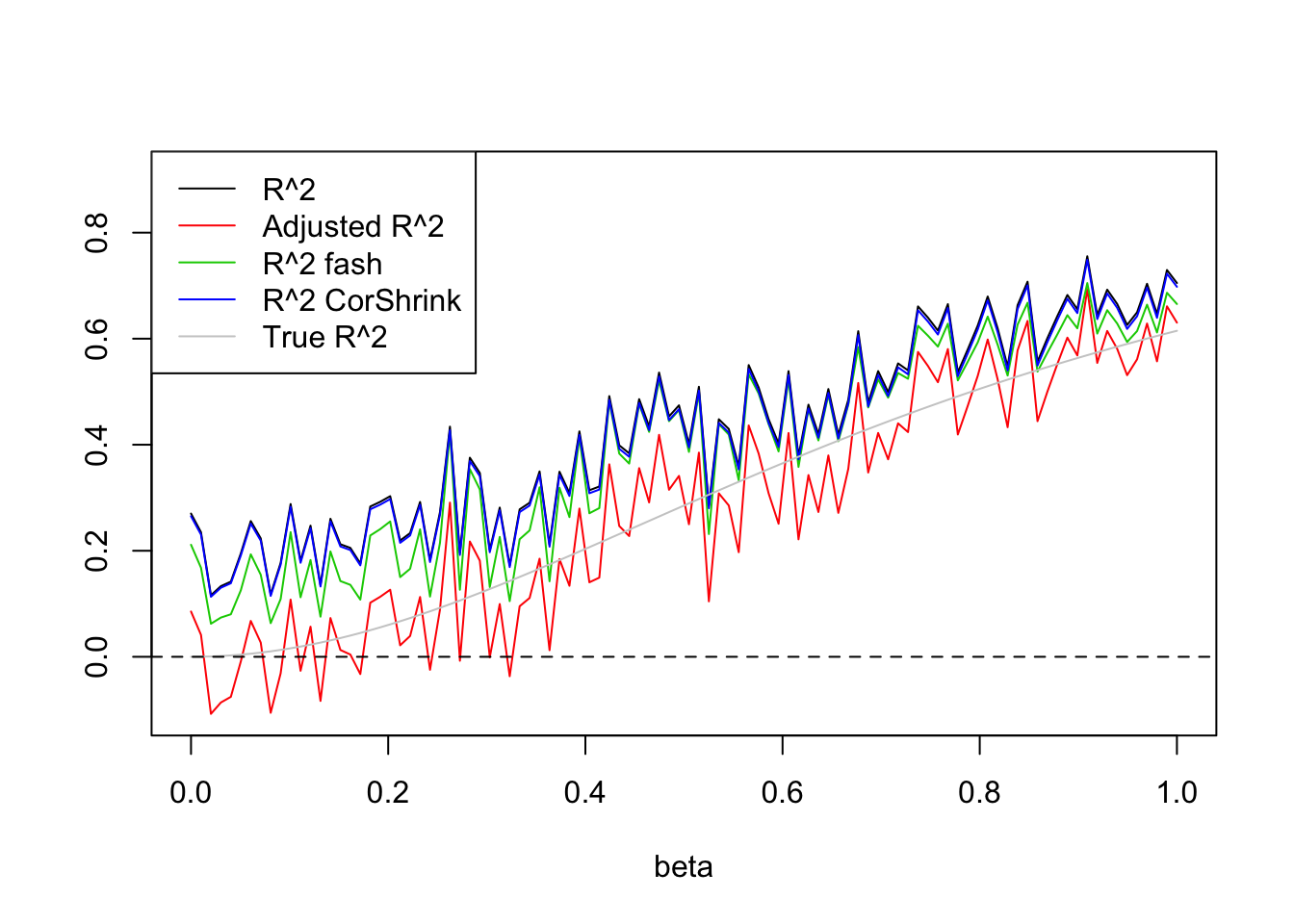

Expand here to see past versions of unnamed-chunk-10-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))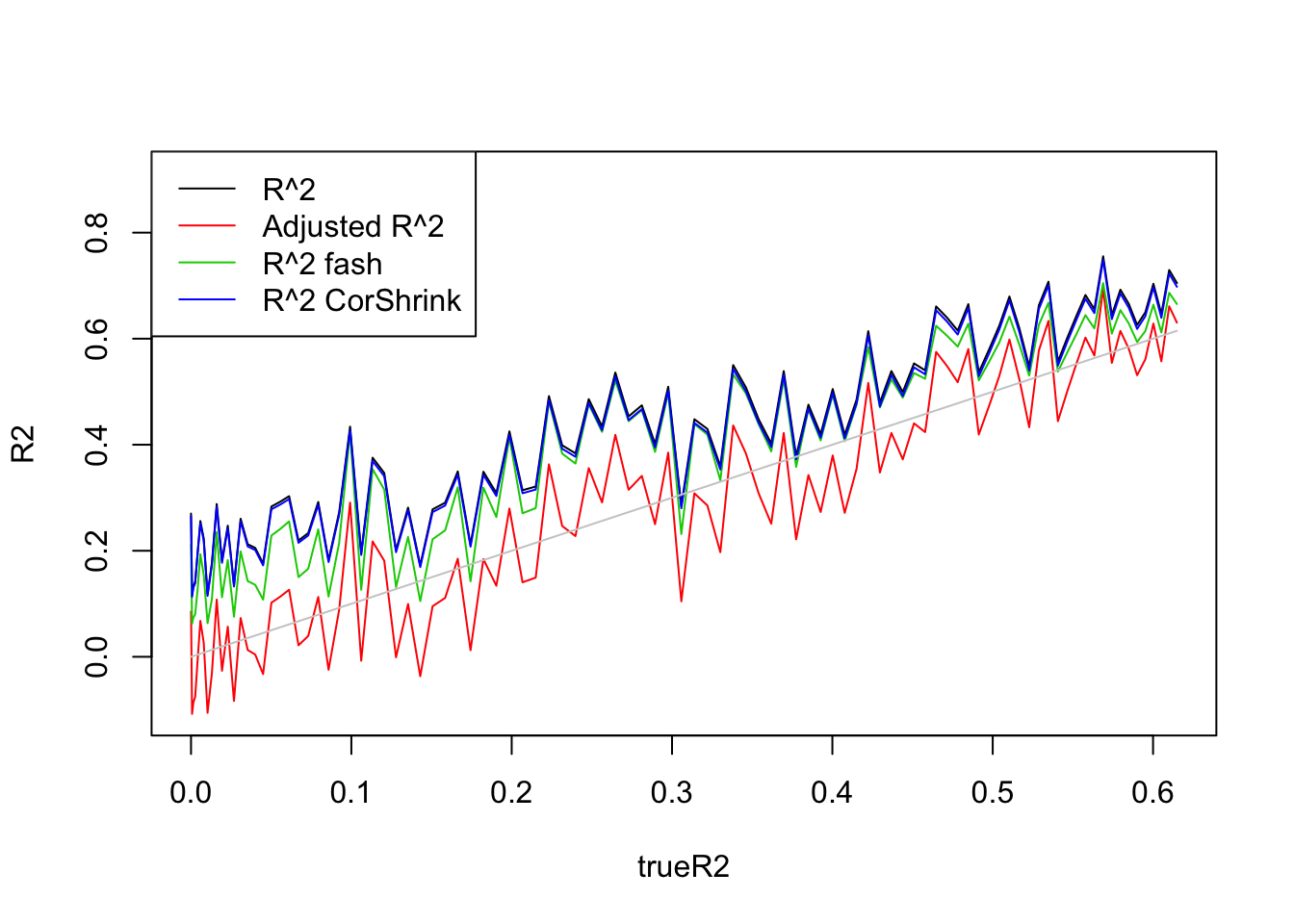

Expand here to see past versions of unnamed-chunk-10-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

\(n=100,p=50\)

Uniform(0,1):

set.seed(1234)

n=100
p=50
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))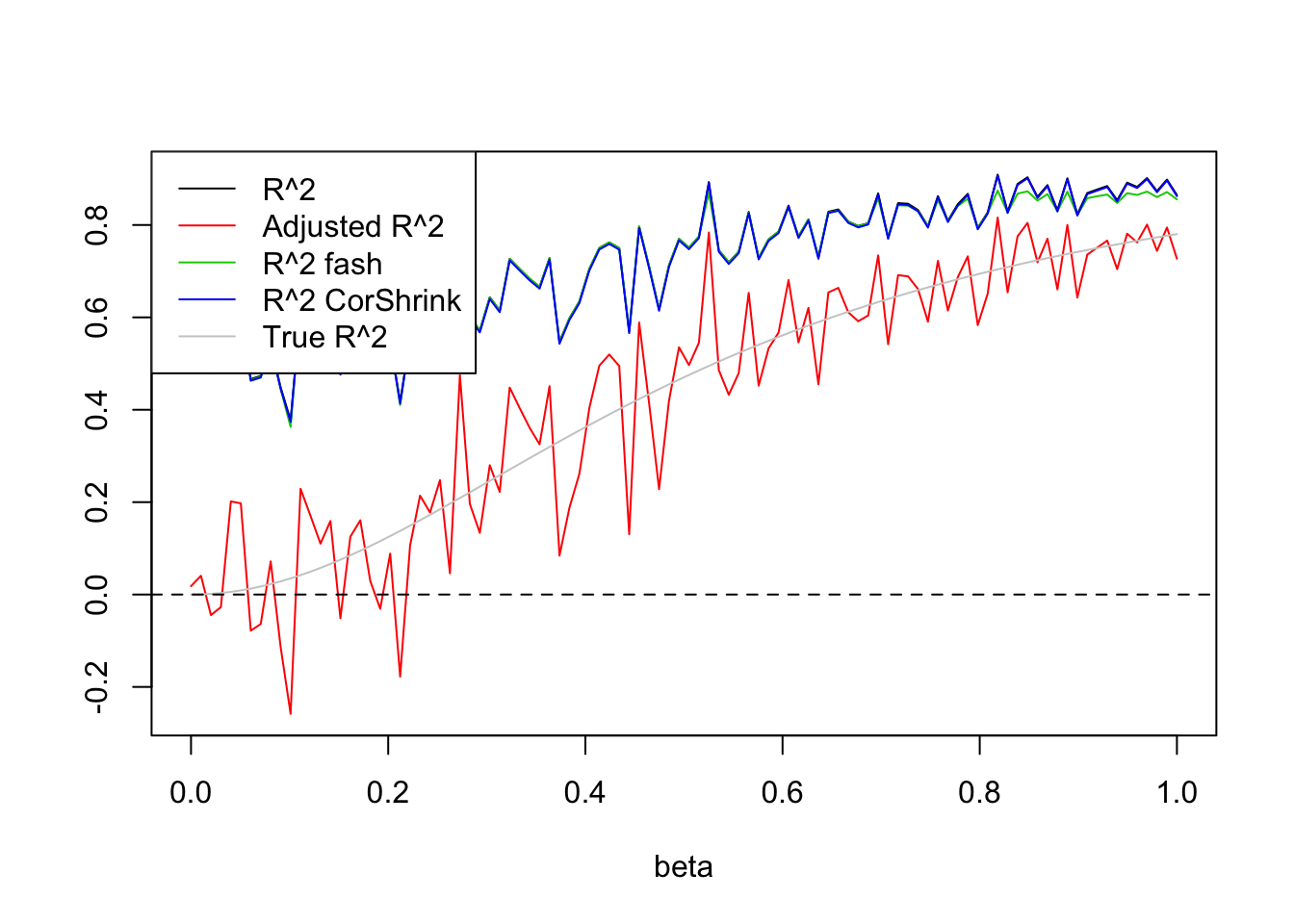

Expand here to see past versions of unnamed-chunk-11-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))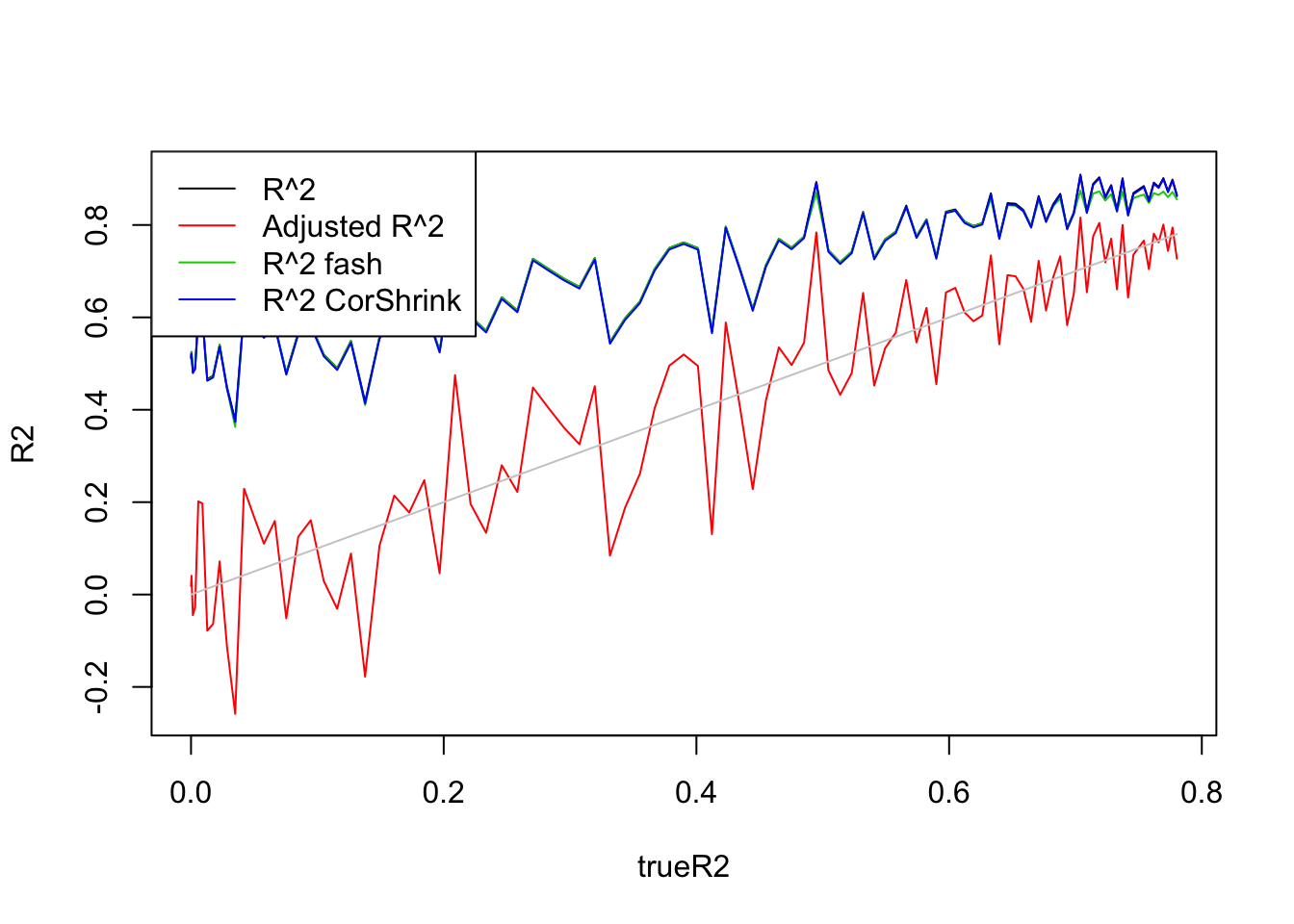

Expand here to see past versions of unnamed-chunk-11-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

\(n=30, p=3\)

Uniform(0,5):

set.seed(1234)

n=30
p=3
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,5,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}
R2.fash=ash_r2(R2,n,p)
R2a.fash=ash_ar2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2


plot(beta.list,R2,ylim=range(c(R2,R2a,R2s,R2as,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2a,col=2)
#lines(beta.list,R2a.fash,col=3)
lines(beta.list,R2.fash,col=3)
lines(beta.list,R2.cor,col=4)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink','True R^2'),lty=c(1,1,1,1,1),col=c(1,2,3,4,'grey80'))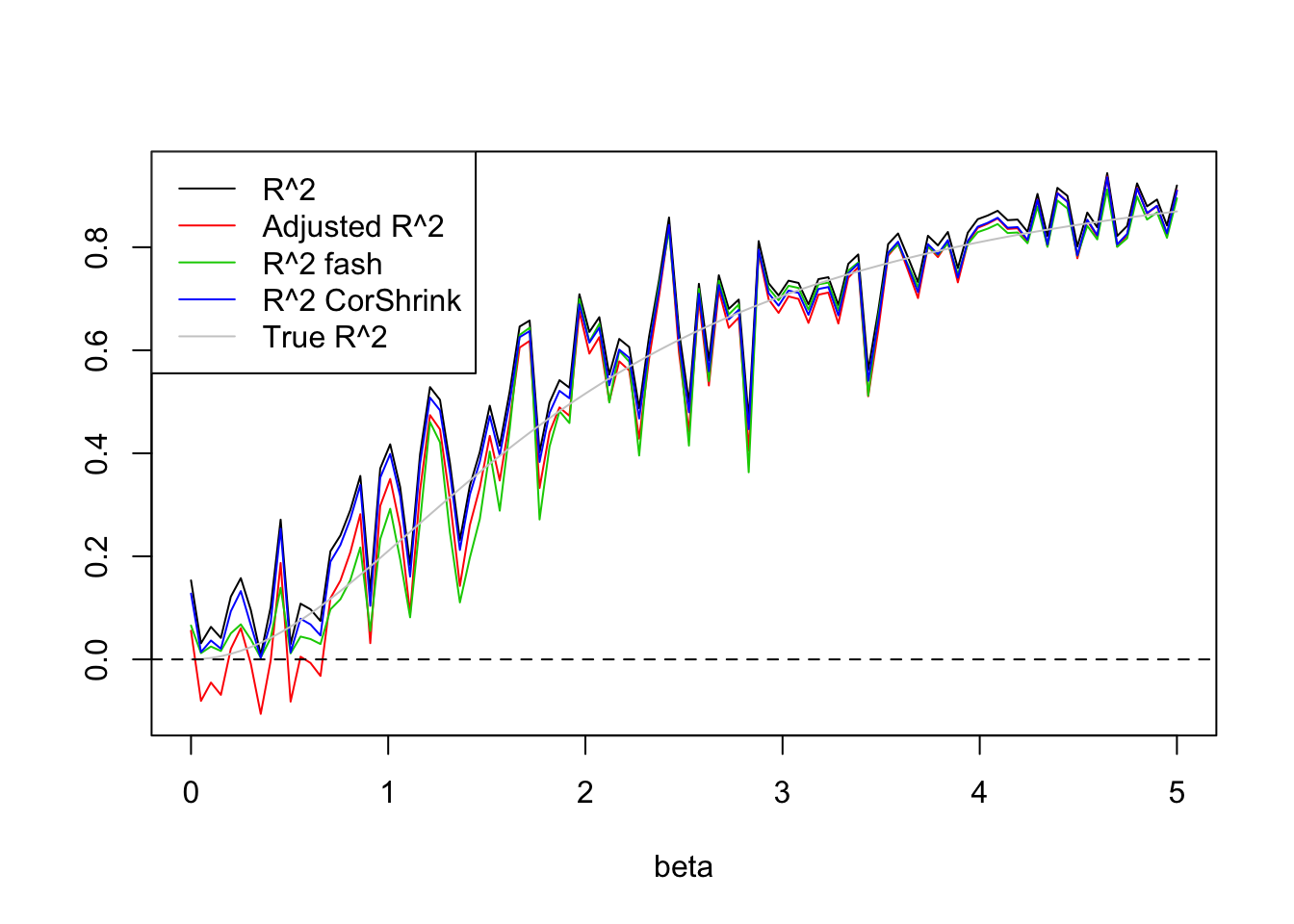

Expand here to see past versions of unnamed-chunk-12-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

plot(trueR2,R2,type='l',ylim=range(c(R2,R2a,R2s,R2as,trueR2)))
lines(trueR2,R2a,col=2)
lines(trueR2,R2.fash,col=3)
lines(trueR2,R2.cor,col=4)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','Adjusted R^2','R^2 fash','R^2 CorShrink'),lty=c(1,1,1,1),col=c(1,2,3,4))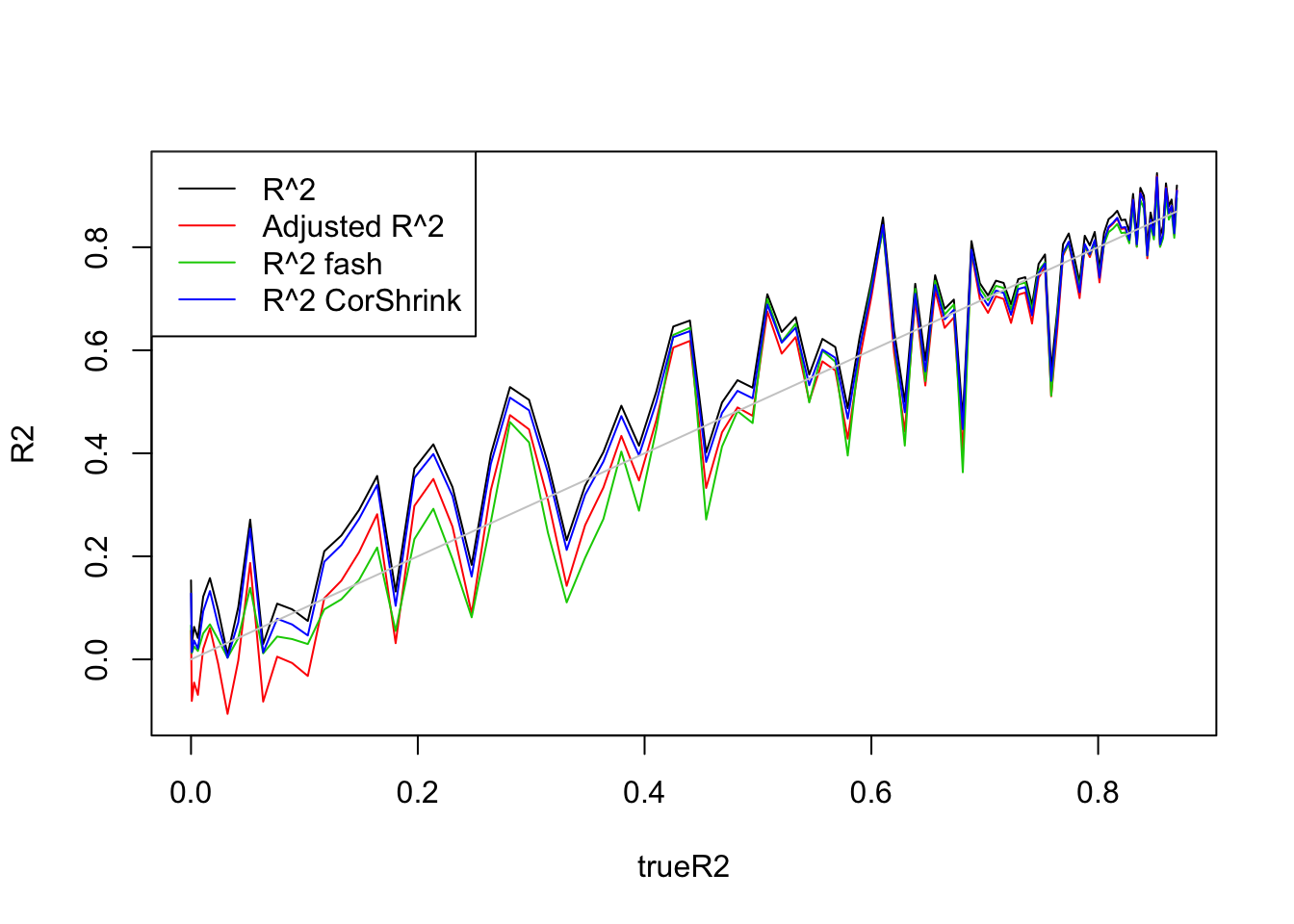

Expand here to see past versions of unnamed-chunk-12-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

Summary1

When generating X from Uniform(0,1), \(var(X\beta)\) is small and fash can shrink all \(R^2\) to 0. This happens when \(n,p\) are small. If \(p=20\), then this does not happen.
CorShrink does not shrink \(R^2\). I can not really tell the difference from plots between Corshrink \(R^2\) and \(R&2\).
Adjusted \(R^2\) is a good shrinkage estimator of \(R^2\).

Sign of correlations

Randomize signs of \(R\) and see if corshrink gives the same results.

Random sample n/2 \(R^2\)s and set the sign of \(R\) to negative.

\(n=100,p=1\)

Uniform(0,1):

library(CorShrink)
set.seed(1234)

n=100
p=1
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X*beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}

R2.cor=(CorShrinkVector(sqrt(R2),n))^2
idx=sample(1:100,50)
R=sqrt(R2)
R[idx]=-R[idx]
R2.cor.sign=(CorShrinkVector(R,n))^2

plot(beta.list,R2,ylim=range(c(R2,R2.cor.sign,R2.cor,trueR2)),main='',xlab='beta',ylab='',type='l')
lines(beta.list,R2.cor,col=2)
lines(beta.list,R2.cor.sign,col=3)
lines(beta.list,trueR2,col='grey80')
abline(h=0,lty=2)
legend('topleft',c('R^2','R^2 CorShrink','R^2 CorShrink Random Sign','True R^2'),lty=c(1,1,1,1),col=c(1,2,3,'grey80'))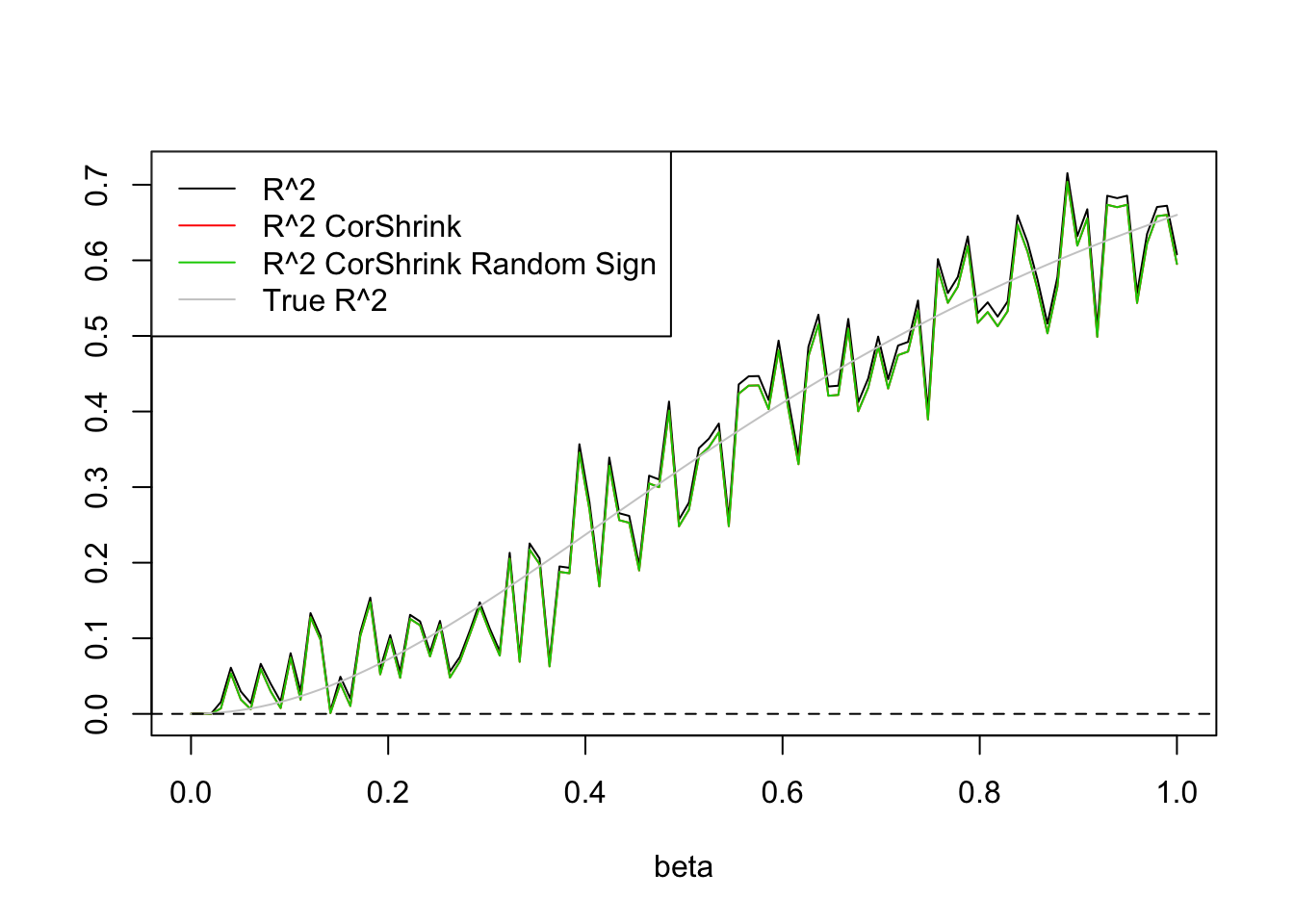

Expand here to see past versions of unnamed-chunk-13-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

plot(trueR2,R2,type='l',ylim=range(c(R2,R2.cor.sign,R2.cor,trueR2)))
lines(trueR2,R2.cor,col=2)
lines(trueR2,R2.cor.sign,col=3)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('R^2','R^2 CorShrink','R^2 CorShrink Random Sign'),lty=c(1,1,1),col=c(1,2,3))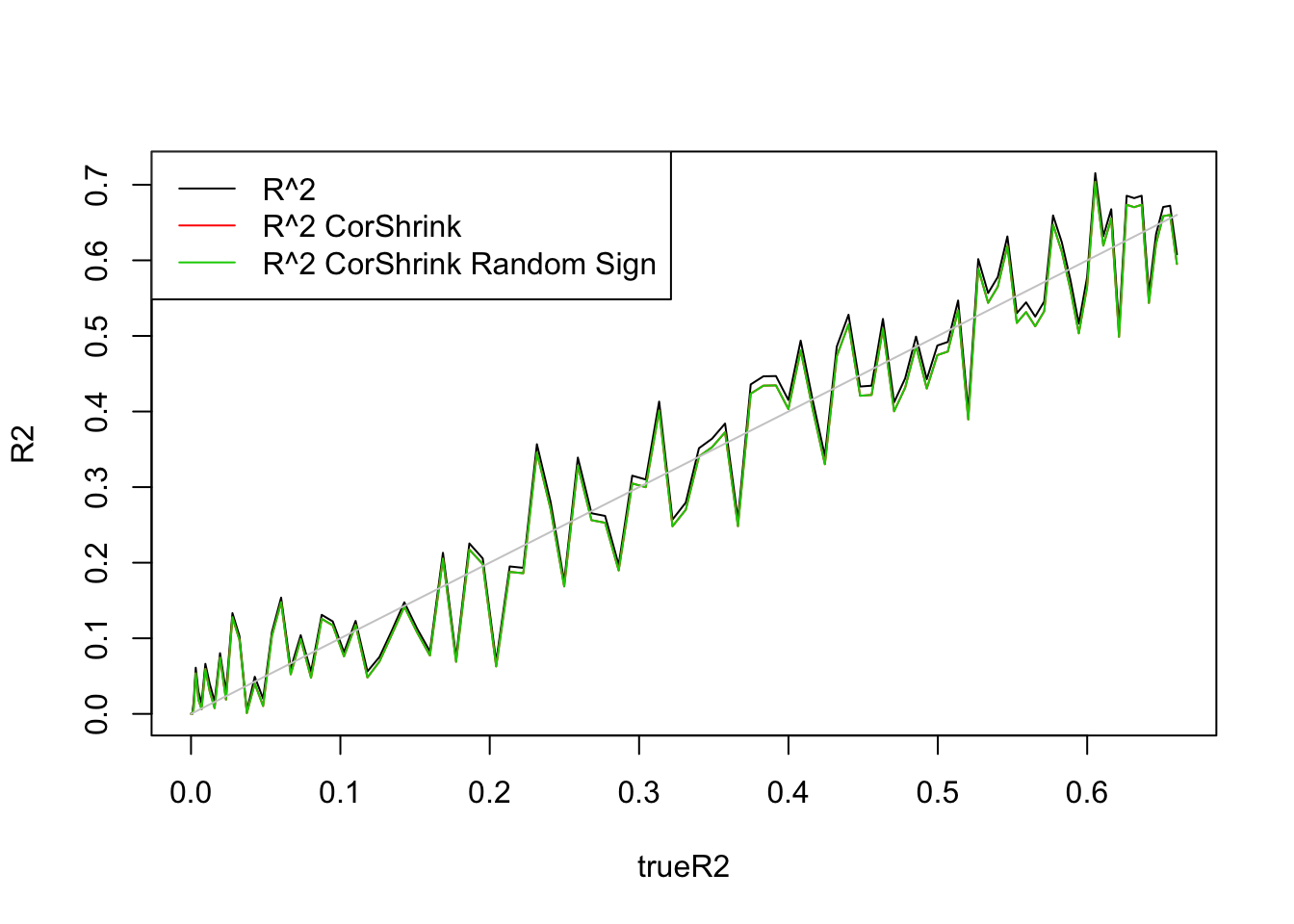

Expand here to see past versions of unnamed-chunk-13-2.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

So signs do not matter.

Estimates of g

Example 0

X from Uniform(0,5) and \(n=100,p=1\)

set.seed(1234)
n=100
p=1
R2=c()
R2a=c()
trueR2=c()
beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}

R2.fash=ash_r2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2

plot(trueR2,R2.fash,type='l',ylim=range(c(R2.fash,R2.cor,trueR2)),ylab = '')
lines(trueR2,R2.cor,col=2)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('fash','Corshrink','True R2'),lty=c(1,1,1),col=c(1,2,'grey80'))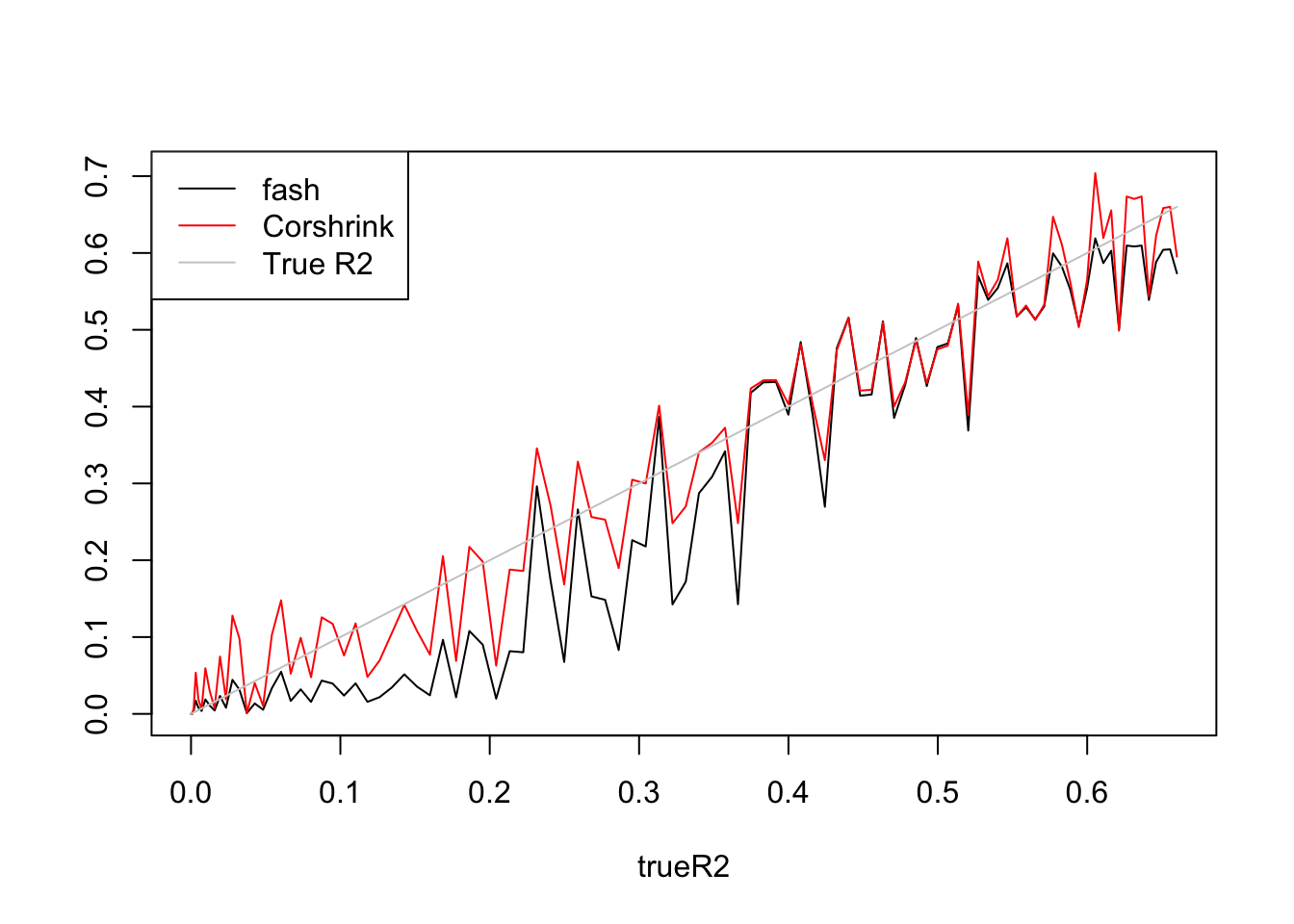

Expand here to see past versions of unnamed-chunk-14-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

fash:

log.ratio=log(1-R2)
ash.fit=ash(log.ratio,1,lik=lik_logF(df1=n-1,df2=n-1))
ash.fit$fitted_g

$pi
 [1] 3.941201e-01 1.339569e-11 1.337869e-11 1.341321e-11 1.372783e-11
 [6] 1.519486e-11 2.151838e-11 6.725142e-11 6.058799e-01 1.814045e-11

$a
 [1]  0.00000000 -0.09507465 -0.13445586 -0.19014930 -0.26891172
 [6] -0.38029861 -0.53782345 -0.76059722 -1.07564690 -1.52119443

$b
 [1] 0.00000000 0.09507465 0.13445586 0.19014930 0.26891172 0.38029861
 [7] 0.53782345 0.76059722 1.07564690 1.52119443

attr(,"class")
[1] "unimix"
attr(,"row.names")
 [1]  1  2  3  4  5  6  7  8  9 10

Fitted g concentrates at \(0.4*\delta_0+0.6*Uniform(-1.07,1.07)\)

Corshrink:

R=sqrt(R2)
corvec=R
corvec_trans = 0.5 * log((1 + corvec)/(1 - corvec))
corvec_trans_sd = rep(sqrt(1/(n - 1) + 2/(n - 
            1)^2), length(corvec_trans))

ash.control=list()
ash.control.default = list(pointmass = TRUE, mixcompdist = "normal", 
        nullweight = 10, fixg = FALSE, mode = 0, optmethod = "mixEM", 
        prior = "nullbiased", gridmult = sqrt(2), outputlevel = 2, 
        alpha = 0, df = NULL, control = list(K = 1, method = 3, 
            square = TRUE, step.min0 = 1, step.max0 = 1, mstep = 4, 
            kr = 1, objfn.inc = 1, tol = 1e-05, 
            trace = FALSE))
ash.control <- utils::modifyList(ash.control.default, ash.control)
    

fit = do.call(ashr::ash, append(list(betahat = corvec_trans, 
        sebetahat = corvec_trans_sd), ash.control))
fit$fitted_g

$pi
 [1] 1.198336e-01 3.102514e-09 3.098655e-09 3.055578e-09 2.825173e-09
 [6] 1.905128e-09 2.187591e-09 7.621847e-08 3.302451e-07 3.196176e-09
[11] 0.000000e+00 0.000000e+00 9.715355e-07 5.124079e-01 3.677565e-01
[16] 5.913347e-07 0.000000e+00 0.000000e+00

$mean
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

$sd
 [1] 0.000000000 0.009663507 0.013666263 0.019327015 0.027332527
 [6] 0.038654030 0.054665053 0.077308060 0.109330107 0.154616120
[11] 0.218660214 0.309232240 0.437320427 0.618464480 0.874640855
[16] 1.236928959 1.749281710 2.473857919

attr(,"class")
[1] "normalmix"
attr(,"row.names")
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18

Fitted g concentrates at \(0.12*\delta_0+0.5*N(0,0.62^2)+0.37*N(0,0.87^2)\)

Example 1

X from Uniform(0,1) and \(n=100,p=5\)

set.seed(1234)
n=100
p=5
R2=c()
R2a=c()
trueR2=c()
beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,1),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}

R2.fash=ash_r2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2

plot(trueR2,R2.fash,type='l',ylim=range(c(R2.fash,R2.cor,trueR2)),ylab = '')
lines(trueR2,R2.cor,col=2)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('fash','Corshrink','True R2'),lty=c(1,1,1),col=c(1,2,'grey80'))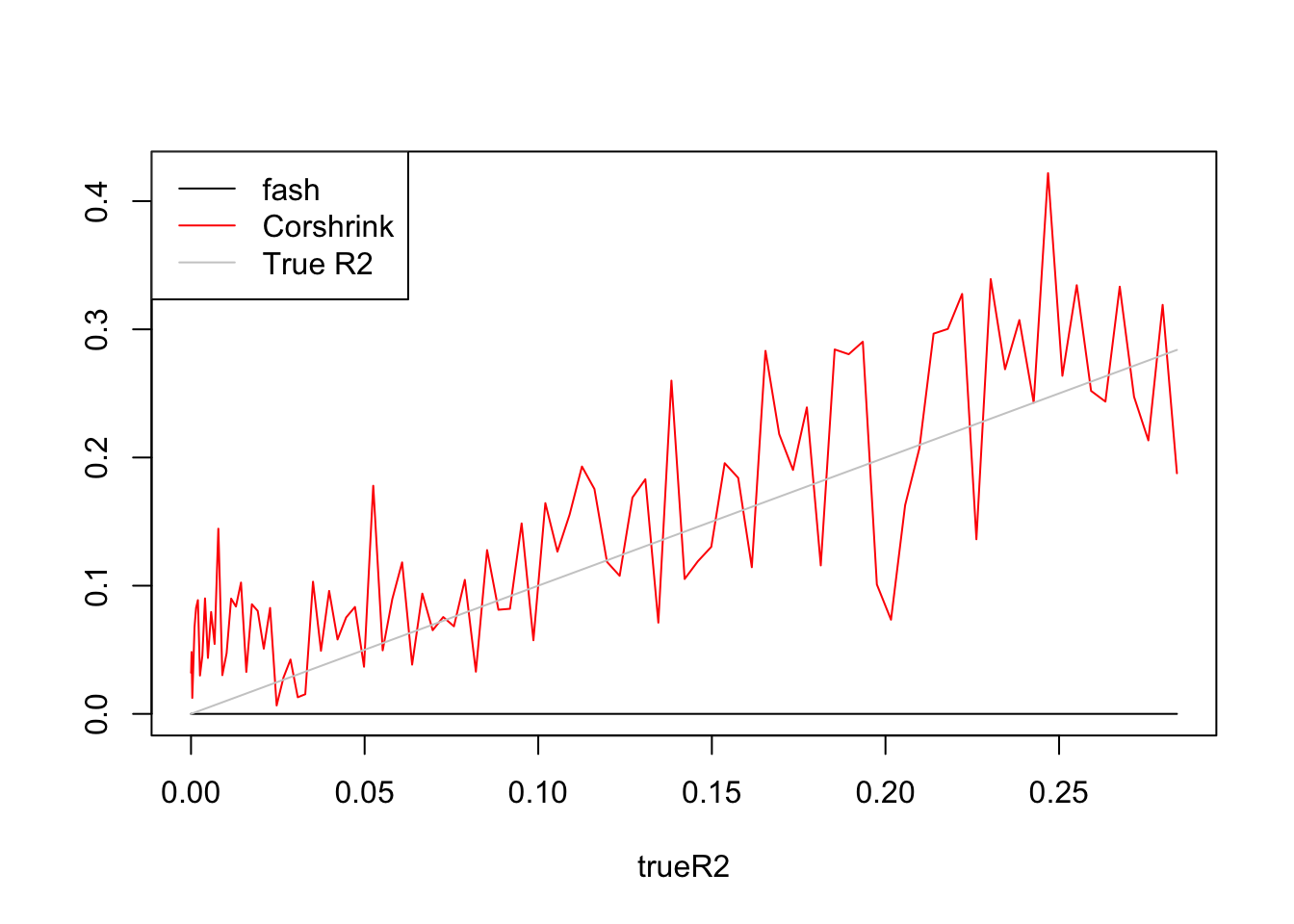

Expand here to see past versions of unnamed-chunk-17-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

fash:

log.ratio=log(1-R2)
ash.fit=ash(log.ratio,1,lik=lik_logF(df1=n-1,df2=n-1))
ash.fit$fitted_g

$pi
[1] 1 0 0 0 0 0 0 0

$a
[1]  0.0000000 -0.1000000 -0.1414214 -0.2000000 -0.2828427 -0.4000000
[7] -0.5656854 -0.8000000

$b
[1] 0.0000000 0.1000000 0.1414214 0.2000000 0.2828427 0.4000000 0.5656854
[8] 0.8000000

attr(,"class")
[1] "unimix"
attr(,"row.names")
[1] 1 2 3 4 5 6 7 8

Fitted g is at point mass at 0.

Corshrink:

R=sqrt(R2)
corvec=R
corvec_trans = 0.5 * log((1 + corvec)/(1 - corvec))
corvec_trans_sd = rep(sqrt(1/(n - 1) + 2/(n - 
            1)^2), length(corvec_trans))

ash.control=list()
ash.control.default = list(pointmass = TRUE, mixcompdist = "normal", 
        nullweight = 10, fixg = FALSE, mode = 0, optmethod = "mixEM", 
        prior = "nullbiased", gridmult = sqrt(2), outputlevel = 2, 
        alpha = 0, df = NULL, control = list(K = 1, method = 3, 
            square = TRUE, step.min0 = 1, step.max0 = 1, mstep = 4, 
            kr = 1, objfn.inc = 1, tol = 1e-05, 
            trace = FALSE))
ash.control <- utils::modifyList(ash.control.default, ash.control)
    

fit = do.call(ashr::ash, append(list(betahat = corvec_trans, 
        sebetahat = corvec_trans_sd), ash.control))
fit$fitted_g

$pi
 [1] 9.802685e-02 3.574714e-08 3.546272e-08 3.428903e-08 2.954403e-08
 [6] 1.308498e-08 5.872701e-09 2.297127e-07 0.000000e+00 0.000000e+00
[11] 0.000000e+00 0.000000e+00 9.018827e-01 8.912271e-05 1.659427e-14
[16] 9.609965e-07 0.000000e+00

$mean
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

$sd
 [1] 0.000000000 0.009016022 0.012750581 0.018032044 0.025501162
 [6] 0.036064089 0.051002323 0.072128177 0.102004647 0.144256355
[11] 0.204009293 0.288512709 0.408018586 0.577025418 0.816037173
[16] 1.154050837 1.632074345

attr(,"class")
[1] "normalmix"
attr(,"row.names")
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17

Fitted g concentrates at \(0.9*N(0,0.41^2)\)

Example 2

X from Uniform(0,5) and \(n=100,p=5\)

set.seed(1234)
n=100
p=5
R2=c()
R2a=c()
trueR2=c()

beta.list=seq(0,1,length.out = 100)
X=matrix(runif(n*(p),0,5),n,p)
for (i in 1:length(beta.list)) {
  beta=rep(beta.list[i],p)
  y=X%*%beta+rnorm(n)
  datax=data.frame(X=X,y=y)
  mod=lm(y~.,datax)
  mod.sy=summary(mod)
  R2[i]=mod.sy$r.squared
  R2a[i]=mod.sy$adj.r.squared
  trueR2[i]=1-(1)/(1+var(X%*%beta))
}

R2.fash=ash_r2(R2,n,p)
R2.cor=(CorShrinkVector(sqrt(R2),n))^2

plot(trueR2,R2.fash,type='l',ylim=range(c(R2.fash,R2.cor,trueR2)),ylab='')
lines(trueR2,R2.cor,col=2)
lines(trueR2,trueR2,col='grey80')
legend('topleft',c('fash','Corshrink','True R2'),lty=c(1,1,1),col=c(1,2,'grey80'))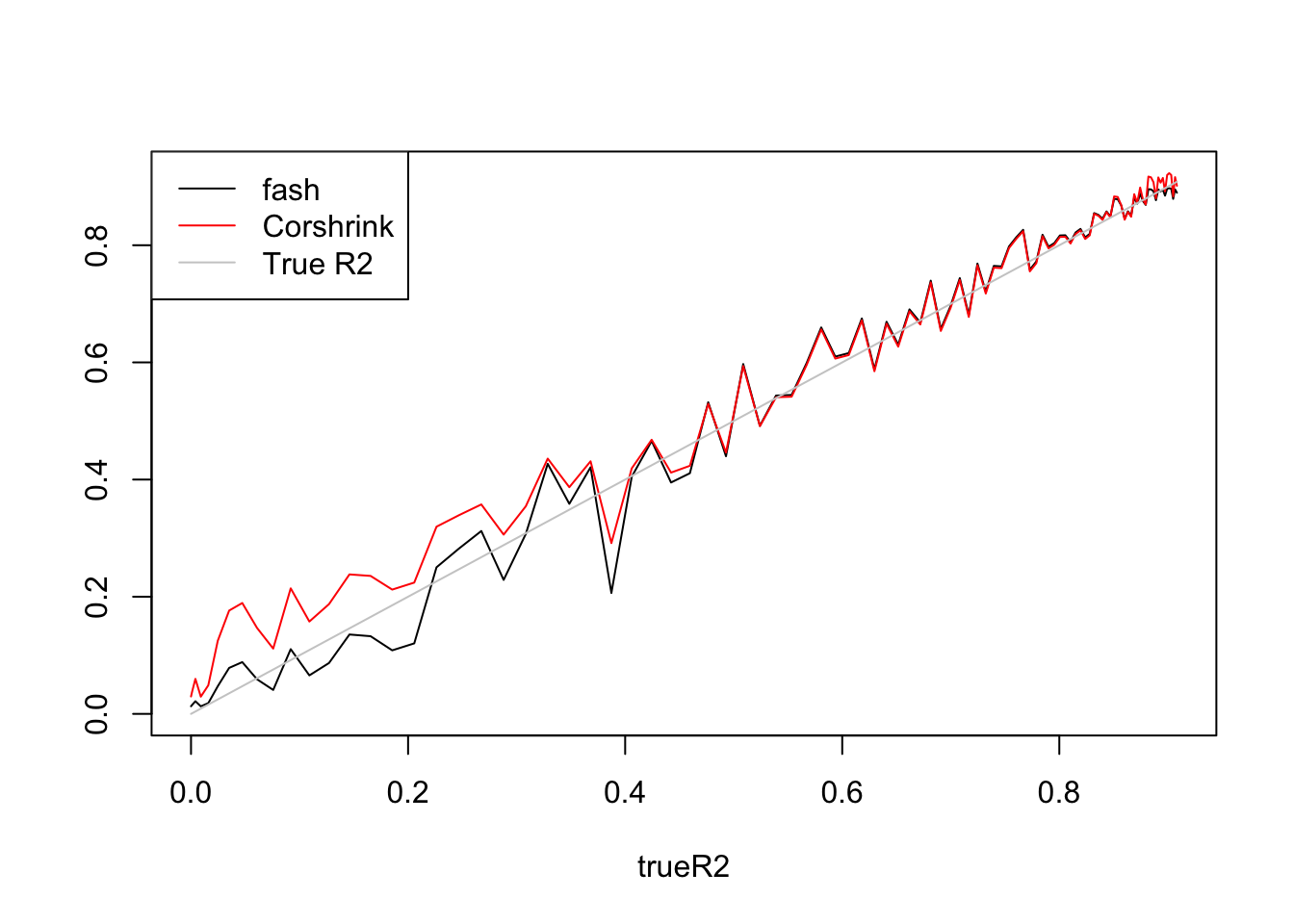

Expand here to see past versions of unnamed-chunk-20-1.png:

Version	Author	Date
c6f9a91	Dongyue Xie	2019-02-10

fash:

log.ratio=log(1-R2)
ash.fit=ash(log.ratio,1,lik=lik_logF(df1=n-1,df2=n-1))
ash.fit$fitted_g

$pi
 [1] 1.925080e-01 3.447647e-11 3.471171e-11 3.517280e-11 3.606265e-11
 [6] 3.774646e-11 4.082196e-11 4.558961e-11 5.172612e-11 6.290321e-11
[11] 1.055638e-10 8.074920e-01 4.531427e-10 4.122839e-11

$a
 [1]  0.00000000 -0.07447264 -0.10532021 -0.14894527 -0.21064043
 [6] -0.29789055 -0.42128085 -0.59578110 -0.84256171 -1.19156219
[11] -1.68512342 -2.38312439 -3.37024683 -4.76624878

$b
 [1] 0.00000000 0.07447264 0.10532021 0.14894527 0.21064043 0.29789055
 [7] 0.42128085 0.59578110 0.84256171 1.19156219 1.68512342 2.38312439
[13] 3.37024683 4.76624878

attr(,"class")
[1] "unimix"
attr(,"row.names")
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14

Fitted g concentrates at \(0.19*\delta_0+0.81*Uniform(-2.38,2.38)\).

Corshrink:

R=sqrt(R2)
corvec=R
corvec_trans = 0.5 * log((1 + corvec)/(1 - corvec))
corvec_trans_sd = rep(sqrt(1/(n - 1) + 2/(n - 
            1)^2), length(corvec_trans))

ash.control=list()
ash.control.default = list(pointmass = TRUE, mixcompdist = "normal", 
        nullweight = 10, fixg = FALSE, mode = 0, optmethod = "mixEM", 
        prior = "nullbiased", gridmult = sqrt(2), outputlevel = 2, 
        alpha = 0, df = NULL, control = list(K = 1, method = 3, 
            square = TRUE, step.min0 = 1, step.max0 = 1, mstep = 4, 
            kr = 1, objfn.inc = 1, tol = 1e-05, 
            trace = FALSE))
ash.control <- utils::modifyList(ash.control.default, ash.control)
    

fit = do.call(ashr::ash, append(list(betahat = corvec_trans, 
        sebetahat = corvec_trans_sd), ash.control))
fit$fitted_g

$pi
 [1] 8.739018e-02 1.585320e-10 1.795248e-10 2.290505e-10 3.656616e-10
 [6] 8.673704e-10 3.820458e-09 3.574858e-08 5.461574e-07 5.361614e-06
[11] 2.307459e-06 8.830531e-07 2.605247e-06 4.894297e-07 0.000000e+00
[16] 5.058173e-06 9.125923e-01 2.335972e-07 0.000000e+00 0.000000e+00

$mean
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

$sd
 [1] 0.000000000 0.007669231 0.010845930 0.015338461 0.021691860
 [6] 0.030676923 0.043383720 0.061353845 0.086767440 0.122707690
[11] 0.173534880 0.245415381 0.347069760 0.490830762 0.694139520
[16] 0.981661524 1.388279041 1.963323048 2.776558081 3.926646095

attr(,"class")
[1] "normalmix"
attr(,"row.names")
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Fitted g concentrates at \(0.91*N(0,1.39^2)\)

Summary2

Fash uses a mixture of point mass and uniform distributions as prior while CorShrink uses a mixture of point mass and normal distirbutions. Fash in these examples put more weights on point mass in fitted g than CorShrink.

Thoughts

Applying fash to shrink \(R^2\) replies on F distribution, which is from the ratio of two variances. F distribution replies on normal assumption and independence of two normal populations. However, \(var(\sigma^2)\) and \(var(y)=var(X\beta)+var(\sigma^2)\) are not independent. So rigourously speaking, using fash is not appropriate here.
Corshirnk depends on Fisher transformation which has bivariate normal assumption. Since \(R^2=r^2_{y,\hat y}\), we can apply Corshirnk if \(y,\hat y\) is bivariate normal distributed. By saying \(y,\hat y\) is bivariate normal distributed, I mean \(y,\hat y\) are \(n\) i.i.d samples from a bivariate normal distribution. However, this can hardly be true because \(\hat y=Hy\) where \(H=X(X^TX)^{-1}X^T\), so the \(n\) samples \(y,\hat y\) are not independently generated.
From the examples above, adjusted \(R^2\) is a good estimate of true \(R^2\). It gives estimate close to ture \(R^2\) which can be seen from the True \(R^2\) - estimated \(R^2\) plot. It’s pitfall it that it’s no longer necessatily positive - it can be negative.

Session information

sessionInfo()

R version 3.5.1 (2018-07-02)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.6

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] CorShrink_0.1-6 ashr_2.2-7     

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.0        plyr_1.8.4        compiler_3.5.1   
 [4] git2r_0.23.0      workflowr_1.1.1   R.methodsS3_1.7.1
 [7] R.utils_2.7.0     iterators_1.0.10  tools_3.5.1      
[10] digest_0.6.18     corrplot_0.84     evaluate_0.11    
[13] gtable_0.2.0      lattice_0.20-35   Matrix_1.2-14    
[16] foreach_1.4.4     yaml_2.2.0        parallel_3.5.1   
[19] gridExtra_2.3     stringr_1.3.1     knitr_1.20       
[22] REBayes_1.3       rprojroot_1.3-2   grid_3.5.1       
[25] glmnet_2.0-16     rmarkdown_1.10    reshape2_1.4.3   
[28] corpcor_1.6.9     magrittr_1.5      whisker_0.3-2    
[31] backports_1.1.2   codetools_0.2-15  htmltools_0.3.6  
[34] MASS_7.3-51.1     assertthat_0.2.0  stringi_1.2.4    
[37] Rmosek_8.0.69     doParallel_1.0.14 pscl_1.5.2       
[40] truncnorm_1.0-8   SQUAREM_2017.10-1 R.oo_1.22.0

This reproducible R Markdown analysis was created with workflowr 1.1.1

Shrink R squared - examples

Dongyue Xie

2019-01-21

R Function

Compare Shrunk \(R^2\) with True \(R2\).

Compare fash and corshrink

1-d case

Multiple regression

Summary1

Sign of correlations

Estimates of g

Example 0

Example 1

Example 2

Summary2

Thoughts

Session information