Mash vs. Flash

Code

# FLASH v MASH ------------------------------------------------------
flash_v_mash <- function(Y, true_Y, nfactors) {
  data <- flash_set_data(Y, S = 1)
  fl <- fit_flash(data, nfactors)
  m <- fit_mash(Y)

  # Sample from FLASH fit
  fl_sampler <- flash_lf_sampler(Y, fl, ebnm_fn=ebnm_pn, fixed="factors")

  nsamp <- 200
  fl_samp <- fl_sampler(nsamp)

  res <- list()
  res$fl_mse <- flash_pm_mse(fl_samp, true_Y)
  res$m_mse <- mash_pm_mse(m, true_Y)
  res$fl_ci <- flash_ci_acc(fl_samp, true_Y)
  res$m_ci <- mash_ci_acc(m, true_Y)
  res$fl_lfsr <- flash_lfsr(fl_samp, true_Y)
  res$m_lfsr <-  mash_lfsr(m, true_Y)
  res
}

plot_res <- function(res) {
  old_par <- par("mfrow")
  par(mfrow=c(1, 2))
  x <- seq(0.025, 0.475, by=0.05)
  plot(x, res$fl_lfsr, type='l', ylim=c(0, 0.6), xlab="FLASH", ylab="lfsr")
  abline(0, 1)
  plot(x, res$m_lfsr, type='l', ylim=c(0, 0.6), xlab="MASH", ylab="lfsr")
  abline(0, 1)
  par(mfrow=old_par)
}


# Fit using FLASH ---------------------------------------------------
fit_flash <- function(data, nfactors) {
  p <- ncol(data$Y)
  fl <- flash_add_greedy(data, nfactors, var_type = "zero")
  fl <- flash_add_fixed_f(data, diag(rep(1, p)), fl)
  flash_backfit(data, fl, nullcheck = F, var_type = "zero")
}

# Fit using MASH ---------------------------------------------------
fit_mash <- function(Y) {
  data <- mash_set_data(Y)
  U.c = cov_canonical(data)
  m.1by1 <- mash_1by1(data)
  strong <- get_significant_results(m.1by1, 0.05)
  U.pca <- cov_pca(data, 5, strong)
  U.ed <- cov_ed(data, U.pca, strong)
  mash(data, c(U.c,U.ed))
}


# MSE of posterior means (FLASH) ------------------------------------
flash_pm_mse <- function(fl_samp, true_Y) {
  n <- nrow(true_Y)
  p <- ncol(true_Y)
  nsamp <- length(fl_samp)

  post_means <- matrix(0, nrow=n, ncol=p)
  for (i in 1:nsamp) {
    post_means <- post_means + fl_samp[[i]]
  }
  post_means <- post_means / nsamp
  sum((post_means - true_Y)^2) / (n * p)
}
# Compare with just using FLASH LF:
# sum((flash_get_lf(fl)- true_flash_Y)^2) / (n * p)


# MSE for MASH ------------------------------------------------------
mash_pm_mse <- function(m, true_Y) {
  n <- nrow(true_Y)
  p <- ncol(true_Y)
  sum((get_pm(m) - true_Y)^2) / (n * p)
}


# CI coverage for FLASH ---------------------------------------------
flash_ci_acc <- function(fl_samp, true_Y) {
  n <- nrow(true_Y)
  p <- ncol(true_Y)
  nsamp <- length(fl_samp)

  flat_samp <- matrix(0, nrow=n*p, ncol=nsamp)
  for (i in 1:nsamp) {
    flat_samp[, i] <- as.vector(fl_samp[[i]])
  }
  CI <- t(apply(flat_samp, 1, function(x) {quantile(x, c(0.025, 0.975))}))
  sum((as.vector(true_Y) > CI[, 1])
      & (as.vector(true_Y < CI[, 2]))) / (n * p)
}

# CI coverage for MASH ----------------------------------------------
mash_ci_acc <- function(m, true_Y) {
  sum((true_Y > get_pm(m) - 1.96 * get_psd(m))
      & (true_Y < get_pm(m) + 1.96 * get_psd(m))) / (n * p)
}


# LFSR for FLASH ----------------------------------------------------
flash_lfsr <- function(fl_samp, true_Y, step=0.05) {
  n <- nrow(true_Y)
  p <- ncol(true_Y)
  nsamp <- length(fl_samp)

  lfsr <- matrix(0, nrow=n, ncol=p)
  for (i in 1:nsamp) {
    lfsr <- lfsr + (fl_samp[[i]] > 0) + 0.5*(fl_samp[[i]] == 0)
  }
  signs <- lfsr >= nsamp / 2
  correct_signs <- true_Y > 0
  gotitright <- signs == correct_signs
  lfsr <- pmin(lfsr, 100 - lfsr) / 100

  nsteps <- floor(.5 / step)
  fsr_by_lfsr <- rep(0, nsteps)
  for (k in 1:nsteps) {
    idx <- (lfsr >= (step * (k - 1)) & lfsr < (step * k))
    fsr_by_lfsr[k] <- ifelse(sum(idx) == 0, 0,
                             1 - sum(gotitright[idx]) / sum(idx))
  }
  fsr_by_lfsr
}


# LFSR for MASH -----------------------------------------------------
mash_lfsr <- function(m, true_Y, step=0.05) {
  lfsr <- get_lfsr(m)
  signs <- get_pm(m) > 0
  correct_signs <- true_Y > 0
  gotitright <- signs == correct_signs

  nsteps <- floor(.5 / step)
  fsr_by_lfsr <- rep(0, nsteps)
  for (k in 1:nsteps) {
    idx <- (lfsr >= (step * (k - 1)) & lfsr < (step * k))
    fsr_by_lfsr[k] <- ifelse(sum(idx) == 0, 0,
                             1 - sum(gotitright[idx]) / sum(idx))
  }
  fsr_by_lfsr
}

# Simulate from FLASH model -----------------------------------------
n <- 1000
p <- 10
flash_factors <- 5

# Use one factor of all ones and one more interesting factor
nfactors <- 2
k <- p + nfactors
ff <- matrix(0, nrow=k, ncol=p)
ff[1, ] <- rep(10, p)
ff[2, ] <- c(seq(10, 2, by=-2), rep(0, p - 5))
diag(ff[3:k, ]) <- 3
ll <- matrix(rnorm(n * k), nrow=n, ncol=k)
true_flash_Y <- ll %*% ff
flash_Y <- true_flash_Y + rnorm(n*p)
# RESULTS
flash_res <- flash_v_mash(flash_Y, true_flash_Y, flash_factors)

fitting factor/loading 1

fitting factor/loading 2

fitting factor/loading 3

fitting factor/loading 4

fitting factor/loading 5

 - Computing 1000 x 463 likelihood matrix.
 - Likelihood calculations took 0.10 seconds.
 - Fitting model with 463 mixture components.
 - Model fitting took 0.14 seconds.
 - Computing posterior matrices.
 - Computation allocated took 0.02 seconds.

# Simulate from basic FLASH model -----------------------------------
ff <- ff[1:nfactors, ]
ll <- matrix(rnorm(n * nfactors), nrow=n, ncol=nfactors)
true_basic_Y <- ll %*% ff
basic_Y <- true_basic_Y + rnorm(n*p)
# RESULTS
basic_res <- flash_v_mash(basic_Y, true_basic_Y, flash_factors)

fitting factor/loading 1

fitting factor/loading 2

fitting factor/loading 3

 - Computing 1000 x 463 likelihood matrix.
 - Likelihood calculations took 0.10 seconds.
 - Fitting model with 463 mixture components.

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in mixIP(matrix_lik = structure(c(4.36775456085054e-15, 0, 0,
0, : Optimization step yields mixture weights that are either too small,
or negative; weights have been corrected and renormalized after the
optimization.

 - Model fitting took 0.20 seconds.
 - Computing posterior matrices.
 - Computation allocated took 0.25 seconds.

# Simulate from MASH model ------------------------------------------
Sigma <- list()
Sigma[[1]] <- matrix(1, nrow=p, ncol=p)
Sigma[[2]] <- matrix(0, nrow=p, ncol=p)
for (i in 1:p) {
  for (j in 1:p) {
    Sigma[[2]][i, j] <- max(1 - abs(i - j) / 4, 0)
  }
}
for (k in 1:p) {
  Sigma[[k + 2]] <- matrix(0, nrow=p, ncol=p)
  Sigma[[k + 2]][k, k] <- 1
}
which_sigma <- sample(1:12, 1000, T, prob=c(.3, .3, rep(.4/p, p)))
true_mash_Y <- matrix(0, nrow=n, ncol=p)
for (i in 1:n) {
  true_mash_Y[i, ] <- 5*mvrnorm(1, rep(0, p), Sigma[[which_sigma[i]]])
}
mash_Y <- true_mash_Y + rnorm(n * p)
# RESULTS
mash_res <- flash_v_mash(mash_Y, true_mash_Y, flash_factors)

fitting factor/loading 1

fitting factor/loading 2

fitting factor/loading 3

fitting factor/loading 4

fitting factor/loading 5

 - Computing 1000 x 400 likelihood matrix.
 - Likelihood calculations took 0.09 seconds.
 - Fitting model with 400 mixture components.
 - Model fitting took 0.53 seconds.
 - Computing posterior matrices.
 - Computation allocated took 0.02 seconds.

In each case below, I follow the vignettes to produce a MASH fit (I use both canonical and data-driven covariance matrices). I fit a FLASH object (fixing the standard errors) by adding up to 10 factors greedily, then adding \(p\) fixed one-hot vectors, and finally backfitting.

The two fits perform similarly. The MASH fit does somewhat better on data generated from the MASH model; more surprisingly, it performs comparably to FLASH on data generated from both the standard two-factor FLASH model. Both do poorly on the “augmented FLASH model” (described below), with MSEs near 1 (which would be obtained by simply using \(Y\) as an estimate).

Flash Model

First I simulate from the basic FLASH model \(Y = LF + E\) with \(E_{ij} \sim N(0, 1)\). Here, \(Y \in \mathbb{R}^{1000 \times 10}\), \(L \in \mathbb{R}^{1000 \times 2}\) has i.i.d. \(N(0, 1)\) entries, and \(F\) is as follows:

     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]   10   10   10   10   10   10   10   10   10    10
[2,]   10    8    6    4    2    0    0    0    0     0

The MSE of the FLASH fit is 0.2, vs. 0.21 for the MASH fit. The proportion of 95% confidence intervals that contain the true value \(LF_{ij}\) is 0.94 for FLASH and 0.96 for MASH. The true false sign rate vs lfsr appears as follows:

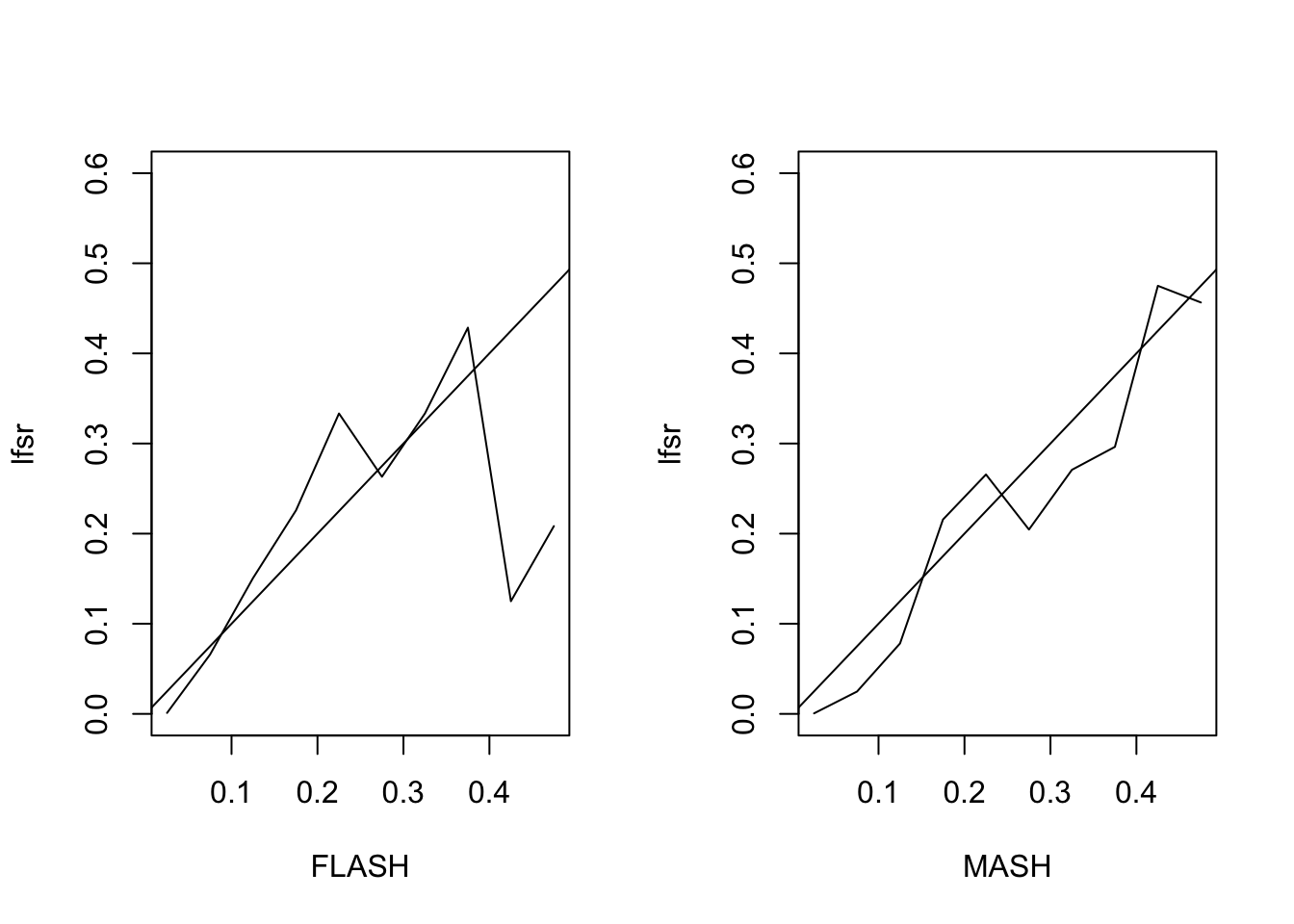
Augmented Flash Model

Next I simulate from the “augmented” FLASH model \[ Y = L \begin{pmatrix} F \\ 3I_{10} \end{pmatrix} + E \] with \(F\) as above.

The MSE of the FLASH fit is 0.93, vs. 1.05 for the MASH fit. The proportion of 95% confidence intervals that contain the true value is 0.94 for FLASH and 0.93 for MASH. The true false sign rate vs lfsr appears as follows:

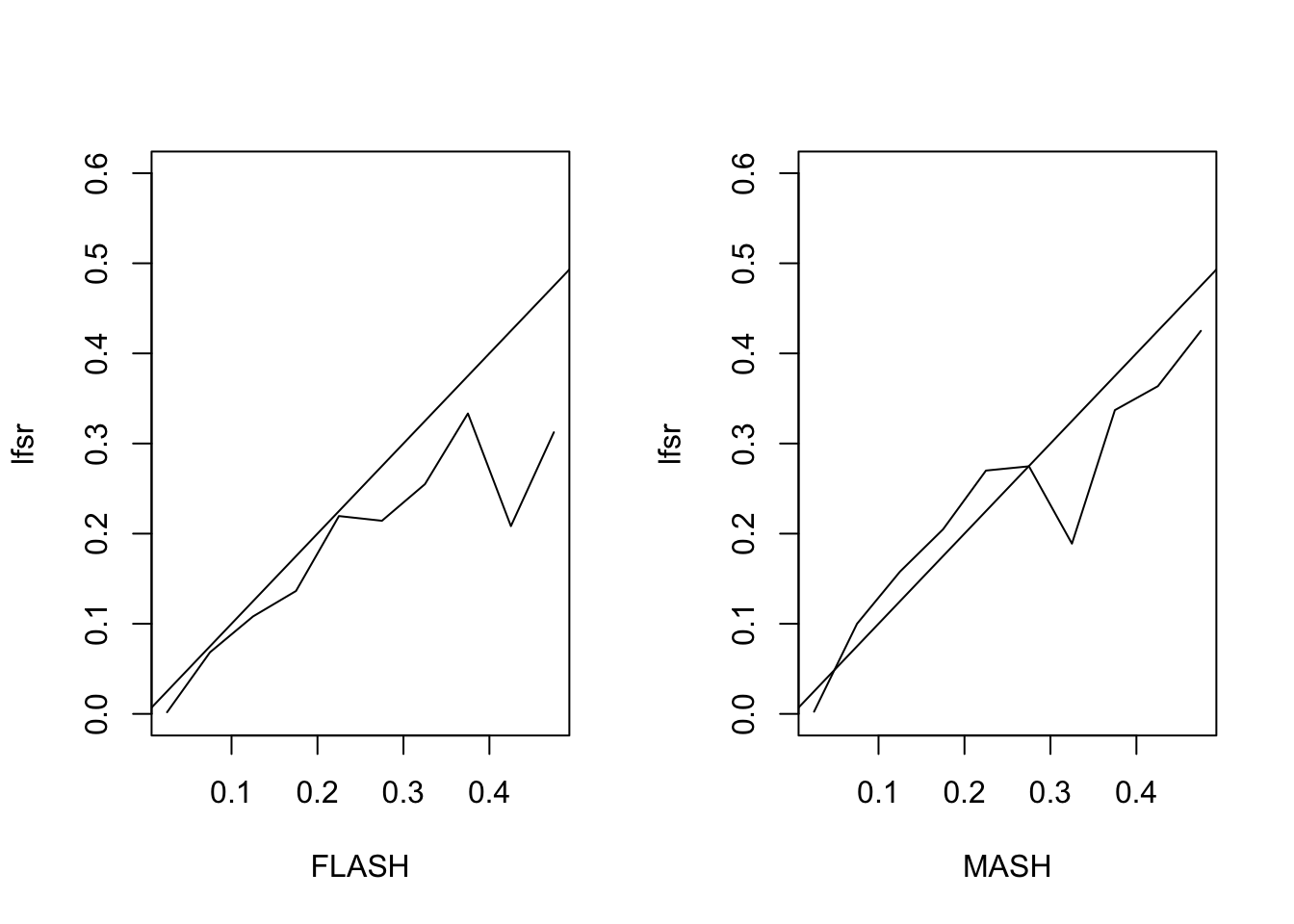
MASH Model

Finally I simulate from the MASH model \[ X \sim \sum \pi_i N(0, \Sigma_i),\ Y = X + E \] with \(E_{ij} \sim N(0, 1)\). I set \(\Sigma_1\) to be the all ones matrix, \(\Sigma_2\) to be a banded covariance matrix with non-zero entries on the first three off-diagonals, and \(\Sigma_3\) through \(\Sigma_{12}\) to have a single non-zero entry (corresponding to tissue-specific effects). \(\pi\) is set to \((0.3, 0.3, 0.04, 0.04, \ldots, 0.04)\).

The MSE of the FLASH fit is 0.56, vs. 0.43 for the MASH fit. The proportion of 95% confidence intervals that contain the true value is 0.9 for FLASH and 0.94 for MASH. The true false sign rate vs lfsr appears as follows:

Session information

sessionInfo()

R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] MASS_7.3-48  mashr_0.2-7  ashr_2.2-7   flashr_0.5-8

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.16             pillar_1.2.1            
 [3] plyr_1.8.4               compiler_3.4.3          
 [5] git2r_0.21.0             workflowr_1.0.1         
 [7] R.methodsS3_1.7.1        R.utils_2.6.0           
 [9] iterators_1.0.9          tools_3.4.3             
[11] testthat_2.0.0           digest_0.6.15           
[13] tibble_1.4.2             evaluate_0.10.1         
[15] memoise_1.1.0            gtable_0.2.0            
[17] lattice_0.20-35          rlang_0.2.0             
[19] Matrix_1.2-12            foreach_1.4.4           
[21] commonmark_1.4           yaml_2.1.17             
[23] parallel_3.4.3           mvtnorm_1.0-7           
[25] ebnm_0.1-11              withr_2.1.1.9000        
[27] stringr_1.3.0            roxygen2_6.0.1.9000     
[29] xml2_1.2.0               knitr_1.20              
[31] REBayes_1.2              devtools_1.13.4         
[33] rprojroot_1.3-2          grid_3.4.3              
[35] R6_2.2.2                 rmarkdown_1.8           
[37] rmeta_3.0                ggplot2_2.2.1           
[39] magrittr_1.5             whisker_0.3-2           
[41] backports_1.1.2          scales_0.5.0            
[43] codetools_0.2-15         htmltools_0.3.6         
[45] assertthat_0.2.0         softImpute_1.4          
[47] colorspace_1.3-2         stringi_1.1.6           
[49] Rmosek_7.1.3             lazyeval_0.2.1          
[51] munsell_0.4.3            doParallel_1.0.11       
[53] pscl_1.5.2               truncnorm_1.0-8         
[55] SQUAREM_2017.10-1        ExtremeDeconvolution_1.3
[57] R.oo_1.21.0