MASH v FLASH simulation: detailed study

Independent effects

Effects were nonnull for all conditions and generated independently from a \(N(0, \sigma^2)\) distribution. I simulated \((1)\) small independent effects (\(\sigma^2 = 2^2\)), \((2)\) large independent effects (\(\sigma^2 = 5^2\)), and \((3)\) independent effects of varying sizes (with \(\sigma^2\) ranging from \(1^2\) to \(5^2\)).

Notice that cases 1 and 2 are covered by “canonical” covariance matrices in MASH, but 3 is not.

Identical effects

Effects were nonnull for all conditions, with an effect size that was identical across conditions. The unique effect size was generated from a \(N(0, \sigma^2)\) distribution. Similar to the above, I simulated \((4)\) small identical effects (\(\sigma^2 = 2^2\)) and \((5)\) large identical effects (\(\sigma^2 = 5^2\)).

Both of these cases are covered by canonical covariance matrices in MASH.

Rank-one effects

These are similar to “identical effects” in that the covariance matrix has rank one (so that conditions 2-20 are always fixed multiples of condition 1), but here, the effect sizes vary.

\((6)\) The effect size for condition 1 was generated from a \(N(0, 1)\) distribution, and conditions 1-20 were multiples evenly spaced between 1 and 5.

Unlike identical effects, rank-one effects are not directly modeled by canonical covariance matrices.

Unique effects

Effects were nonnull in one condition only, with the nonnull effect simulated from a \(N(0, \sigma^2)\) distribution. I simulated \((7)\) small effects (\(\sigma^2 = 3^2\)) unique to condition 1 and \((8)\) large effects (\(\sigma^2 = 8^2\)) unique to condition 2.

These effects are directly modeled by canonical covariance matrices.

Shared effects

Effects were nonnull in several conditions. The nonnull effects were either identical across conditions or fixed multiples of one another. I included \((9)\) medium effects (\(\sigma^2 = 3^2\)) identical across 3 conditions (3-5), \((10)\) small effects (\(\sigma^2 = 2^2\)) identical across 10 conditions (1-10), and \((11)\) effects of differing sizes over 5 conditions (6-10), with variances ranging from \(2^2\) to \(4^2\).

None of these effects are modeled by canonical covariance matrices.

Other covariance structures

I included two more covariance structures in which effects were nonnull across all conditions: \((12)\) a banded (Toeplitz) covariance matrix with bandwidth 5, with covariances equal to \(5^2\) along the diagonal and decreasing to \(2^2\) along the fourth off-diagonals, and \((13)\) a random covariance matrix \(A^T A\), with the entries of \(A\) independently generated from a \(N(0, 2^2)\) distribution.

Fitting methods

For each simulation, I fitted a MASH model and two FLASH models using the “one-hots last” method described in my larger simulation study. One FLASH model used the point-normal approach to solve the ebnm problem (ebnm_fn = ebnm_pn); the other used ashr (ebnm_fn = ebnm_ash).

Results: RRMSE

Here I give a detailed breakdown of the relative root mean-squared errors (that is, the RMSE for each fit object, divided by the RMSE that would be obtained by simply using the observed data \(Y\) to estimate the “true effects” \(X\)). In addition to calculating the RRMSE separately for each covariance type, I also separately consider null effects and nonnull effects.

MASH does much better in shrinking null effects towards zero, particularly for tests that are null across all conditions or that are unique to a single condition (covariance types 7-8). MASH also does consistently better in estimating nonnull effects when effects are independent across conditions (types 1-3). (In such cases, FLASH does worse than the naive estimate \(\hat{X} = Y\).)

Results for other covariance types are more varied: MASH appears to do better on identical effects (types 4-5, whose covariance structures are included as “canonical”), but worse on rank-one effects (type 6, which is not accounted for by canonical covariance matrices). FLASH seems to outperform MASH on shared effects (types 9-11), but (somewhat surprisingly) MASH does better on banded and random covariance matrices (types 12-13), with an RRMSE near 1 (whereas FLASH is again outperformed by the naive estimate \(\hat{X} = Y\)).

In general, the ash fits perform very similarly to the point-normal fits.

RRMSE for null effects is as follows (where “null” below refers to tests that are null across all conditions):

par(mar = c(5,4,4,6))

legend.names <- c("FL-pn", "FL-ash", "MASH")
legend.args <- list(x="right", bty="n", inset=c(-0.25,0), xpd=T)
barplot(all.rrmses[,nullidx], names.arg = null.names, beside=T,
        ylim=c(0, 1), ylab="RRMSE", main="RRMSE for null effects",
        legend.text=legend.names, args.legend=legend.args)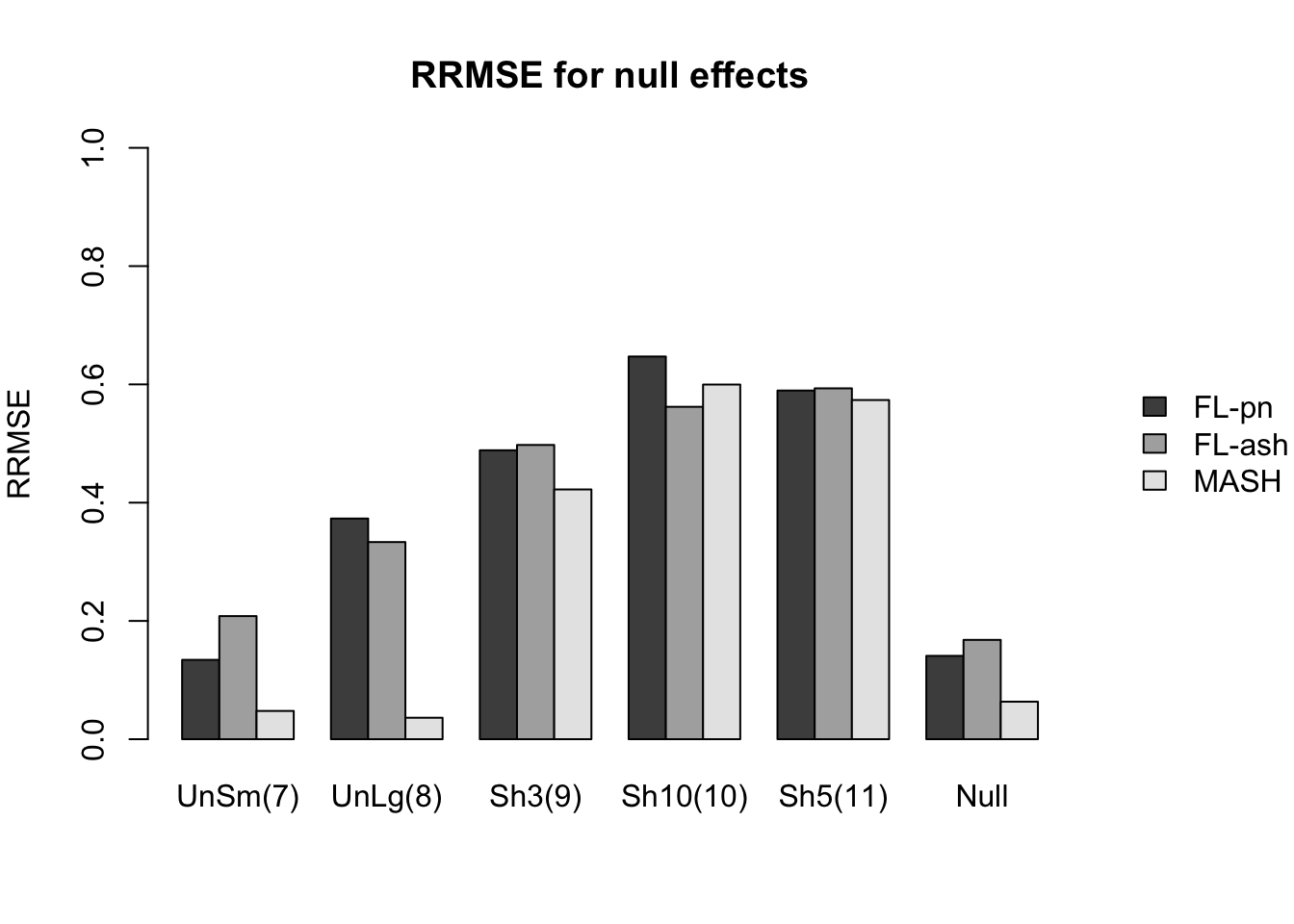

And RRMSE for nonnull effects is as follows.

par(mar = c(5,4,4,6))
barplot(all.rrmses[,indididx], names.arg = indid.names, beside=T,
        ylim=c(0, 2), ylab="RRMSE", main="RRMSE for nonnull effects",
        legend.text=legend.names, args.legend=legend.args)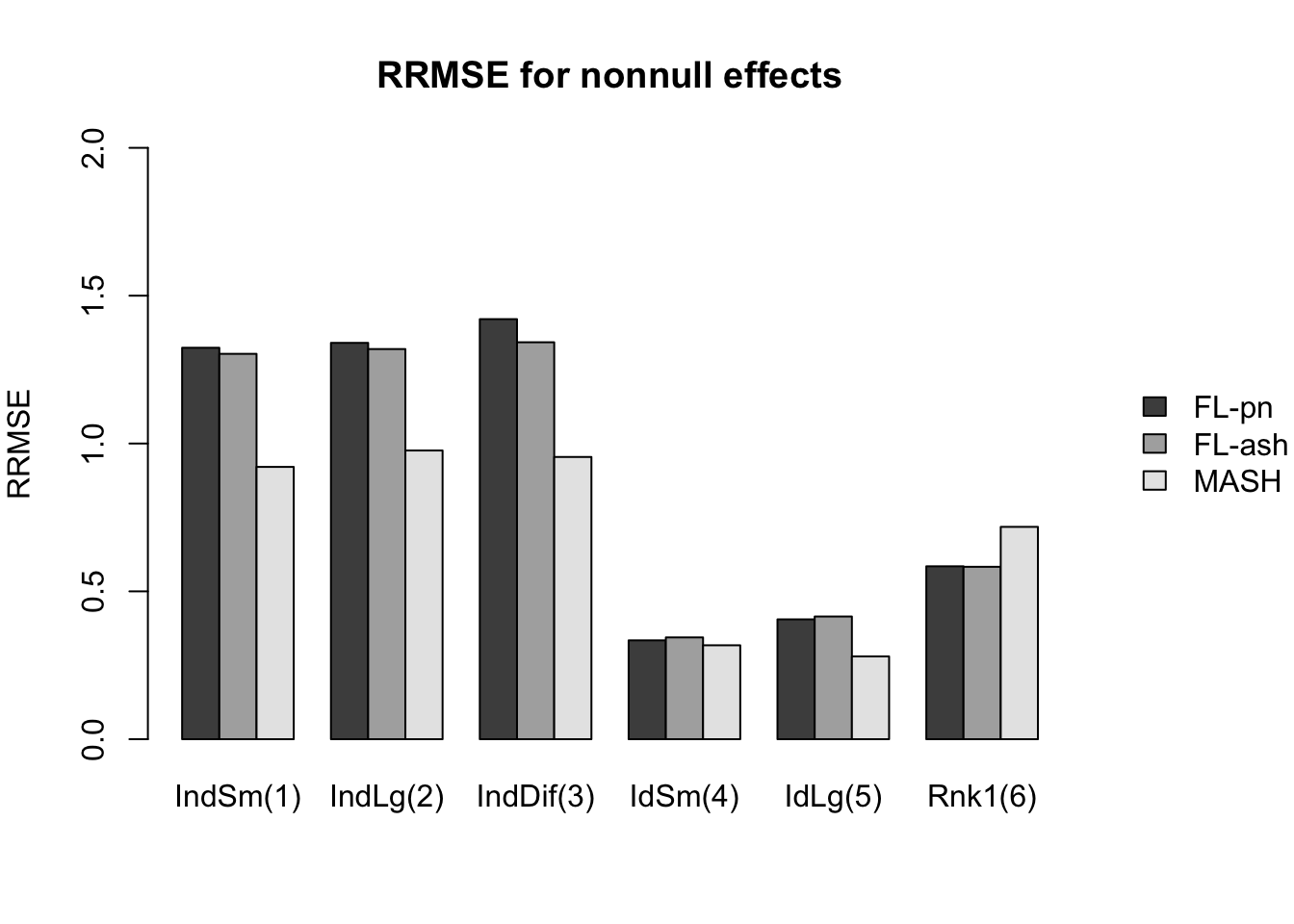

barplot(all.rrmses[,unshidx], names.arg = unsh.names, beside=T,
        ylim=c(0, 2), ylab="RRMSE", main="",
        legend.text=legend.names, args.legend=legend.args)

barplot(all.rrmses[,otheridx], names.arg = other.names, beside=T,
        ylim=c(0, 2), ylab="RRMSE", main="",
        legend.text=legend.names, args.legend=legend.args)

Results: FPR/TPR

As in the larger simulation study, I evaluate true and false positive rates using the built-in function get_lfsr() for MASH and by simulating from the posterior for FLASH. Here I use a significance threshold of 0.05.

The FLASH fits appear to have significantly higher power for independent effects (covariance types 1-3) and shared effects (9-11), and have equal or slightly higher power for all other covariance types. However, this higher power is counterbalanced by much higher false positive rates across all covariance types.

As above, the ash fits are not convincingly better than the point-normal fits.

The false positive rates for various null effects are as follows.

par(mar = c(5,4,4,6))
barplot(all.prs[,nullidx], names.arg = null.names, beside=T,
        ylim=c(0, 0.25), ylab="FPR", main="FPR for null effects",
        legend.text=legend.names, args.legend=legend.args)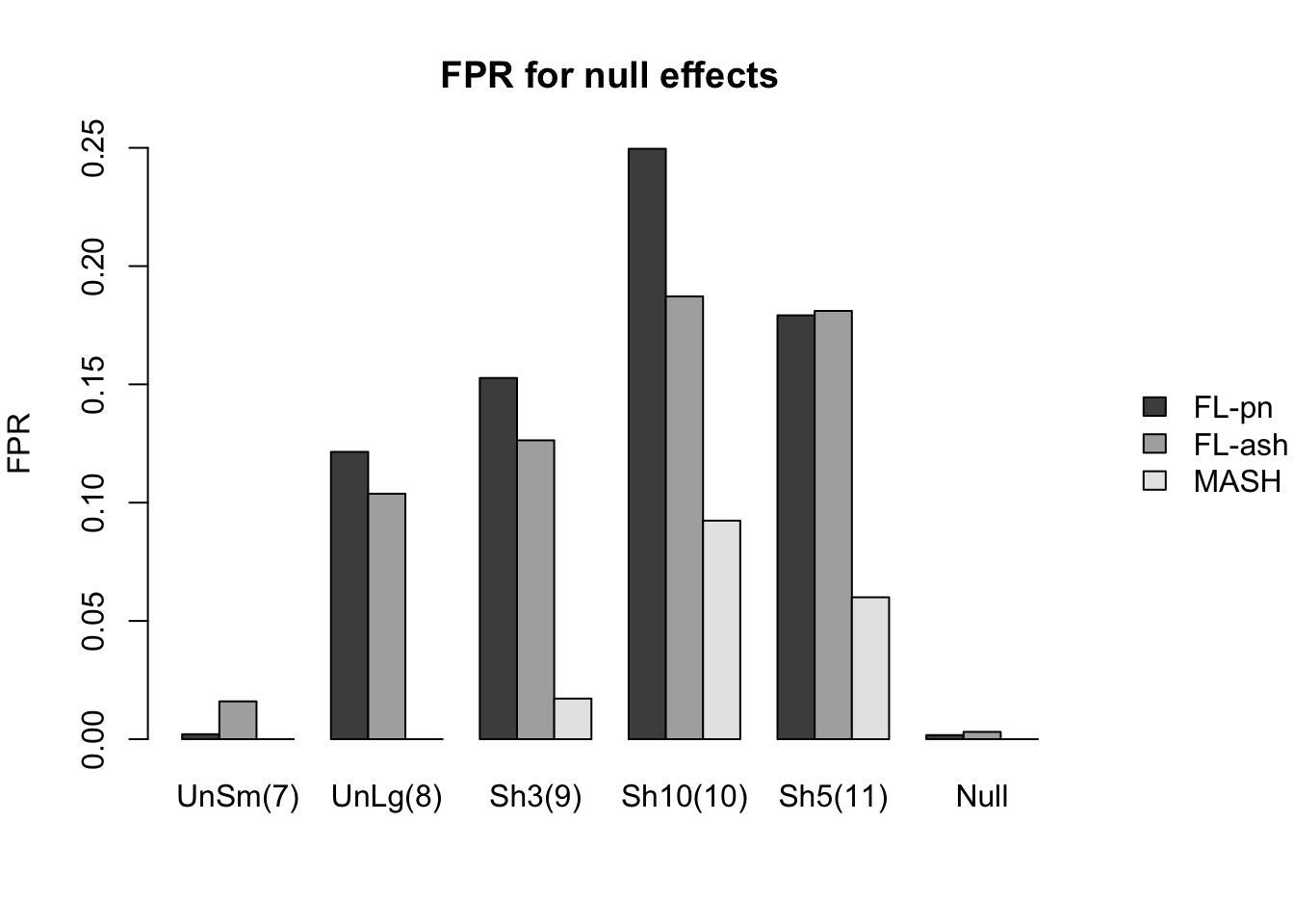

And the true positive rates are as follows.

par(mar = c(5,4,4,6))
barplot(all.prs[,unshidx], names.arg = unsh.names, beside=T,
        ylim=c(0, 1), ylab="TPR", main="TPR for nonnull effects",
        legend.text=legend.names, args.legend=legend.args)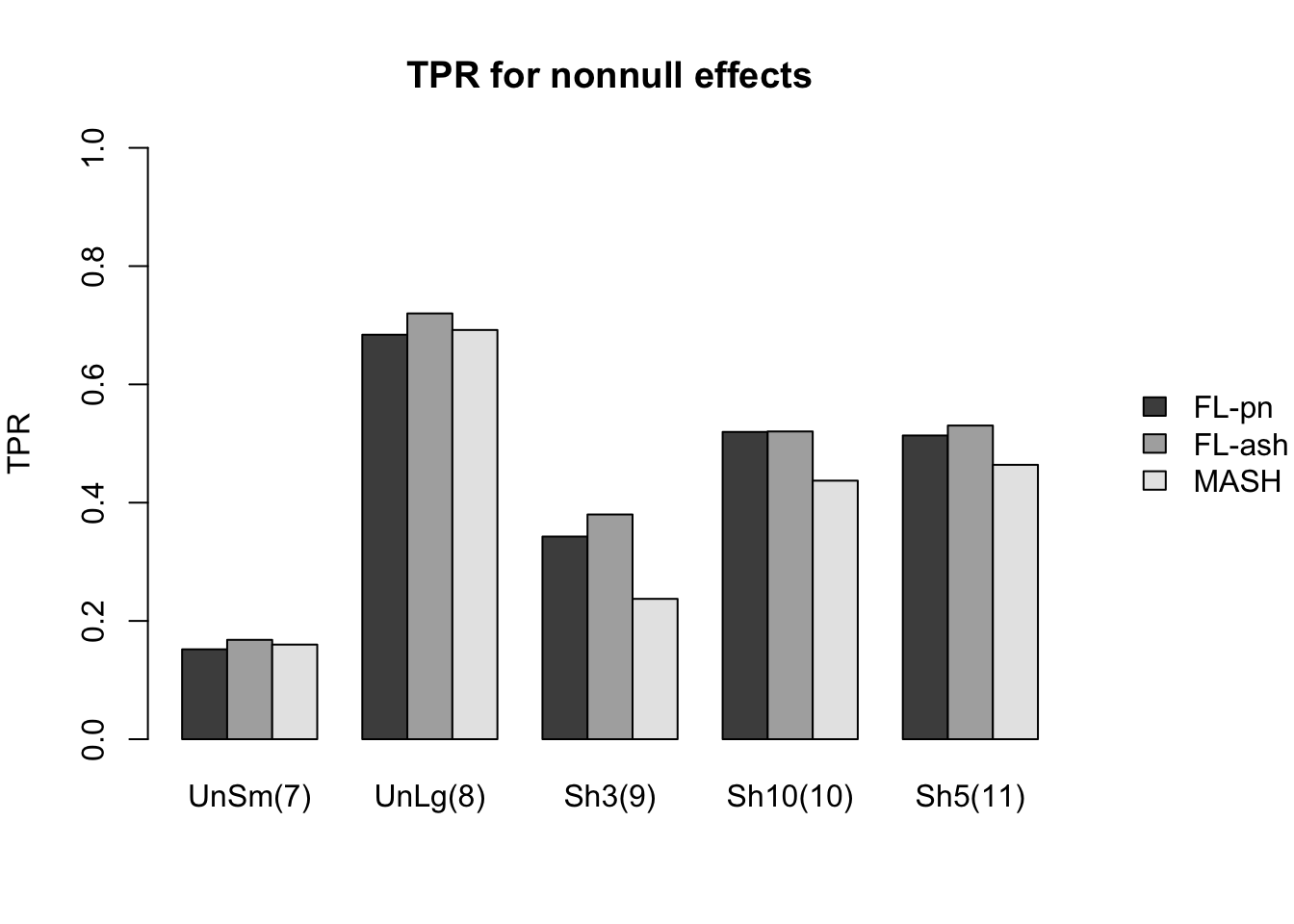

barplot(all.prs[,indididx], names.arg = indid.names, beside=T,
        ylim=c(0, 1), ylab="TPR", main="",
        legend.text=legend.names, args.legend=legend.args)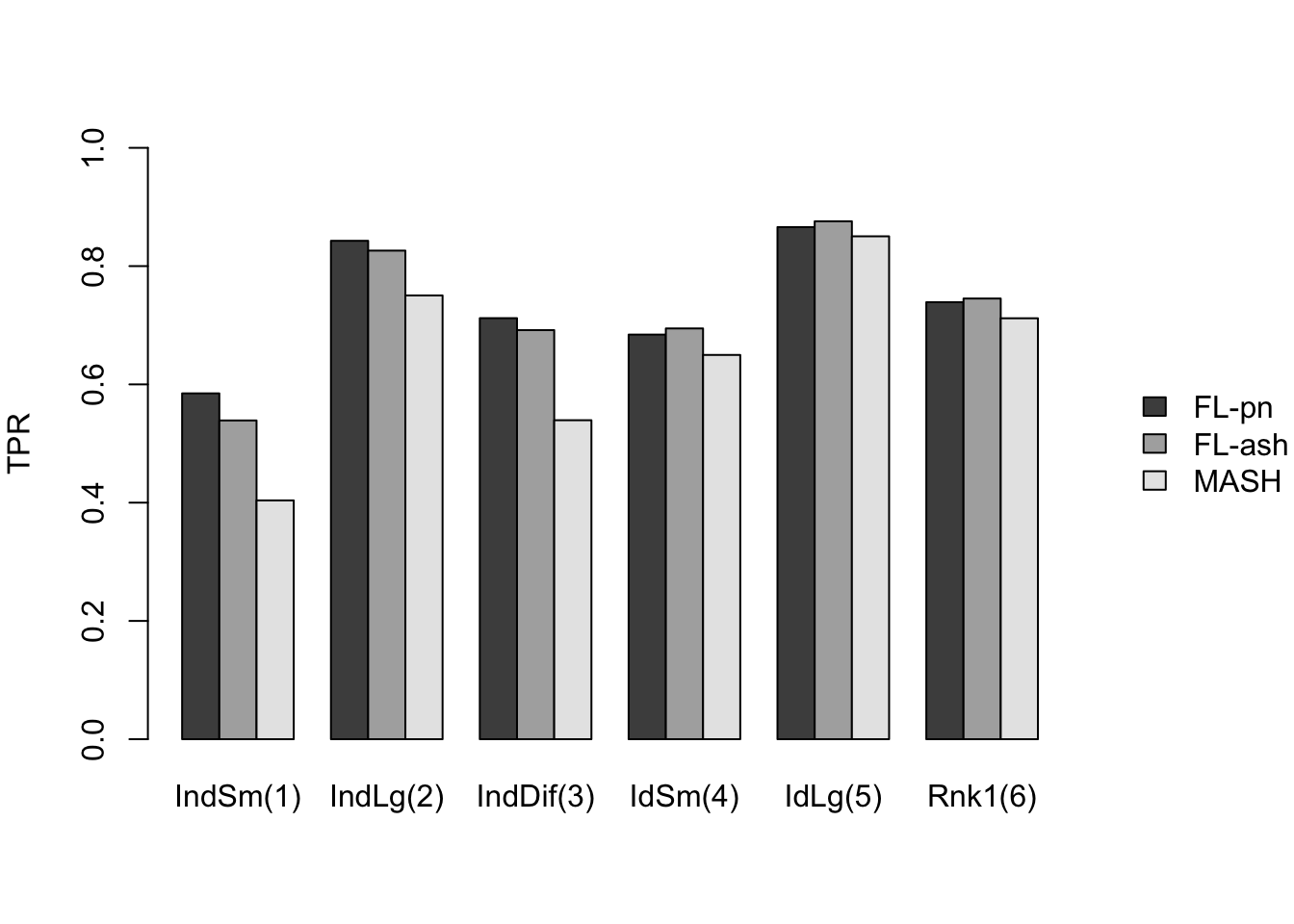

barplot(all.prs[,otheridx], names.arg = other.names, beside=T,
        ylim=c(0, 1), ylab="TPR", main="",
        legend.text=legend.names, args.legend=legend.args)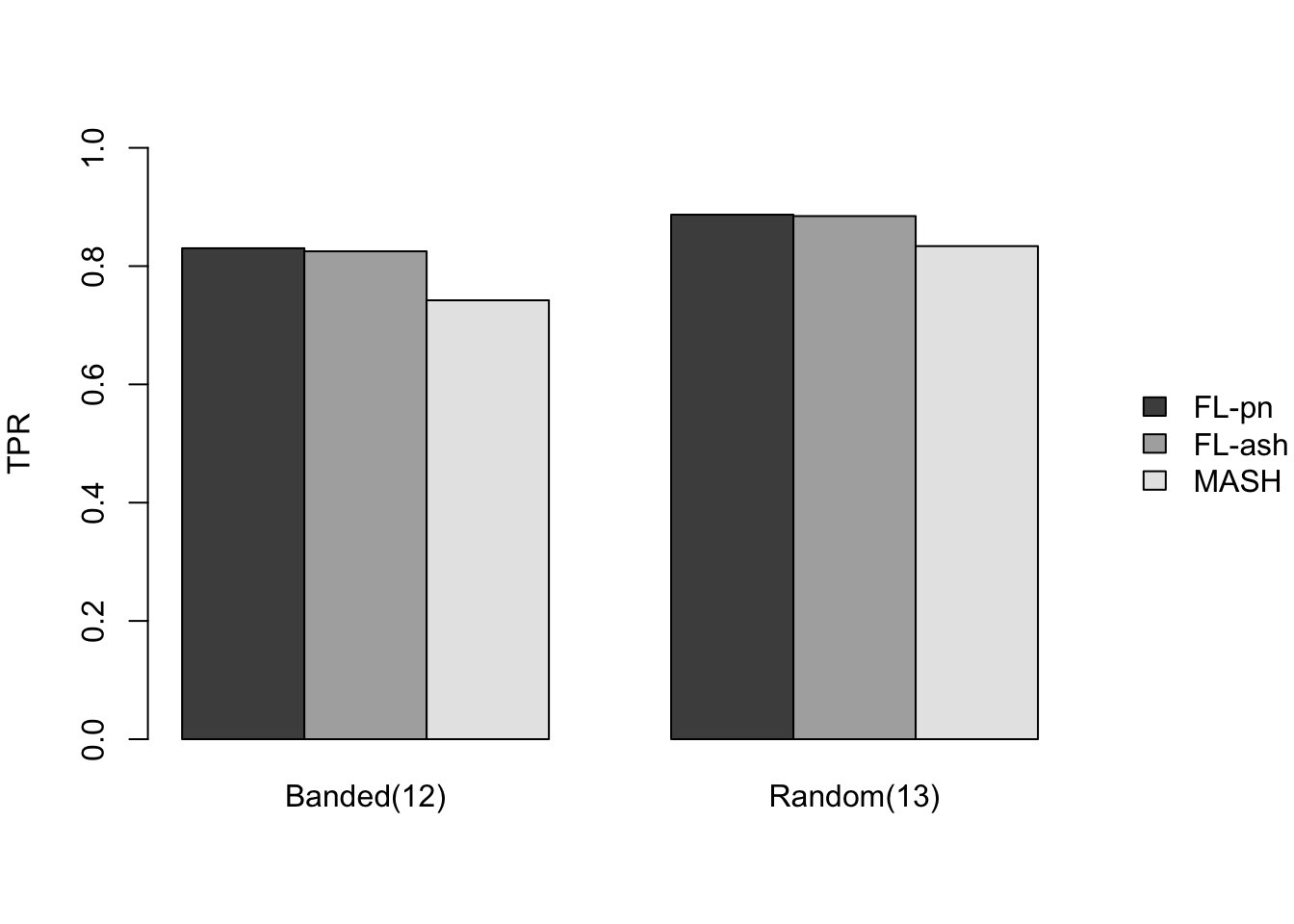

Session information

sessionInfo()

R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] workflowr_1.0.1   Rcpp_0.12.17      digest_0.6.15    
 [4] rprojroot_1.3-2   R.methodsS3_1.7.1 backports_1.1.2  
 [7] git2r_0.21.0      magrittr_1.5      evaluate_0.10.1  
[10] stringi_1.1.6     whisker_0.3-2     R.oo_1.21.0      
[13] R.utils_2.6.0     rmarkdown_1.8     tools_3.4.3      
[16] stringr_1.3.0     yaml_2.1.17       compiler_3.4.3   
[19] htmltools_0.3.6   knitr_1.20