SVM (Support Vector Machines)

$ \newcommand{\R}{\mathbb{R}} $

Give a data set $\{(x_i, y_i)\}_{i=1}^m$:

  • $x_i \in X \subset \R^n$ (input/feature vectors)
  • $y_i \in \{-1,+1\}$ (class labels)

In SVM, we want to find a separating hyperplane in forms of $f_{w,b}(x) = \langle x, w \rangle + b = 0$:

  • $f_{w,b} (x_i) > 0$ if $y_i = +1$
  • $f_{w,b} (x_i) < 0$ if $y_i = -1$
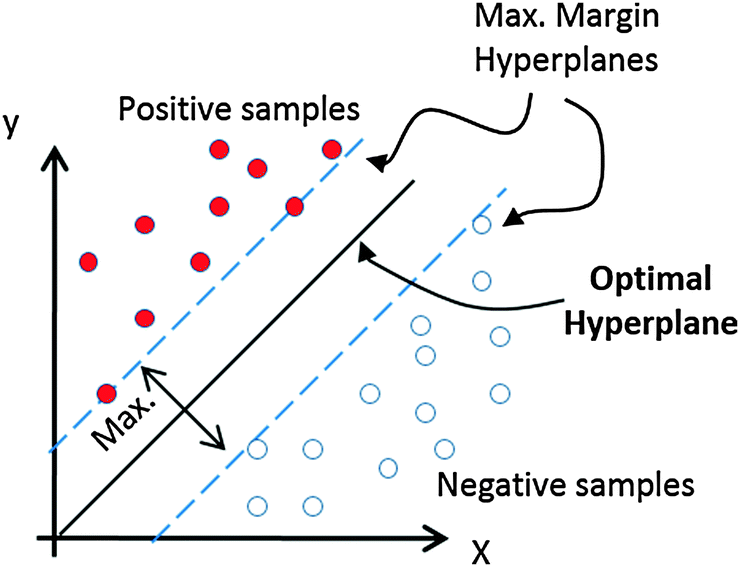svm (from Fernandez-Lozano et al., Royal Soc. Chem. 2014)

  • Separating hyperplane: $f_{w,b}(x) = 0$
  • Supporting hyperplanes: $f_{w,b}(x) = \pm 1$

Q. Derive that the margin (the gap between two supporting hyperplanes) is expressed as $\frac{2}{\|w\|_2}$

Max. Margin Hyperplane

We want to find a hyperplane defined with $(w,b)$ such that the margin $\frac{2}{\|w\|}$ will be maximize: roughly speaking, it will be a safer (or more robust) choice to classify unseen data points.

Hinge Loss Function

Due to the construction of the sep. hyperplane, a point $(x_i,y_i)$ is correctly classified if

$$ y_i \cdot f_{w,b}(x_i) \ge 0. $$

We want to find parameters $(w,b)$ satisfying this condition for all $i=1,\dots,m$.

In practice, we try to find a more robust classifier:

$$ y_i \cdot f_{w,b}(x_i) \ge 1, \;\; i=1,\dots,m. $$

That is,

$$ 1 - y_i f_{w,b}(x_i) \begin{cases} \le 0 & \text{if correctly classified} \\ > 0 & \text{if misclassified} \end{cases} $$

So we can define an classification error function, $$ \ell(x_i,y_i;w,b) = (1- y_i f_{w,b}(x_i))_+ = \max\{0, 1-y_i f_{w,b}(x_i)\} . $$

This is called the hinge loss function.

svm (from Wikipedia)

SVM

Minimizing the hinge loss of all data points and maximizing the margin can be described as:

\begin{equation} \begin{aligned} \min_{w,b} \;\; \frac{1}{m} \sum_{i=1}^m \max\{0, 1 - y_i (\langle w, x_i\rangle + b)\} + \frac{\lambda}{2} \|w\|^2 . \end{aligned} \end{equation}

with a balancing parameter $\lambda>0$ to be specified.

  • This formulation can be difficult to handle since the first term is not differentiable.

SVM (QP Formulation)

We can rewrite the above formulation equivalently to

\begin{equation} \begin{aligned} \min_{w \in \R^n,b\in \R,\xi \in \R^m} &\;\; \frac{1}{m} \sum_{i=1}^m \xi_i + \frac{\lambda}{2} \|w\|^2 \\ \text{s.t.} &\;\; \xi_i \ge 1 - y_i(\langle w, x_i\rangle + b), \;\; i=1,\dots, m,\\ &\;\; \xi_i \ge 0, \;\; i=1,\dots,m. \end{aligned} \end{equation}
In [5]:
using MNIST

Xtr,Ytr = traindata()
Xtr = Xtr' ./255;
In [9]:
using PyPlot

figure(figsize = (10,5))
for k=1:3, i = 0:9
    j = find(Ytr .== i)[k]
    img = reshape(Xtr[j,:], 28, 28)
    subplot(5,10,10*(k-1) + i+1)
    imshow(img,cmap="gray")
    axis("off")
end
In [10]:
# Reduce the size of X
using StatsBase

m, n = size(Xtr)
println("m=$m, n=$n")

s = 1000
idx = sample(1:m, s)

X = Xtr[idx,:]
Y = Ytr[idx];

m, n = size(X)
println("Reduced: m=$m, n=$n")

m=60000, n=784
Reduced: m=1000, n=784
In [11]:
# Make it binary classfication problem
# even vs odd

oddind = map(isodd, round(Int64,Y))
Y[oddind] = -1
Y[!oddind] = +1

np = length(find(Y.==1))
nn = s - np;
println("No. classes: +1=$np, -1=$nn")

No. classes: +1=485, -1=515

Q. Solve the above SVM problem with the MNIST data using JuMP.

In [13]:
w_val = getValue(w);
b_val = getValue(b);

println("b_val = $b_val")

pred = [dot(vec(X[i,:]),w_val) + b_val for i=1:m]
correct = Y.*pred
@printf "Prediction accuracy on the training set = %.2f %%" sum(correct .> 0) / m

b_val = -1.063506990789158
Prediction accuracy on the training set = 0.94 %
In [14]:
Xtt, Ytt = testdata()
Xtt = Xtt' ./255;
m = size(Xtt,1)
oddind = map(isodd, round(Int64,Ytt))
Ytt[oddind] = -1
Ytt[!oddind] = +1

pred = [dot(vec(Xtt[i,:]),w_val) + b_val for i=1:m]
correct = Ytt.*pred
@printf "Prediction accuracy on the test set (size=%d) = %.2f %%" m (sum(correct .> 0)/m)

Prediction accuracy on the test set (size=10000) = 0.88 %

SVM and Feature Maps

Consider a more general version of the SVM:

\begin{equation}\label{eq:svmphi} \begin{aligned} \min_{w \in \R^n,b\in \R,\xi \in \R^m} &\;\; \frac{1}{m} \sum_{i=1}^m \xi_i + \frac{\lambda}{2} \|w\|^2 \\ \text{s.t.} &\;\; \xi_i \ge 1 - y_i(\langle w, \phi(x_i)\rangle + b), \;\; i=1,\dots, m,\\ &\;\; \xi_i \ge 0, \;\; i=1,\dots,m. \end{aligned} \end{equation}

where $\phi: X \to \mathcal H$ is a feature map which transforms an input vector into a function.

$\mathcal H$ is a Hilbert space where inner products are well-defined.

The purpose of using $\phi$ is to transform input vectors into another space, so that linear classifier will work:

svm (from Wikipedia)

Often, finding such mapping $\phi$ is not trivial. We'd rather define $\phi$ implicitly, by defining the inner products $ \langle \phi(x_i), \phi(x_j) \rangle$.

SVM Dual Formulation

The primal formulation: $$ \begin{aligned} \min_{w \in \R^n,b\in \R,\xi \in \R^m} &\;\; \frac{1}{\lambda'} \sum_{i=1}^m \xi_i + \frac{1}{2} \|w\|^2 \\ \text{s.t.} &\;\; \xi_i \ge 1 - y_i(\langle w, \phi(x_i)\rangle + b), \;\; i=1,\dots, m,\\ &\;\; \xi_i \ge 0, \;\; i=1,\dots,m. \end{aligned} $$ with $\lambda' = m\lambda$.

The Lagrangian function: with Lagrange multipliers $\alpha \ge 0$ and $\beta \ge 0$, $$ L(w,b,\xi; \alpha,\beta) = \frac{1}{\lambda'} \sum_{i=1}^m \xi_i + \frac{1}{2} \|w\|^2 - \sum_{i=1}^m \alpha_i (\xi_i - 1 + y_i(\langle w, \phi(x_i)\rangle + b) - \sum_{i=1}^m \beta_i \xi_i $$

The dual objective is defined as $$ g(\alpha,\beta) = \inf_{w,b,\xi} L(w,b,\xi; \alpha,\beta) $$

Since $L$ is convex in terms of the primal variables $(w,b,\xi)$, the infimum must satisfy:

(i) Lagrangian optimality $$ \begin{cases} \frac{\partial L}{\partial w} &= w - \sum_i \alpha_i y_i \phi(x_i) = 0 & \Rightarrow w = \sum_i \alpha_i y_i \phi(x_i)\\ \frac{\partial L}{\partial b} &= - \sum_i \alpha_i y_i = 0 & \Rightarrow \sum_i \alpha_i y_i = 0\\ \frac{\partial L}{\partial \xi_i} &= \frac{1}{\lambda'} - \alpha_i -\beta_i = 0 & \Rightarrow \beta_i = \frac{1}{\lambda'} - \alpha_i \ge 0 \end{cases} $$

We only need the Lagrangian optimality for dual formulation, but we can go further to write other parts of the KKT conditions:

(ii) Complementary slackness $$ \begin{cases} \alpha_i (\xi_i - 1 + y_i(\langle w, \phi(x_i)\rangle + b)) = 0 & i=1,\dots,m\\ \beta_i \xi_i = 0 & i=1,\dots,m. \end{cases} $$

(iii) Feasibility $$ \xi \ge 0, \;\; i=1,\dots,m. $$

Using this, the dual problem $$ \begin{aligned} \max_{\alpha \in \R^m,\beta \in \R^m} &\;\; g(\alpha,\beta) \\ & \alpha \ge 0, \beta \ge 0 \end{aligned} $$

can be simplified to \begin{equation} \begin{aligned} \min_{\alpha \in \R^m} &\;\; \frac12 \alpha^T D_Y K D_Y \alpha - e^T \alpha\ & \;\; \sum_i^m y_i \alpha_i = 0 \ & \;\; 0 \le \alpha_i \le \frac{1}{m\lambda} \;\; i=1,\dots,m \end{aligned} \end{equation}

where $D_Y = \text{diag}(Y)$ and $K$ is an $m\times m$ kernel matrix,

$$ K_{ij} = \langle \phi(x_i), \phi(x_j) \rangle, \;\; i, j \in \{1,\dots, m\}. $$

The mapping $\phi$ appears only in terms of inner products!

Kernel Functions

Popular choices:

  • Linear kernel: $K_{ij} = \langle x_i, x_j \rangle$
  • Polynomial kernel of degree $d$: $K_{ij} = (x_i^T x_j + c)^d$
  • Gaussian (or RBF, Radial Basis Function) kernel: $K_{ij} = \exp( - \gamma \|x_i - x_j\|_2^2)$
In [17]:
m,n = size(X)

nw = nprocs()
if(nw<4)
    addprocs(4-nw)
end

start = time()

γ = .001

# parallel Gaussian kernel
K = SharedArray(Float64, (m,m))
@sync @parallel for i=1:m
    for j=i:m
        diff = vec(X[i,:]-X[j,:])
        K[i,j] = exp(-γ*dot(diff,diff))
        K[j,i] = K[i,j]
    end
end

# # Non-parallel Gaussian kernel
# K = eye(m)
# for i=1:m, j=(i+1):m
#     diff = vec(X[i,:]-X[j,:])
#     K[i,j] = exp(-γ*dot(diff,diff))
#     K[j,i] = K[i,j]
# end

# linear kernel
# for i=1:m, j=i:m
#         K[i,j] = dot(vec(X[i,:]), vec(X[j,:]))
#         K[j,i] = K[i,j]
# end

print(time() - start)

6.629415035247803

Q. Solve the SVM dual formulation using JuMP and the kernel matrix.

From the KKT conditions, we had $$ w = \sum_i \alpha_i y_i \phi(x_i)\\ $$

The predictions are to be made for a data point $(x,y)$ by $$ y (\langle \phi(x), w \rangle +b) $$

First, $$ \langle \phi(x), w \rangle = \sum_i \alpha_i y_i \langle \phi(x), \phi(x_i) \rangle $$

From the KKT conditions again, we had $$ \begin{cases} \alpha_i (\xi_i - 1 + y_i(\langle w, \phi(x_i)\rangle + b)) = 0 & i=1,\dots,m \\ \beta_i \xi_i = 0 & i=1,\dots,m. \end{cases} $$ with $$ \beta_i = \frac{1}{\lambda'} - \alpha_i $$

Let call the set $$ \text{SV} = \{i : 0 < \alpha_i < \frac{1}{\lambda'} \}. $$

Then the above condition implies that for all $i \in \text{SV}$, $- 1 + y_i(\langle w, \phi(x_i)\rangle + b) = 0$. $$ \begin{aligned} b &= \frac{1}{|\text{SV}|} \sum_{i \in \text{SV}} (y_i - \langle w, \phi(x_i) \rangle) \\ &= \frac{1}{|\text{SV}|} \sum_{i \in \text{SV}} (y_i - \sum_j \alpha_j y_j \langle \phi(x_i), \phi(x_j) \rangle) \\ &= \frac{1}{|\text{SV}|} \sum_{i \in \text{SV}} (y_i - \sum_j \alpha_j y_j K_{ij}\rangle) \end{aligned} $$

In [24]:
α_val = getValue(α);

ϵ = 1e-12
sv = find((α_val .> ϵ) & (α_val .< 1/(m*λ) -ϵ))

tmp = Y[sv] - K[sv,:]*diagm(Y)*α_val
b_val = sum(tmp) / length(sv)

println("size of SV = $(length(sv)), b = $b_val")

correct = Y.*vec(K*diagm(Y)*α_val + b_val)
# pred = [dot(vec(X[i,:]),w_val) + b_val for i=1:m]
@printf "Prediction accuracy on the training set = %.2f %%" sum(correct .> 0) / m

size of SV = 1000, b = 0.39730212886907446
Prediction accuracy on the training set = 0.81 %
In [ ]:
# Prediction on test set: this takes quite a while.

# m = size(Xtt,1)

# Ktt = SharedArray(Float64, (m, length(sv)))
# @sync @parallel for i=1:m
#     for j=1:length(sv)
#         diff = vec(Xtt[i,:] - X[j,:])
#         Ktt[i,j] = exp(-γ*dot(diff,diff))
#     end
# end

# correct = Ytt.*vec(Ktt*diagm(Y)*α_val + b_val)
# @printf "Prediction accuracy on the test set = %.2f %%" sum(correct .> 0) / m