MATLAB xUnit Test Framework: How to Test Using a Floating-Point Tolerance
MATLAB performs arithmetic operations using the floating-point hardware instructions on your processor. Because almost all floating-point operations are subject to round-off error, arithmetic operations can sometimes produce surprising results. Here's an example.
a = 1 + 0.1 + 0.1 + 0.1
a =
1.3000
a == 1.3
ans =
0
So why doesn't a equal 1.3? Because 0.1, 1.3, and most other decimal fractions do not have exact representations in the binary floating-point number representation your computer uses. The first line above is doing an approximate addition of 1 plus an approximation of 0.1, plus an approximation of 0.1, plus an approximation of 0.1. The second line compares the result of all that with an approximation of 1.3.
If you subtract 1.3 from a, you can see that the computed result for a is extremely close to the floating-point approximation of 1.3, but it is not exactly the same.
a - 1.3
ans = 2.2204e-16
As a general rule, when comparing the results of floating-point calculations for equality, it is necessary to use a tolerance value. Two types of tolerance comparisons are commonly used: absolute tolerance and relative tolerance. An absolute tolerance comparison of a and b looks like:
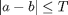
A relative tolerance comparison looks like:
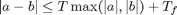
where Tf is called the floor tolerance. It acts as an absolute tolerance when a and b are very close to 0.
For example, suppose that a is 100, b is 101, and T is 0.1. Then a and b would not be considered equal using an absolute tolerance, because 1 > 0.1. However, a and b would be considered equal using a relative tolerance, because they differ by only 1 part in 100.
MATLAB xUnit provides the utility assertion functions called assertElementsAlmostEqual and assertVectorAlmostEqual. These functions make it easy to write tests involving floating-point tolerances.
assertElementsAlmostEqual(A,B) applies the tolerance test independently to every element of A and B. The function uses a relative tolerance test by default, but you make it use an absolute tolerance test, or change the tolerance values used, by passing additional arguments to it.
assertVectorsAlmostEqual(A,B) applies the tolerance test to the vectors A and B in the L2-norm sense. For example, suppose A is [1 1e10], B is [2 1e10], and the tolerance is 1e-8. Then A and B would fail an elementwise relative tolerance comparison, because the relative difference between the first elements is 0.5. However, they would pass a vector relative tolerance comparison, because the relative vector difference between A and B is only about 1 part in 1e10.
The examples_general directory contains a portion of a unit test for the sin function. The output of sin can sometimes be a bit surprising because of floating-point issues. For example:
sin(pi)
ans = 1.2246e-16
That's very close but not exactly equal to 0. Here's how the sin unit test uses assertElementsAlmostEqual to write the sin(pi) test with a minimum of fuss.
cd examples_general type testSin
function testSin assertElementsAlmostEqual(sin(pi), 0);
Run the test using runxunit.
runxunit testSin
Test suite: testSin Test suite location: C:\Users\psexton\Documents\GitHub\matlab-xunit-doctest\doc\examples_general\testSin.m 20-Feb-2014 19:59:11 Starting test run with 1 test case. . PASSED in 0.014 seconds.