Examples of (discrete) orthogonal basis: Fourier basis
\[\left\lbrace \frac{1}{\sqrt{\pi}} \sin(nx), \frac{1}{\sqrt{\pi}} \cos(nx), \frac{1}{\sqrt{2\pi}}\middle| \forall n \in \mathbb{N}, \forall x\in [-\pi, \pi]\right\rbrace\]

Nicolás Guarín-Zapata
email: nguarinz@eafit.edu.co
github: nicoguaro
April 16, 2017
Inner products let us extend geometrical notions such as length of a vector or angle between vectors for vector spaces that are more abstract than \(\mathbb{R}^2\) or \(\mathbb{R}^3\). It also let us define the orthogonality between vectors. Inner product spaces generalize the notion of Euclidean spaces to any dimension.
An orthogonal basis for an inner product spaces \(V\), is a basis for \(V\) whose vectors are mutually orthogonal. The angle between vectors (\(\theta\)) is defined using the inner product as
\[\theta = \arccos\left(\frac{\langle x, y\rangle}{\Vert x\Vert\, \Vert y\Vert}\right) \, .\]
If they have magnitude 1, then the base is called orthonormal.
\[\left\lbrace \frac{1}{\sqrt{\pi}} \sin(nx), \frac{1}{\sqrt{\pi}} \cos(nx), \frac{1}{\sqrt{2\pi}}\middle| \forall n \in \mathbb{N}, \forall x\in [-\pi, \pi]\right\rbrace\]

\[\left\lbrace (-1)^n e^{x^2}\frac{d^n}{dx^n} e^{-x^2},\middle| \forall n \in \mathbb{N}, \forall x\in [-\infty, \infty]\right\rbrace\]
with orthogonality as
\[\int\limits_{-\infty}^{\infty} H_m(x) H_n(x) e^{-x^2} dx = \sqrt{\pi}s^n n! \delta_{mn}\]
They are defined by the recursion relation
\[T_0(x) = 1,\, T_1(x) = x,\, T_{n+1} = 2x T_n(x) - T_{n-1}(x),\quad \forall x\in [-1,1]\]
with orthogonality as
\[\int\limits_{-1}^{1} T_m(x) T_n(x) \frac{dx}{\sqrt{1 - x^2}} = \begin{cases} 0 &n\neq m \\ \pi &n=m=0\\ \pi/2 &n=m\neq 0\end{cases}\]
From Wikipedia
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
Fourier analysis has many scientific applications:
Signal Processing. It may be the best application of Fourier analysis.
Approximation Theory. We use Fourier series to write a function as a trigonometric polynomial.
Control Theory. The Fourier series of functions in the differential equation often gives some prediction about the behavior of the solution of differential equation. They are useful to find out the dynamics of the solution.
Partial Differential equation. We use it to solve higher order partial differential equations by the method of separation of variables.
Some examples include:
JPG image compression.
MP3 sound compression.
Image processing to remove periodic or anisotropic artifacts such as jaggies from interlaced video.
X-ray crystallography to reconstruct a crystal structure from its diffraction pattern.
A Fourier series allow us to represent a (periodic) function as the sum of sine and cosine functions.
For a function \(f(x)\) defined over \([x_0, x_0 + P]\), that is continuous or piecewise continuous, we write
\[ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty}\left[ a_n \cos\left(\frac{2\pi nx}{P}\right) + b_n \sin\left(\frac{2\pi nx}{P}\right) \right]\]
where the coefficients are obtained computing the inner product with the elements of the base, i.e.
\[a_0 = \frac{2}{P}\int_{x_0}^{x_0+P} f(x)\, dx\\ a_n = \frac{2}{P}\int_{x_0}^{x_0+P} \cos\left(\frac{2\pi nx}{P}\right) f(x)\, dx\\ b_n = \frac{2}{P}\int_{x_0}^{x_0+P} \sin\left(\frac{2\pi nx}{P}\right) f(x)\, dx\]
A set \(\lbrace \phi(k, x)\rbrace\) with \(x\) and \(k\) defined over \((a, b)\), and \((c, d)\) are orthogonal with weight \(w(x)\) (\(w(x)\) real) if:
\[\int\limits_{a}^{b} w(x) \phi^* (k, x) \phi(k', x)\, dx = \delta(k - k')\, , \quad x\in(a, b),\, k\in(c, d)\, .\]
If the basis is complete we can write a function \(f(x)\) as
\[f(x) = \int\limits_{a}^{b} C(k) \phi(k', x)\, dx\, ,\]
with
\[C(x) = \int\limits_{a}^{b} C(x') w(x')\phi(k, x')\, dx'\, .\]
\(C(k)\) is known as the tranform of \(f(x)\).
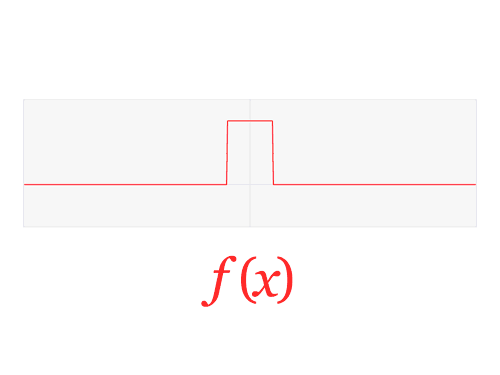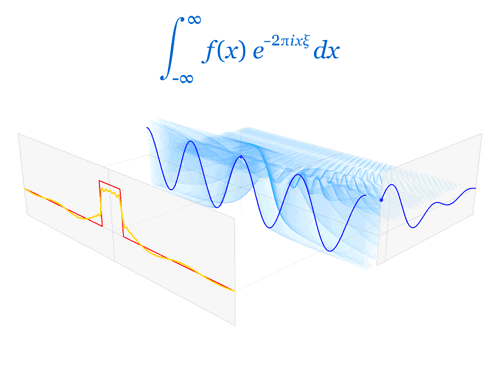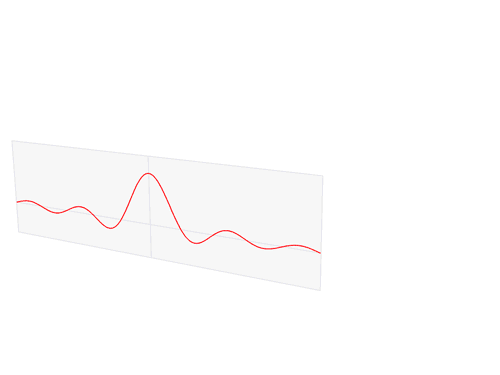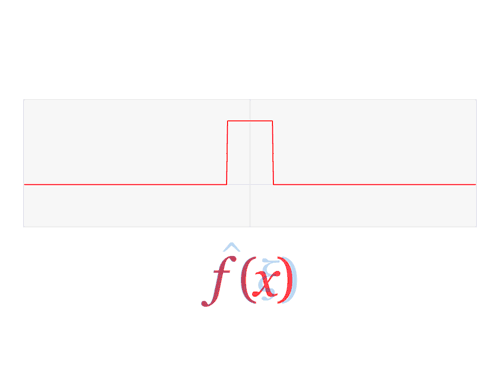
When we choose the basis functions \(\lbrace \frac{e^{ikx}}{\sqrt{2\pi}}\rbrace\), we can write a function \(f(x)\), that is piecewise continuous and does not grow faster than exponentially, as
\[f(x) = \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty}F(k) e^{ikx}\, dx\, .\]
Using the orthonormality condition
\[\int\limits_{-\infty}^{\infty} e^{i(k -k') x}dx = 2\pi \delta(k - k')\, ,\]
we can write
\[F(k) = \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty}f(x) e^{-ikx}\, dx\, .\]
We can compute the Fourier transform of a Gaussian function
\[f(x) = e^{-\alpha^2 x^2},\quad x\in(-\infty, \infty)\]
Using the definition and proceeding with the integral we get
\begin{align} F(k) &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty} e^{-\alpha^2(x^2 + ikx/\alpha^2)} dx\\ &= \frac{e^{-k/4\alpha^2}}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty} e^{-\alpha^2(x + ikx/2\alpha^2)^2} dx\\ &= \frac{1}{\sqrt{\pi} \alpha} e^{-k^2/4\alpha^2} \, . \end{align}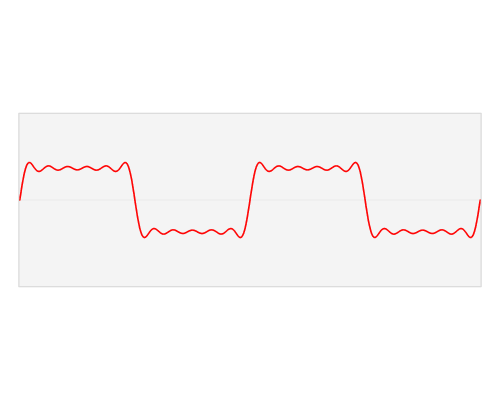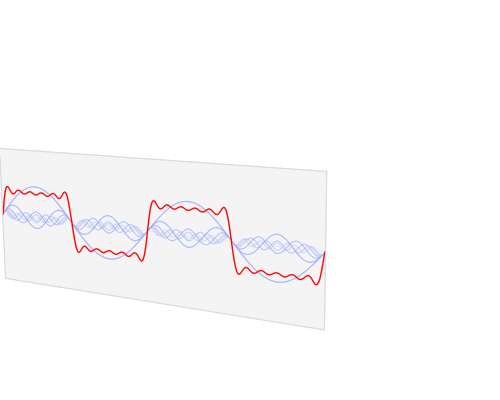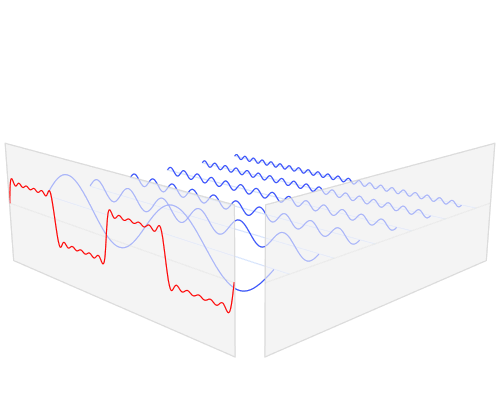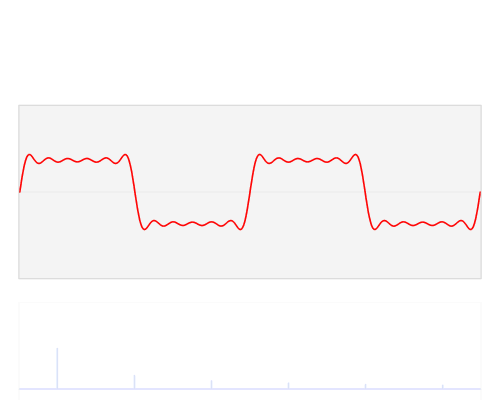
Alonso Sepúlveda Soto. Física matemática. Ciencia y Tecnología. Universidad de Antioquia, 2009.
Pierre Guilleminot's. Fourier series visualisation with d3.js., 2016.
Wikipedia contributors. "Fourier analysis." Wikipedia, The Free Encyclopedia
Wikipedia contributors. "Hermite polynomials." Wikipedia, The Free Encyclopedia.
Wikipedia contributors. "Fourier series." Wikipedia, The Free Encyclopedia.
Wikipedia contributors. "Chebyshev polynomials." Wikipedia, The Free Encyclopedia.
Wikipedia contributors. "Fourier transform." Wikipedia, The Free Encyclopedia.