Differential expression analysis for studies with 2 groups
John Blischak
2018-01-26
Last updated: 2018-05-17
Code version: ed562e1
Analyze proteomics data set that compares 2 groups.
library("Biobase")
library("ggplot2")
library("limma")
eset <- readRDS("../data/ch02.rds")Studies with 2 groups (Video)
Describe the scientific question, the experimental design, and the data collected for the 2-group study. Introduce the ExpressionSet object that contains the data. Review the quality control procedures covered in past Bioconductor courses (specifically comparing distributions and PCA).
Plot a differentially expressed gene
Create boxplots of a few pre-selected genes (one clearly DE, one clearly not, and one in between). Use pData to select the phenotype variables and exprs to access the expression data.
# Plot protein #3
boxplot(exprs(eset)[3, ] ~ pData(eset)$spikein, main = fData(eset)$protein[3])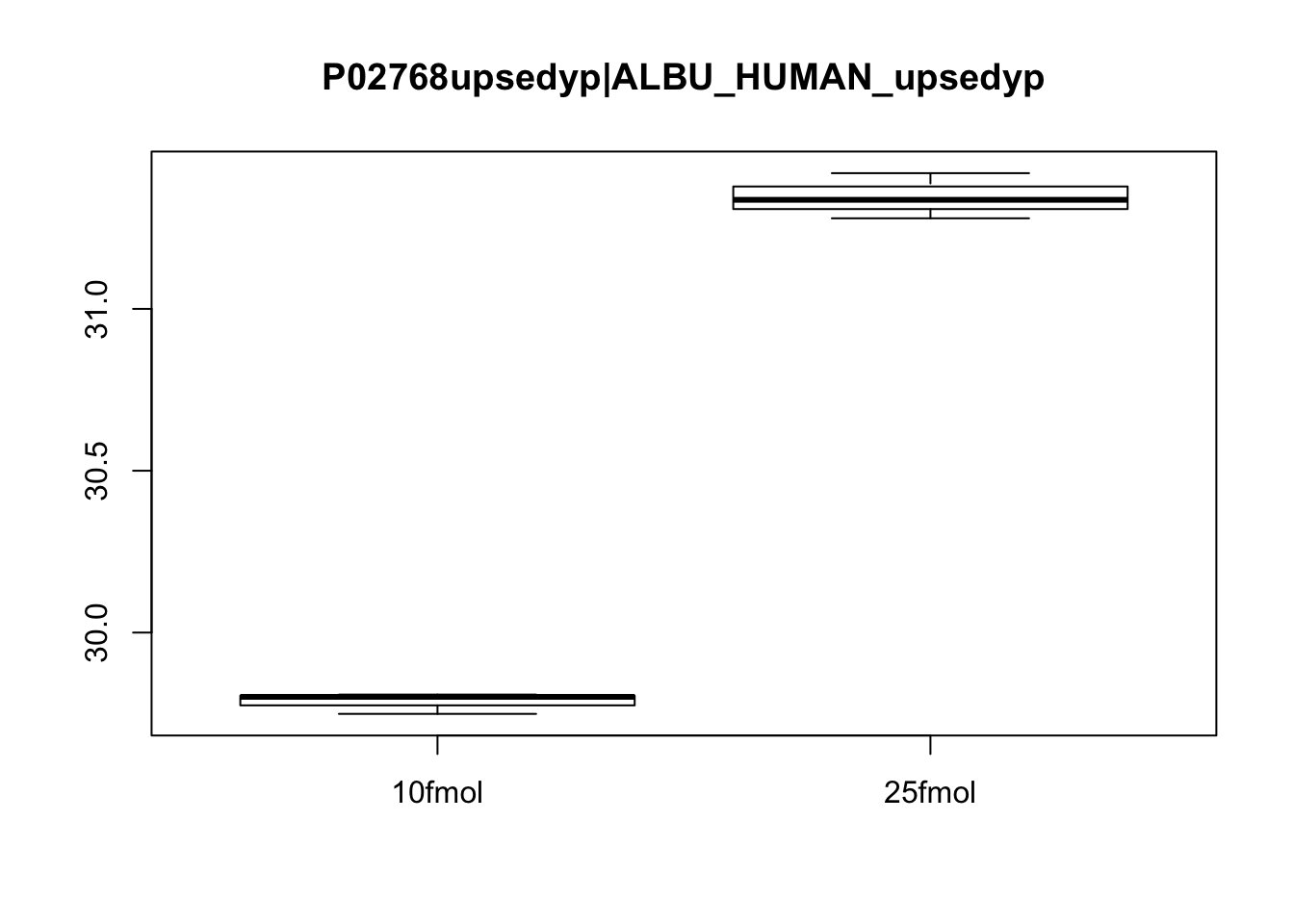
# Plot protein #5
boxplot(exprs(eset)[5, ] ~ pData(eset)$spikein, main = fData(eset)$protein[5])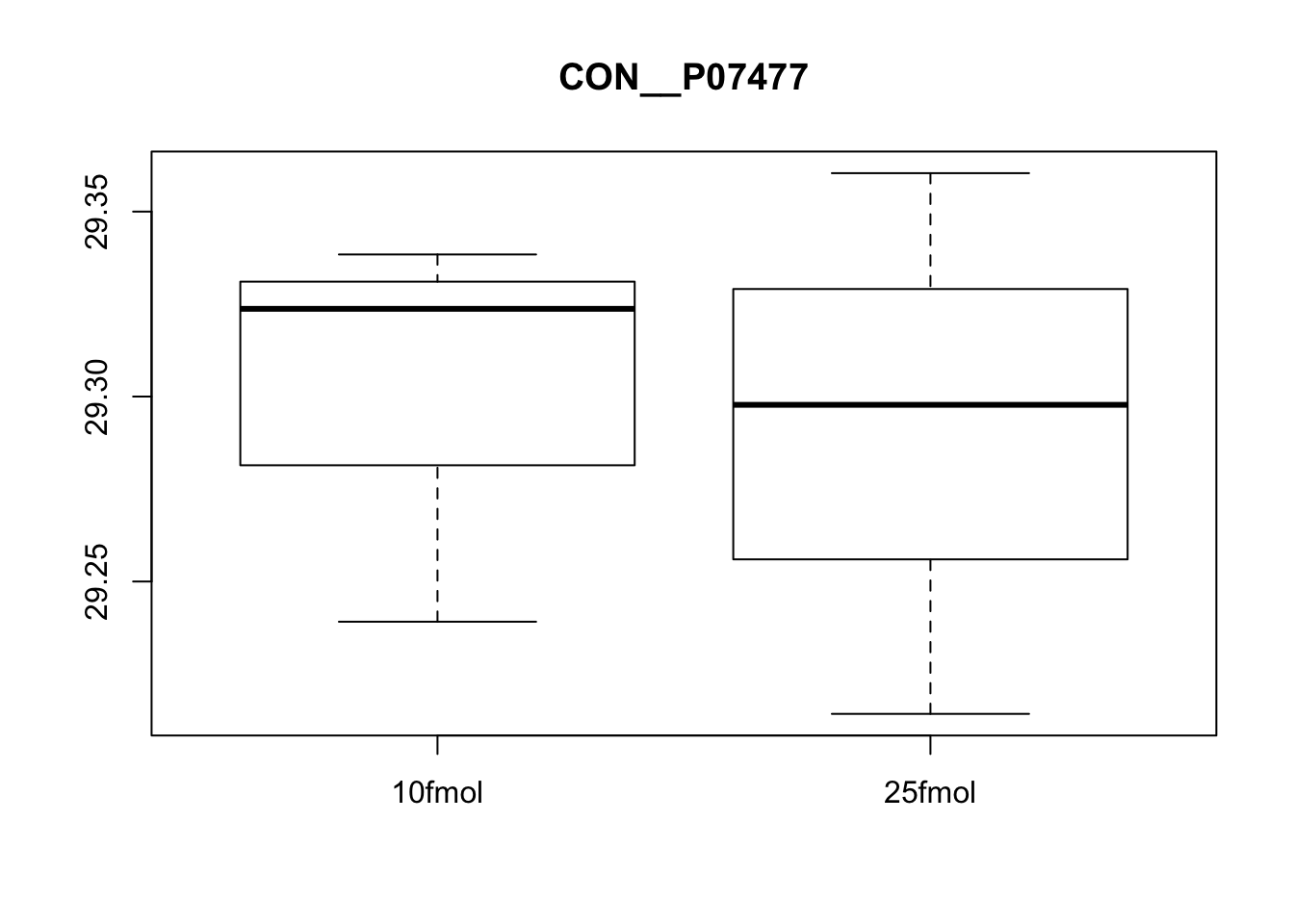
# Plot protein #463
boxplot(exprs(eset)[463, ] ~ pData(eset)$spikein, main = fData(eset)$protein[463])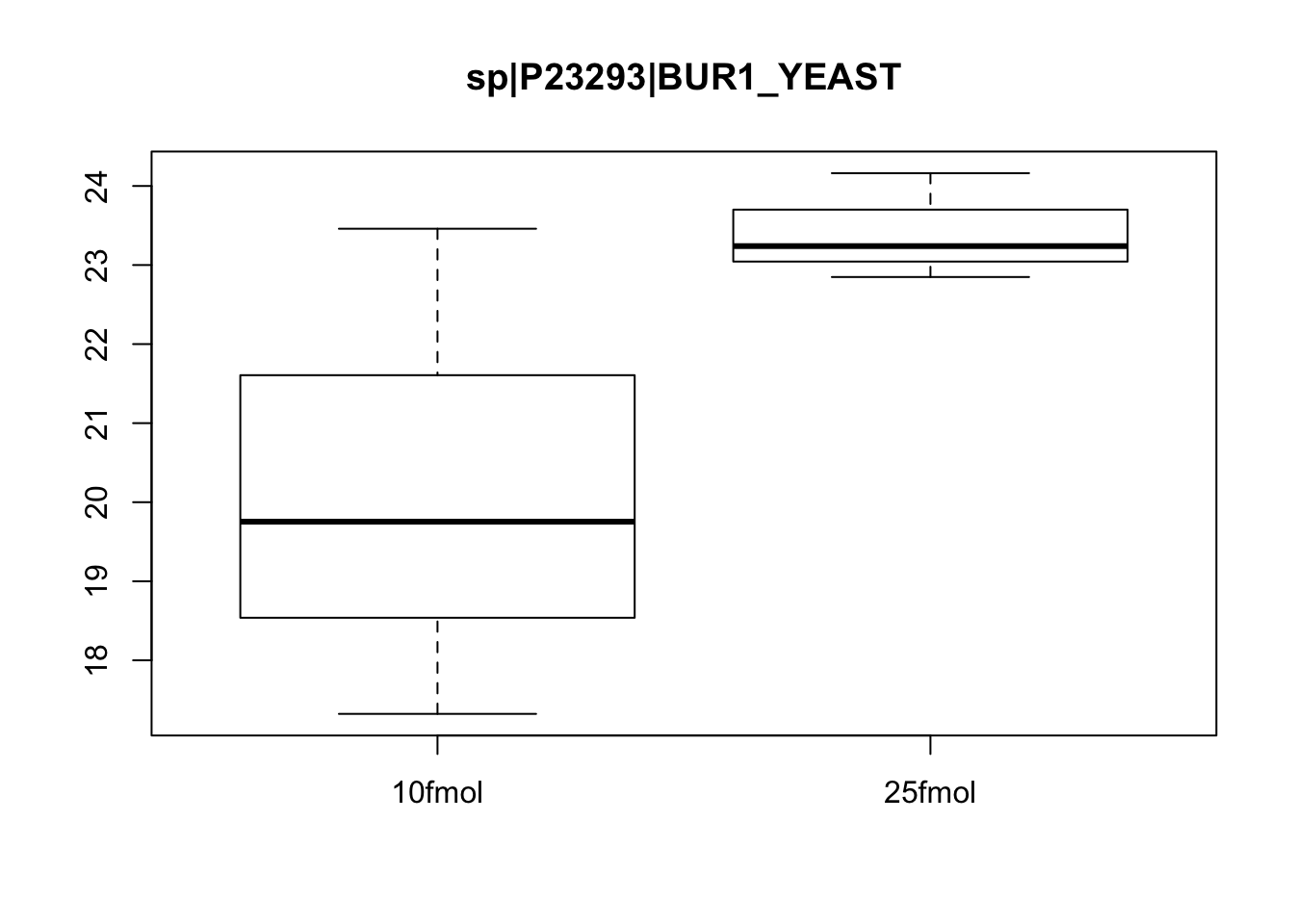
Create a density plot to compare distribution across samples
Use limma::plotDensities to confirm that the distribution of gene expression levels is consistent across the samples.
plotDensities(eset, group = pData(eset)$spikein, legend = "topright")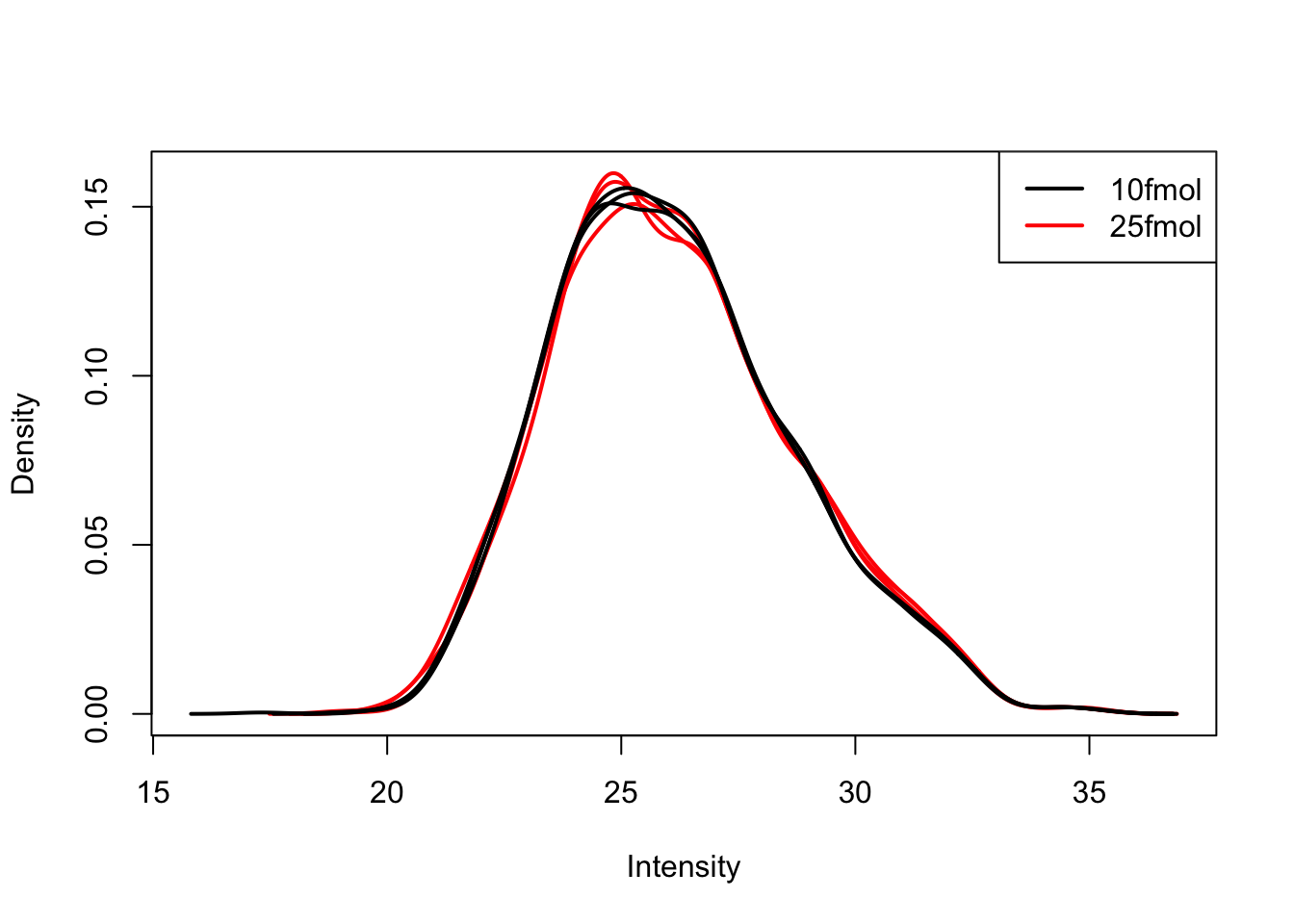
Create a PCA plot to assess source of variation
Use prcomp to compute principal components and then plot PC1 vs. PC2 to confirm that the biological effect is the main source of variation.
# Perform PCA
pca <- prcomp(t(exprs(eset)), scale. = TRUE)
# Combine the PCs with the phenotype data
d <- data.frame(pData(eset), pca$x)
# Plot PC1 vs. PC2 colored by spikein
ggplot(d, aes(x = PC1, y = PC2, color = spikein)) +
geom_point()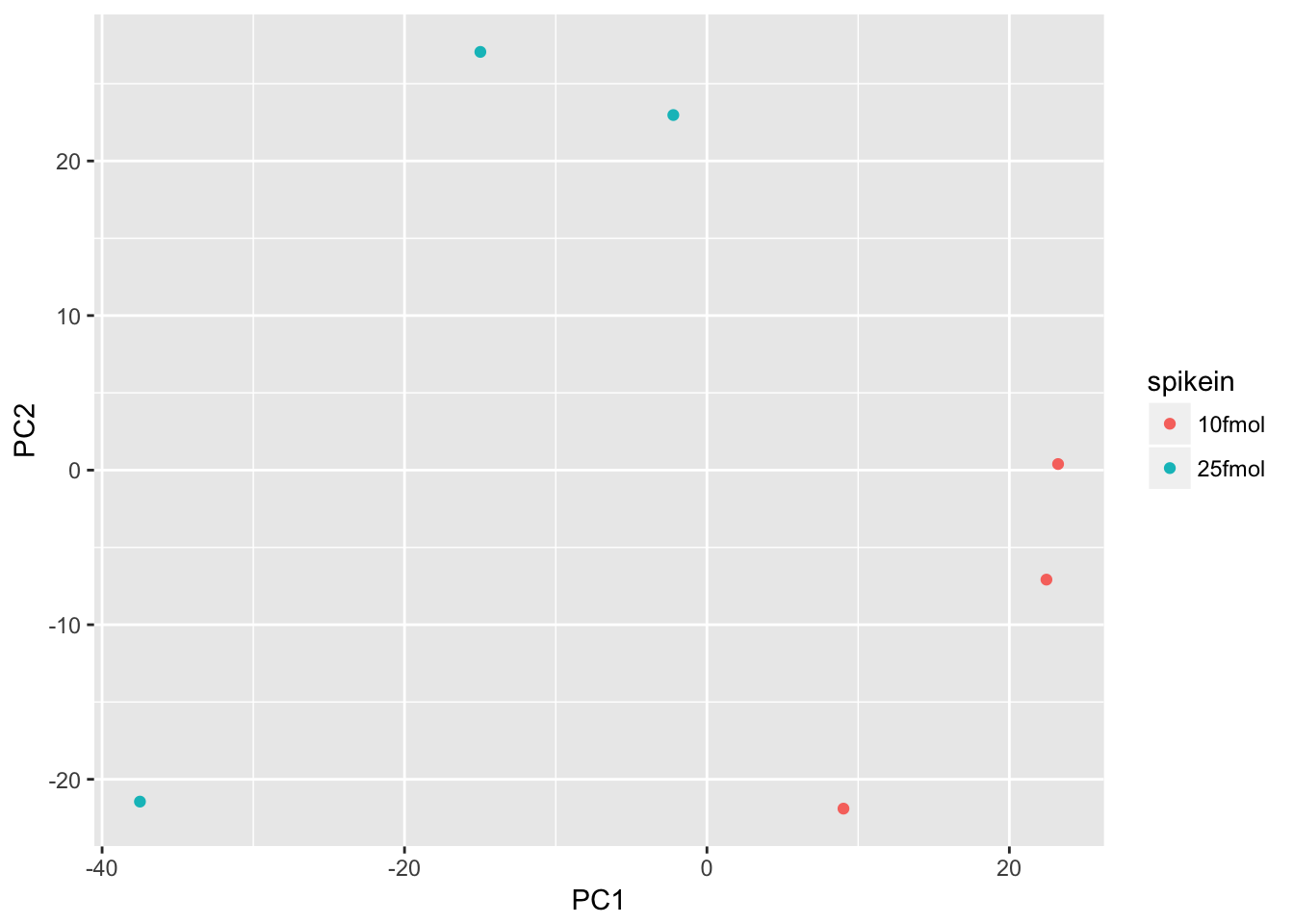
limma for differential expression (Video)
Describe the standard limma workflow. Describe the 2 main techniques for constructing the linear model: treatment-contrasts versus group-means parametrizations.
Create design matrix for treatment-contrasts parametrization
Use model.matrix to create a linear model with an intercept and one binary variable. Use colSums to reason about how this relates to the samples (e.g. the intercept represents the mean across samples because it is 1 for every sample).
# Create a design matrix with an intercept and a coefficient for spikein
design <- model.matrix(~spikein, data = pData(eset))
design (Intercept) spikein25fmol
spikein.25fmol.r1 1 1
spikein.25fmol.r2 1 1
spikein.25fmol.r3 1 1
spikein.10fmol.r1 1 0
spikein.10fmol.r2 1 0
spikein.10fmol.r3 1 0
attr(,"assign")
[1] 0 1
attr(,"contrasts")
attr(,"contrasts")$spikein
[1] "contr.treatment"# How many samples are modeled by each coefficient in the design matrix?
colSums(design) (Intercept) spikein25fmol
6 3 Fit and test model for treatment-contrasts parametrization
Use limma::lmFit, limma::eBayes, and limma::decideTests to fit and test the model.
# Fit the model coefficients
fit <- lmFit(eset, design)
head(fit$coefficients) (Intercept) spikein25fmol
1 21.19598 0.134121520
2 32.48541 -0.004568881
3 29.78624 1.559134985
4 25.25850 0.706384928
5 29.30042 -0.009631149
6 22.12669 1.089862564# Compute moderated t-statistics
fit <- eBayes(fit)
# Count the number of differentially expressed genes
results <- decideTests(fit[, "spikein25fmol"])
summary(results) spikein25fmol
-1 9
0 1879
1 56Create design matrix and contrasts matrix for group-means parametrization
Use model.matrix to create a linear model with two binary variables (and no intercept). Use colSums to reason about how this relates to the samples (e.g. each of the terms represents the mean for its group of samples because it is the only term that is 1 for those samples). Use limma::makeContrasts to create a contrasts matrix based on this new linear model.
# Create a design matrix with no intercept and one coefficient for each spikein
design <- model.matrix(~0 + spikein, data = pData(eset))
design spikein10fmol spikein25fmol
spikein.25fmol.r1 0 1
spikein.25fmol.r2 0 1
spikein.25fmol.r3 0 1
spikein.10fmol.r1 1 0
spikein.10fmol.r2 1 0
spikein.10fmol.r3 1 0
attr(,"assign")
[1] 1 1
attr(,"contrasts")
attr(,"contrasts")$spikein
[1] "contr.treatment"# How many samples are modeled by each coefficient in the design matrix?
colSums(design)spikein10fmol spikein25fmol
3 3 # Create a contrast that comapres the 25 fmol versus the 10 fmol samples
cont_mat <- makeContrasts(spike_effect = spikein25fmol - spikein10fmol, levels = design)
cont_mat Contrasts
Levels spike_effect
spikein10fmol -1
spikein25fmol 1Fit and test model for group-means parametrization
Use limma::lmFit, limma::contrasts.fit, limma::eBayes, and limma::decideTests to fit and test the model. Confirm that the results are identical to the more traditional linear modelling approach used previously.
# Fit the model coefficients
fit <- lmFit(eset, design)
head(fit$coefficients) spikein10fmol spikein25fmol
1 21.19598 21.33010
2 32.48541 32.48084
3 29.78624 31.34538
4 25.25850 25.96488
5 29.30042 29.29079
6 22.12669 23.21656# Fit the contrasts
fit2 <- contrasts.fit(fit, contrasts = cont_mat)
head(fit2$coefficients) Contrasts
spike_effect
1 0.134121520
2 -0.004568881
3 1.559134985
4 0.706384928
5 -0.009631149
6 1.089862564# Compute moderated t-statistics
fit2 <- eBayes(fit2)
# Count the number of differentially expressed genes
results <- decideTests(fit2)
summary(results) spike_effect
-1 9
0 1879
1 56Visualizing the results (Video)
Describe how to access the results with topTable and describe the columns. Demonstrate some common visualizations.
Create a histogram of p-values
Use geom_histogram to plot P.Value column from limma::topTable. Ask question to confirm they understand that the p-value distribution corresponds to the number of differentially expressed genes identified.
# View the top 10 diffentially expressed proteins
topTable(fit2) protein logFC AveExpr t
32 P06396upsedyp|GELS_HUMAN_upsedyp 1.861560 29.47426 27.52384
33 P06732upsedyp|KCRM_HUMAN_upsedyp 1.534331 29.14056 27.01624
28 P02787upsedyp|TRFE_HUMAN_upsedyp 1.596815 30.67280 26.77212
52 P68871upsedyp|HBB_HUMAN_upsedyp 1.485236 28.84136 25.03177
29 P02788upsedyp|TRFL_HUMAN_upsedyp 1.502014 31.02911 24.79491
38 P10599upsedyp|THIO_HUMAN_upsedyp 1.473717 28.31979 24.30523
14 P00709upsedyp|LALBA_HUMAN_upsedyp 1.468805 28.42487 24.18606
41 P15559upsedyp|NQO1_HUMAN_upsedyp 1.541838 27.32908 23.91733
10 O00762upsedyp|UBE2C_HUMAN_upsedyp 1.554906 28.71986 23.25450
3 P02768upsedyp|ALBU_HUMAN_upsedyp 1.559135 30.56581 23.07978
P.Value adj.P.Val B
32 5.176104e-07 0.0002584916 7.311601
33 5.719561e-07 0.0002584916 7.221913
28 6.004868e-07 0.0002584916 7.177897
52 8.609292e-07 0.0002584916 6.846476
29 9.059136e-07 0.0002584916 6.798845
38 1.008053e-06 0.0002584916 6.698332
14 1.034938e-06 0.0002584916 6.673445
41 1.098739e-06 0.0002584916 6.616701
10 1.277099e-06 0.0002584916 6.472931
3 1.329689e-06 0.0002584916 6.434105# Extract the results for all tested proteins
stats <- topTable(fit2, number = nrow(fit2), sort.by = "none")
# Plot a histogram of the p-values
ggplot(stats, aes(x = P.Value)) +
geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.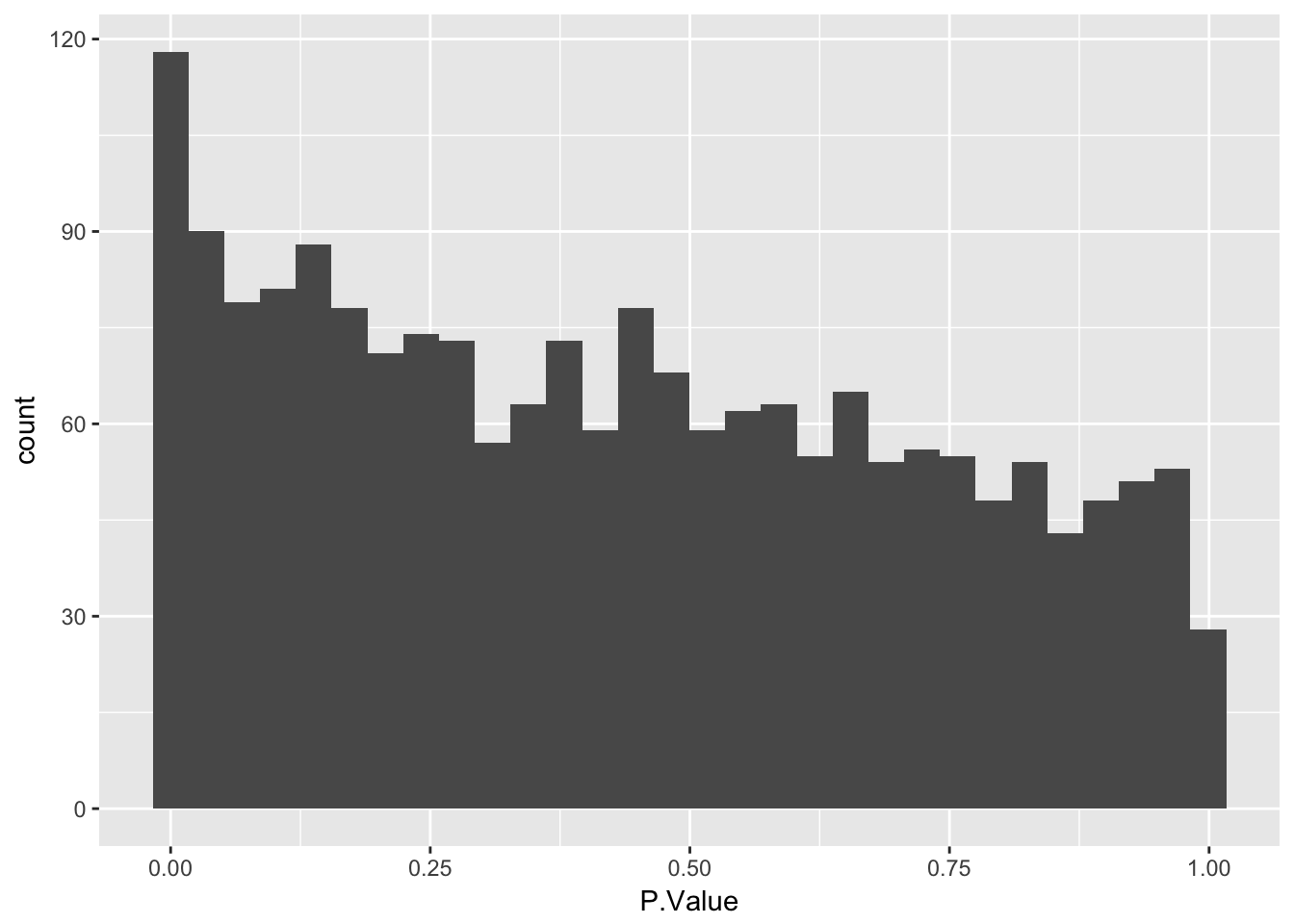
Create a volcano plot
Use geom_point() to plot -log10(P.Value) vs. logFC. Mention limma::volcanoPlot after exercise is completed.
# Create a variable to indicate differential expression
stats$significant <- stats$adj.P.Val < 0.05
# Create a volcano plot
ggplot(stats, aes(x = logFC, y = -log10(P.Value), color = significant)) +
geom_point()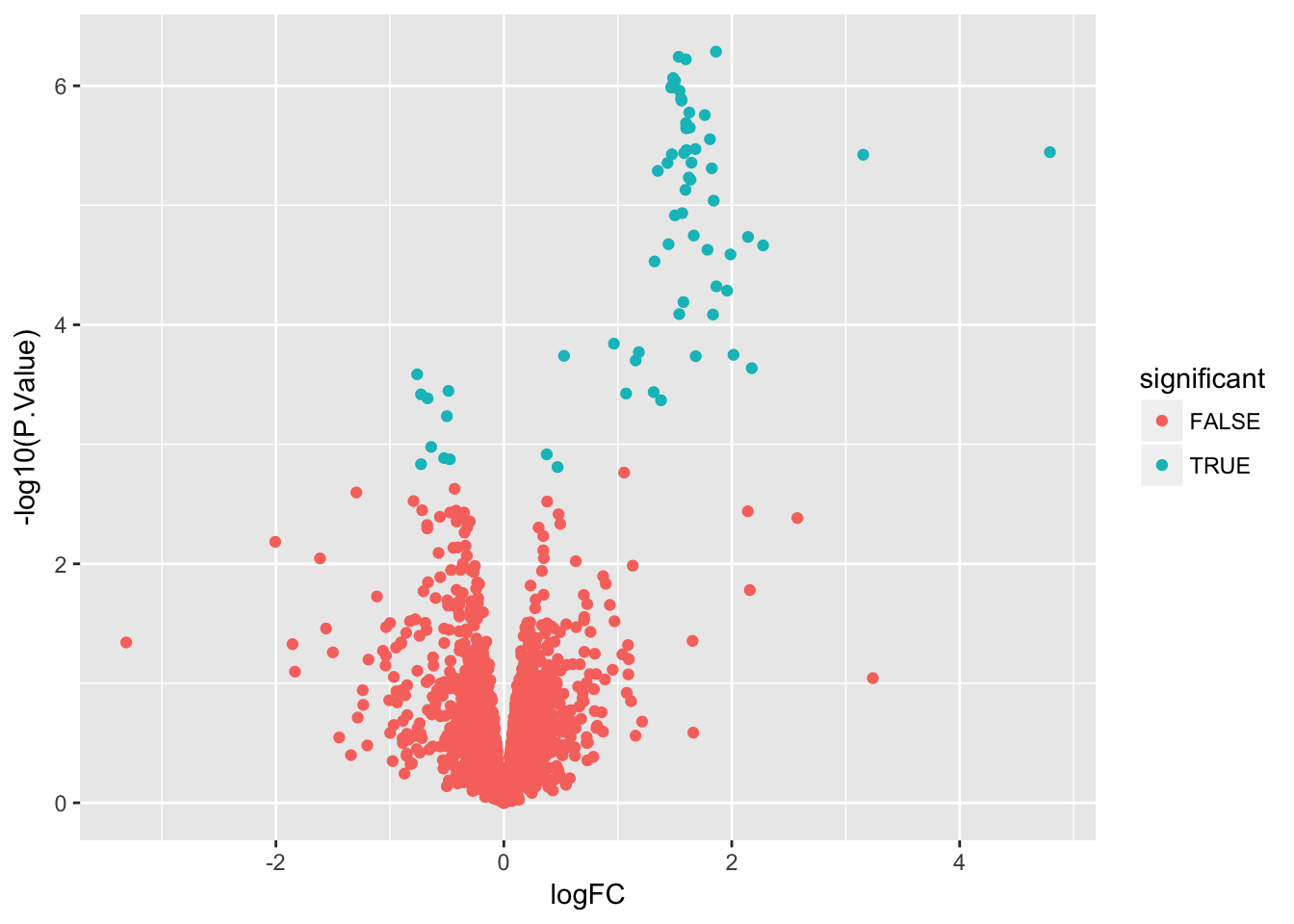
Session information
sessionInfo()R version 3.3.3 (2017-03-06)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: OS X Yosemite 10.10.5
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] tidyr_0.7.2 limma_3.30.13 ggplot2_2.2.1
[4] Biobase_2.34.0 BiocGenerics_0.20.0
loaded via a namespace (and not attached):
[1] Rcpp_0.12.14 knitr_1.20 magrittr_1.5 tidyselect_0.2.3
[5] munsell_0.4.3 colorspace_1.3-2 rlang_0.2.0 stringr_1.3.0
[9] plyr_1.8.4 tools_3.3.3 grid_3.3.3 gtable_0.2.0
[13] git2r_0.21.0 htmltools_0.3.6 yaml_2.1.16 lazyeval_0.2.1
[17] rprojroot_1.3-2 digest_0.6.13 tibble_1.4.2 purrr_0.2.4
[21] glue_1.2.0 evaluate_0.10.1 rmarkdown_1.9 labeling_0.3
[25] stringi_1.1.7 pillar_1.2.2 scales_0.5.0 backports_1.1.2 This R Markdown site was created with workflowr