Posterior Inference with Gaussian Derivative Likelihood: Model and Result
Lei Sun
2017-06-14
Last updated: 2018-05-12
workflowr checks: (Click a bullet for more information)-
✔ R Markdown file: up-to-date
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
-
✔ Environment: empty
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
-
✔ Seed:
set.seed(12345)The command
set.seed(12345)was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible. -
✔ Session information: recorded
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
-
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.✔ Repository version: ddf9062
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can usewflow_publishorwflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.Ignored files: Ignored: .DS_Store Ignored: .Rhistory Ignored: .Rproj.user/ Ignored: analysis/.DS_Store Ignored: analysis/BH_robustness_cache/ Ignored: analysis/FDR_Null_cache/ Ignored: analysis/FDR_null_betahat_cache/ Ignored: analysis/Rmosek_cache/ Ignored: analysis/StepDown_cache/ Ignored: analysis/alternative2_cache/ Ignored: analysis/alternative_cache/ Ignored: analysis/ash_gd_cache/ Ignored: analysis/average_cor_gtex_2_cache/ Ignored: analysis/average_cor_gtex_cache/ Ignored: analysis/brca_cache/ Ignored: analysis/cash_deconv_cache/ Ignored: analysis/cash_fdr_1_cache/ Ignored: analysis/cash_fdr_2_cache/ Ignored: analysis/cash_fdr_3_cache/ Ignored: analysis/cash_fdr_4_cache/ Ignored: analysis/cash_fdr_5_cache/ Ignored: analysis/cash_fdr_6_cache/ Ignored: analysis/cash_plots_cache/ Ignored: analysis/cash_sim_1_cache/ Ignored: analysis/cash_sim_2_cache/ Ignored: analysis/cash_sim_3_cache/ Ignored: analysis/cash_sim_4_cache/ Ignored: analysis/cash_sim_5_cache/ Ignored: analysis/cash_sim_6_cache/ Ignored: analysis/cash_sim_7_cache/ Ignored: analysis/correlated_z_2_cache/ Ignored: analysis/correlated_z_3_cache/ Ignored: analysis/correlated_z_cache/ Ignored: analysis/create_null_cache/ Ignored: analysis/cutoff_null_cache/ Ignored: analysis/design_matrix_2_cache/ Ignored: analysis/design_matrix_cache/ Ignored: analysis/diagnostic_ash_cache/ Ignored: analysis/diagnostic_correlated_z_2_cache/ Ignored: analysis/diagnostic_correlated_z_3_cache/ Ignored: analysis/diagnostic_correlated_z_cache/ Ignored: analysis/diagnostic_plot_2_cache/ Ignored: analysis/diagnostic_plot_cache/ Ignored: analysis/efron_leukemia_cache/ Ignored: analysis/fitting_normal_cache/ Ignored: analysis/gaussian_derivatives_2_cache/ Ignored: analysis/gaussian_derivatives_3_cache/ Ignored: analysis/gaussian_derivatives_4_cache/ Ignored: analysis/gaussian_derivatives_5_cache/ Ignored: analysis/gaussian_derivatives_cache/ Ignored: analysis/gd-ash_cache/ Ignored: analysis/gd_delta_cache/ Ignored: analysis/gd_lik_2_cache/ Ignored: analysis/gd_lik_cache/ Ignored: analysis/gd_w_cache/ Ignored: analysis/knockoff_10_cache/ Ignored: analysis/knockoff_2_cache/ Ignored: analysis/knockoff_3_cache/ Ignored: analysis/knockoff_4_cache/ Ignored: analysis/knockoff_5_cache/ Ignored: analysis/knockoff_6_cache/ Ignored: analysis/knockoff_7_cache/ Ignored: analysis/knockoff_8_cache/ Ignored: analysis/knockoff_9_cache/ Ignored: analysis/knockoff_cache/ Ignored: analysis/knockoff_var_cache/ Ignored: analysis/marginal_z_alternative_cache/ Ignored: analysis/marginal_z_cache/ Ignored: analysis/mosek_reg_2_cache/ Ignored: analysis/mosek_reg_4_cache/ Ignored: analysis/mosek_reg_5_cache/ Ignored: analysis/mosek_reg_6_cache/ Ignored: analysis/mosek_reg_cache/ Ignored: analysis/pihat0_null_cache/ Ignored: analysis/plot_diagnostic_cache/ Ignored: analysis/poster_obayes17_cache/ Ignored: analysis/real_data_simulation_2_cache/ Ignored: analysis/real_data_simulation_3_cache/ Ignored: analysis/real_data_simulation_4_cache/ Ignored: analysis/real_data_simulation_5_cache/ Ignored: analysis/real_data_simulation_cache/ Ignored: analysis/rmosek_primal_dual_2_cache/ Ignored: analysis/rmosek_primal_dual_cache/ Ignored: analysis/seqgendiff_cache/ Ignored: analysis/simulated_correlated_null_2_cache/ Ignored: analysis/simulated_correlated_null_3_cache/ Ignored: analysis/simulated_correlated_null_cache/ Ignored: analysis/simulation_real_se_2_cache/ Ignored: analysis/simulation_real_se_cache/ Ignored: analysis/smemo_2_cache/ Ignored: data/LSI/ Ignored: docs/.DS_Store Ignored: docs/figure/.DS_Store Ignored: output/fig/ Unstaged changes: Deleted: analysis/cash_plots_fdp.Rmd
Expand here to see past versions:
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| rmd | cc0ab83 | Lei Sun | 2018-05-11 | update |
| html | 0f36d99 | LSun | 2017-12-21 | Build site. |
| html | 853a484 | LSun | 2017-11-07 | Build site. |
| html | 4f032ad | LSun | 2017-11-05 | transfer |
| html | 87c16f9 | LSun | 2017-07-03 | Build site. |
| rmd | 8556dea | LSun | 2017-07-03 | wflow_publish(“analysis/gd_lik_2.rmd”) |
| html | a2512ac | LSun | 2017-07-03 | plots |
| rmd | f3fd0b8 | LSun | 2017-07-03 | wflow_commit(“analysis/gd_lik_2.rmd”) |
| html | 921703f | LSun | 2017-06-25 | Build site. |
| rmd | c9aadb6 | LSun | 2017-06-25 | wflow_publish(“analysis/gd_lik_2.rmd”) |
| html | b7c3984 | LSun | 2017-06-24 | Build site. |
| rmd | 1217d1e | LSun | 2017-06-24 | wflow_publish(“analysis/gd_lik_2.rmd”) |
| rmd | e6d5a64 | LSun | 2017-06-17 | GD-Lik |
| html | e6d5a64 | LSun | 2017-06-17 | GD-Lik |
| rmd | 73b4bb7 | LSun | 2017-06-17 | GD-Lik simulations |
| html | 73b4bb7 | LSun | 2017-06-17 | GD-Lik simulations |
GD-ASH Model
Recall the typical GD-ASH model is
\[ \begin{array}{l} \beta_j \sim \sum\pi_k N\left(0, \sigma_k^2\right) \ ;\\ \hat\beta_j = \beta_j + \hat s_j z_j \ ;\\ z_j \sim N\left(0, 1\right), \text{ correlated} \ . \end{array} \] Then we are fitting the empirical distribution of \(z\) with Gaussian derivatives
\[ f(z) = \sum w_l\frac{1}{\sqrt{l!}}\varphi^{(l)}(z) \ . \] Therefore, in essence, we are changing the likelihood of \(\hat\beta_j | \hat s_j, \beta_j\) from correlated \(N\left(\beta_j, \hat s_j^2\right)\) to independent \(\frac{1}{\hat s_j}f\left(\frac{\hat\beta_j - \beta_j}{\hat s_j}\right)\), which using Gaussian derivatives is
\[ \frac{1}{\hat s_j}\sum w_l \frac{1}{\sqrt{l!}} \varphi^{(l)}\left(\frac{\hat\beta_j - \beta_j}{\hat s_j}\right) \ . \] Note that when \(f = \varphi\) it becomes the independent \(N\left(\beta_j, \hat s_j^2\right)\) case.
GD-Lik Model
Therefore, if we use Gaussian derivatives instead of Gaussian as the likelihood, the posterior distribution of \(\beta_j | \hat s_j, \hat\beta_j\) should be
\[ \begin{array}{rcl} f\left(\beta_j \mid \hat s_j, \hat\beta_j\right) &=& \frac{ \displaystyle g\left(\beta_j\right) f\left(\hat\beta_j \mid \hat s_j, \beta_j \right) }{ \displaystyle\int g\left(\beta_j\right) f\left(\hat\beta_j \mid \hat s_j, \beta_j \right) d\beta_j }\\ &=& \frac{ \displaystyle \sum\pi_k\sum w_l \frac{1}{\sigma_k} \varphi\left(\frac{\beta_j - \mu_k}{\sigma_k}\right) \frac{1}{\hat s_j} \frac{1}{\sqrt{l!}} \varphi^{(l)}\left(\frac{\hat\beta_j - \beta_j}{\hat s_j}\right) }{ \displaystyle \sum\pi_k\sum w_l \int \frac{1}{\sigma_k} \varphi\left(\frac{\beta_j - \mu_k}{\sigma_k}\right) \frac{1}{\hat s_j} \frac{1}{\sqrt{l!}} \varphi^{(l)}\left(\frac{\hat\beta_j - \beta_j}{\hat s_j}\right) d\beta_j } \ . \end{array} \] The denominator readily has an analytic form which is
\[ \displaystyle \sum\pi_k \sum w_l \frac{\hat s_j^l}{\left(\sqrt{\sigma_k^2 + \hat s_j^2}\right)^{l+1}} \frac{1}{\sqrt{l!}} \varphi^{(l)}\left(\frac{\hat\beta_j - \mu_k}{\sqrt{\sigma_k^2 + \hat s_j^2}}\right) := \sum \pi_k \sum w_l f_{jkl} \ . \]
Posterior mean
After algebra, the posterior mean is given by
\[ E\left[\beta_j \mid \hat s_j, \hat \beta_j \right] = \int \beta_j f\left(\beta_j \mid \hat s_j, \hat\beta_j\right) d\beta_j = \displaystyle \frac{ \sum \pi_k \sum w_l m_{jkl} }{ \sum \pi_k \sum w_l f_{jkl} } \ , \] where \(f_{jkl}\) is defined as above and \[ m_{jkl} = - \frac{\hat s_j^l \sigma_k^2}{\left(\sqrt{\sigma_k^2 + \hat s_j^2}\right)^{l+2}} \frac{1}{\sqrt{l!}} \varphi^{(l+1)}\left(\frac{\hat\beta_j - \mu_k}{\sqrt{\sigma_k^2 + \hat s_j^2}}\right) + \frac{\hat s_j^l\mu_k}{\left(\sqrt{\sigma_k^2 + \hat s_j^2}\right)^{l+1}} \frac{1}{\sqrt{l!}} \varphi^{(l)}\left(\frac{\hat\beta_j - \mu_k}{\sqrt{\sigma_k^2 + \hat s_j^2}}\right) \ . \]
Local FDR
Assuming \(\mu_k \equiv 0\), the lfdr is given by \[
p\left(\beta_j = 0\mid \hat s_j, \hat \beta_j\right)
=
\frac{
\pi_0
\sum w_l
\frac{1}{\hat s_j}
\frac{1}{\sqrt{l!}}
\varphi^{(l)}\left(\frac{\hat\beta_j}{\hat s_j}\right)
}{
\sum \pi_k
\sum w_l
f_{jkl}
} \ .
\]
Local FSR
Right now the analytic form of lfsr using Gaussian derivatives is unavailable.
Simulation
The correlated \(N\left(0, 1\right)\) \(z\) scores are simulated from the GTEx/Liver data by the null pipeline. In order to get a better sense of the effectiveness of GD-ASH and GD-Lik, we are using data sets more distorted by correlation in the simulation. In particular, we are using an “inflation” batch, defined as the standard error of the correlated \(z\) no less than \(1.2\), and a “deflation” batch, defined as that no greater than \(0.8\). Out of \(1000\) simulated data sets, there are \(109\) inflation ones and \(99\) deflation ones.
In order to create realistic heterskedastic estimated standard error, \(\hat s_j\)’s are also simulated from the same null pipeline. Let \(\sigma^2 = \frac1n \sum\limits_{j = 1}^n \hat s_j^2\) be the average strength of the heteroskedastic noise, and the true effects \(\beta_j\)’s are simulated from \[ 0.6\delta_0 + 0.3N\left(0, \sigma^2\right) + 0.1N\left(0, \left(2\sigma\right)^2\right) \ . \]
Then let \(\hat\beta_j = \beta_j + \hat s_j z_j\). We are using \(\hat\beta_j\), \(\hat s_j\), along with \(\hat z_j = \hat\beta_j / \hat s_j\), \(\hat p_j= 2\left(1 - \Phi\left(\left|\hat z_j\right|\right)\right)\), as the summary statistics fed to GD-ASH and GD-Lik, as well as into BH, qvalue, locfdr, ASH for a comparison.
source("../code/gdash_lik.R")z.mat = readRDS("../output/z_null_liver_777.rds")
se.mat = readRDS("../output/sebetahat_null_liver_777.rds")z.sd = apply(z.mat, 1, sd)
inflation.index = (z.sd >= 1.2)
deflation.index = (z.sd <= 0.8)
z.inflation = z.mat[inflation.index, ]
se.inflation = se.mat[inflation.index, ]
## Number of inflation data sets
nrow(z.inflation)[1] 109z.deflation = z.mat[deflation.index, ]
se.deflation = se.mat[deflation.index, ]
## Number of deflation data sets
nrow(z.deflation)[1] 99Inflation data sets
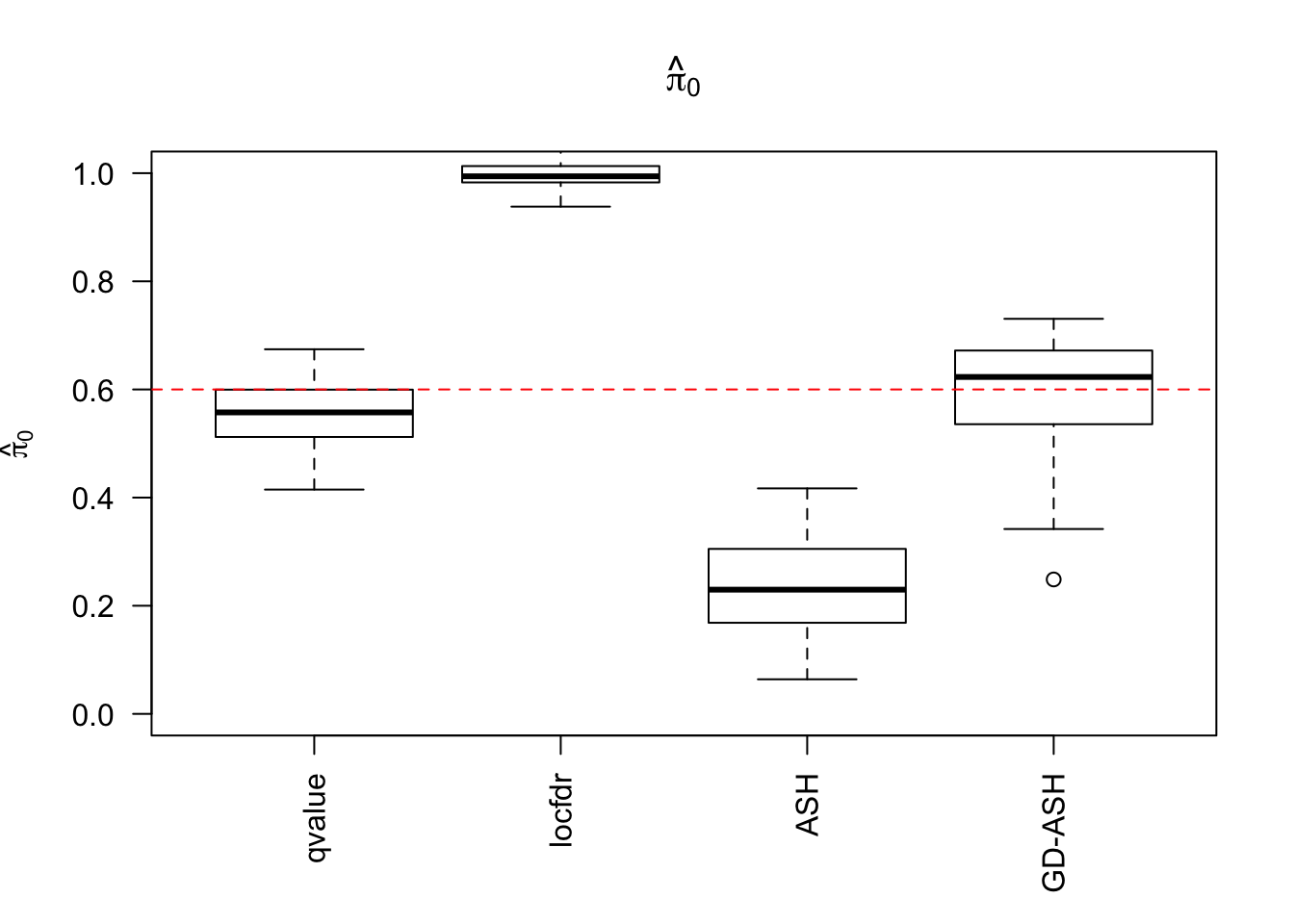
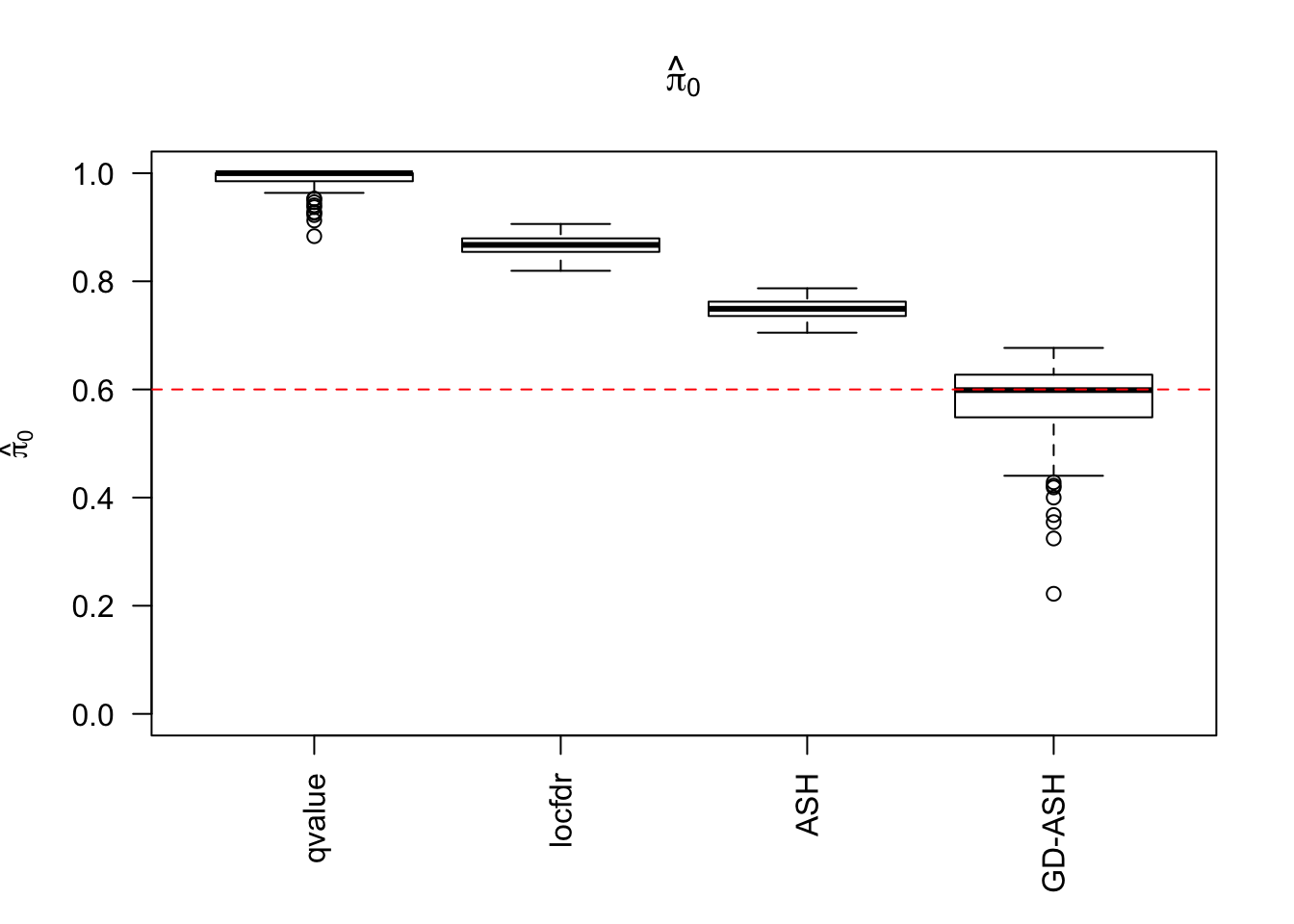
\(\hat \pi_0\)
locfdr overestimates, ASH underestimates, GD-ASH on target, qvalue surprisingly good.
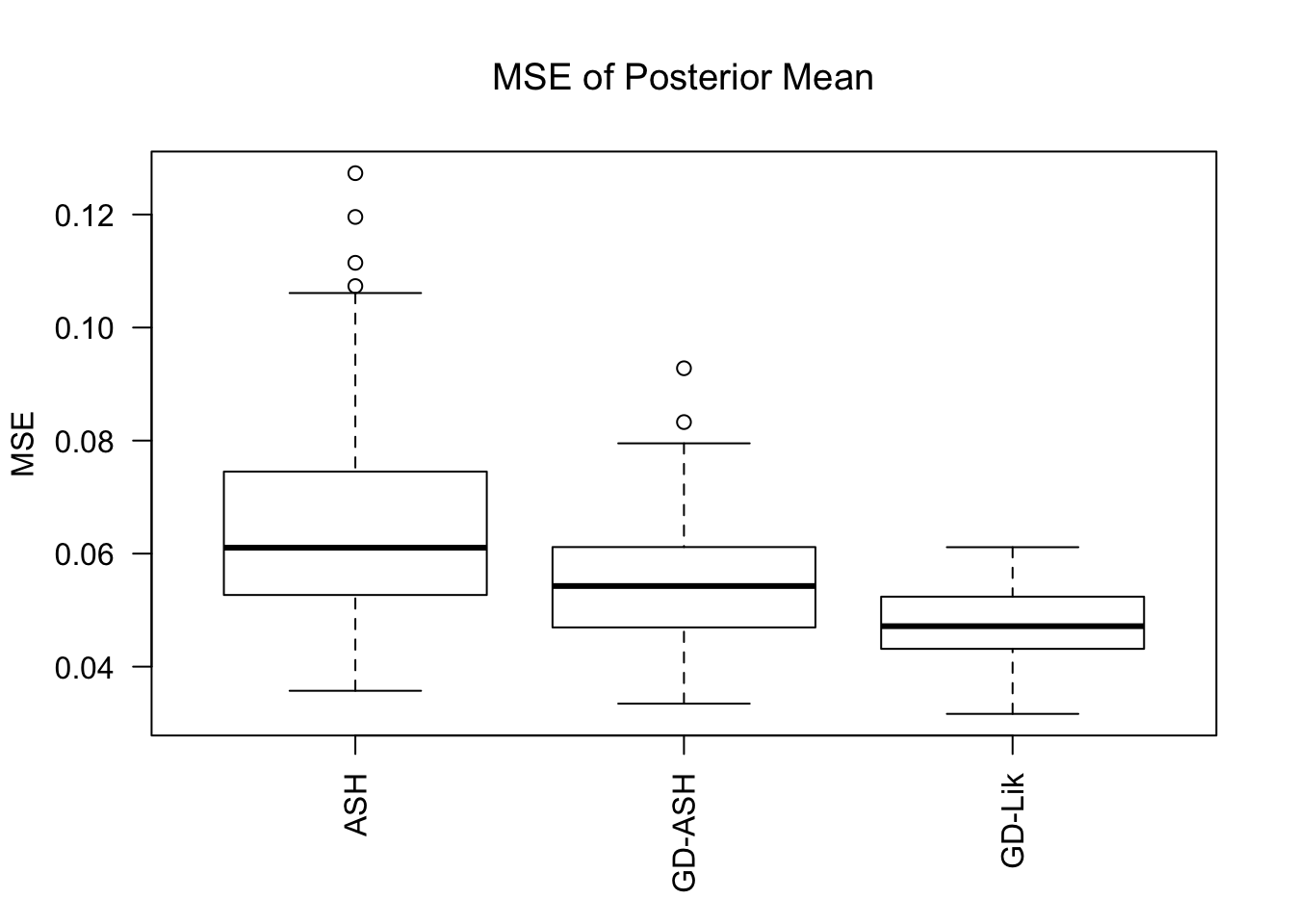
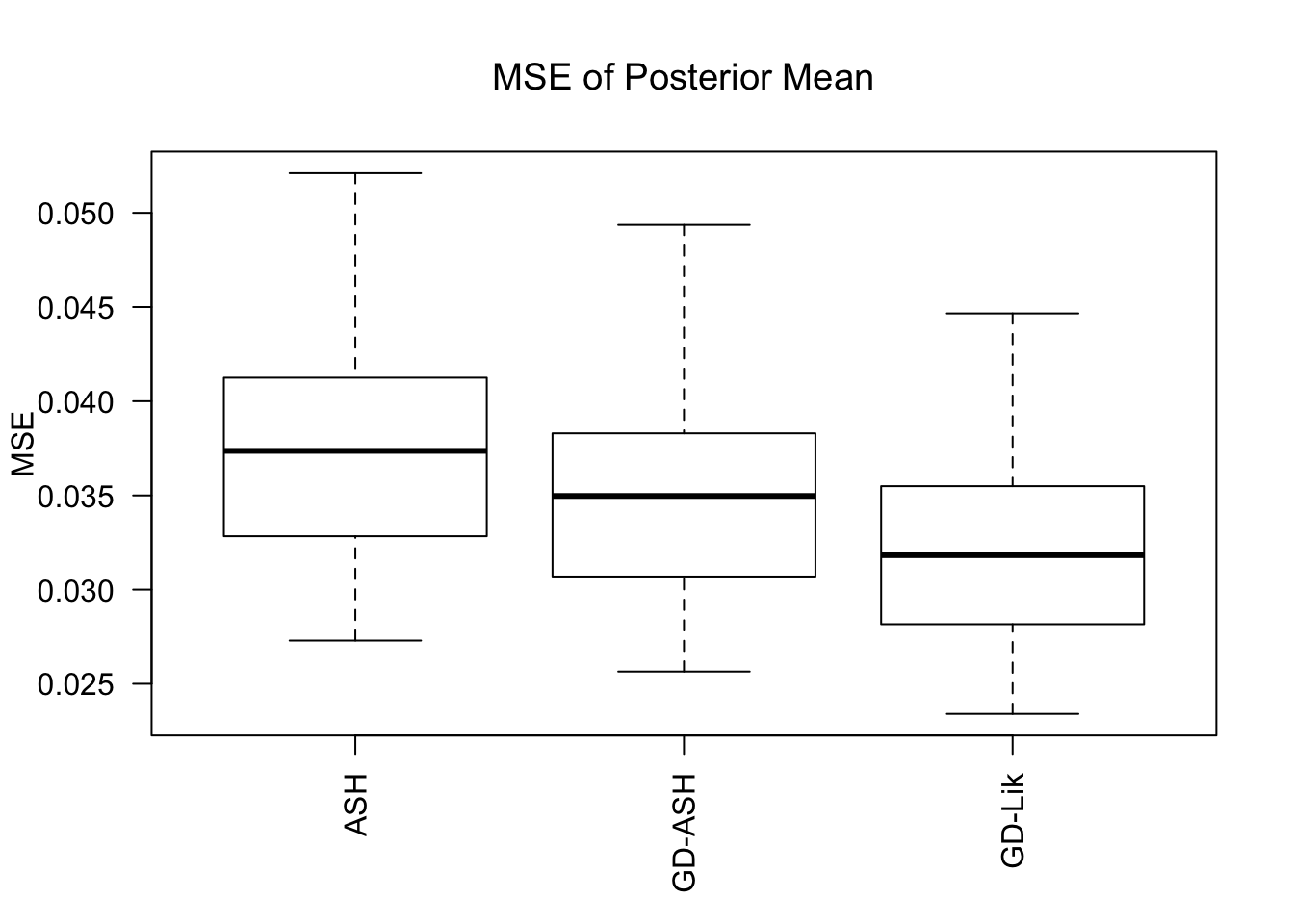
MSE
GD-Lik clearly improves the posterior estimates of GD-ASH.
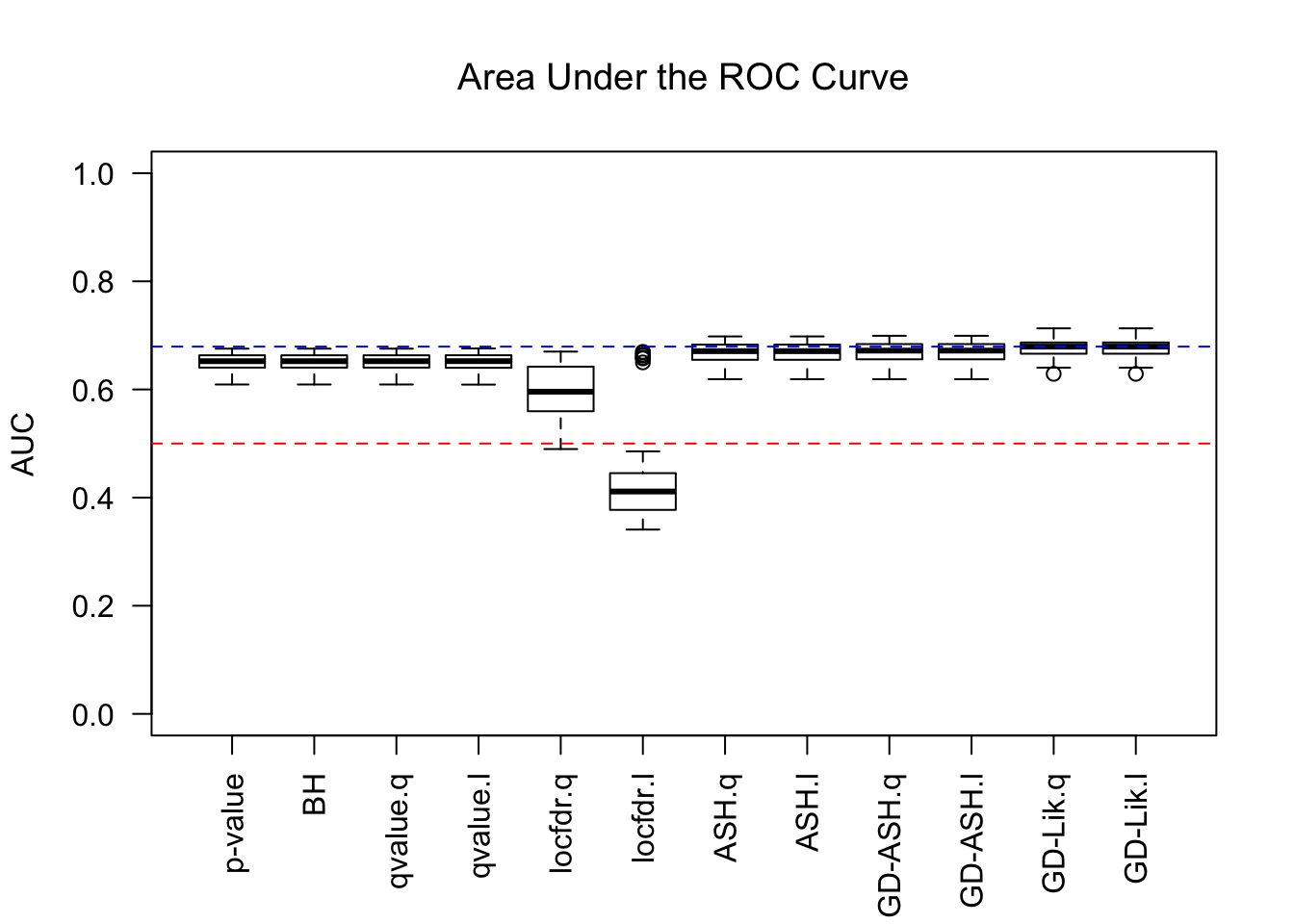
AUC
For almost all methods, .q means using q values, and .l using local FDRs. GD-Lik is the best, yet even the vanilla \(p\) values are not much worse. It indicates that all the methods based on summary statistics indeed make few changes to the order of original \(p\) values. Worth noting is that locfdr doesn’t perform well, and lfdr’s give a drastically different result than q values do, probably due to some artifacts like ties.
q values and positive FDR (pFDR) calibration
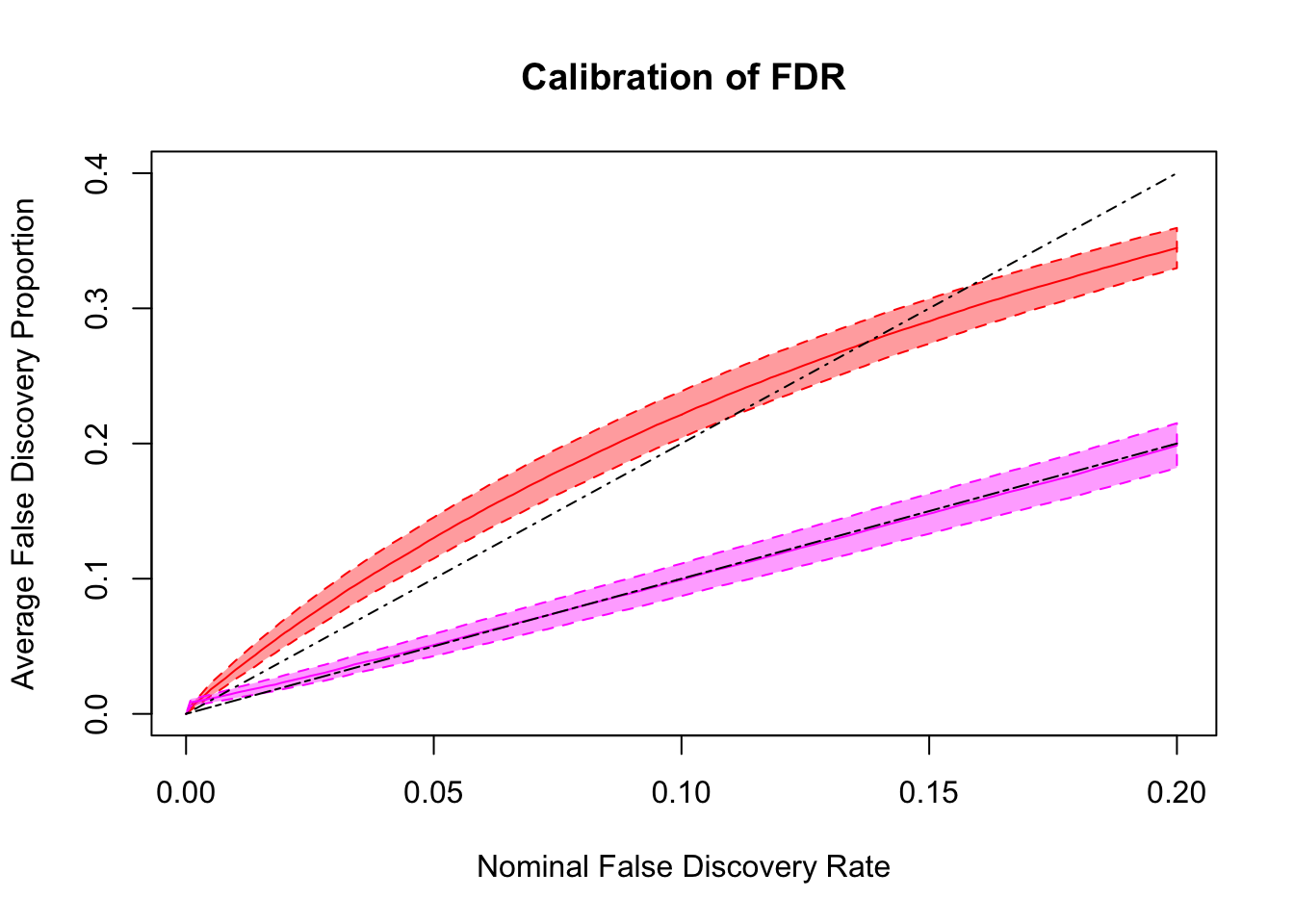
Dashed lines are \(y = x\) and \(y = 2x\). ASH and qvalue are too liberal, and locfdr is too conservative. GD-ASH and BH give very similar results and not far off. BH’s calibrates pFDR relatively well, even though it’s only guaranteed to control FDR under independence. GD-Lik calibrates pFDR almost precisely.
Model and data generation
\[ \begin{array}{l} \hat\beta_j = \beta_j + \sigma_j z_j \\ z_j \sim N(0, 1), \text{ correlated, simulated from real data}\\ \sigma_j : \text{ heteroskedastic, simulated from real data}\\ \beta_j \sim 0.6\delta_0 + 0.3N(0, \sigma^2) + 0.1N\left(0, \left(2\sigma\right)^2\right) \end{array} \]
Expand here to see past versions of inflation qvalue calibration plotting-1.png:
| Version | Author | Date |
|---|---|---|
| 0f36d99 | LSun | 2017-12-21 |
| b7c3984 | LSun | 2017-06-24 |
| 73b4bb7 | LSun | 2017-06-17 |
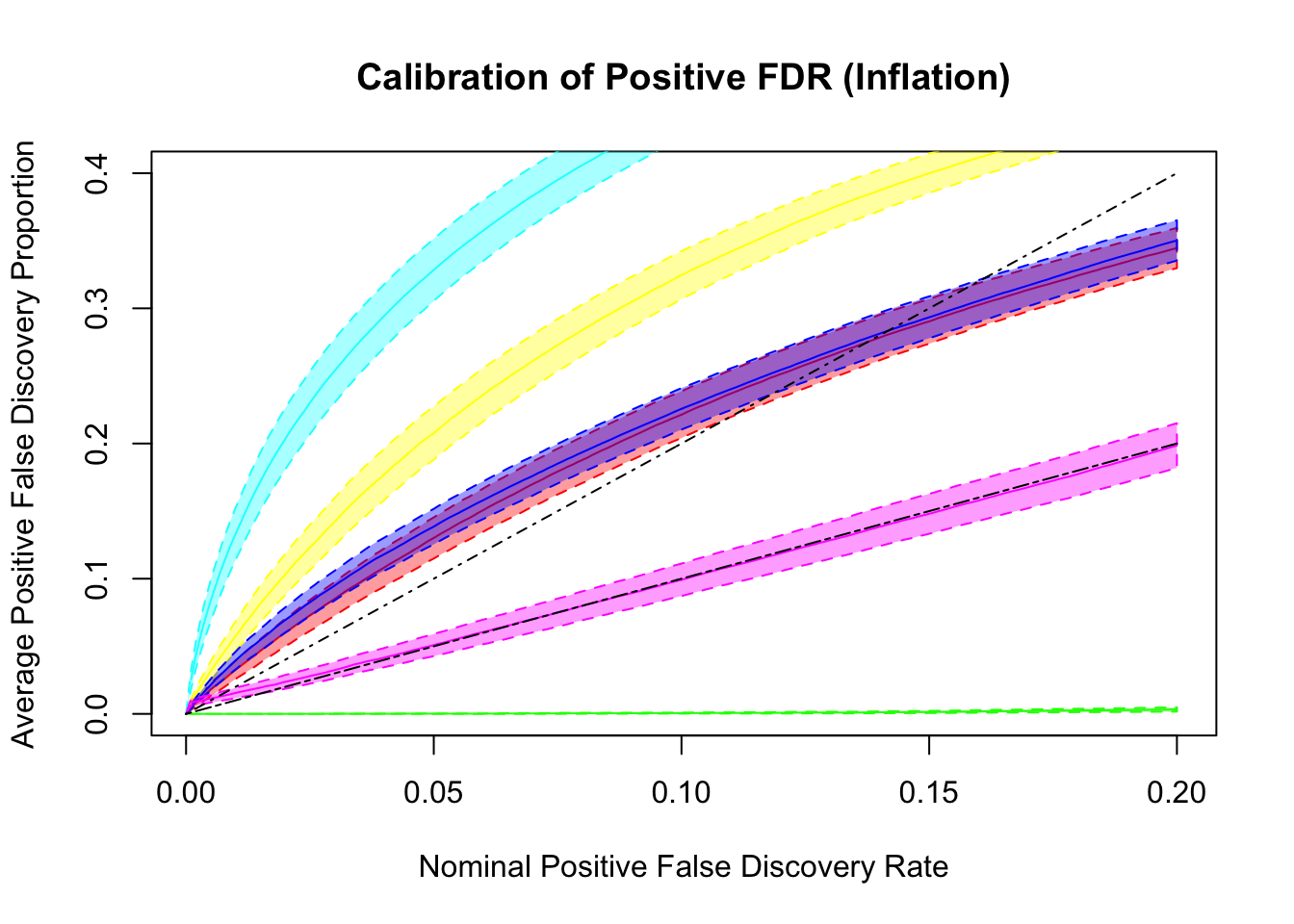
FDR calibration

Expand here to see past versions of inflation FDR calibration plotting-1.png:
| Version | Author | Date |
|---|---|---|
| 0f36d99 | LSun | 2017-12-21 |
| a2512ac | LSun | 2017-07-03 |
Deflation data sets
\(\hat \pi_0\)
Almost all methods except GD-ASH overestimate as expected. GD-ASH occasionally severely underestimates as seen before.
MSE
GD-Lik does better than ASH and GD-ASH but not as significantly as in the inflation case.
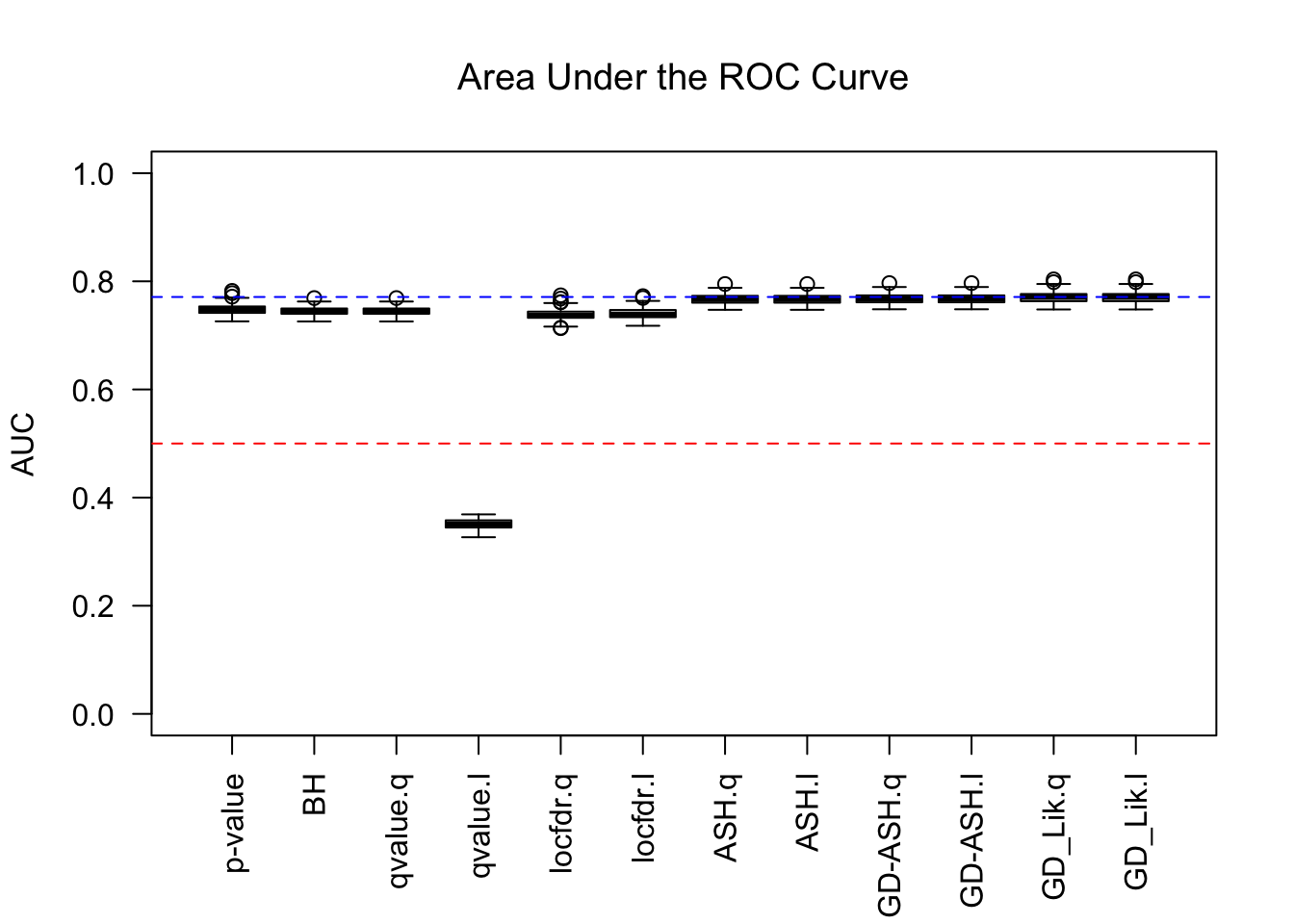
AUC
Similar story as in the inflation case, although this time qvalue’s lfdr behaves weirdly.
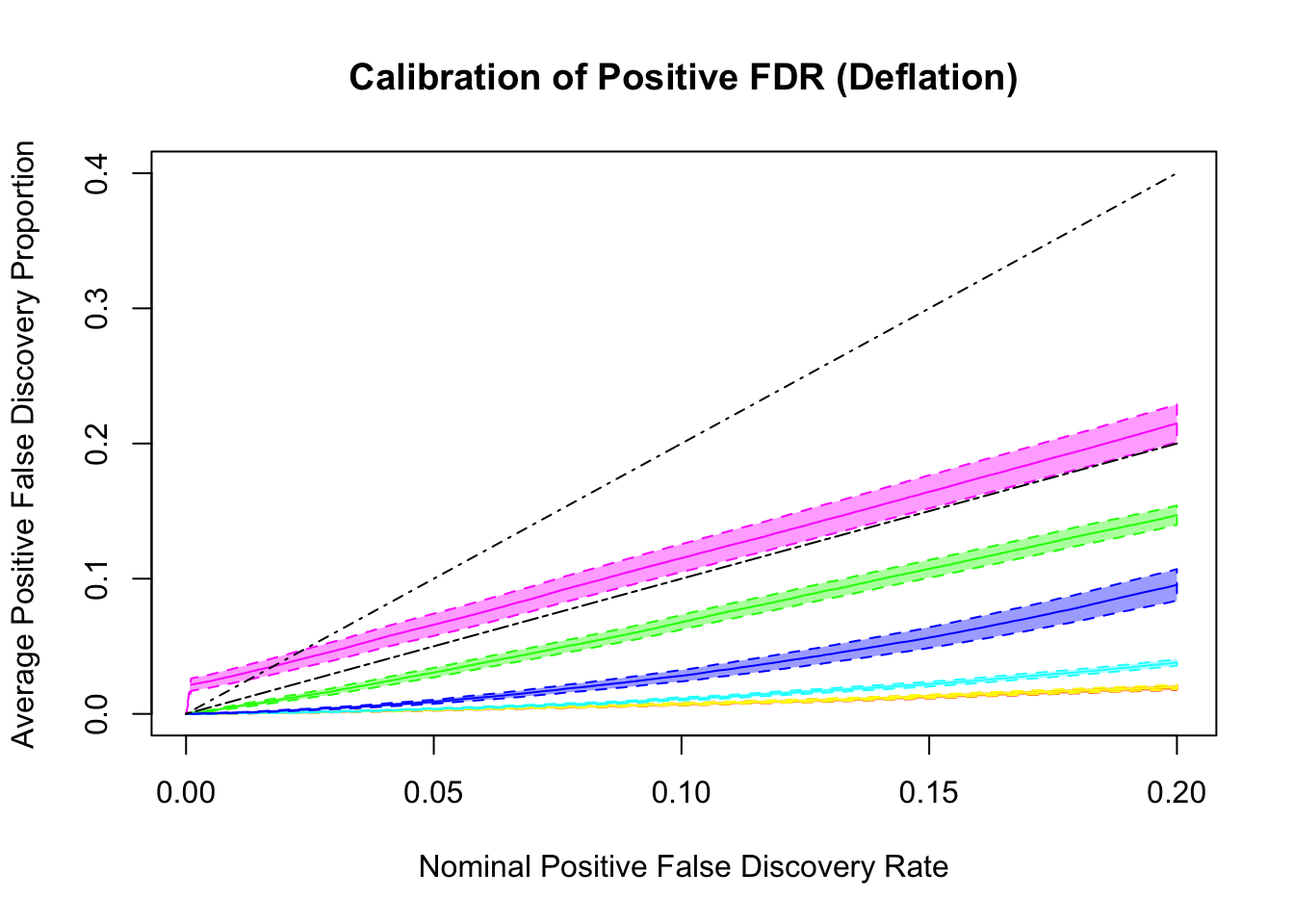
q values and positive FDR (pFDR) calibration
Essentially all methods successfully control pFDR. GD-Lik looks good although off a little. qvalue is the most conservative, followed by ASH, GD-ASH, and locfdr.
Expand here to see past versions of deflation qvalue calibration plotting-1.png:
| Version | Author | Date |
|---|---|---|
| 0f36d99 | LSun | 2017-12-21 |
| b7c3984 | LSun | 2017-06-24 |
| 73b4bb7 | LSun | 2017-06-17 |
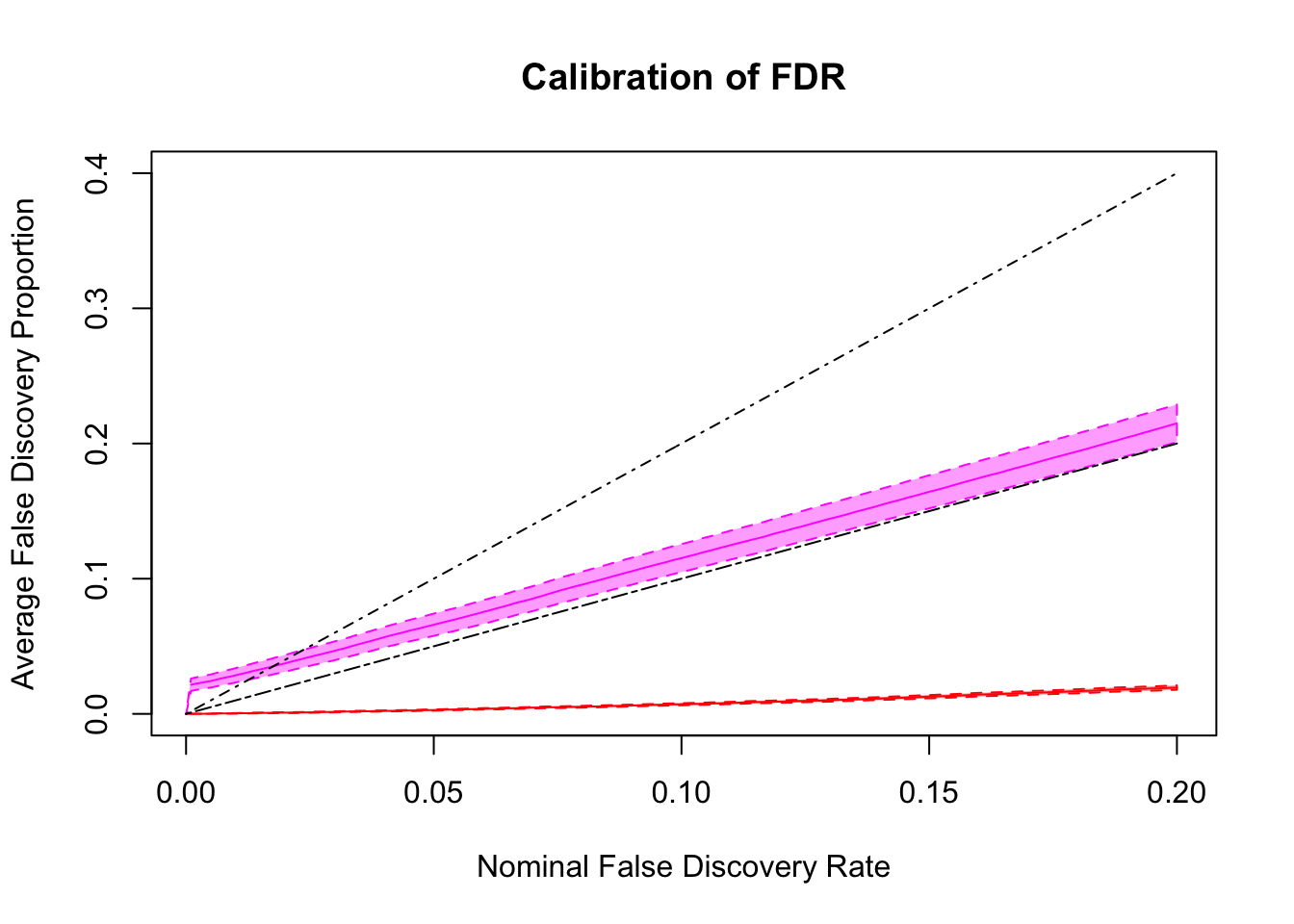
FDR calibration

Expand here to see past versions of deflation FDR calibration plotting-1.png:
| Version | Author | Date |
|---|---|---|
| 0f36d99 | LSun | 2017-12-21 |
| a2512ac | LSun | 2017-07-03 |
Remarks
- Would be nice to come up with a way to calculate
lfsrinGD-Lik. - Many methods are too liberal for inflation cases and too conservative for deflation cases, showing a lack of robustness against correlation. Although, on average they probably seem about right.
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] ashr_2.2-2 Rmosek_8.0.69 PolynomF_1.0-1 CVXR_0.95
[5] REBayes_1.2 Matrix_1.2-12 SQUAREM_2017.10-1 EQL_1.0-0
[9] ttutils_1.0-1
loaded via a namespace (and not attached):
[1] gmp_0.5-13.1 Rcpp_0.12.16 compiler_3.4.3
[4] git2r_0.21.0 workflowr_1.0.1 R.methodsS3_1.7.1
[7] R.utils_2.6.0 iterators_1.0.9 tools_3.4.3
[10] digest_0.6.15 bit_1.1-12 evaluate_0.10.1
[13] lattice_0.20-35 foreach_1.4.4 yaml_2.1.18
[16] parallel_3.4.3 Rmpfr_0.6-1 ECOSolveR_0.4
[19] stringr_1.3.0 knitr_1.20 rprojroot_1.3-2
[22] bit64_0.9-7 grid_3.4.3 R6_2.2.2
[25] rmarkdown_1.9 magrittr_1.5 whisker_0.3-2
[28] MASS_7.3-47 backports_1.1.2 codetools_0.2-15
[31] htmltools_0.3.6 scs_1.1-1 stringi_1.1.6
[34] pscl_1.5.2 doParallel_1.0.11 truncnorm_1.0-7
[37] R.oo_1.21.0
This reproducible R Markdown analysis was created with workflowr 1.0.1





