Knockoff vs Bayesian: Mixture normal signals
Lei Sun
2018-04-03
Last updated: 2018-04-16
Code version: c7c5984
Introduction
The true \(\beta\) are simulated as \(\beta \sim \pi_0\delta_0 + (1 - \pi_0)N(0, \sigma_\beta^2)\).
varbvs.get.lfsr <- function (fit) {
# For each variable, and each hyperparameter setting, get the
# posterior probability that the regression coefficient is exactly
# zero.
p0 <- 1 - fit$alpha
# For each variable, and for each hyperparameter setting, get the
# posterior probability that the regression coefficient is negative.
pn <- with(fit,alpha * pnorm(0,mu,sqrt(s)))
# For each variable, and for each hyperparameter setting, ompute the
# local false sign rate (LFSR) following the formula given in
# Matthew's Biostatistics paper, "False discovery rates: a new deal".
p <- nrow(fit$alpha)
k <- ncol(fit$alpha)
lfsr <- matrix(0,p,k)
b <- pn > 0.5*(1 - p0)
lfsr[b] <- 1 - pn[b]
lfsr[!b] <- p0[!b] + pn[!b]
# Average the average LFSR over the hyperparameter settings, weighted
# by the probability of each hyperparameter setting.
lfsr <- c(lfsr %*% fit$w)
return(lfsr)
}\(n > p\)
n <- 2000
p <- 1000
k <- 200
m <- 100
q <- 0.1Independent design
\(X_{n \times p}\) has independent columns simulated from \(N(0, (1/\sqrt n)^2)\) so they are roughly normalized.
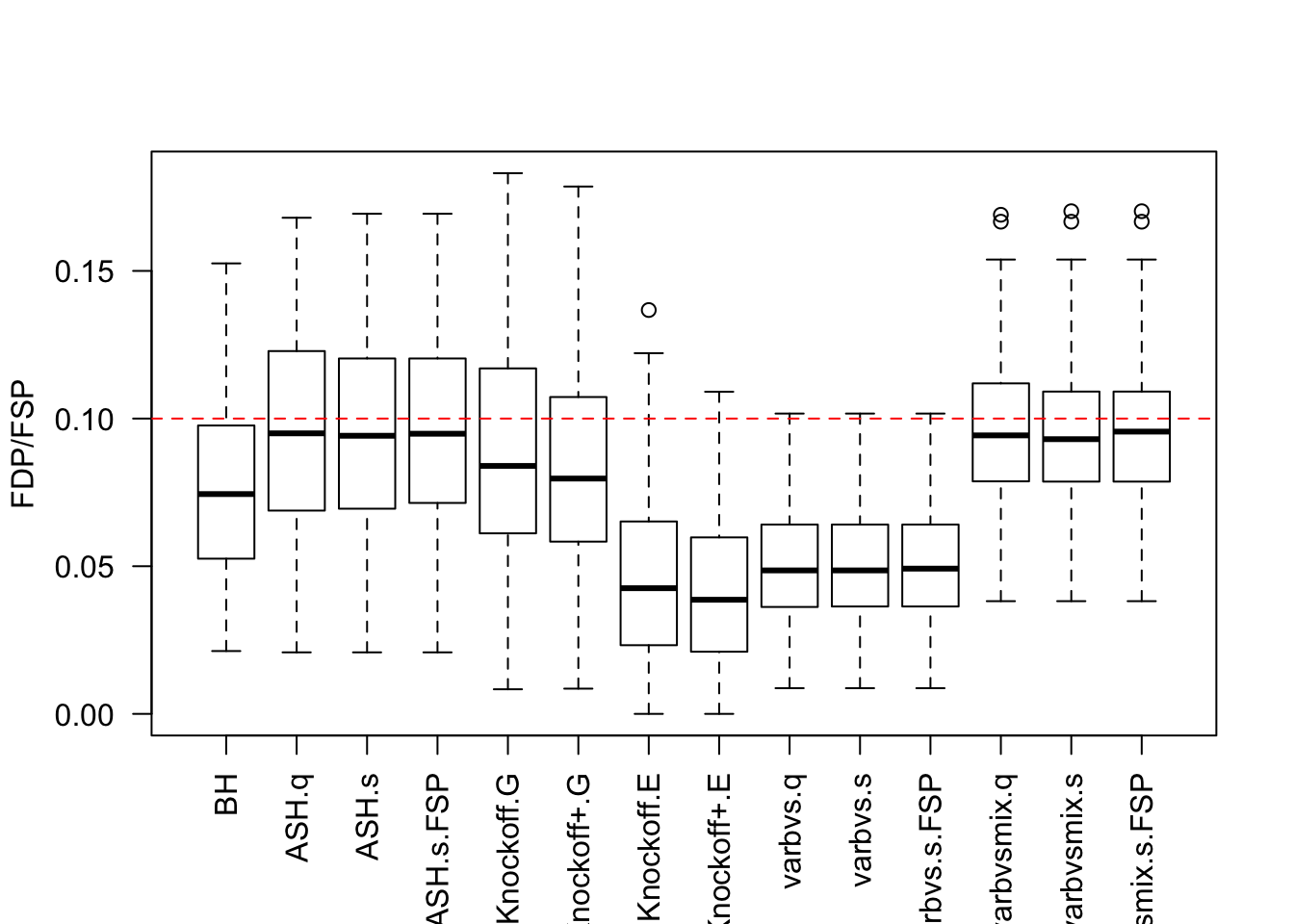
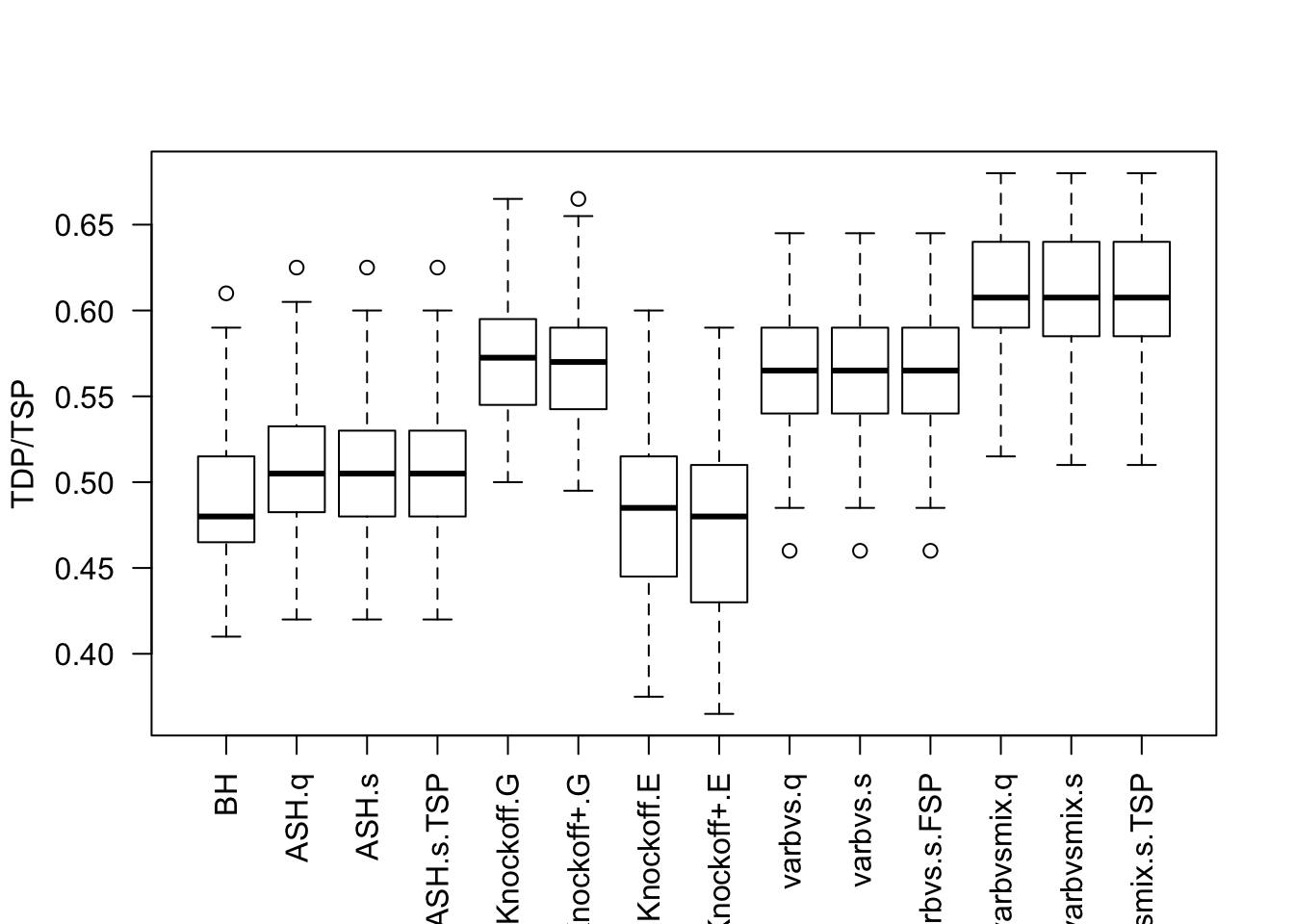
Local correlation / AR model for \(X\)
\(X_{n \times p}\) has correlation \(\Sigma_{ij} = \rho^{|i - j|}\). Each row is independently \(N(0, \frac1n\Sigma)\).
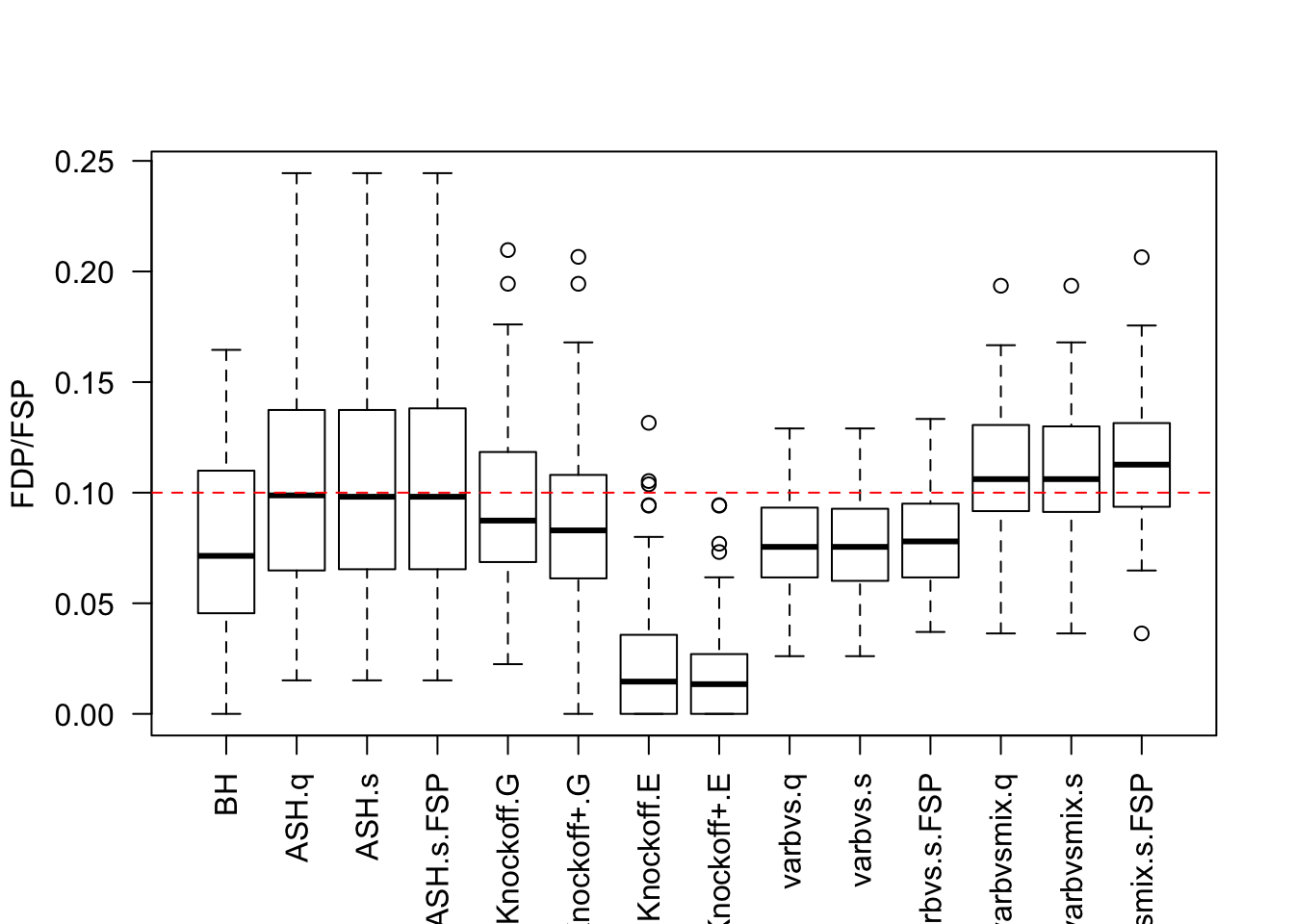
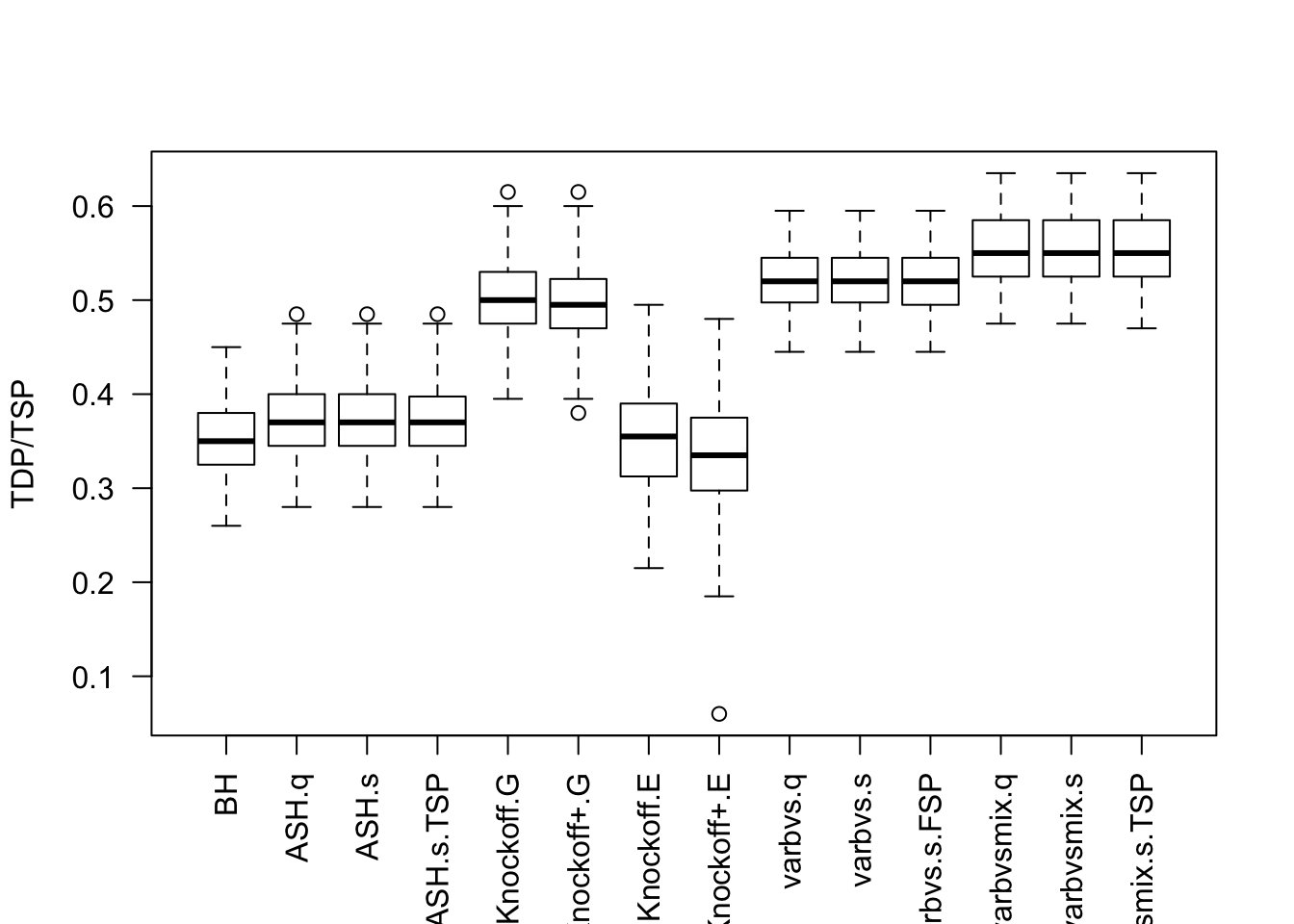
Factor Model for \(X\)
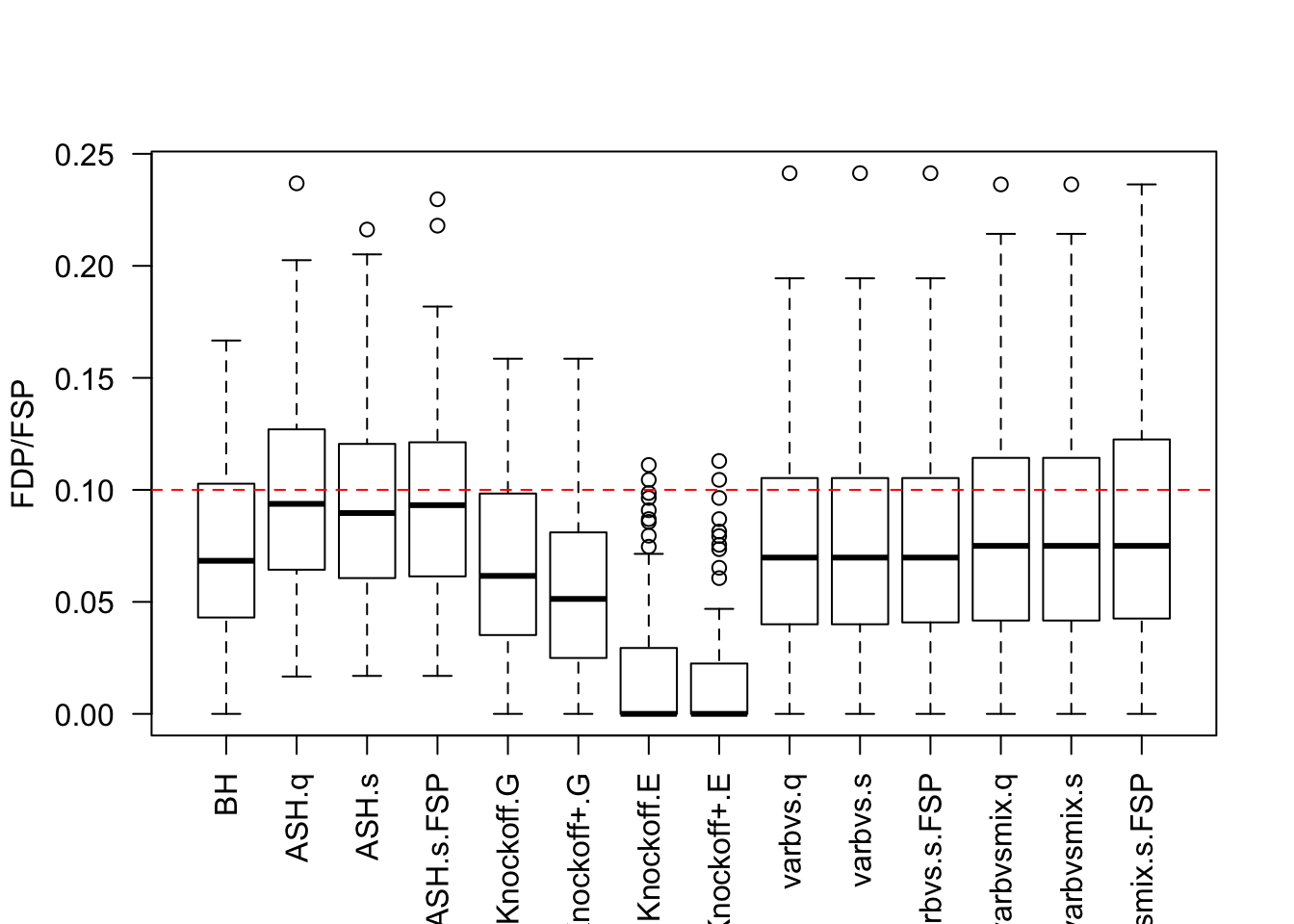
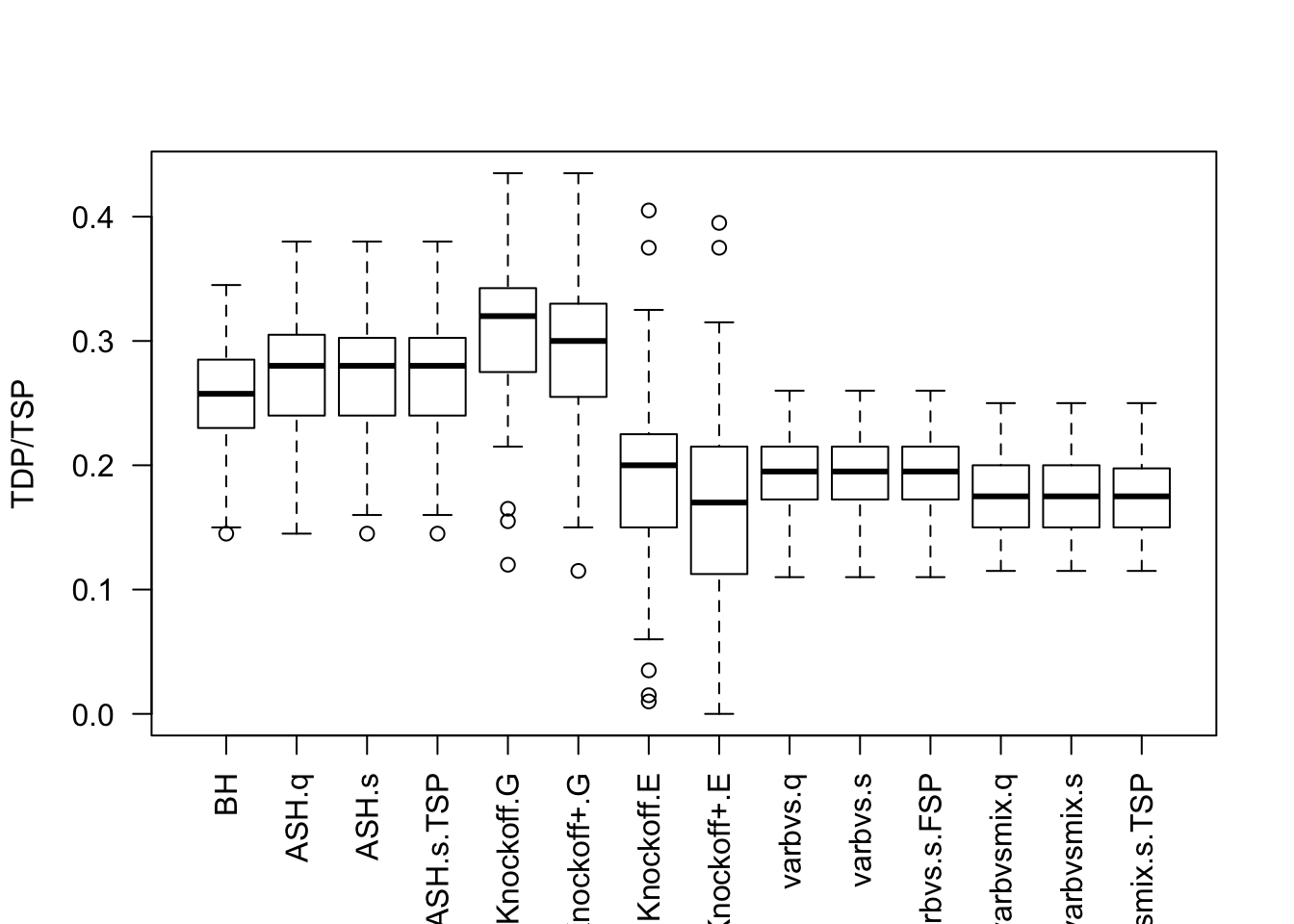
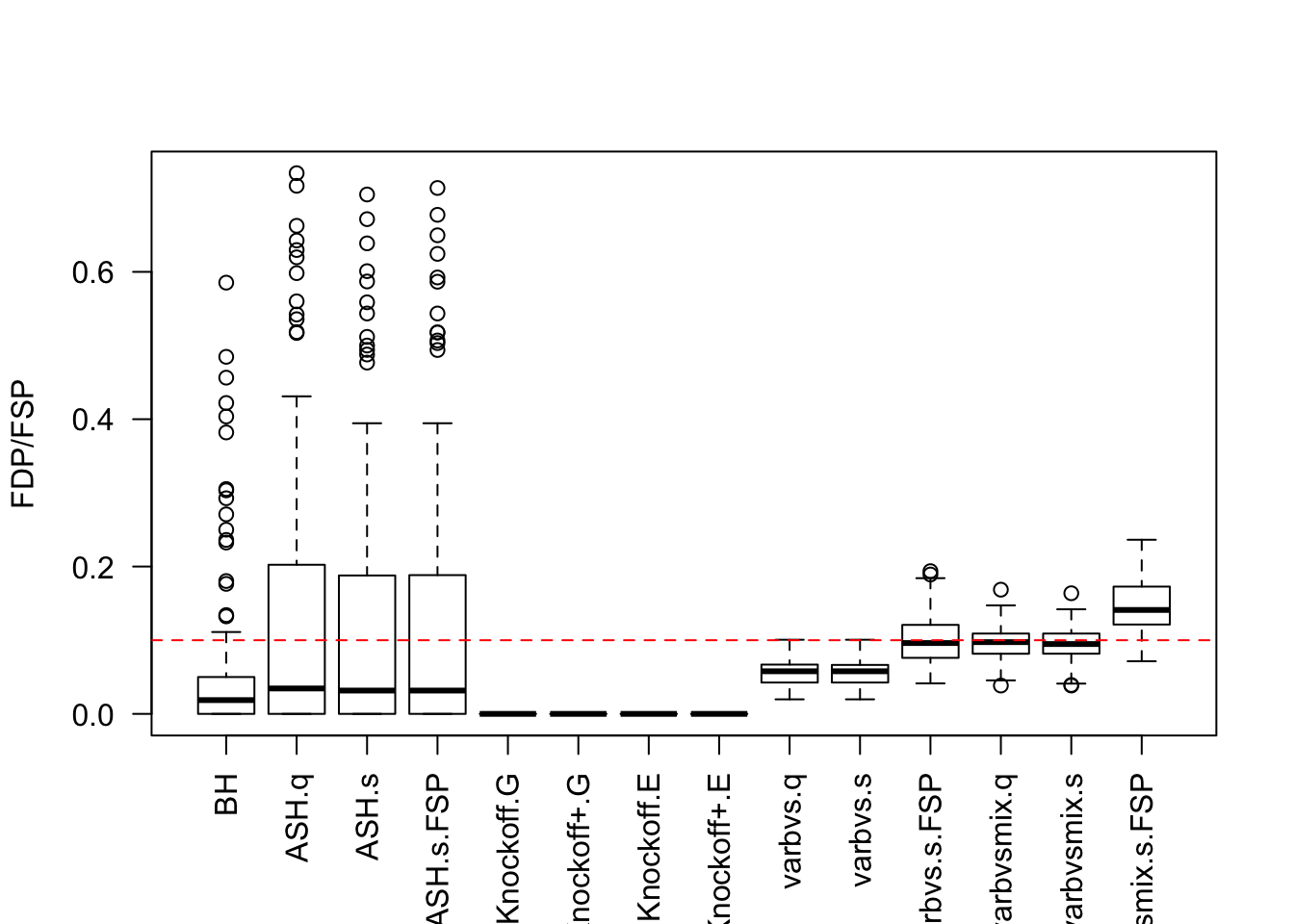
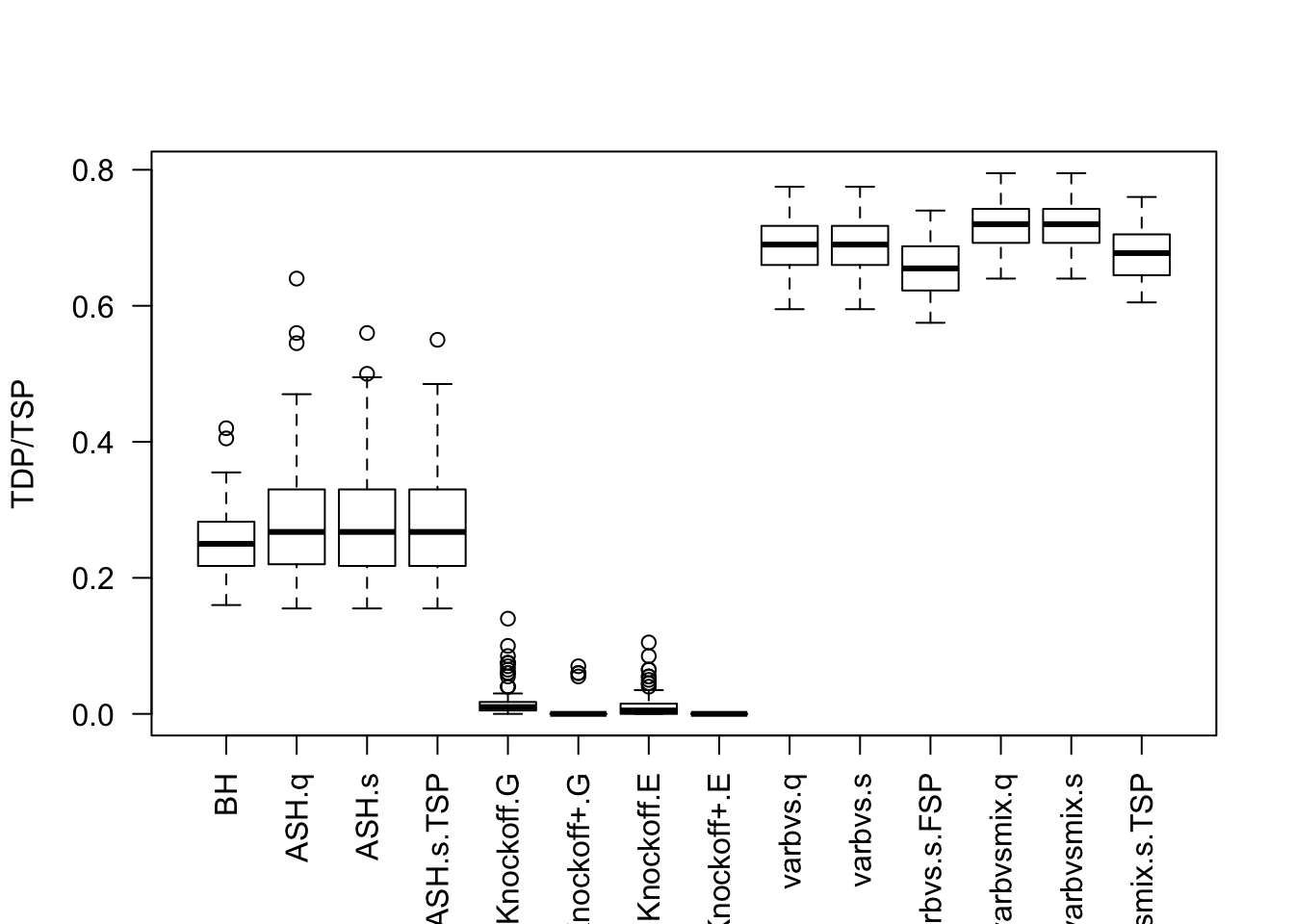
Factor Model for \(\hat\beta\)
Observation
- Model-\(X\) knockoff is very powerful.
- Using estimated distribution of \(X\) rather than the true distribution hurts the power of Model-\(X\) knockoff.
- The power of Model-\(X\) knockoff using estimated distributio of \(X\) is on par with that of
ASHandBH, probably because the presence of small signals makes knockoff less powerful. - Sometimes
equiis better thanSDPwhen generating knockoffs, as shown in previous simulations using factor model for \(X\).
\(n < p\)
n <- 300
p <- 1000
k <- 200
m <- 100
q <- 0.1Independent design
Cov.X <- diag(1 / n, p)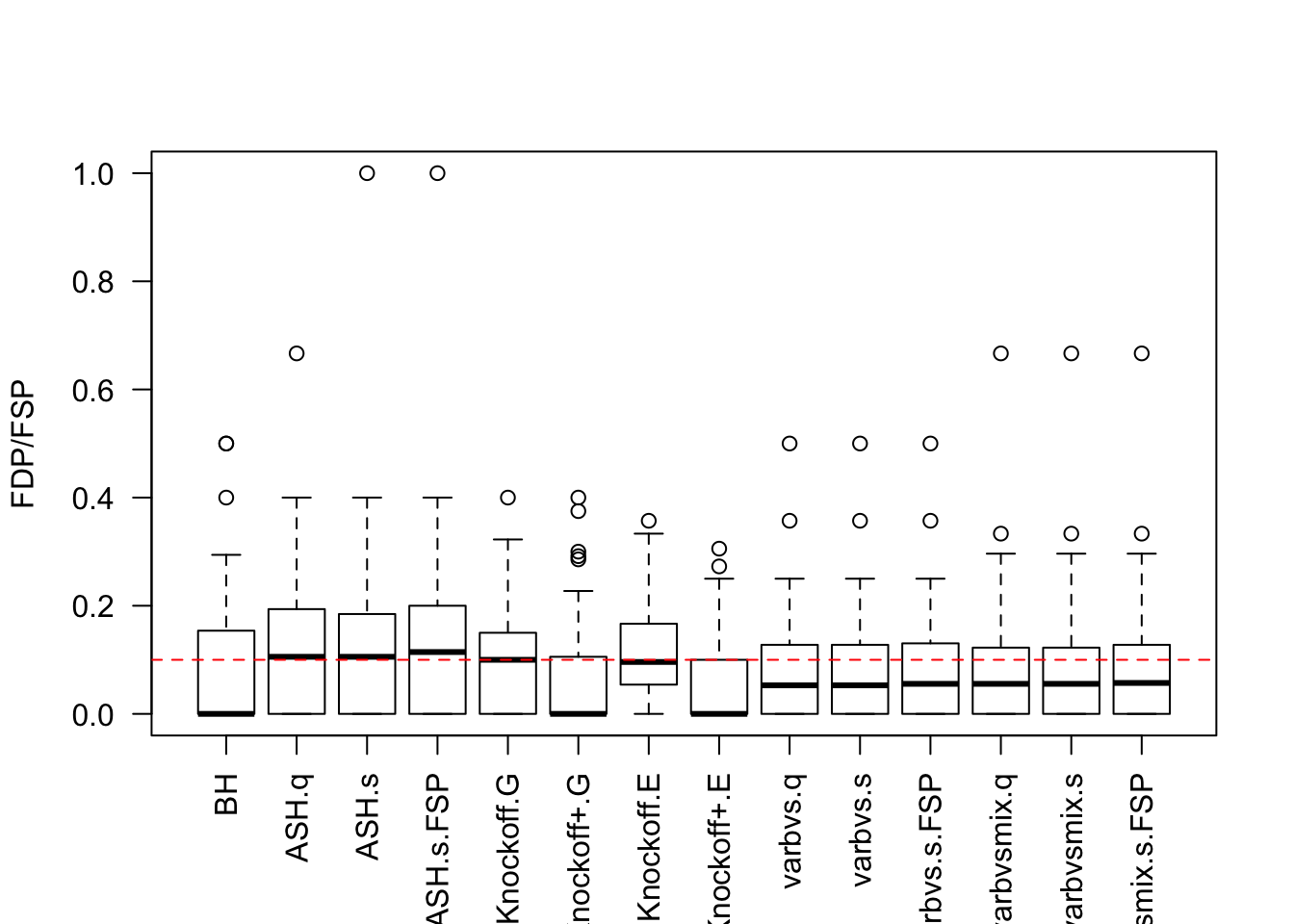
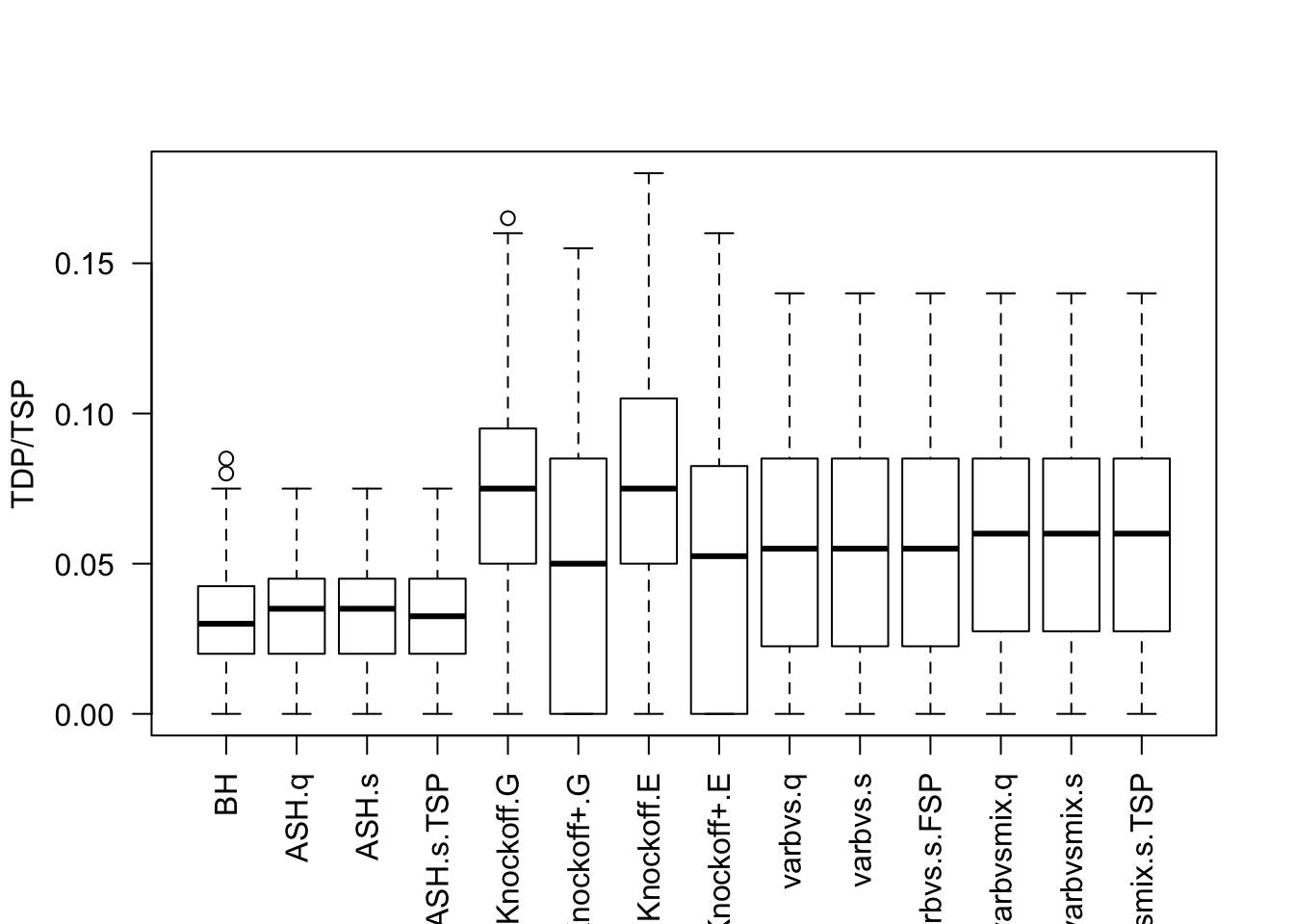
Local correlation design
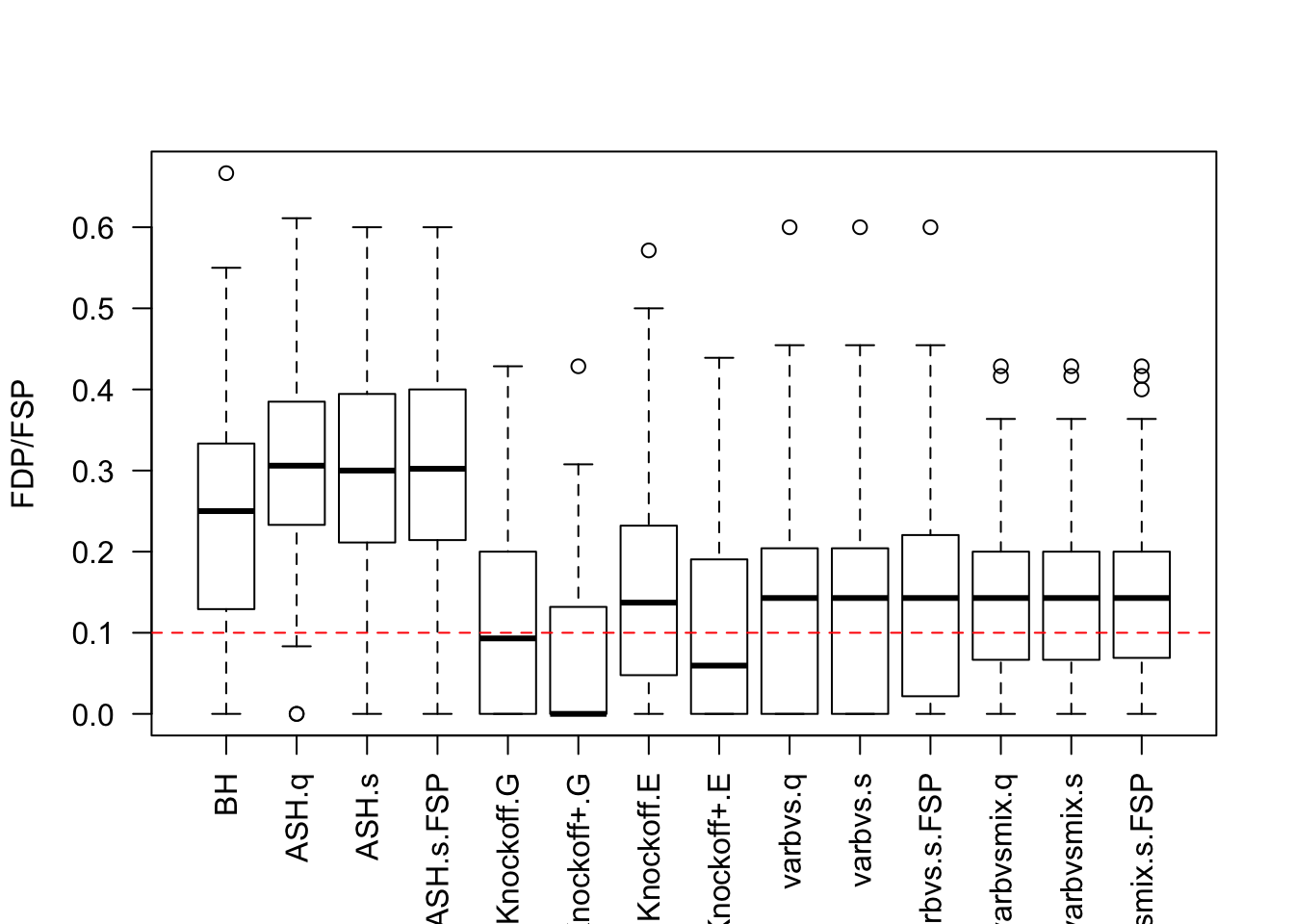

Factor Model for \(X\)
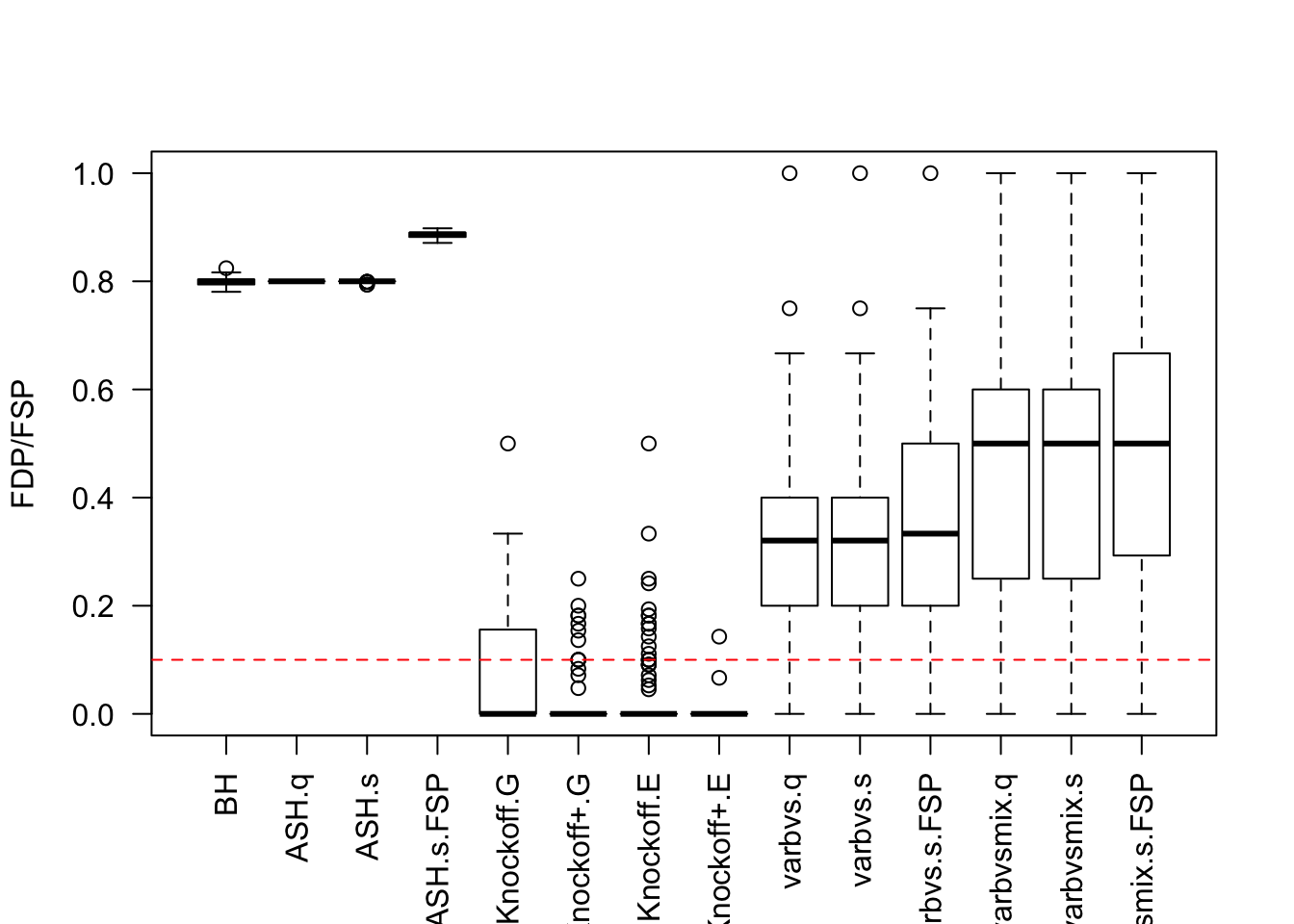
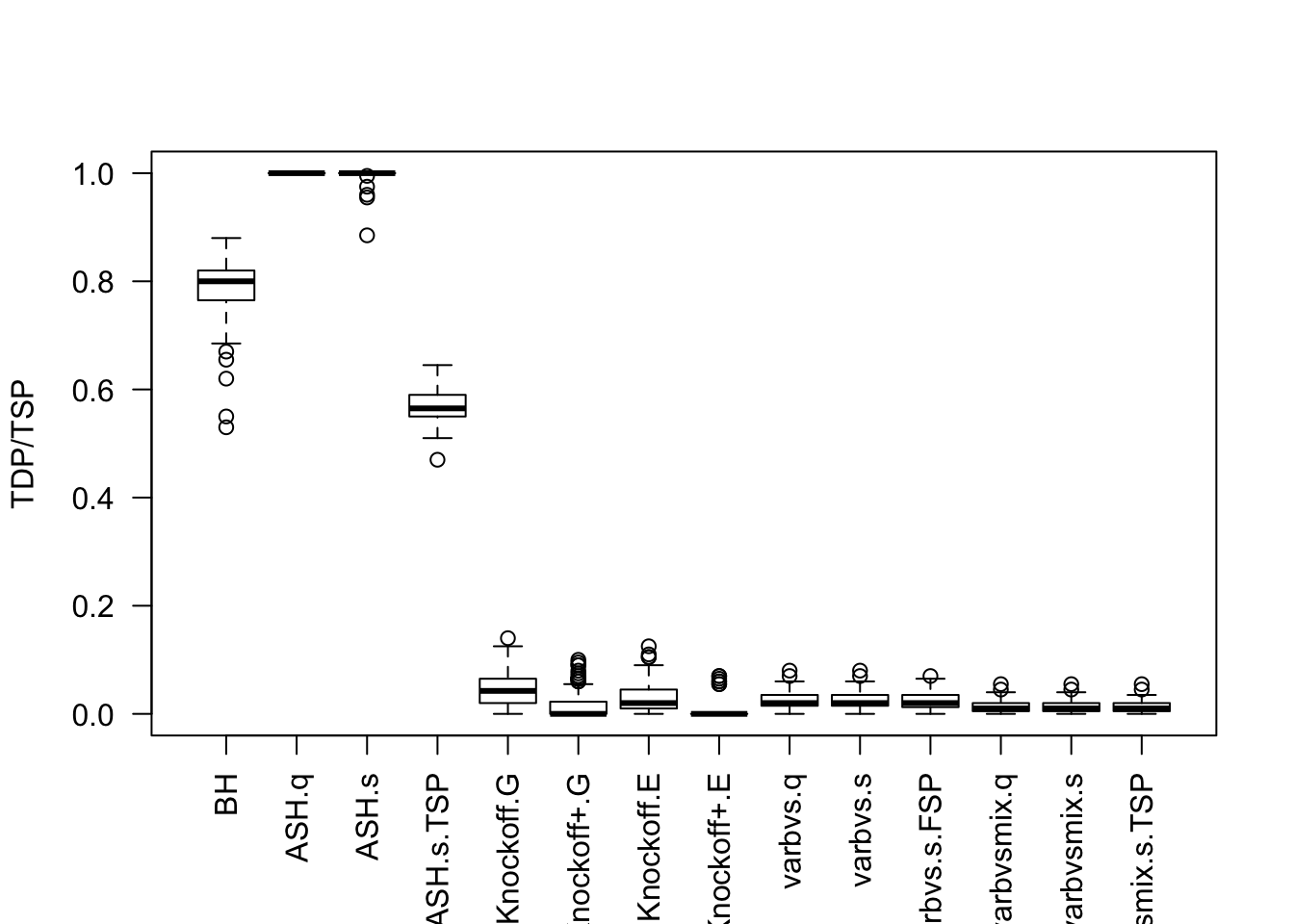
Factor Model for \(\hat\beta\)
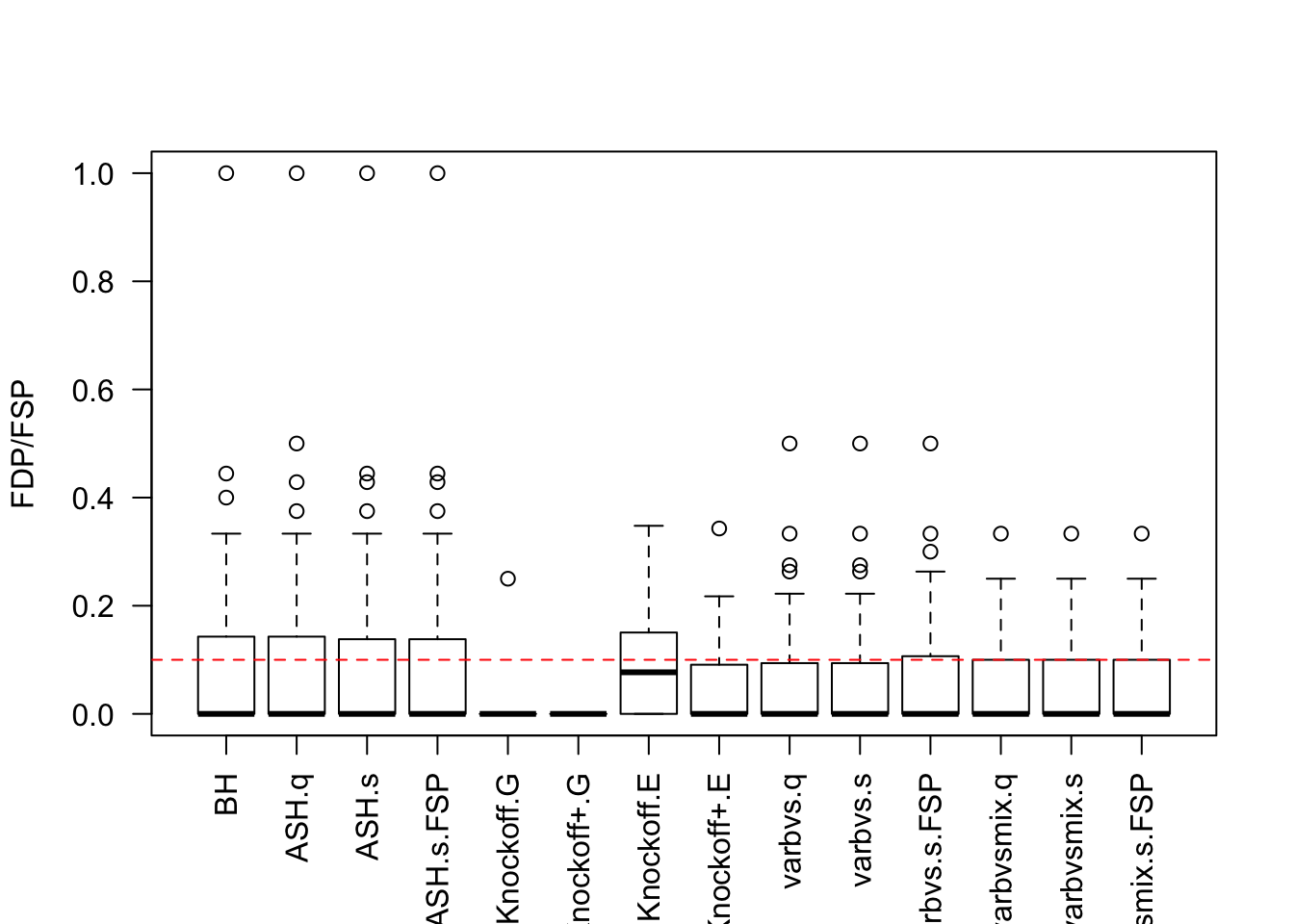
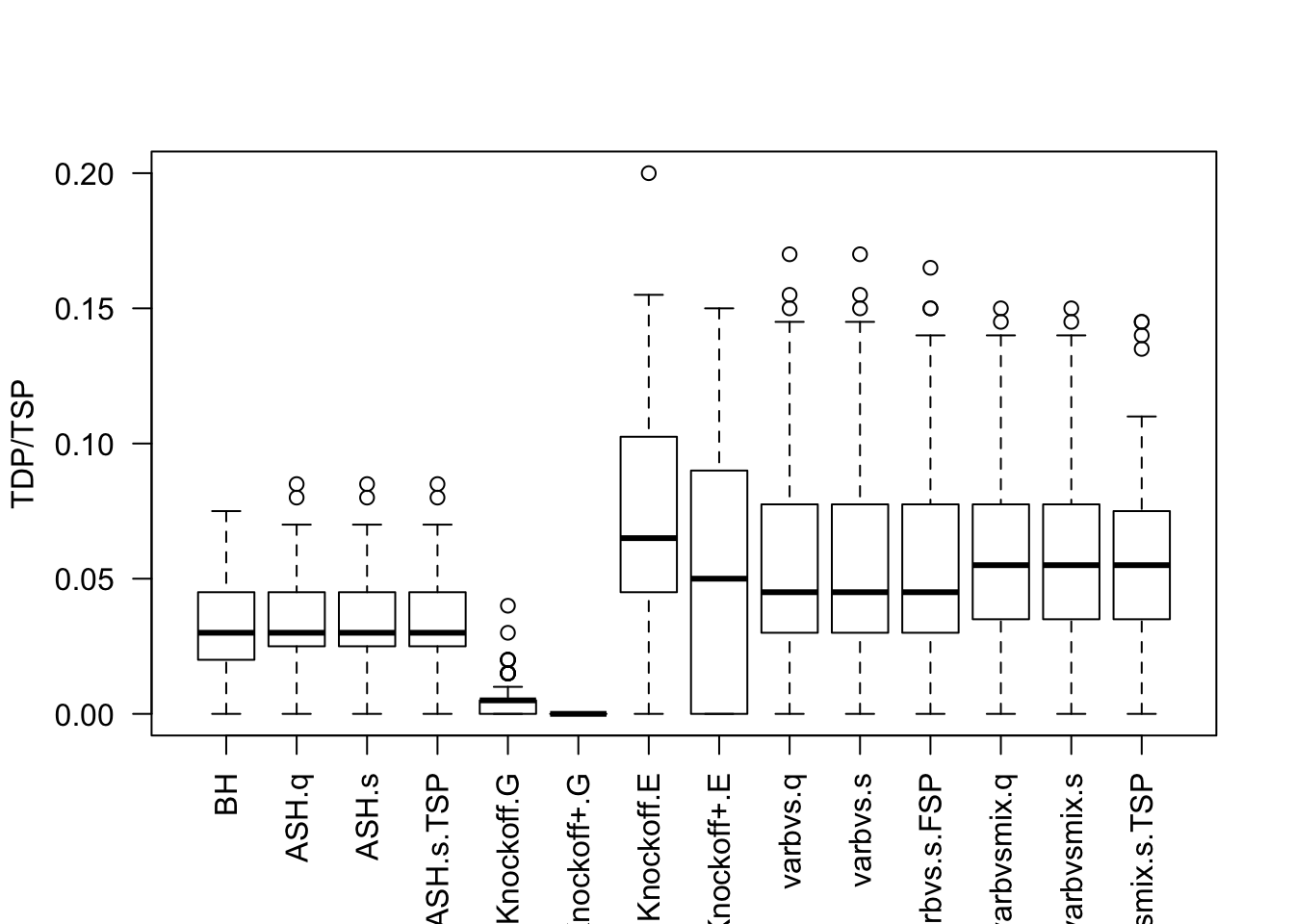
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.3 backports_1.1.2 magrittr_1.5 rprojroot_1.3-2
[5] tools_3.4.3 htmltools_0.3.6 yaml_2.1.18 Rcpp_0.12.16
[9] stringi_1.1.6 rmarkdown_1.9 knitr_1.20 git2r_0.21.0
[13] stringr_1.3.0 digest_0.6.15 evaluate_0.10.1This R Markdown site was created with workflowr