Alternative vs Correlated Null

Introduction

We’ve shown that in many real data sets when we have correlated null \(z\) scores, we can fit their empirical distribution with Gaussian and its derivatives.

But what if we have real signals instead of the global null? Can we fit real signals with Gaussian derivatives with reasonable weights? Let’s start with the most basic case: \(z \sim N(0, \sqrt{2}^2)\) independently. This data set can be seen as generated as follows.

\[ \begin{array}{c} \beta_j \sim N(0, 1)\\ z_j \sim N(\beta_j, 1) \end{array} \]

Illustration

Scale weights \(w_k^s = \sqrt{k!}w_k\), so that \(\text{var}(w_k^s) = \alpha_k = \bar{\rho_{ij}^k}\).

n = 1e4
m = 5
set.seed(777)
zmat = matrix(rnorm(n * m, 0, sd = sqrt(2)), nrow = m)

library(ashr)
source("../code/ecdfz.R")
res = list()
for (i in 1:3) {
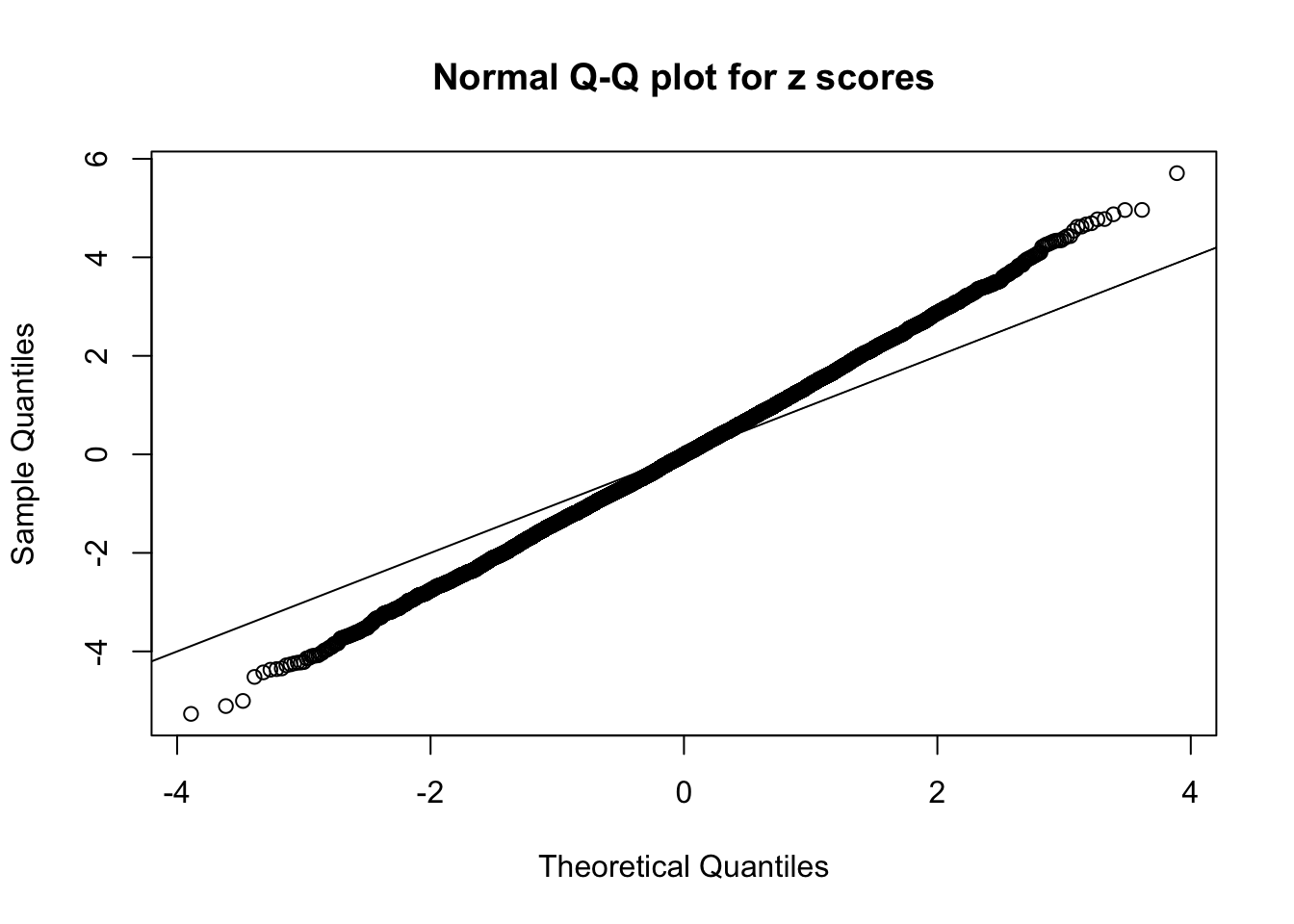
  z = zmat[i, ]
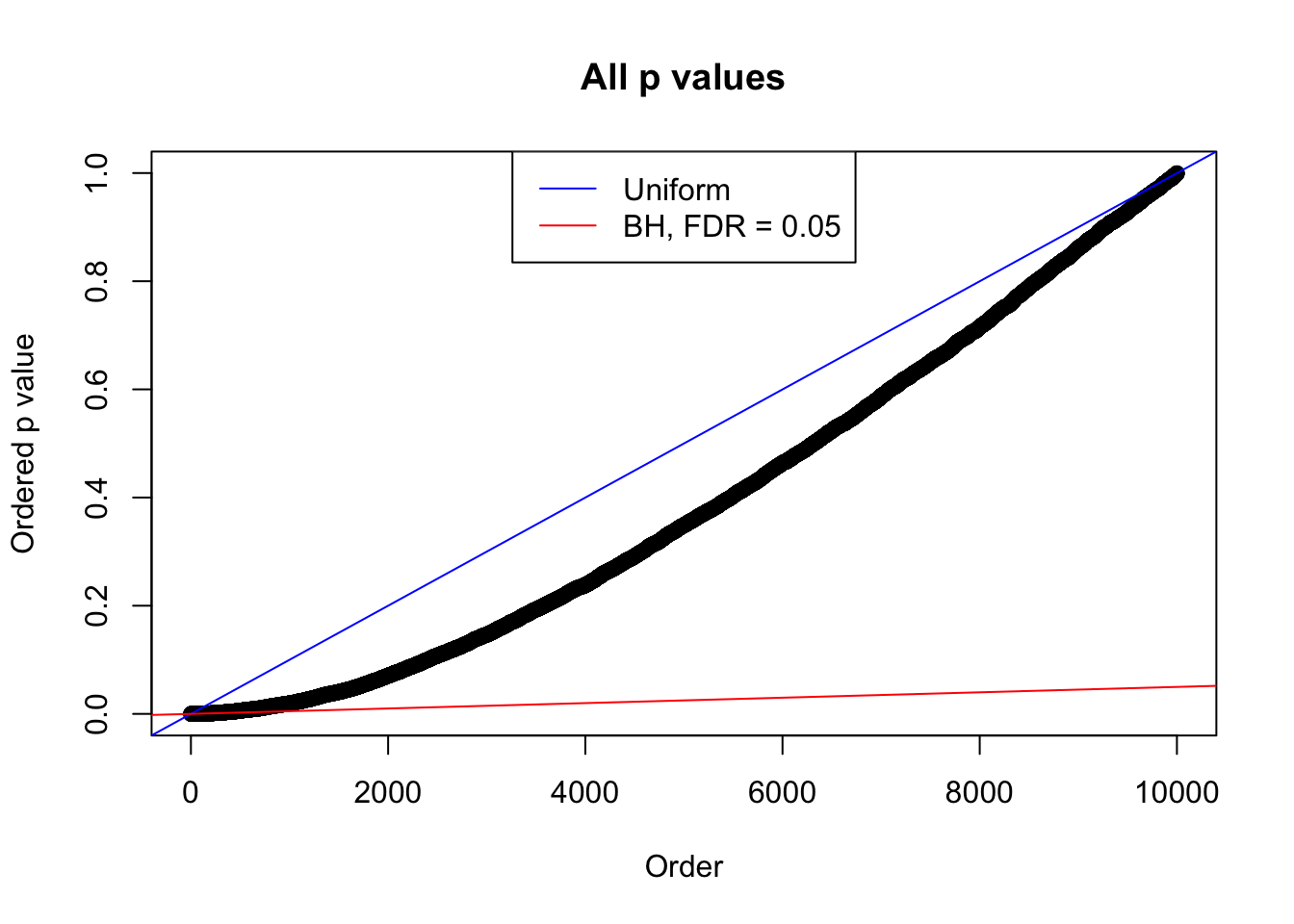
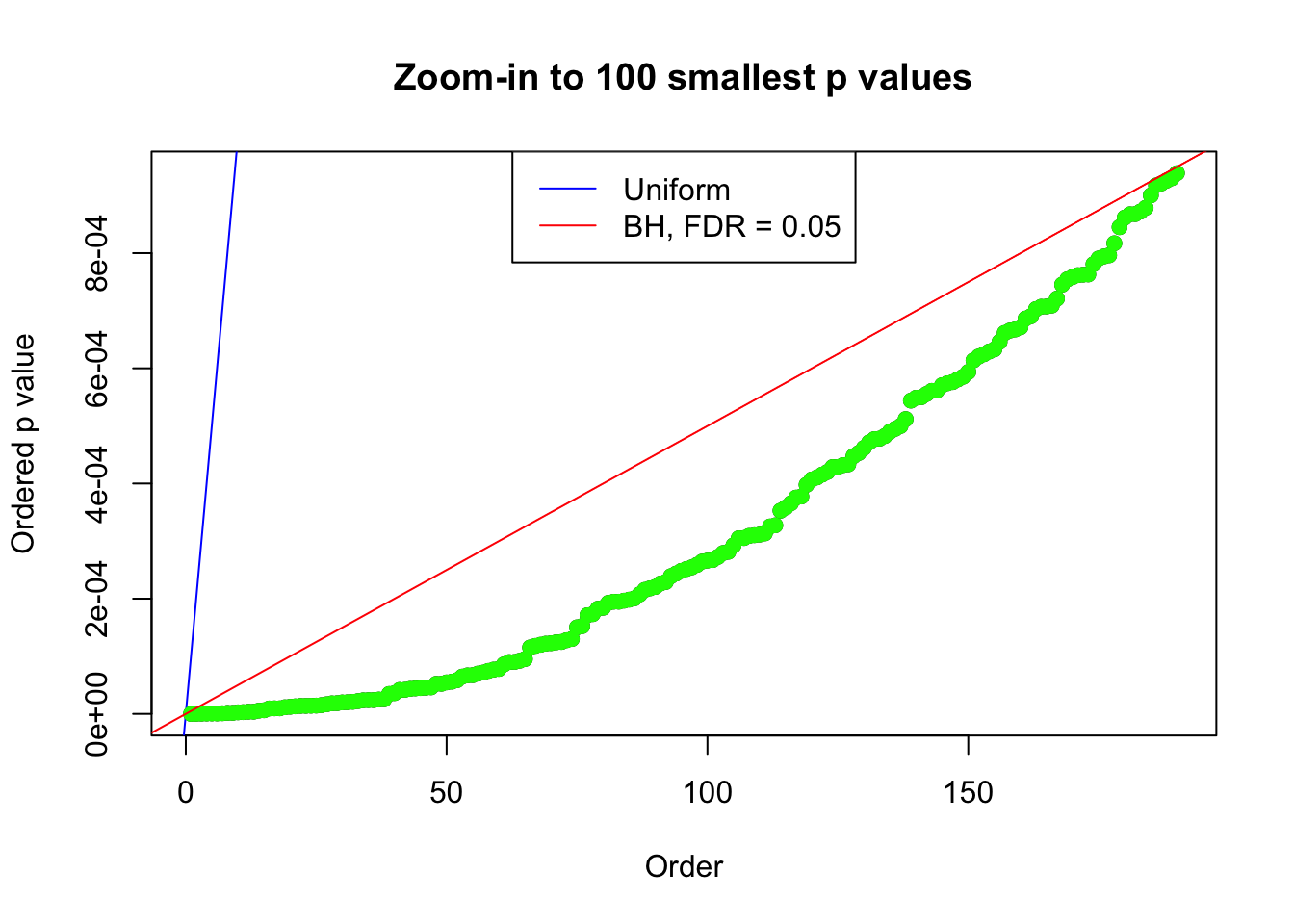
  p = (1 - pnorm(abs(z))) * 2
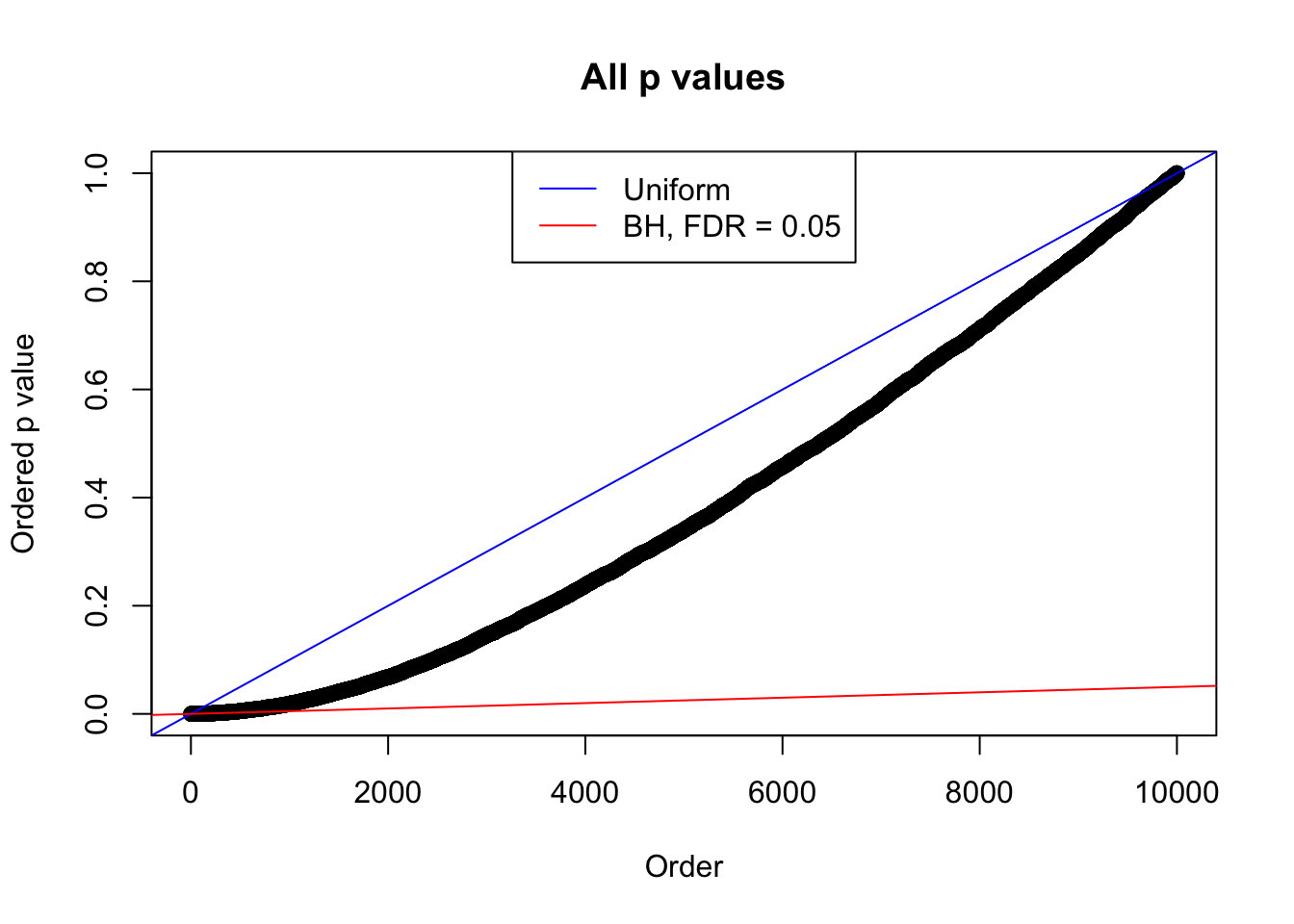
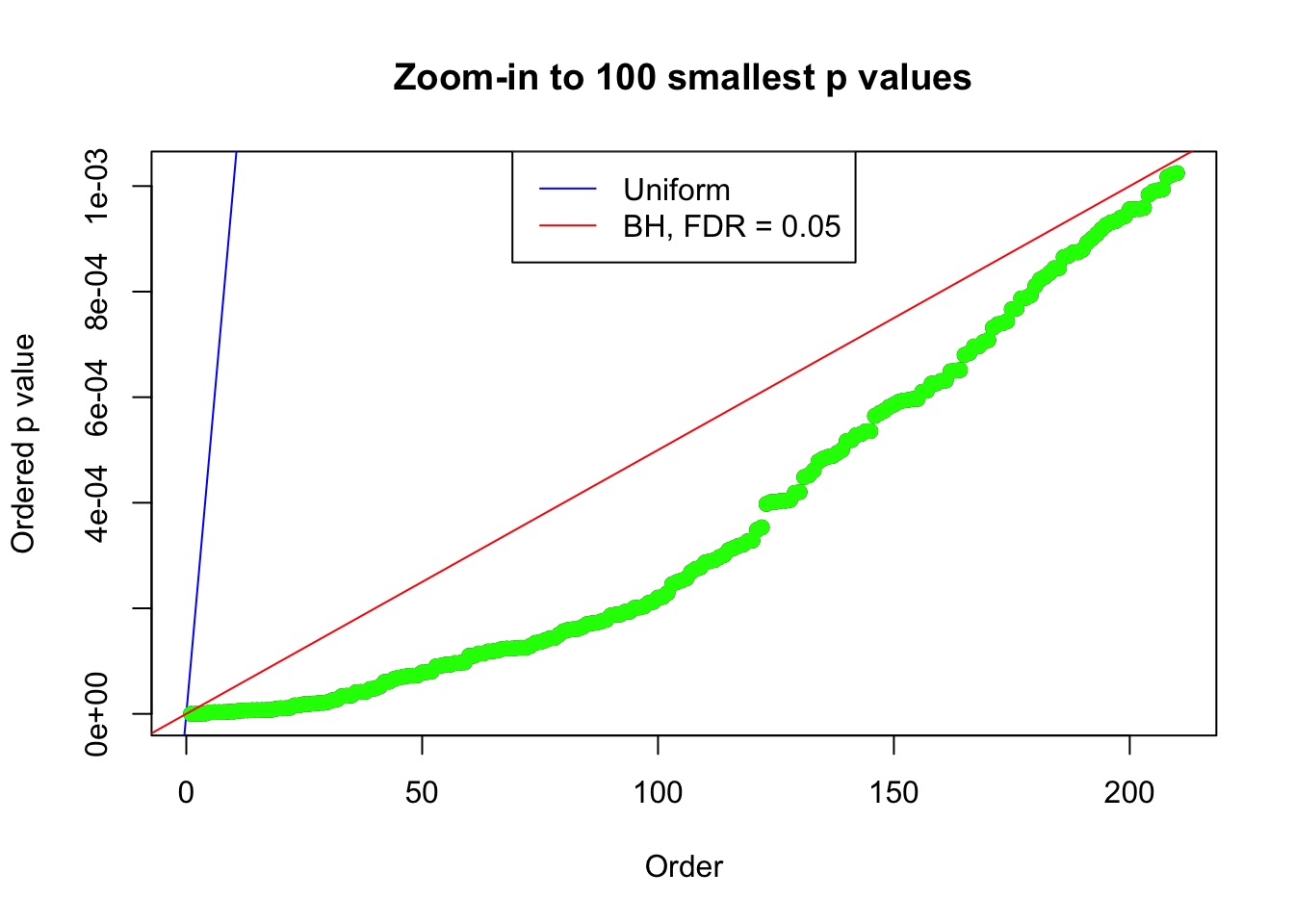
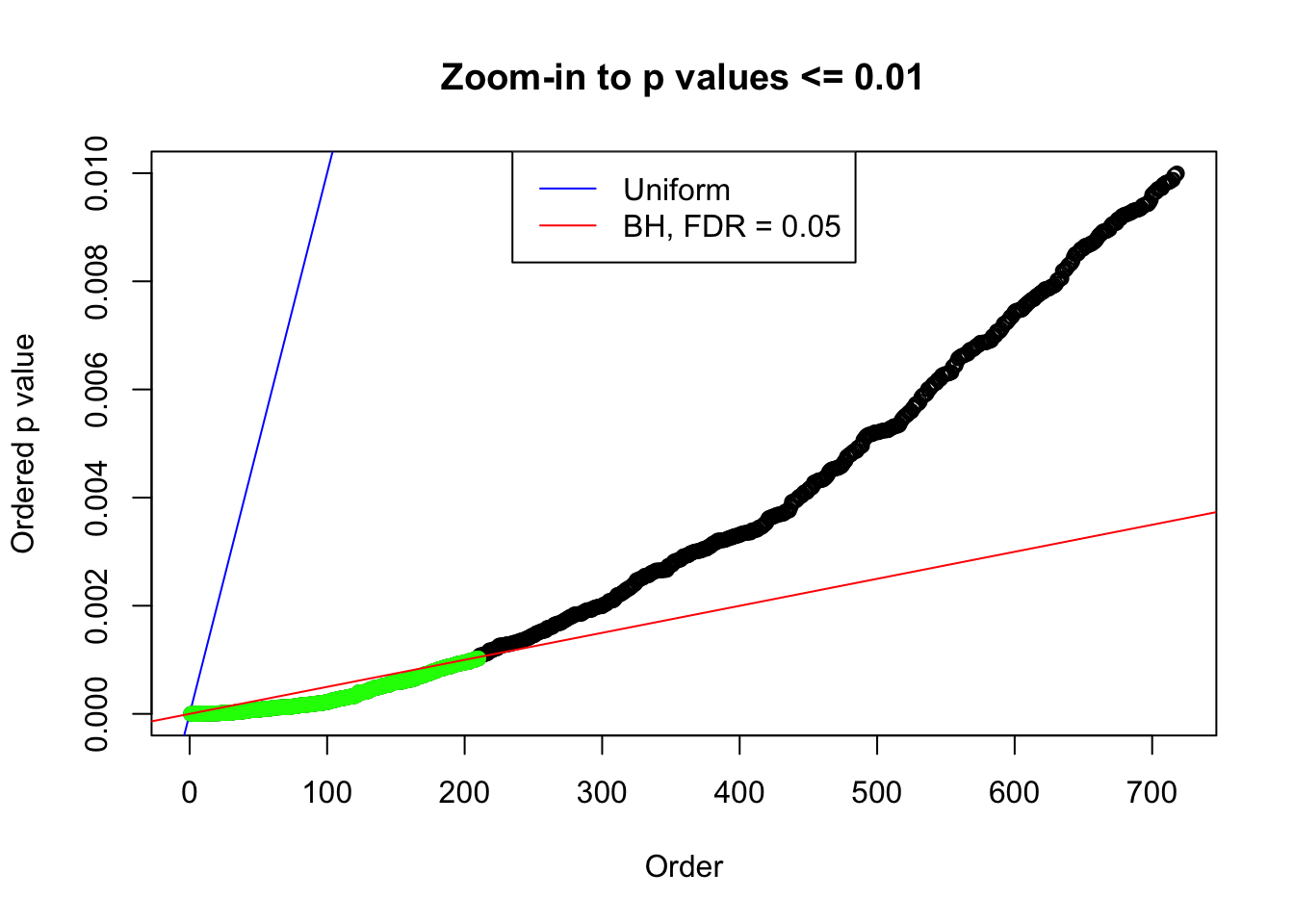
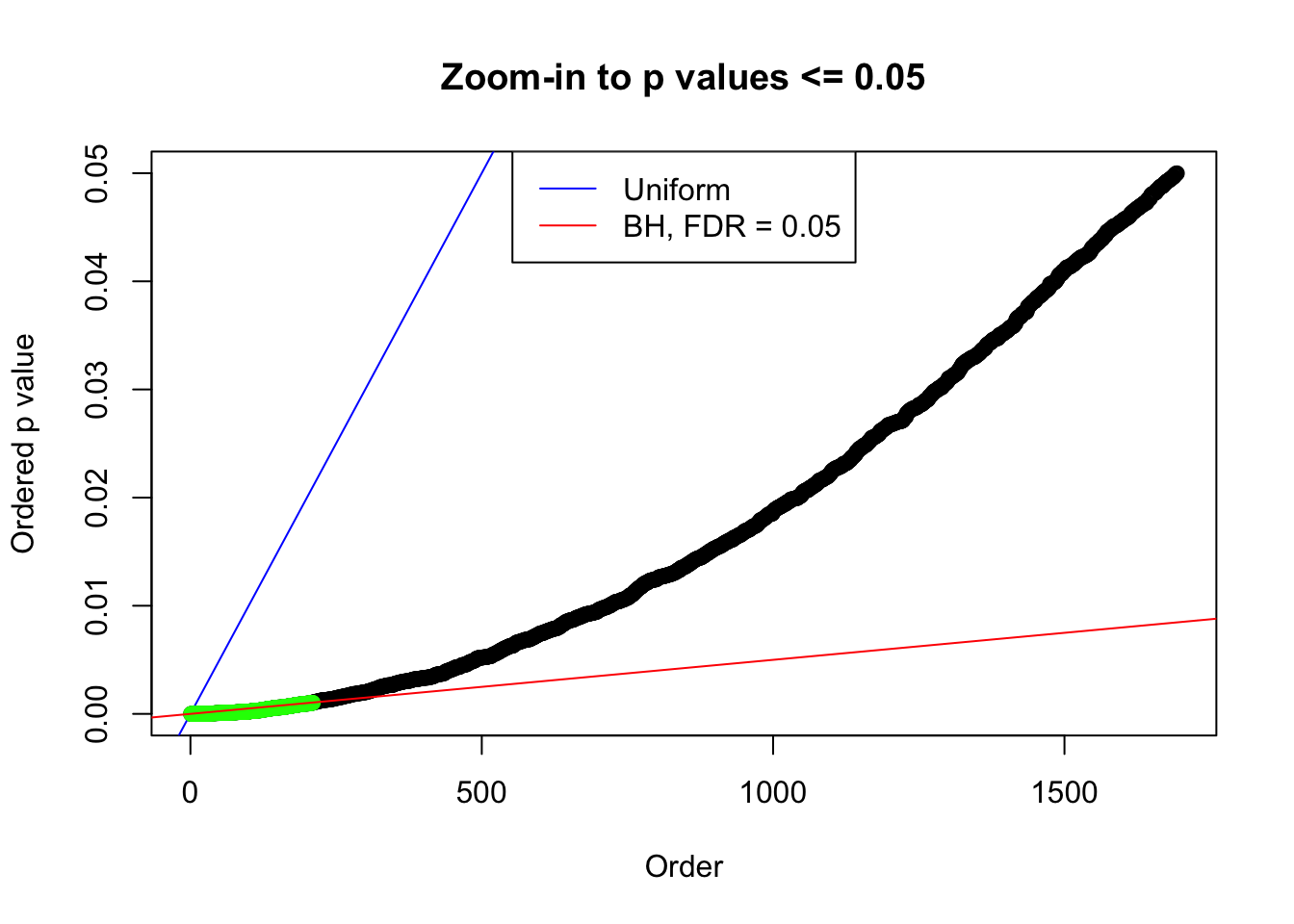
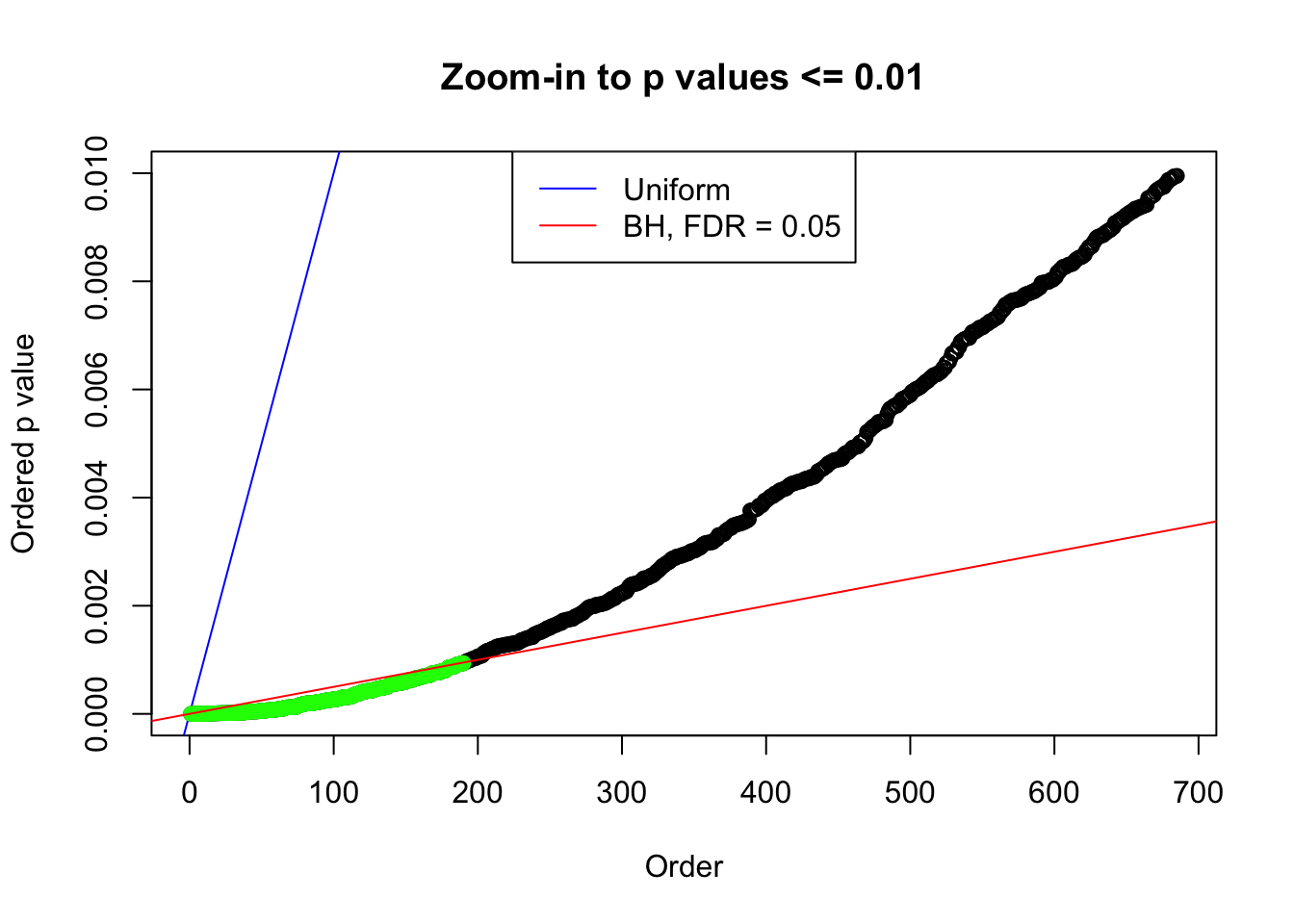
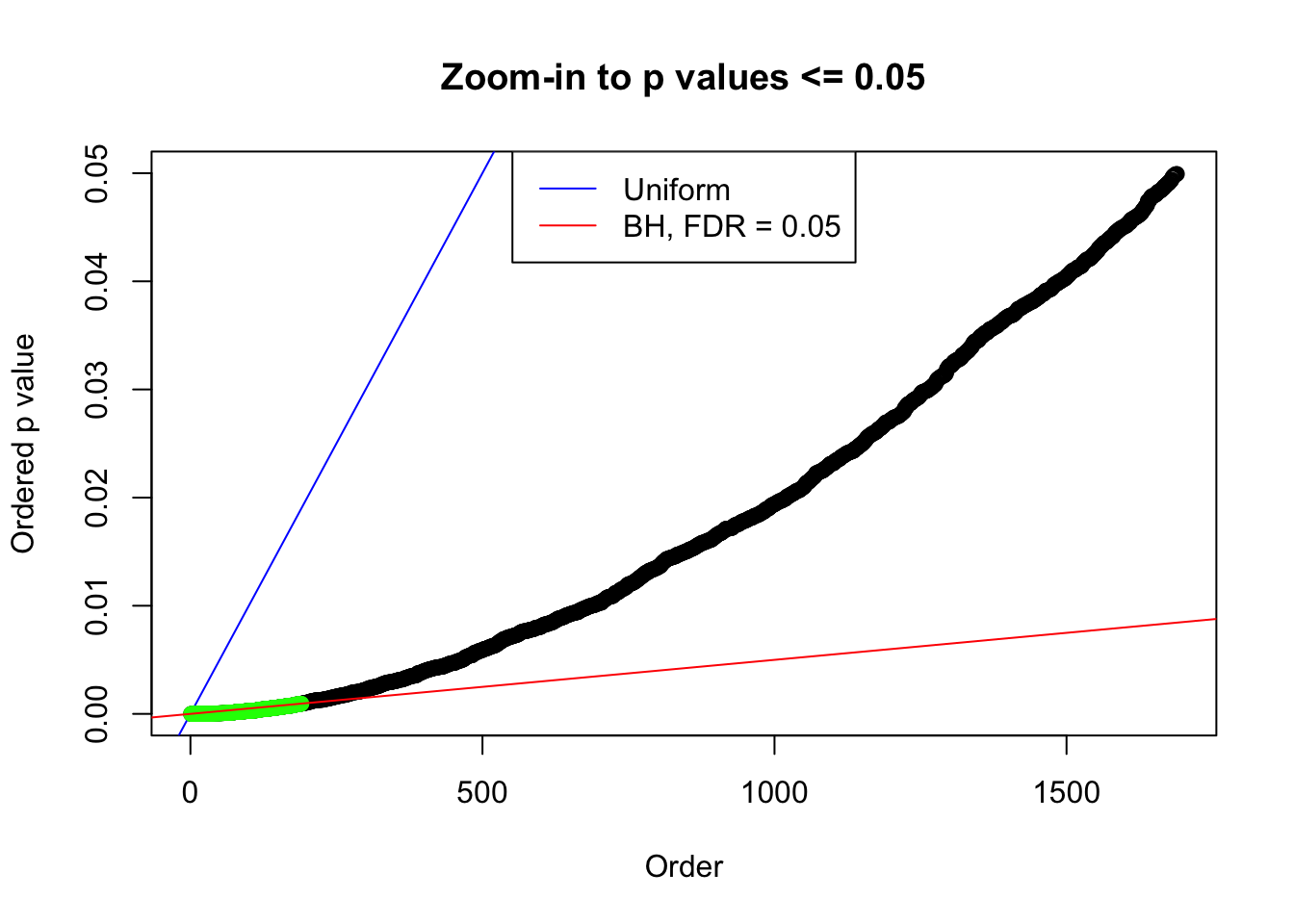
  bh.fd = sum(p.adjust(p, method = "BH") <= 0.05)
  pihat0.ash = get_pi0(ash(z, 1, method = "fdr"))
  ecdfz.fit = ecdfz.optimal(z)
  res[[i]] = list(z = z, p = p, bh.fd = bh.fd, pihat0.ash = pihat0.ash, ecdfz.fit = ecdfz.fit)
}

Number of False Discoveries: 207 ; pihat0 = 0.3309512 
Scaled weights:
1 : -0.0177035771860527 ; 2 : 0.689887136368602 ; 3 : -0.0509478089605657 ; 4 : 0.474815572091947 ; 5 : -0.0255292356243276 ; 6 : 0.197260355735445 ; 7 : 0.0209642526780779 ;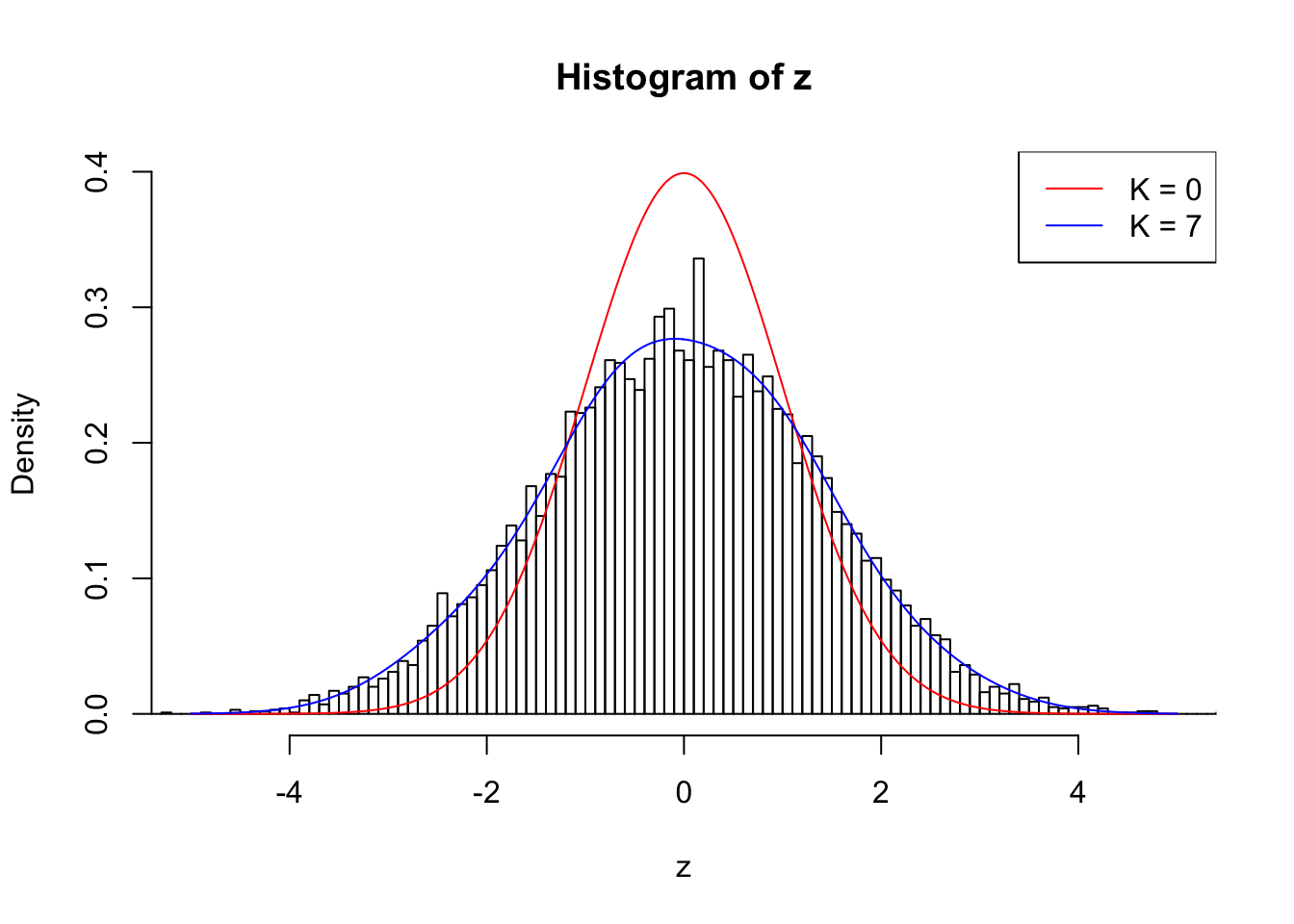

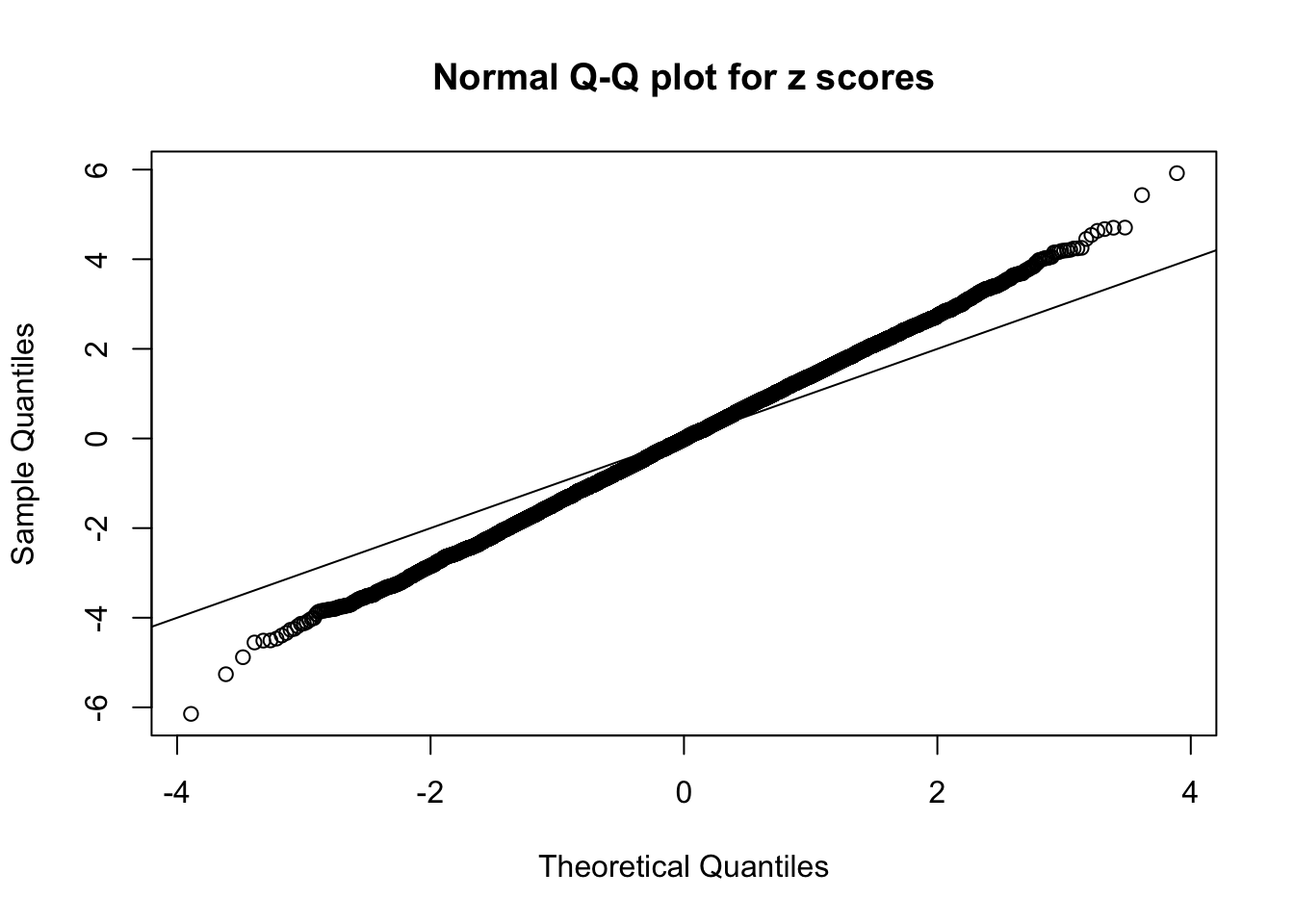
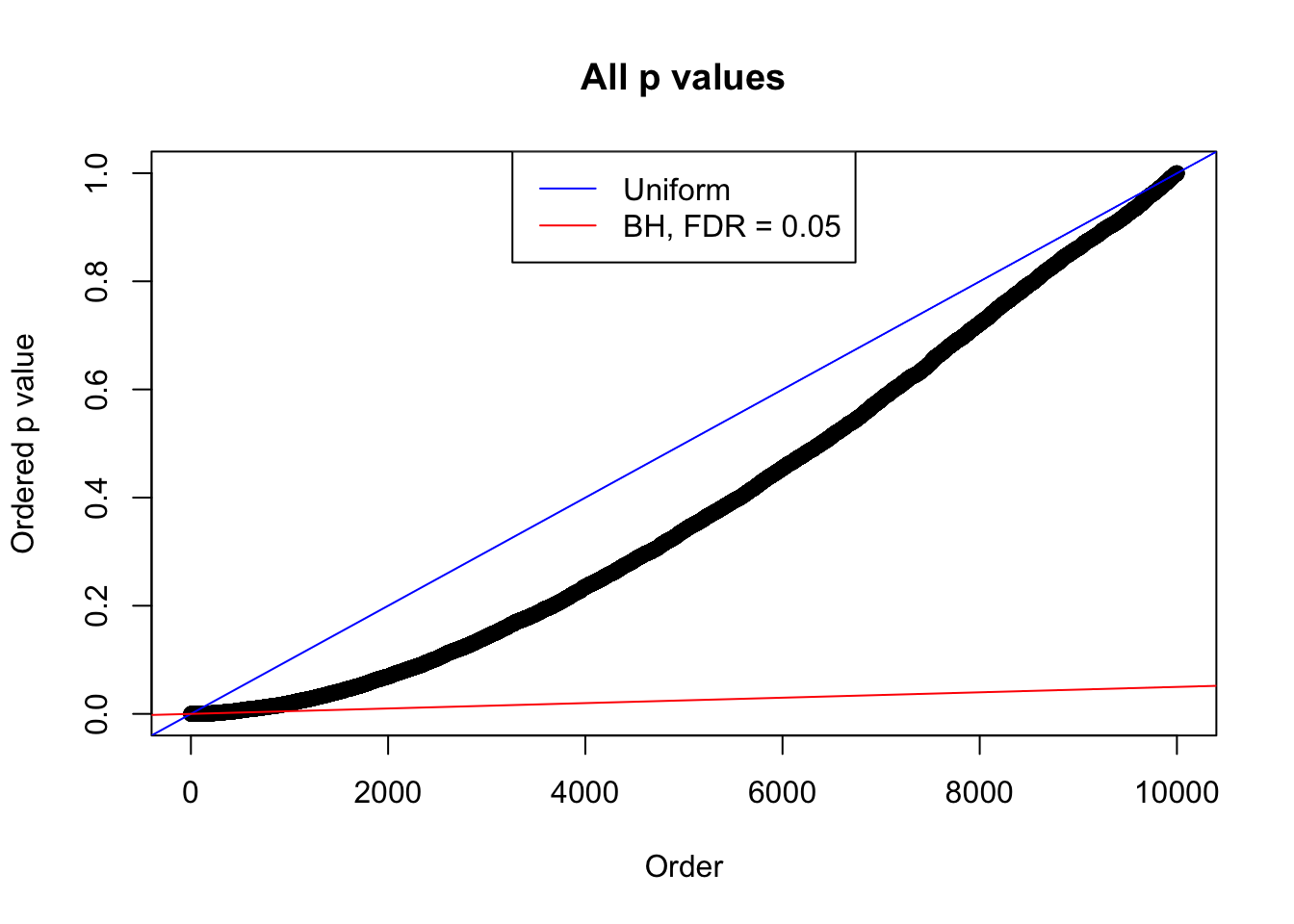
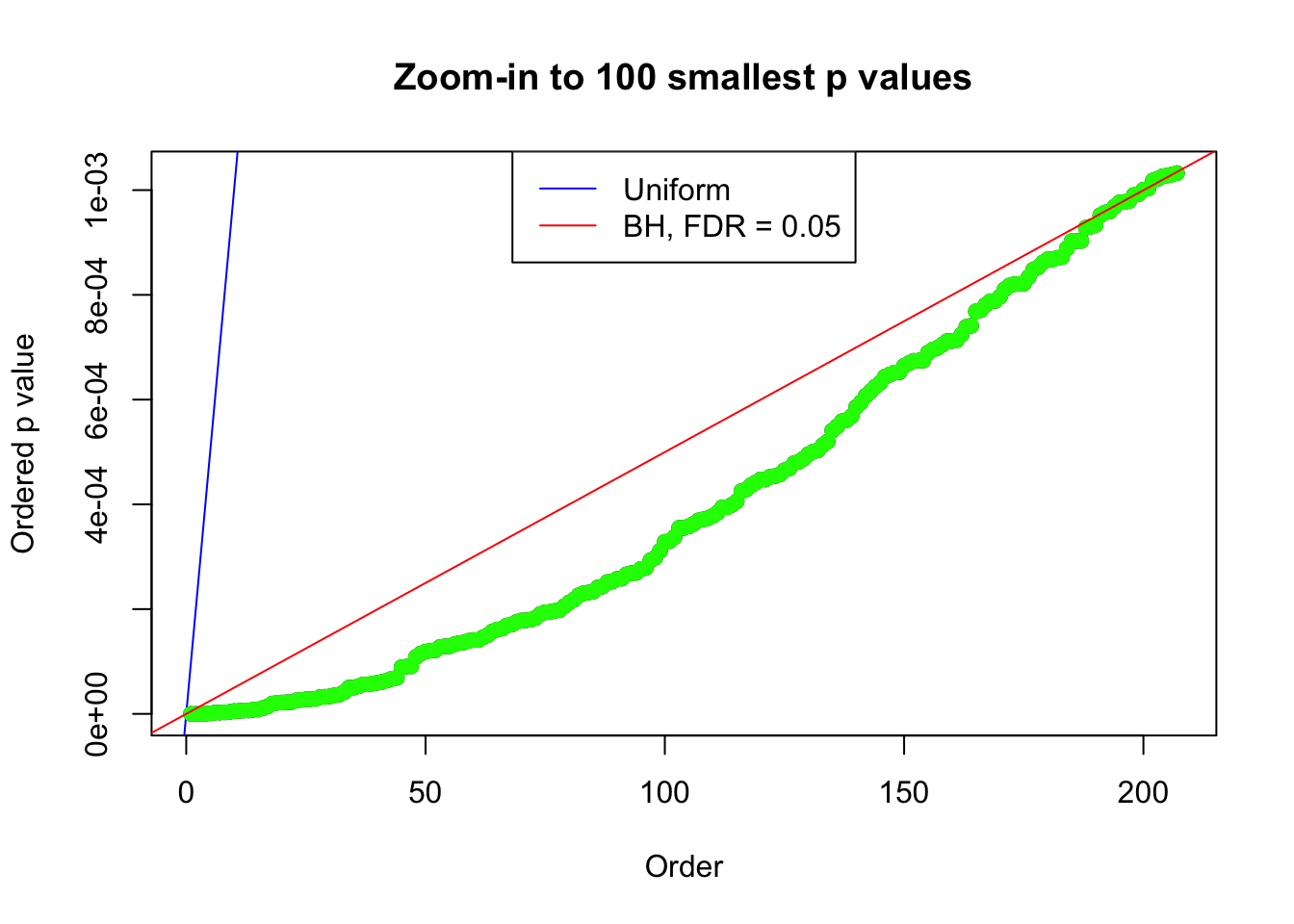
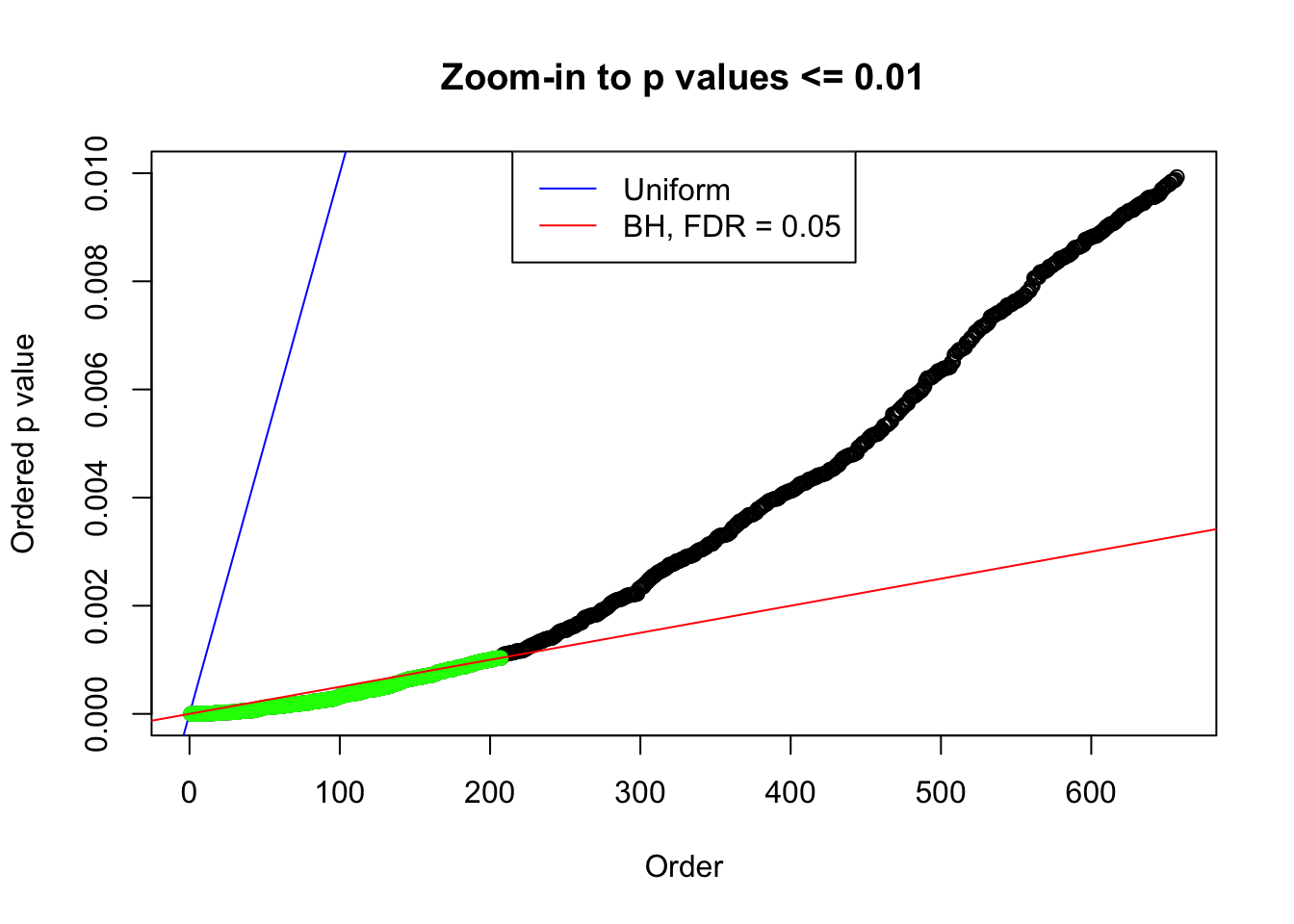
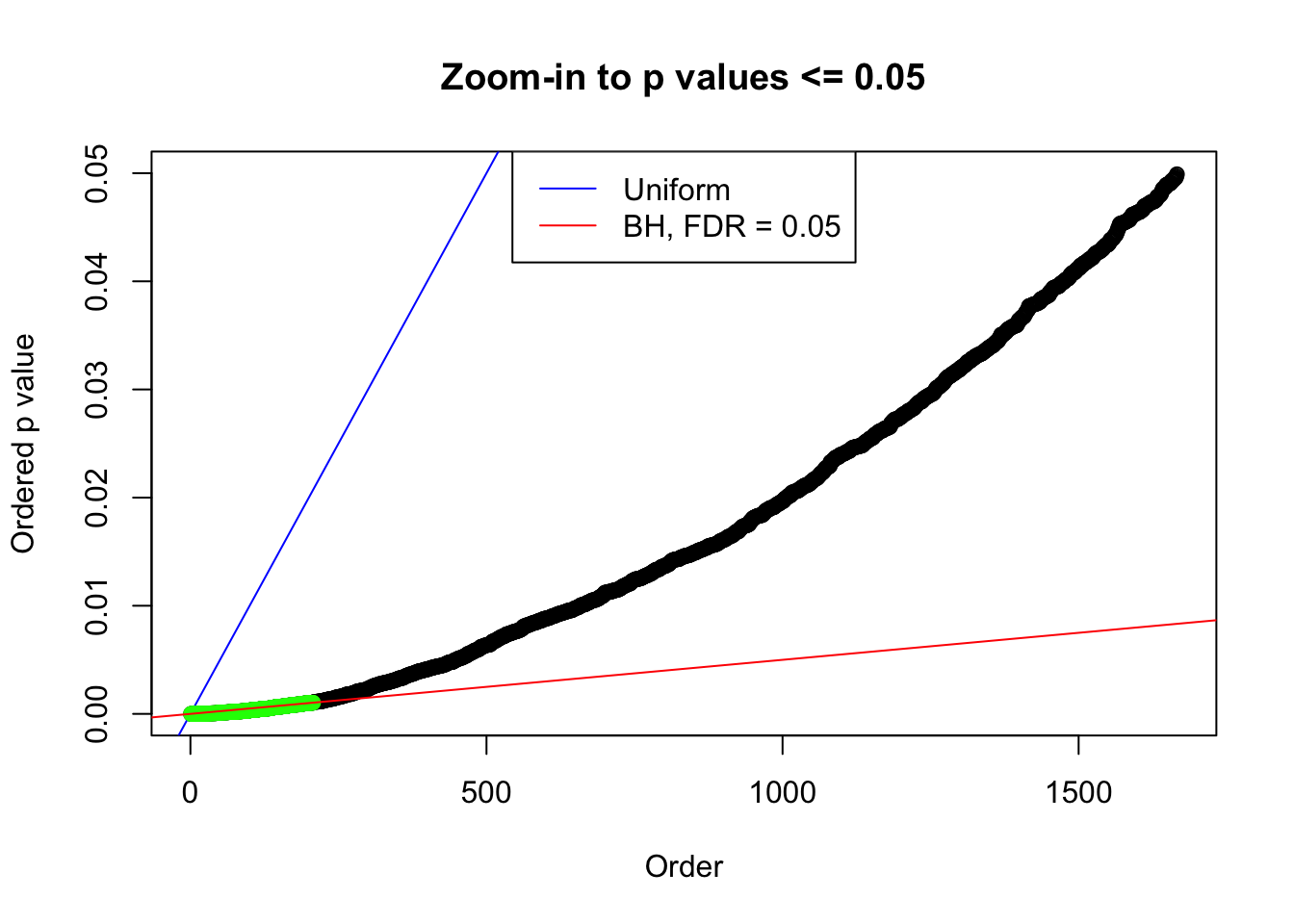
Number of False Discoveries: 210 ; pihat0 = 0.3484933 
Scaled weights:
1 : -0.00737514574580675 ; 2 : 0.710989131104057 ; 3 : -0.0342447864738427 ; 4 : 0.555898827287519 ; 5 : -0.00986066214392825 ; 6 : 0.26603682769249 ; 7 : 0.0306361333022764 ;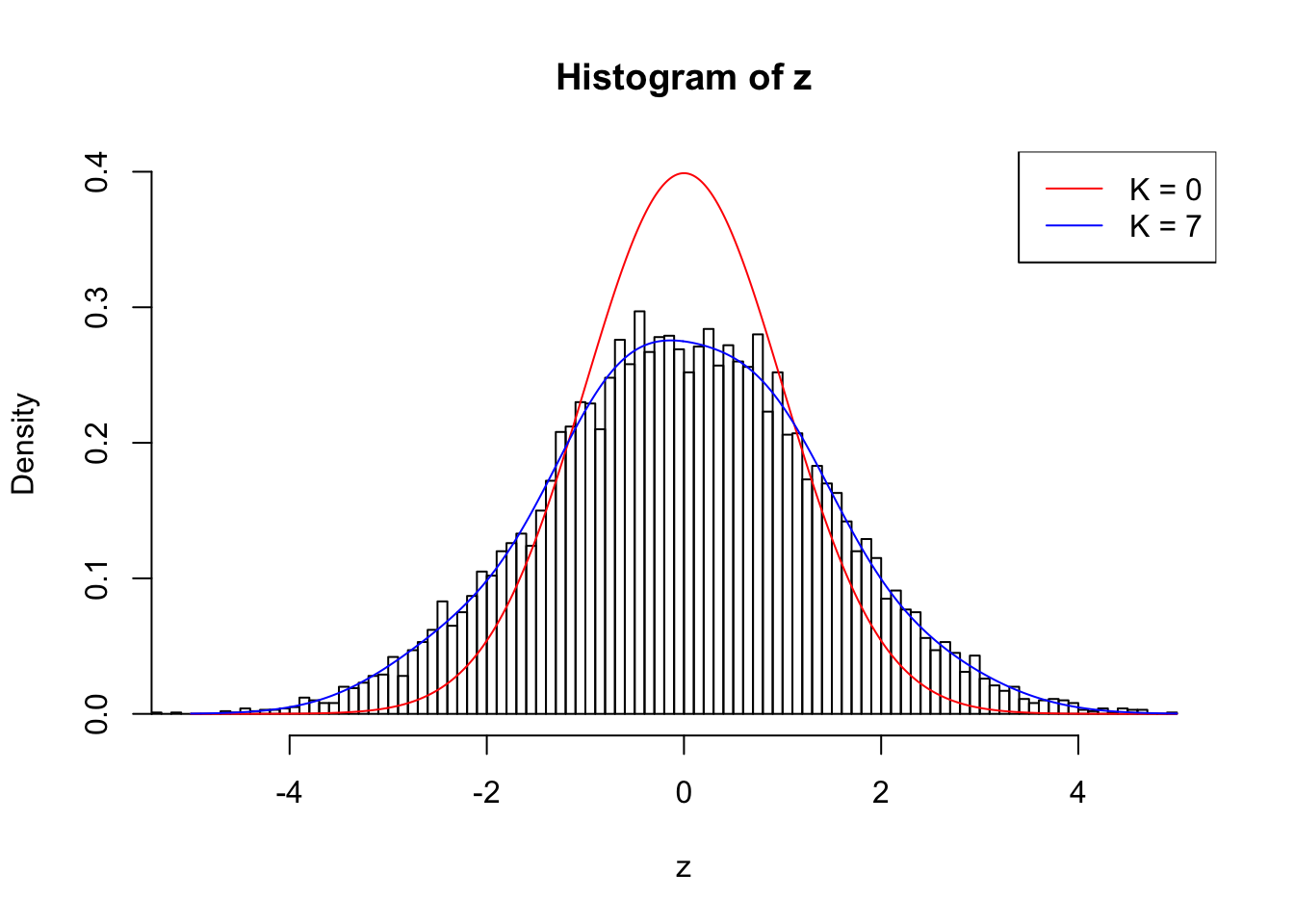

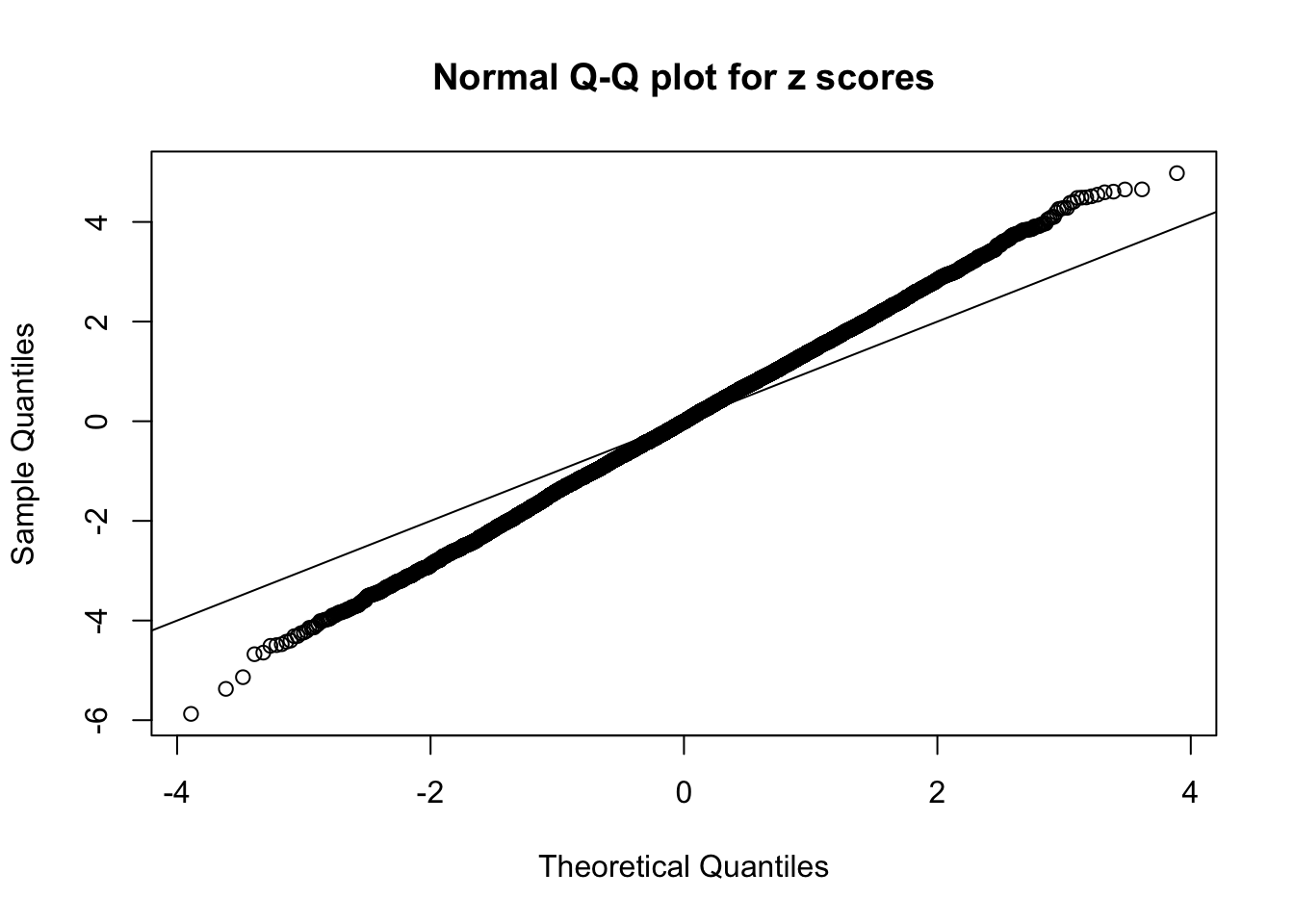
Number of False Discoveries: 190 ; pihat0 = 0.3438938 
Scaled weights:
1 : 0.00366309861970015 ; 2 : 0.686706854397367 ; 3 : 0.0586825498559195 ; 4 : 0.519903434456322 ; 5 : 0.0632968145789646 ; 6 : 0.230863448021081 ; 7 : 0.0428429372260126 ;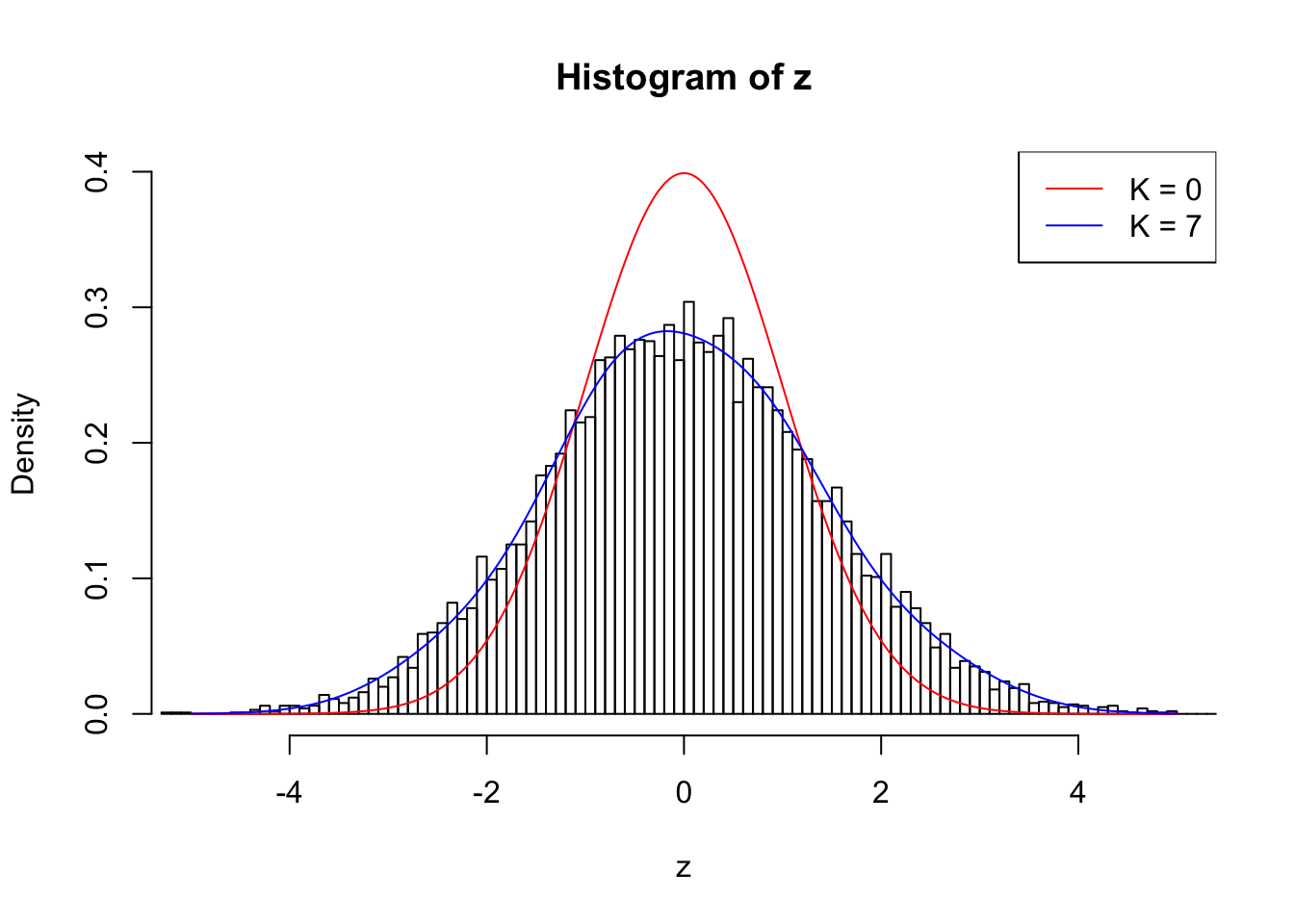

Session information

sessionInfo()

R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.3

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] backports_1.0.5 magrittr_1.5    rprojroot_1.2   tools_3.3.2    
 [5] htmltools_0.3.5 yaml_2.1.14     Rcpp_0.12.10    stringi_1.1.2  
 [9] rmarkdown_1.3   knitr_1.15.1    stringr_1.2.0   digest_0.6.11  
[13] evaluate_0.10