Simulating Correlated \(N(0, 1)\) \(Z\) Scores: More Complicated

Introduction

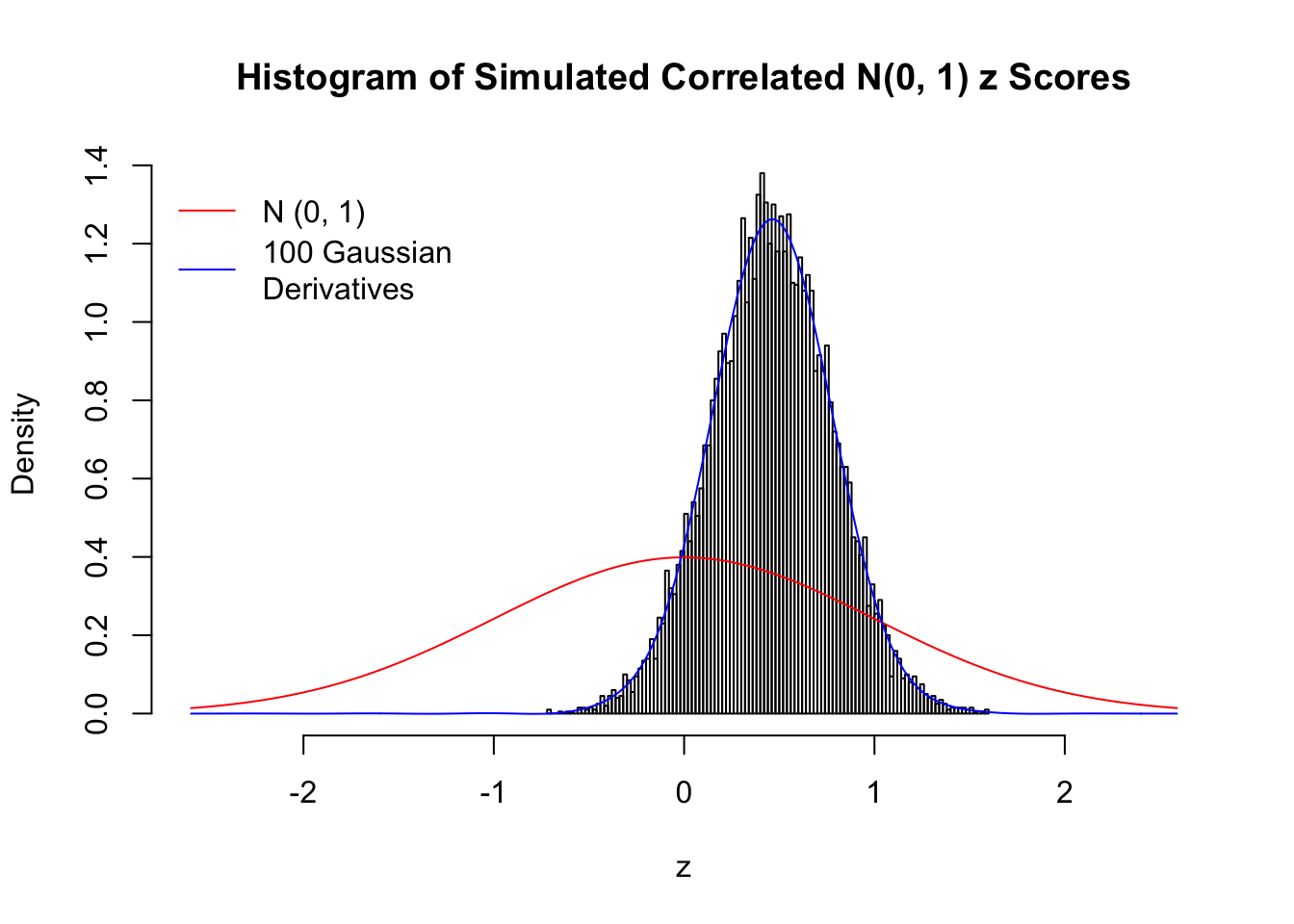
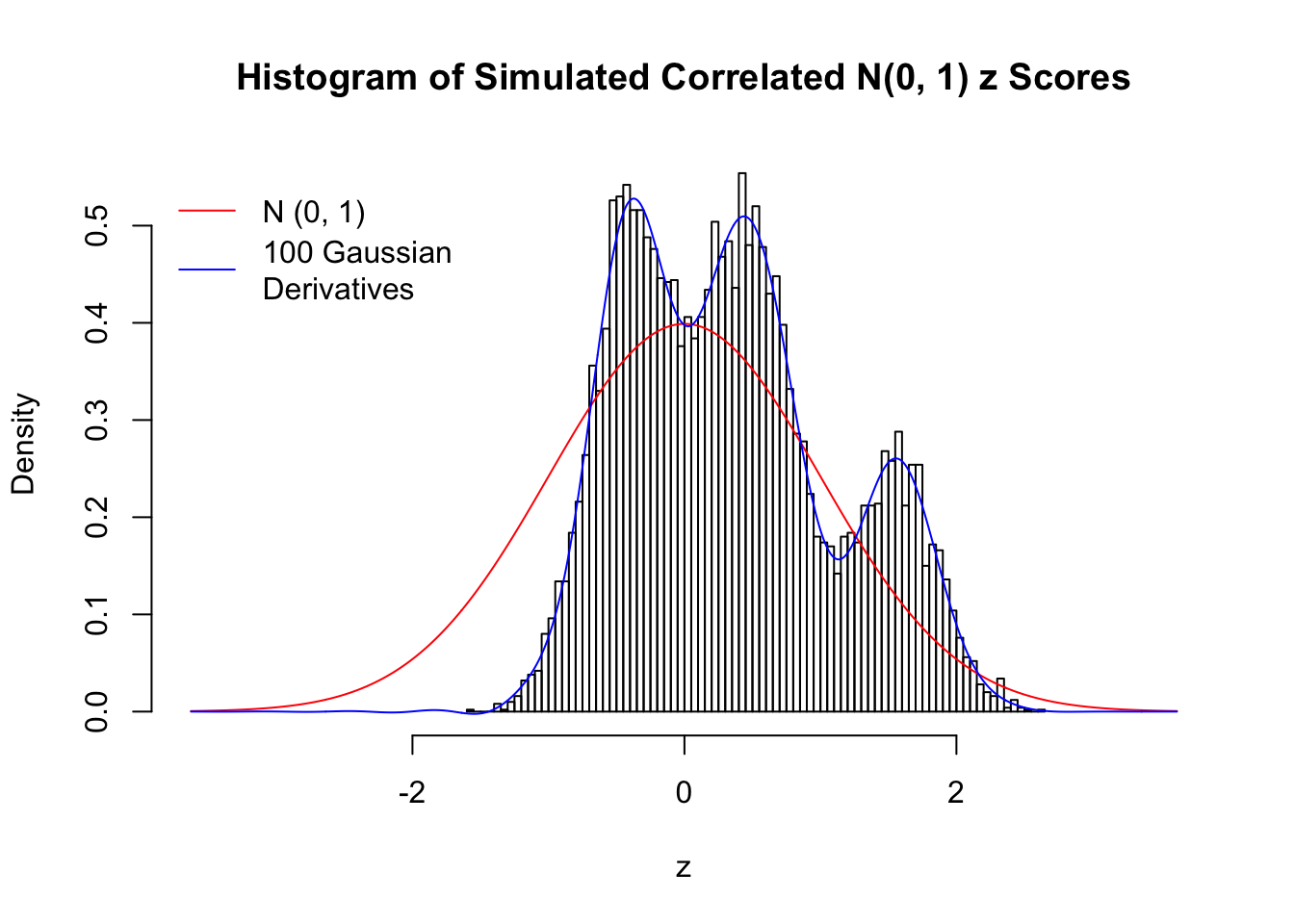
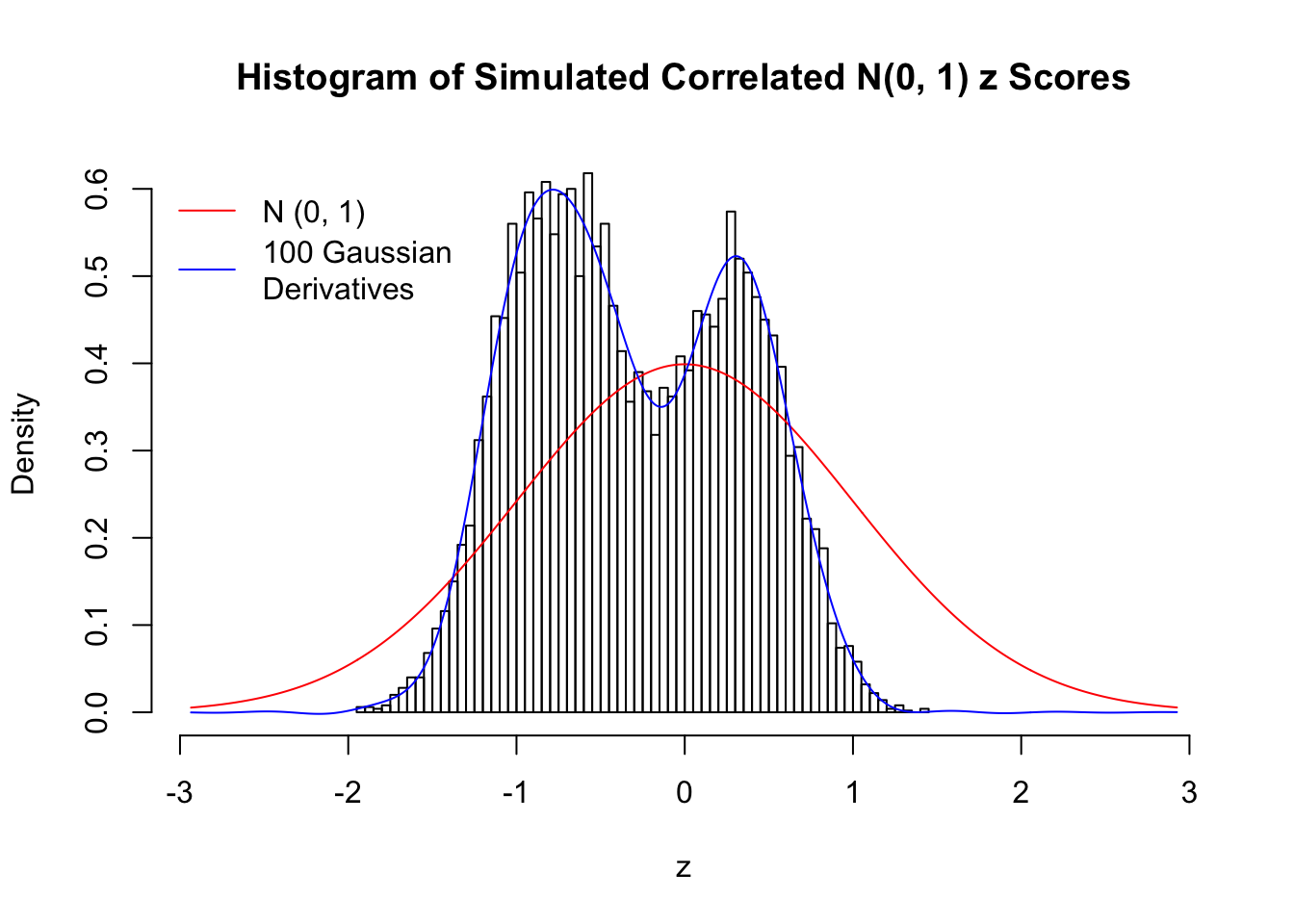
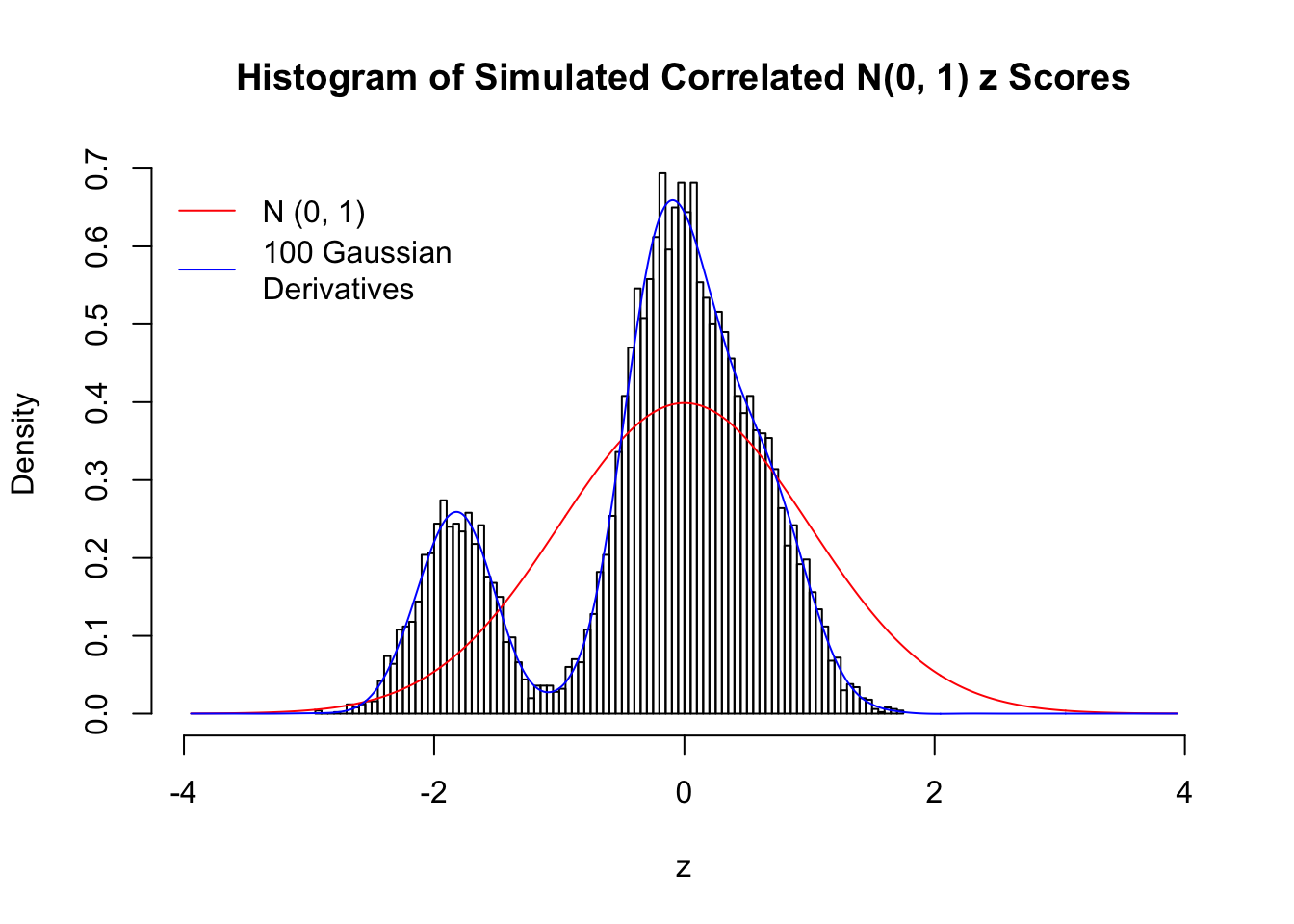
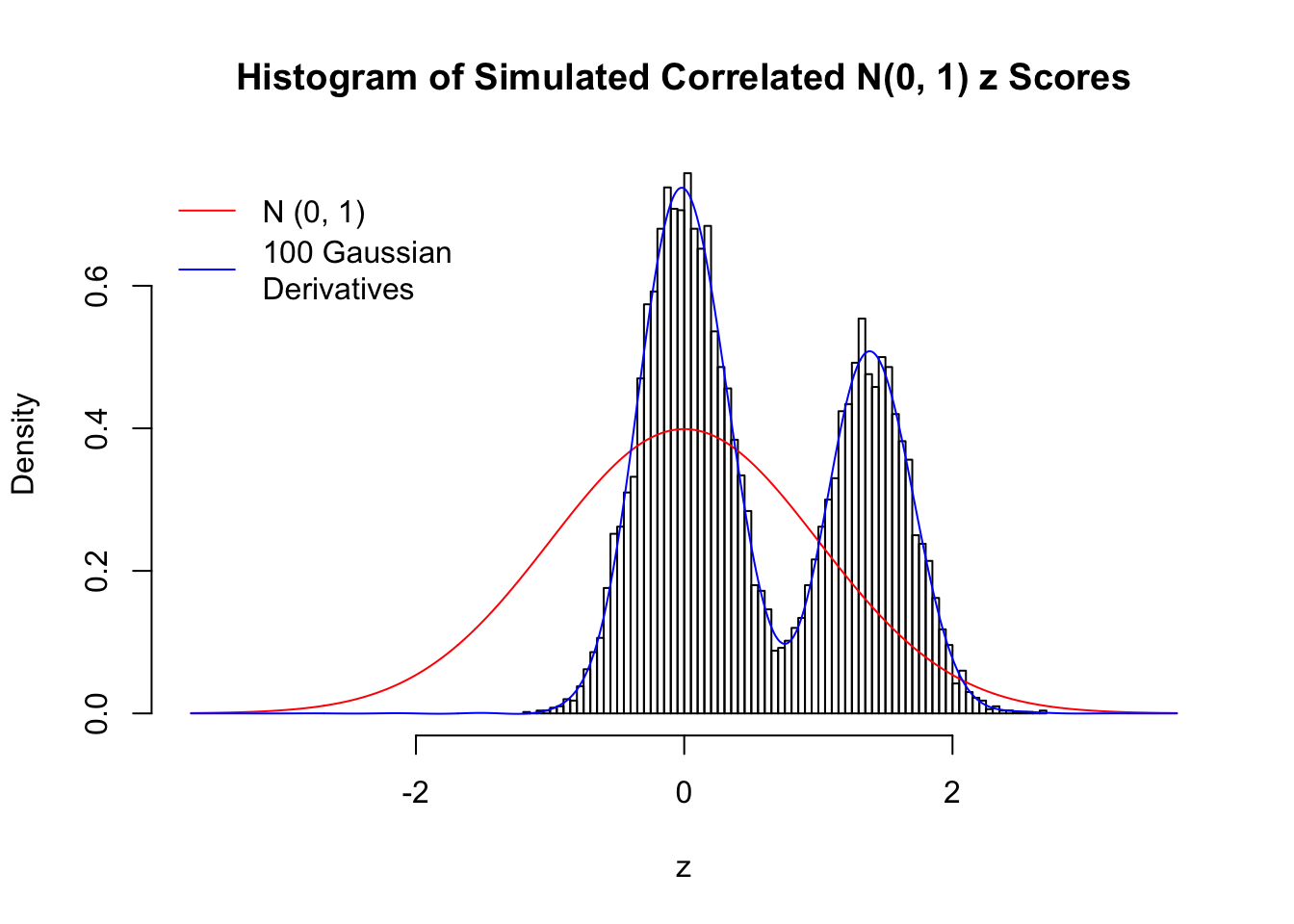
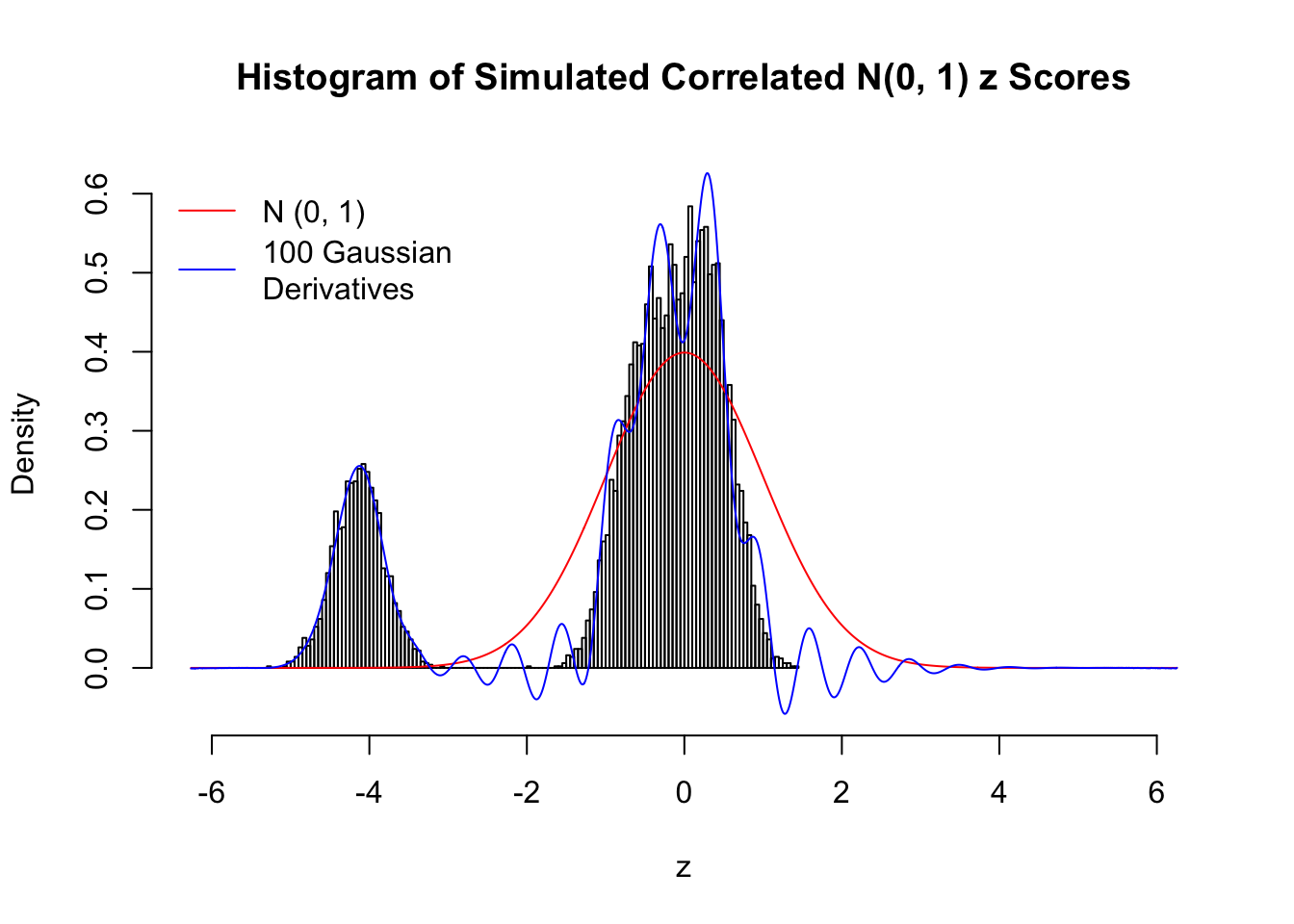
Despite his theory on the connection between Gaussian derivatives and empirical distributions of correlated null \(z\) scores, Dr. Schwartzman in his own research used Gaussian mixtures instead of Gaussian derivatives to fit the empirical distribution. A motivating example of his is a large number of marginally \(N\left(0, 1\right)\) \(z\) scores that are closely correlated with each other within one group, but independent between groups. We now show that data simulated in this way can also be fitted by Gaussian derivatives by the method of moments. To be specific, let \(n\) standard normal random samples be in \(K\) groups, in each group \(k\), given \(x_k\), \(y_{ki}\) iid \(N\left(0, 1\right)\),

\[ z_{ki} = \sqrt{\rho} x_k + \sqrt{1 - \rho} y_{ki} \ . \] In all the simulations, we choose \(n = 10^4\), \(\rho = 0.9\), and for theoretical exploration, \(L = 100\) Gaussian derivatives.

n = 1e4
rho = 0.9
L = 100

Scenario I: One Group

set.seed(777)
K = 1
for (j in 1 : 5) {
  z = z.sim(n, K, rho)
  fit.gd(L, z)
}

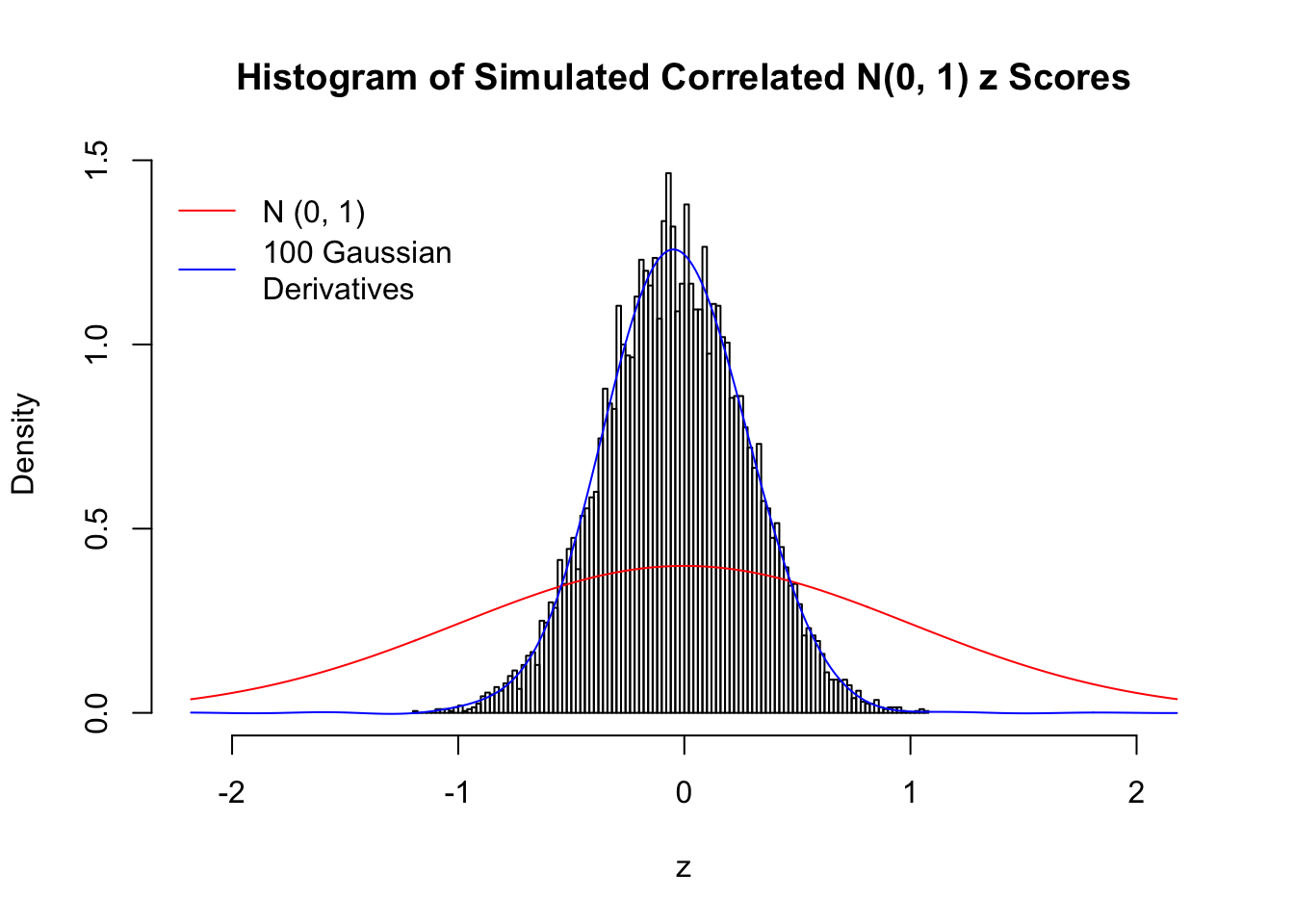
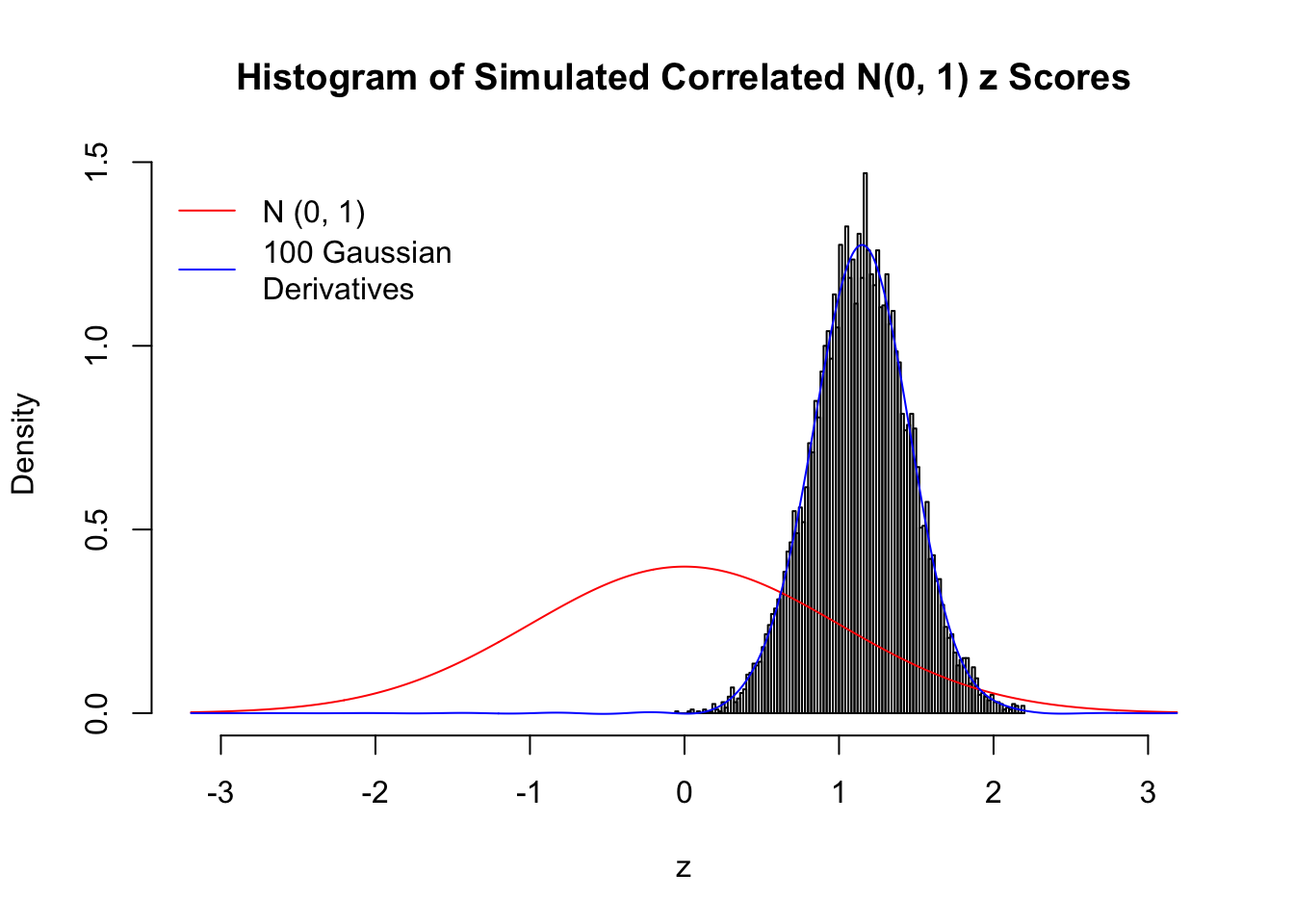
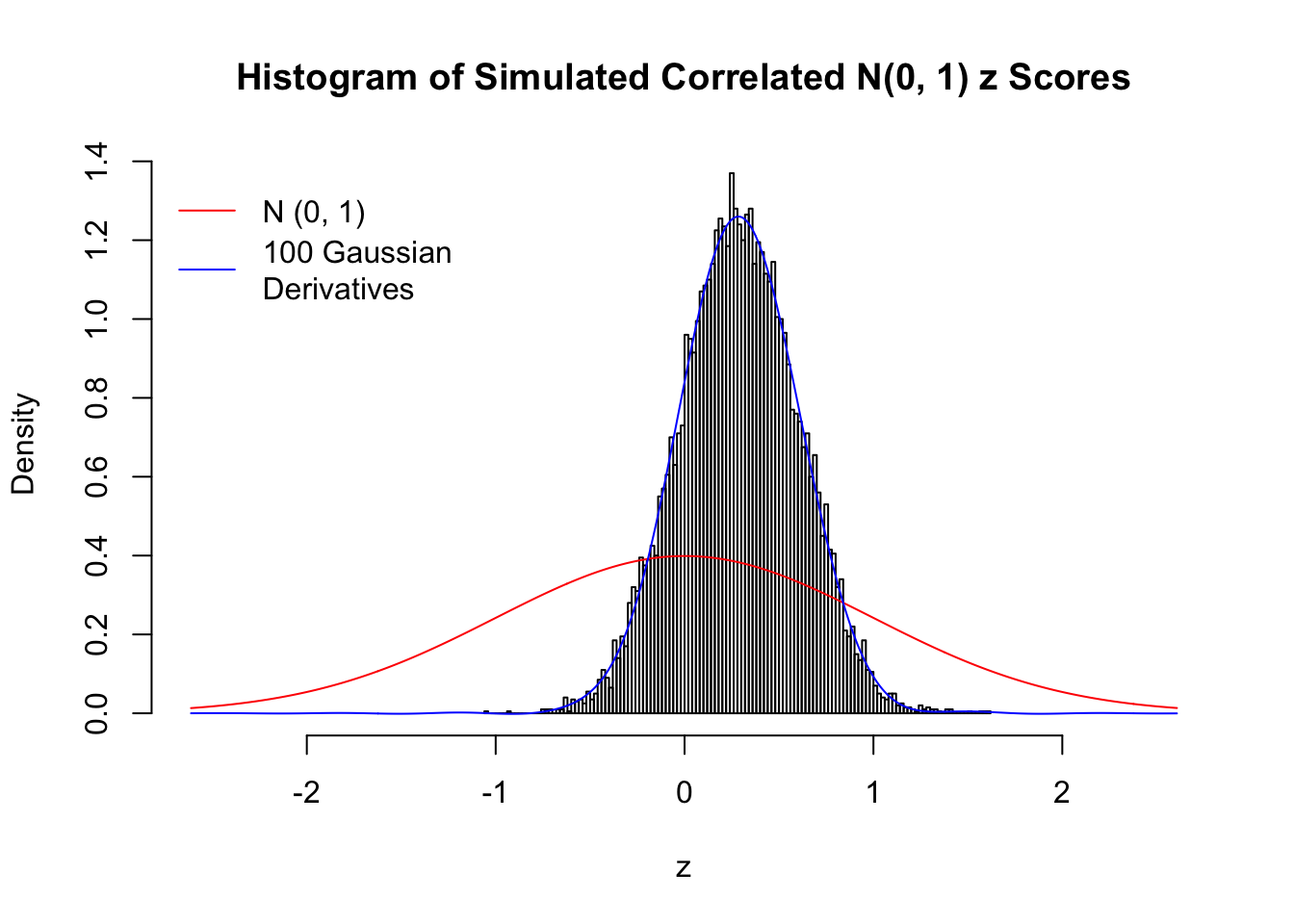
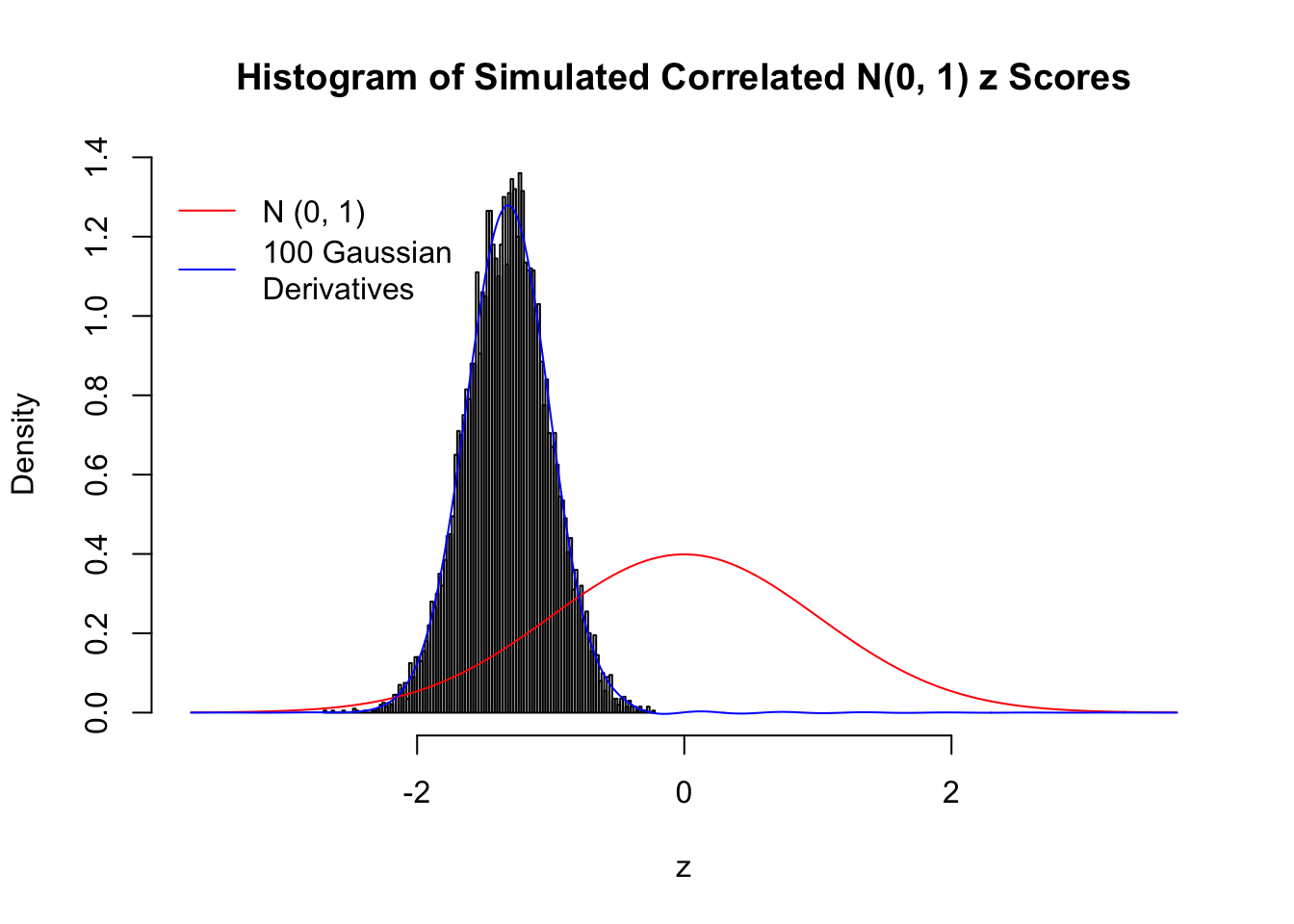
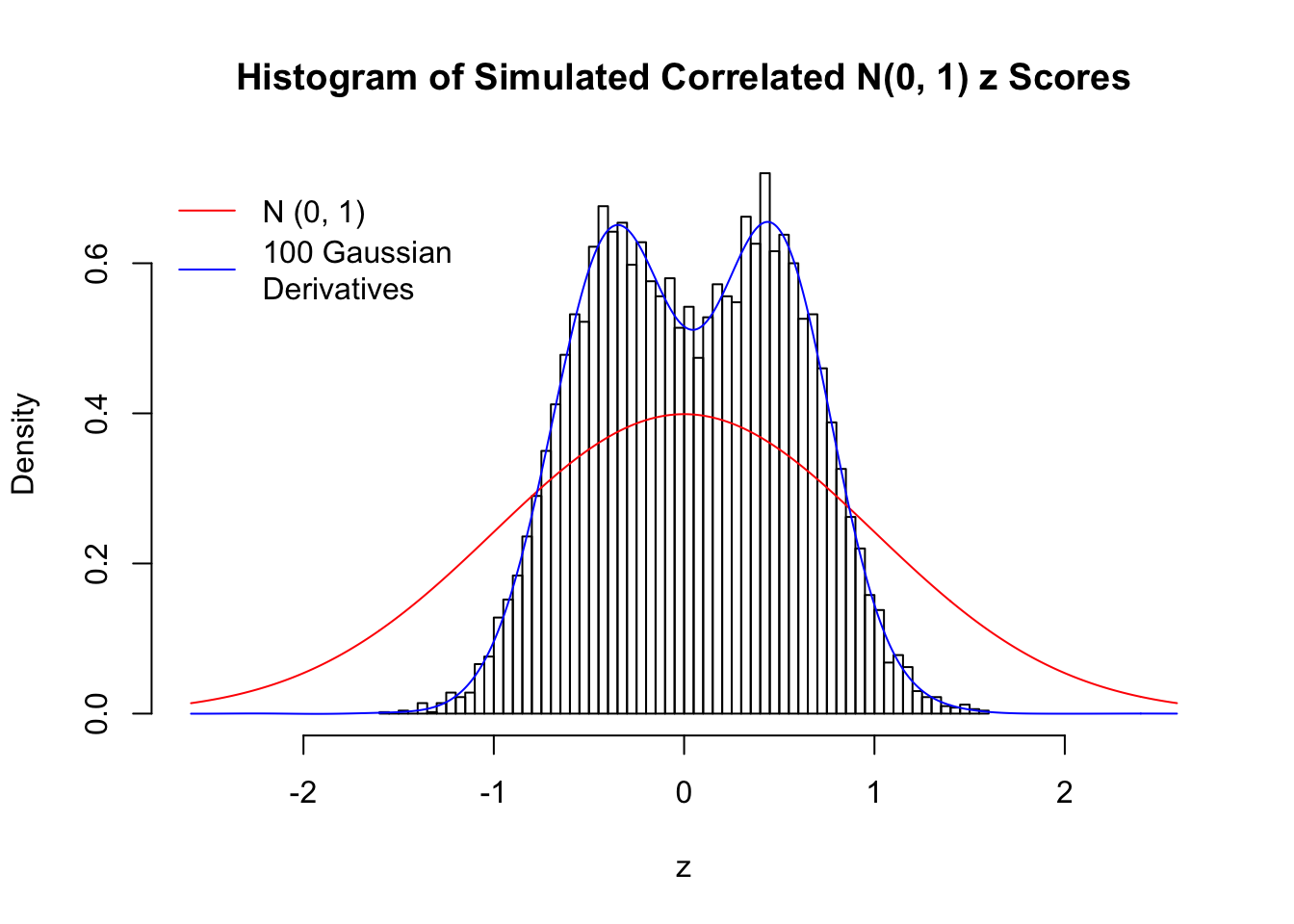
Scenario II: Two Groups

set.seed(777)
K = 2
for (j in 1 : 5) {
  z = z.sim(n, K, rho)
  fit.gd(L, z)
}

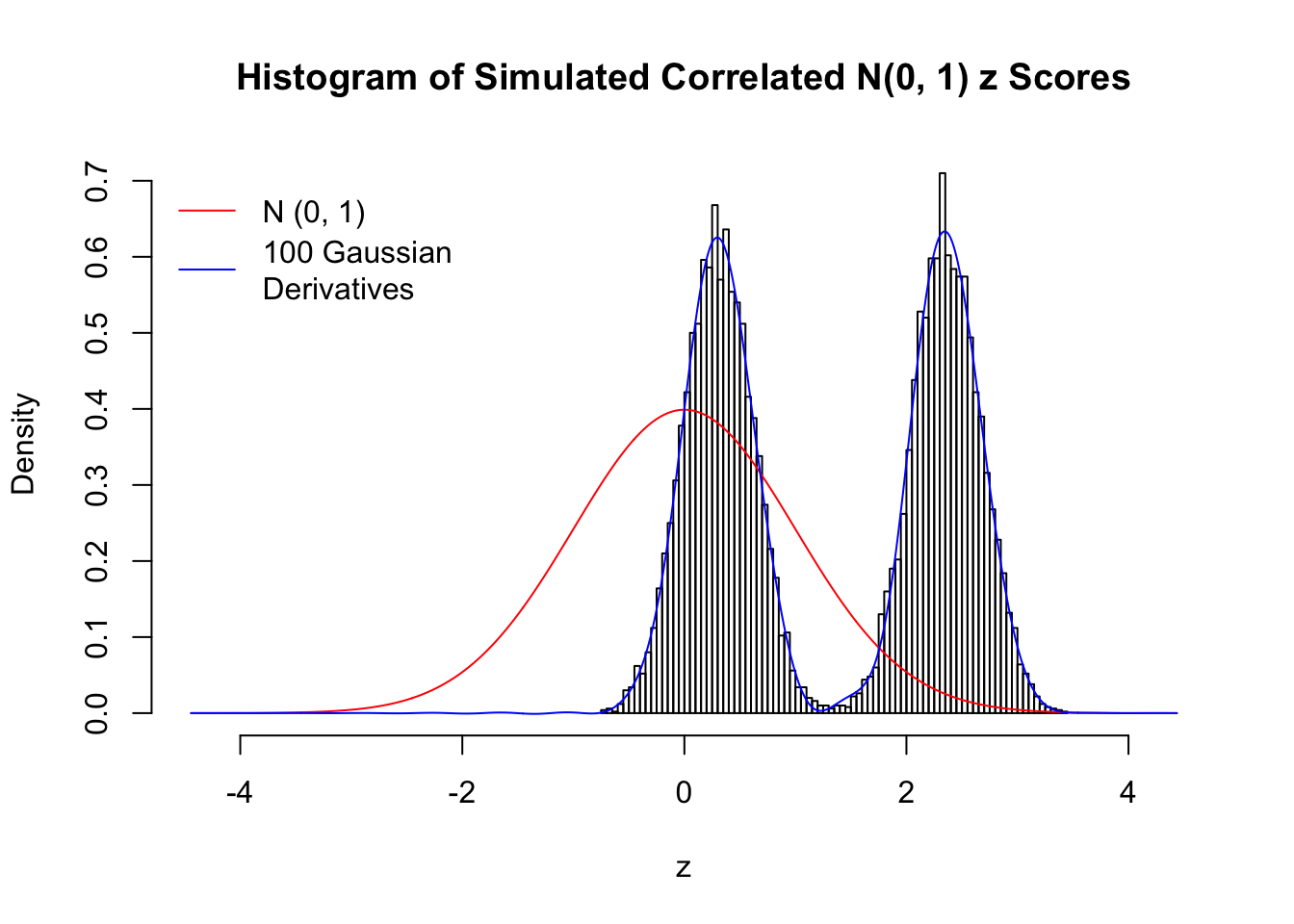
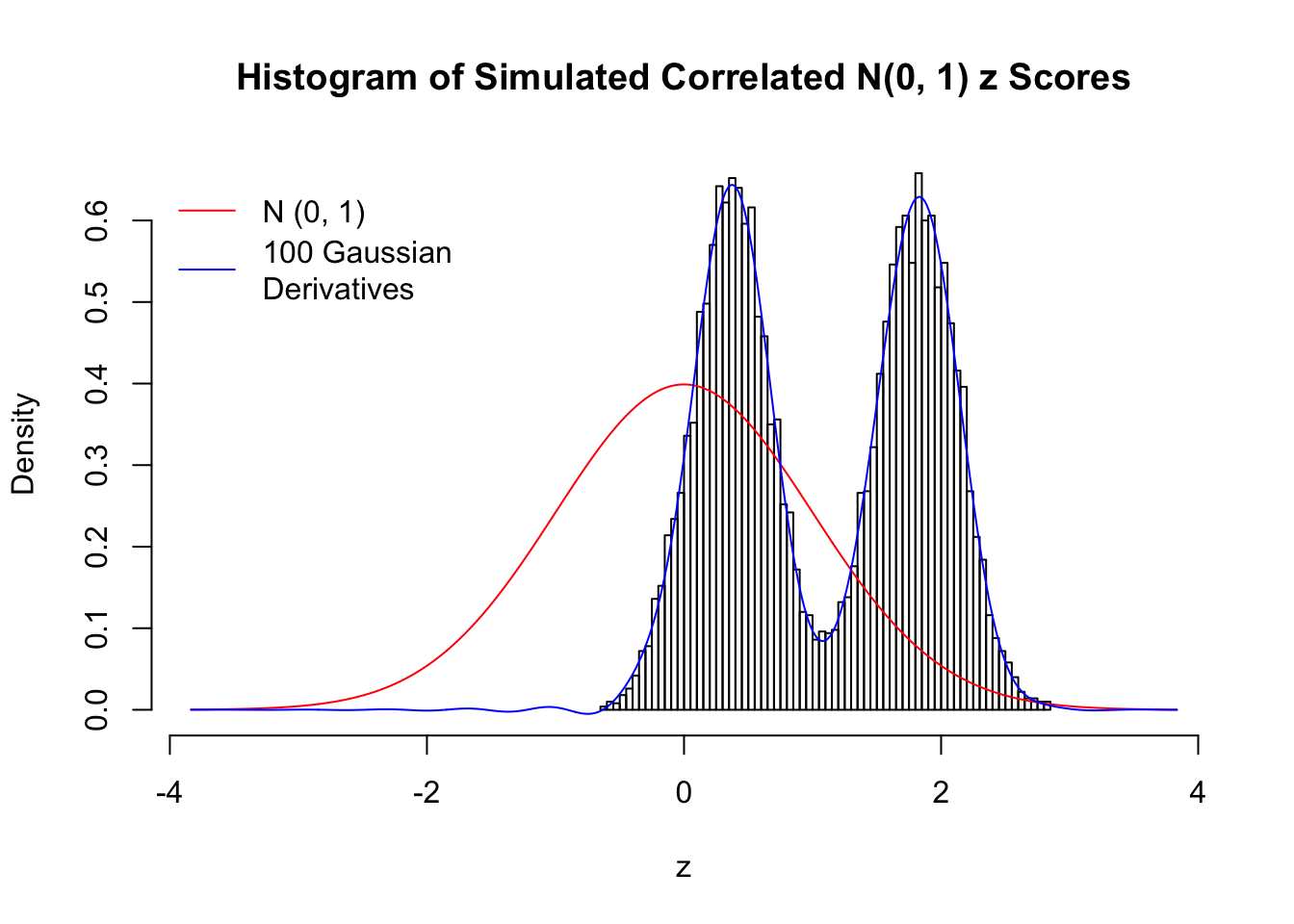
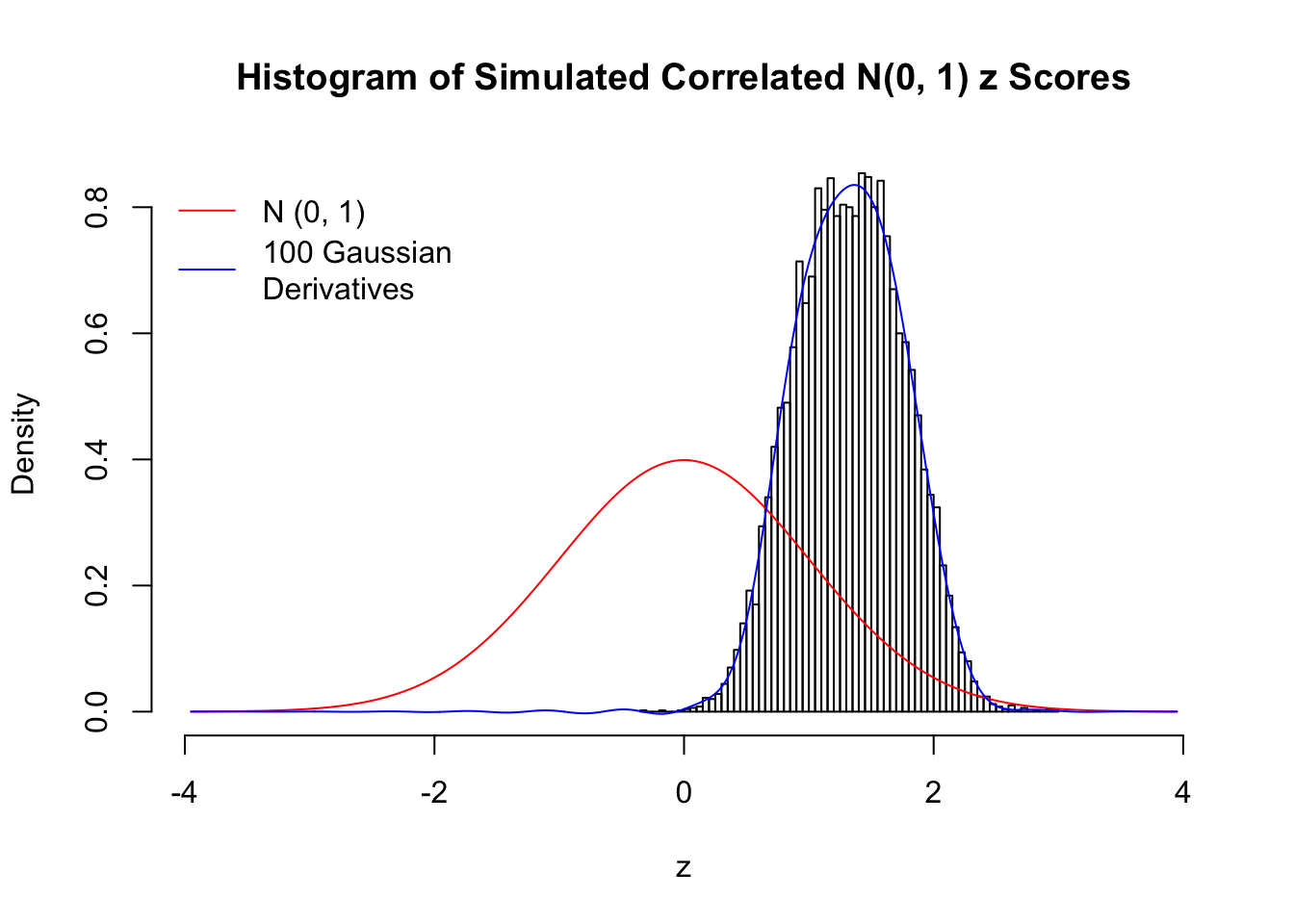
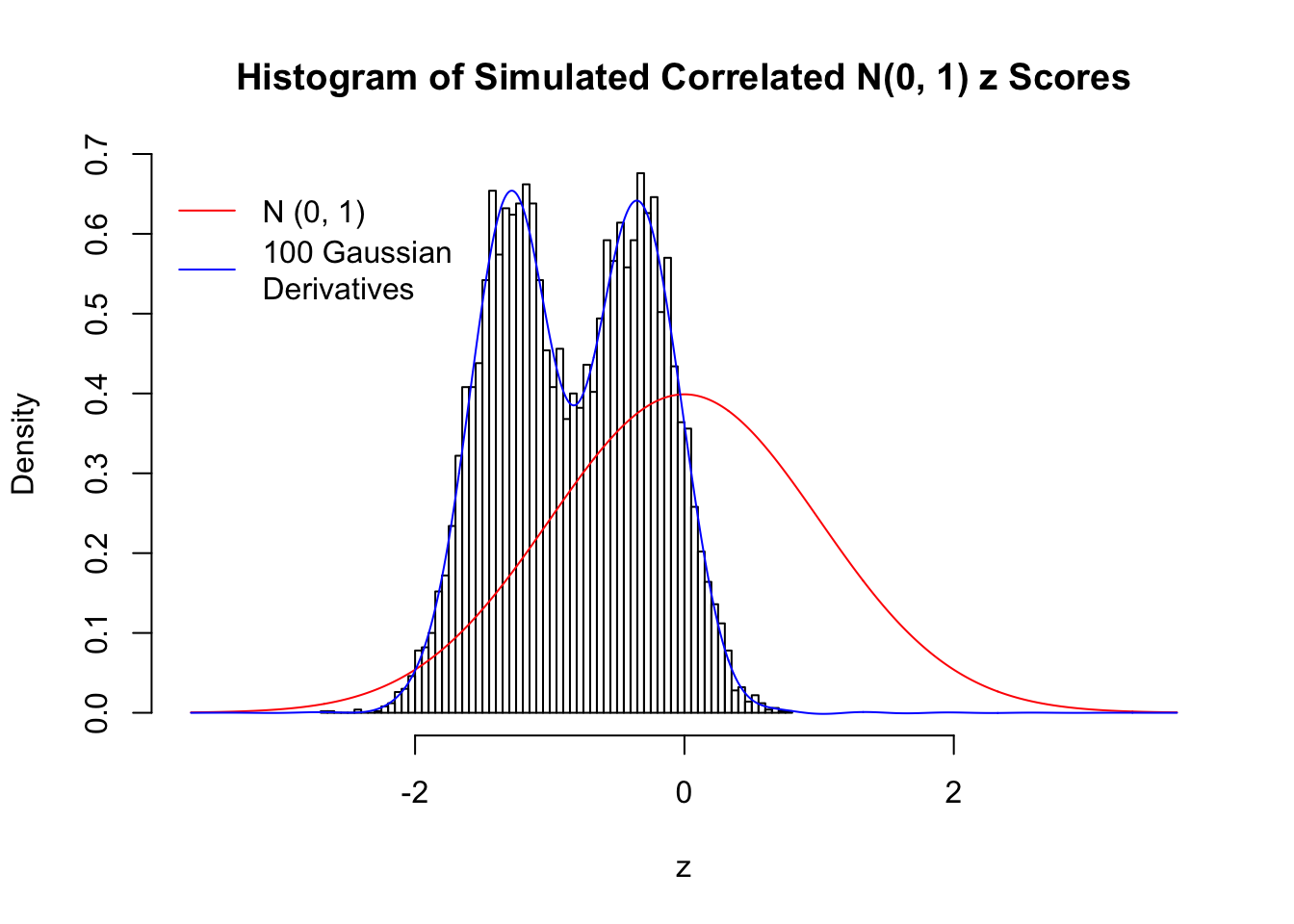
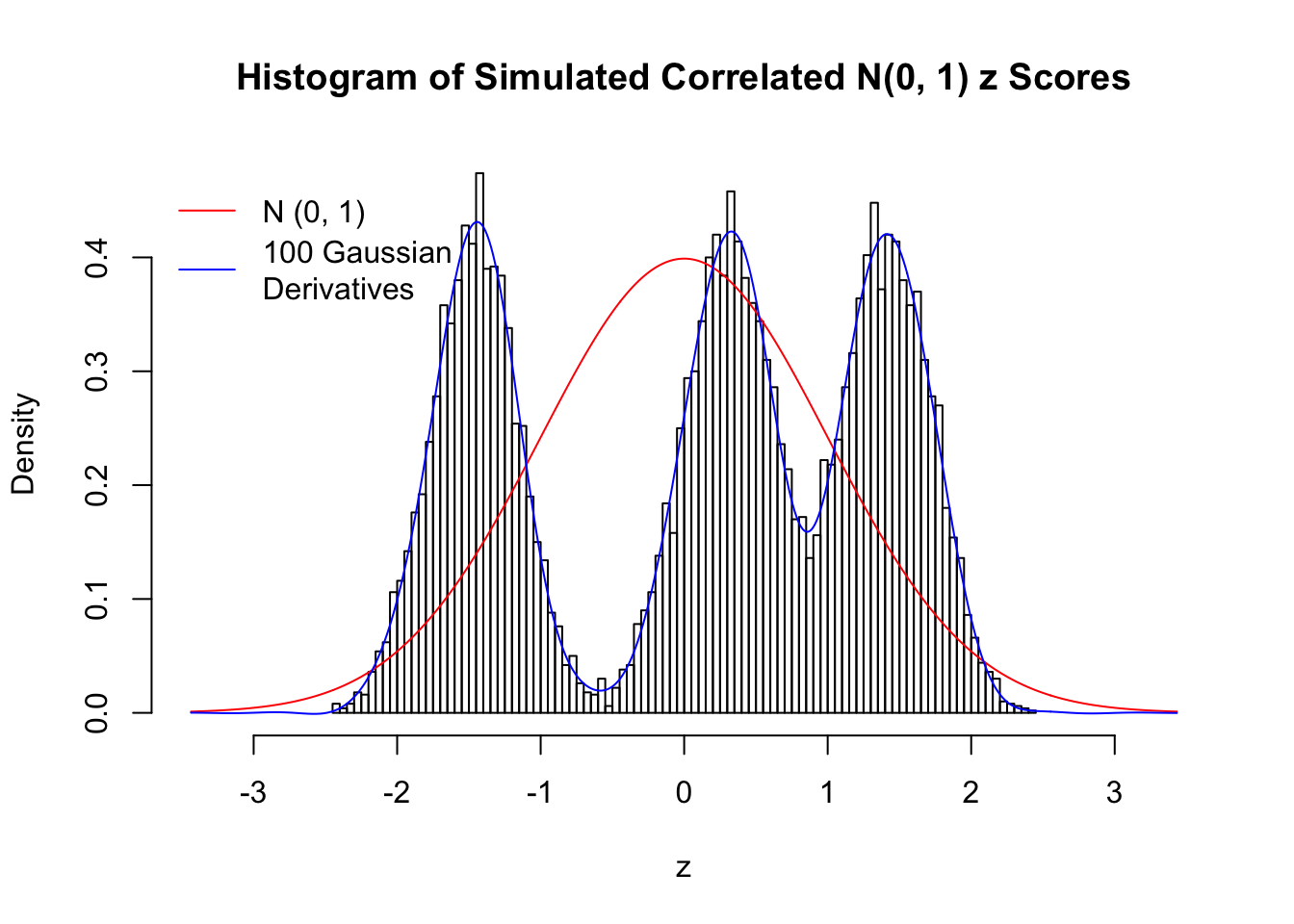
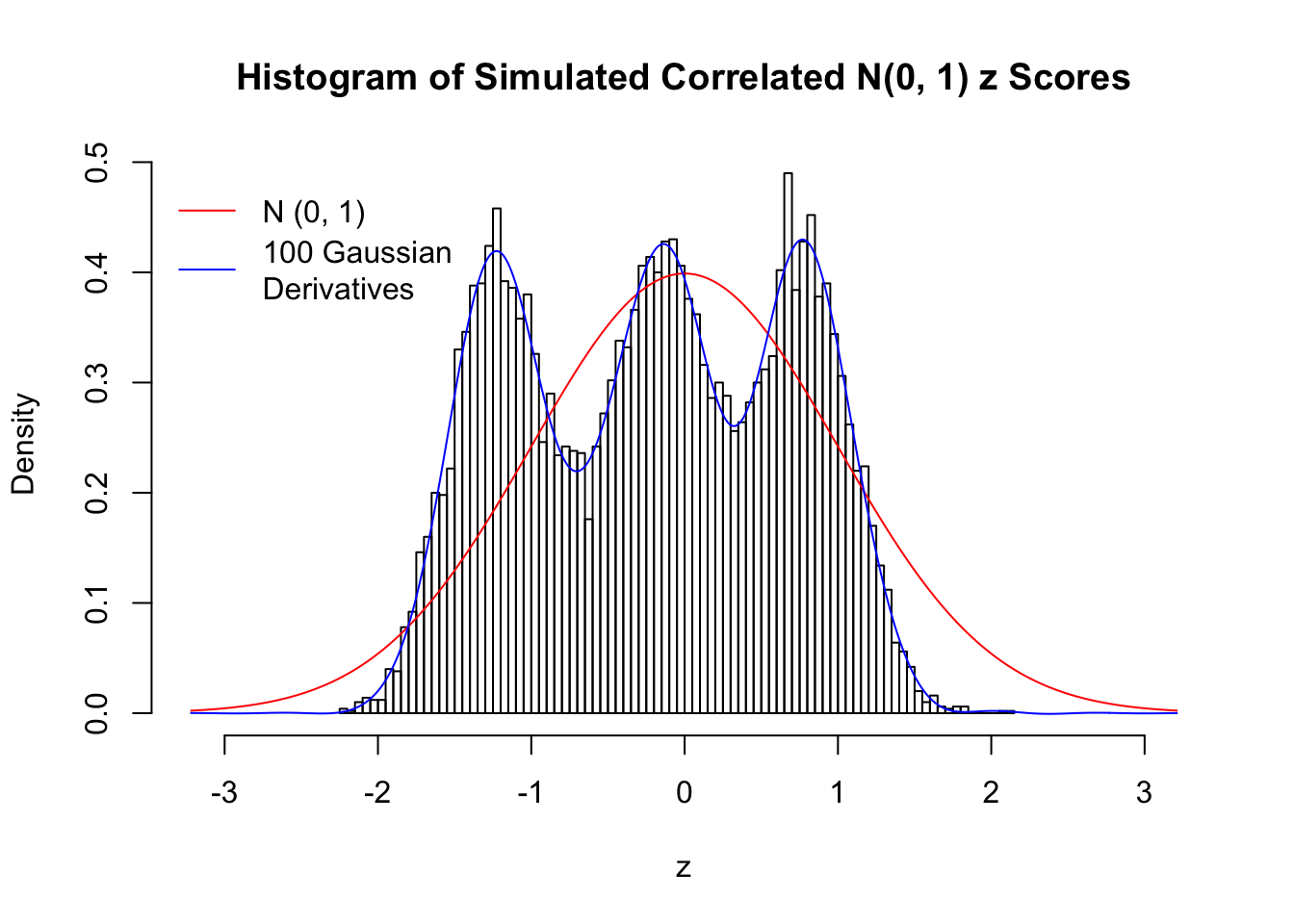
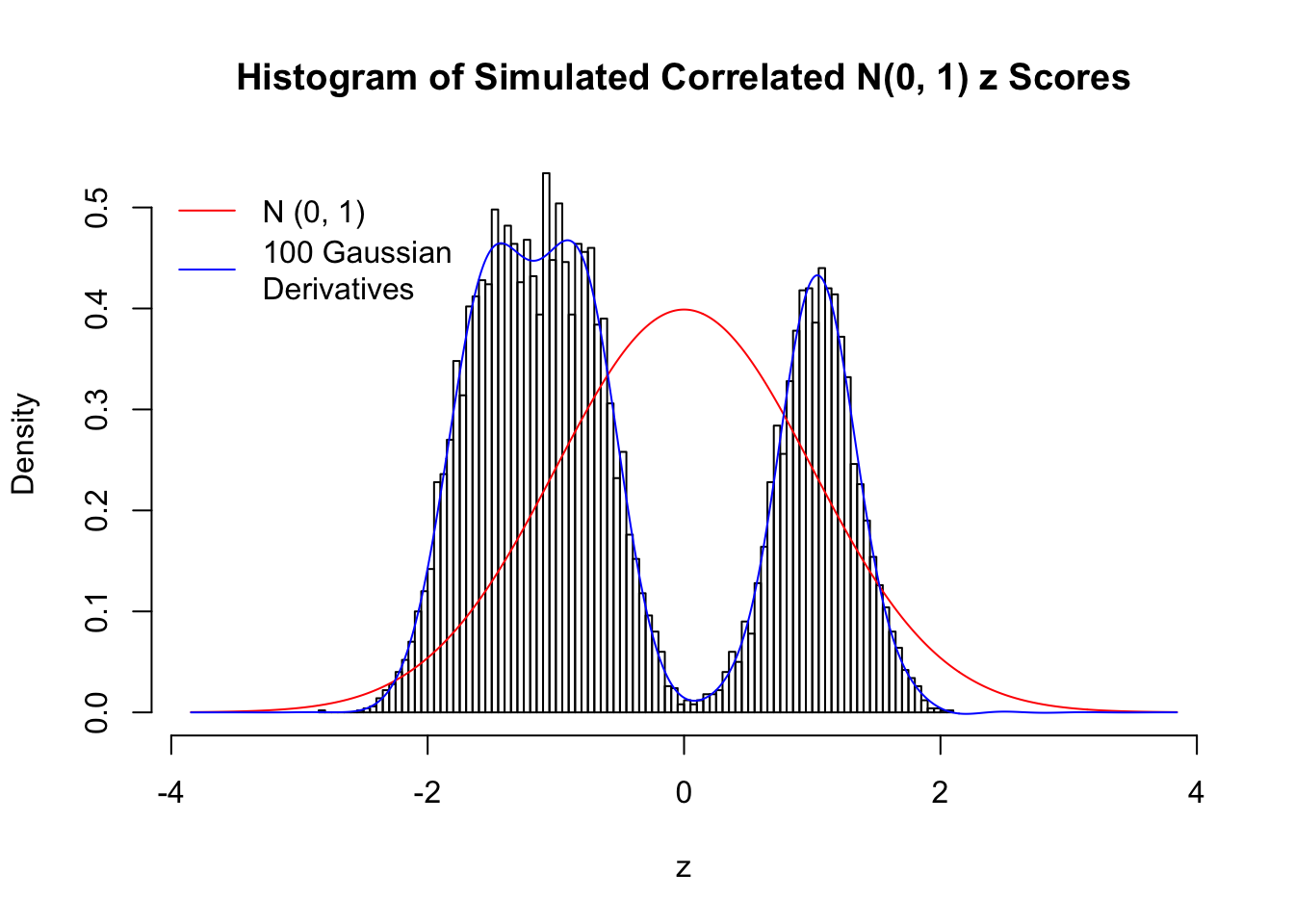
Scenario III: Three Groups

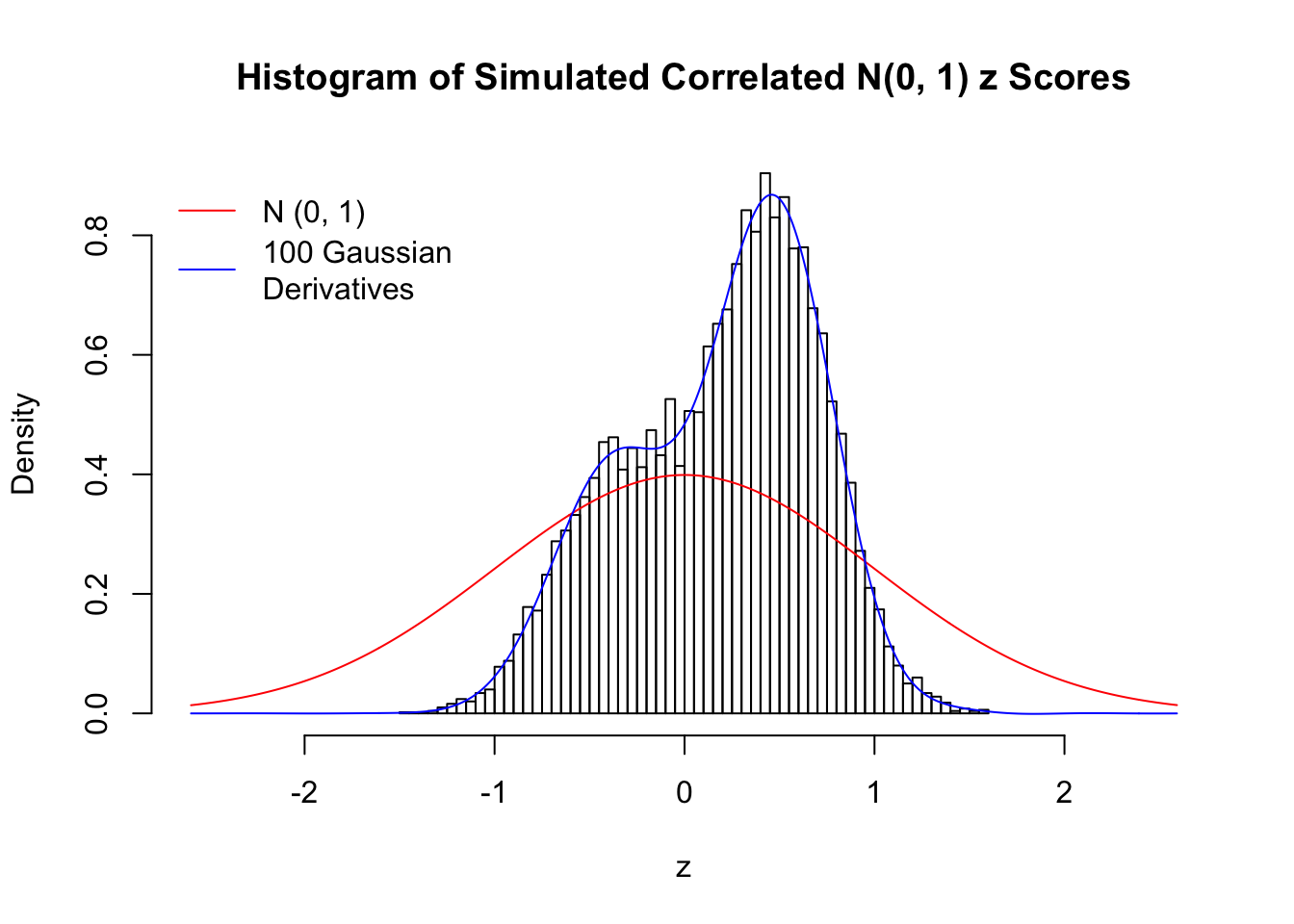
set.seed(777)
K = 3
for (j in 1 : 5) {
  z = z.sim(n, K, rho)
  fit.gd(L, z)
}

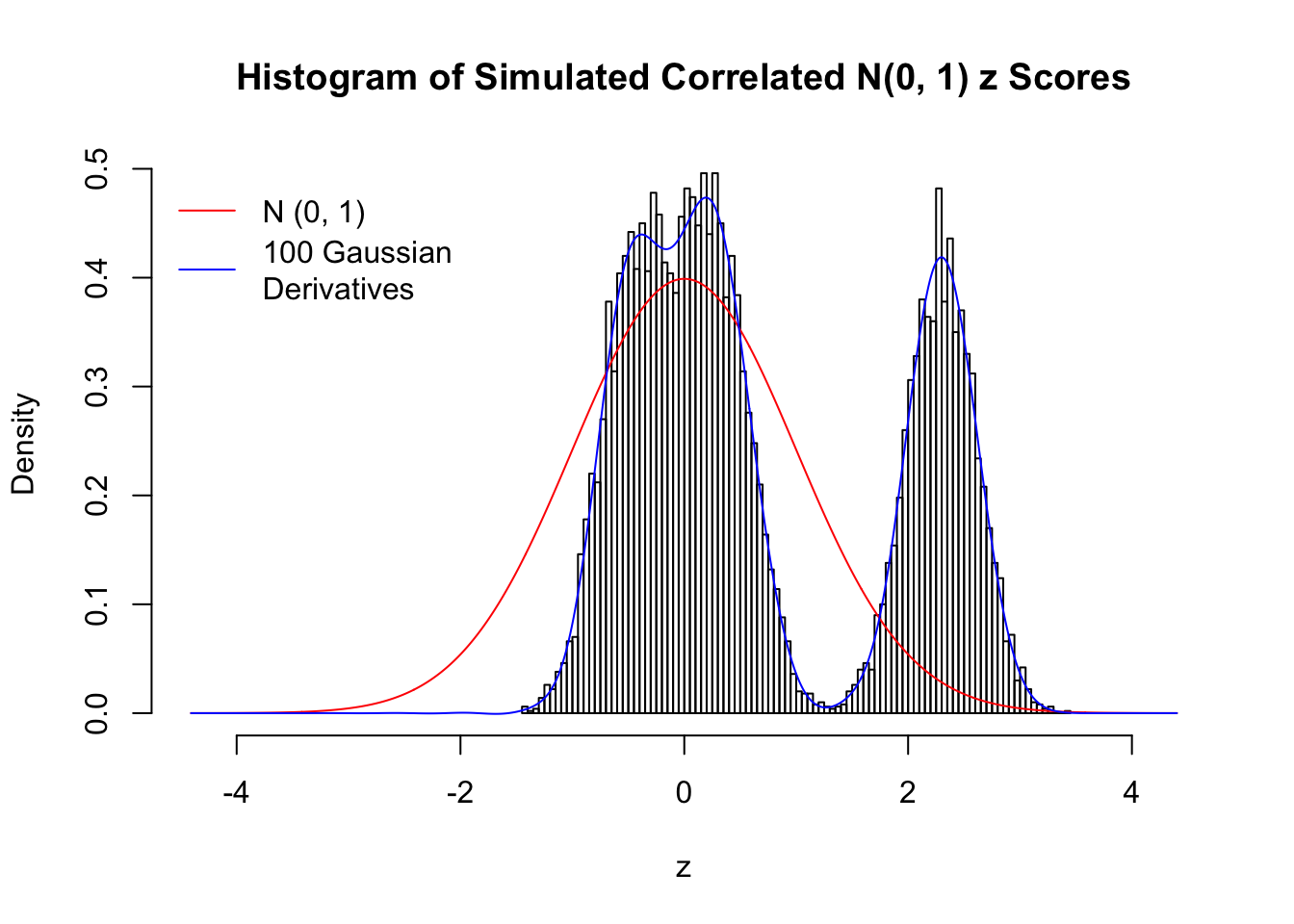
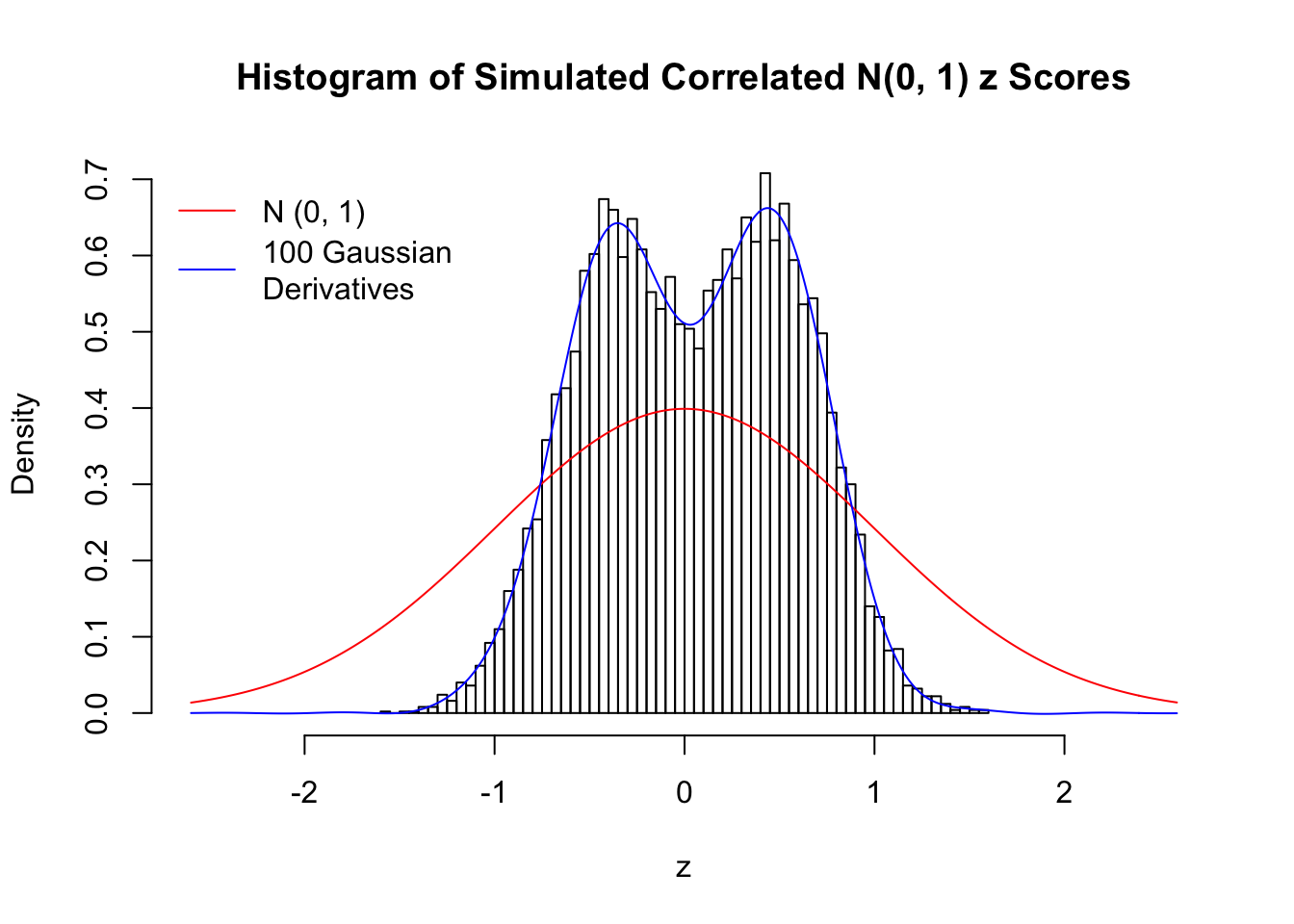
Scenario IV: Four Groups

set.seed(777)
K = 4
for (j in 1 : 5) {
  z = z.sim(n, K, rho)
  fit.gd(L, z)
}

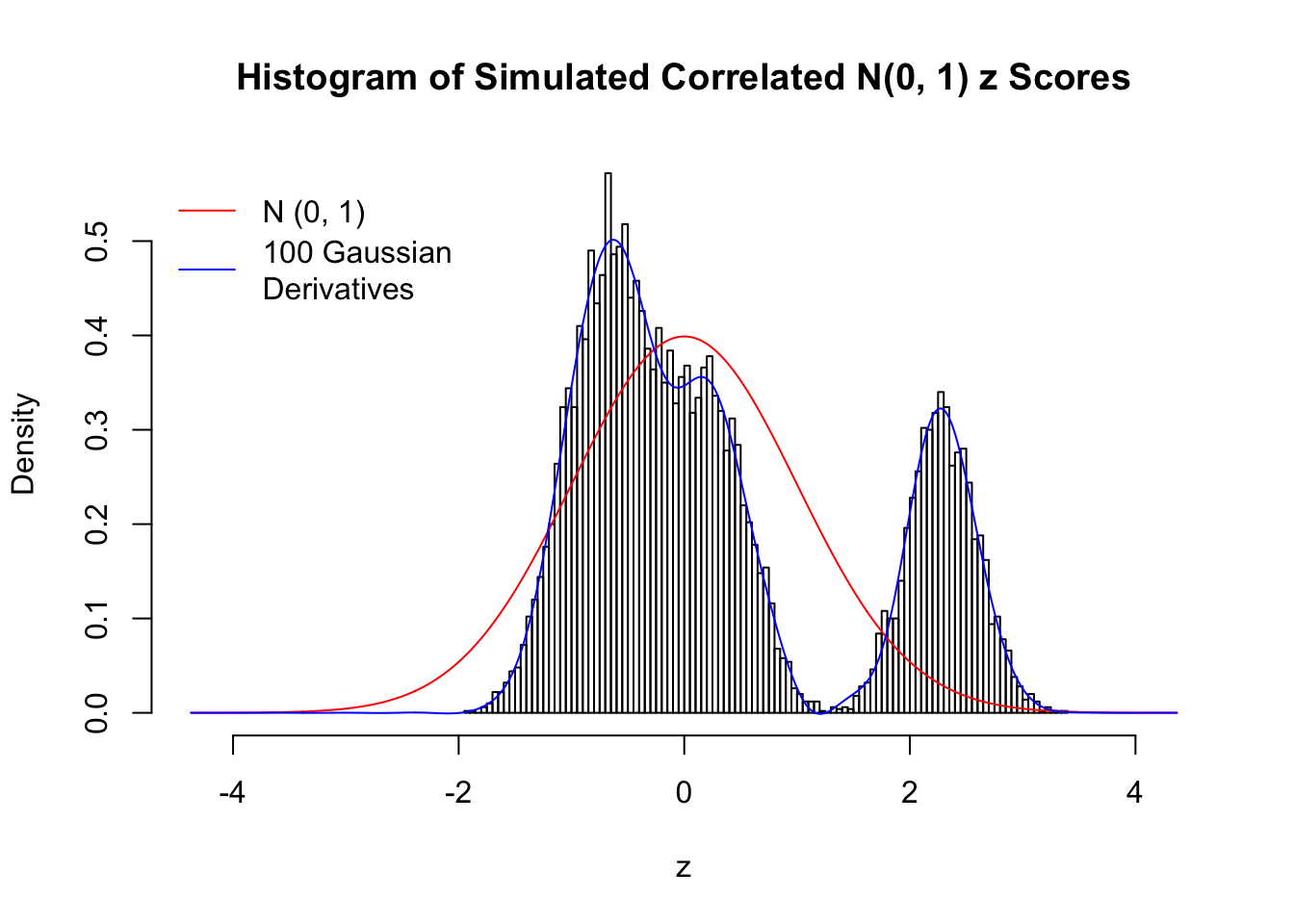
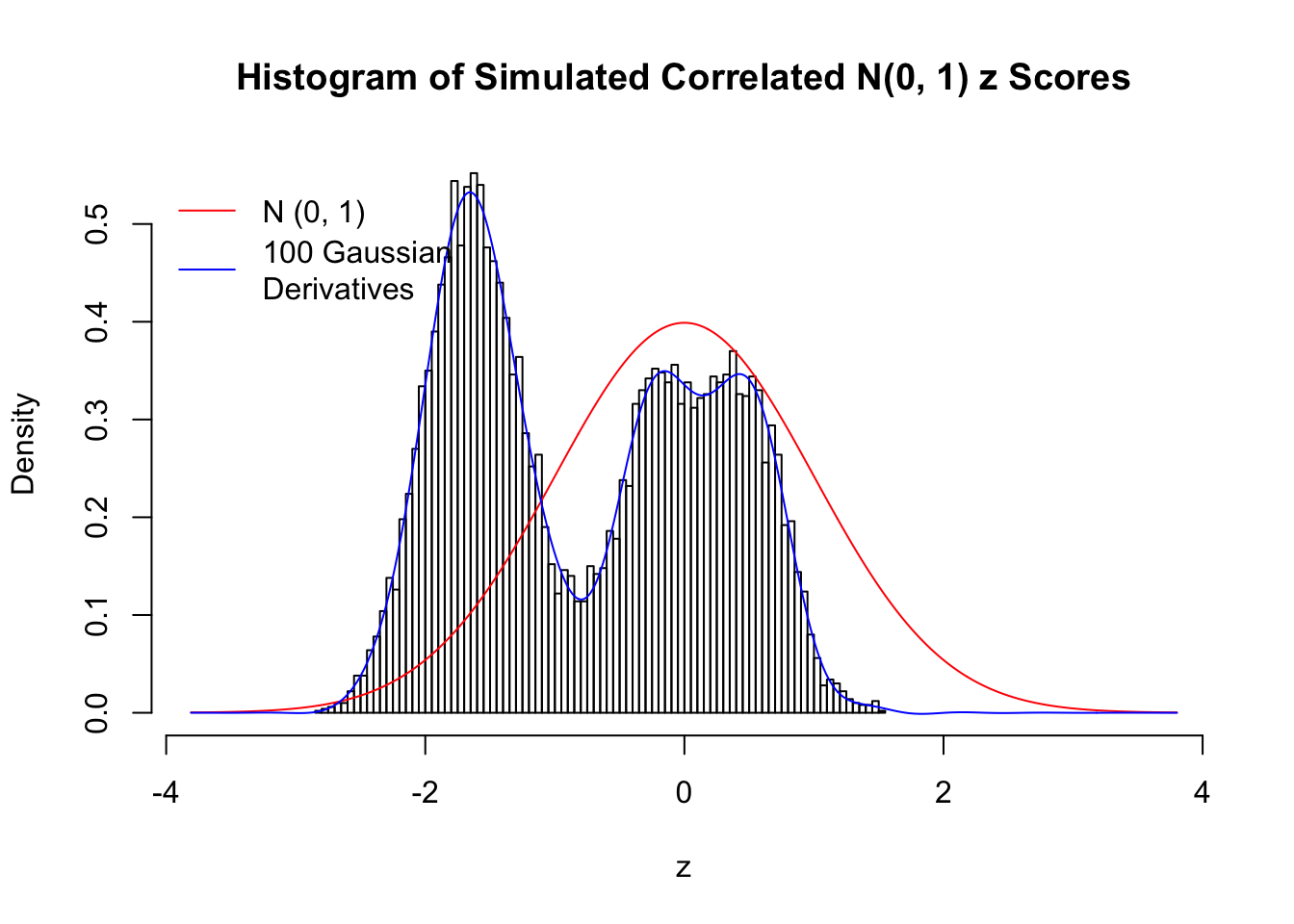
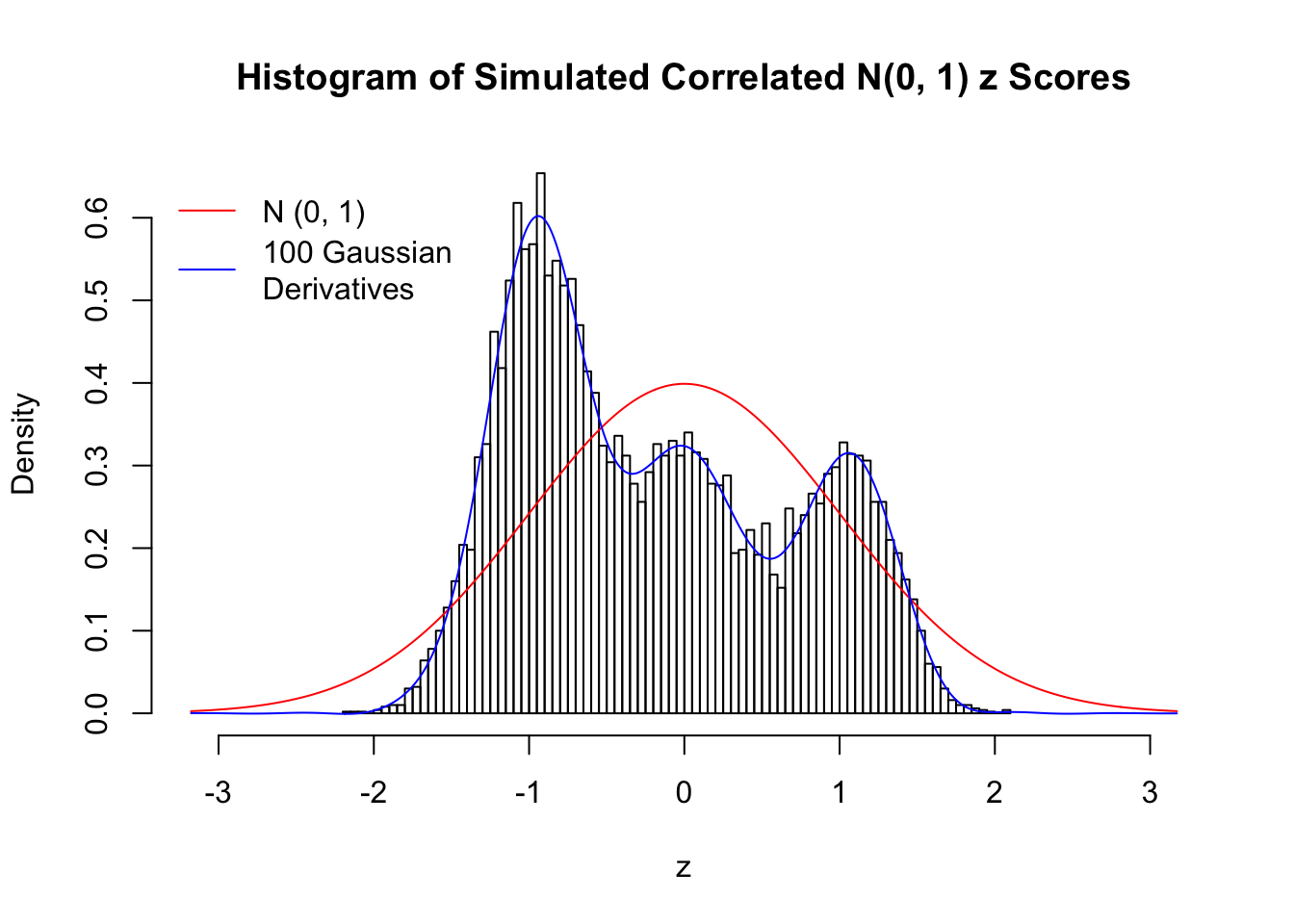
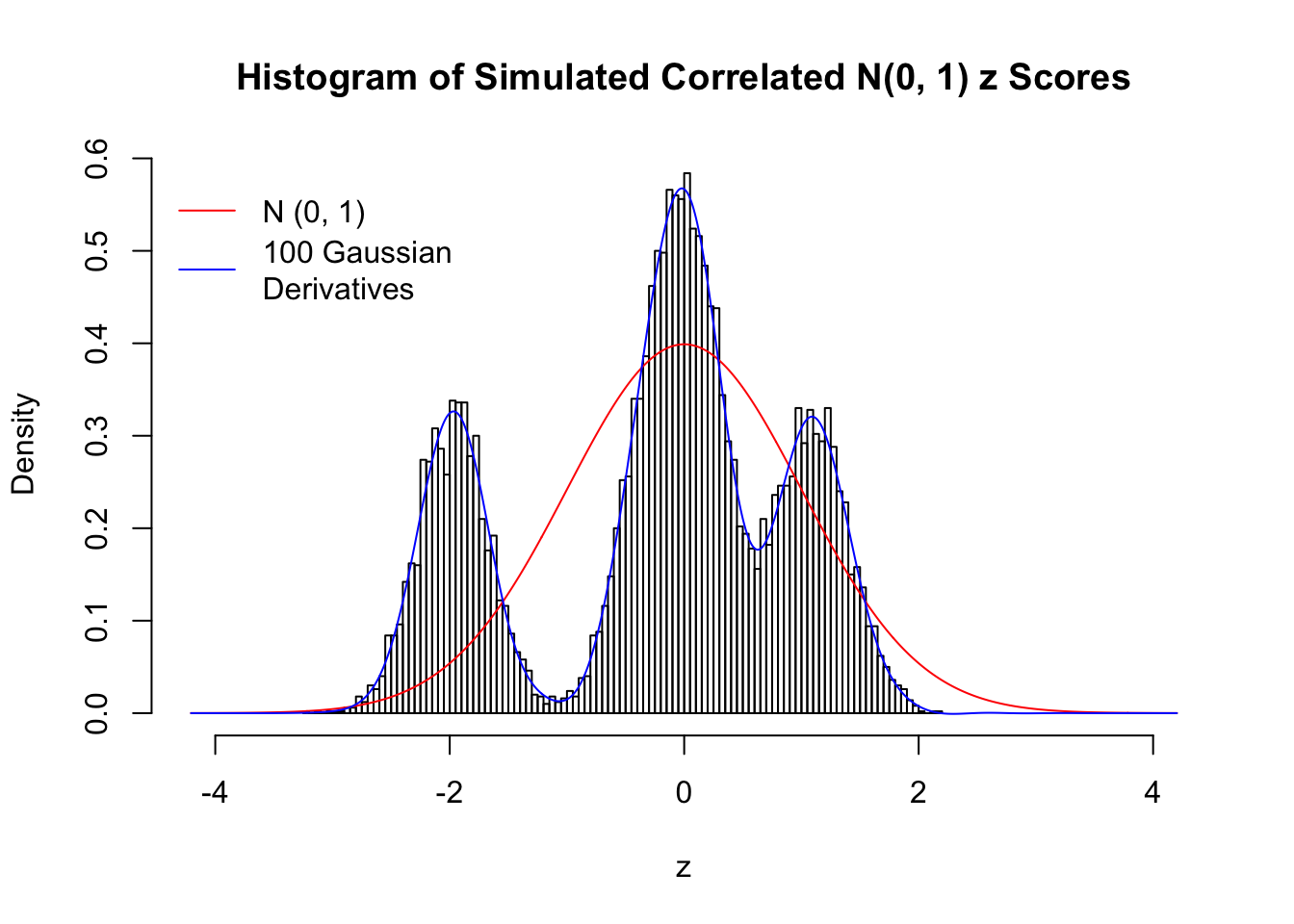
Scenario V: Five Groups

set.seed(777)
K = 5
for (j in 1 : 5) {
  z = z.sim(n, K, rho)
  fit.gd(L, z)
}

Session information

sessionInfo()

R version 3.3.3 (2017-03-06)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.5

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] backports_1.0.5 magrittr_1.5    rprojroot_1.2   tools_3.3.3    
 [5] htmltools_0.3.6 yaml_2.1.14     Rcpp_0.12.10    stringi_1.1.2  
 [9] rmarkdown_1.5   knitr_1.15.1    git2r_0.18.0    stringr_1.2.0  
[13] digest_0.6.12   evaluate_0.10