Diagnostic Plots for ASH on Correlated Null
Lei Sun
2017-04-18
Last updated: 2017-11-07
Code version: 2c05d59
Correlation makes ASH fit less well
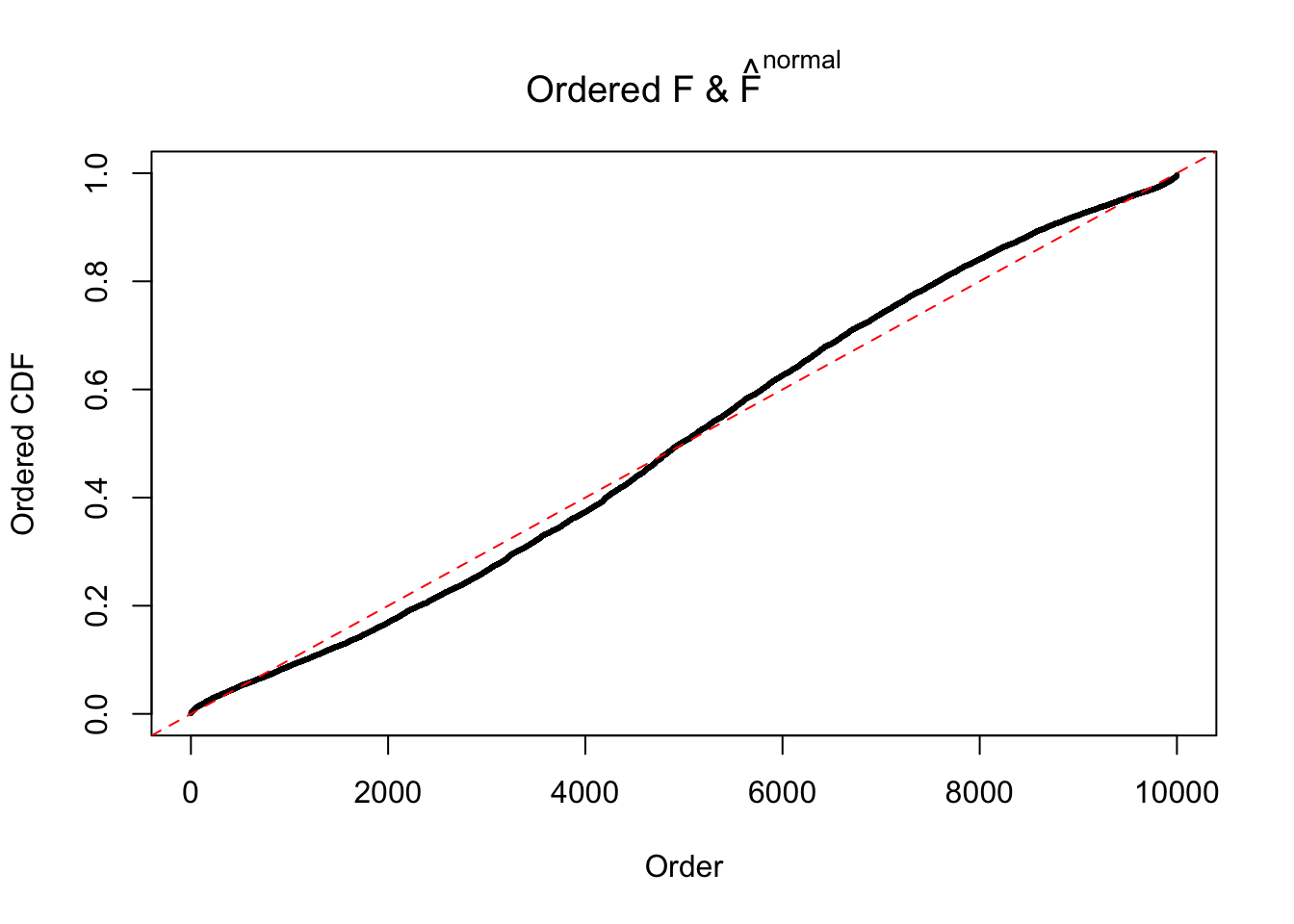
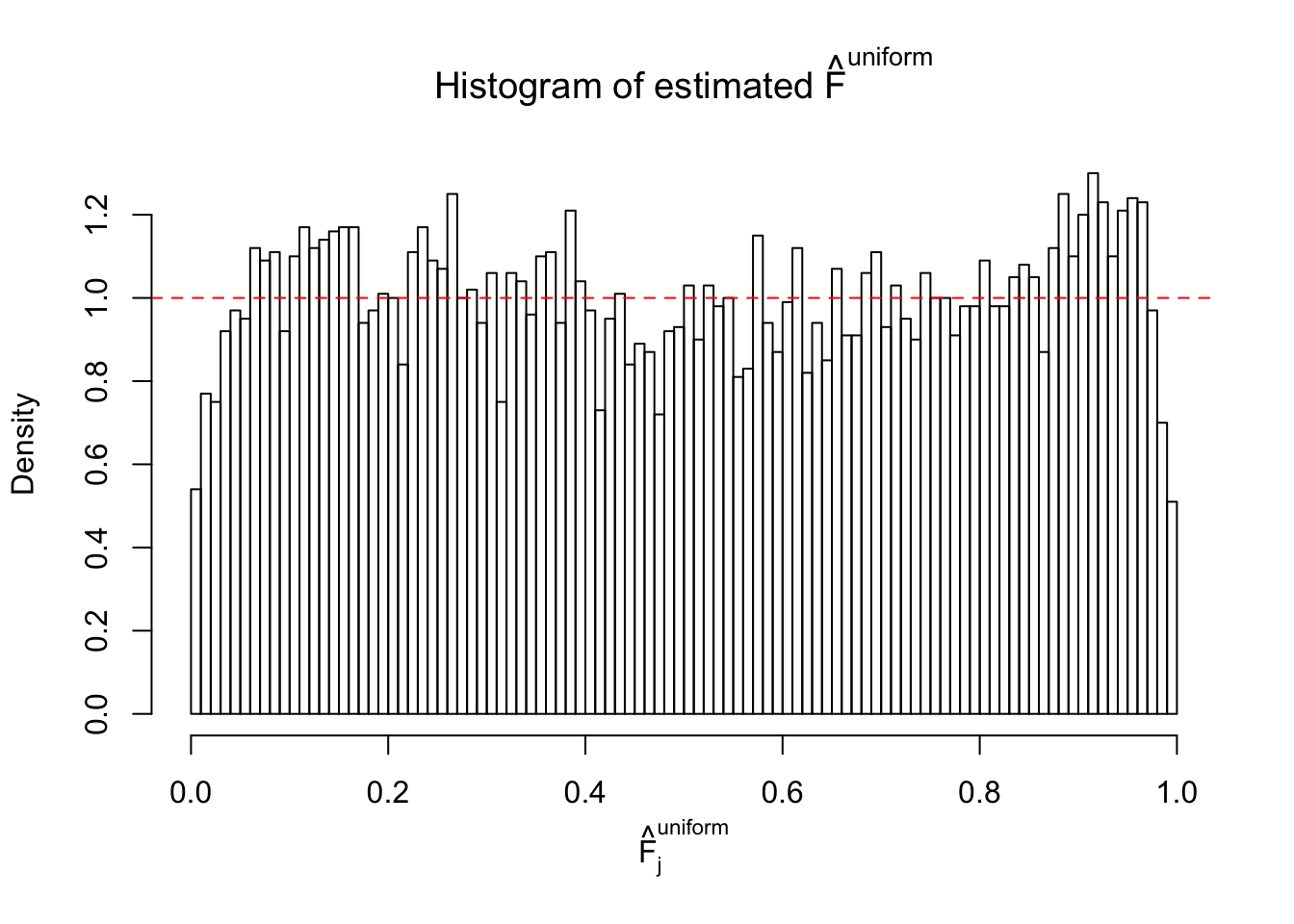
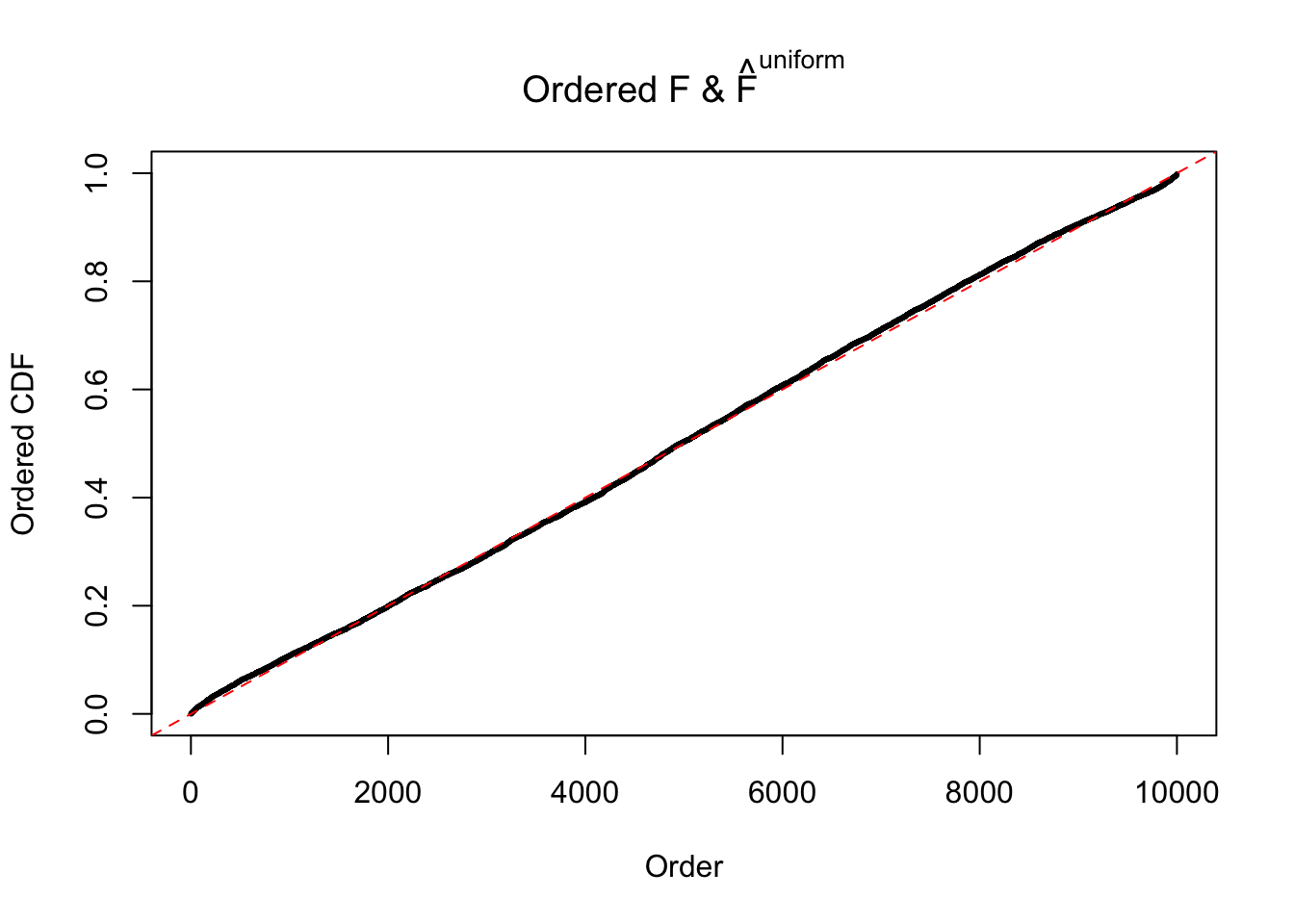
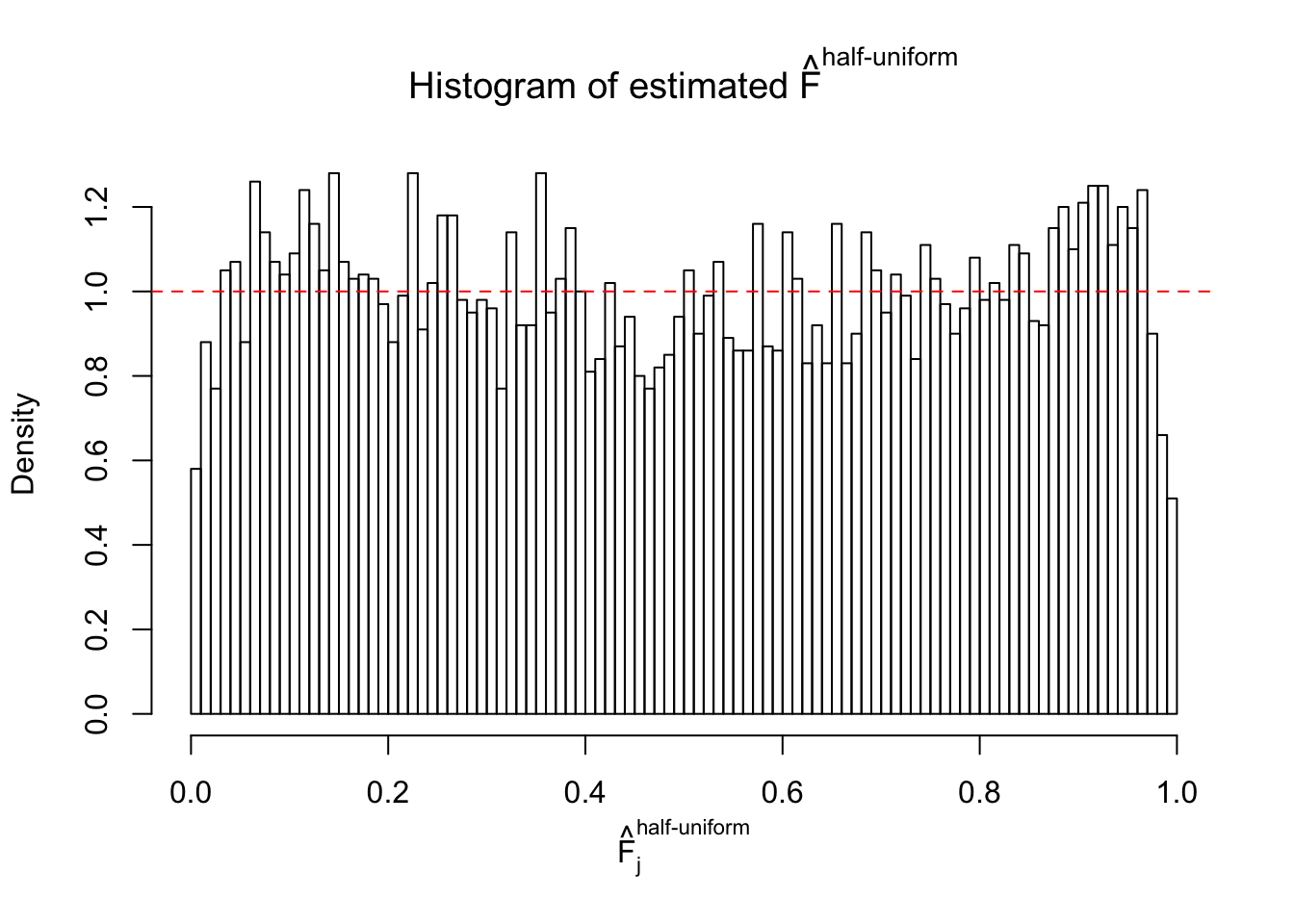
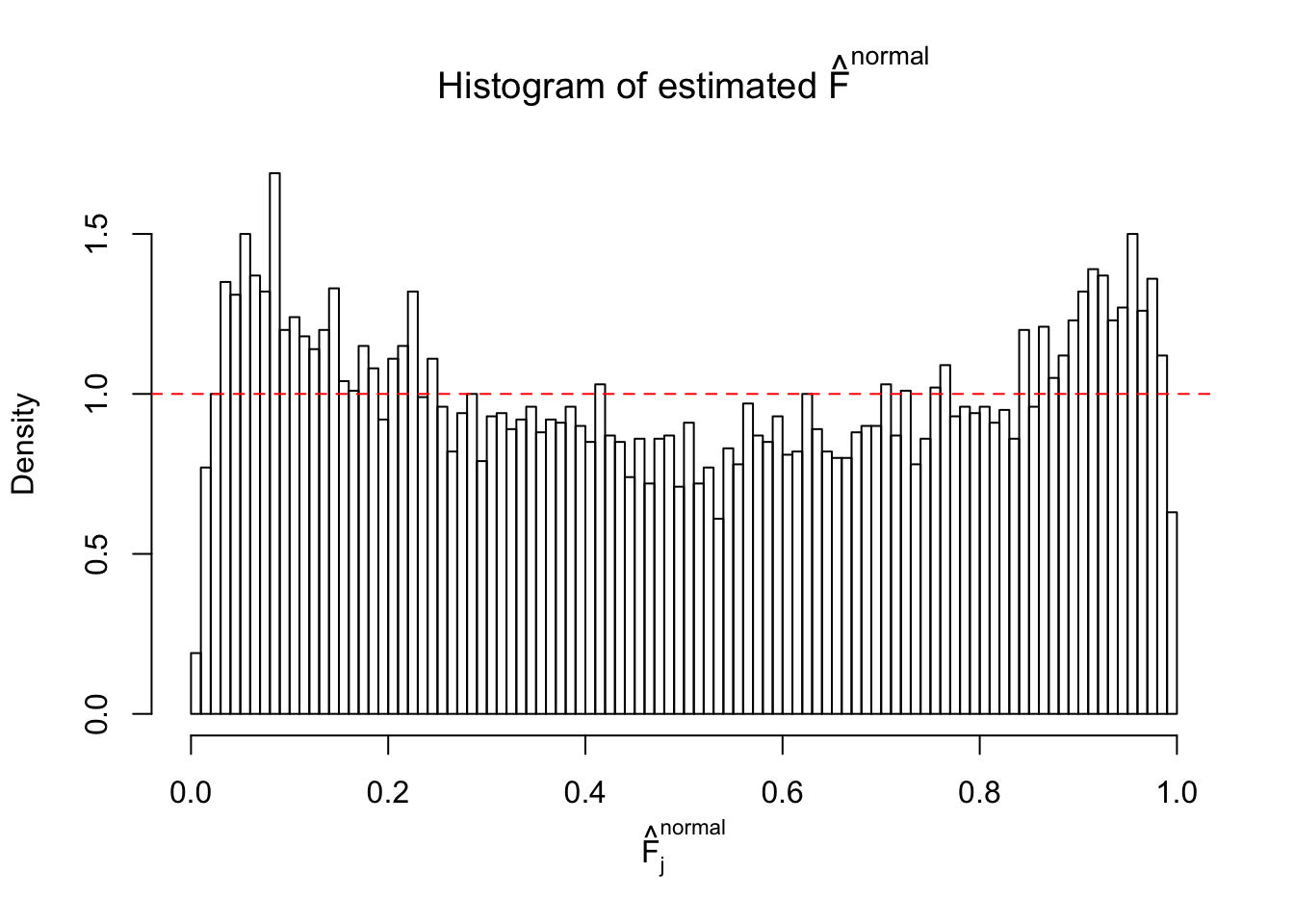
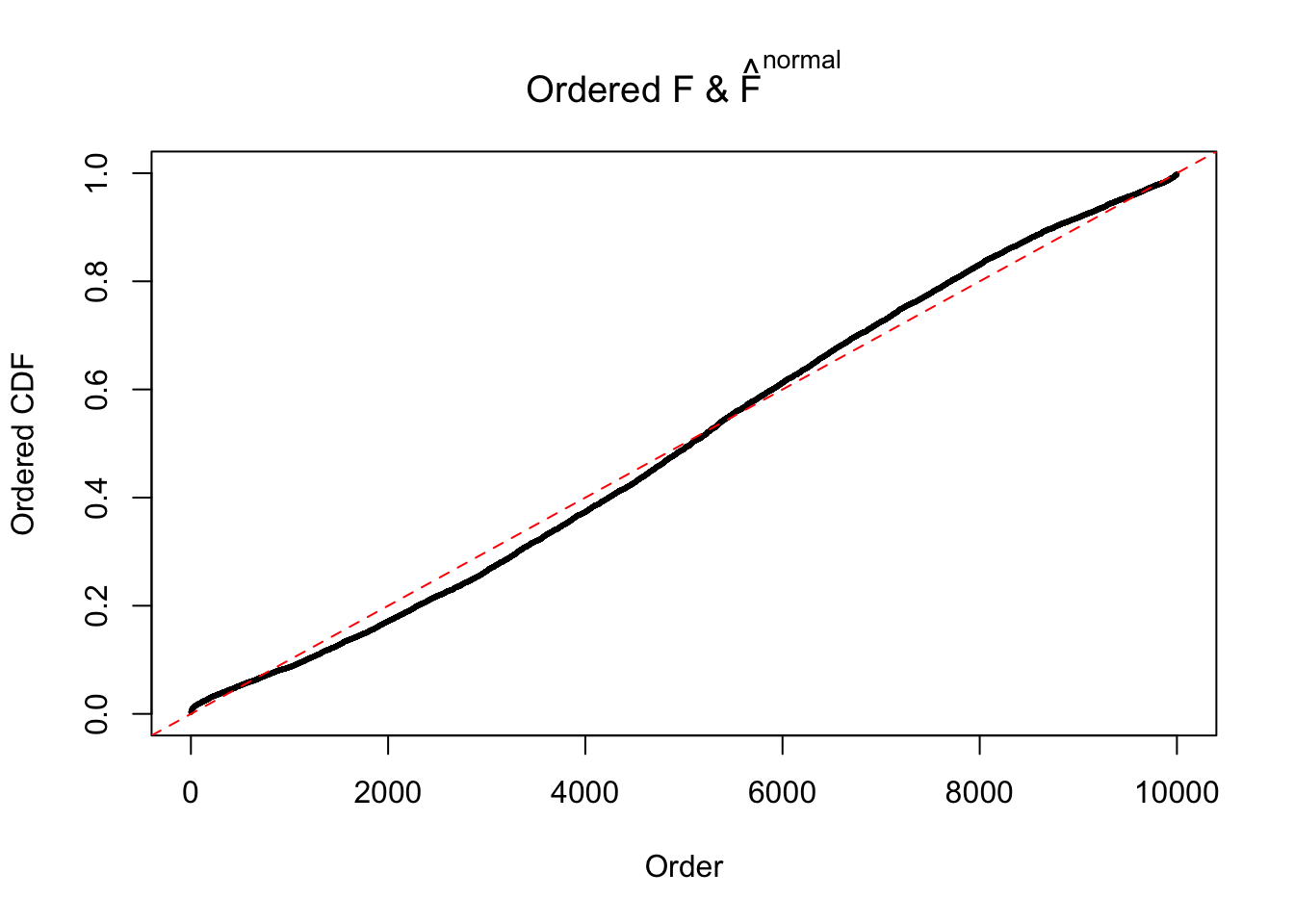
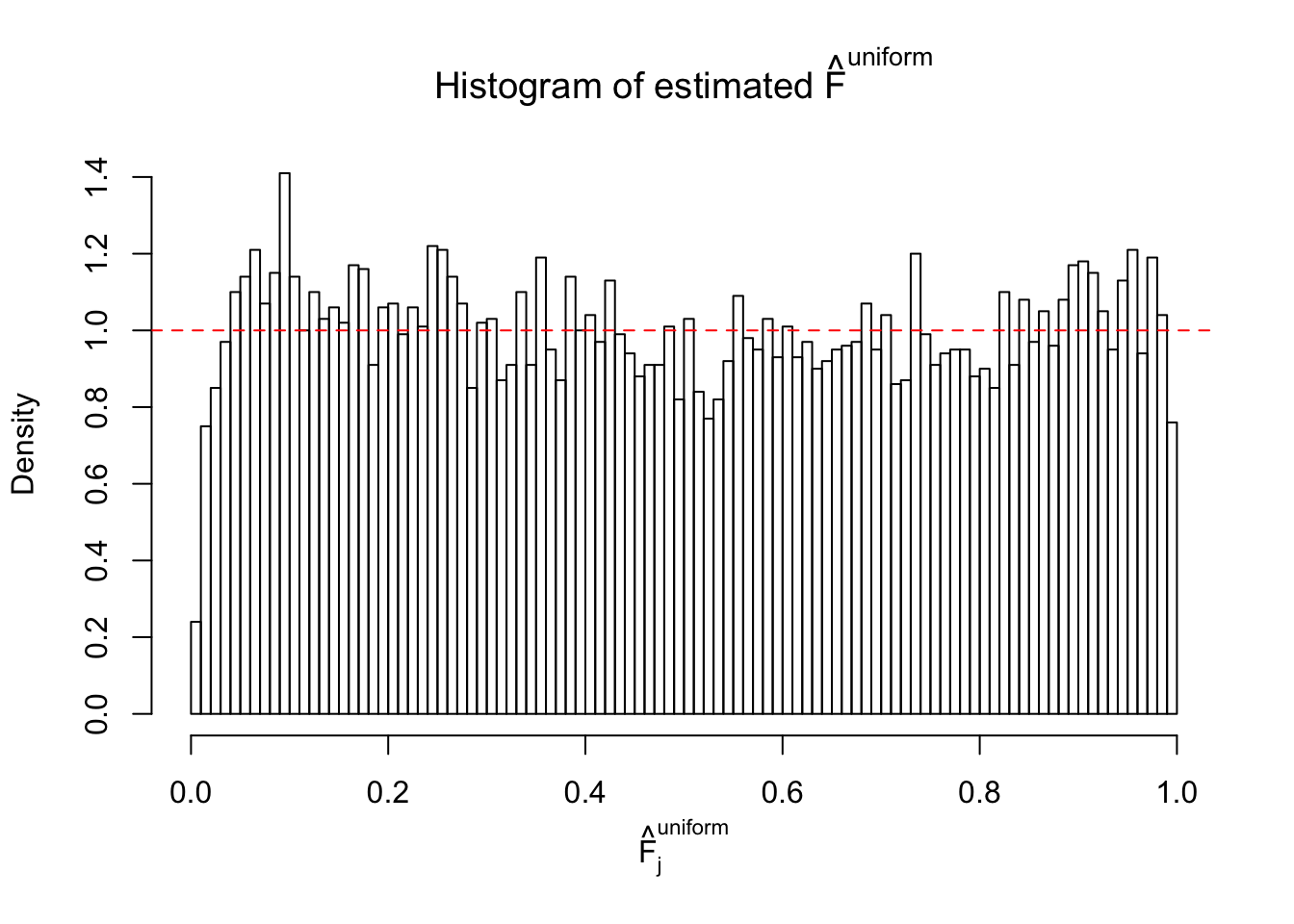
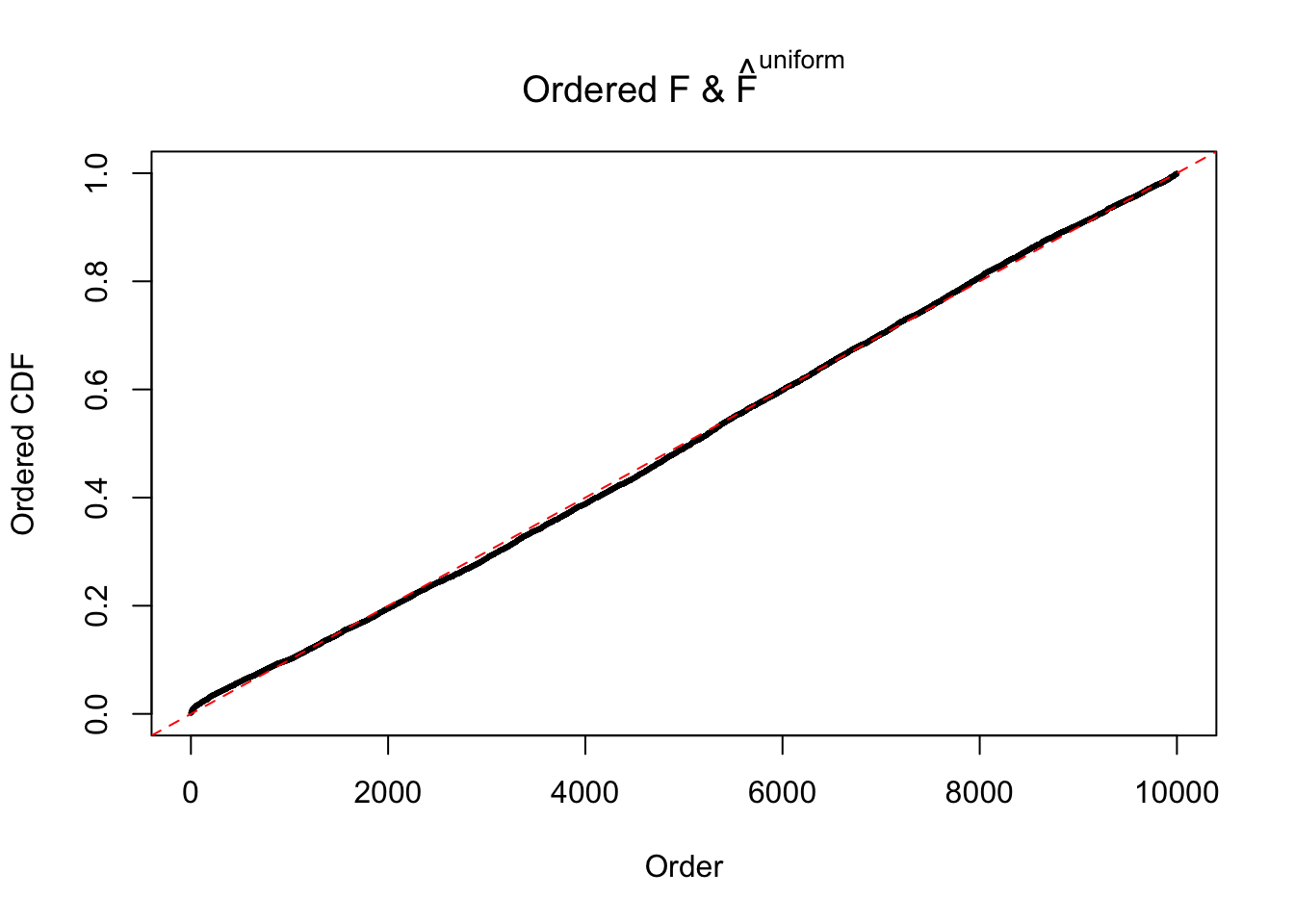
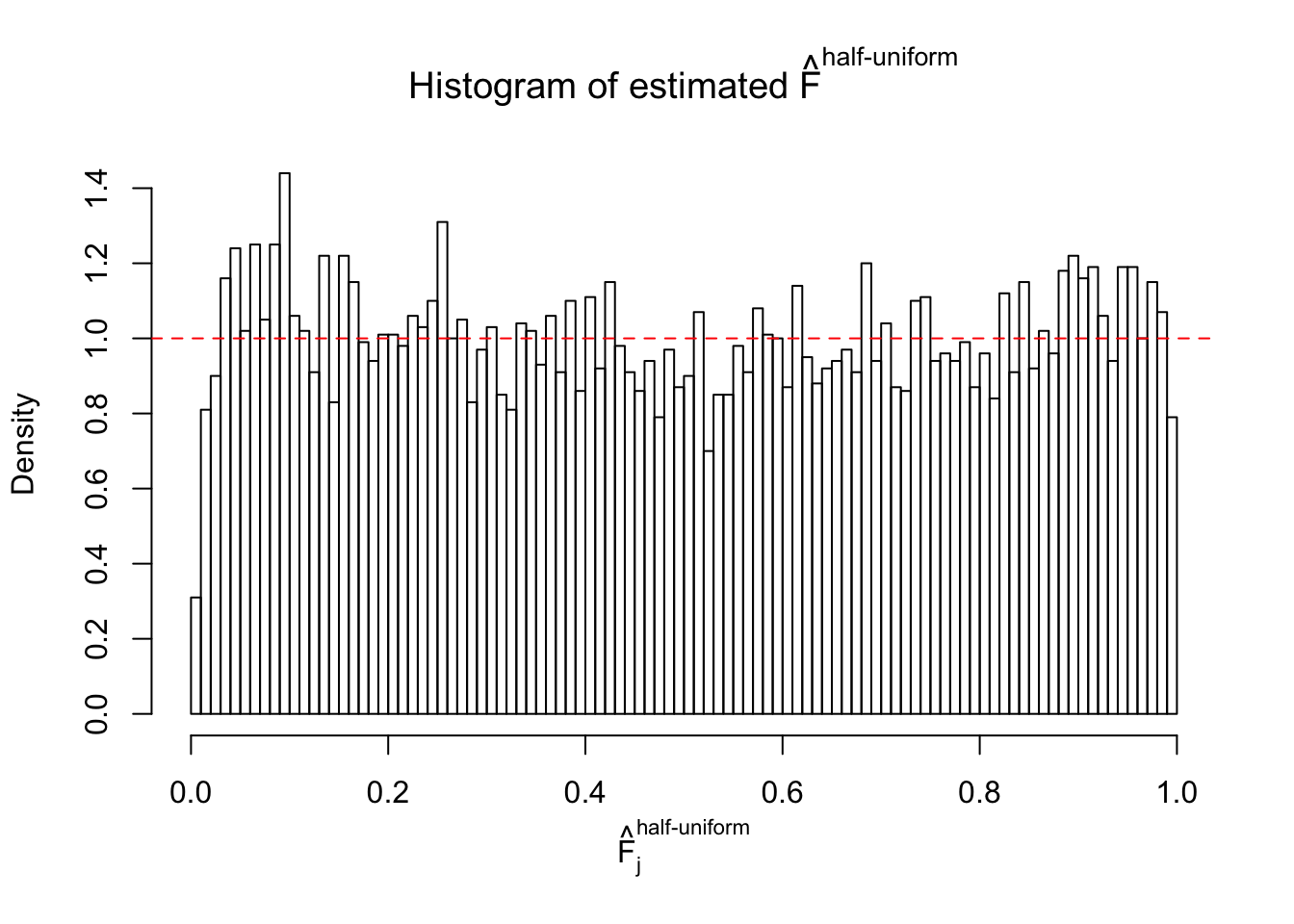
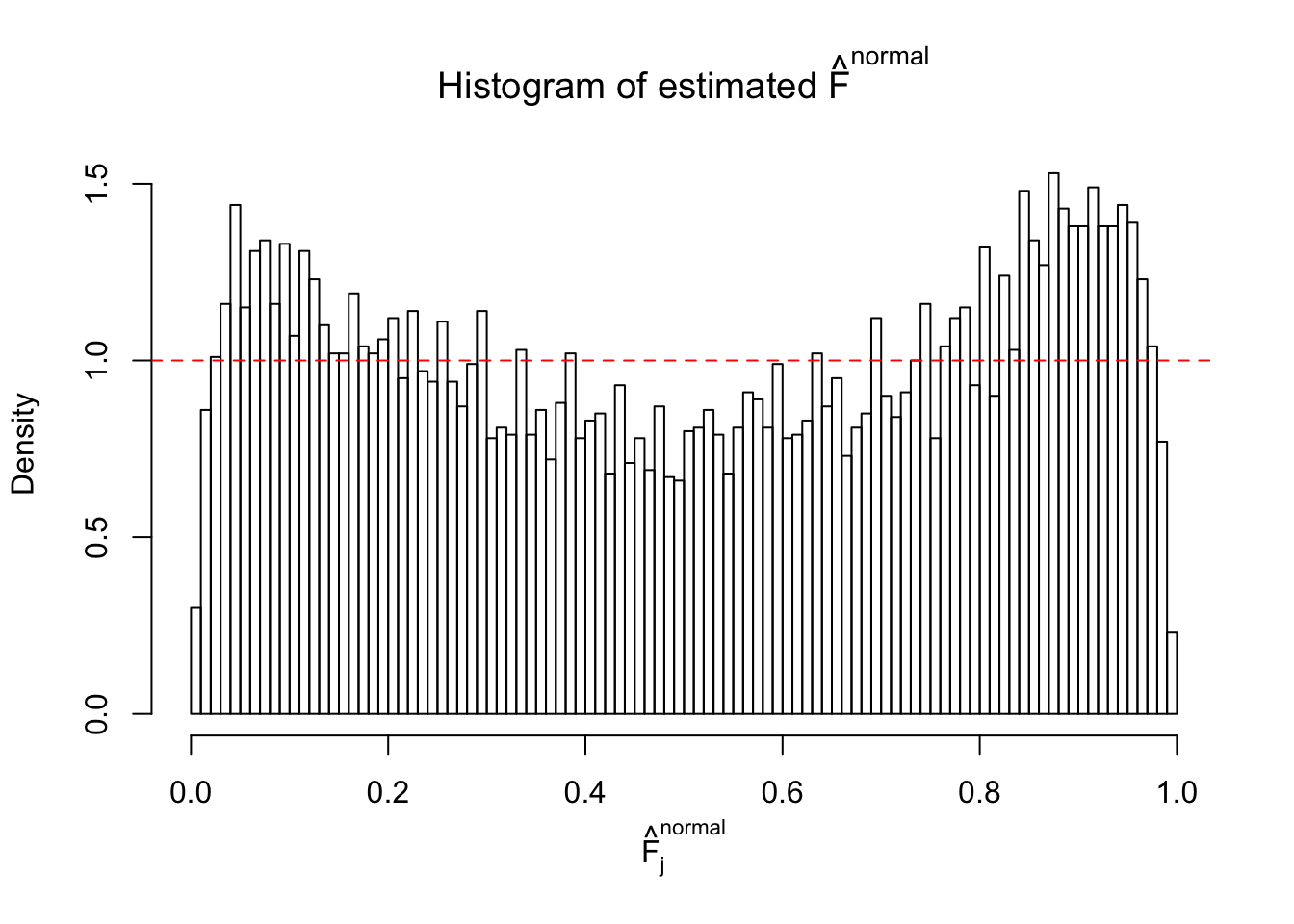
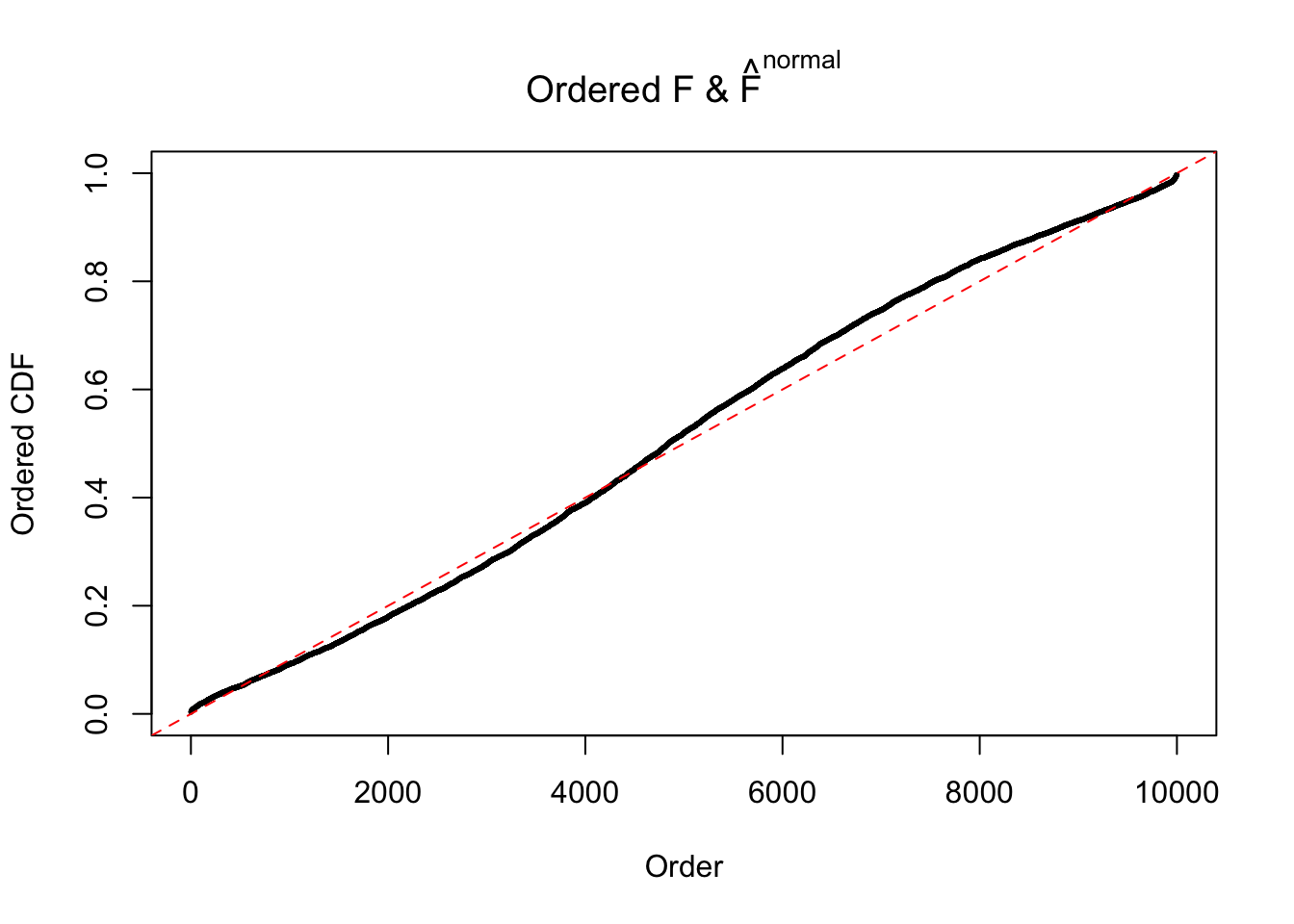
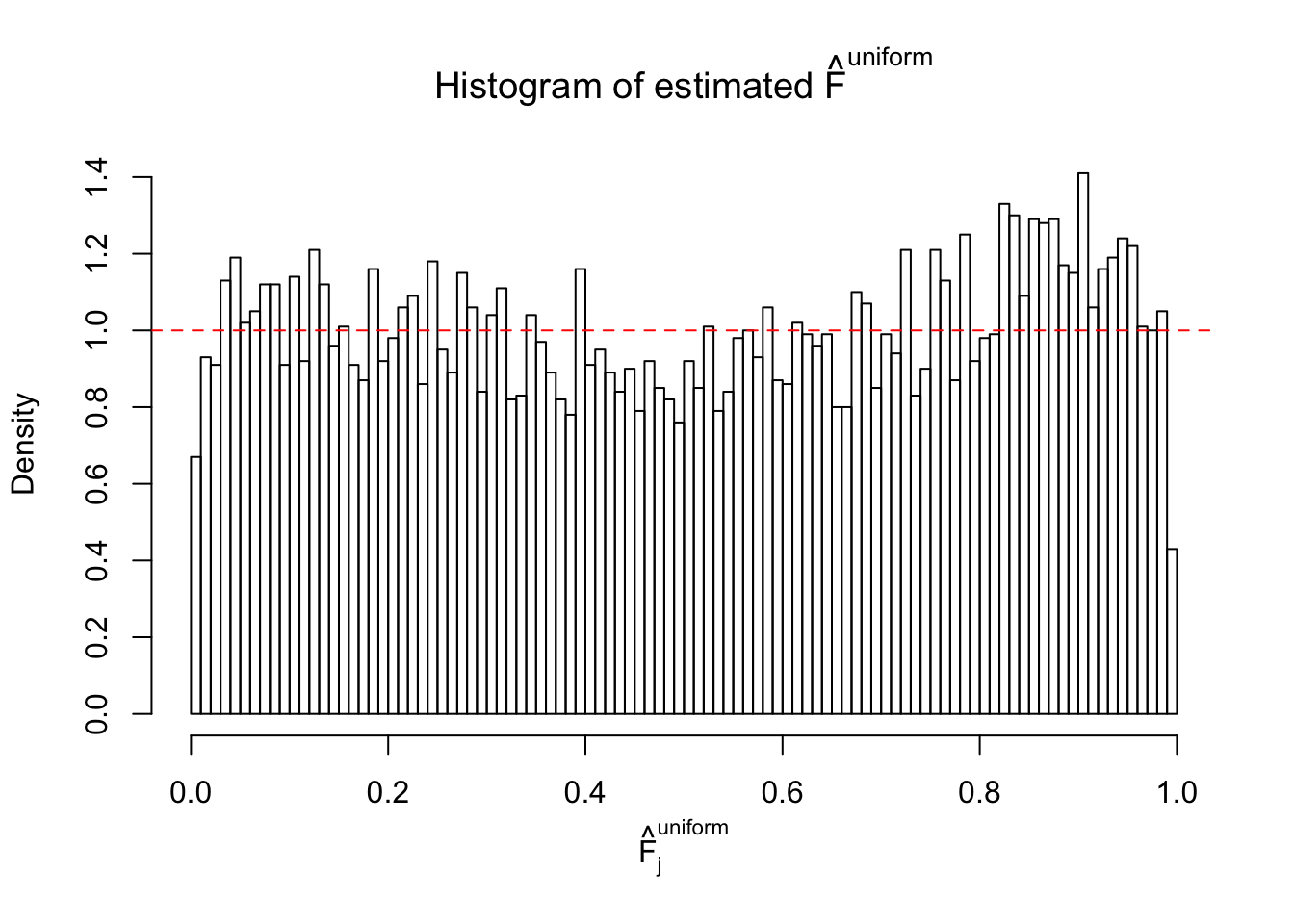
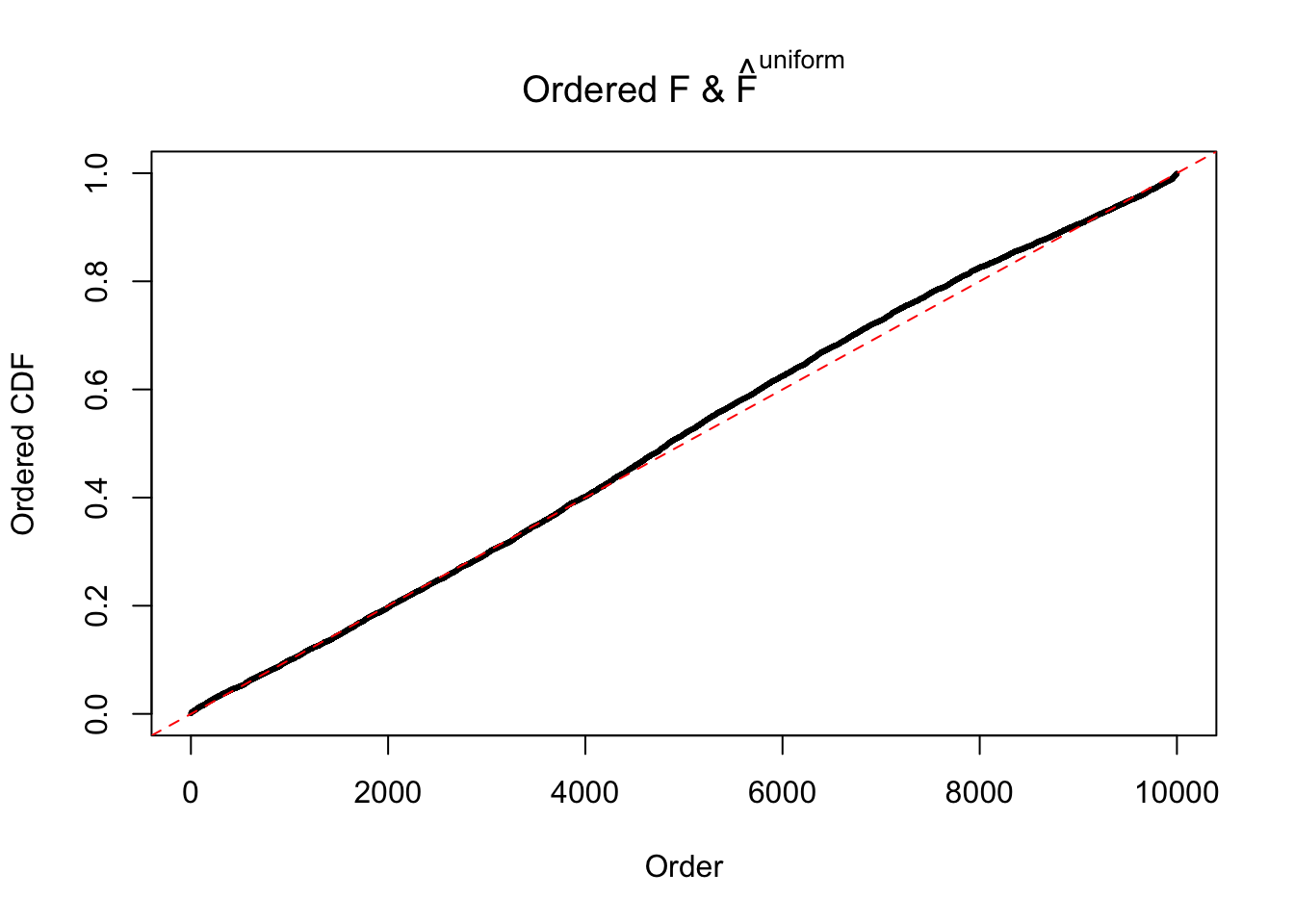
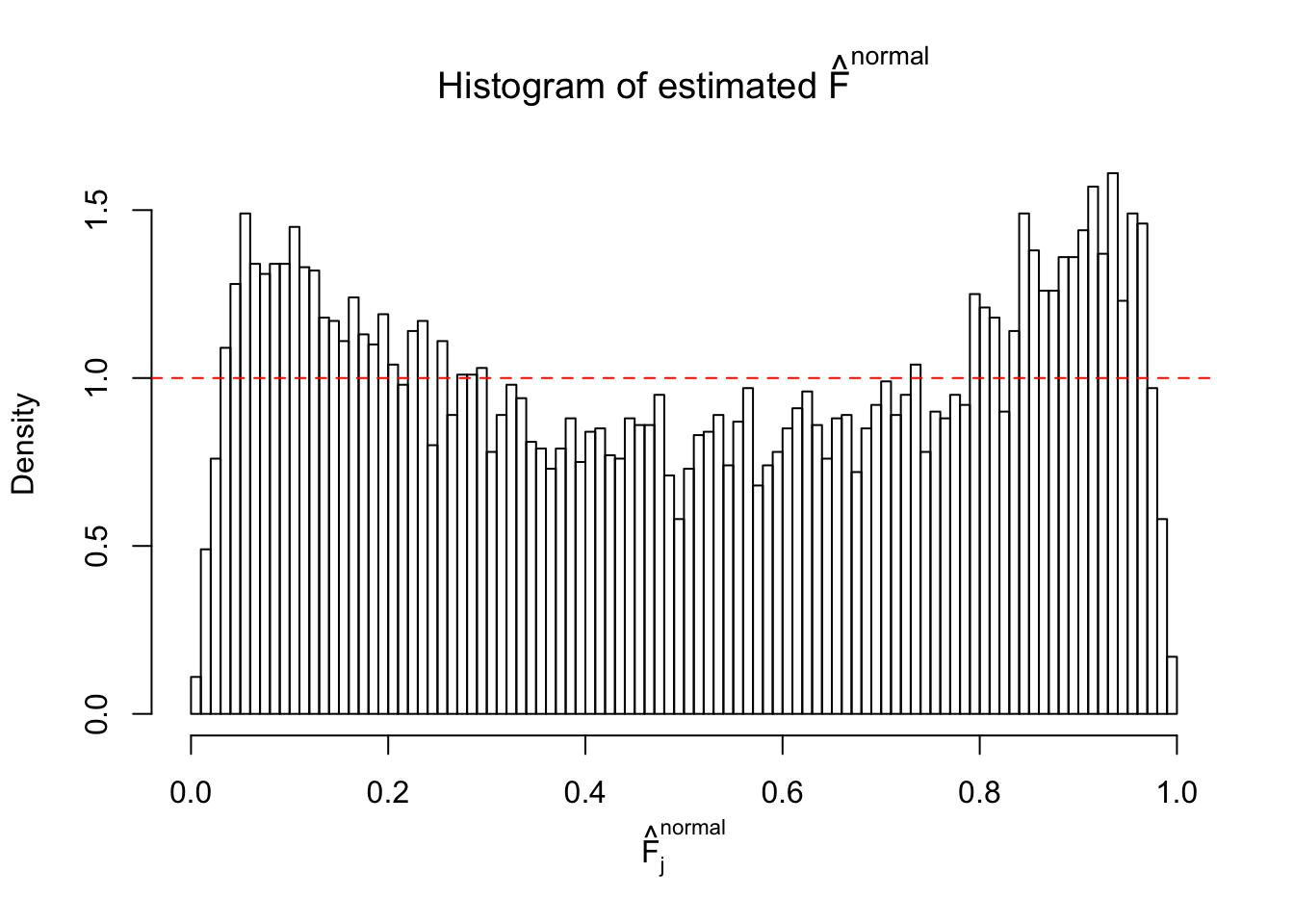
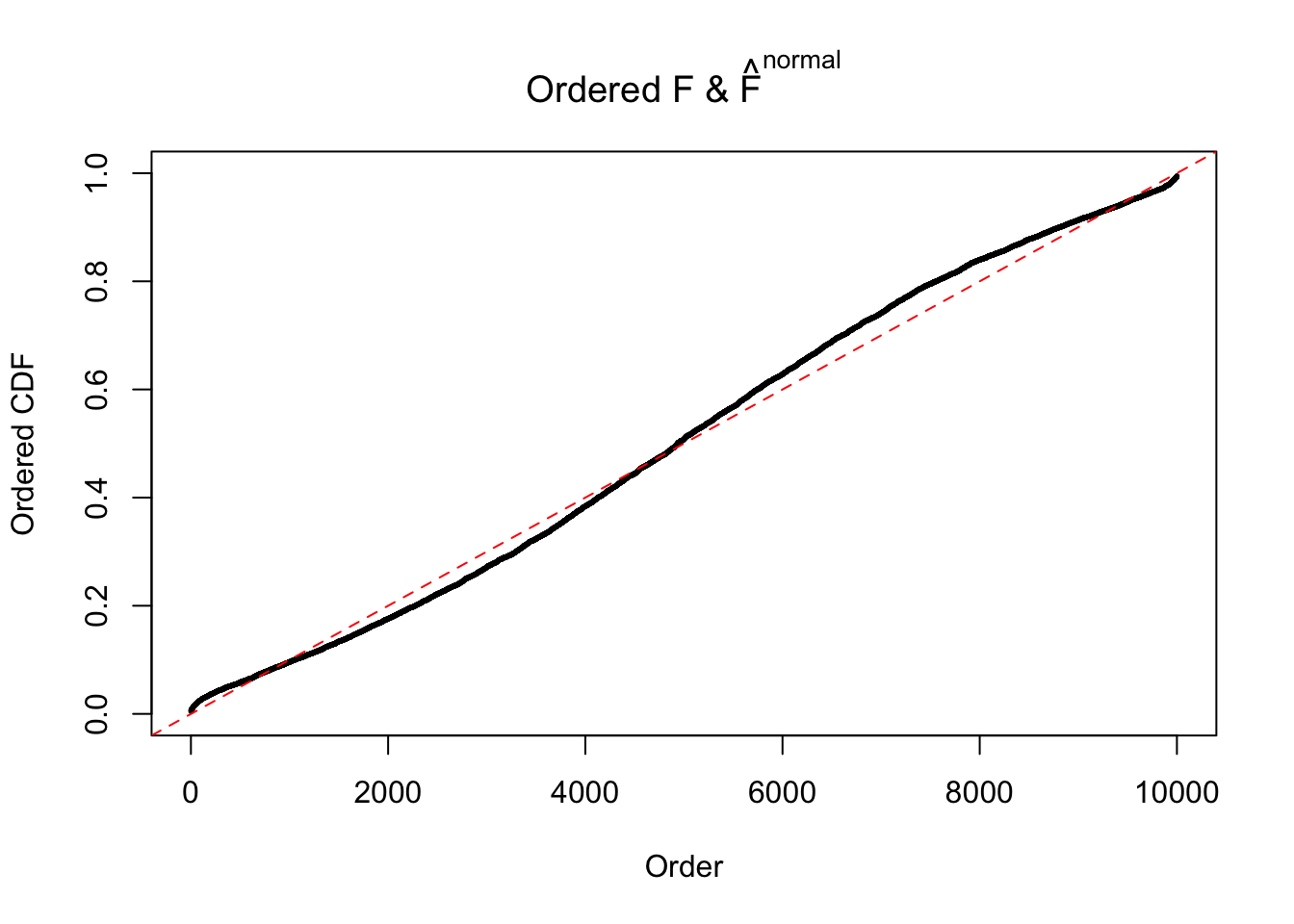
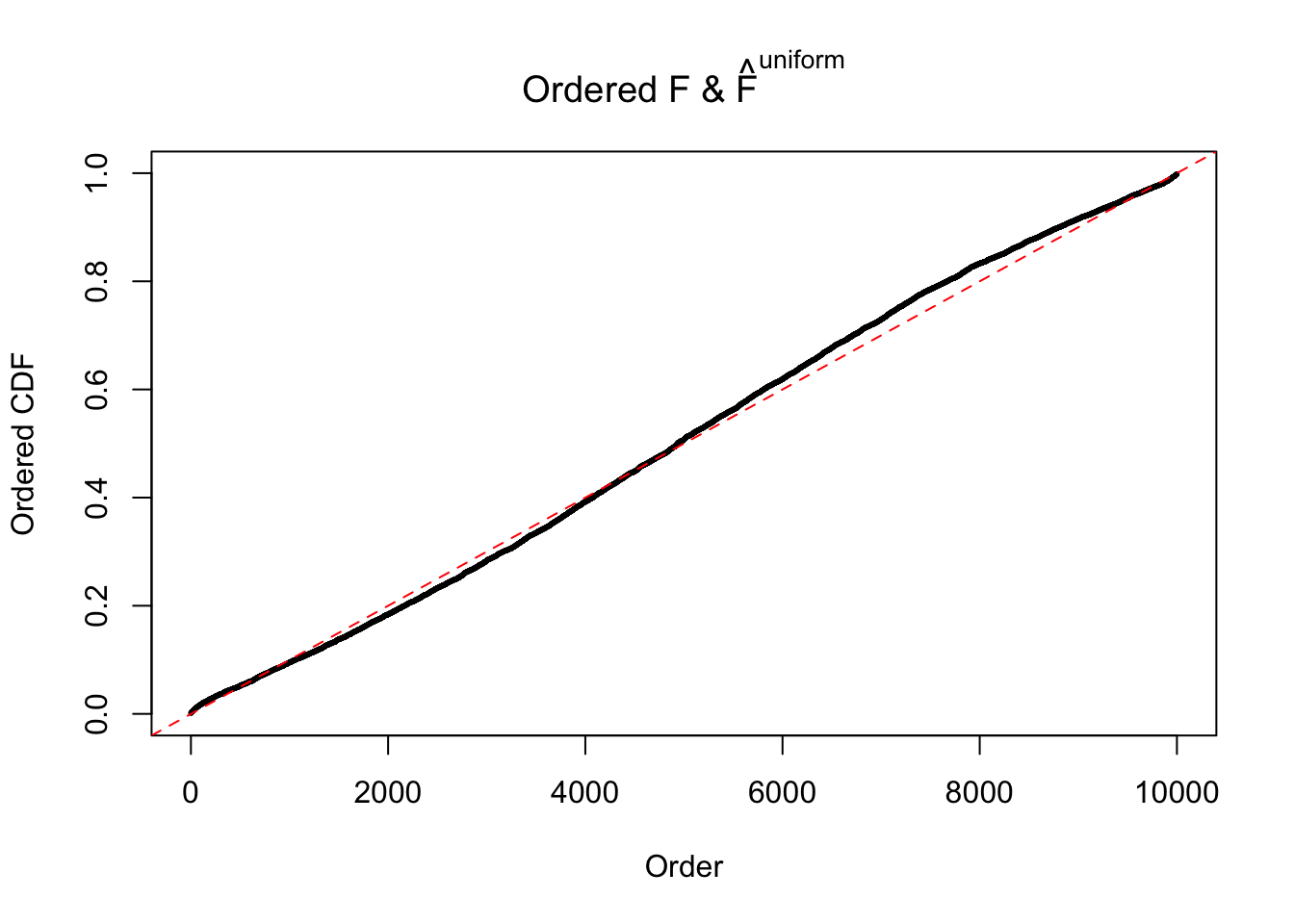
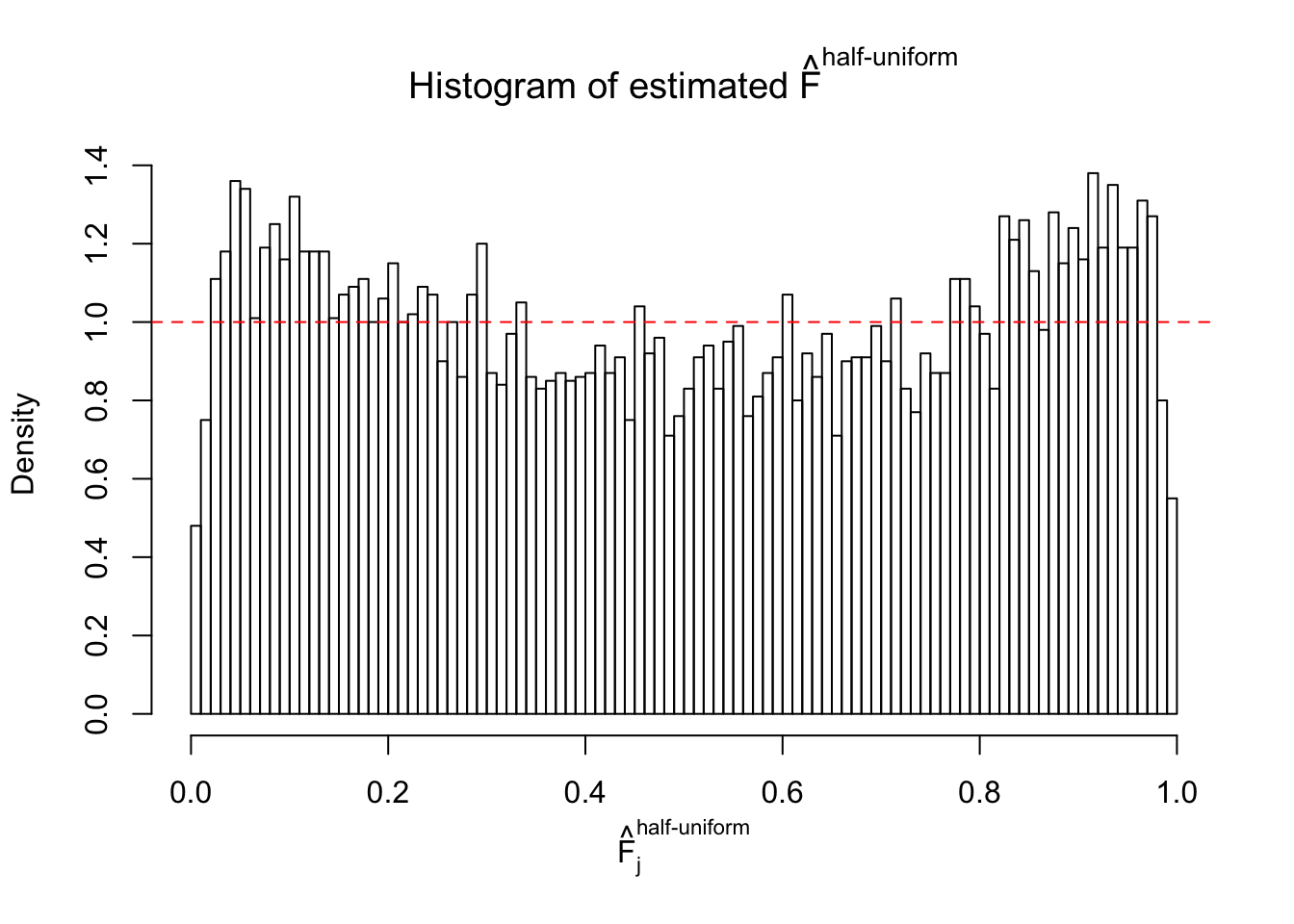
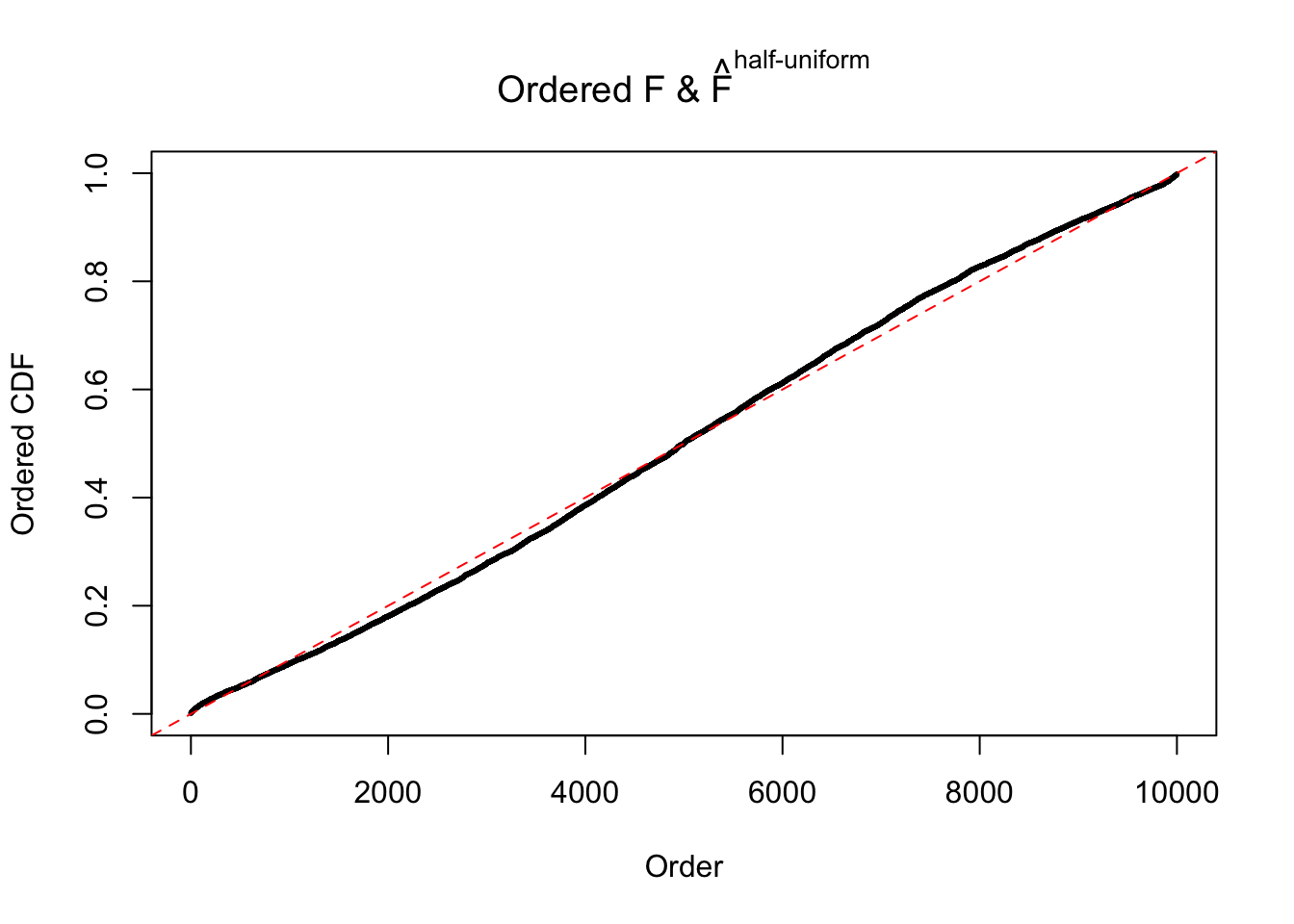
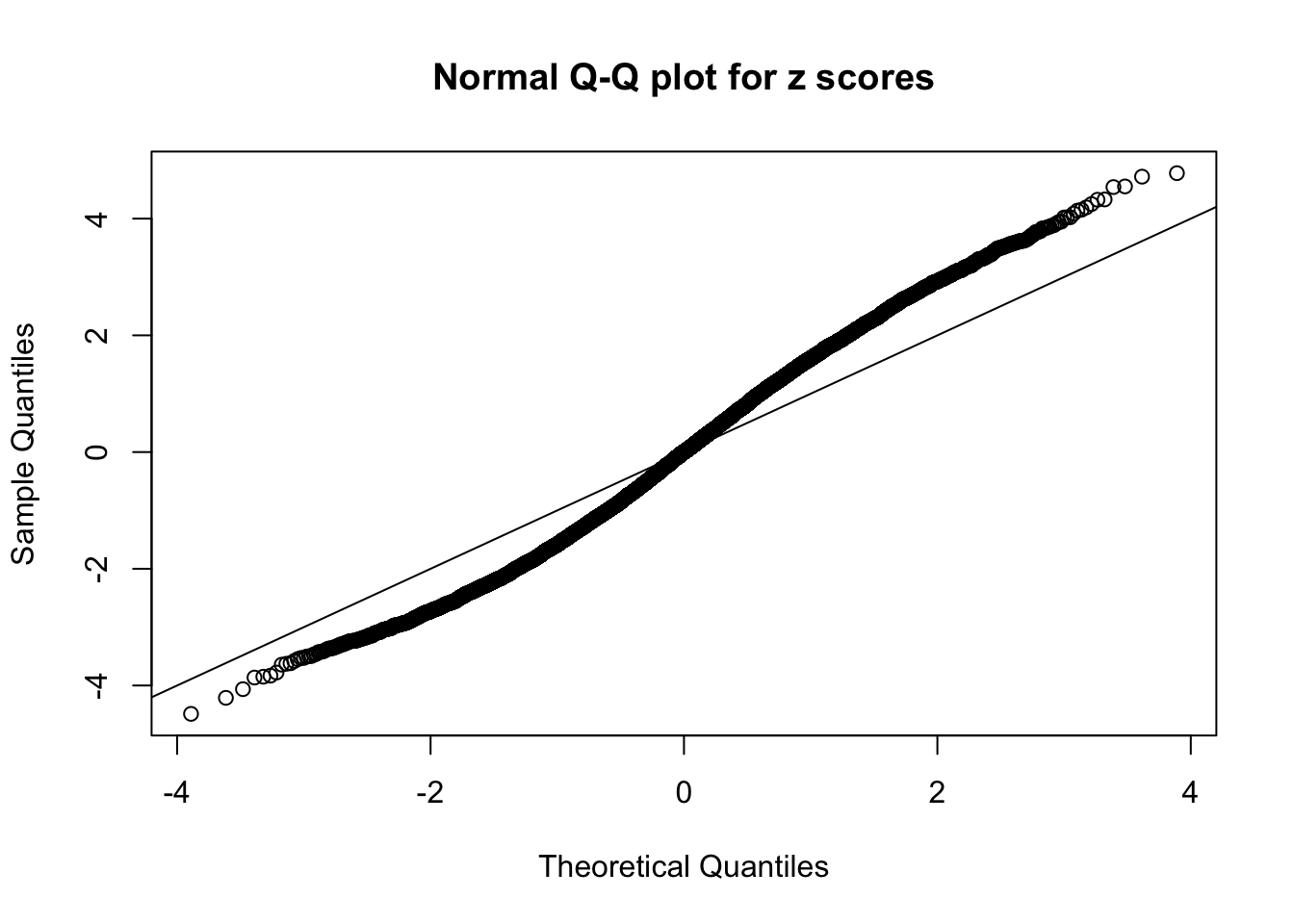
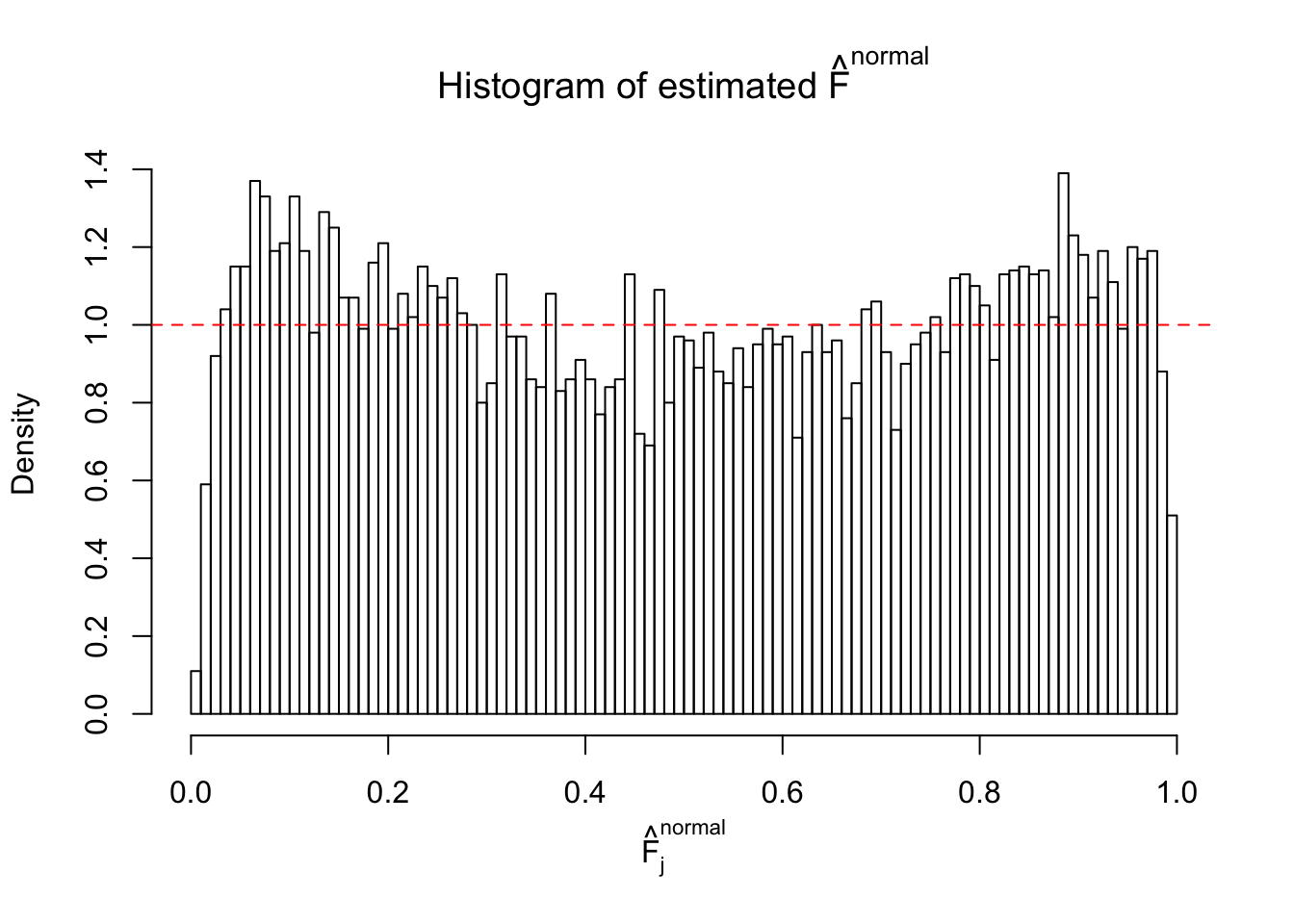
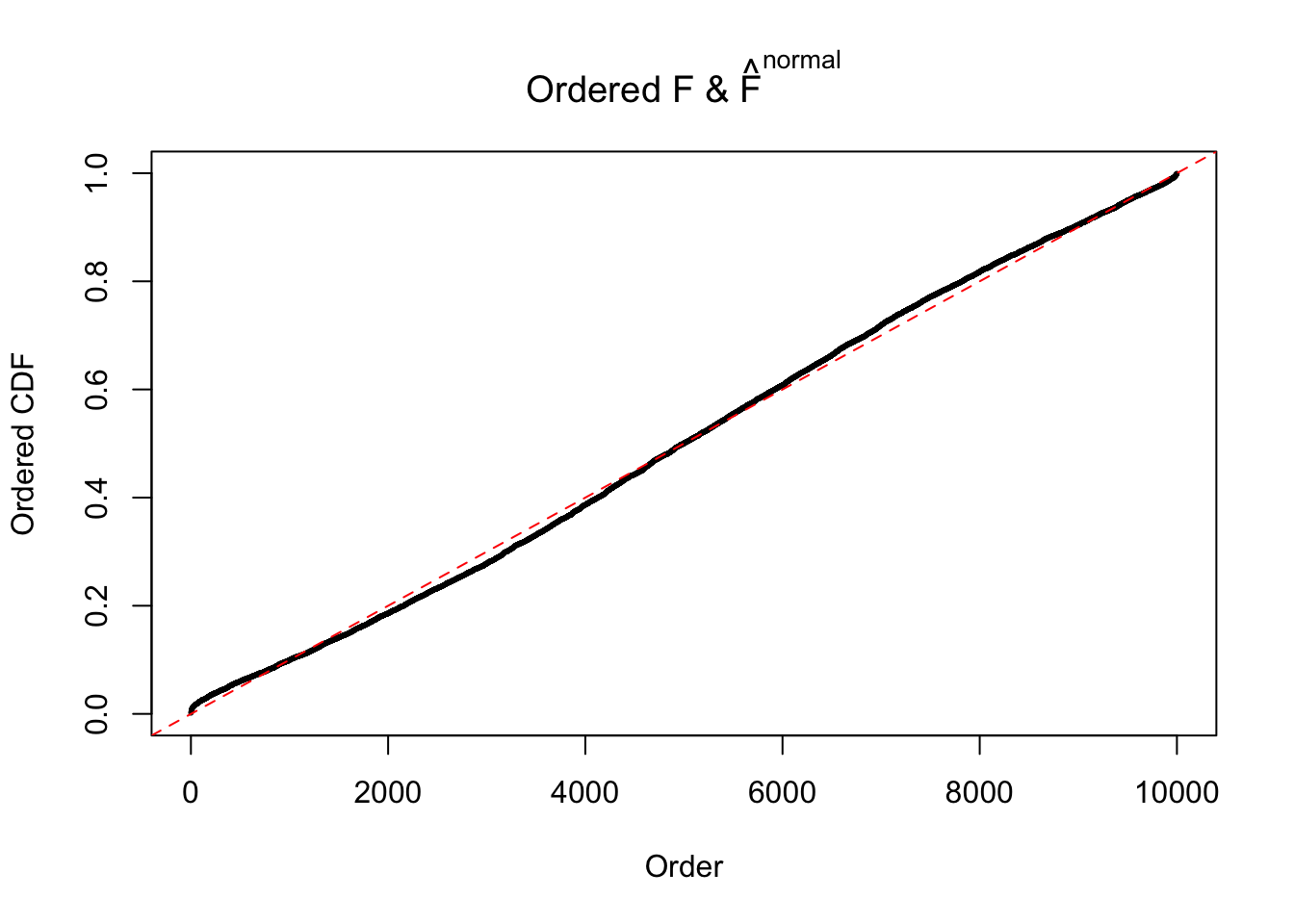
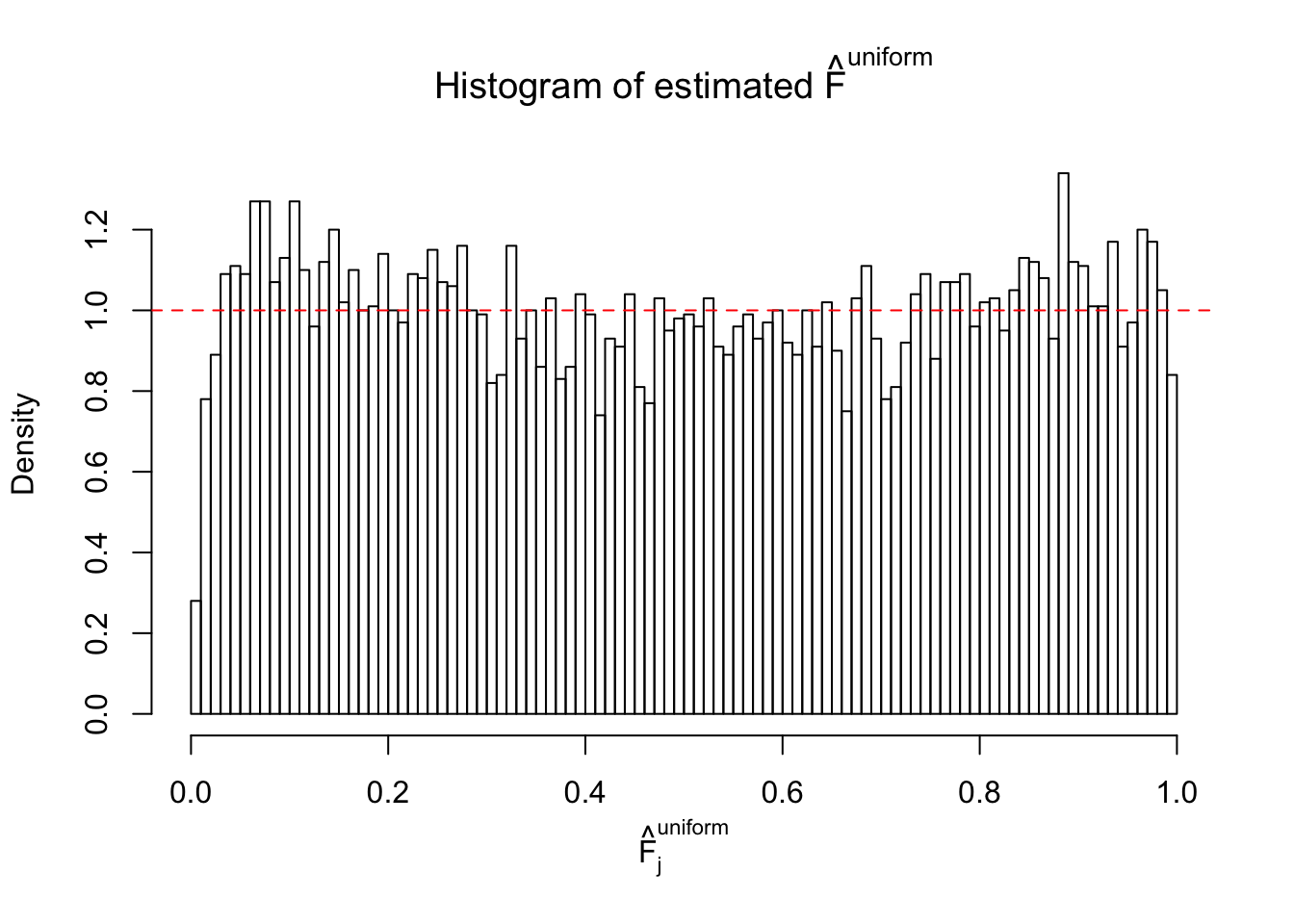
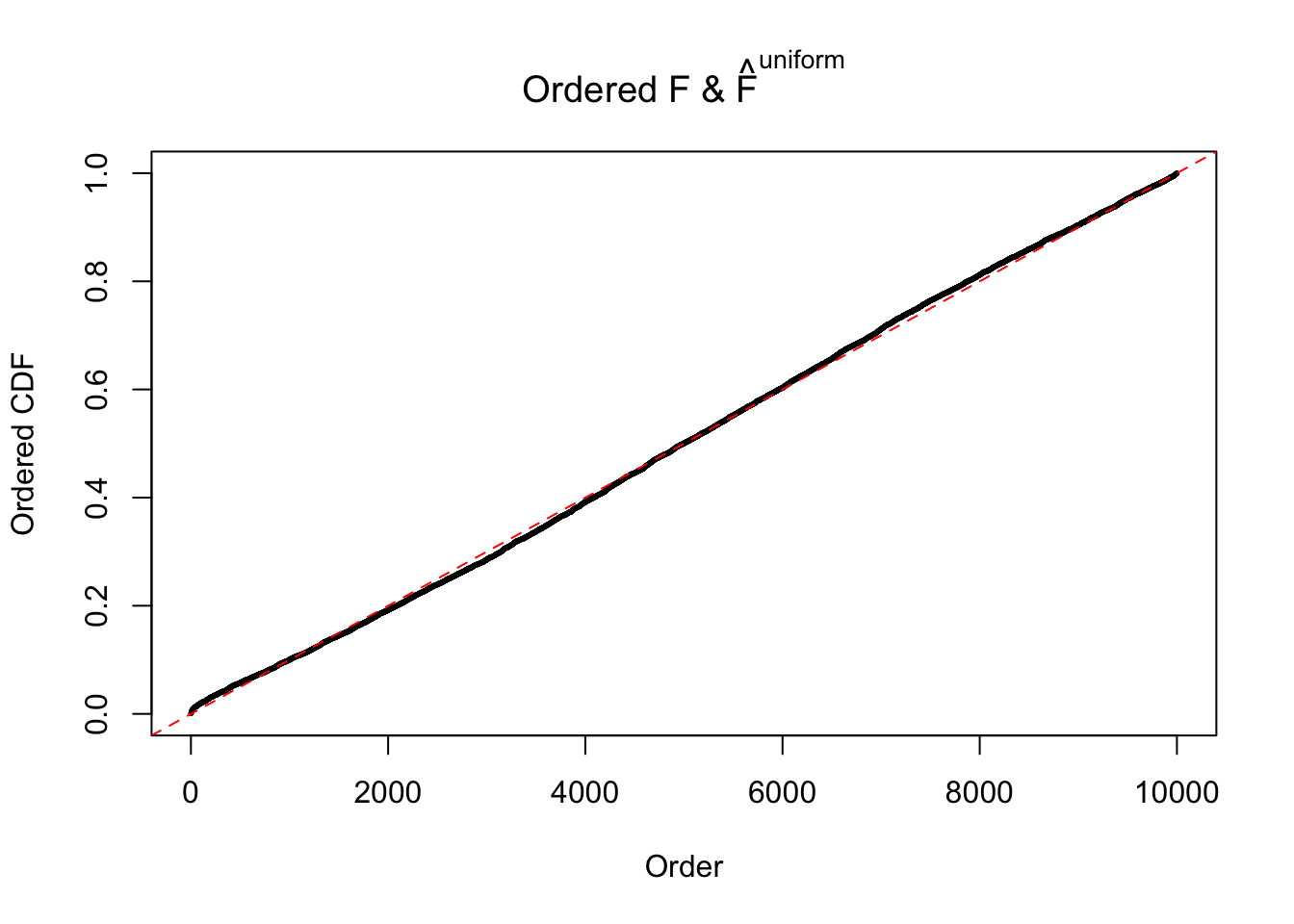
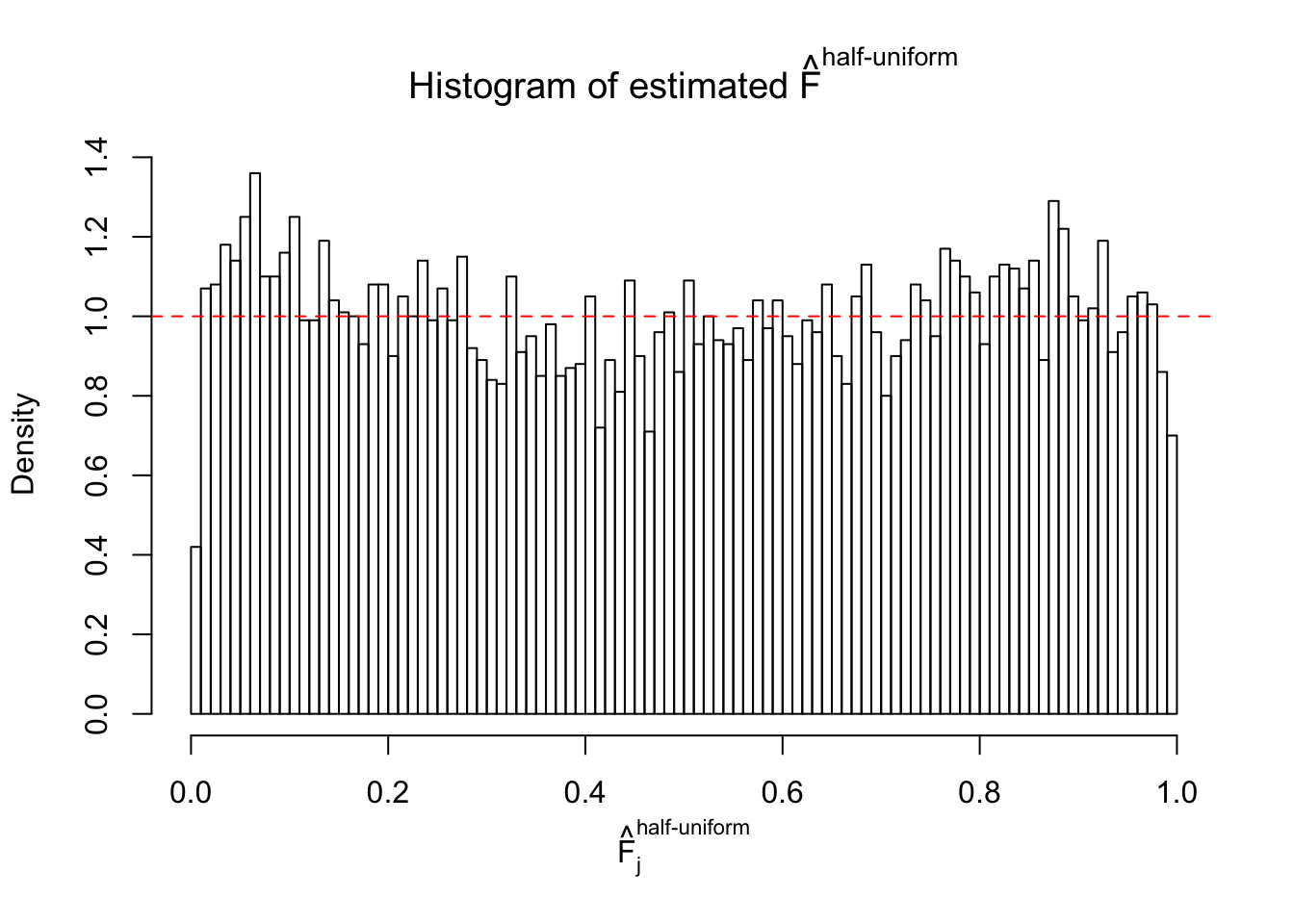
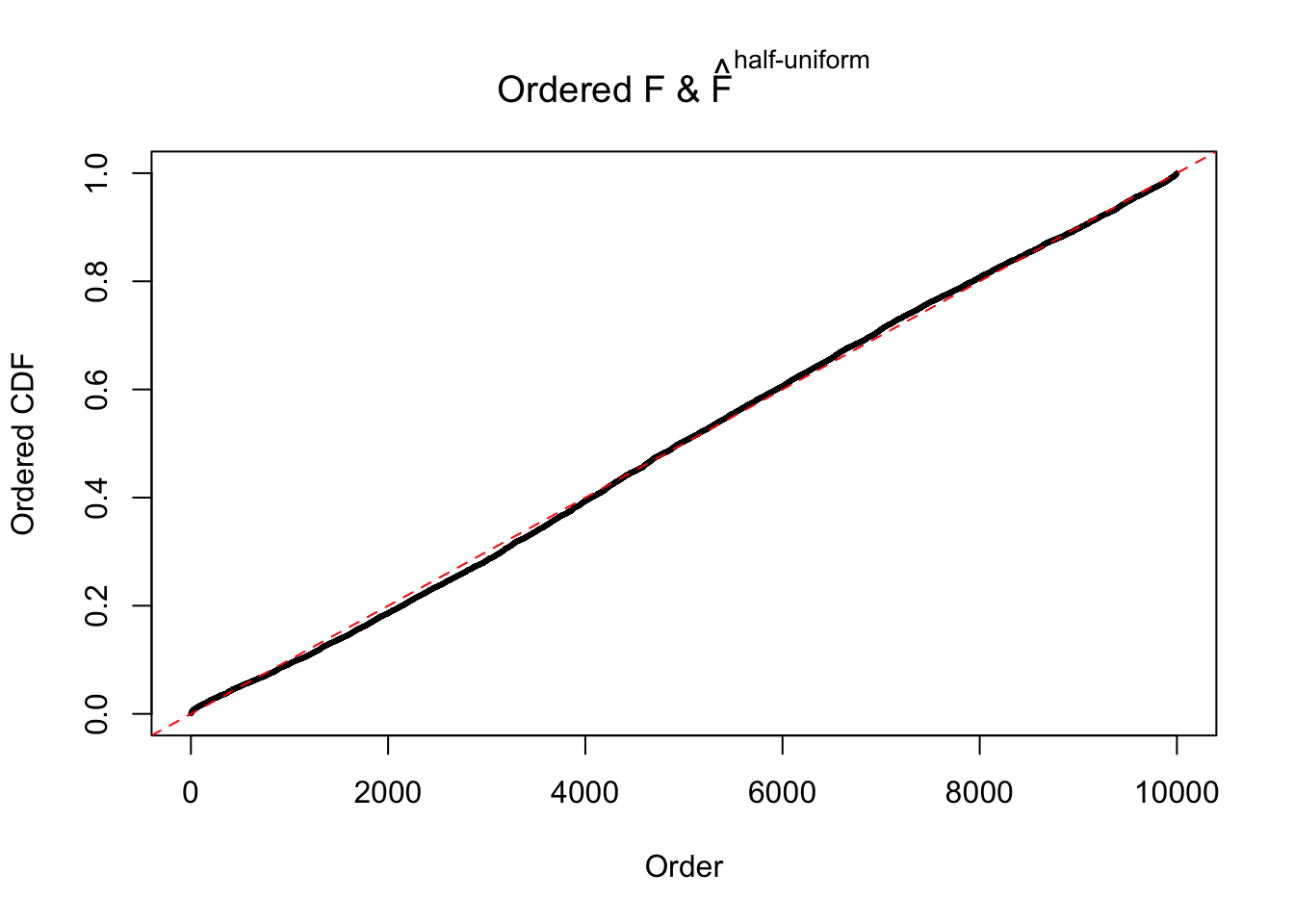
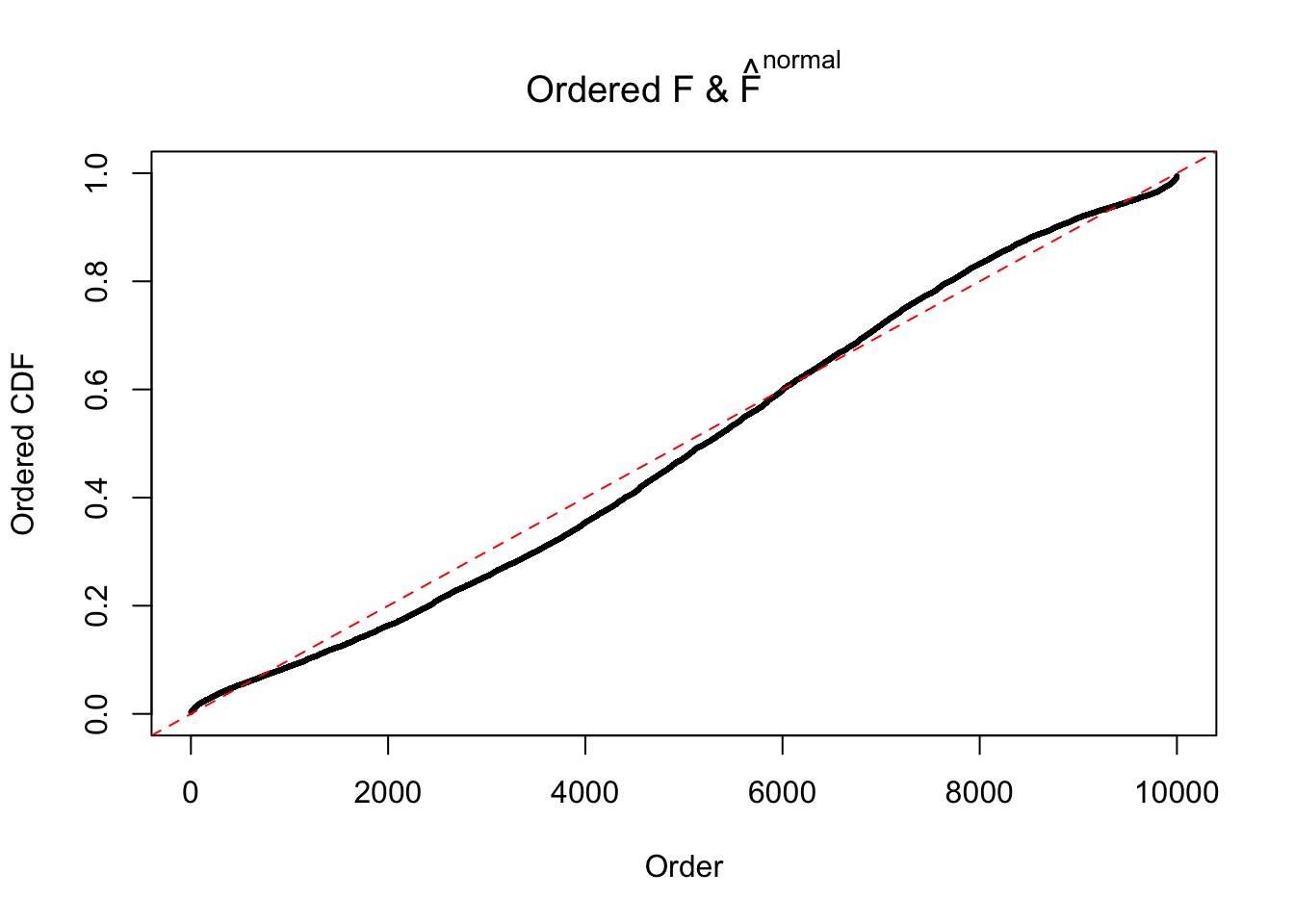
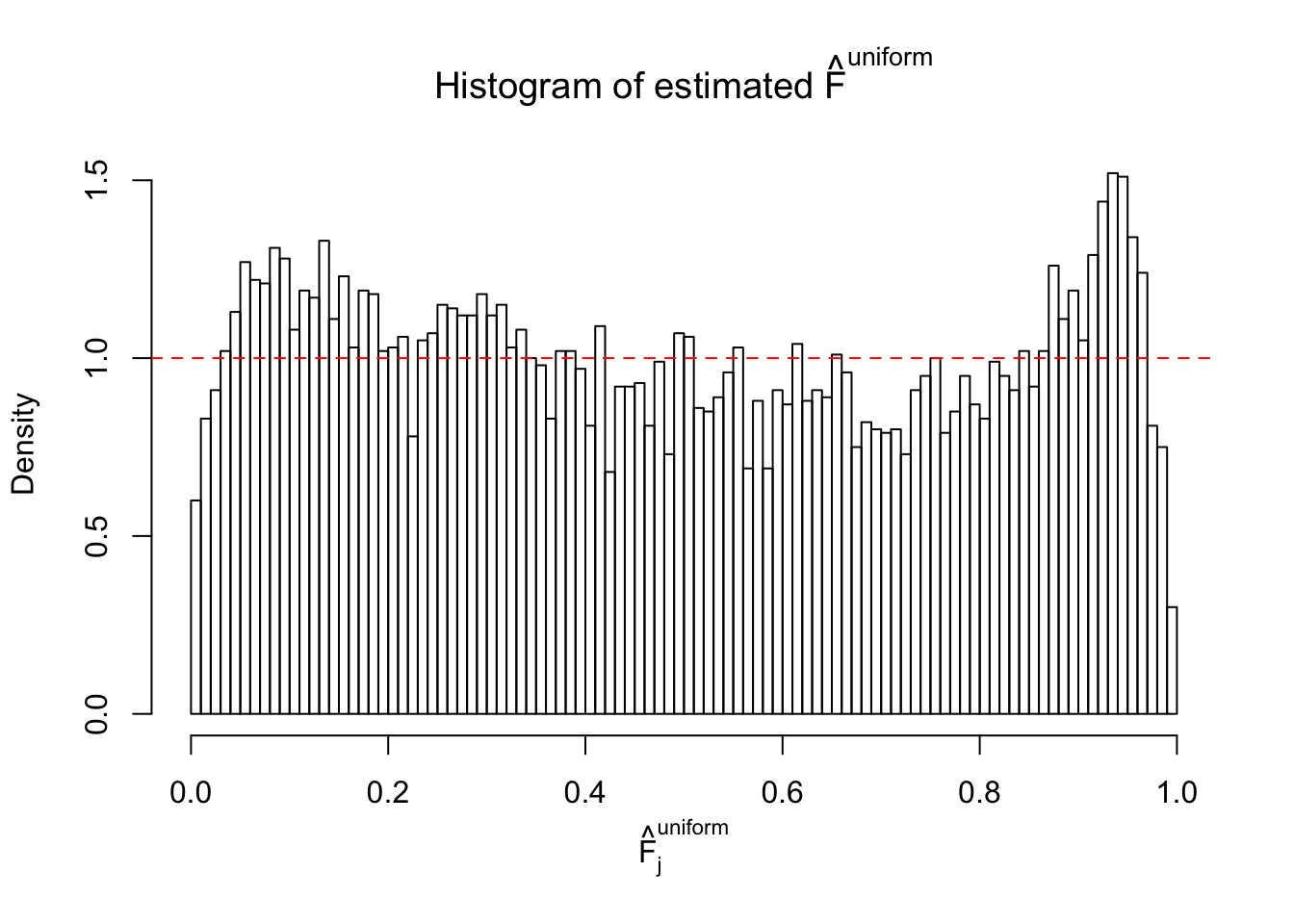
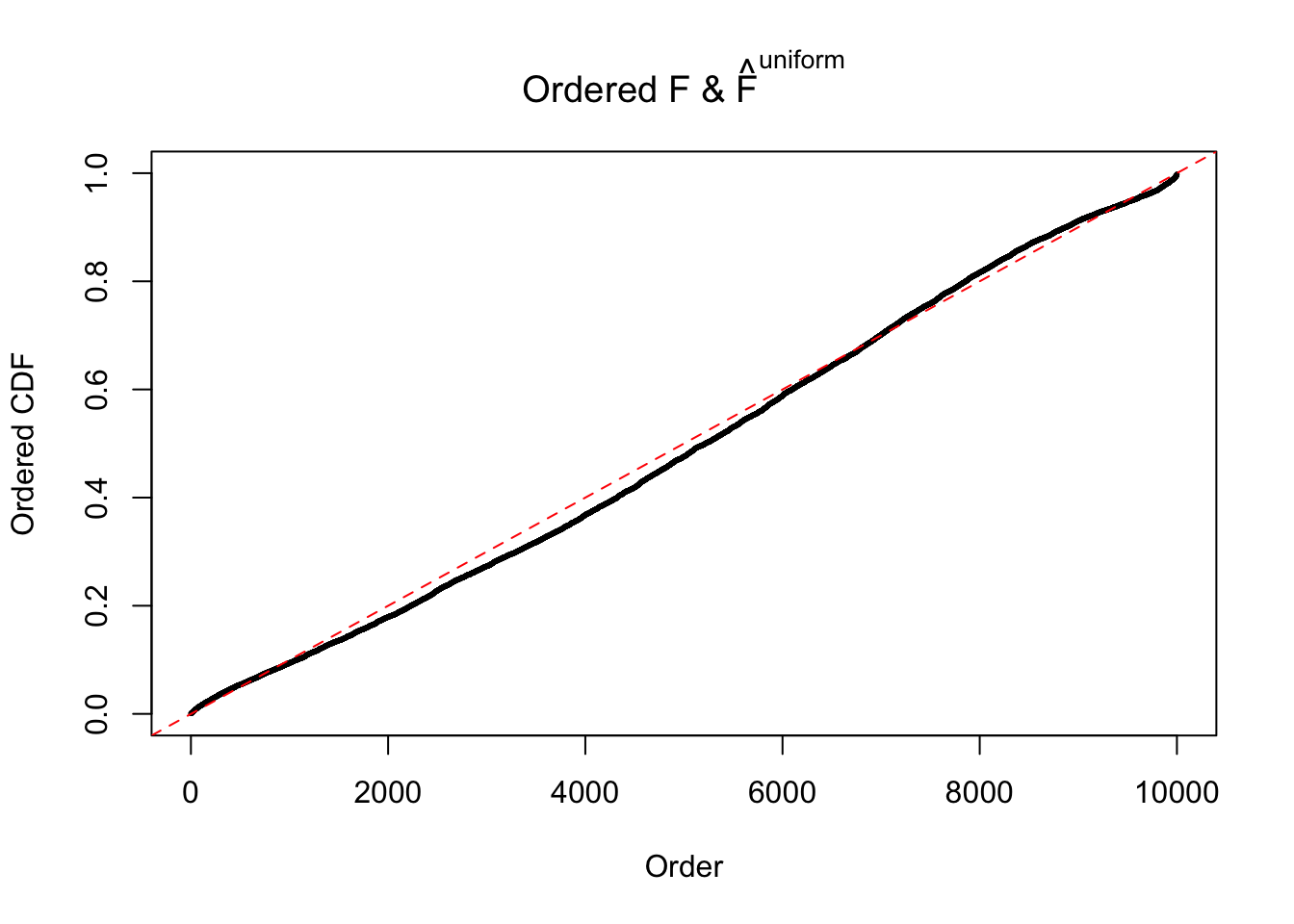
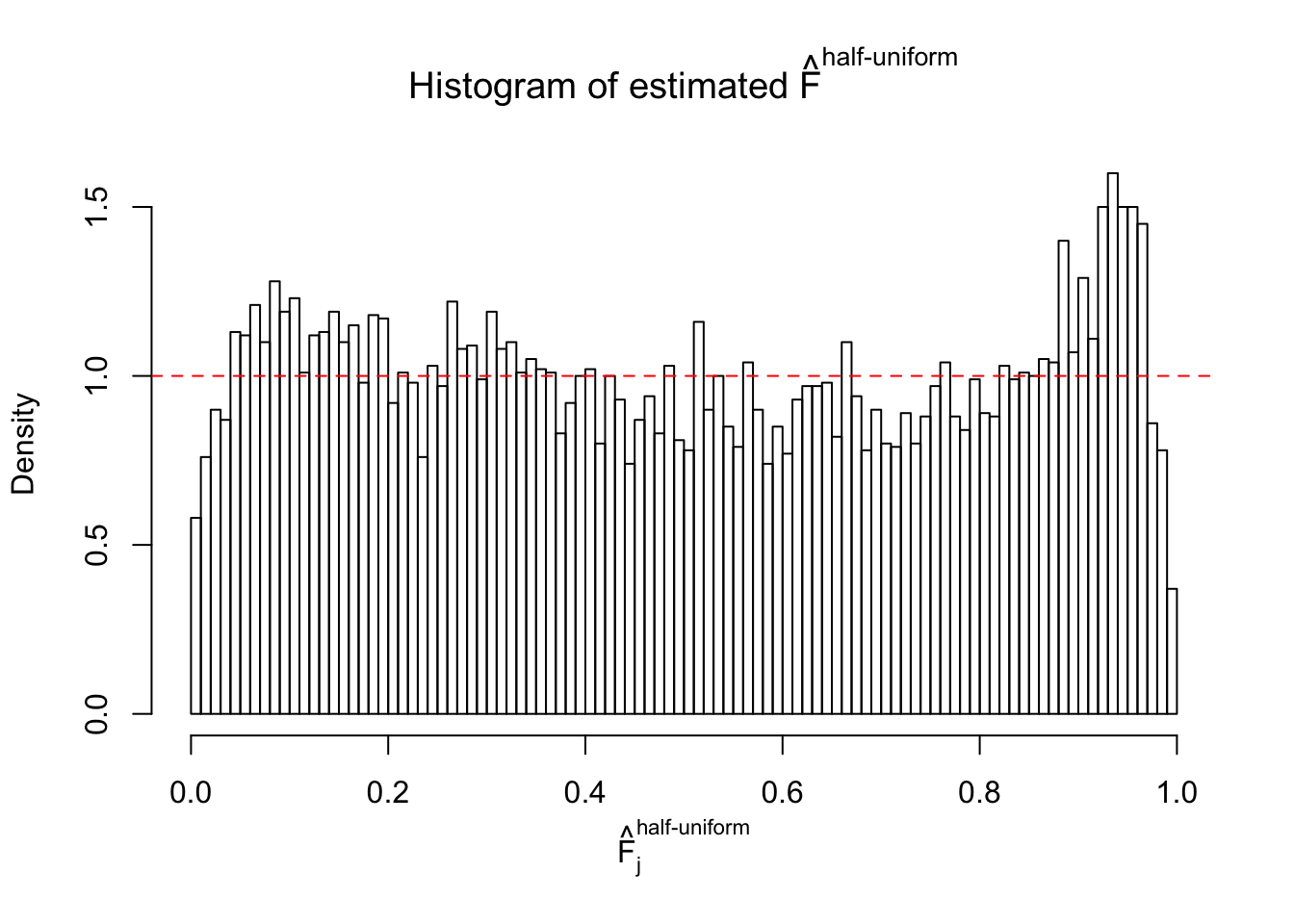
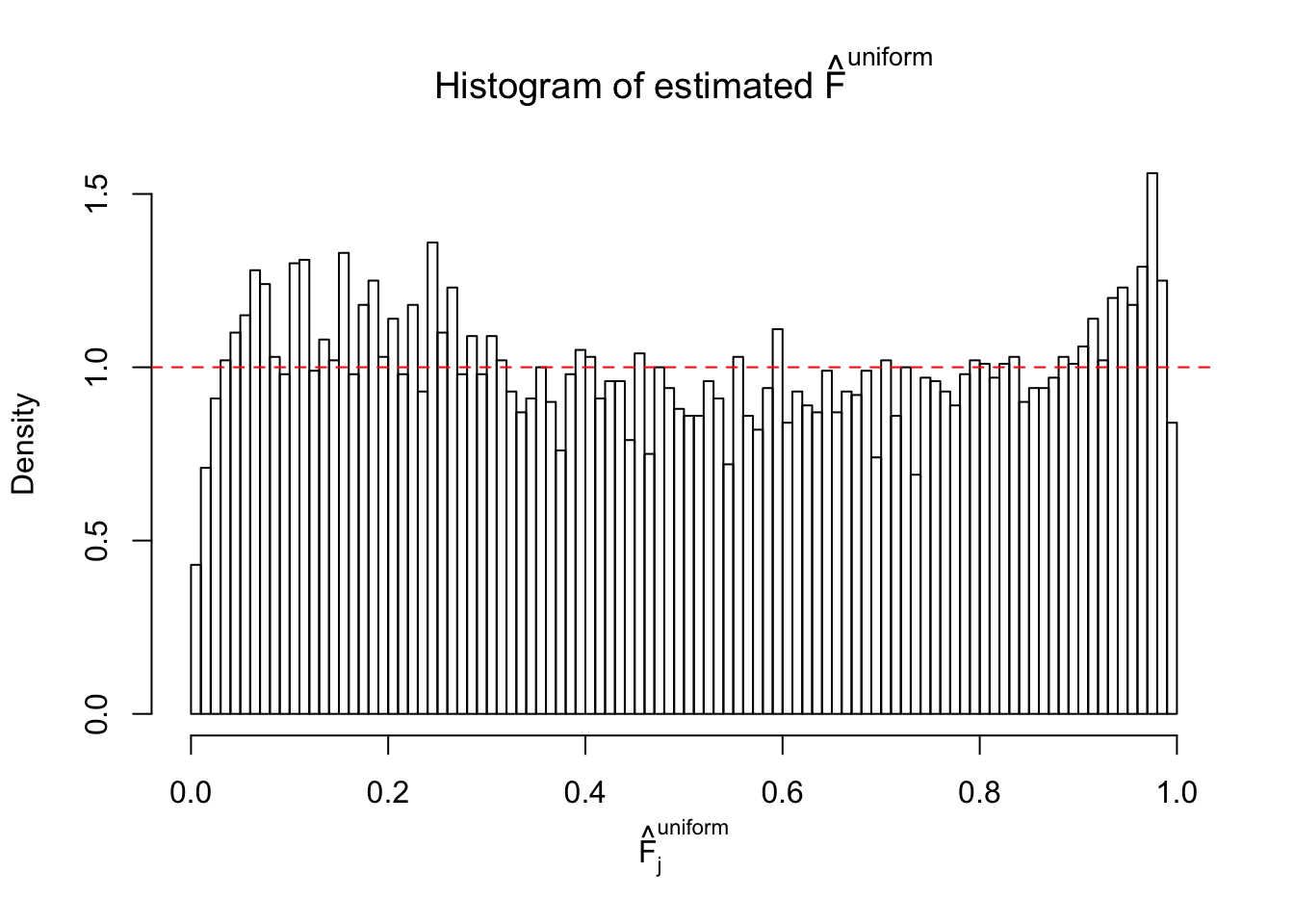
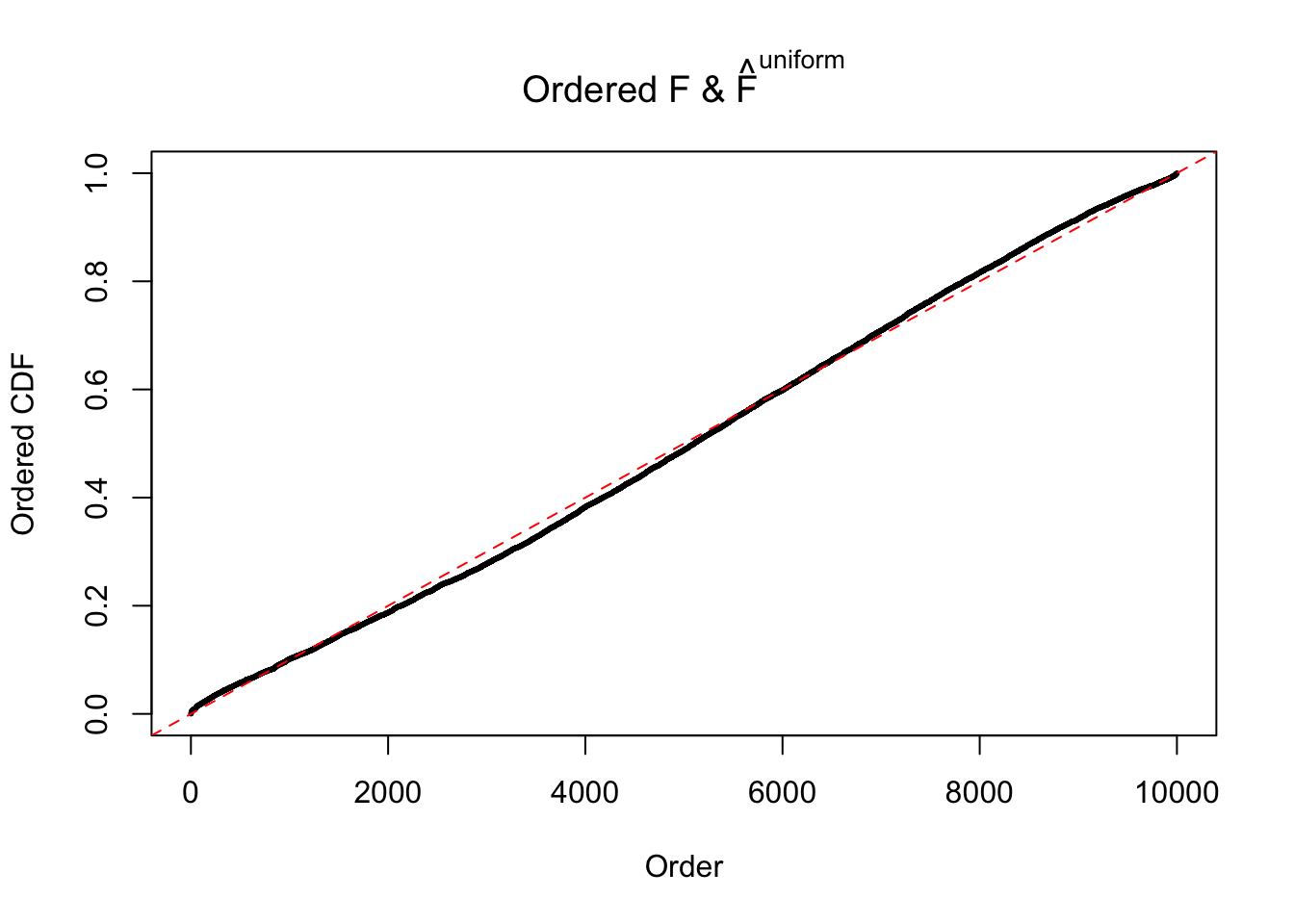
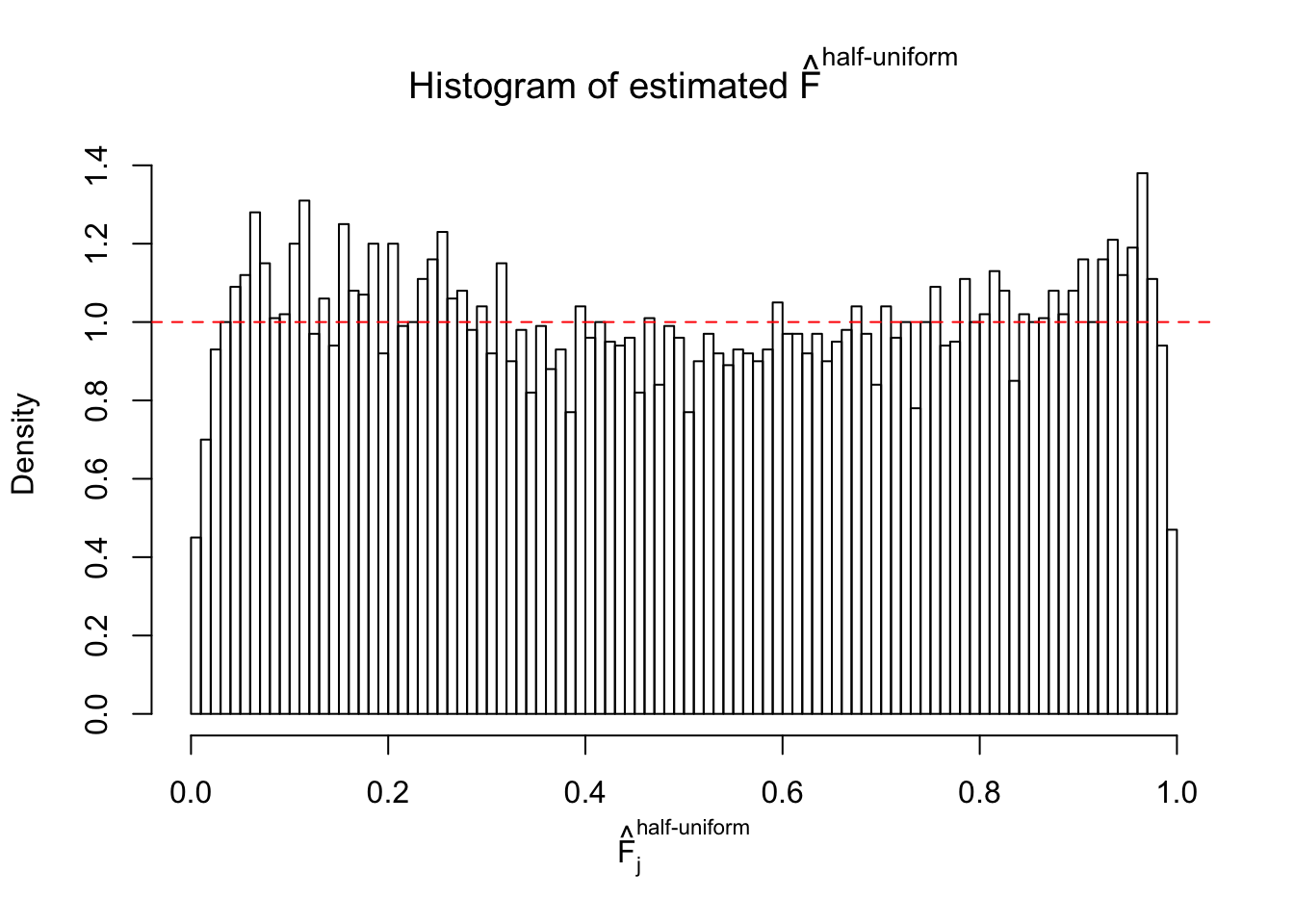
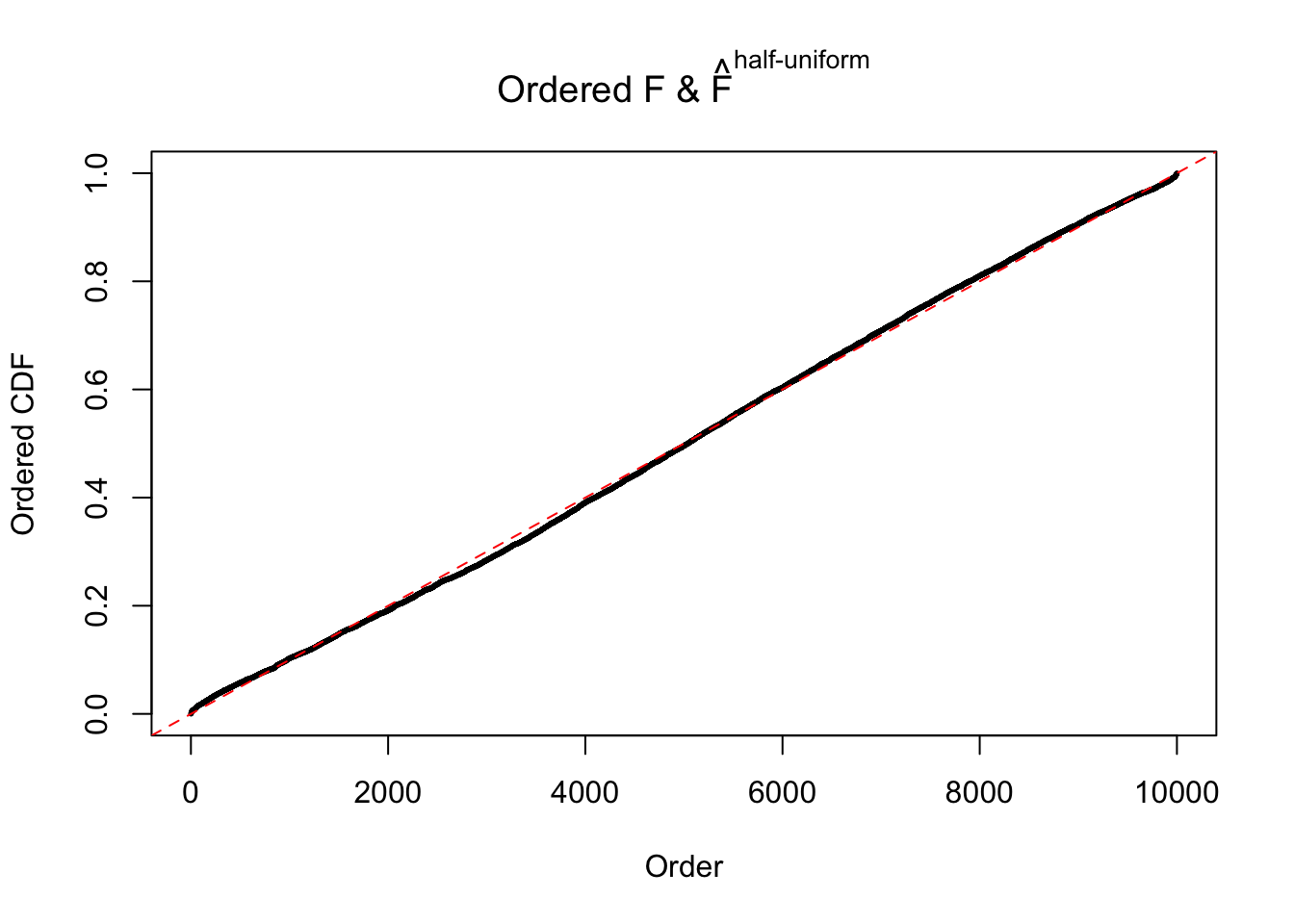
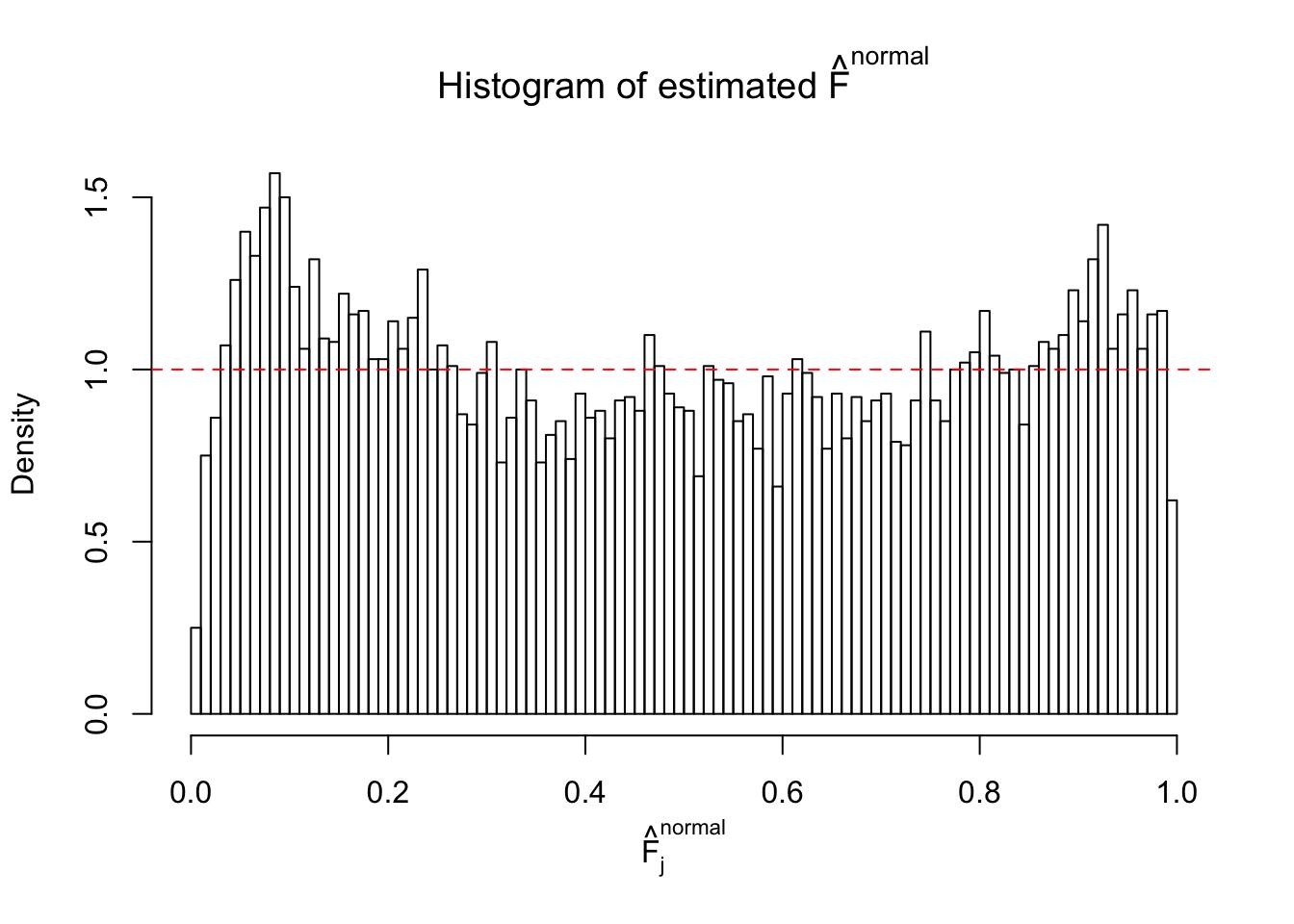
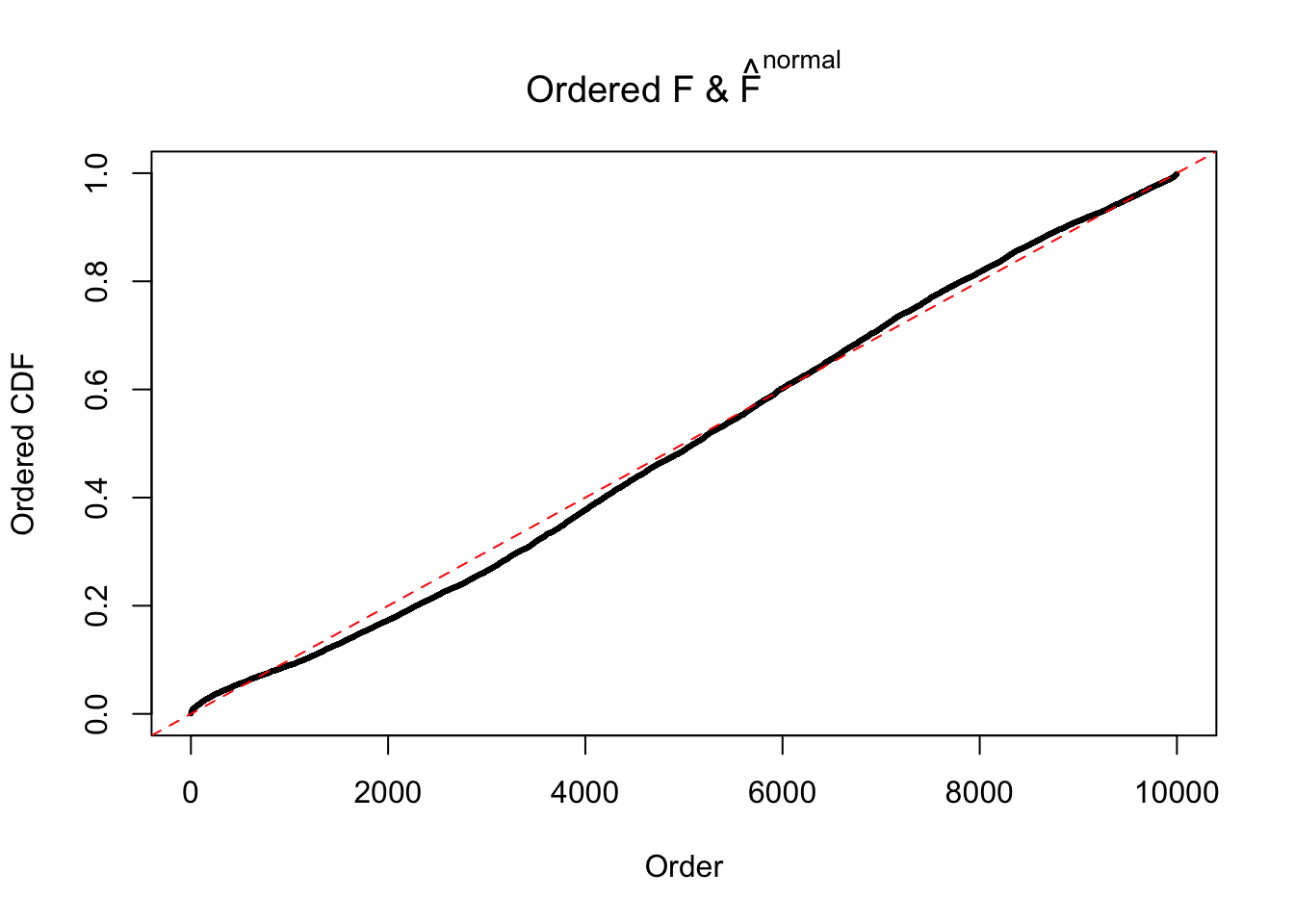
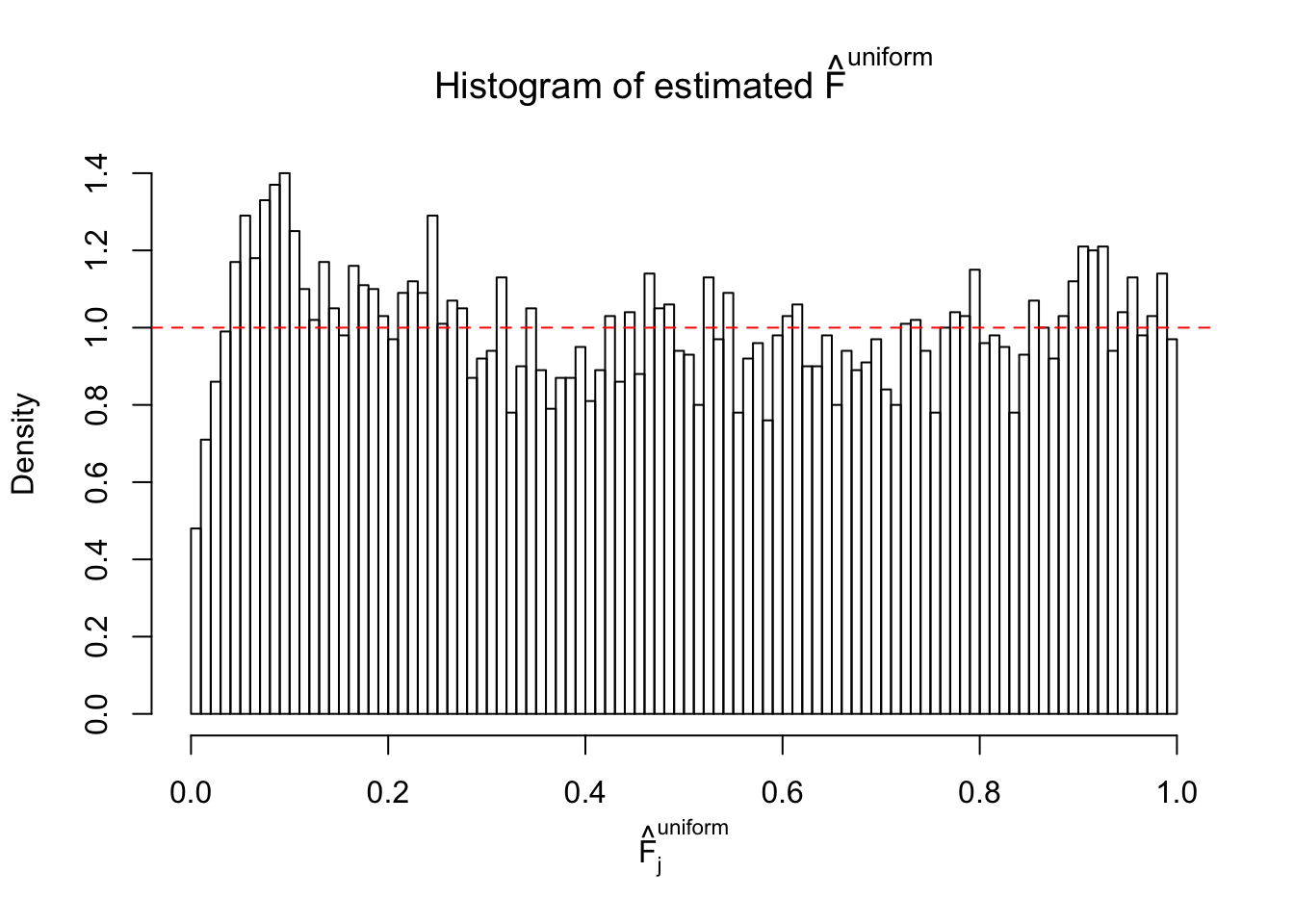
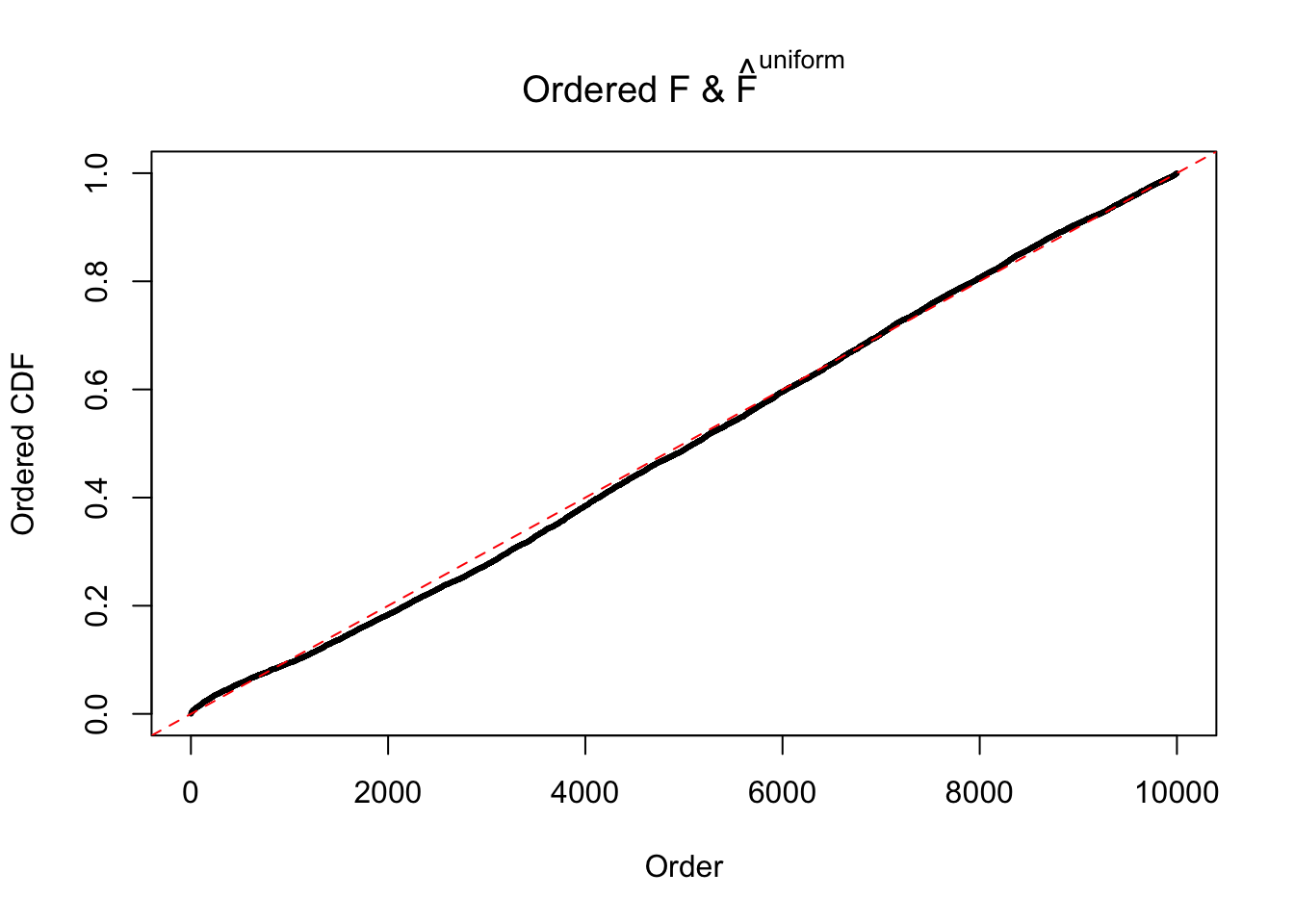
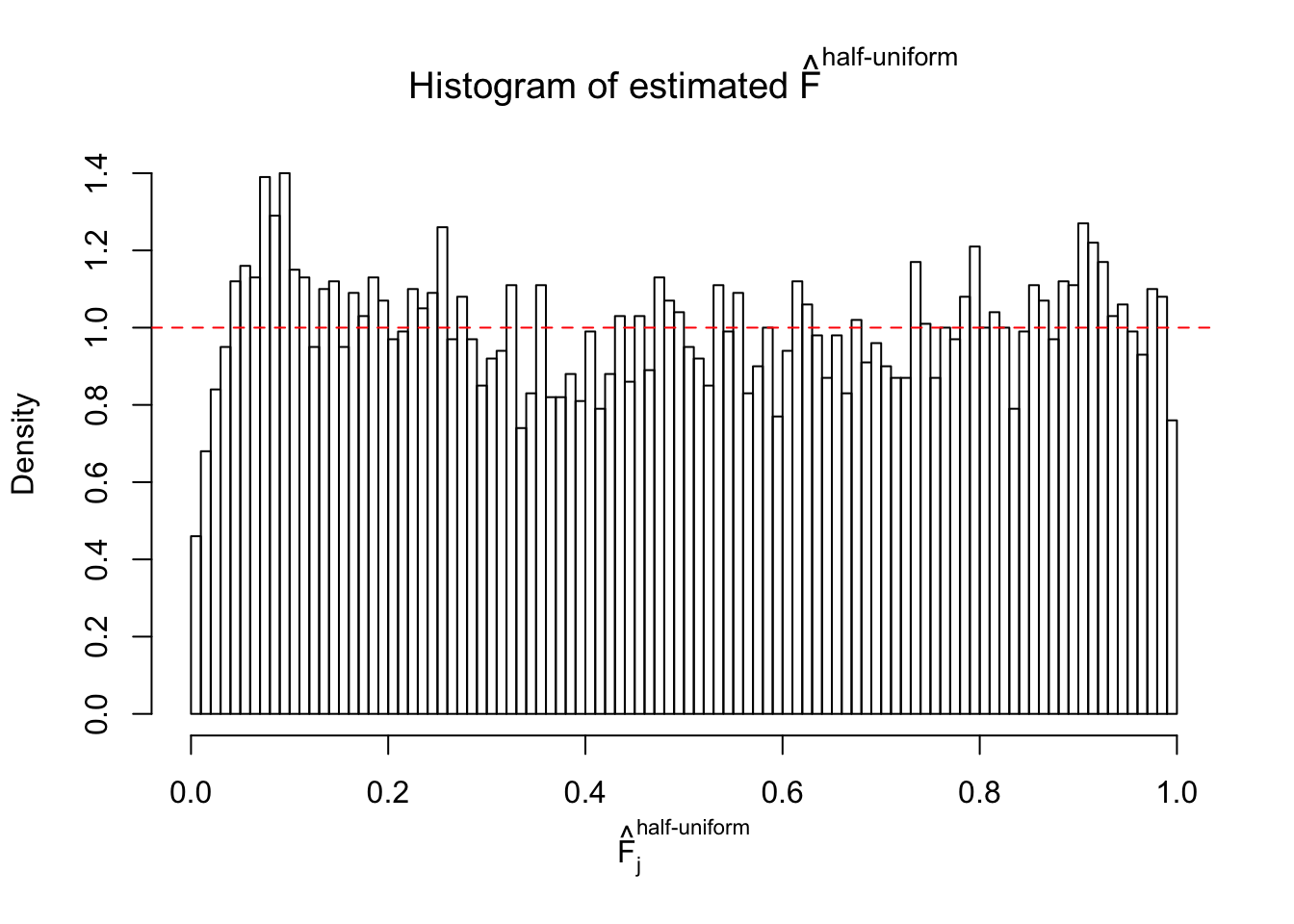
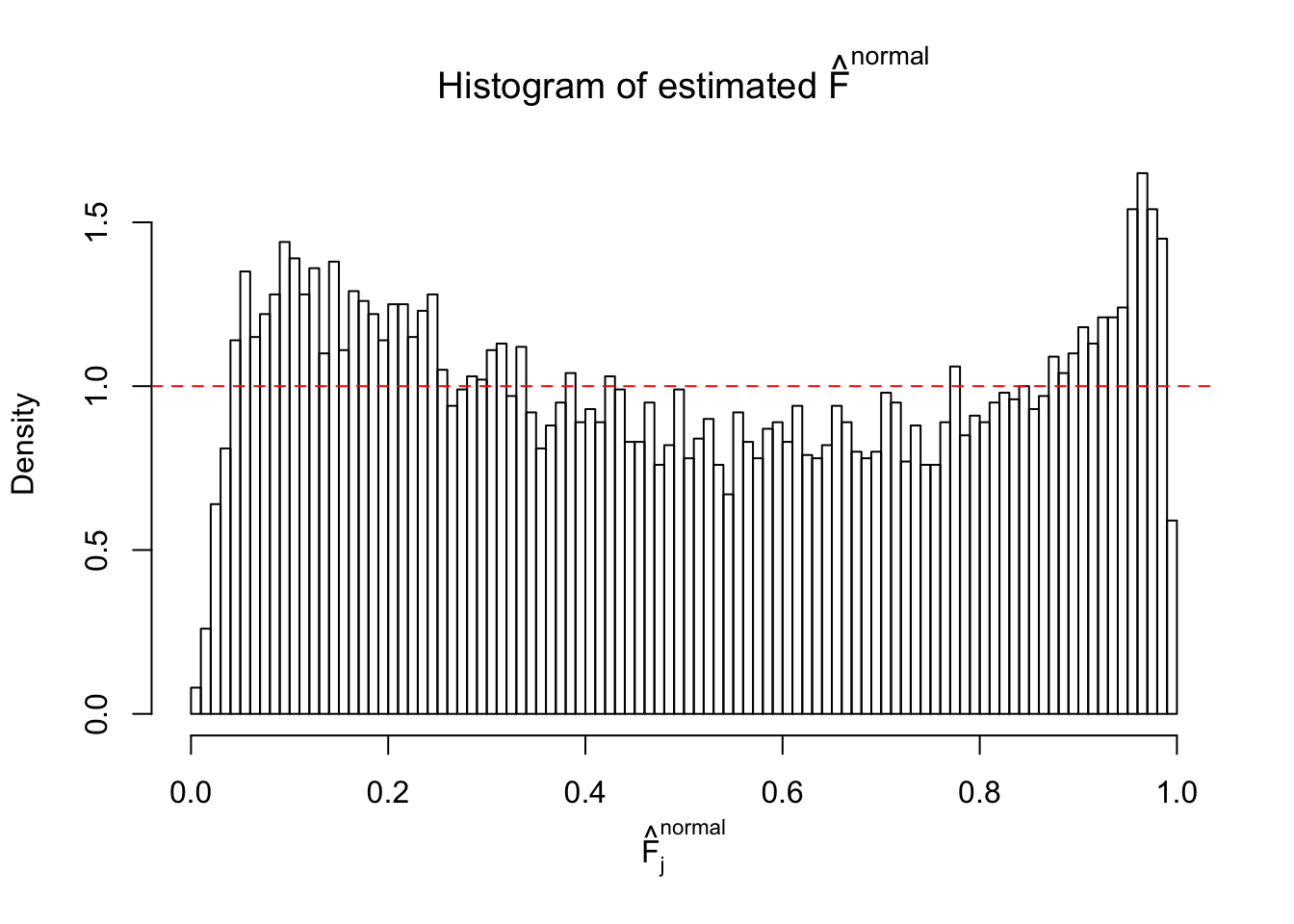
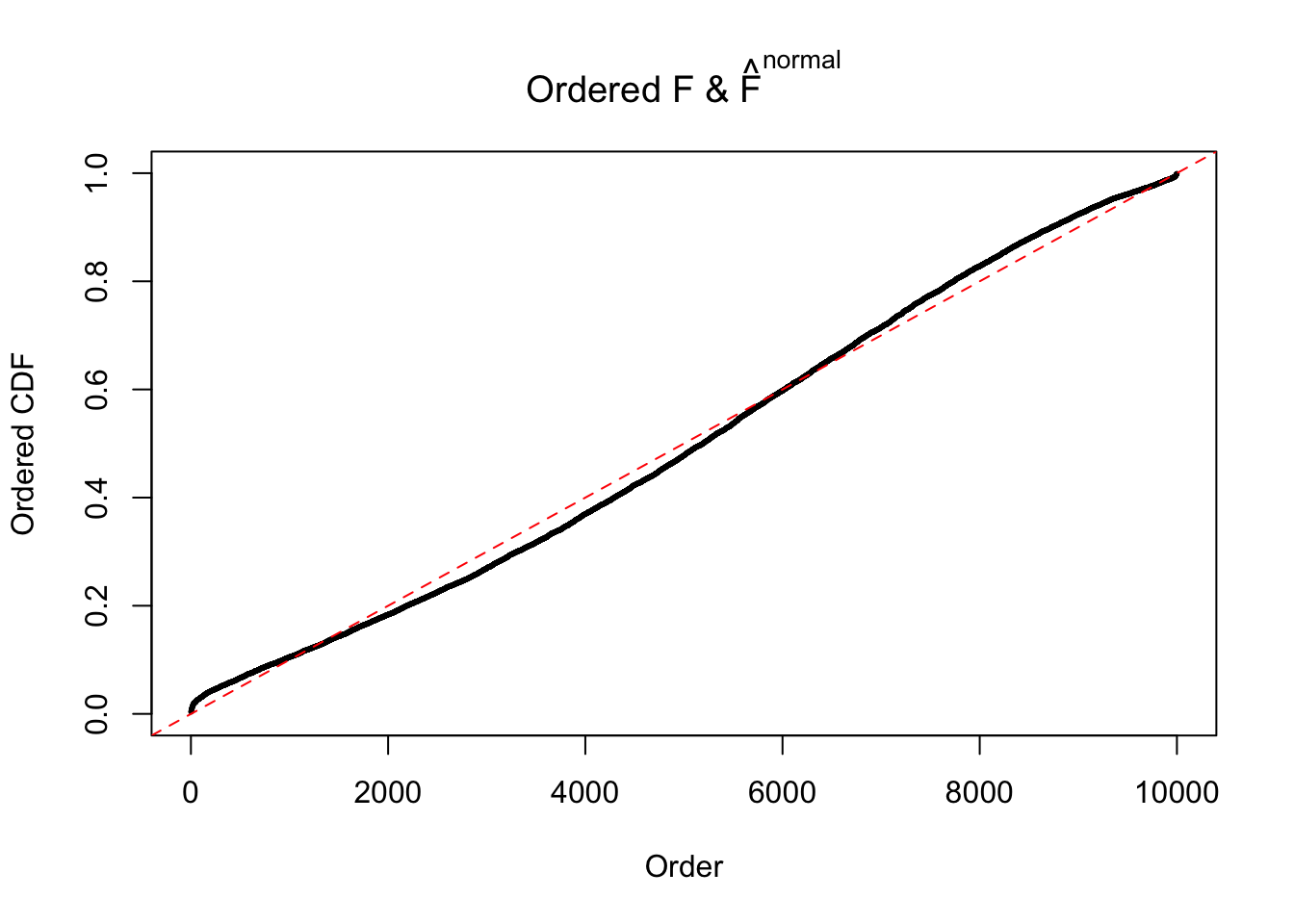
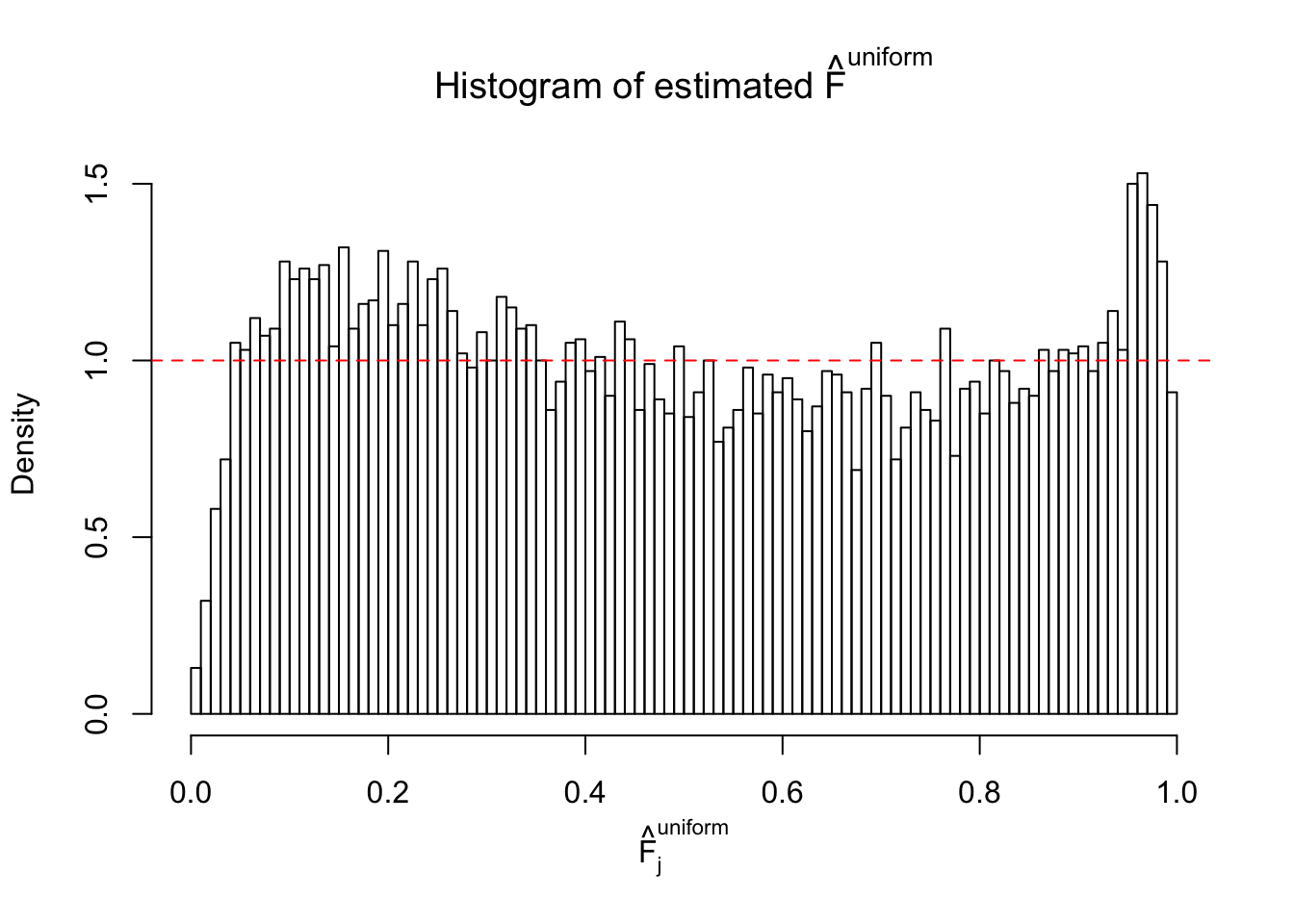
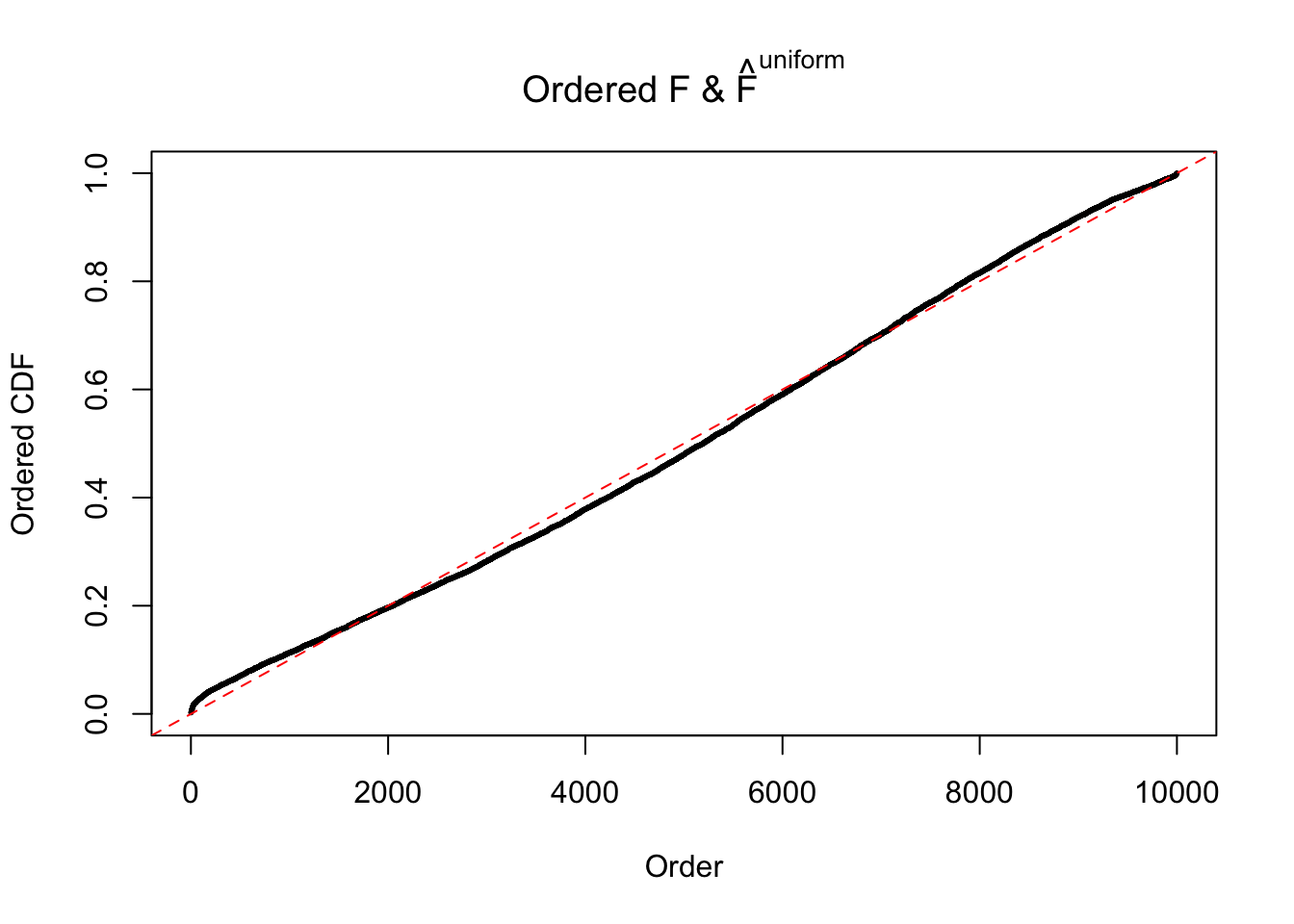
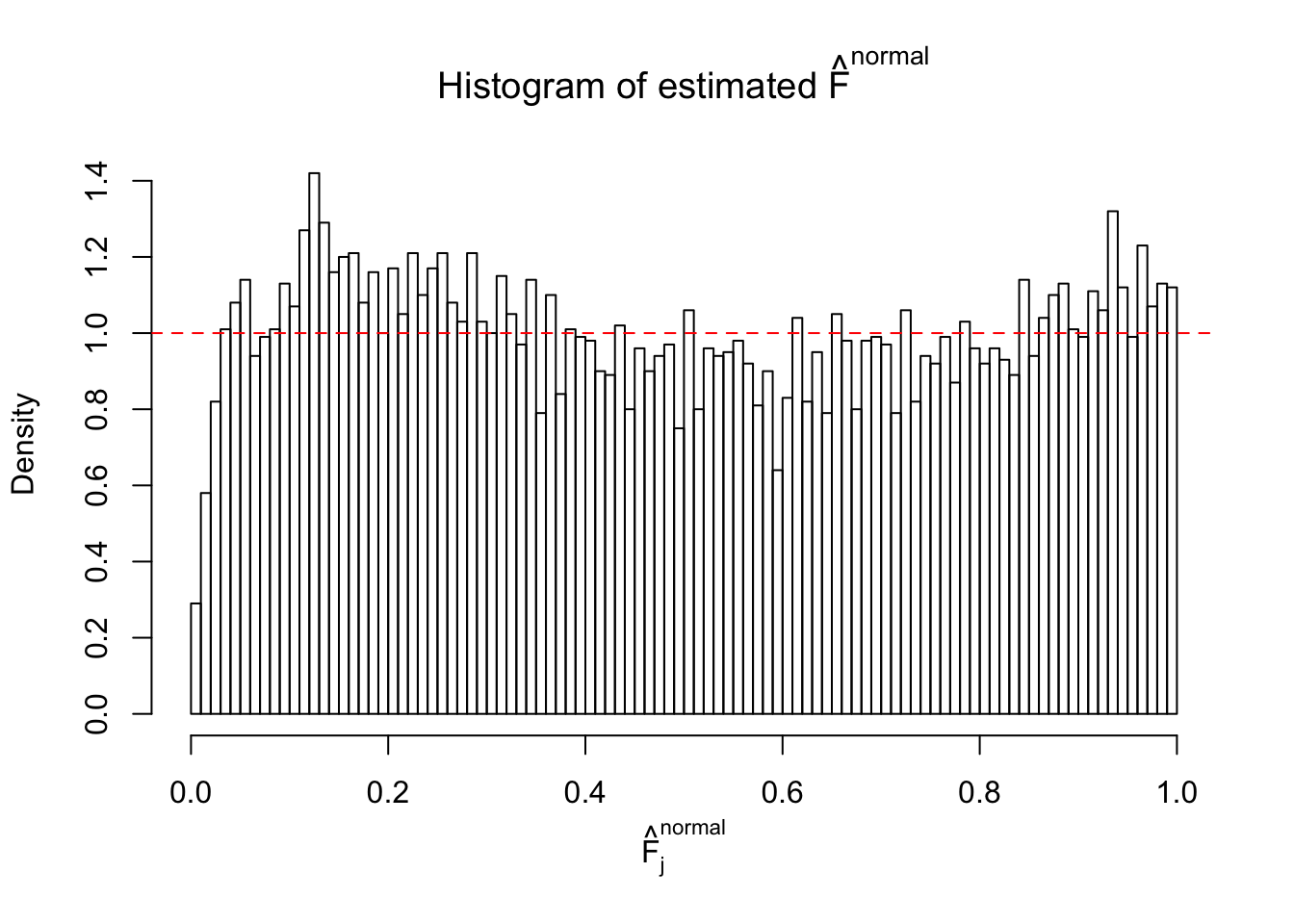
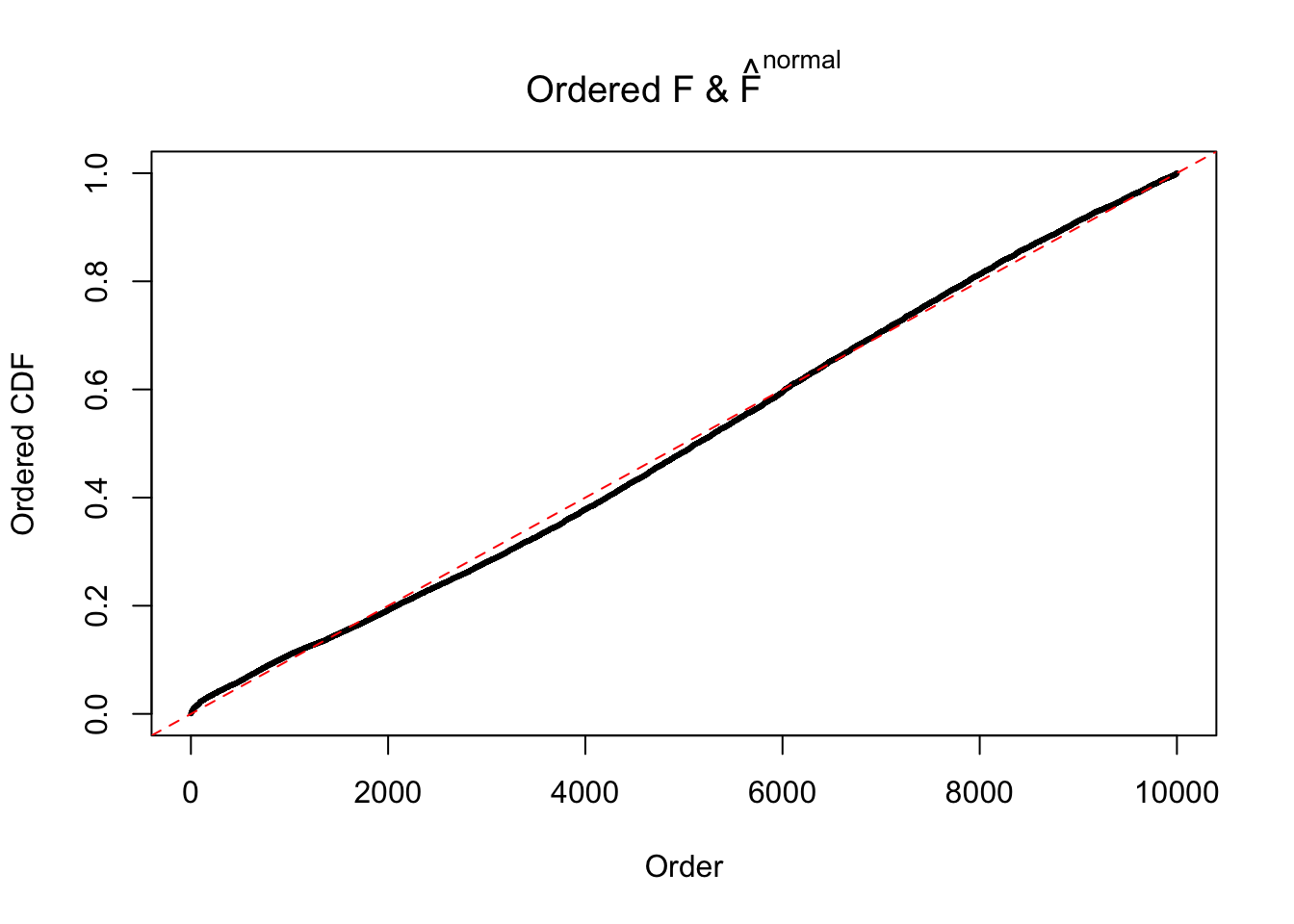
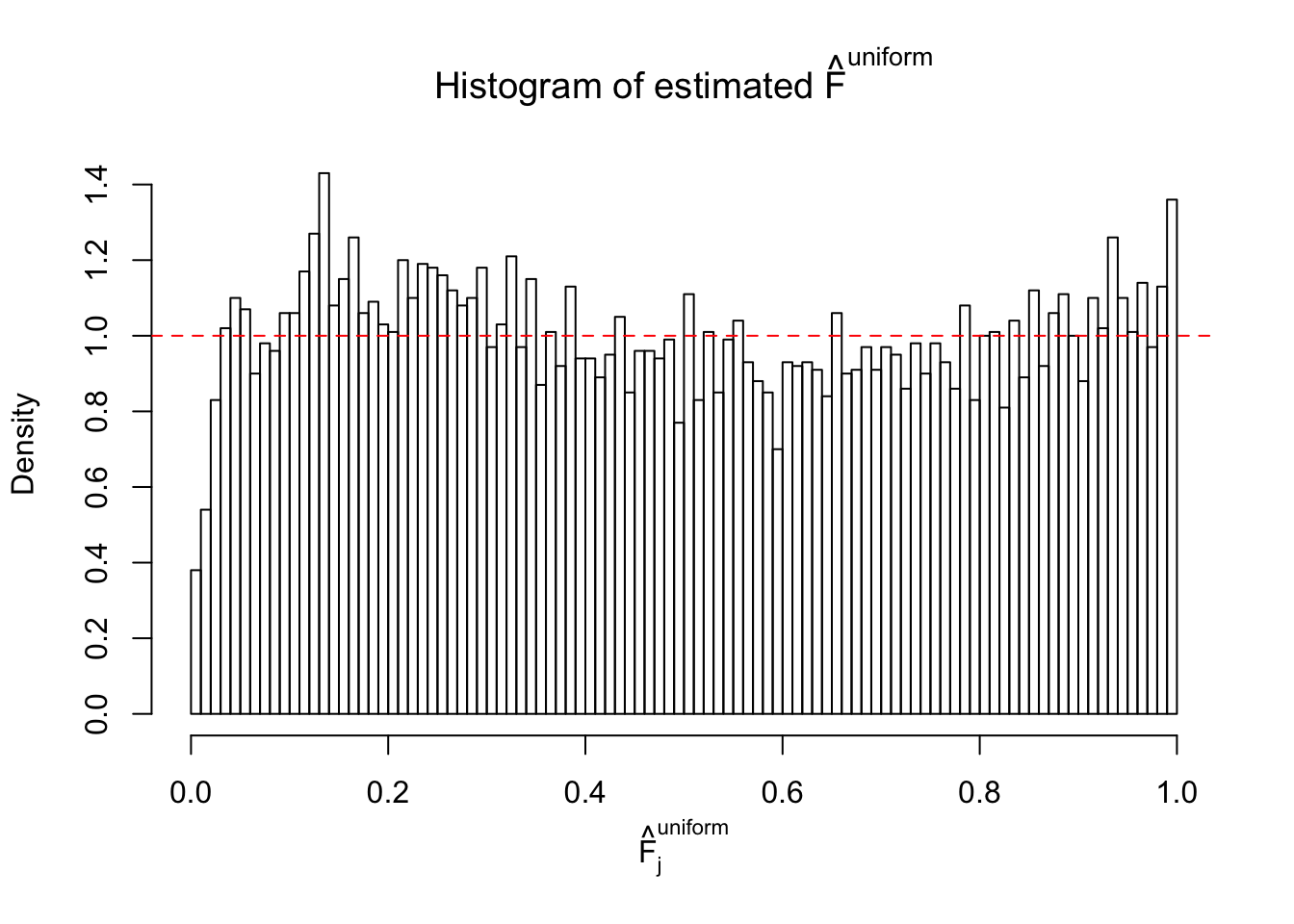
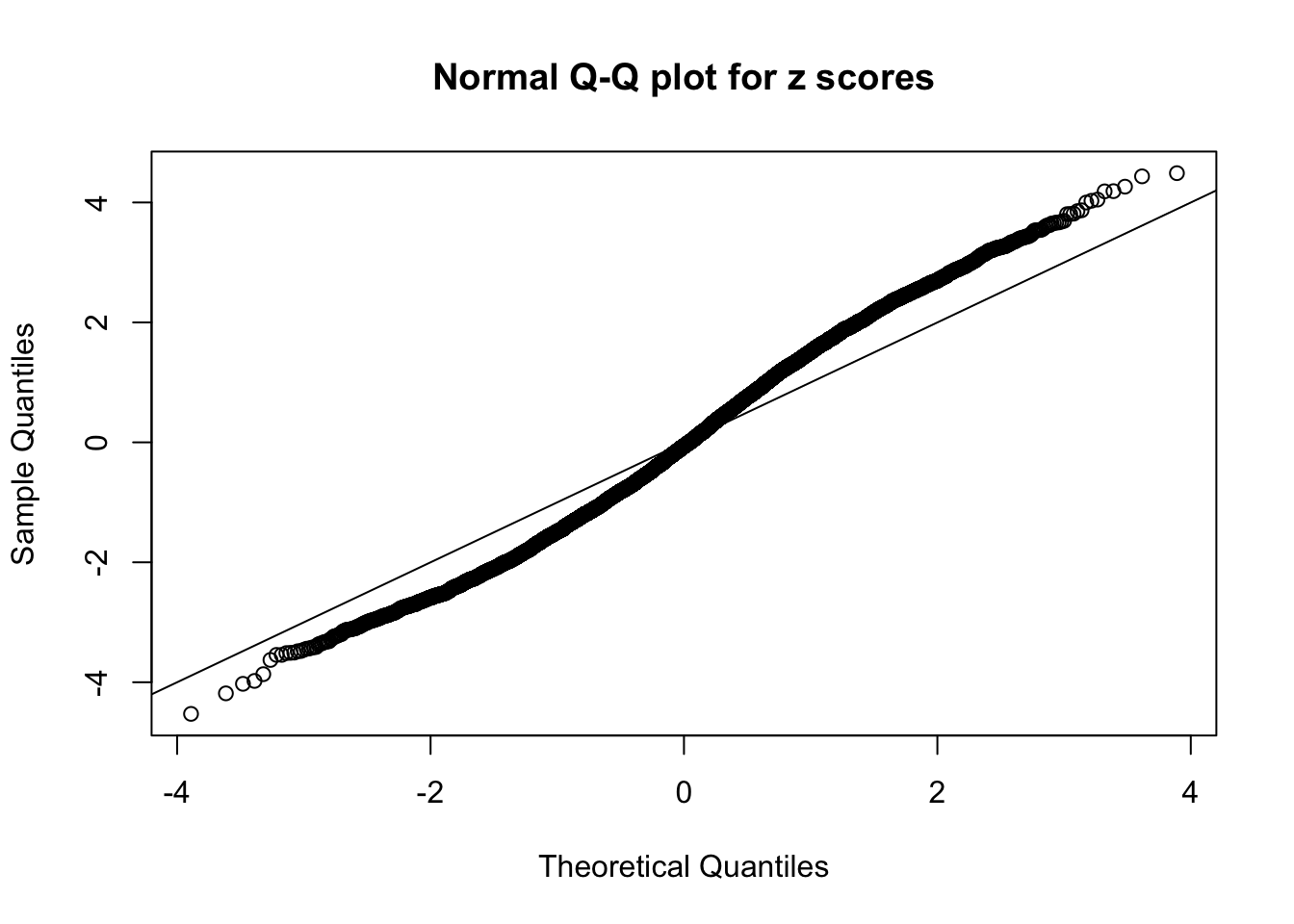
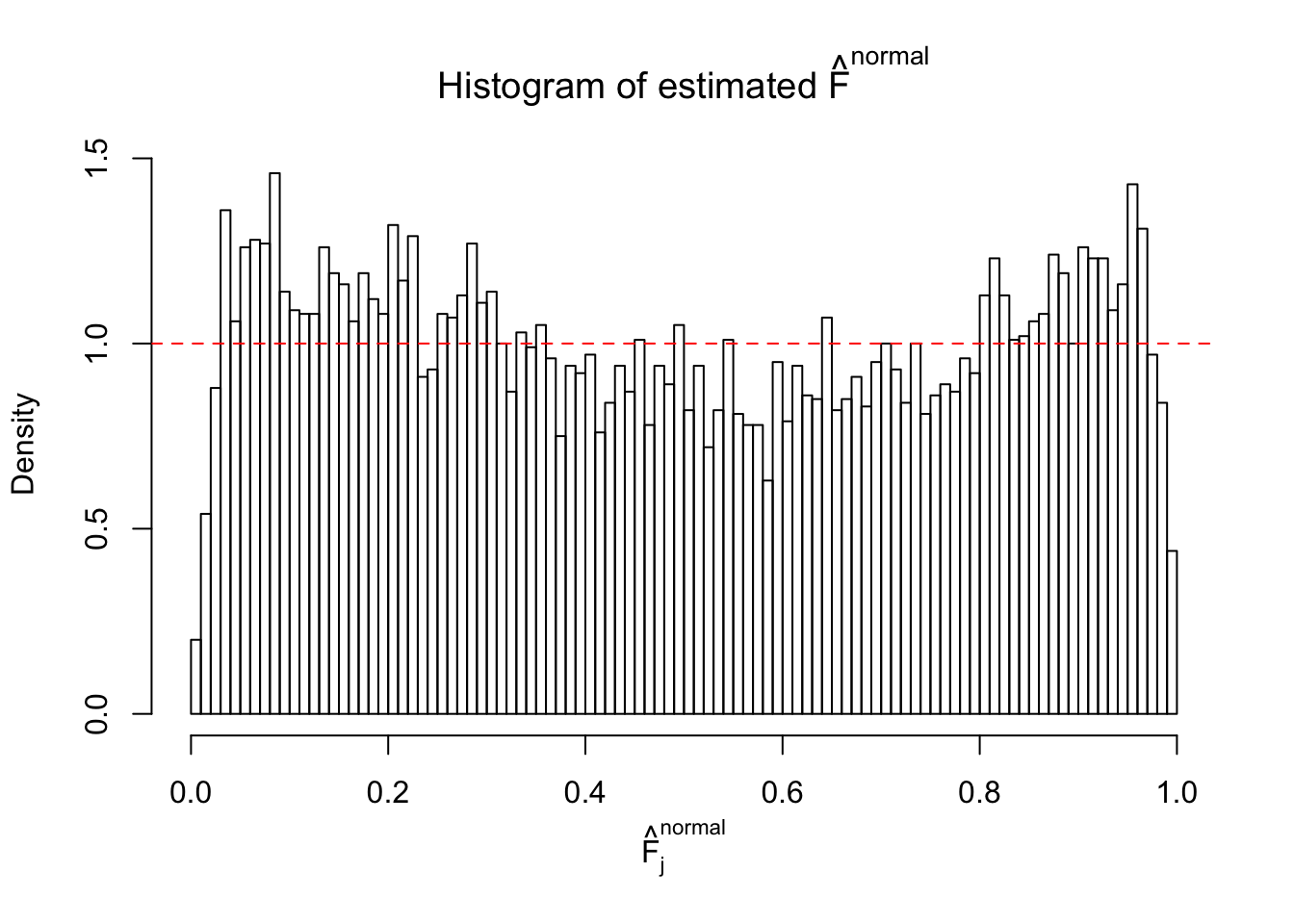
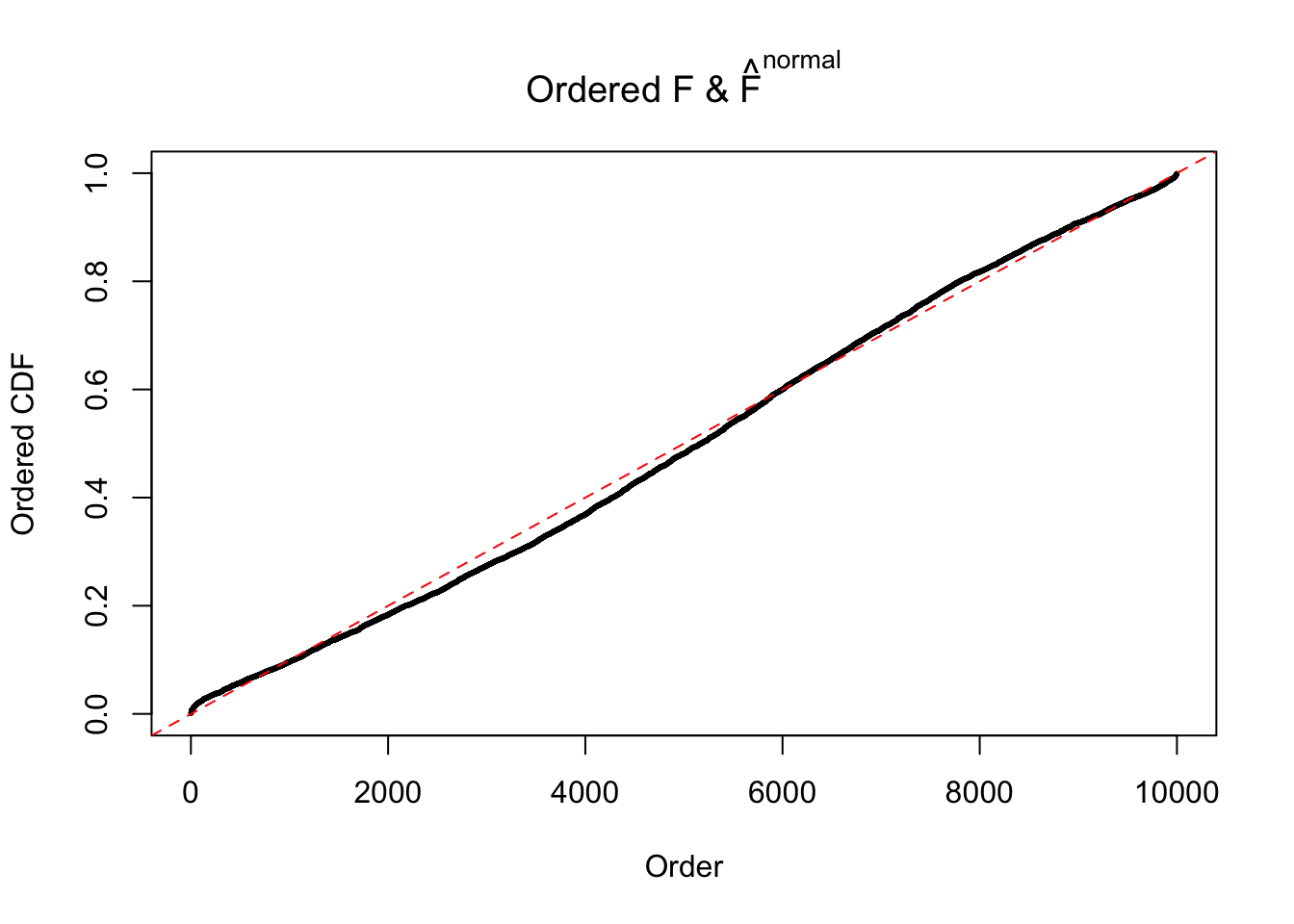
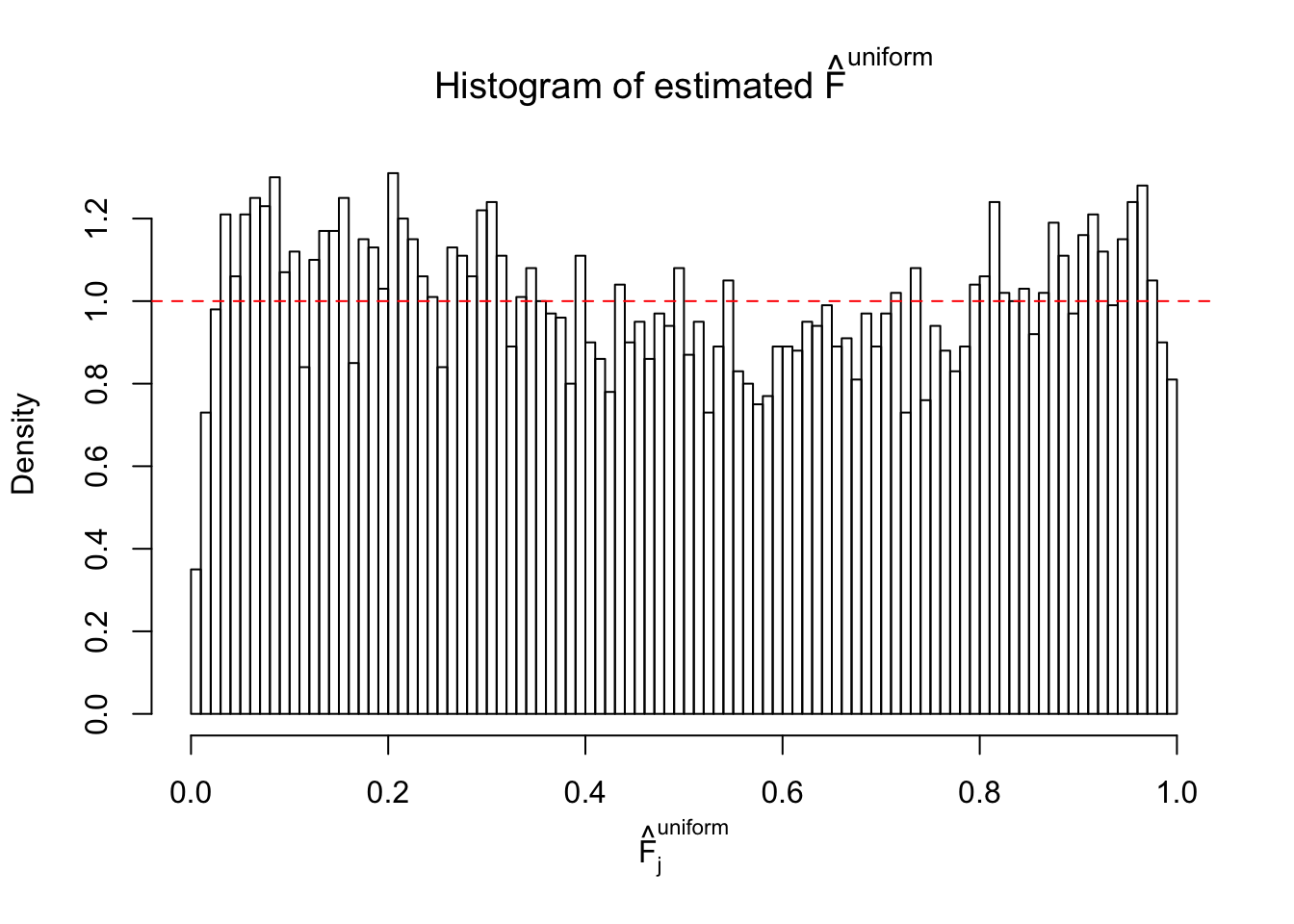
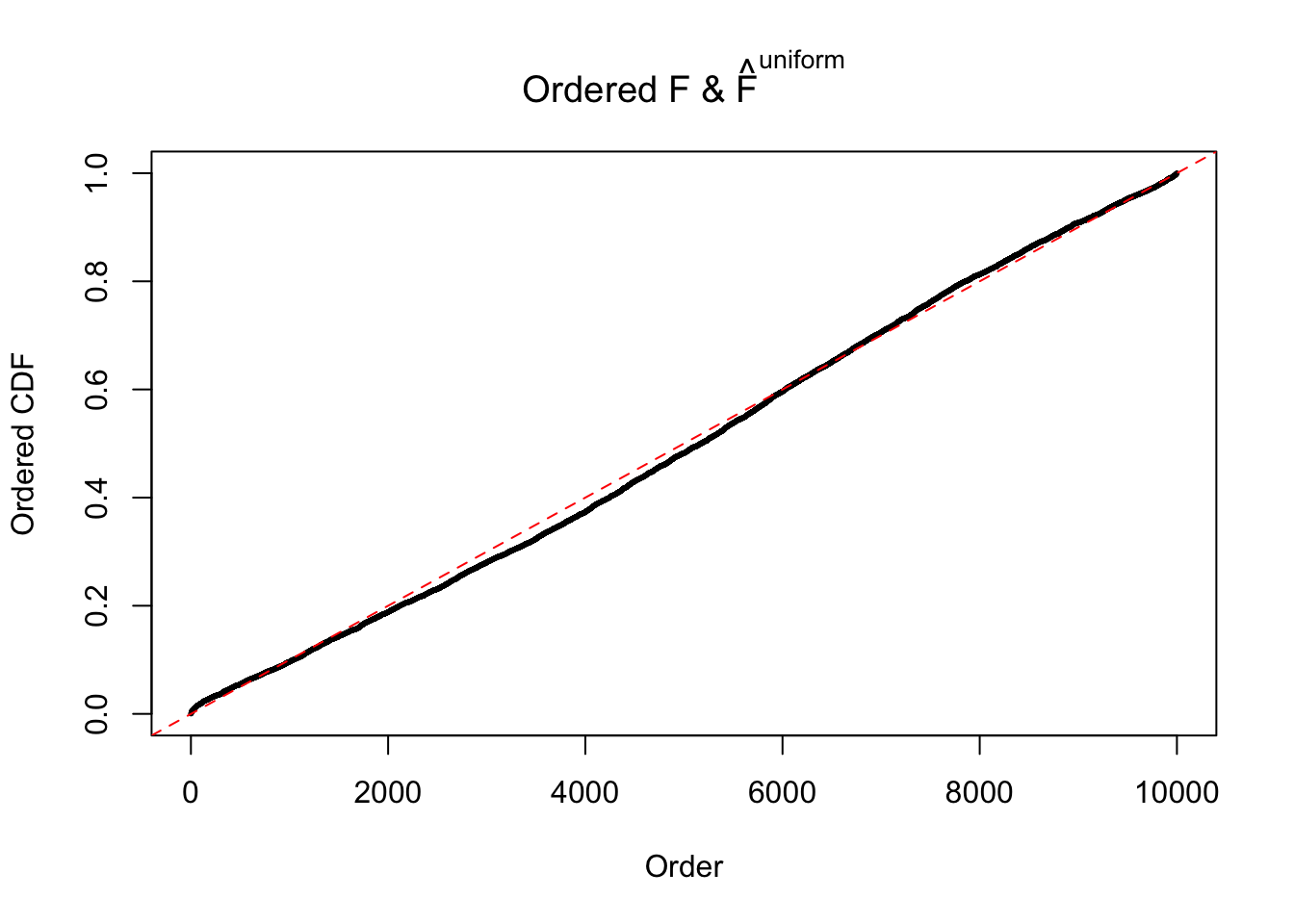
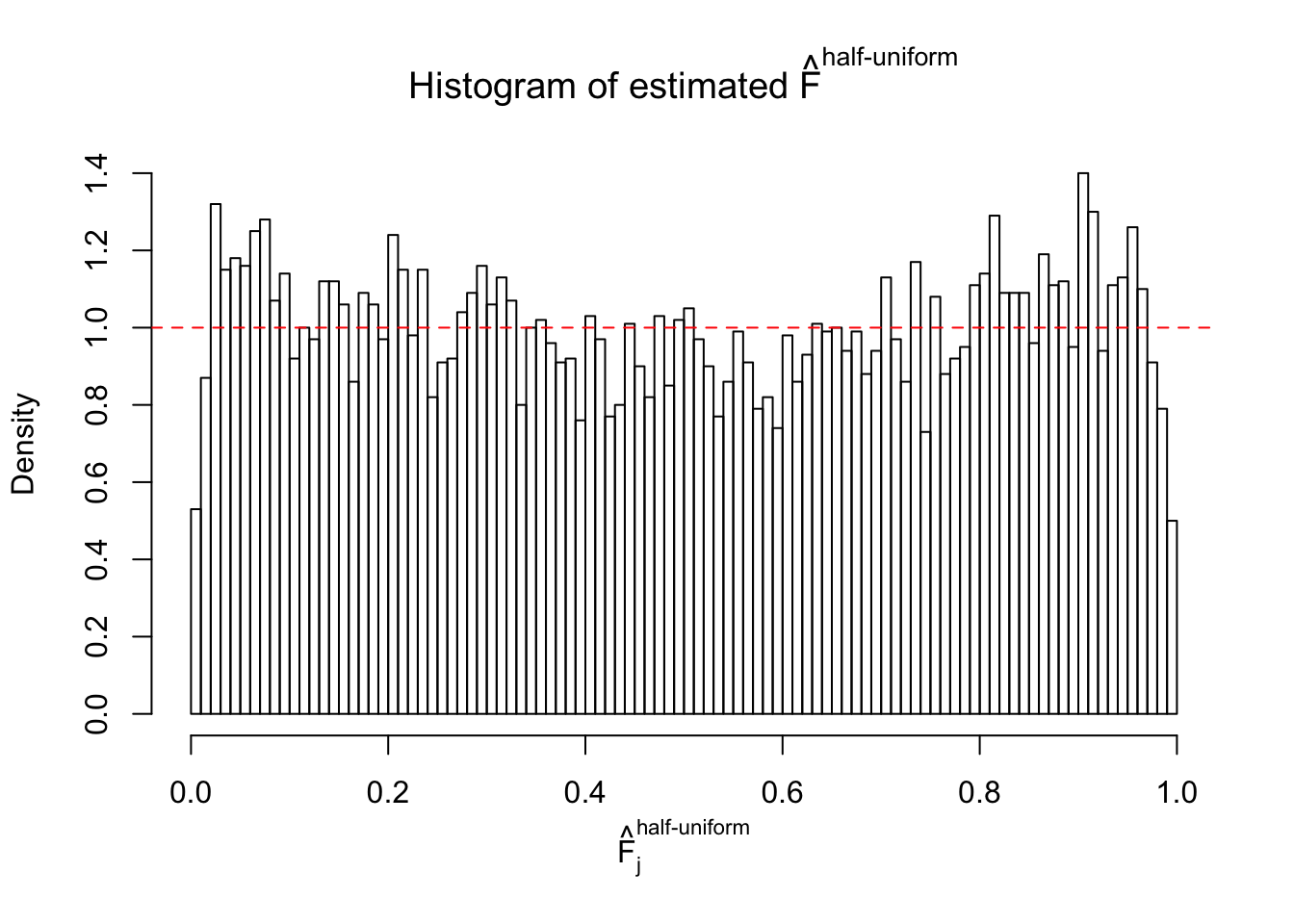
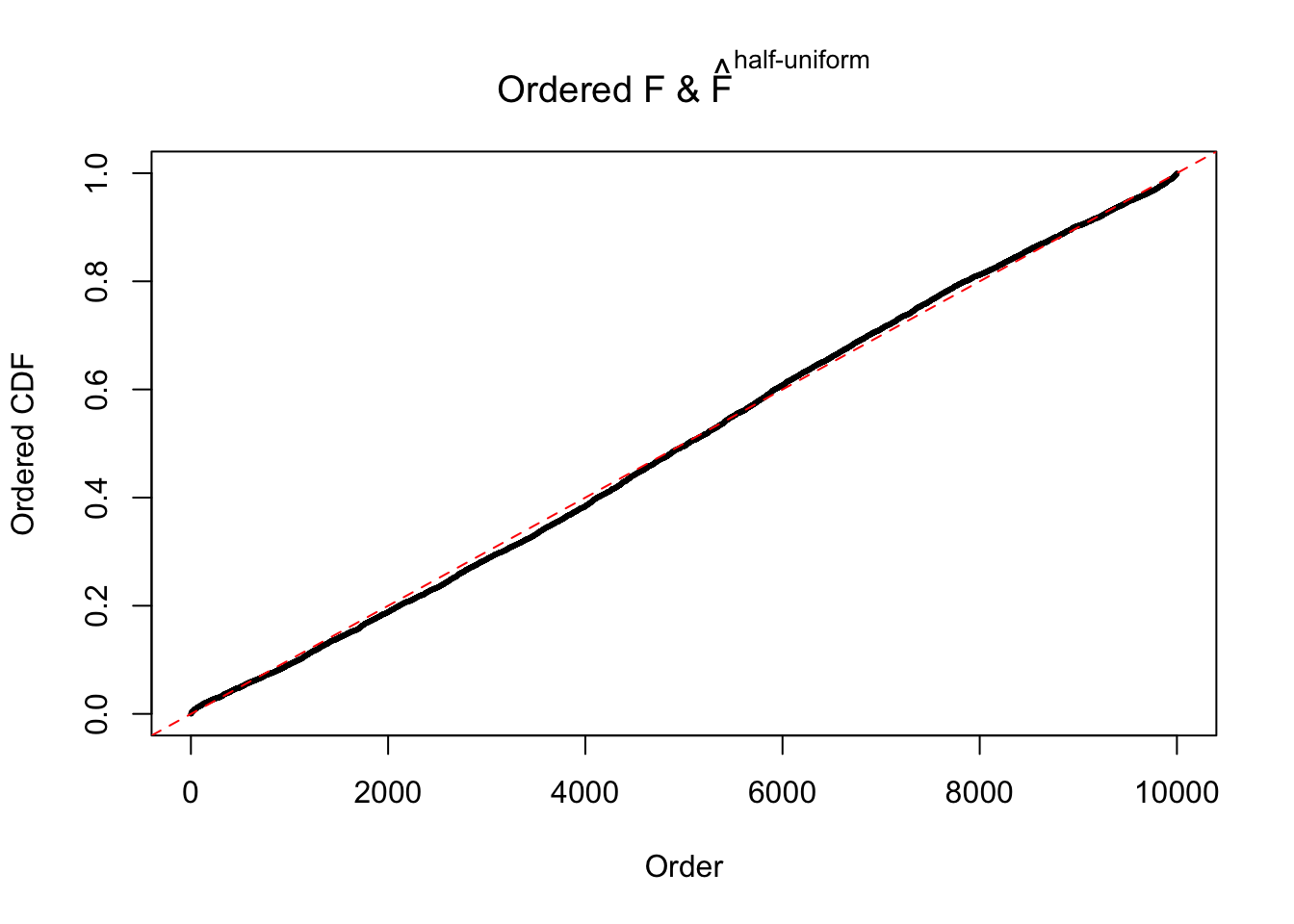
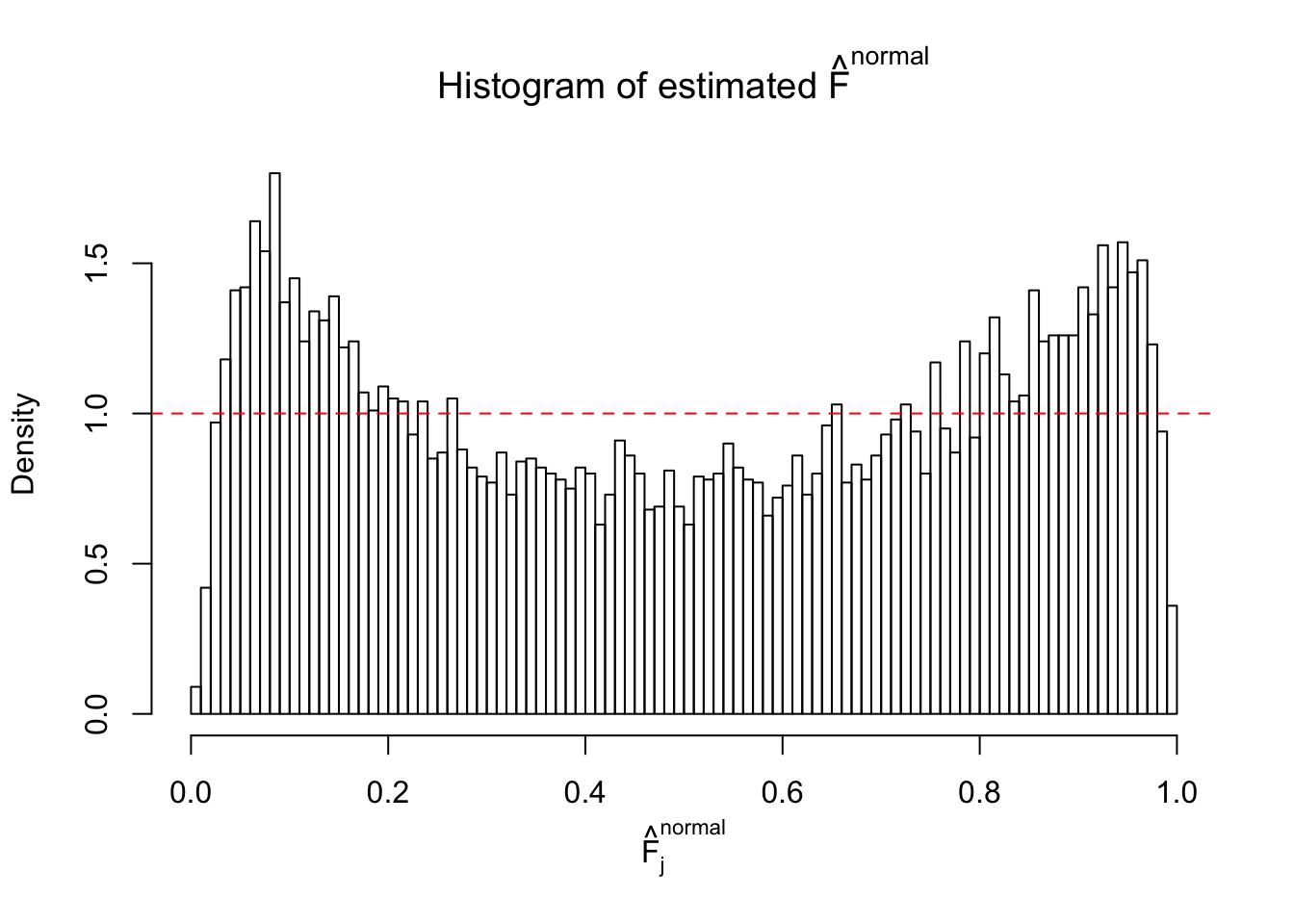
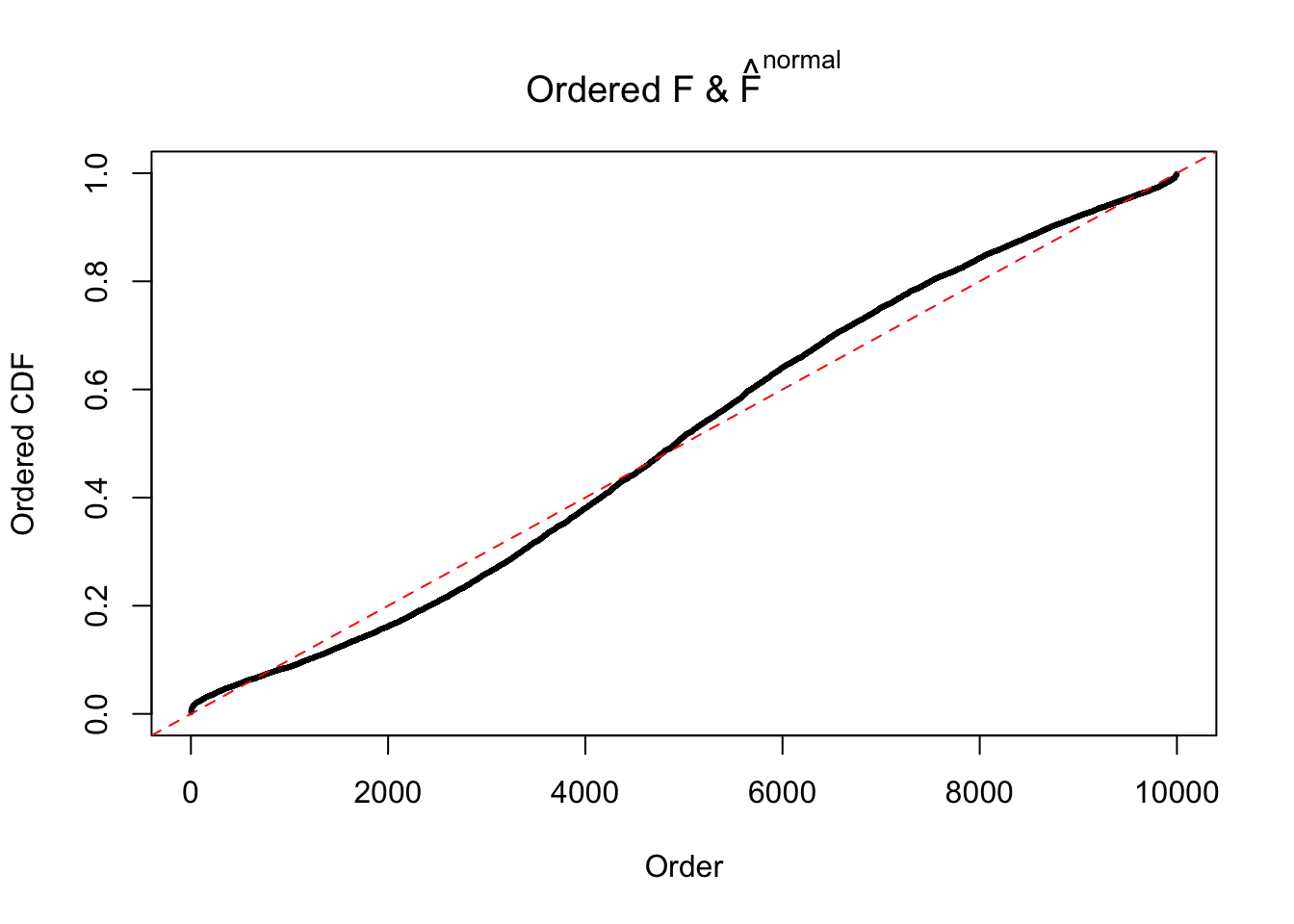
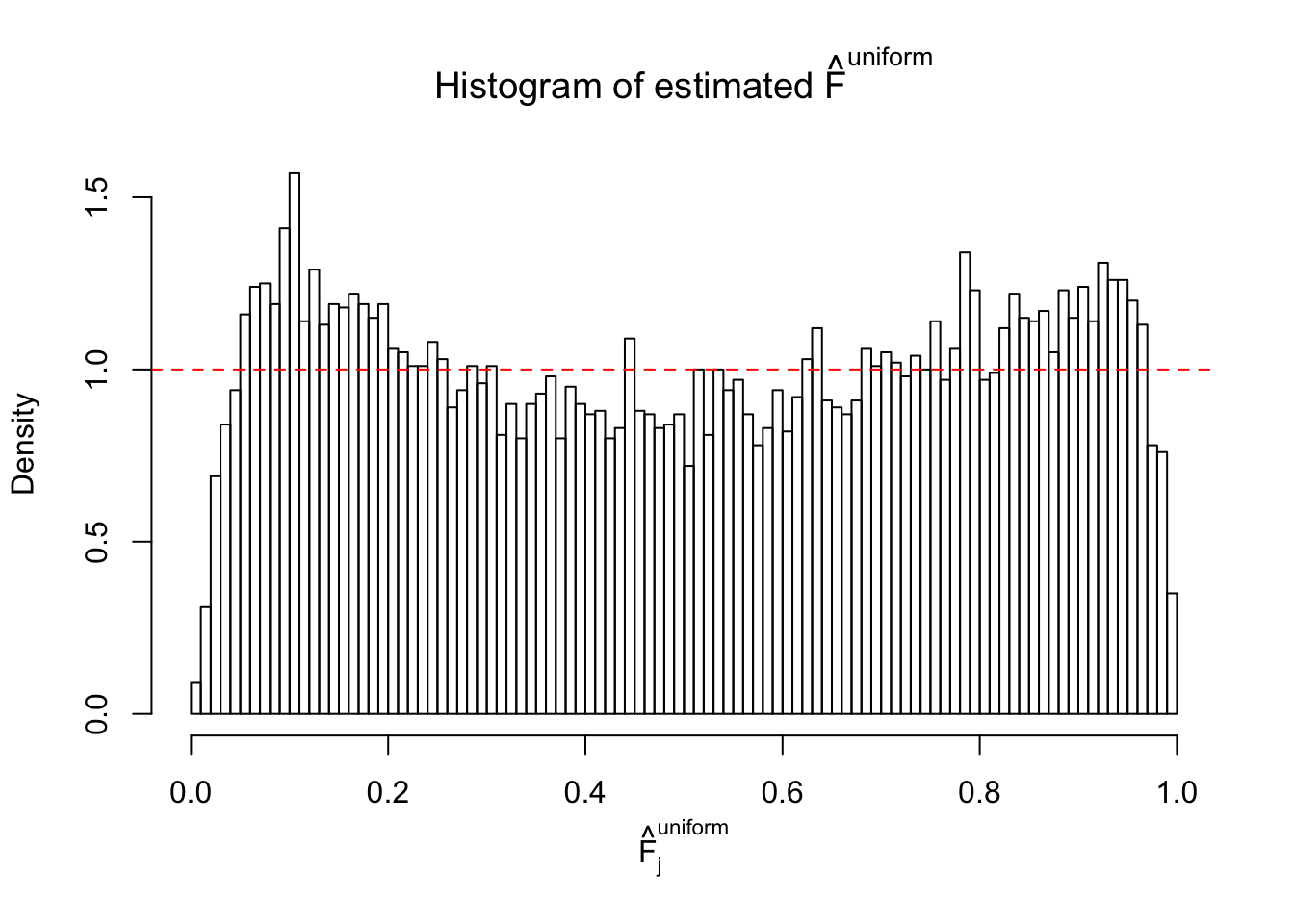
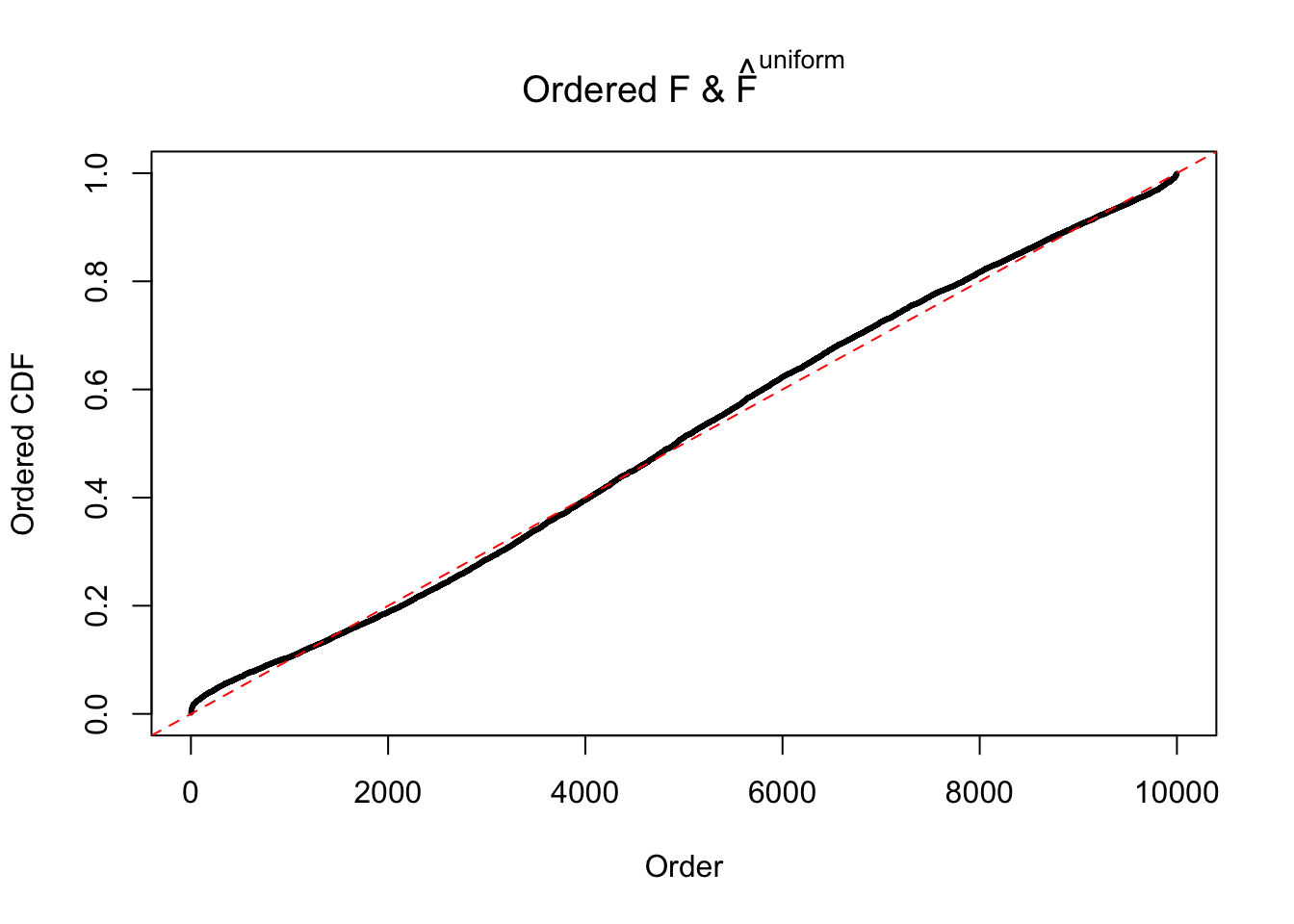
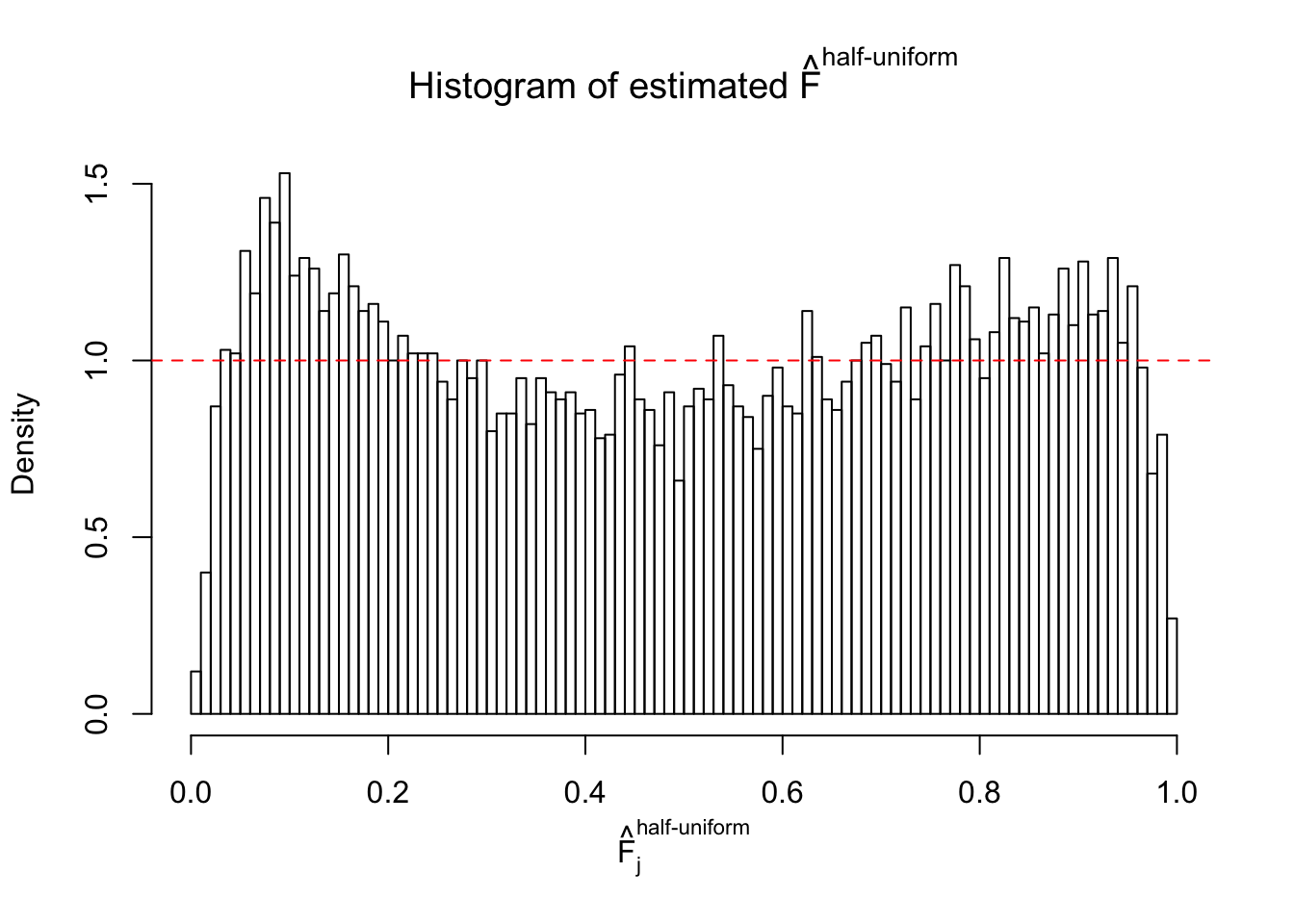
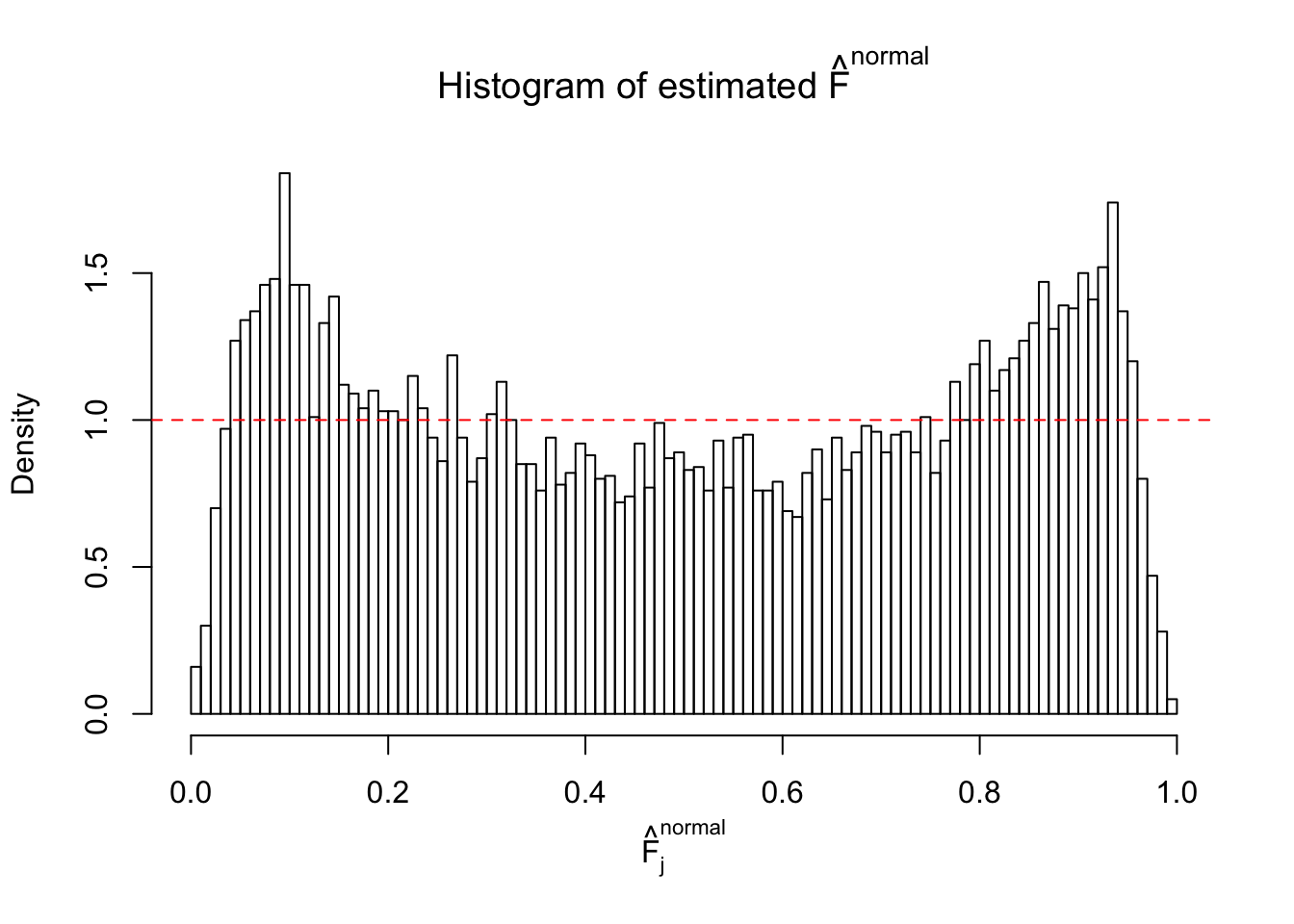
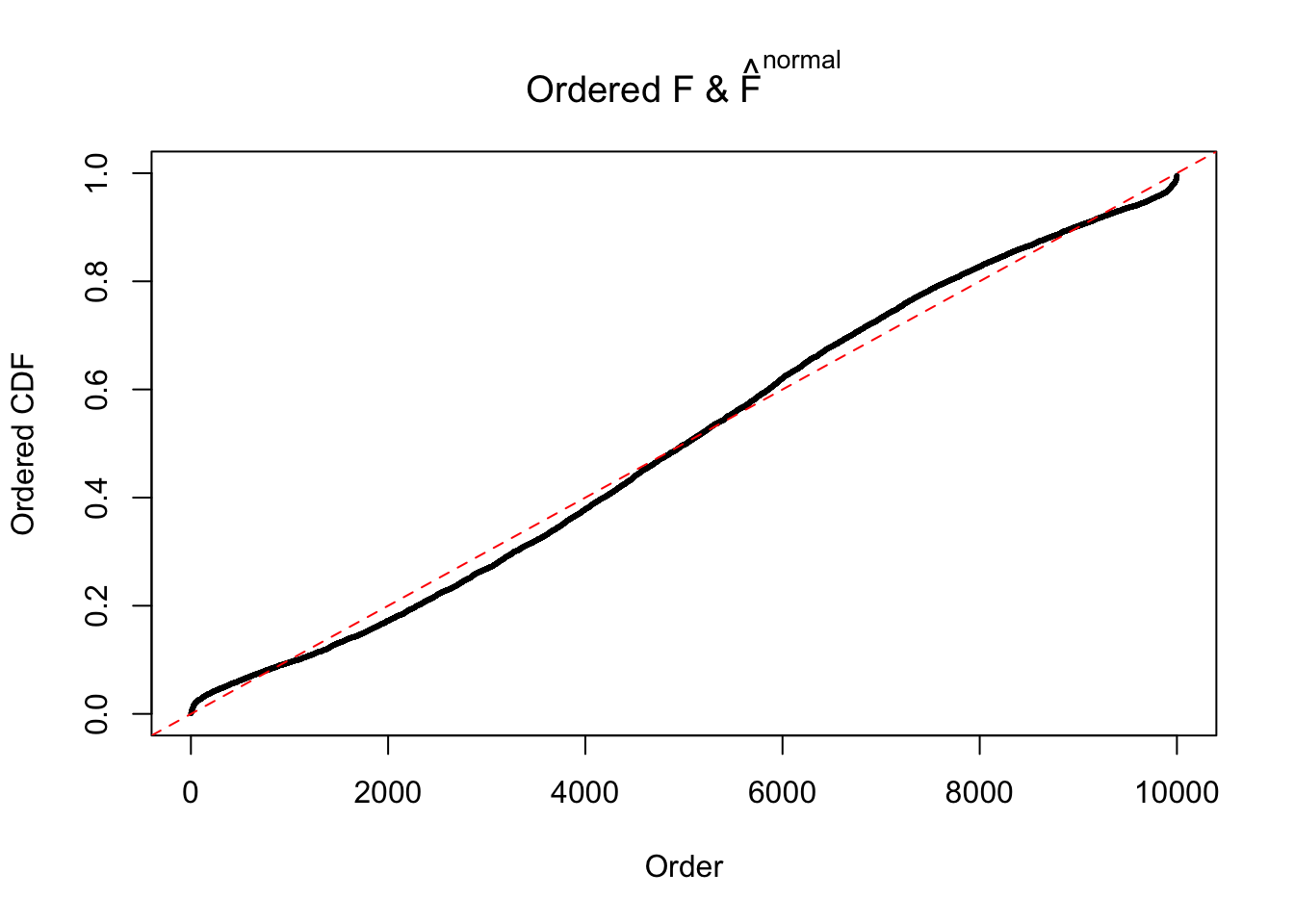
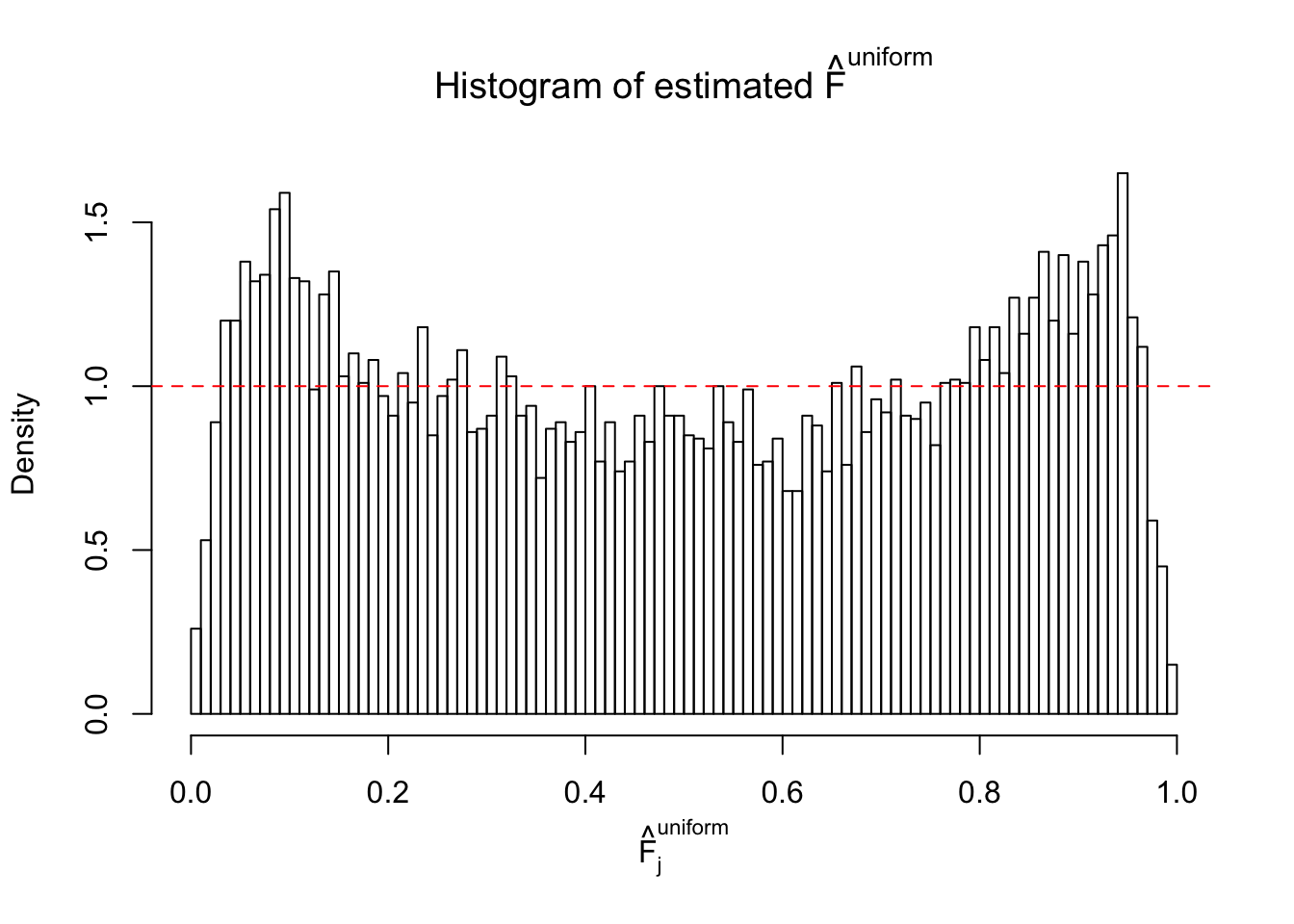
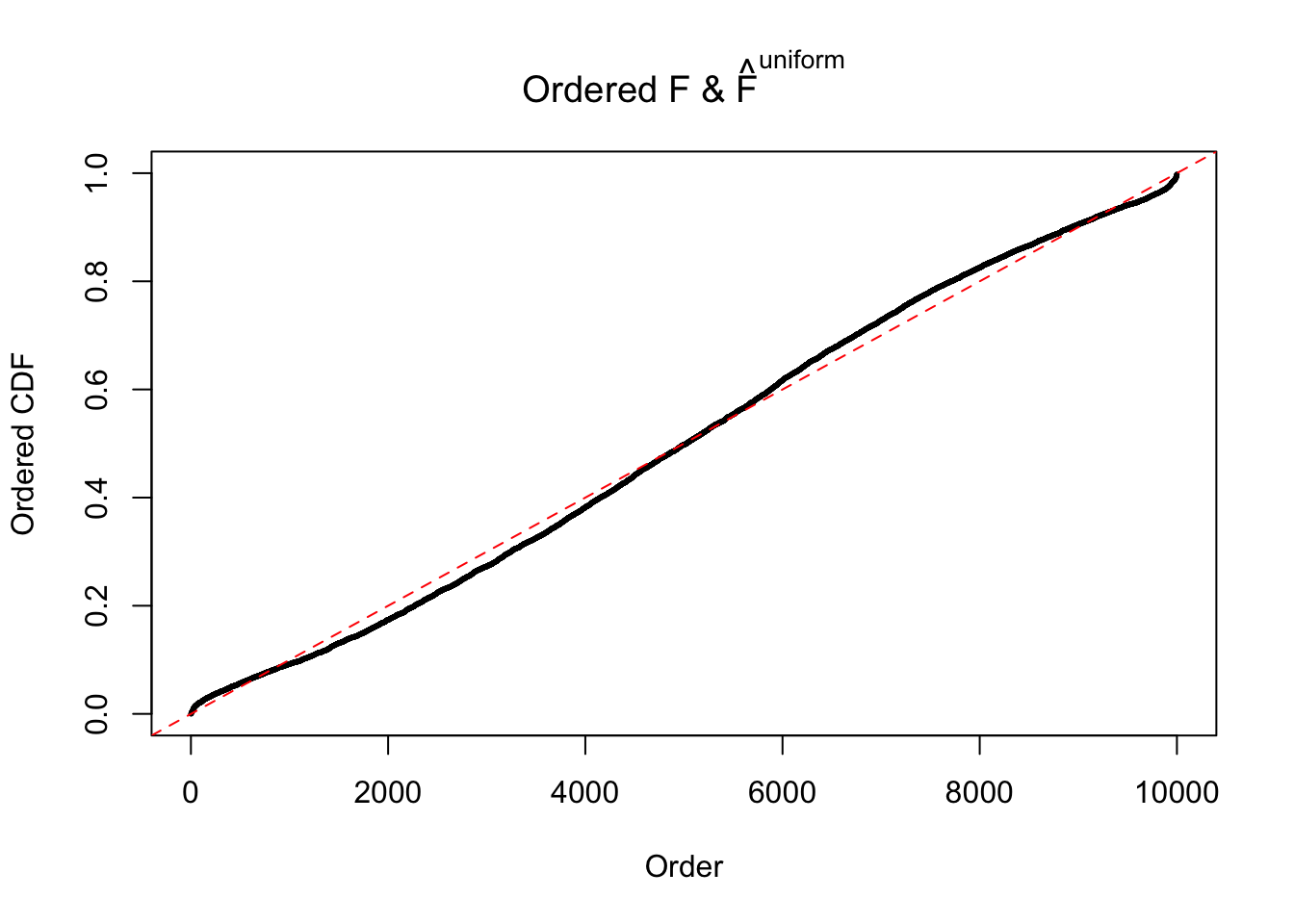
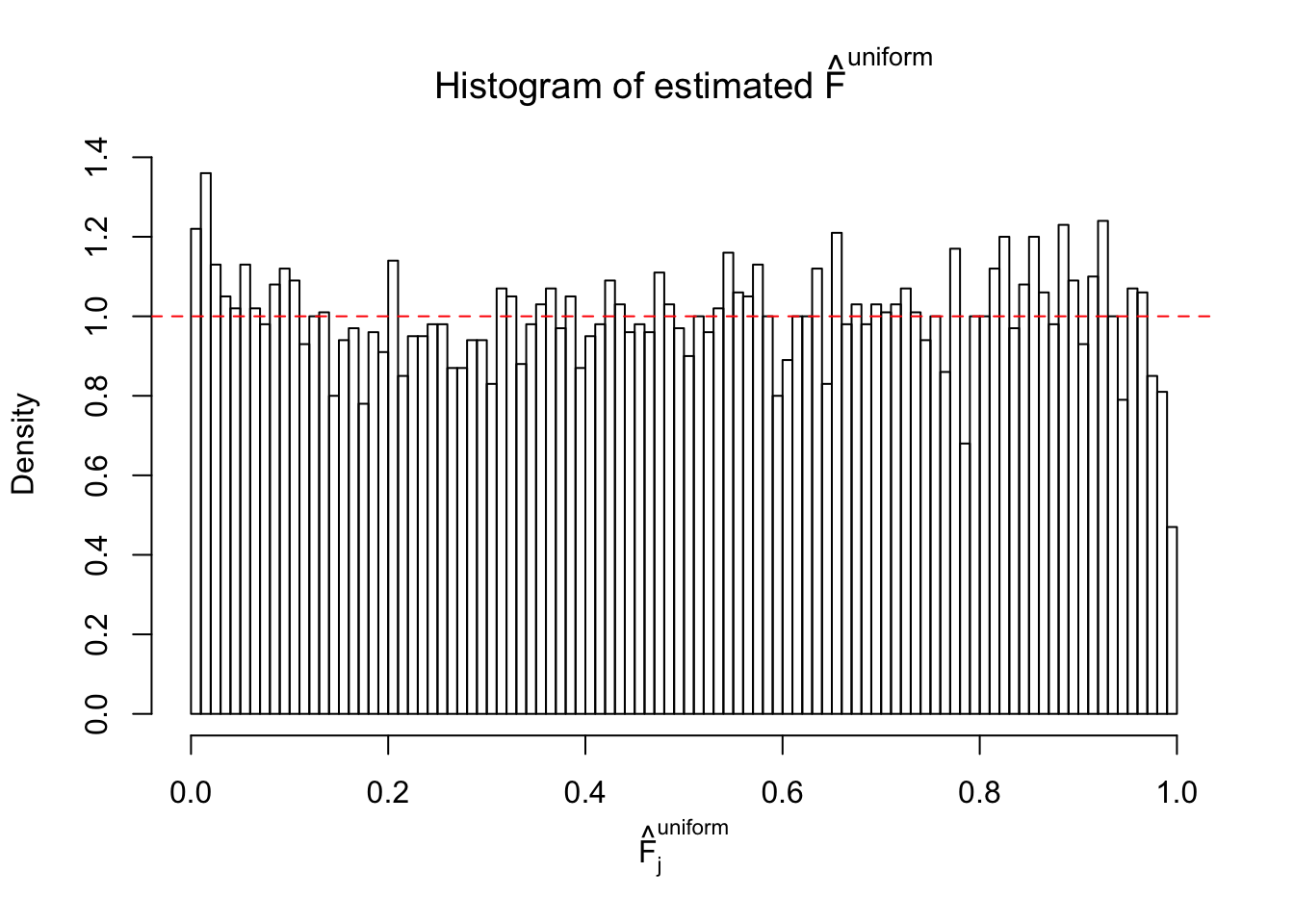
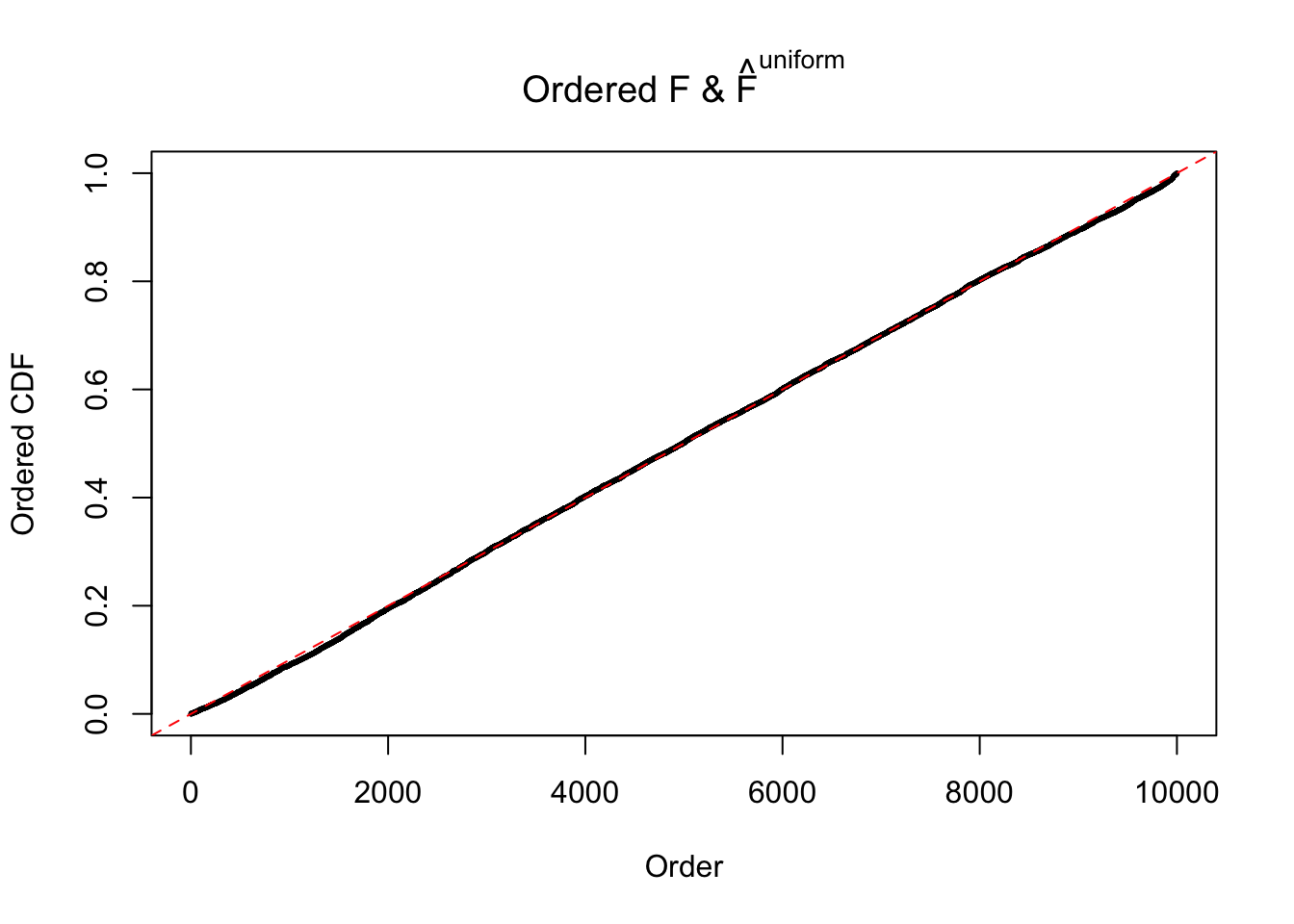
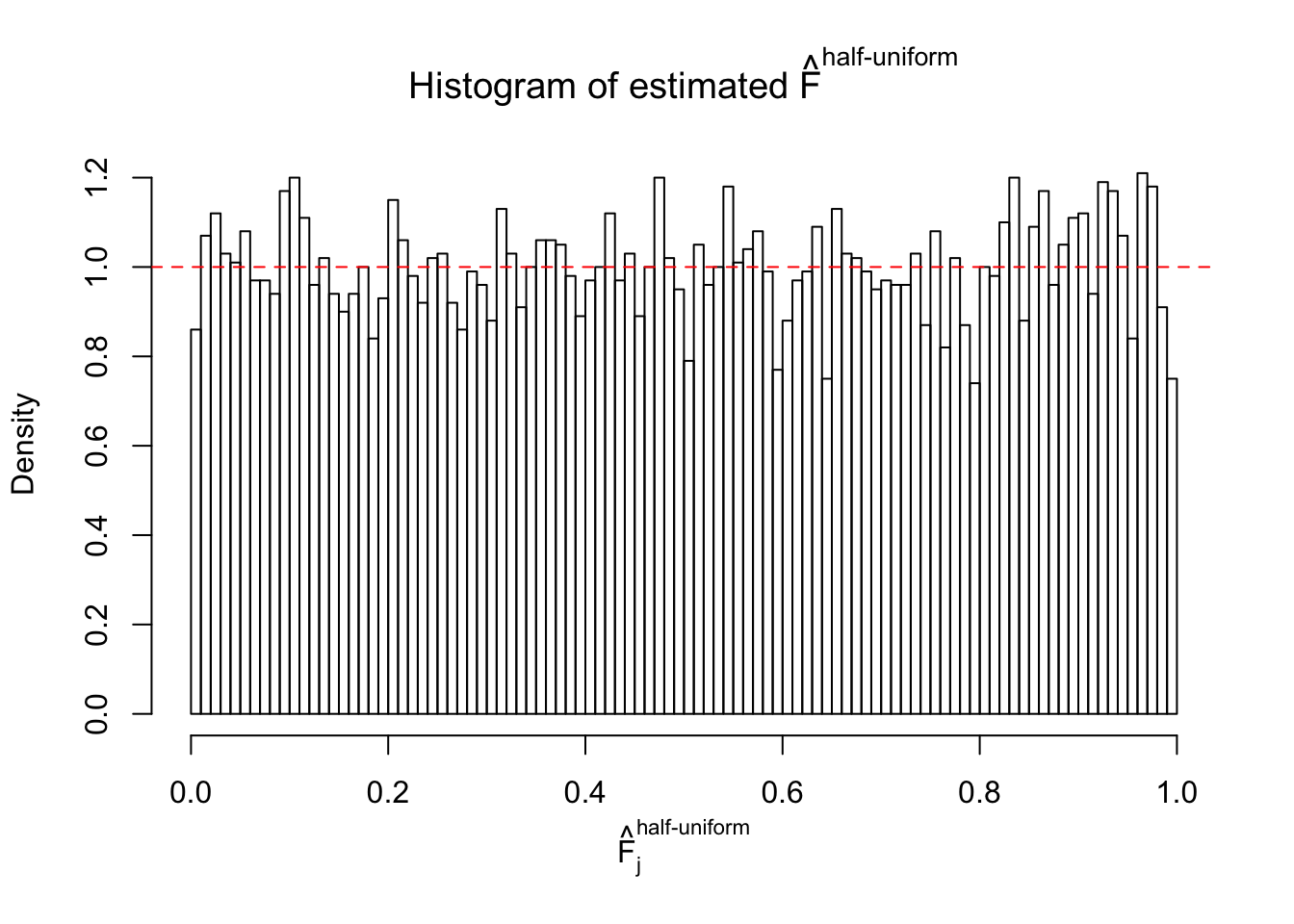
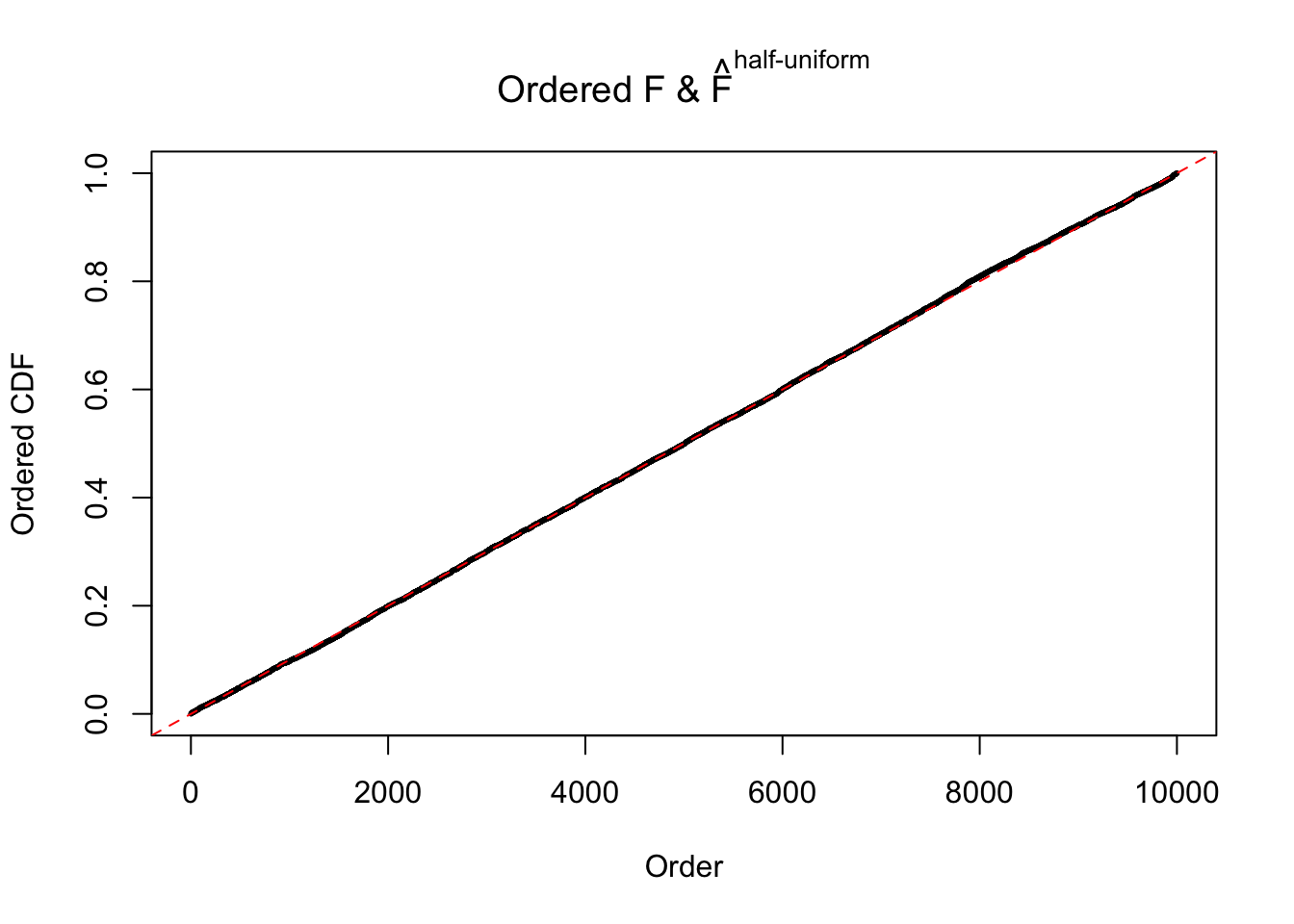
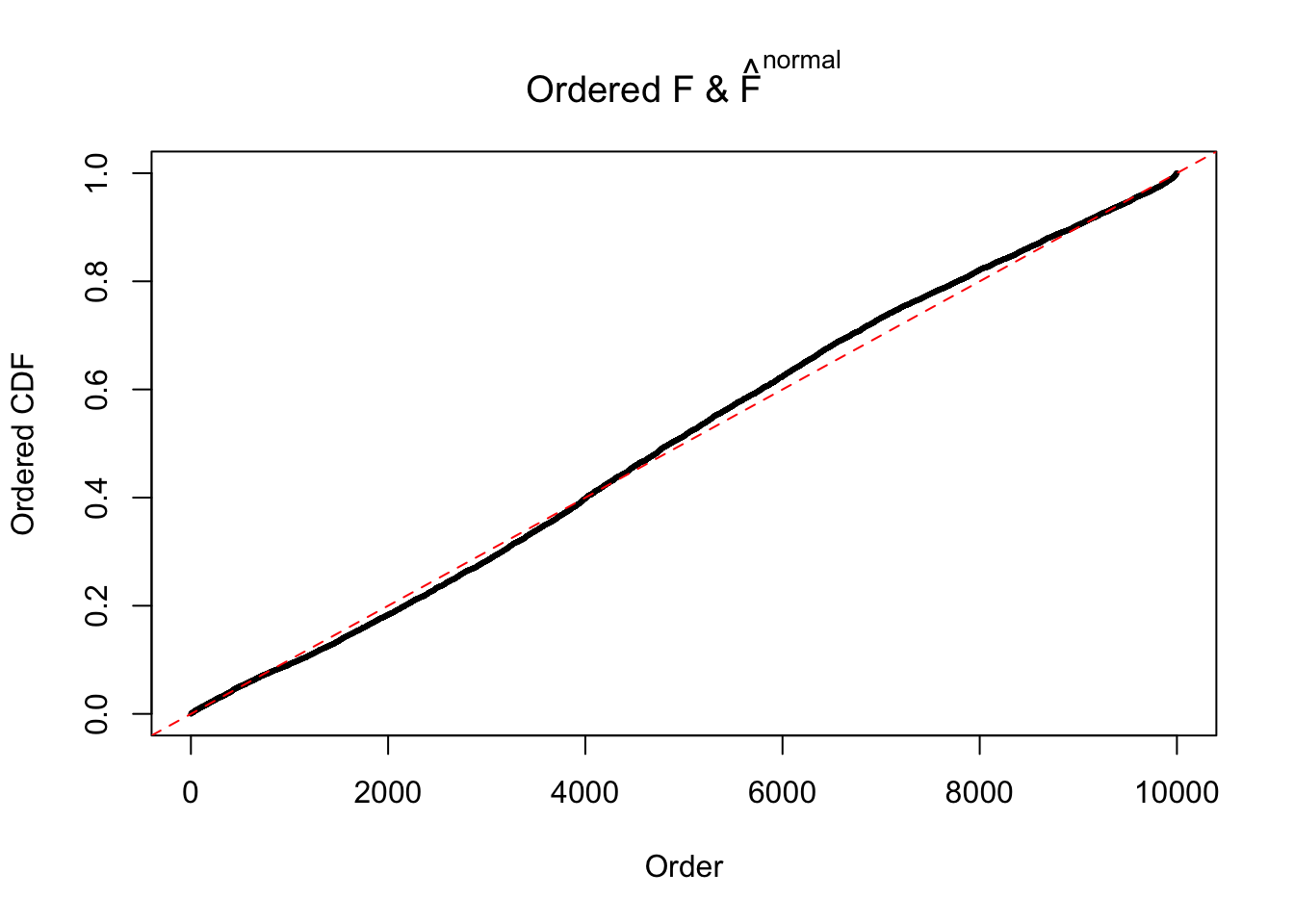
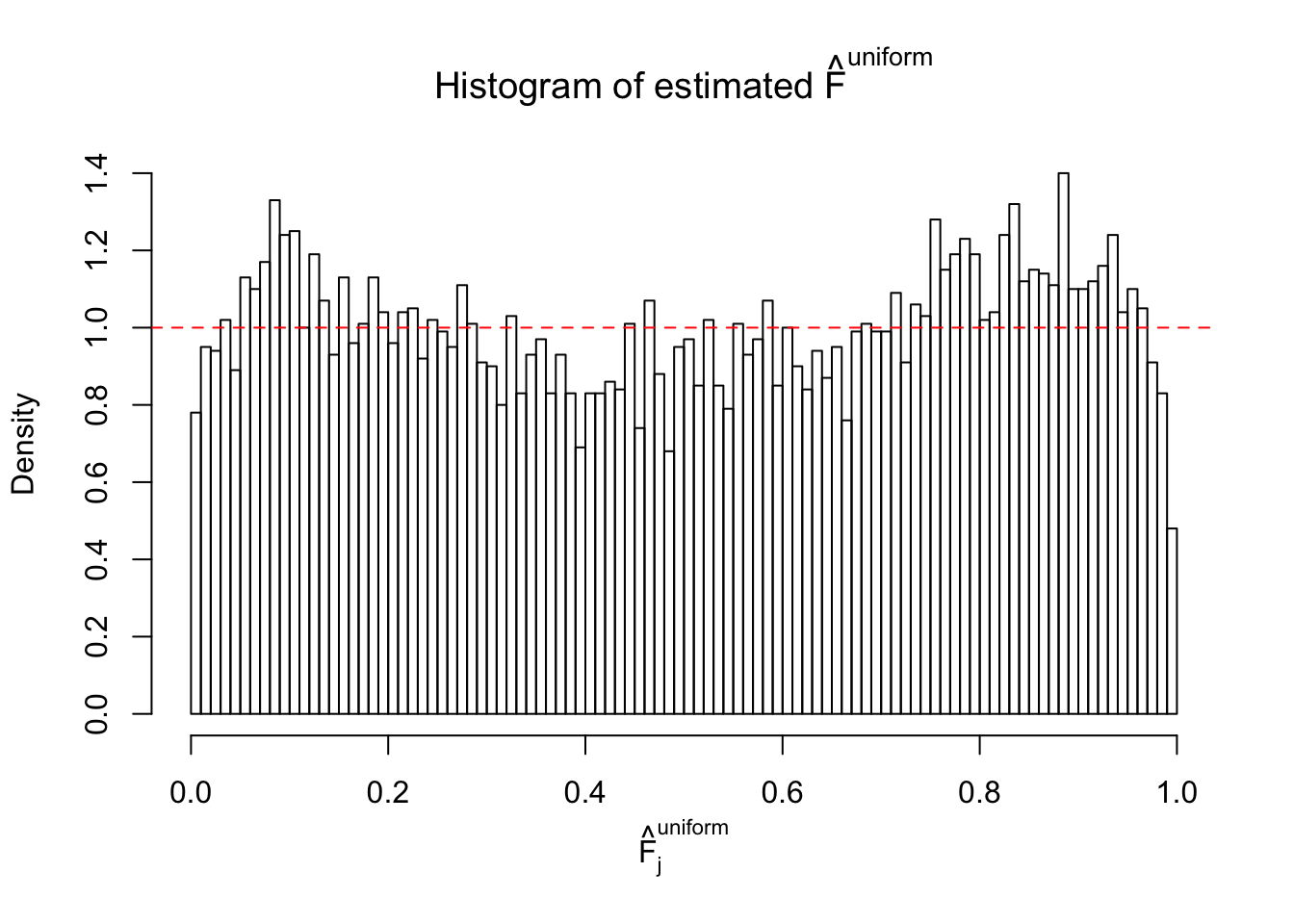
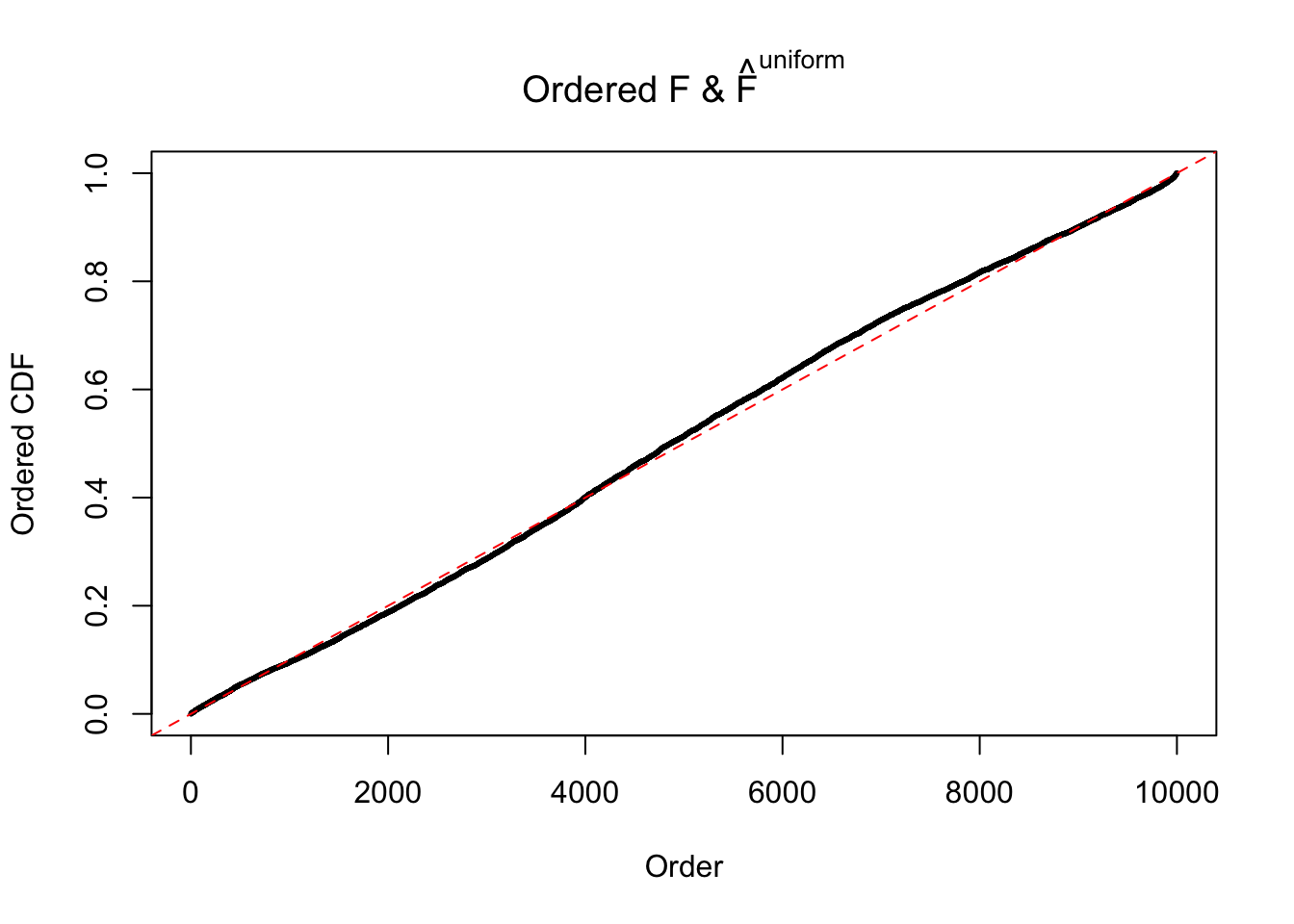
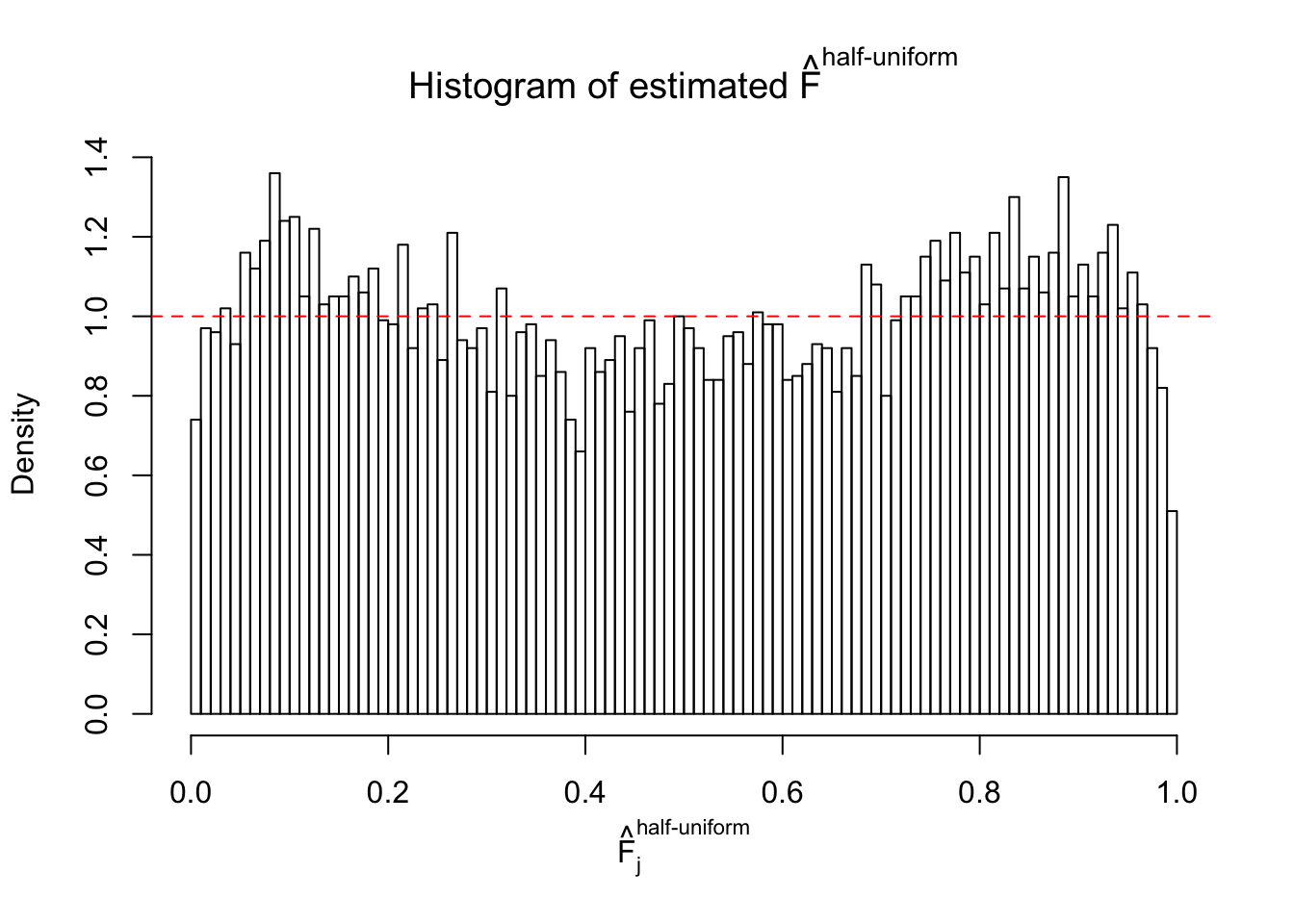
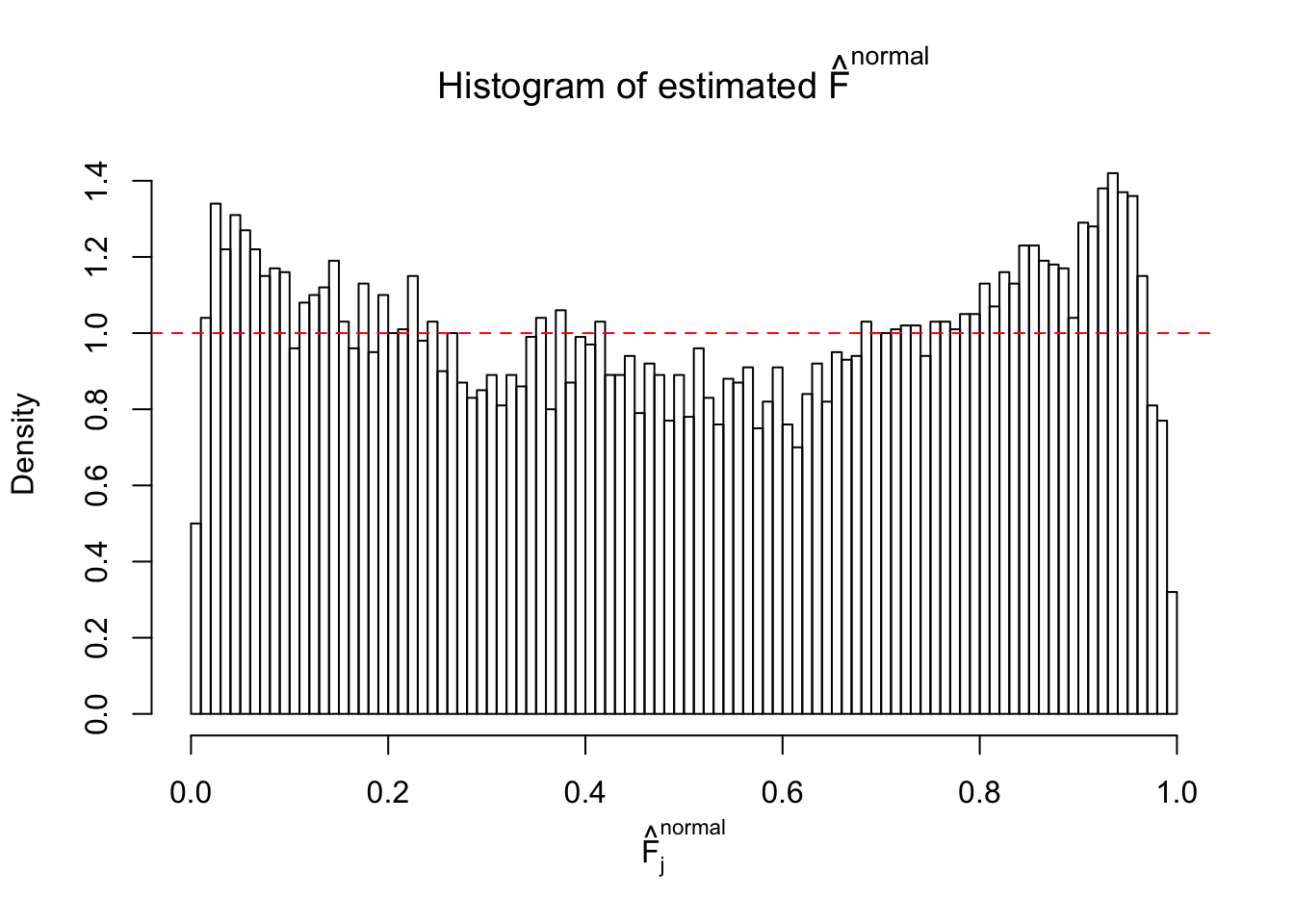
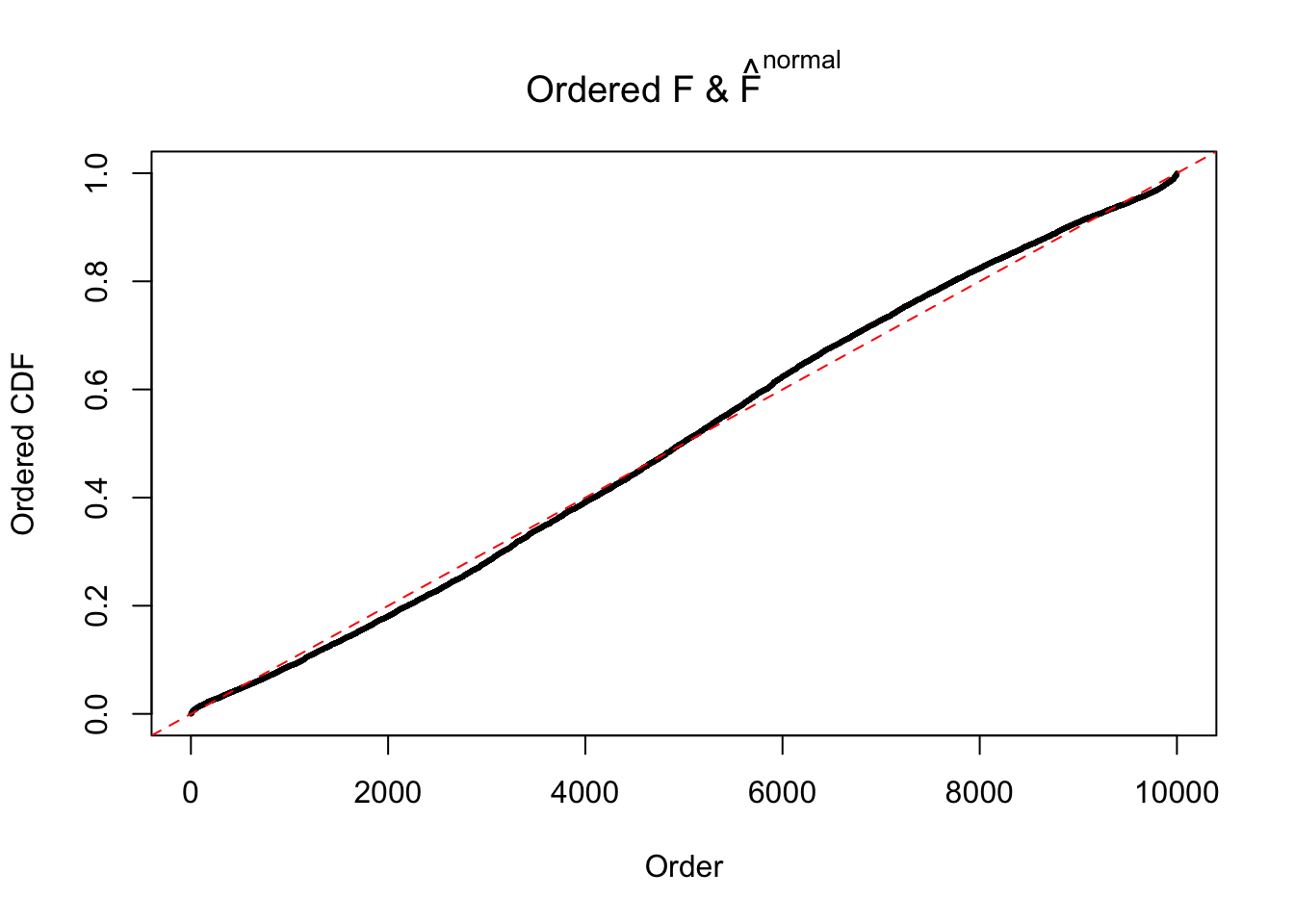
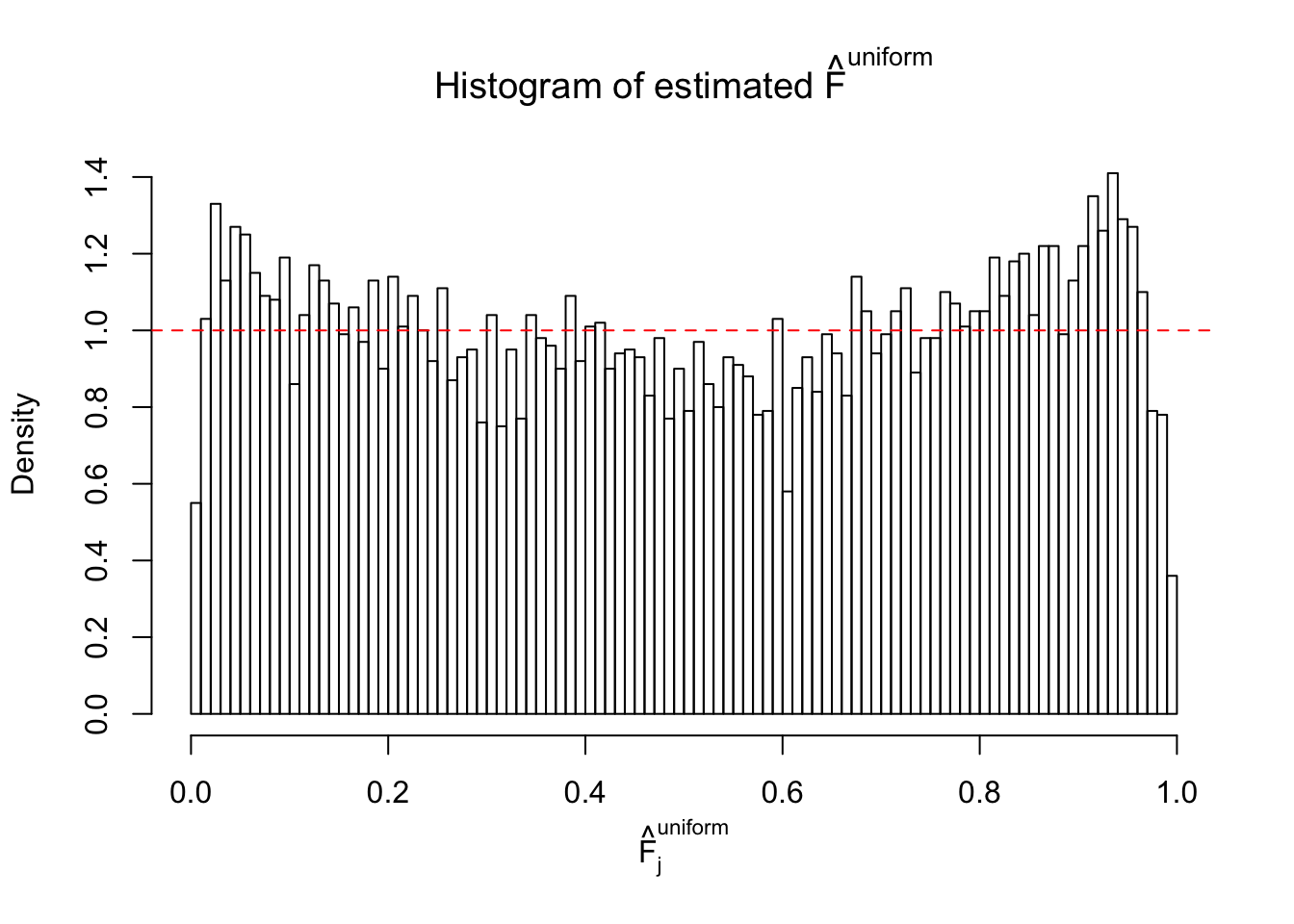
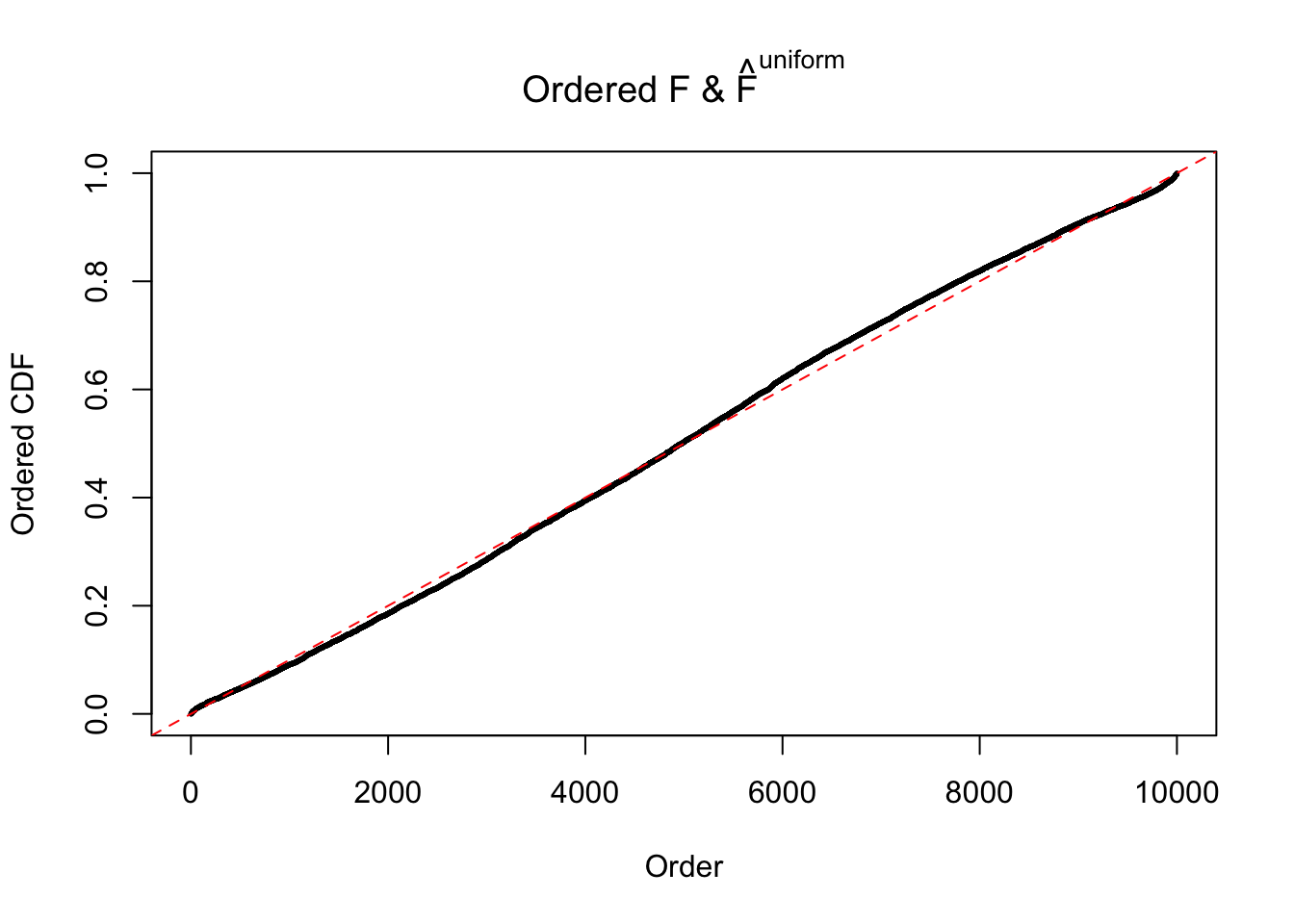
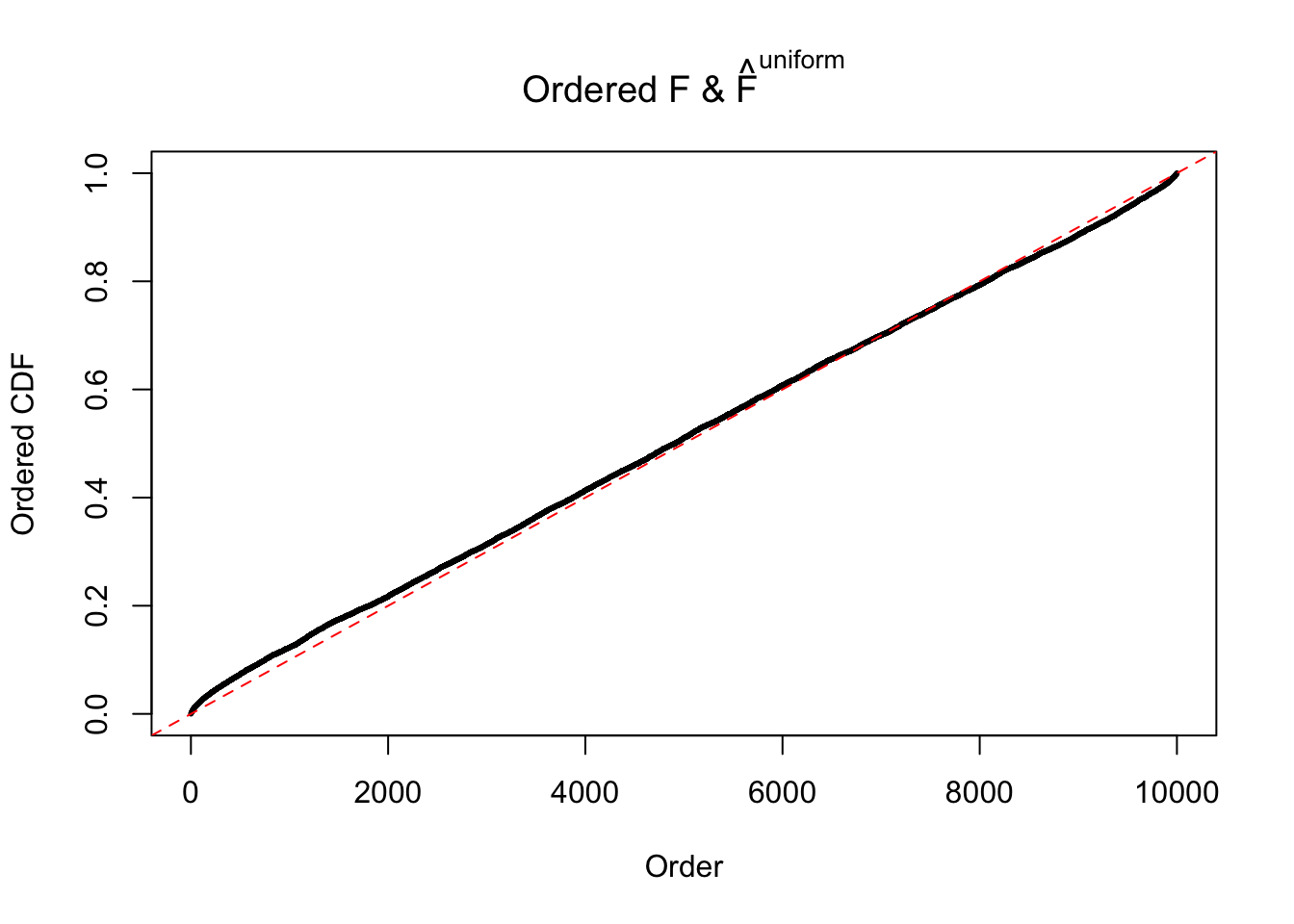
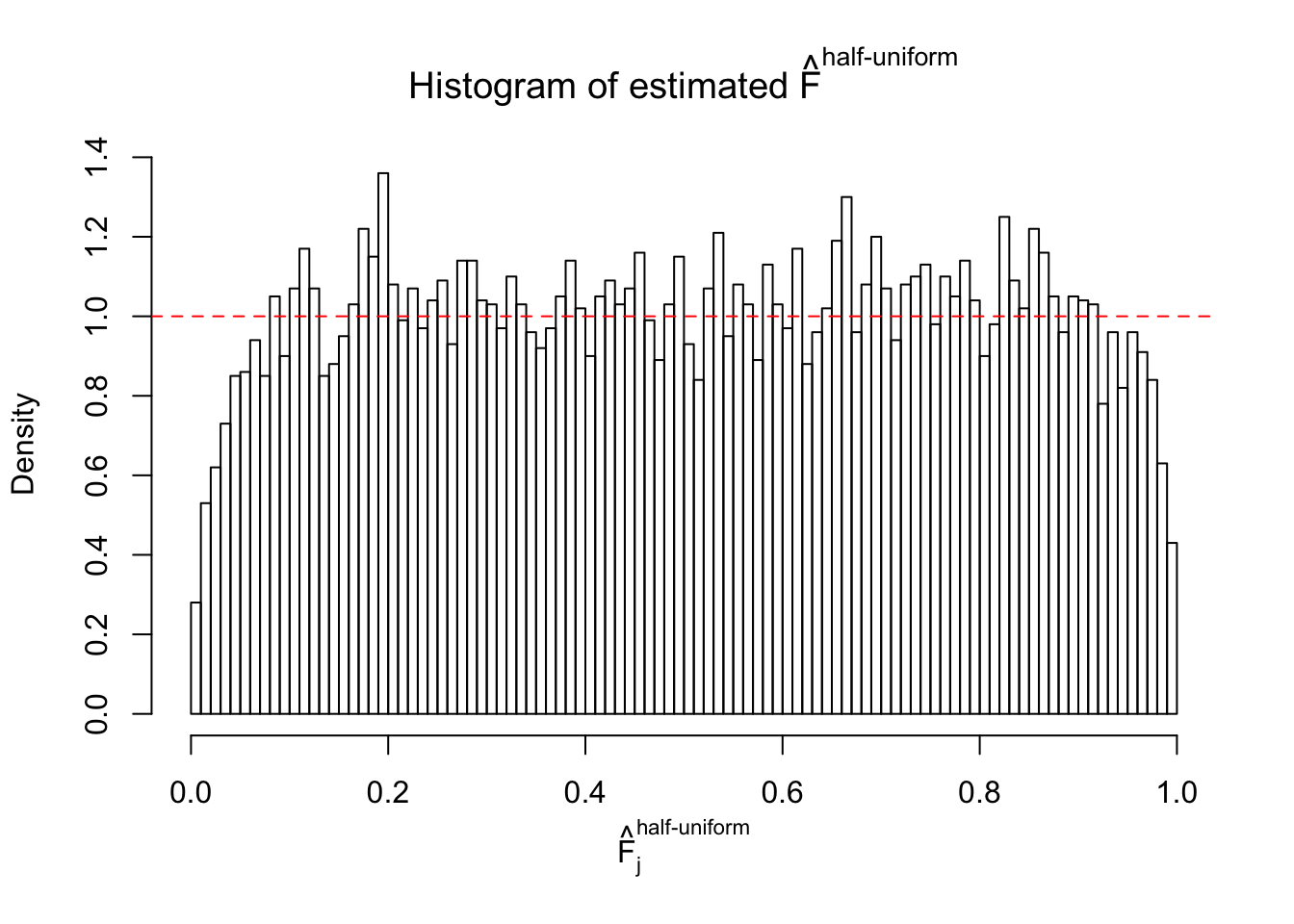
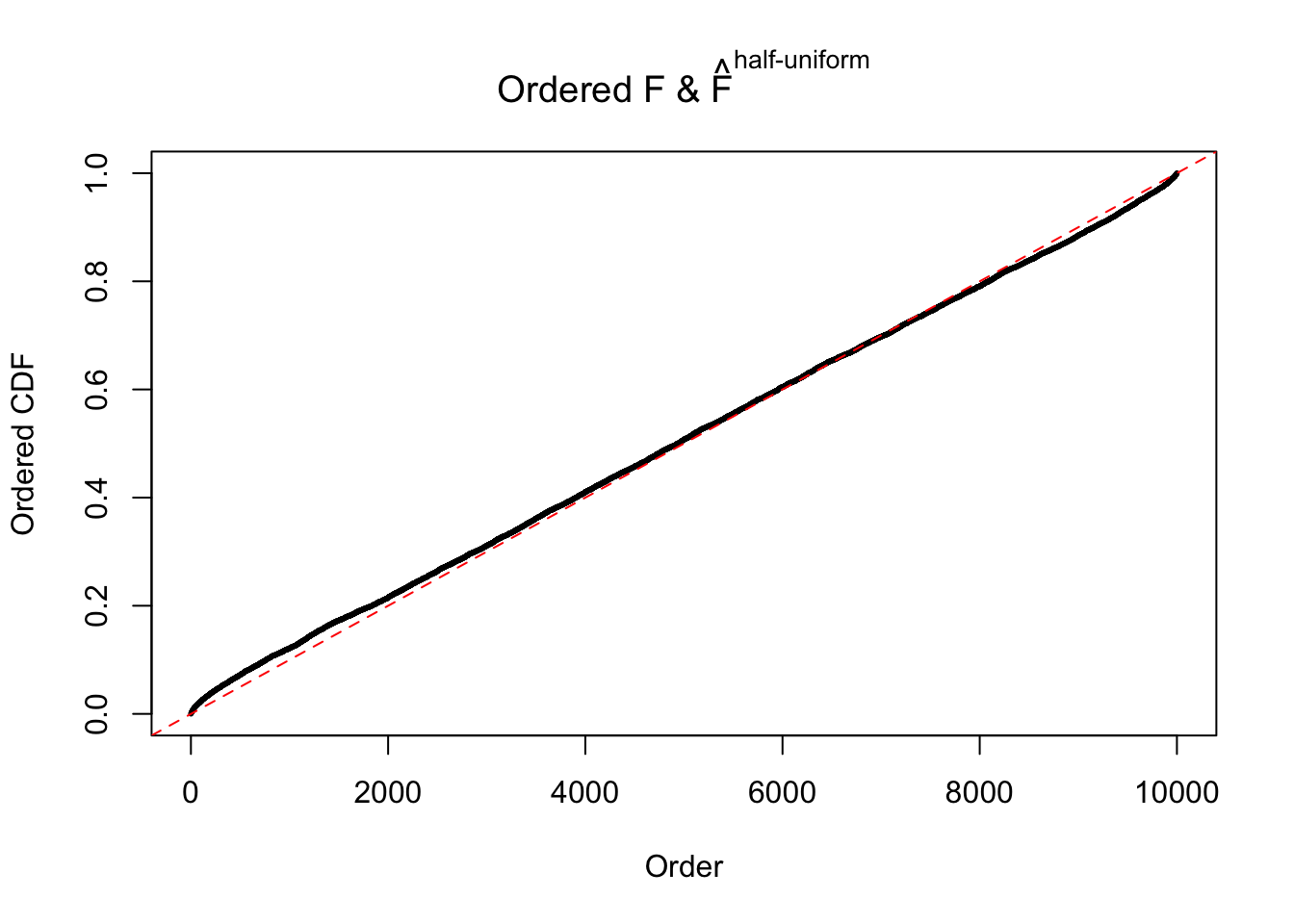
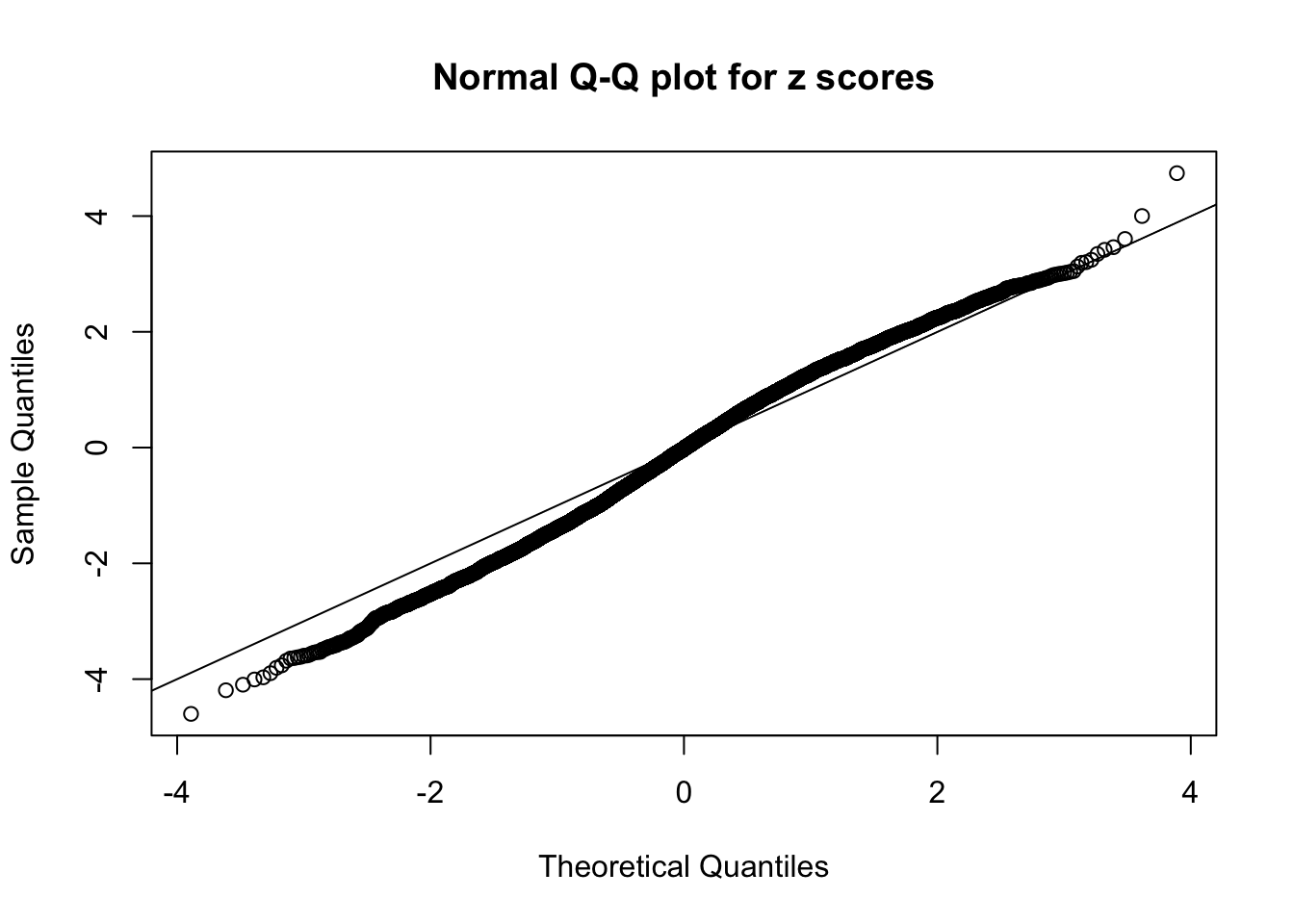
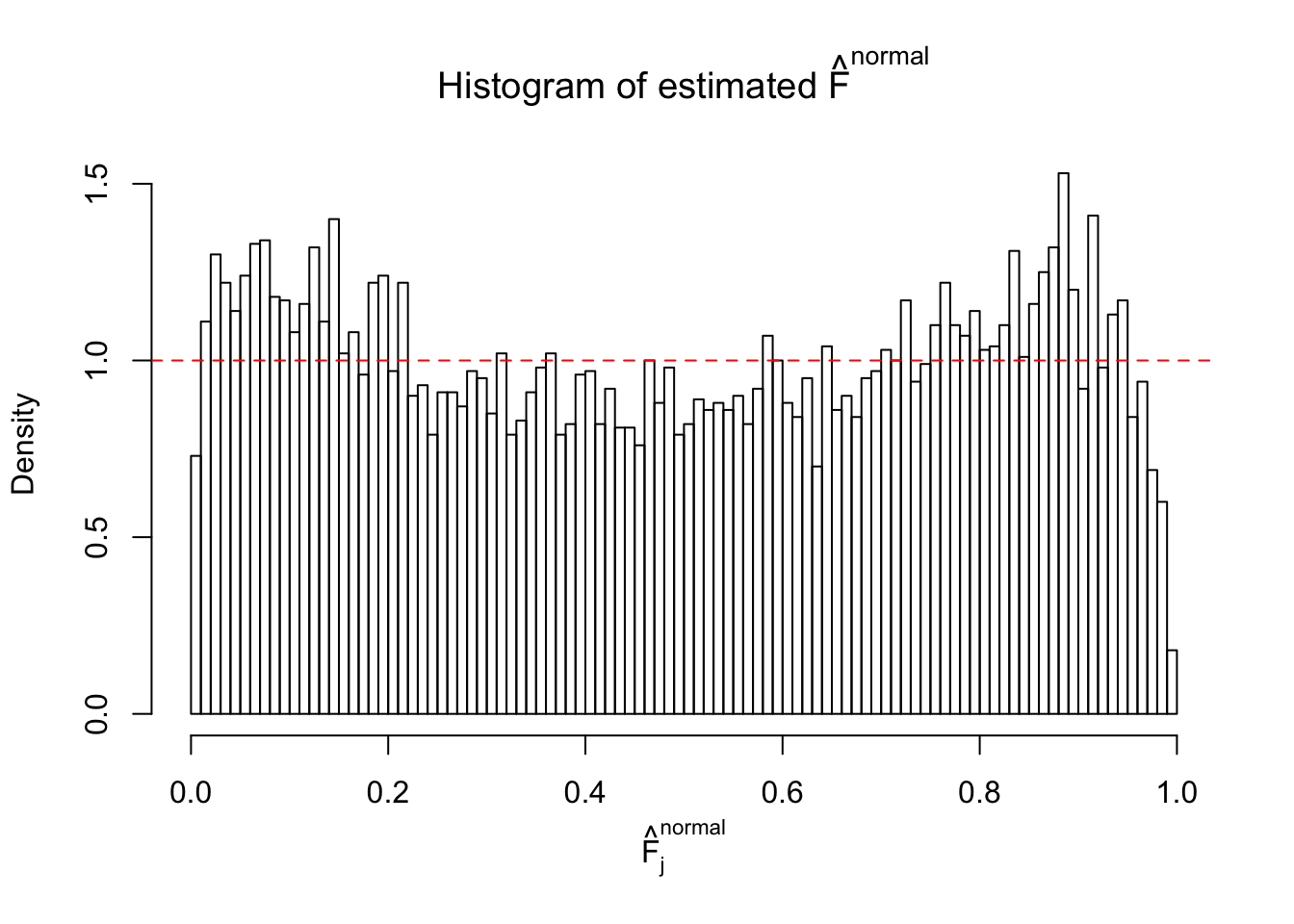
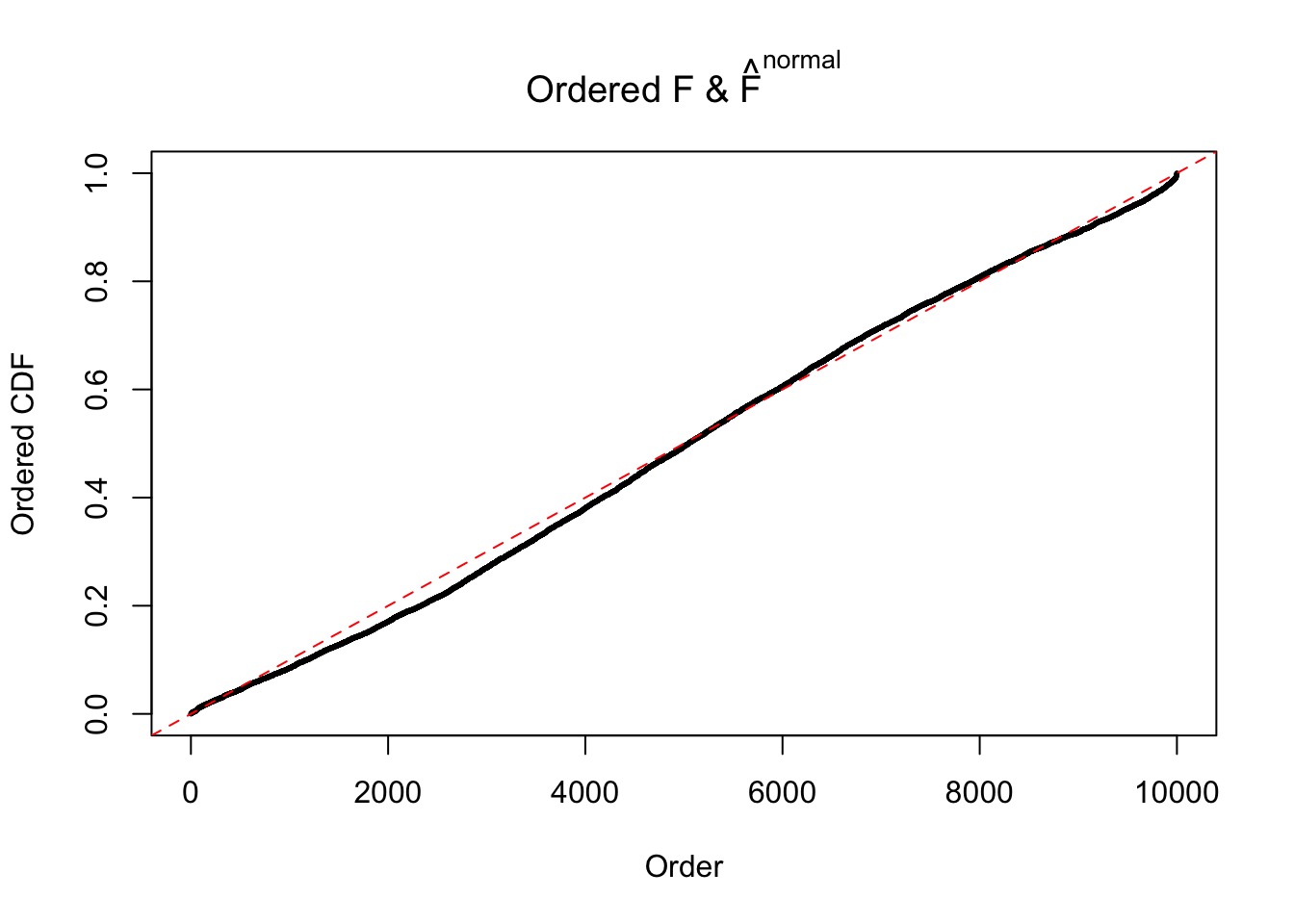
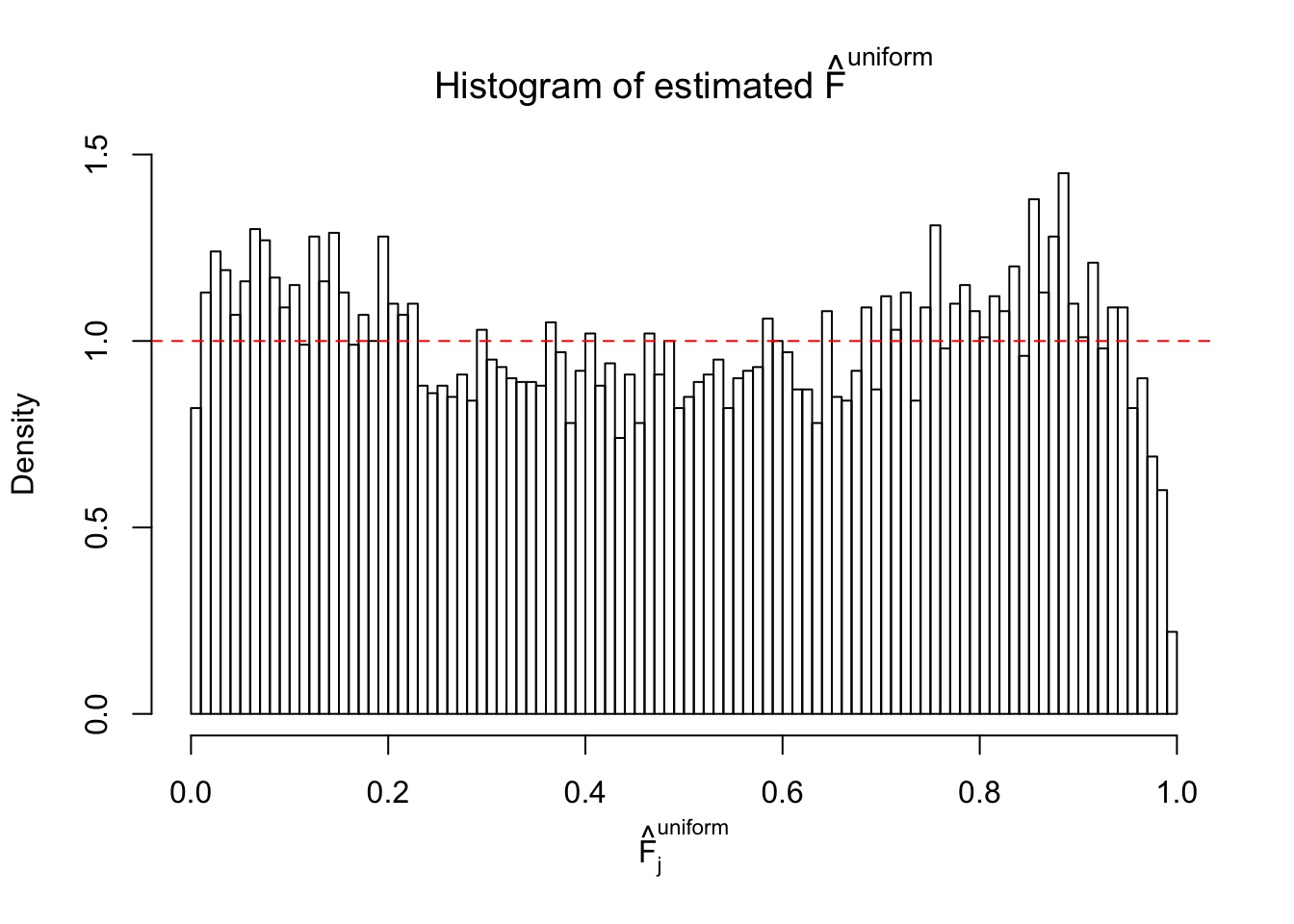
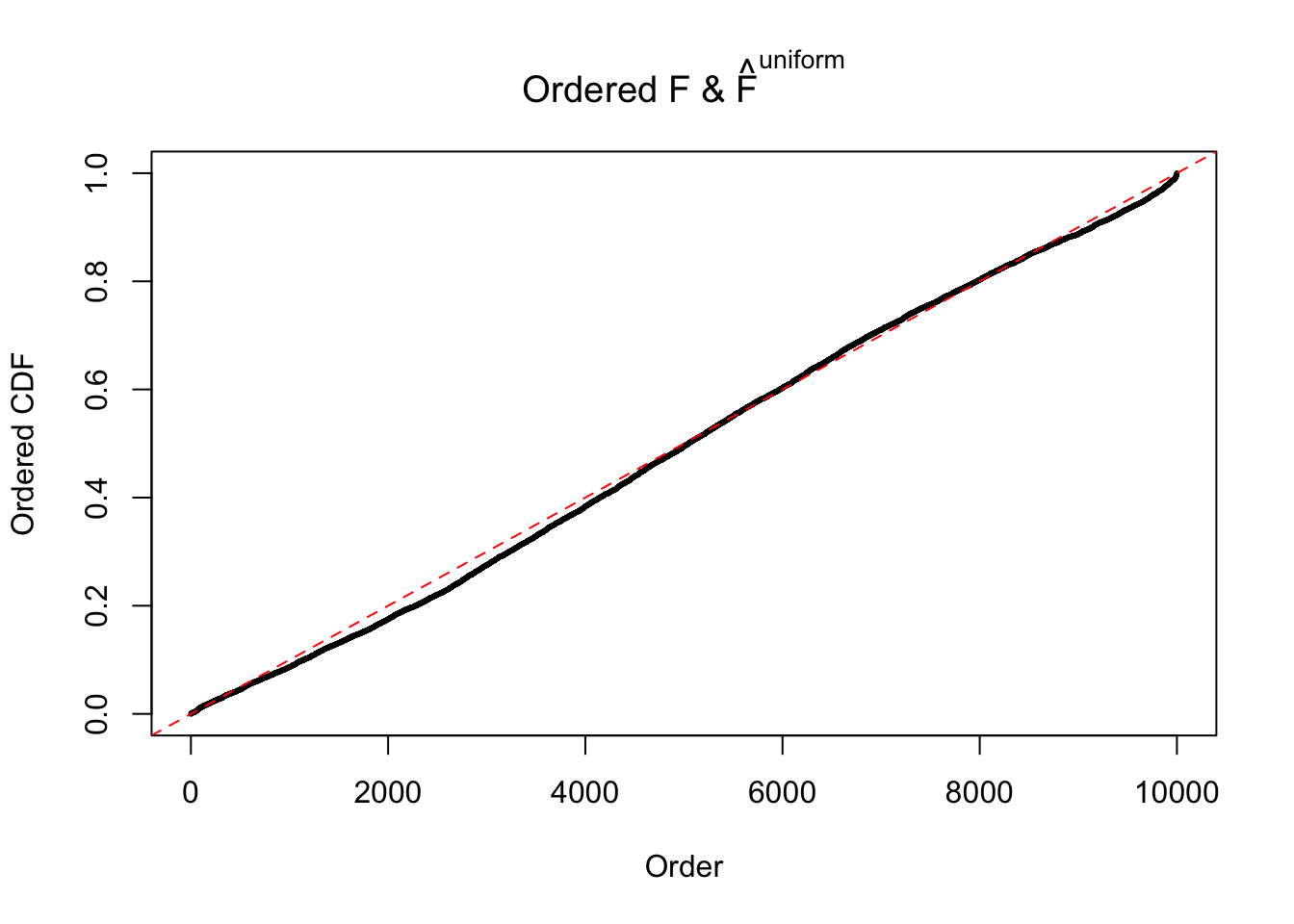
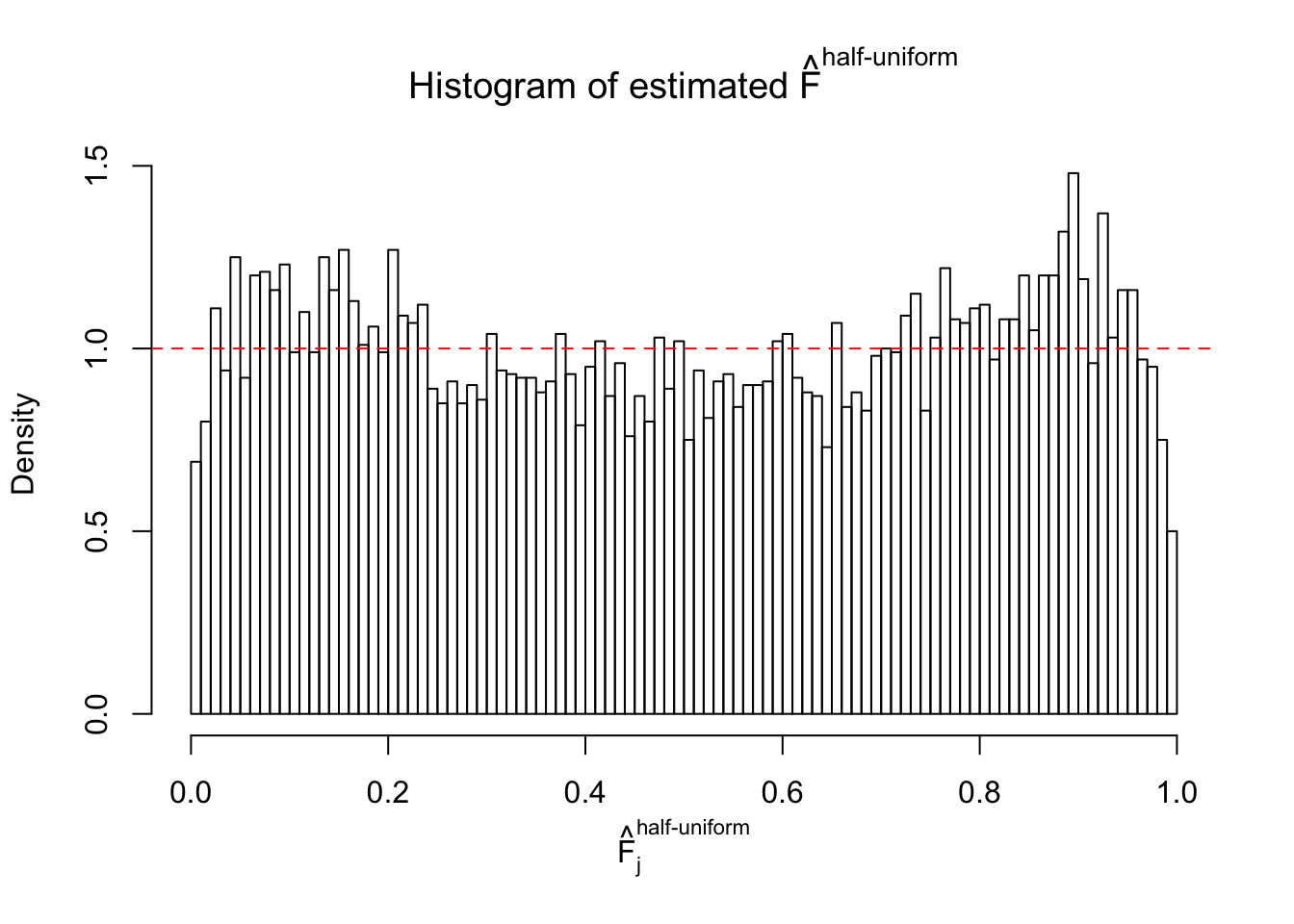
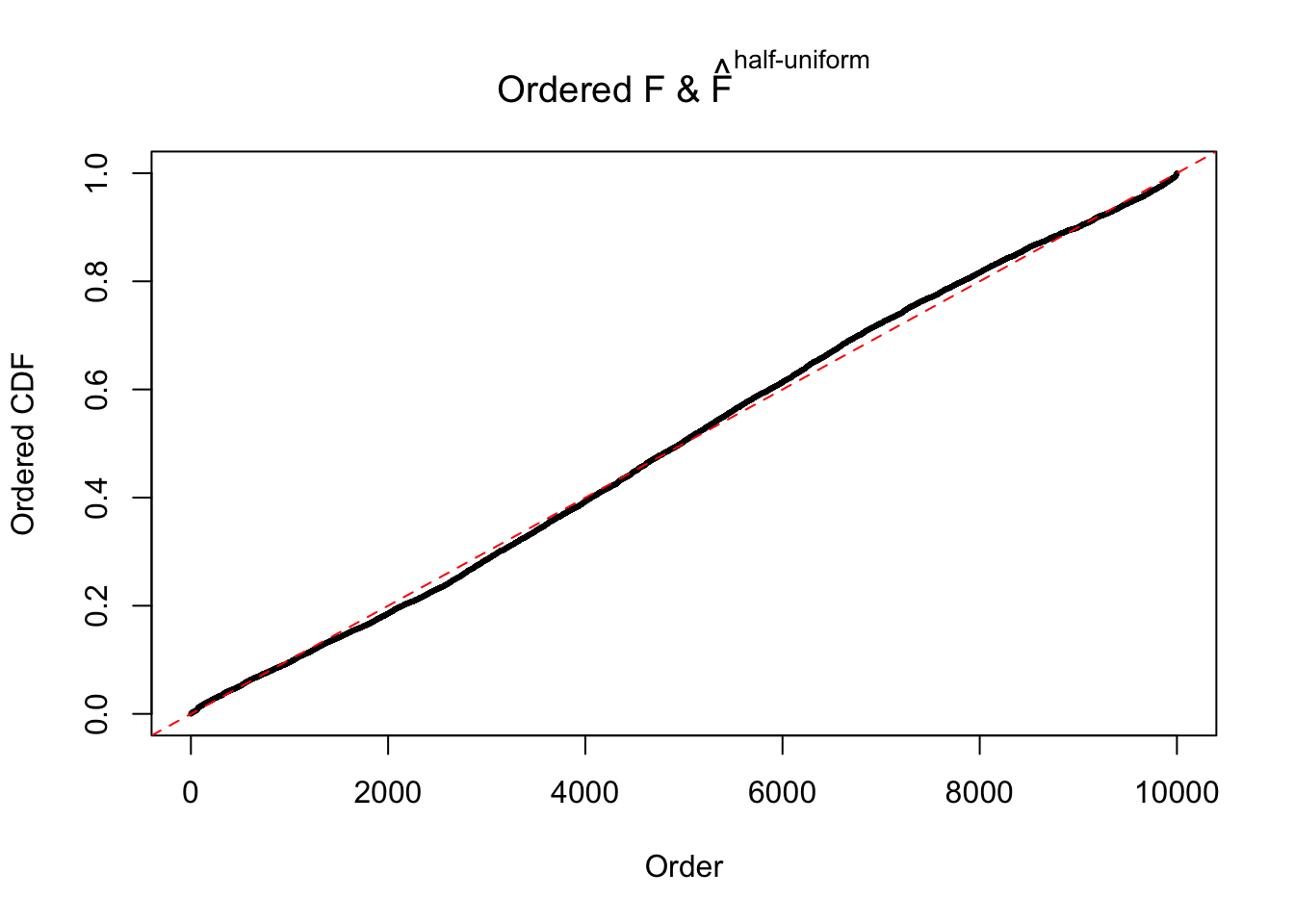
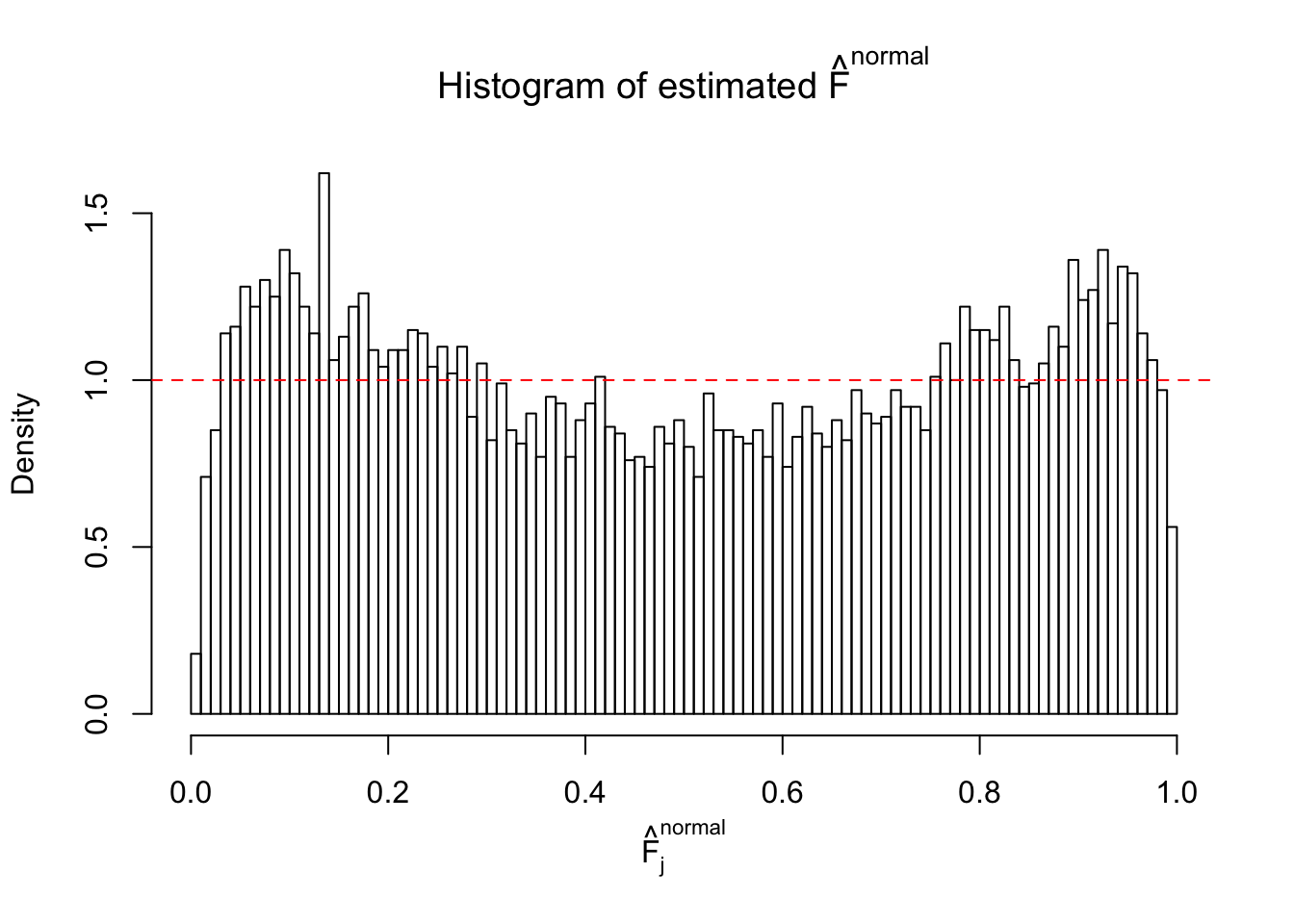
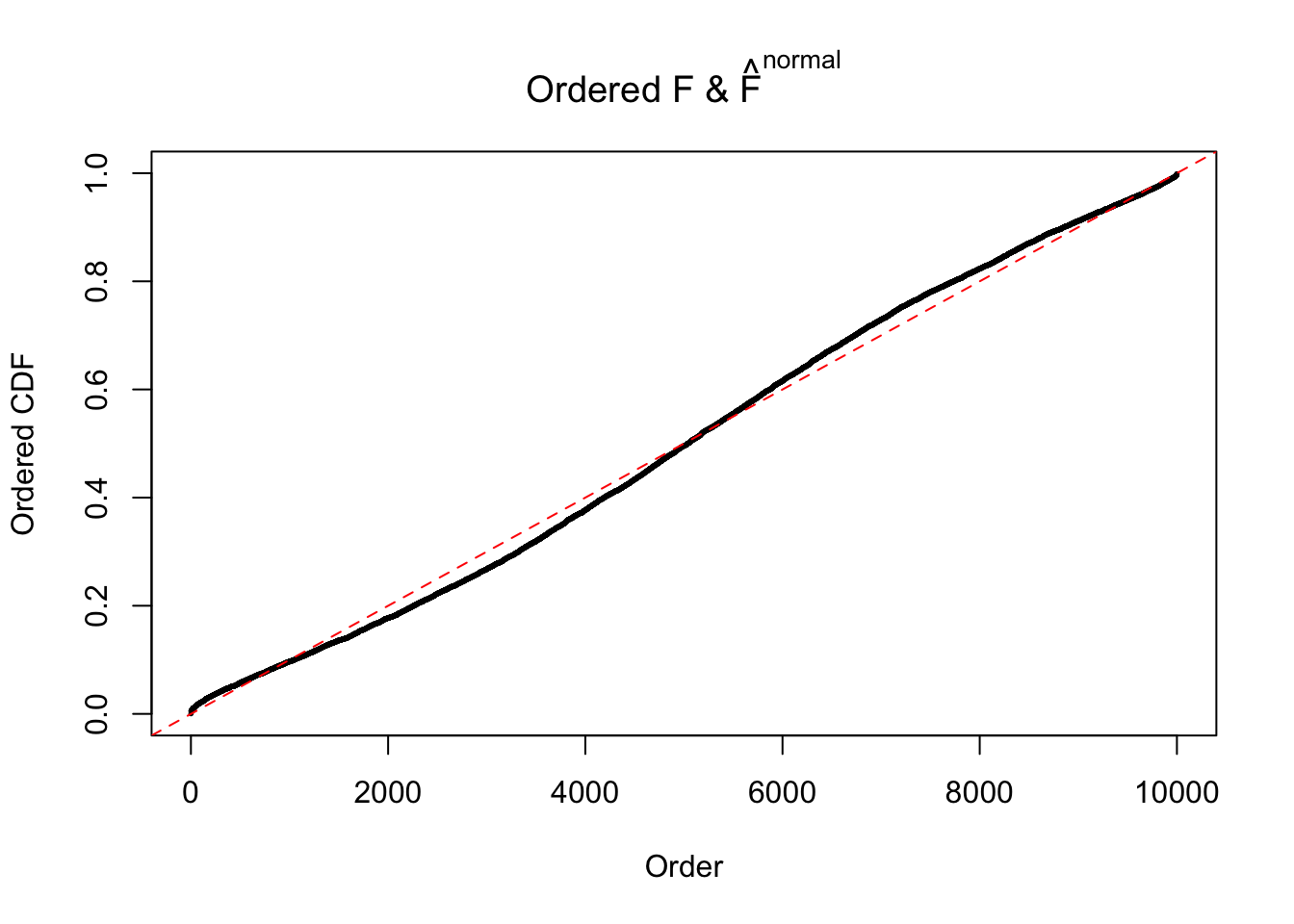
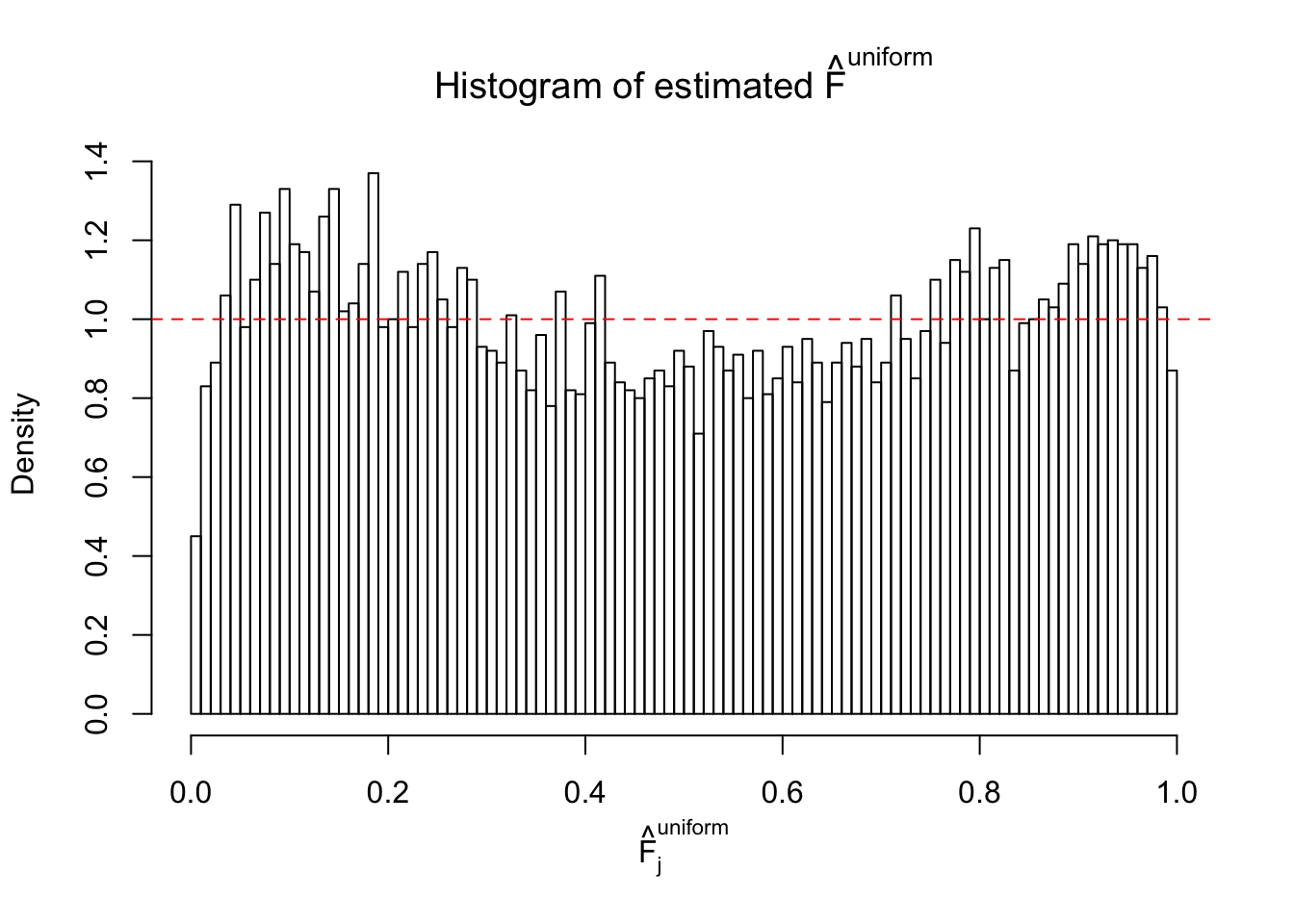
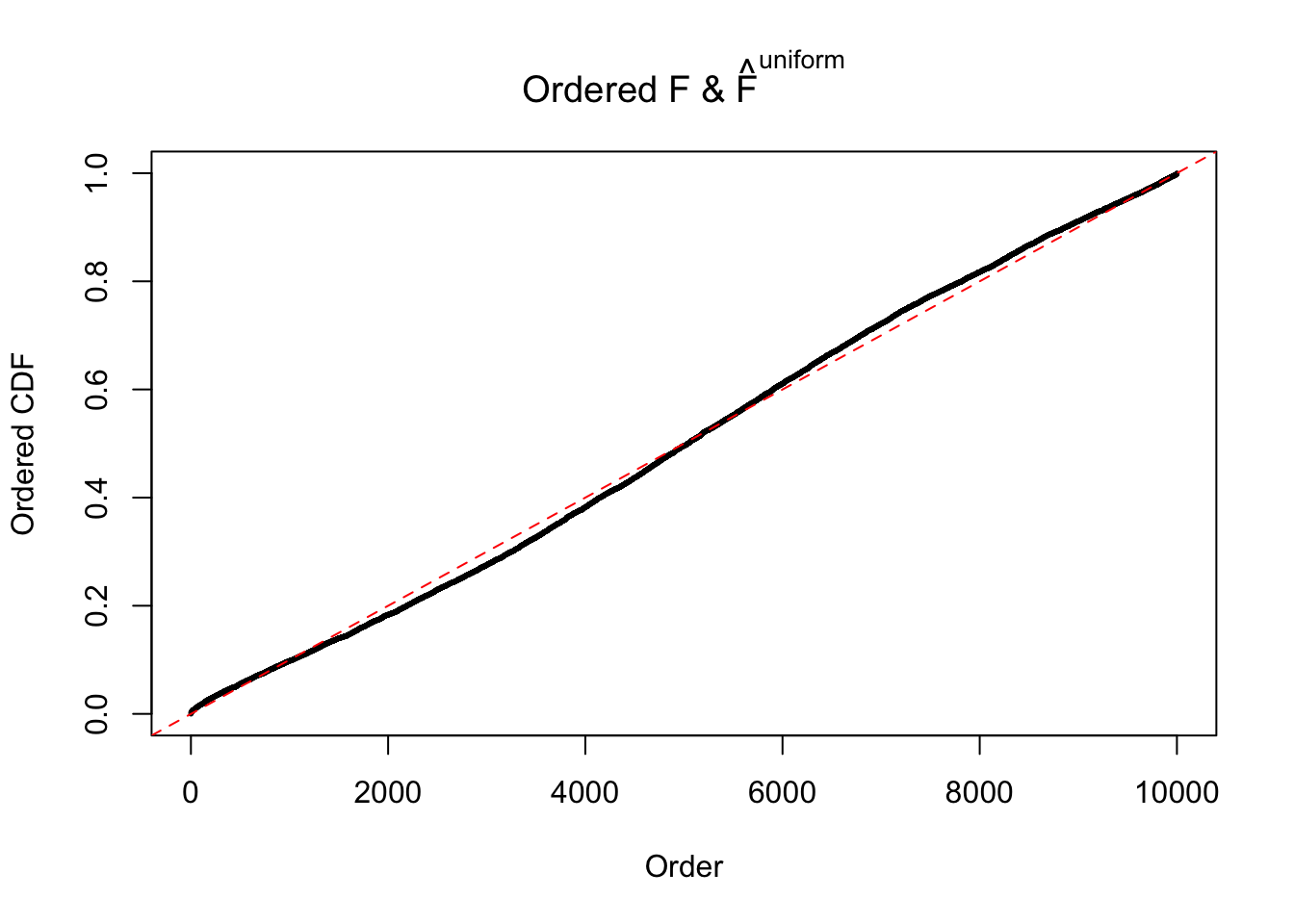
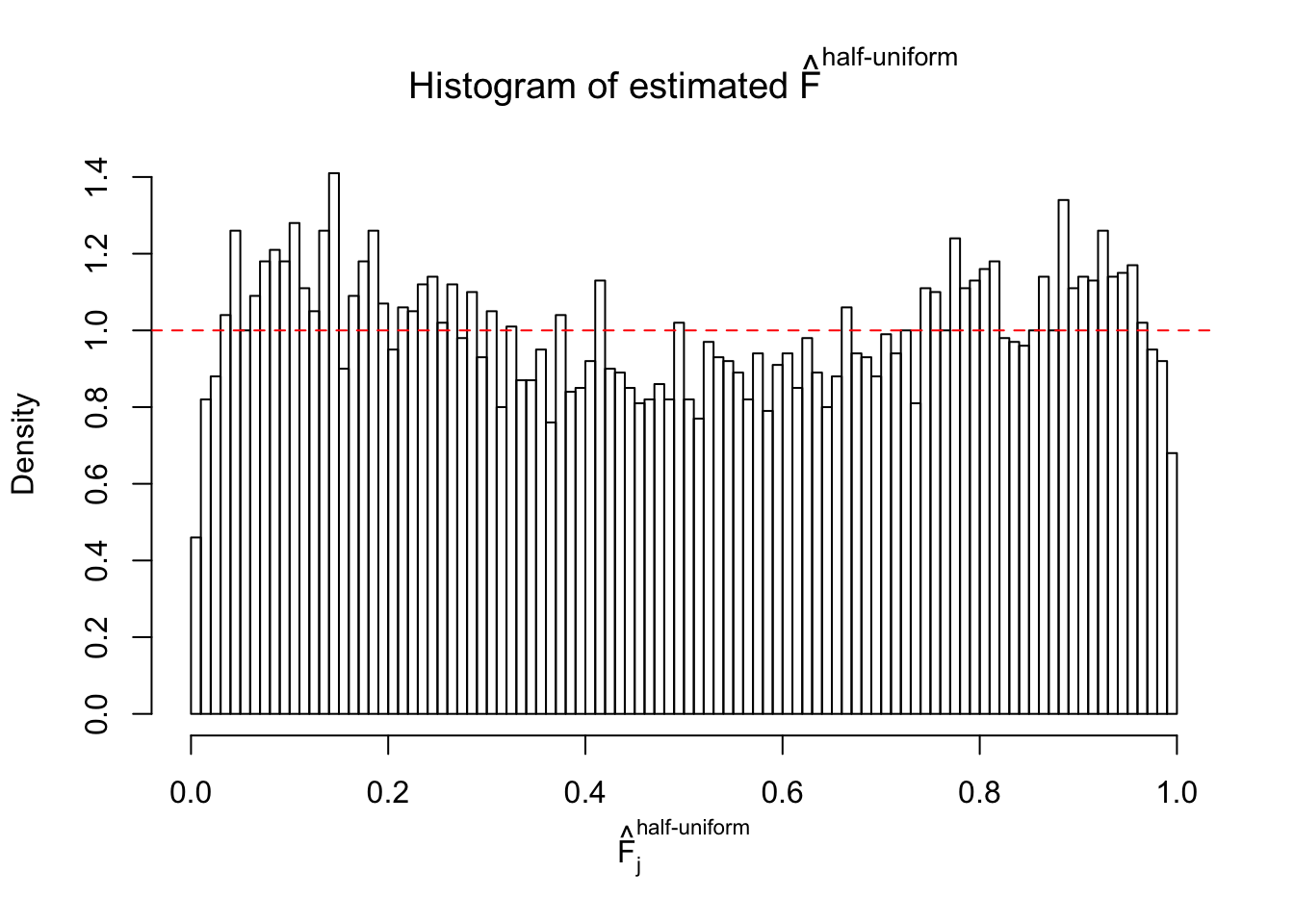
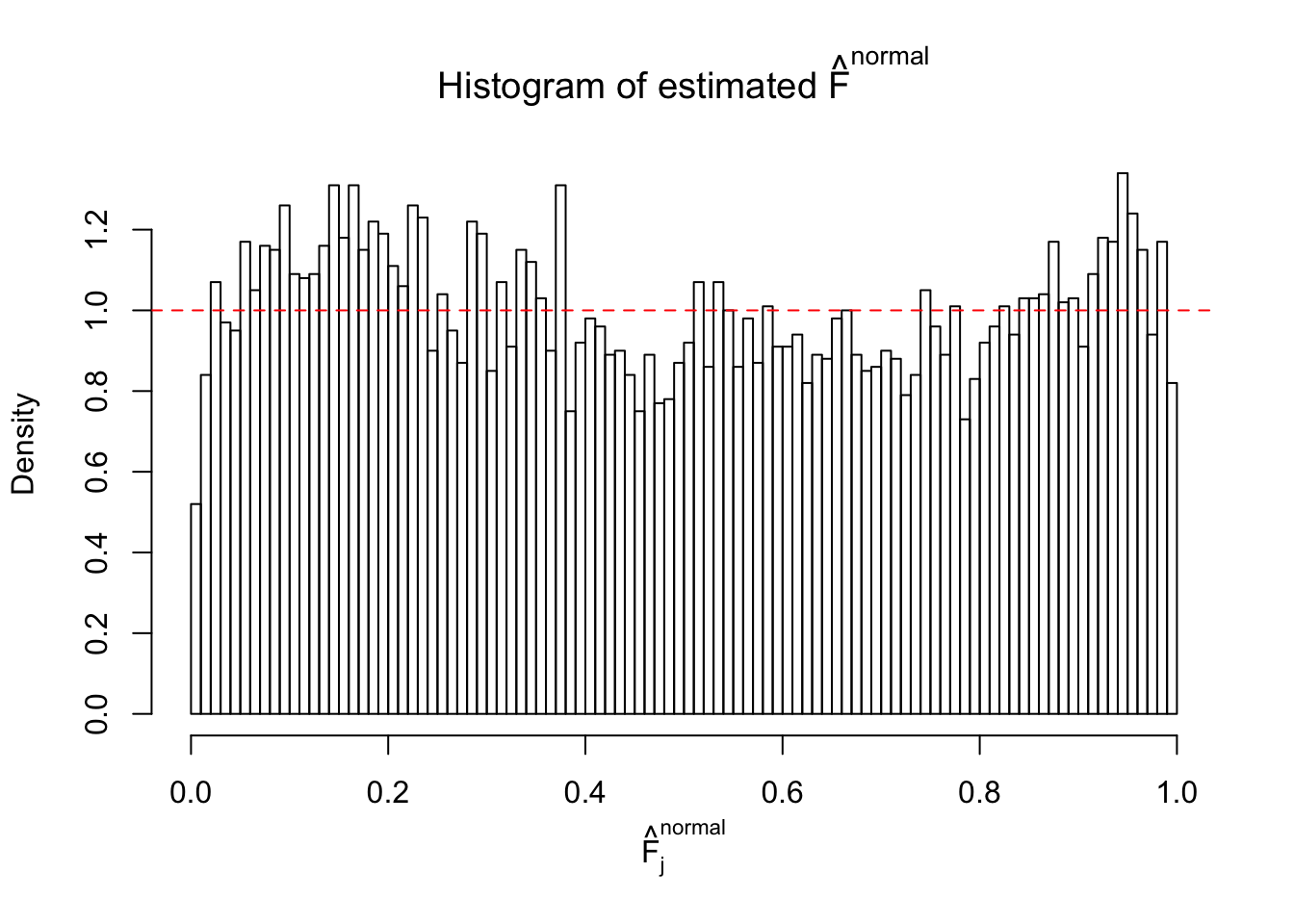
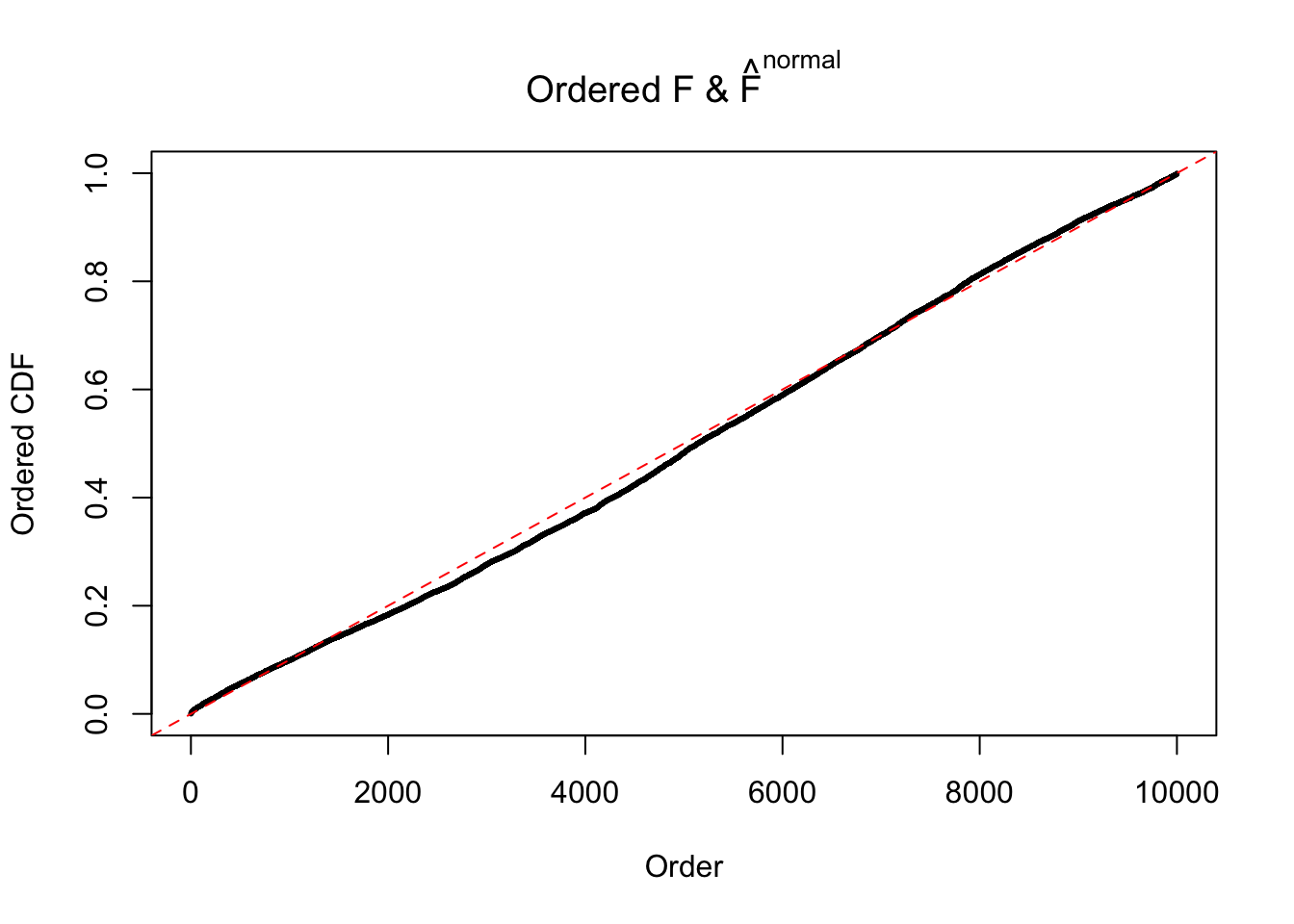
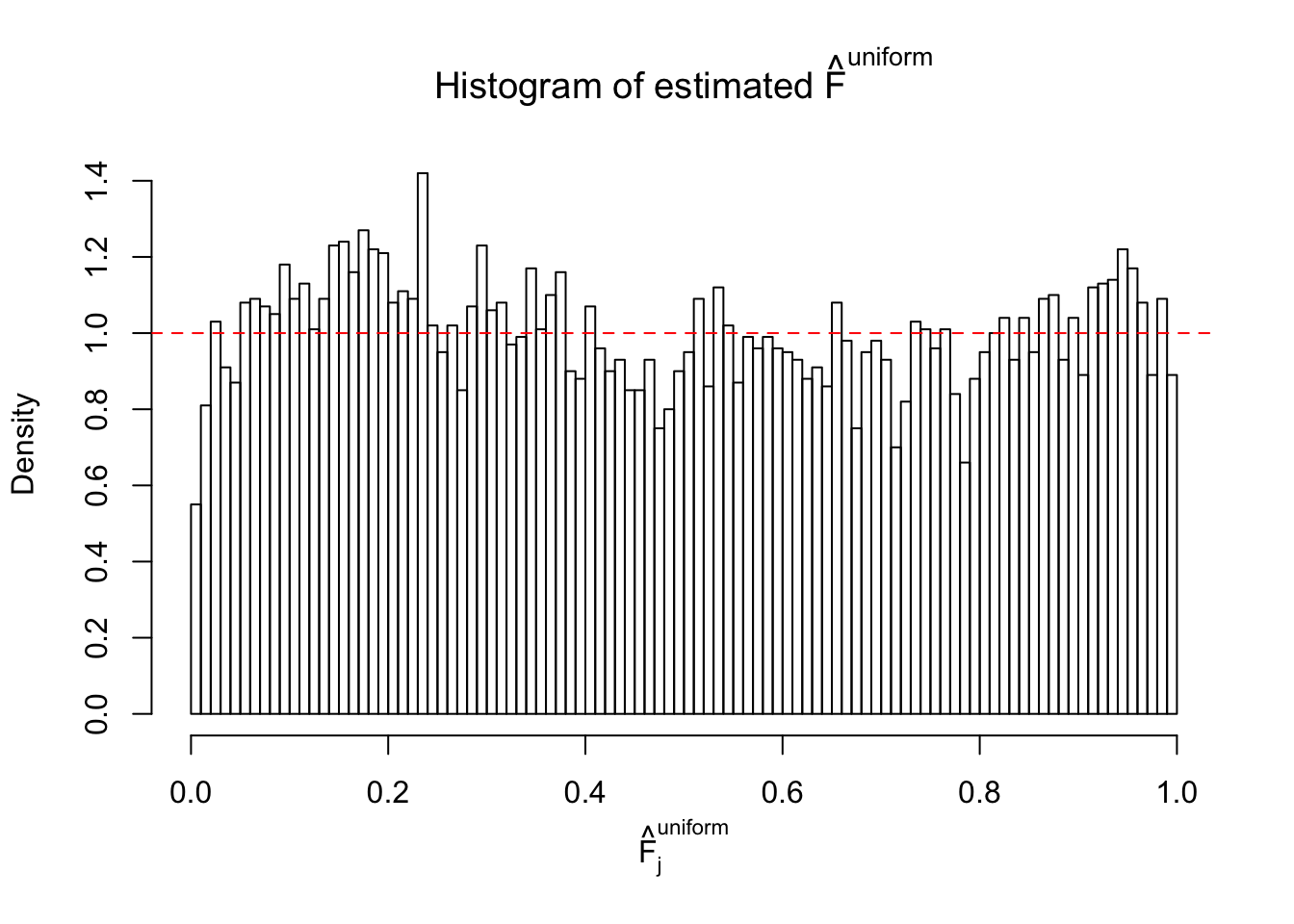
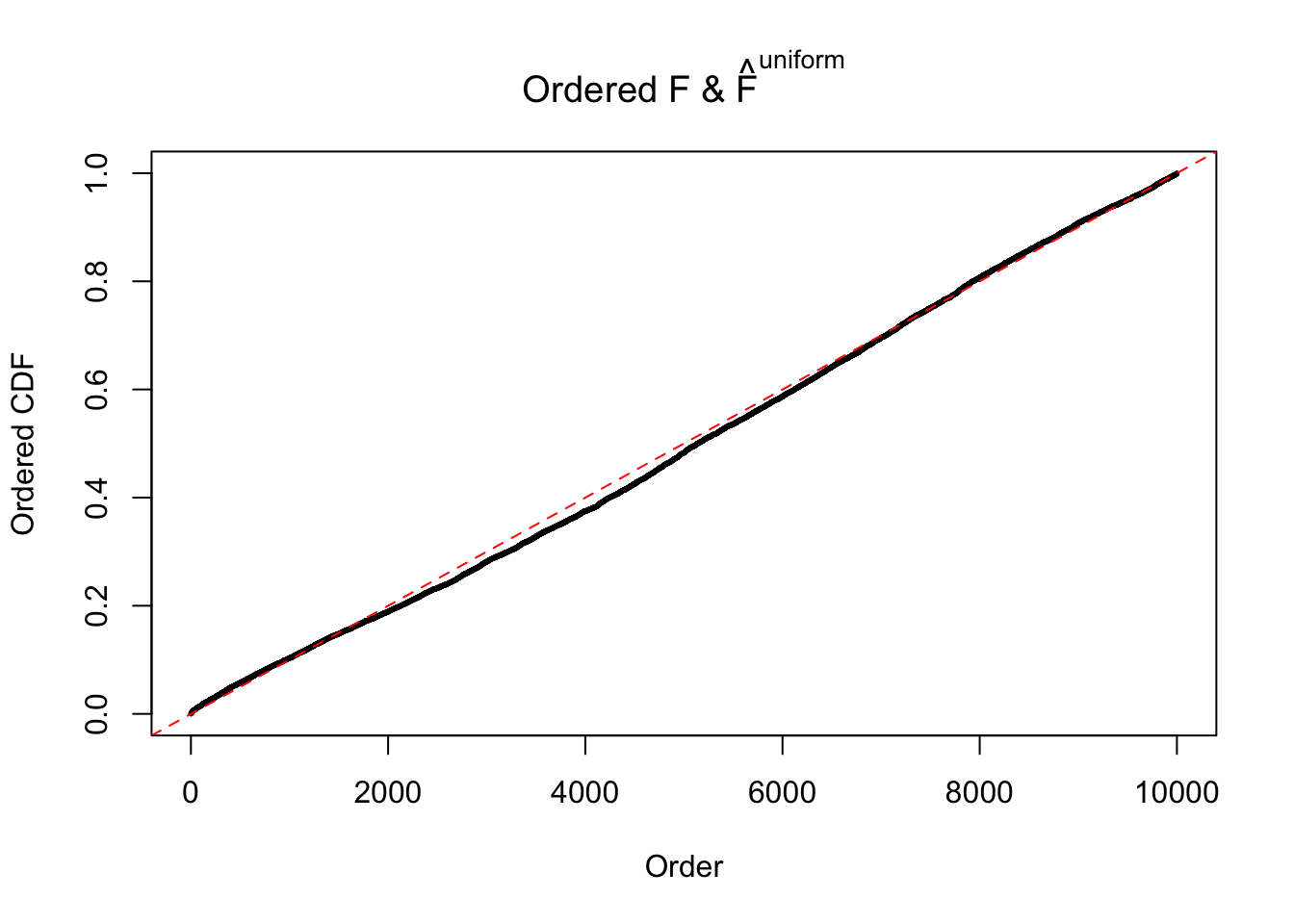
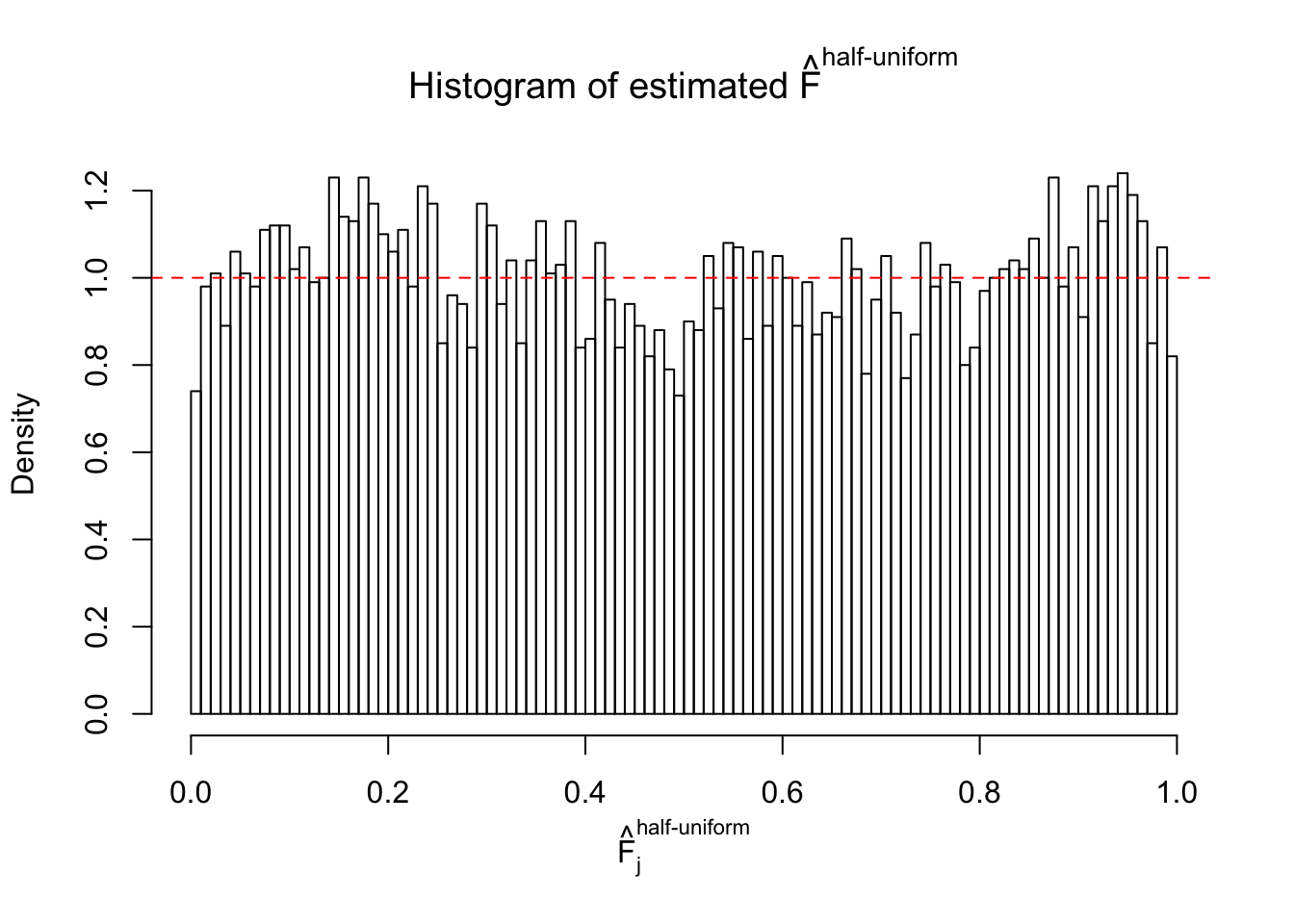
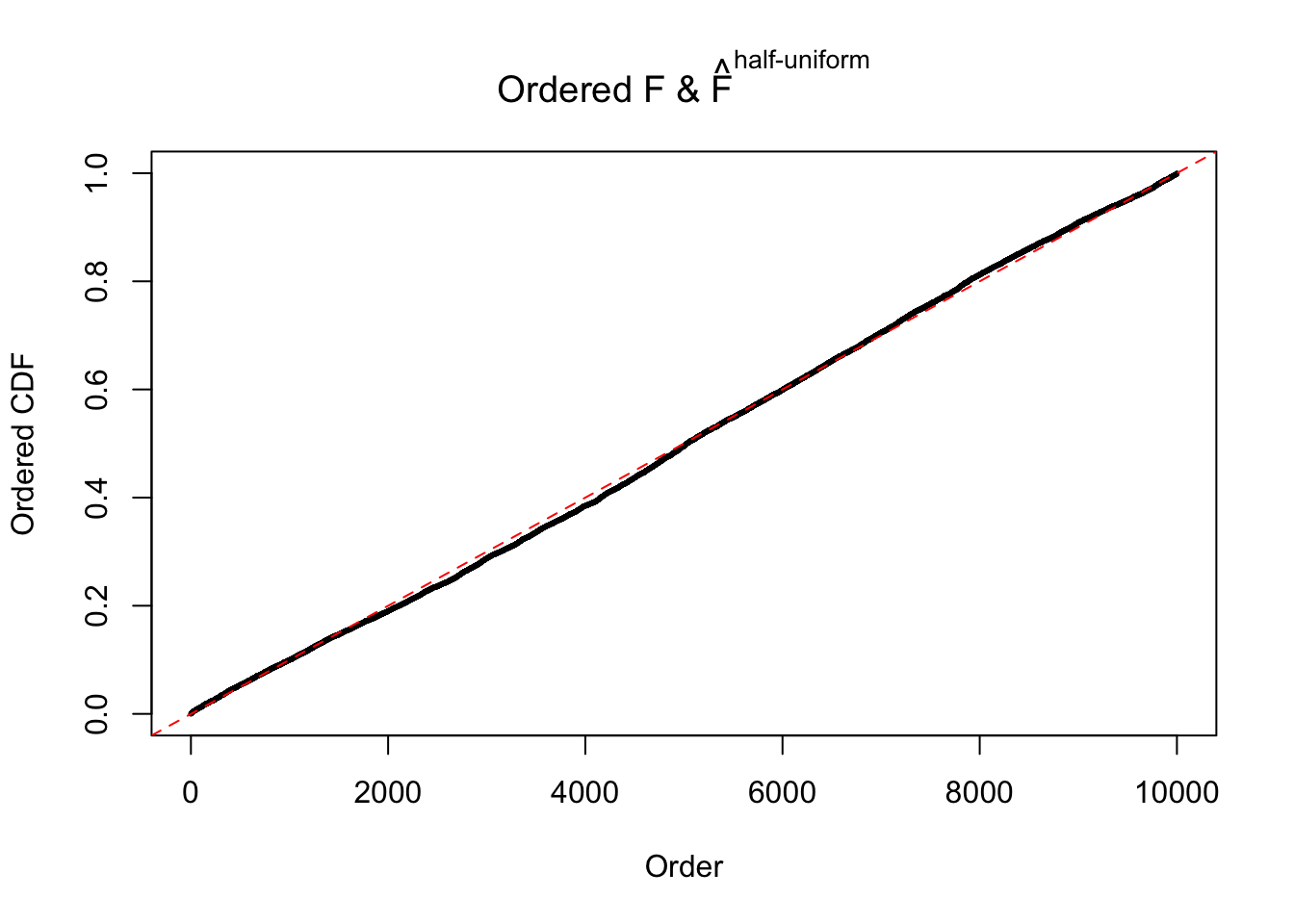
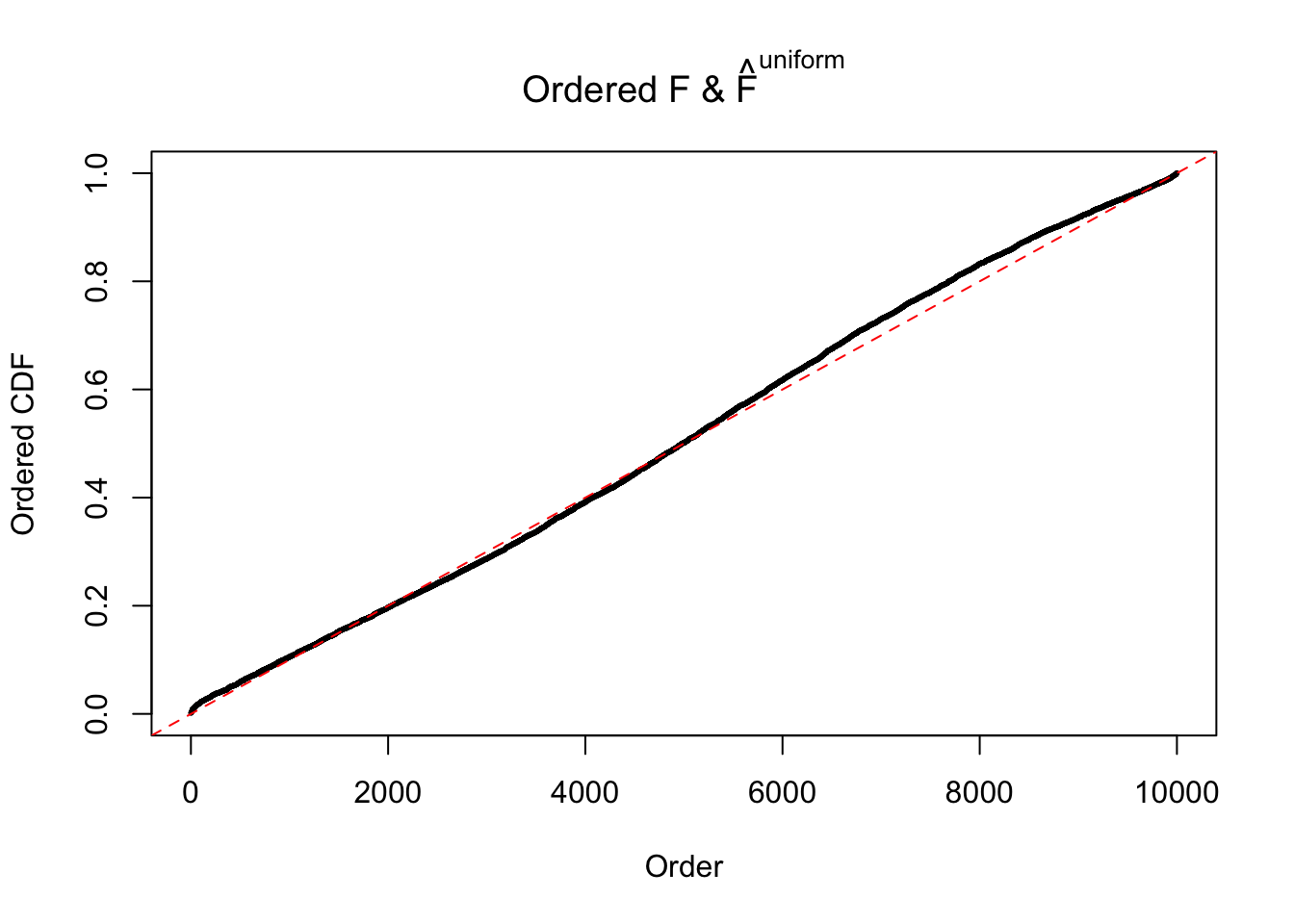
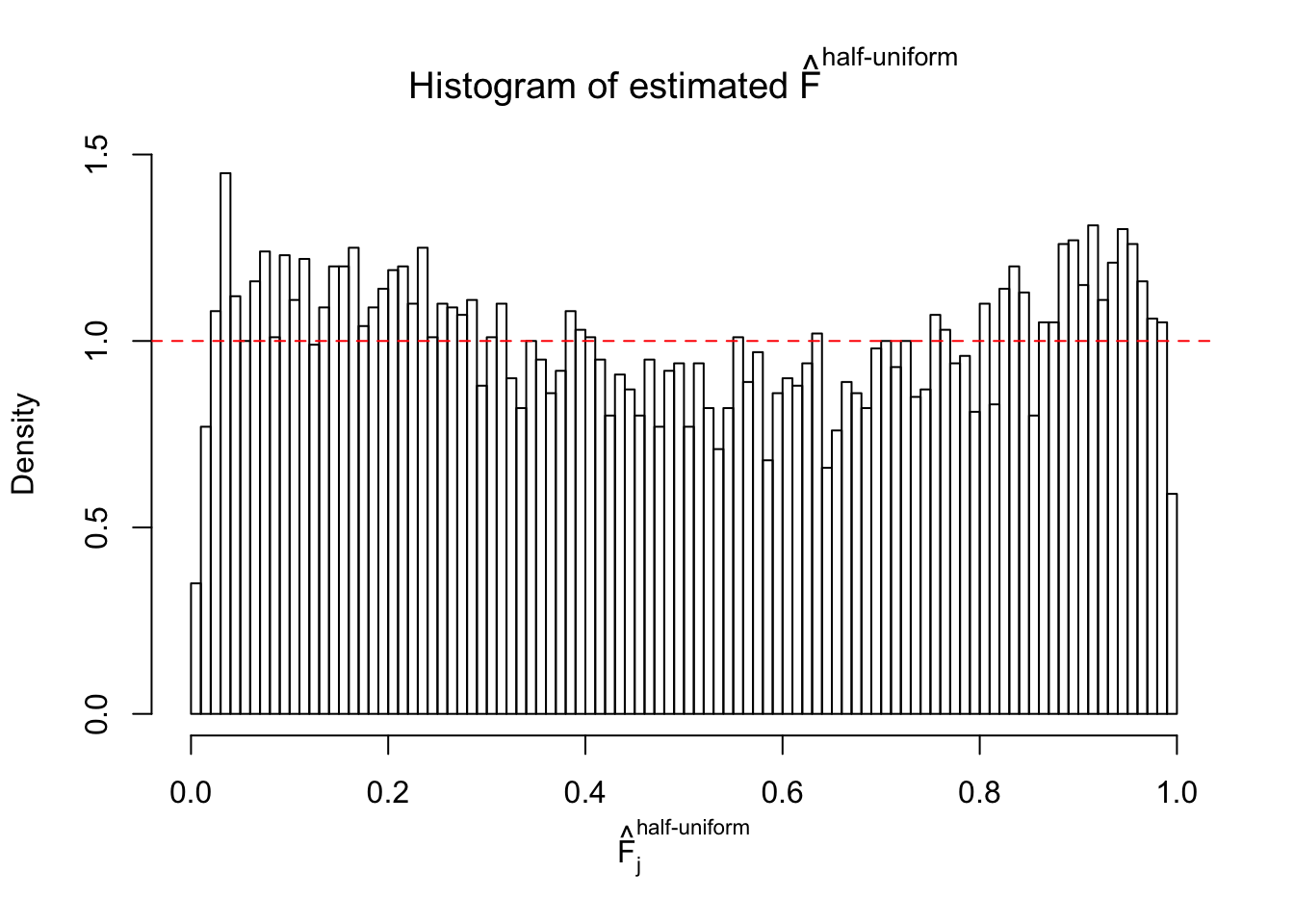
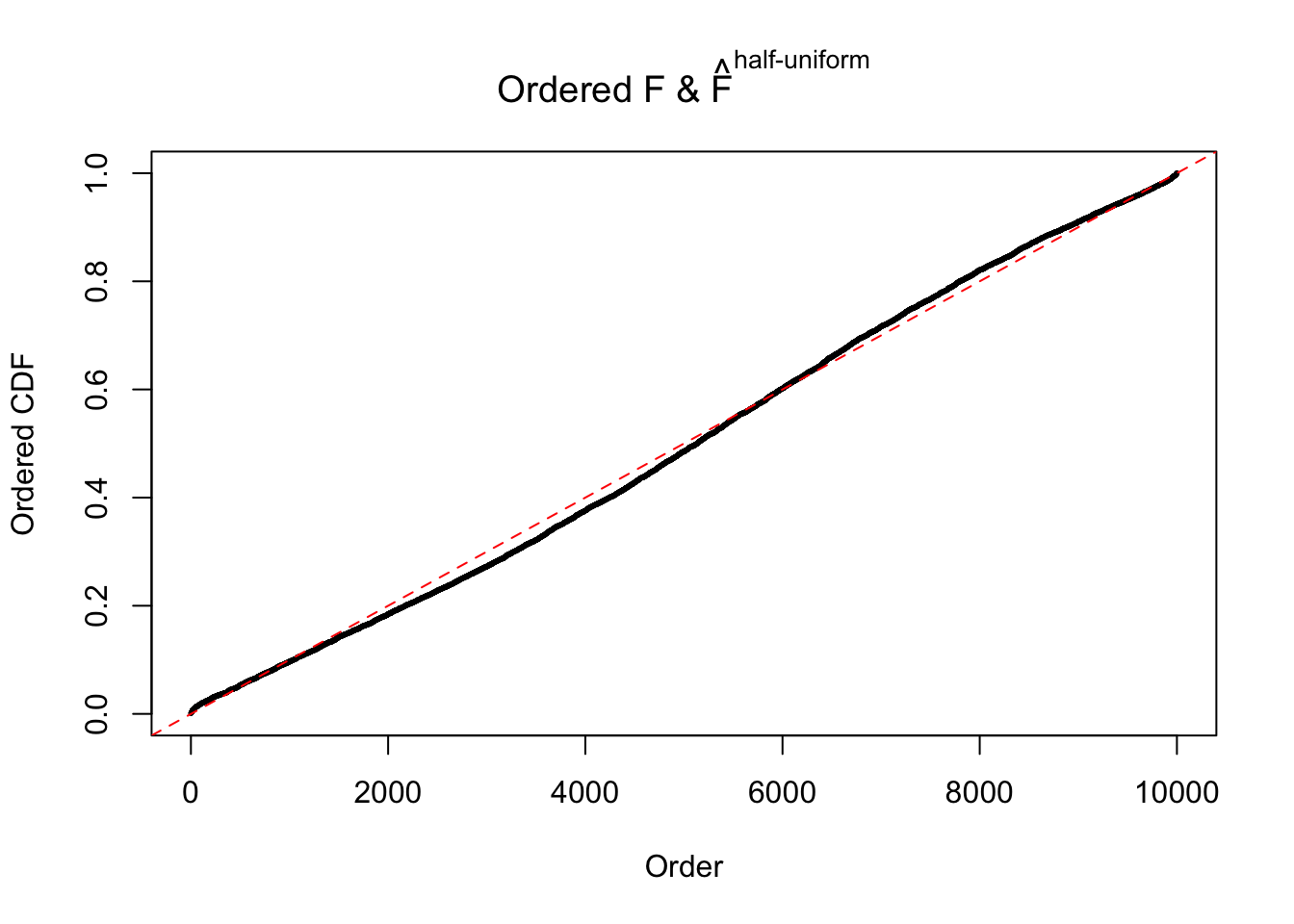
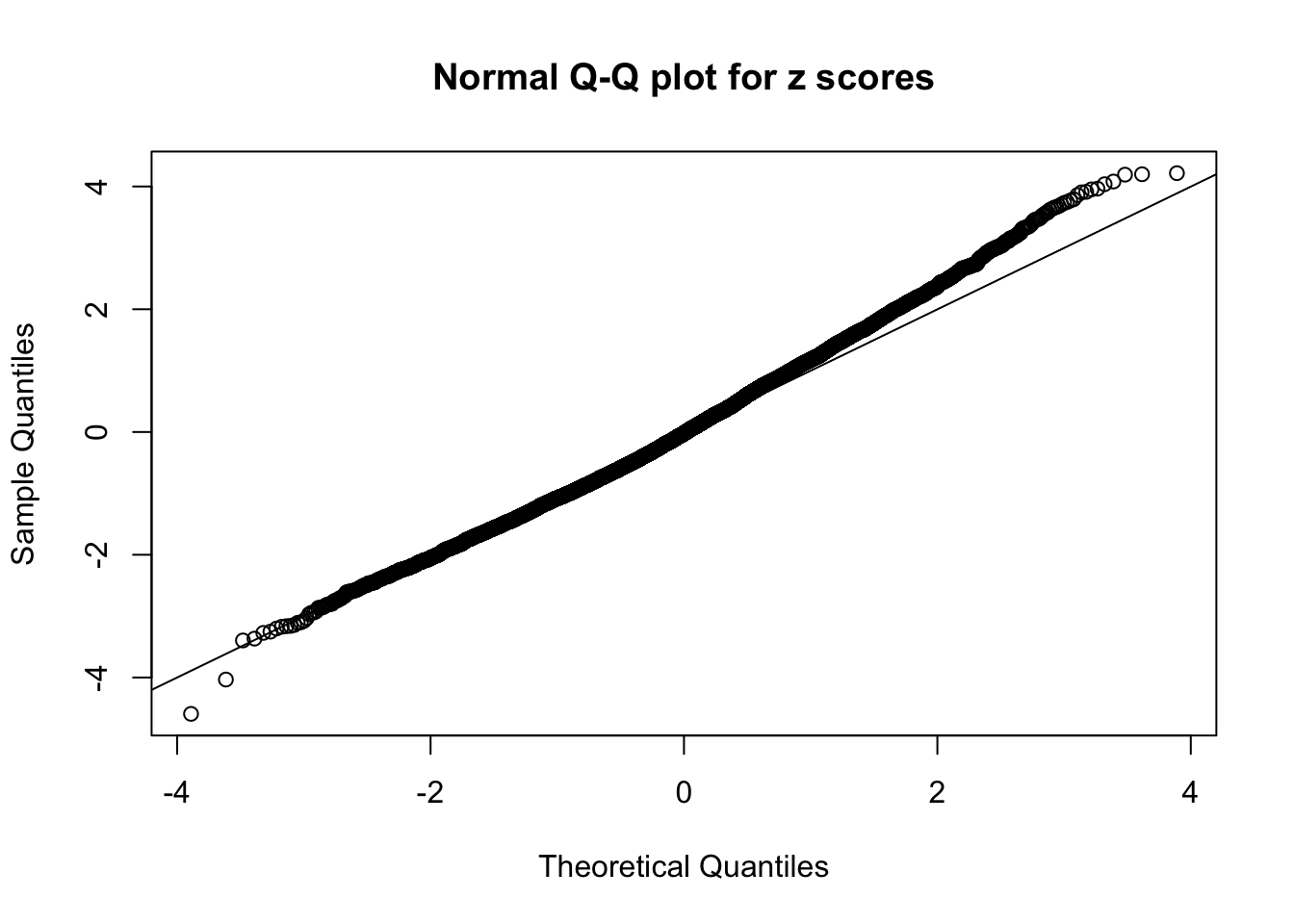
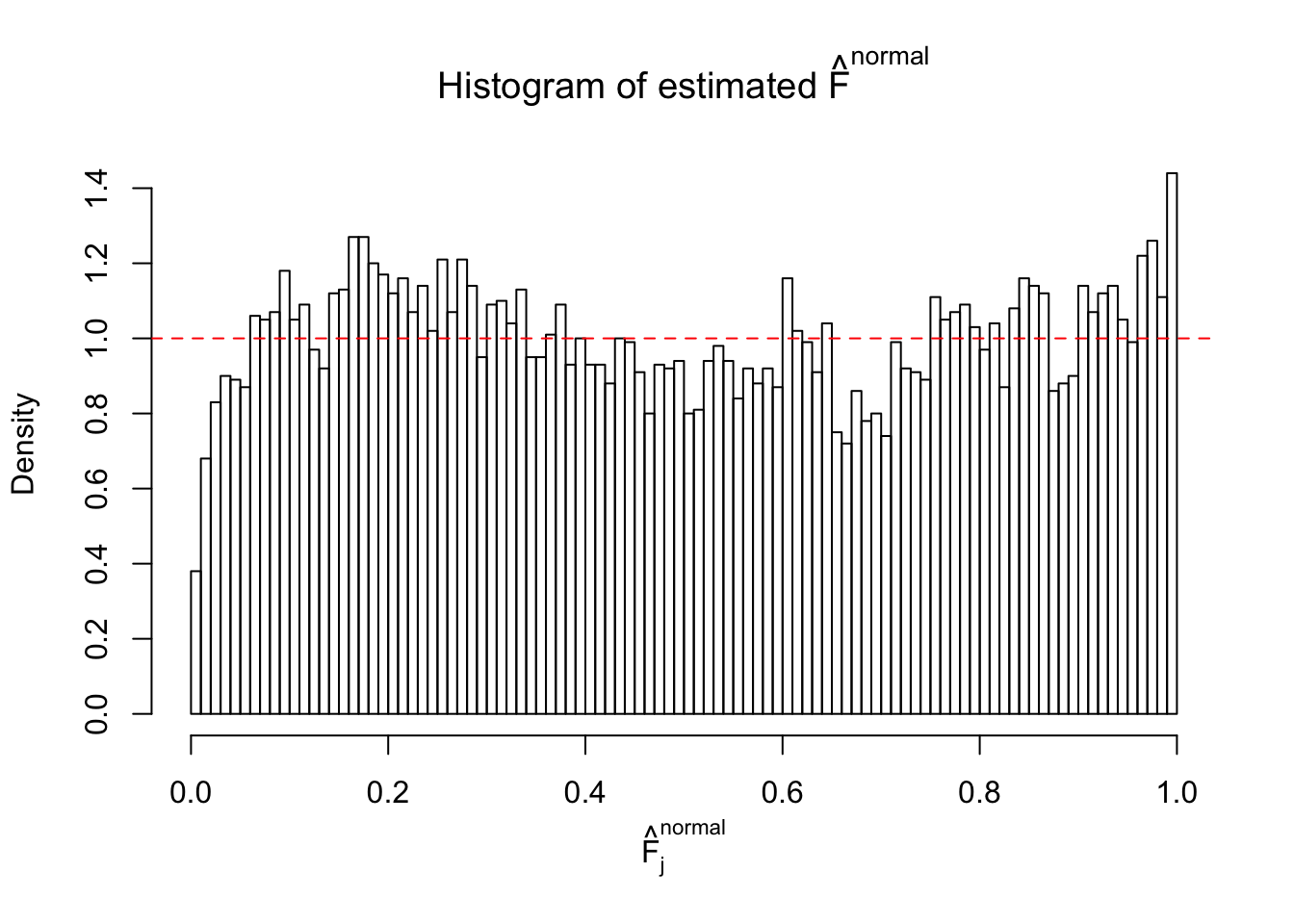
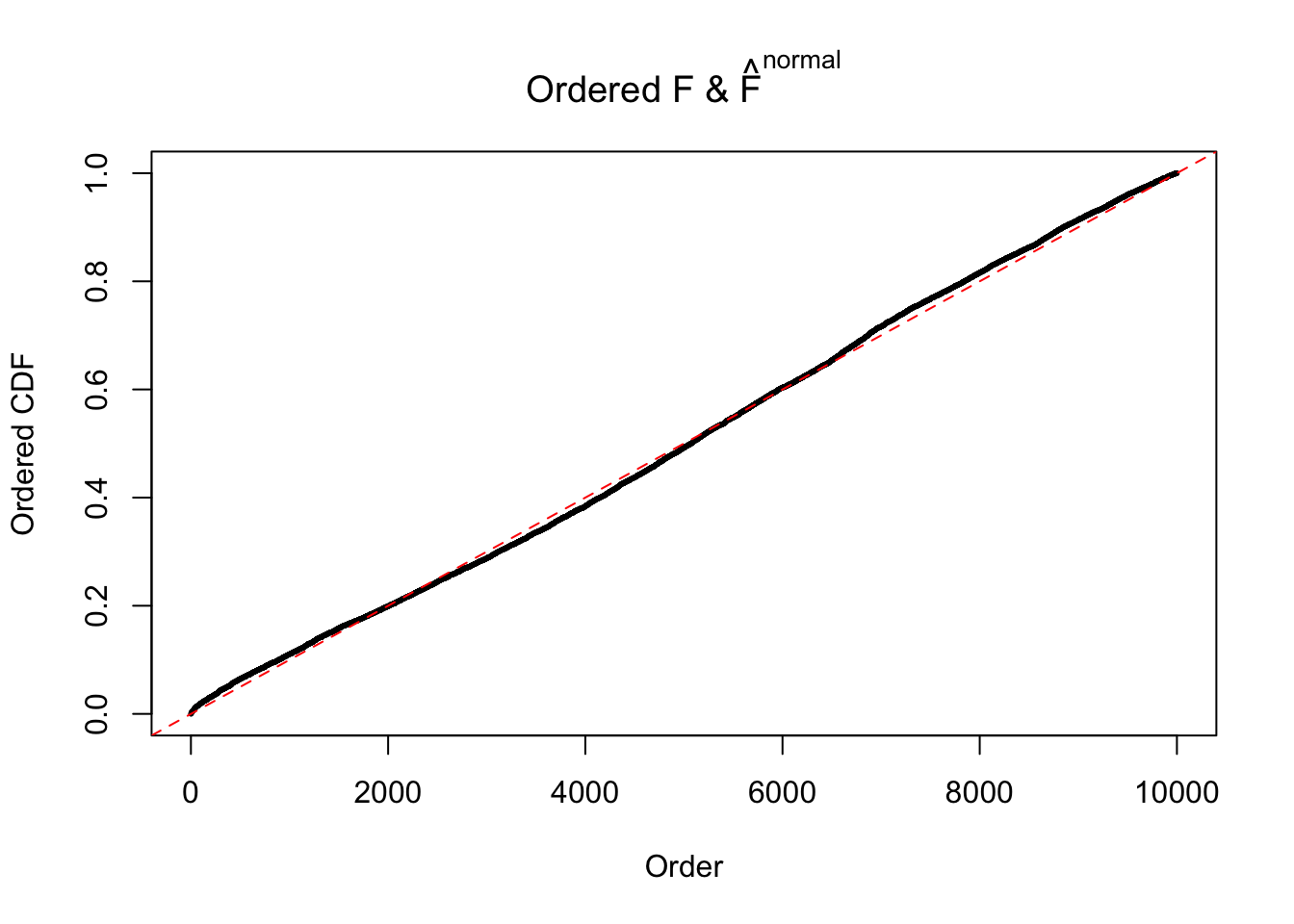
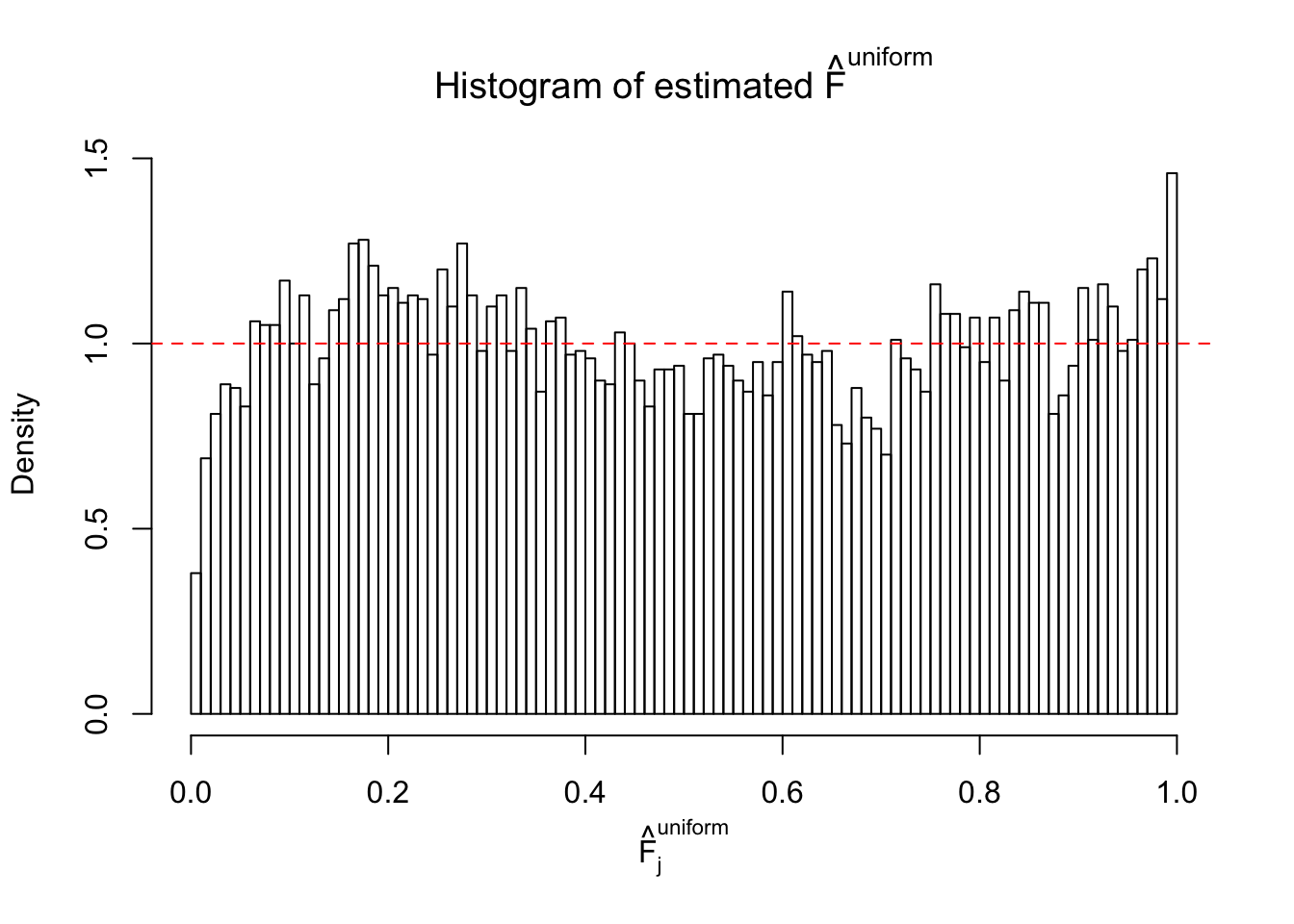
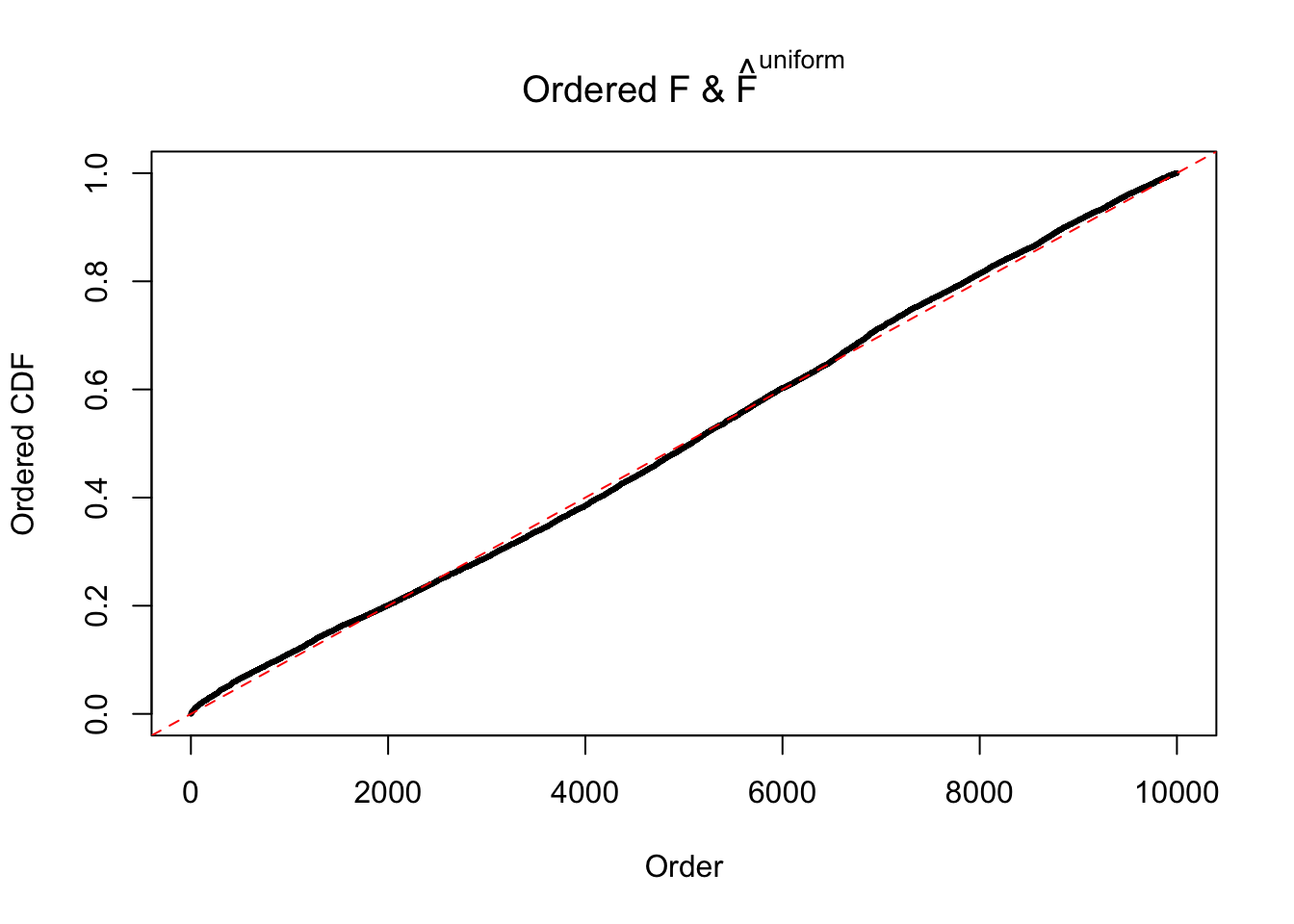
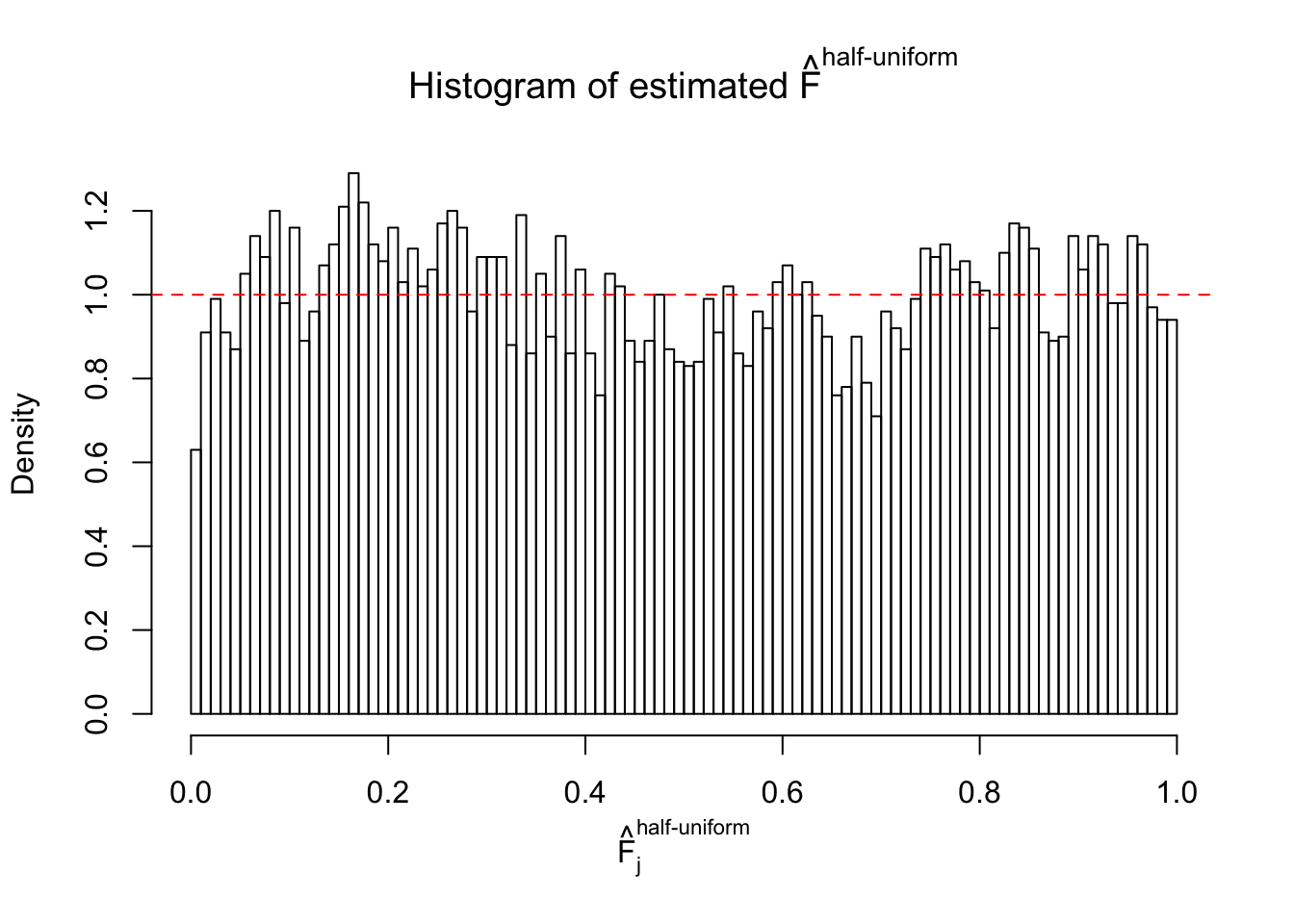
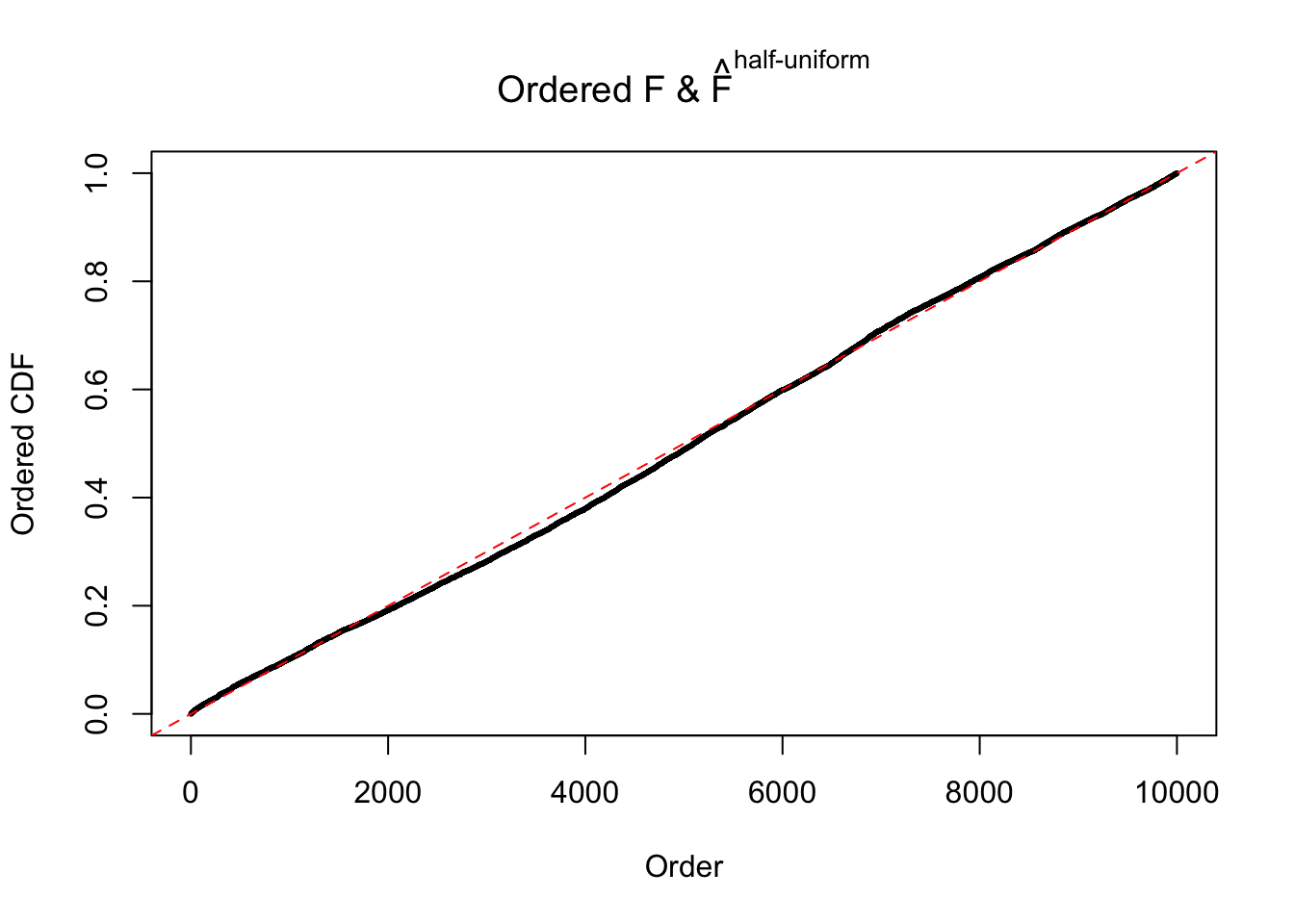
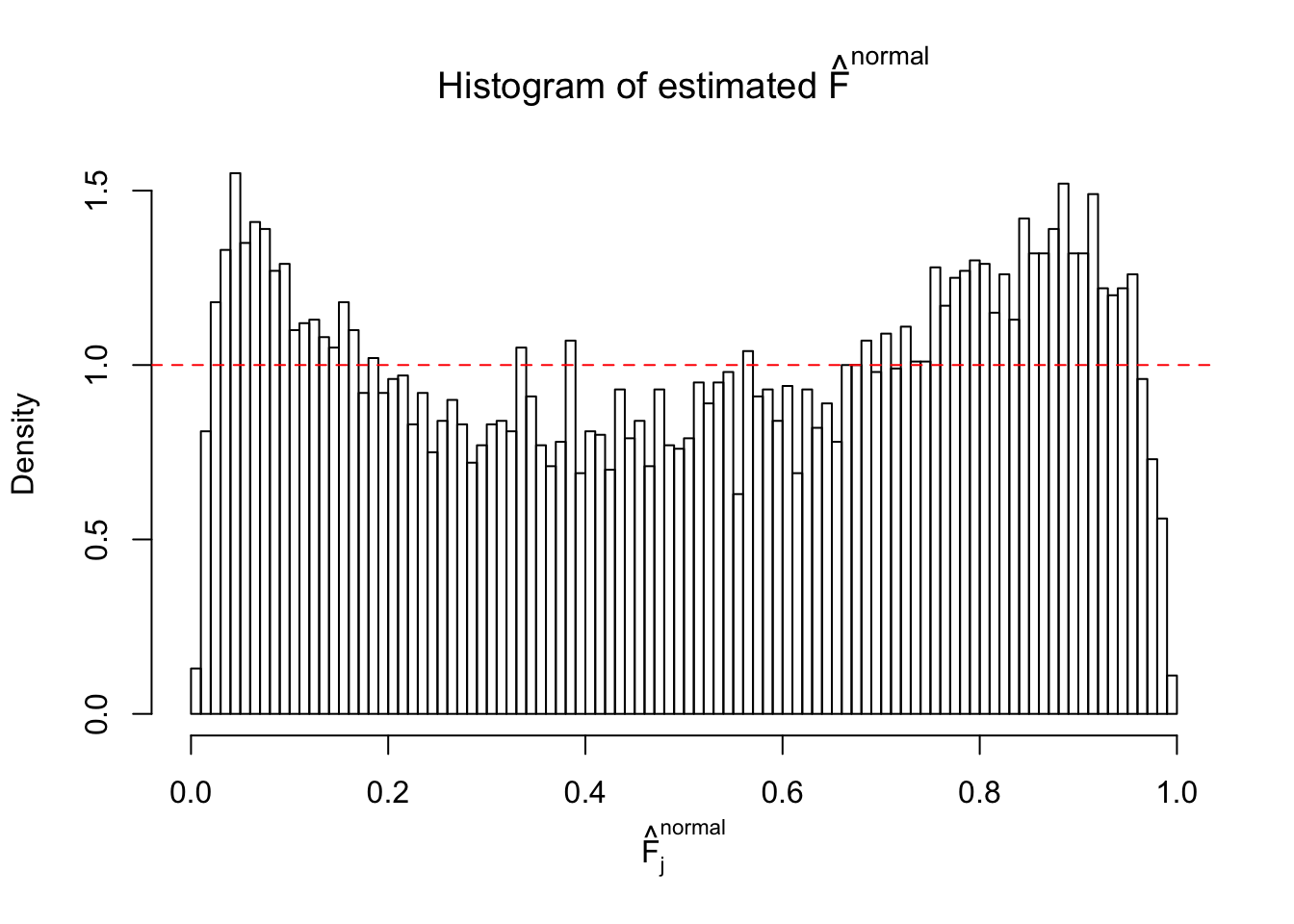
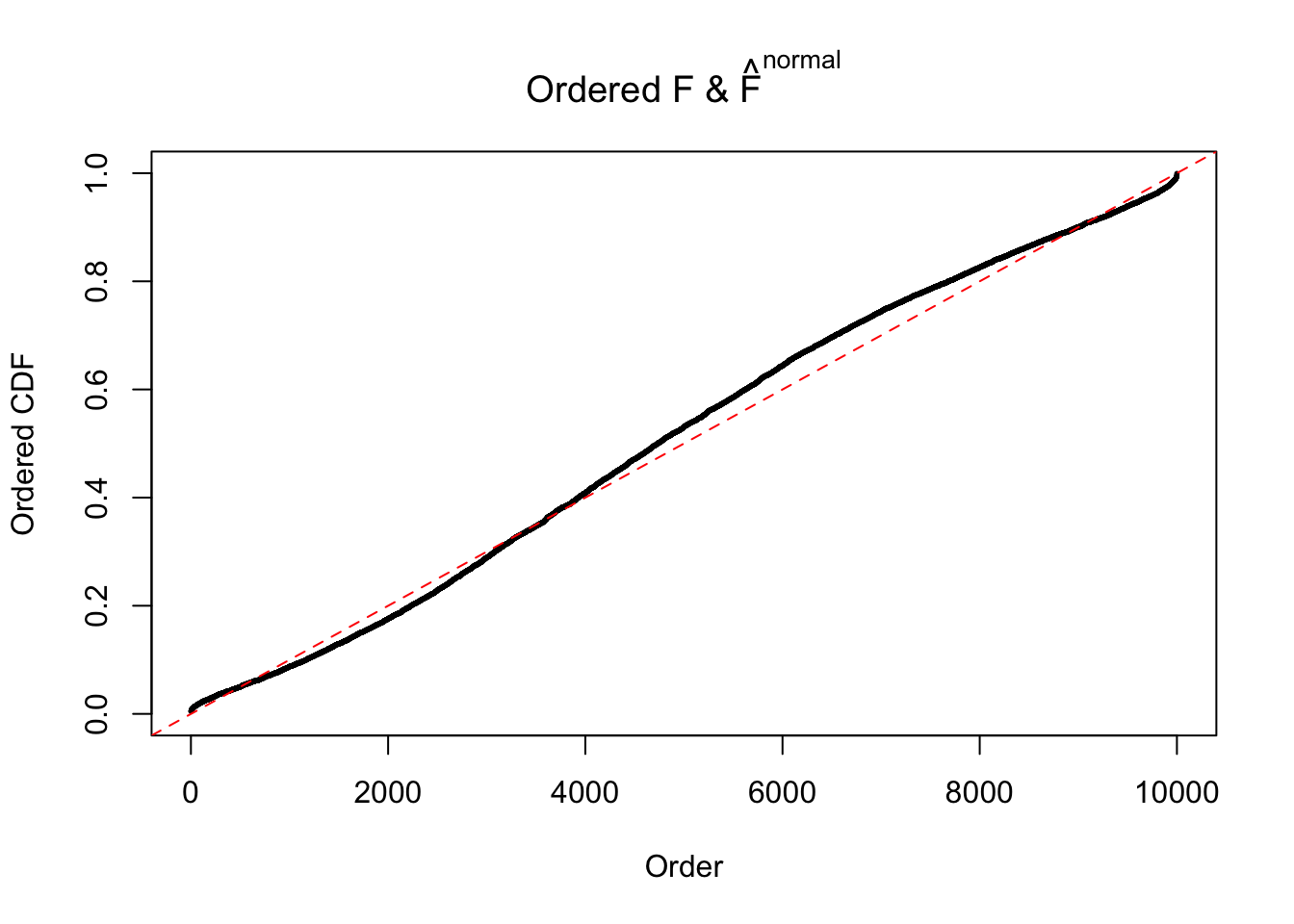
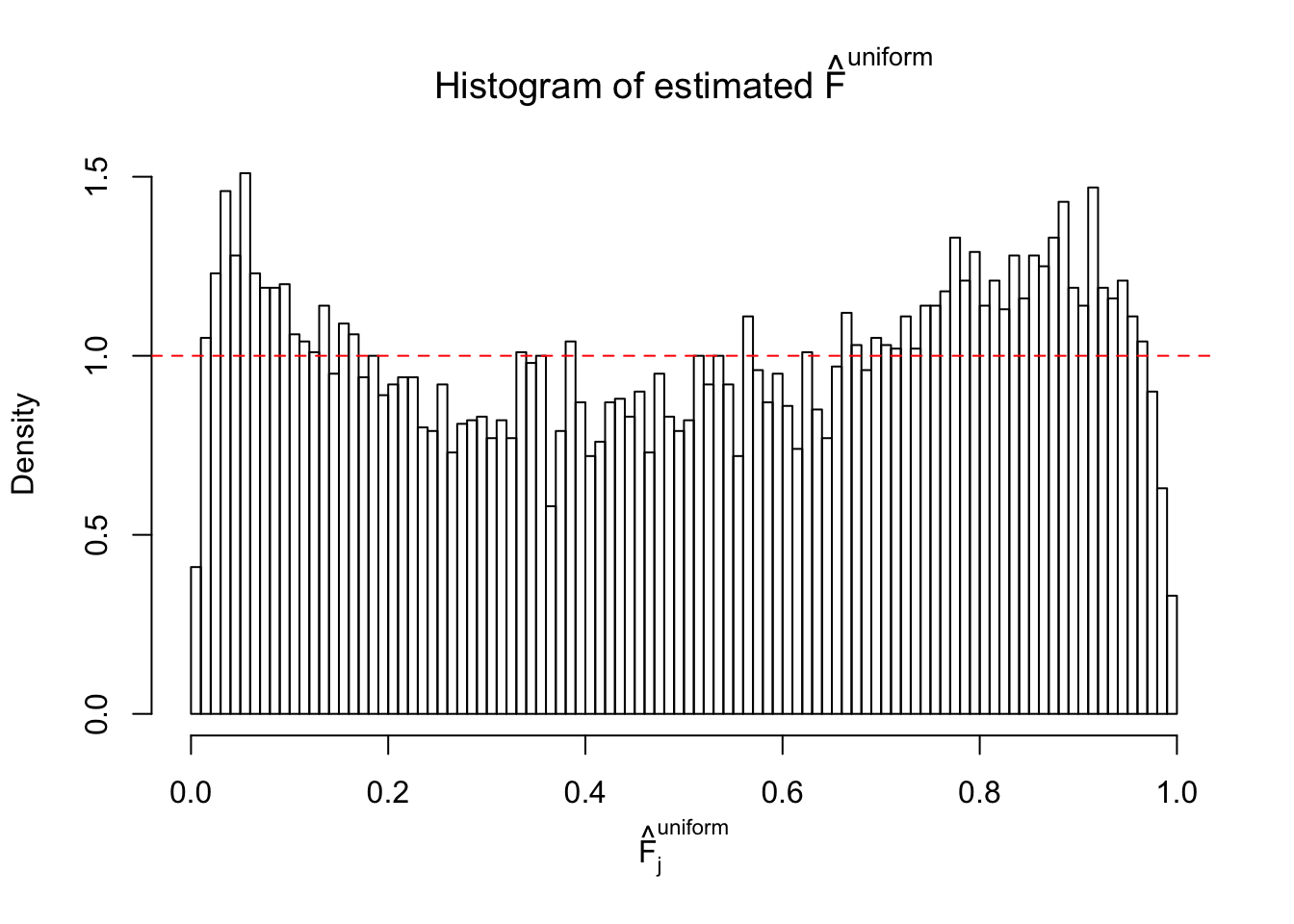
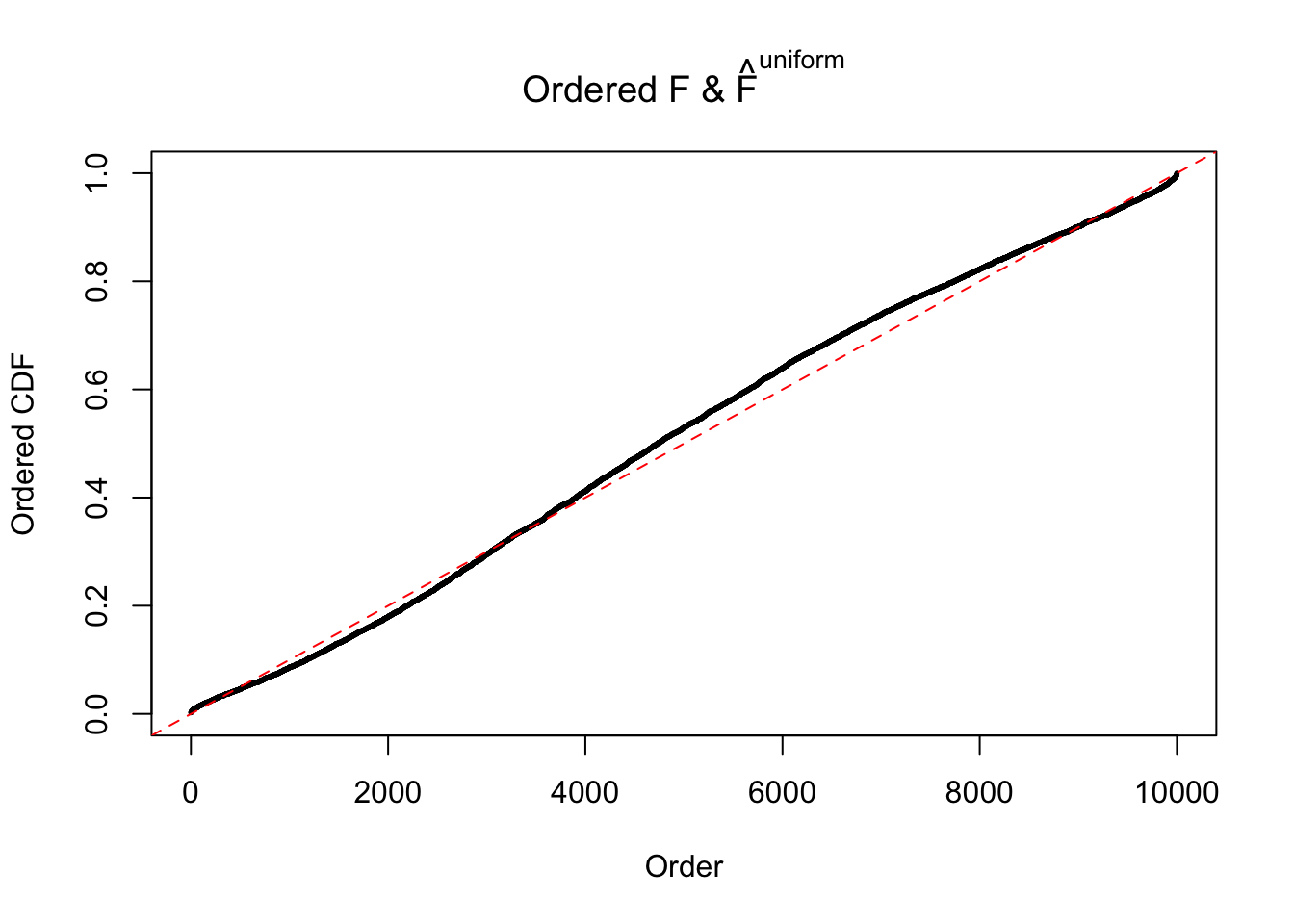
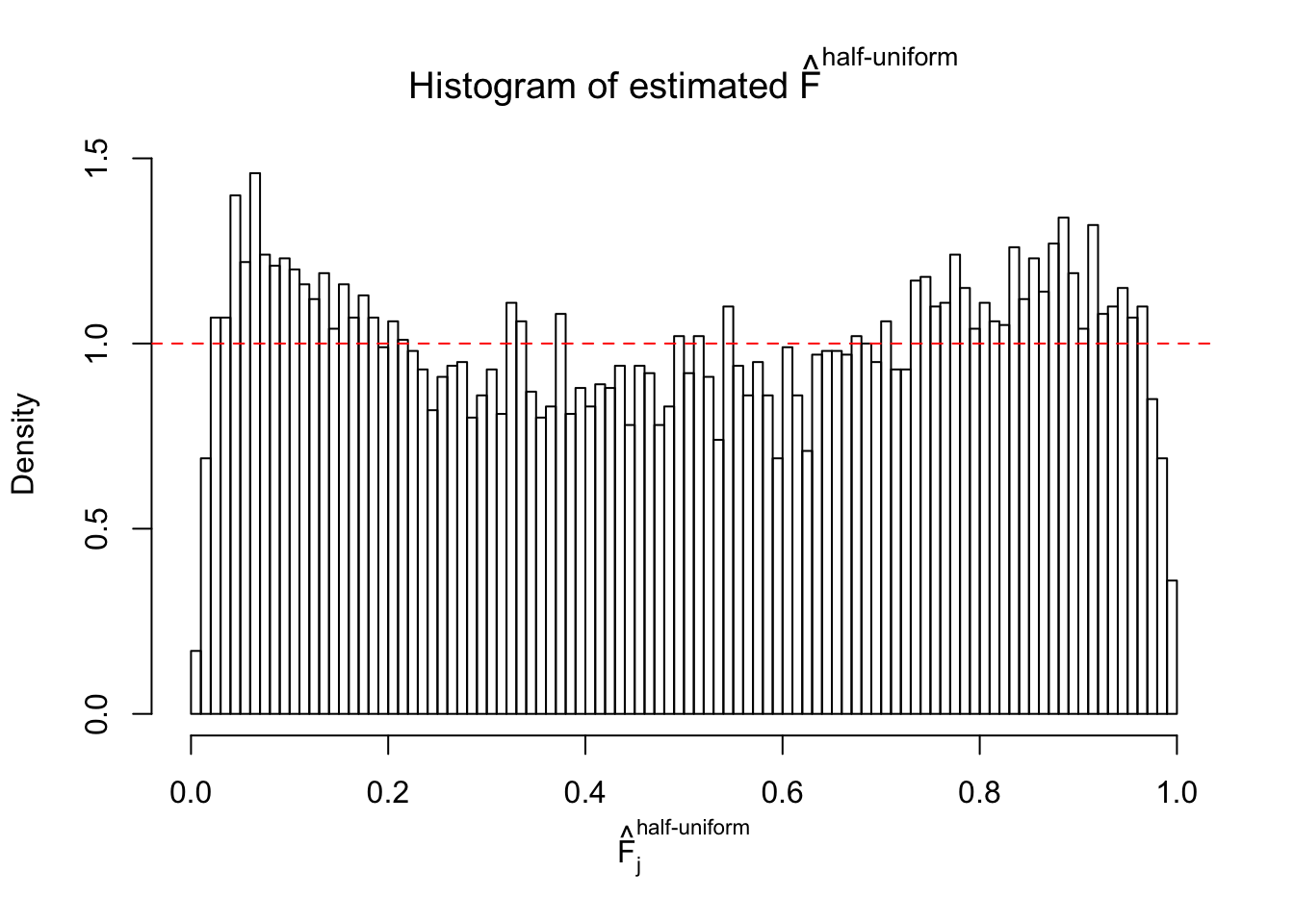
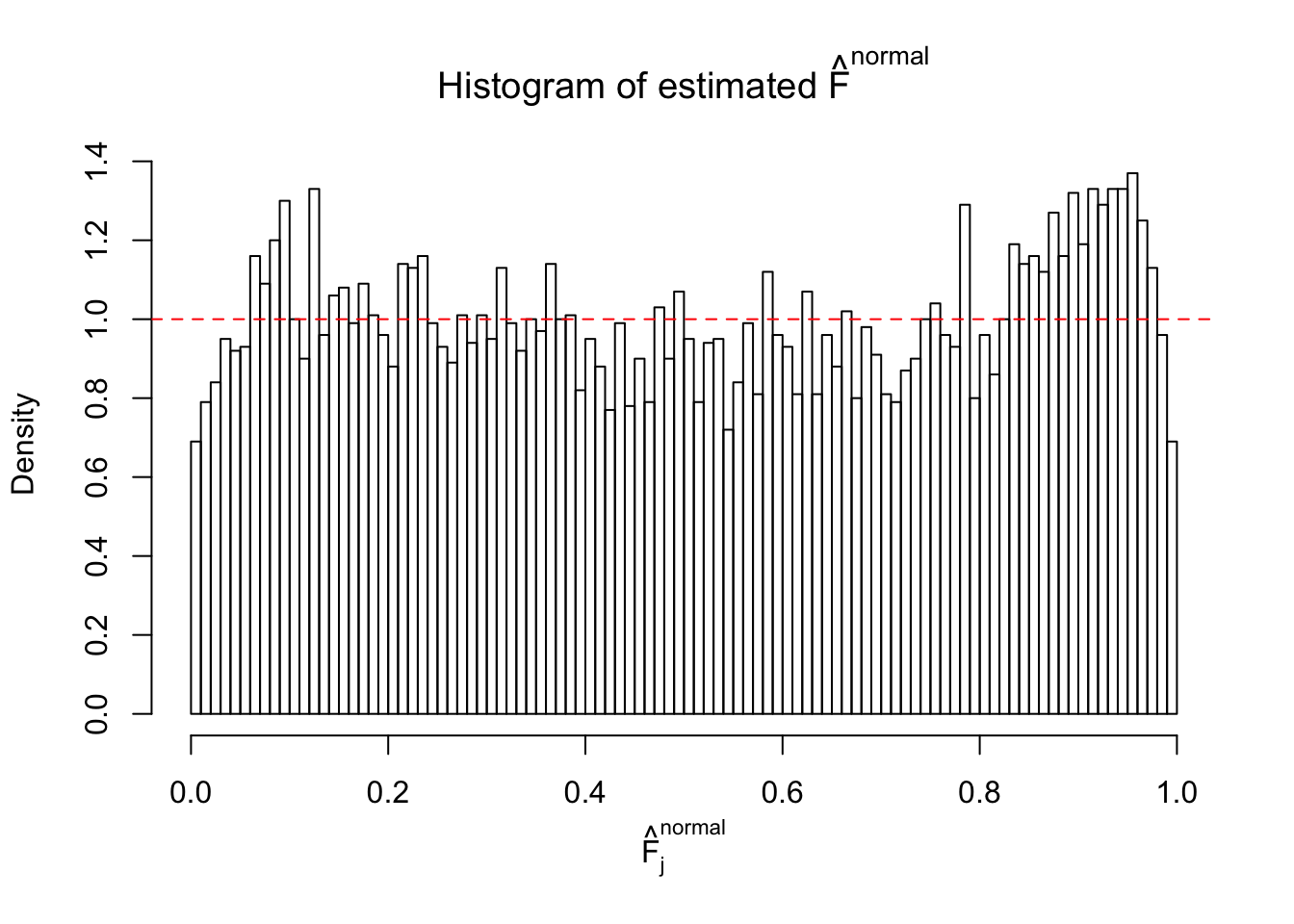
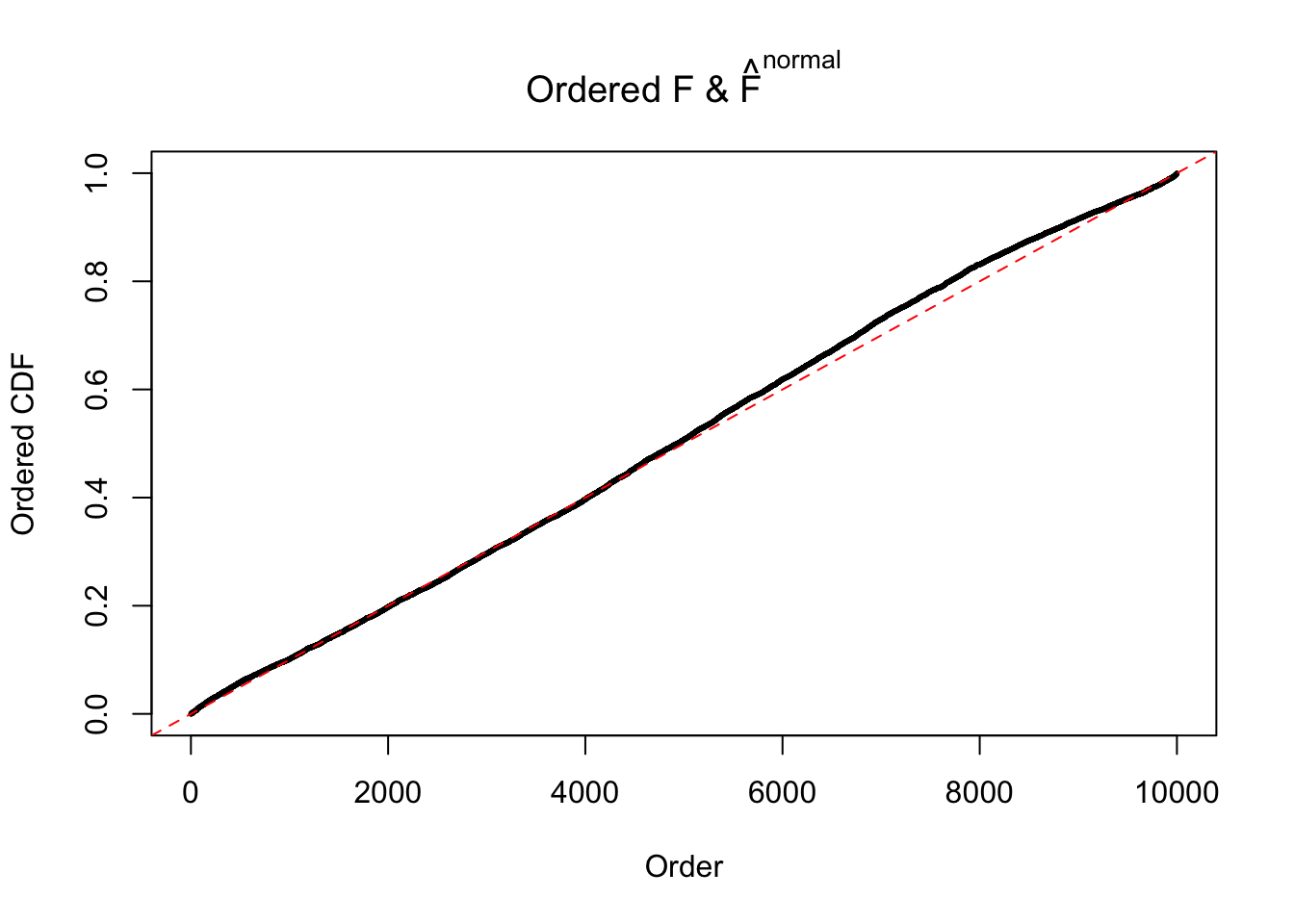
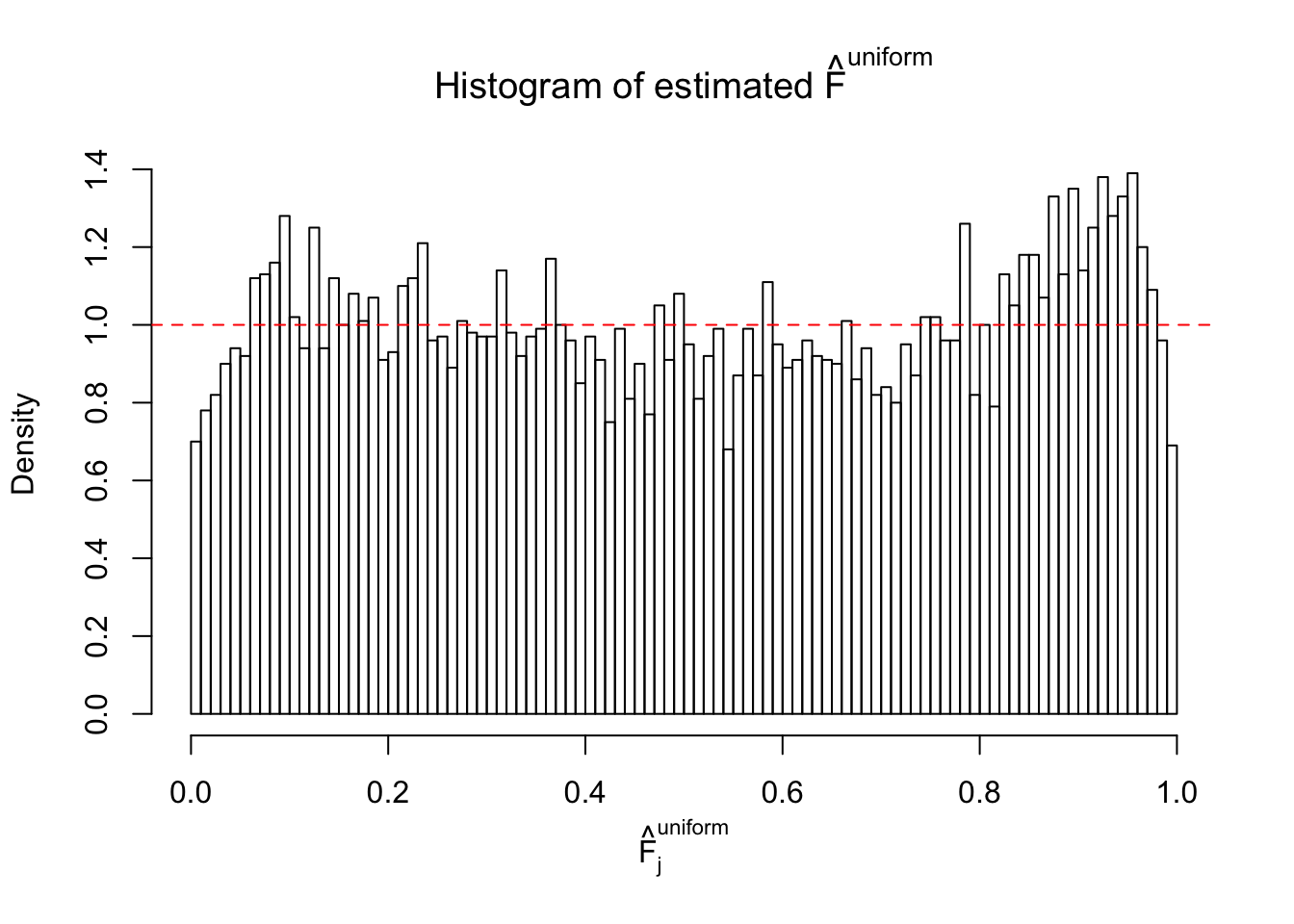
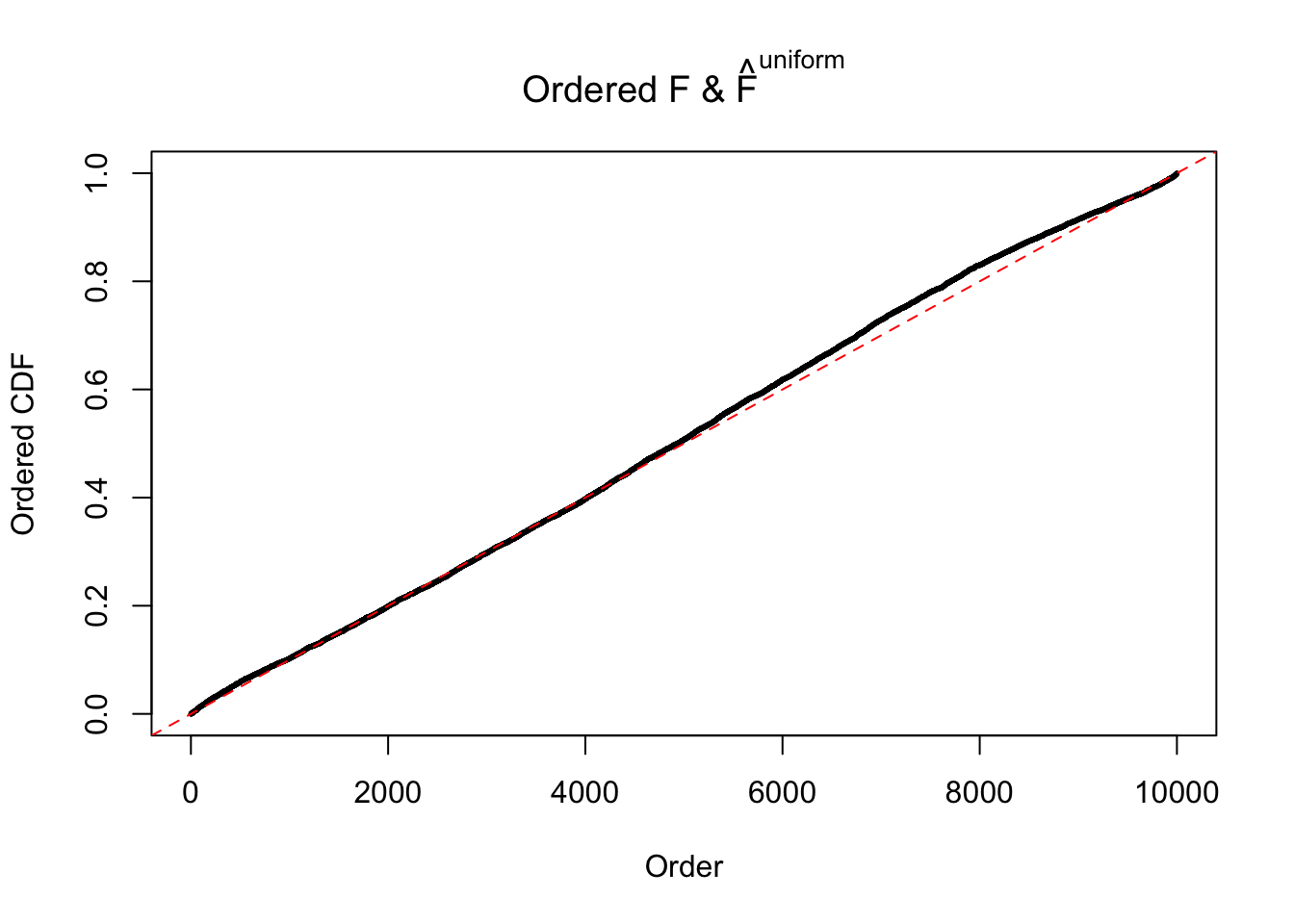
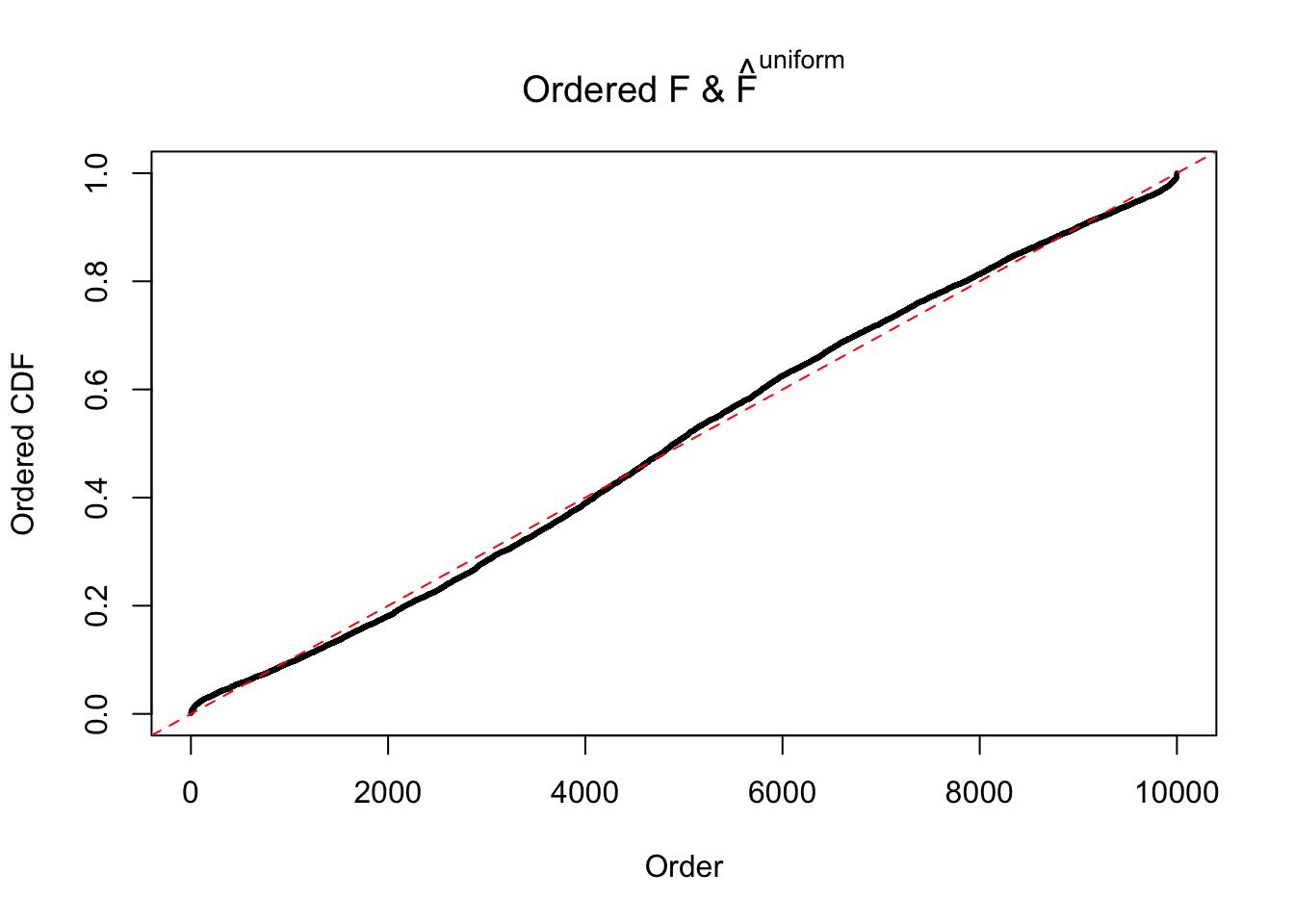
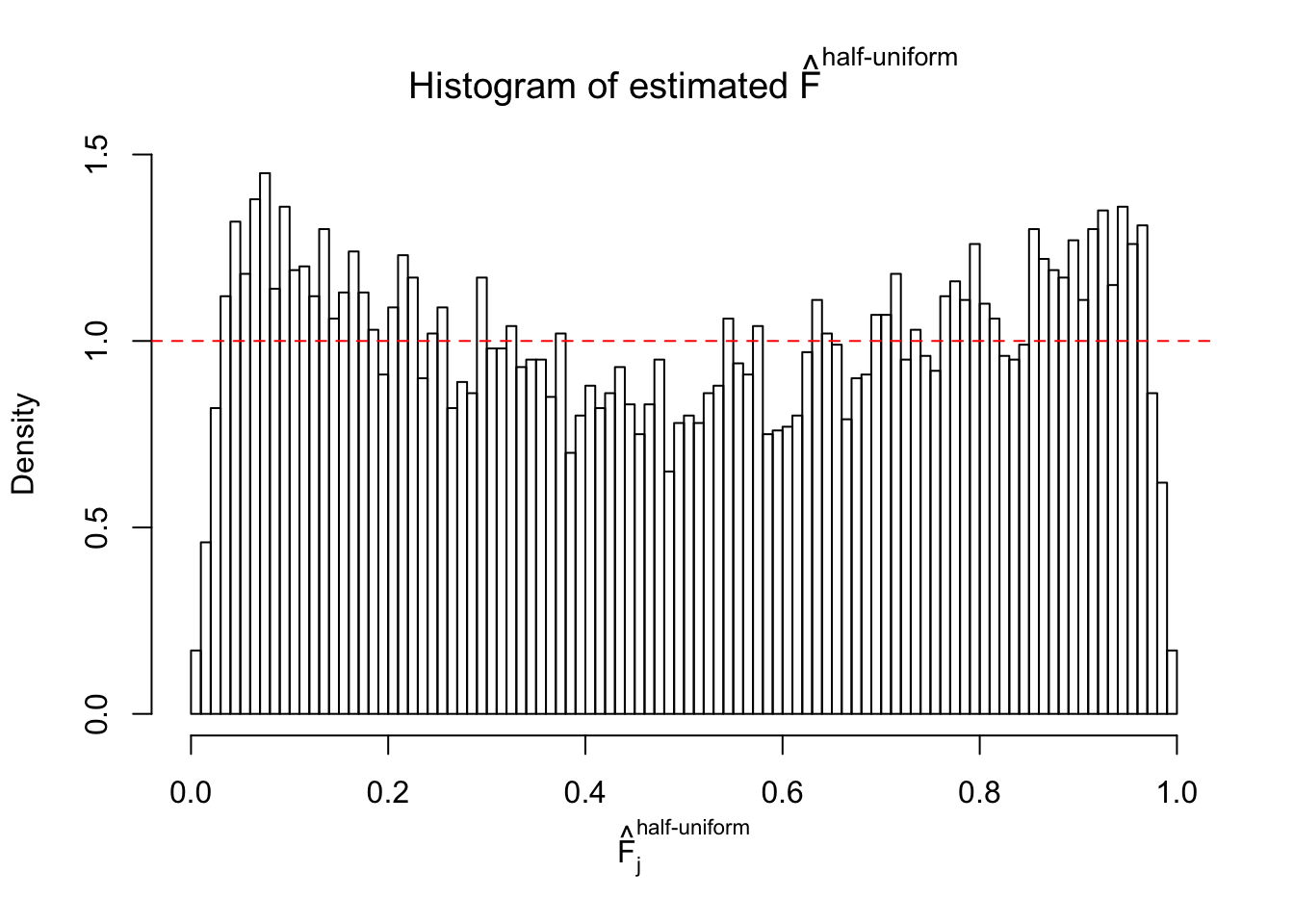
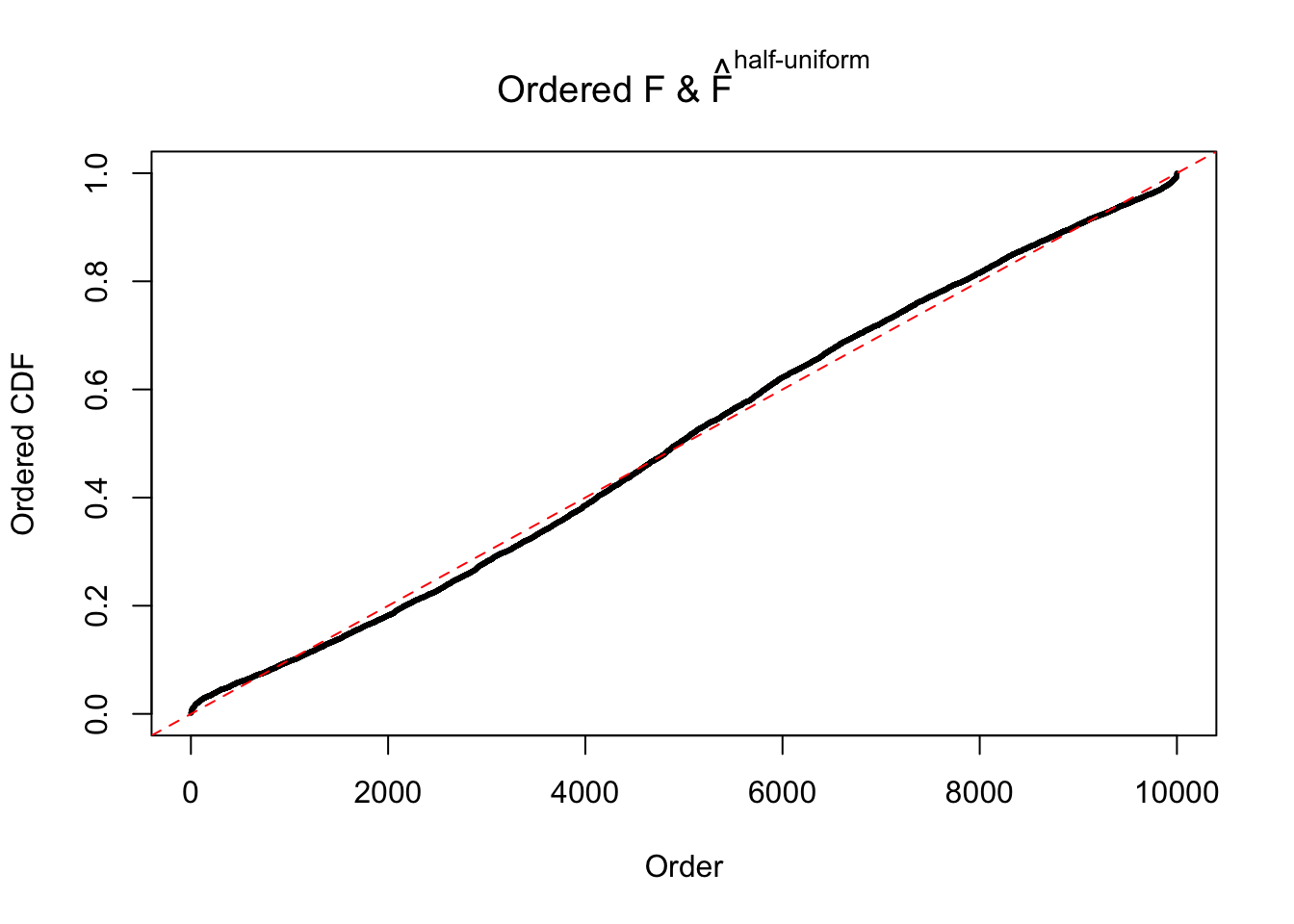
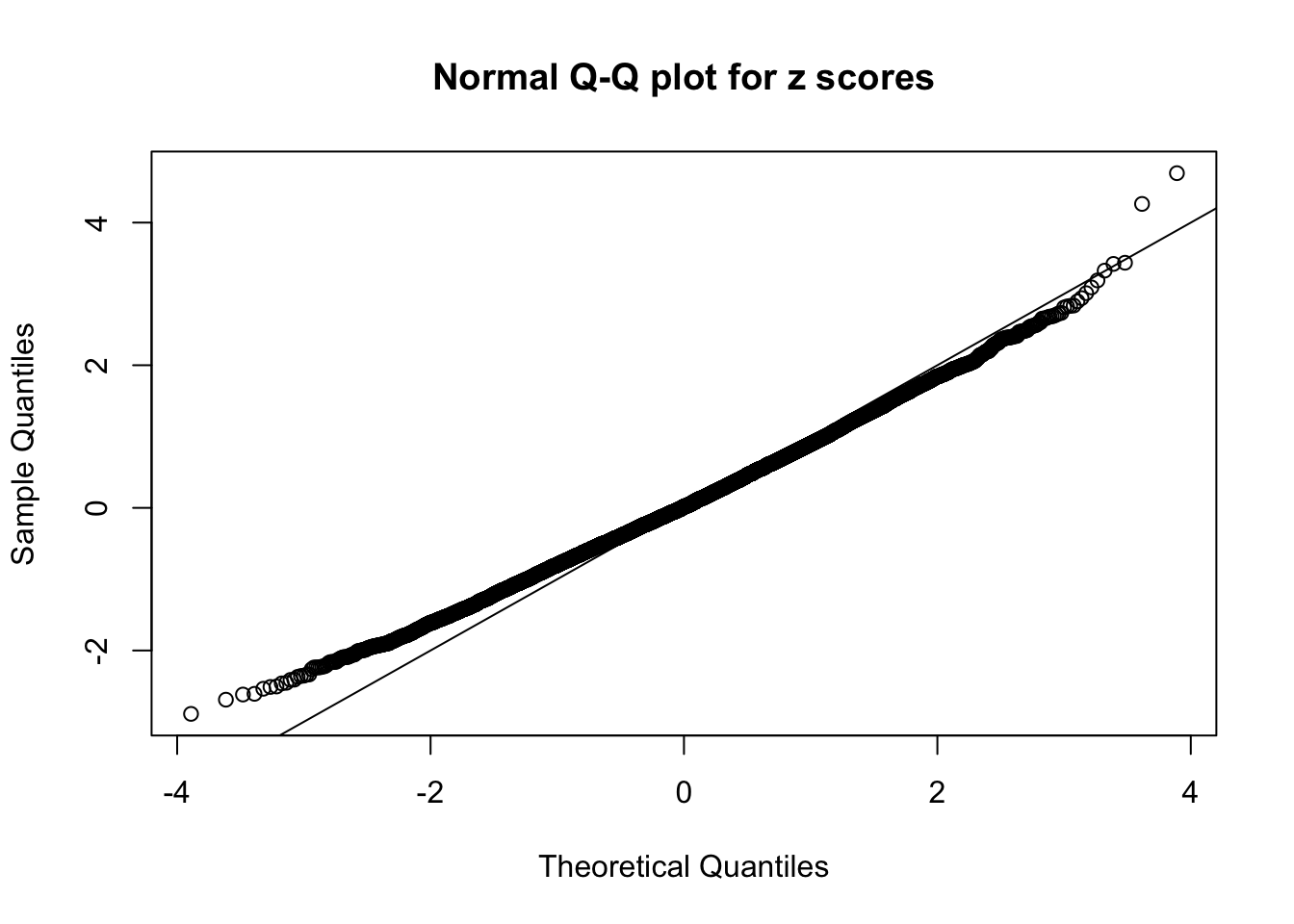
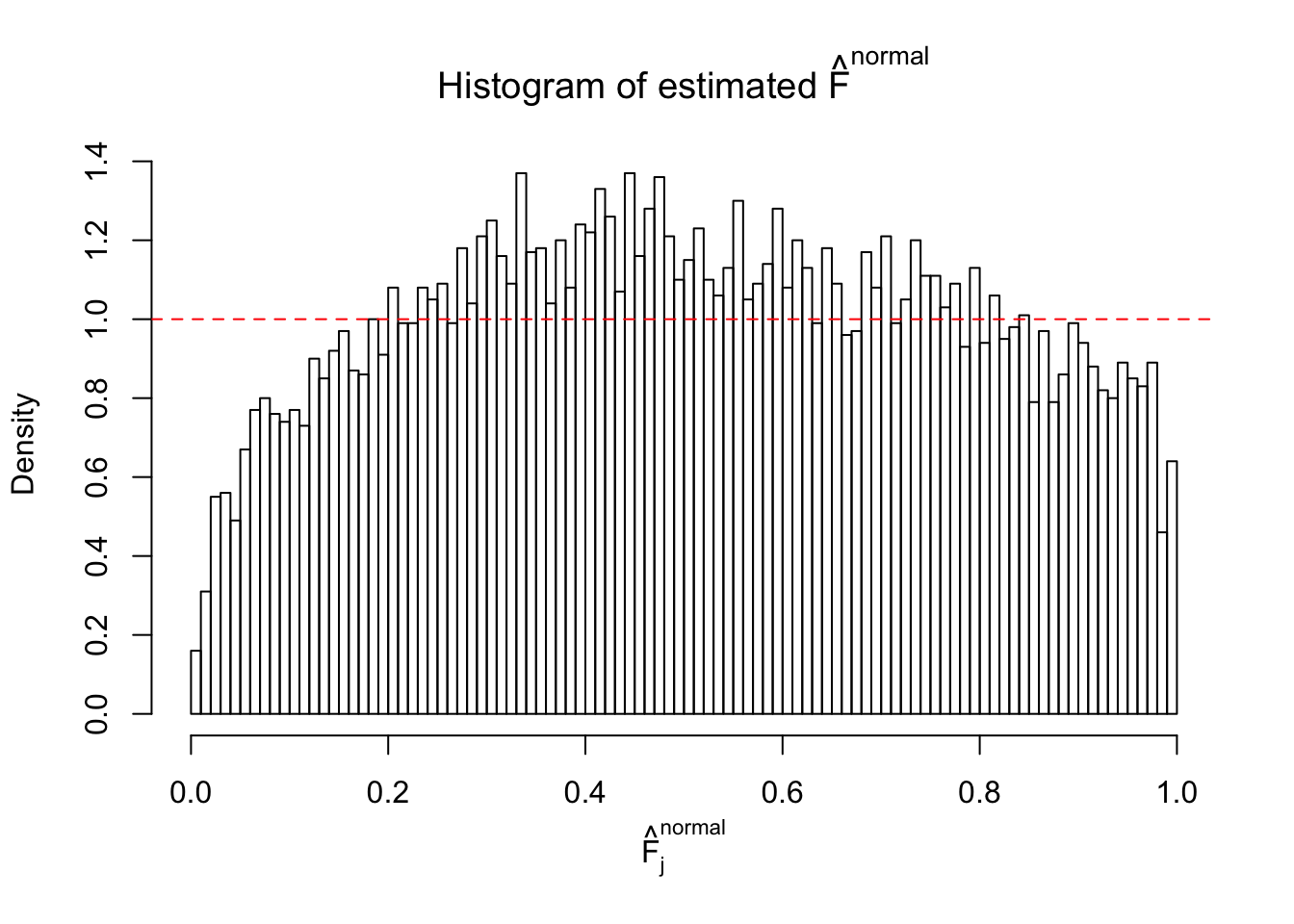
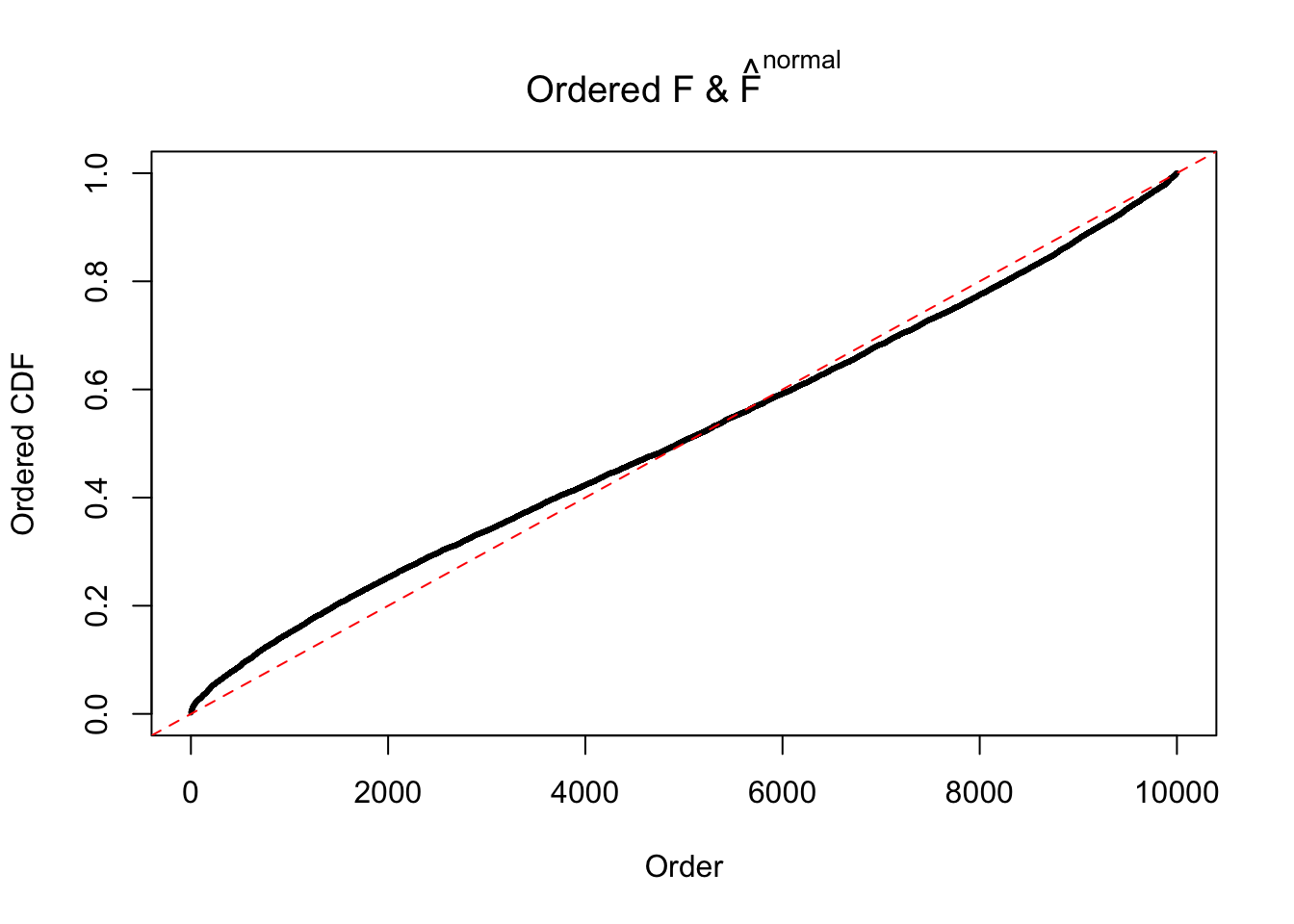
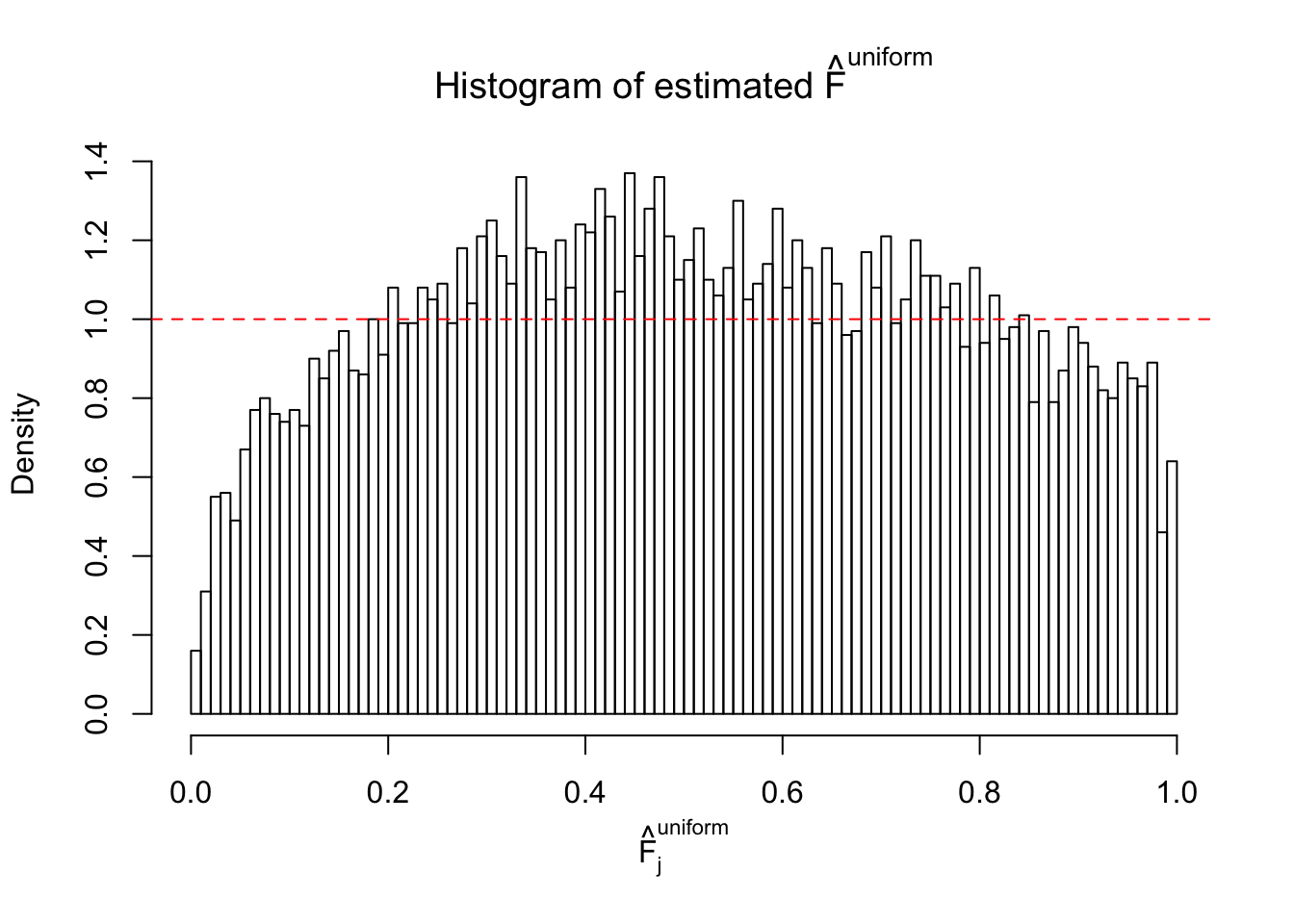
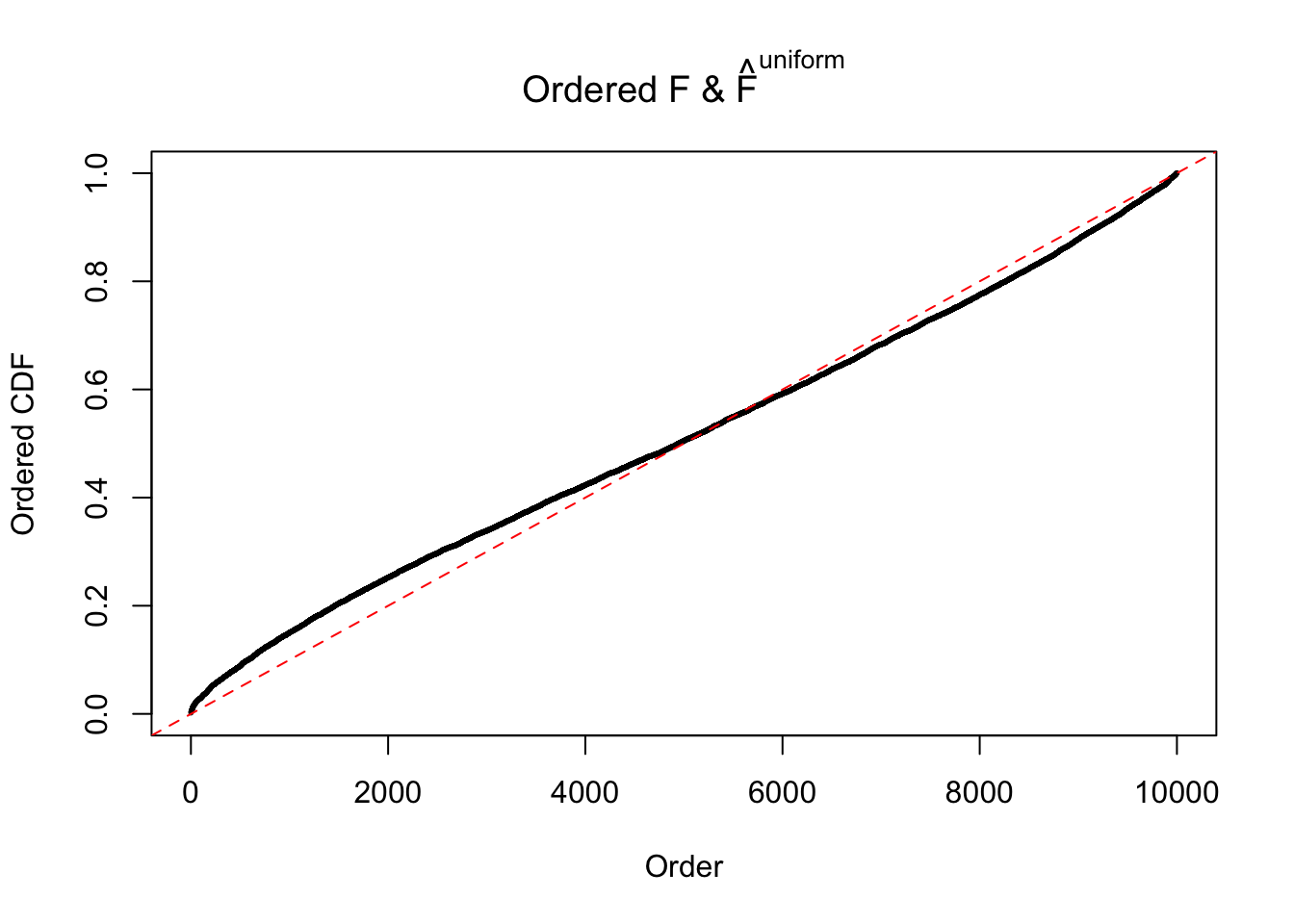
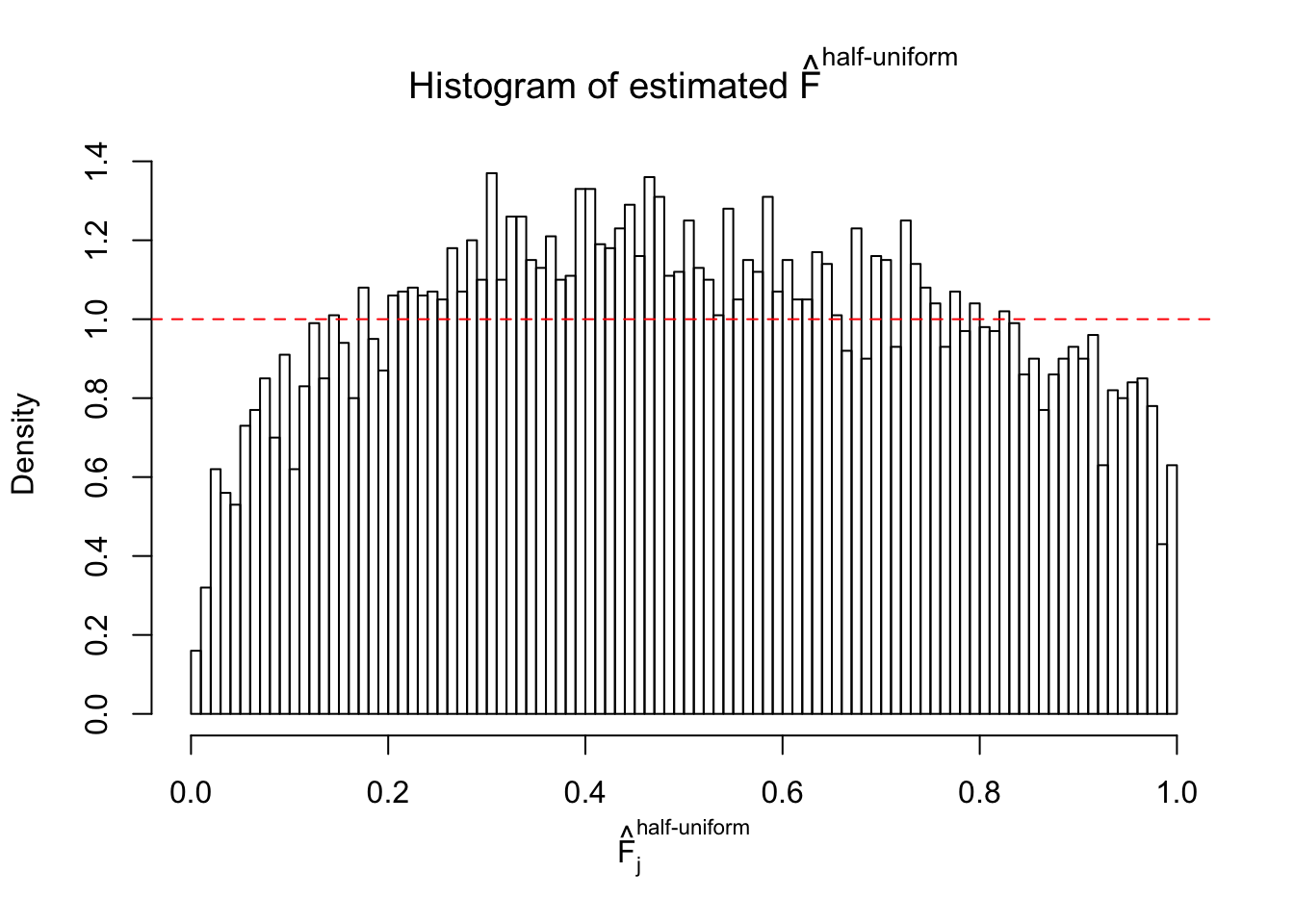
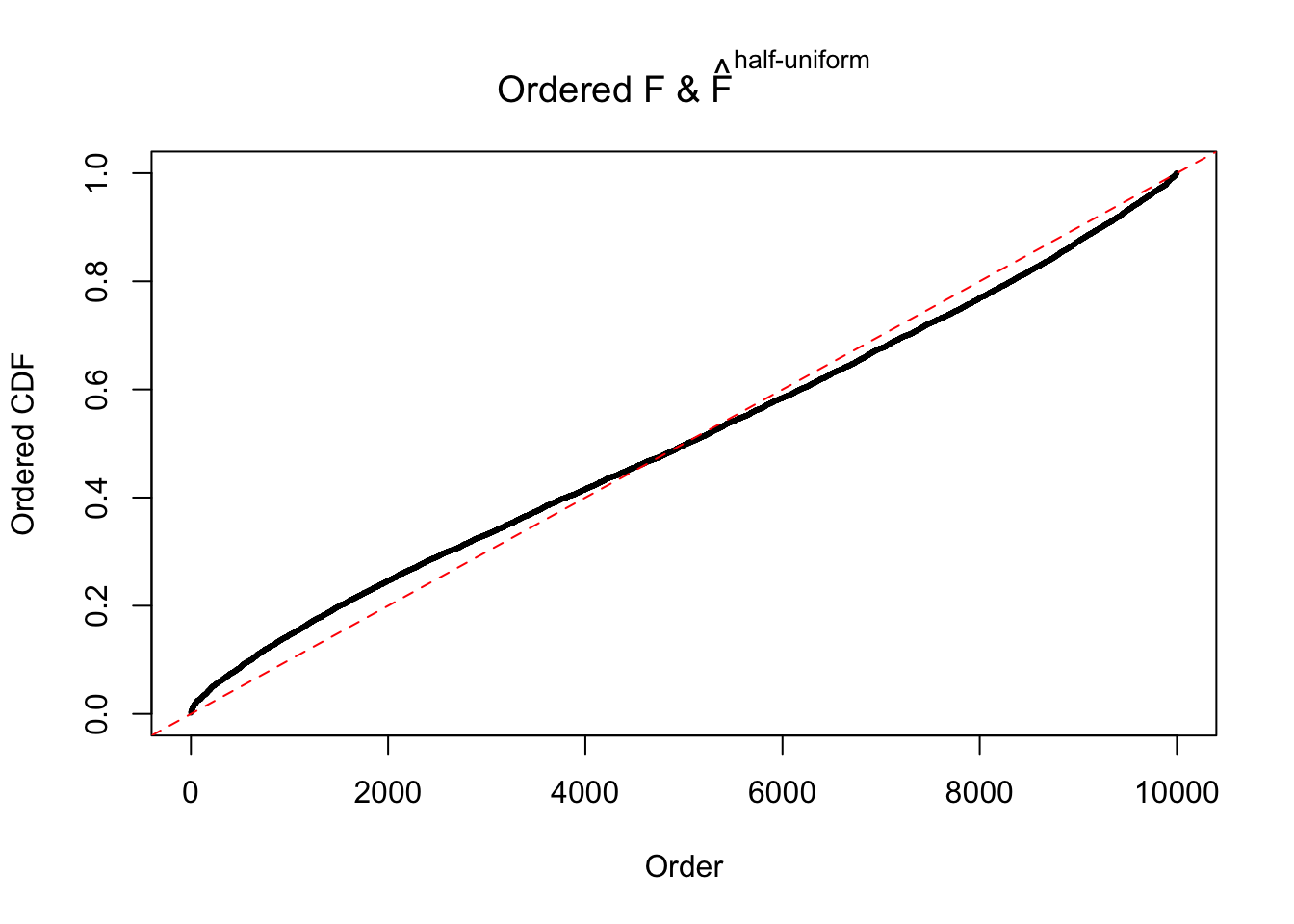
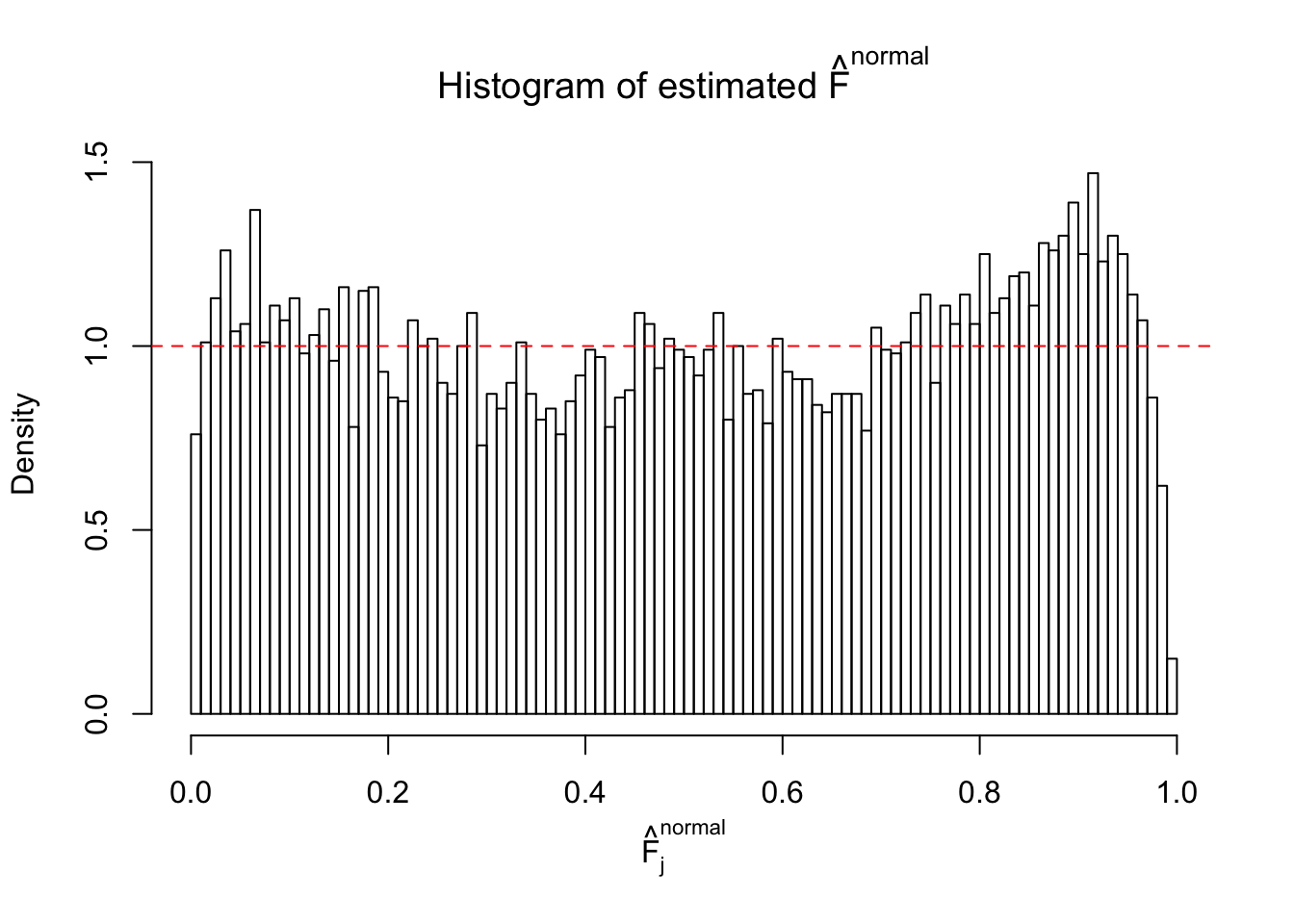
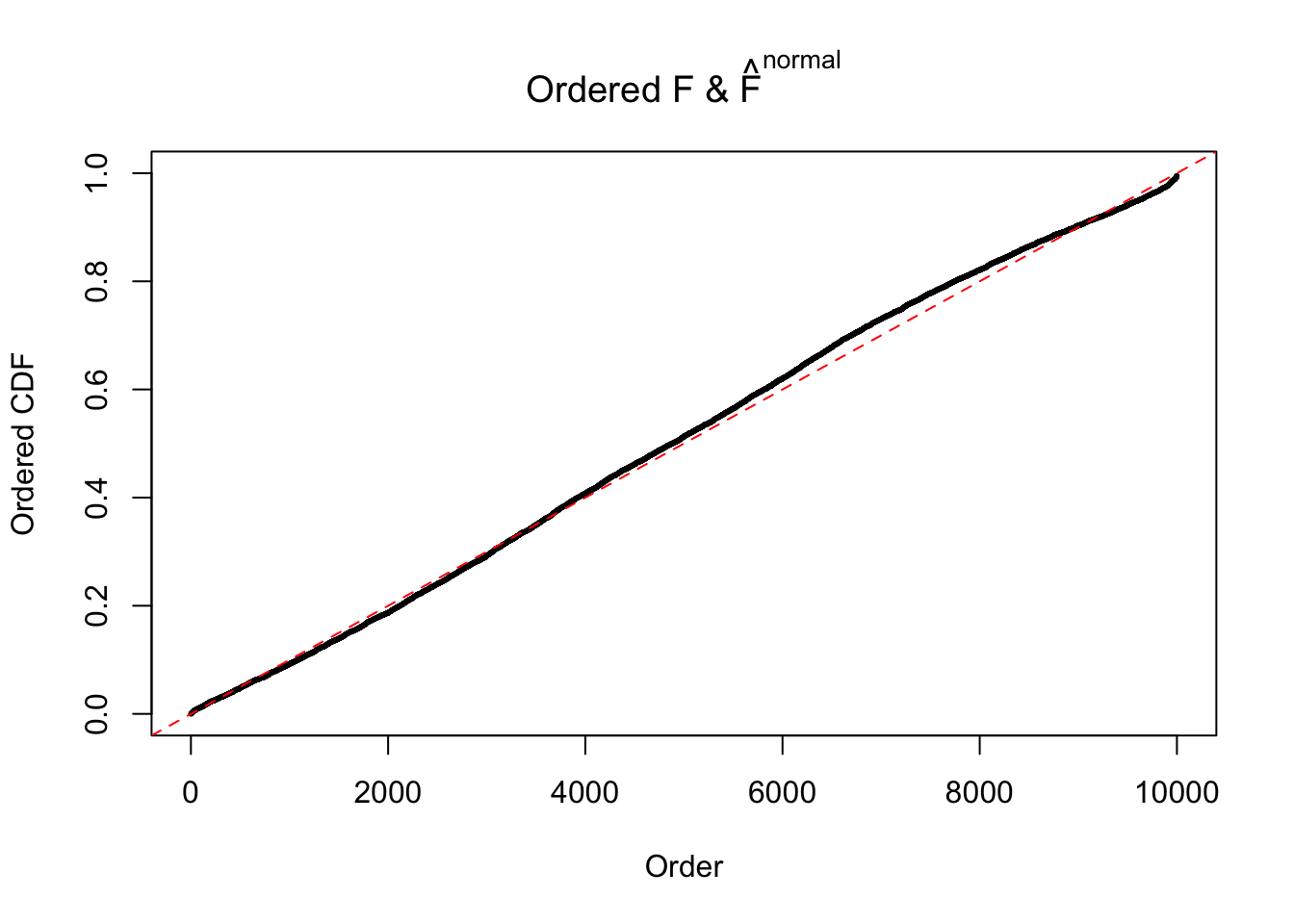
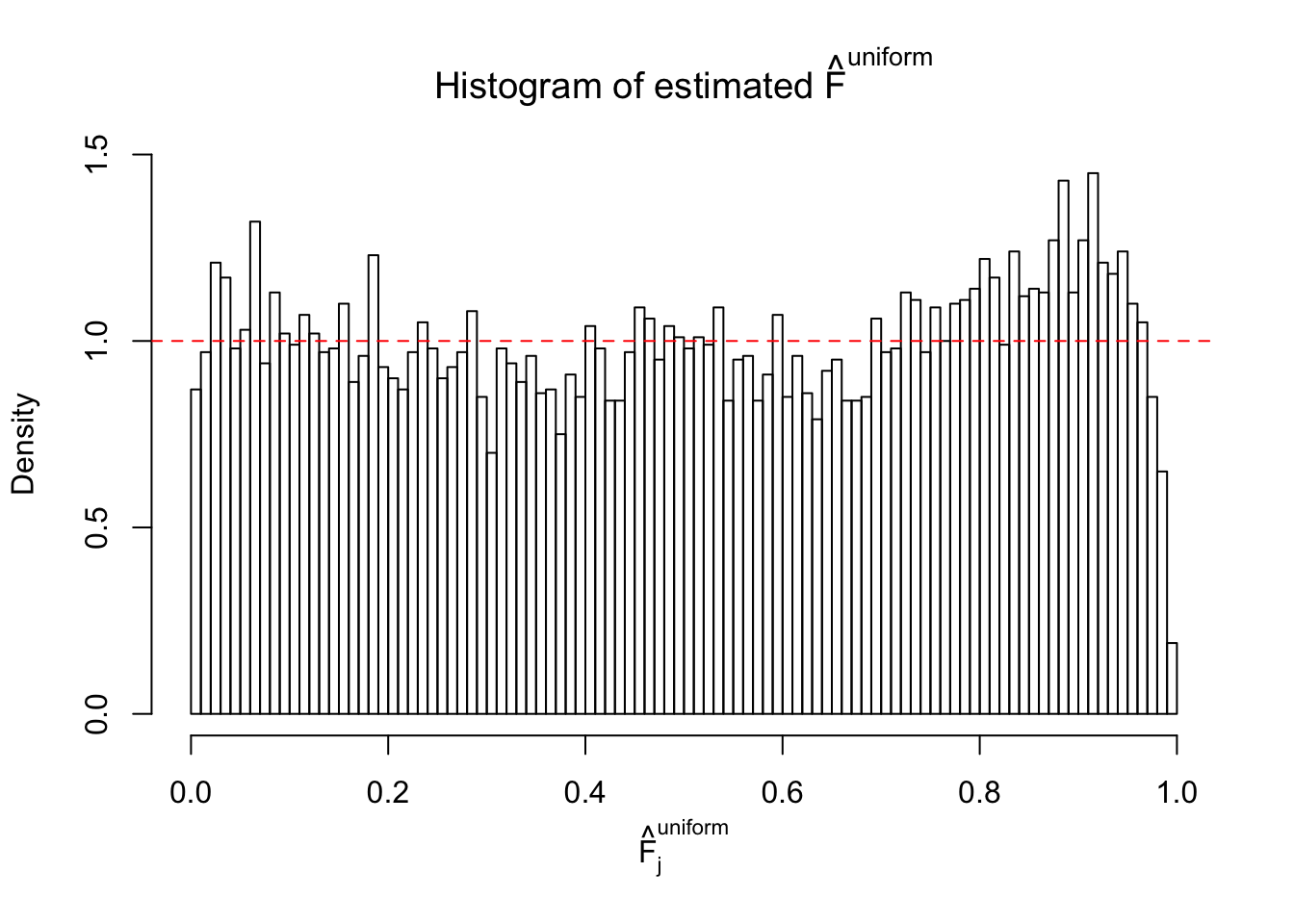
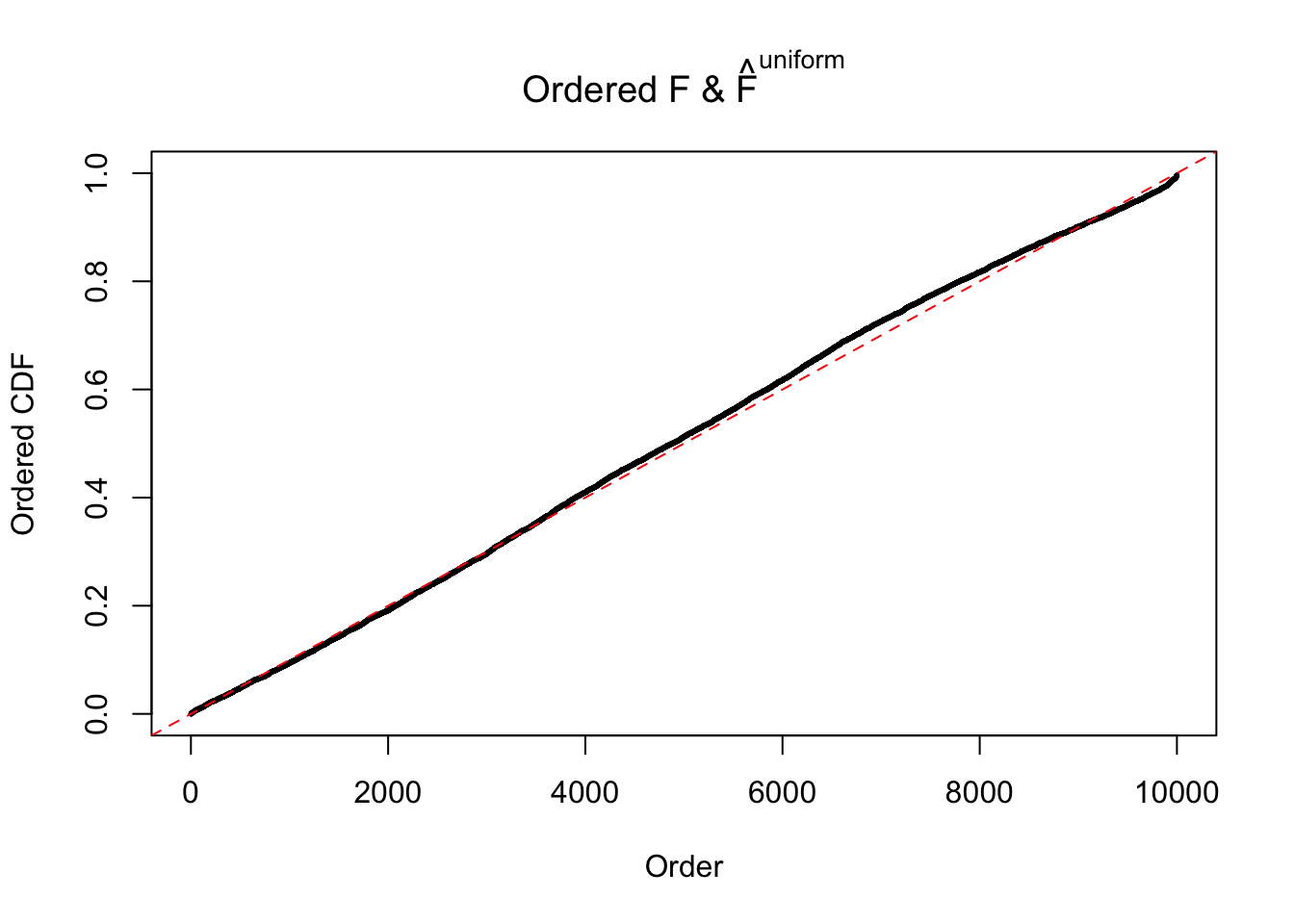
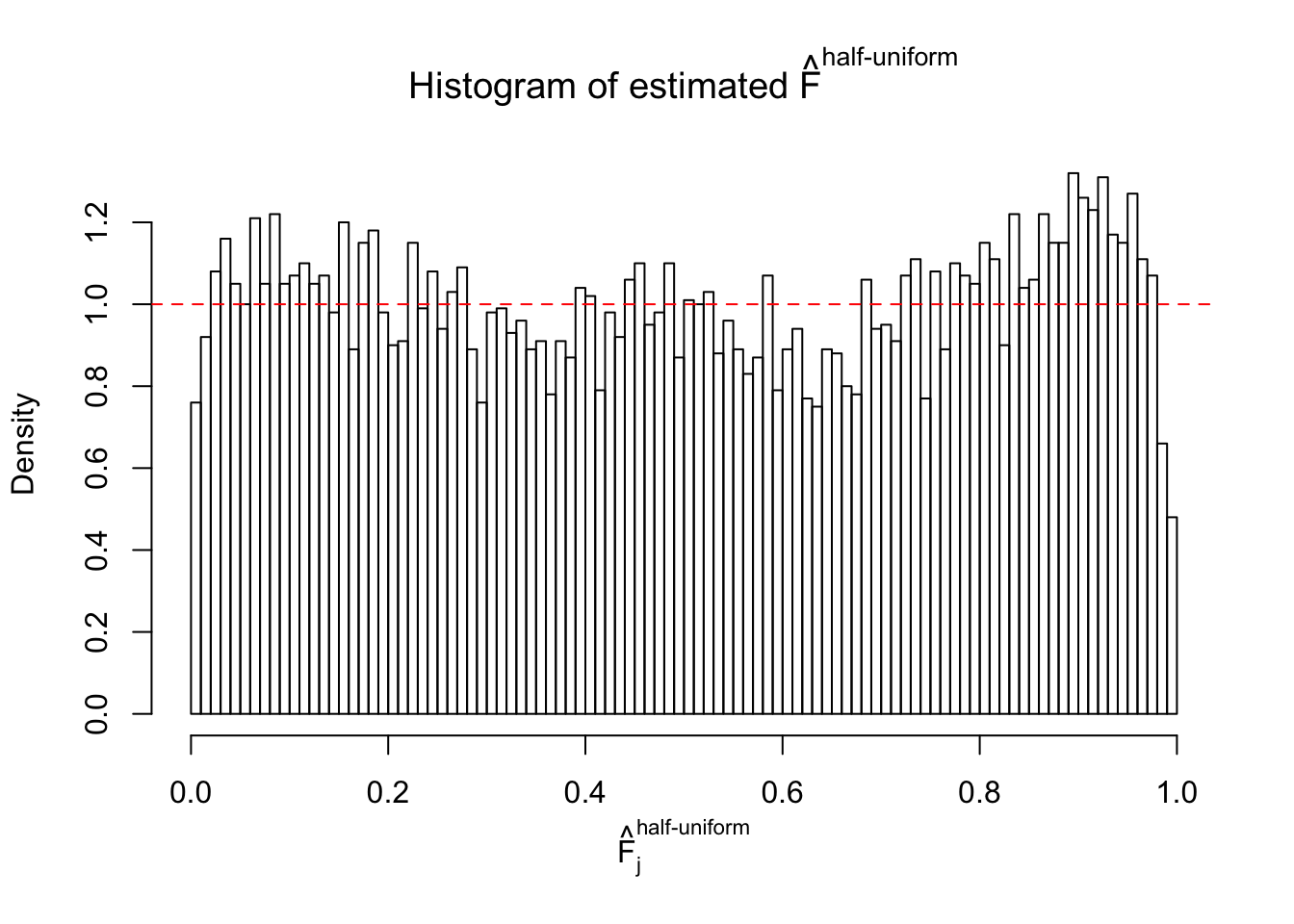
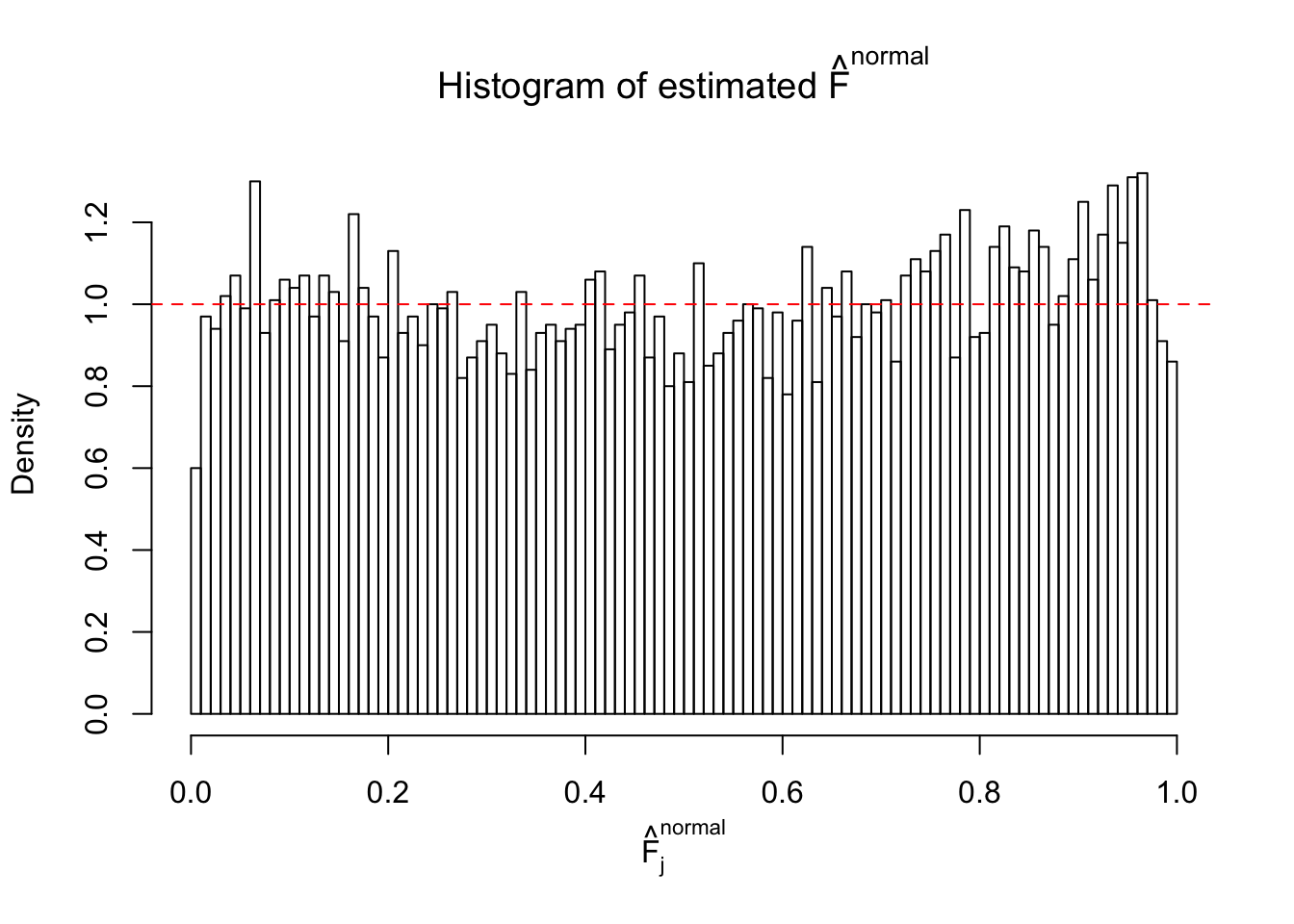
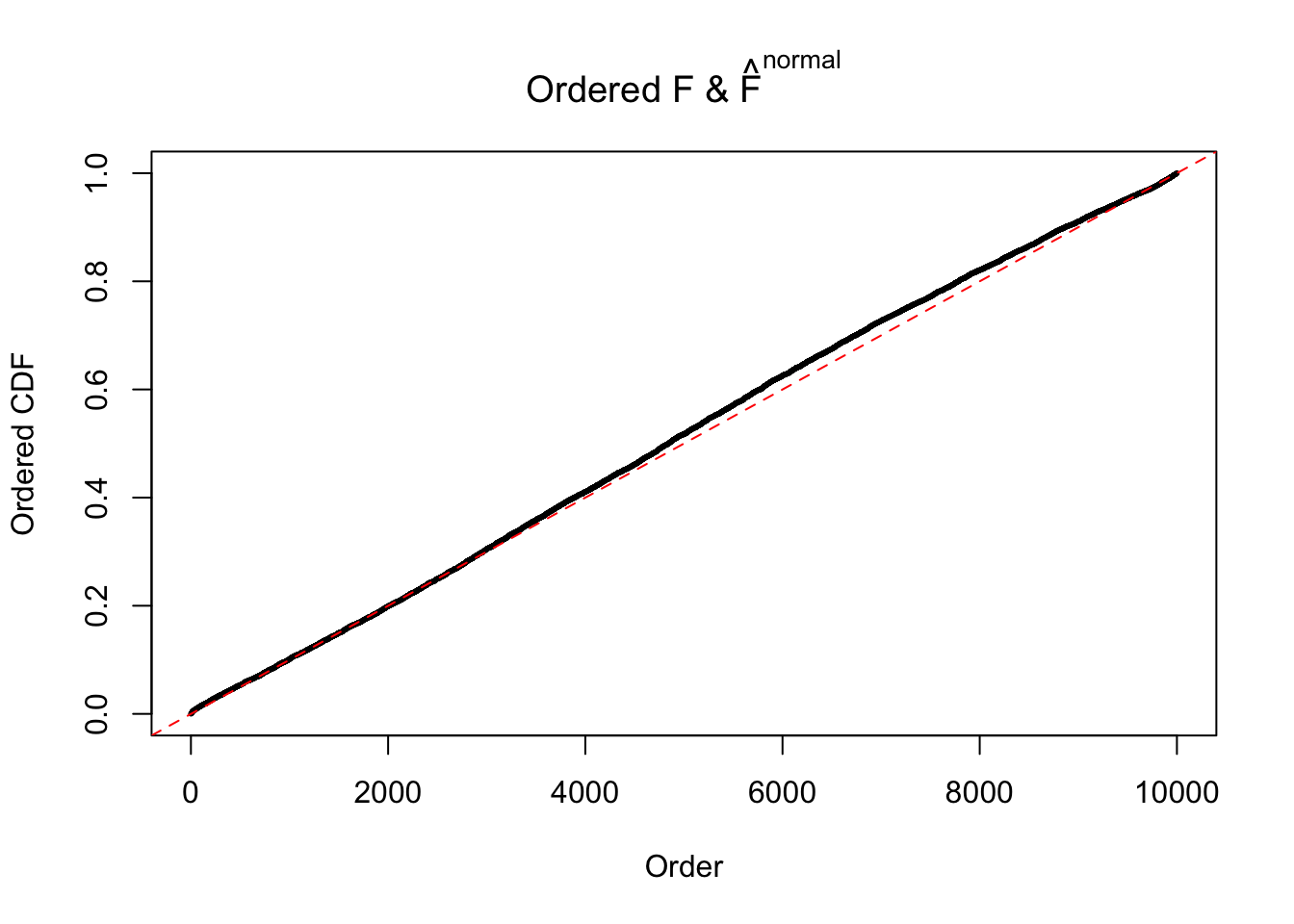
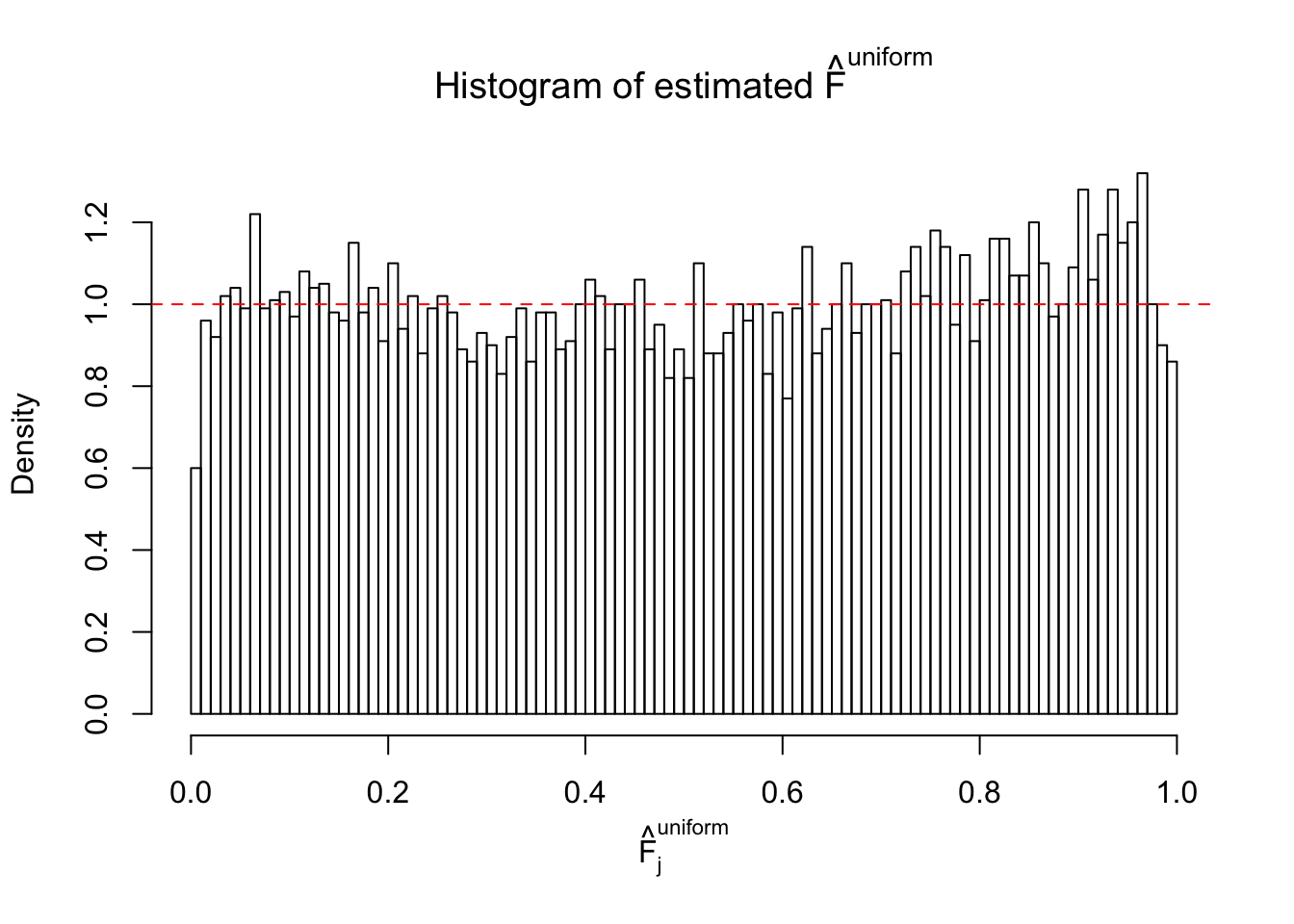
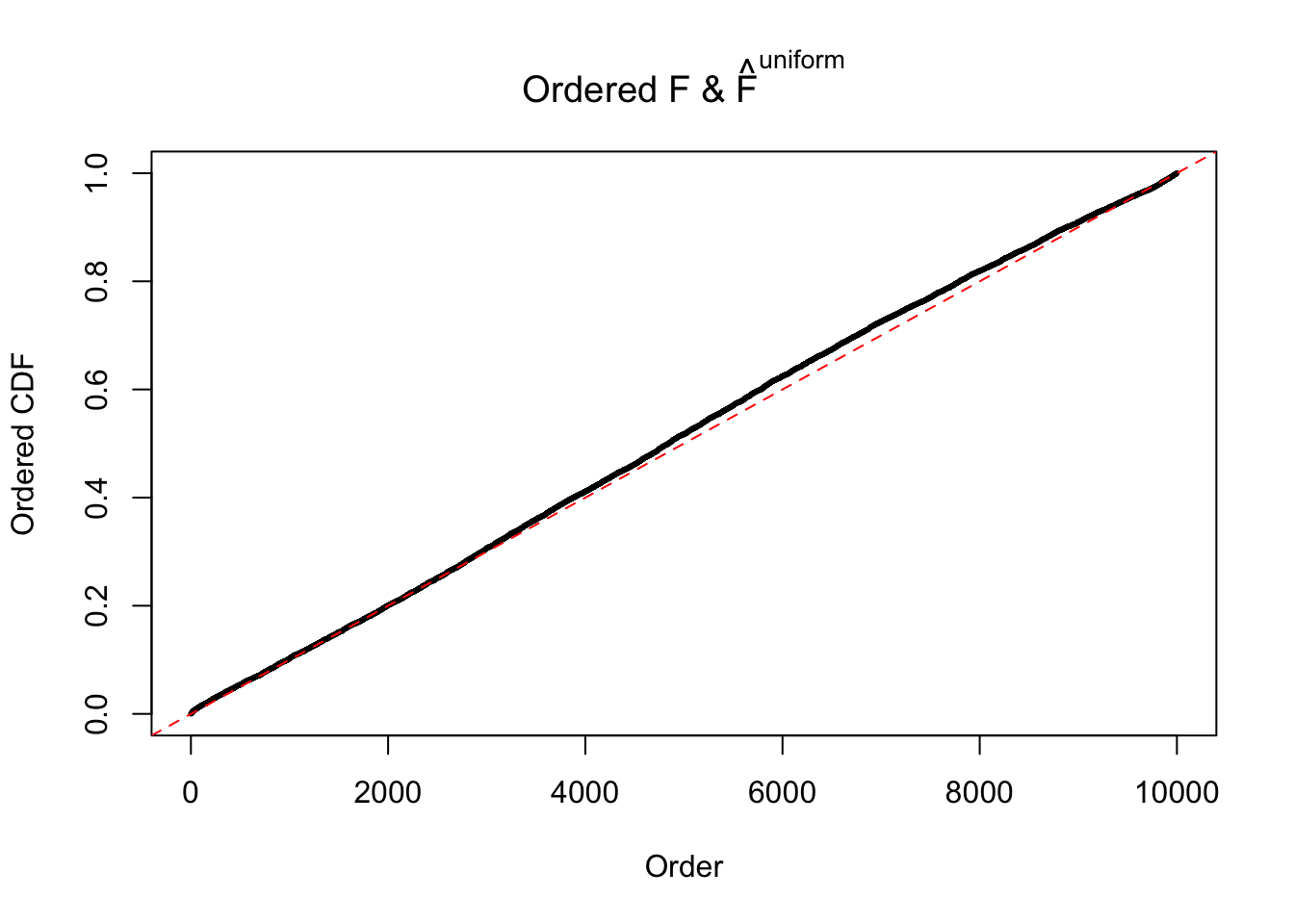
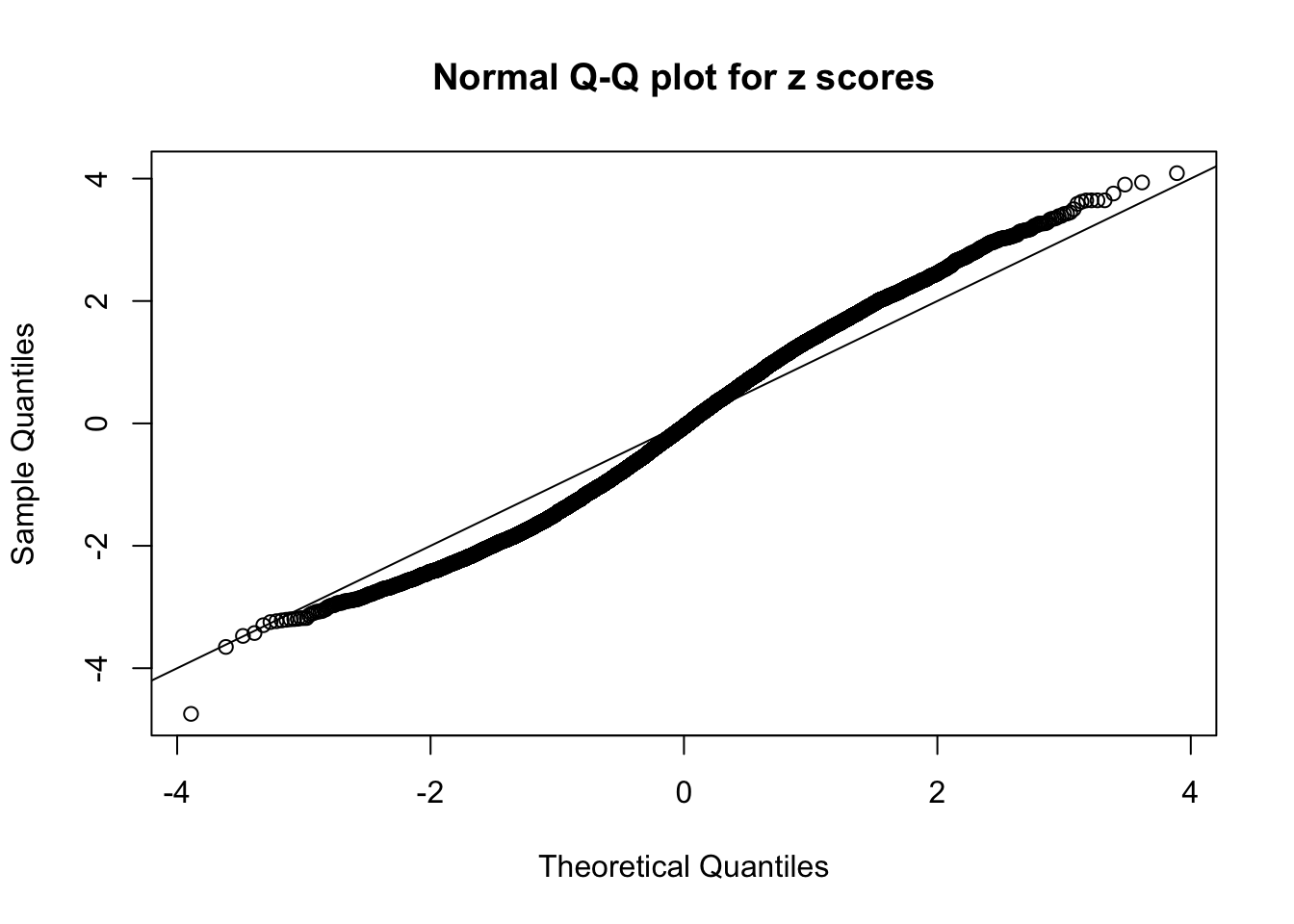
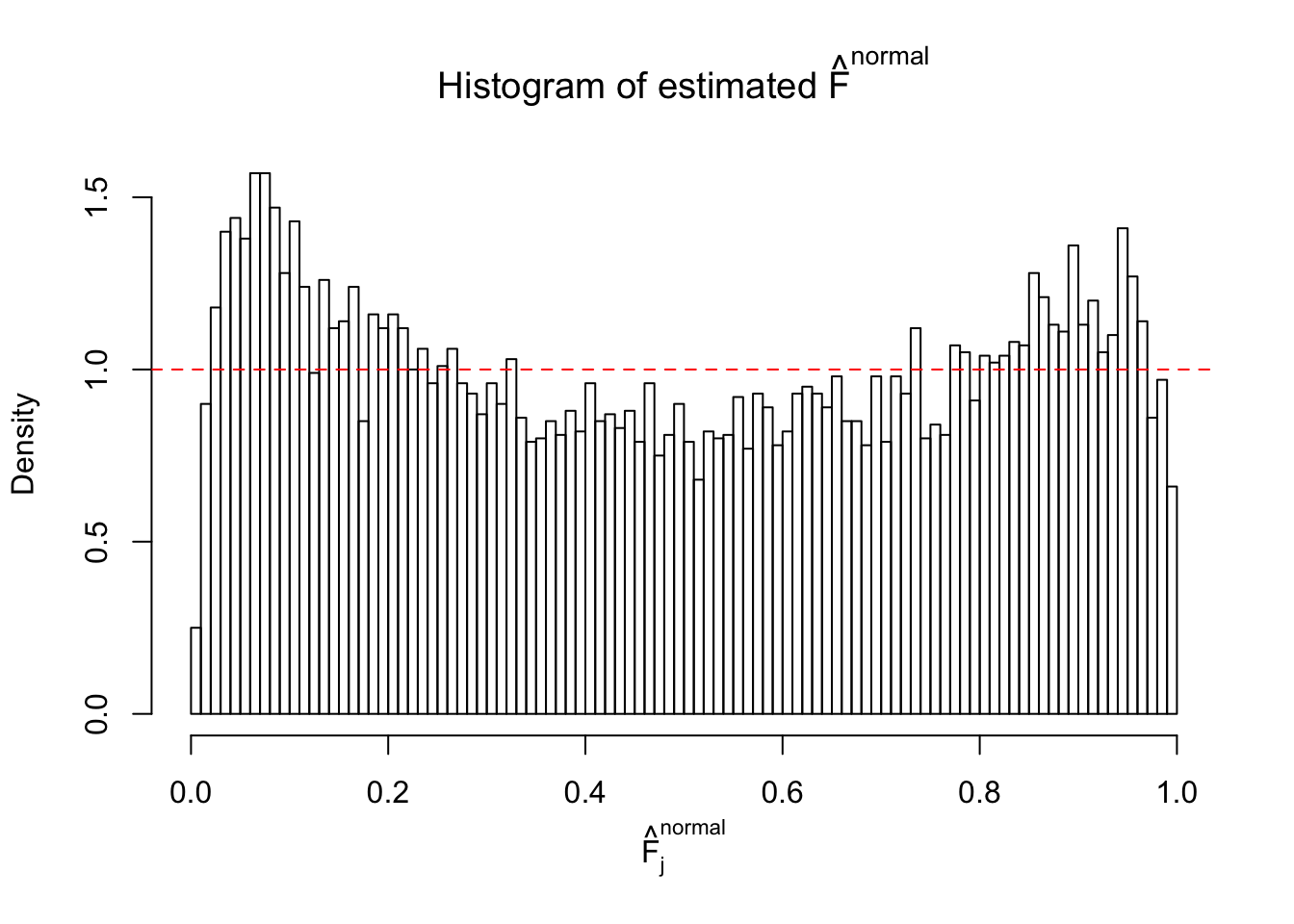
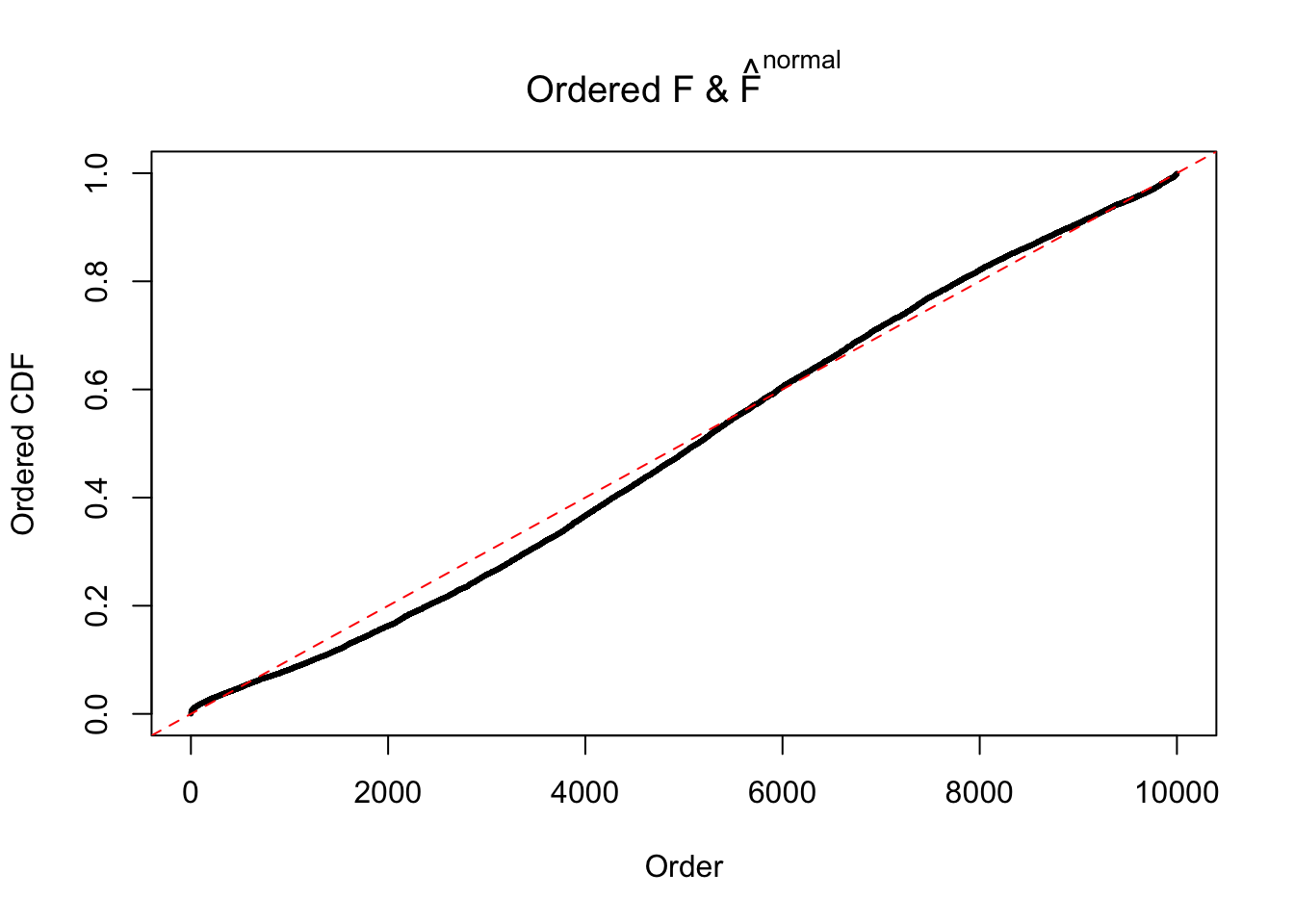
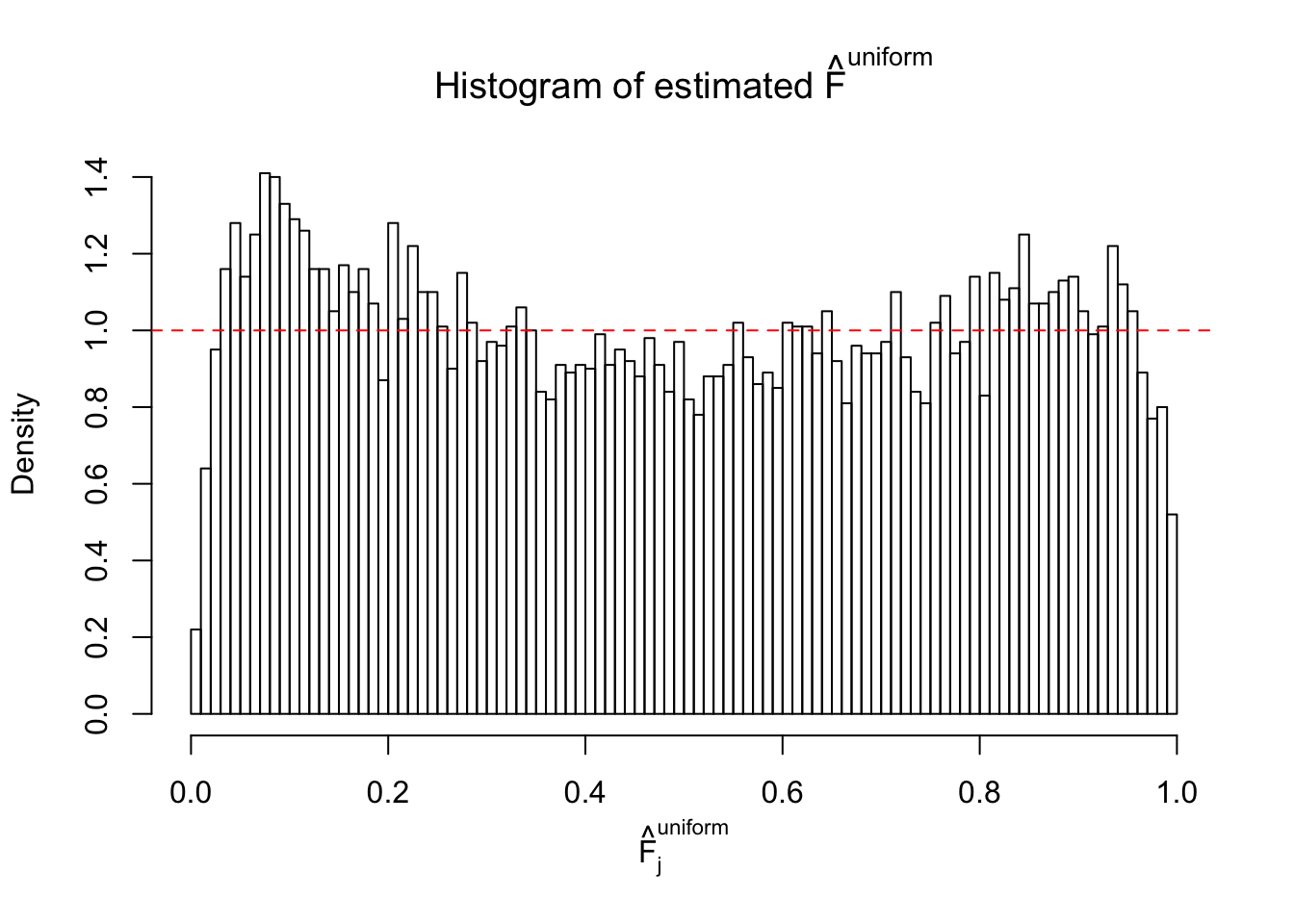
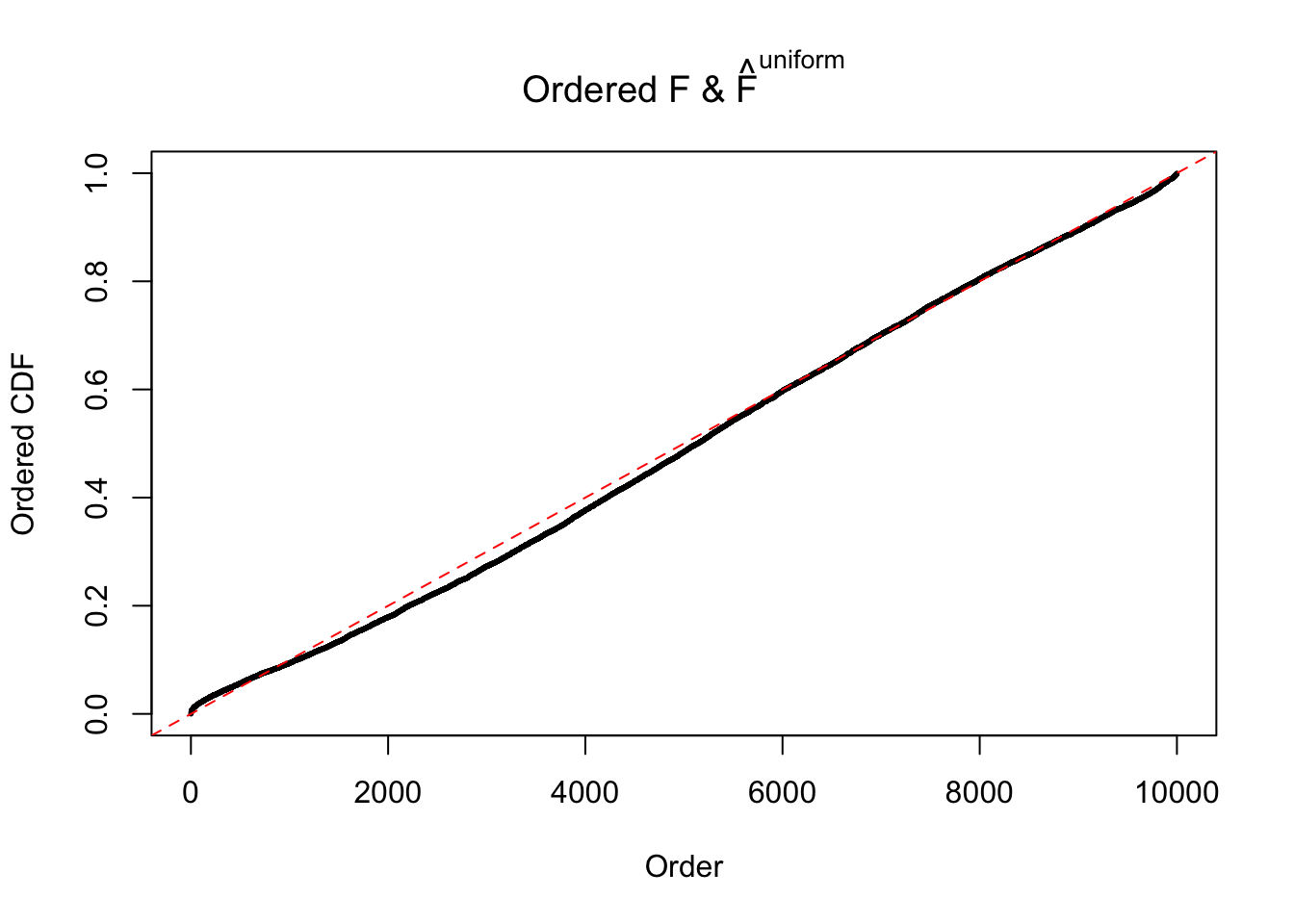
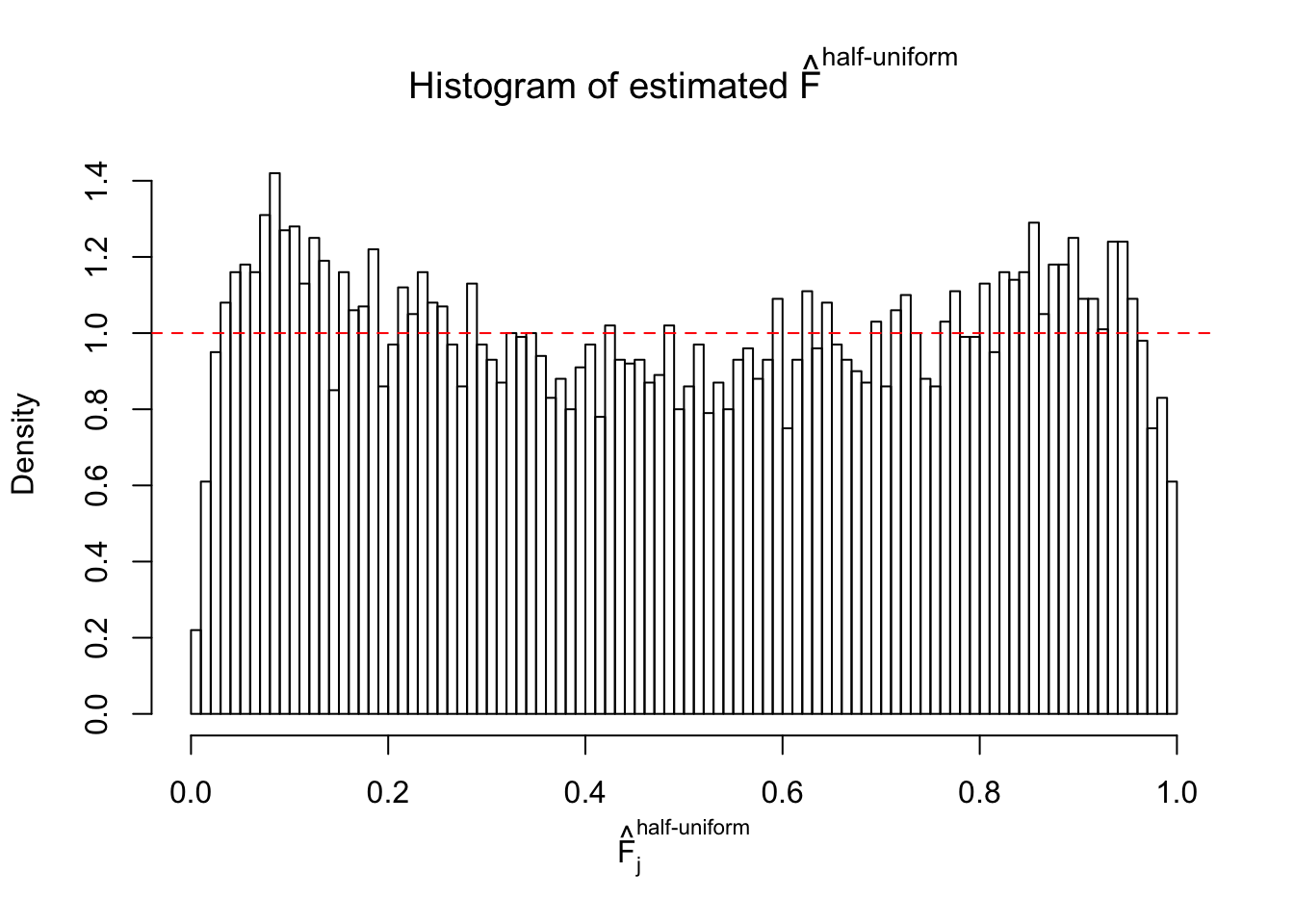
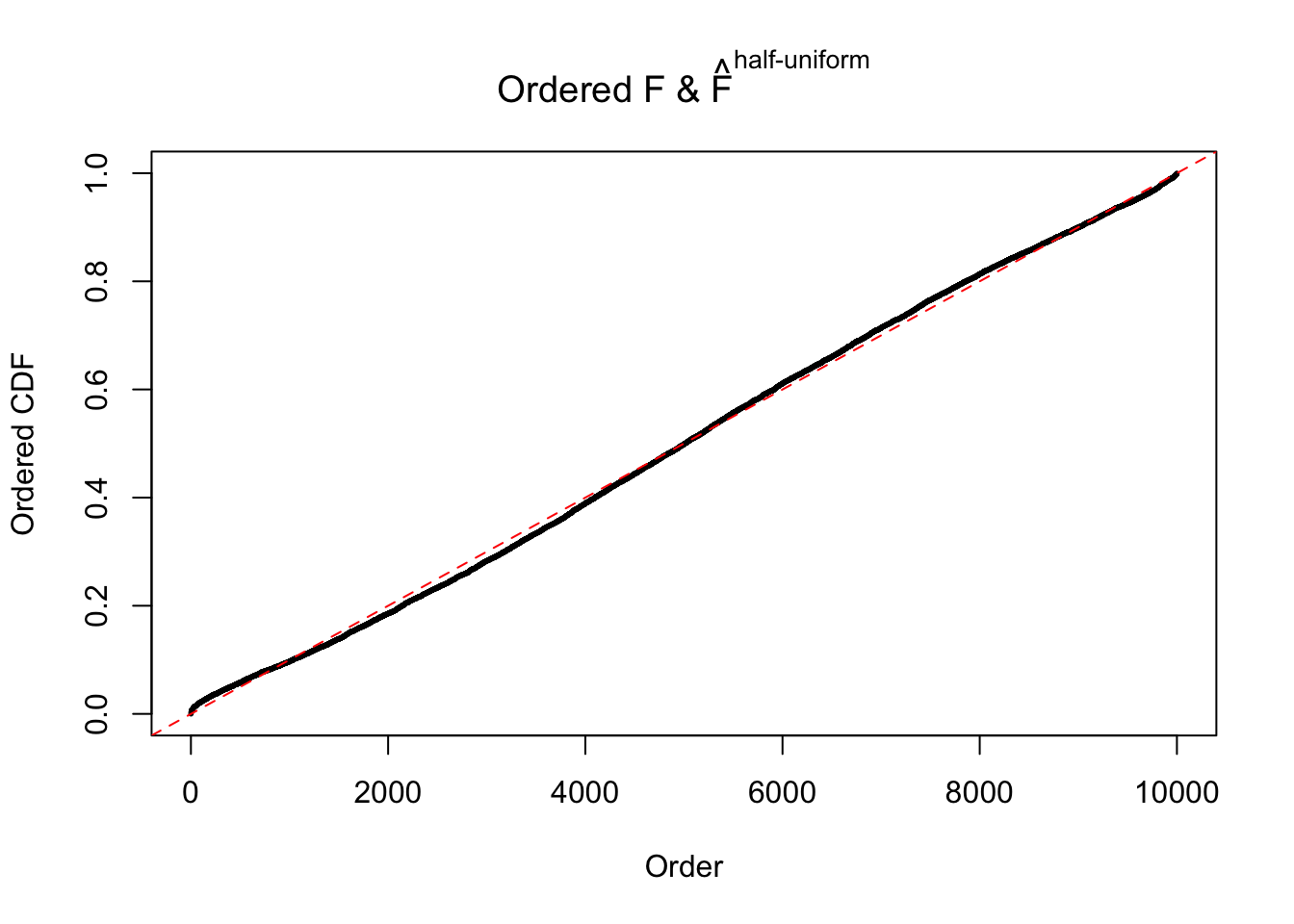
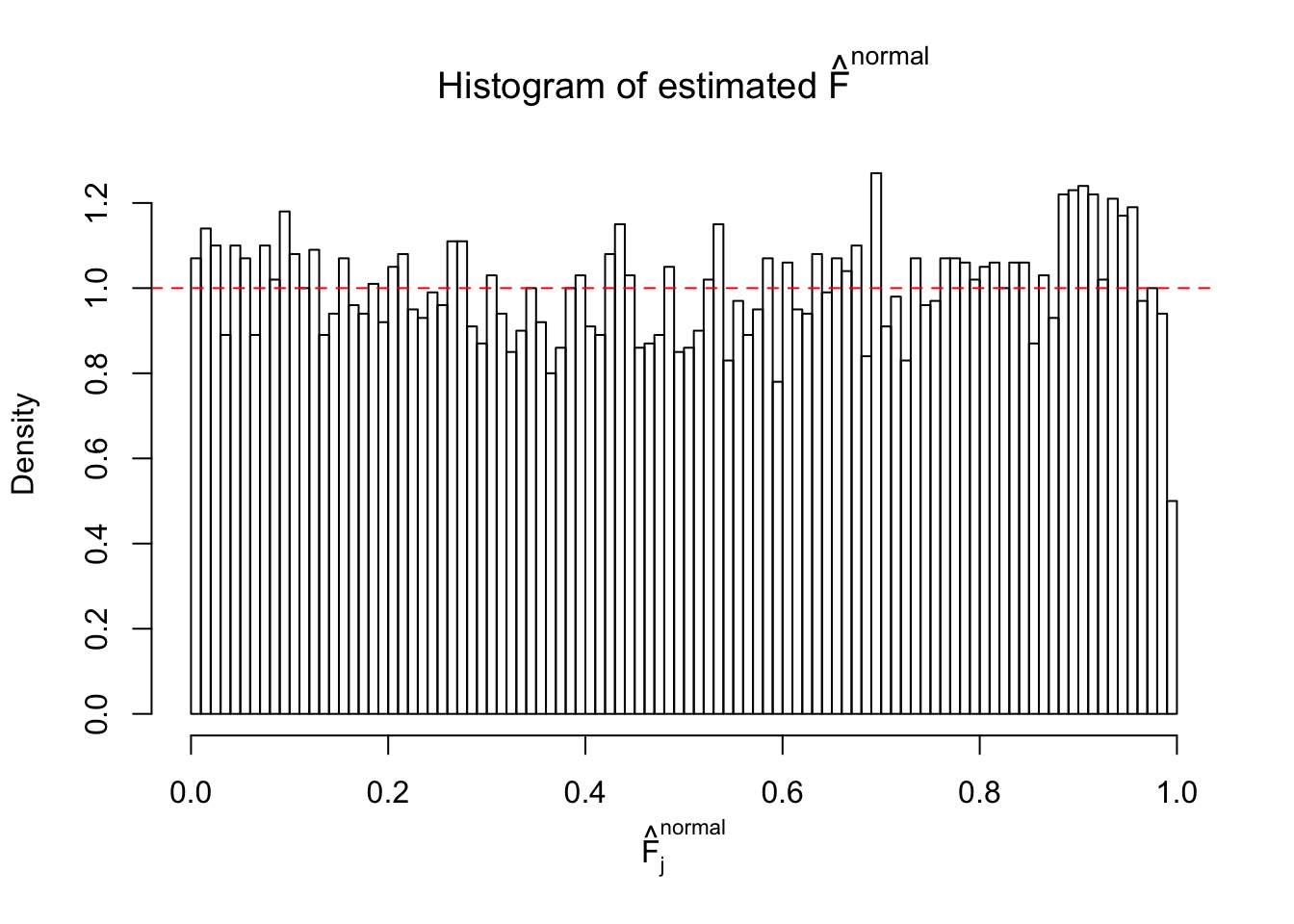
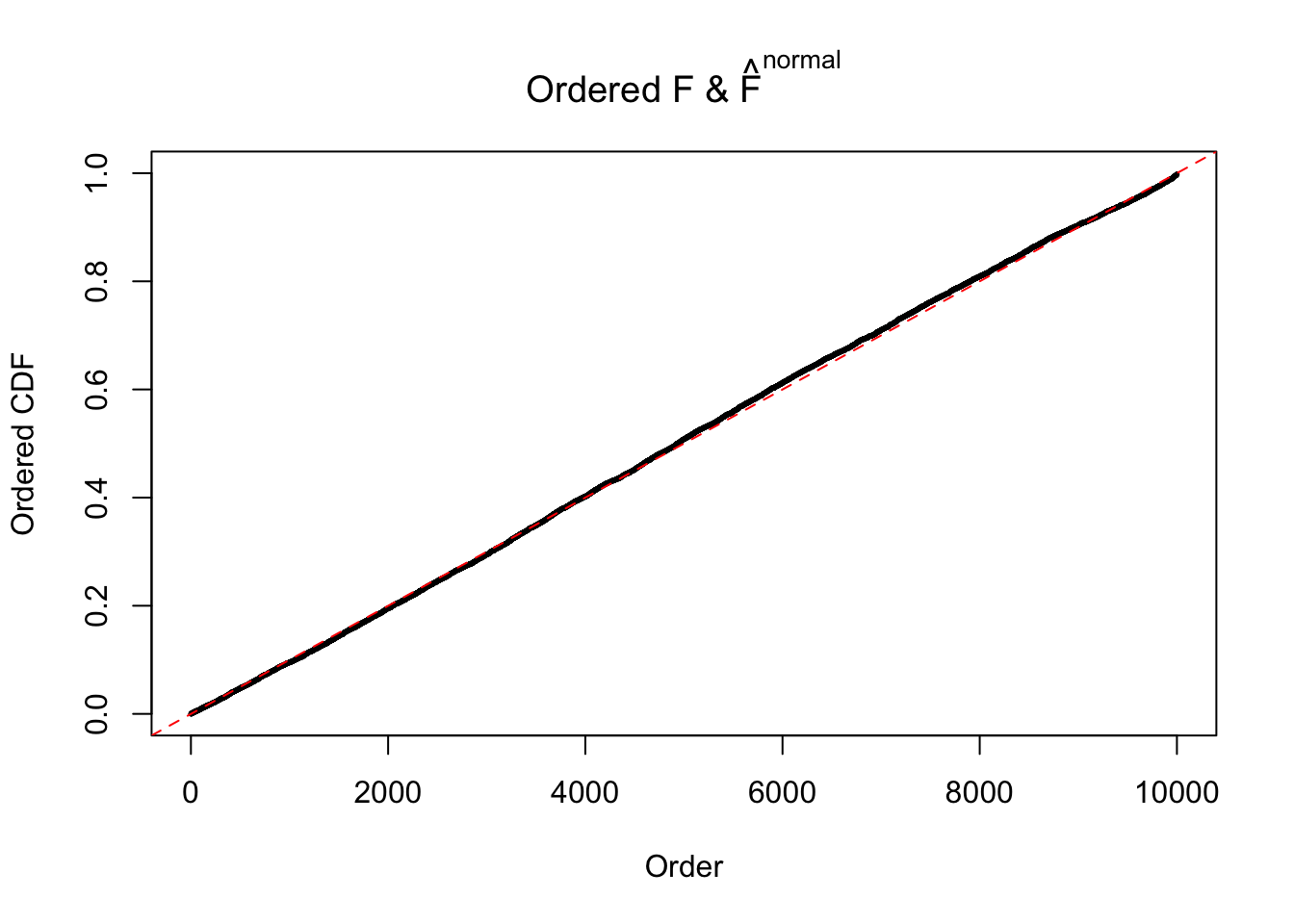
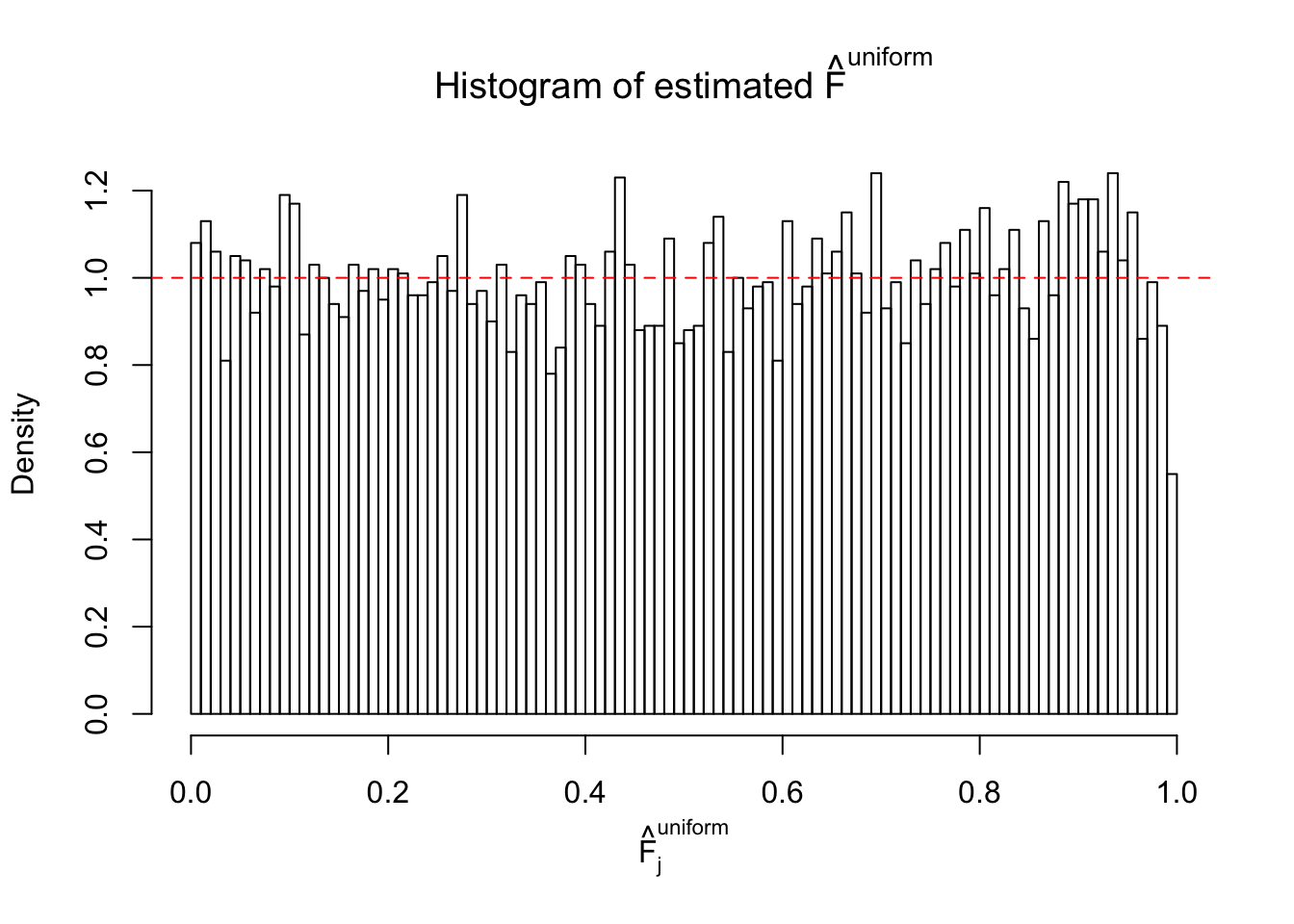
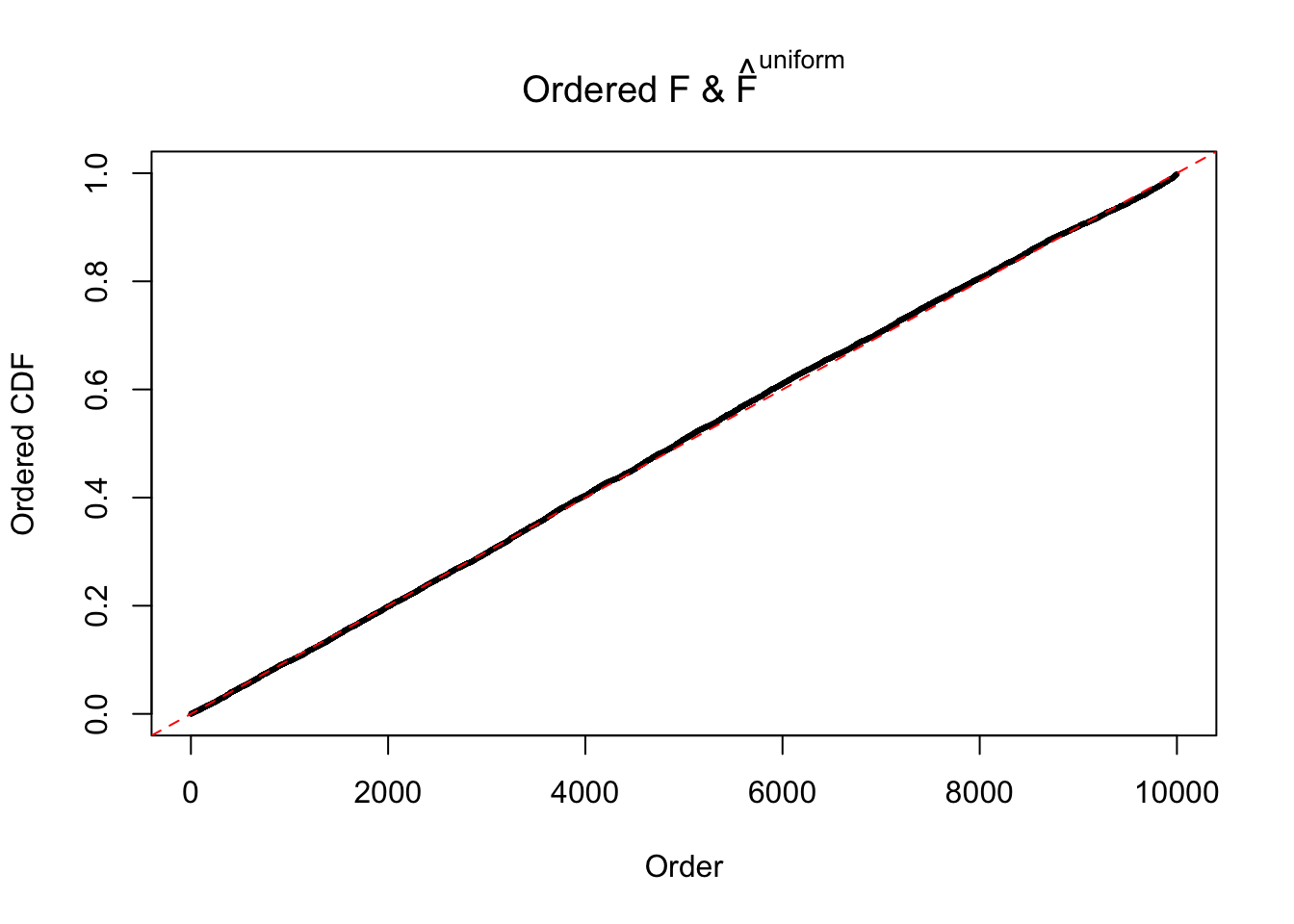
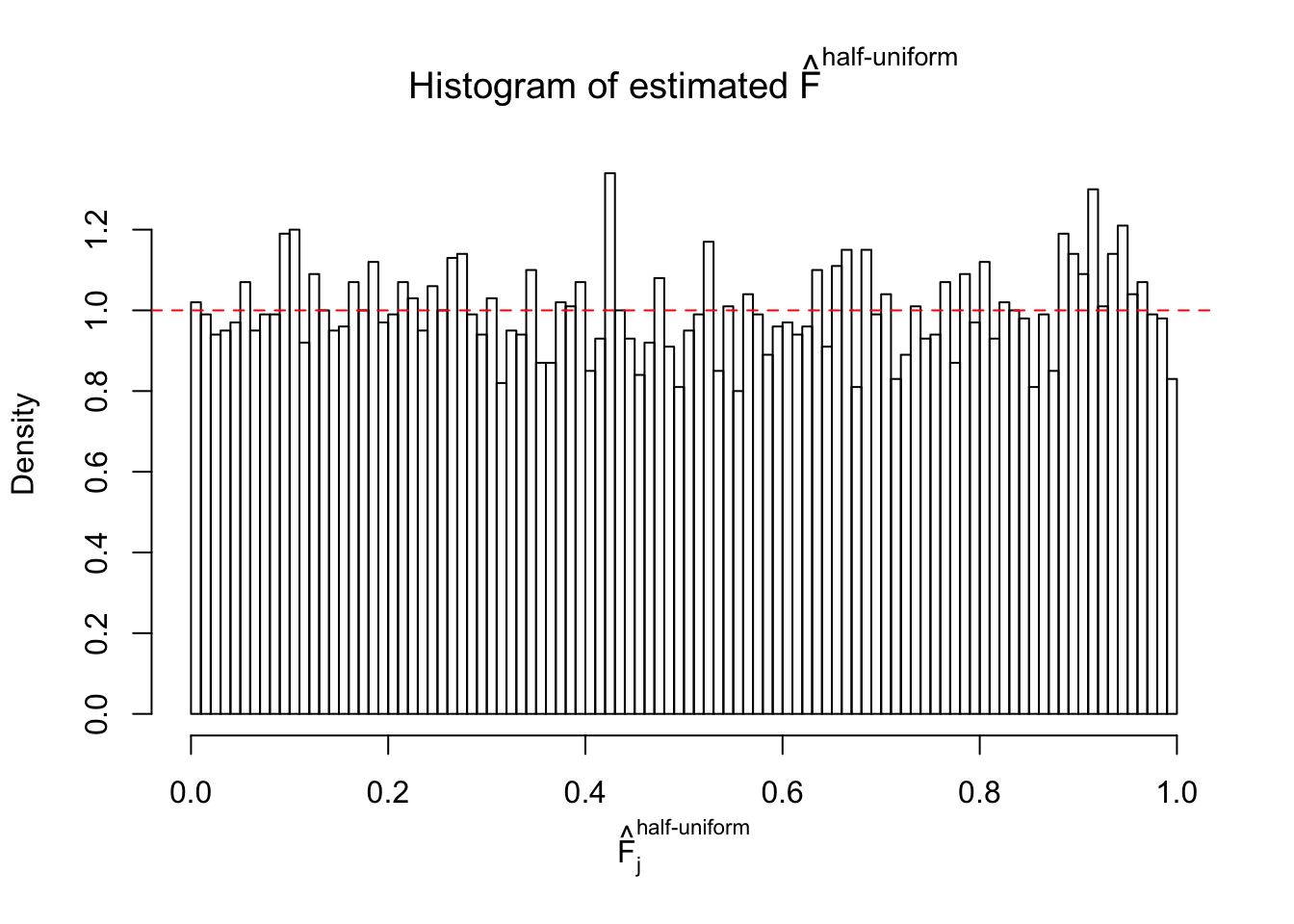
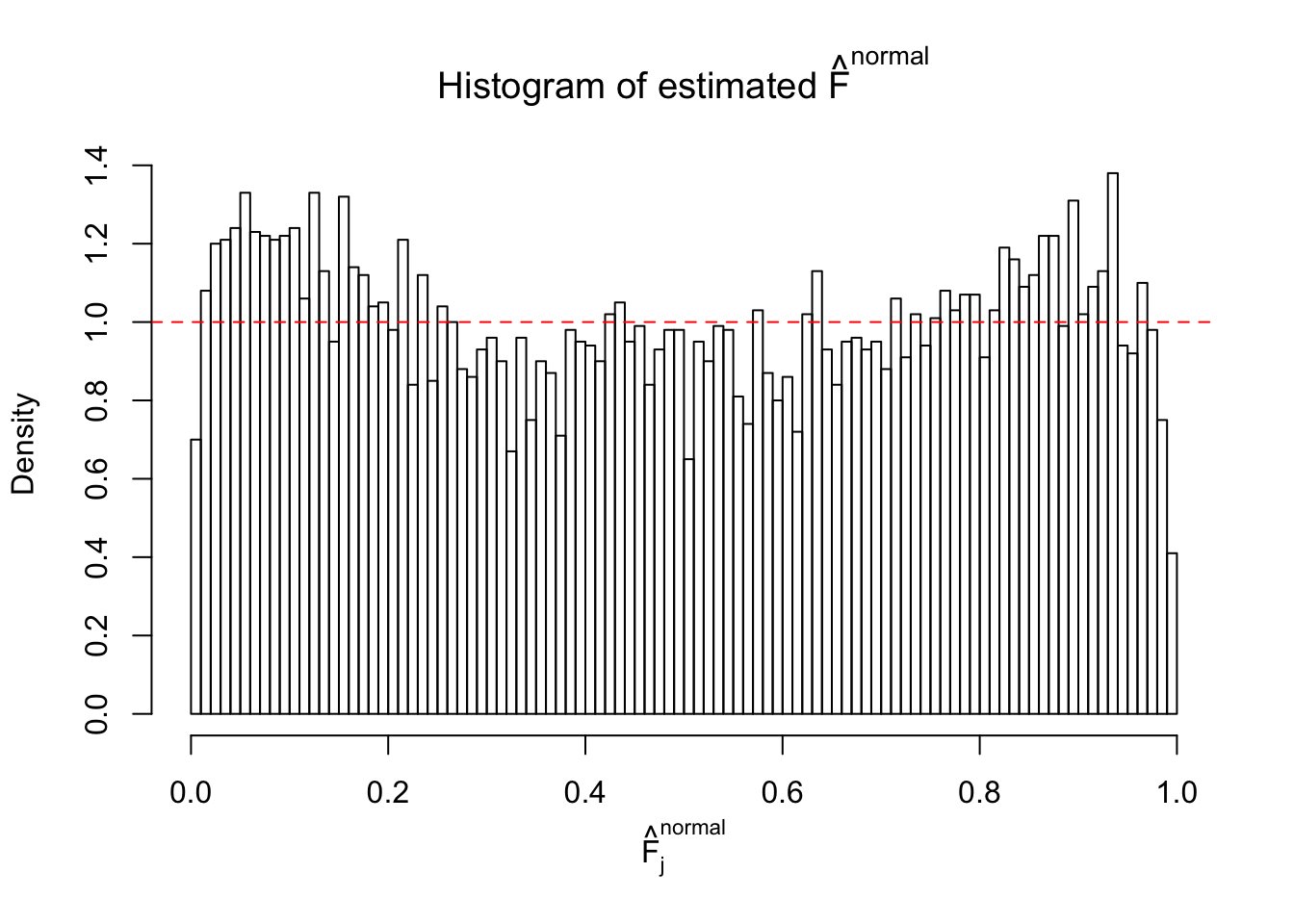
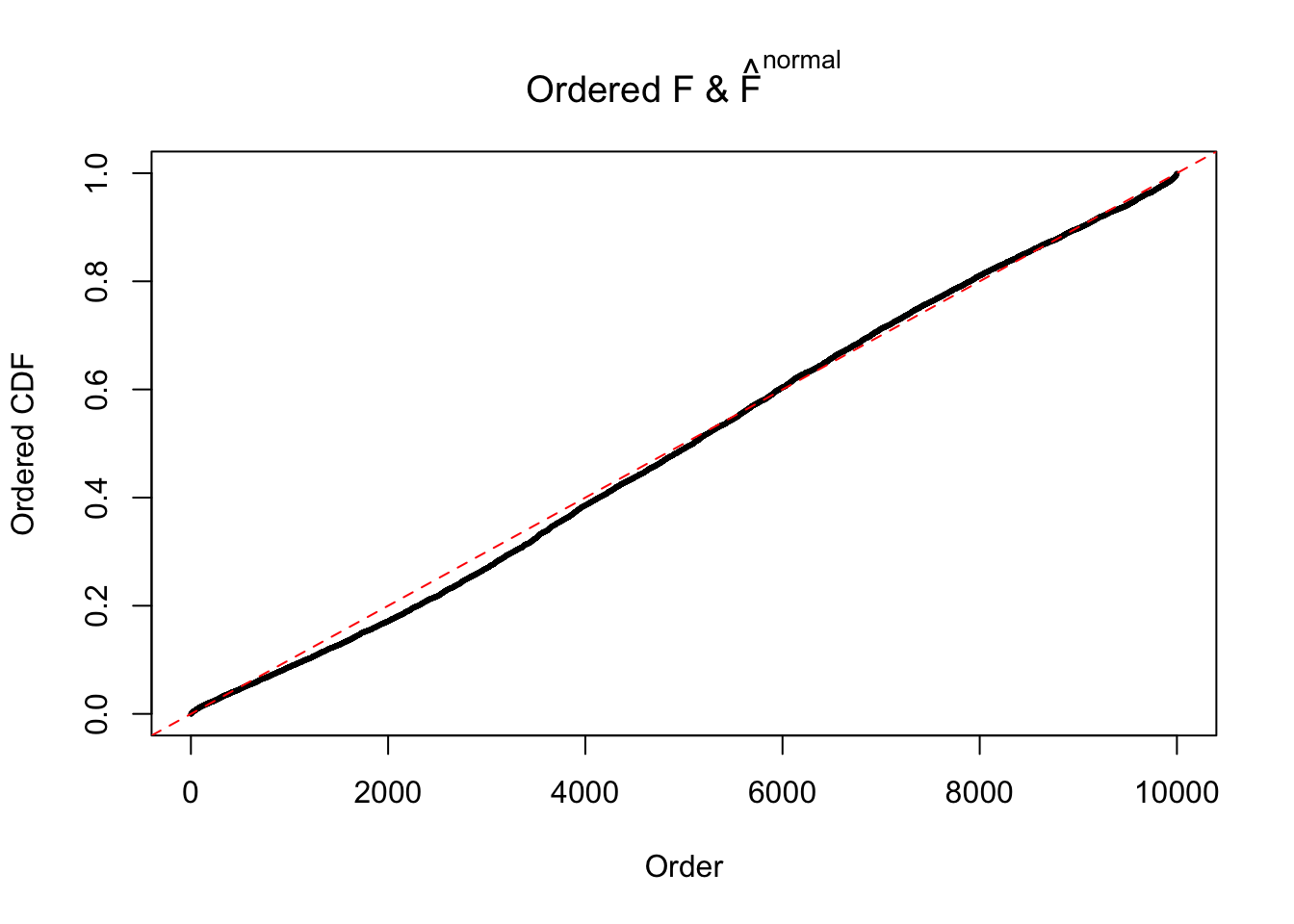
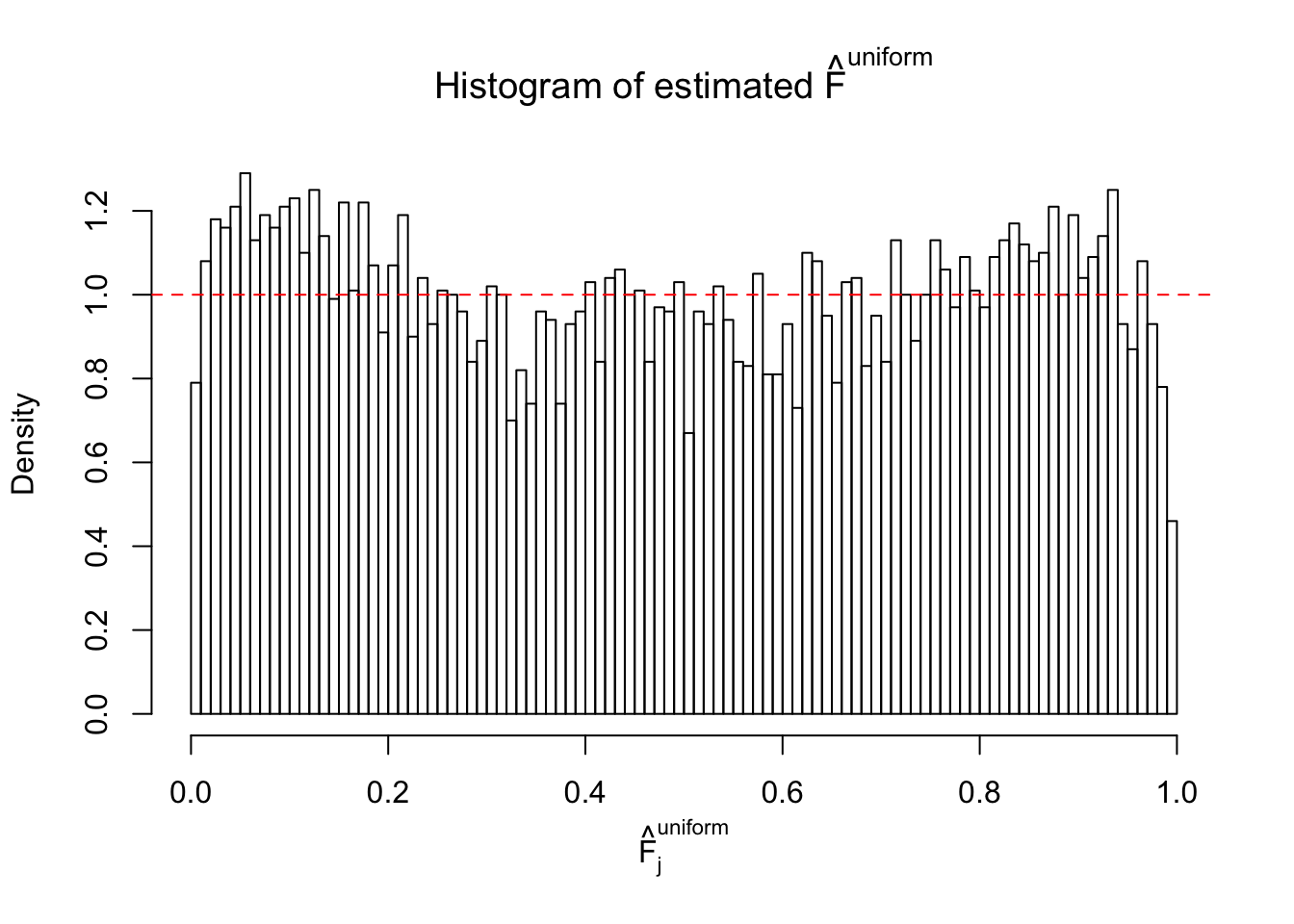
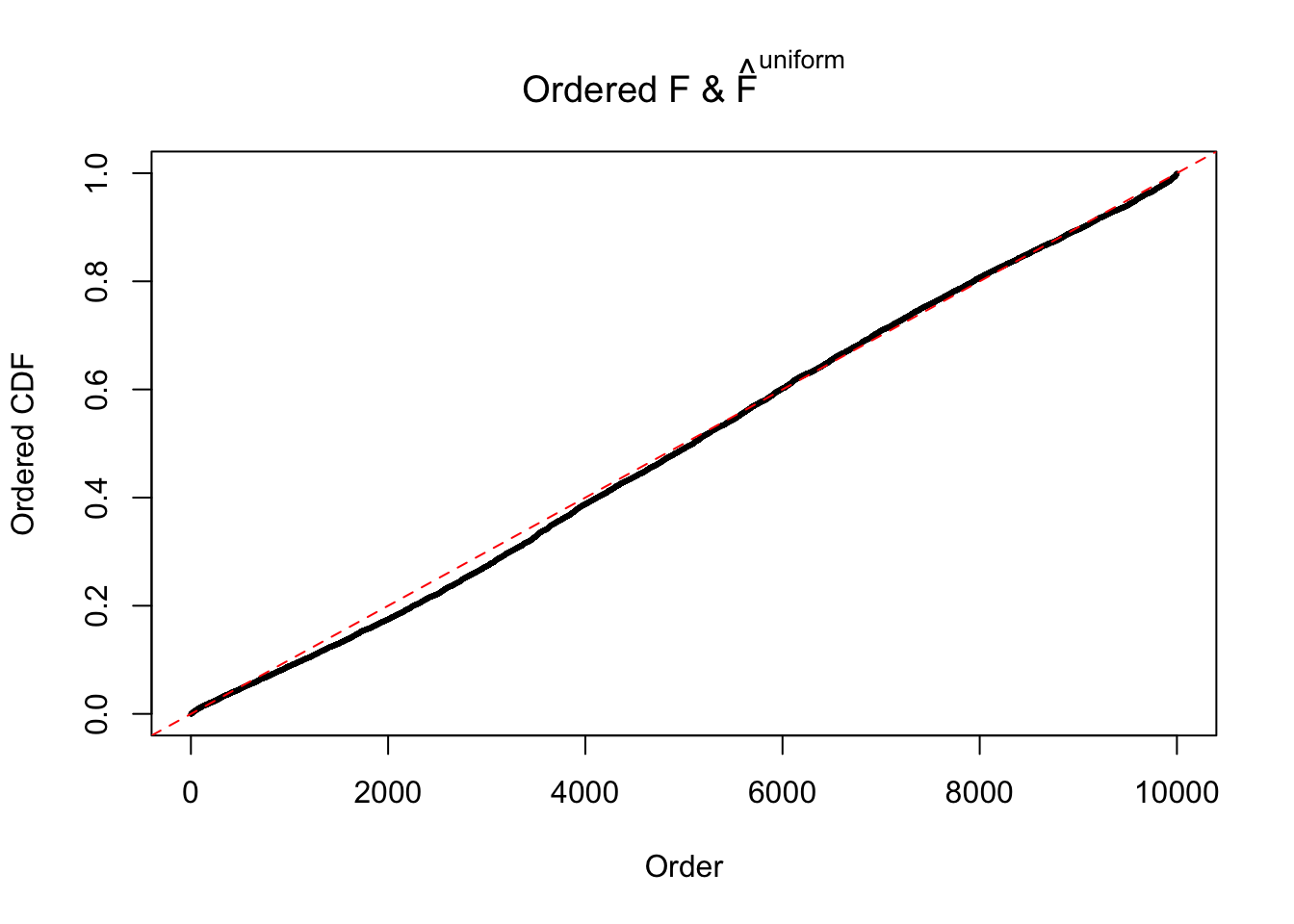
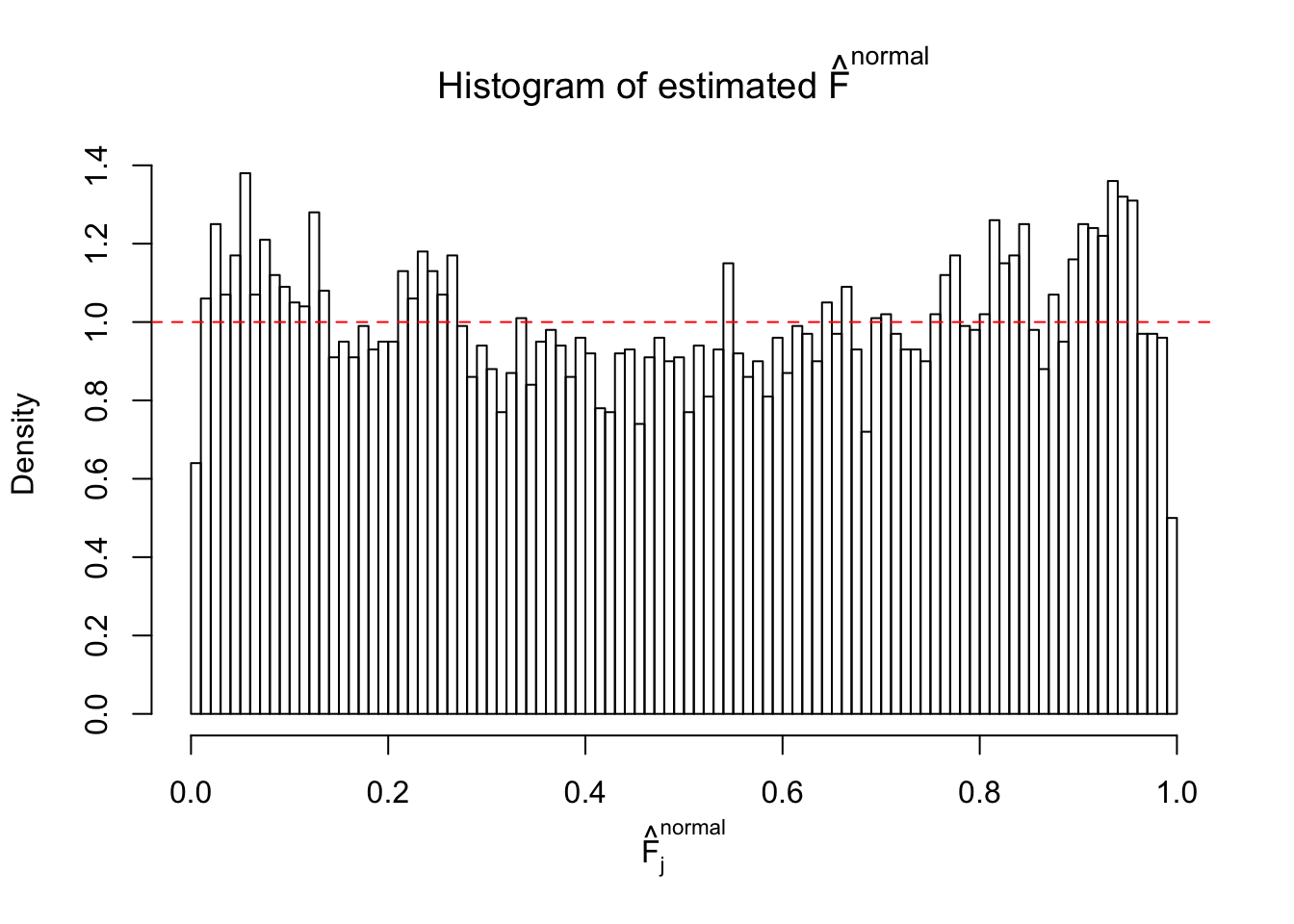
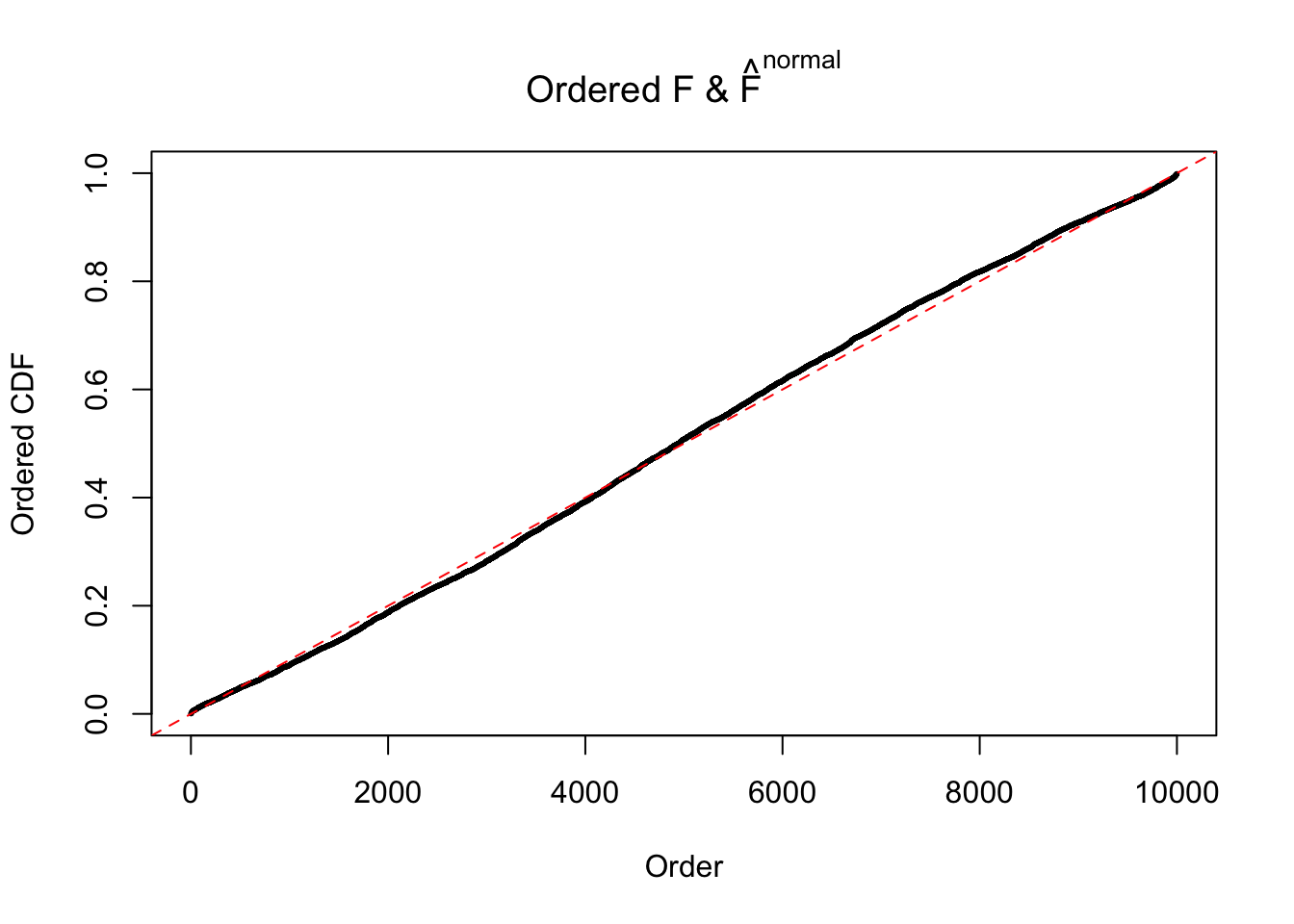
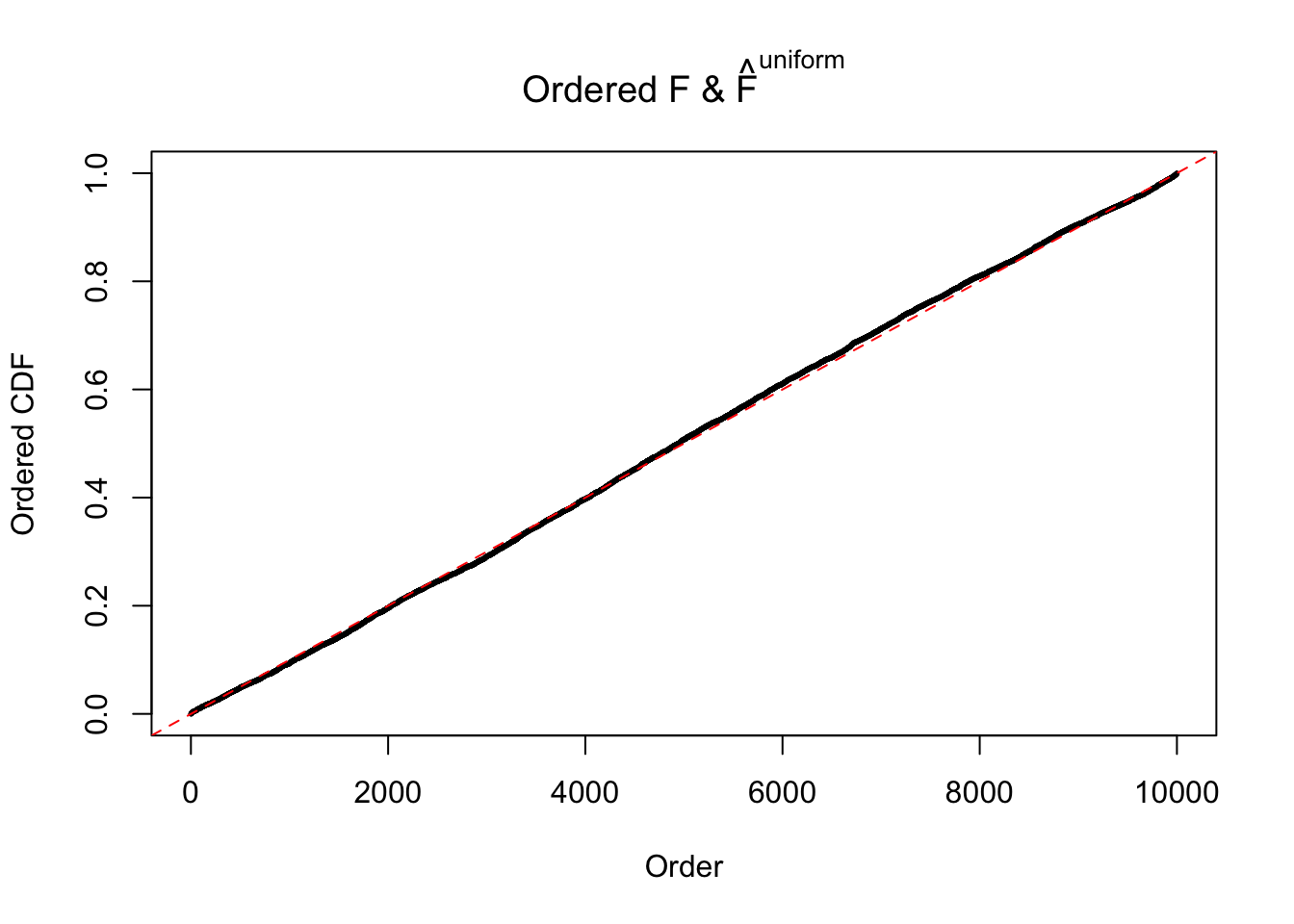
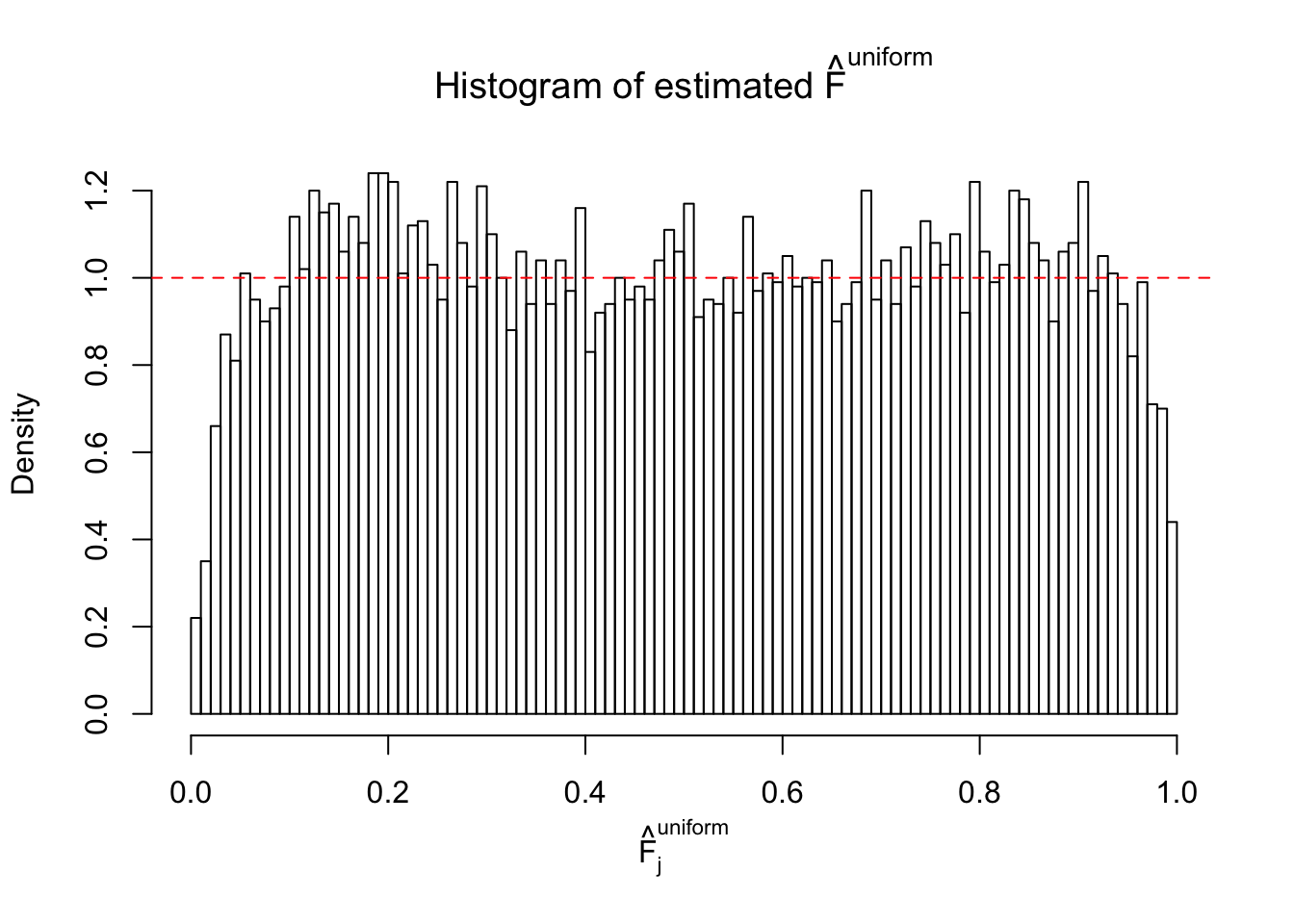
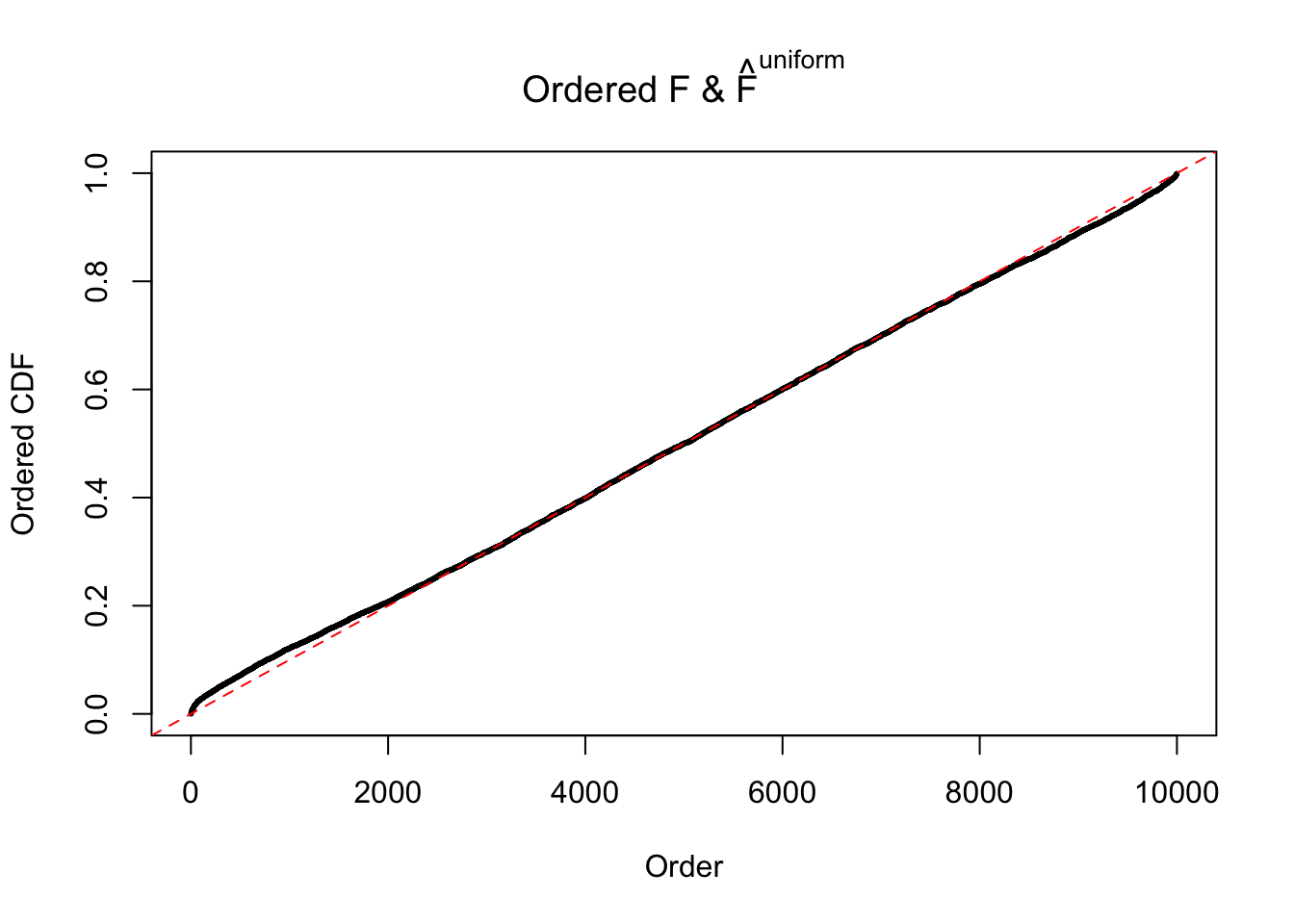
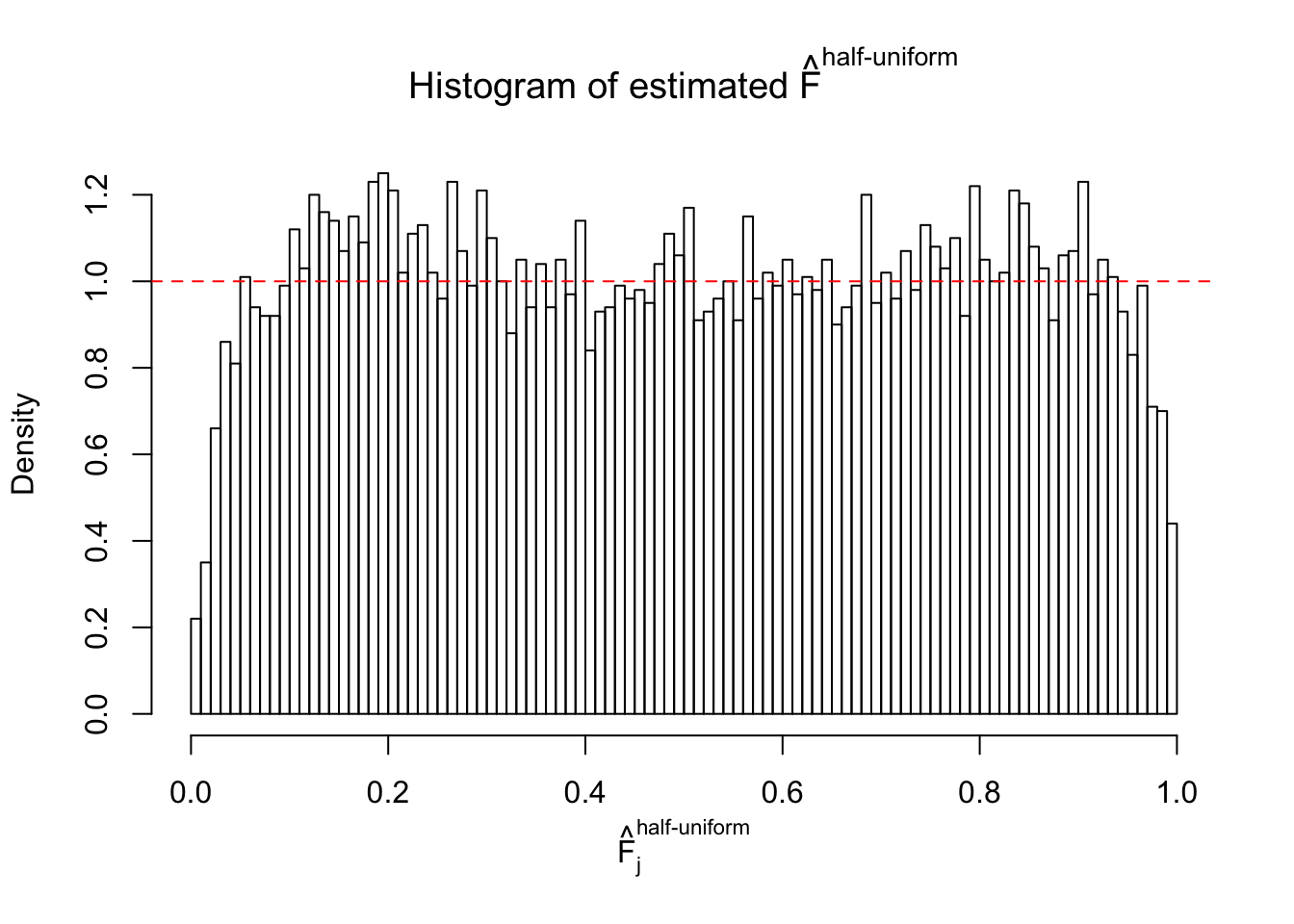
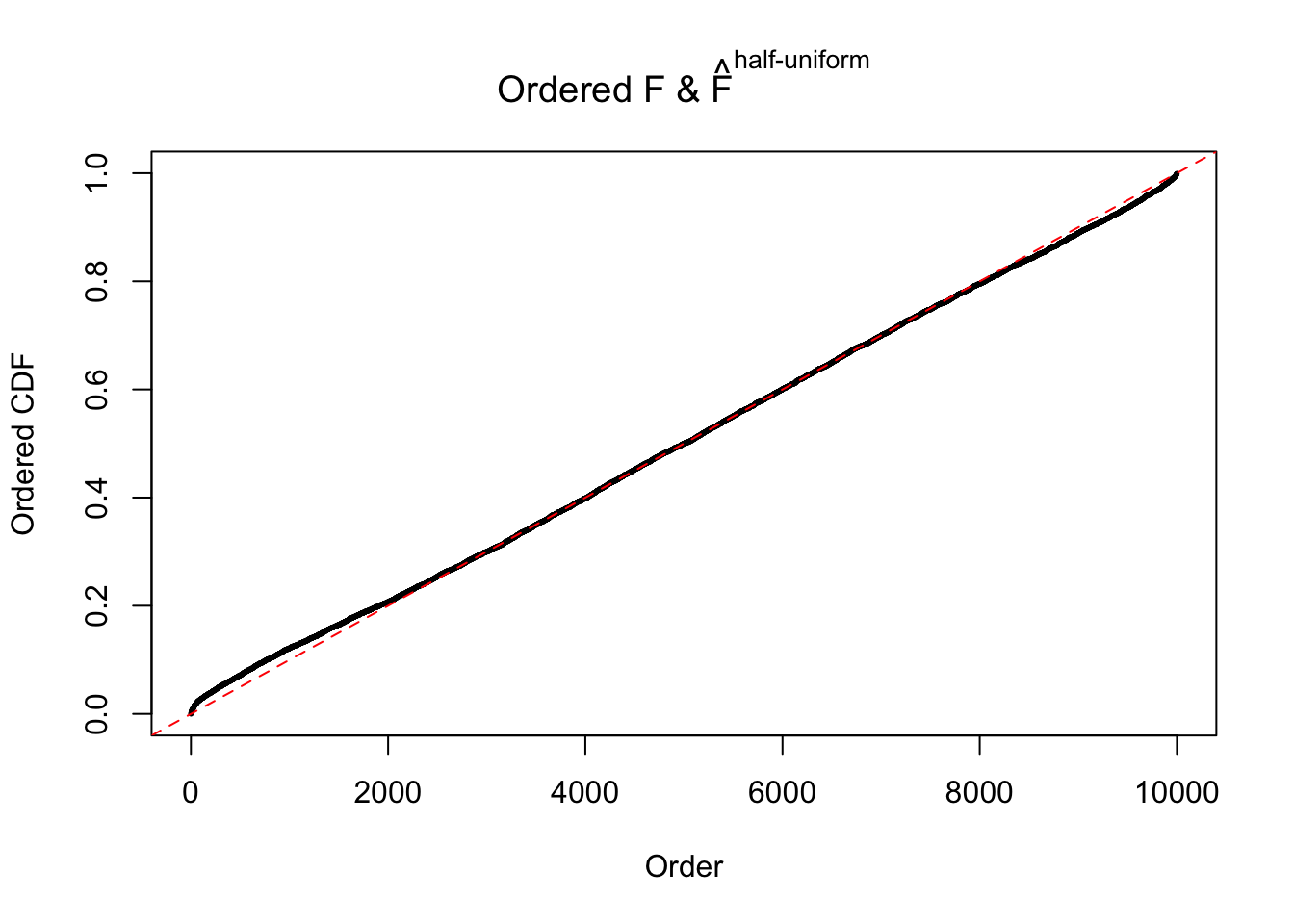
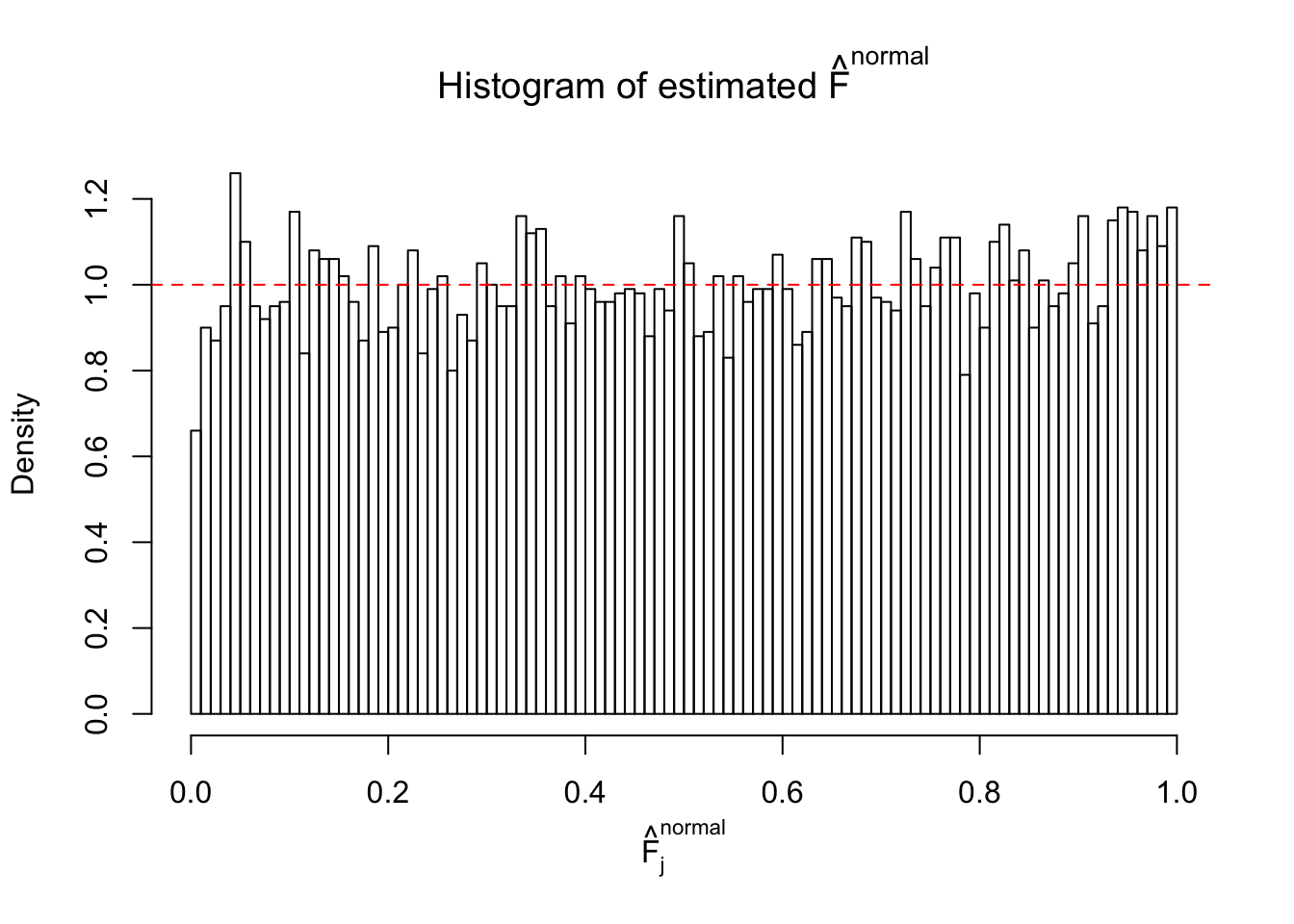
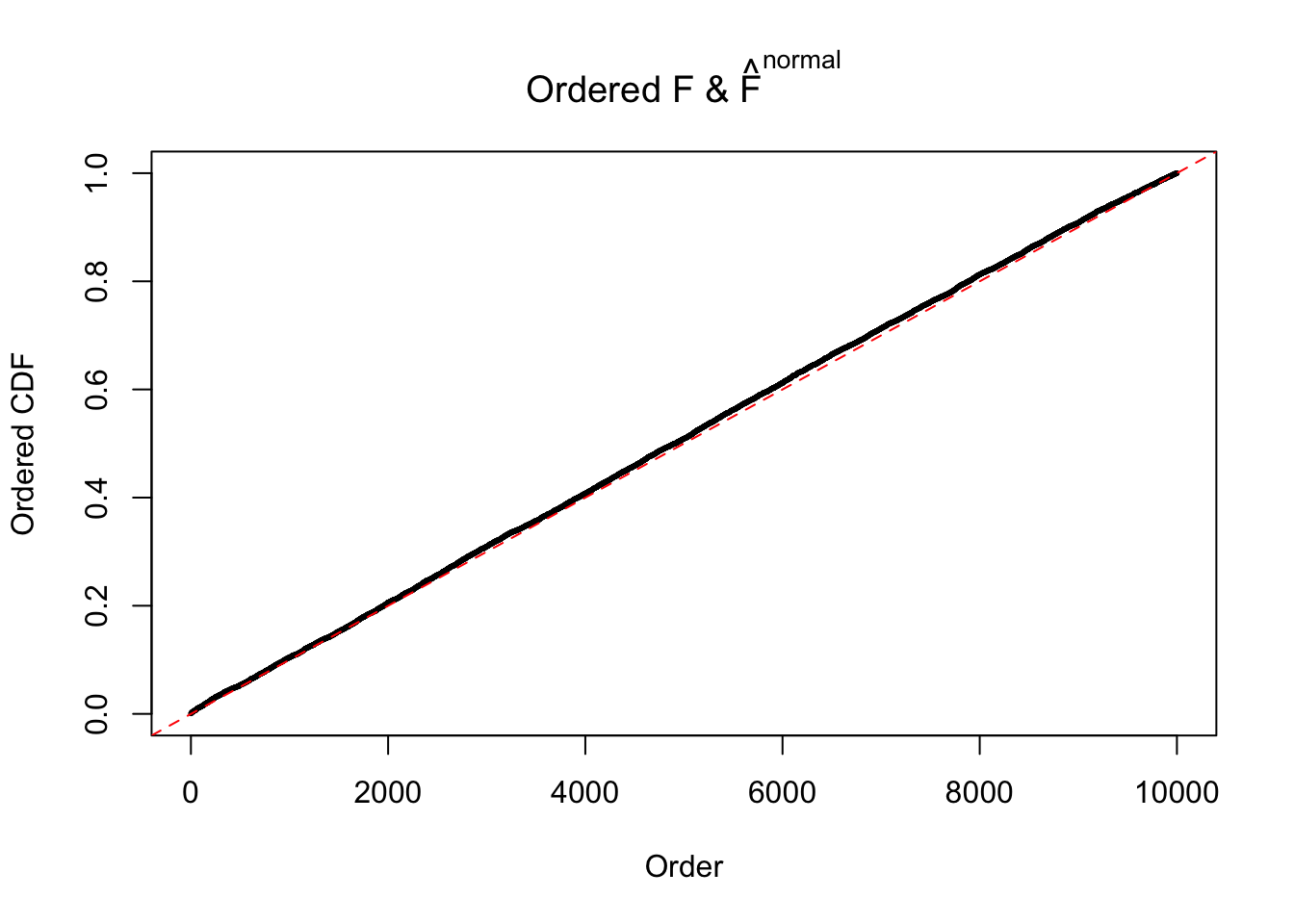
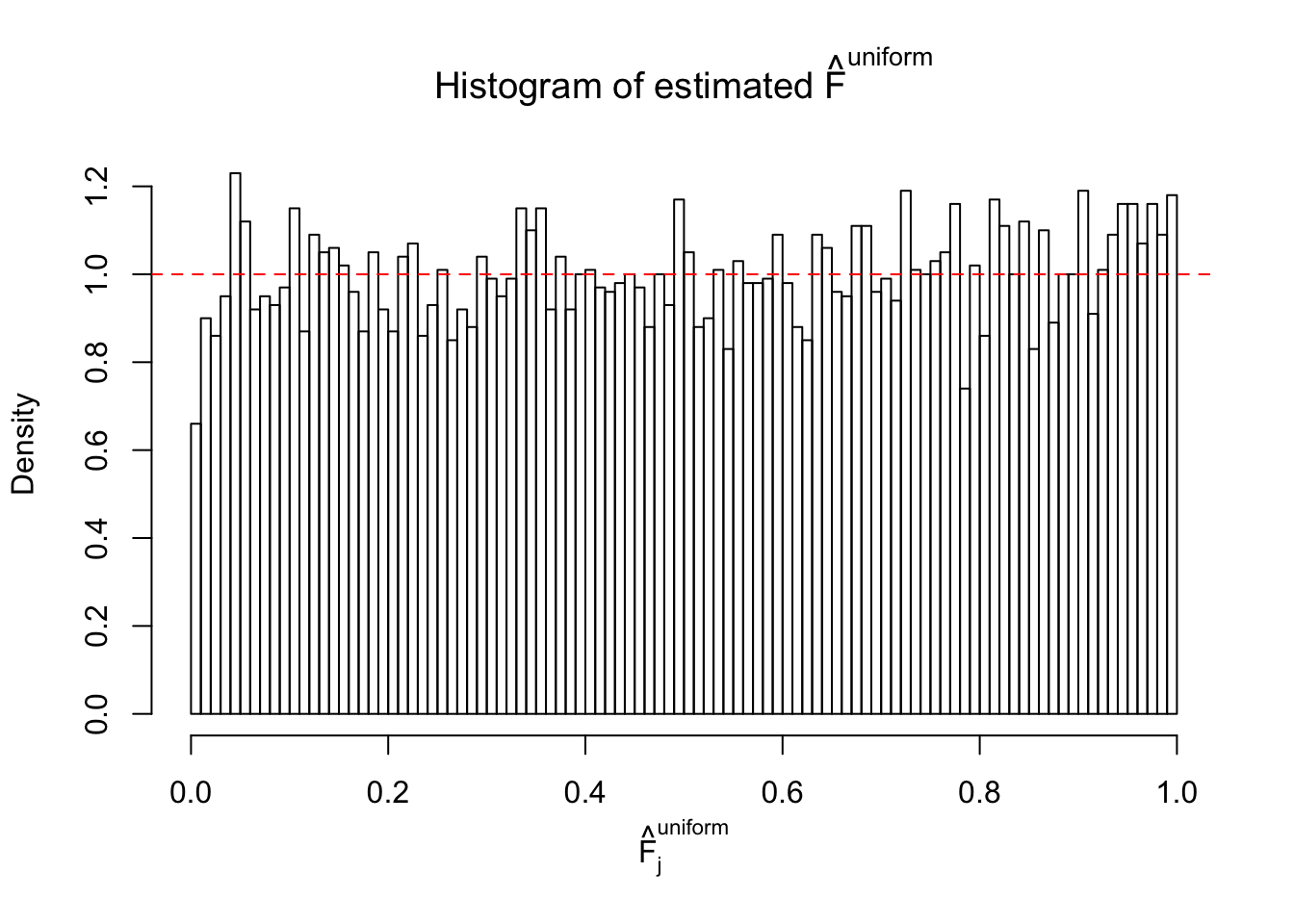
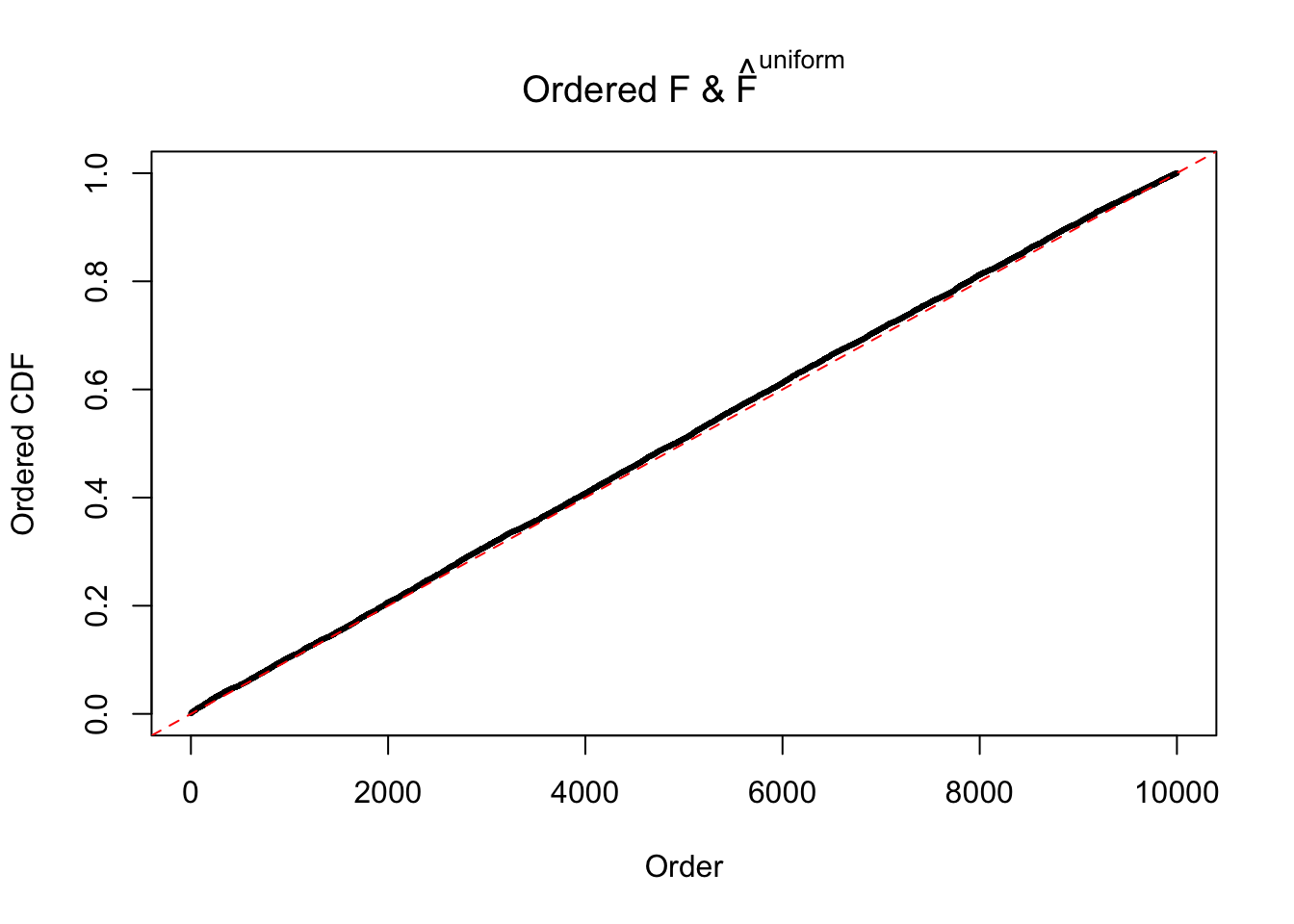
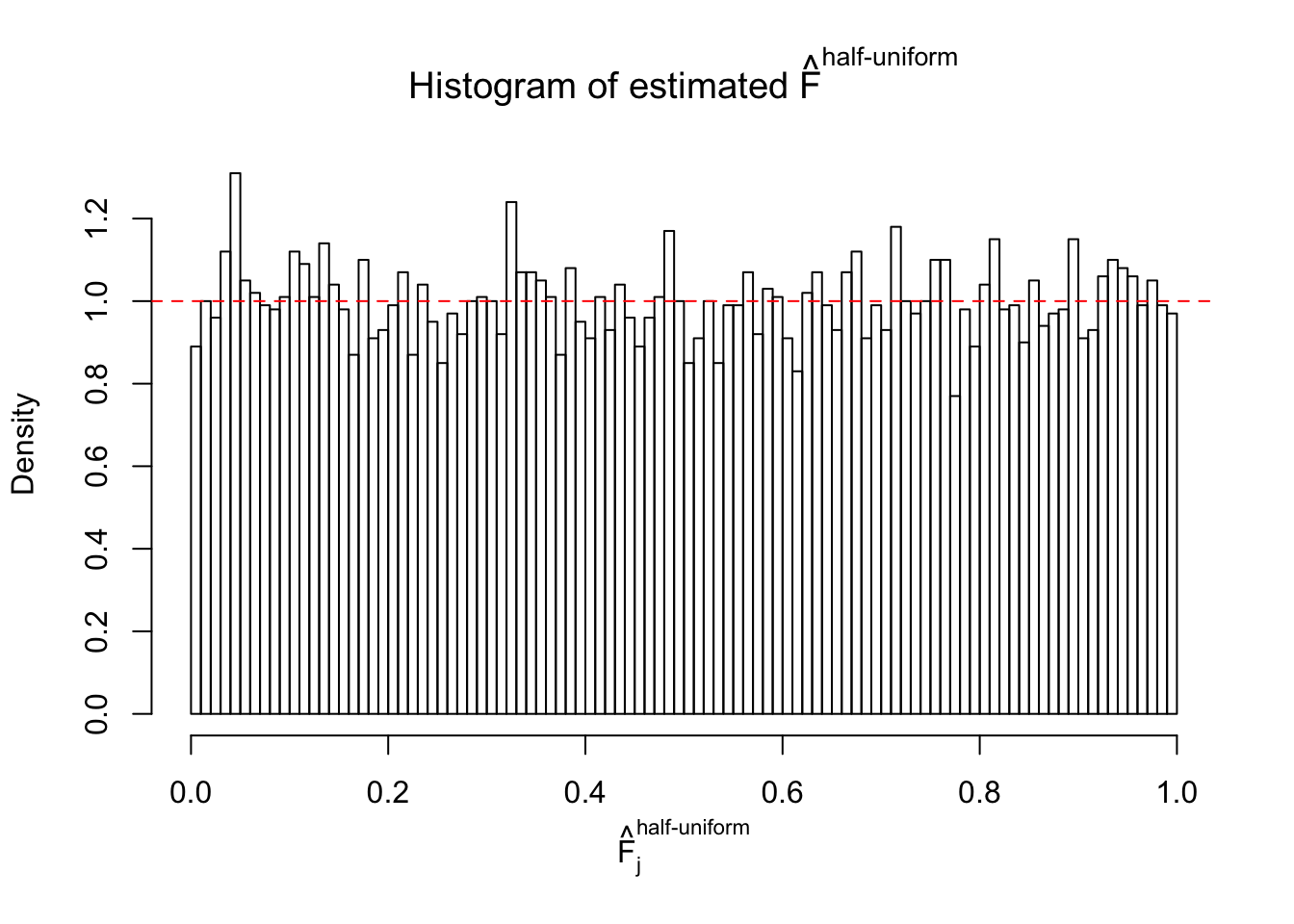
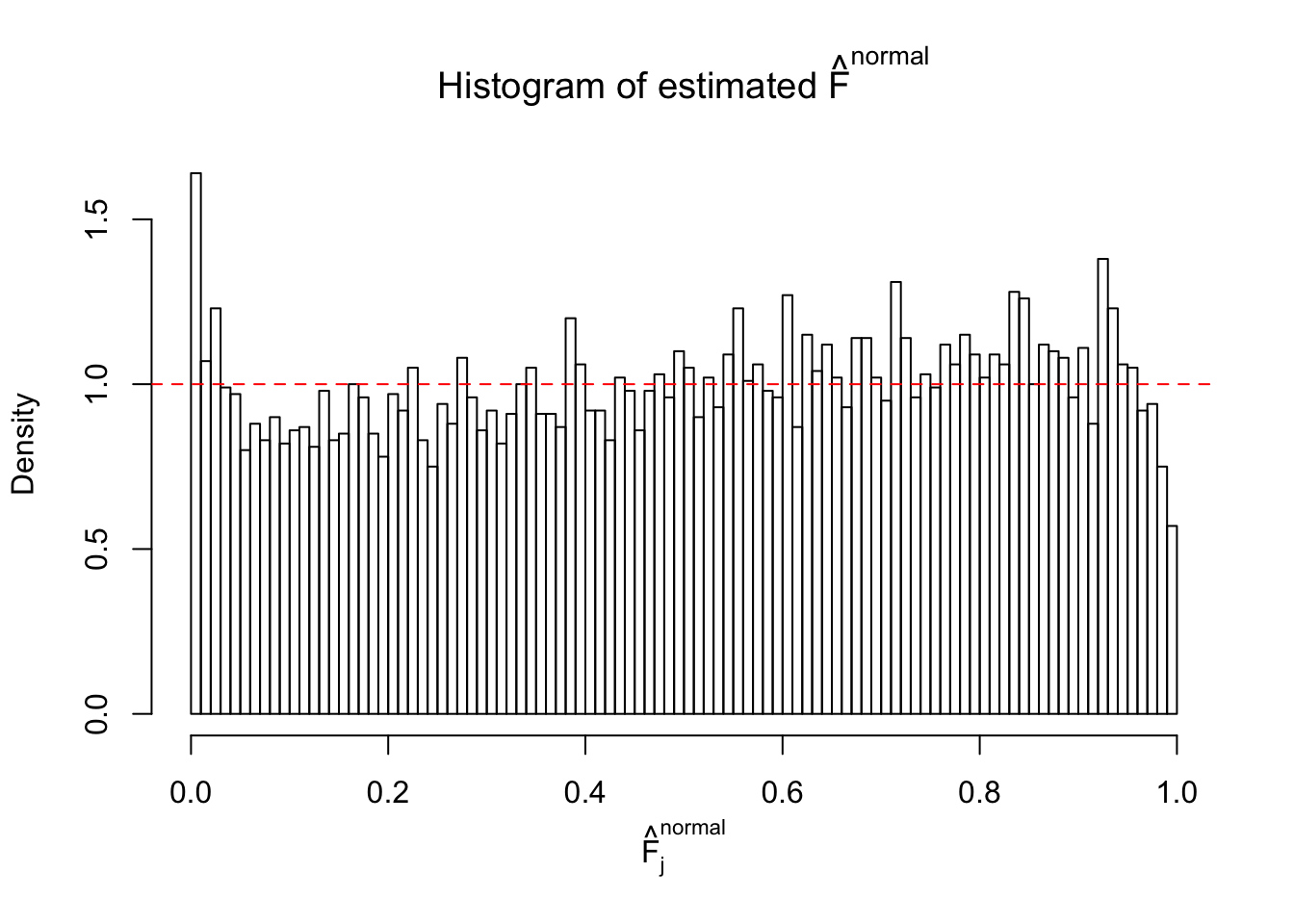
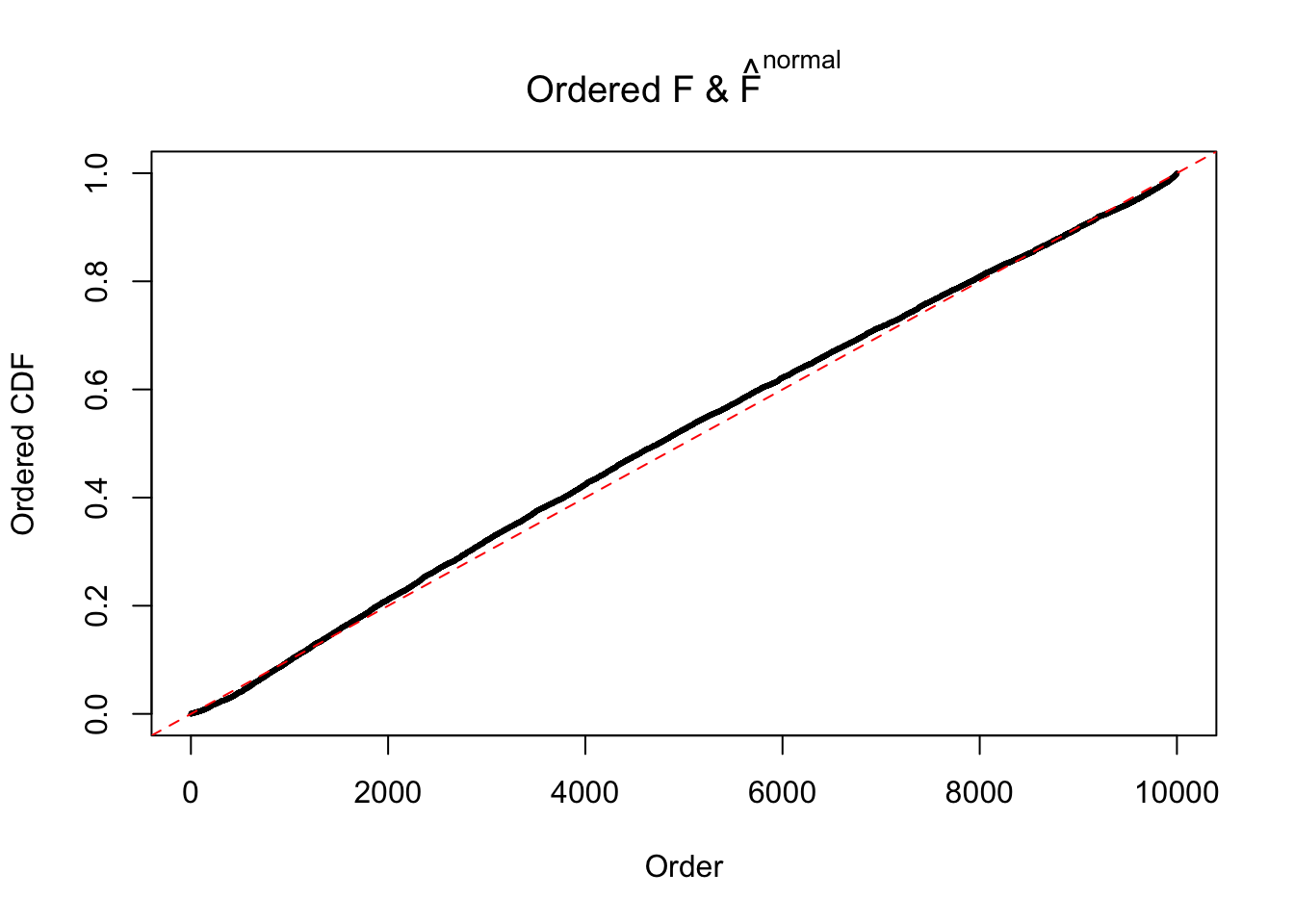
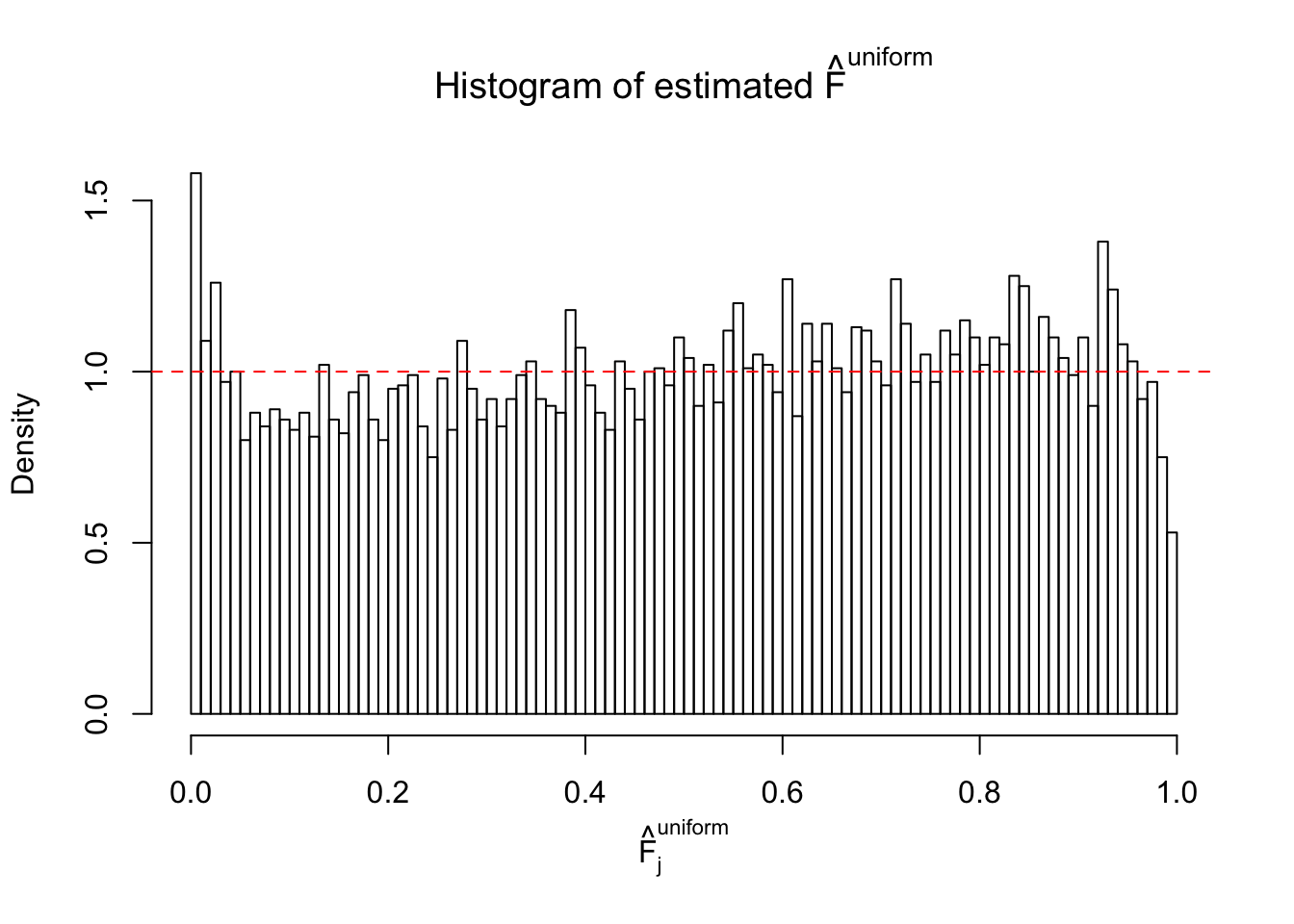
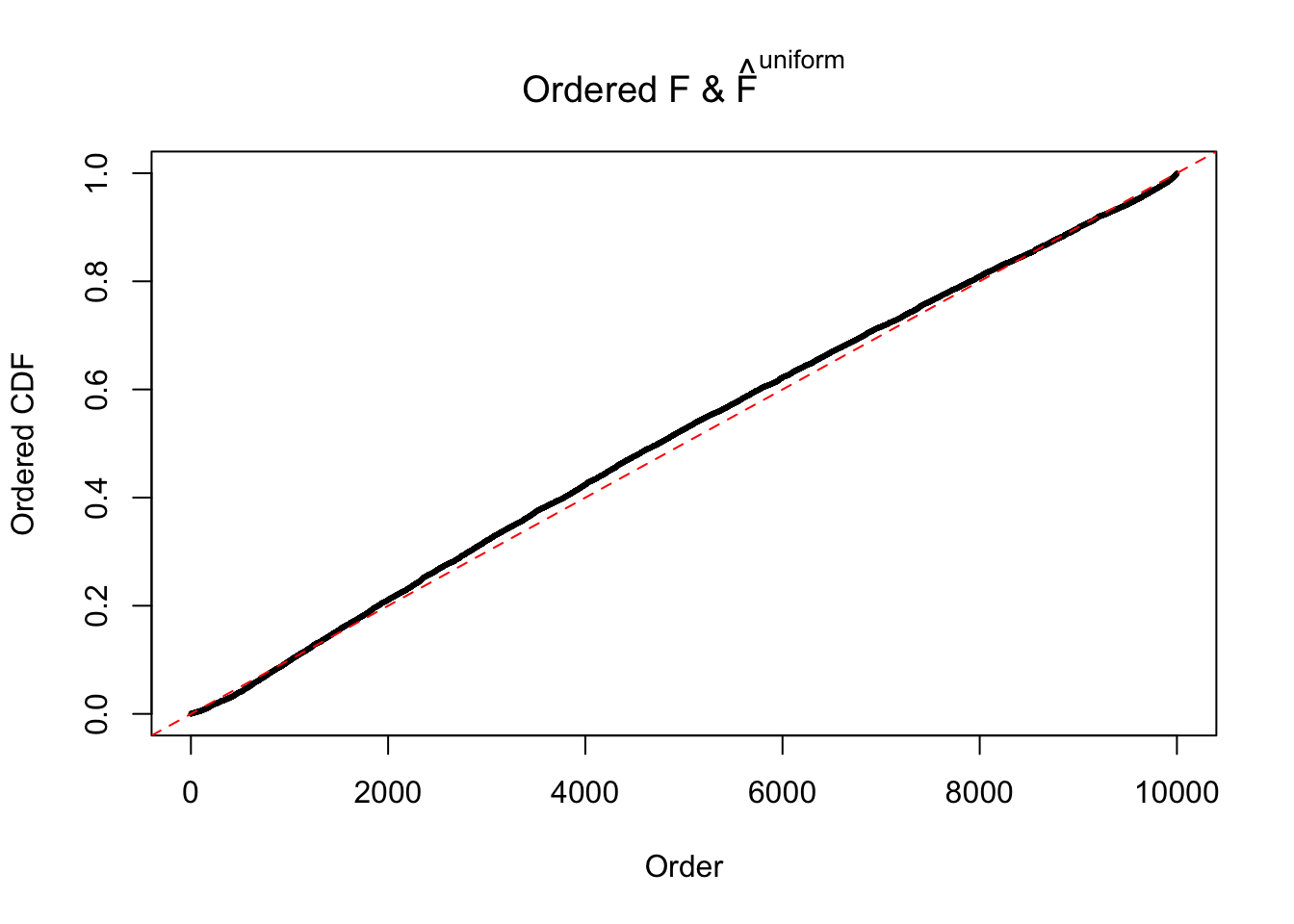
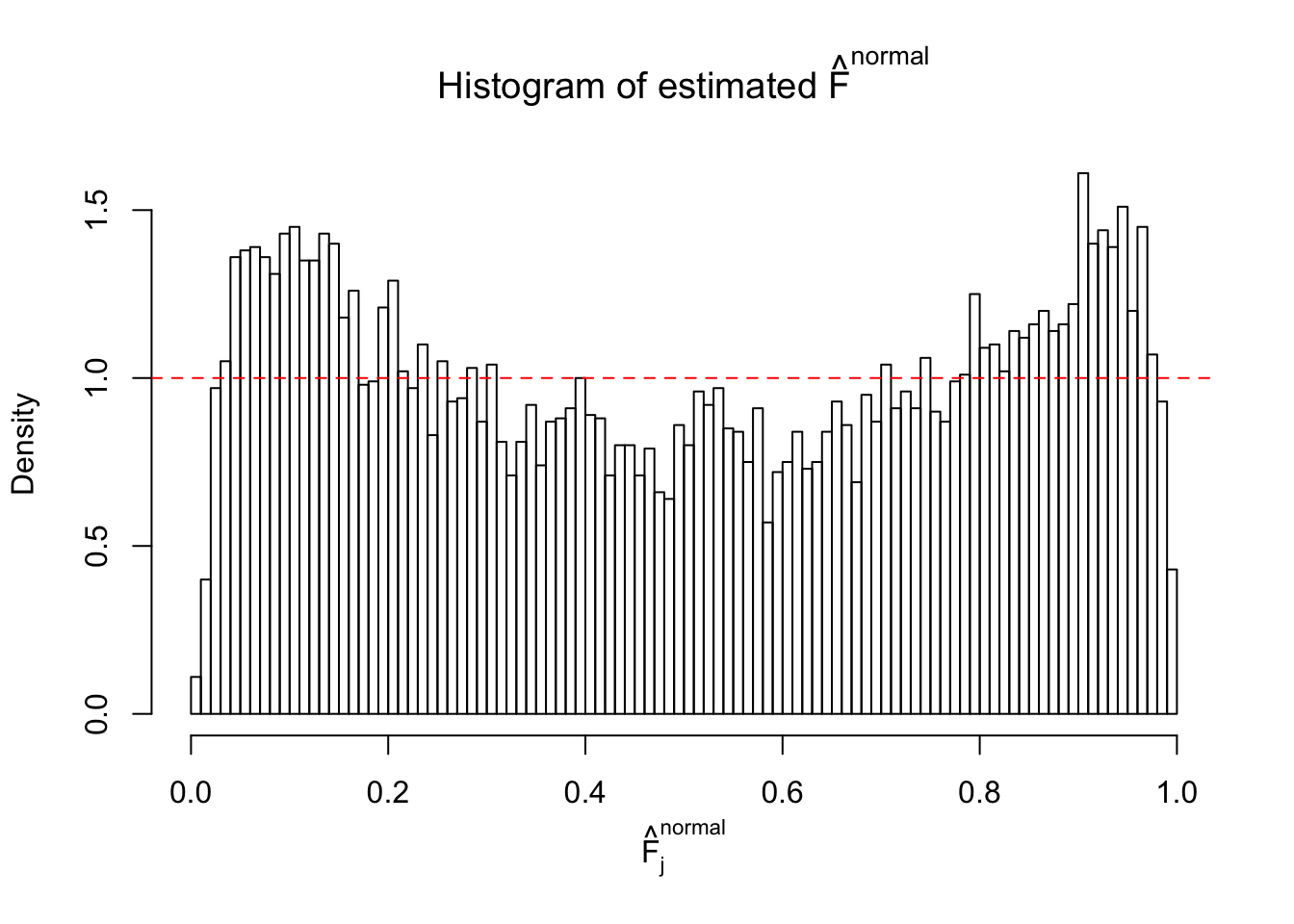
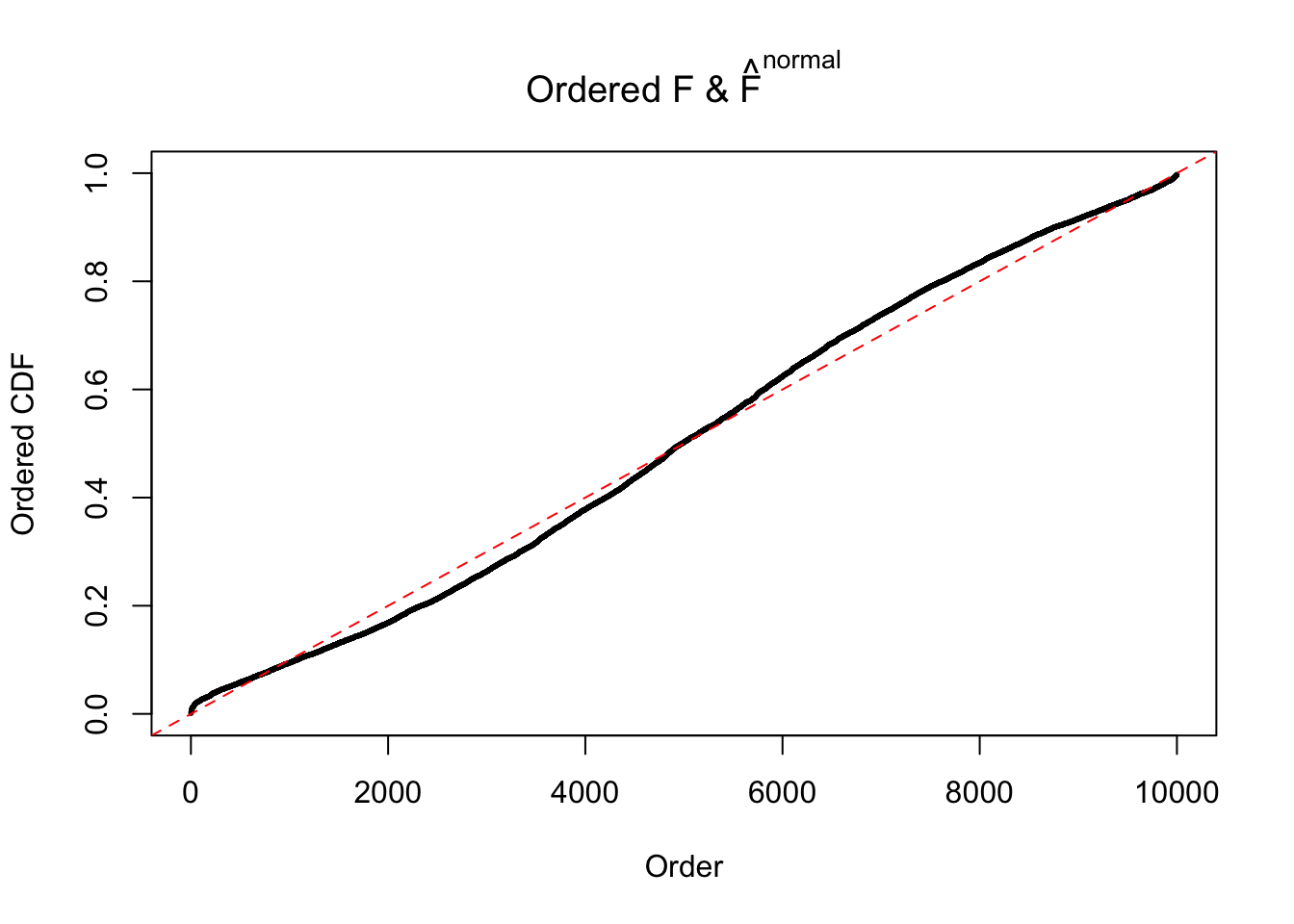
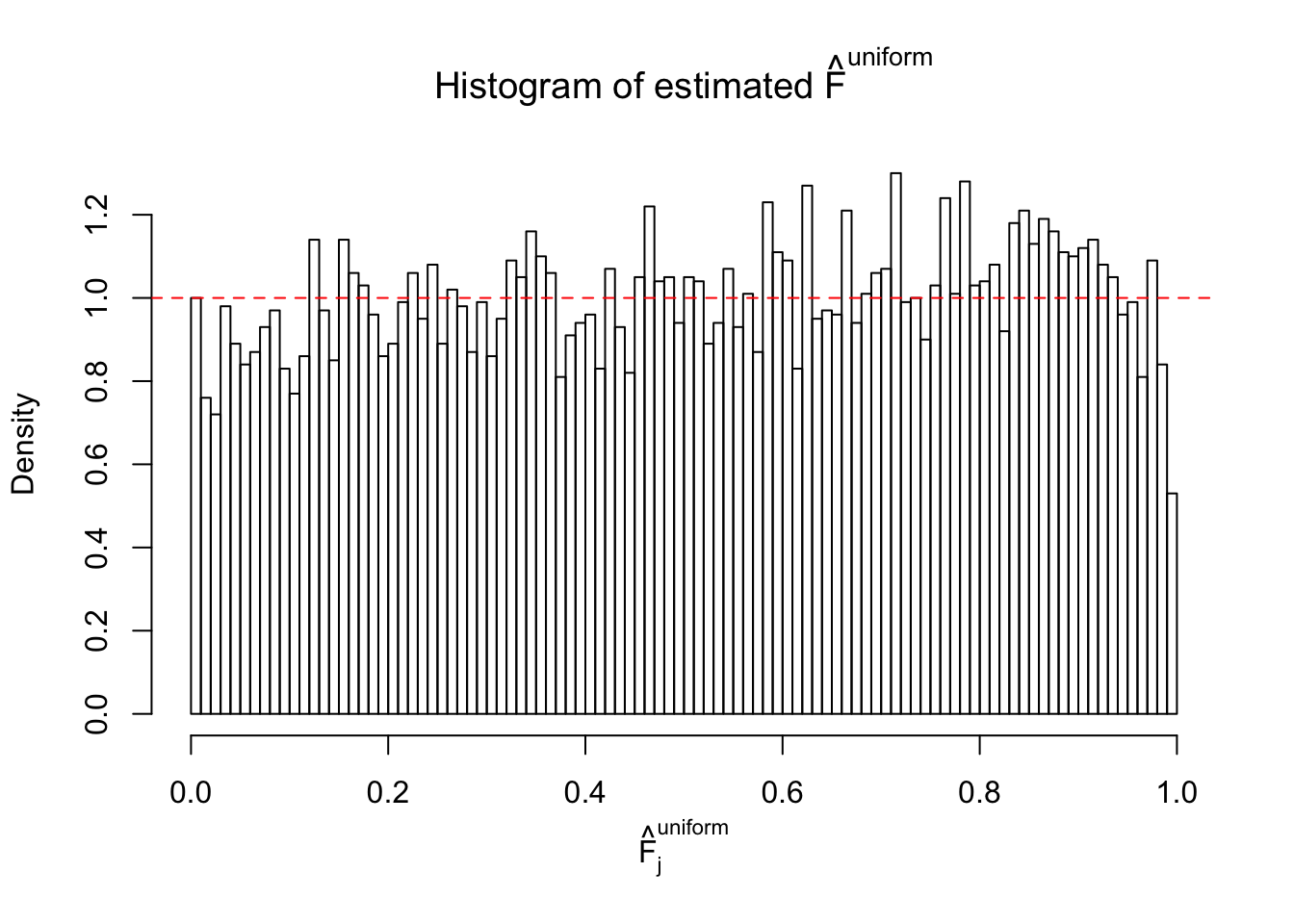
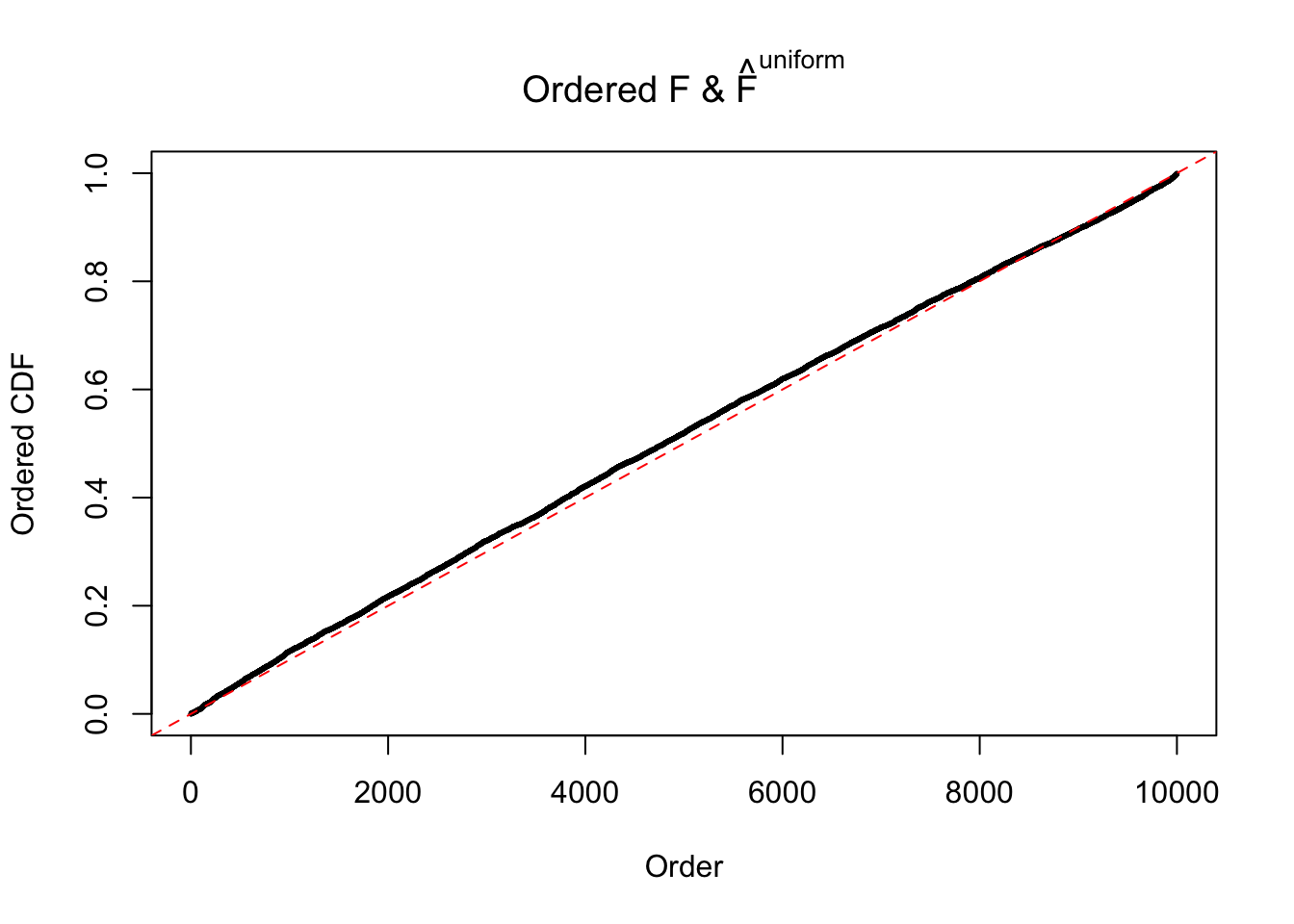
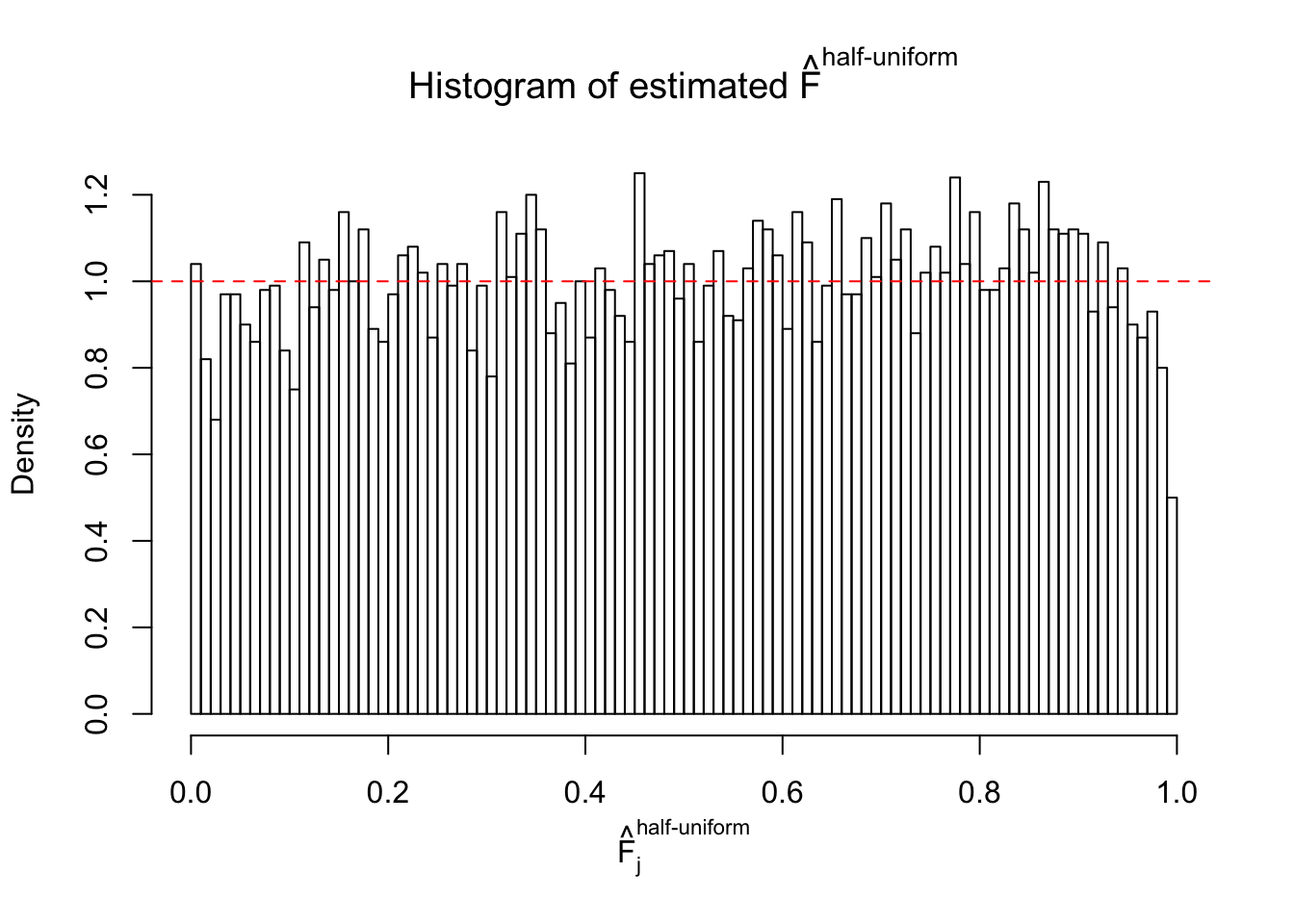
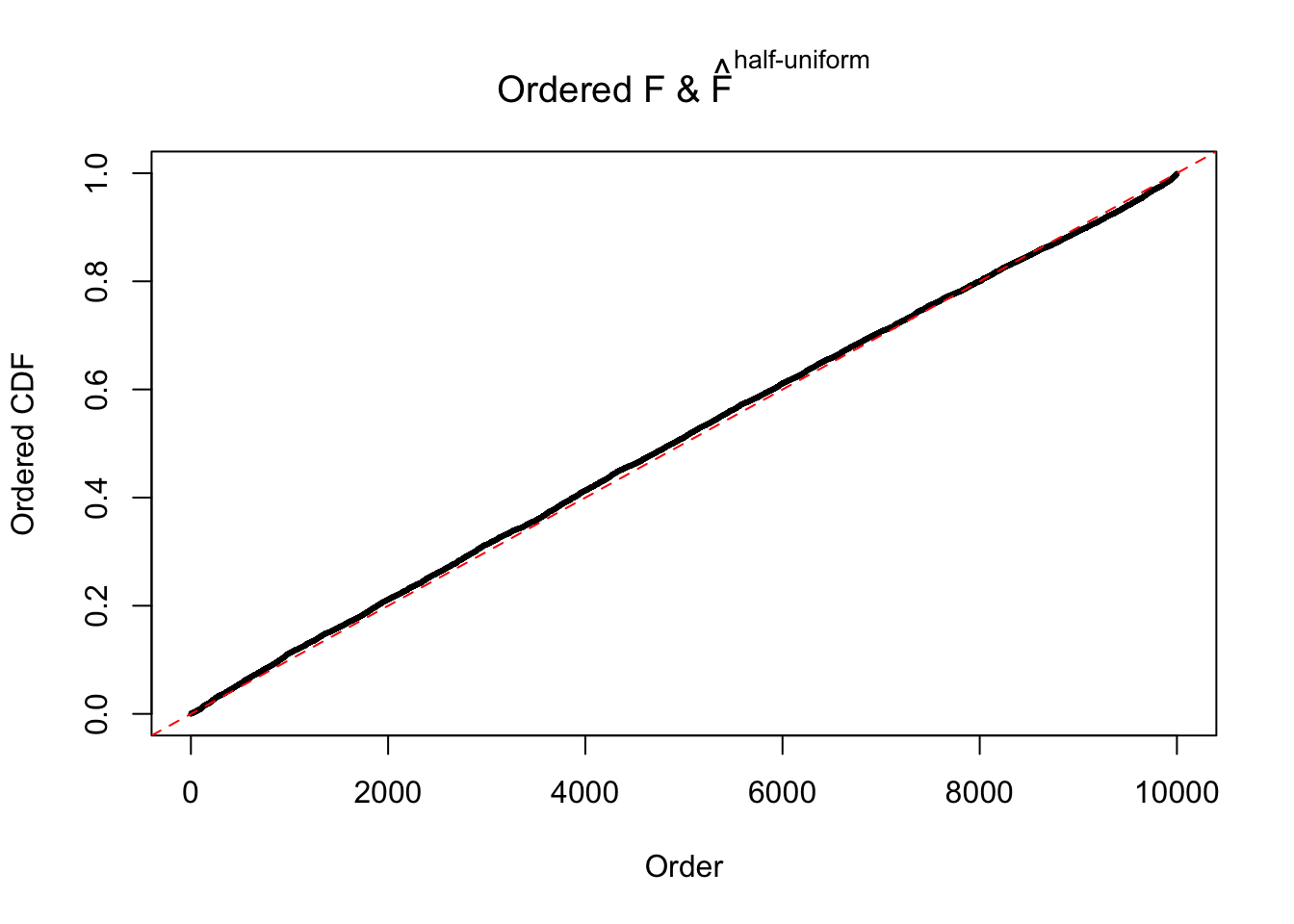
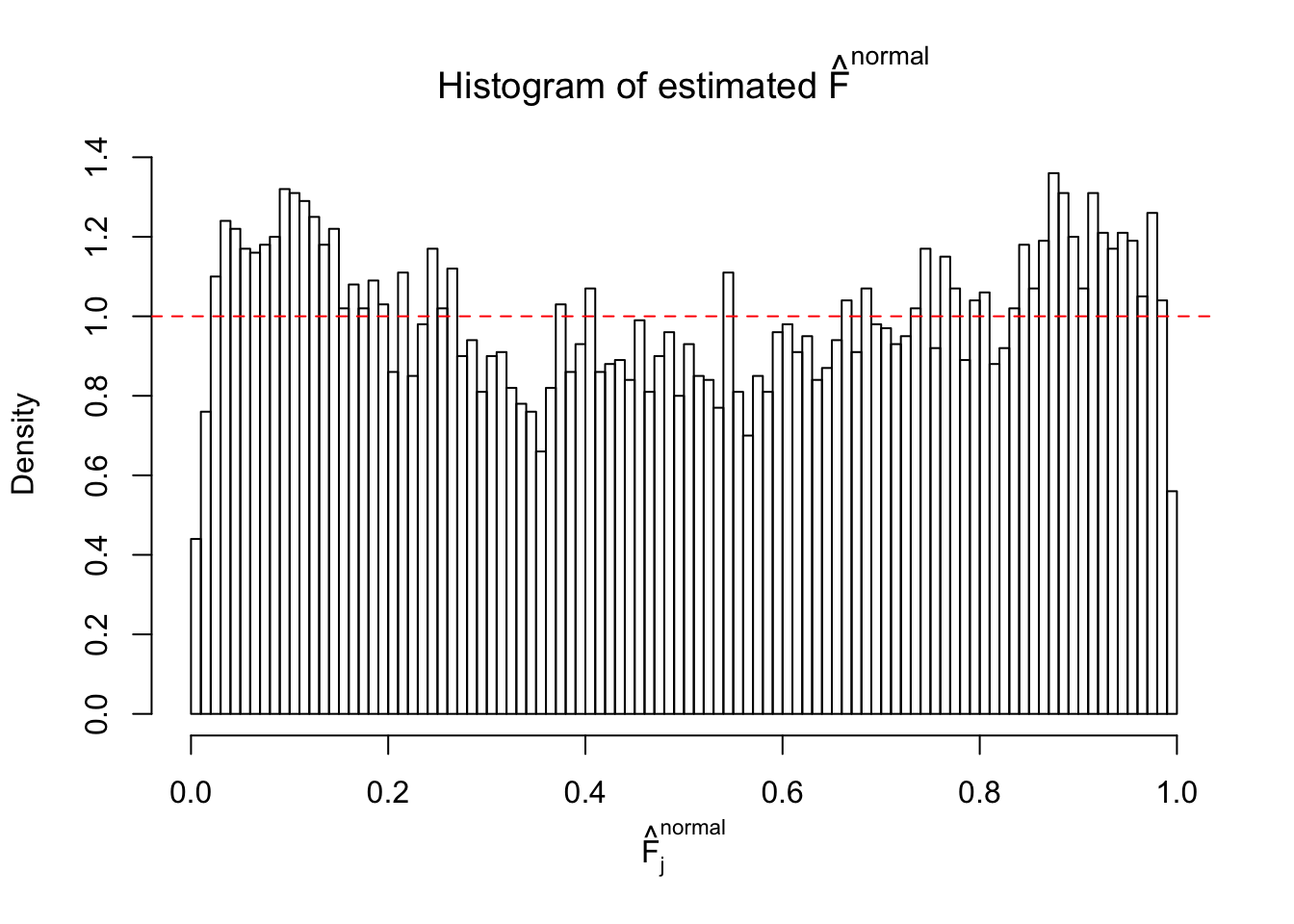
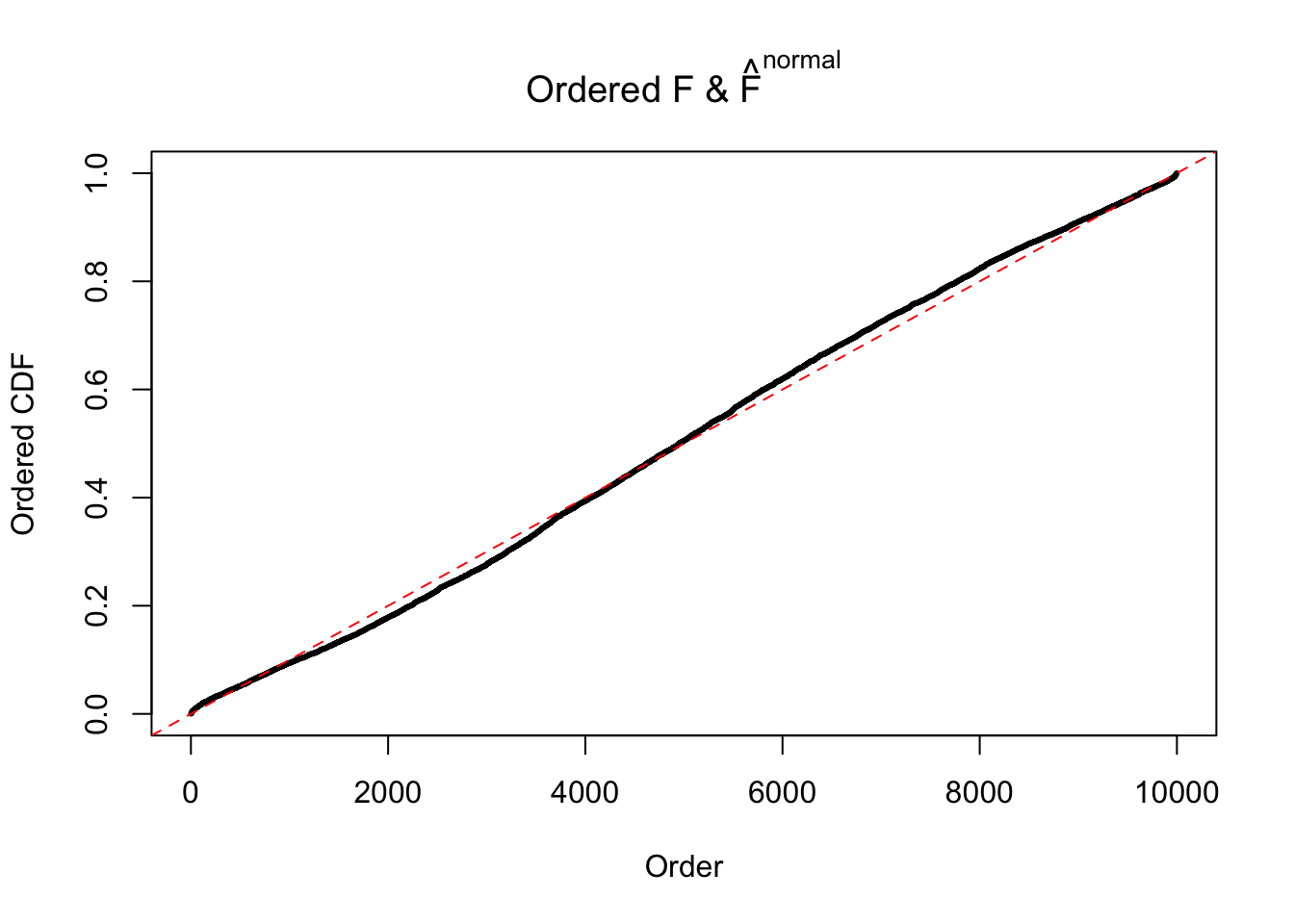
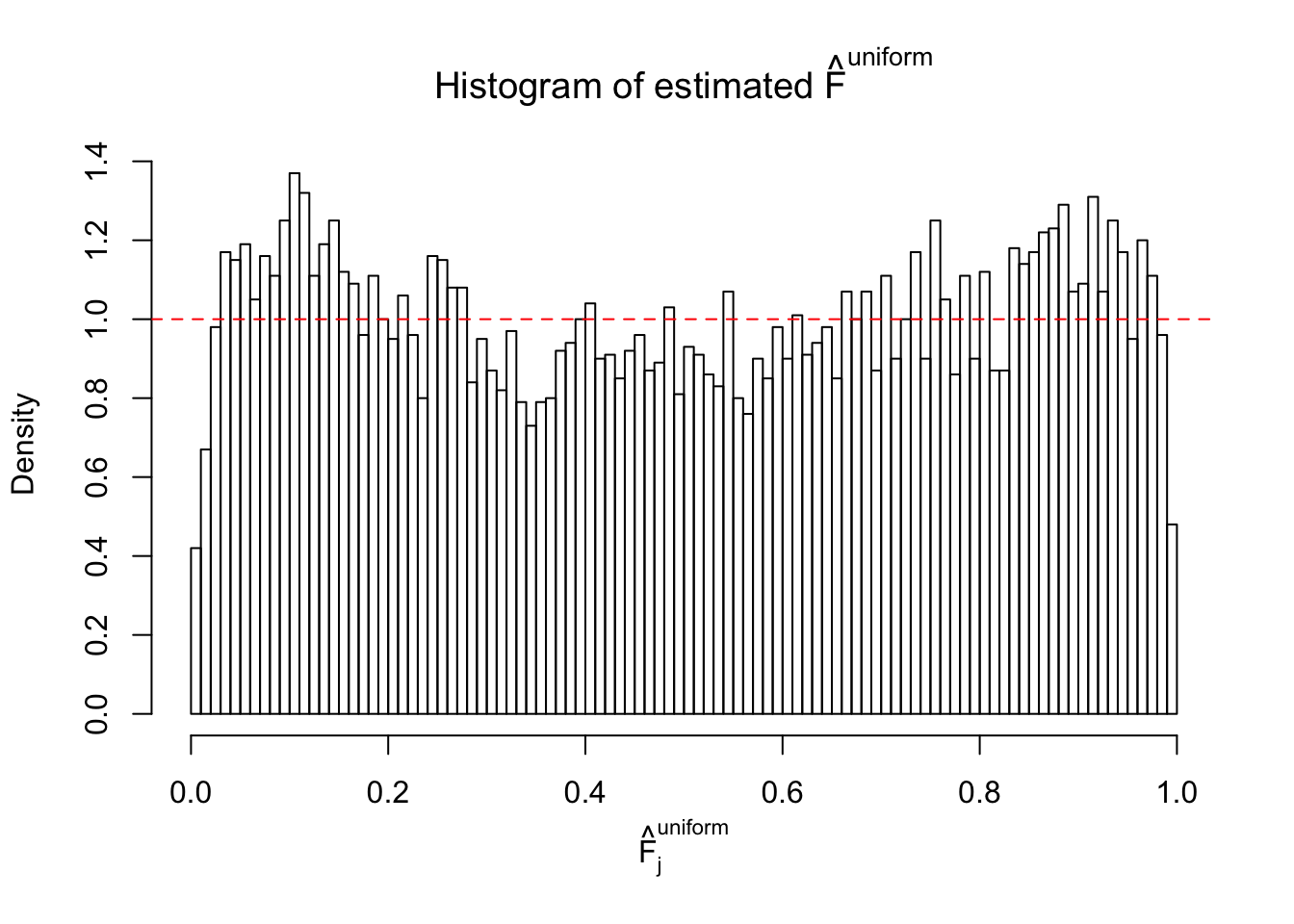
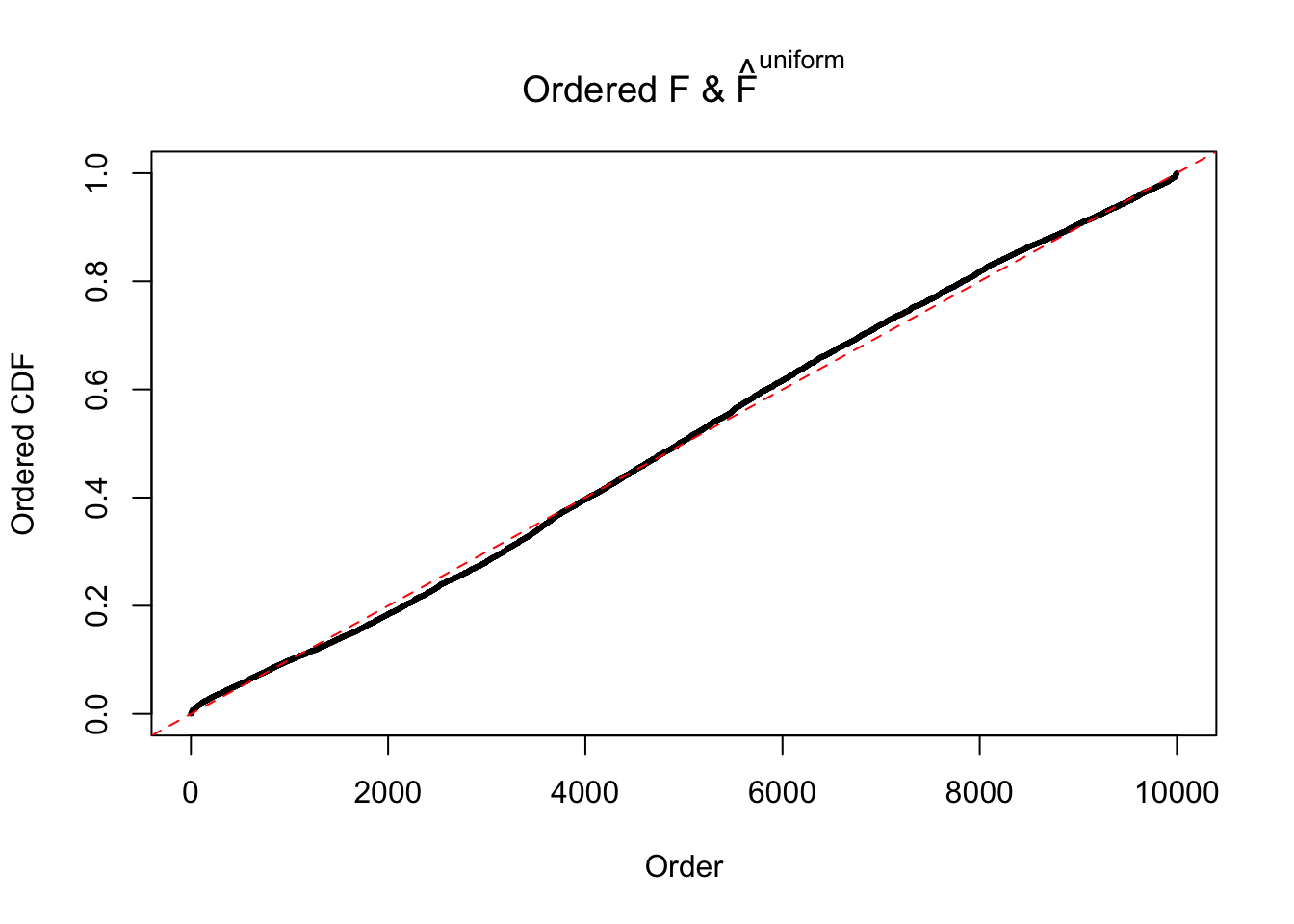
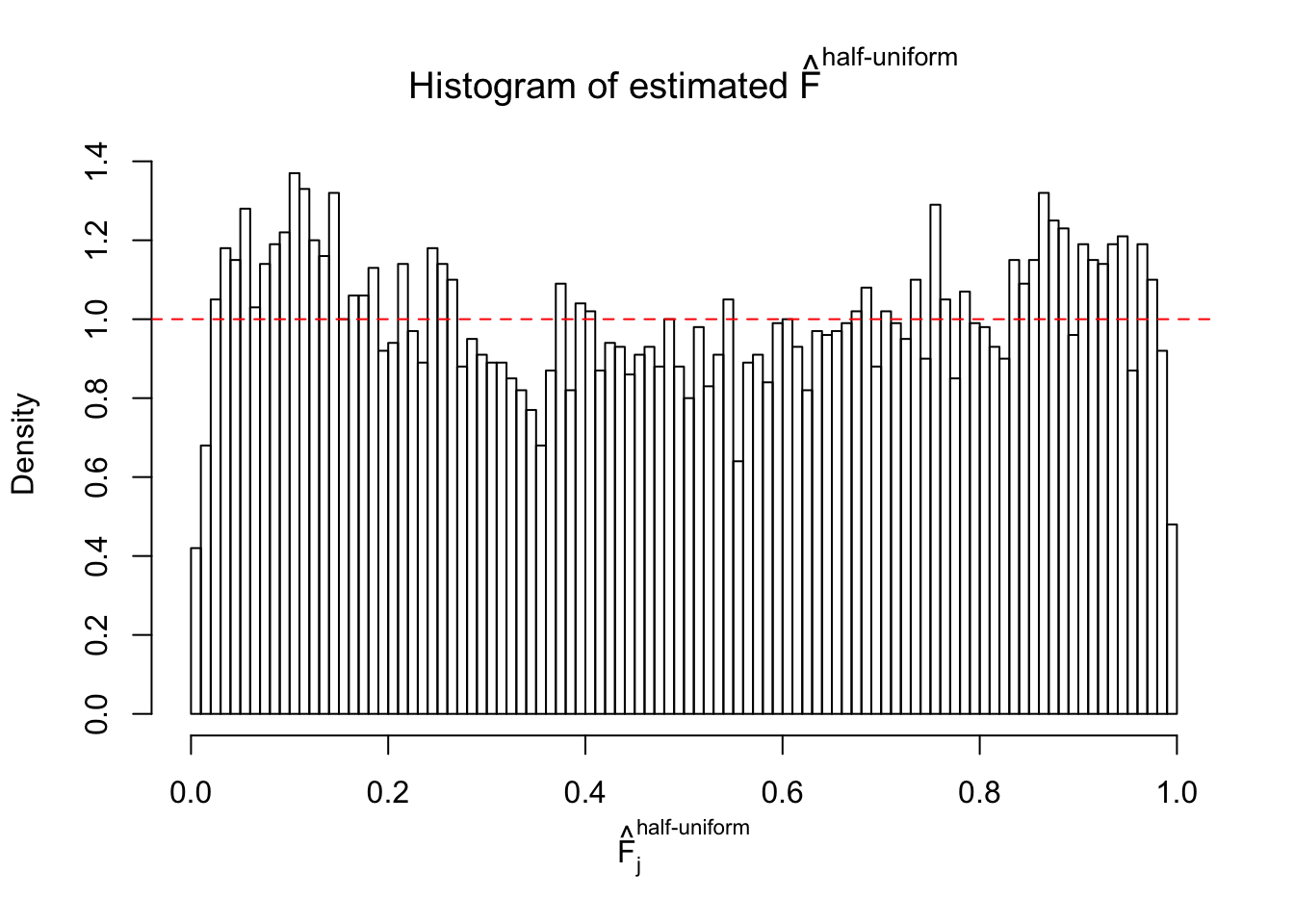
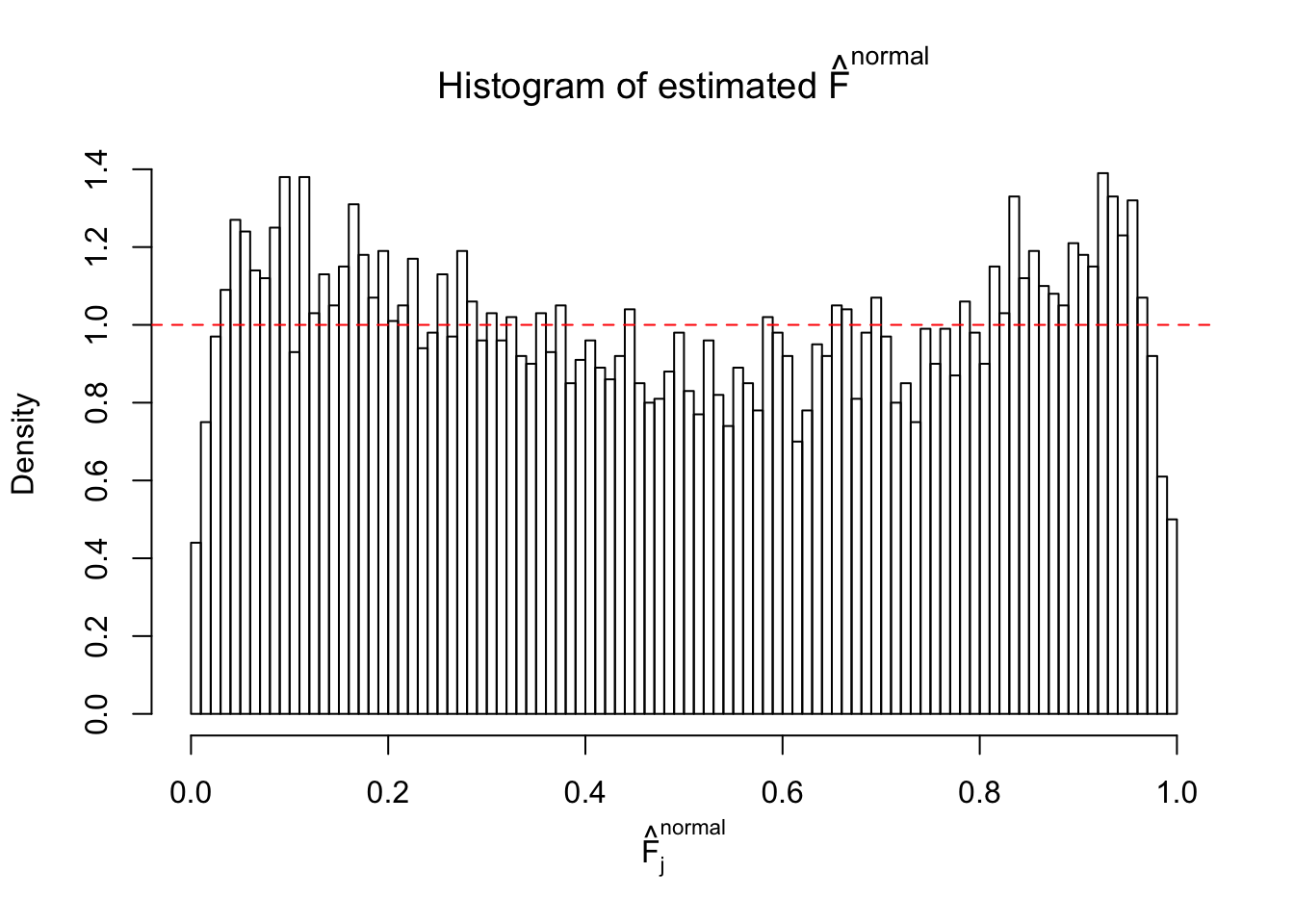
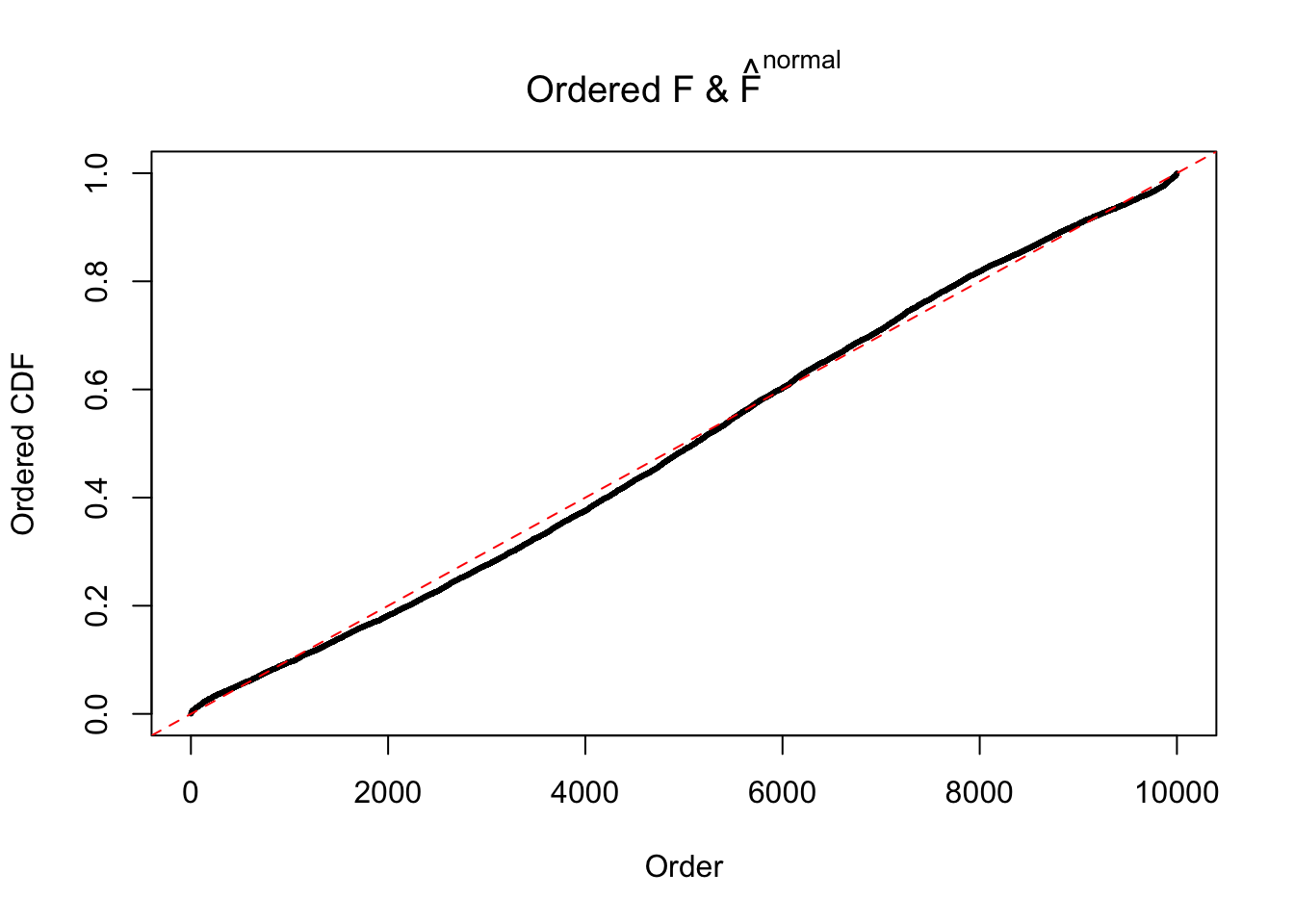
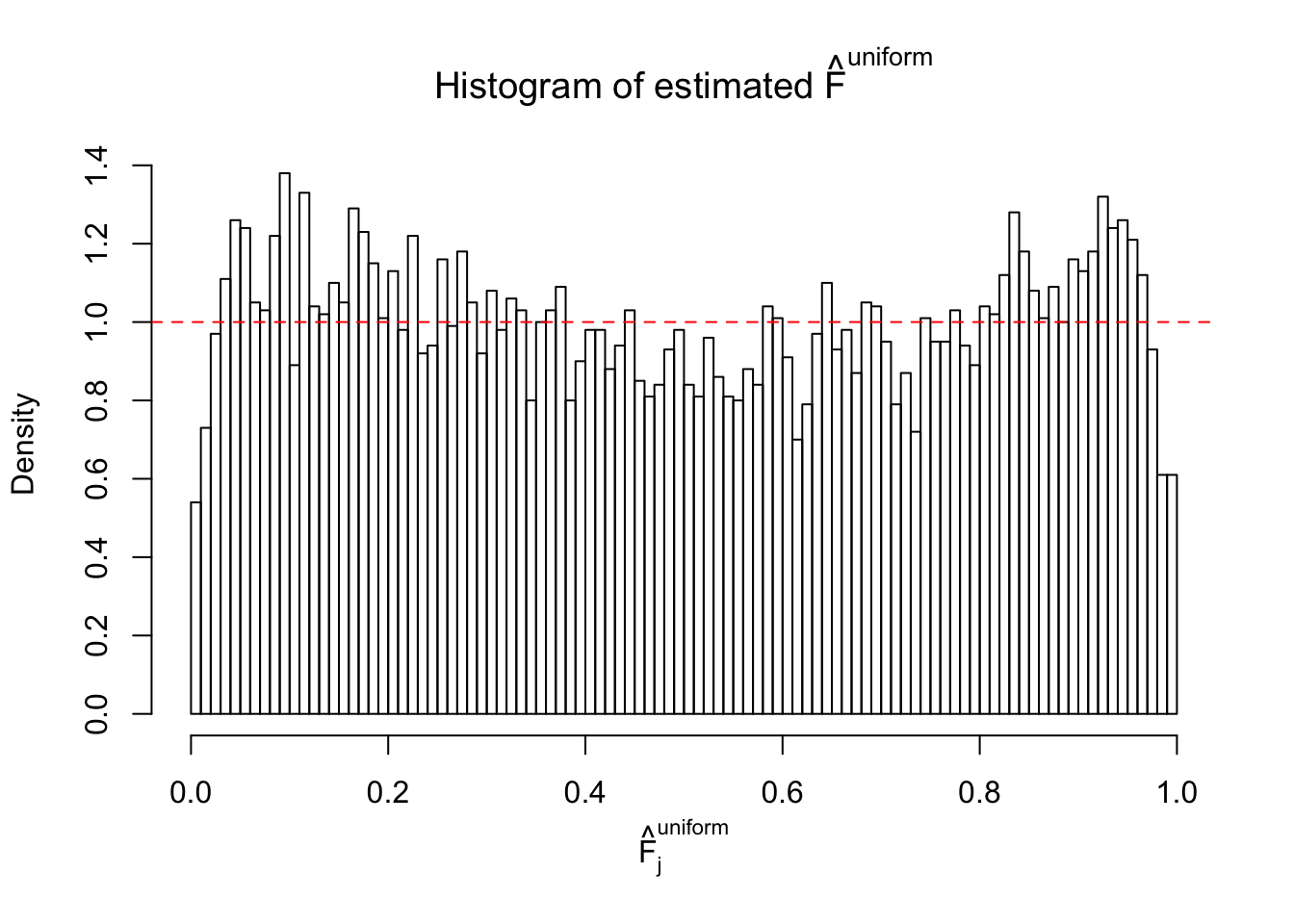
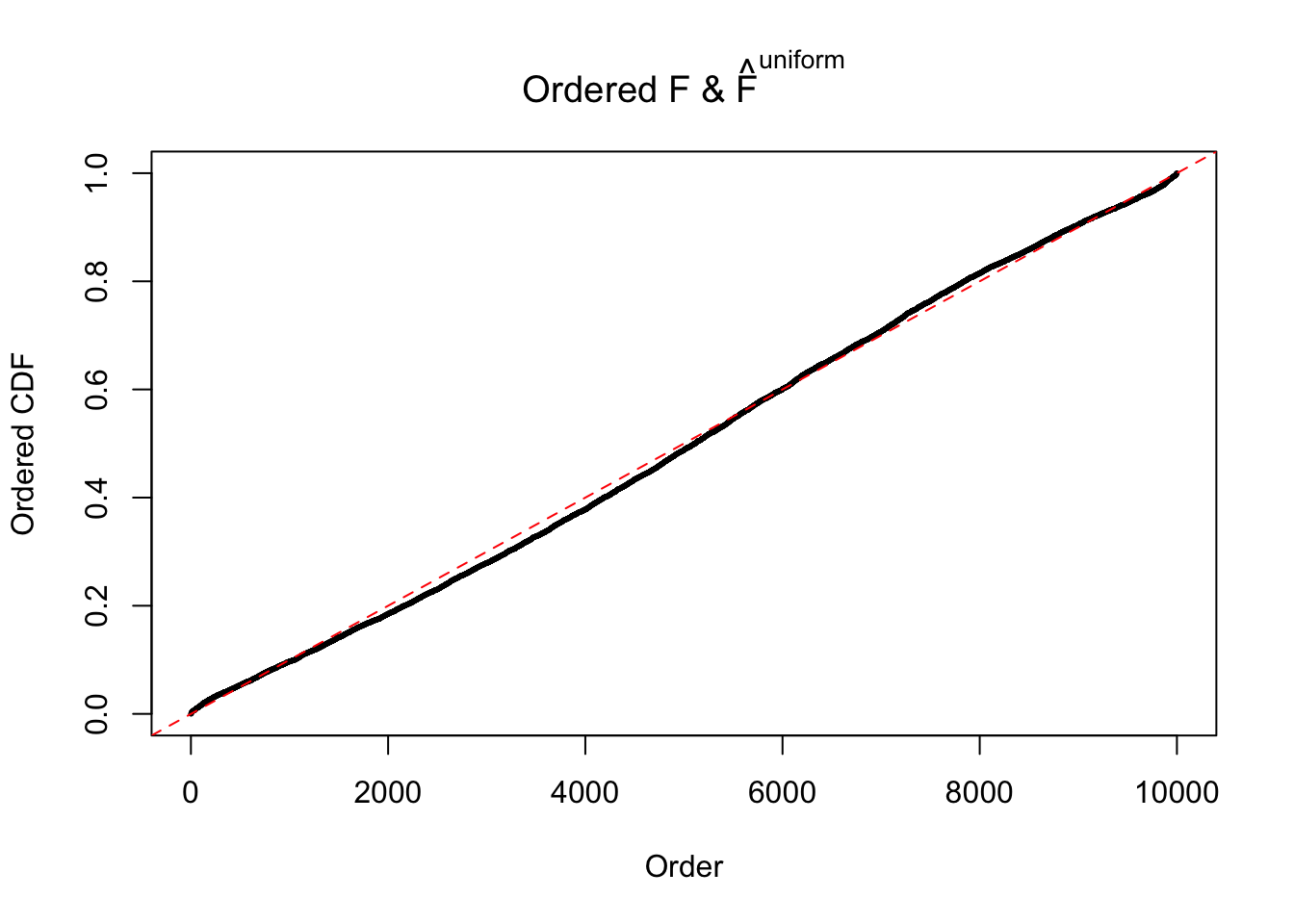
Diagnostic plots for ASH can be used to measure the goodness of fit of ASH. Breaking any of the assumptions behind ASH would make its fit less well, as shown in the non-uniformness of \(\left\{\hat F_j\right\}\), among which some cases have been discussed.
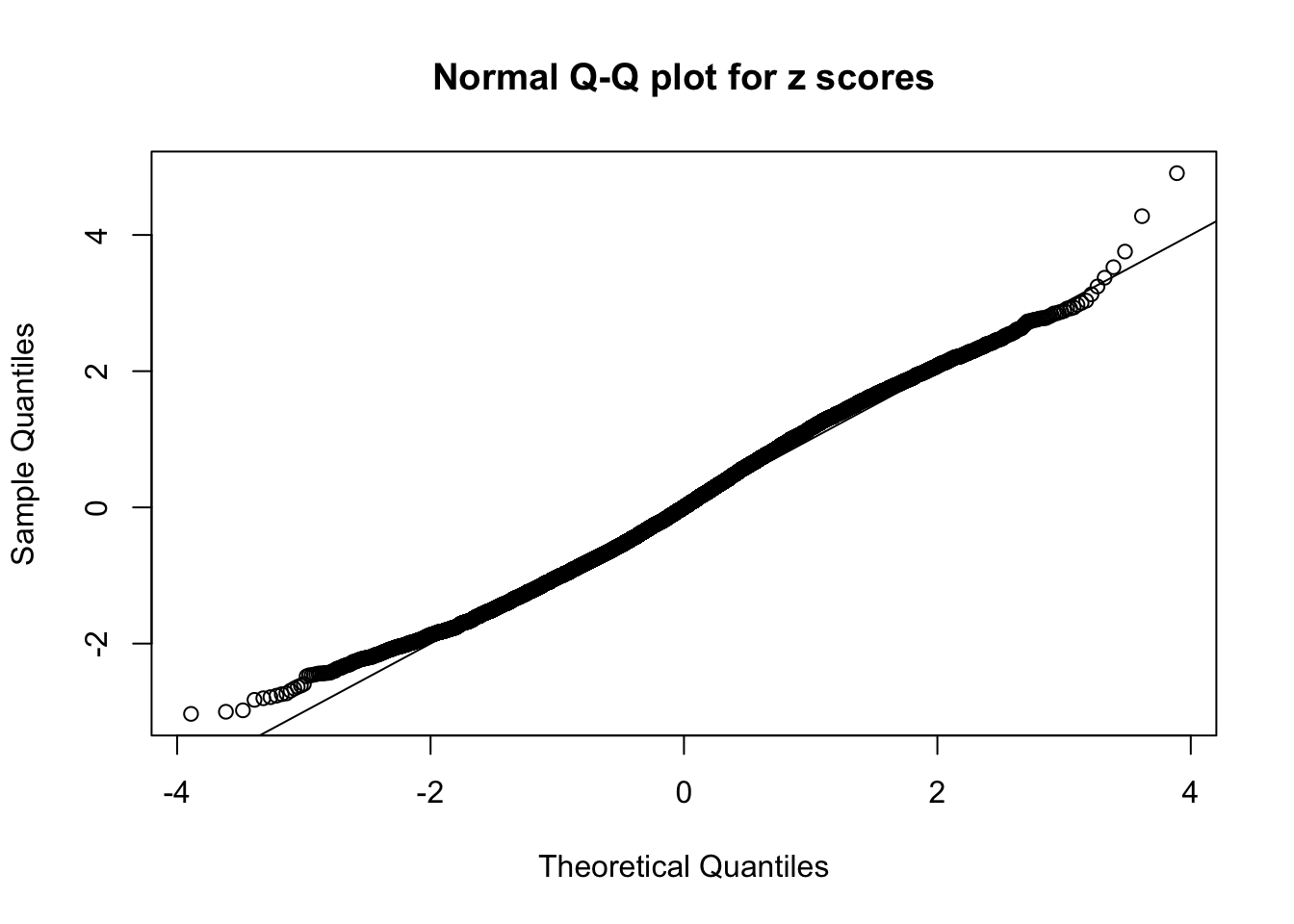
A special case closely related to this project is about correlation. The presence of correlation could affects the accuracy of estimating \(g\), as shown before. Moreover, the correlation will inflate the empirical distribution of the correlated noise, making it less regular, thus less able to be captured by the mixture of normals or uniforms as in ASH.
Dignostic plots for all BH-hostile data sets
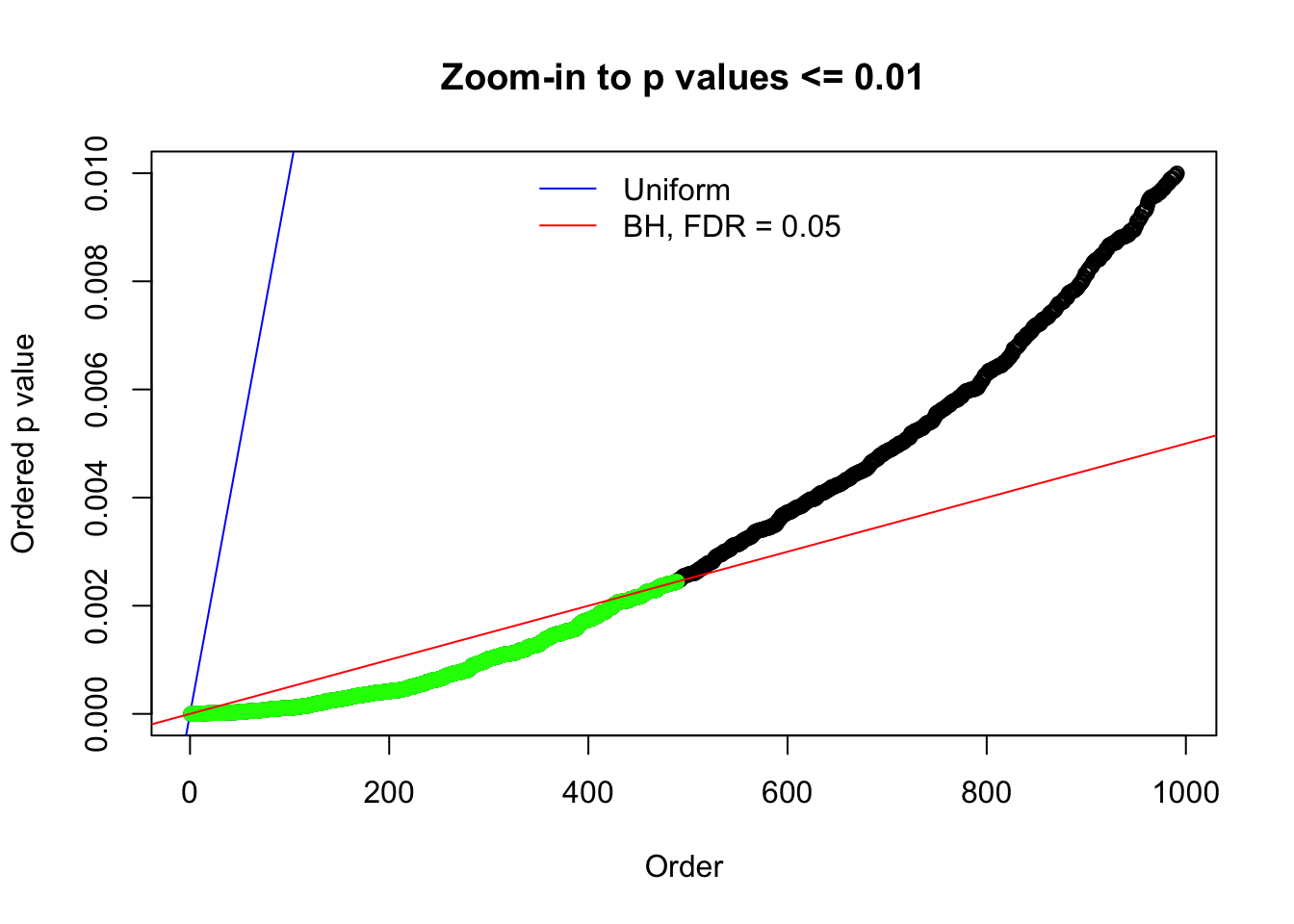
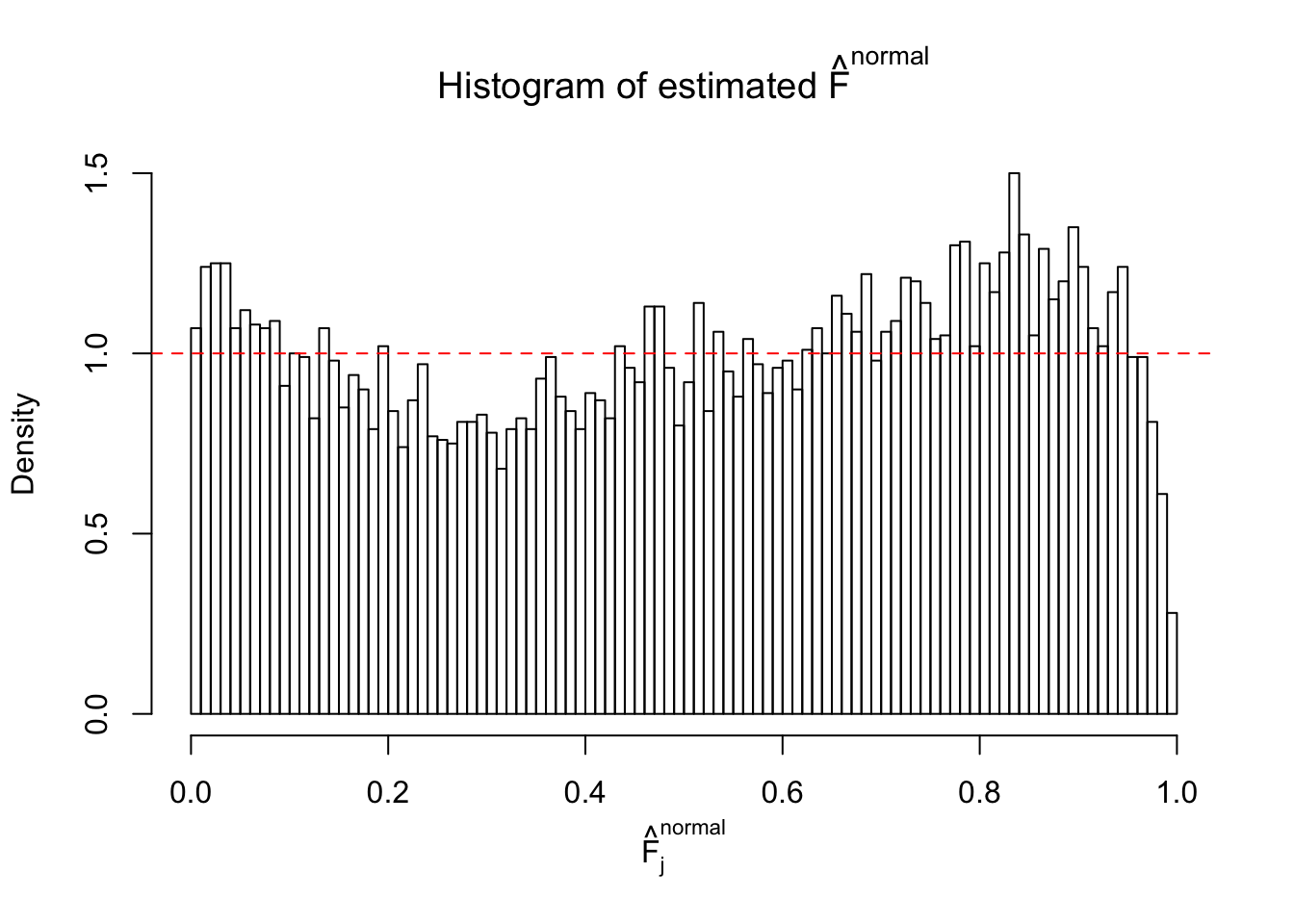
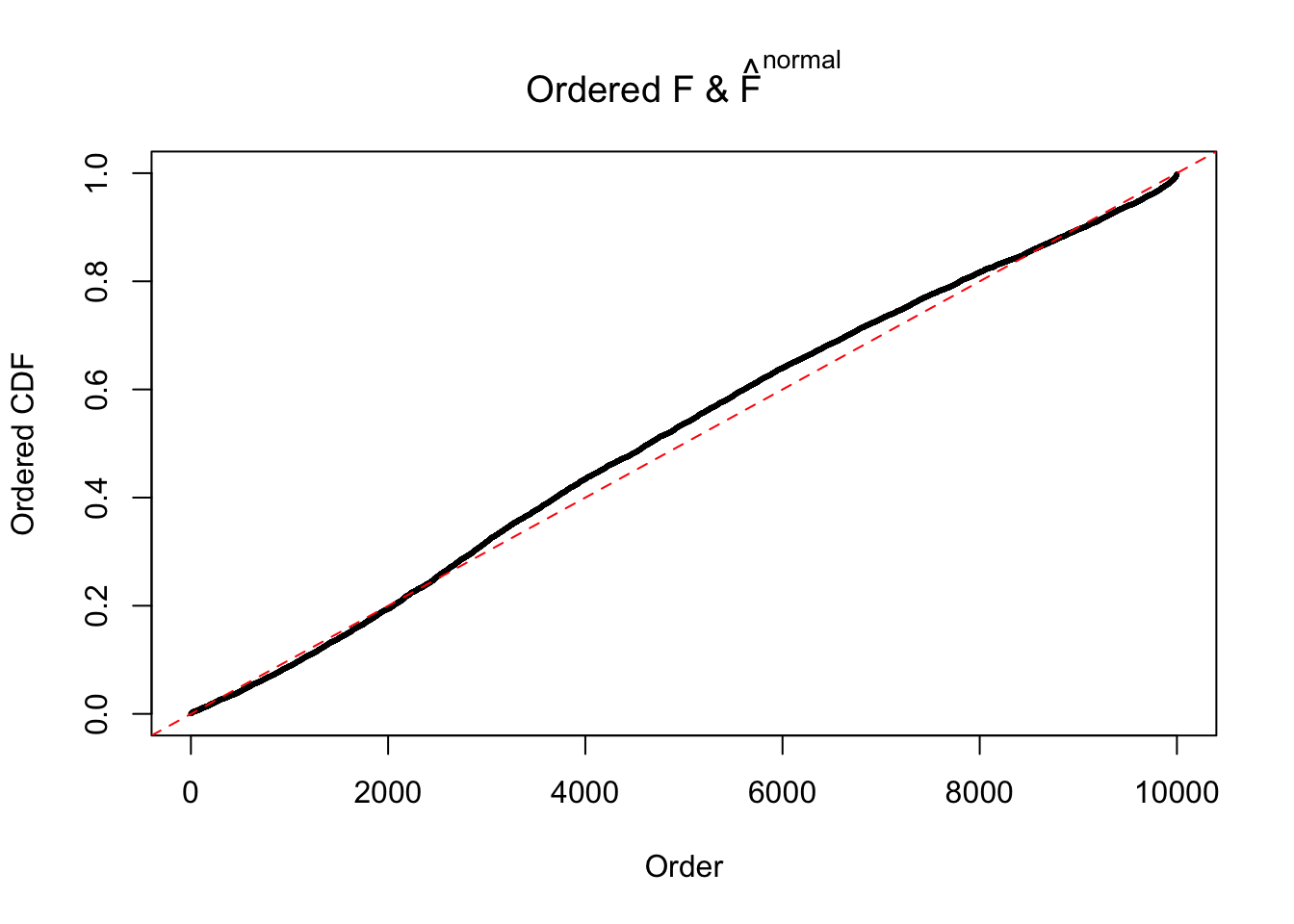
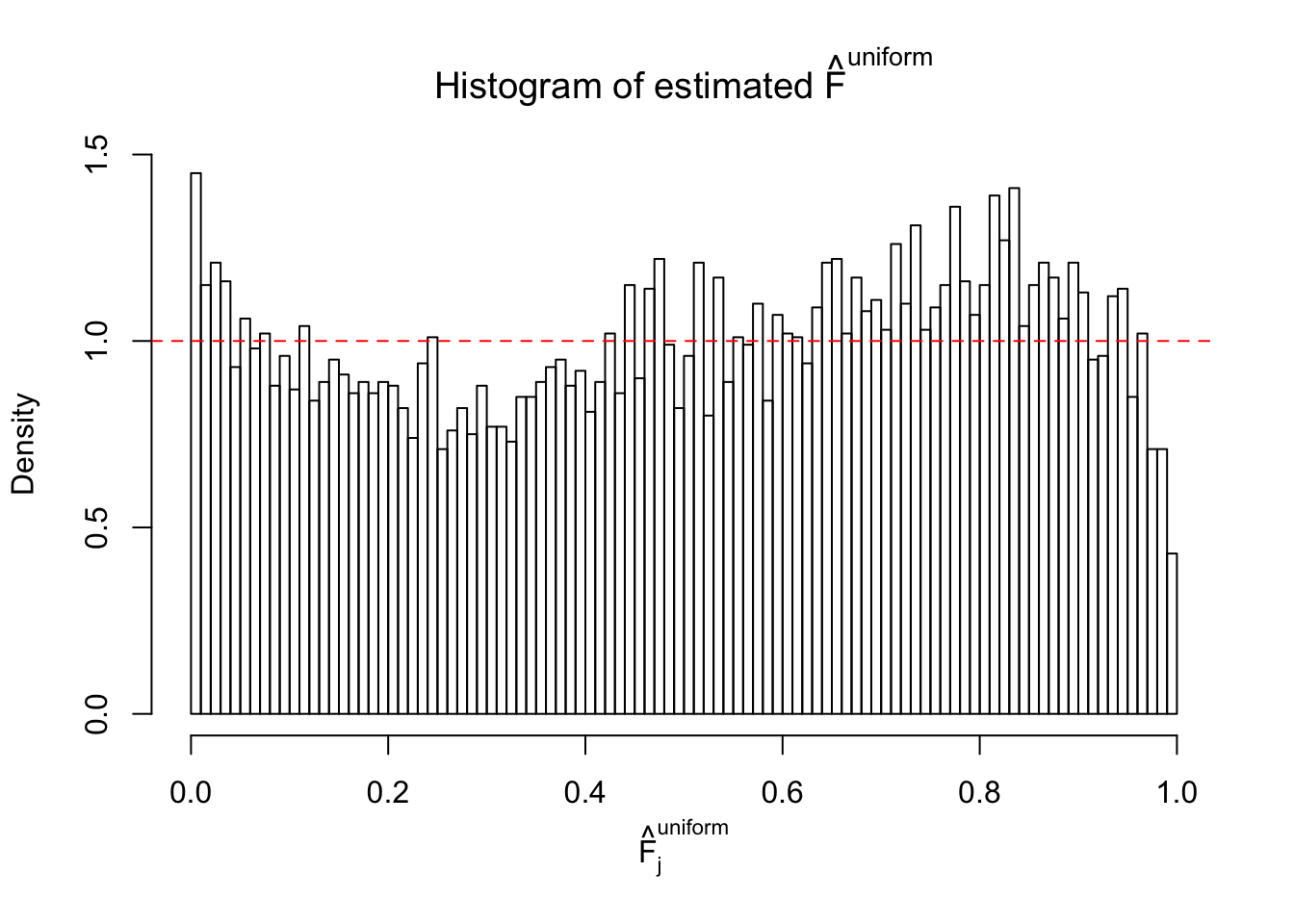
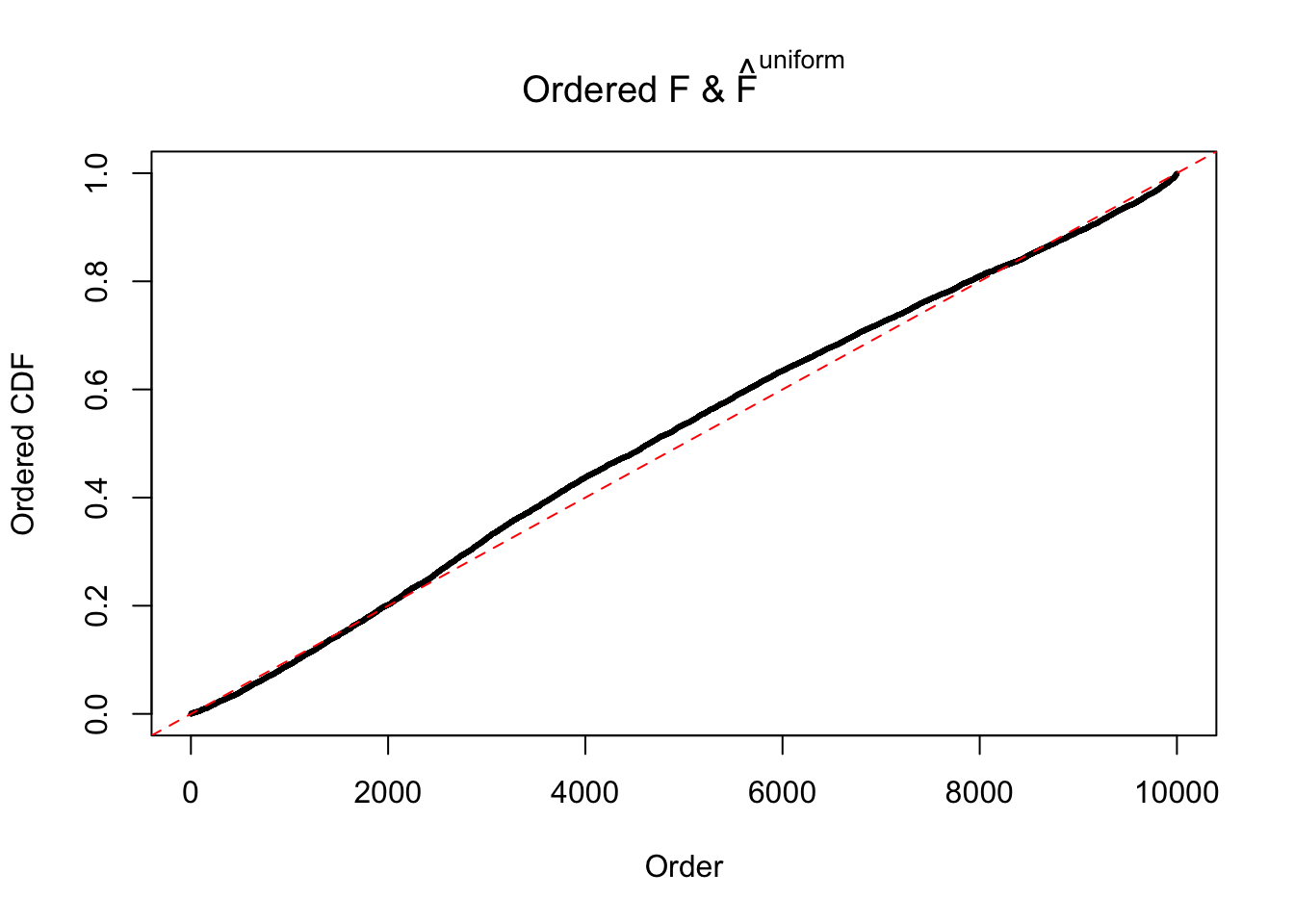
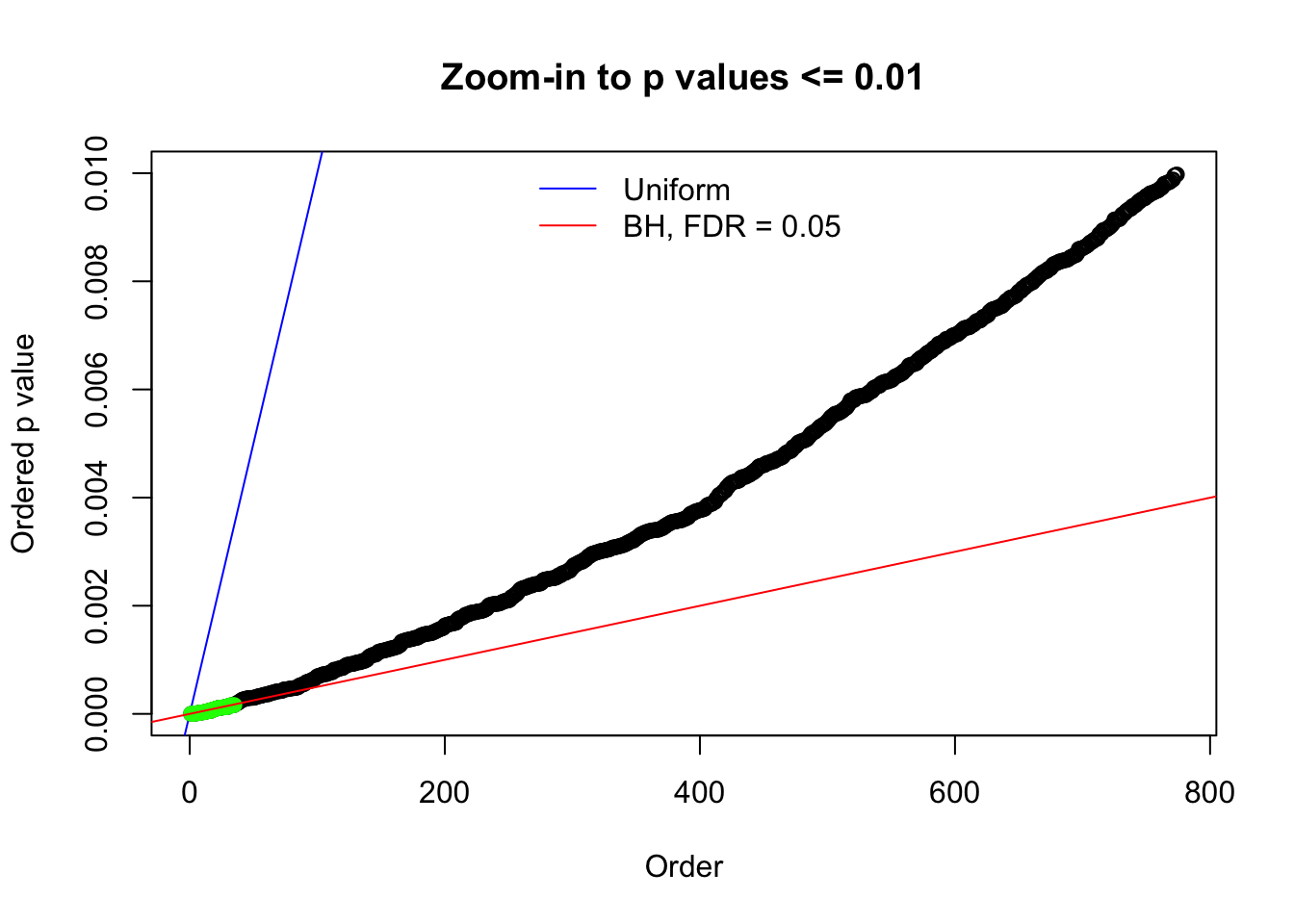
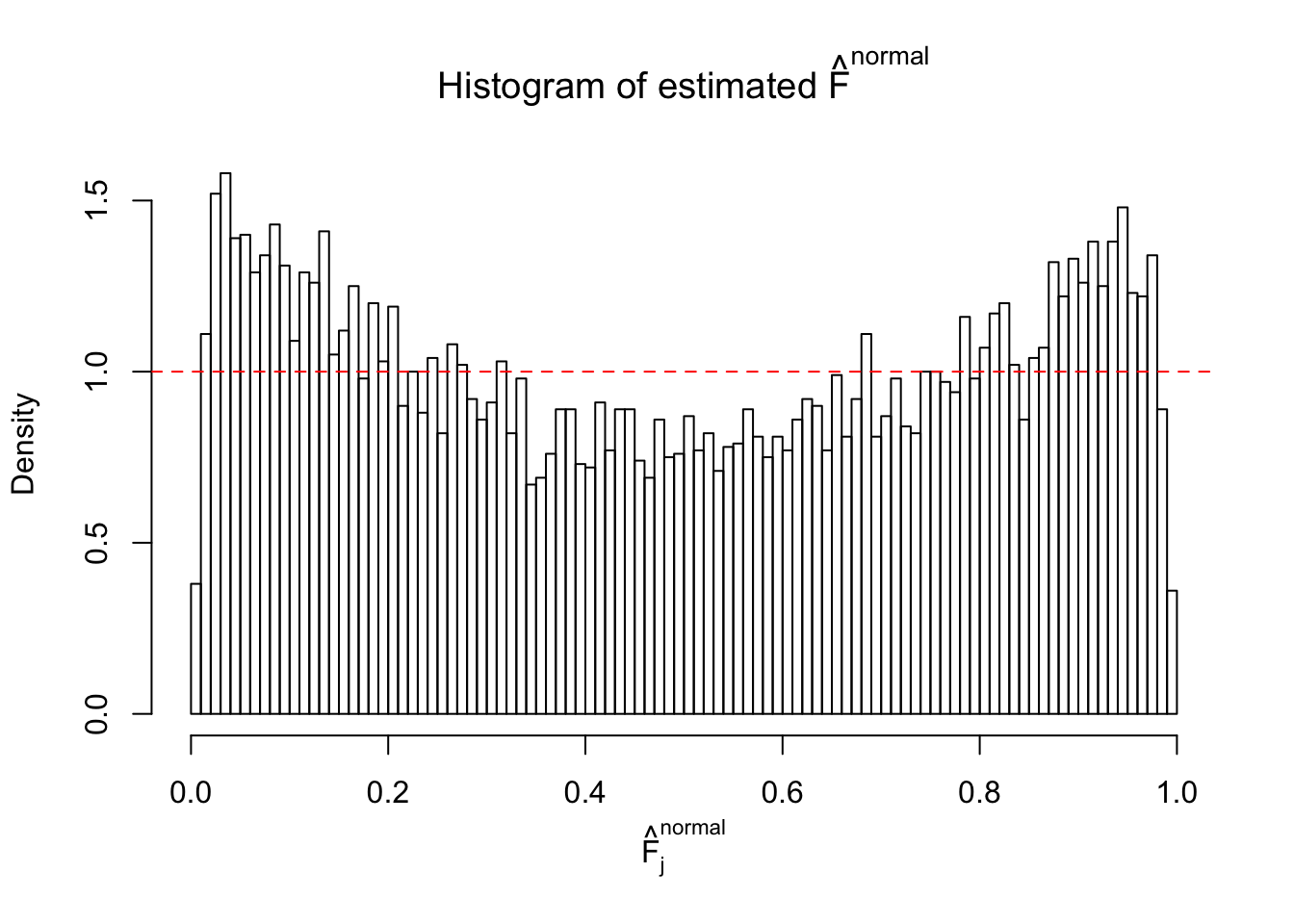
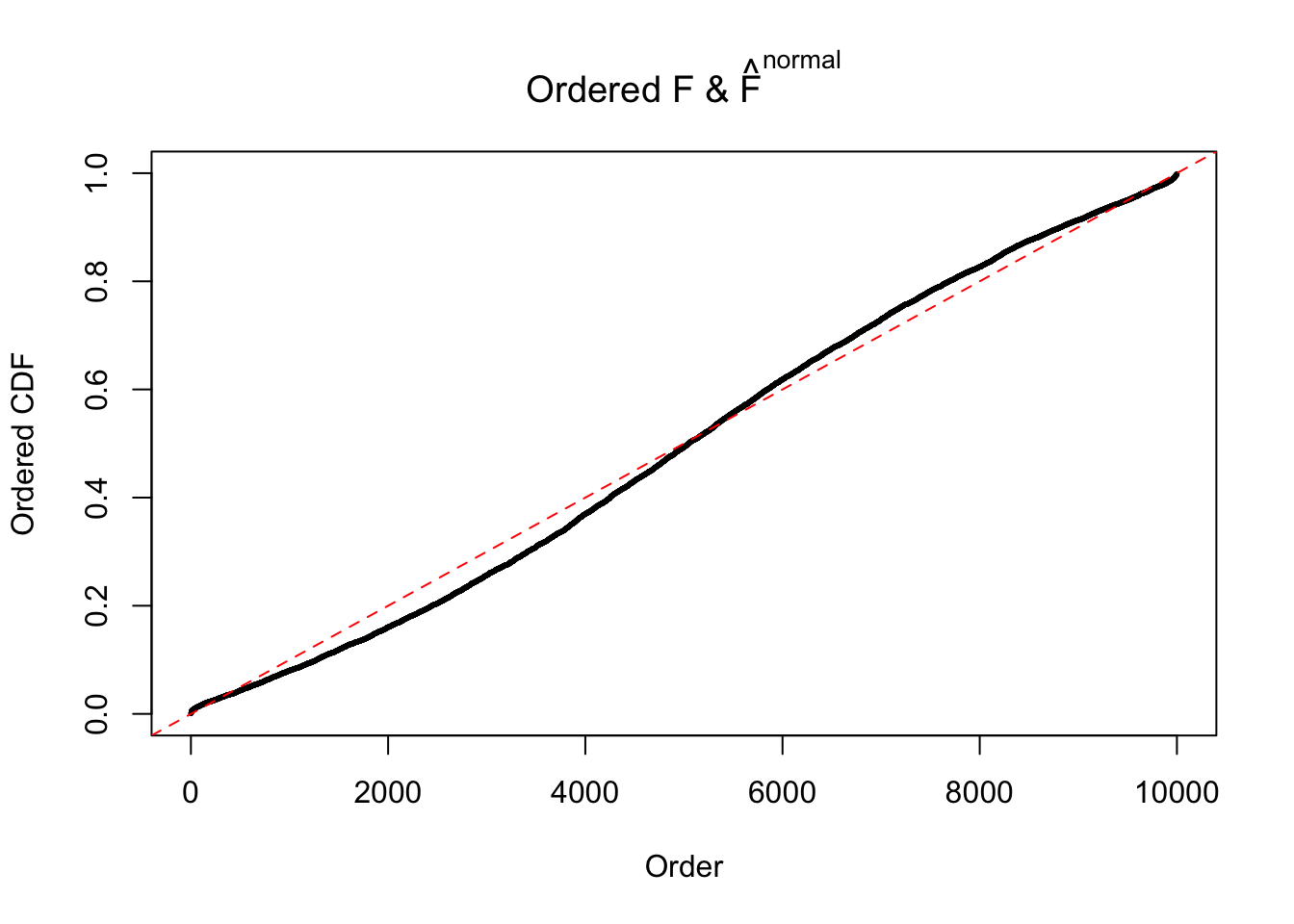
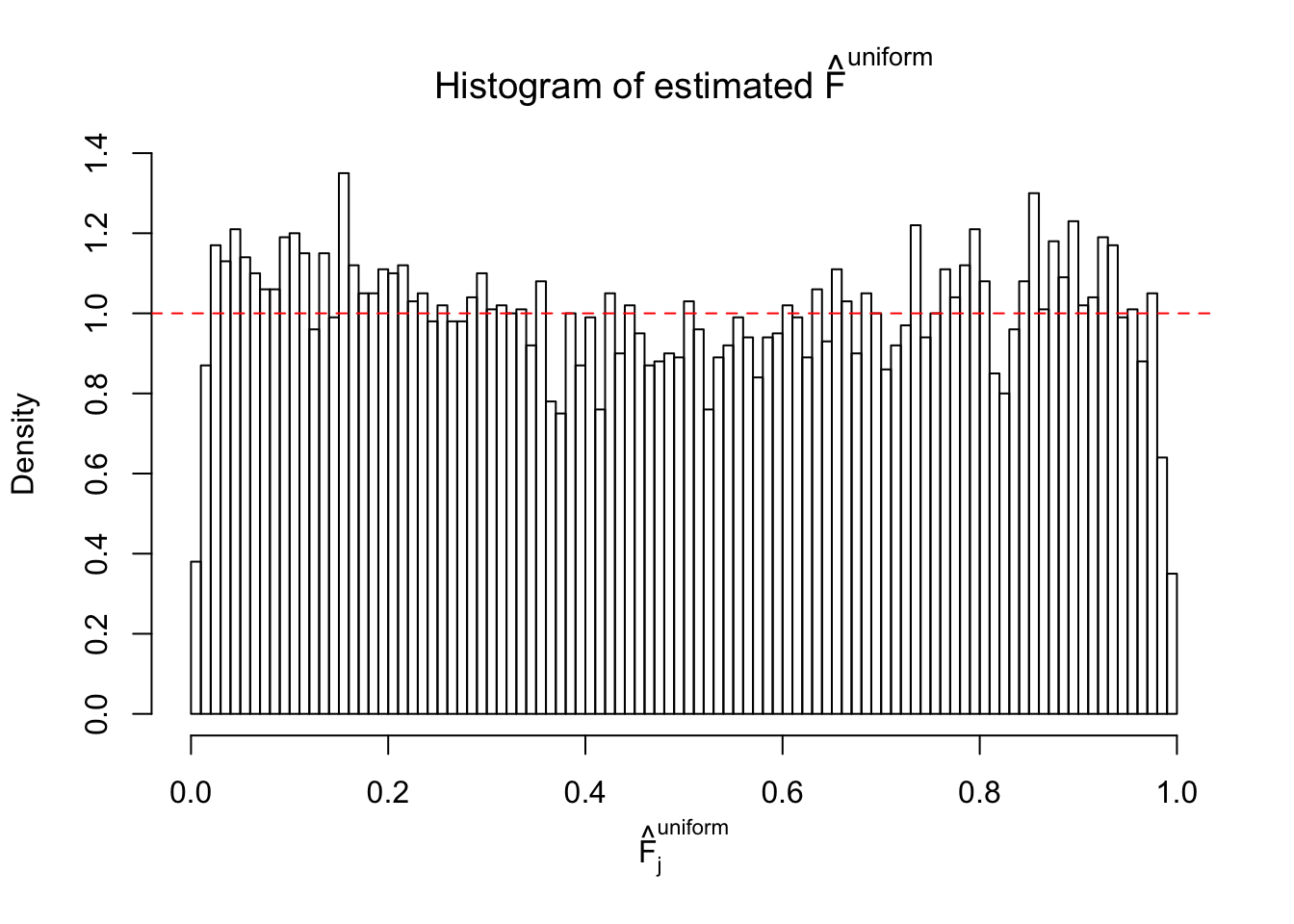
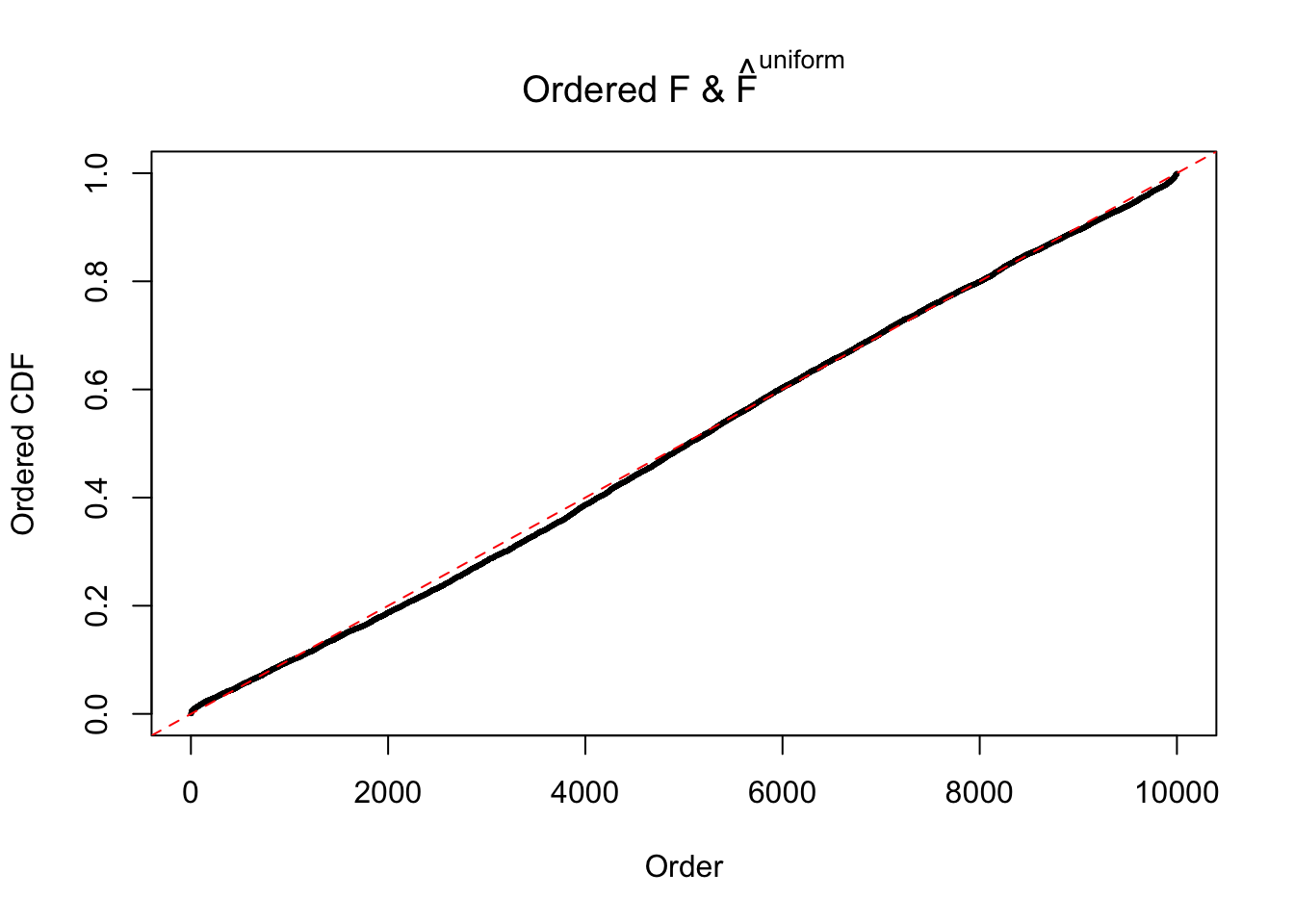
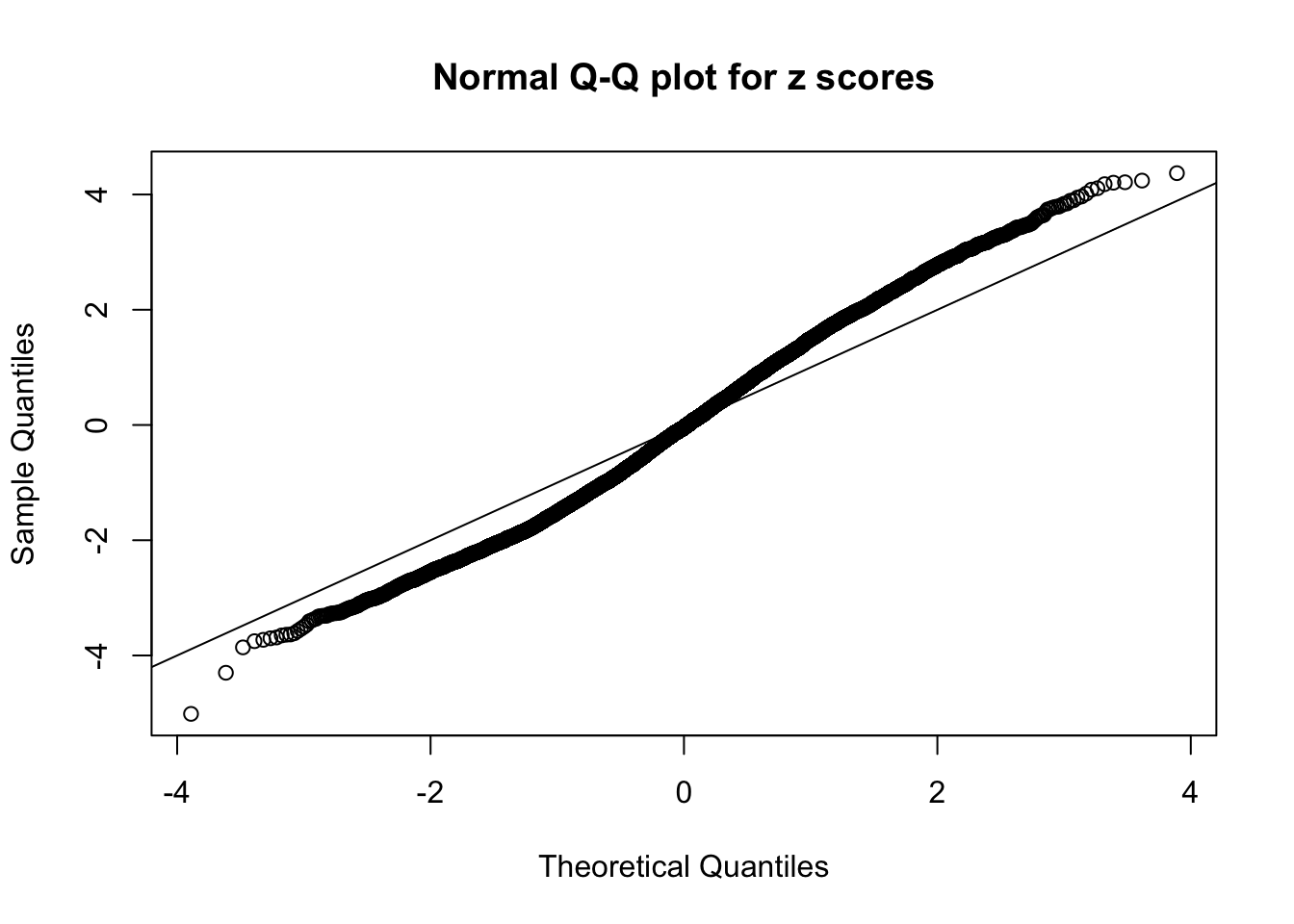
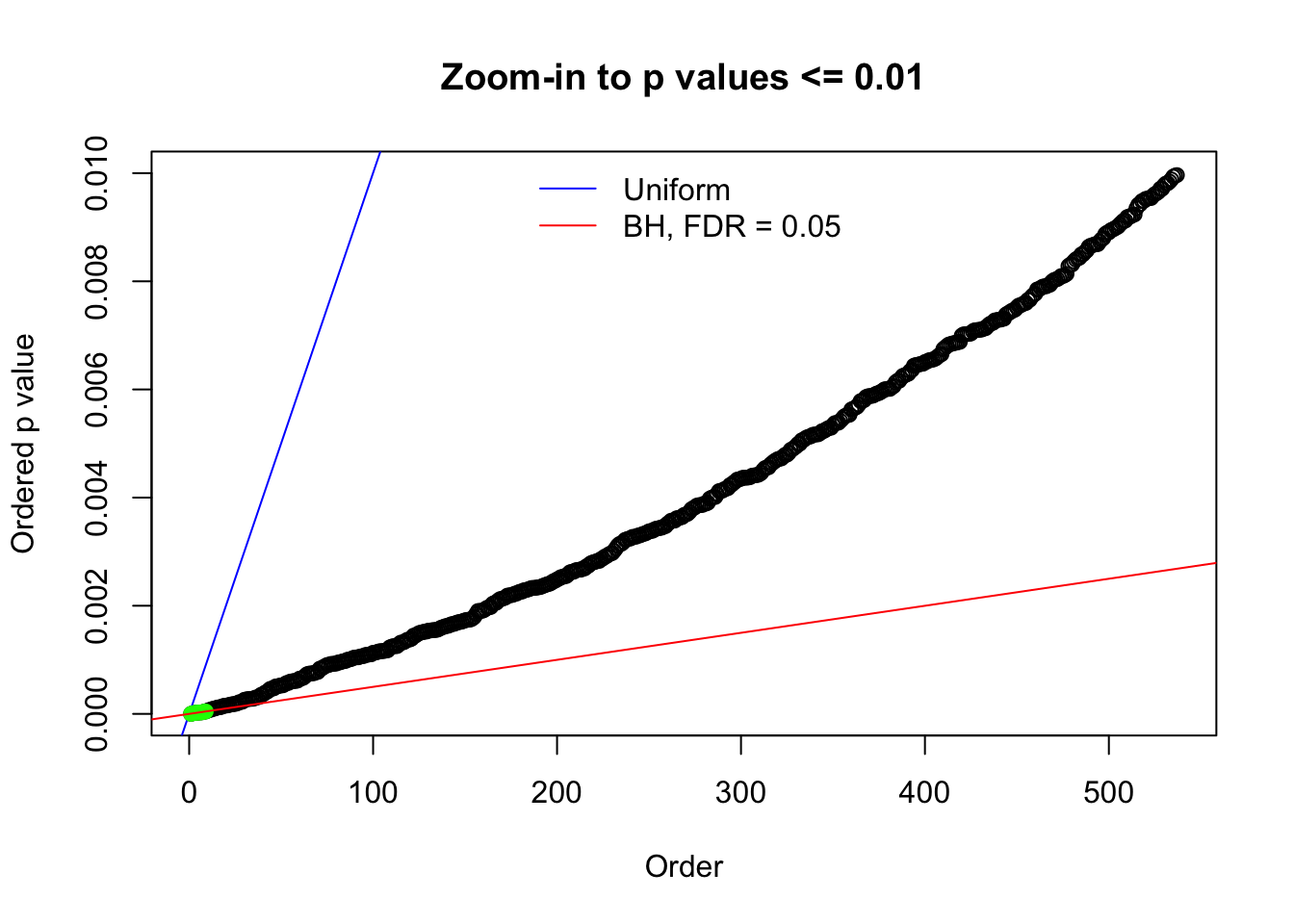
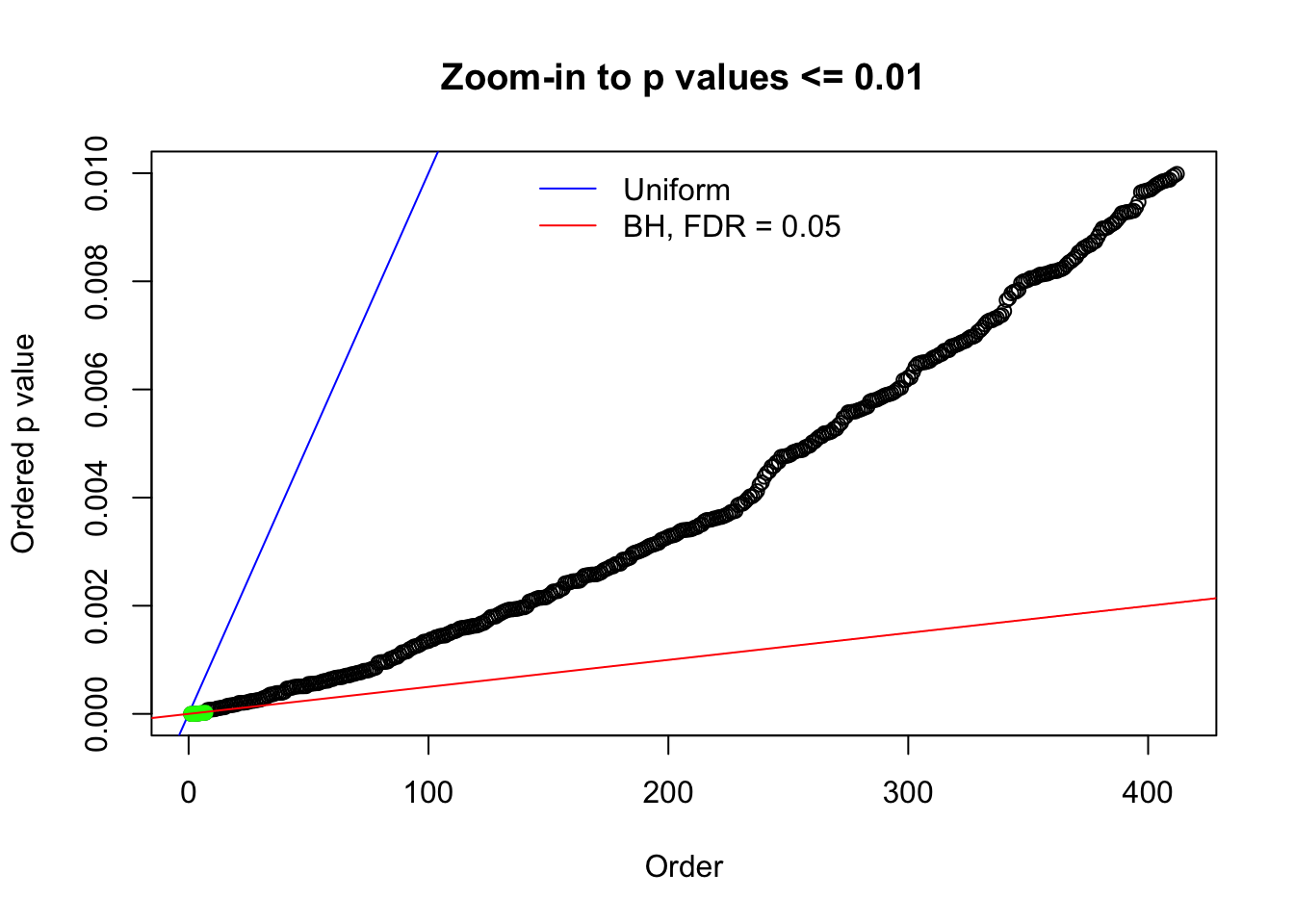
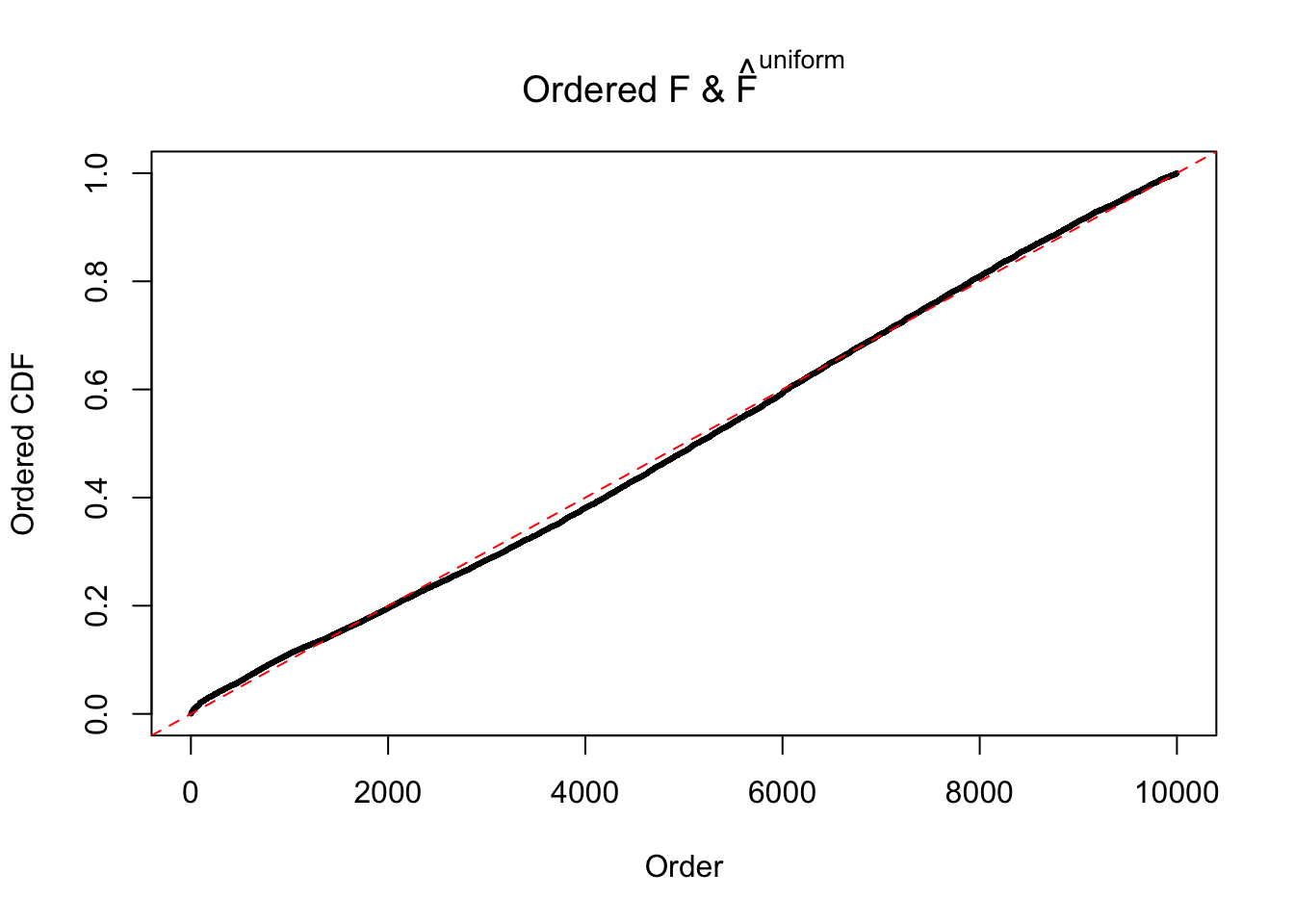
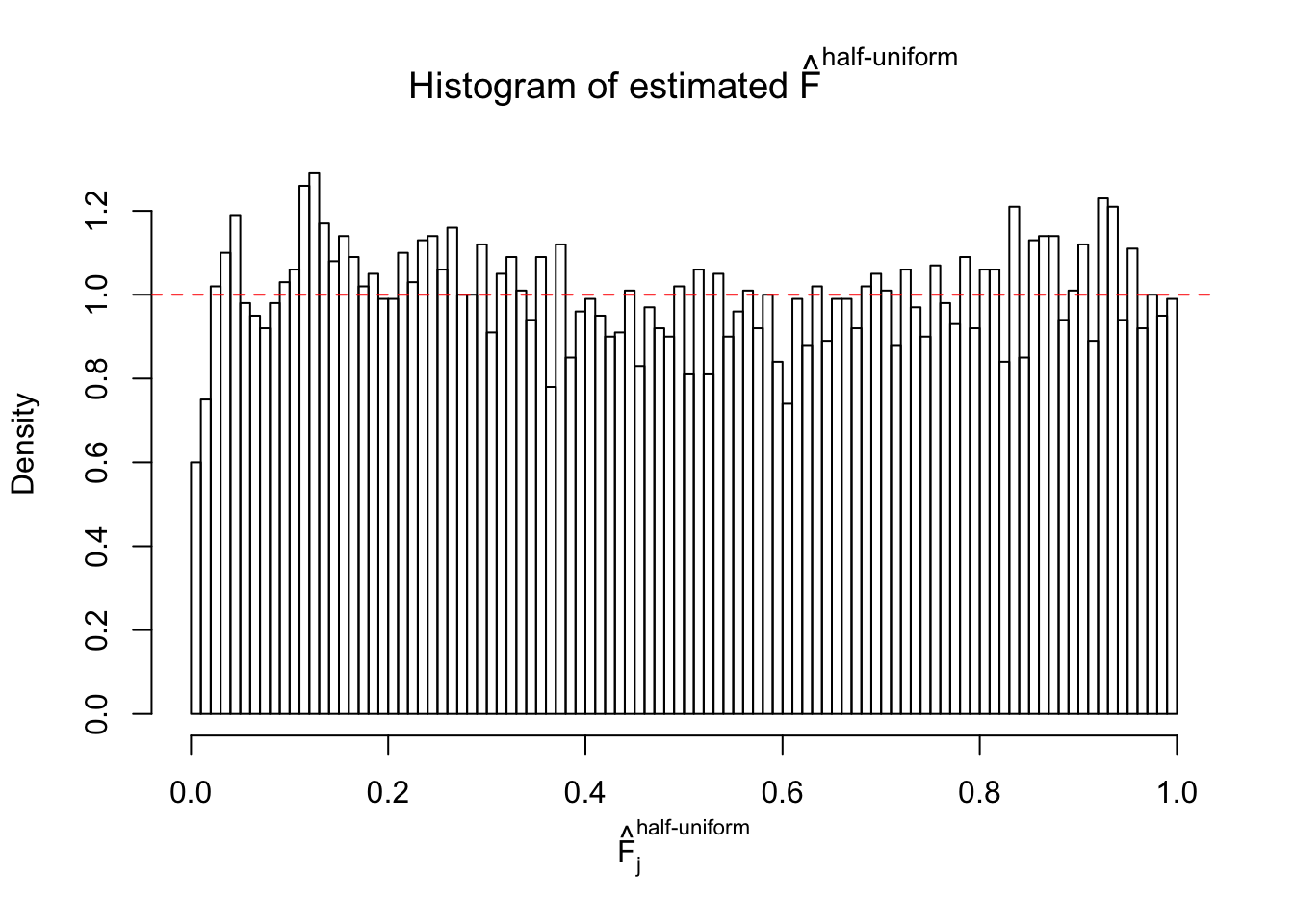
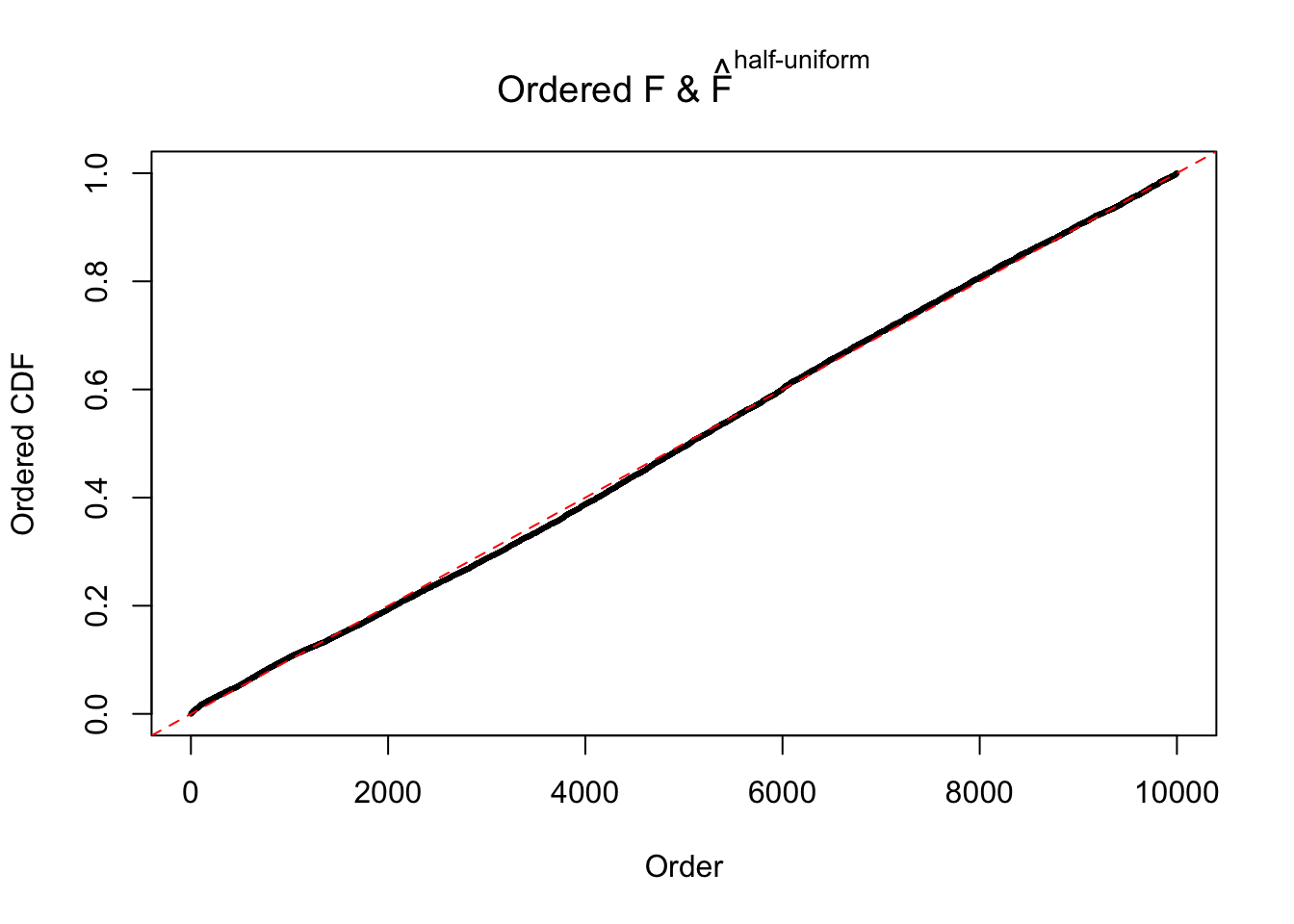
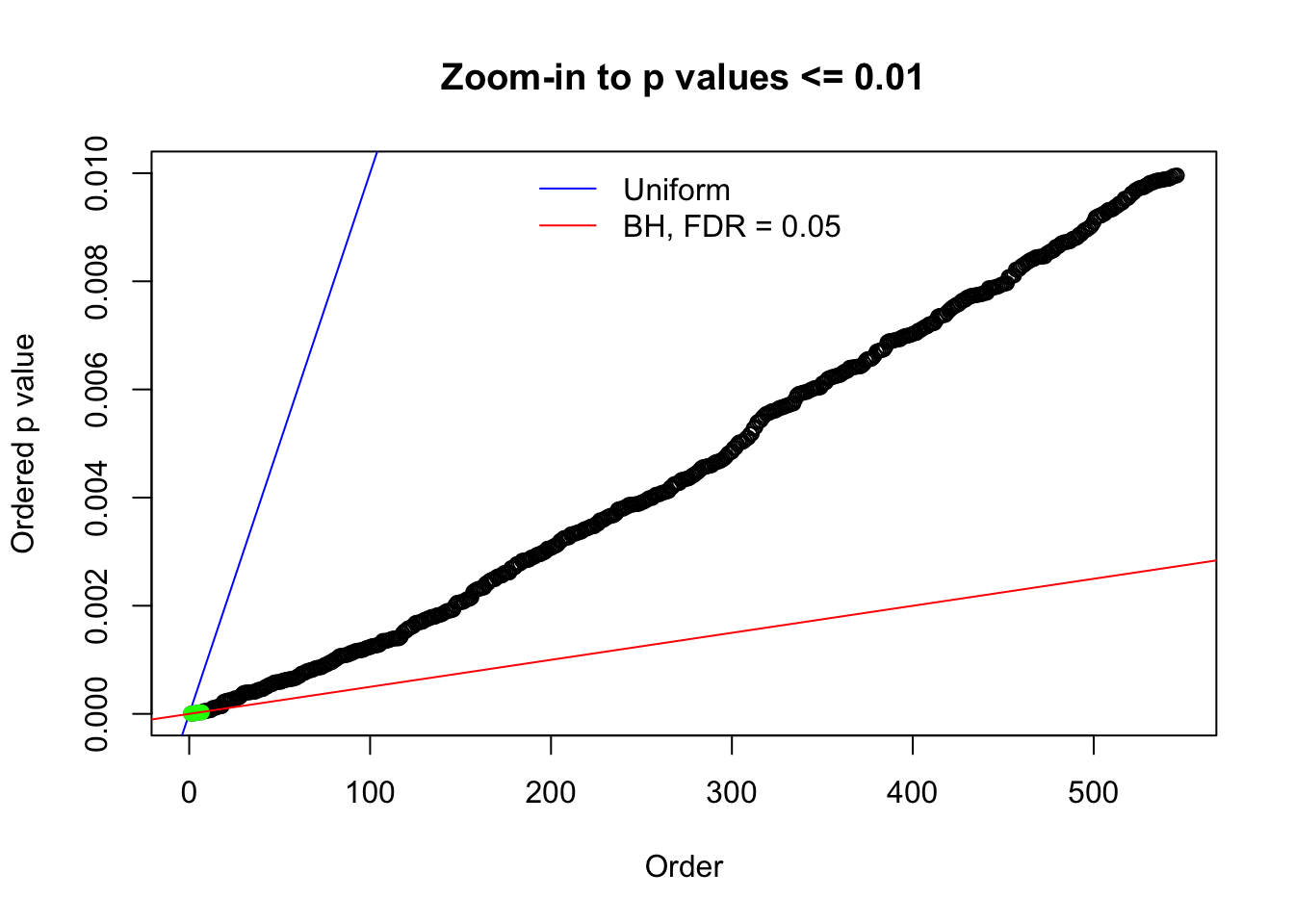
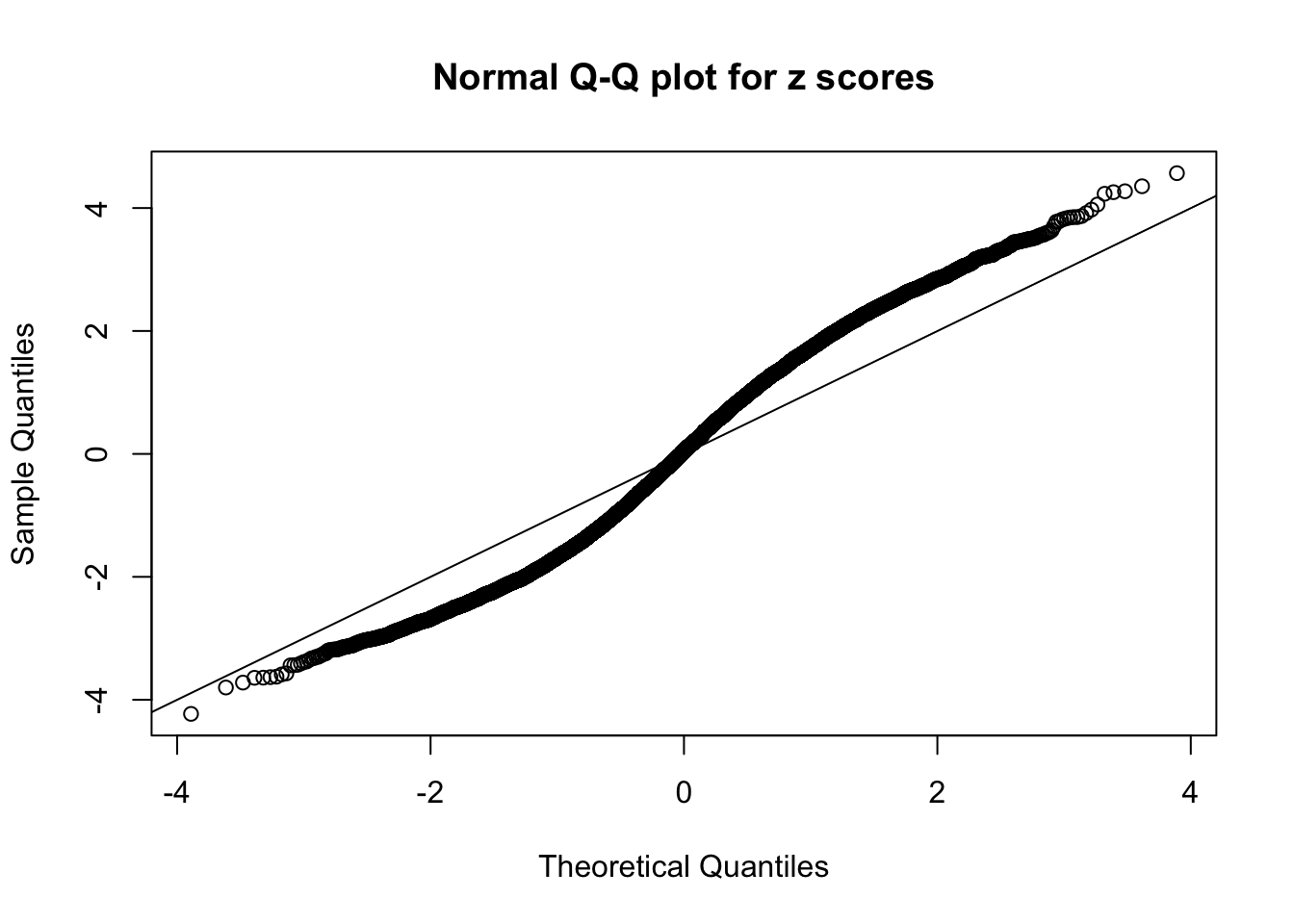
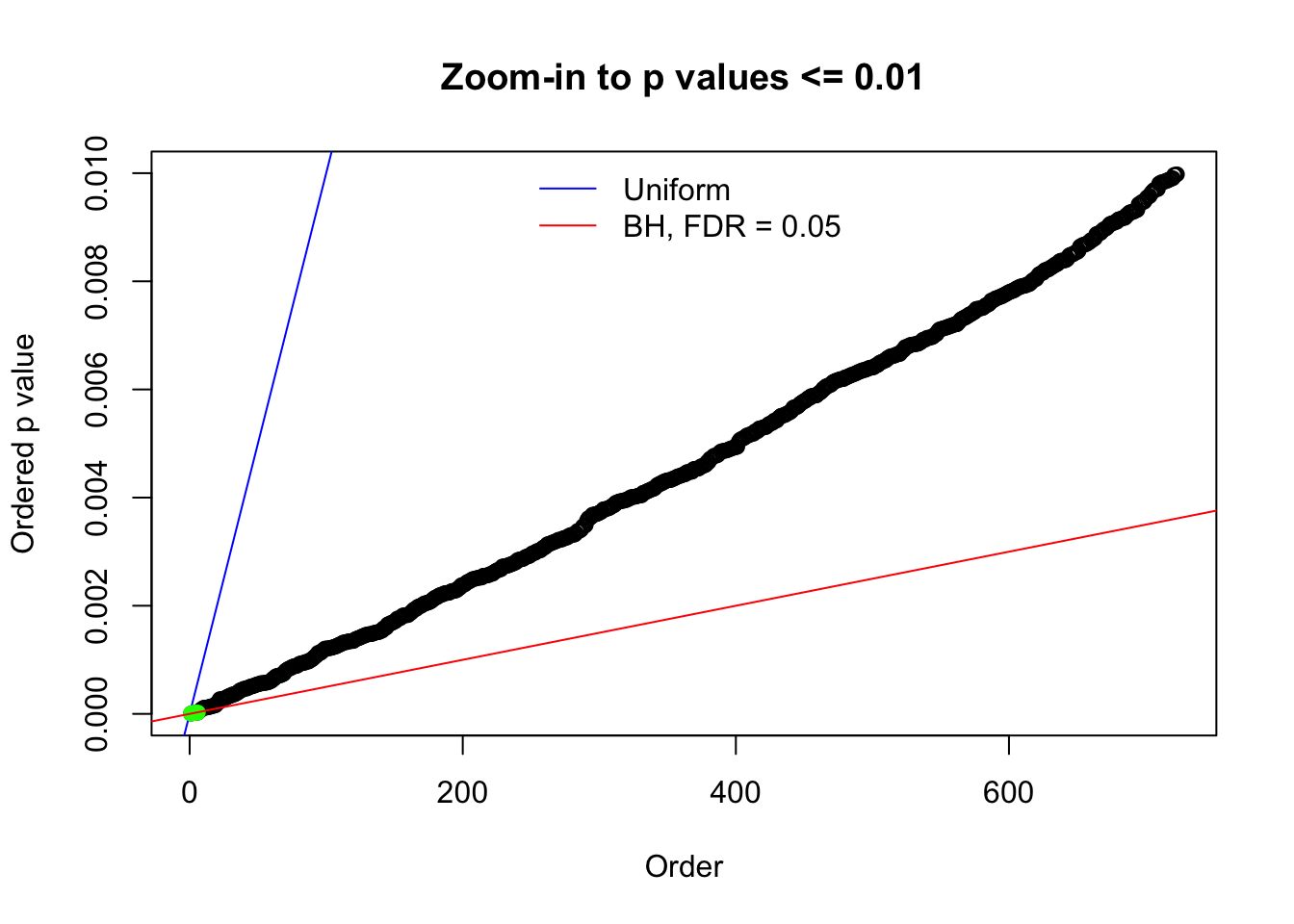
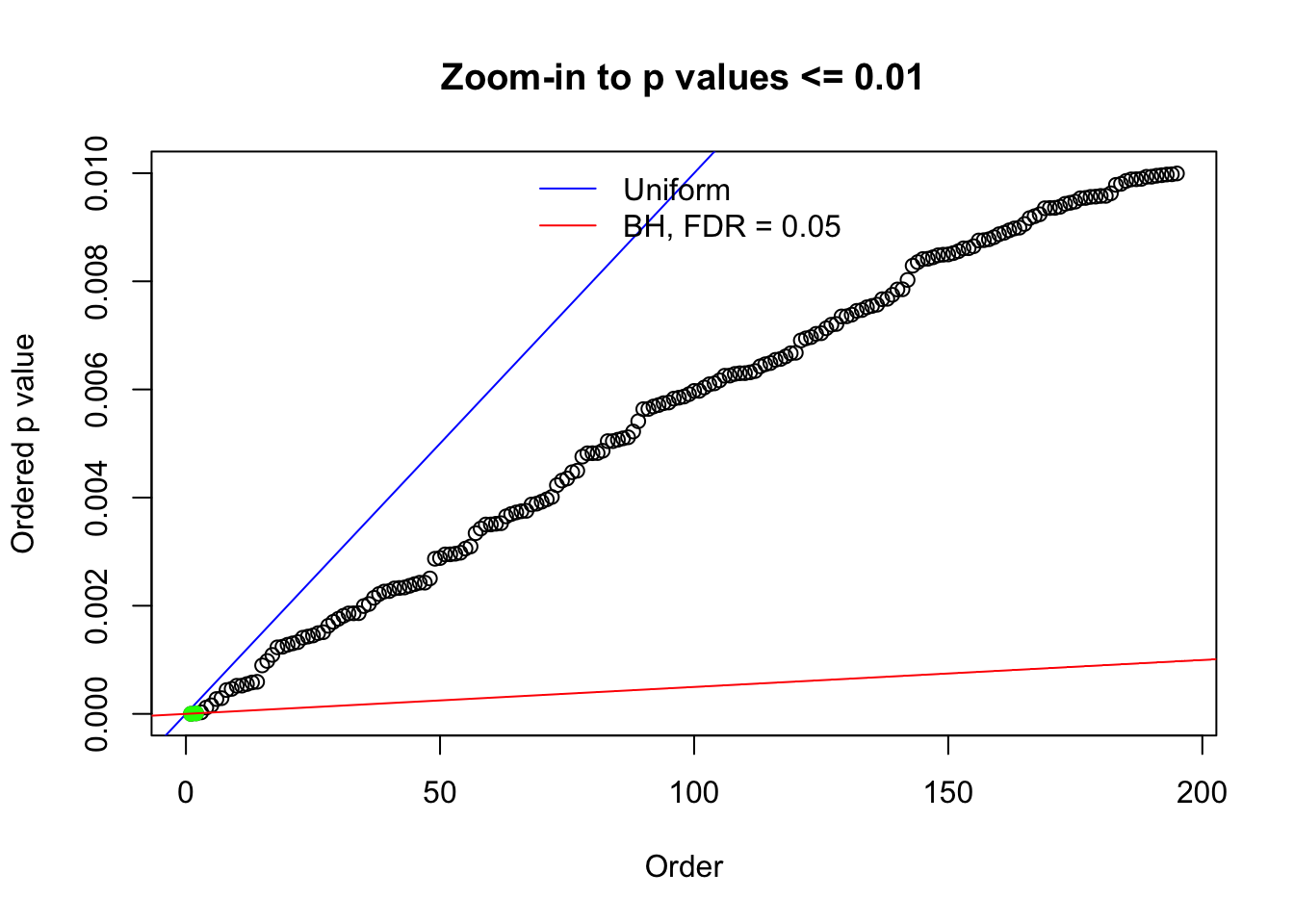
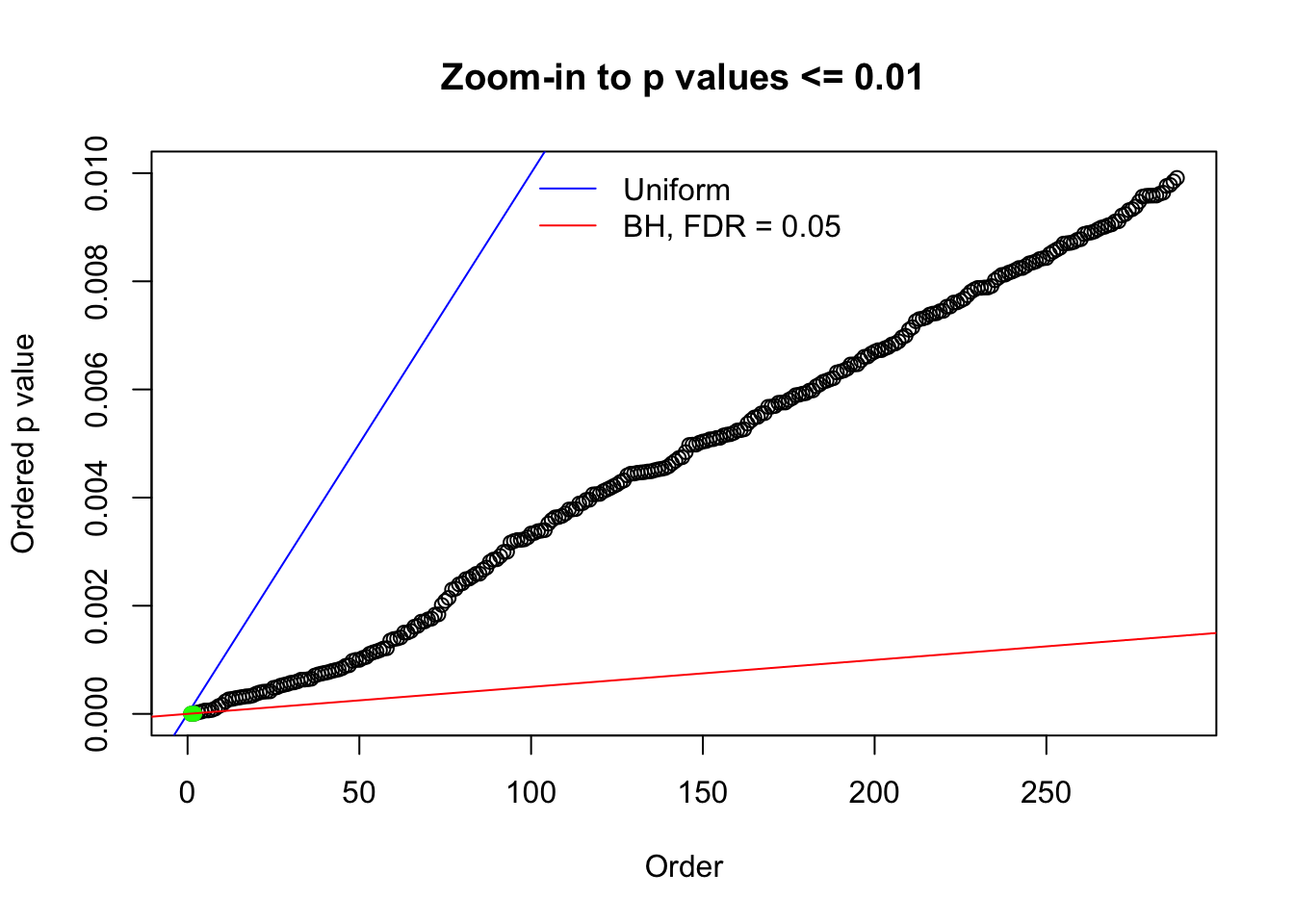
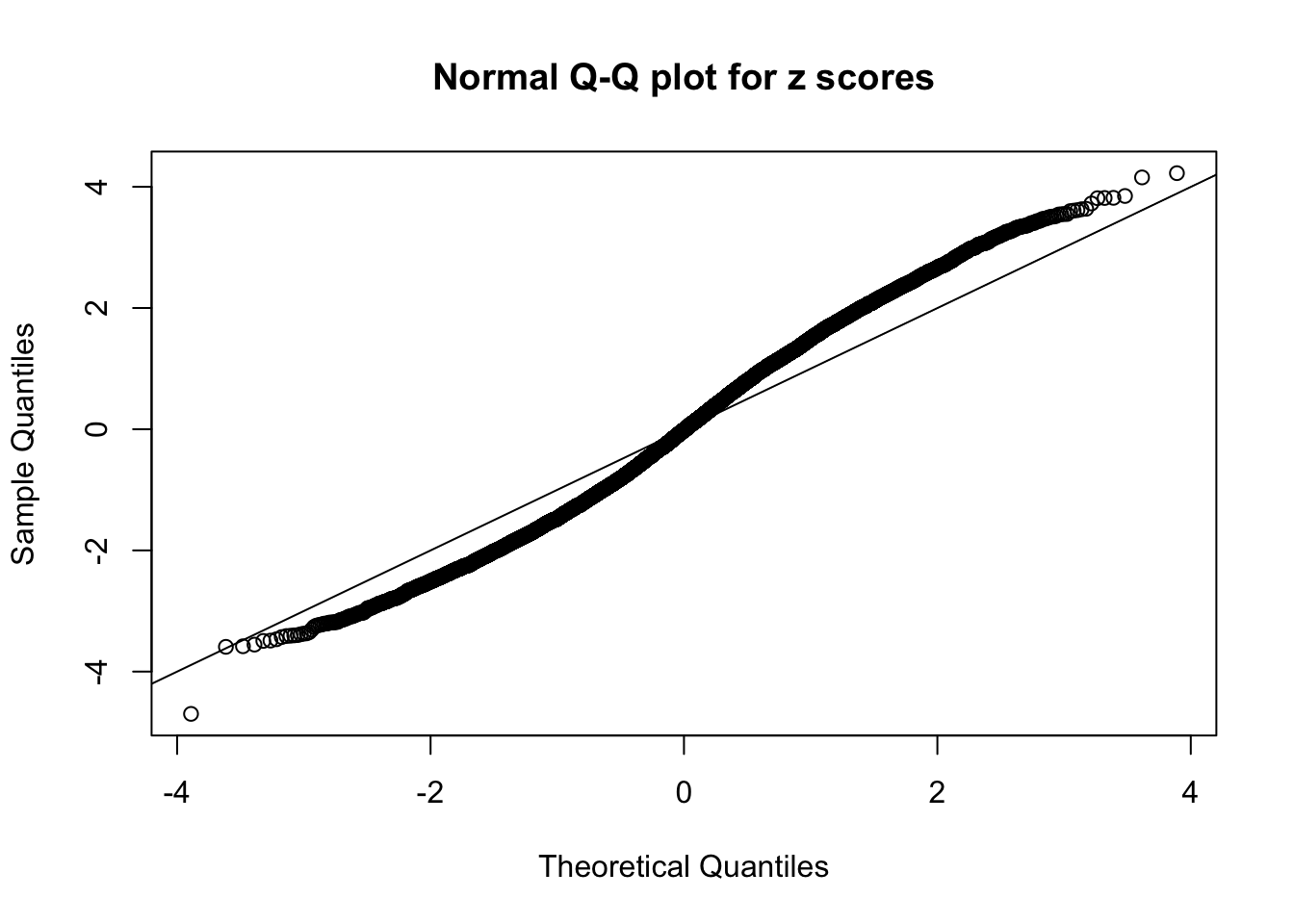
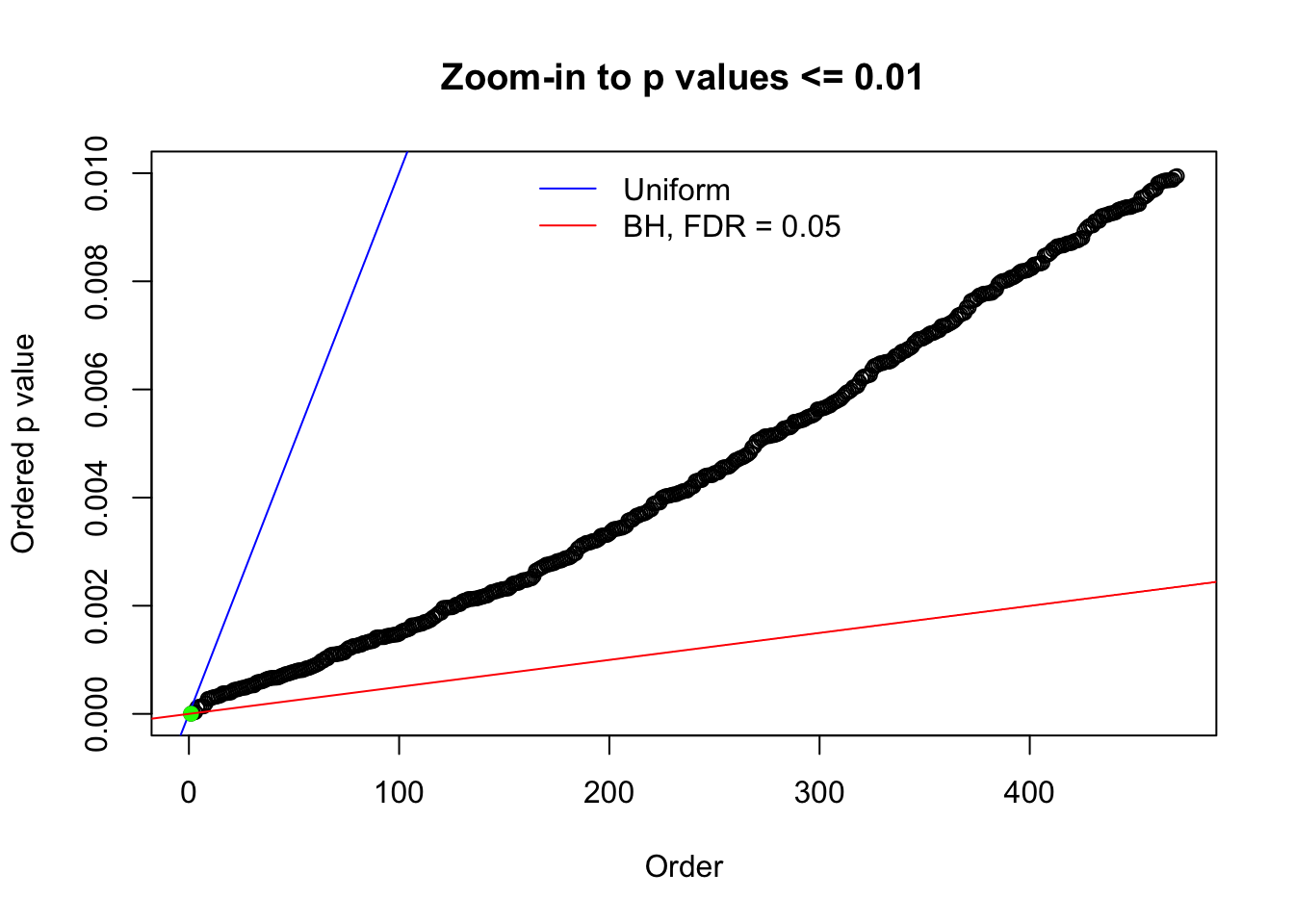
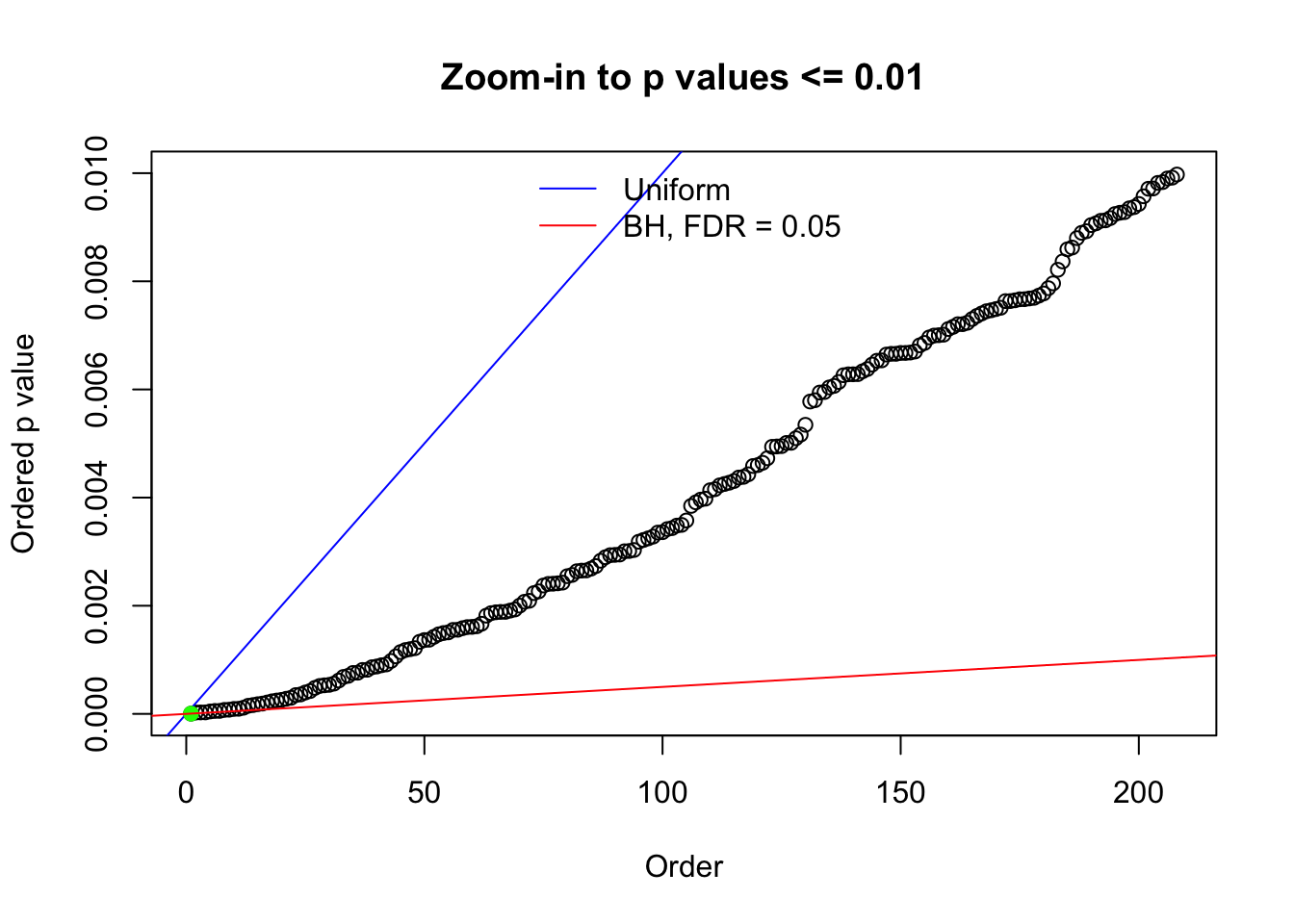
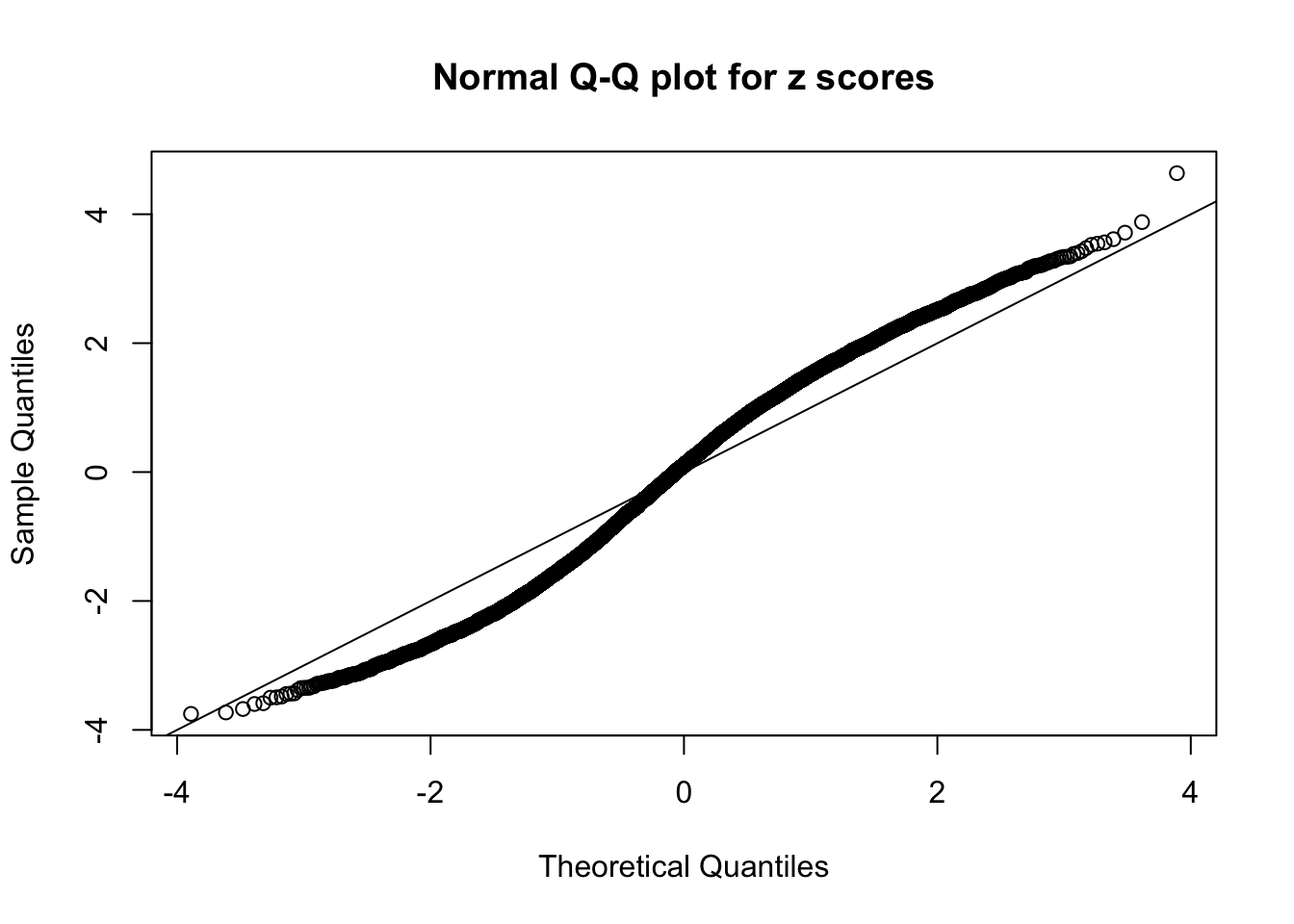
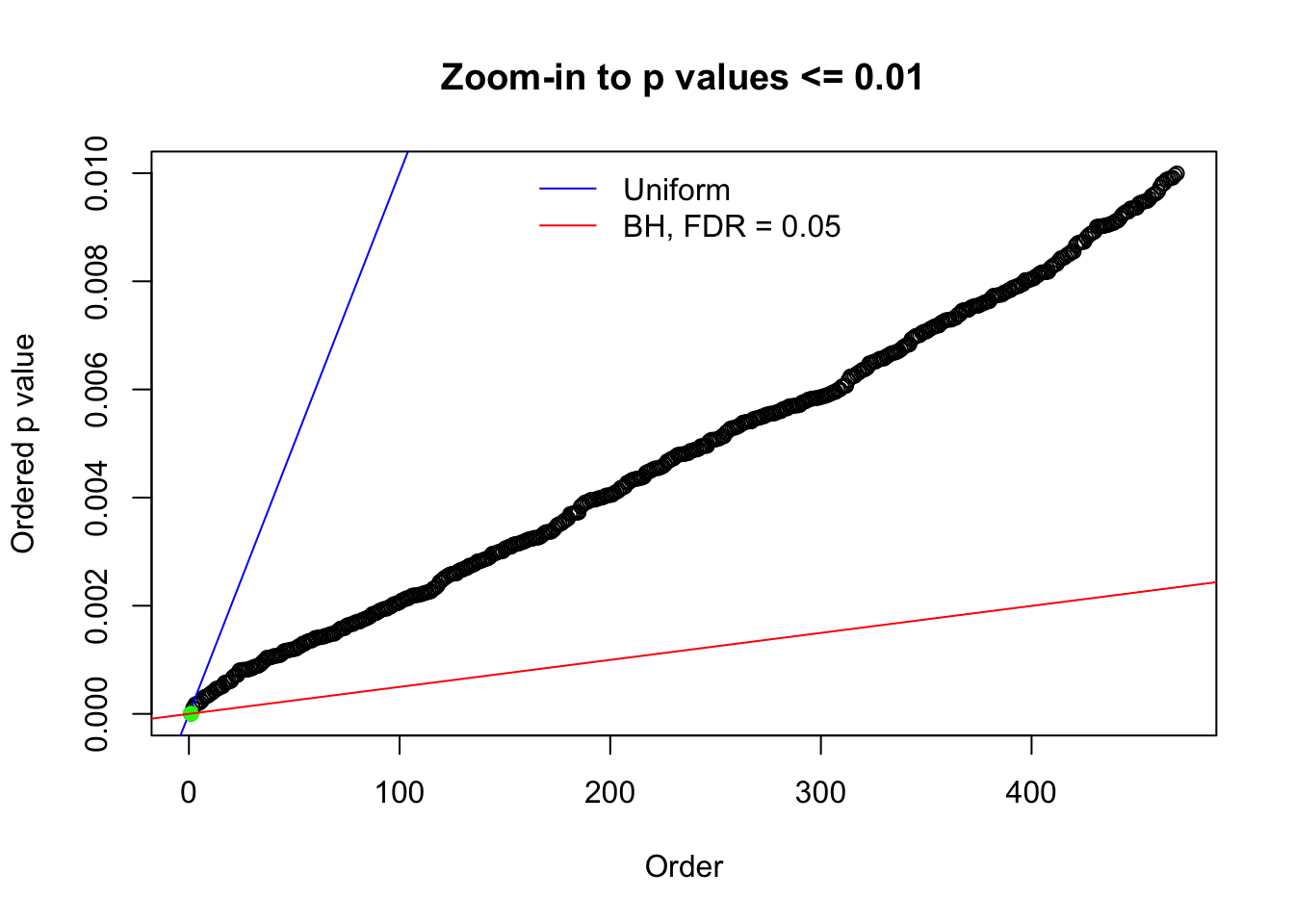
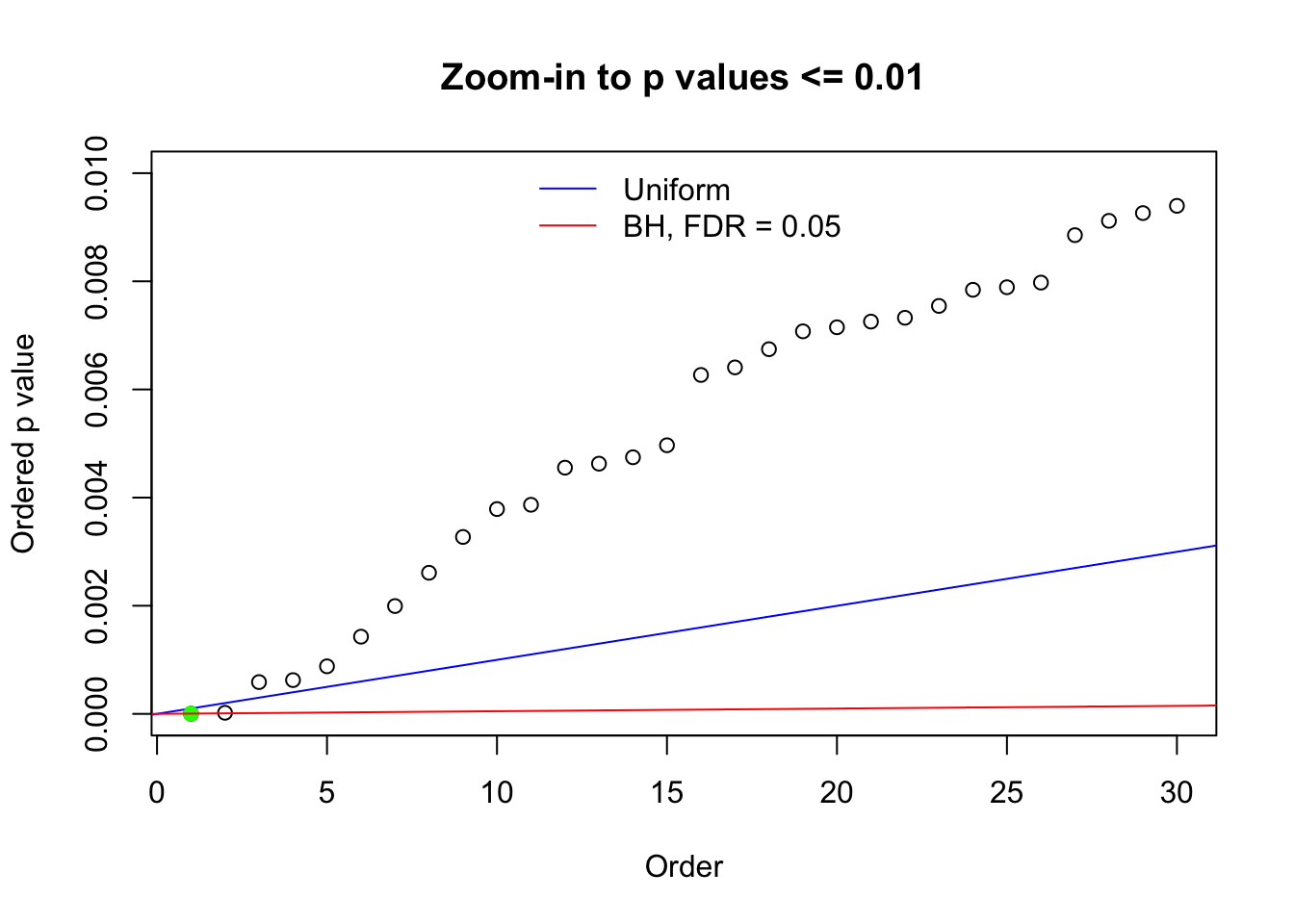
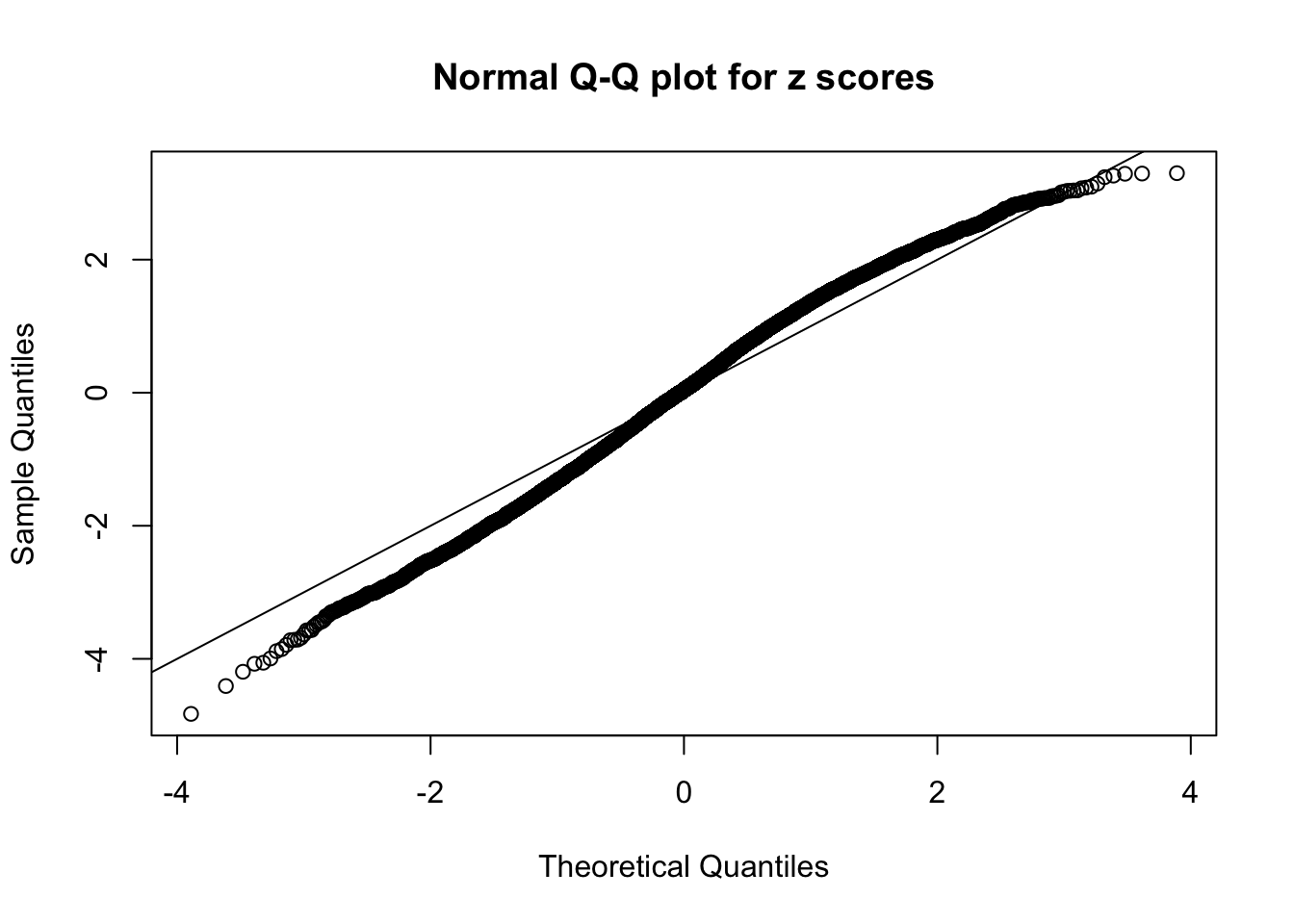
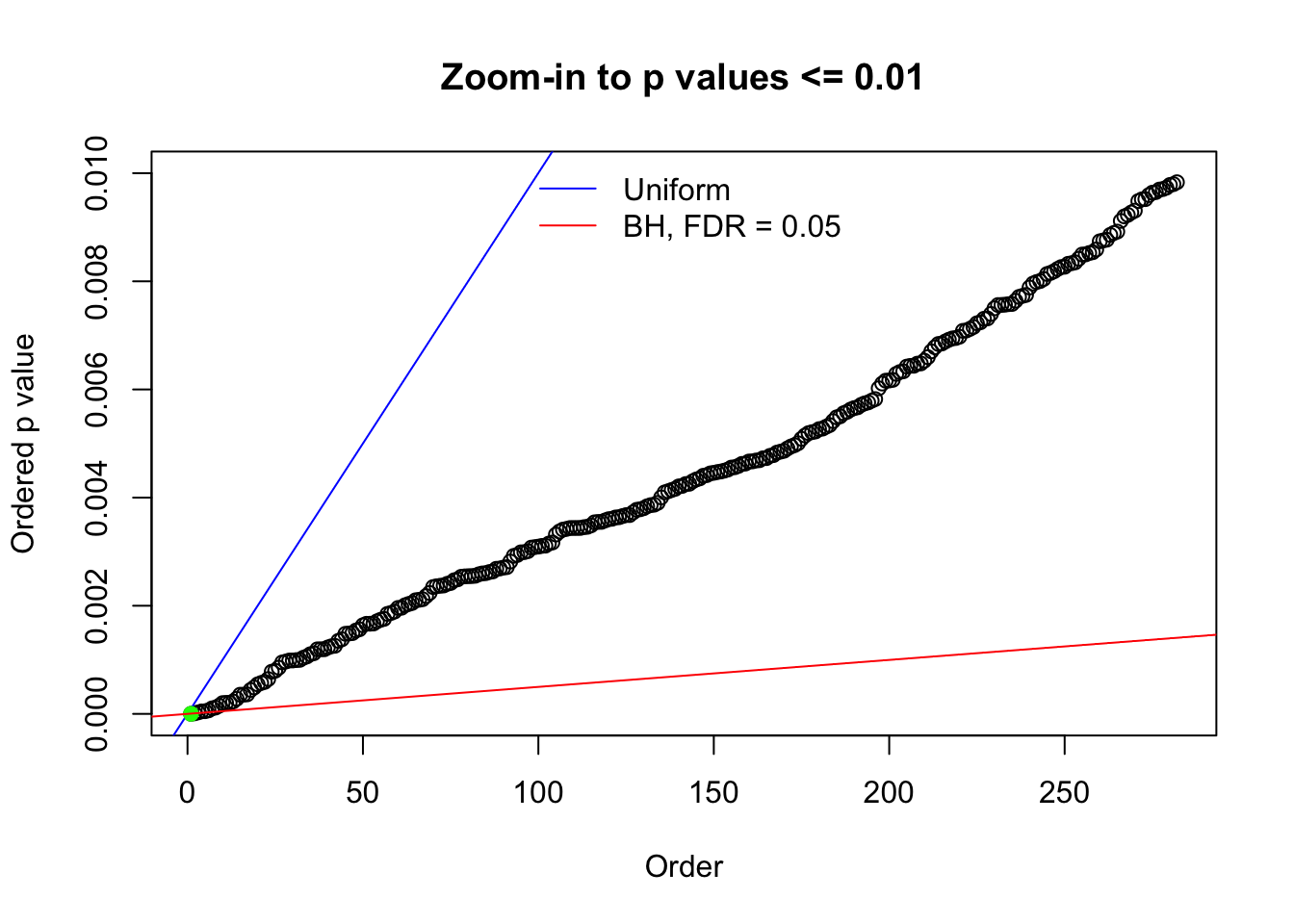
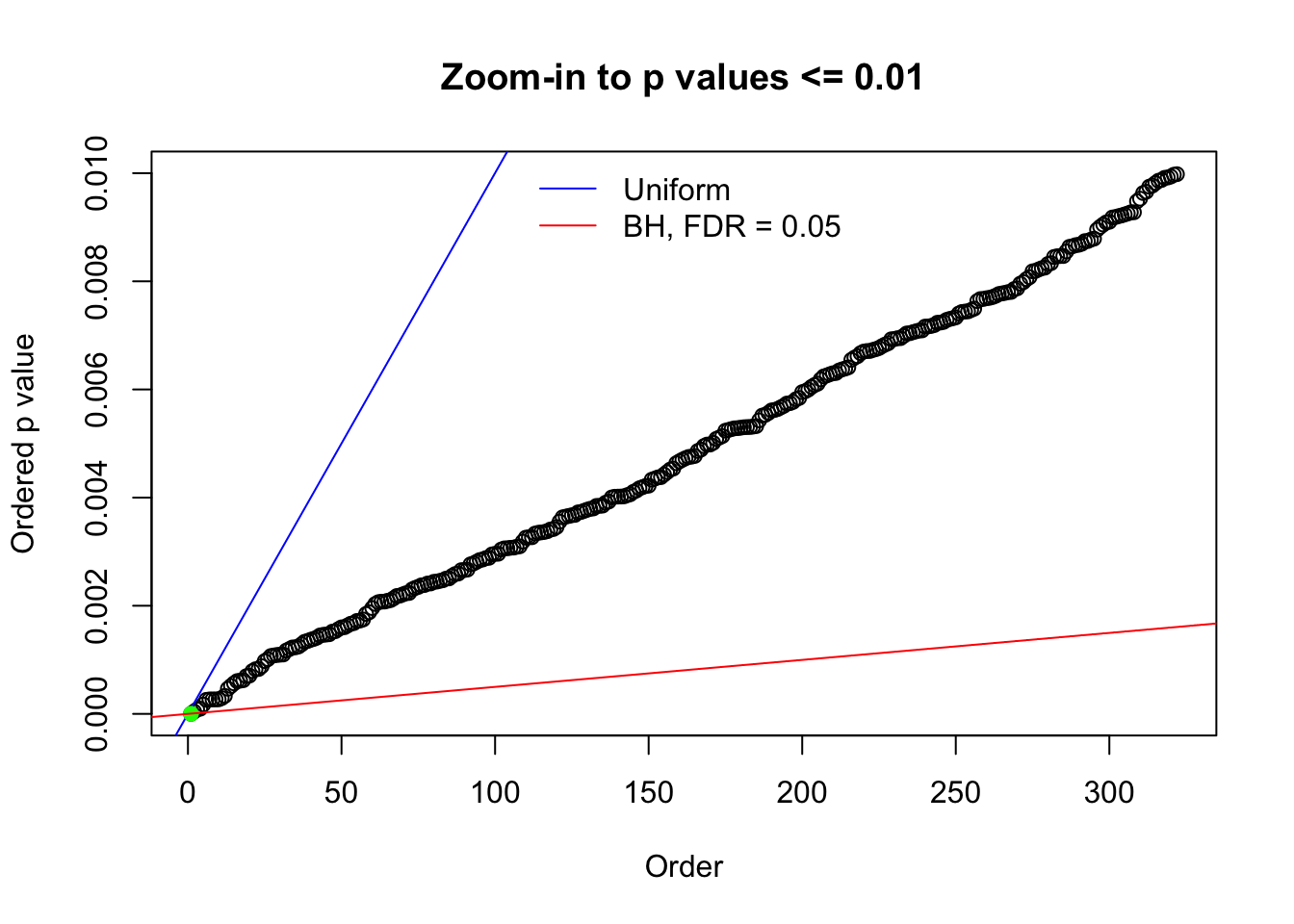
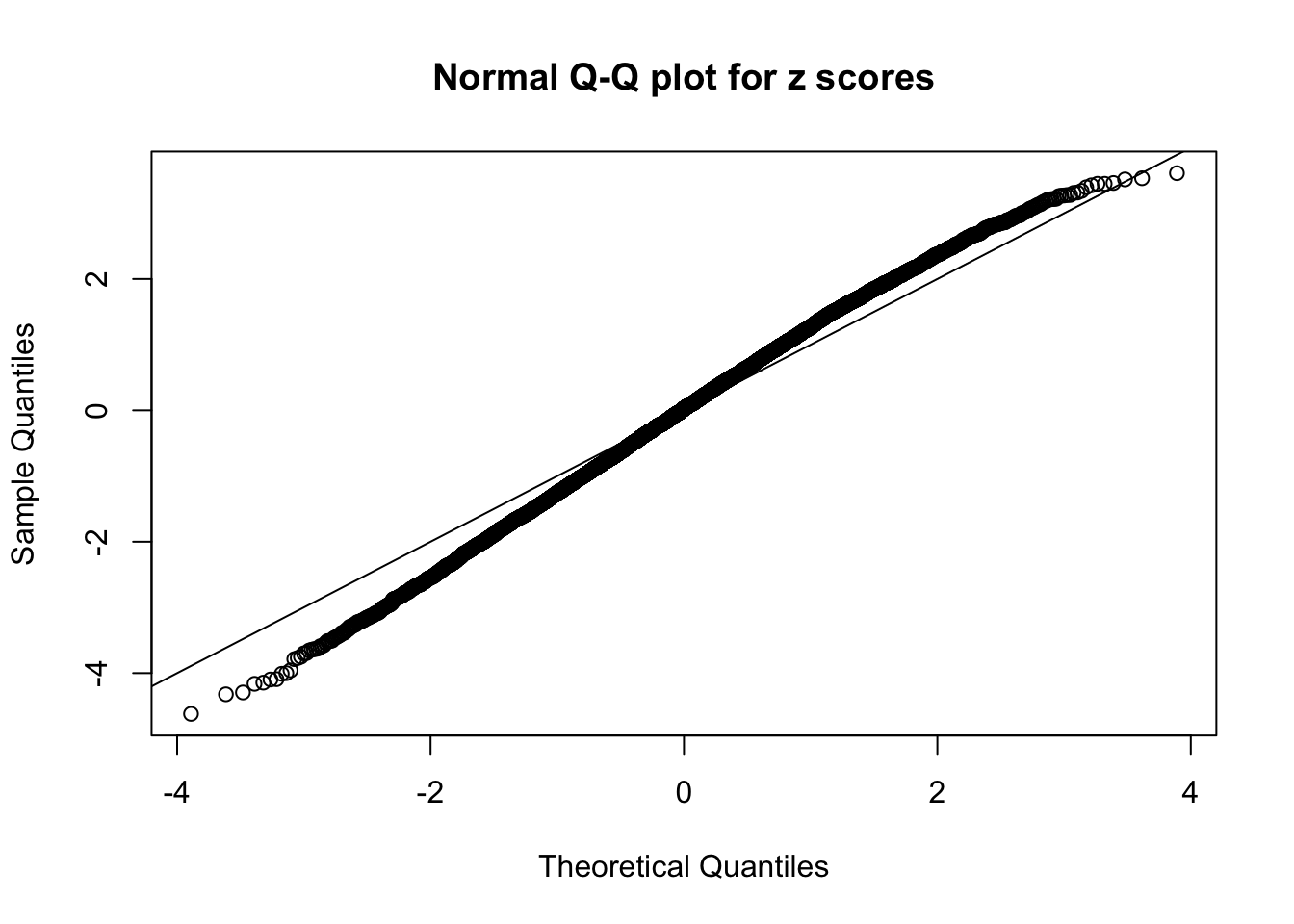
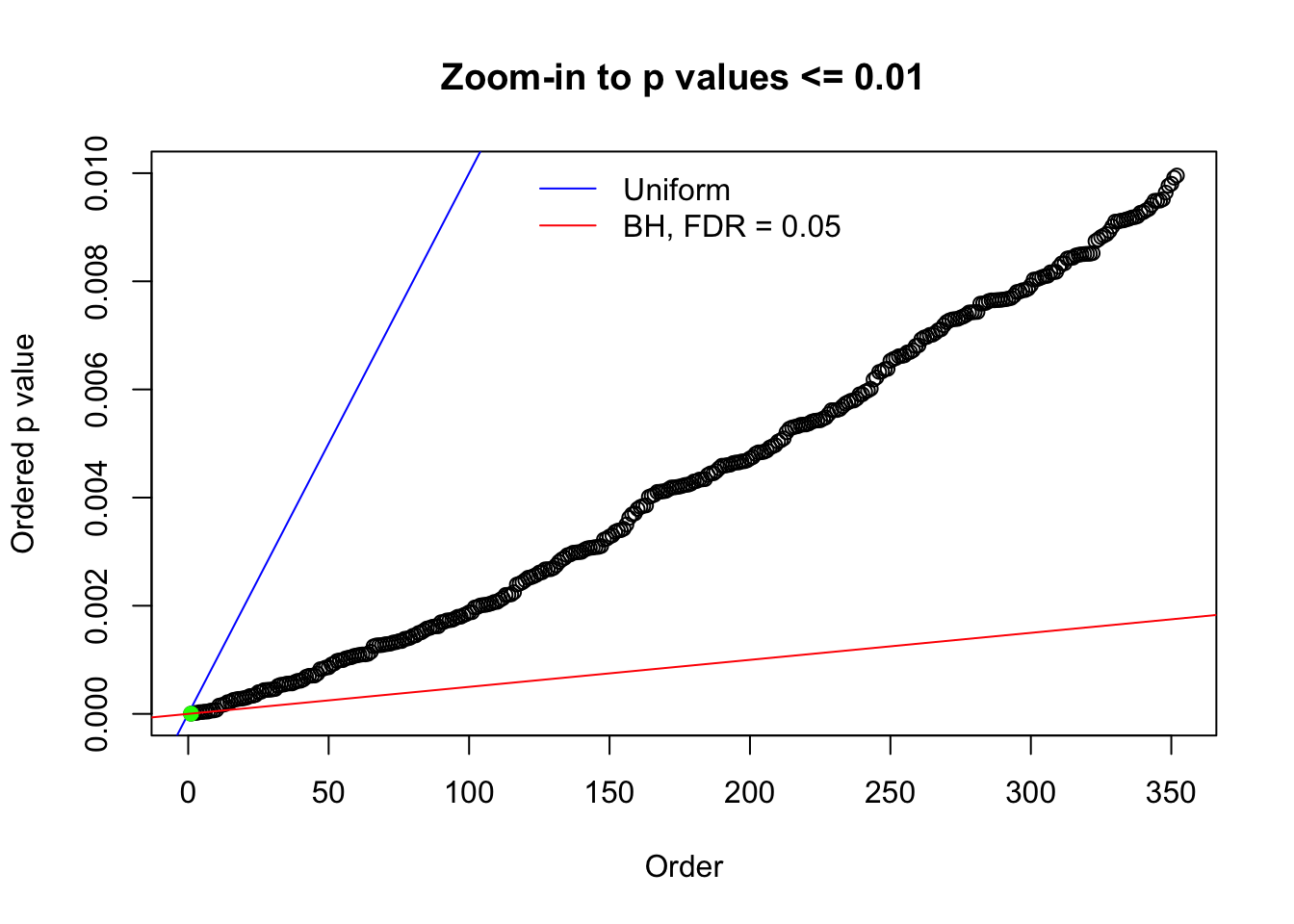
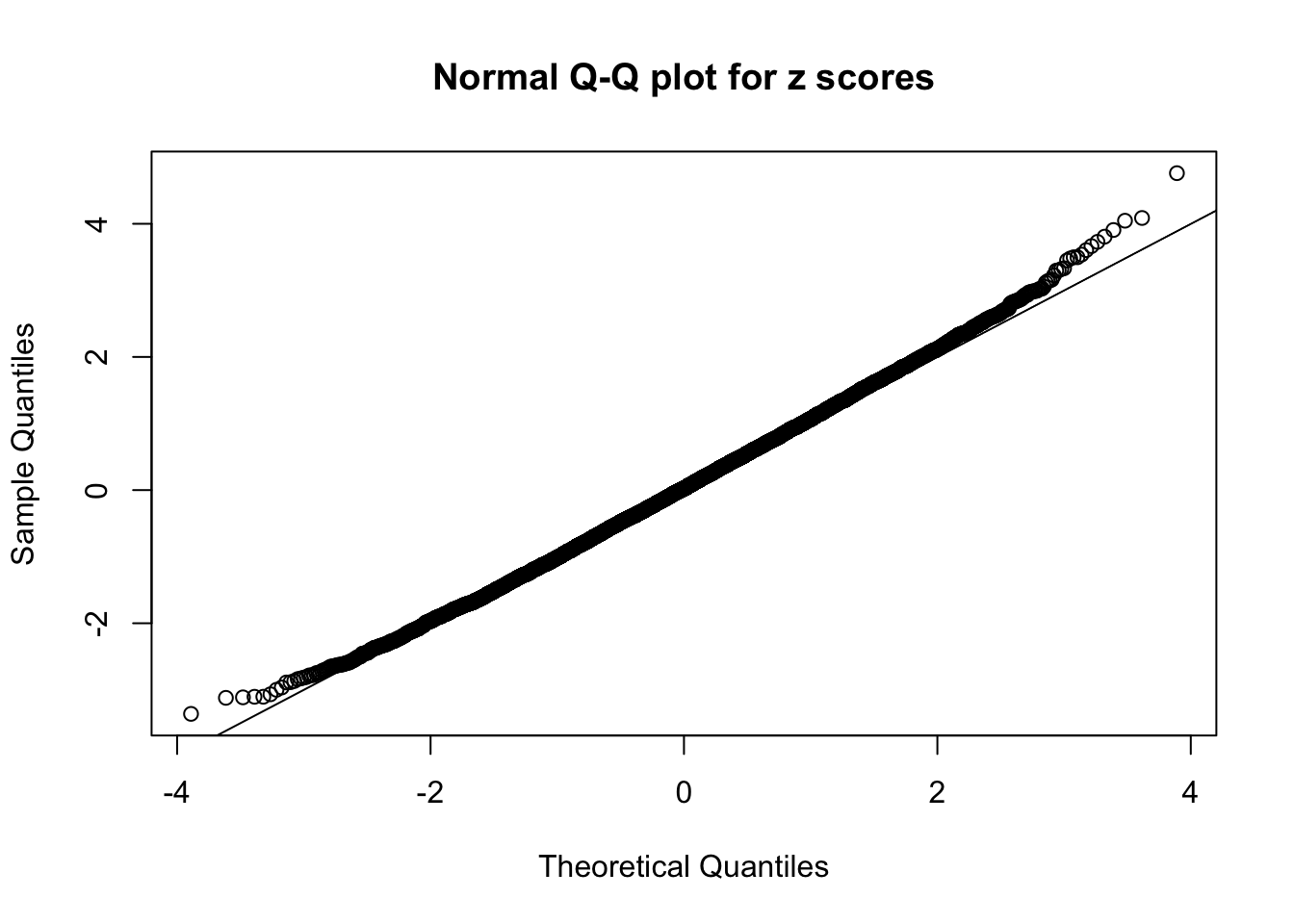
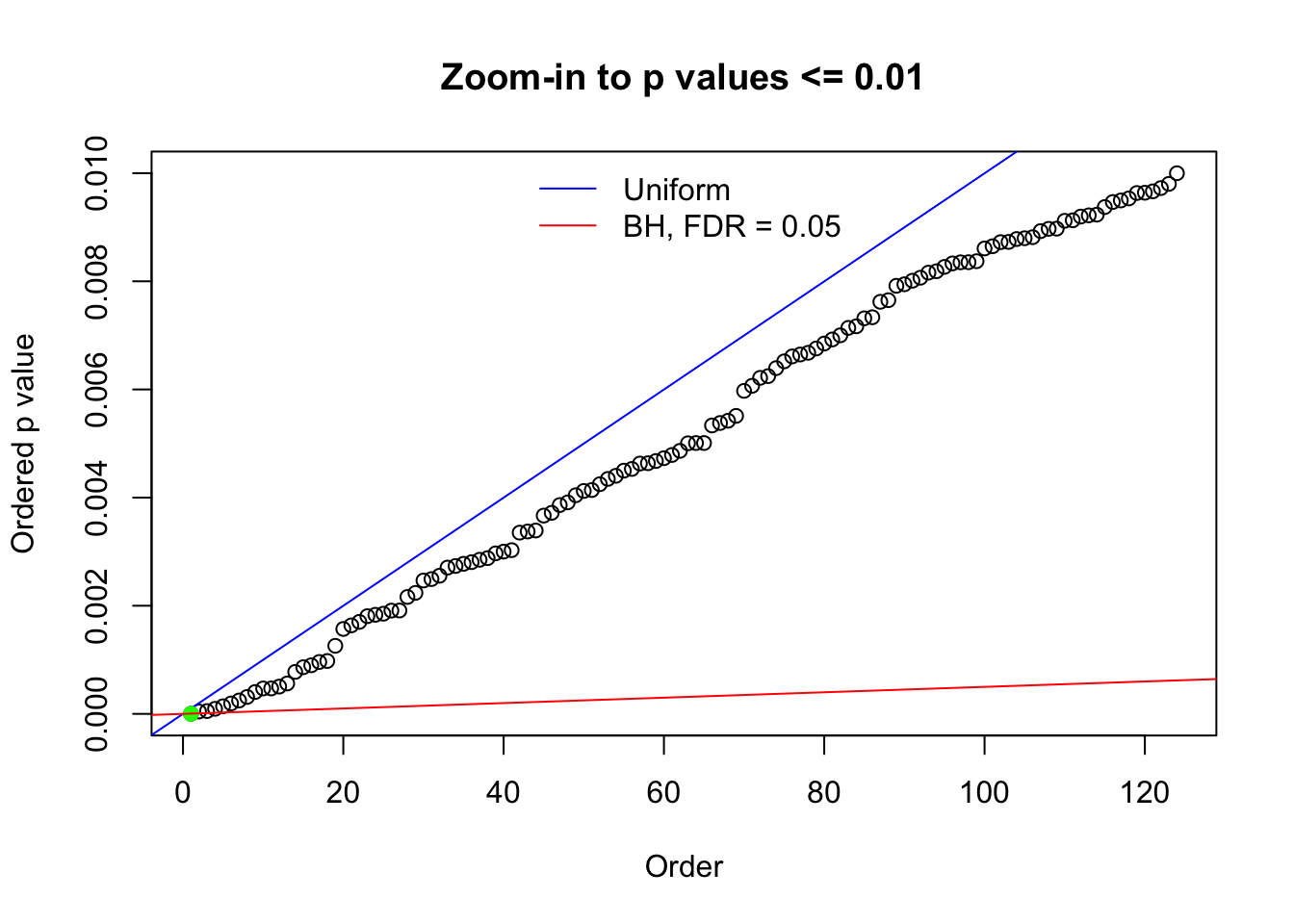
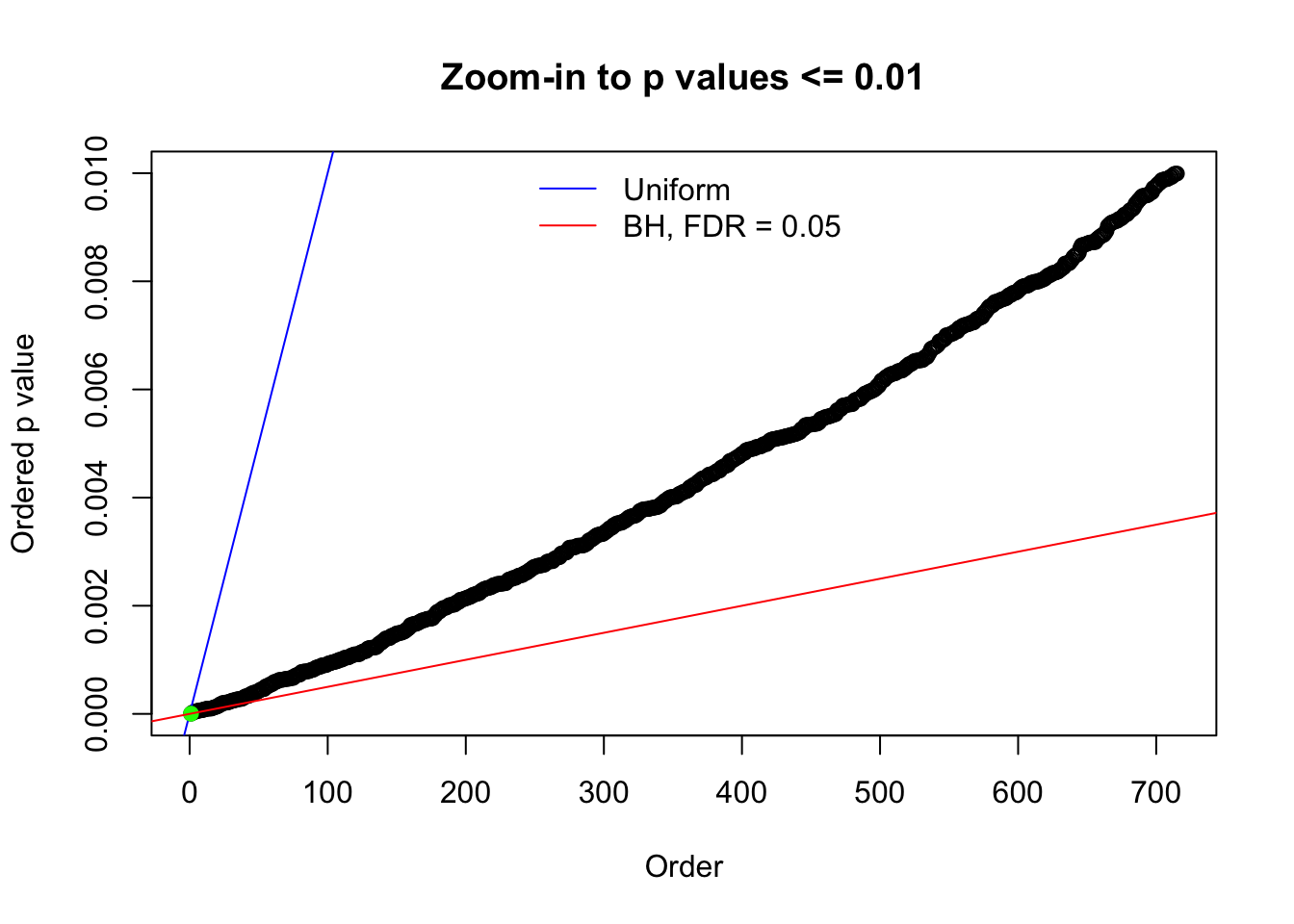
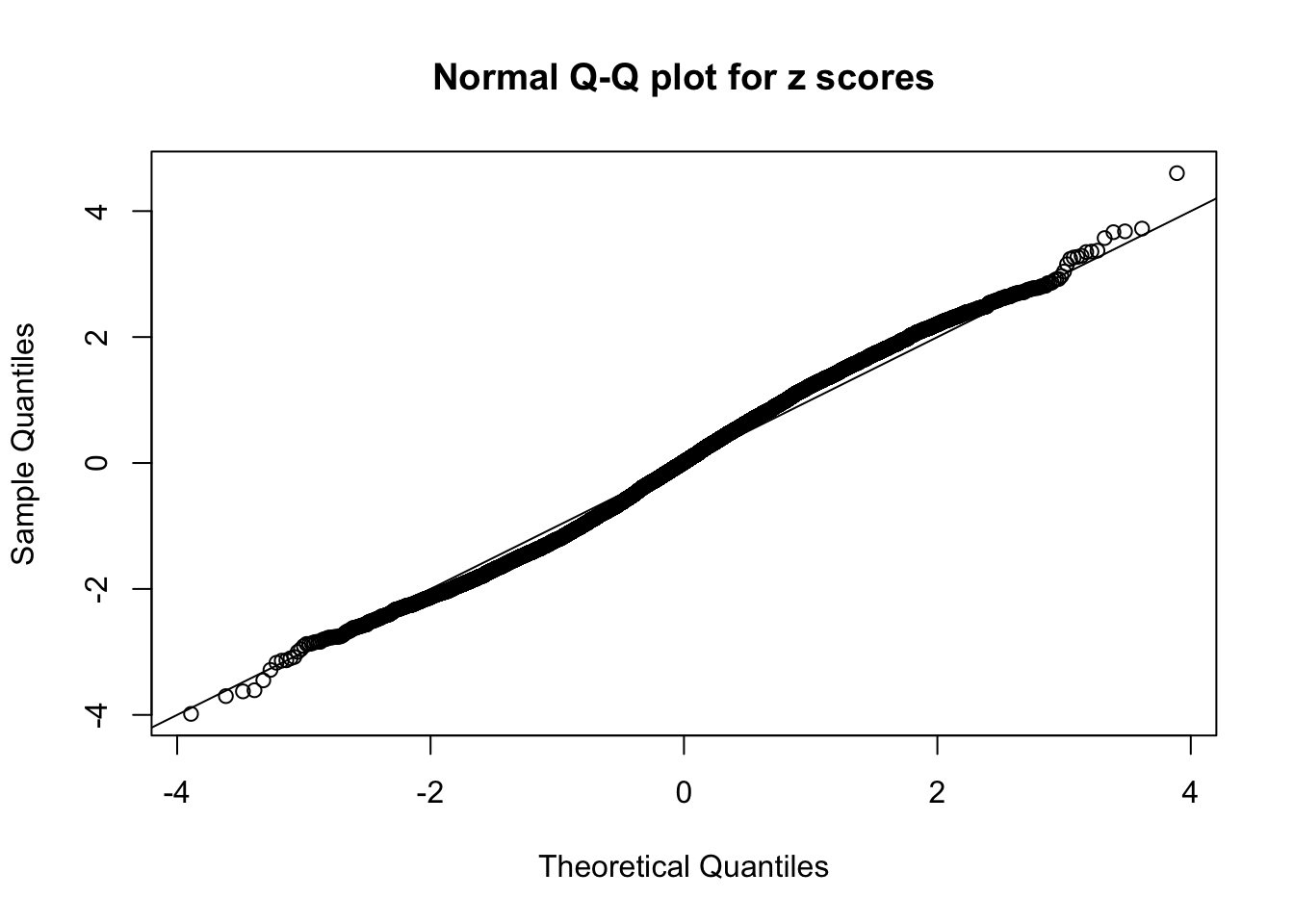
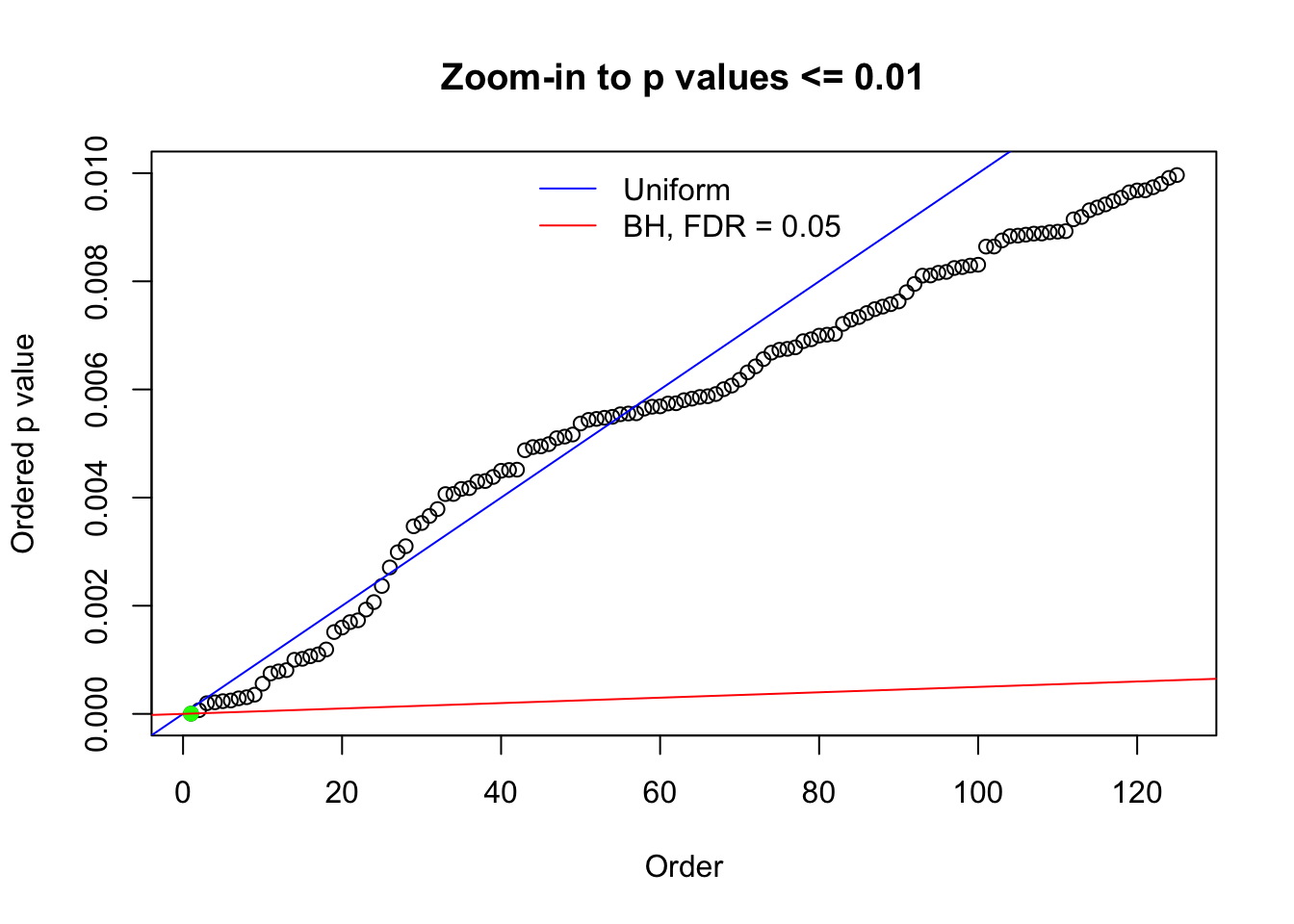
Here we get \(1K\) simulated, correlated null data sets, each having \(10K\) \(z\) scores, \(p\) values associated \(10K\) genes. We choose those data sets most hostile to \(BH\) procedure – those which produce at least false discovery under BH using \(\alpha = 0.05\). And then feed \(\hat\beta_j = z_j, \hat s_j \equiv 1\) to ASH, using a prior of normal mixtures and uniform mixtures, respectively.
If these \(z\) scores are independent, ASH should be able to estimated \(\hat g =\delta_0\) reasonably well. However, with correlation, estimated \(\hat g\) will be different from \(\delta_0\). Moreover, with this estimated \(\hat g\), \(\left\{\hat F_j\right\}\) might not behave like \(\text{Unif}\left[0, 1\right]\).
This is because the pseudo-effect due to the correlation-induced inflation is not regular and not likely to be captured by unimodal mixtures of normals of uniforms. For example, as Matthew’s initial observation which inspired the whole project in the first place, the correlation may only inflate the moderate observations but not the extreme ones. Thus, a mixture of normals, which simultaneously inflates both the moderate and the extreme observations, would be ill-advised.
library(ashr)z = read.table("../output/z_null_liver_777.txt")
p = read.table("../output/p_null_liver_777.txt")
n = nrow(z)
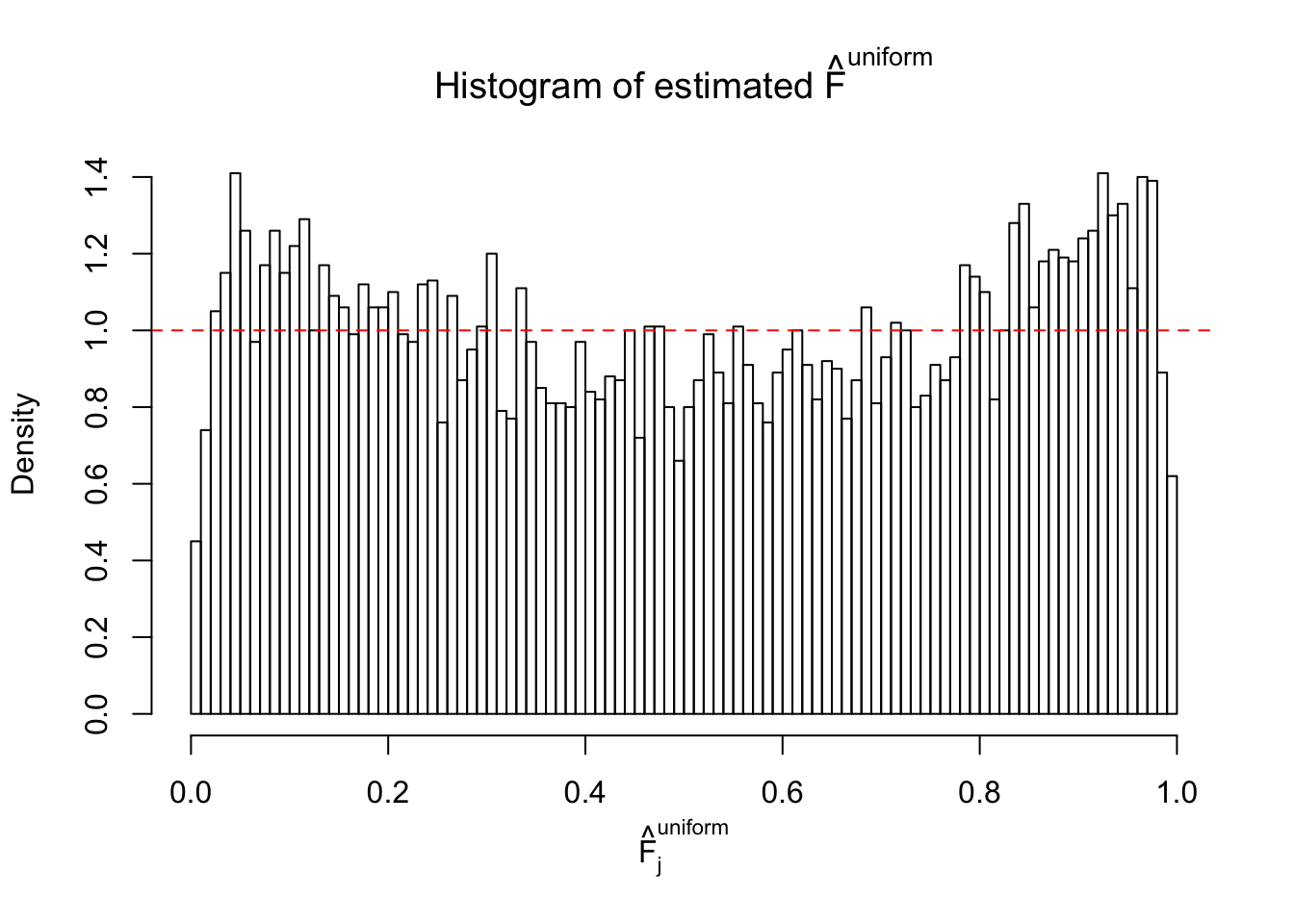
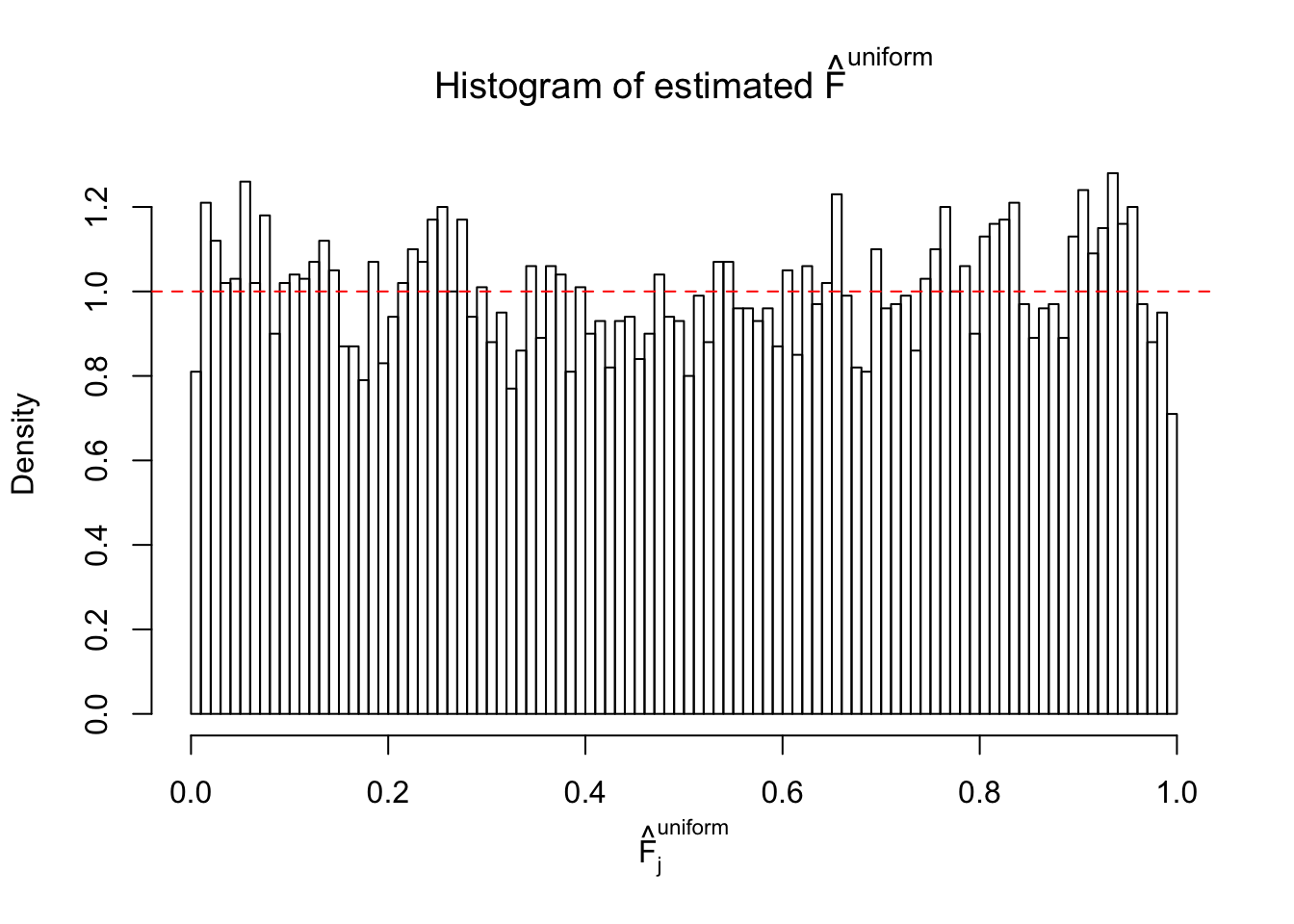
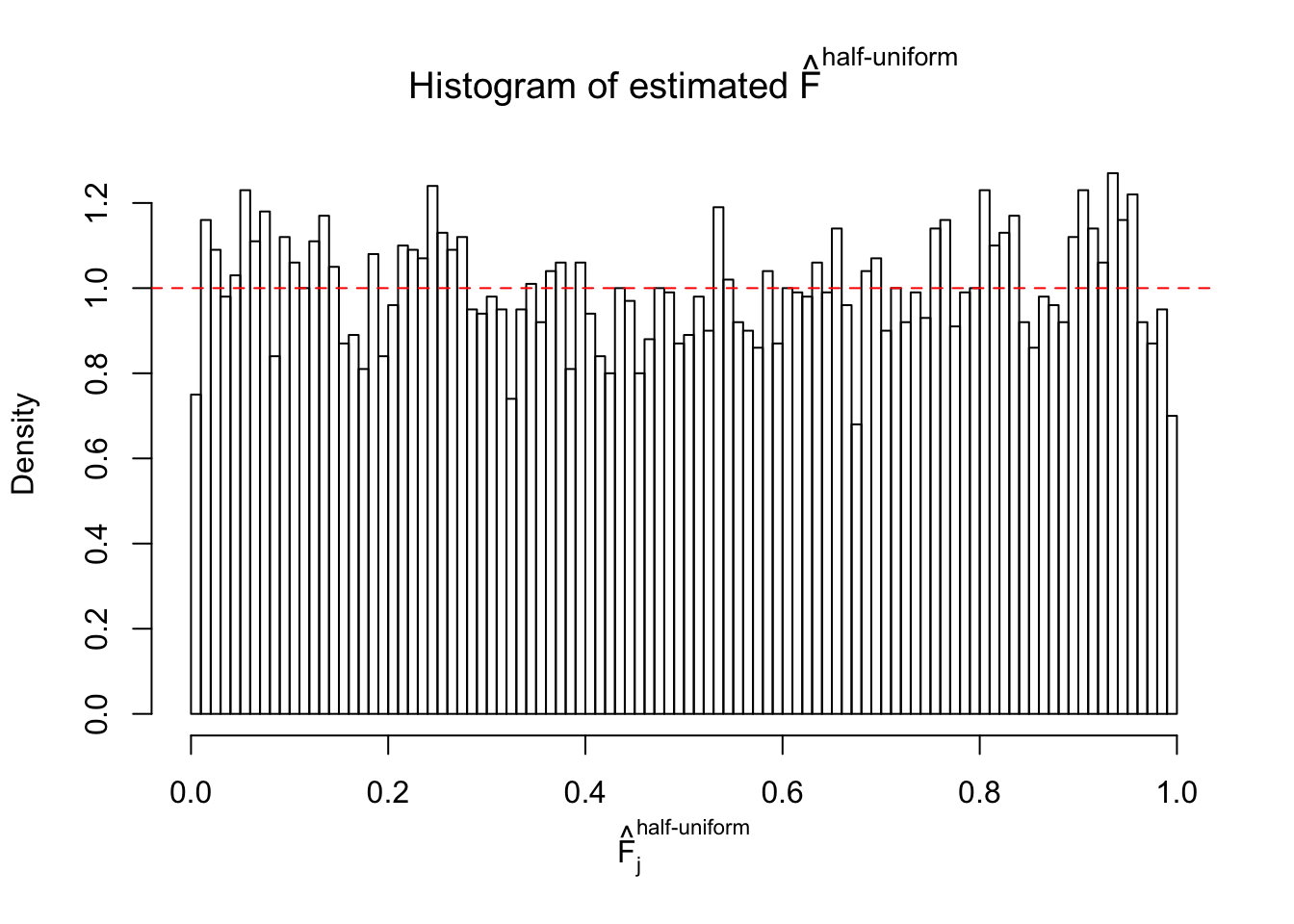
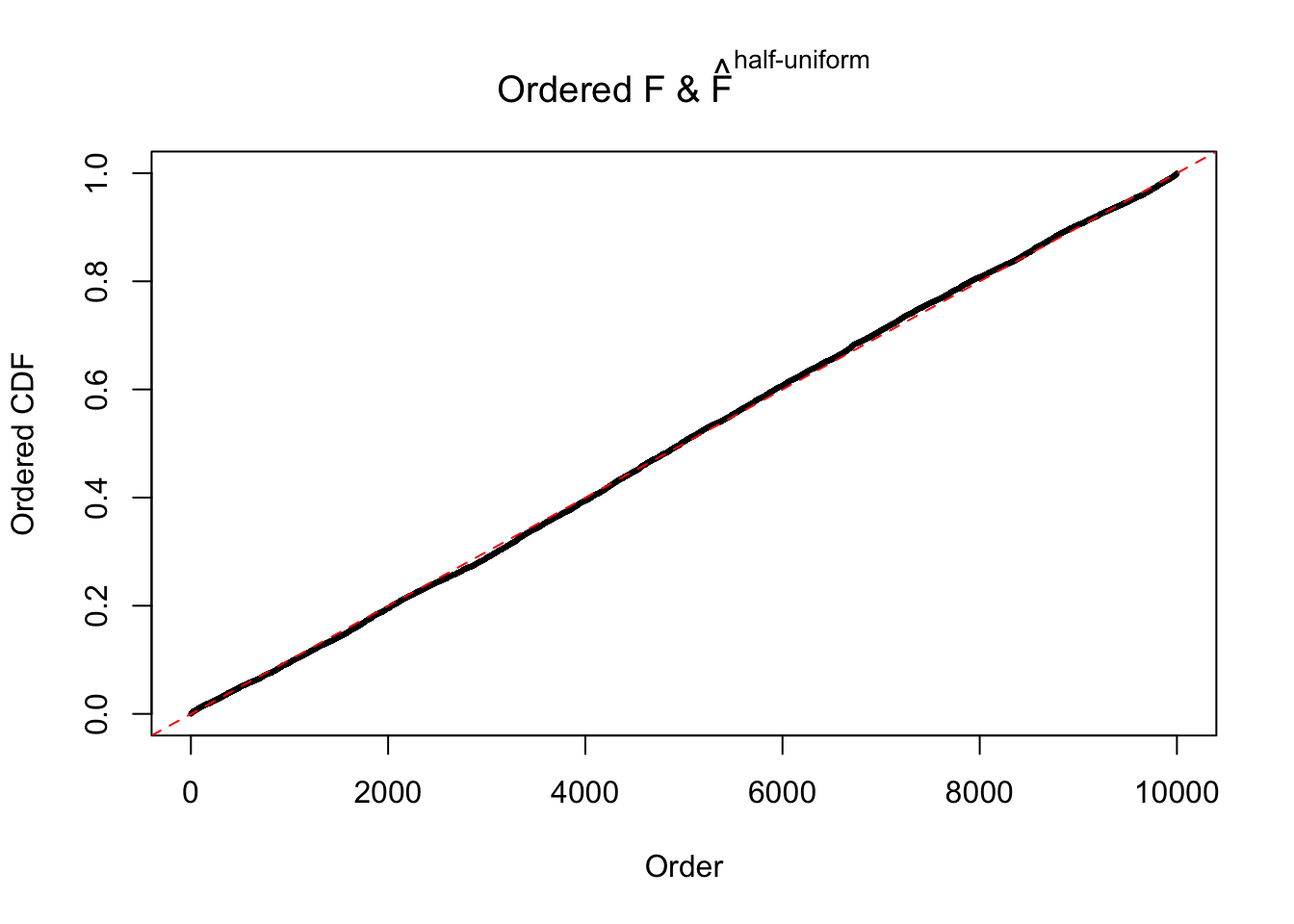
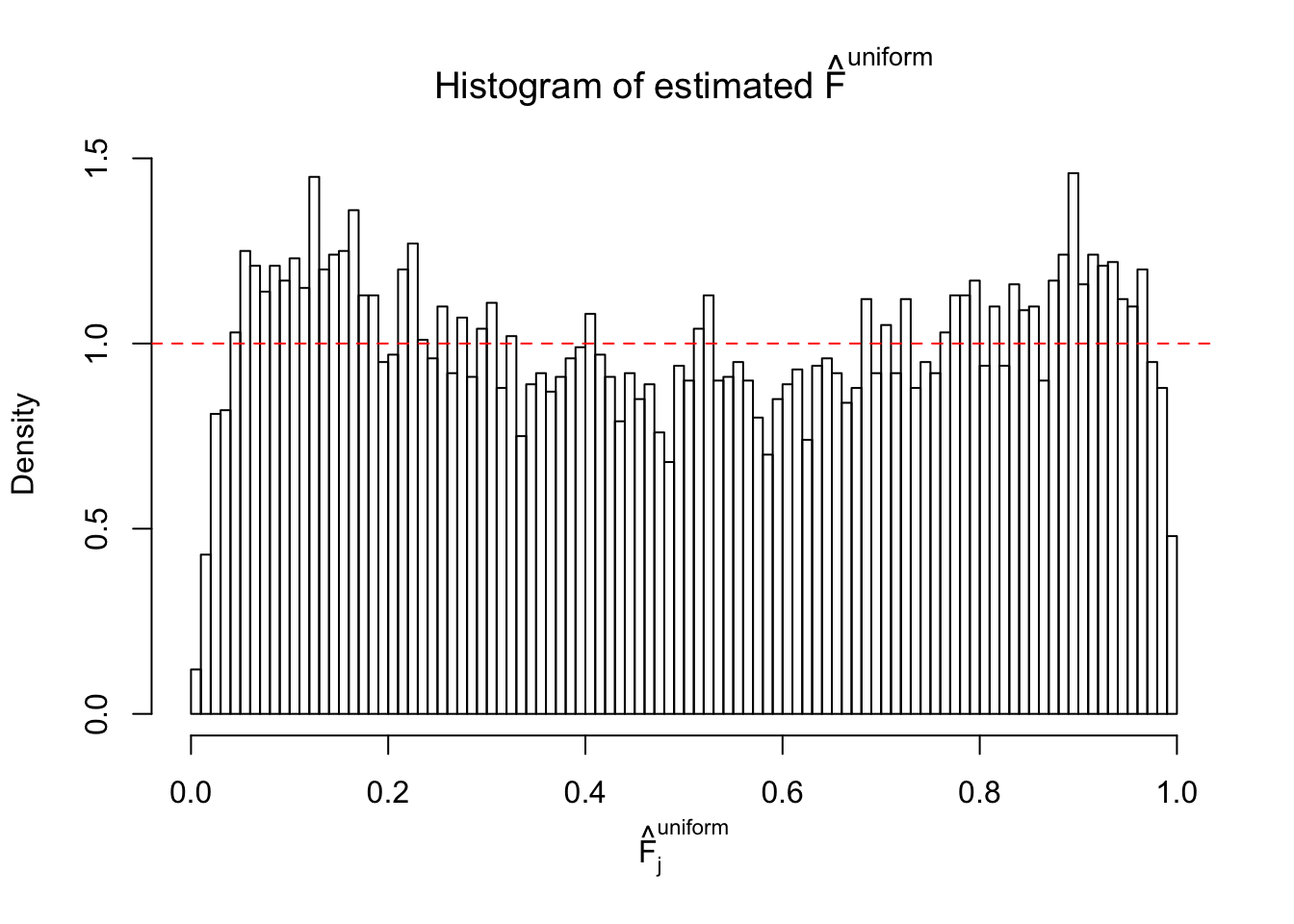
m = ncol(z)It’s worth noting that for the same data set, that is, for the same correlated \(z\) scores, the diagnostic plots of ASH using a mixture uniform prior is usually conspicuously better than those using a mixture normal prior. This might be because uniform mixtures are more flexible than normal mixtures at dealing with irregular distributions, like the “moderates inflated yet extremes not inflated” one. For the same reason, mixcompdist = "halfuniform" is occasionally better than mixcompdist = "uniform".
N0. 1 : Data Set 355 ; Number of False Discoveries: 639 ; pihat0 = 0.01079742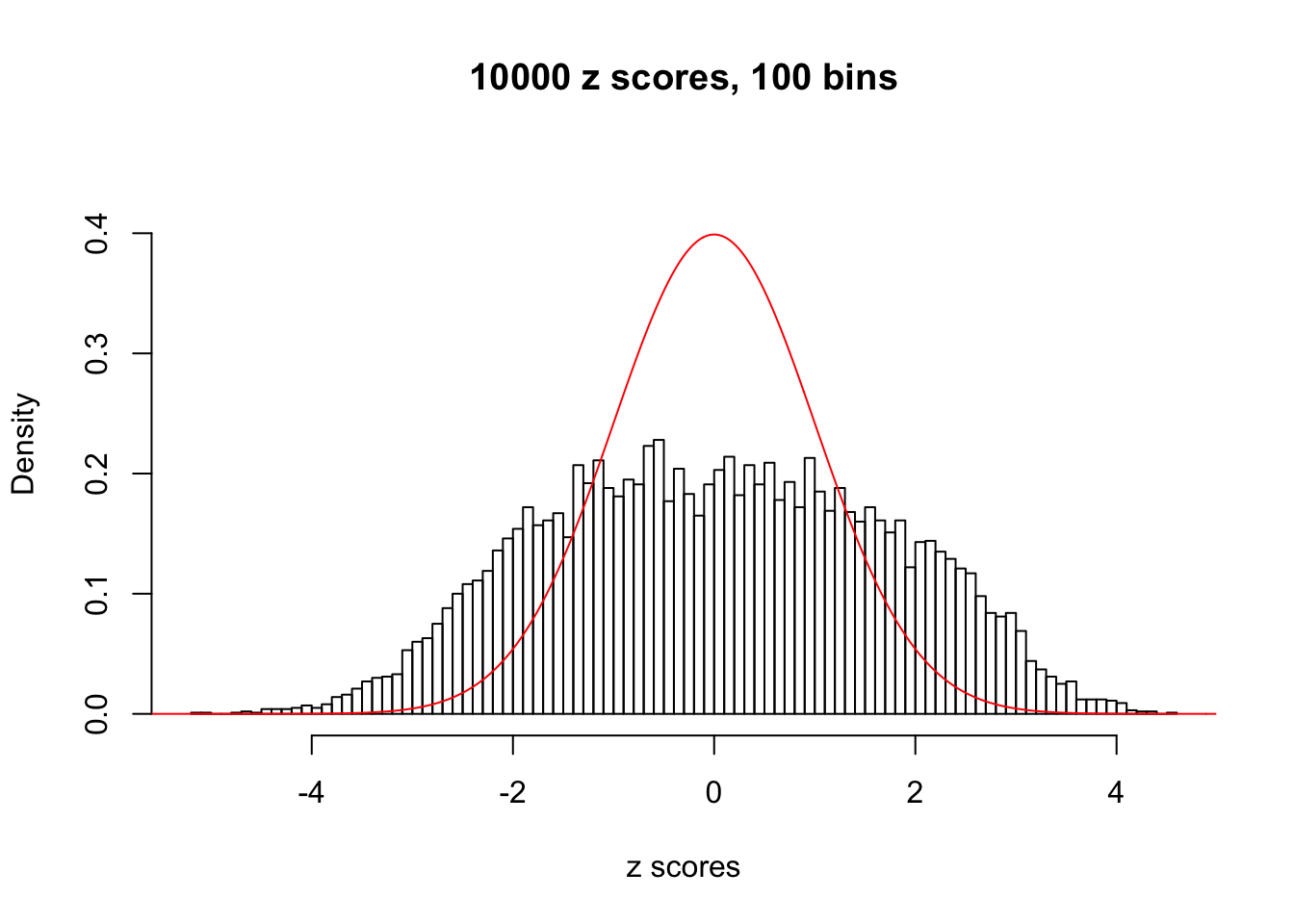
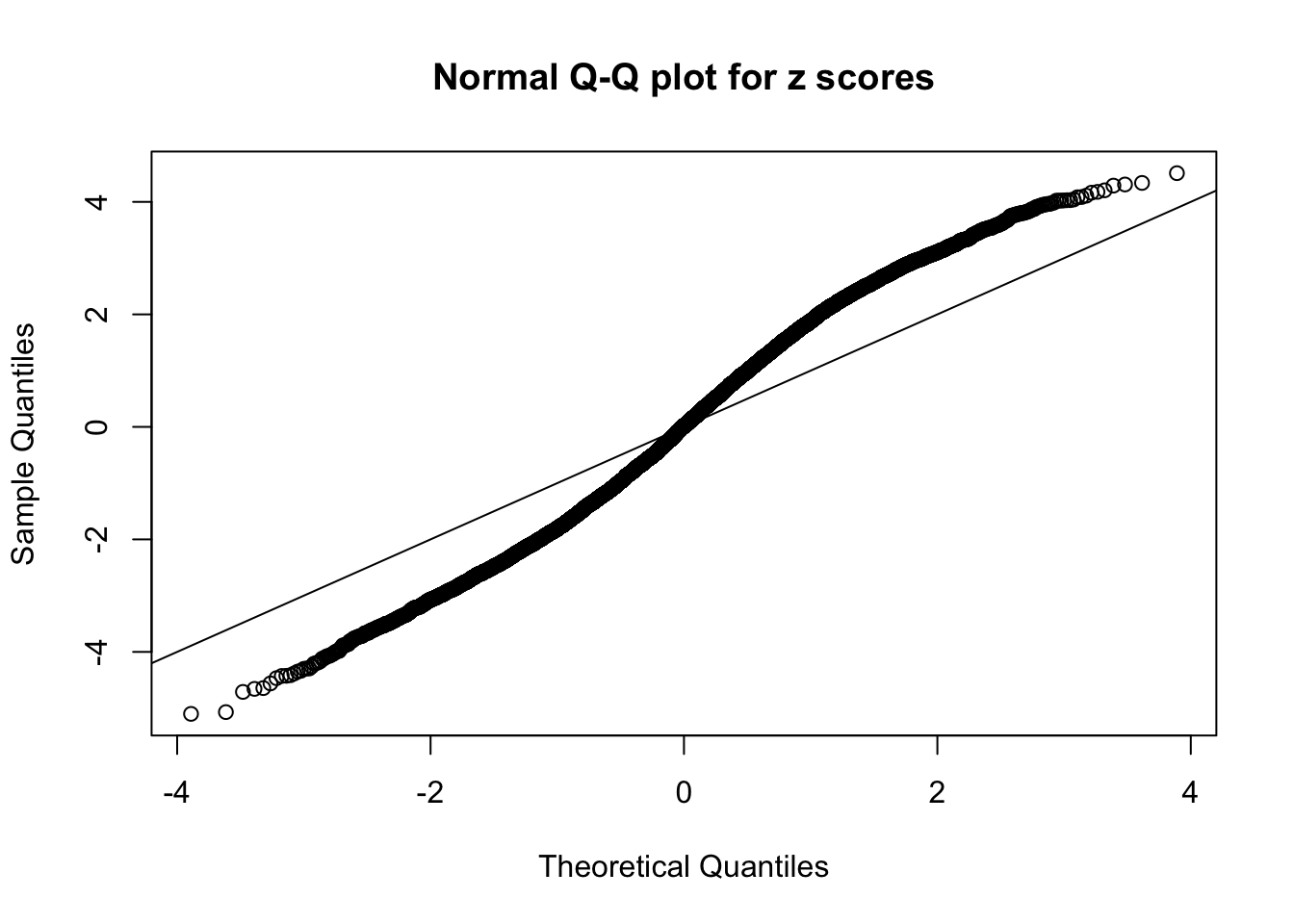
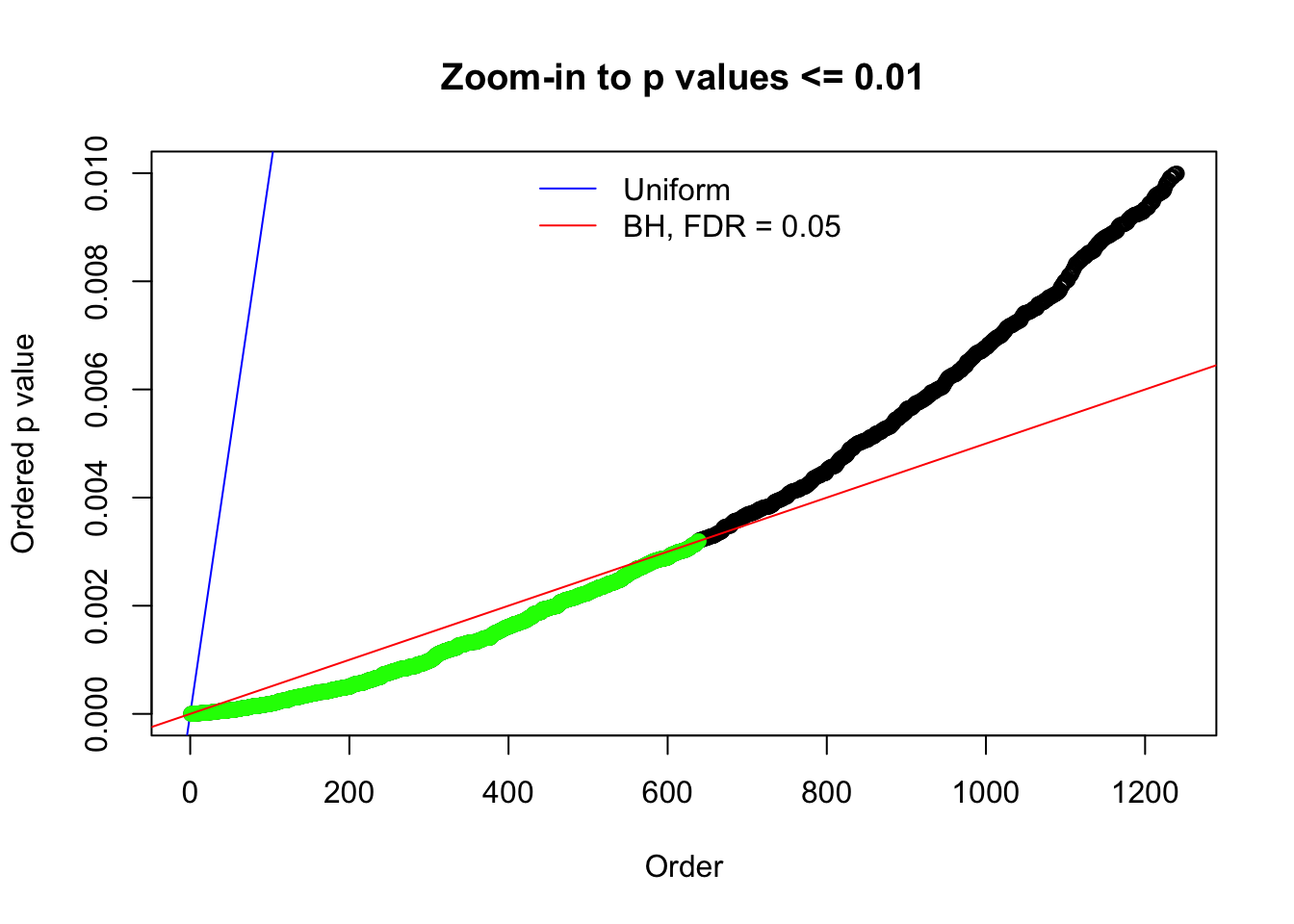
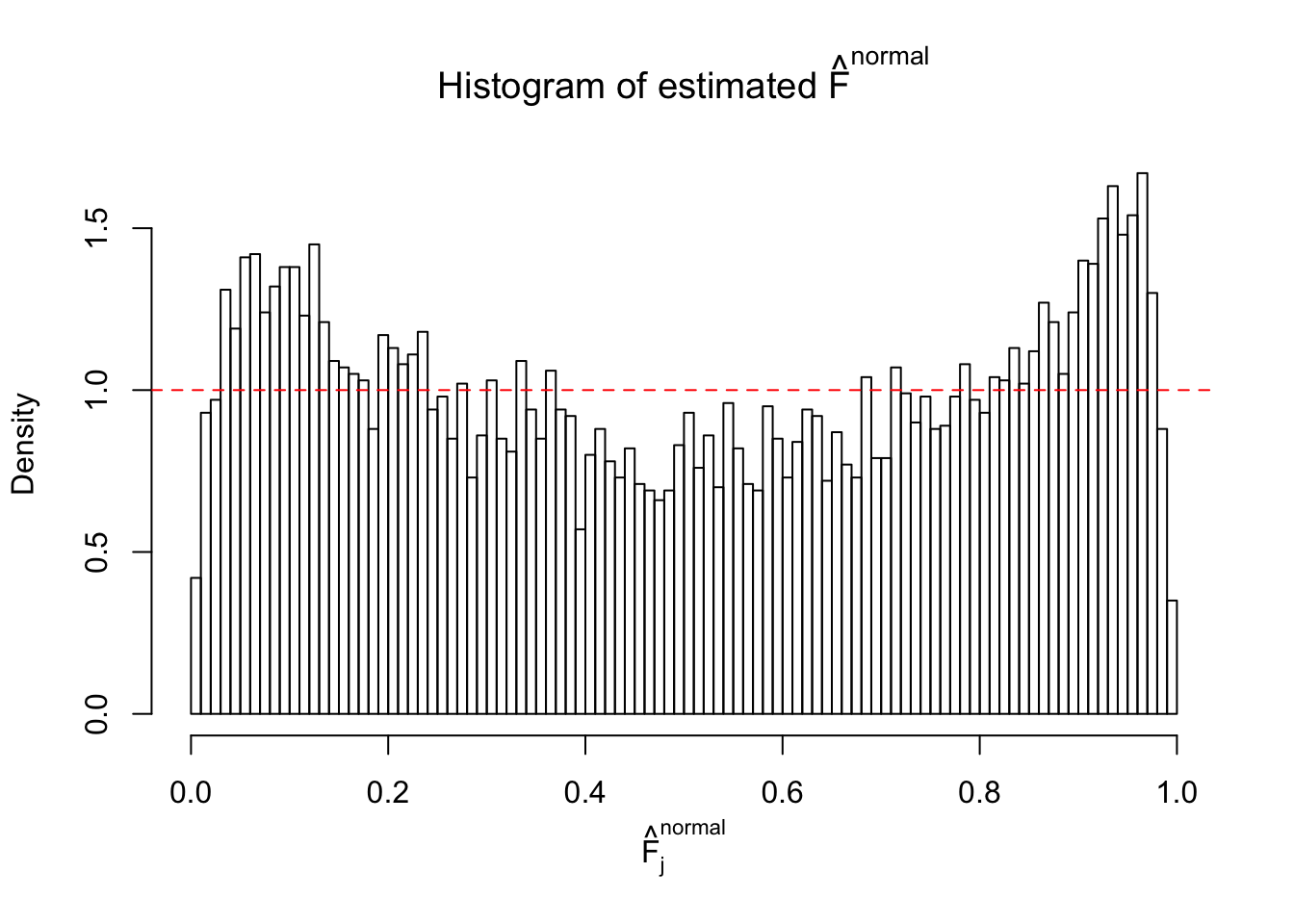
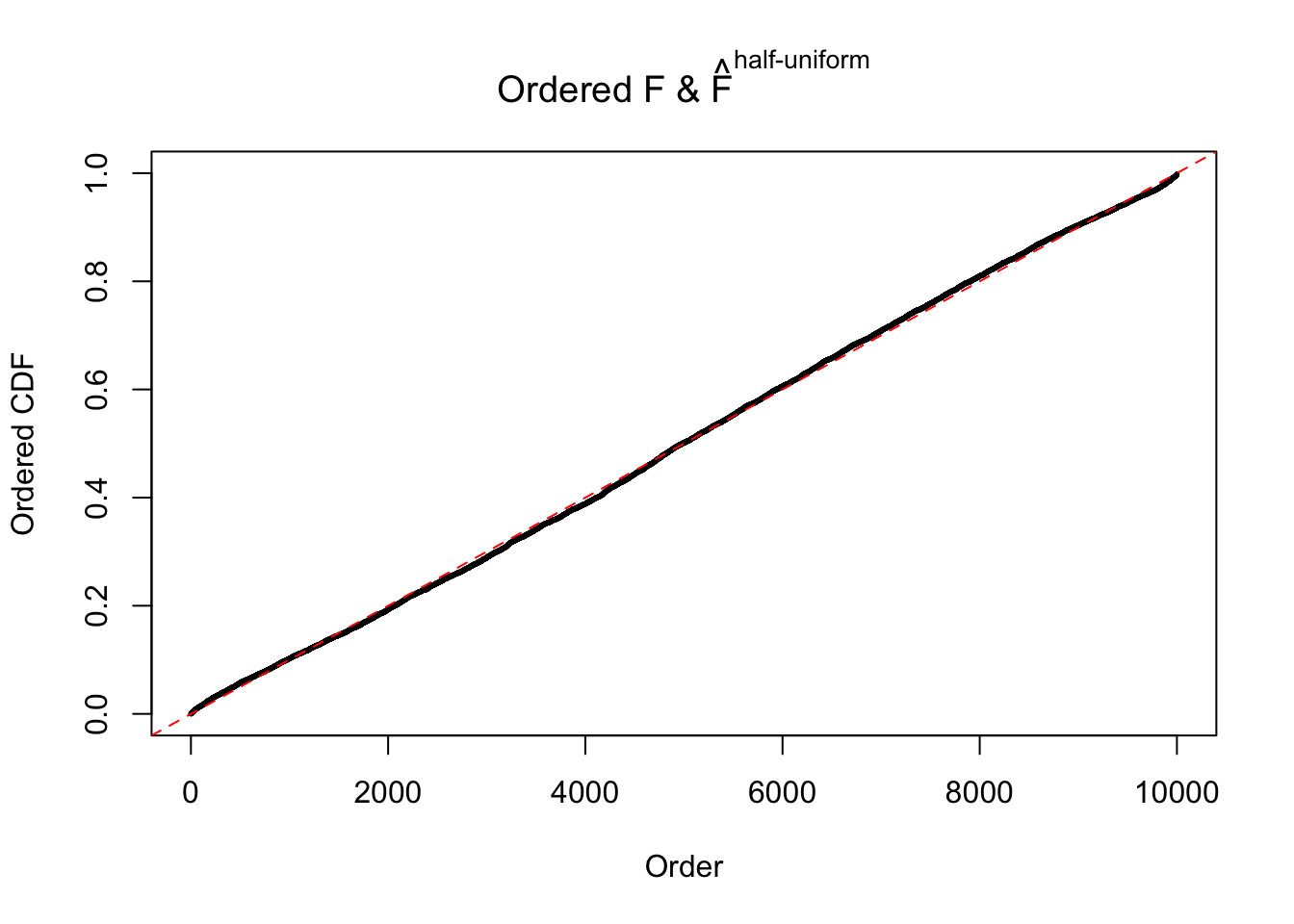
N0. 2 : Data Set 327 ; Number of False Discoveries: 489 ; pihat0 = 0.0477939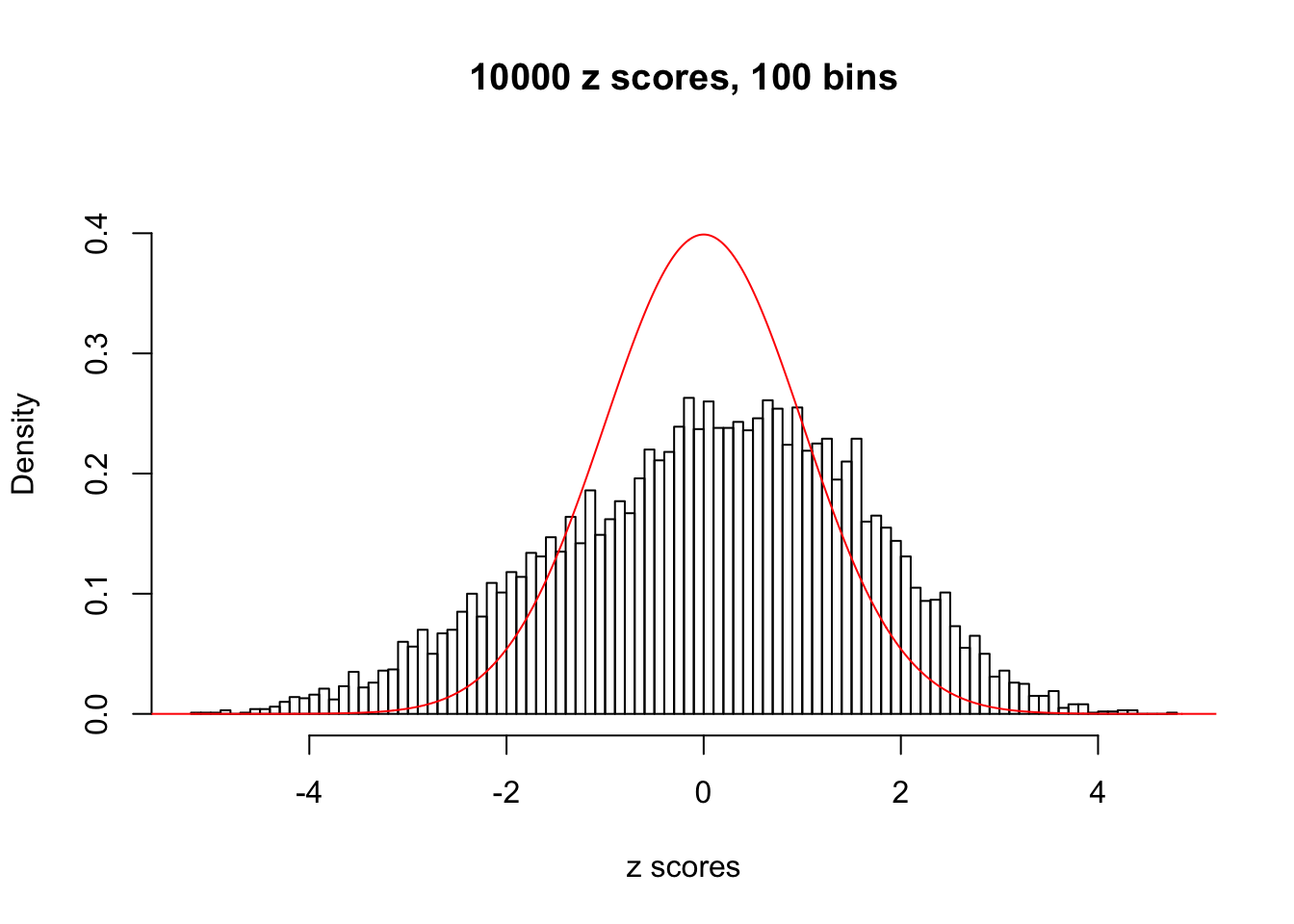
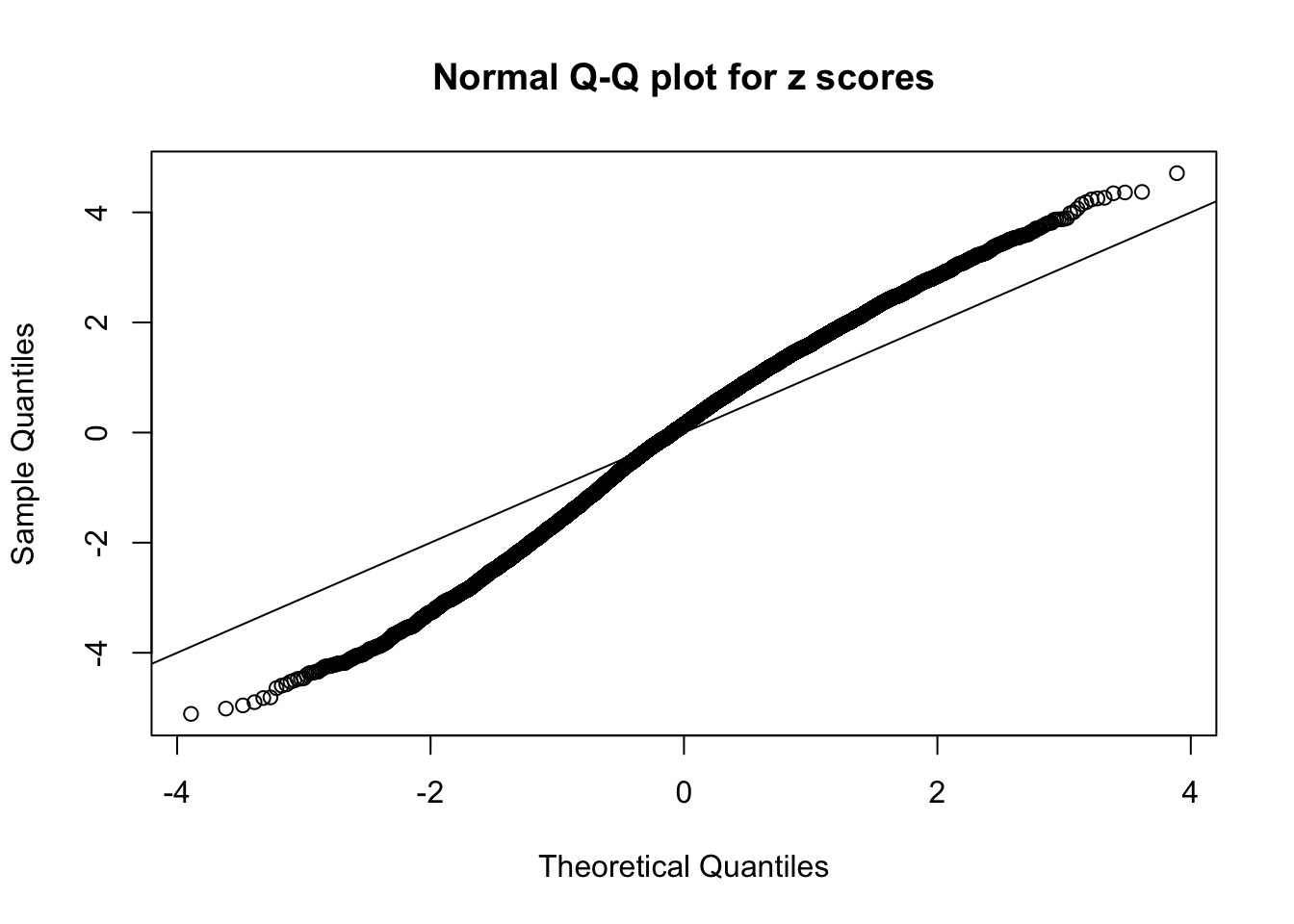
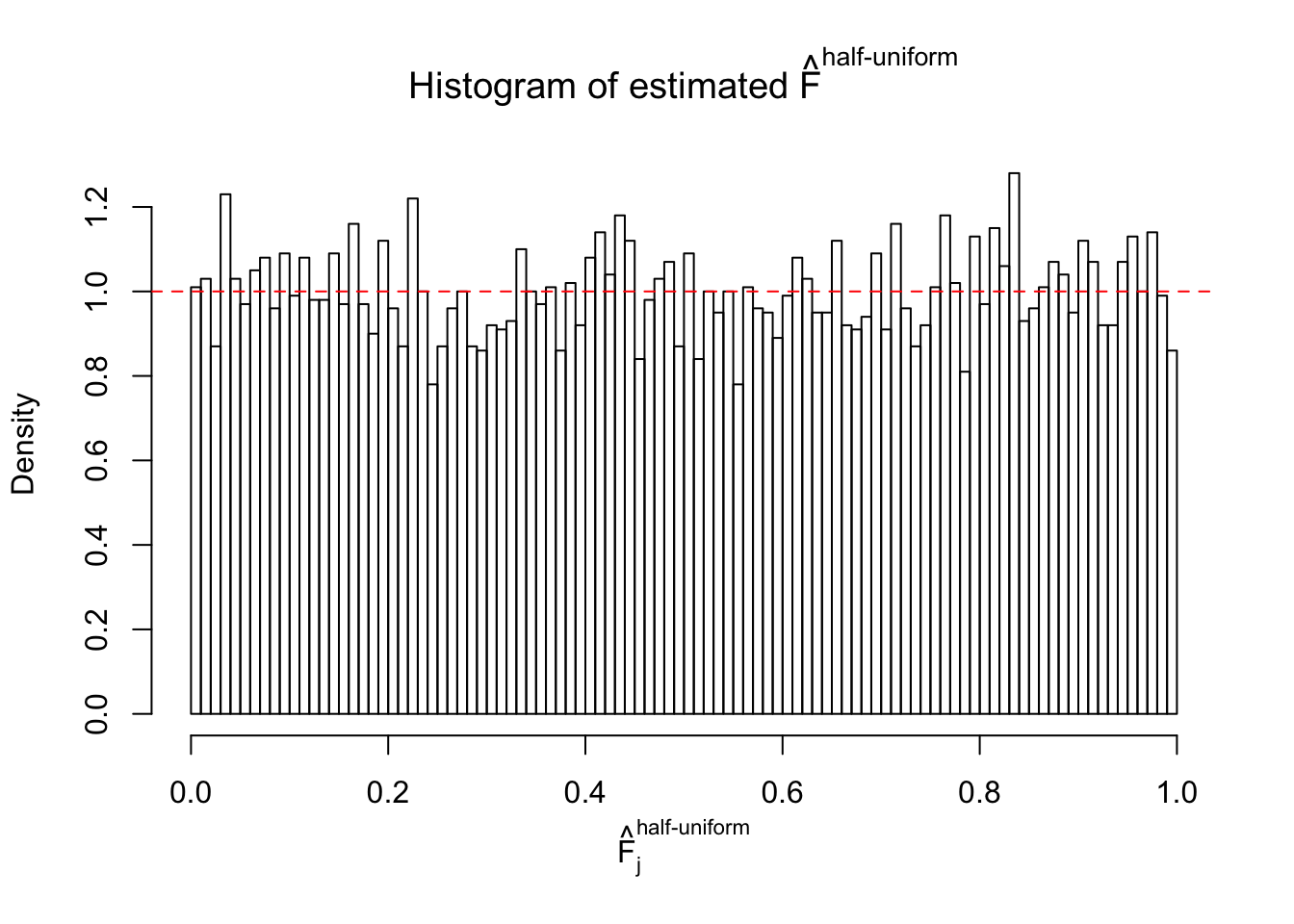
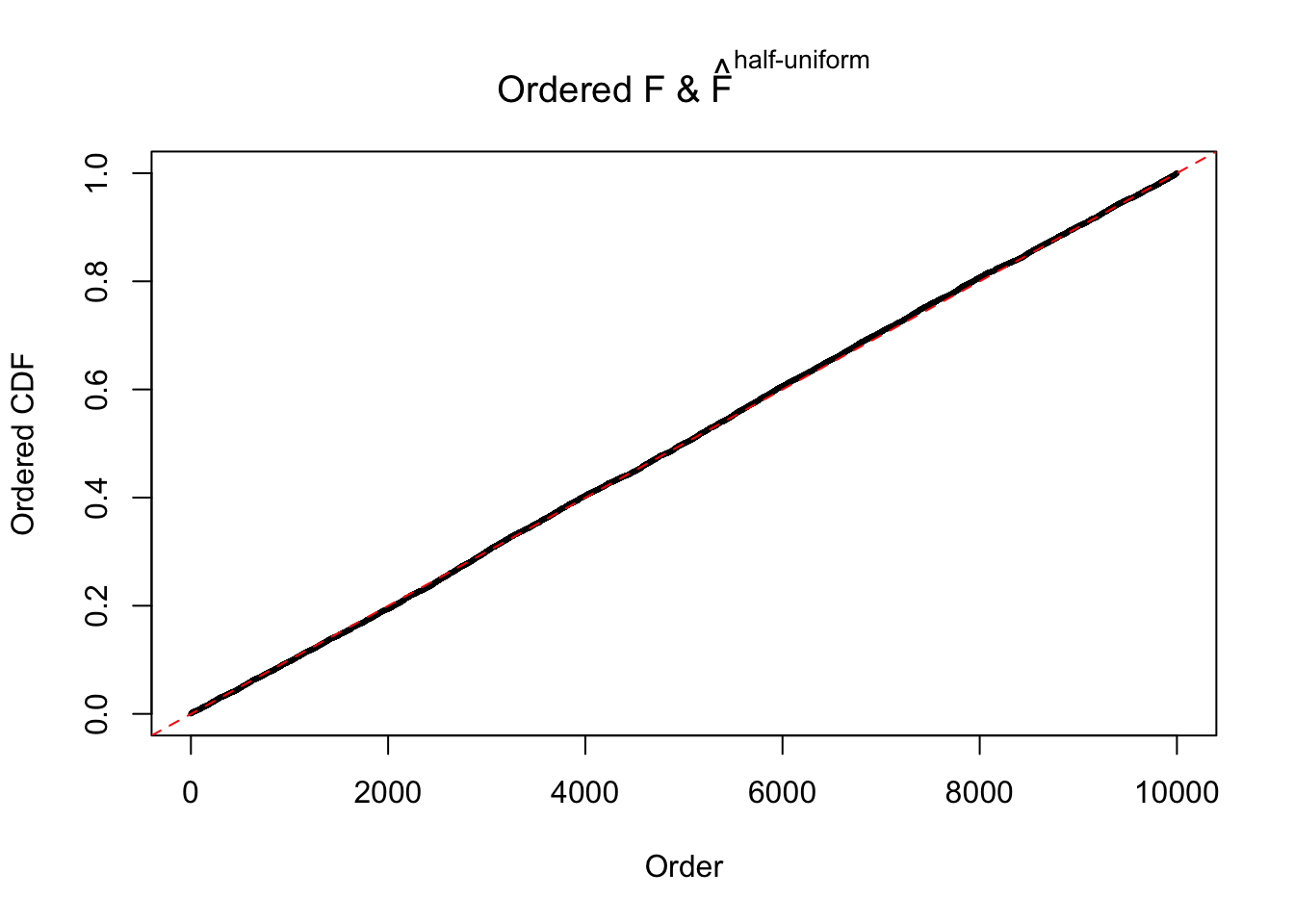
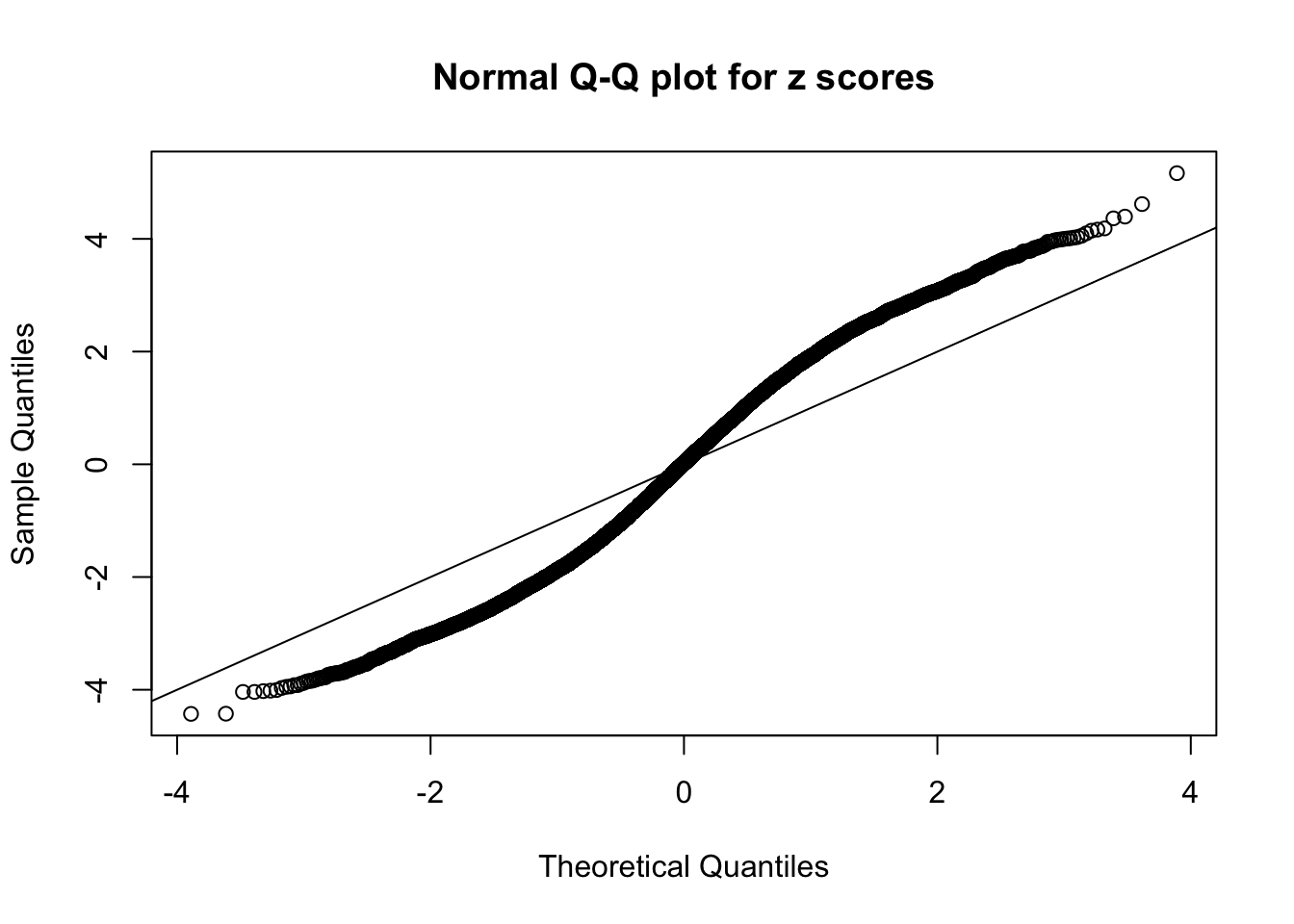
N0. 3 : Data Set 23 ; Number of False Discoveries: 408 ; pihat0 = 0.008419777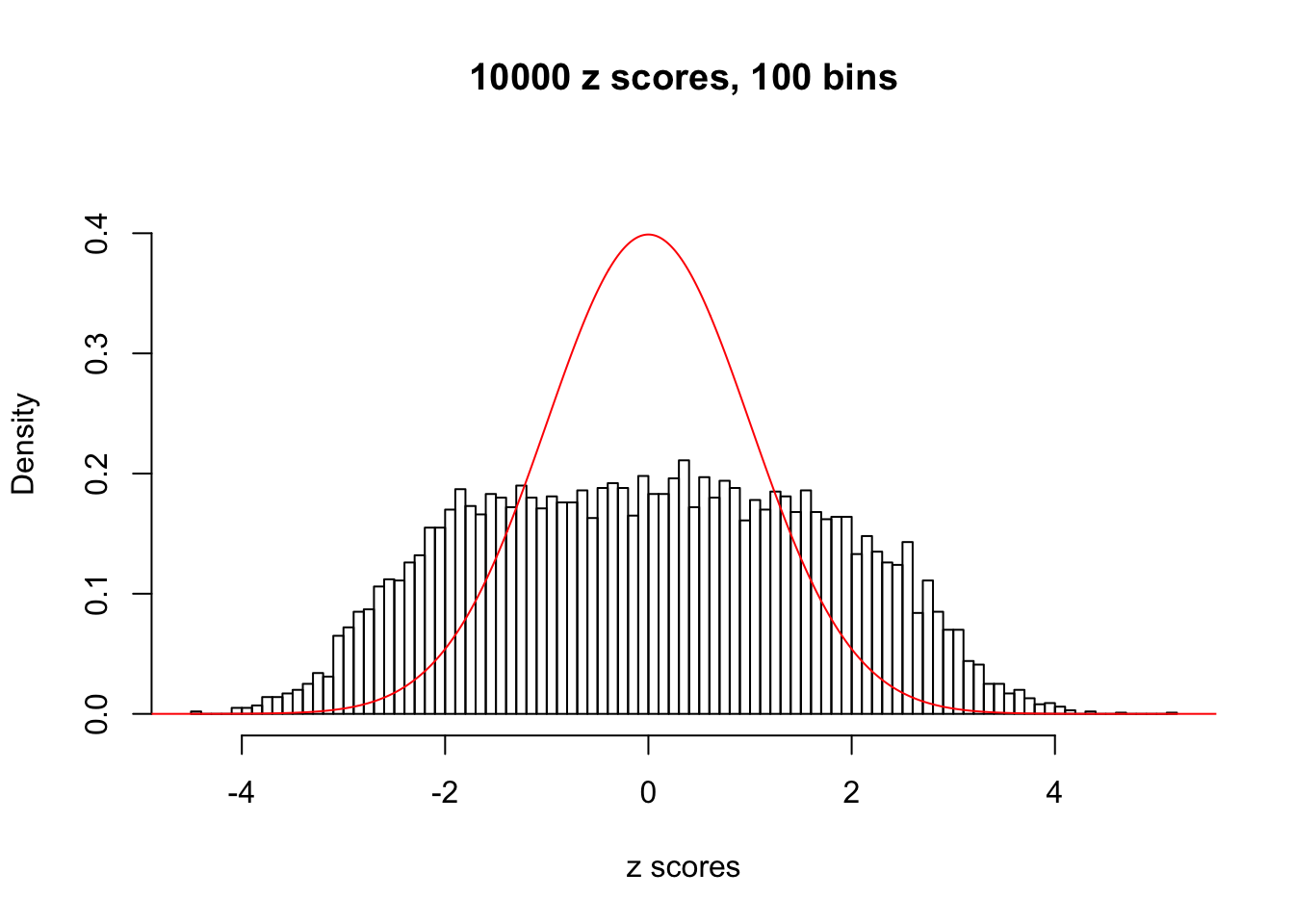
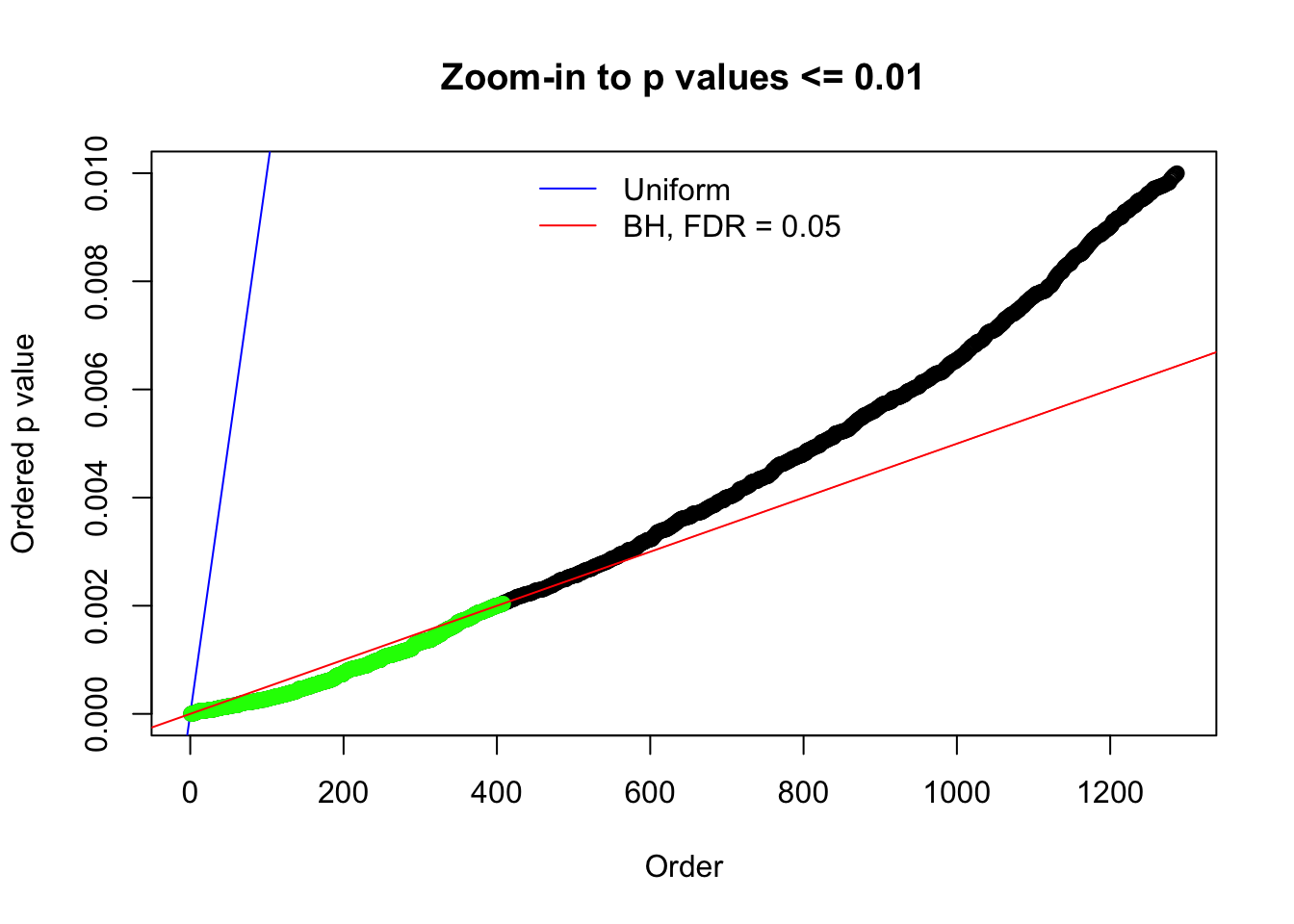
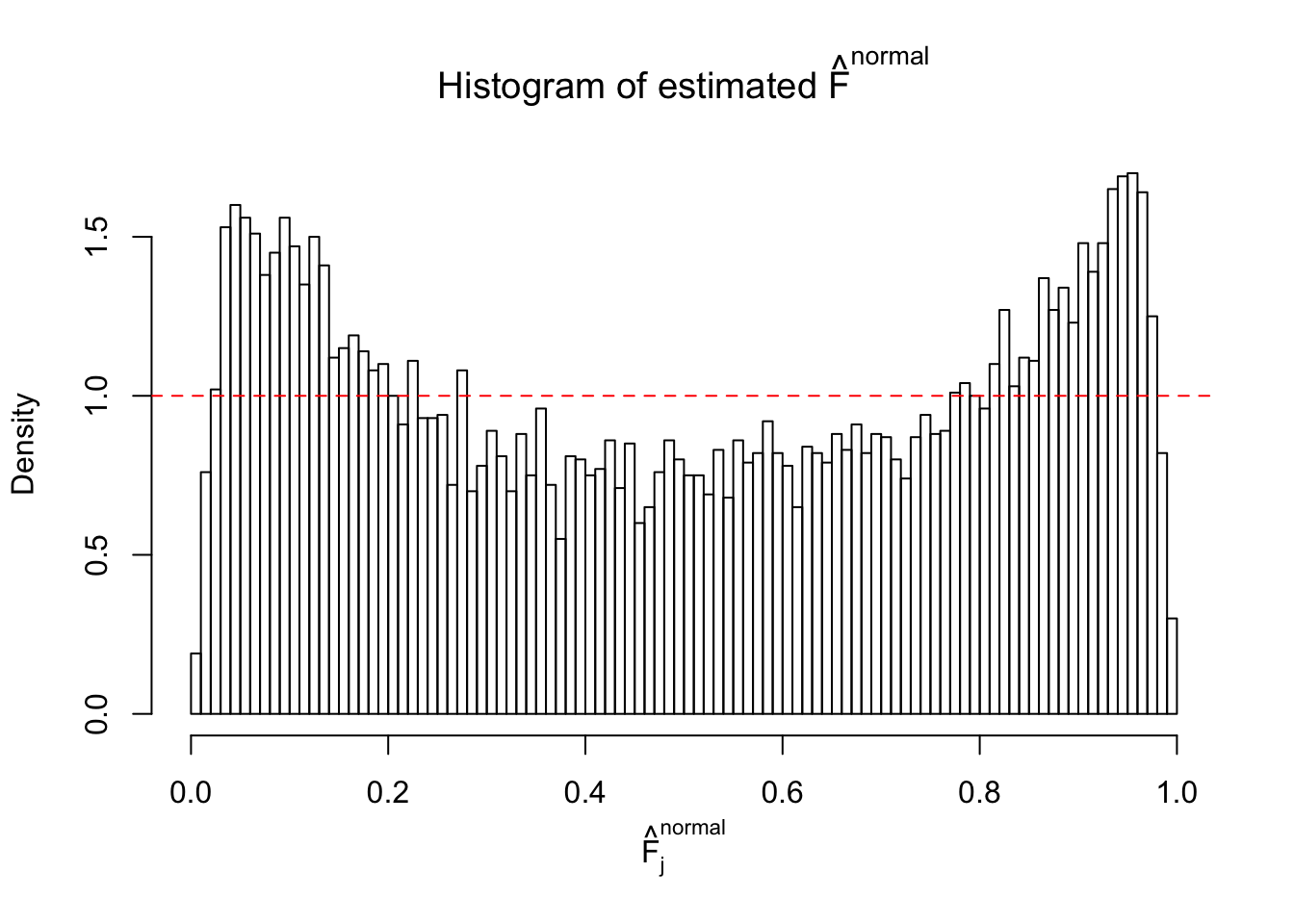
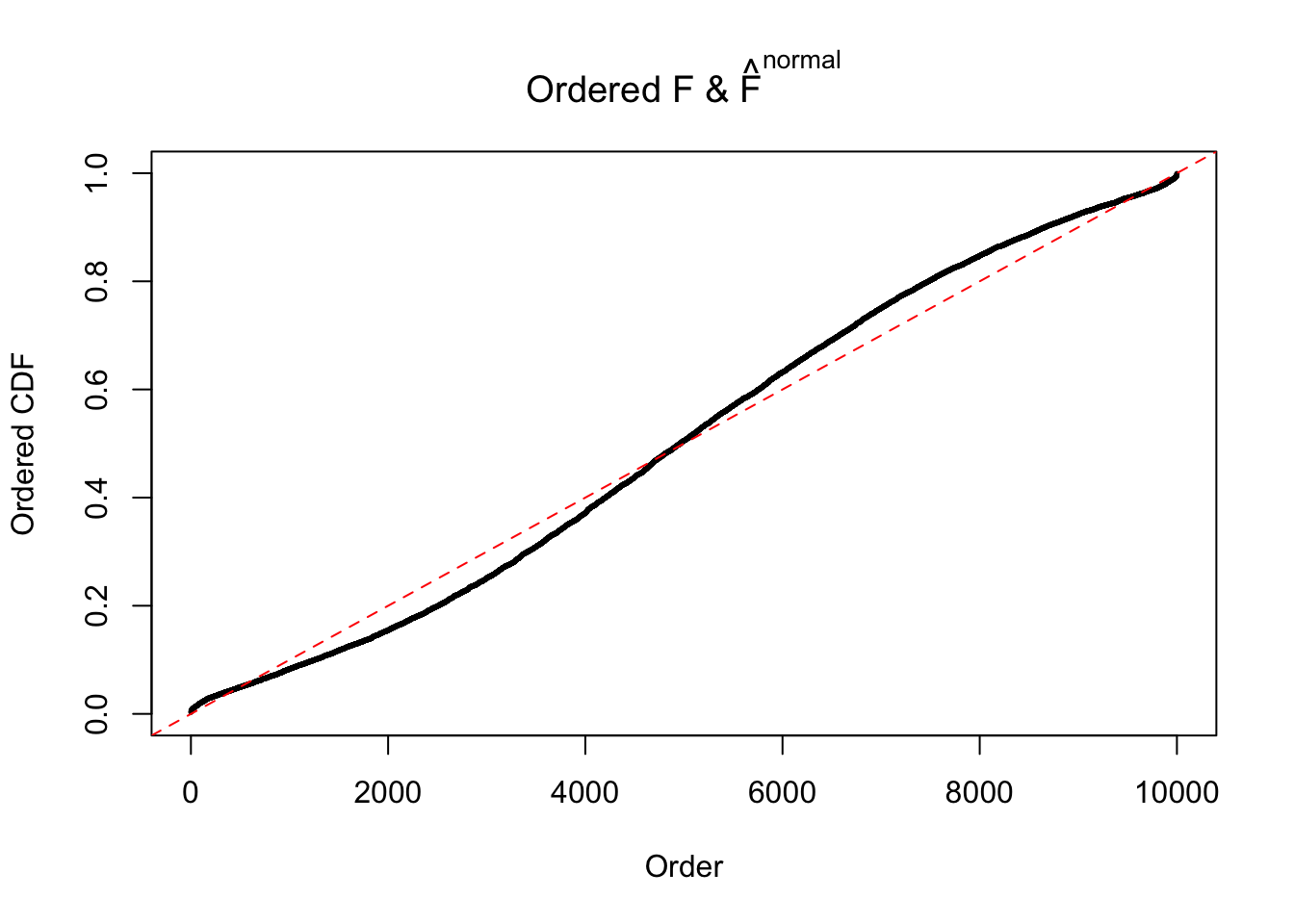
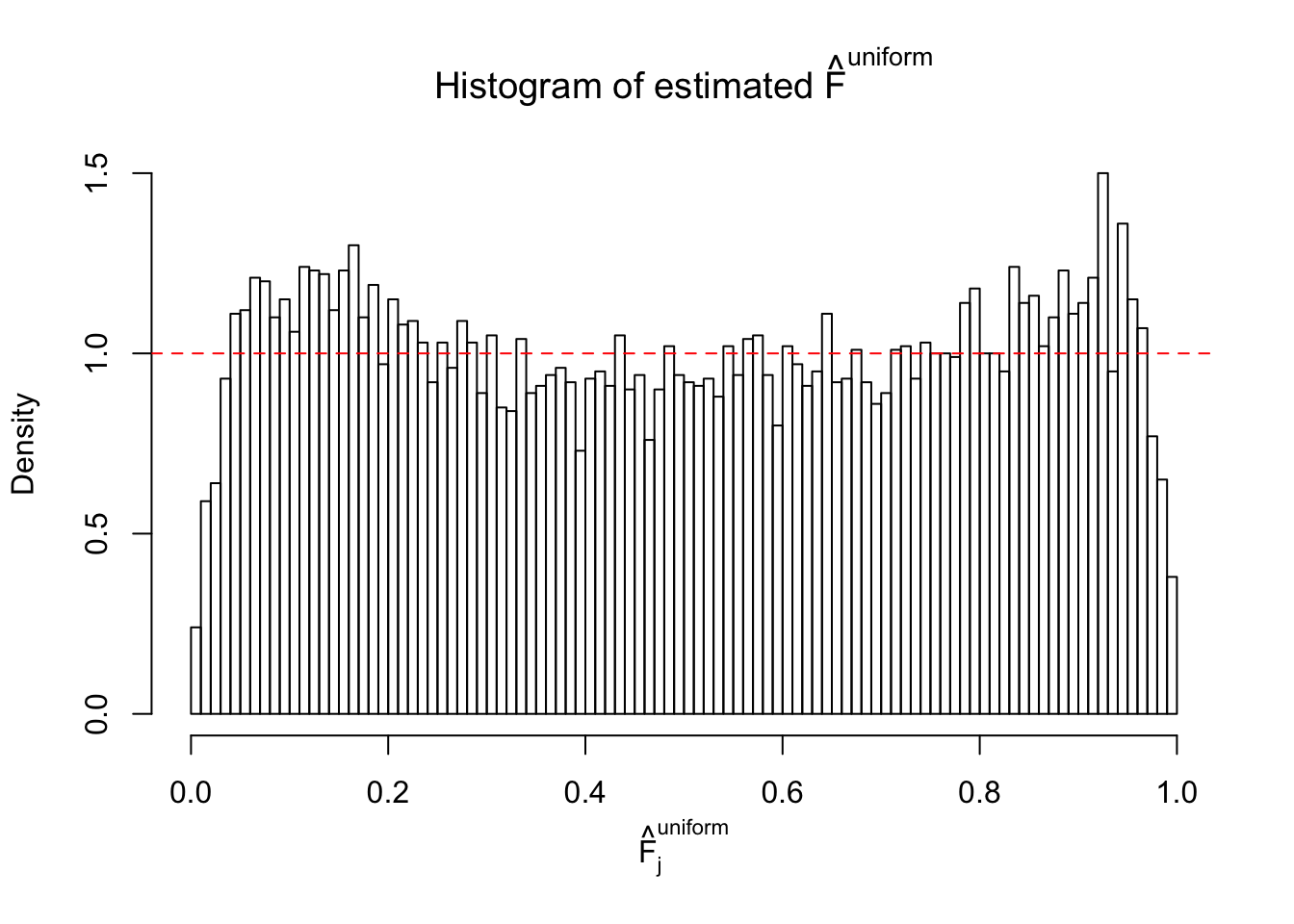
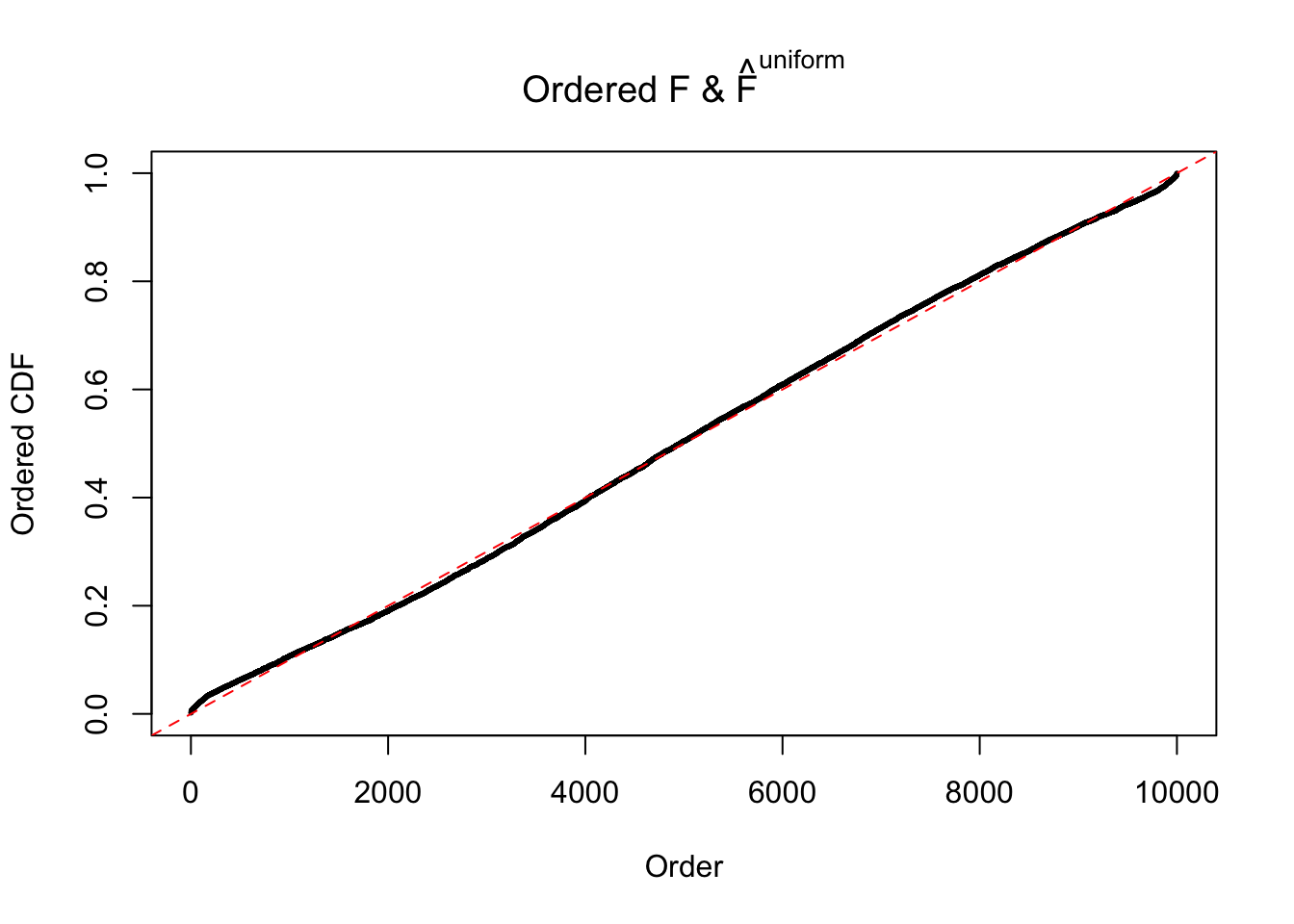
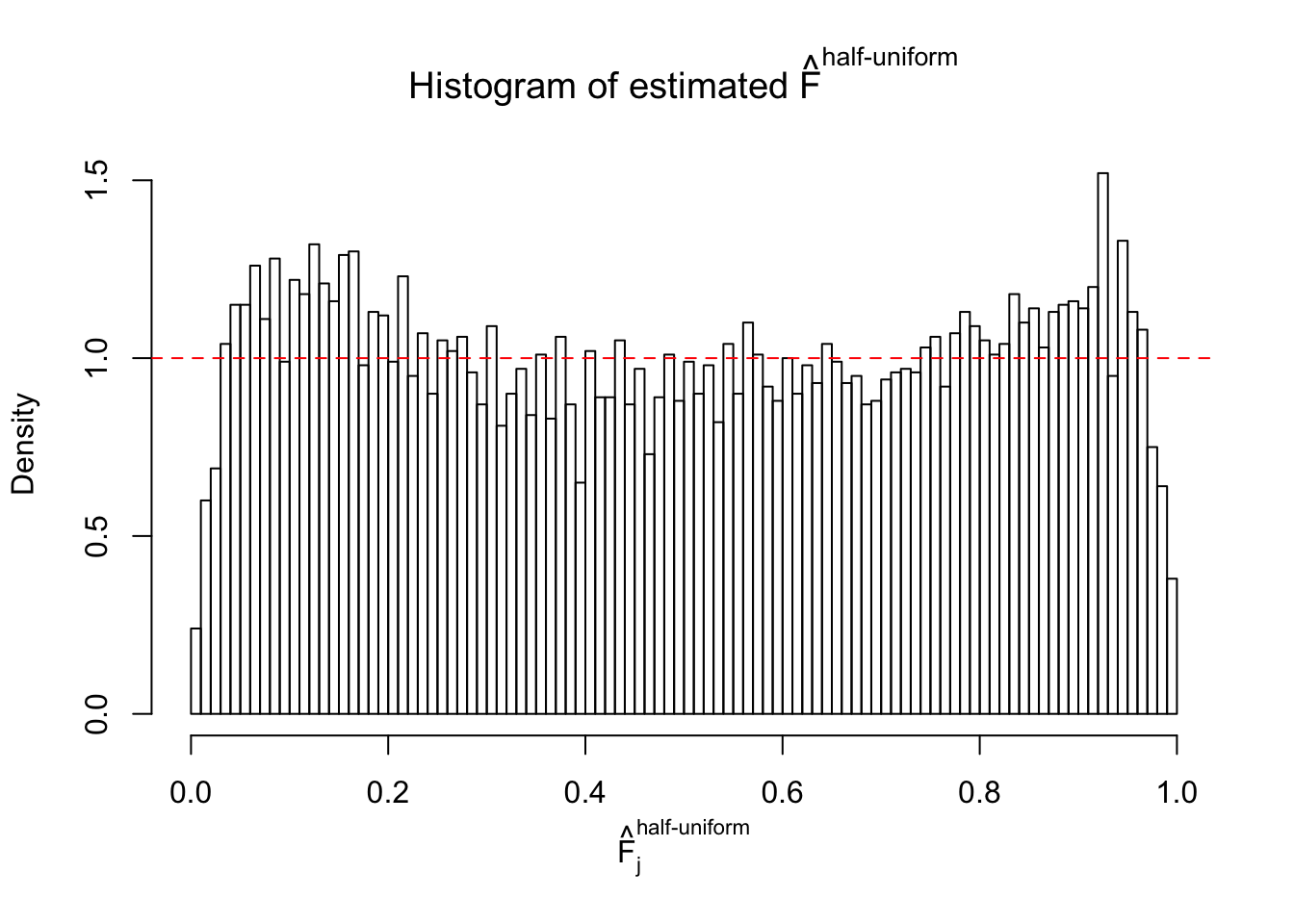
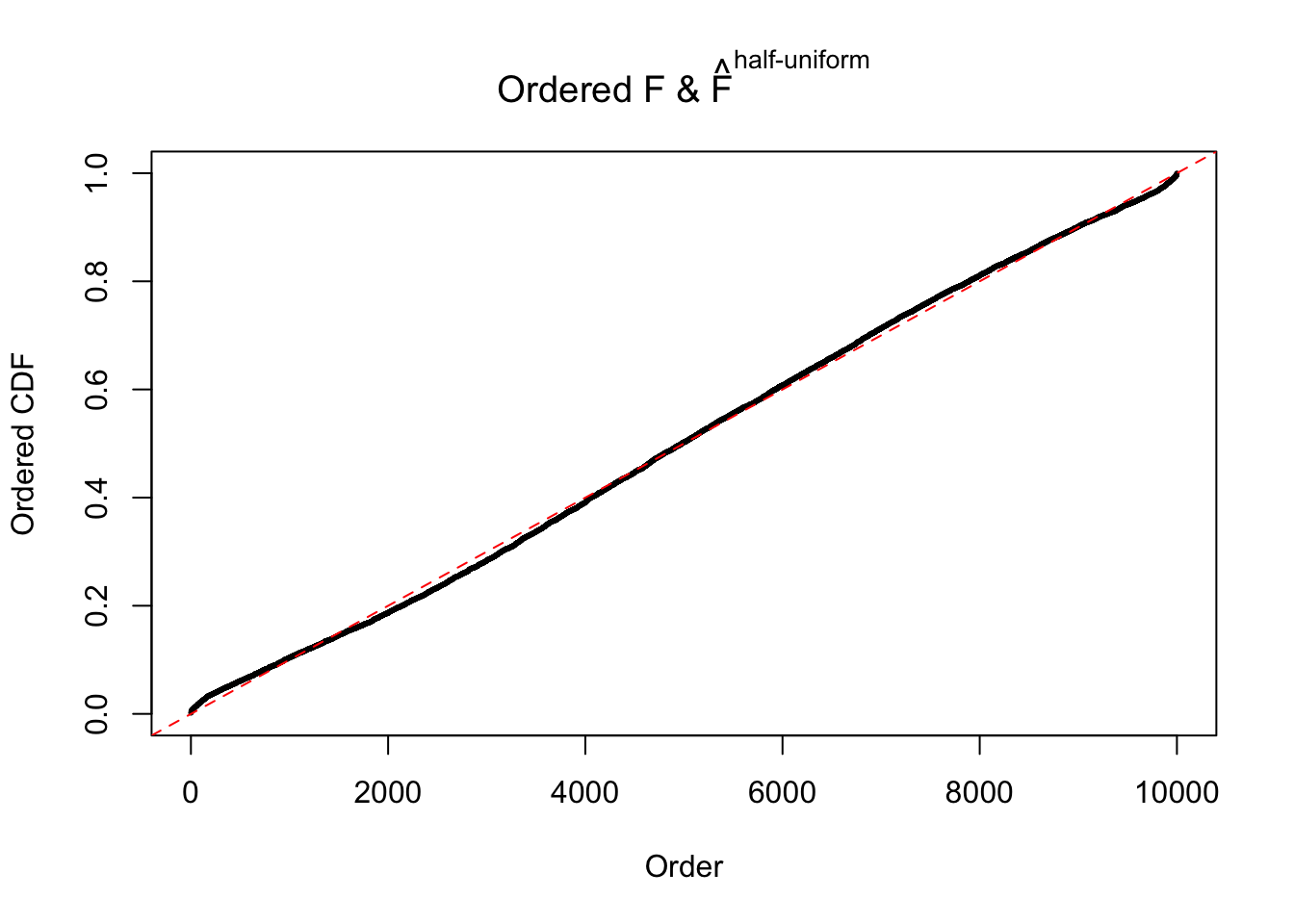
N0. 4 : Data Set 122 ; Number of False Discoveries: 331 ; pihat0 = 0.01544099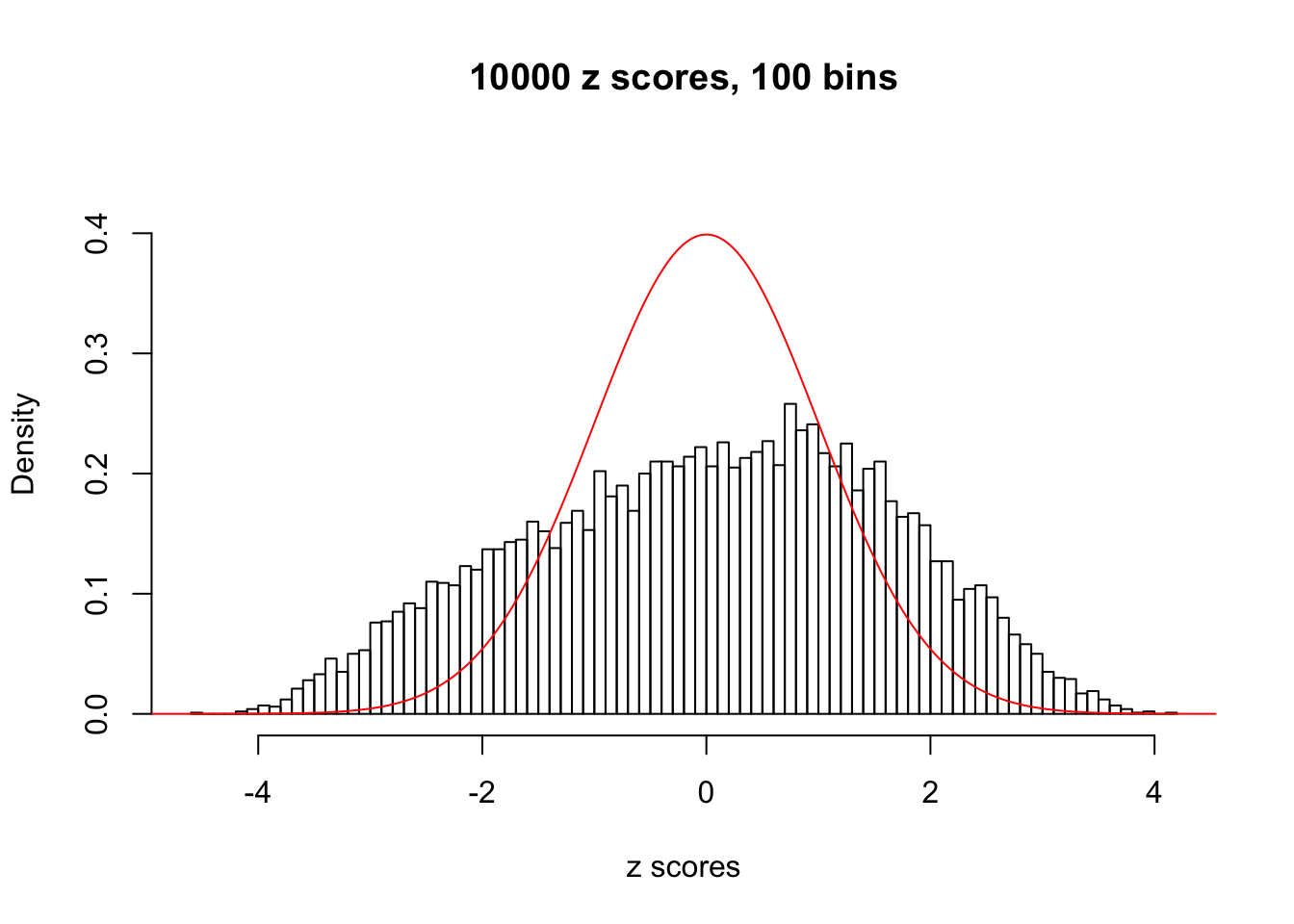
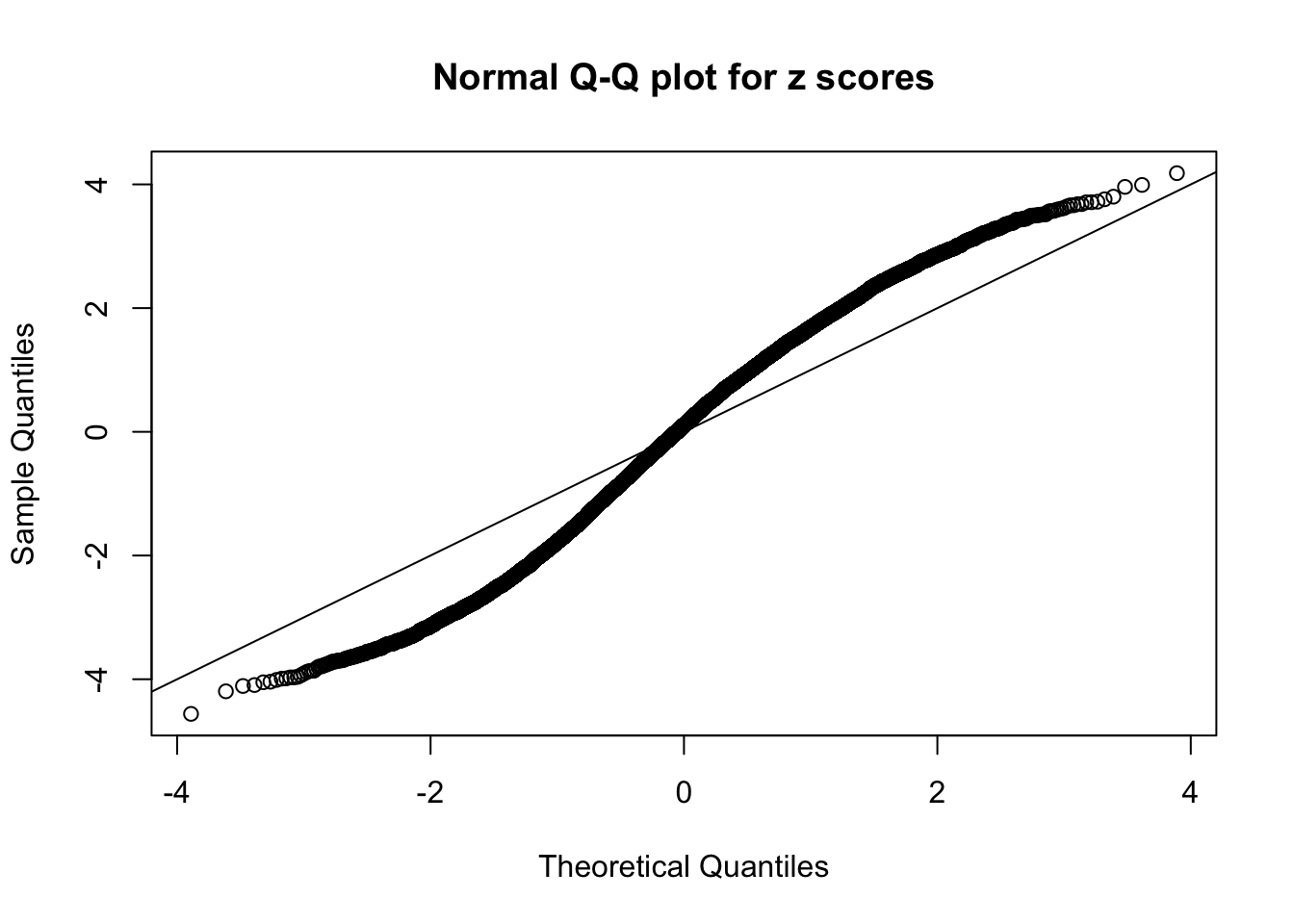
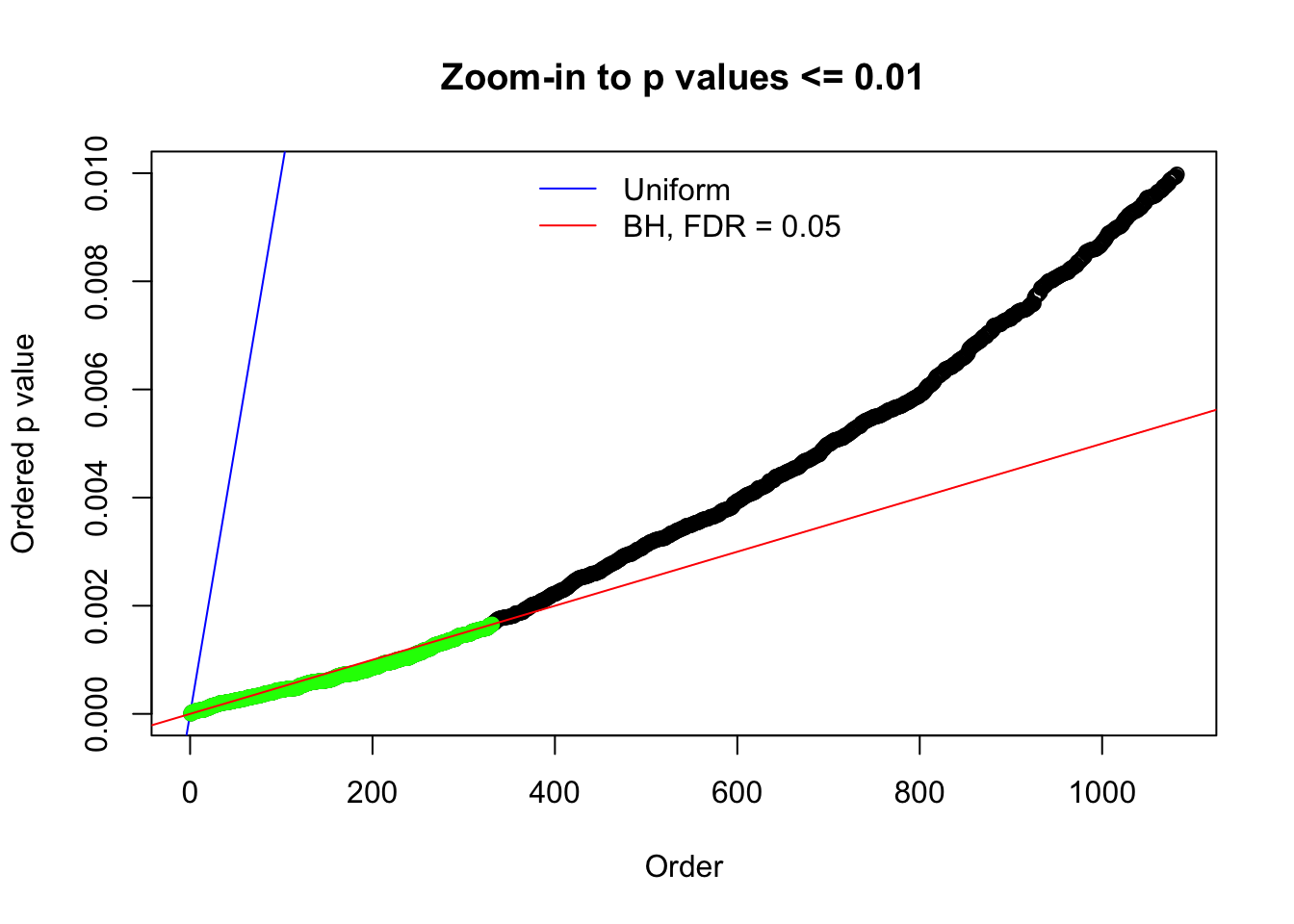
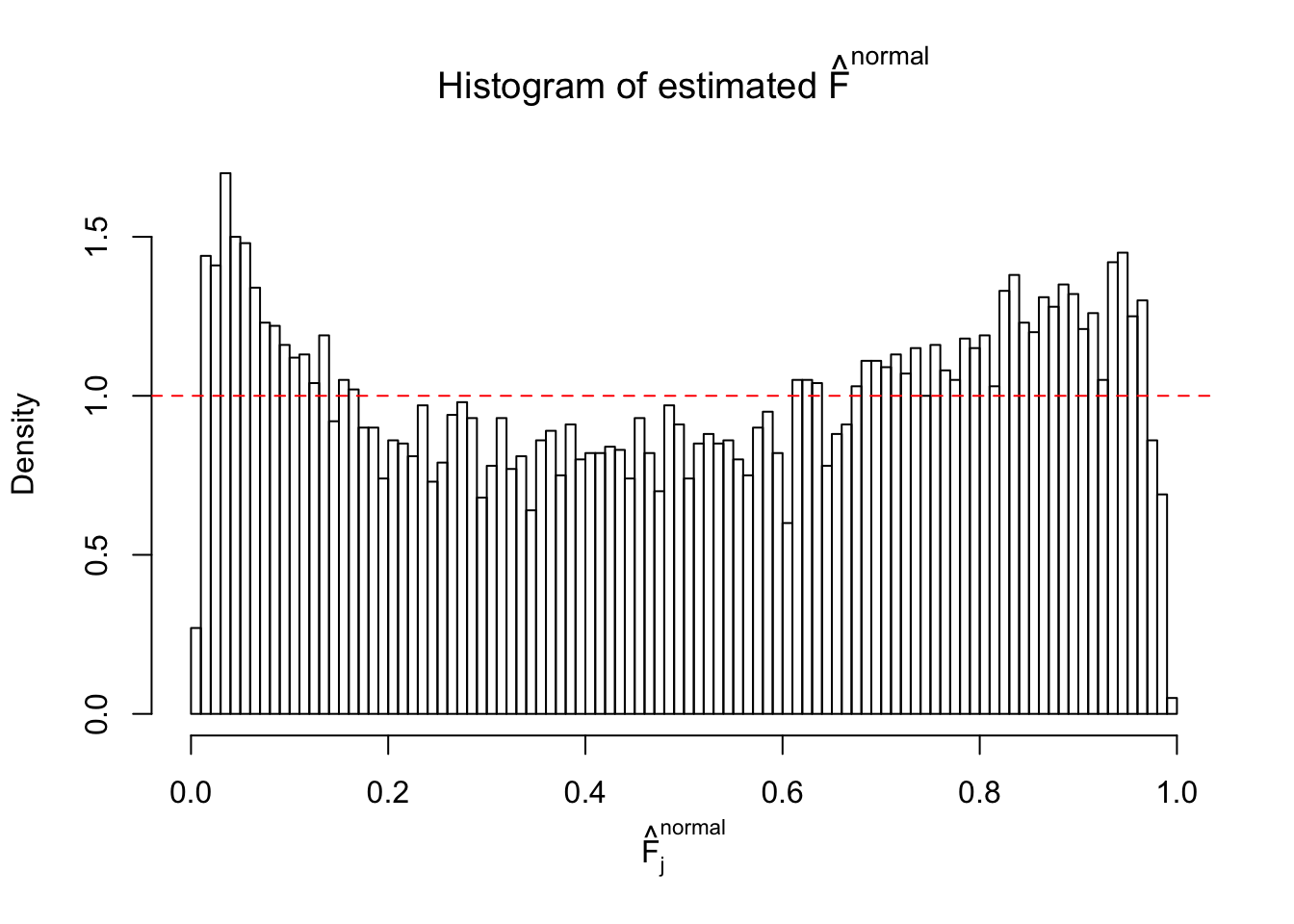
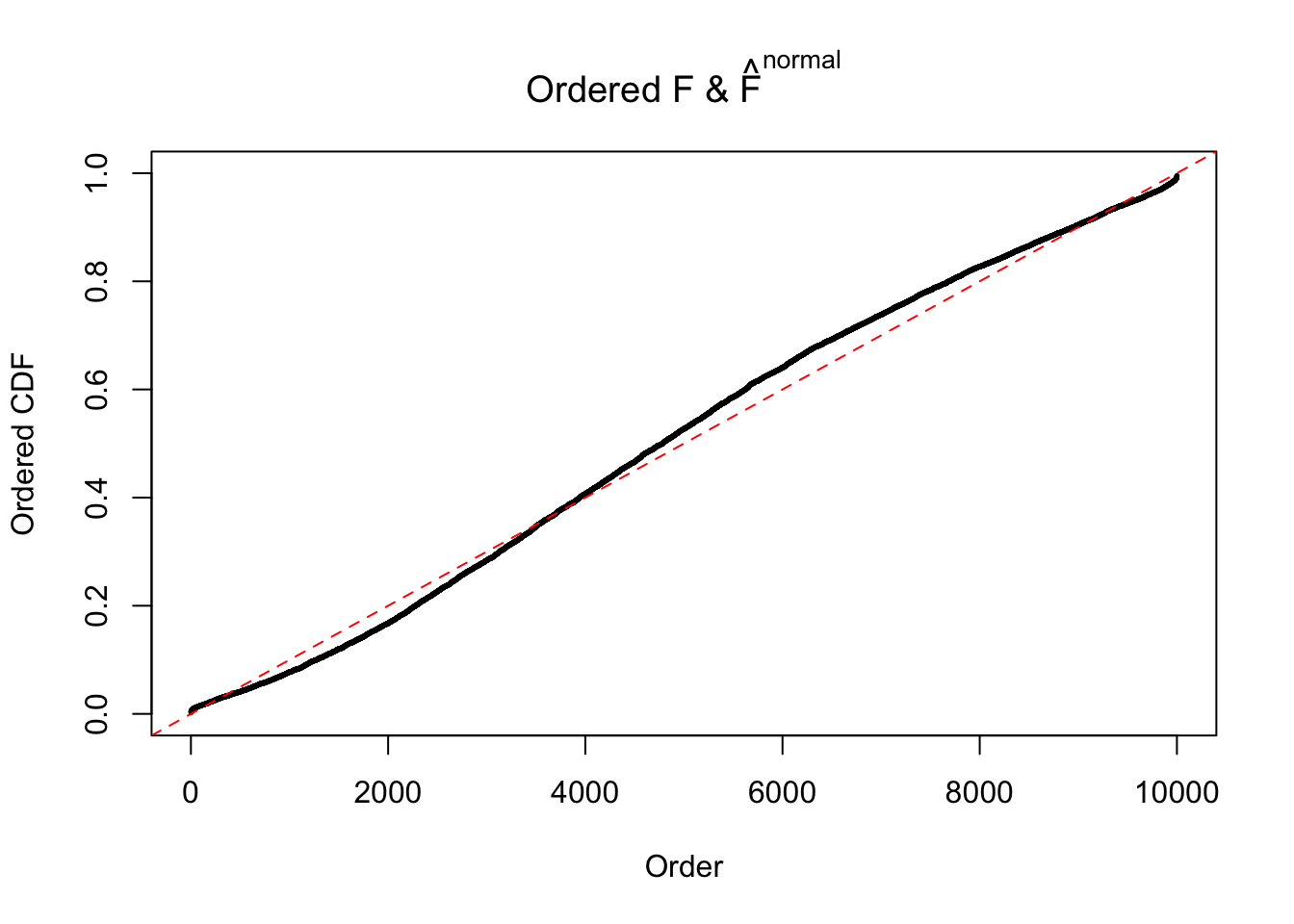
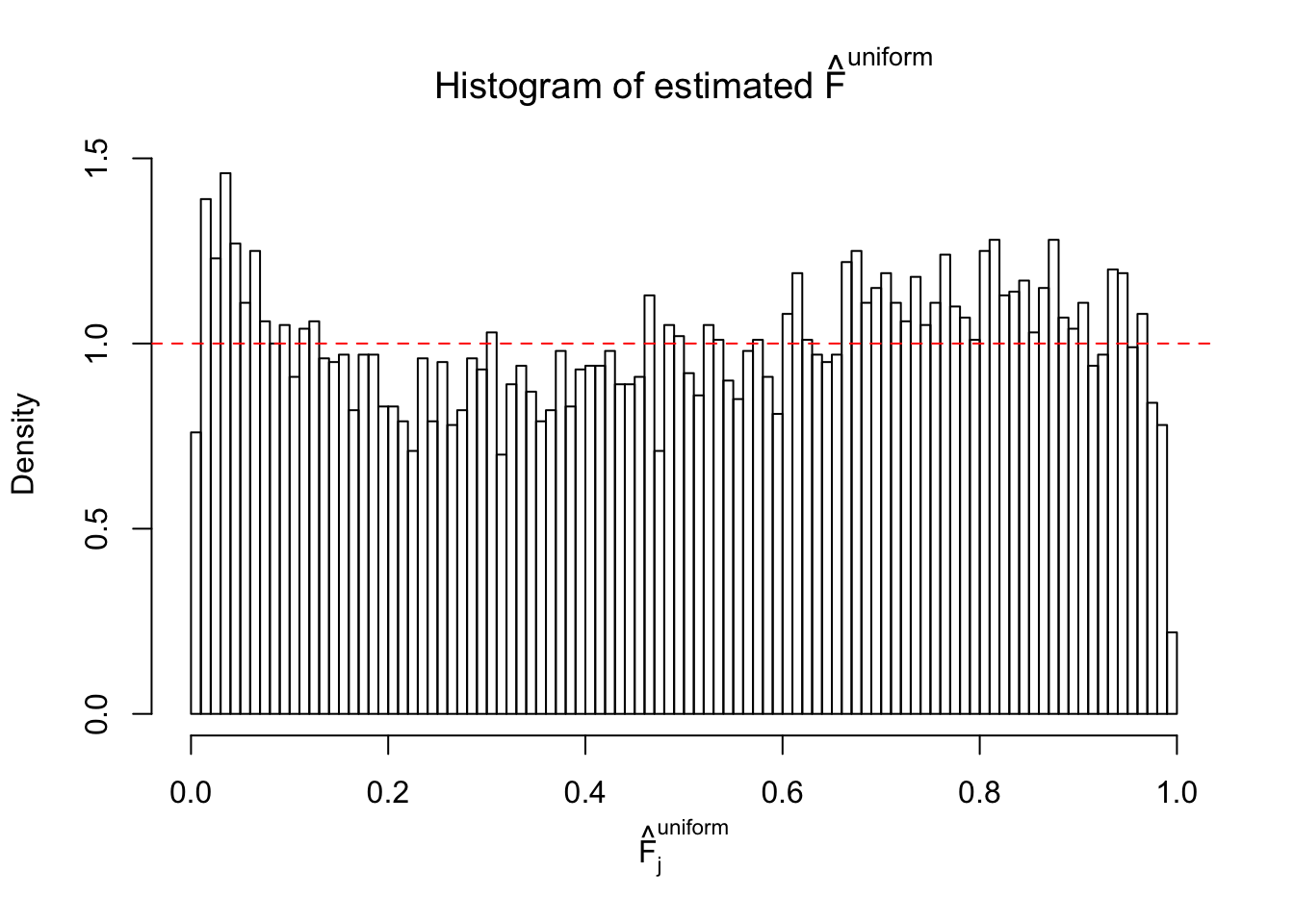
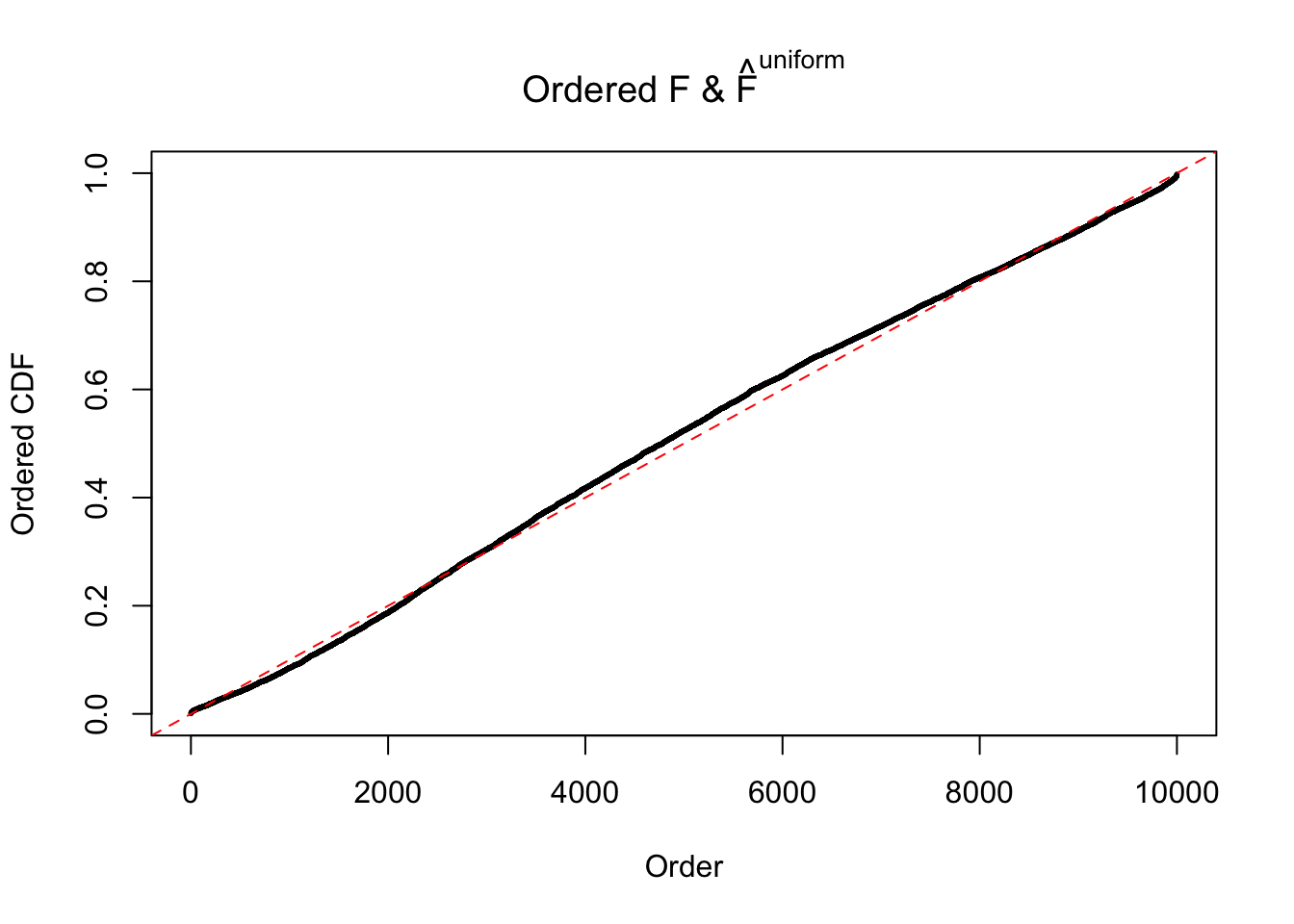
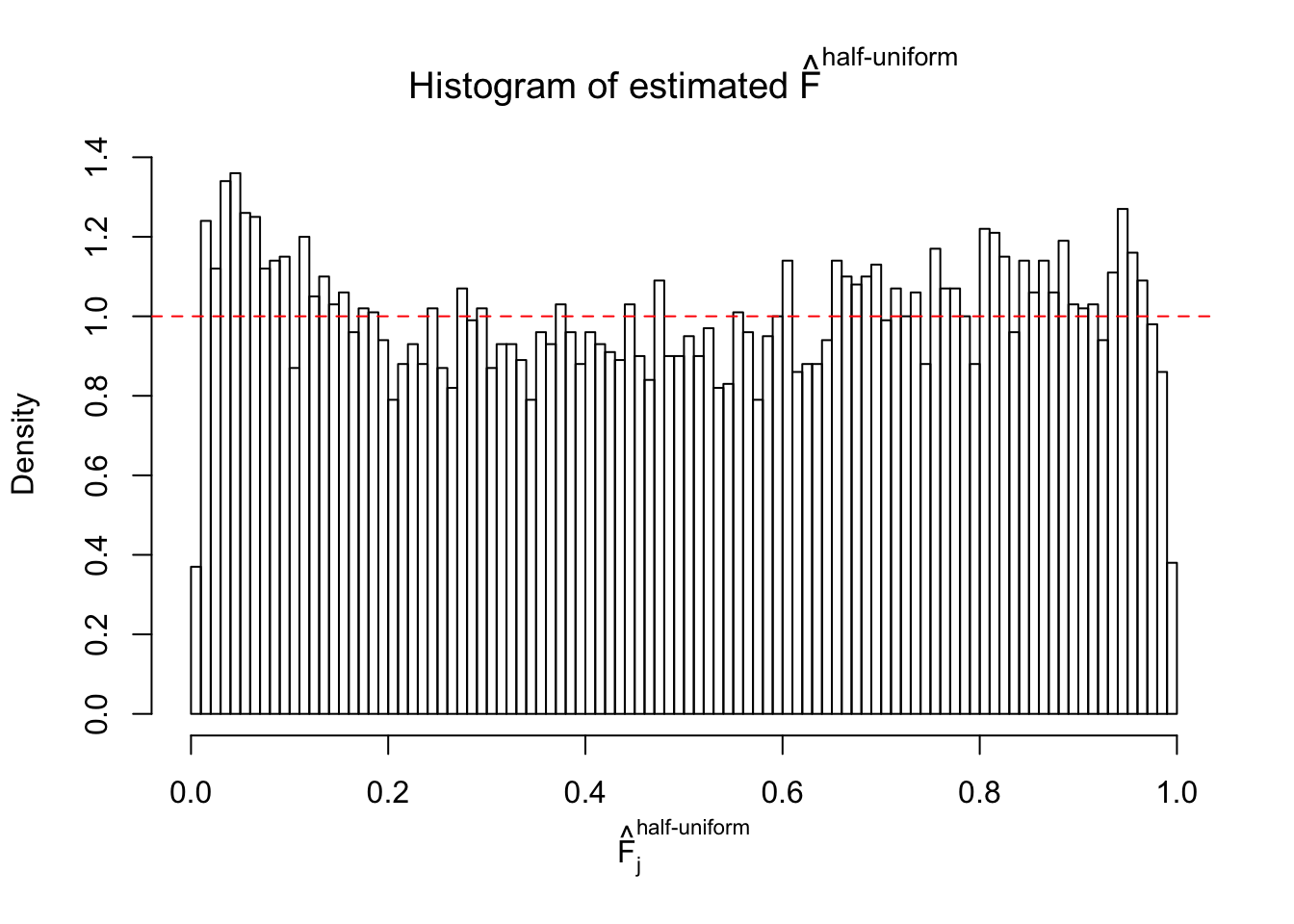
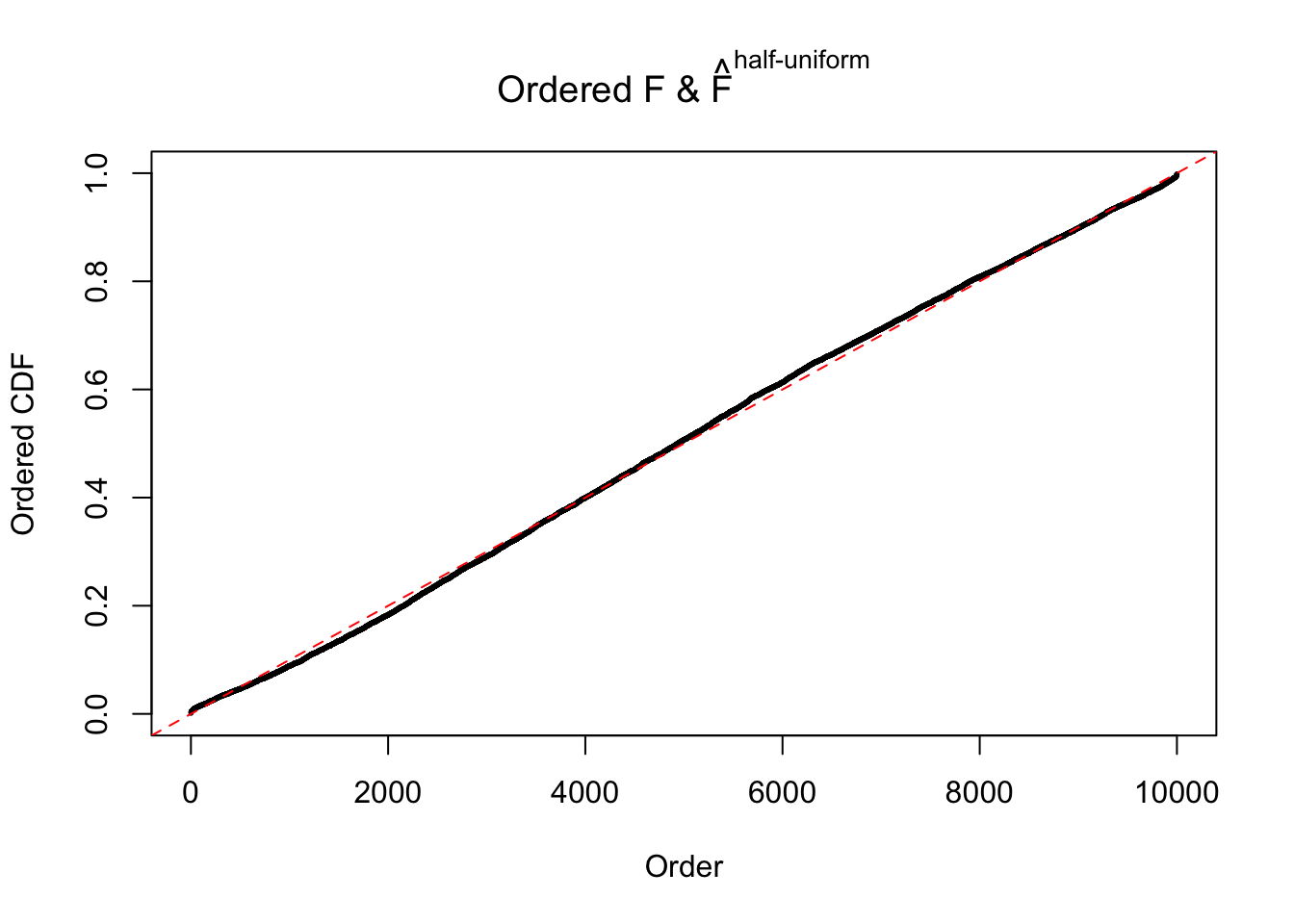
N0. 5 : Data Set 783 ; Number of False Discoveries: 170 ; pihat0 = 0.01516697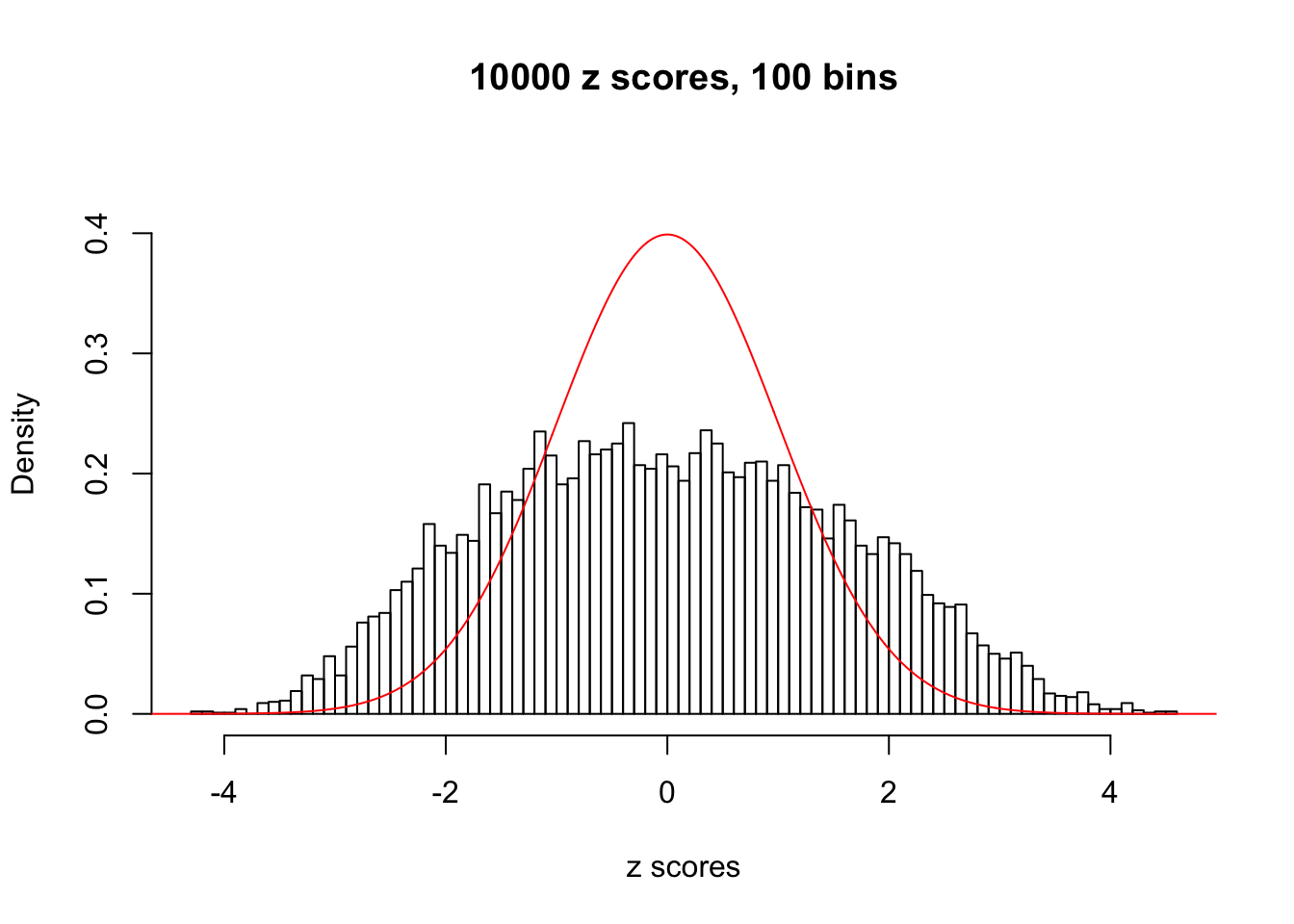
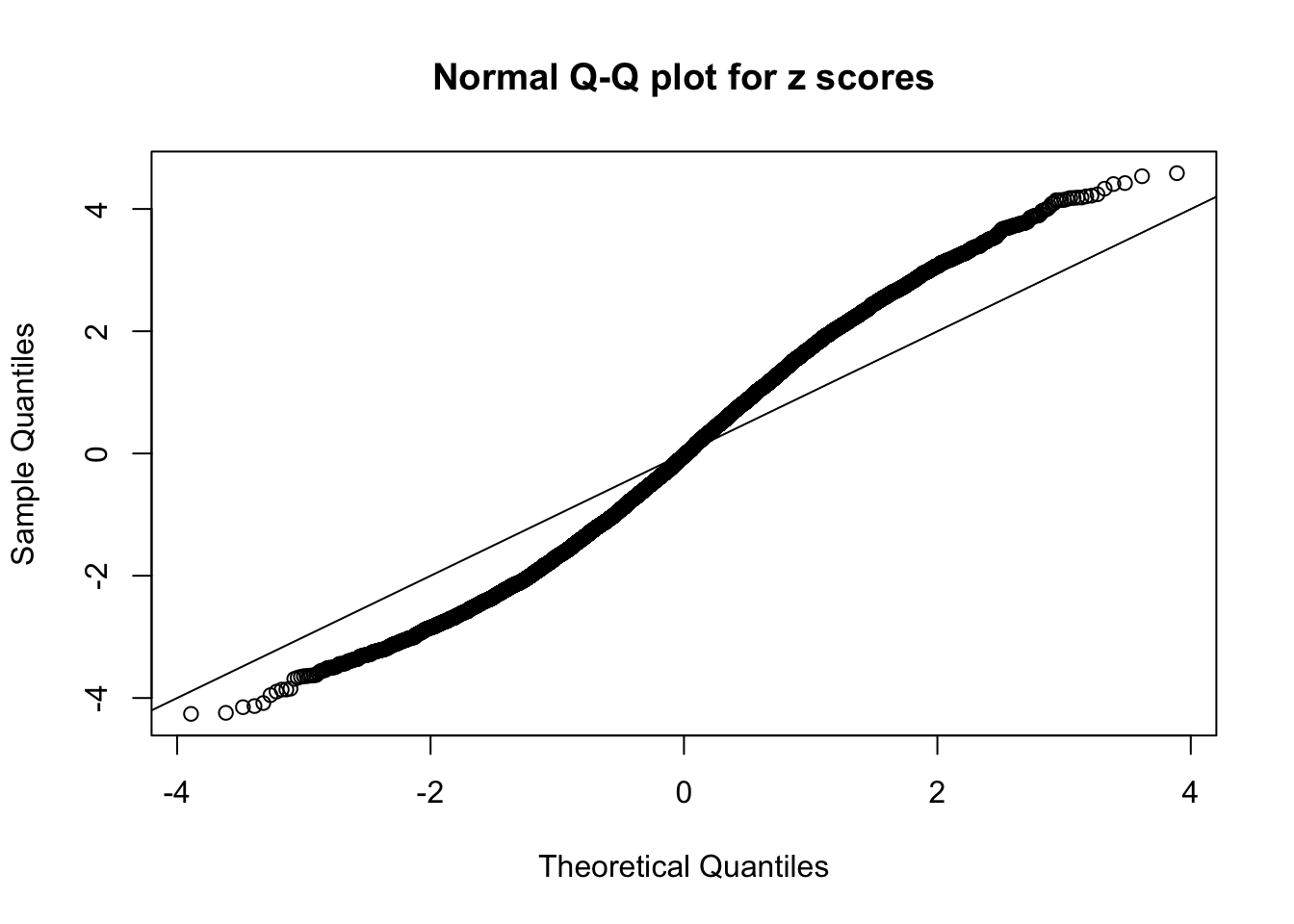
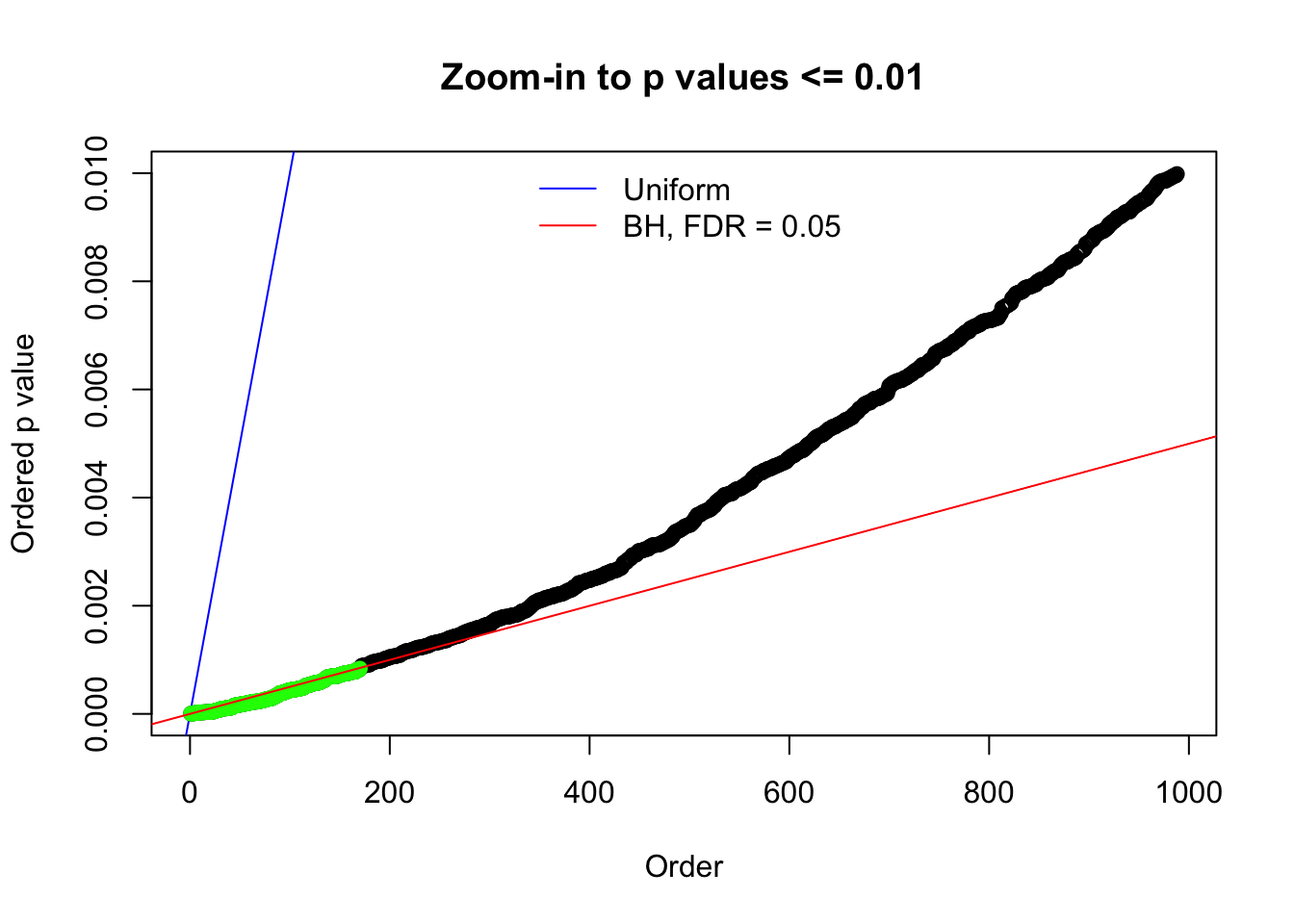
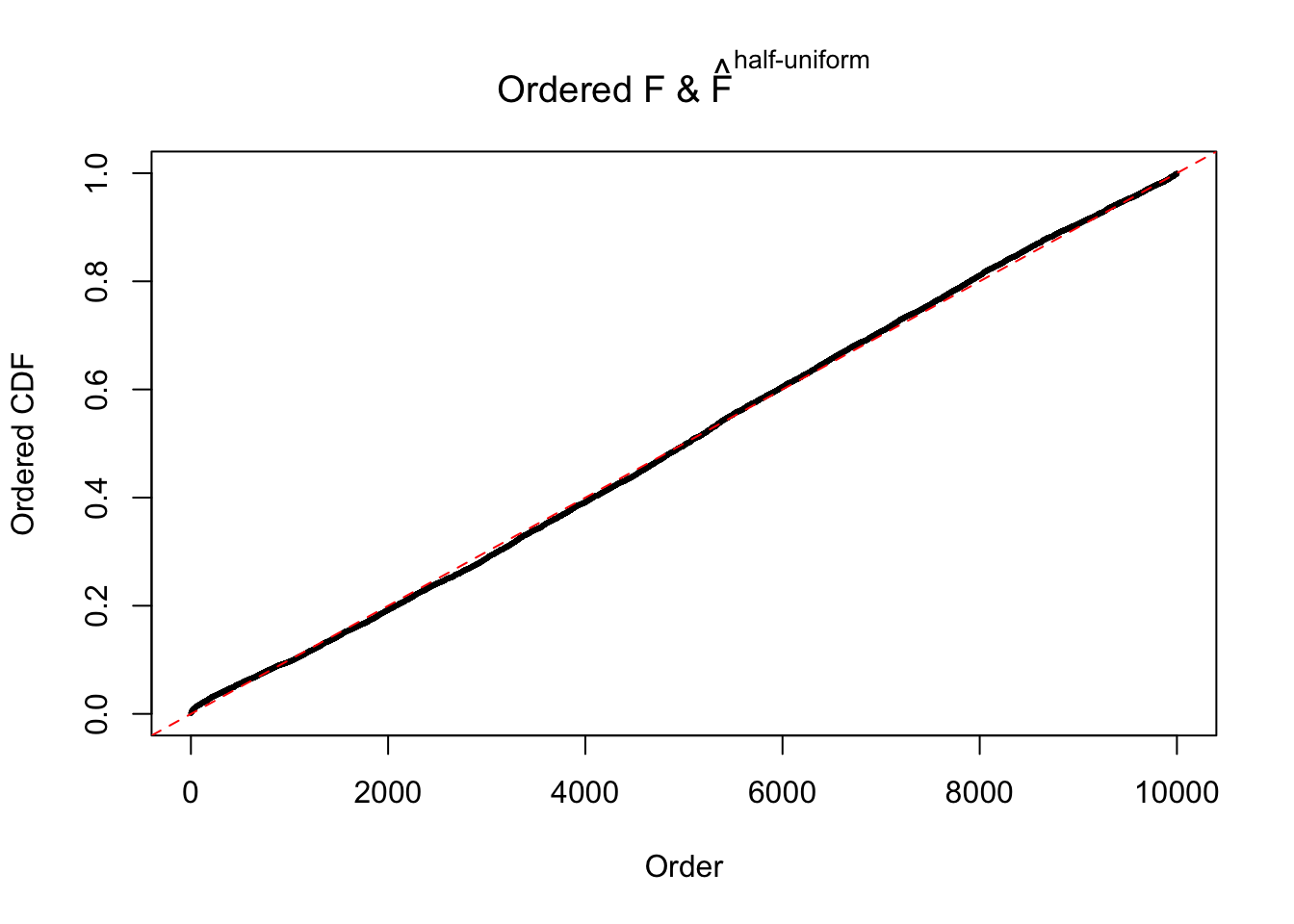
N0. 6 : Data Set 749 ; Number of False Discoveries: 114 ; pihat0 = 0.01482747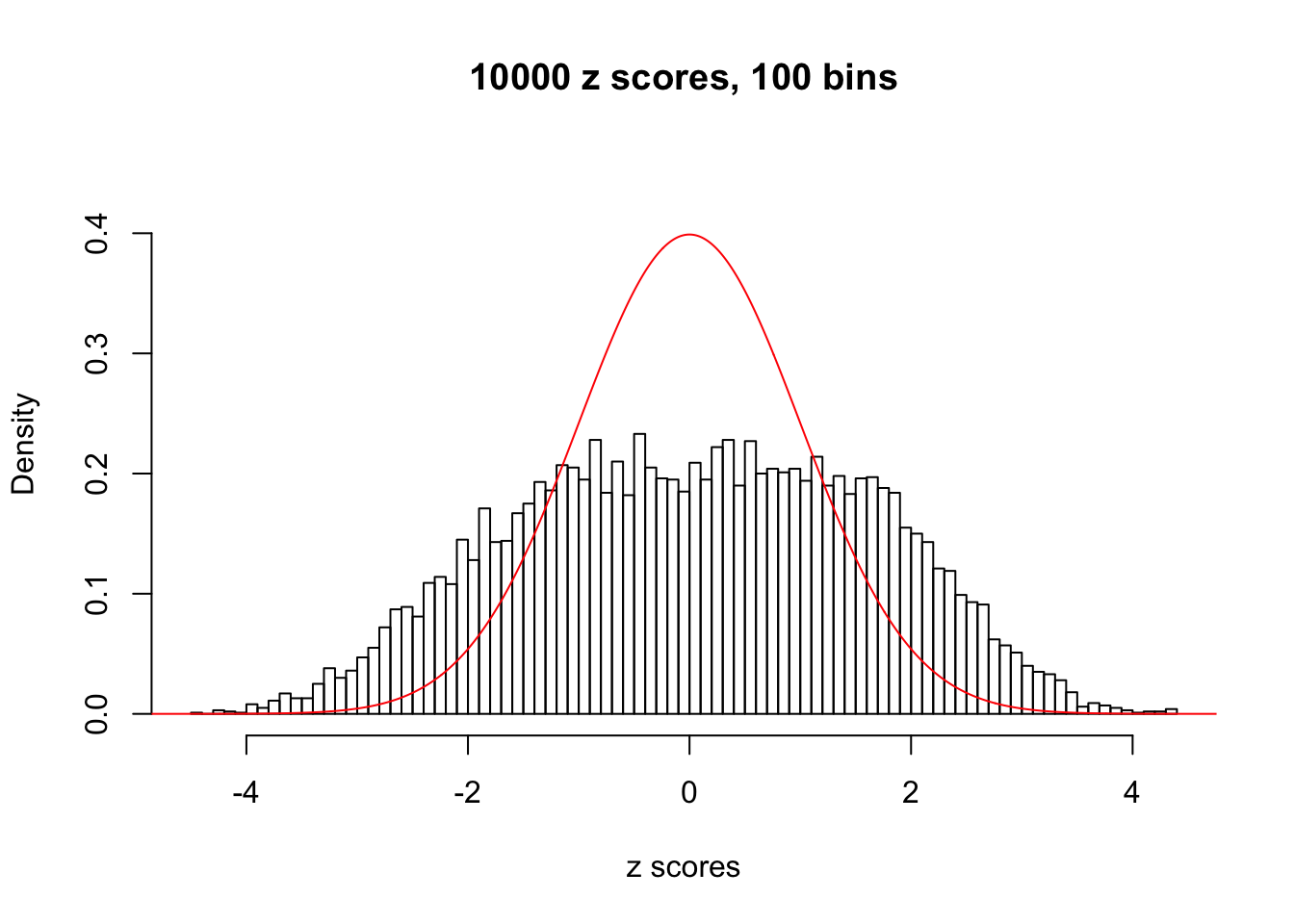
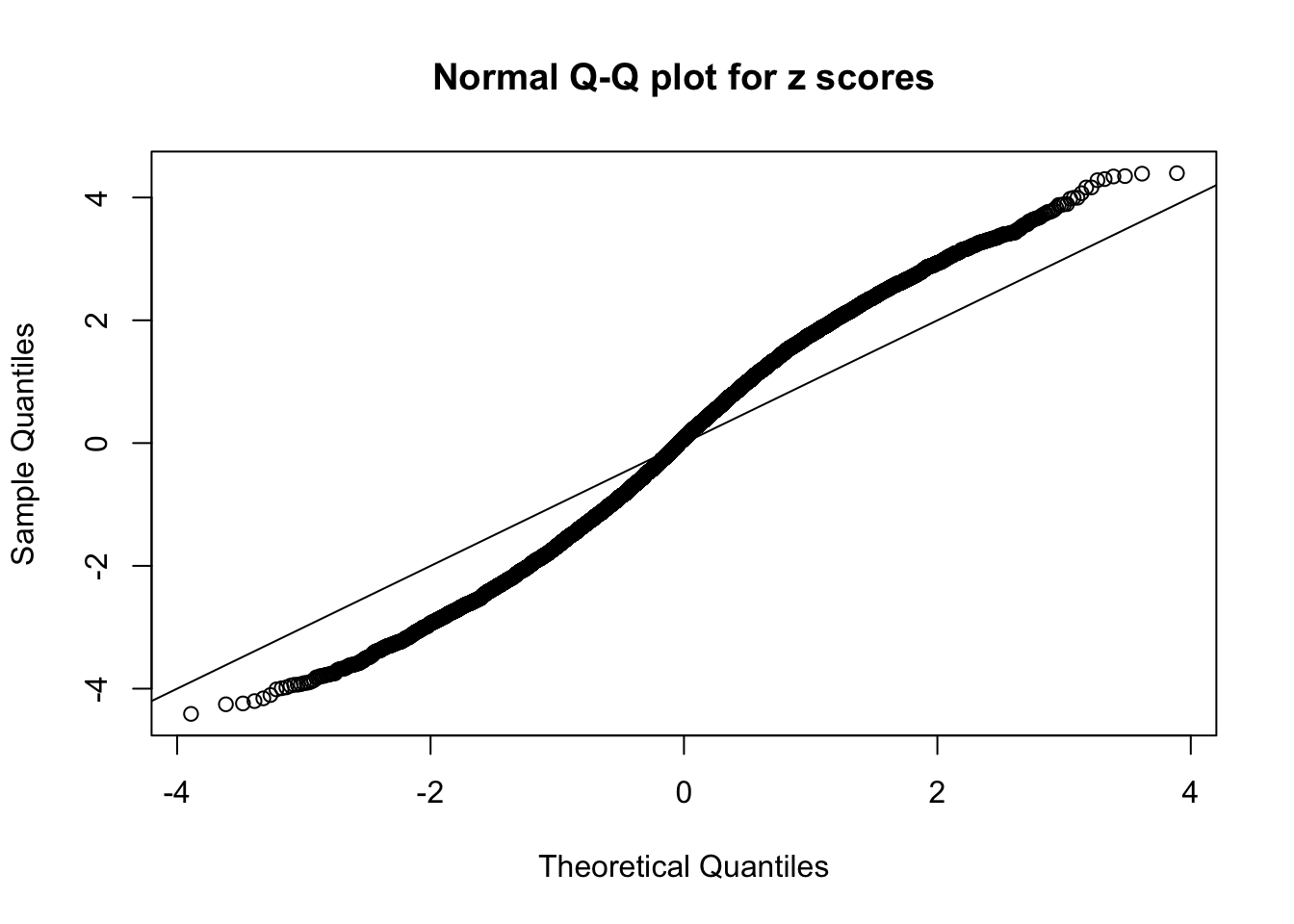
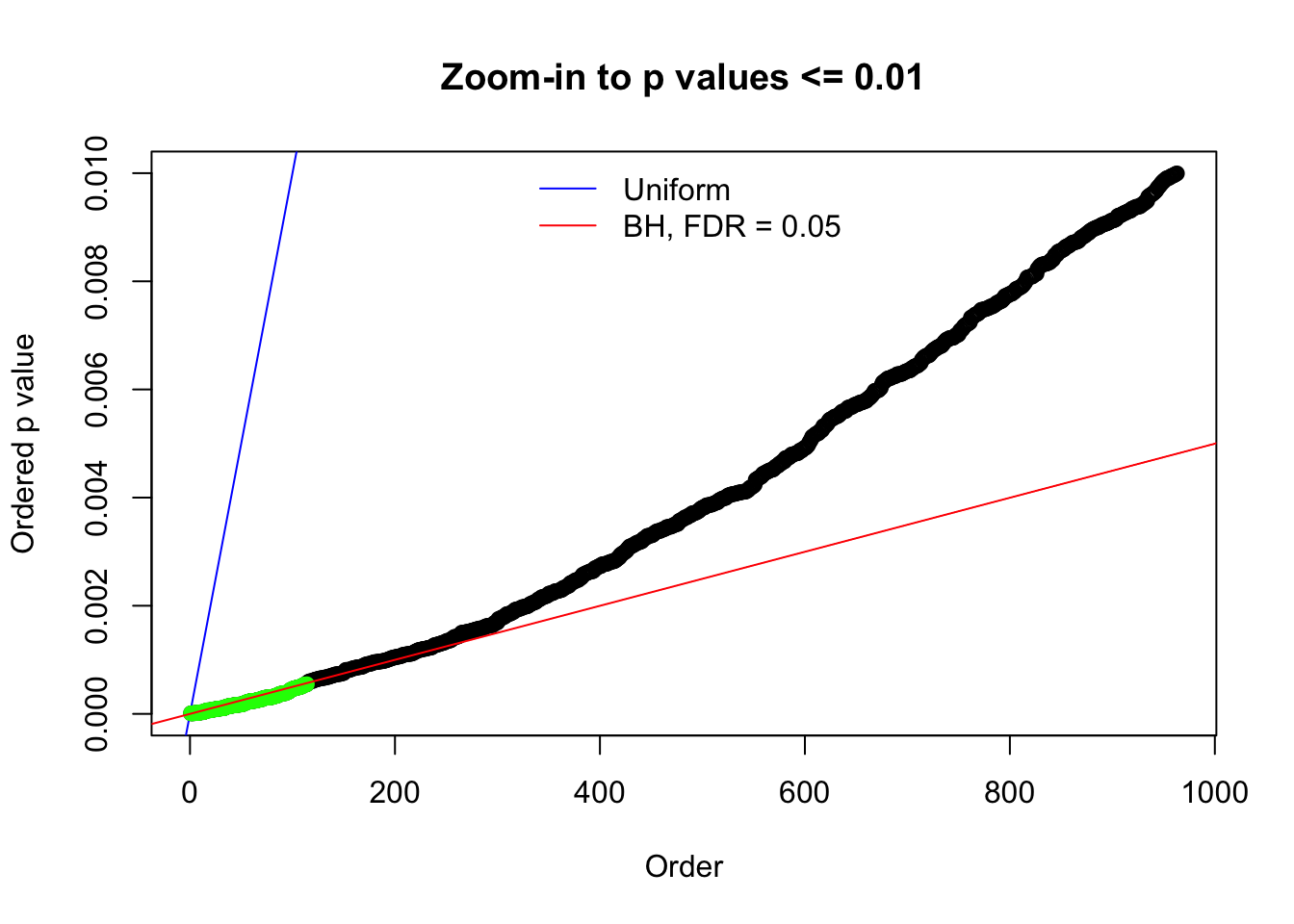
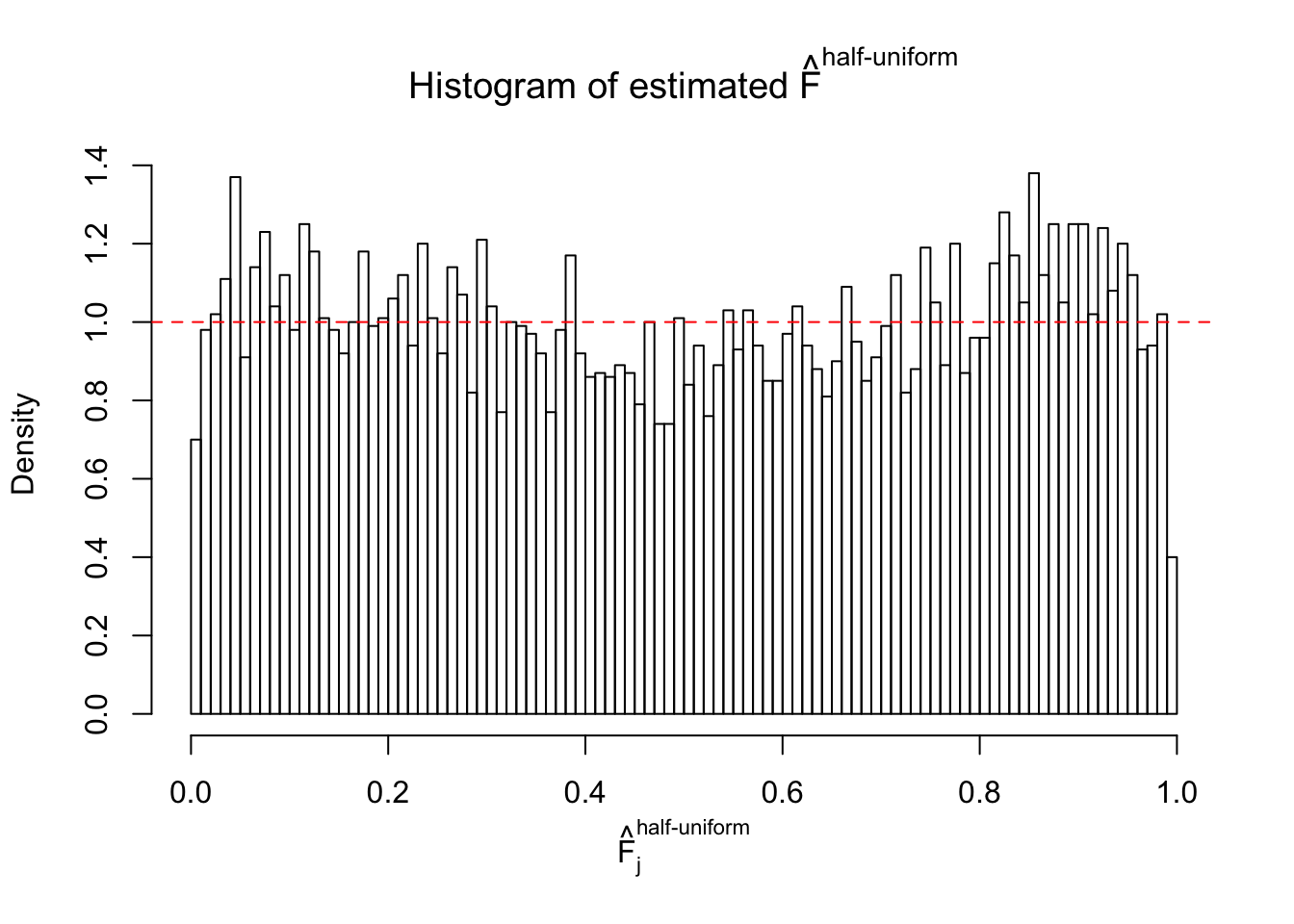
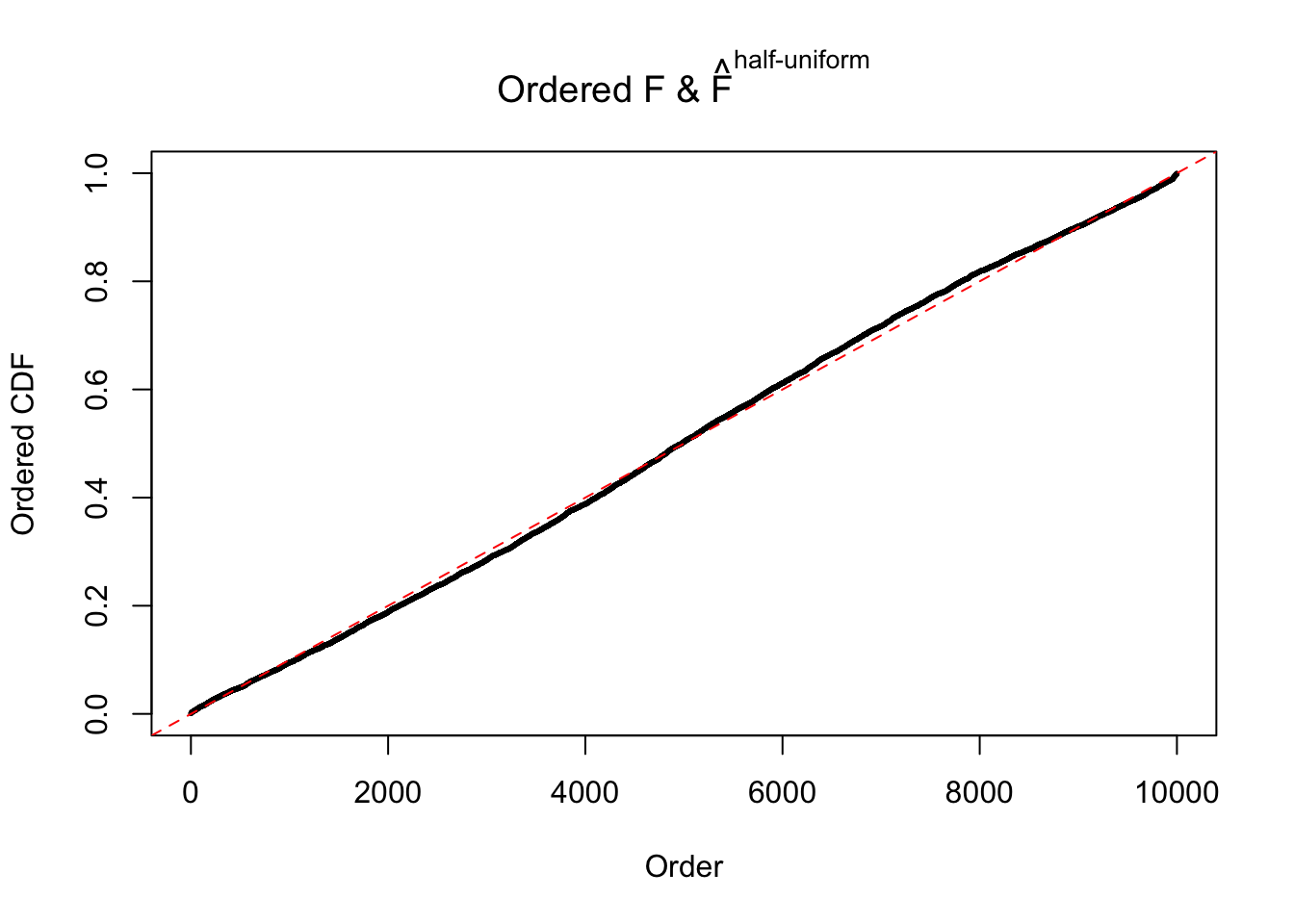
N0. 7 : Data Set 724 ; Number of False Discoveries: 79 ; pihat0 = 0.01451062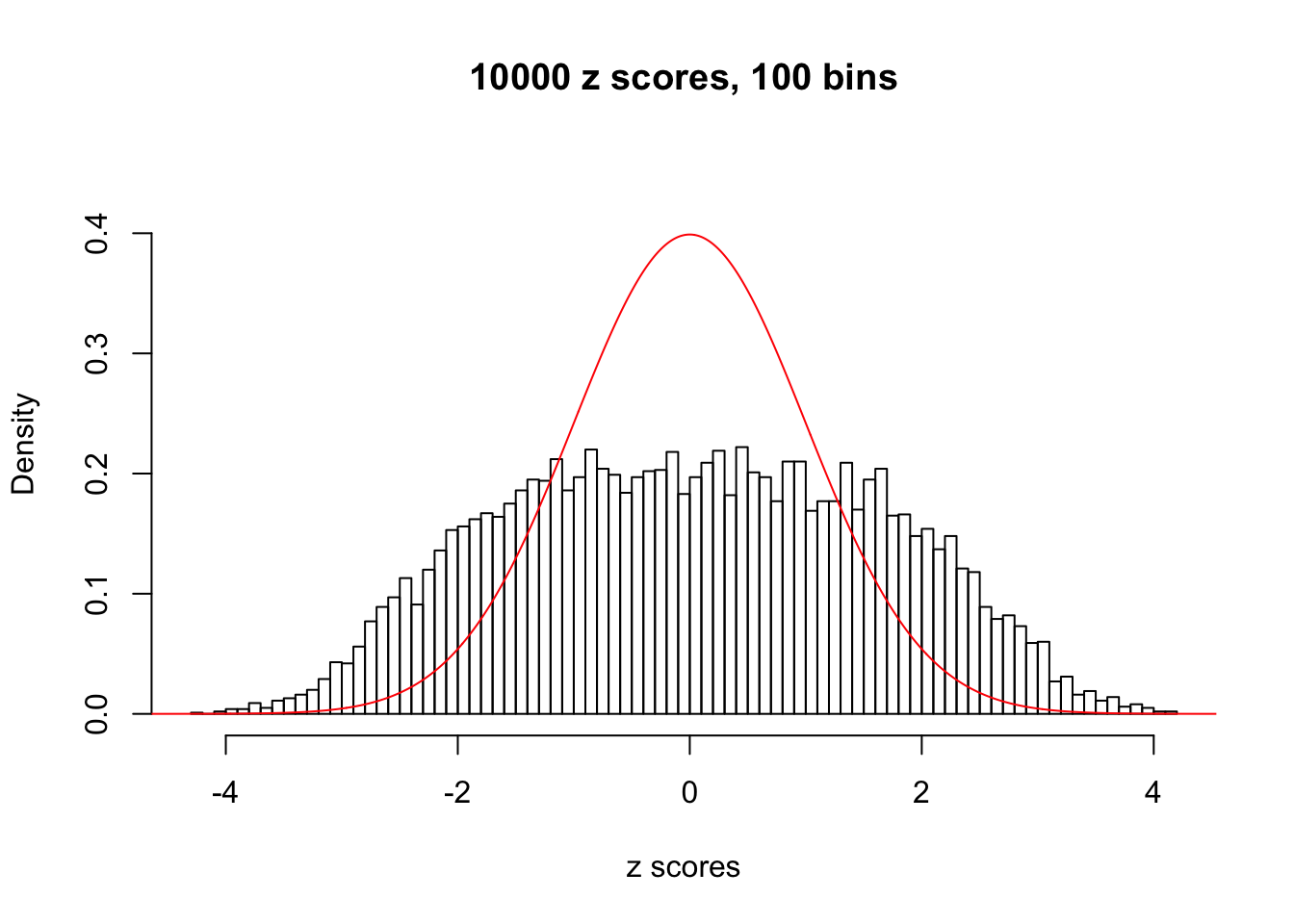
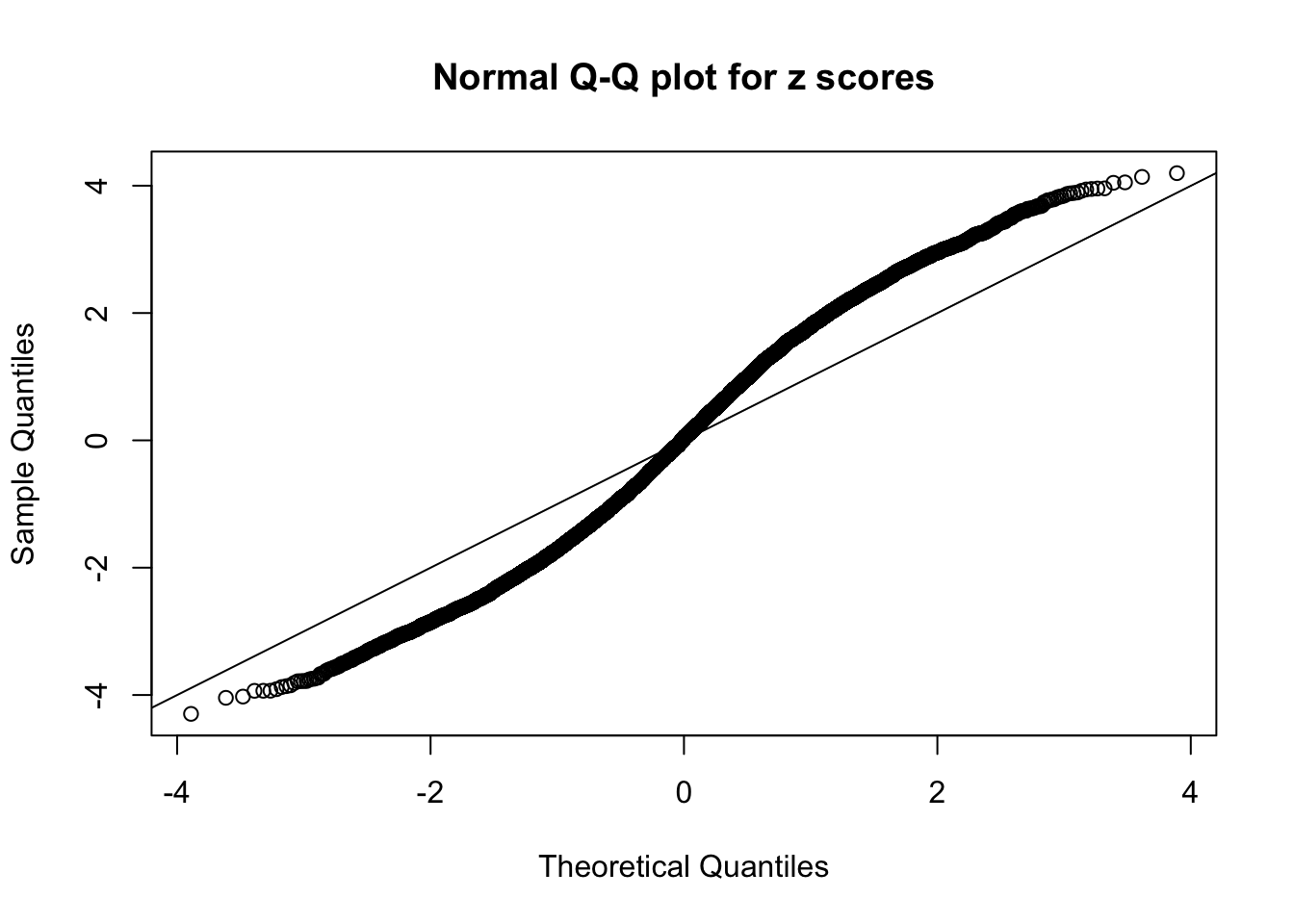
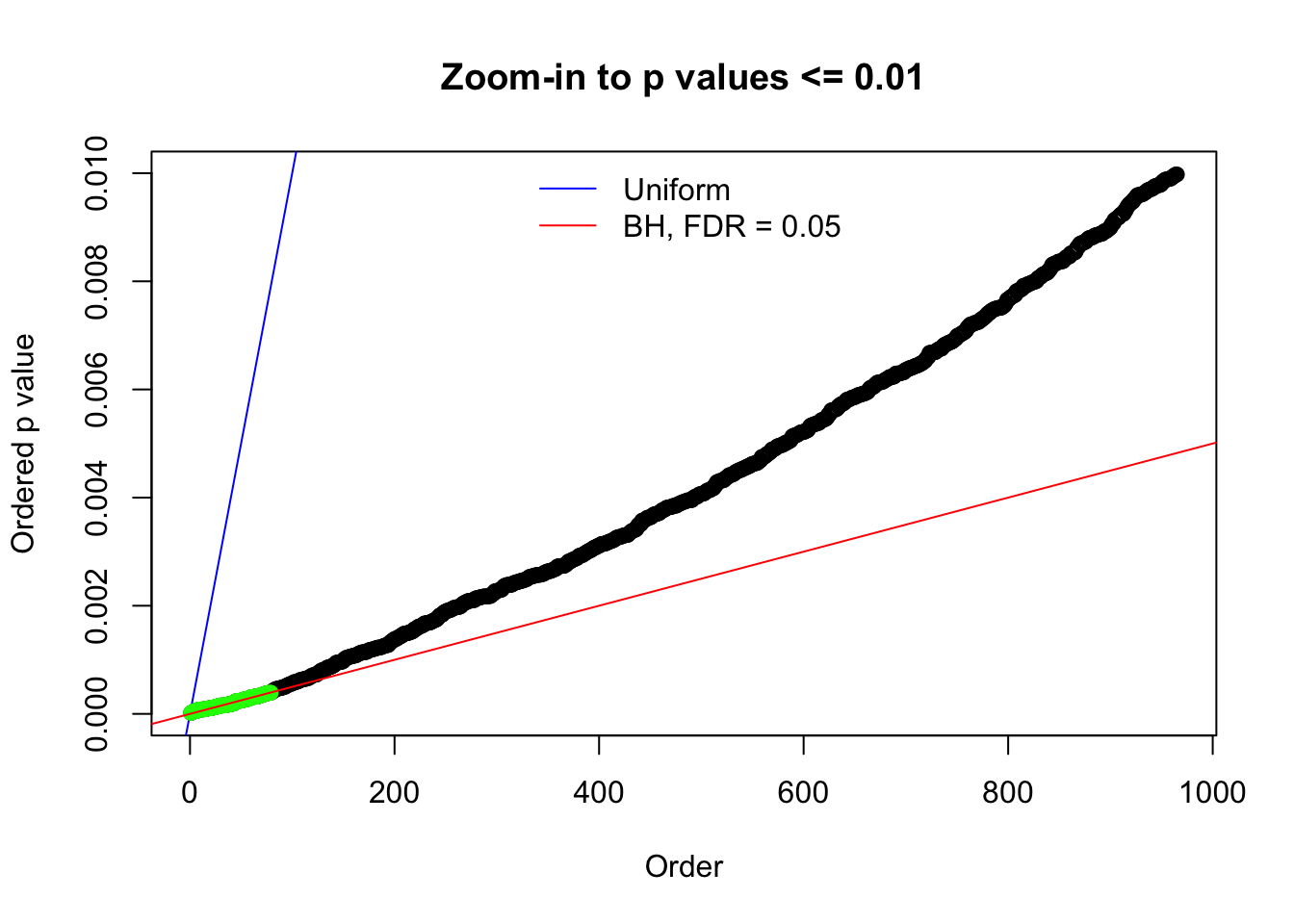
N0. 8 : Data Set 56 ; Number of False Discoveries: 35 ; pihat0 = 0.03811803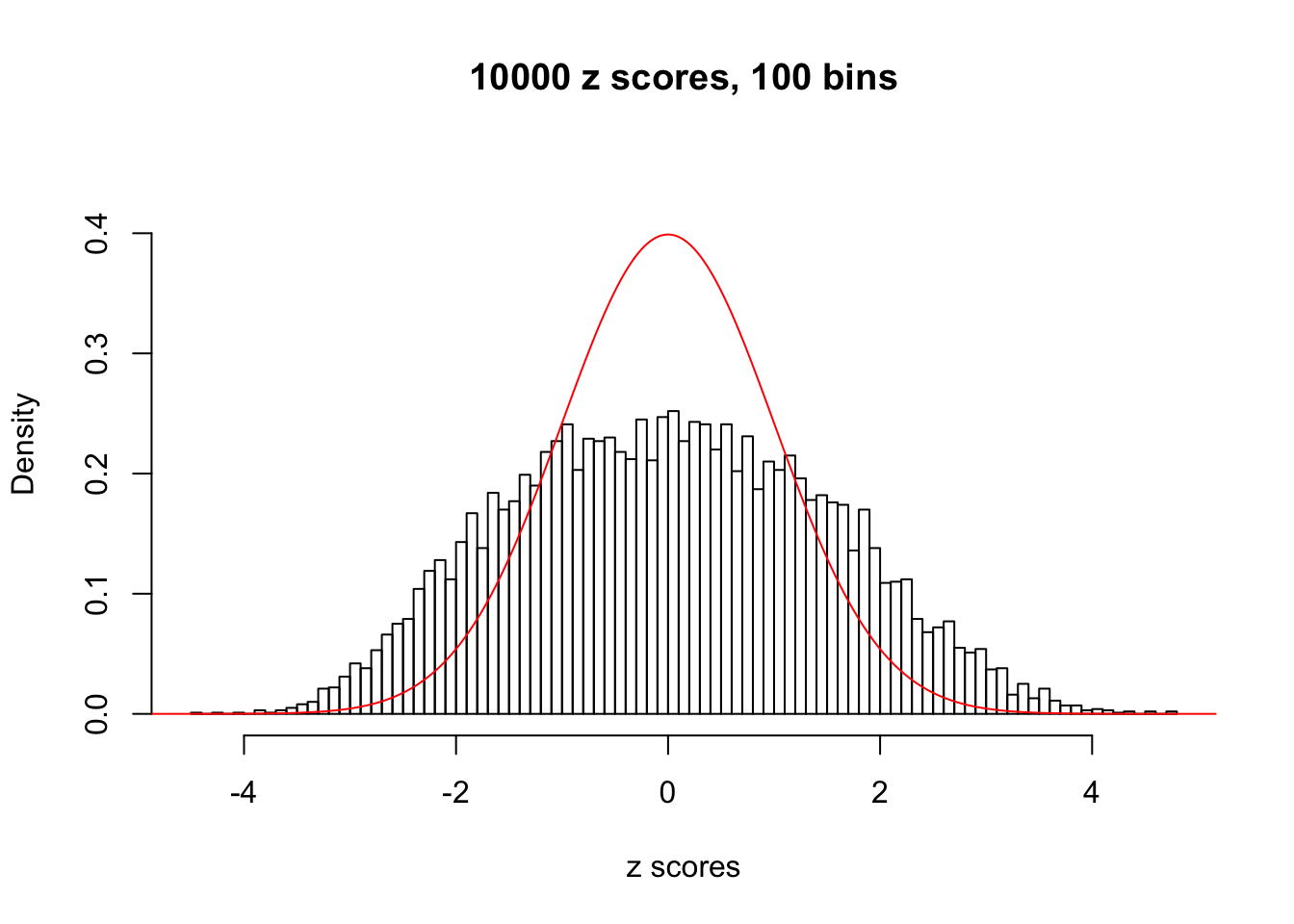
N0. 9 : Data Set 840 ; Number of False Discoveries: 28 ; pihat0 = 0.01433503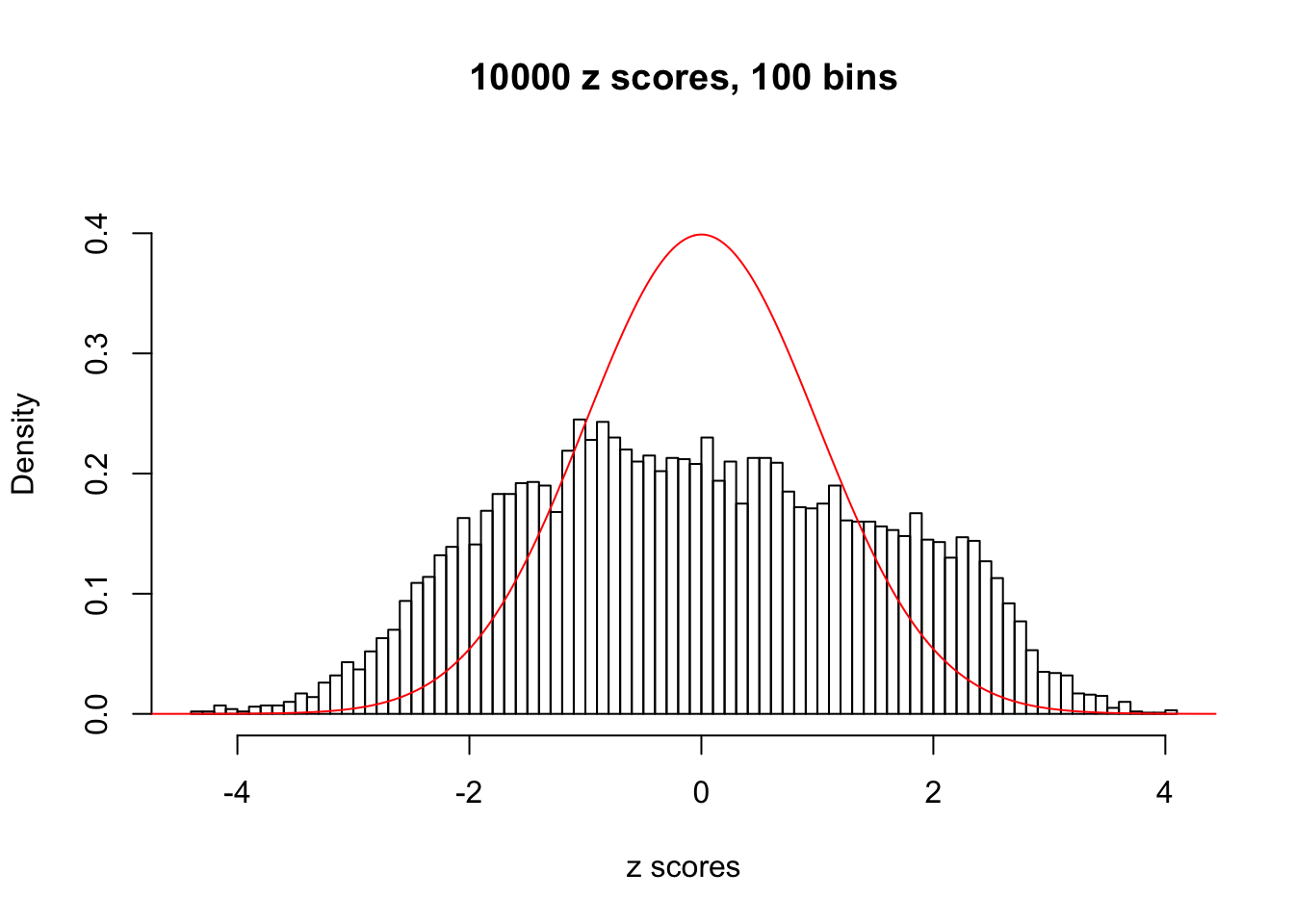
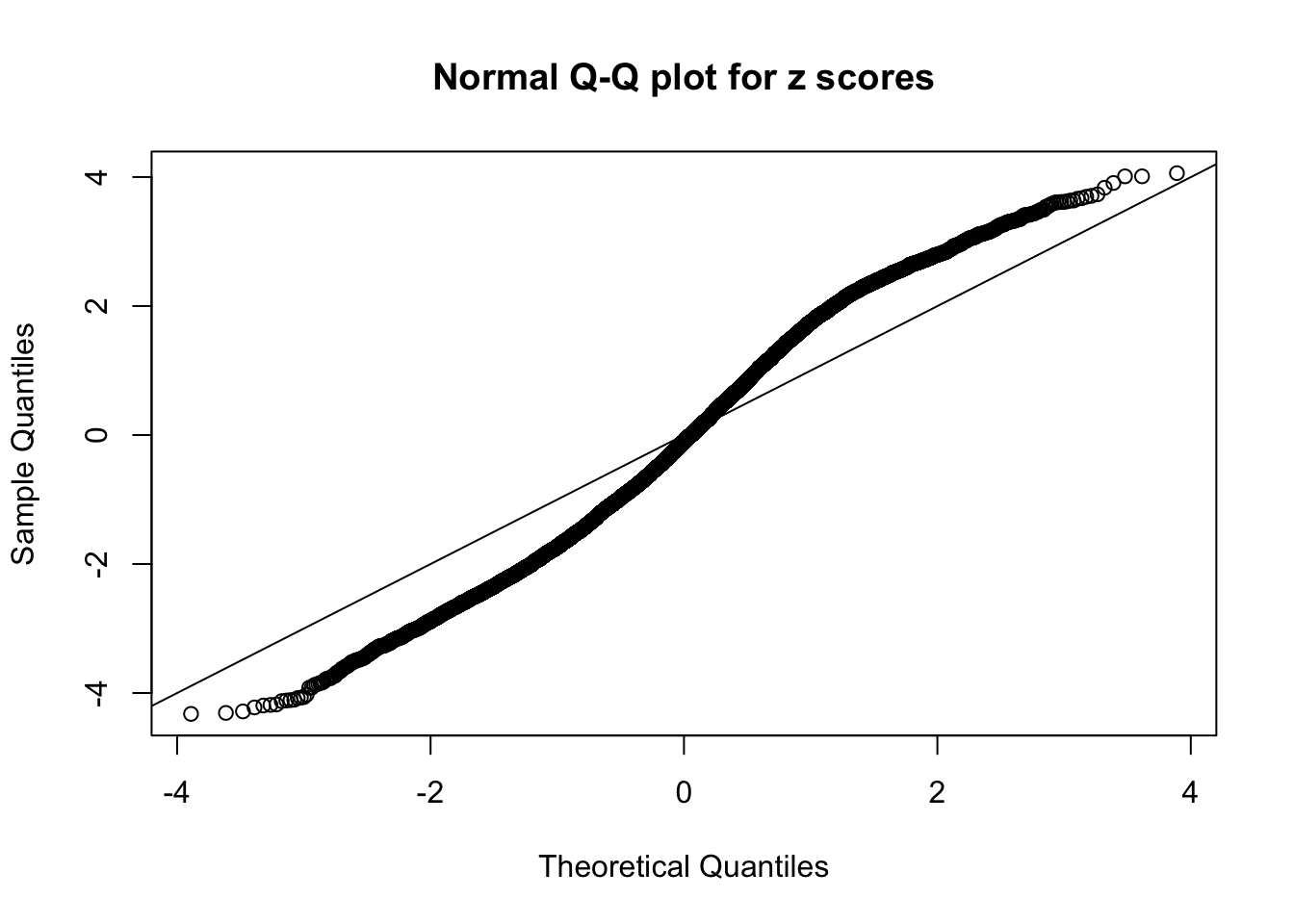
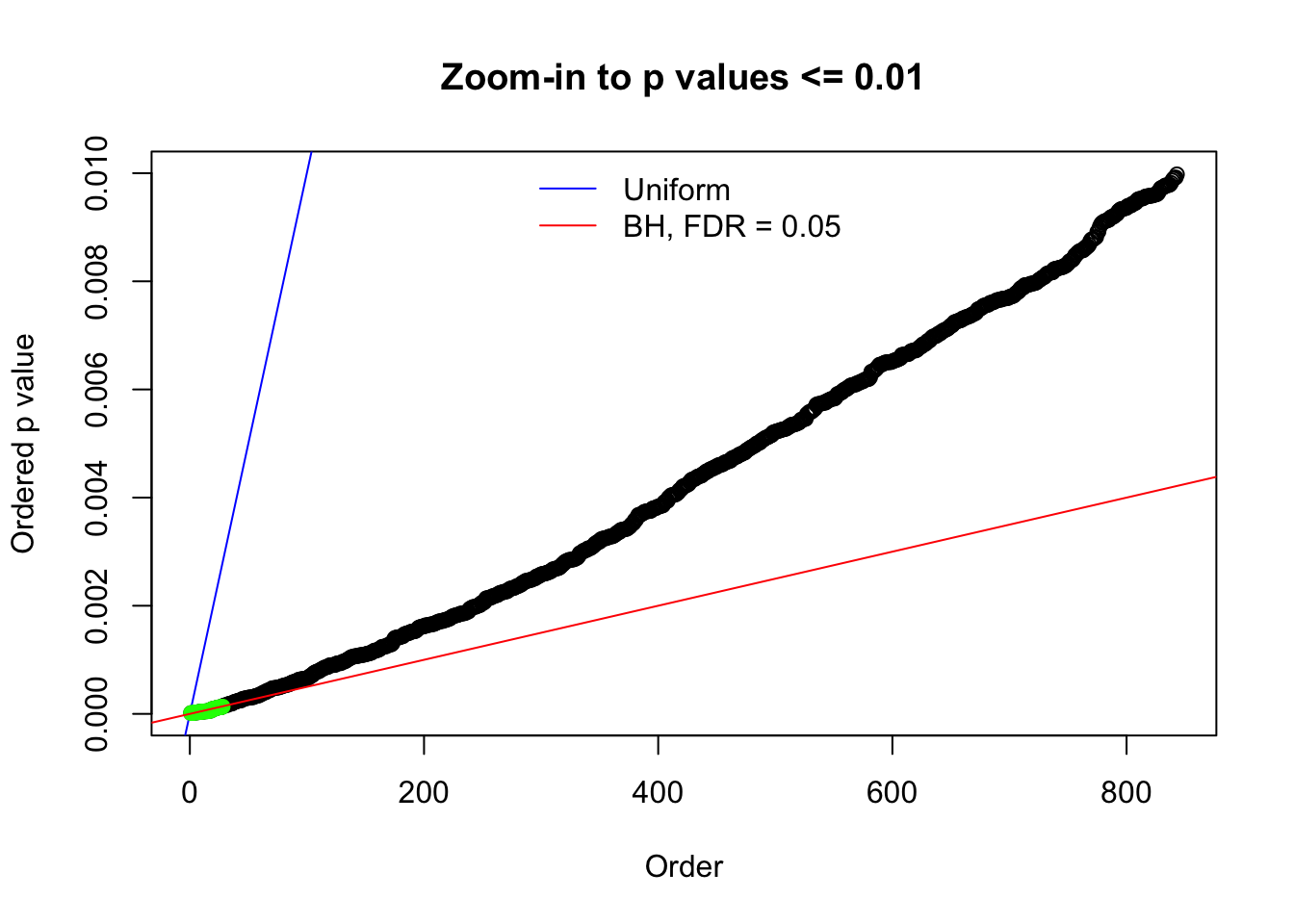
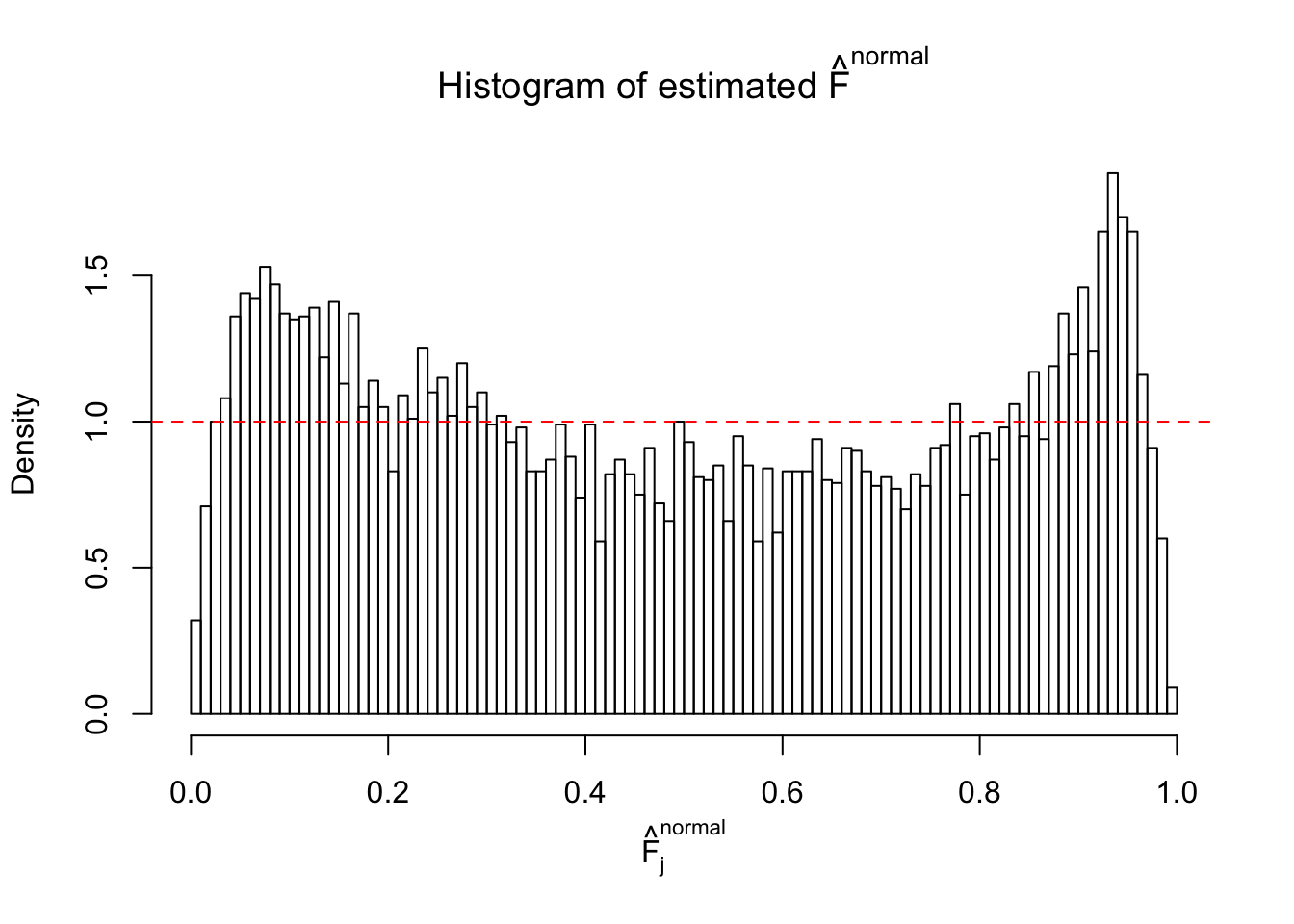
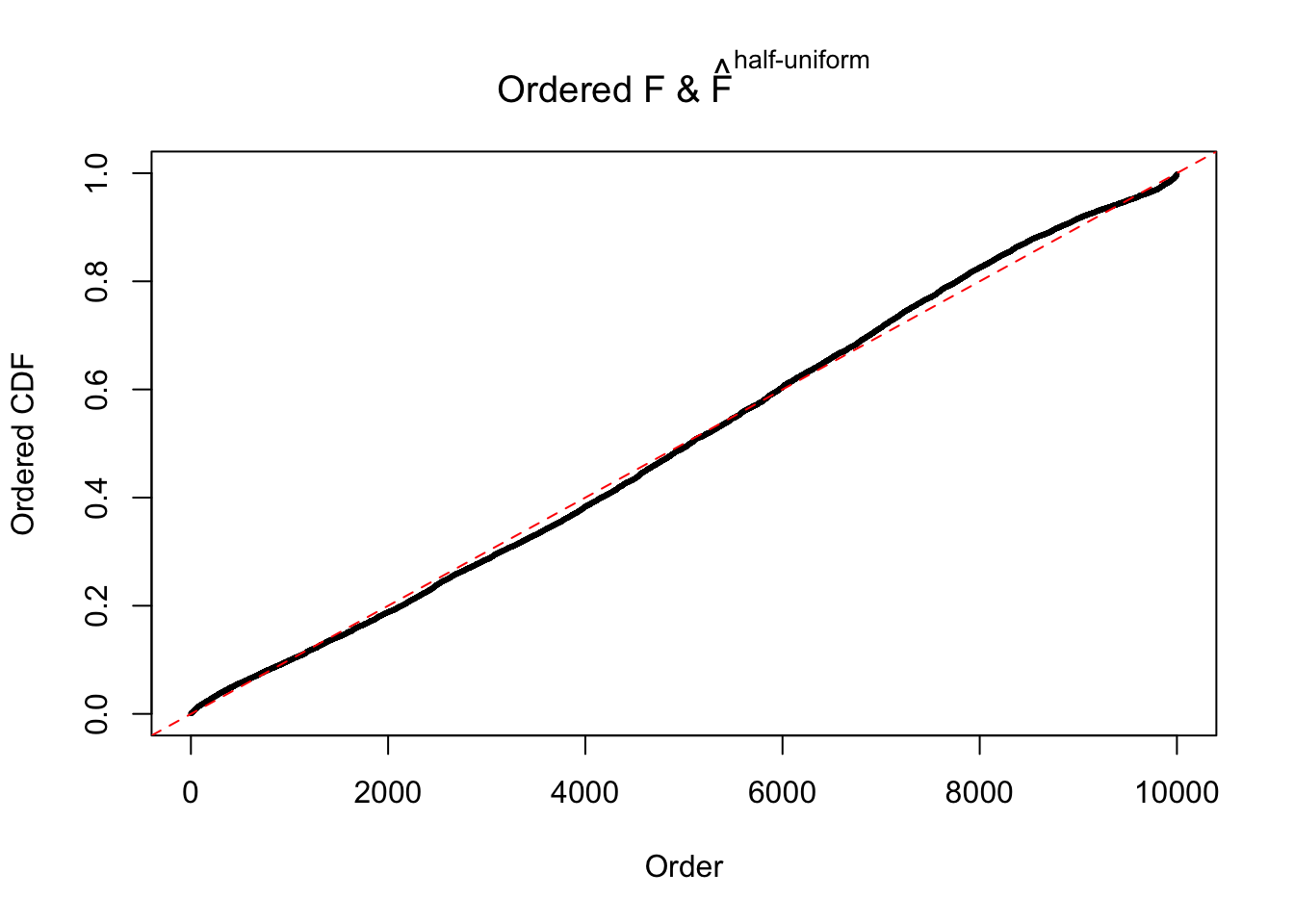
N0. 10 : Data Set 858 ; Number of False Discoveries: 16 ; pihat0 = 0.01340537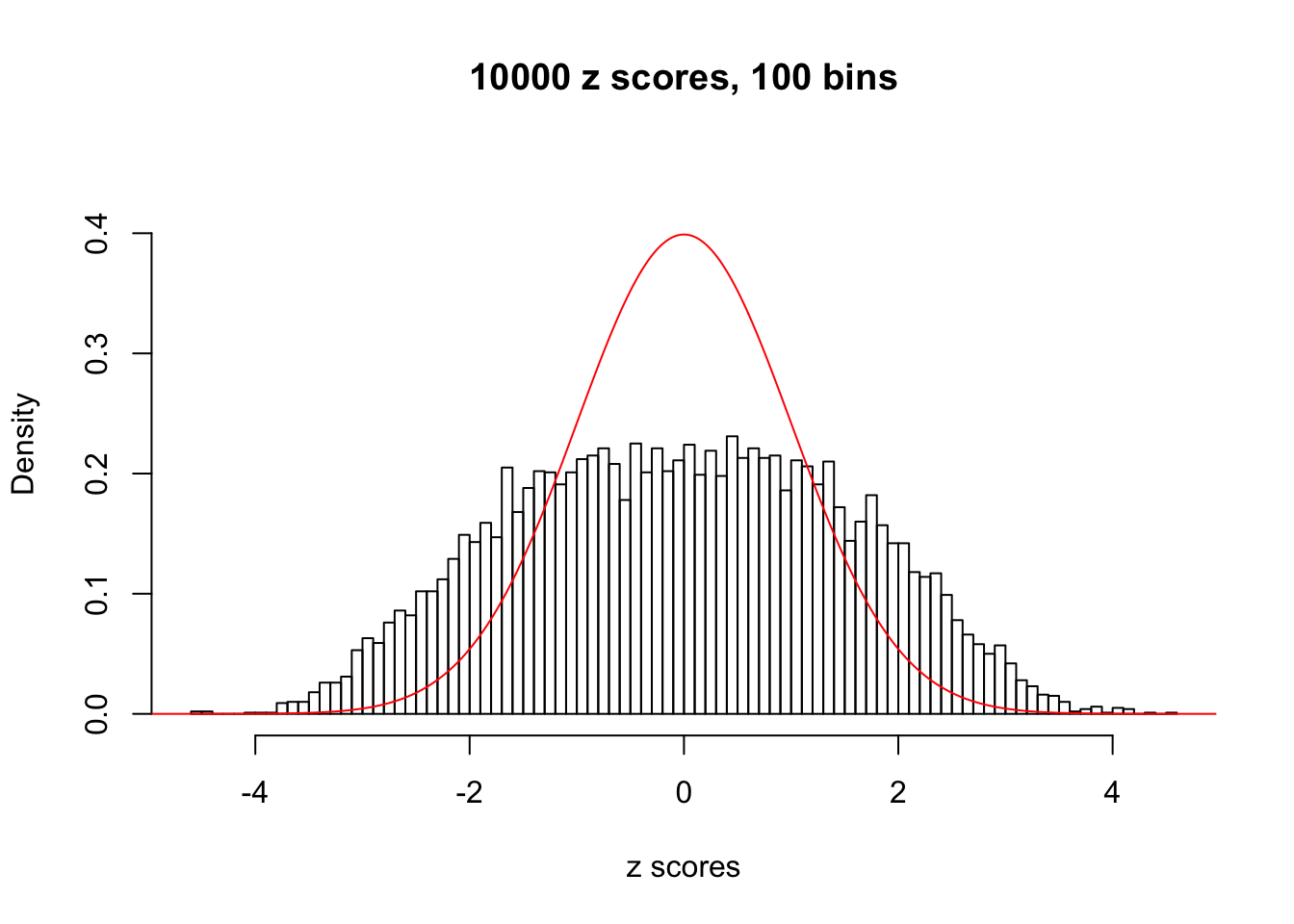
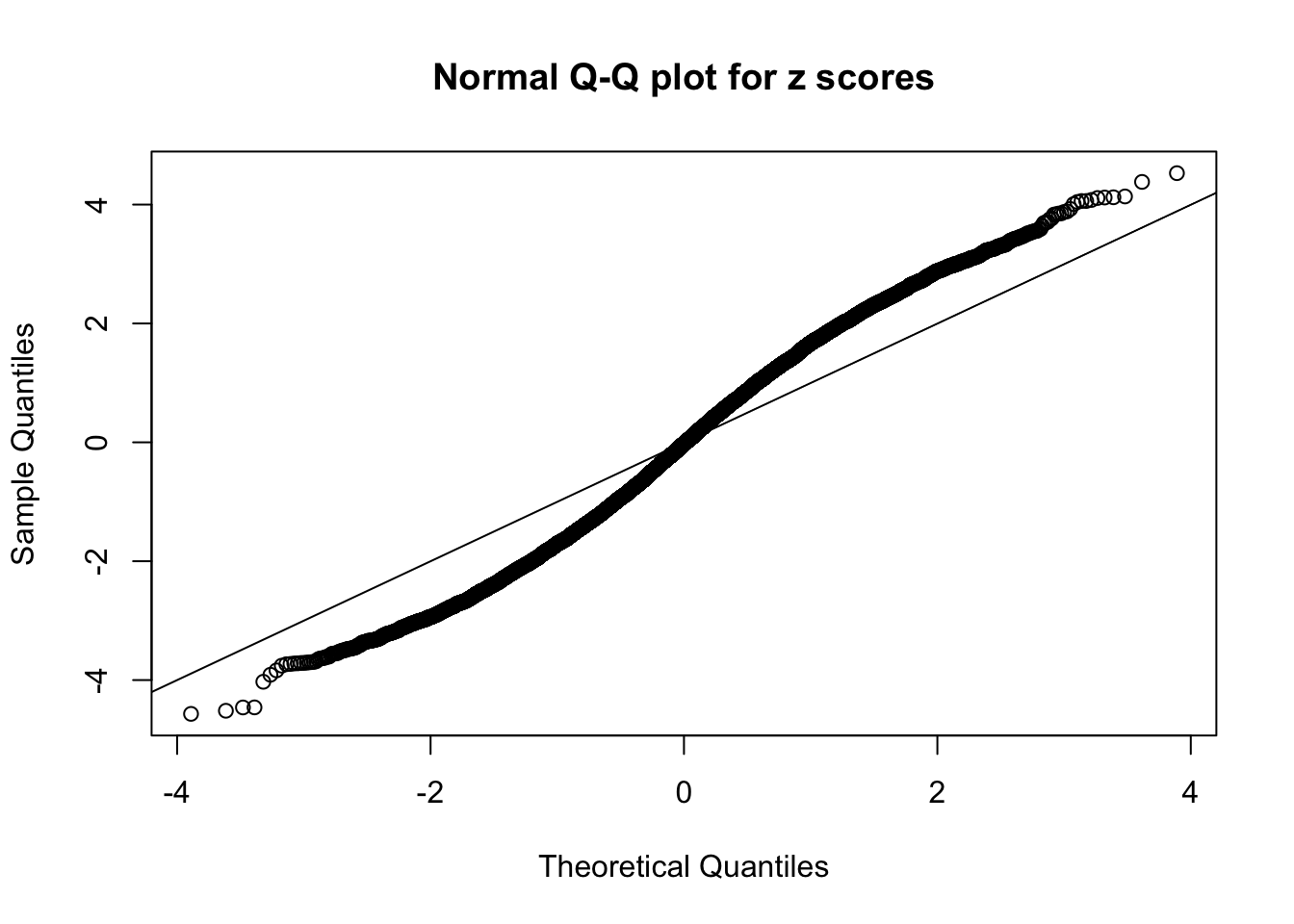
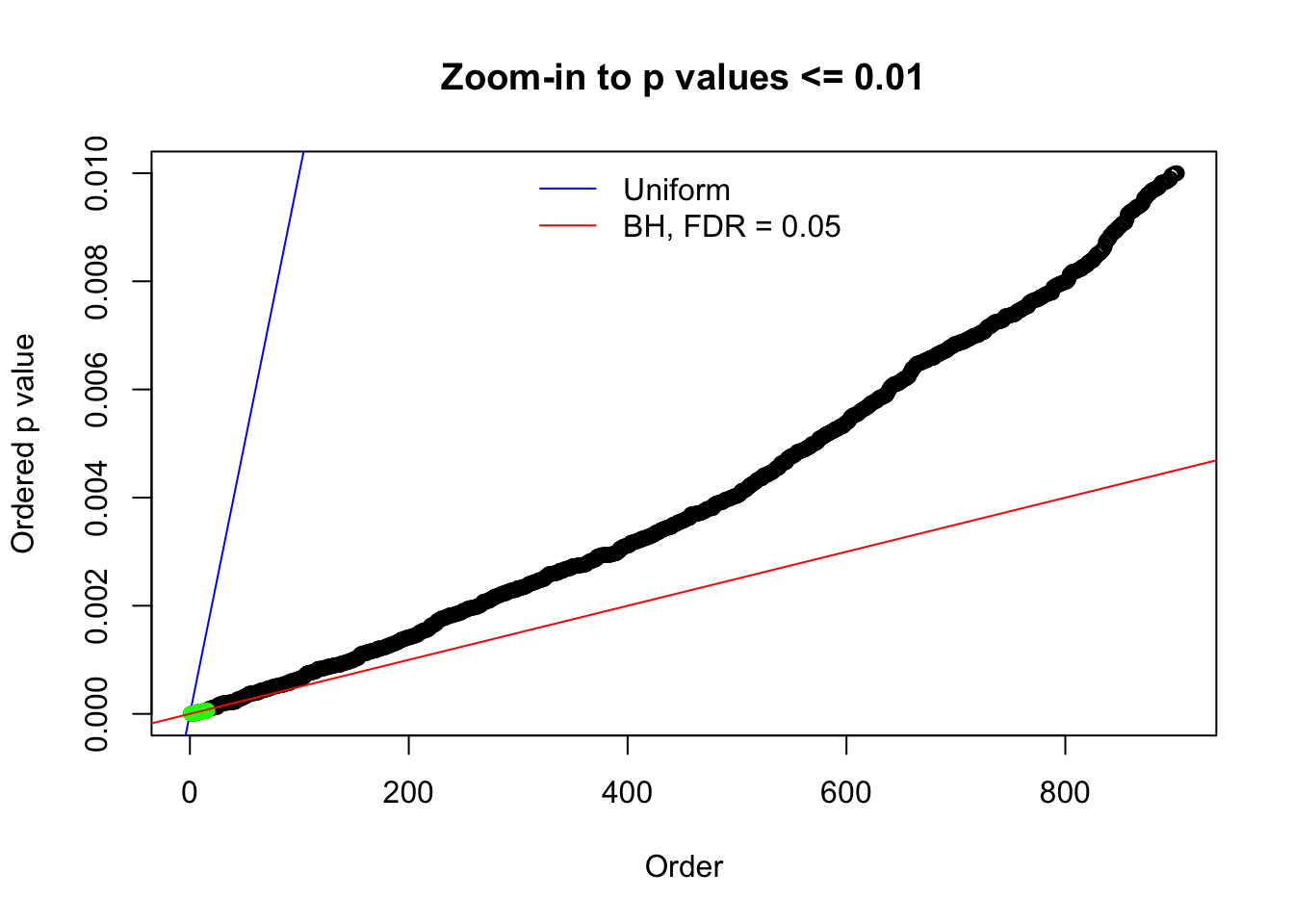
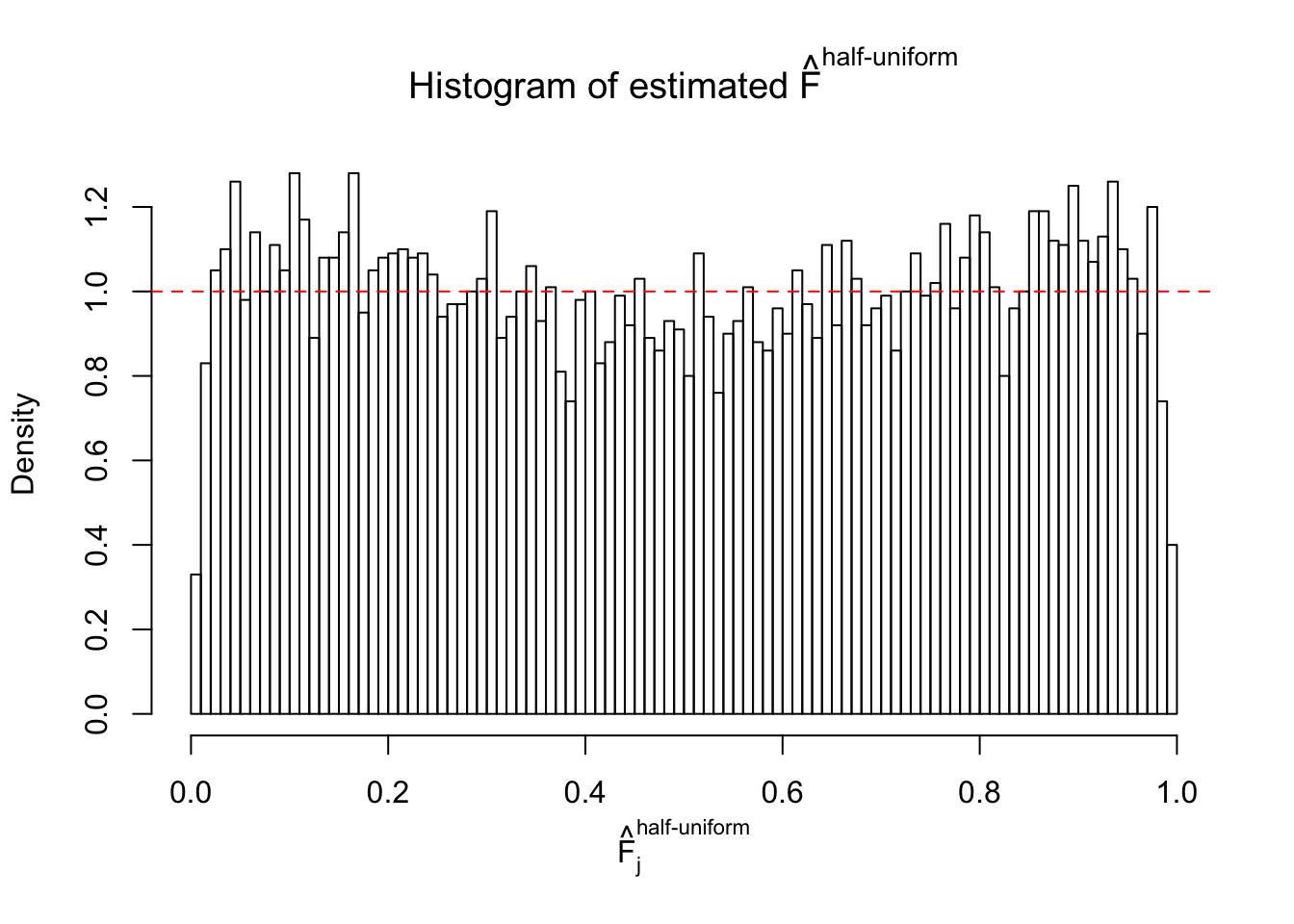
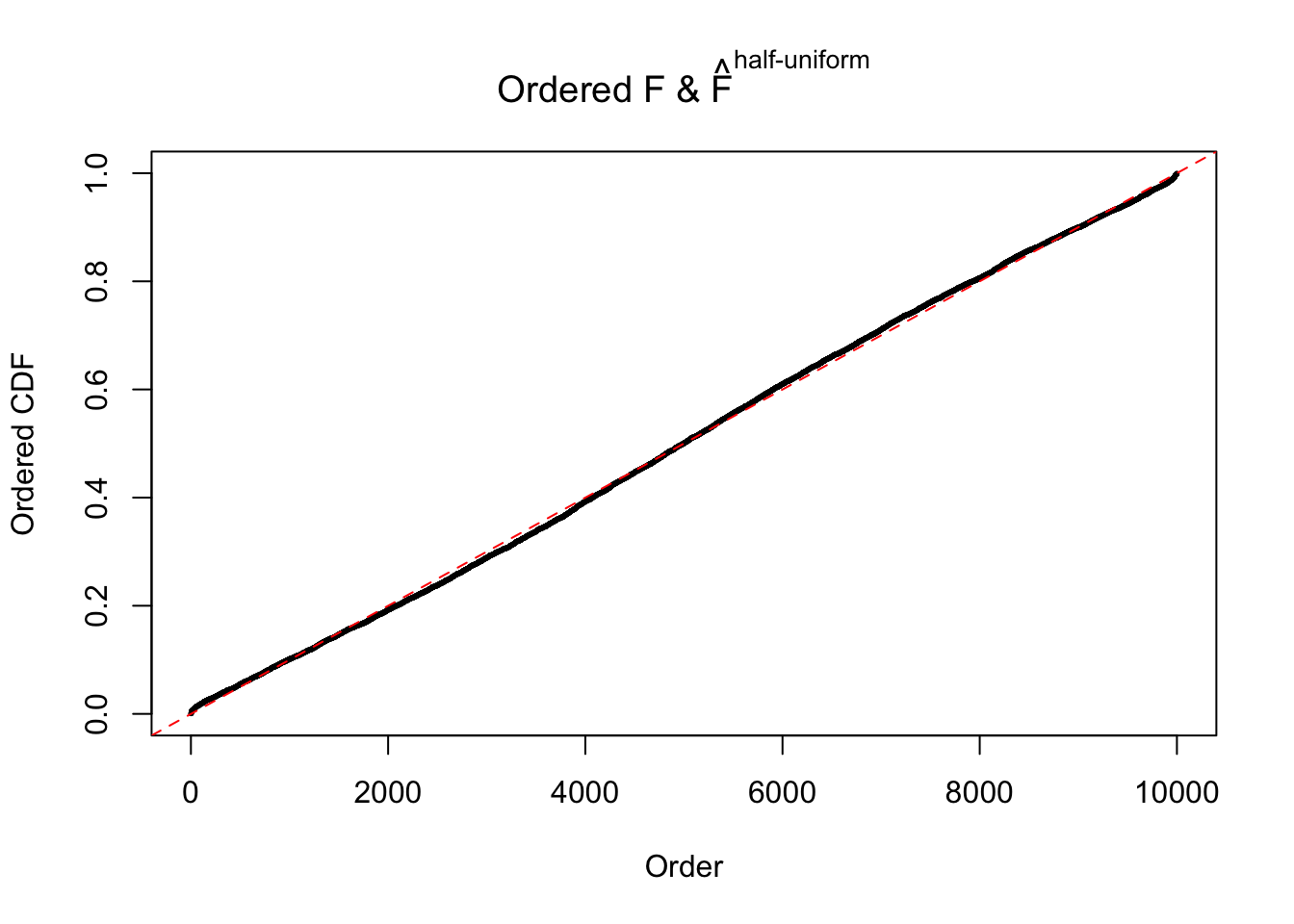
N0. 11 : Data Set 771 ; Number of False Discoveries: 12 ; pihat0 = 0.04069309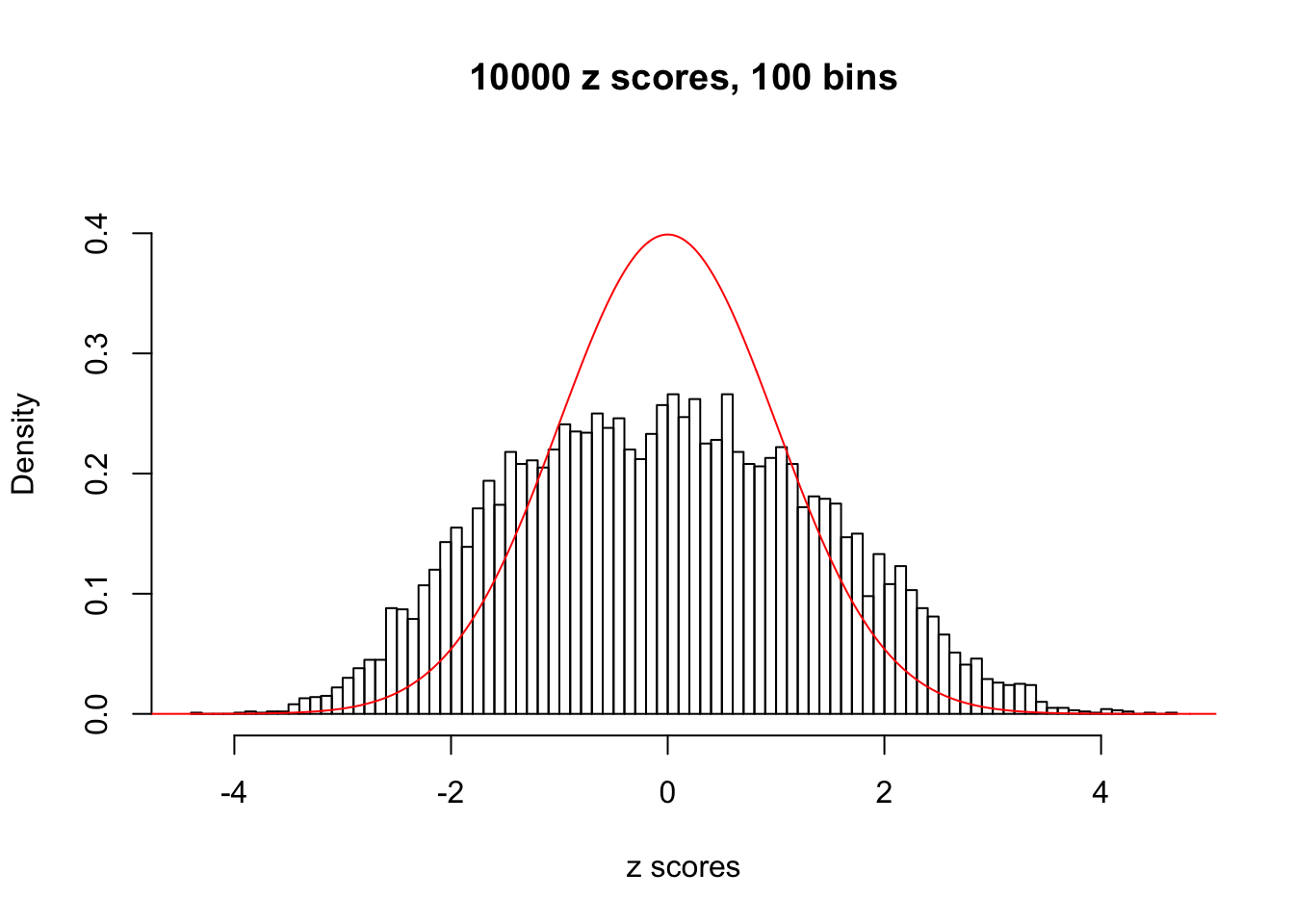
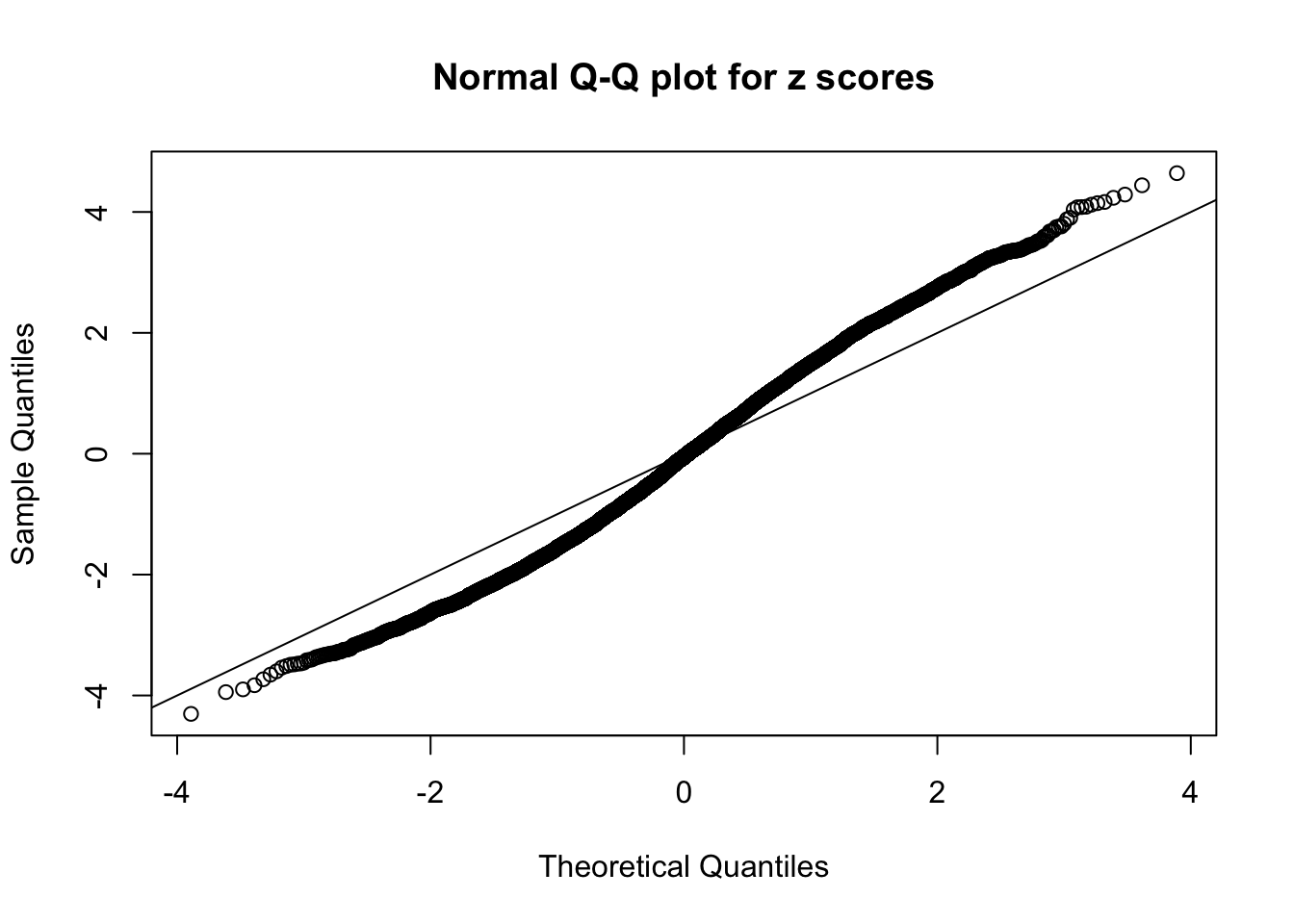
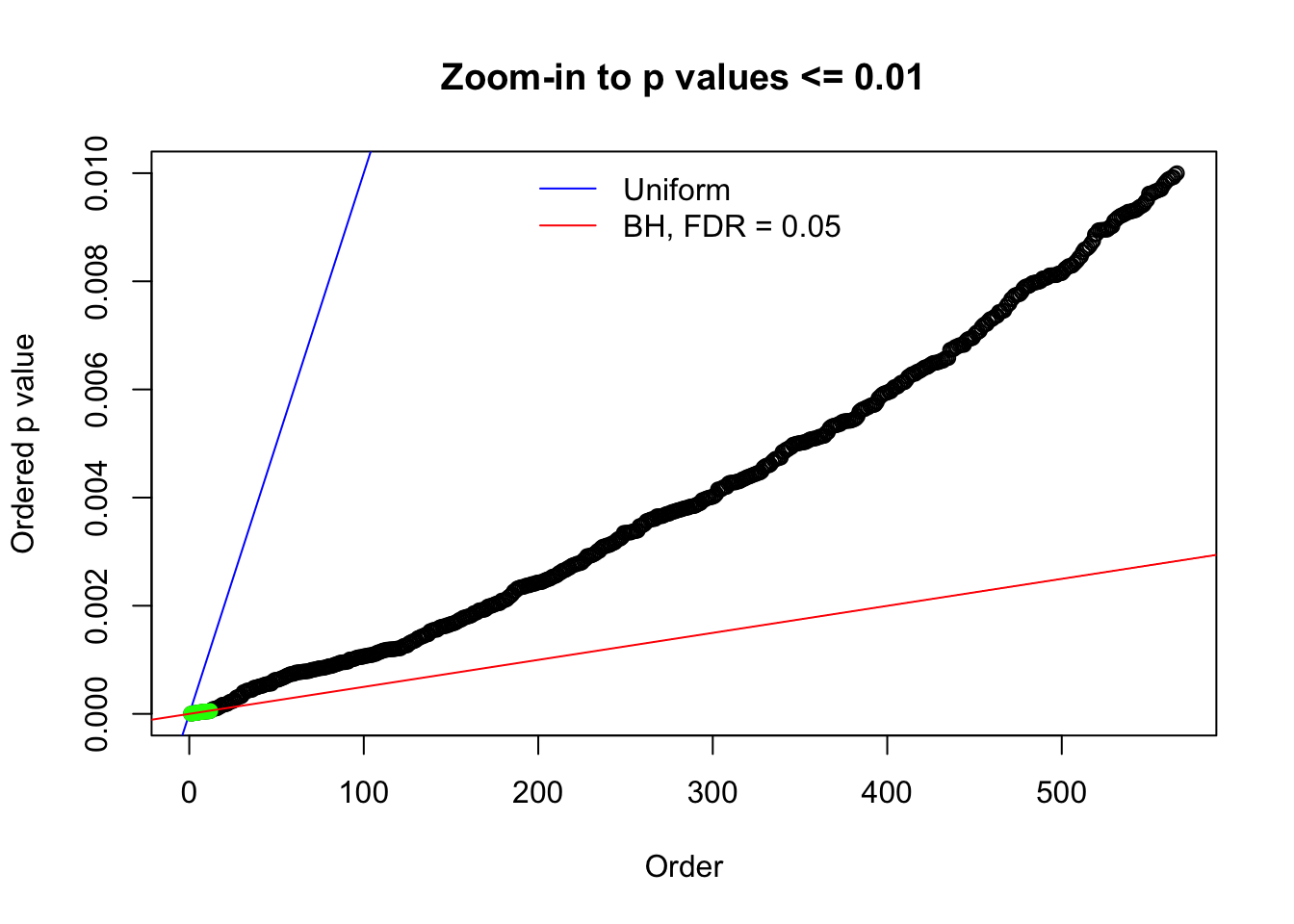
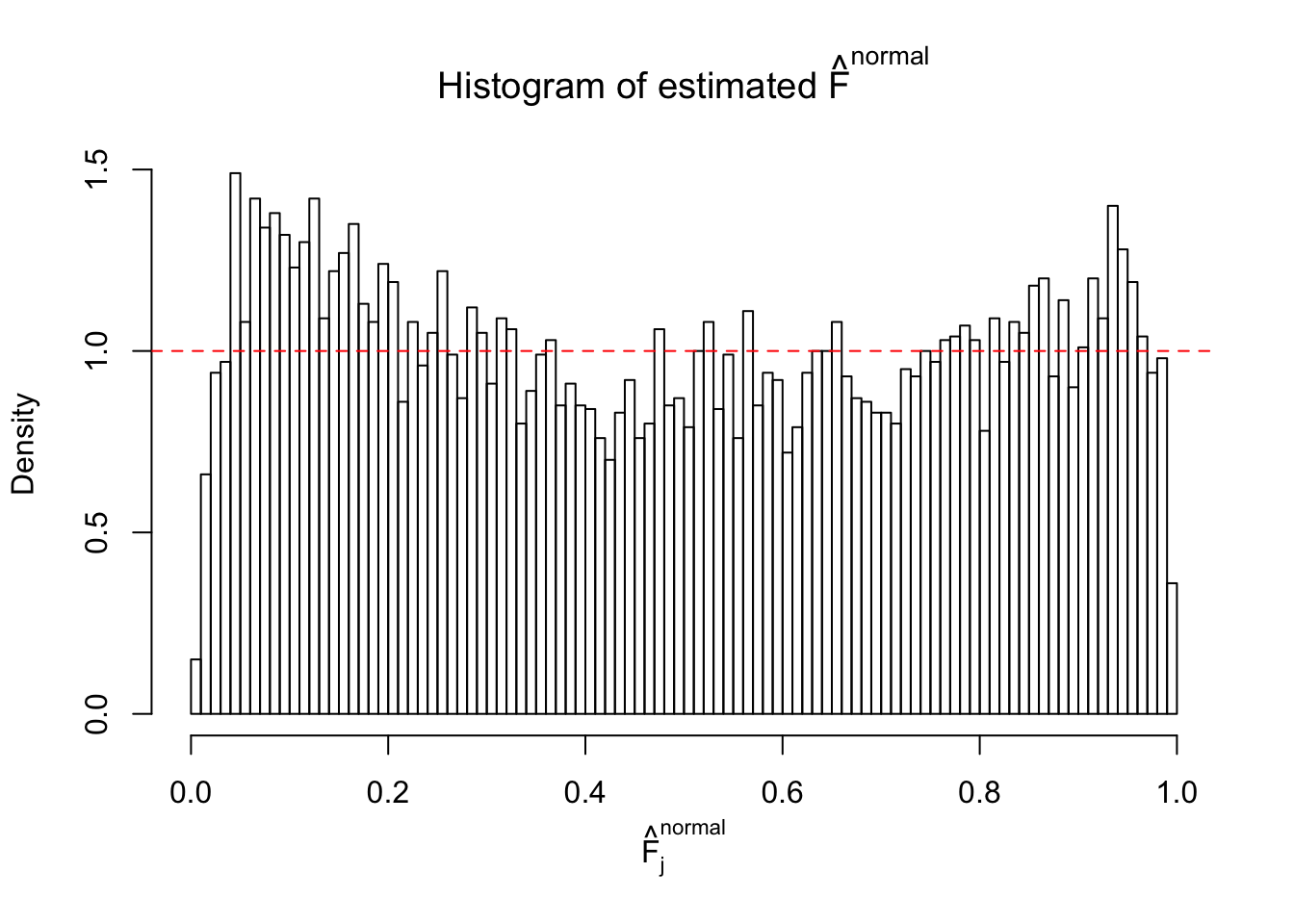
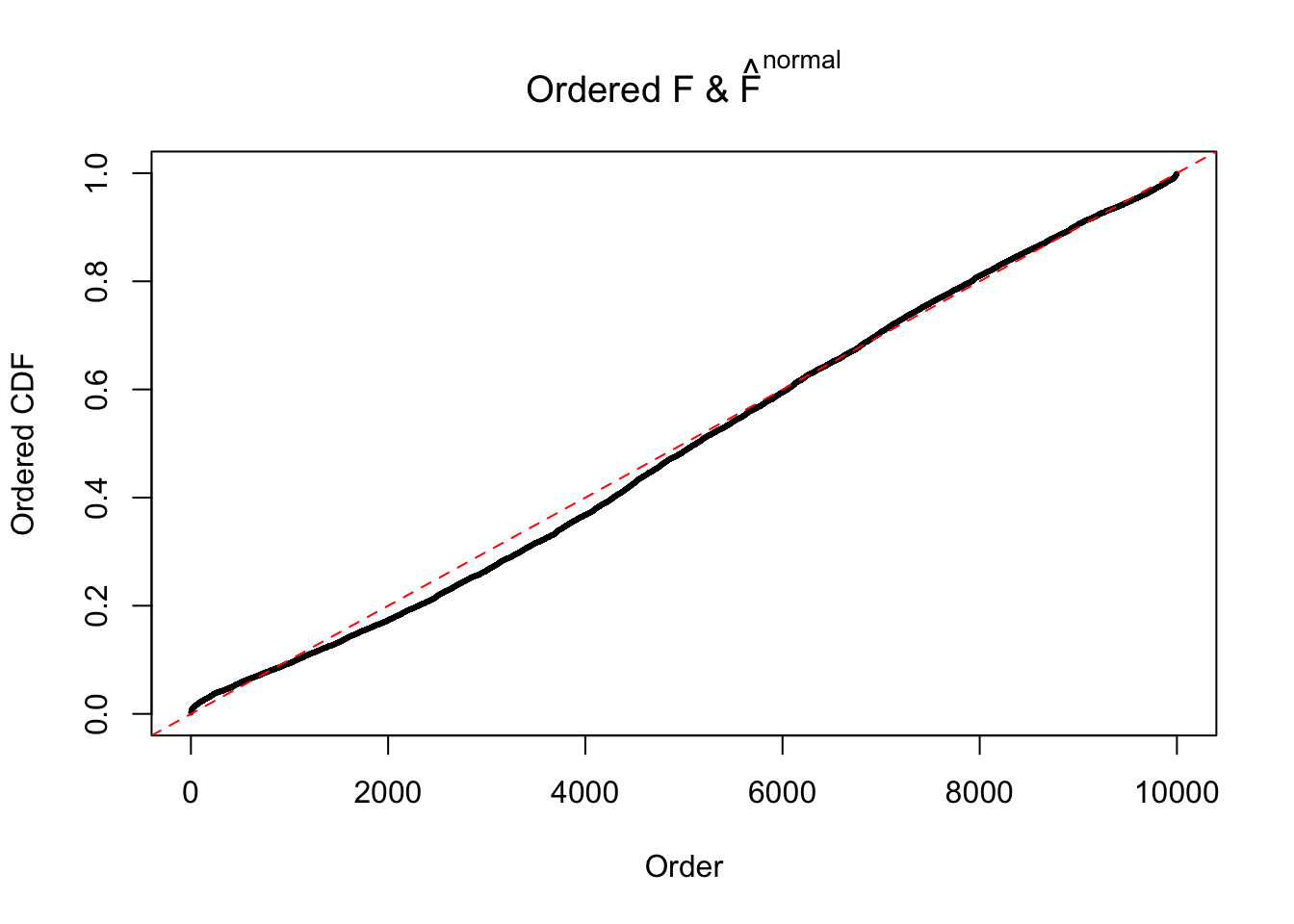
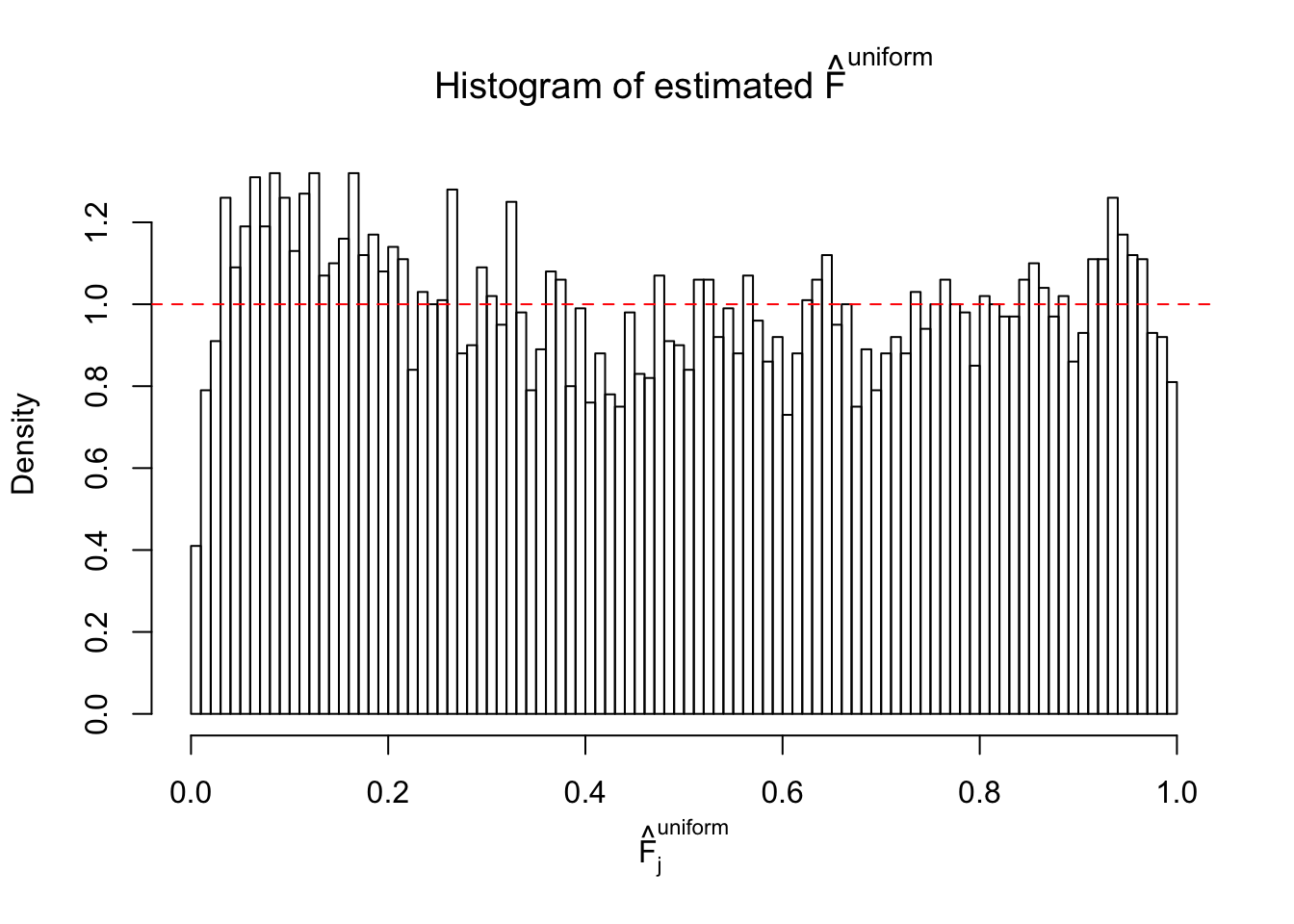
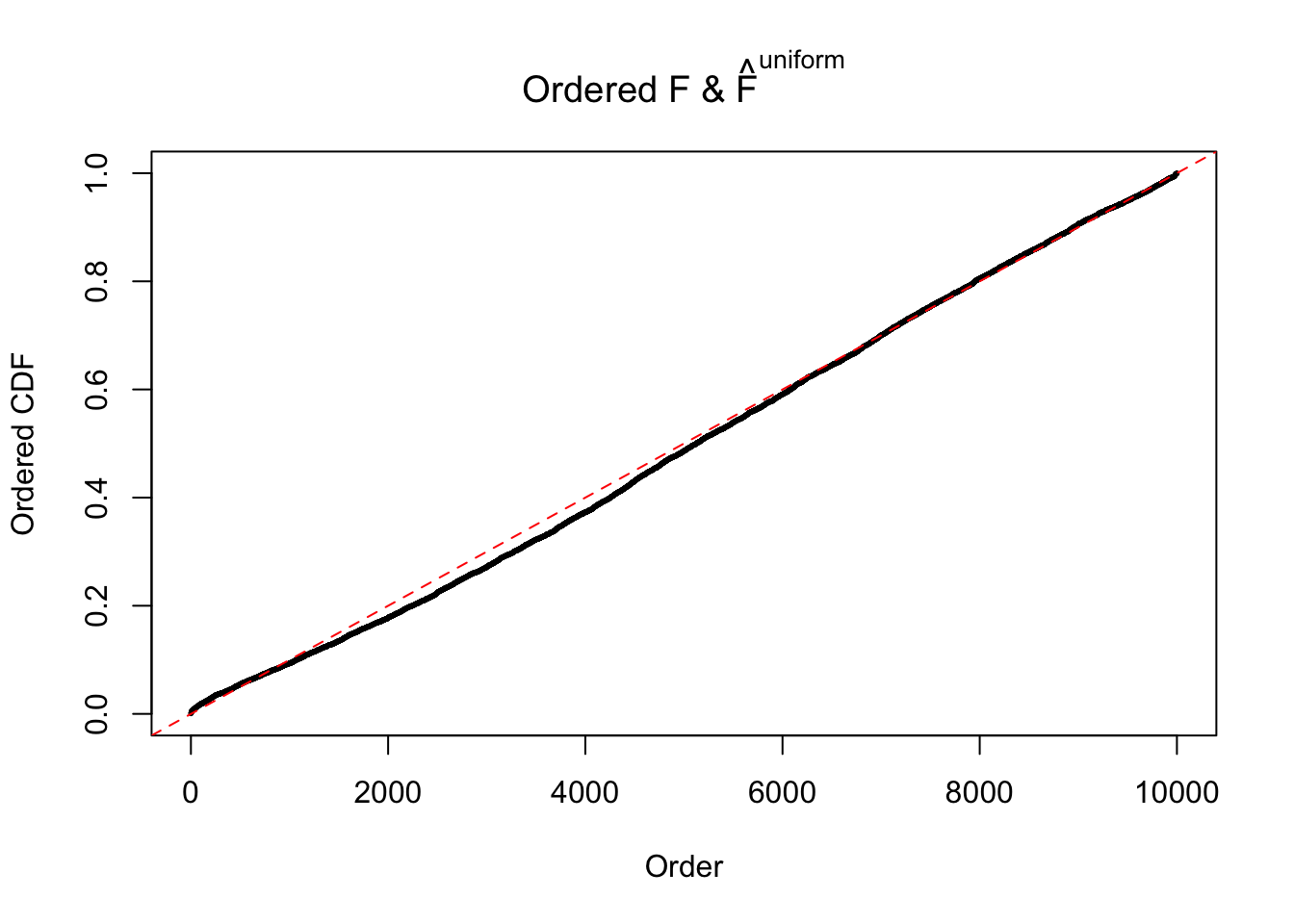
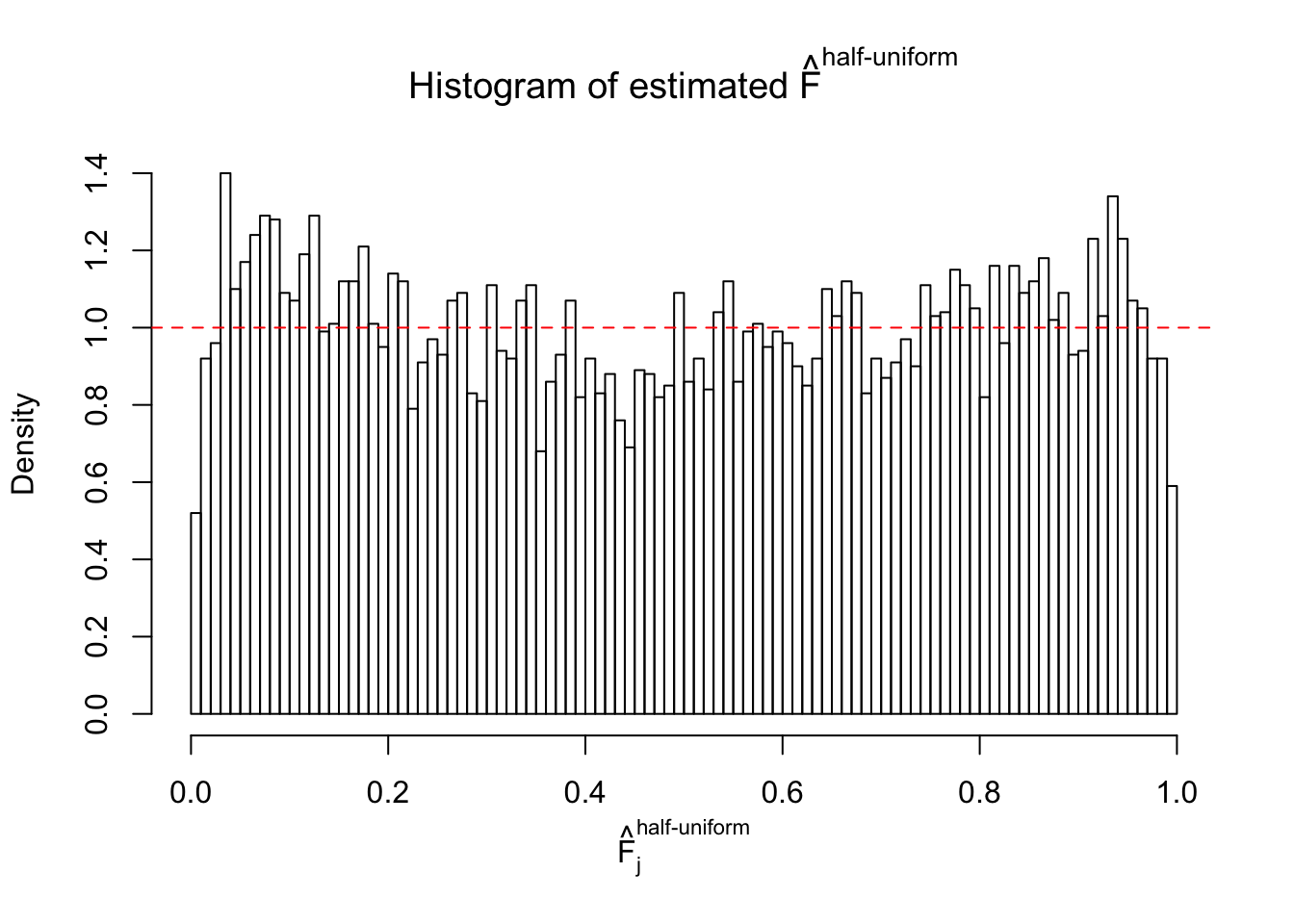
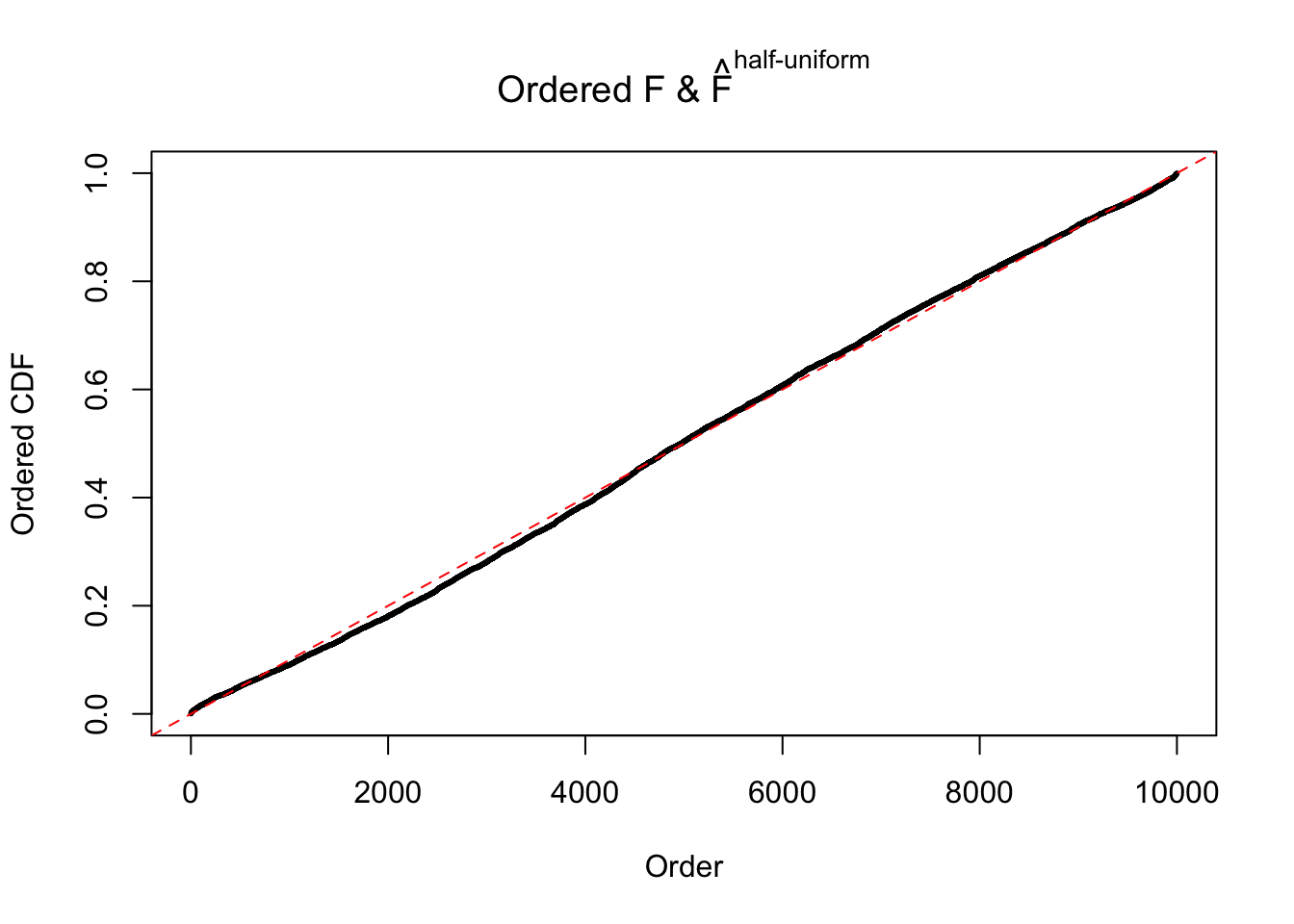
N0. 12 : Data Set 389 ; Number of False Discoveries: 11 ; pihat0 = 0.02694463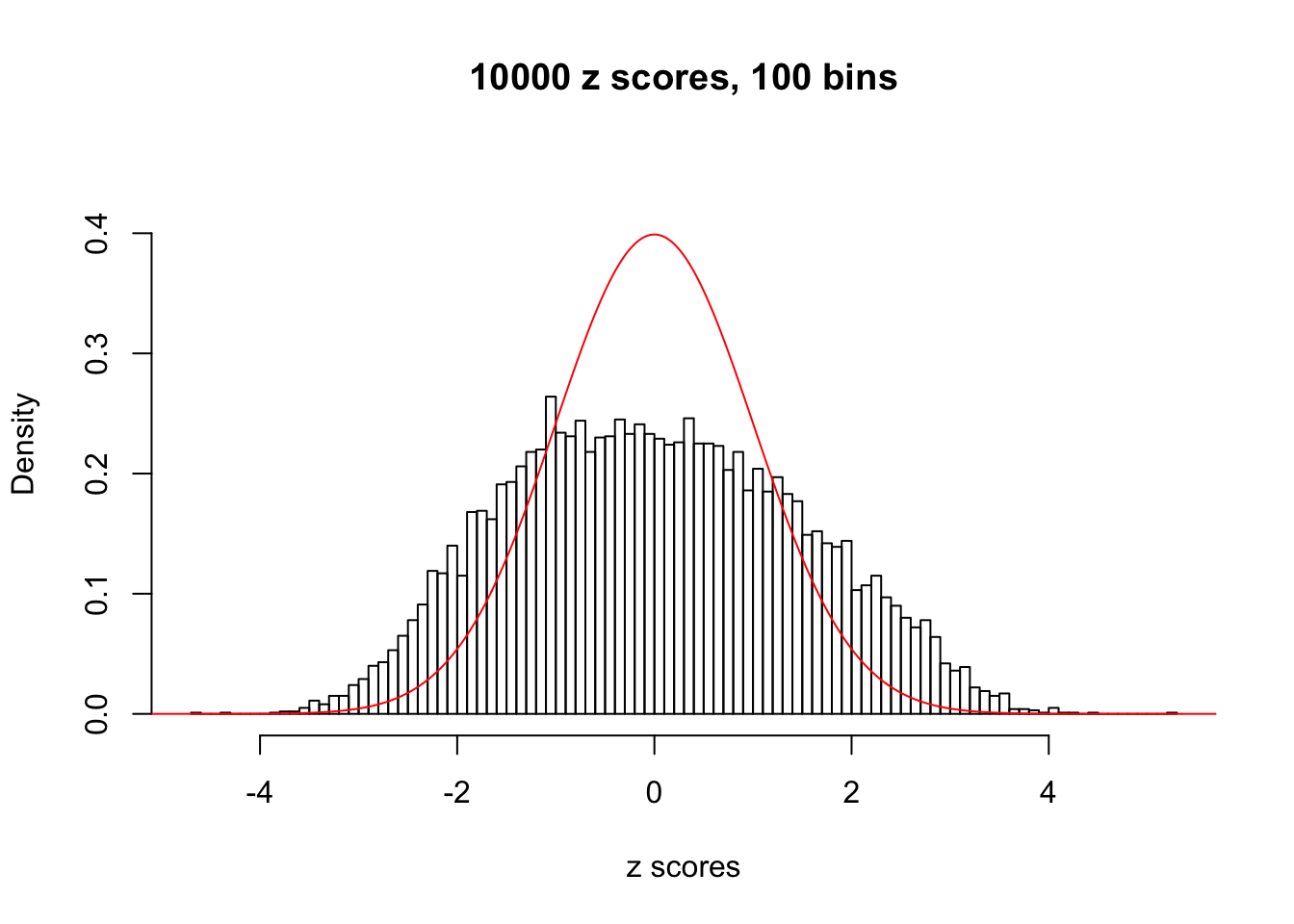
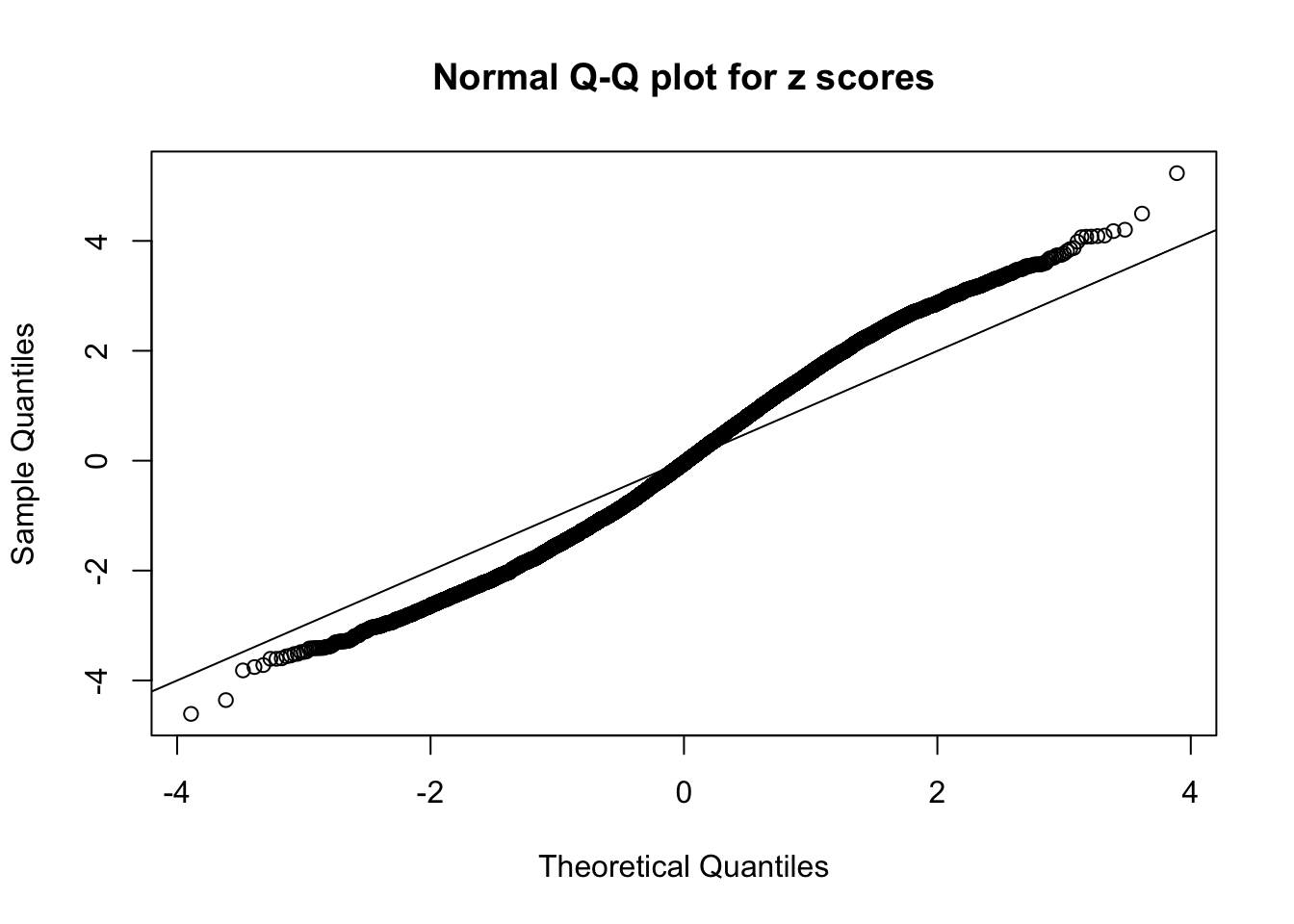
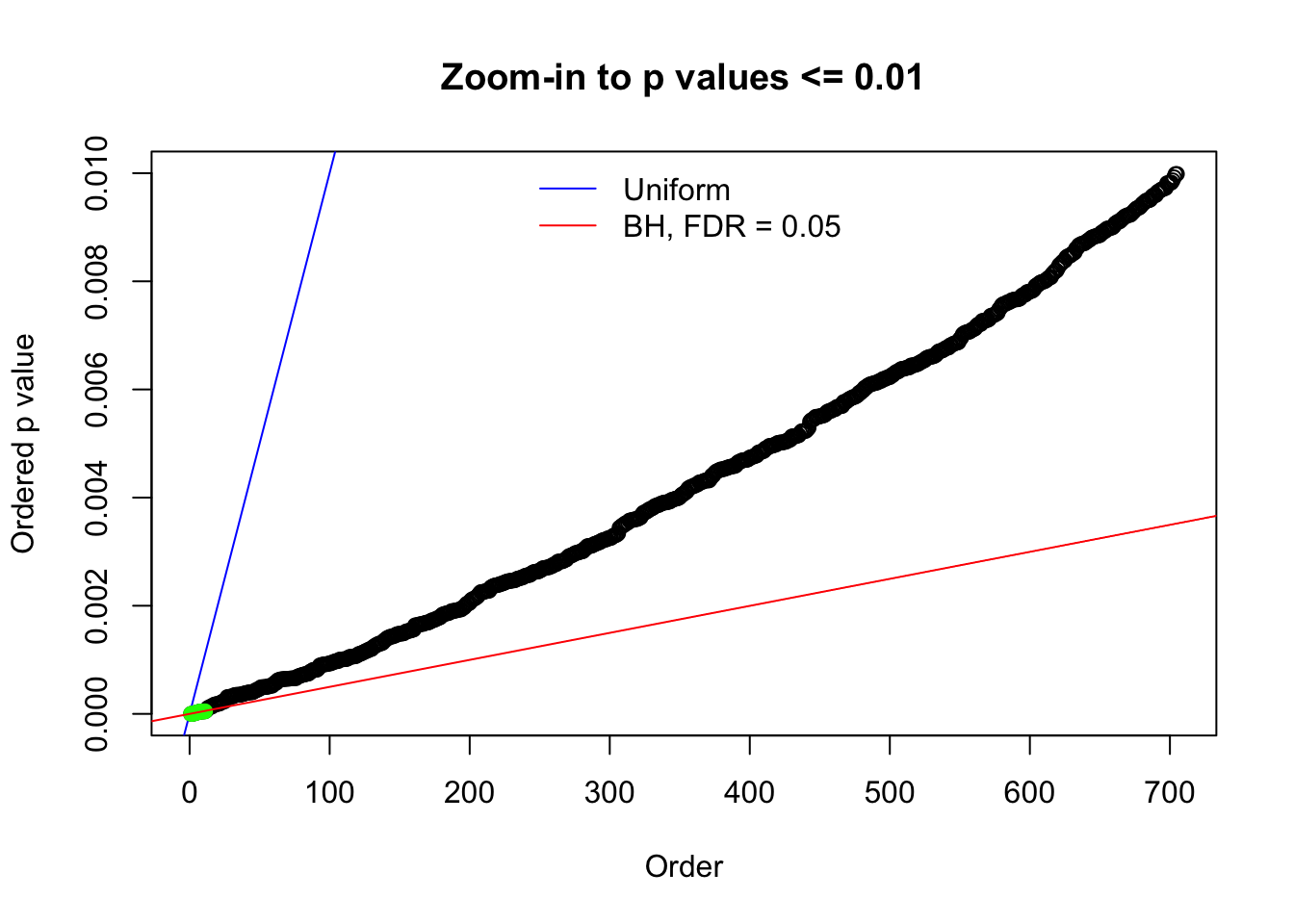
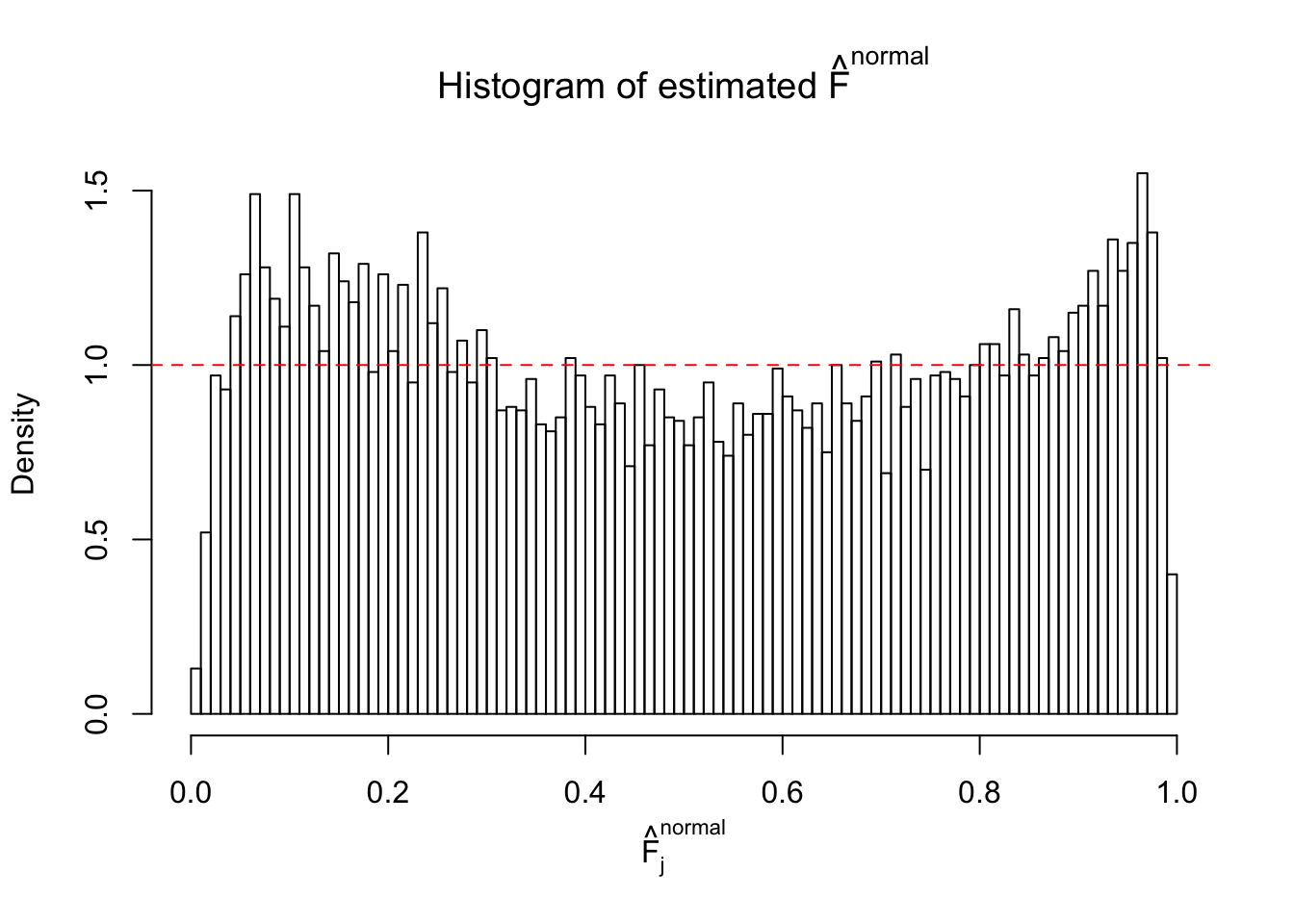
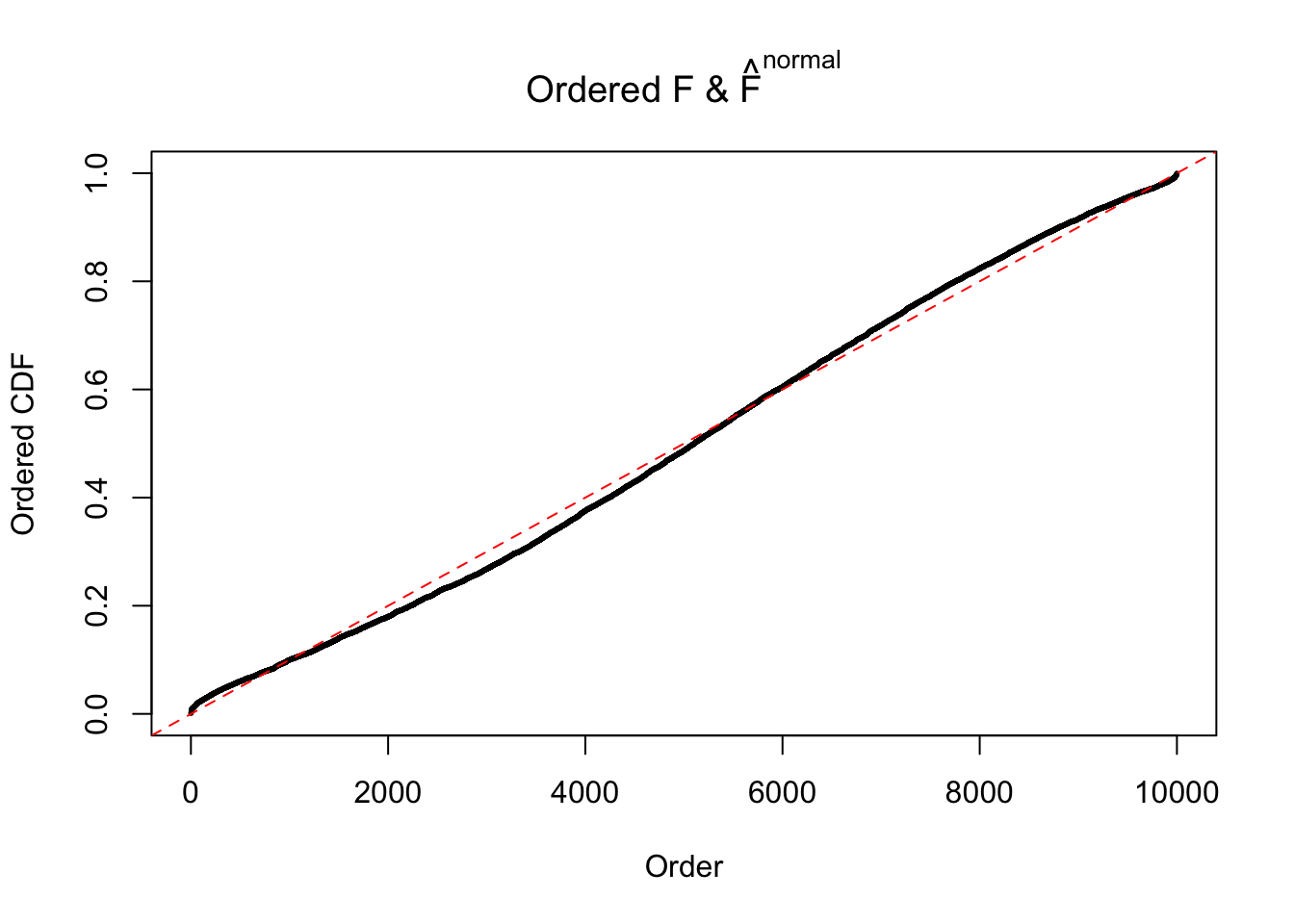
N0. 13 : Data Set 485 ; Number of False Discoveries: 9 ; pihat0 = 0.03190266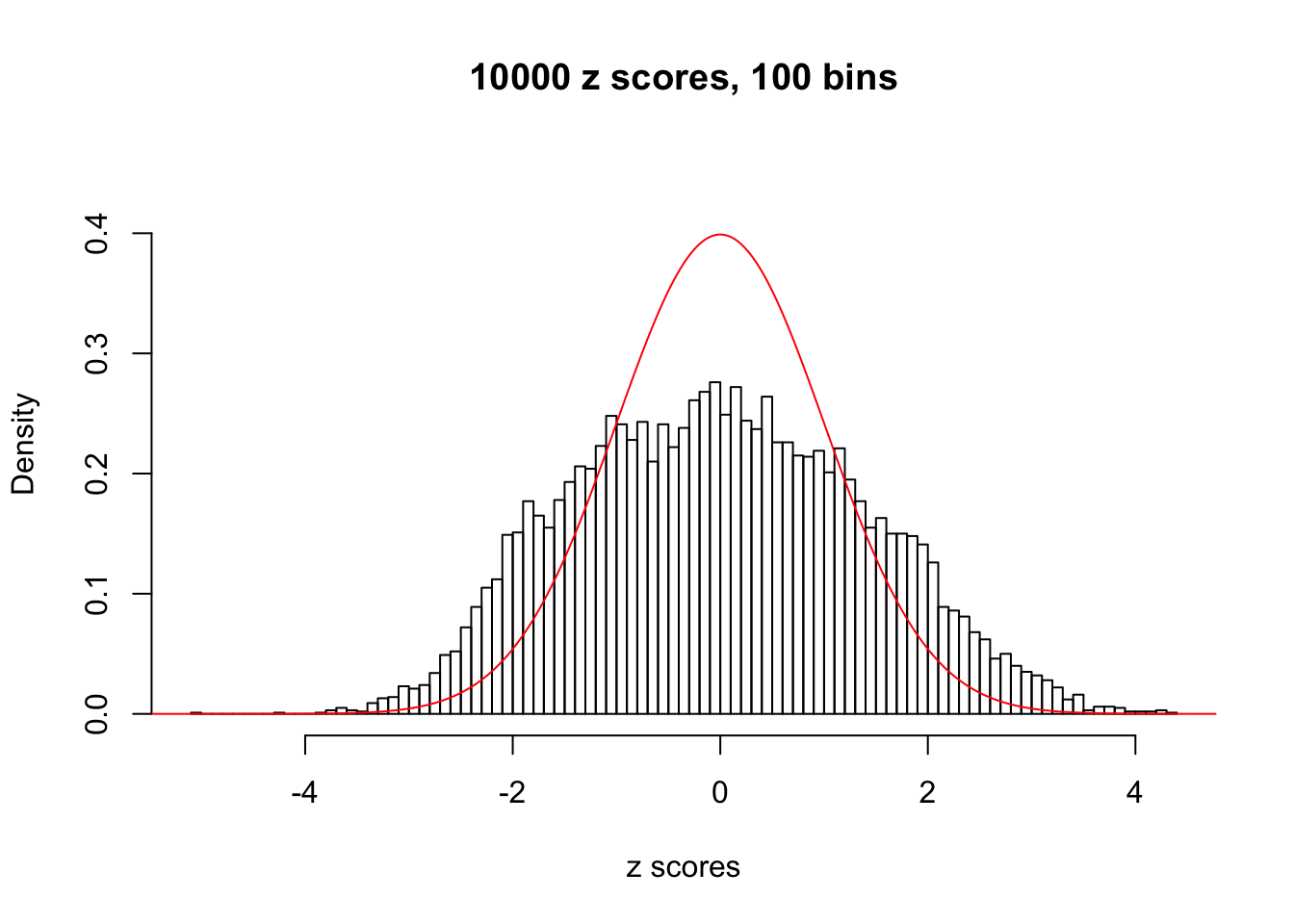
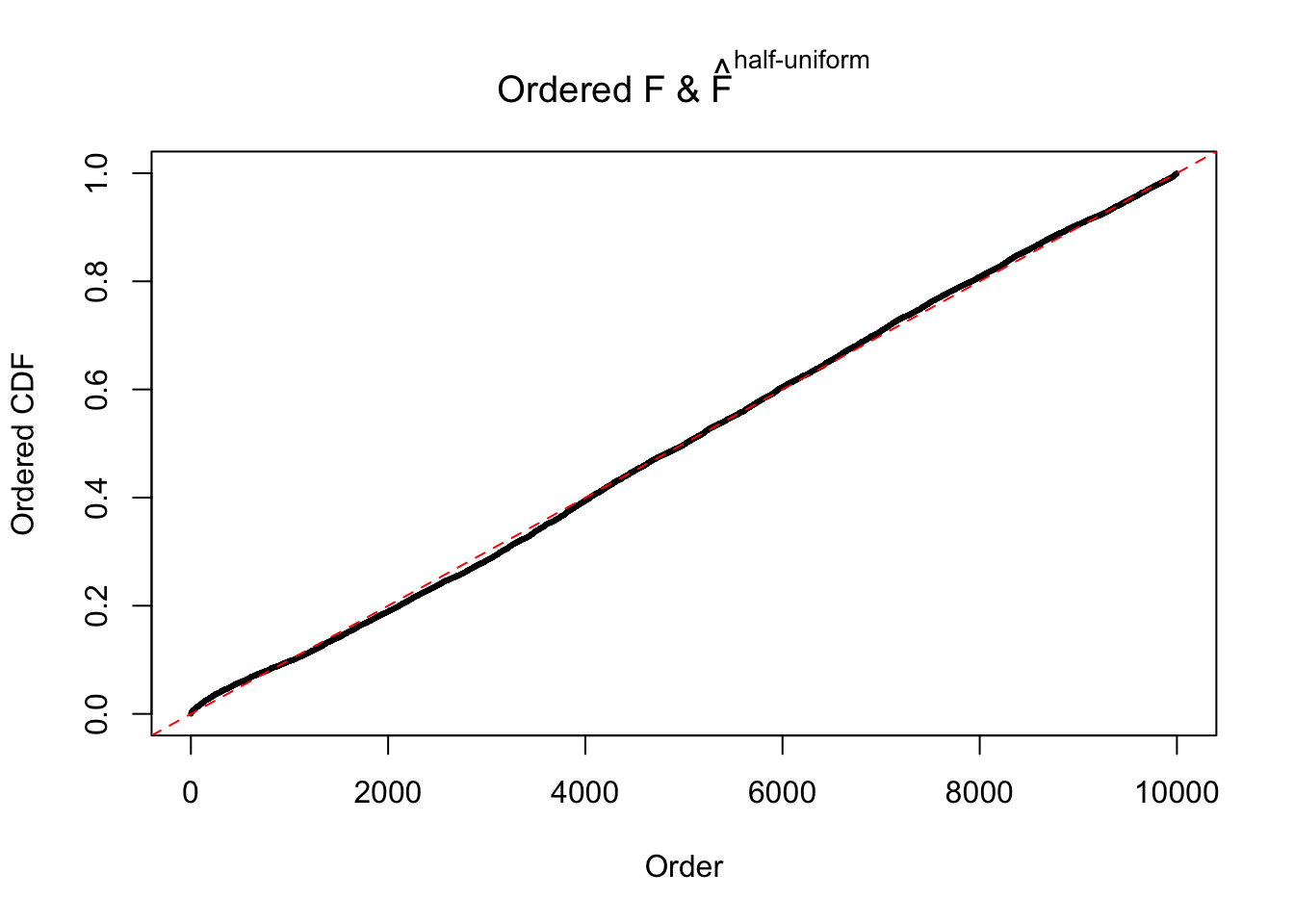
N0. 14 : Data Set 77 ; Number of False Discoveries: 7 ; pihat0 = 0.0240265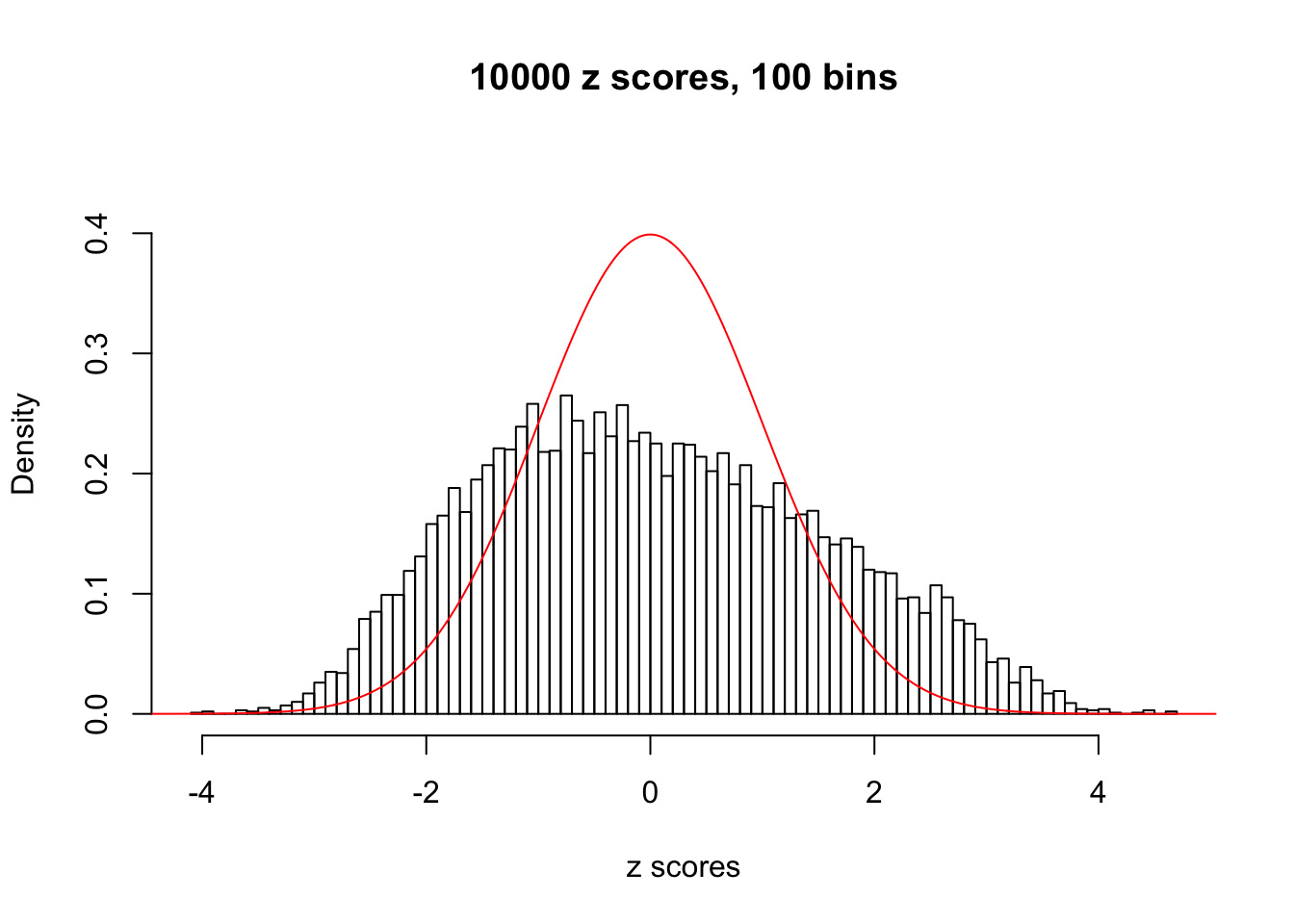
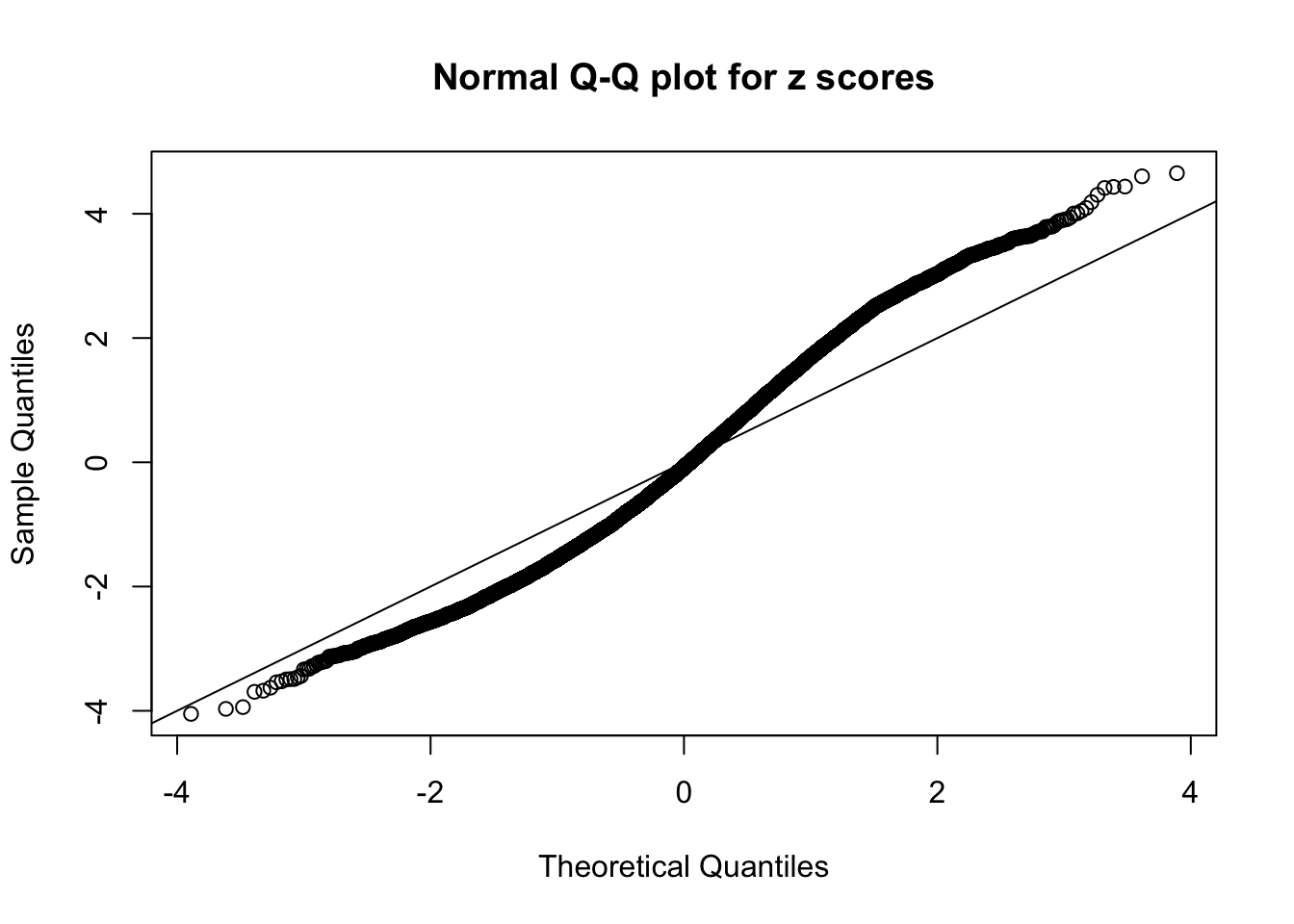
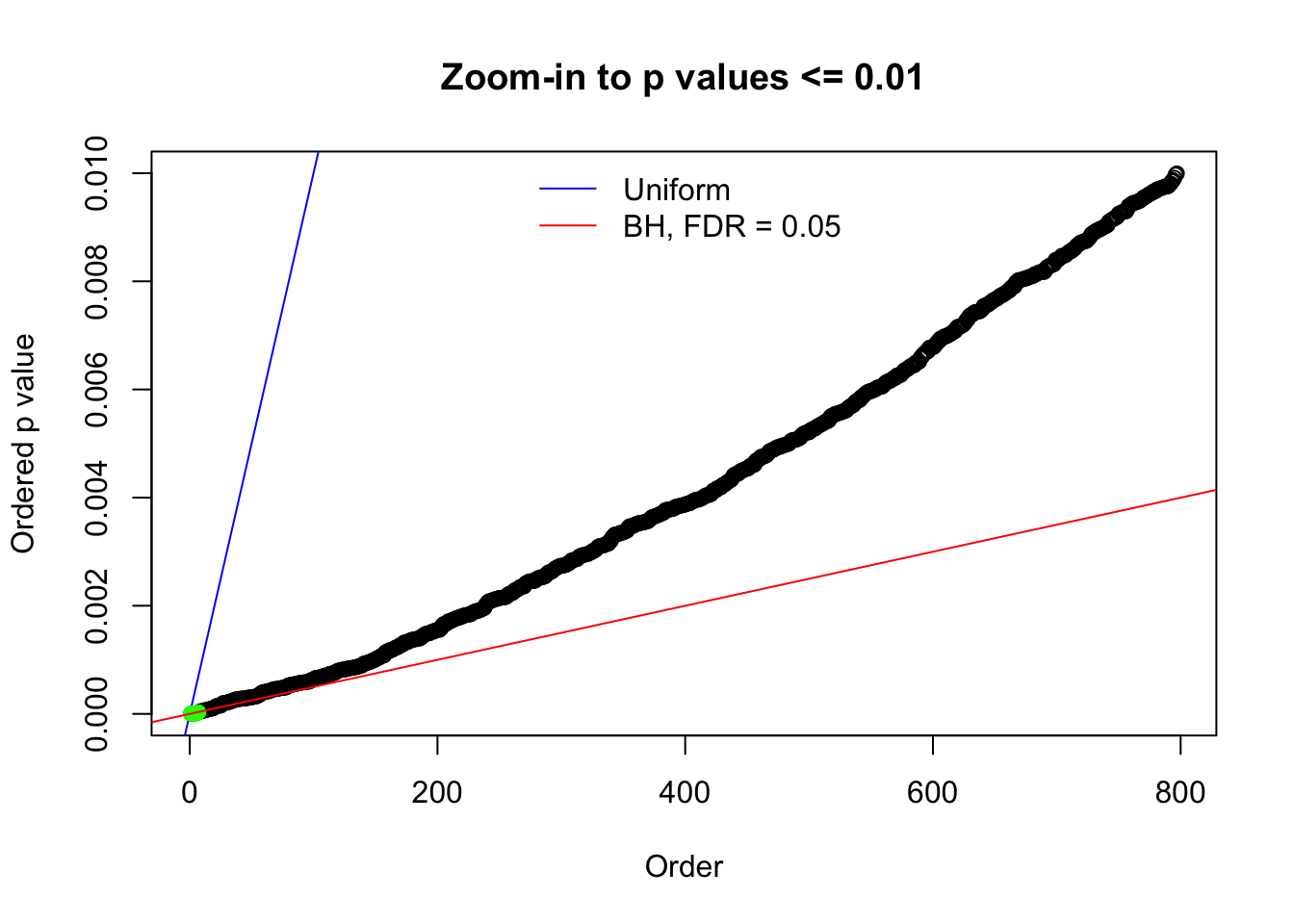
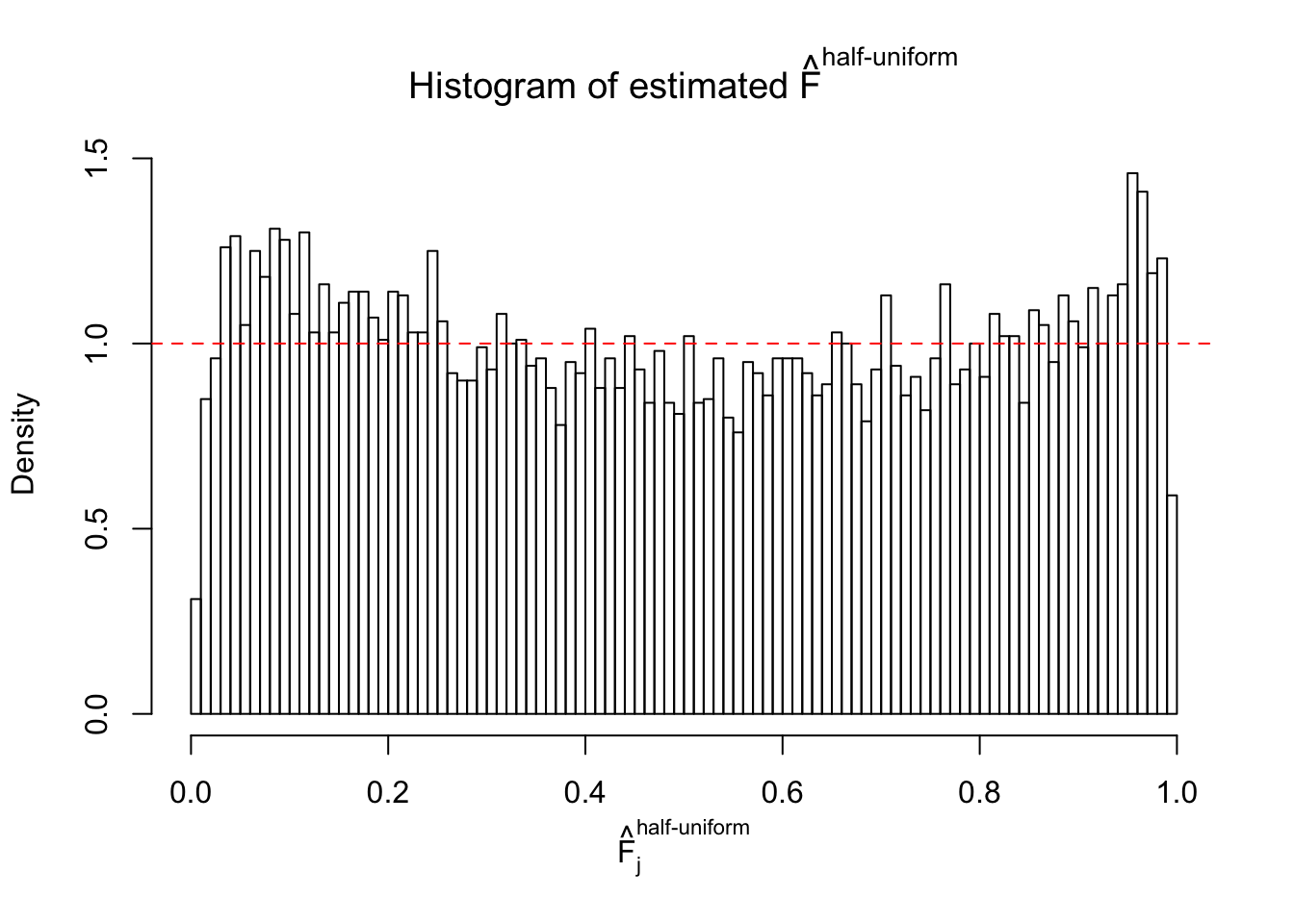
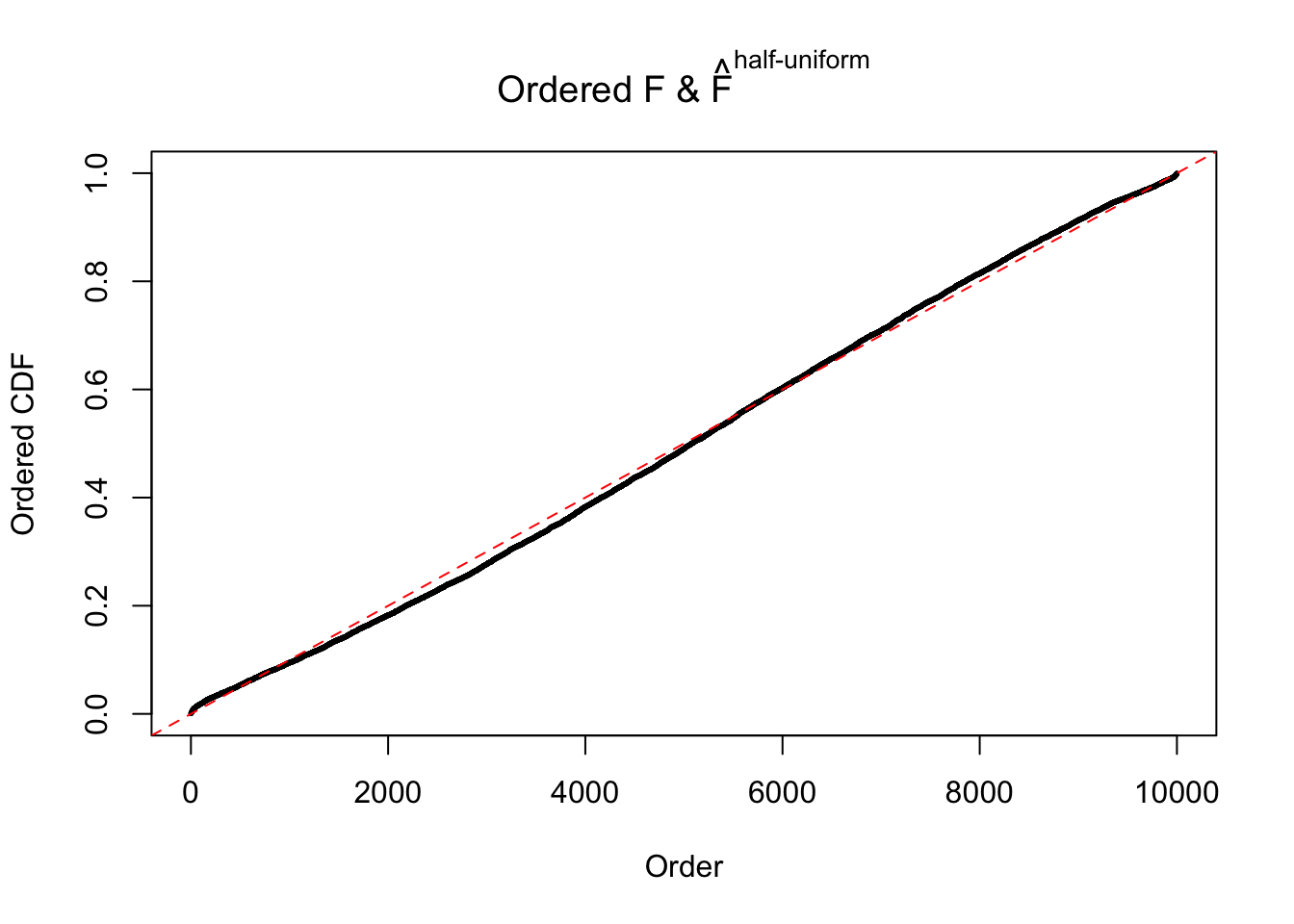
N0. 15 : Data Set 503 ; Number of False Discoveries: 7 ; pihat0 = 0.1290869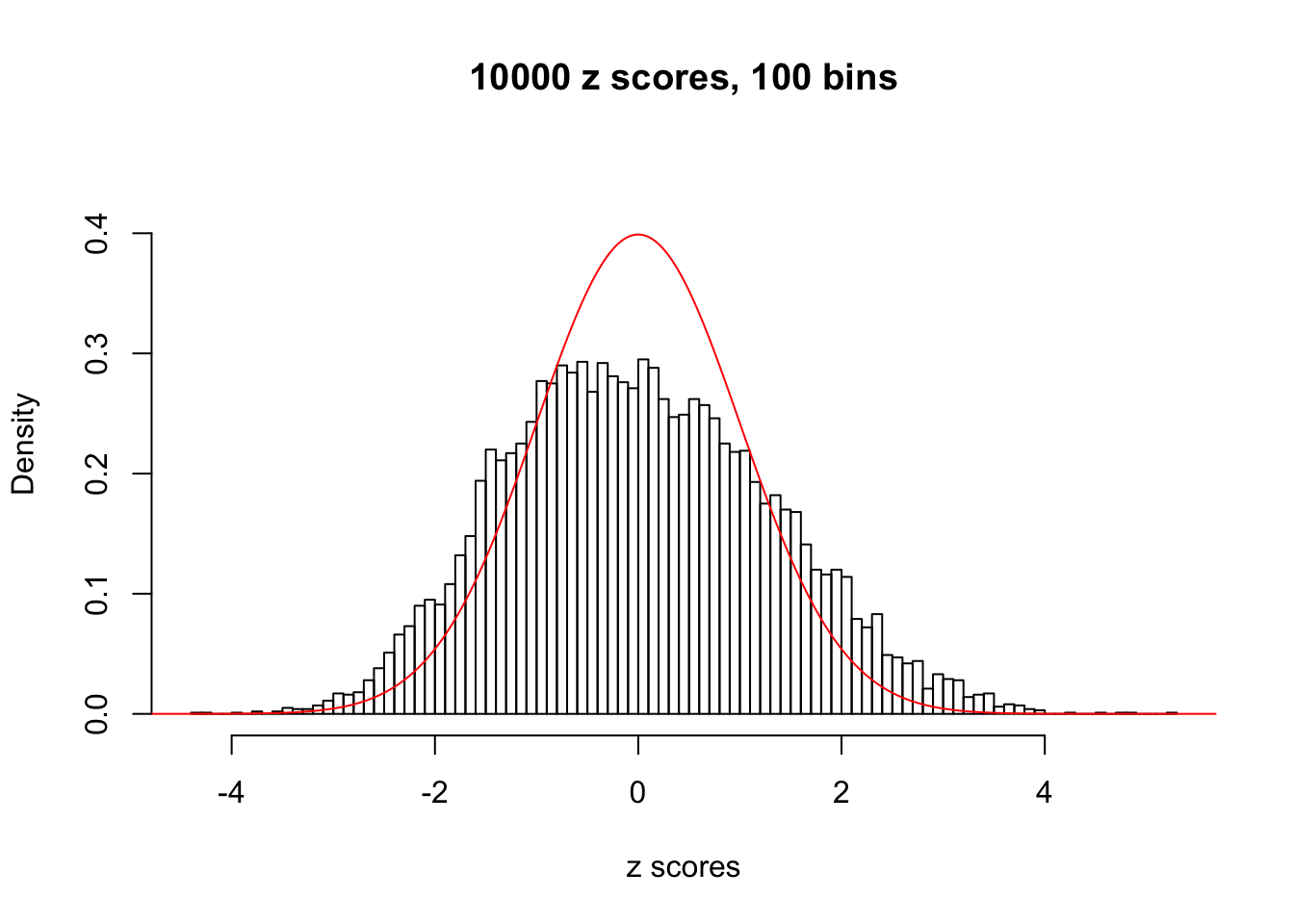
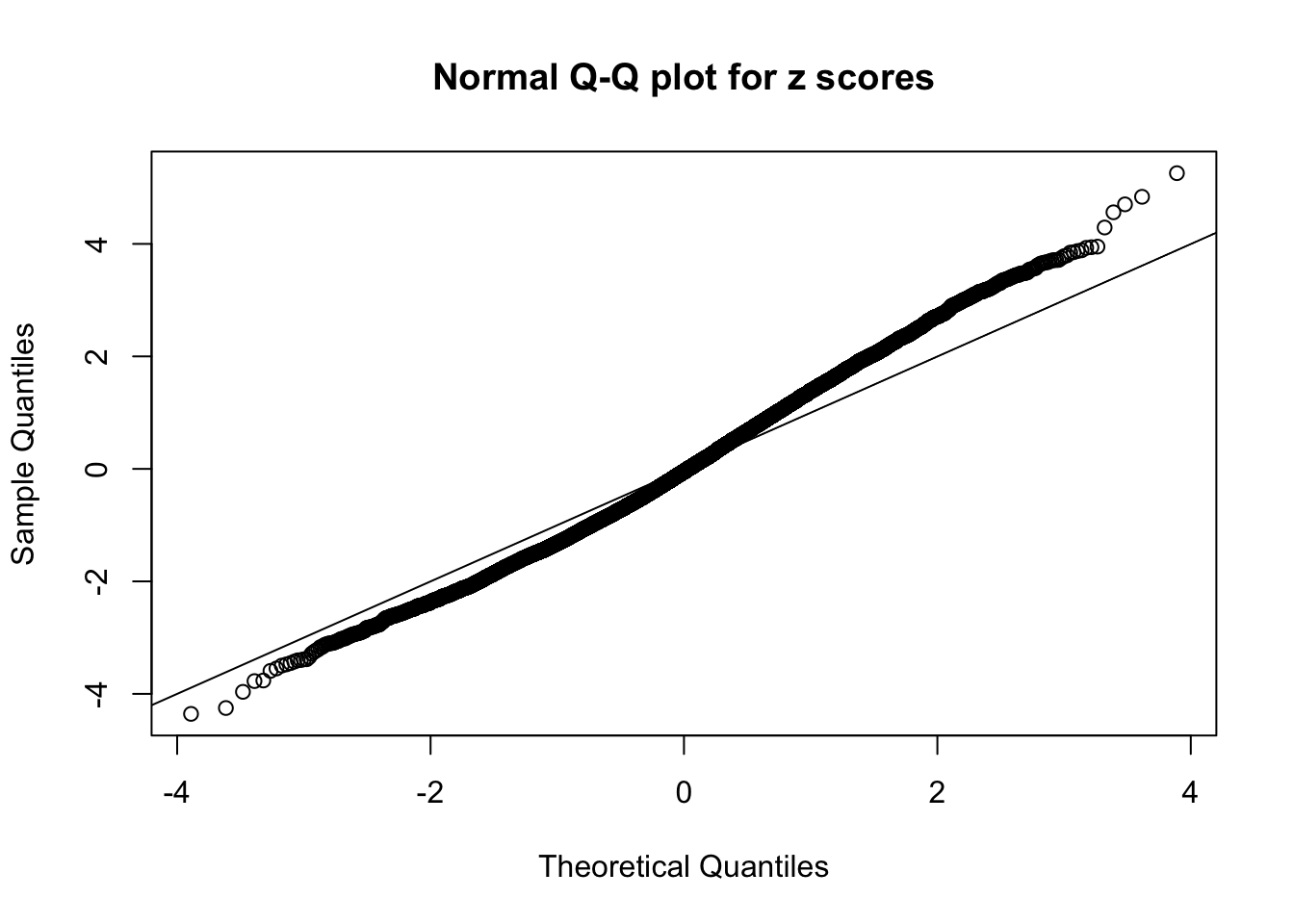
N0. 16 : Data Set 984 ; Number of False Discoveries: 7 ; pihat0 = 0.04373679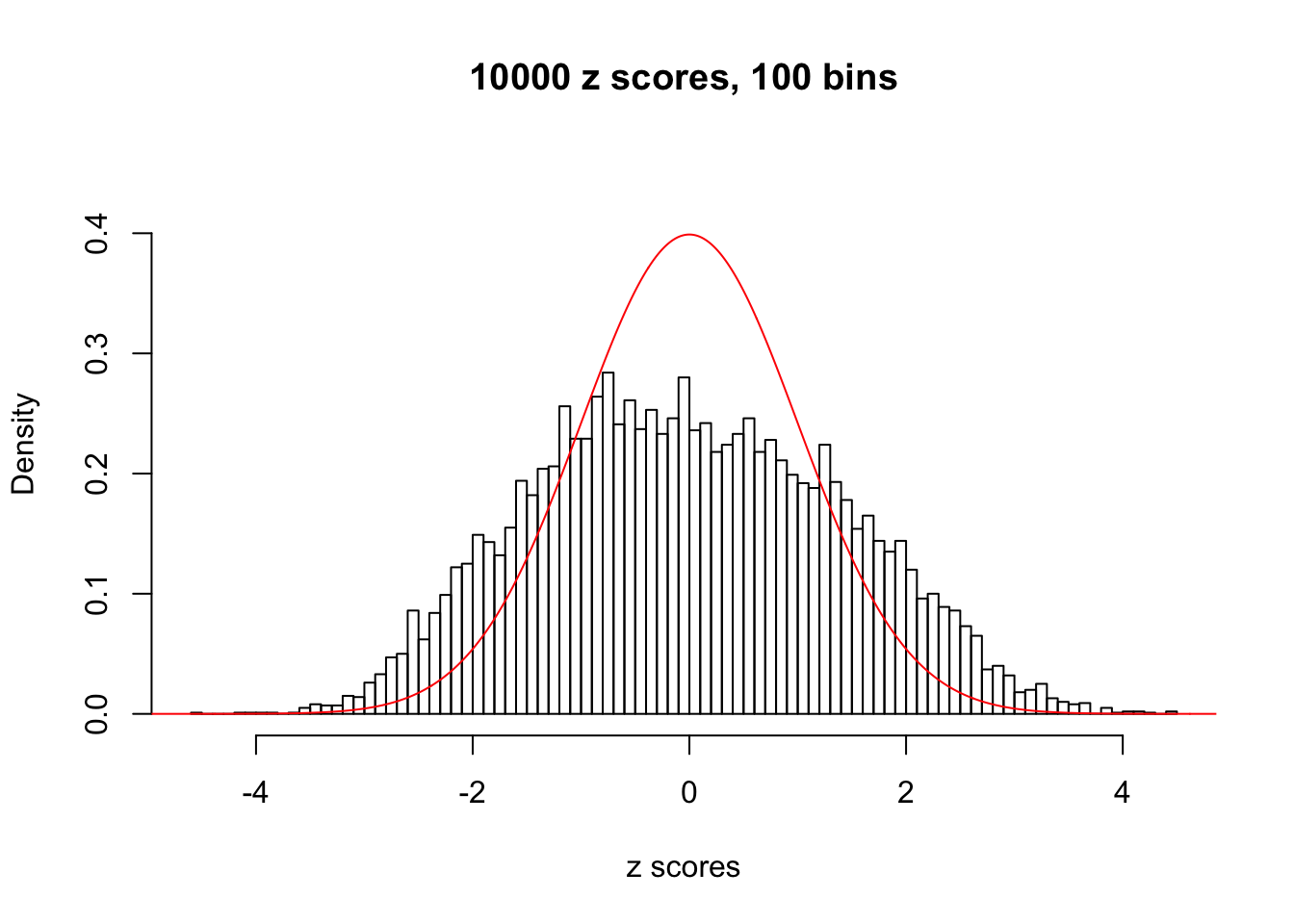
N0. 17 : Data Set 360 ; Number of False Discoveries: 6 ; pihat0 = 0.01242637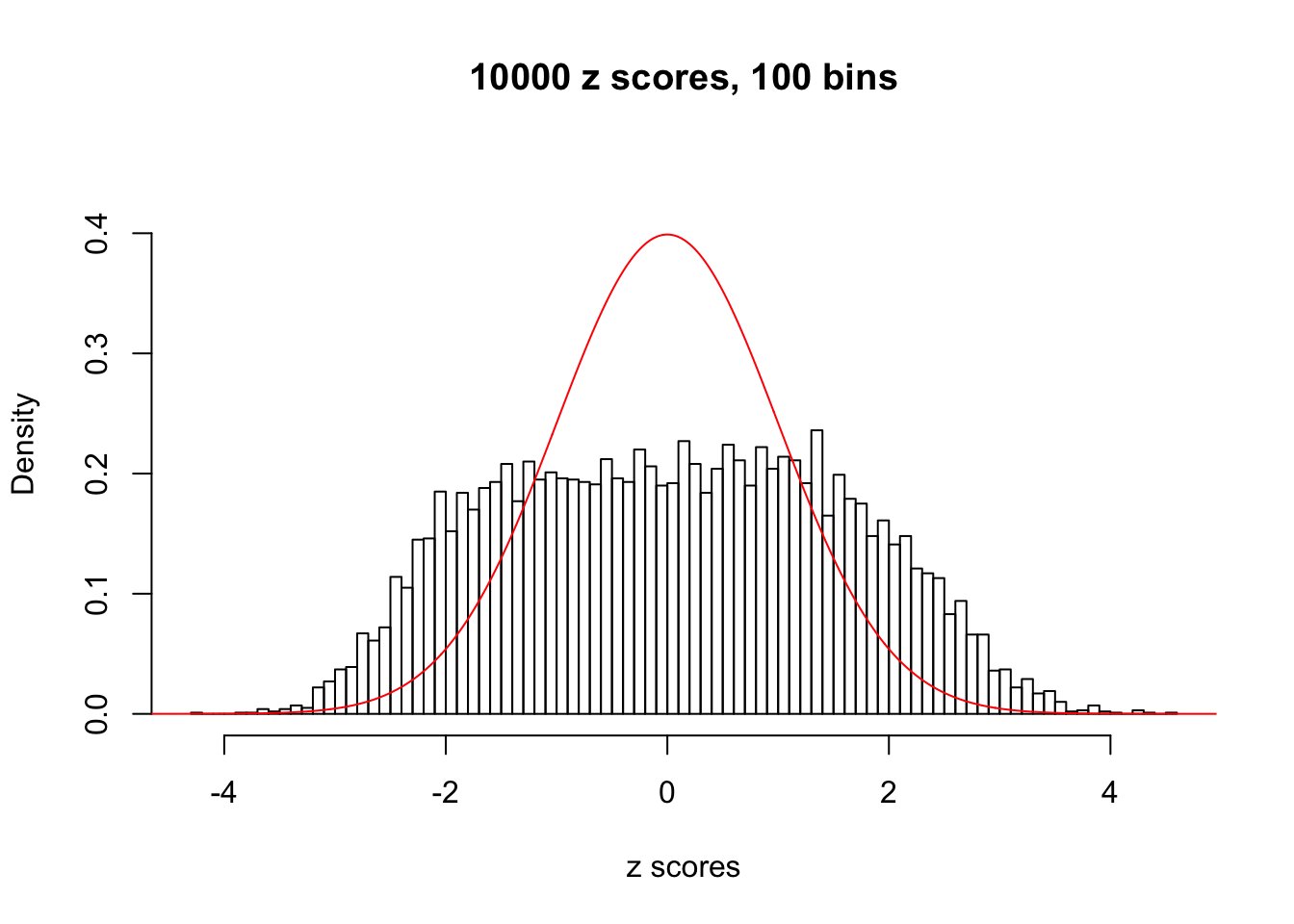
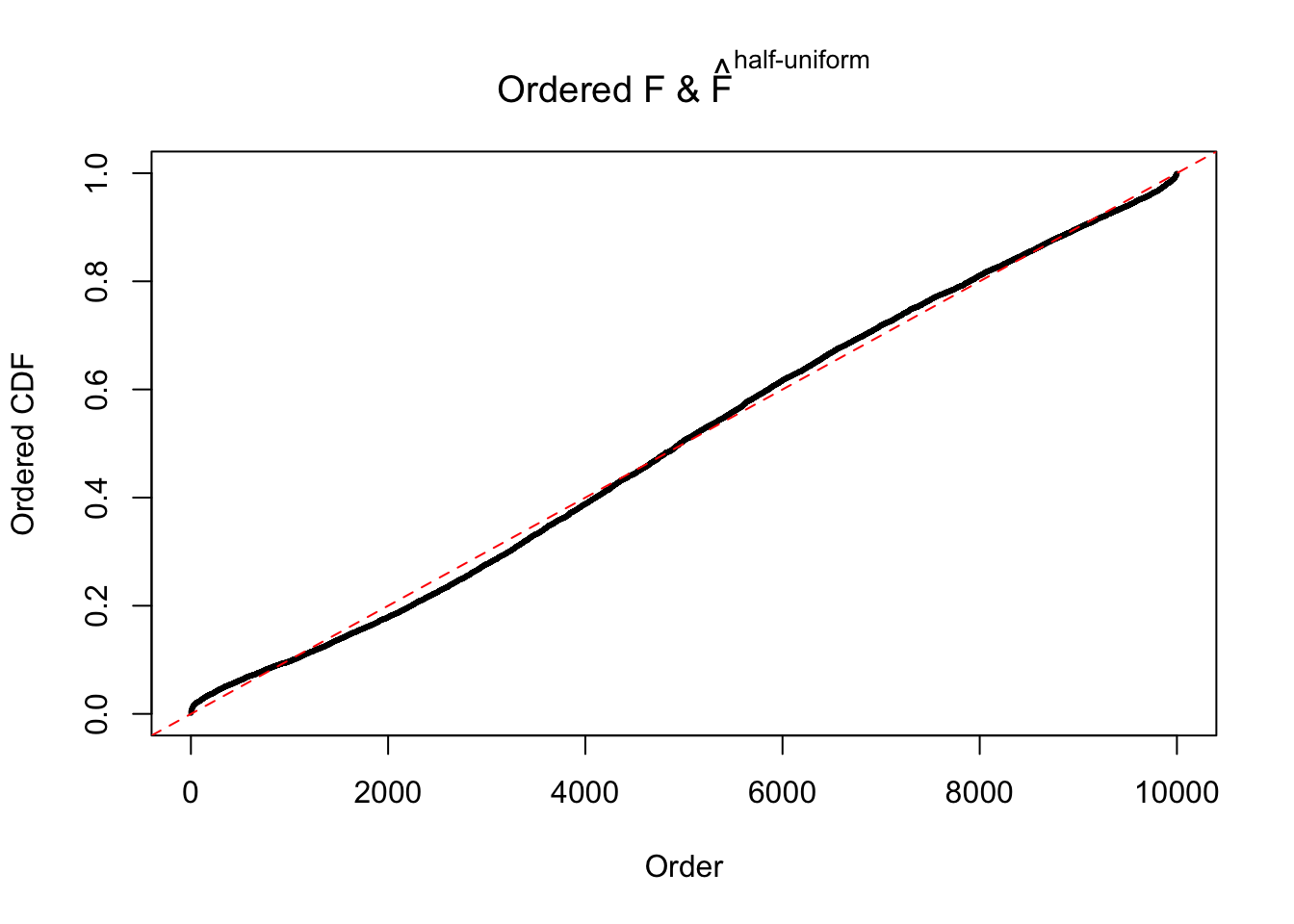
N0. 18 : Data Set 522 ; Number of False Discoveries: 4 ; pihat0 = 0.02361336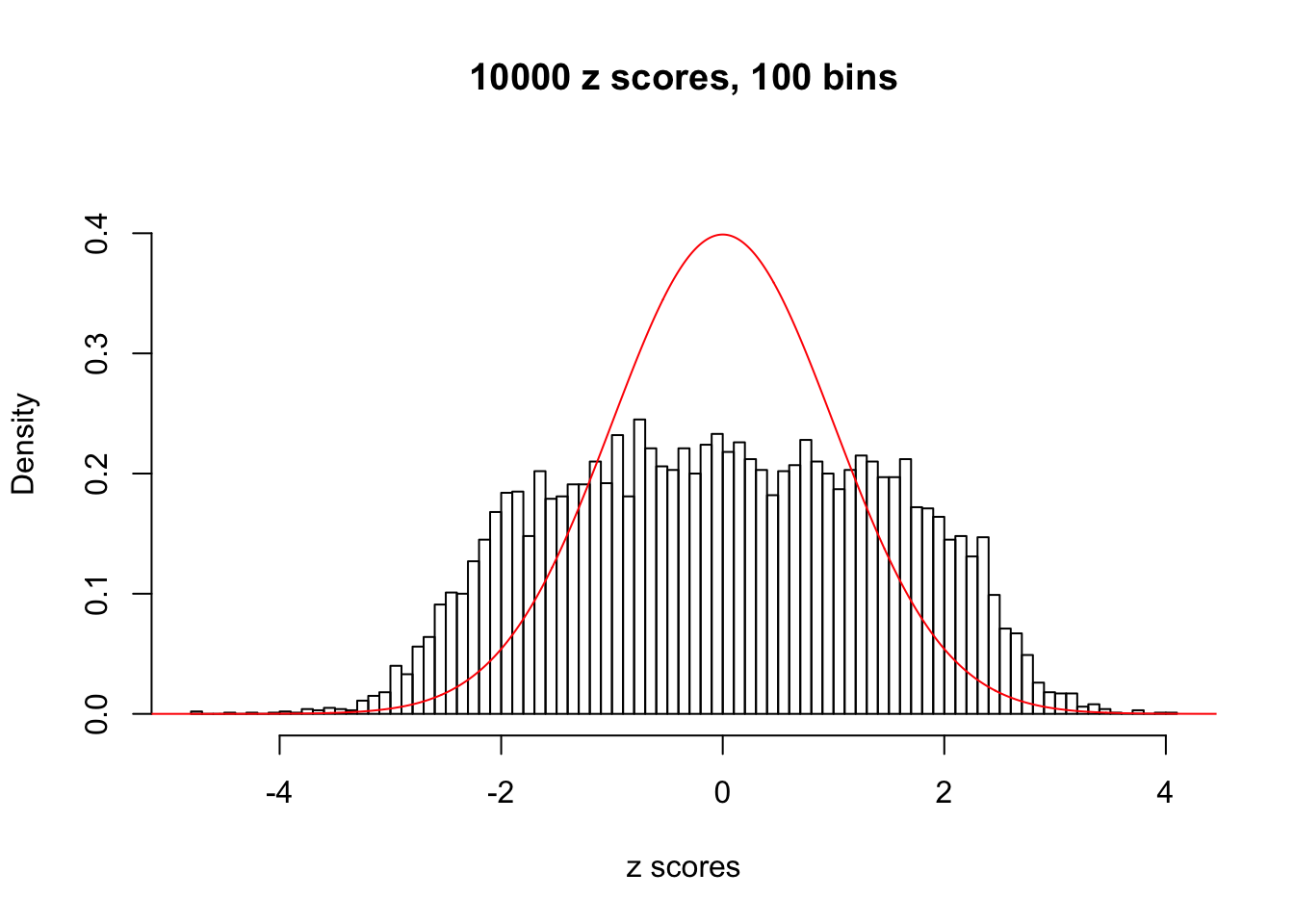
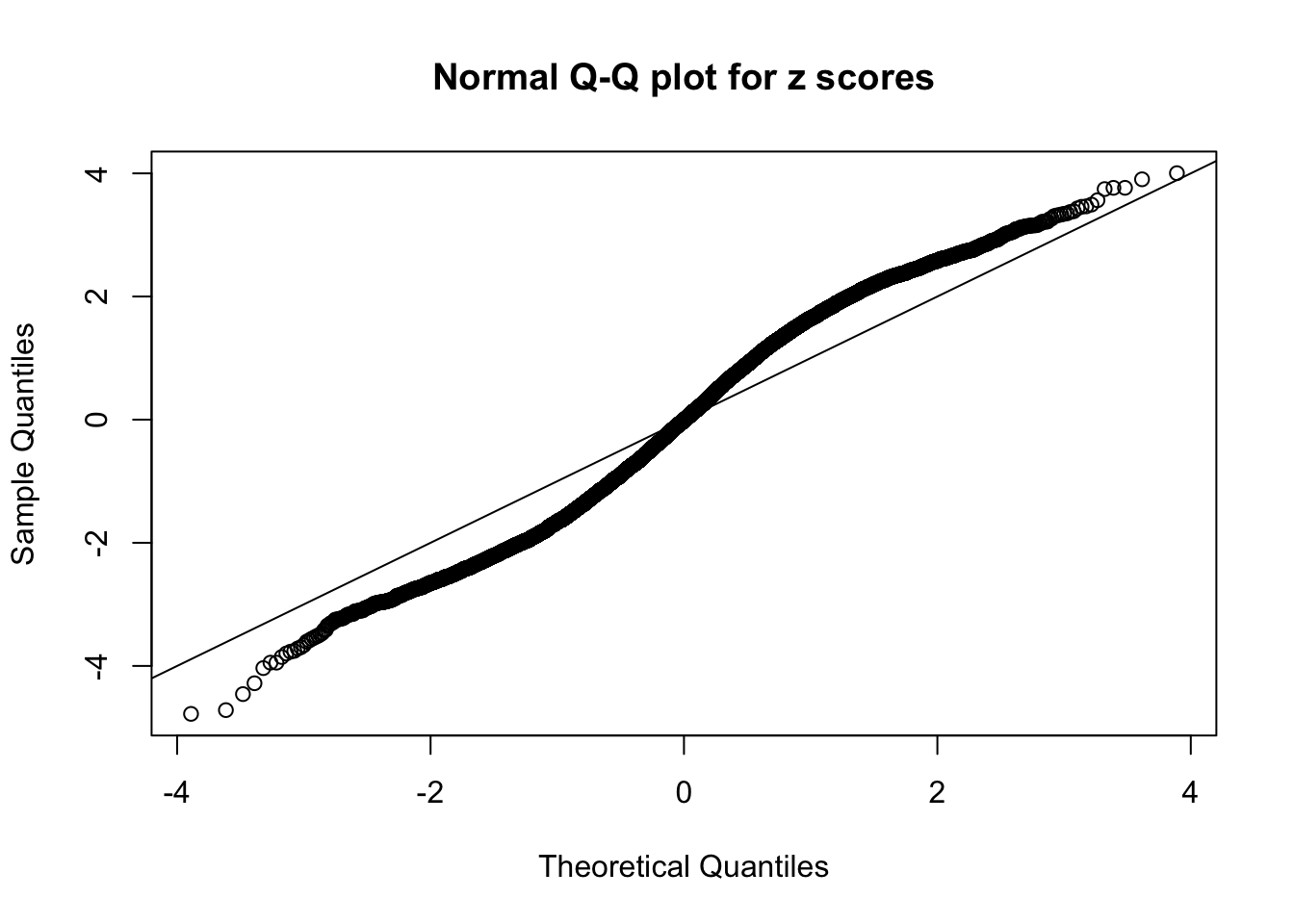
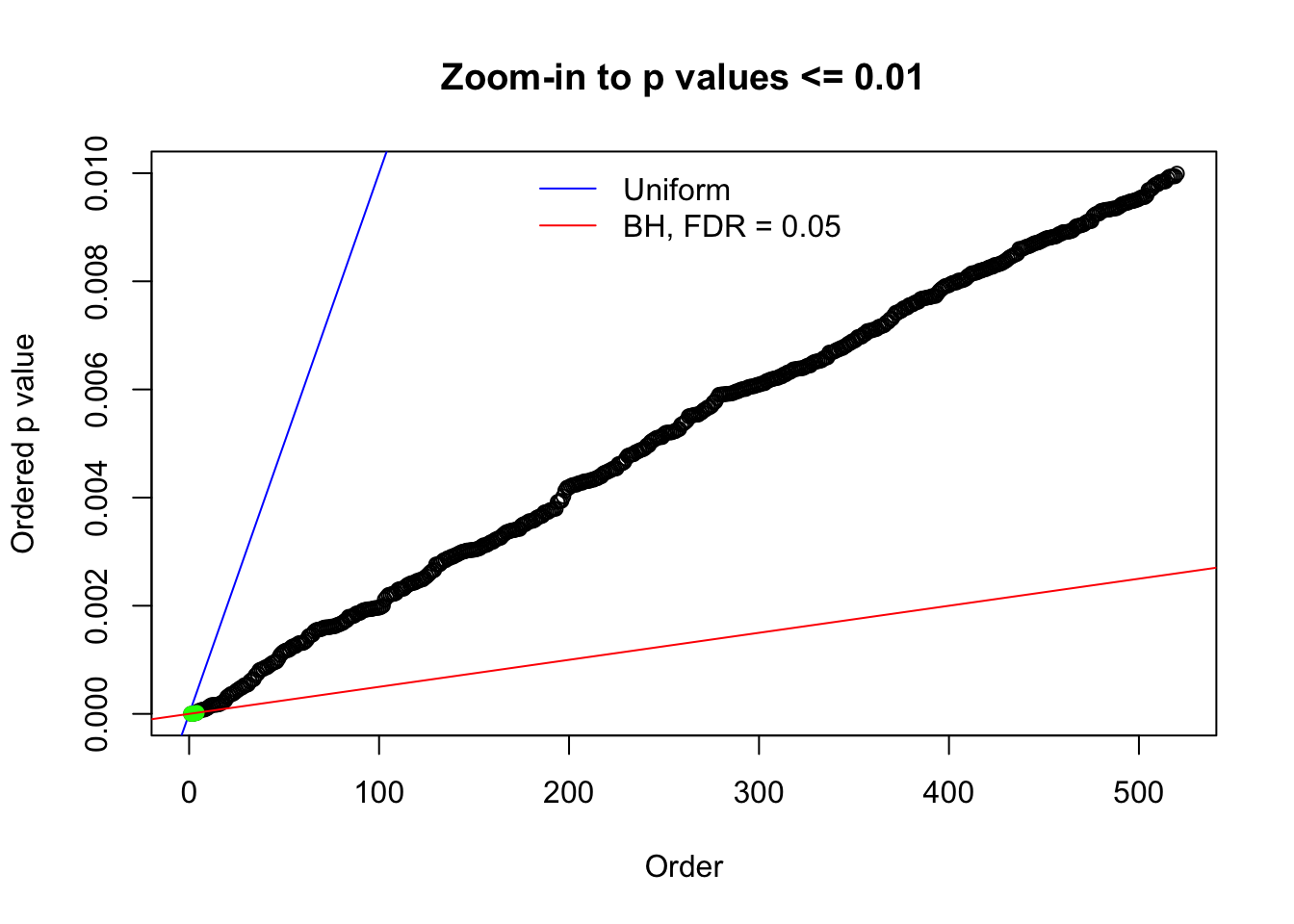
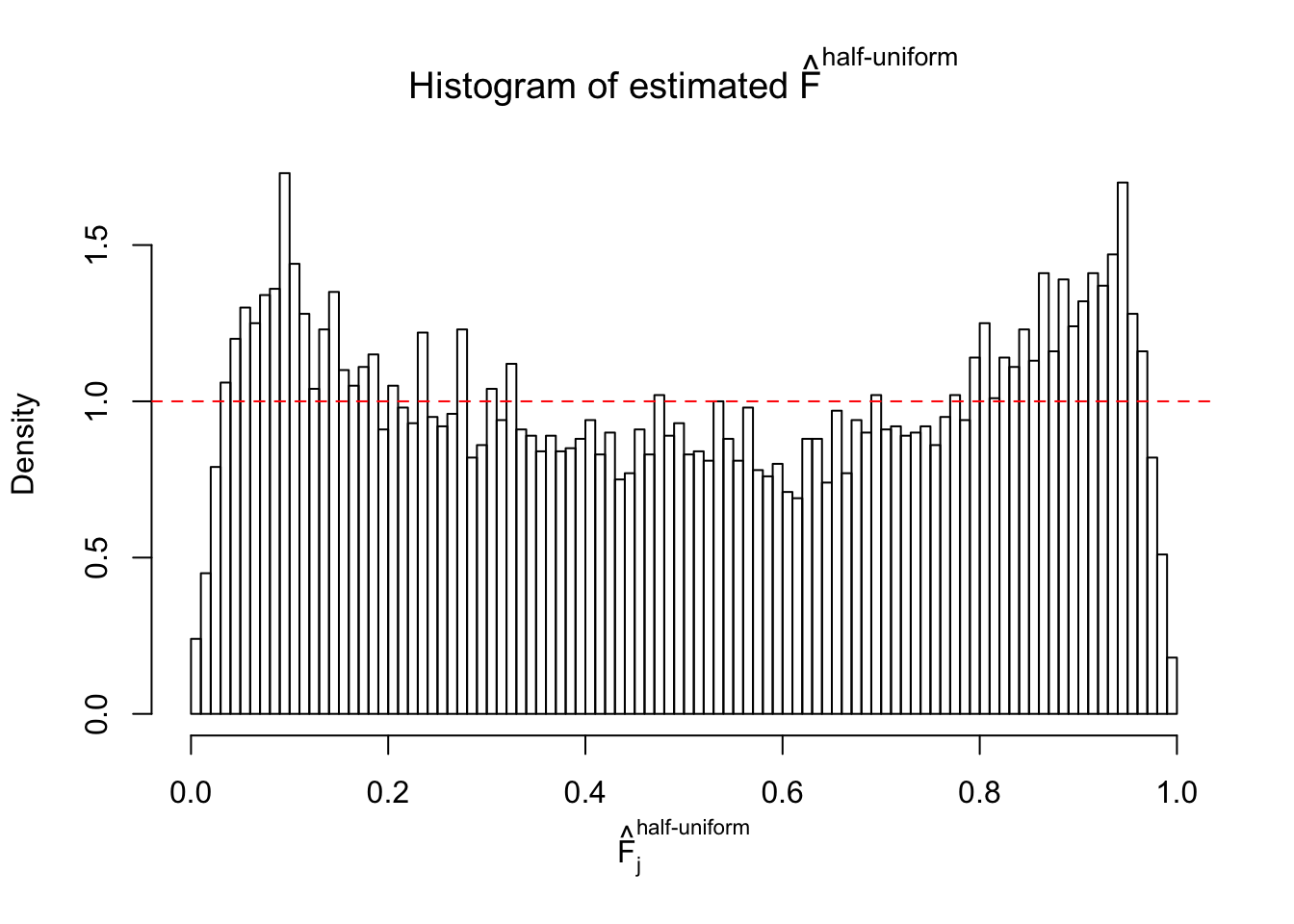
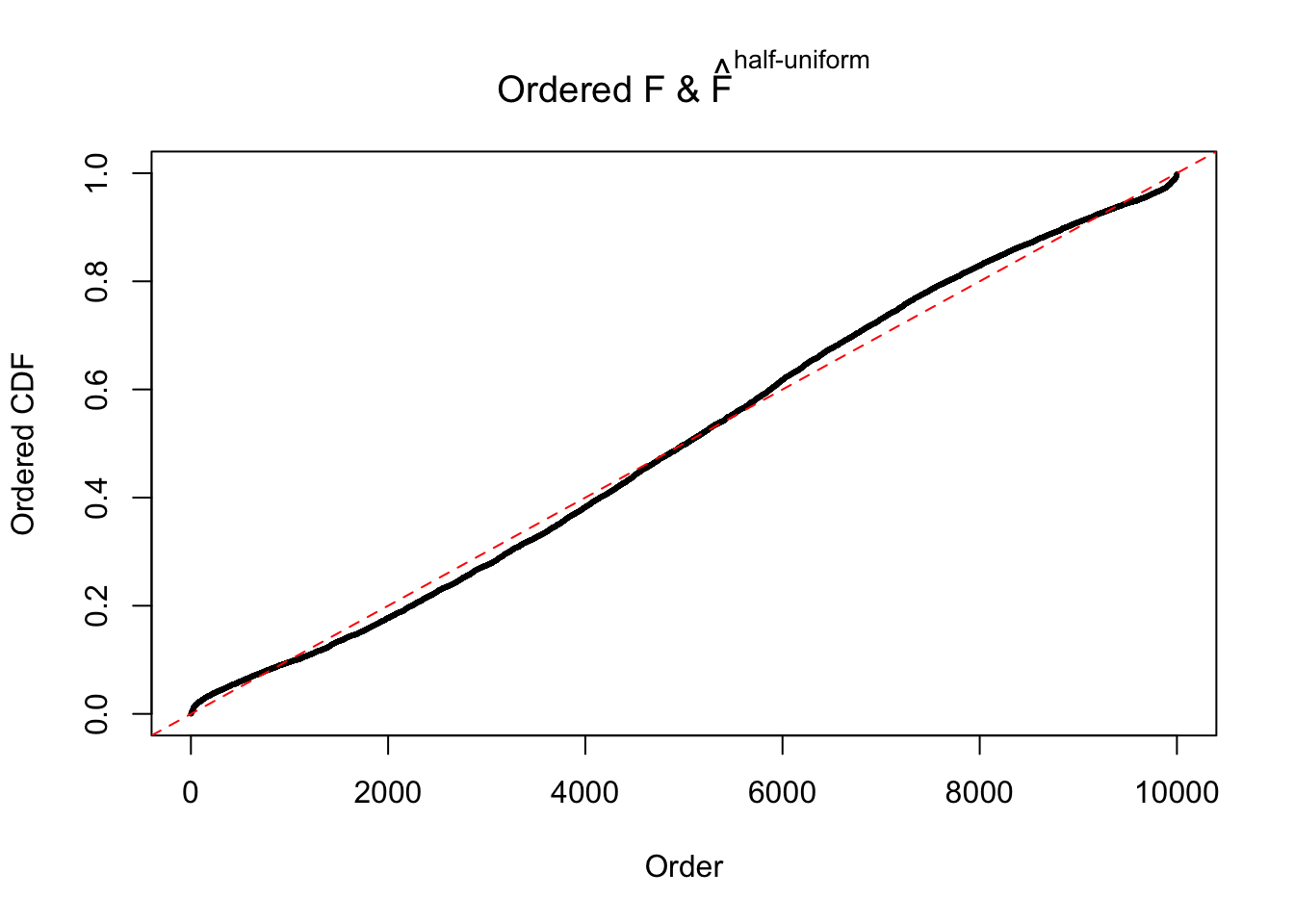
N0. 19 : Data Set 51 ; Number of False Discoveries: 3 ; pihat0 = 0.07300305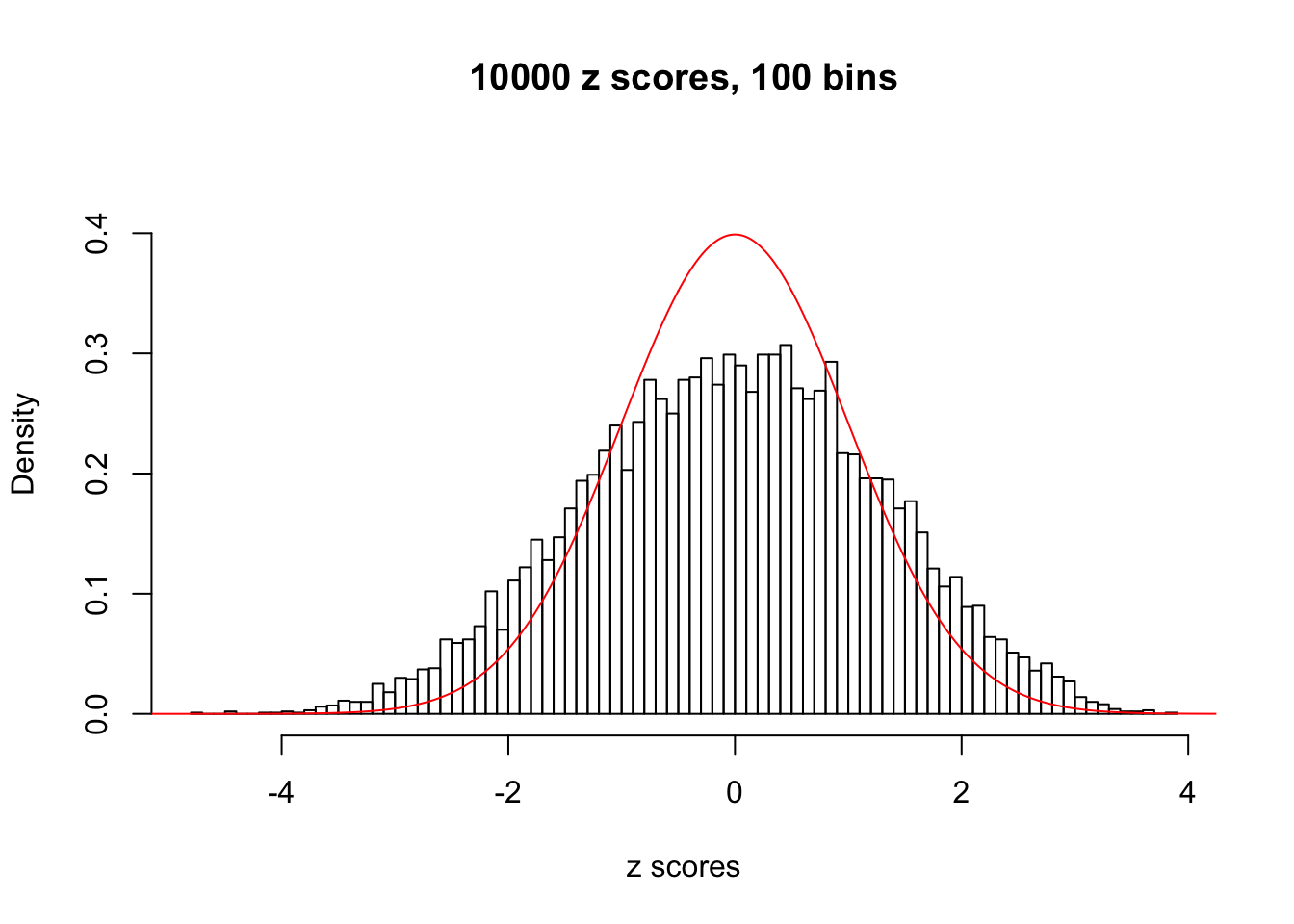
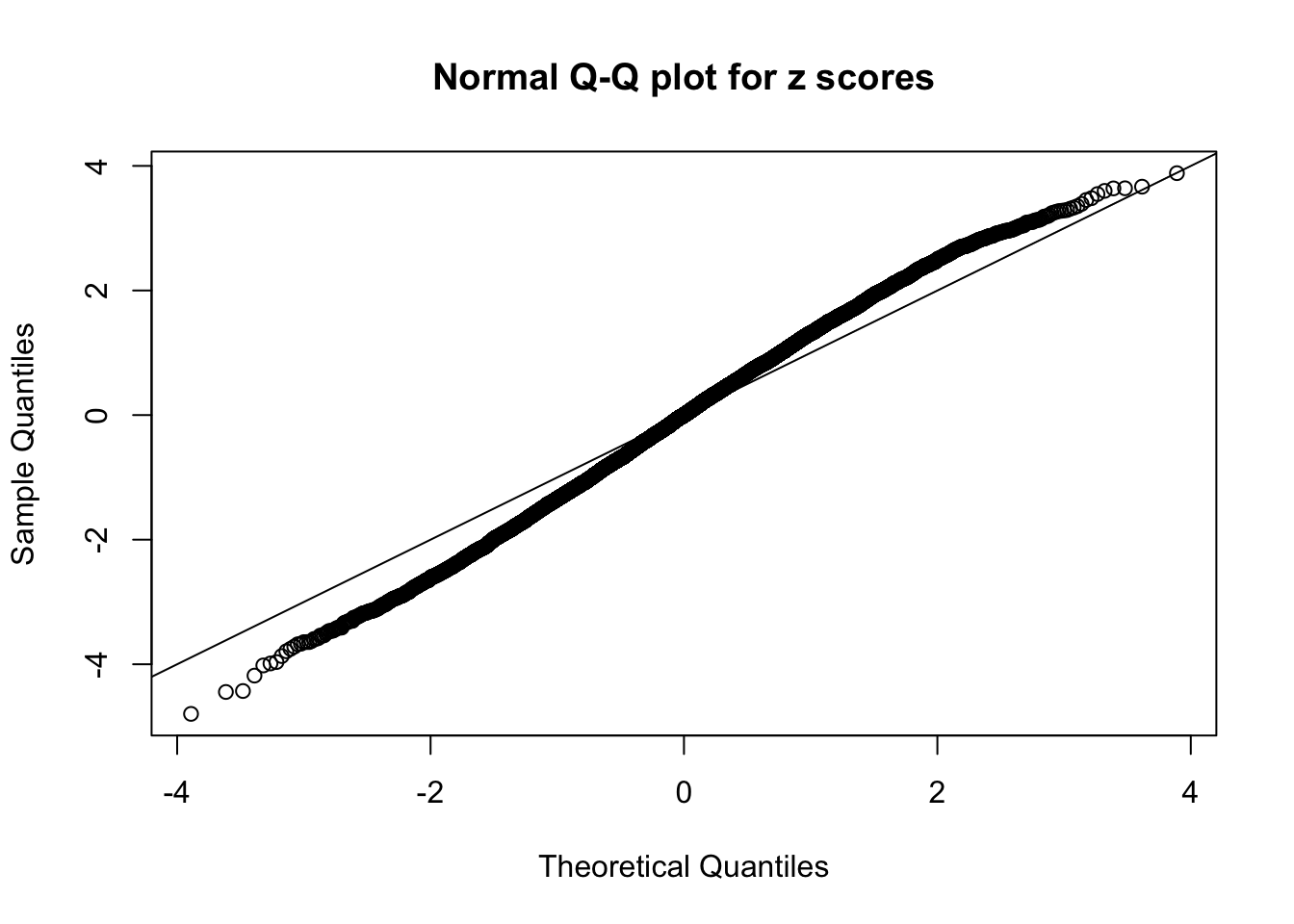
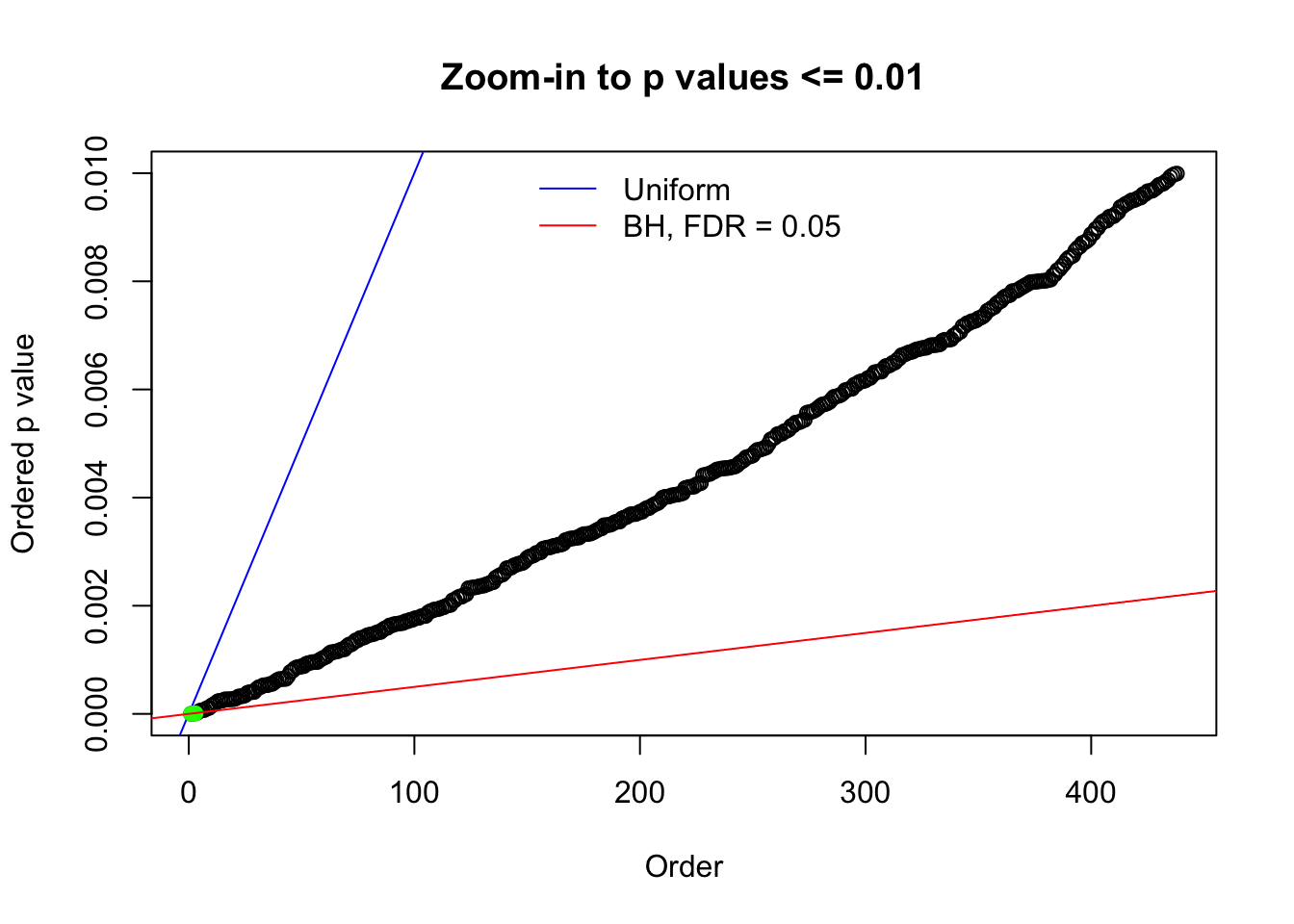
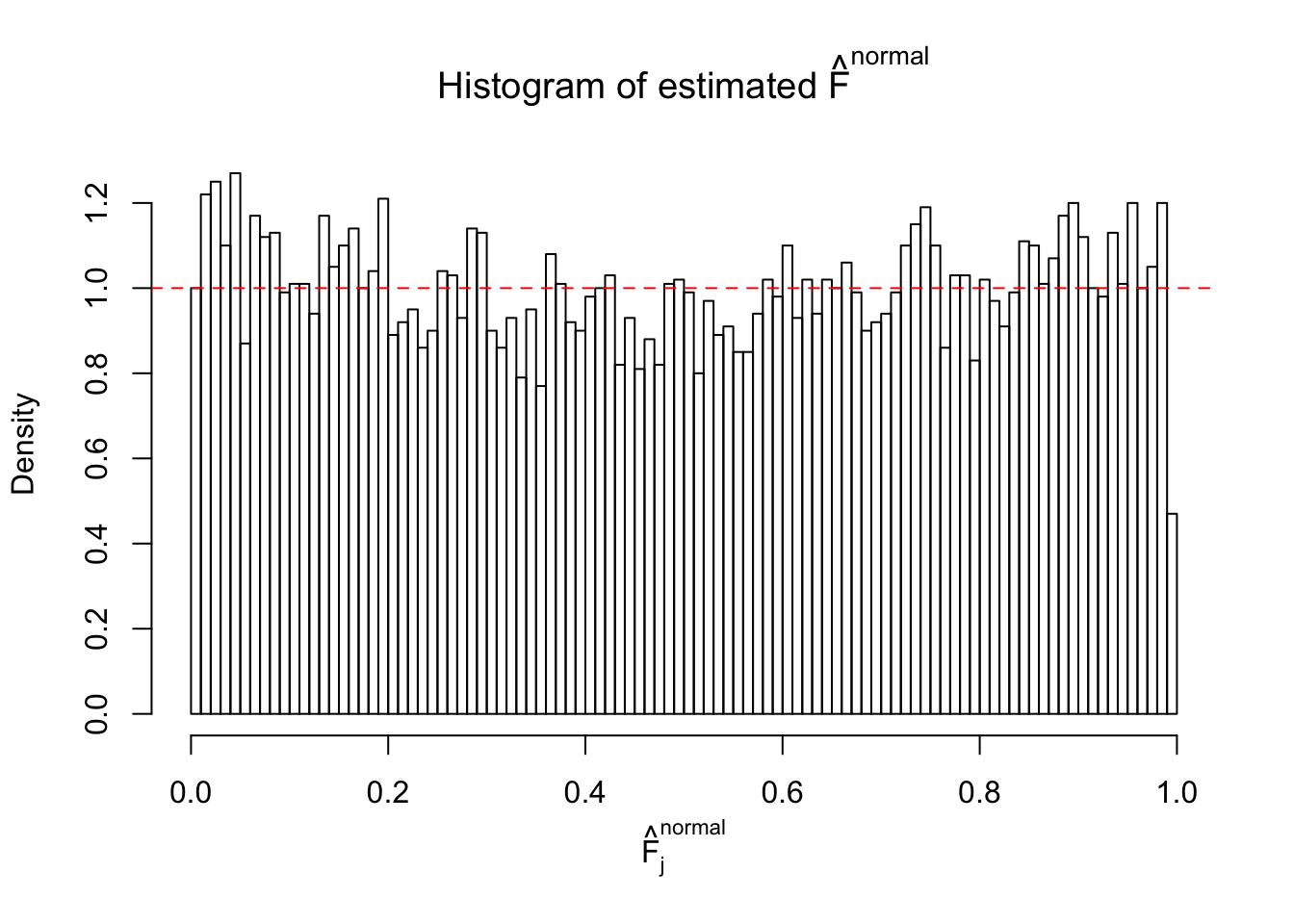
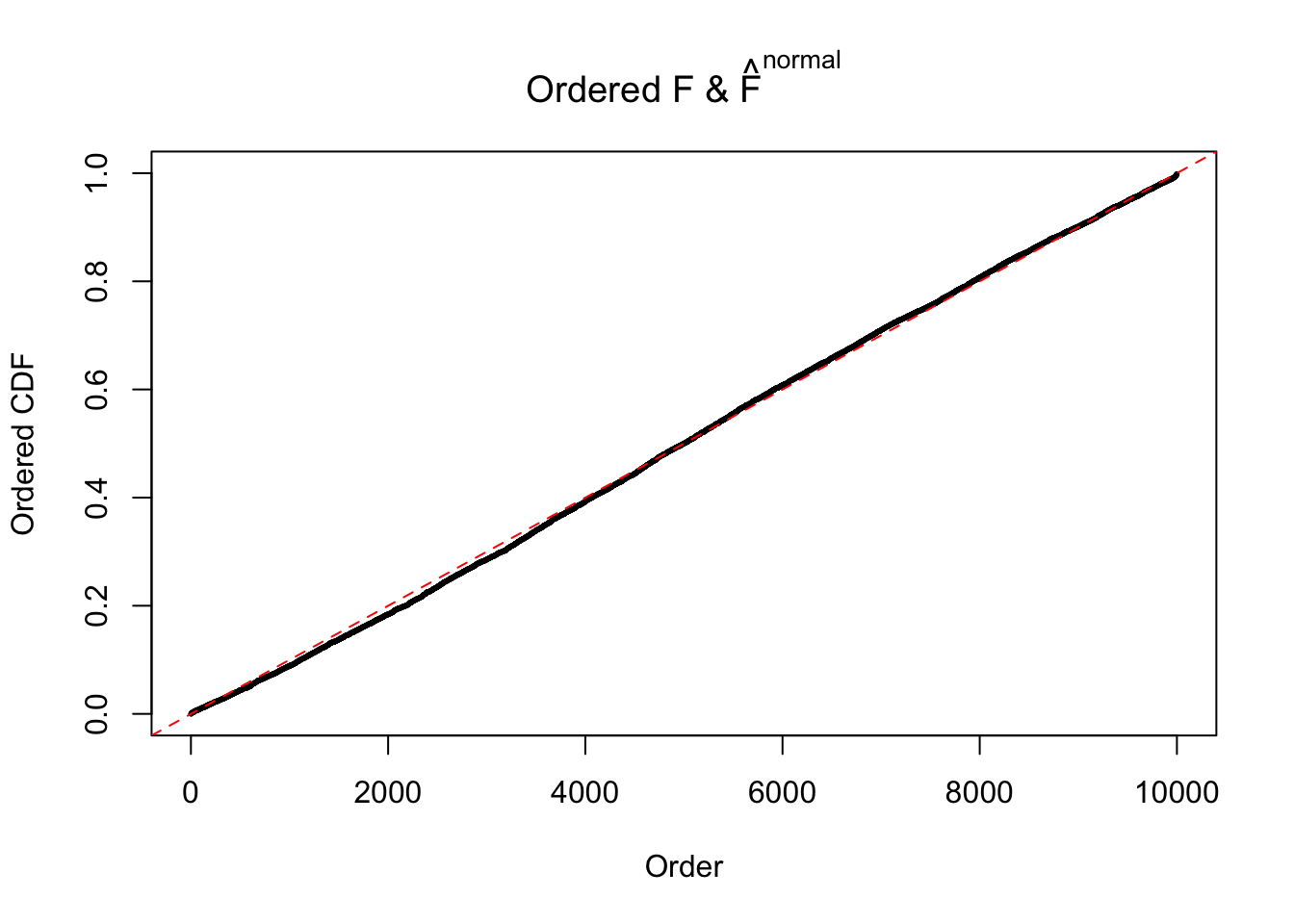
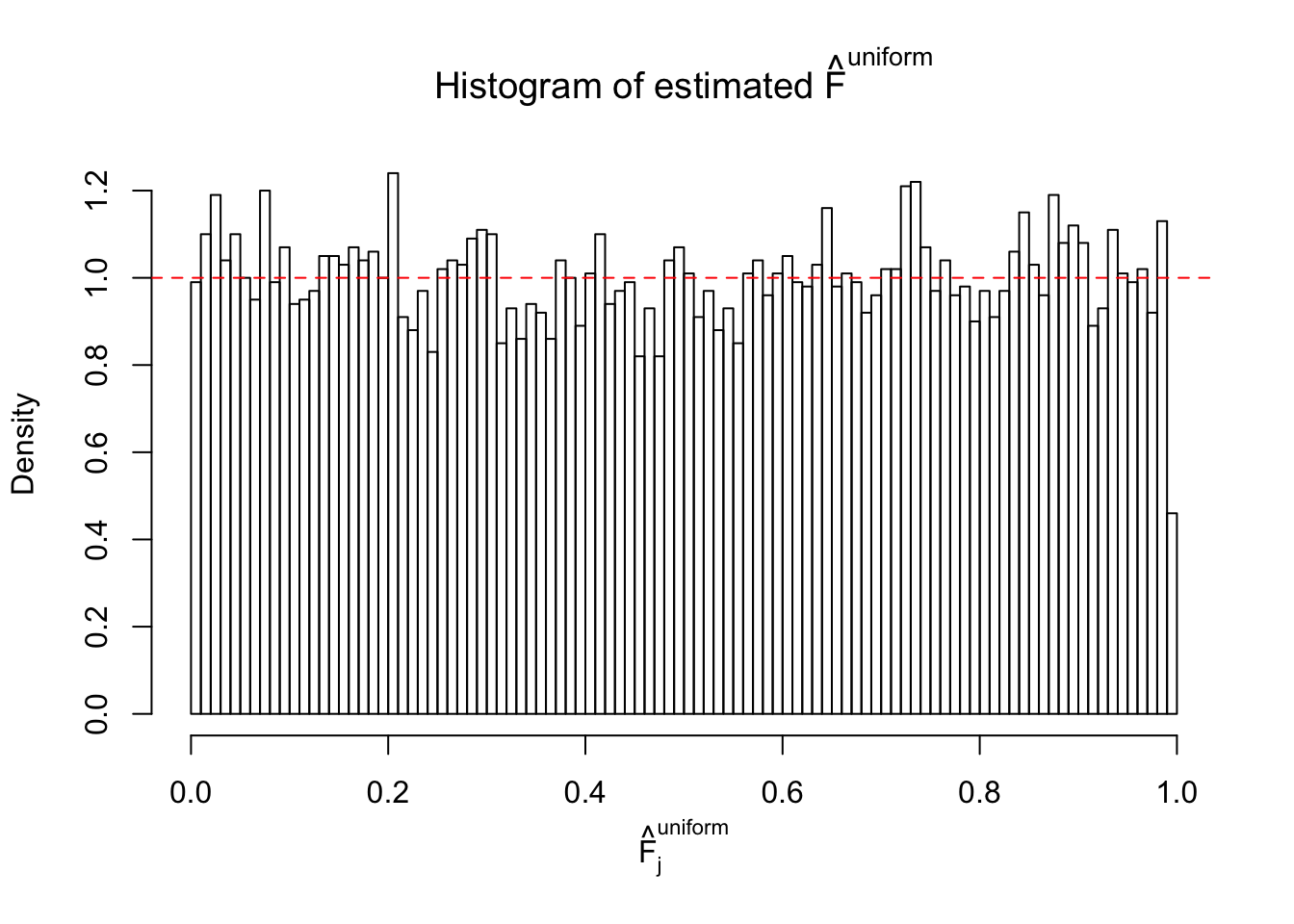
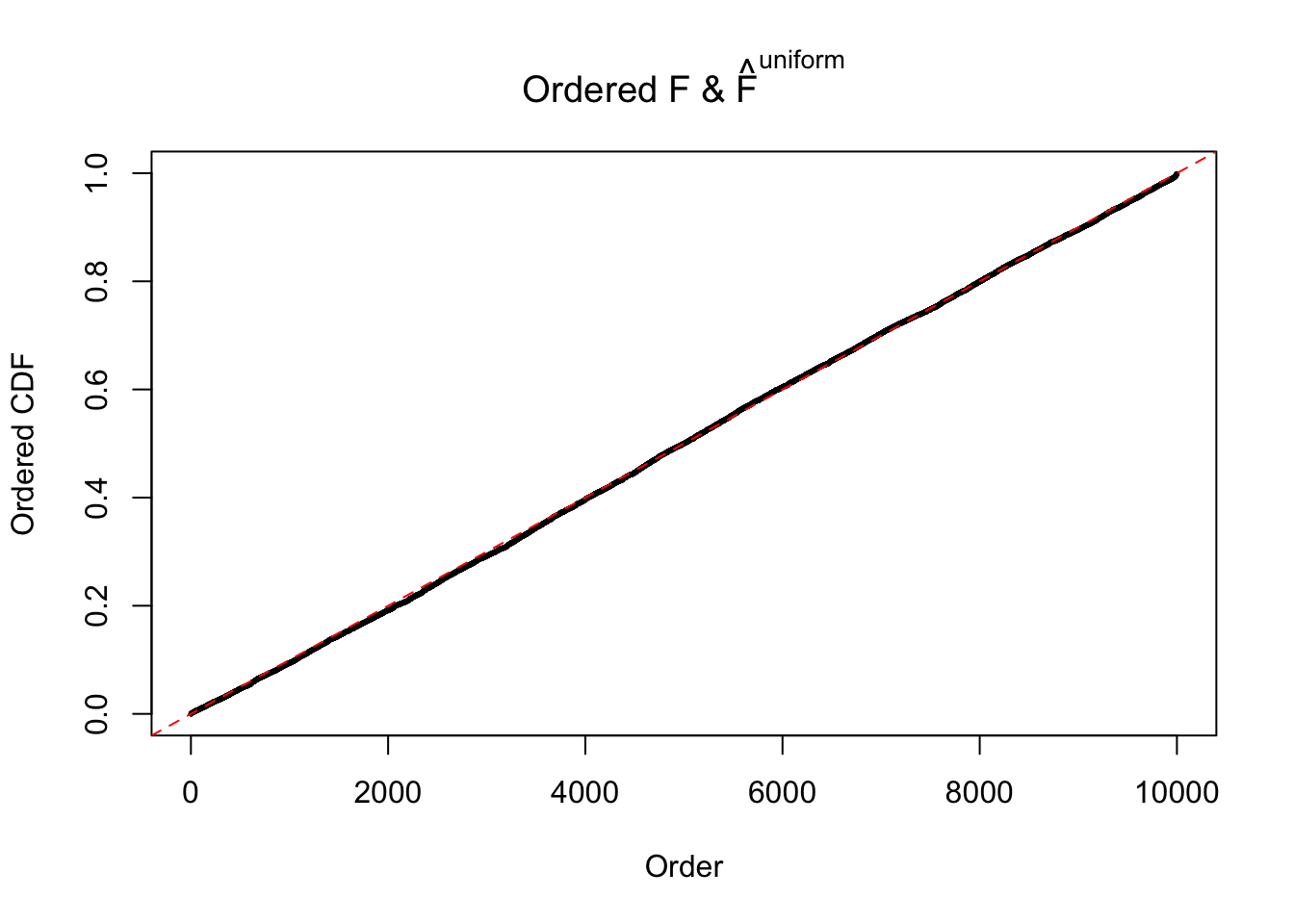
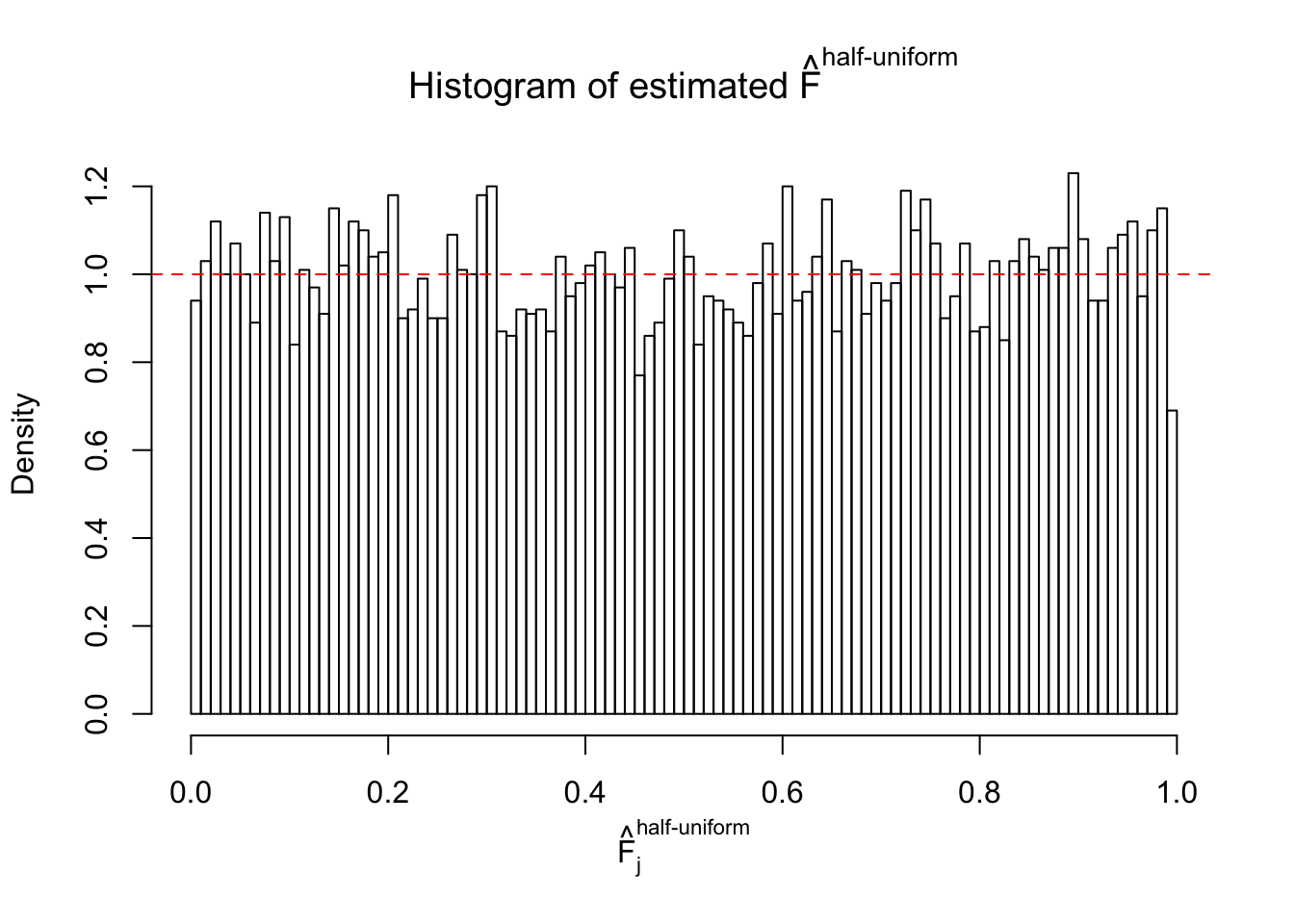
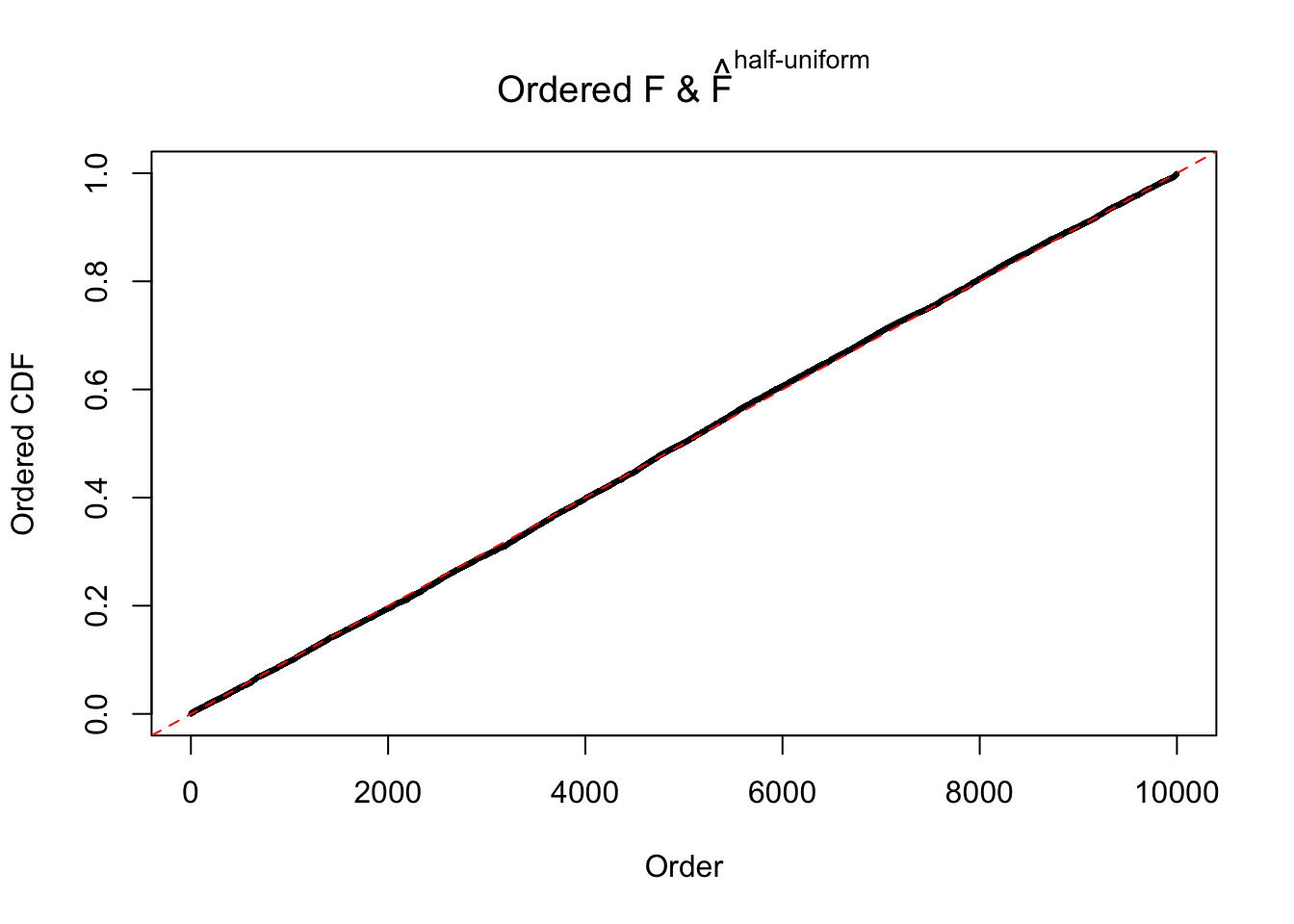
N0. 20 : Data Set 316 ; Number of False Discoveries: 3 ; pihat0 = 0.1078068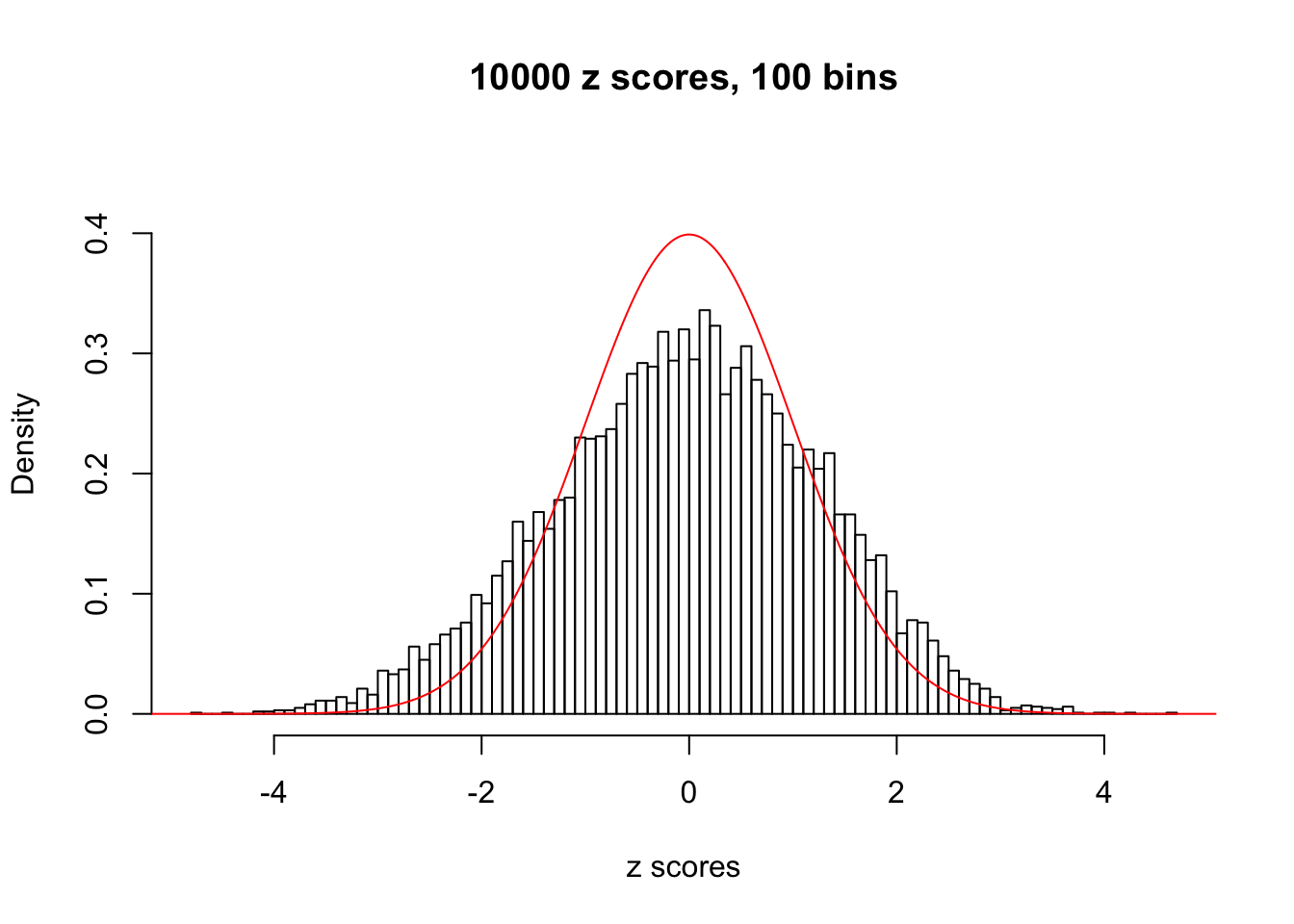
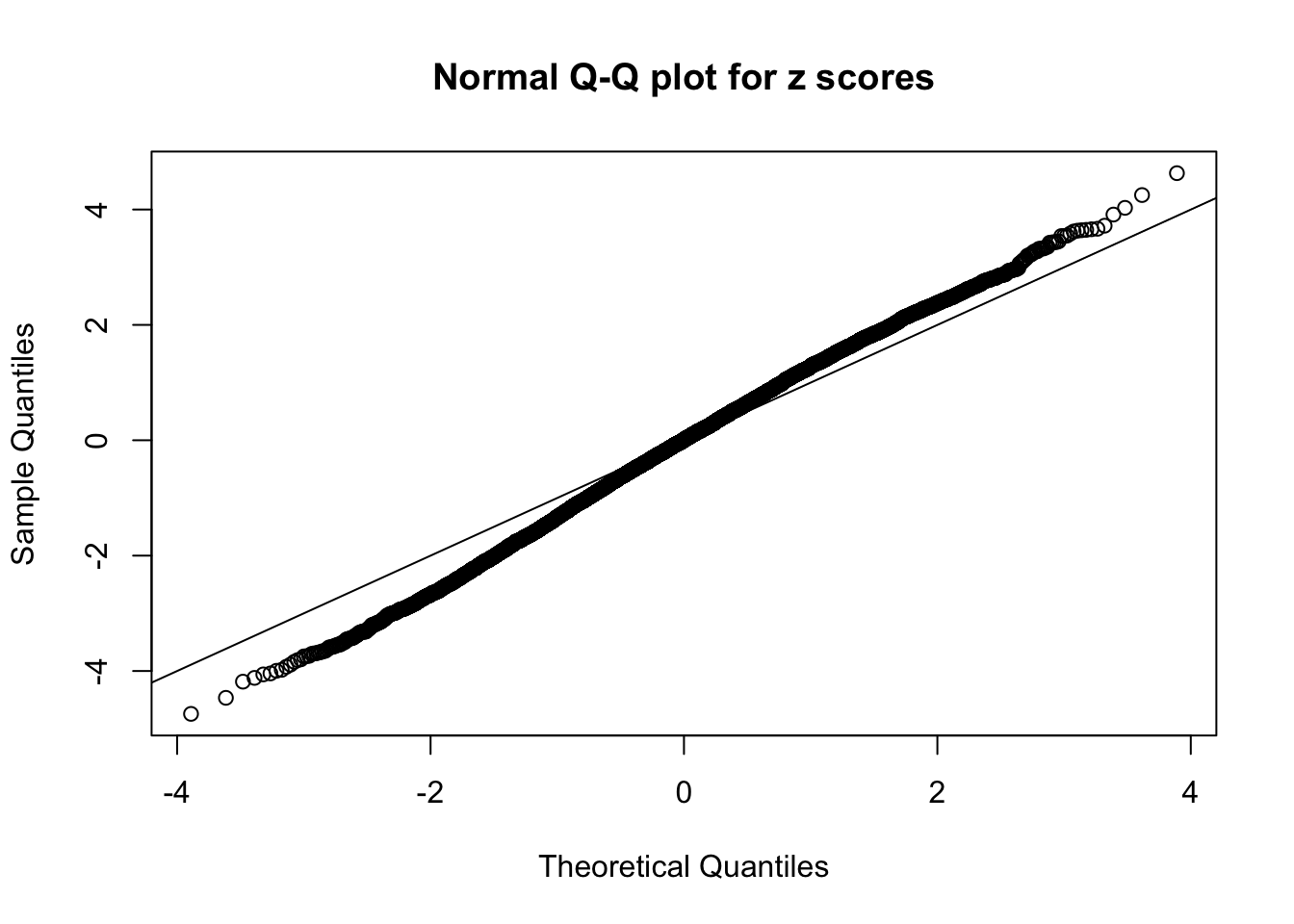
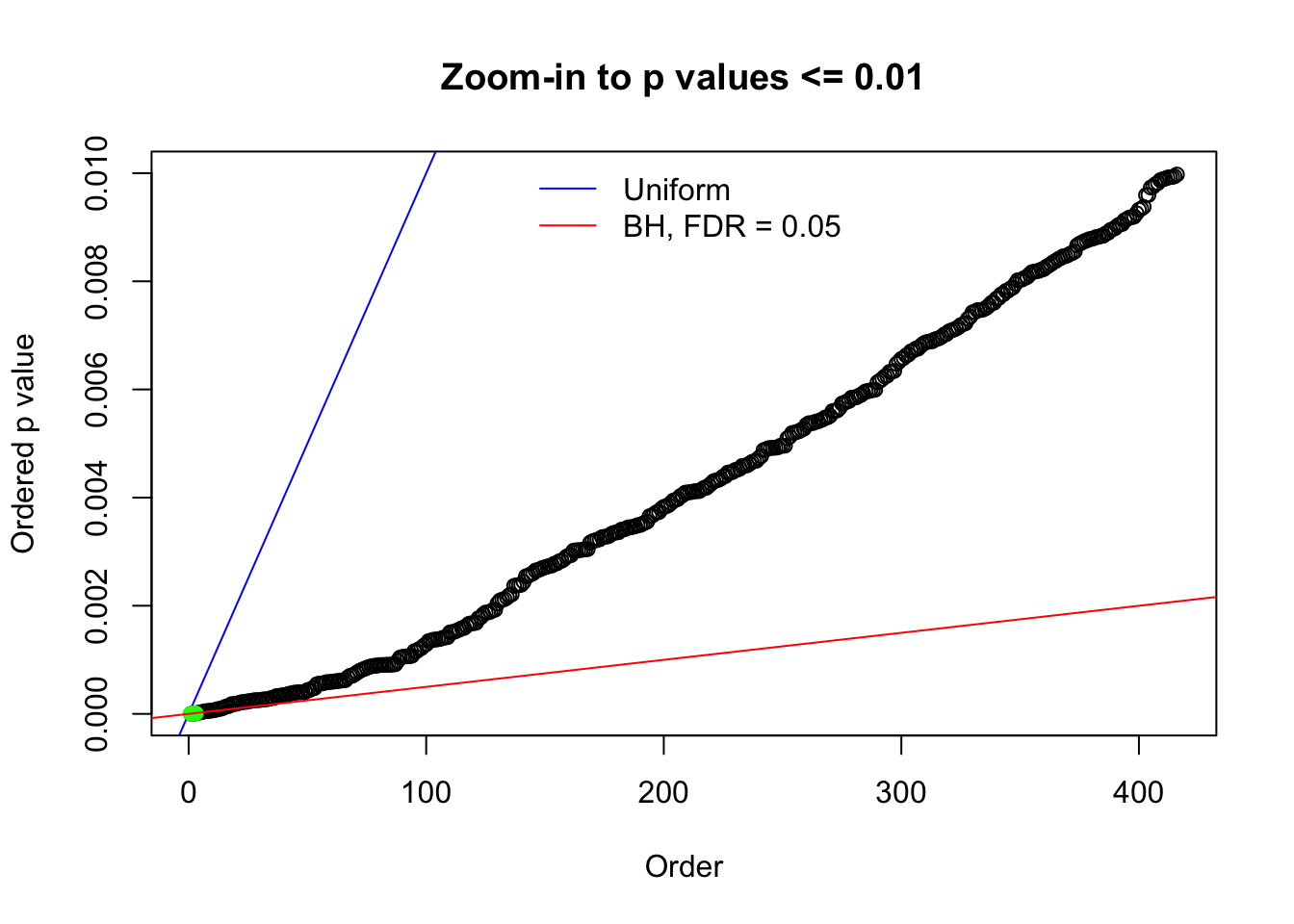
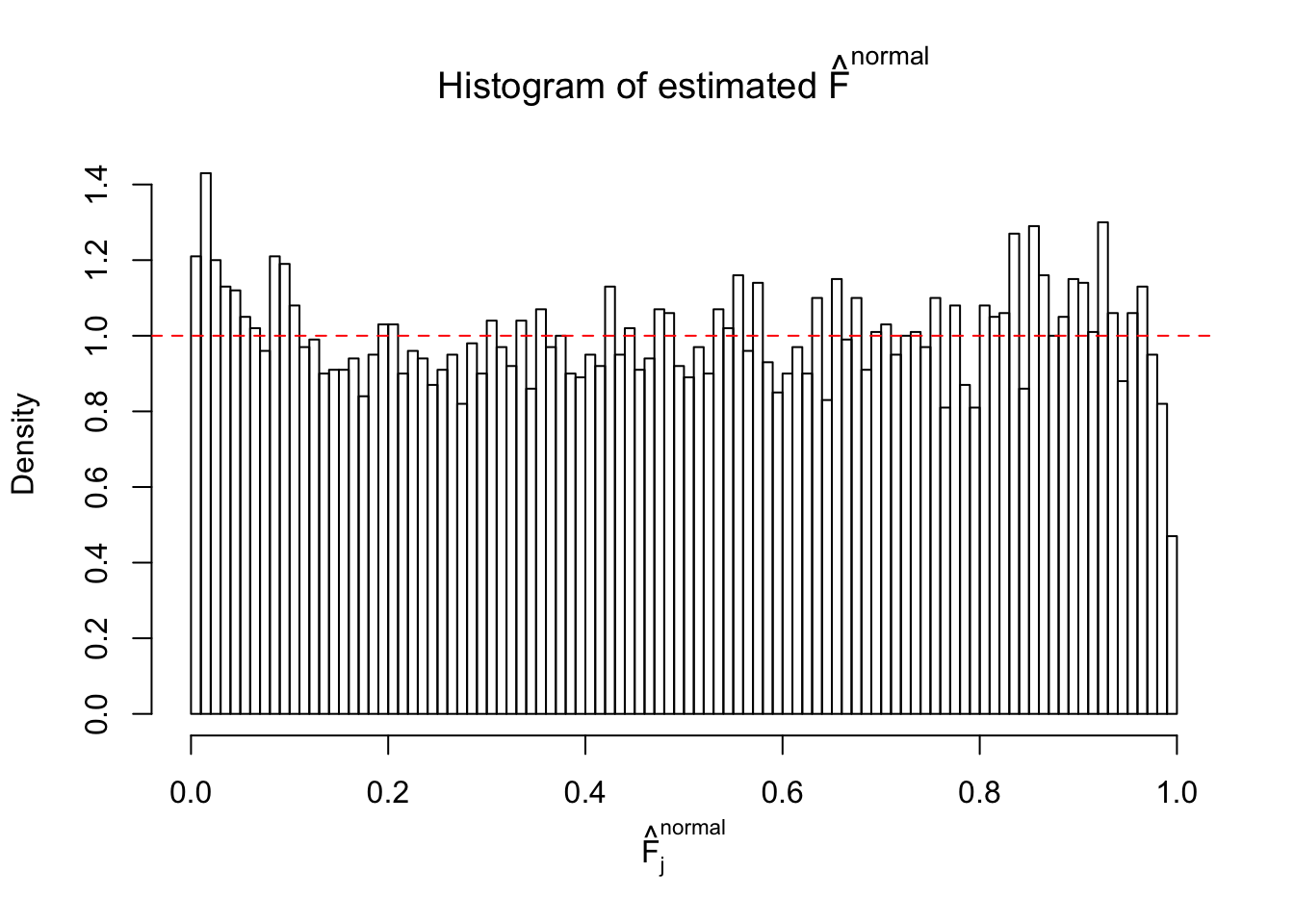
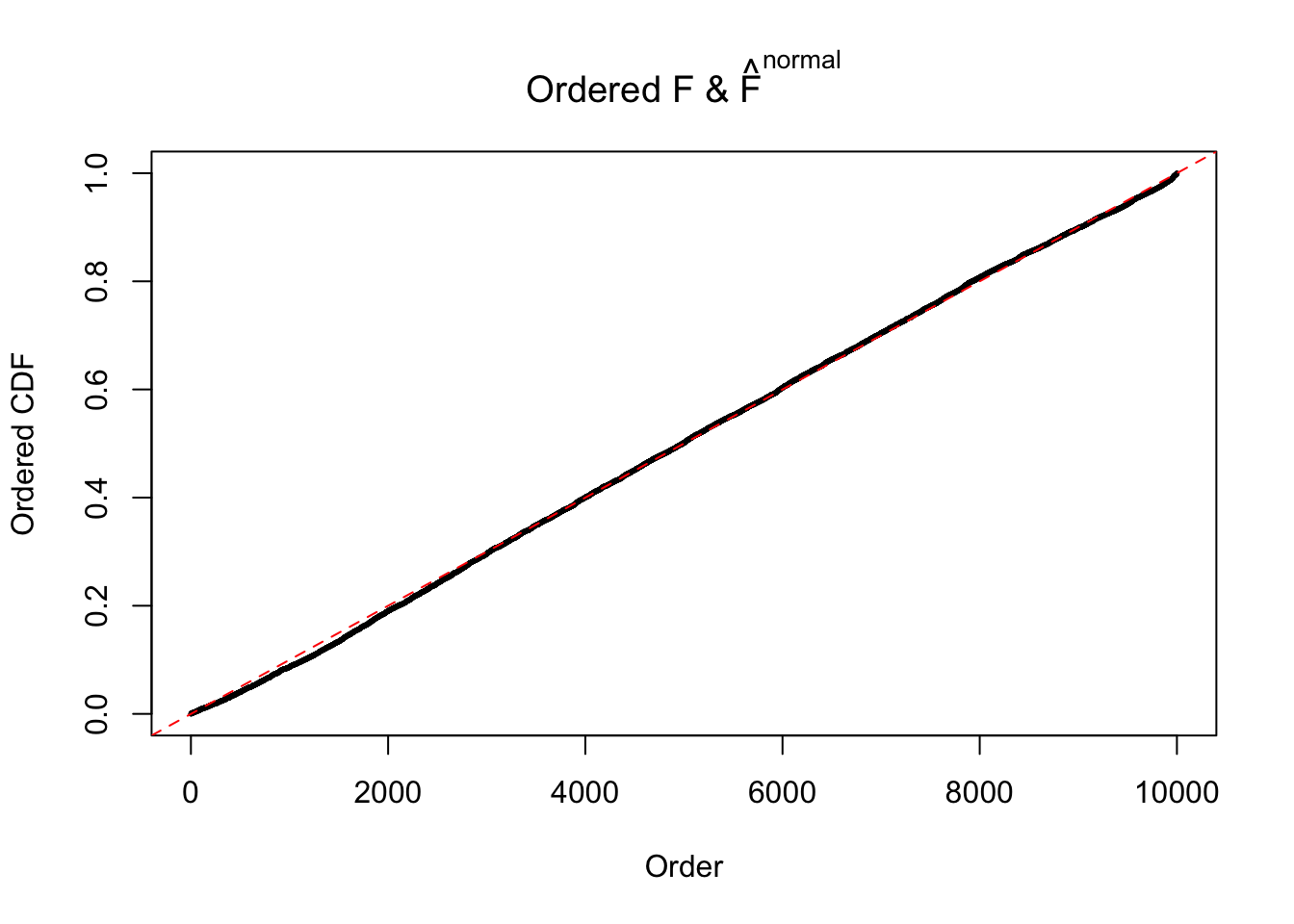
N0. 21 : Data Set 663 ; Number of False Discoveries: 3 ; pihat0 = 0.1696198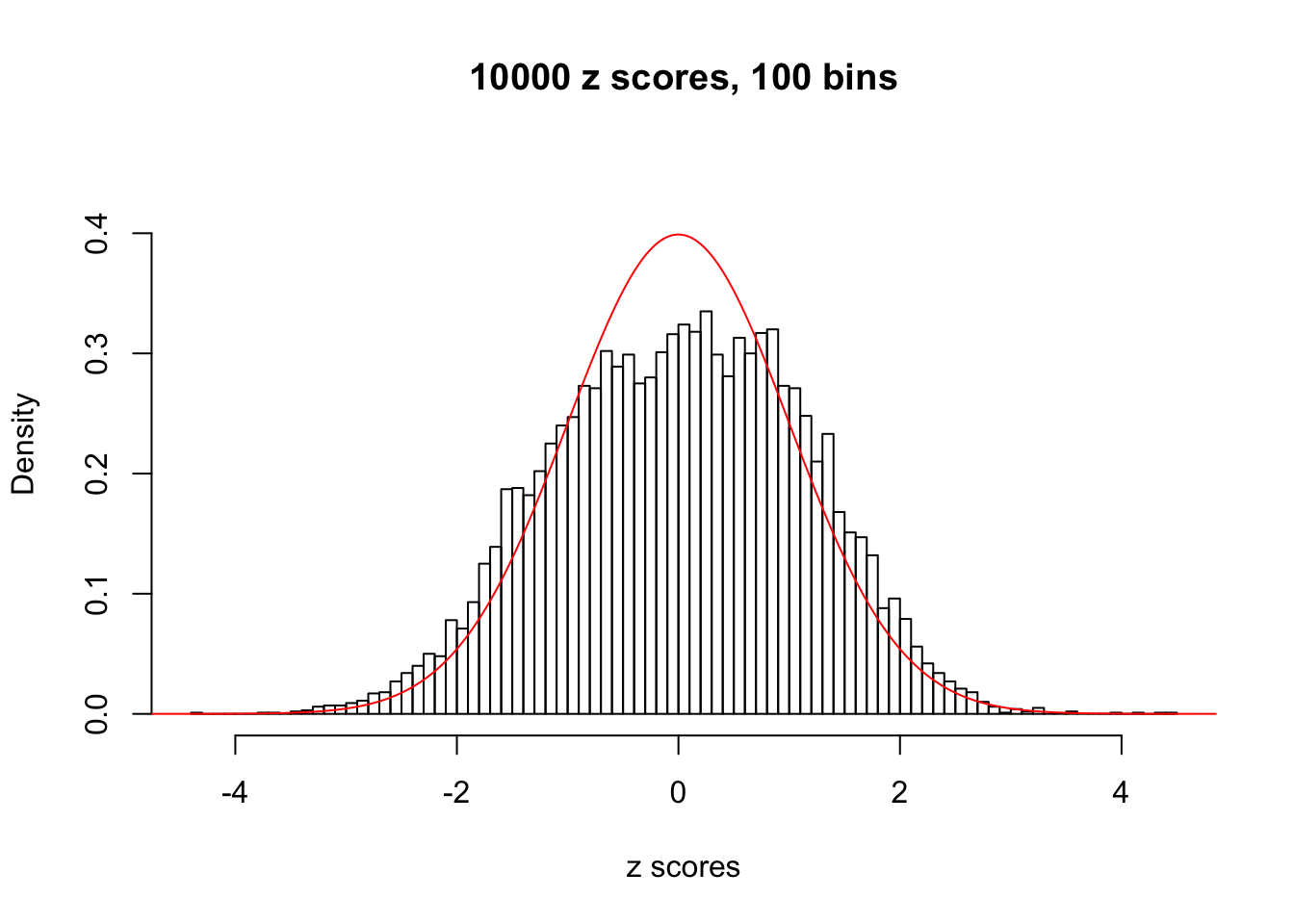
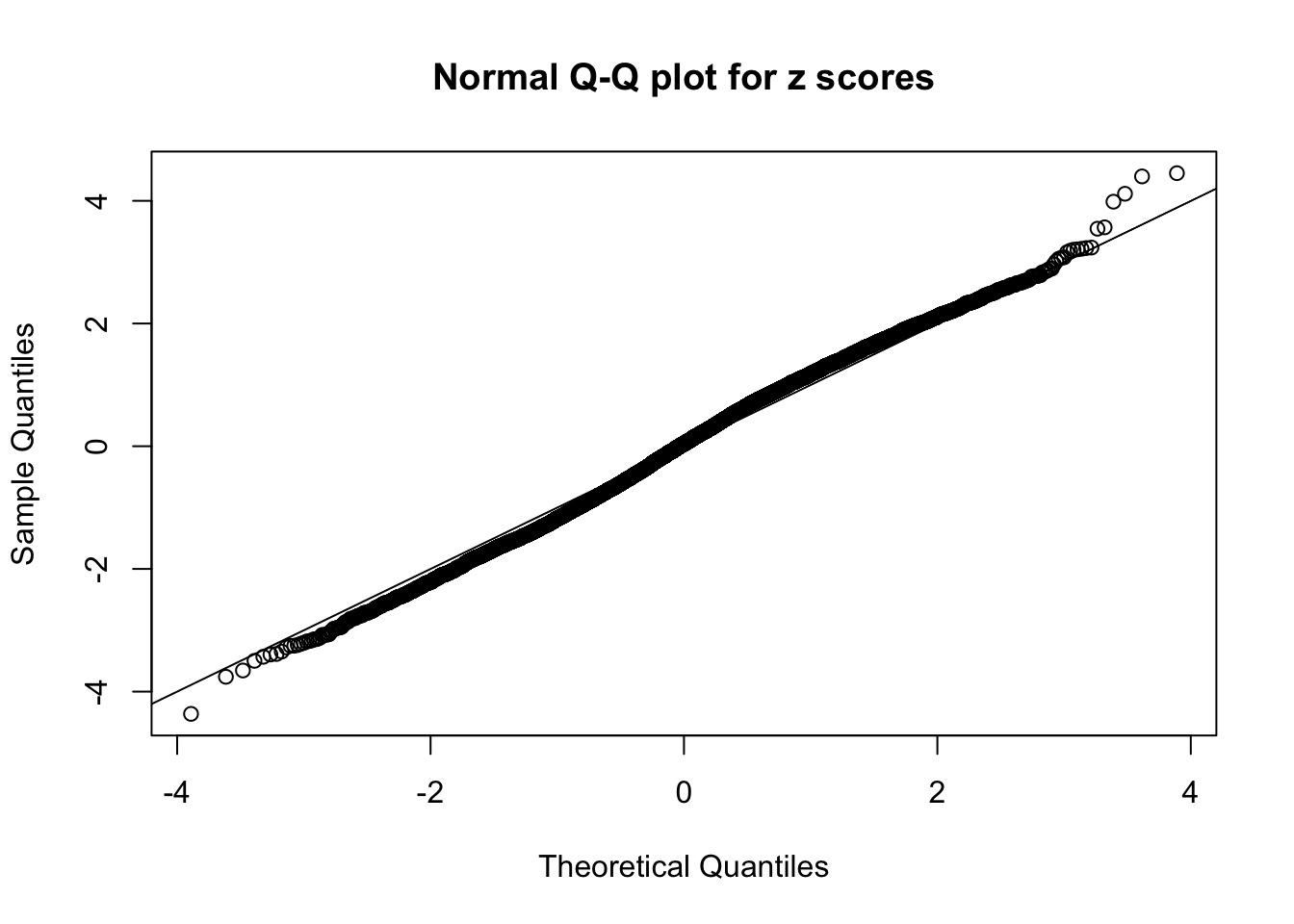
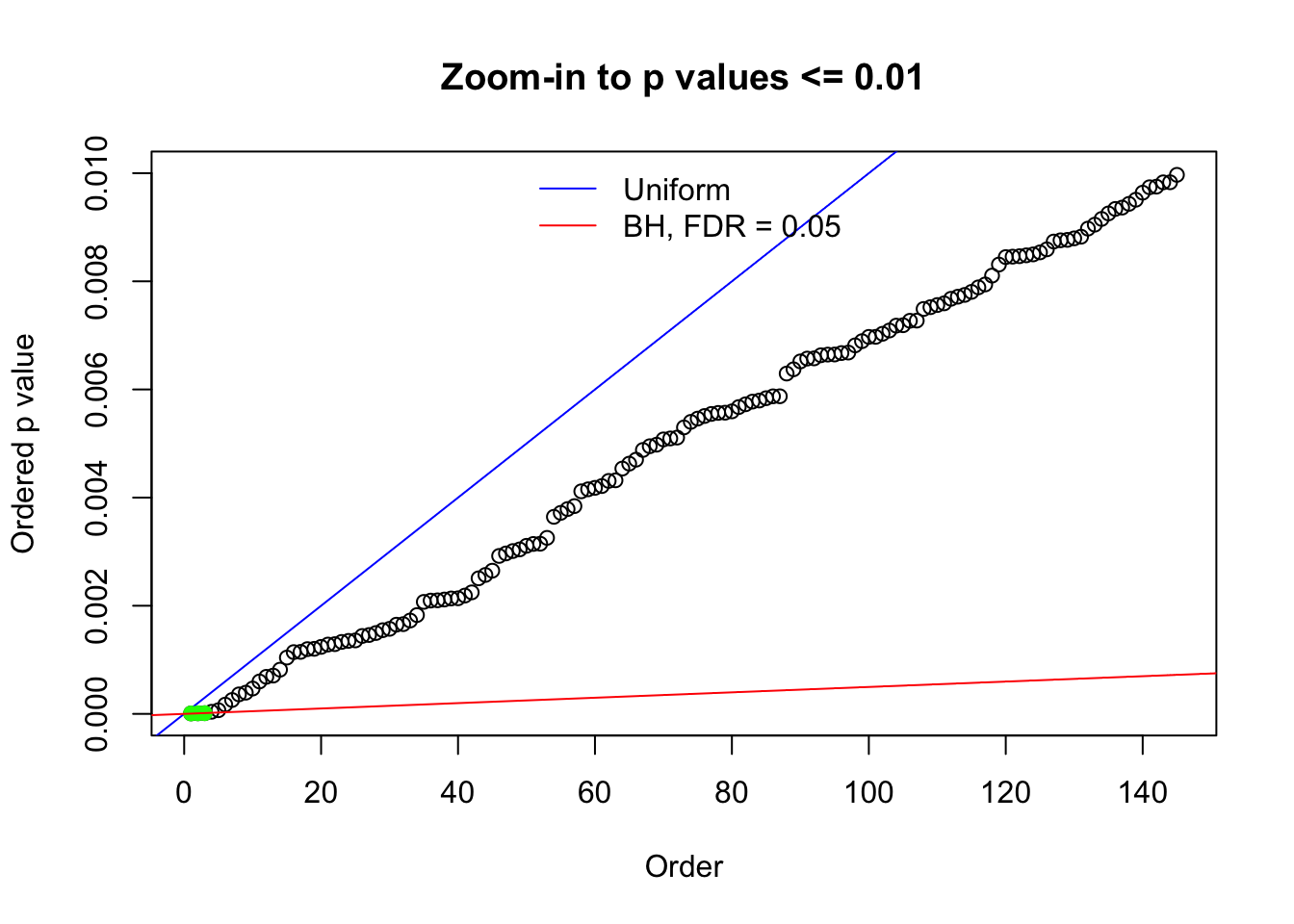
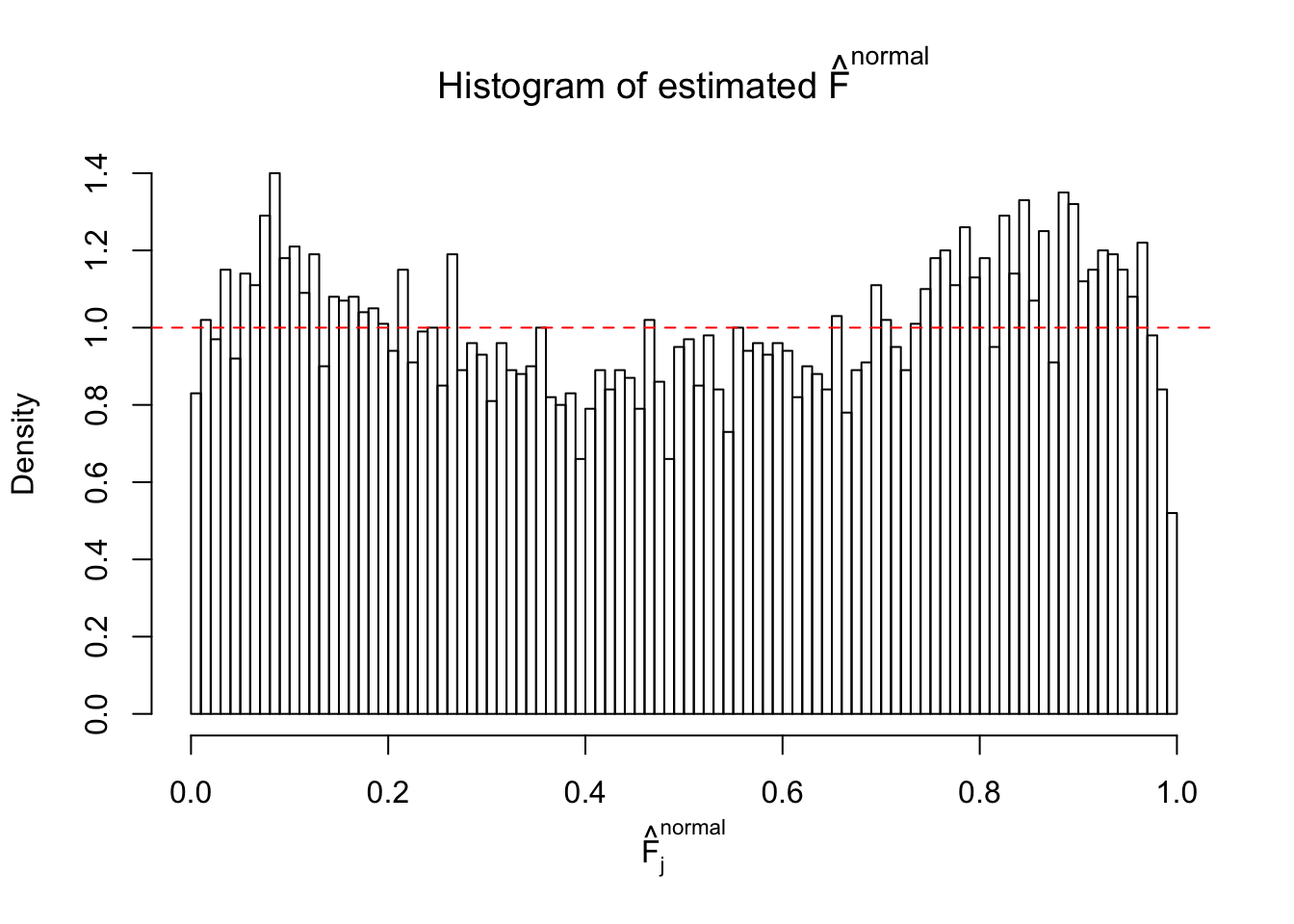
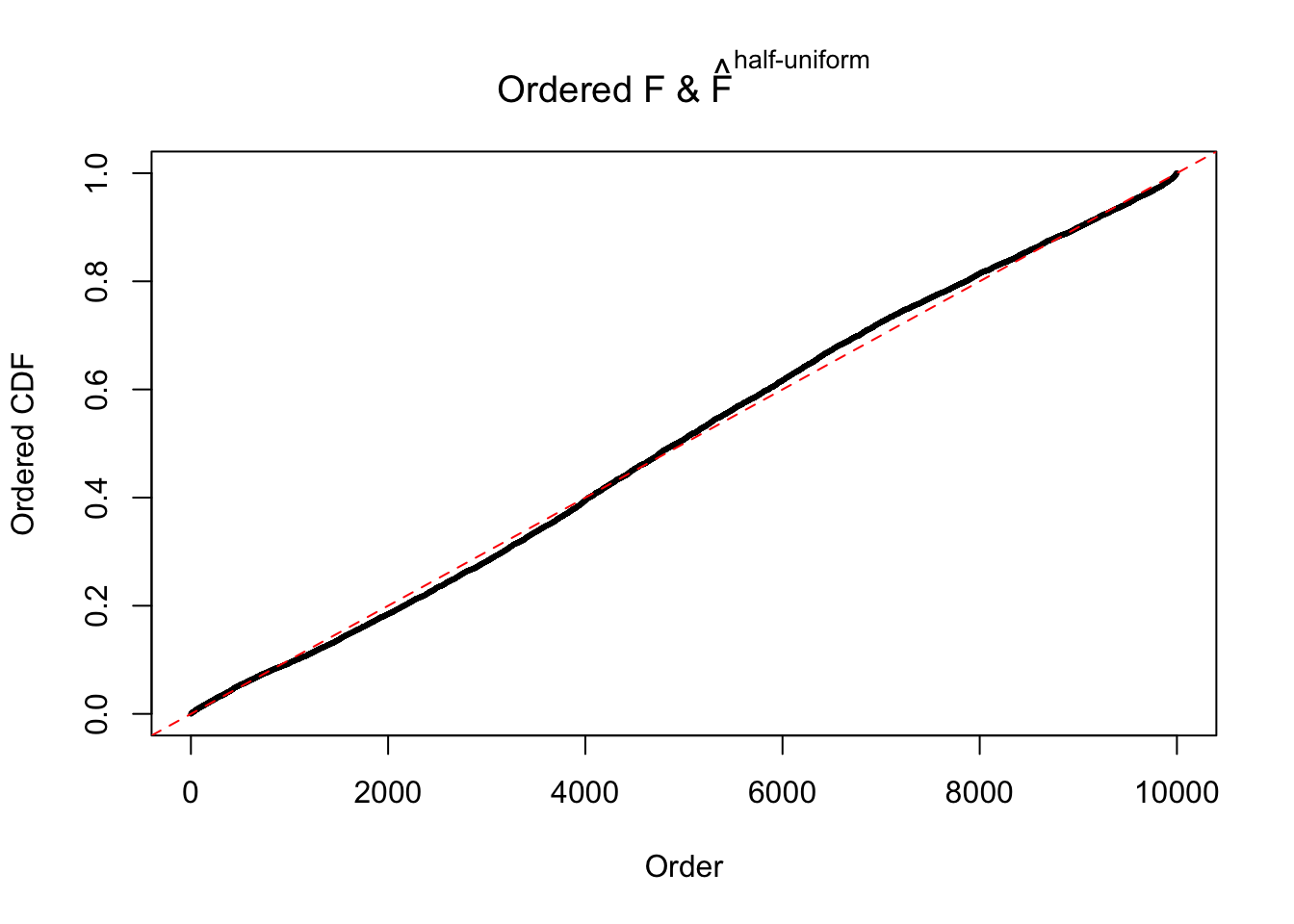
N0. 22 : Data Set 274 ; Number of False Discoveries: 2 ; pihat0 = 0.08298182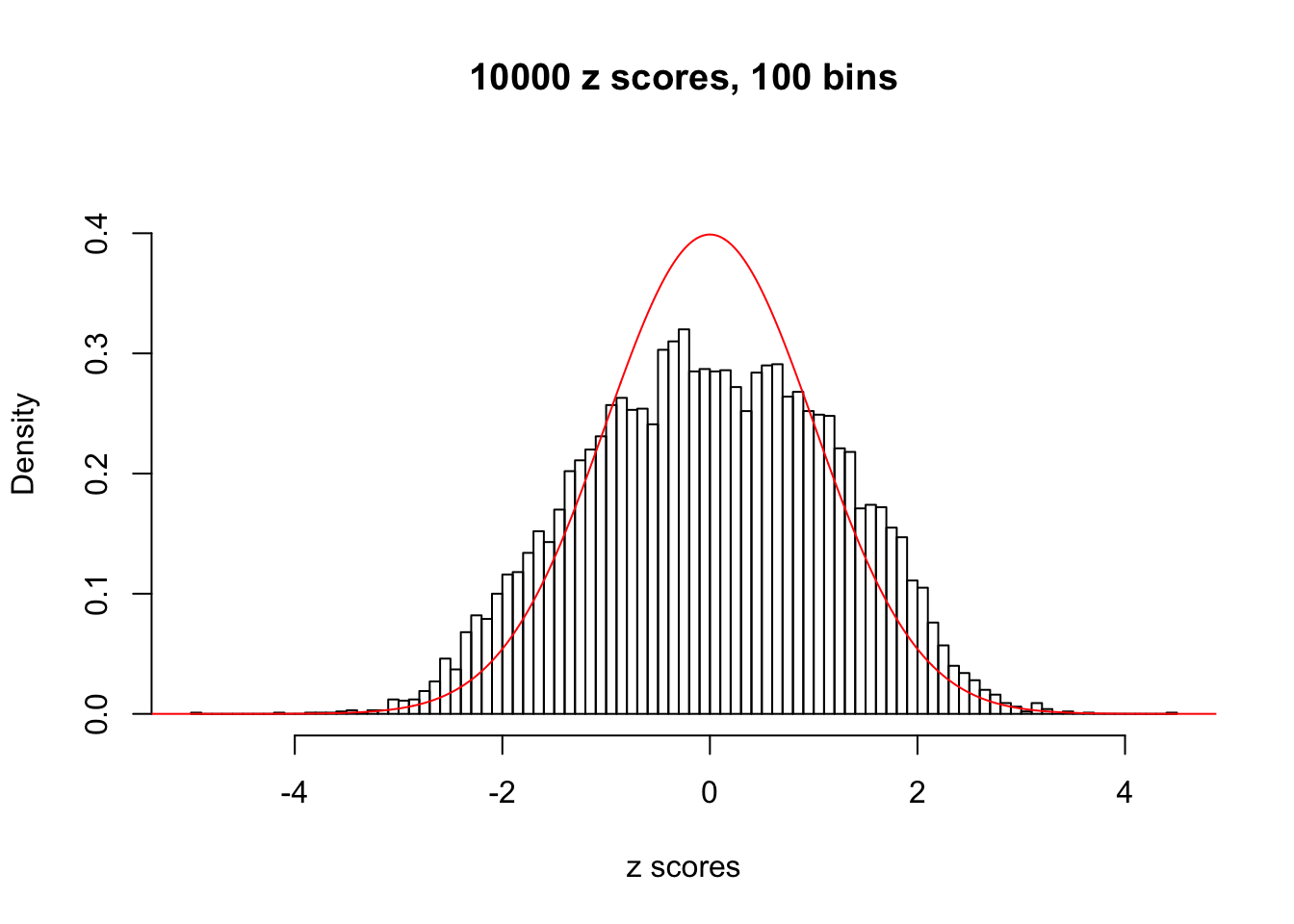
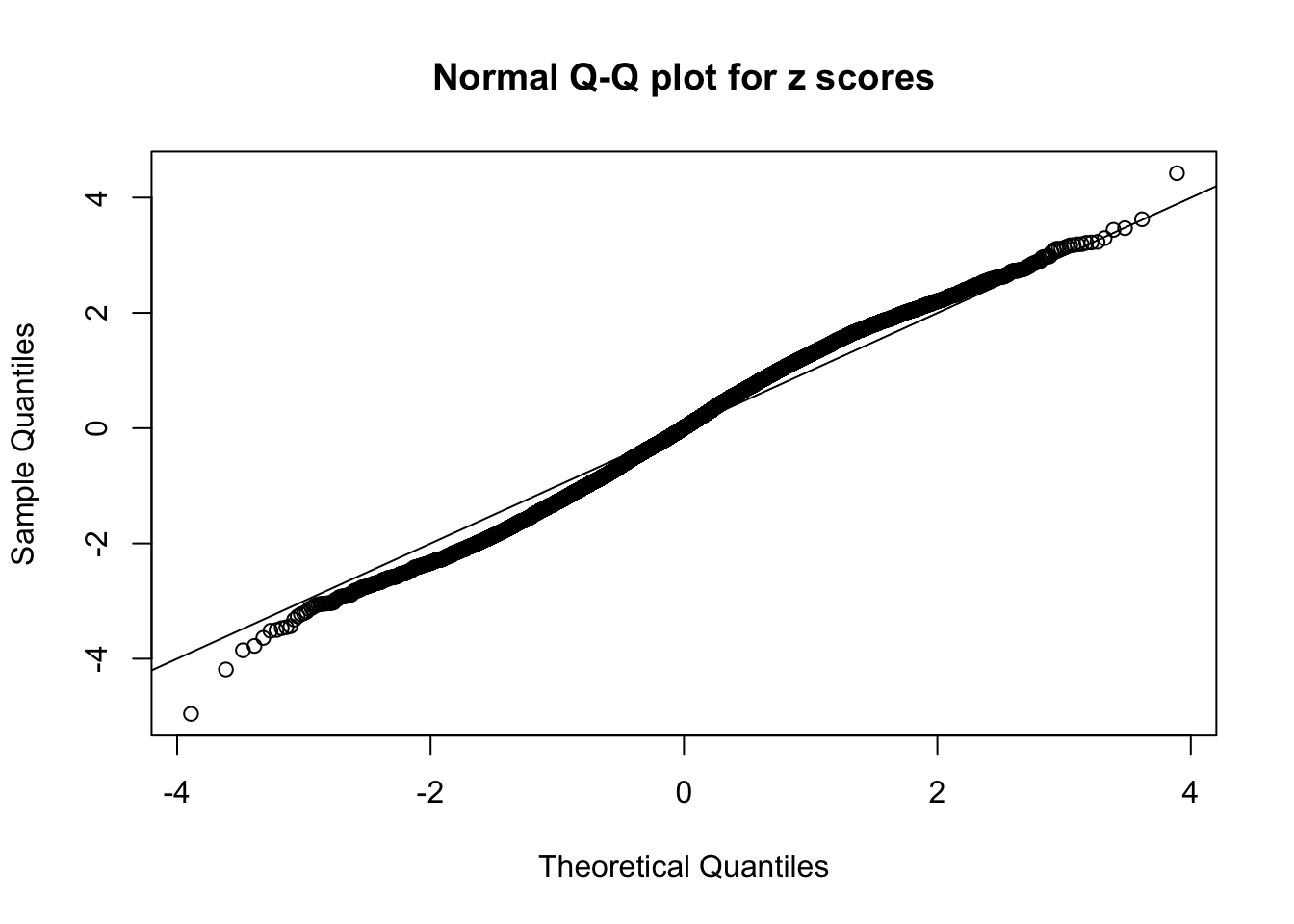
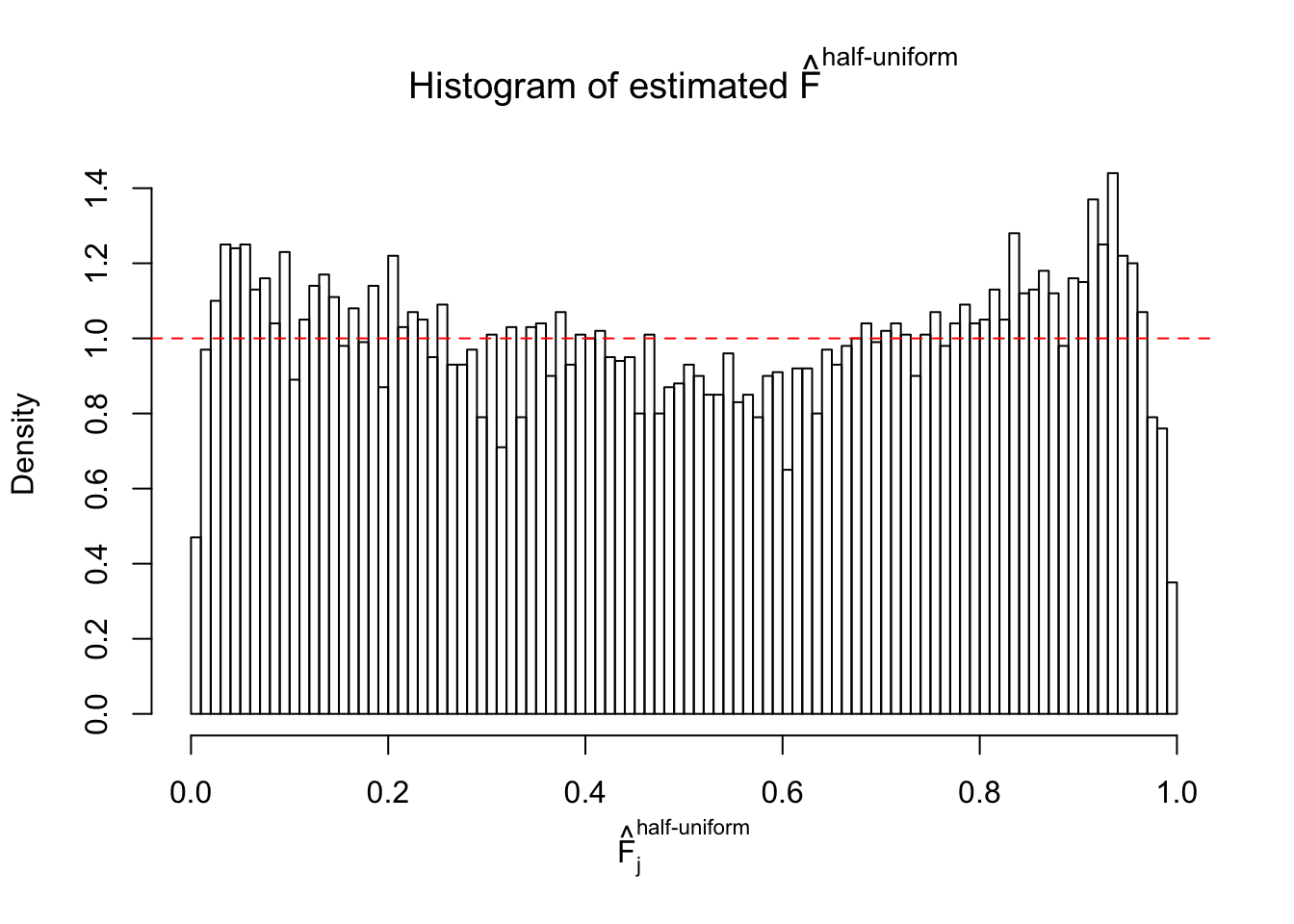
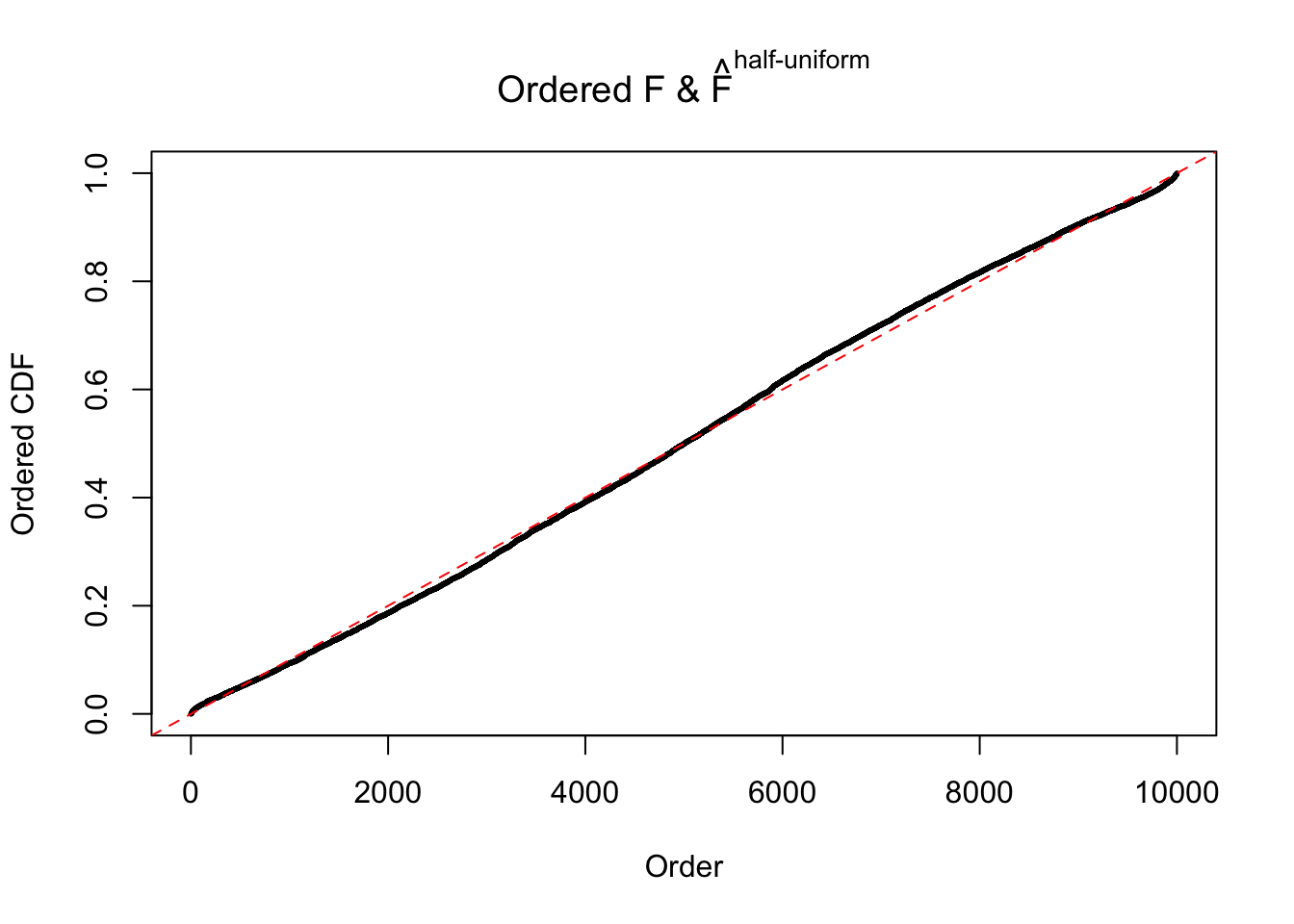
N0. 23 : Data Set 901 ; Number of False Discoveries: 2 ; pihat0 = 0.9997685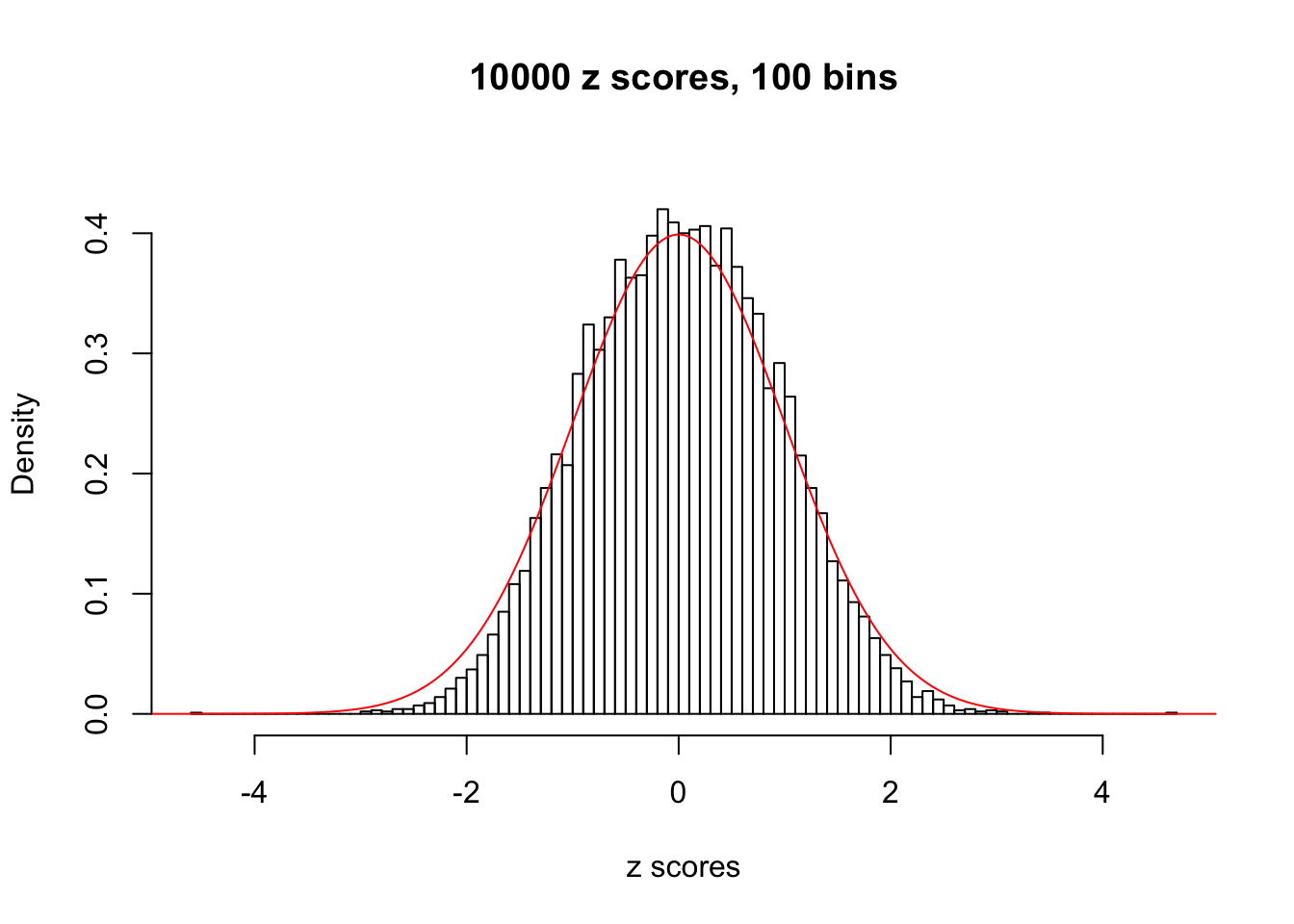
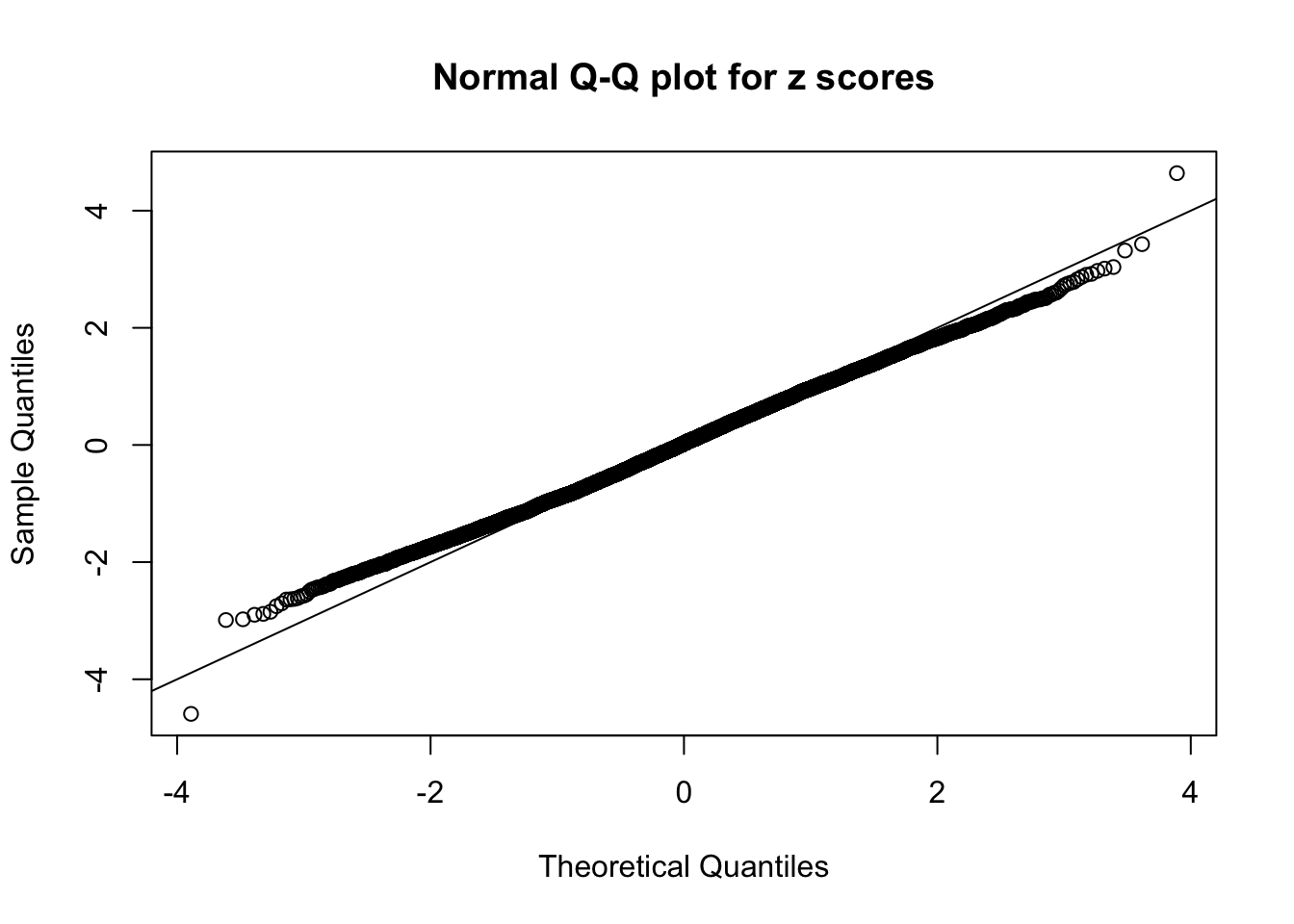
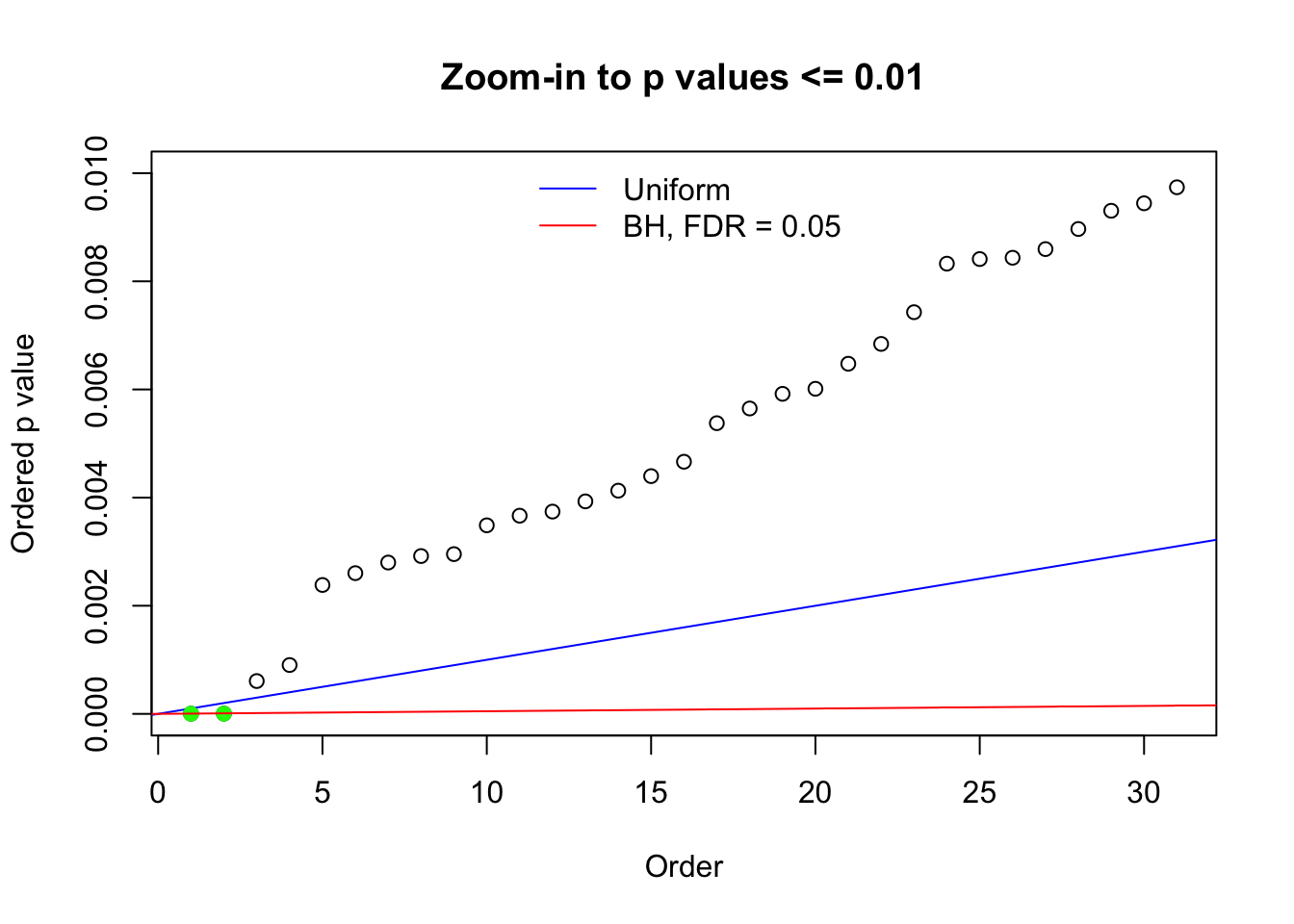
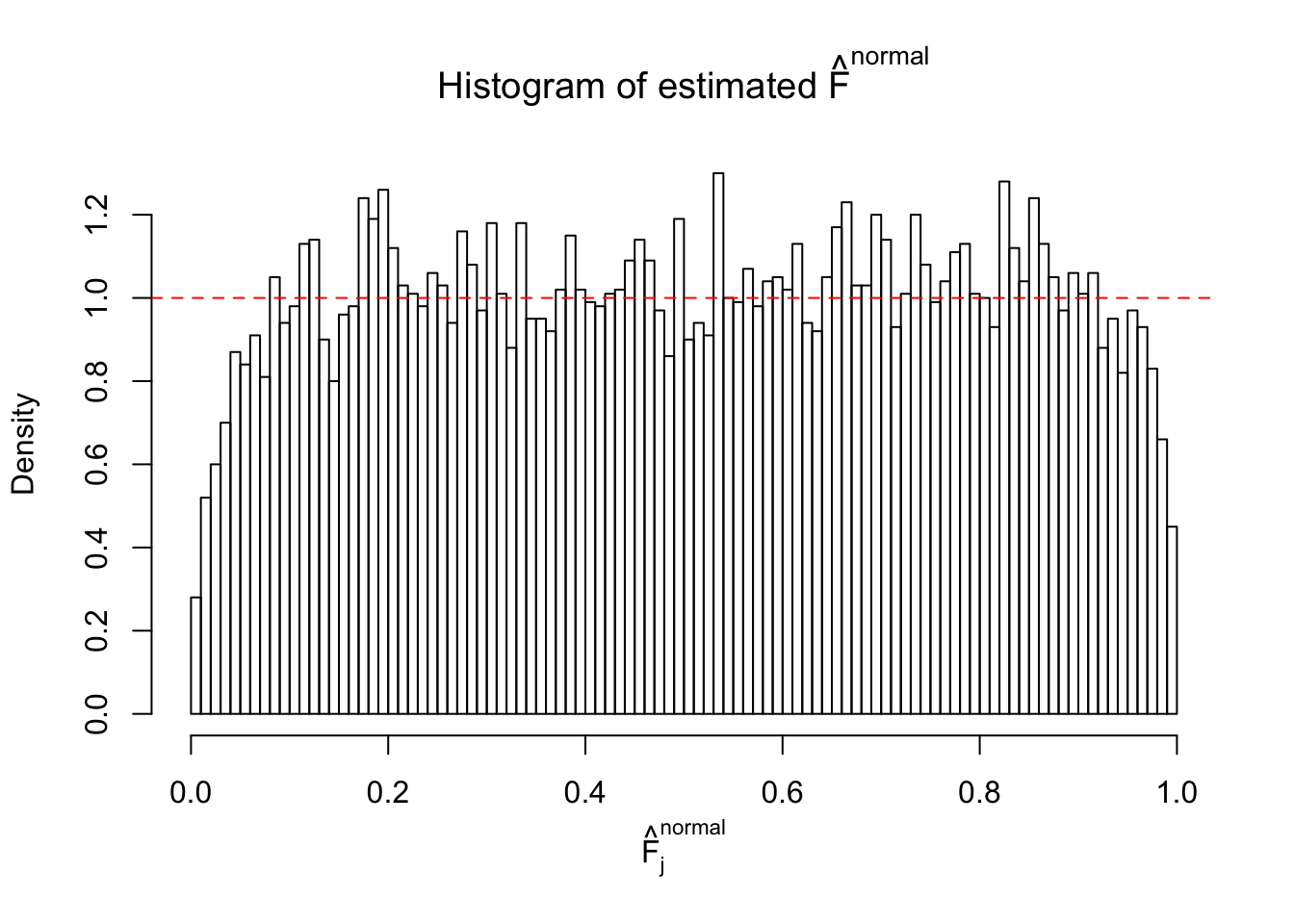
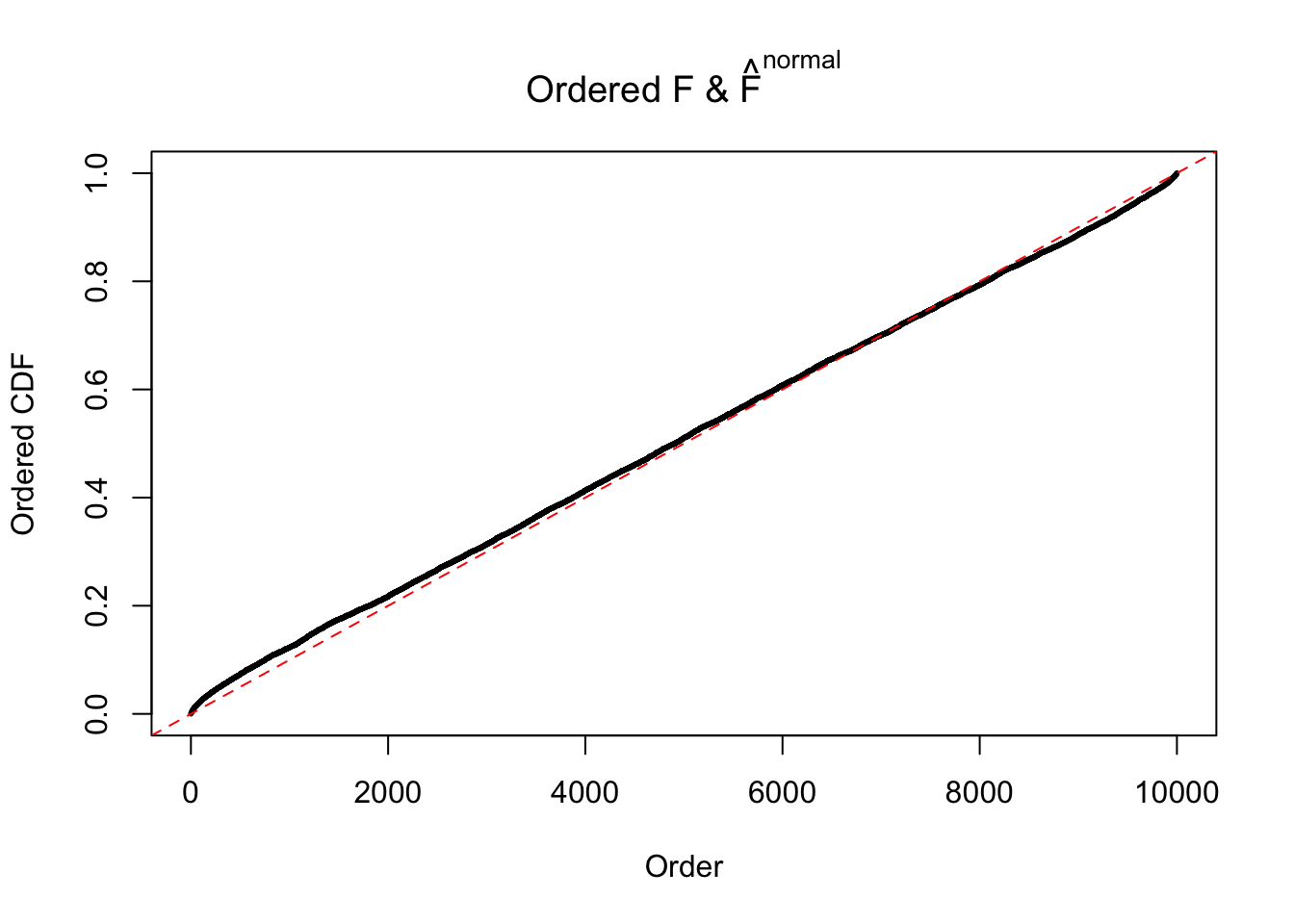
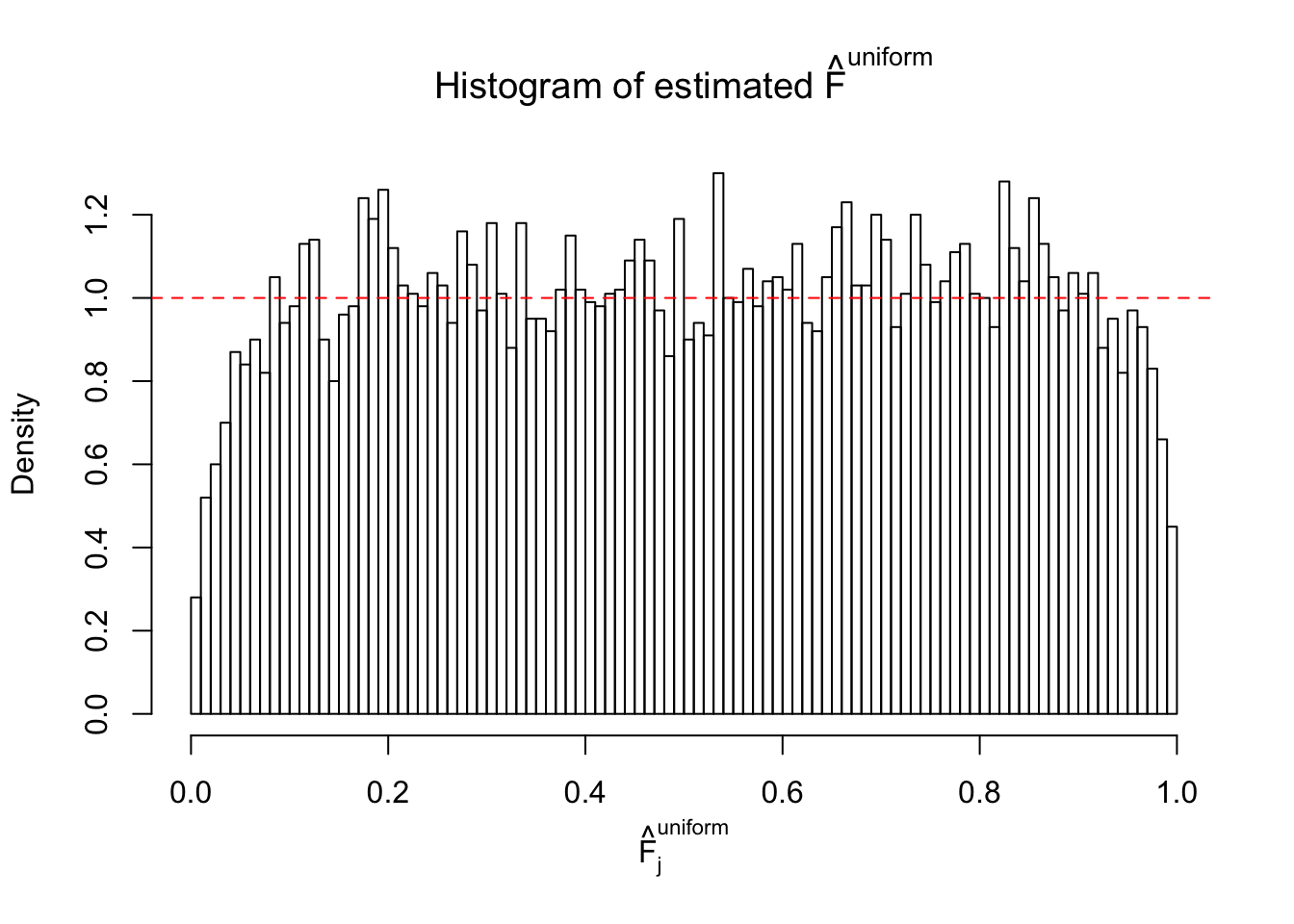
N0. 24 : Data Set 912 ; Number of False Discoveries: 2 ; pihat0 = 0.08821883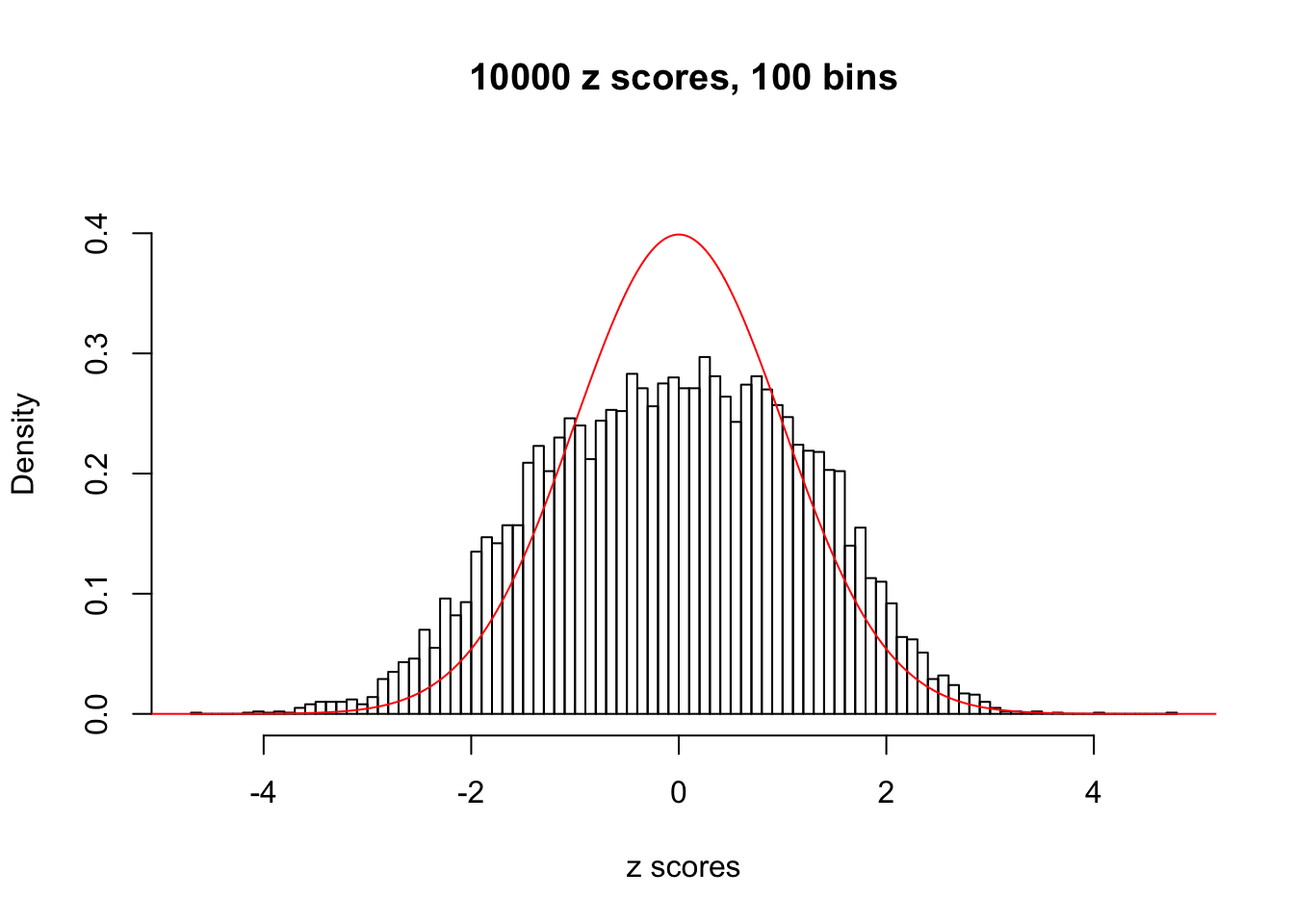
N0. 25 : Data Set 22 ; Number of False Discoveries: 1 ; pihat0 = 0.0328122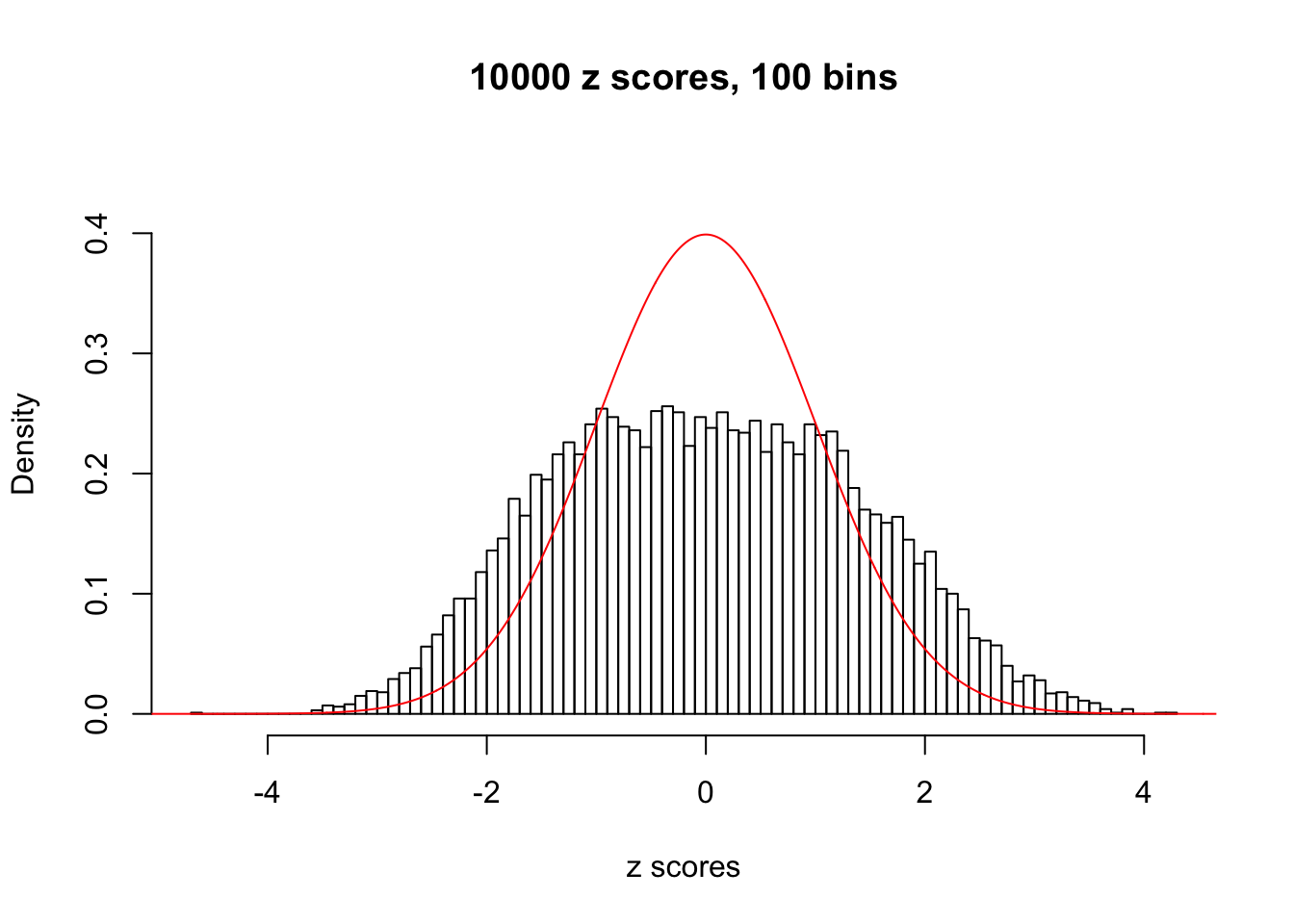
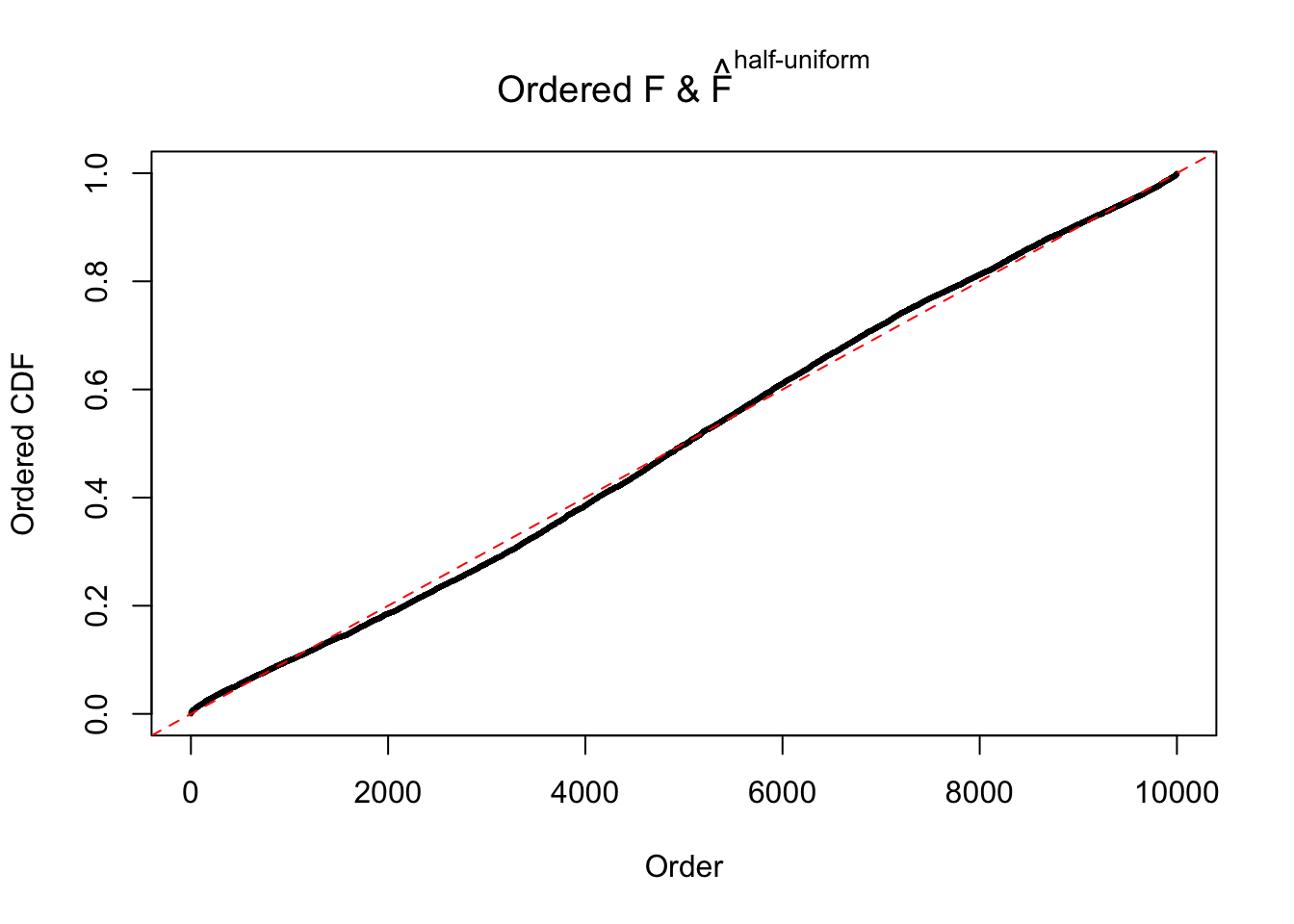
N0. 26 : Data Set 31 ; Number of False Discoveries: 1 ; pihat0 = 0.09577454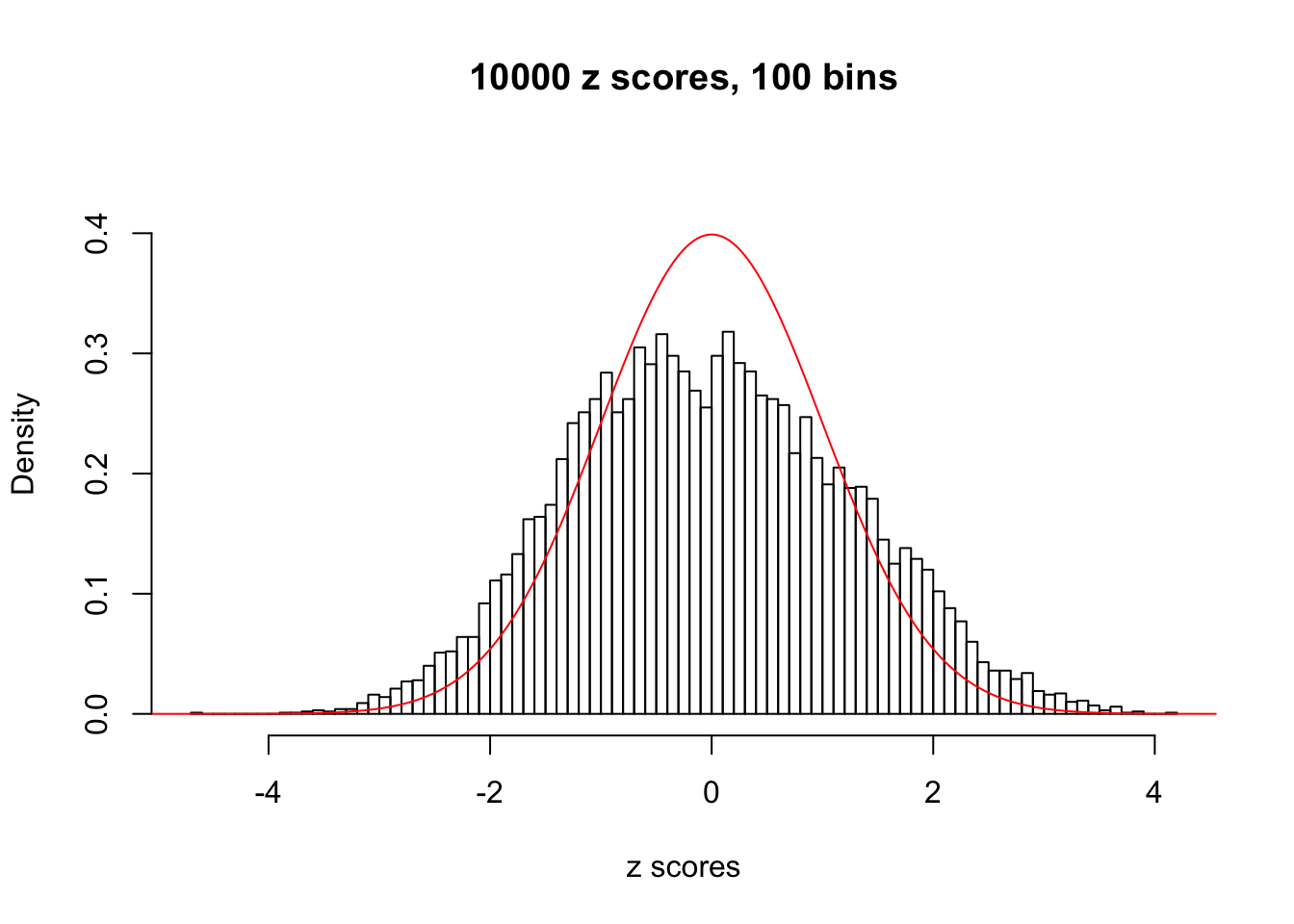
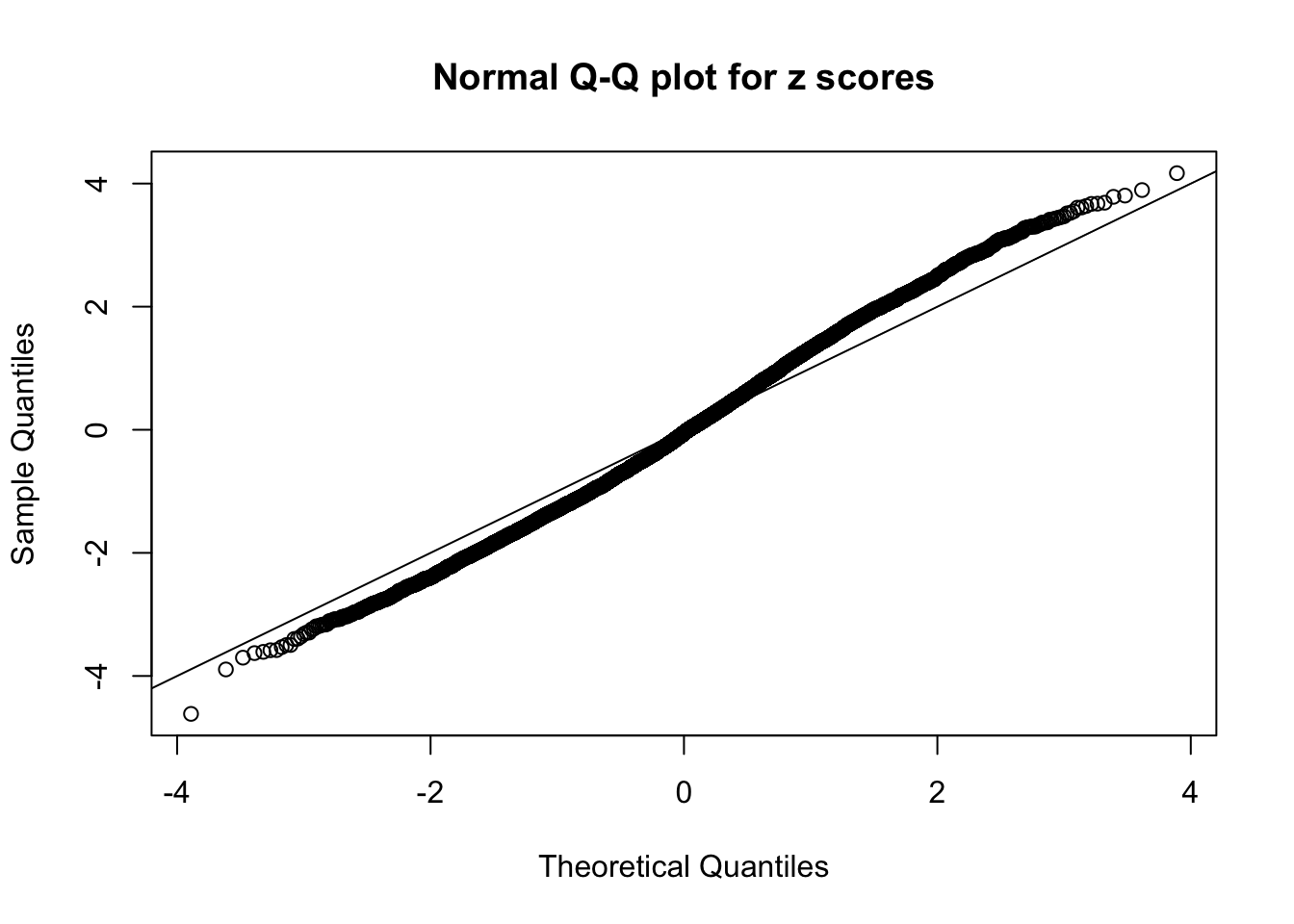
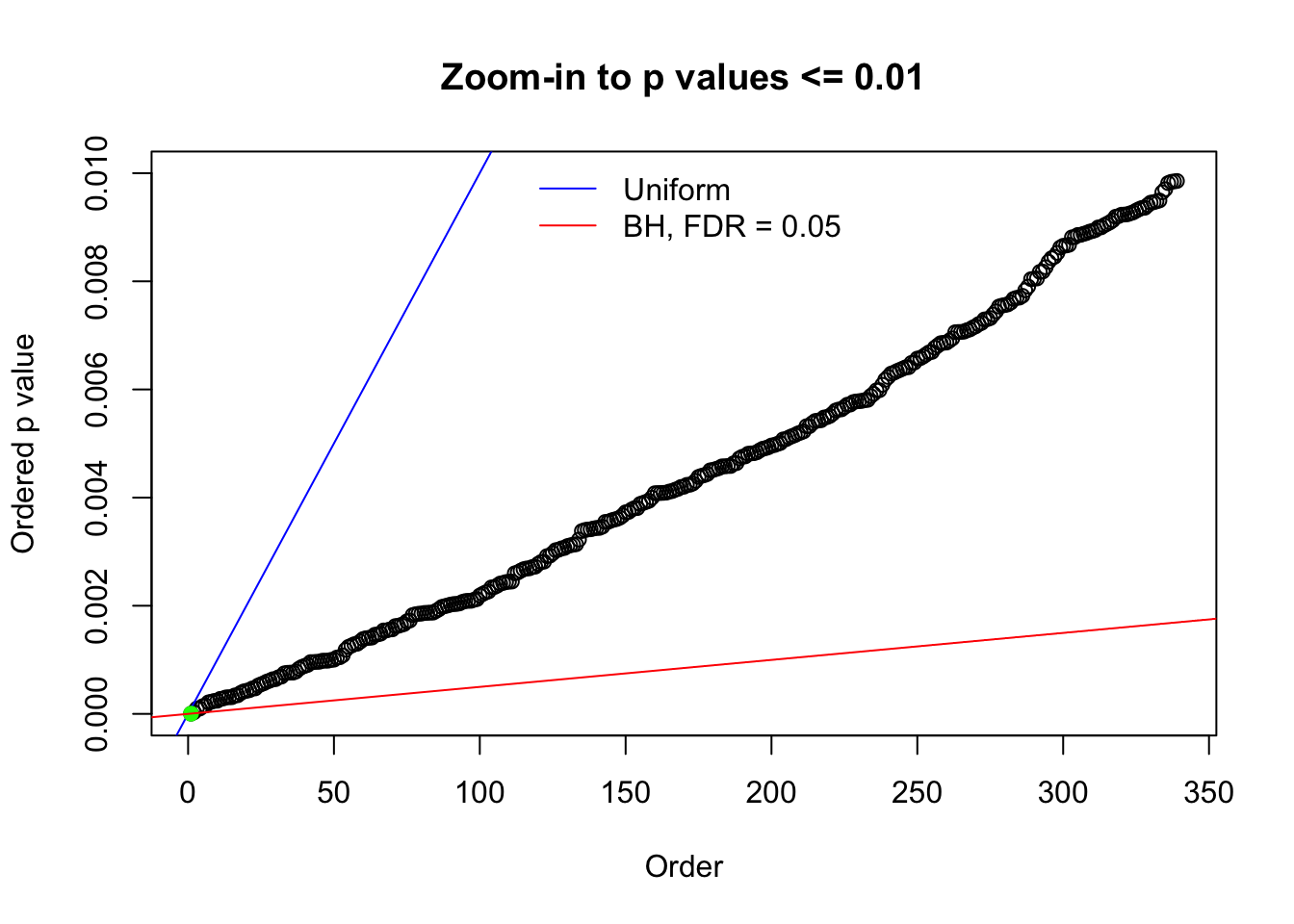
N0. 27 : Data Set 187 ; Number of False Discoveries: 1 ; pihat0 = 0.6662317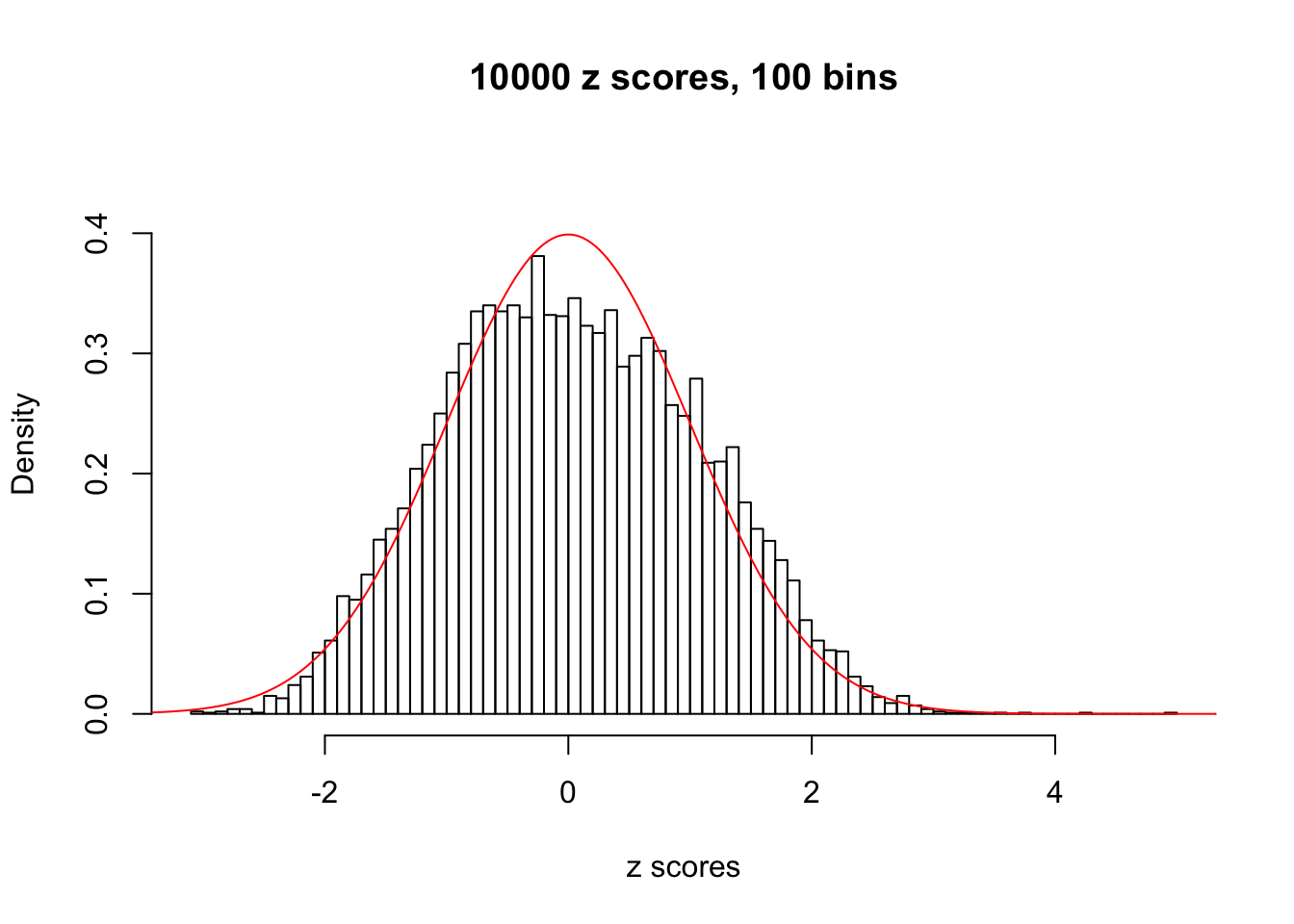
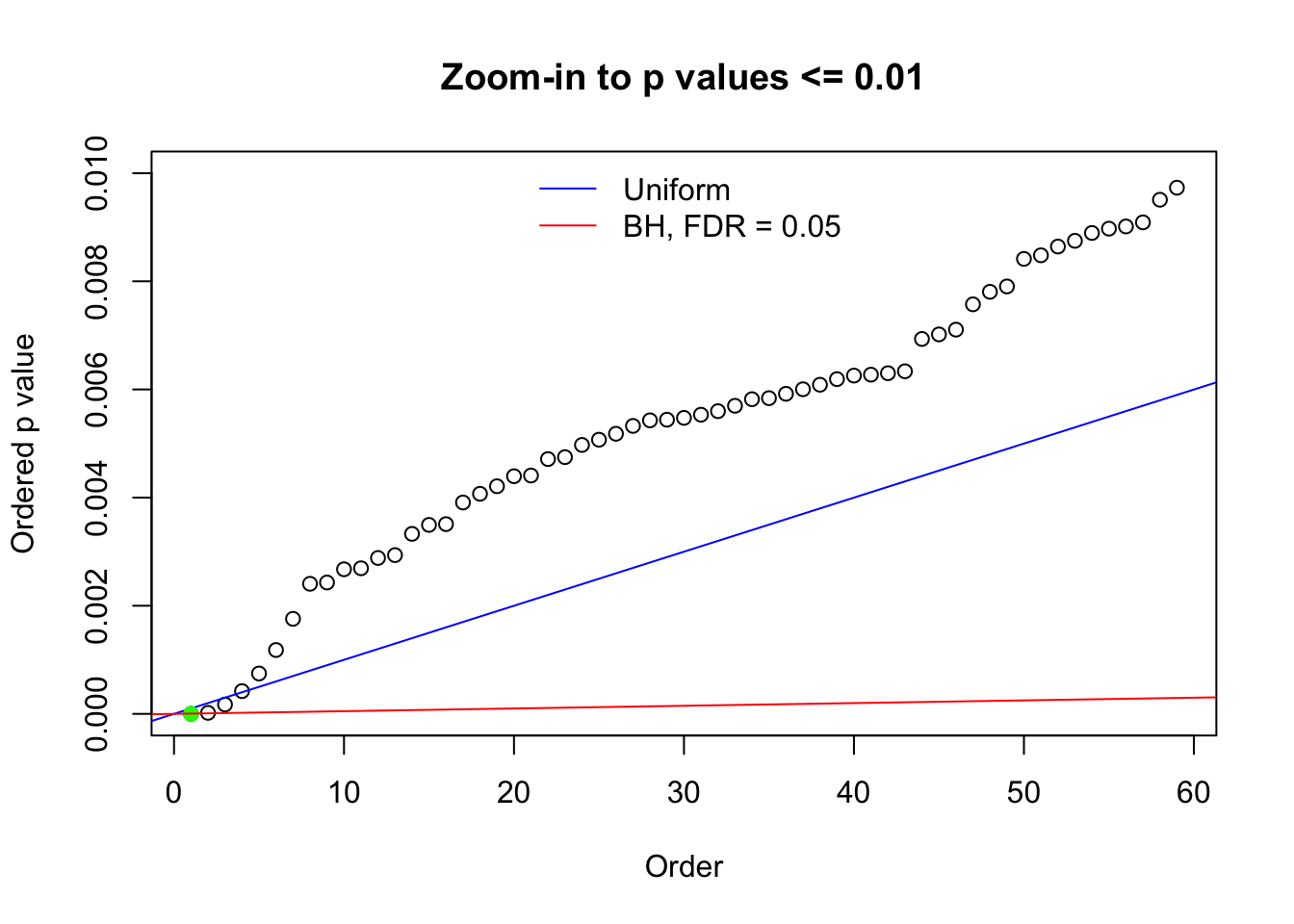
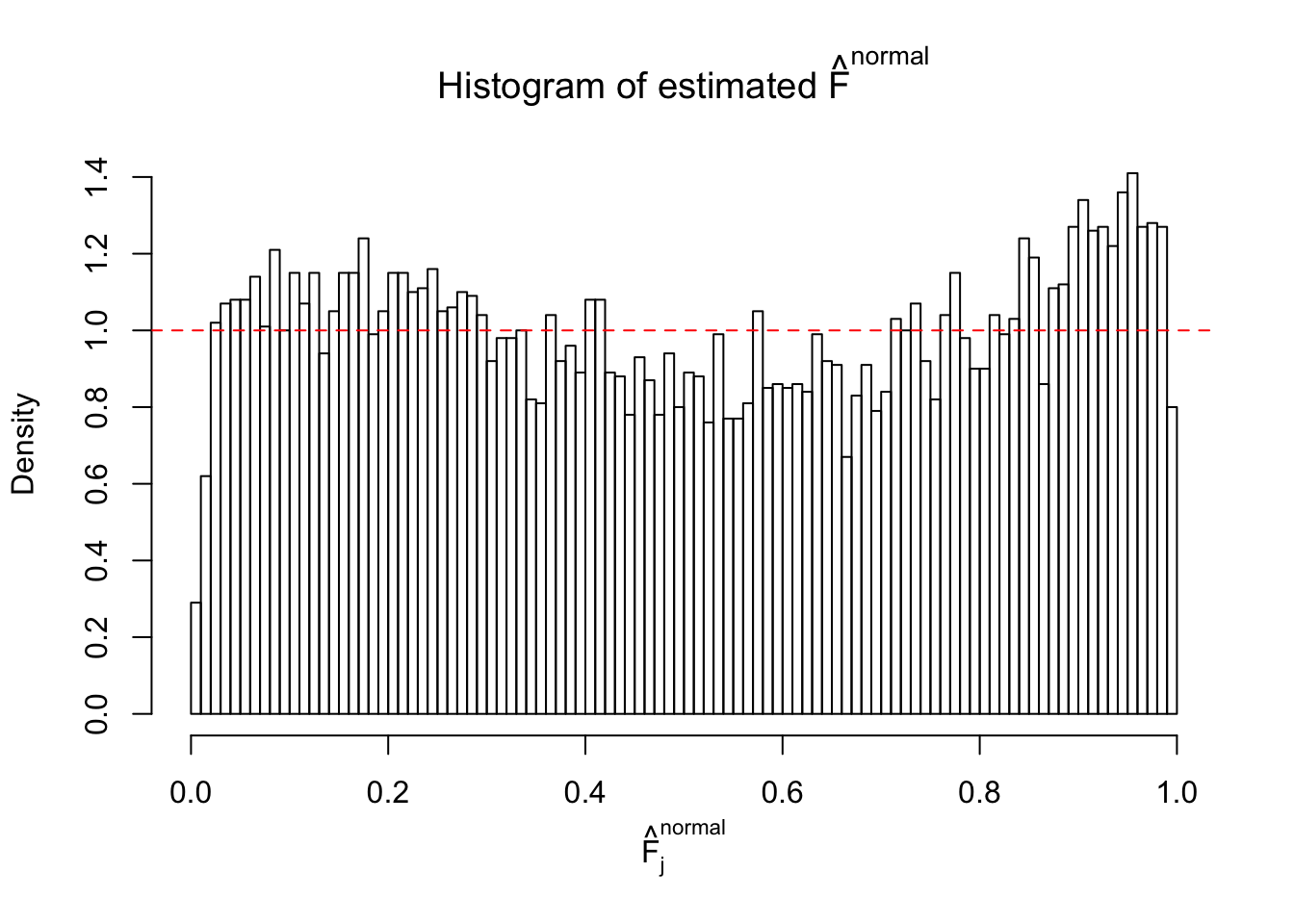
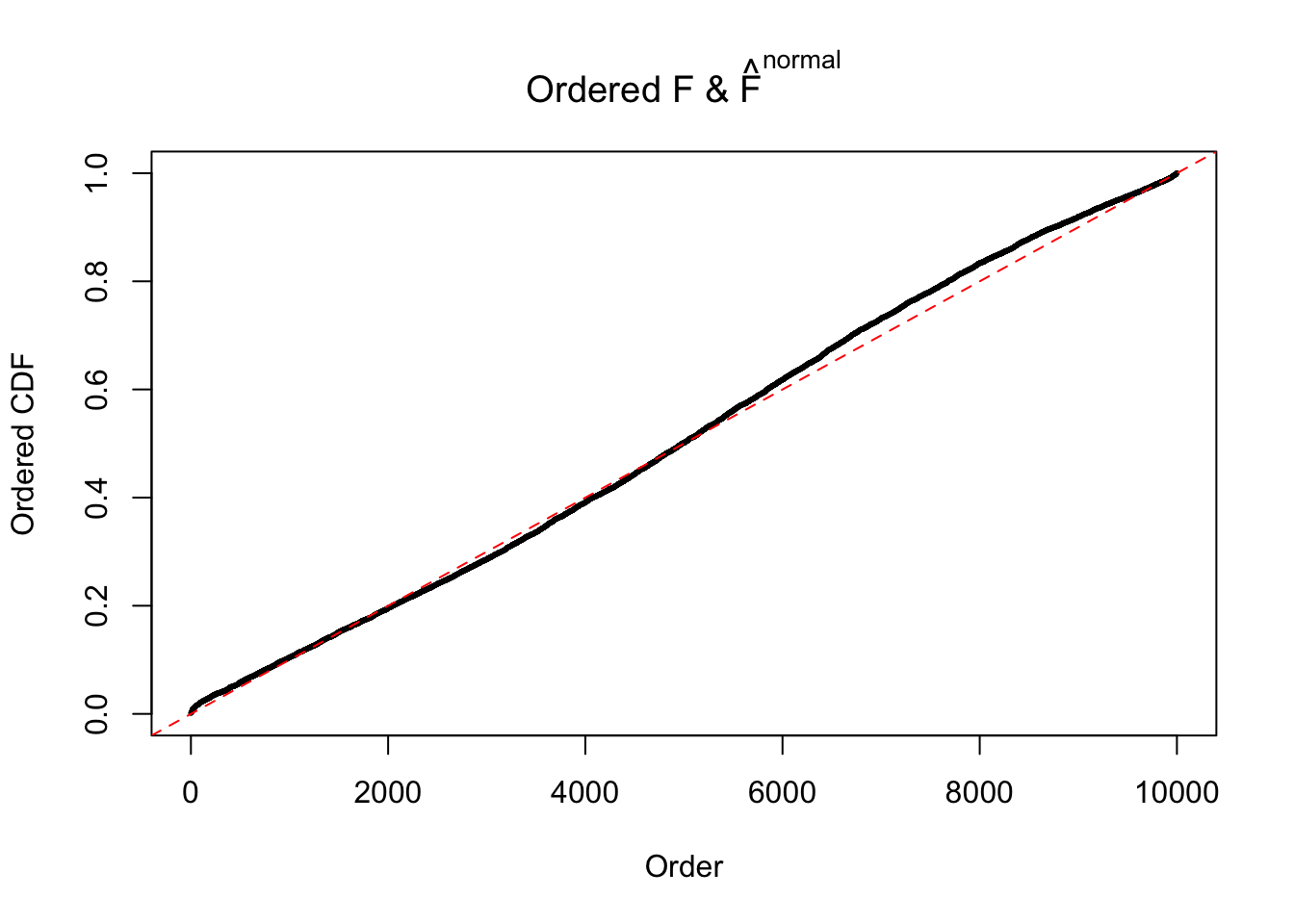
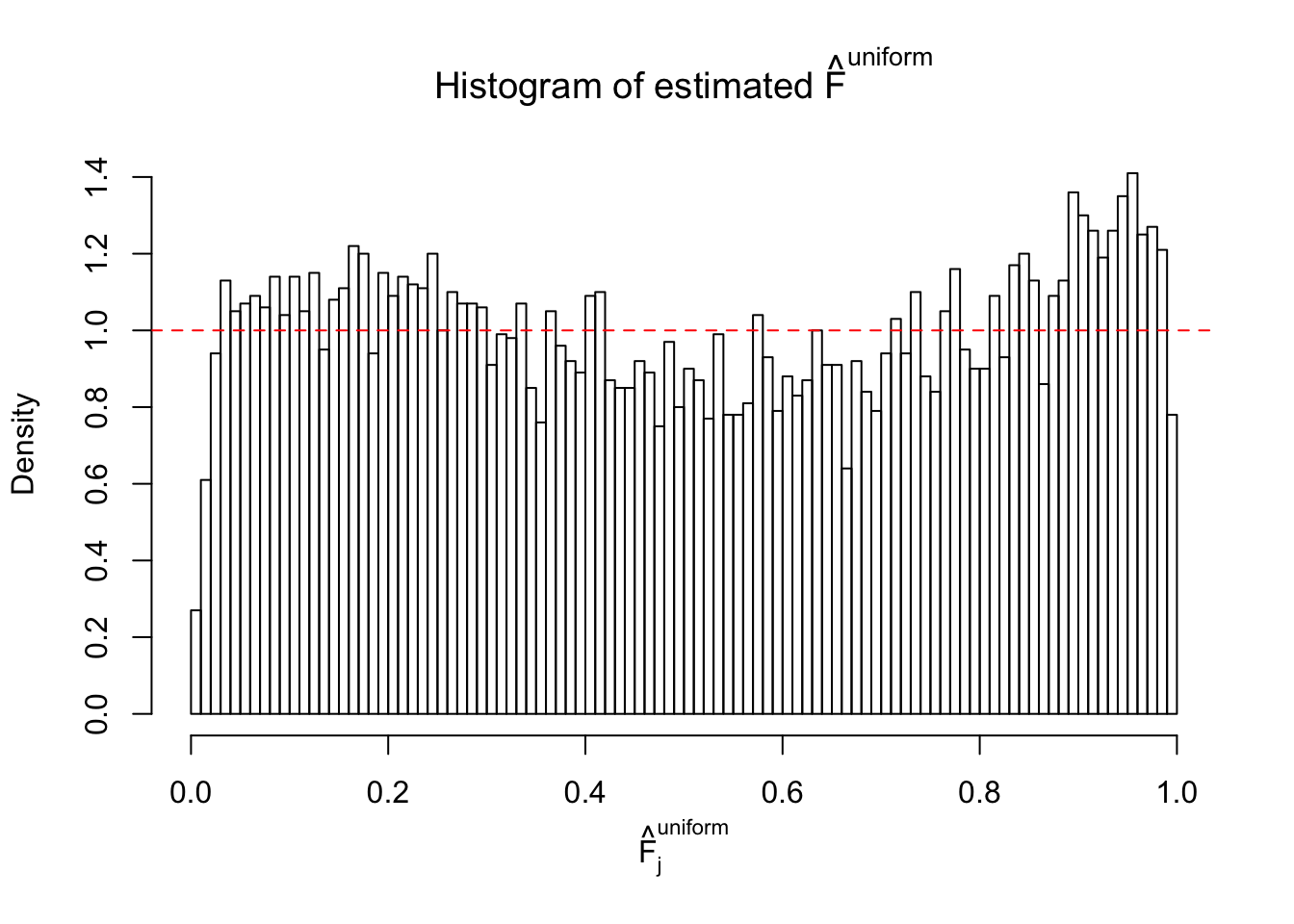
N0. 28 : Data Set 248 ; Number of False Discoveries: 1 ; pihat0 = 0.4583919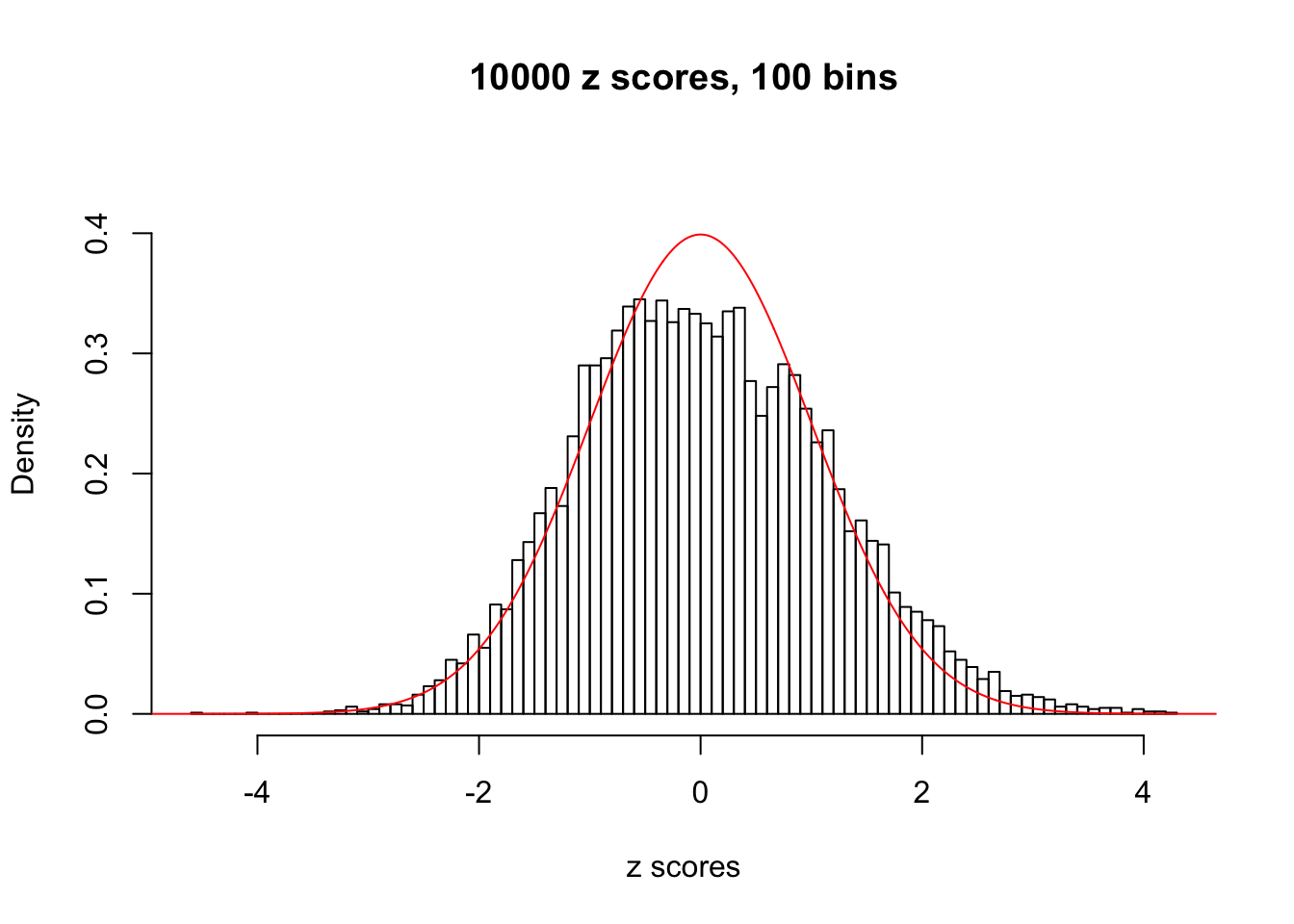
N0. 29 : Data Set 269 ; Number of False Discoveries: 1 ; pihat0 = 0.03060497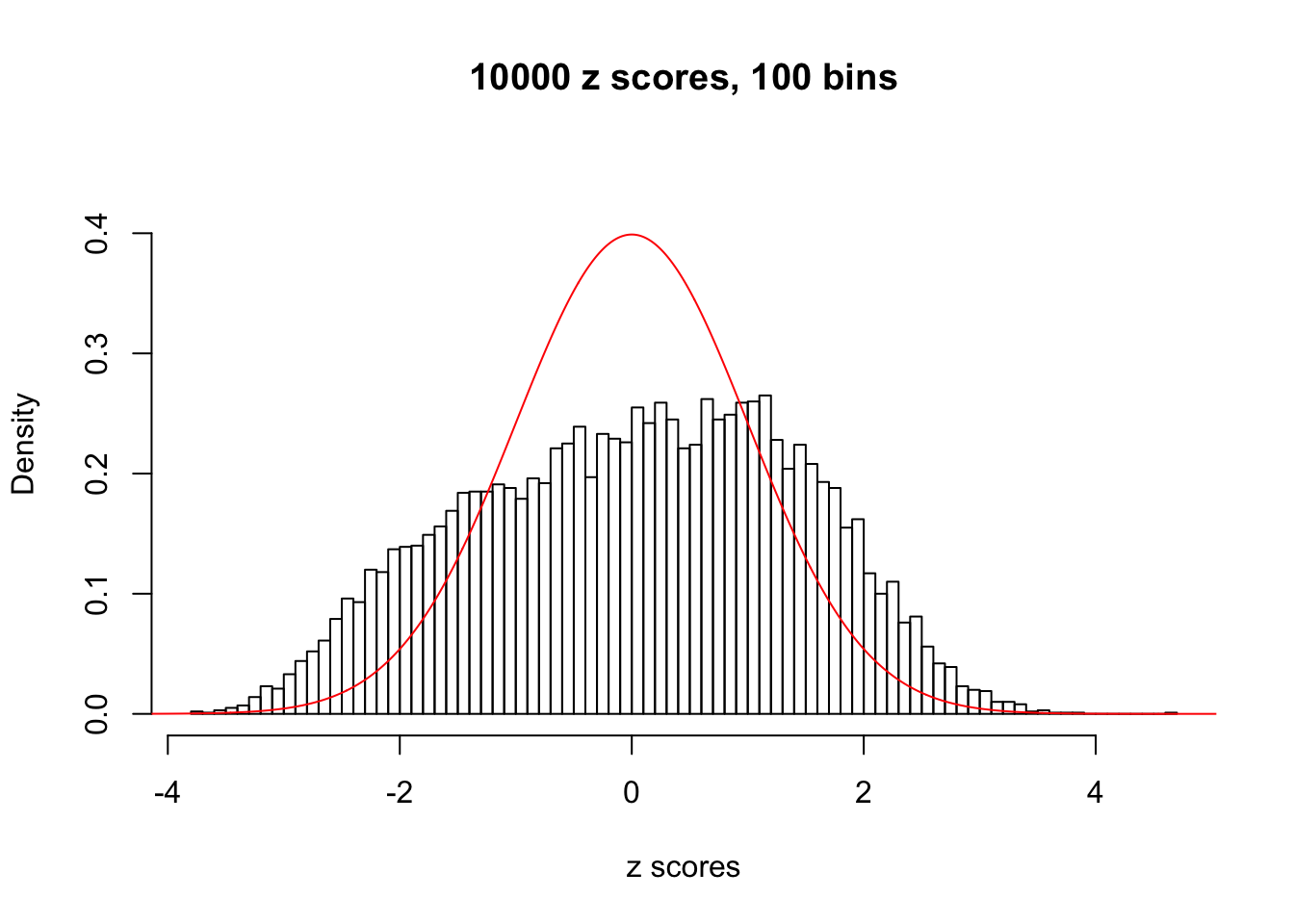
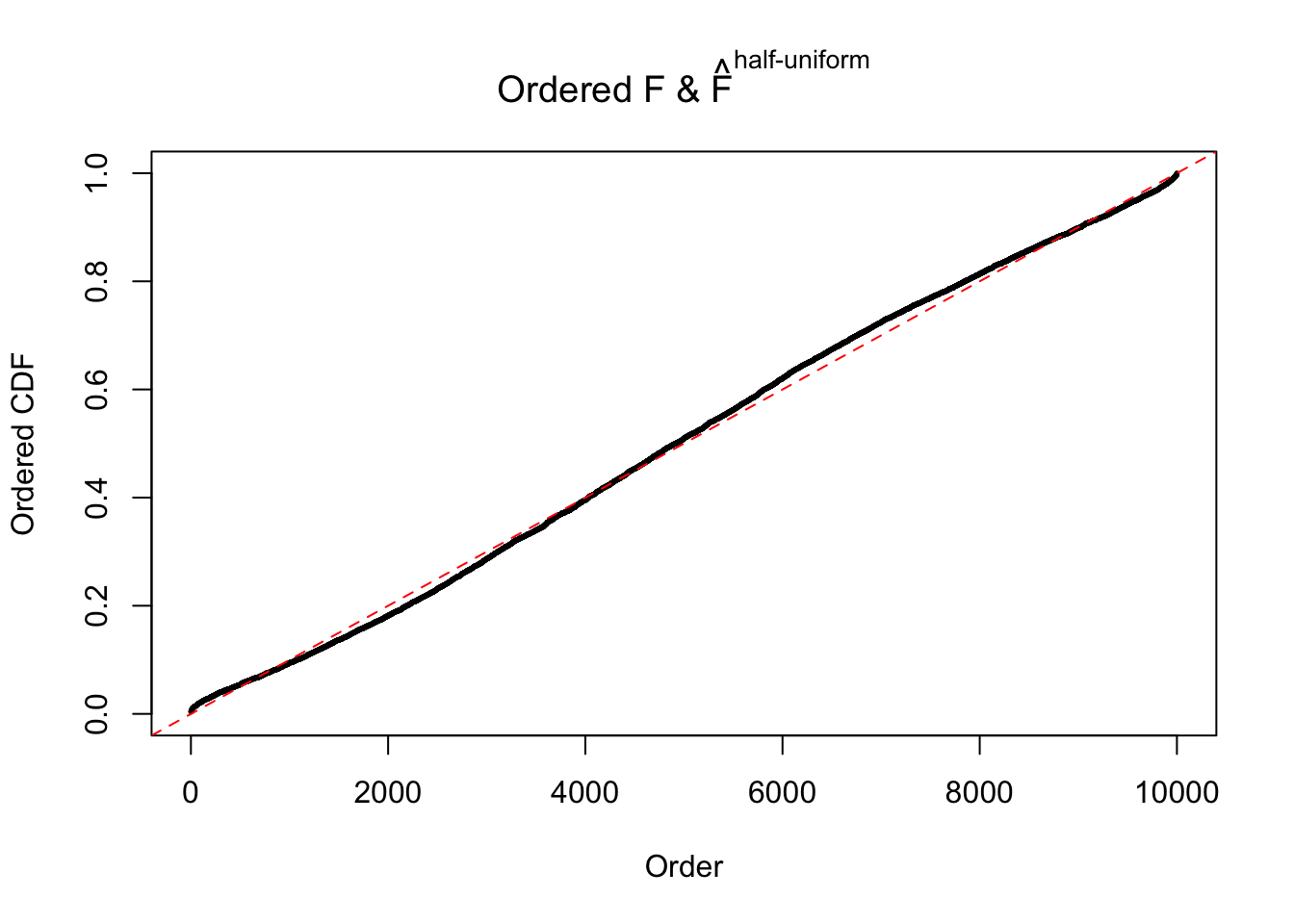
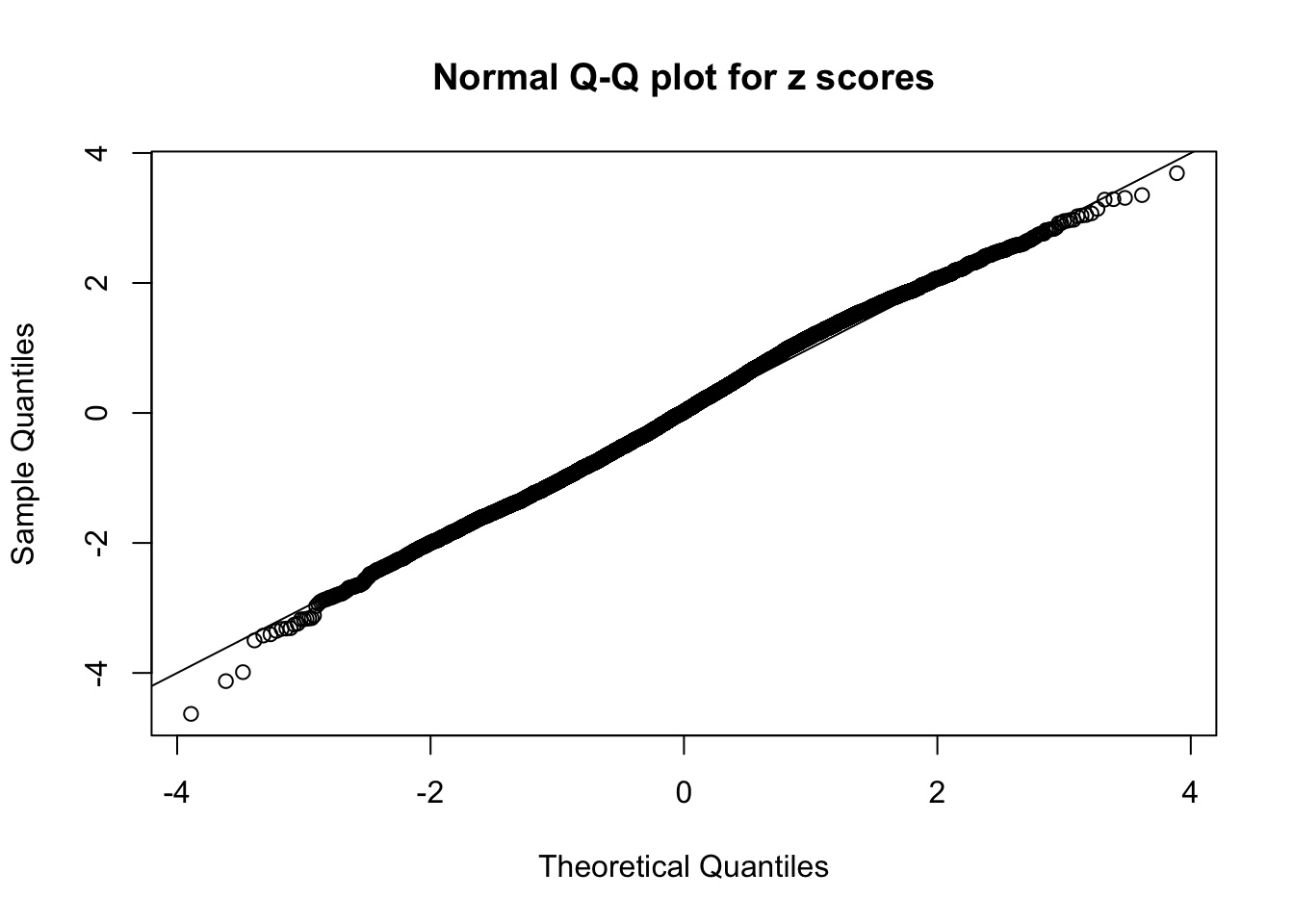
N0. 30 : Data Set 285 ; Number of False Discoveries: 1 ; pihat0 = 0.5178013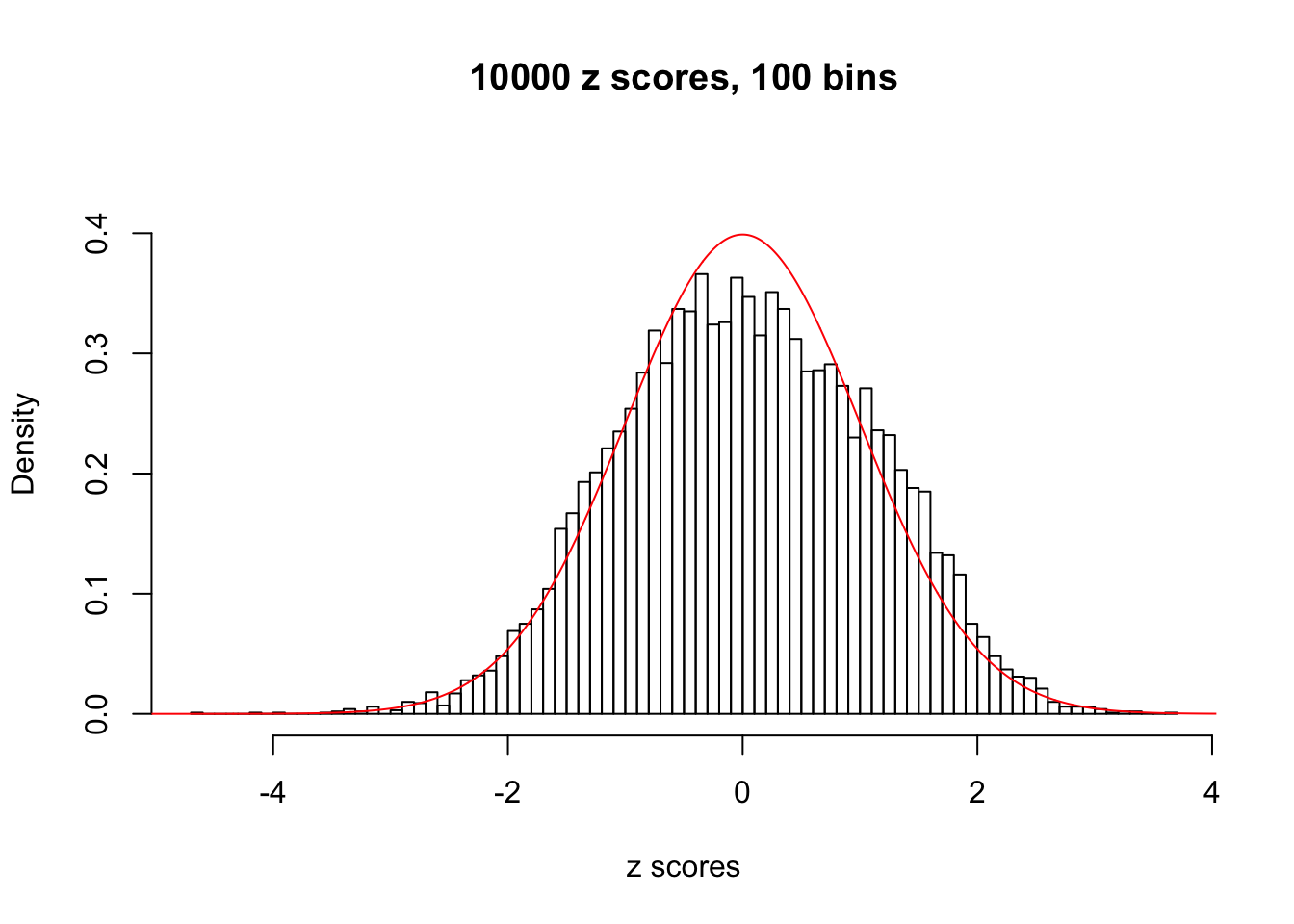
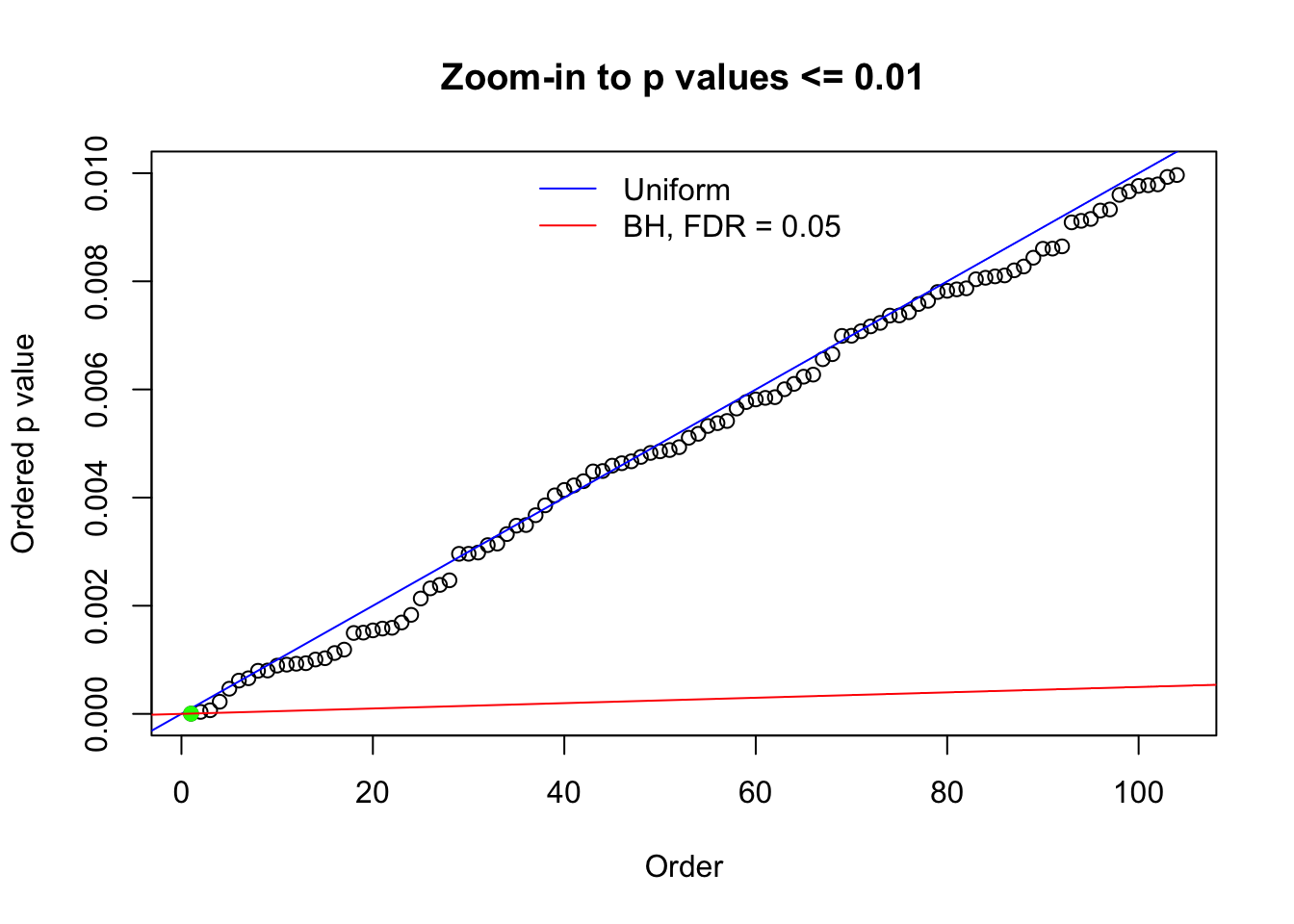
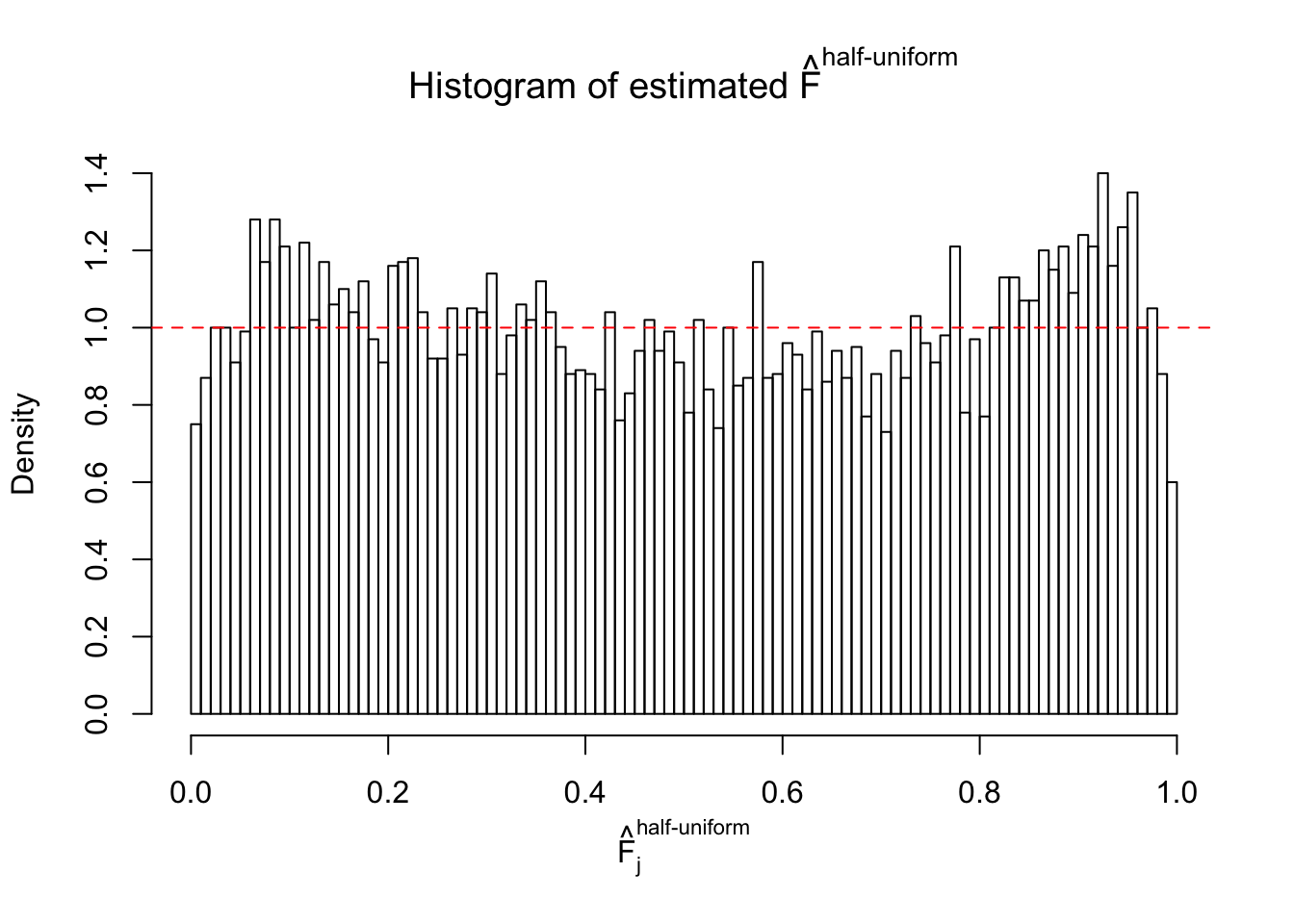
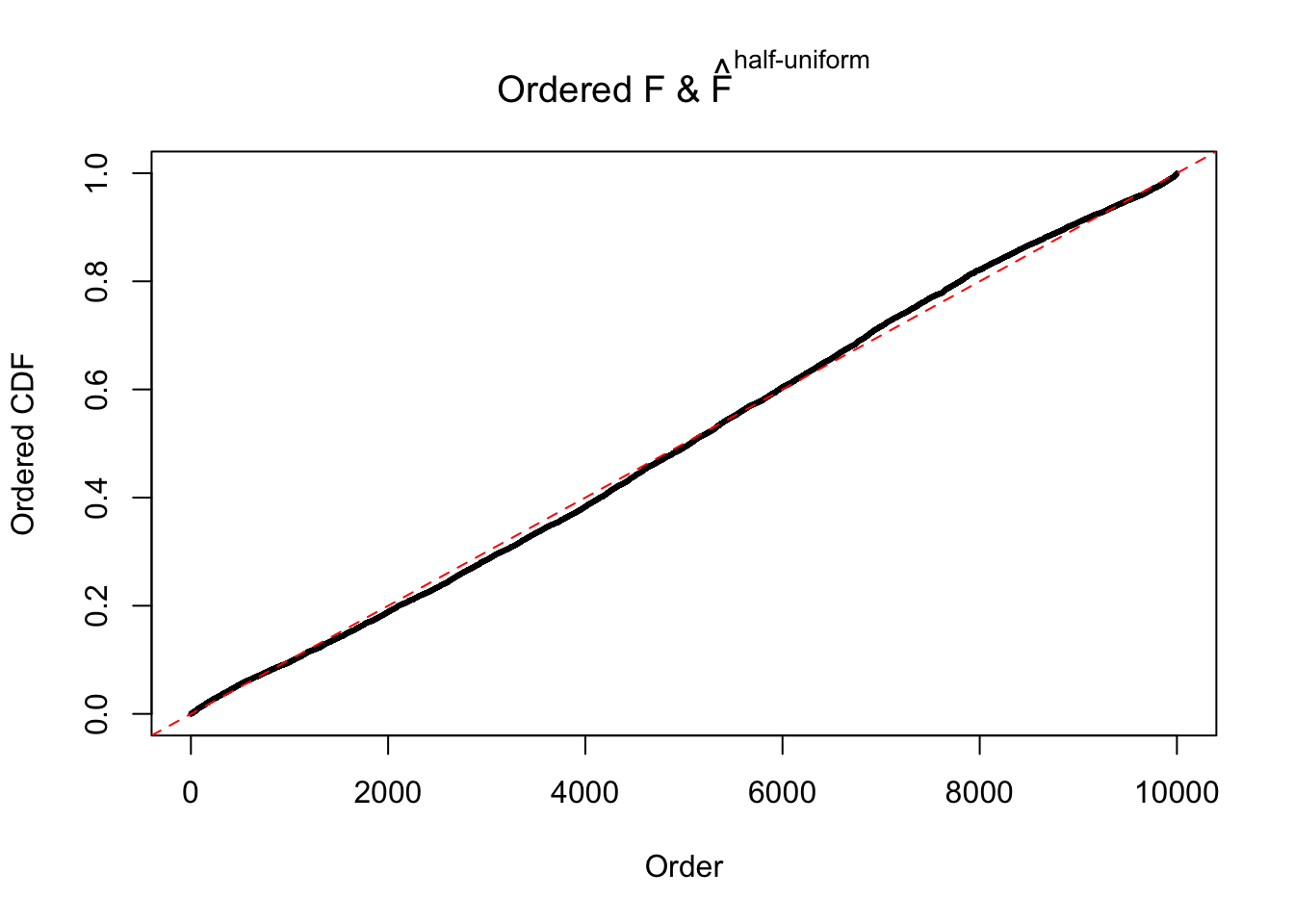
N0. 31 : Data Set 403 ; Number of False Discoveries: 1 ; pihat0 = 0.03166538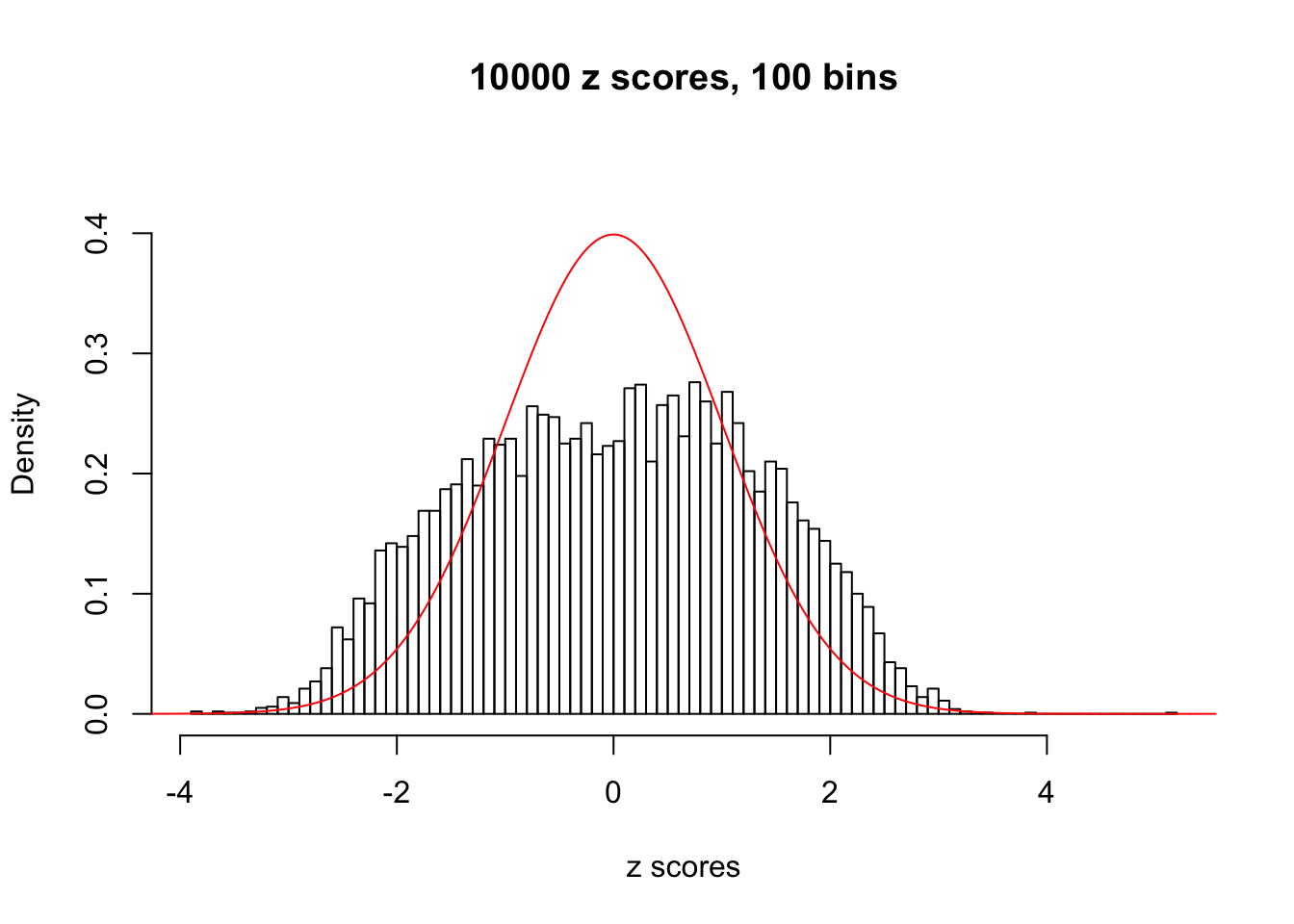
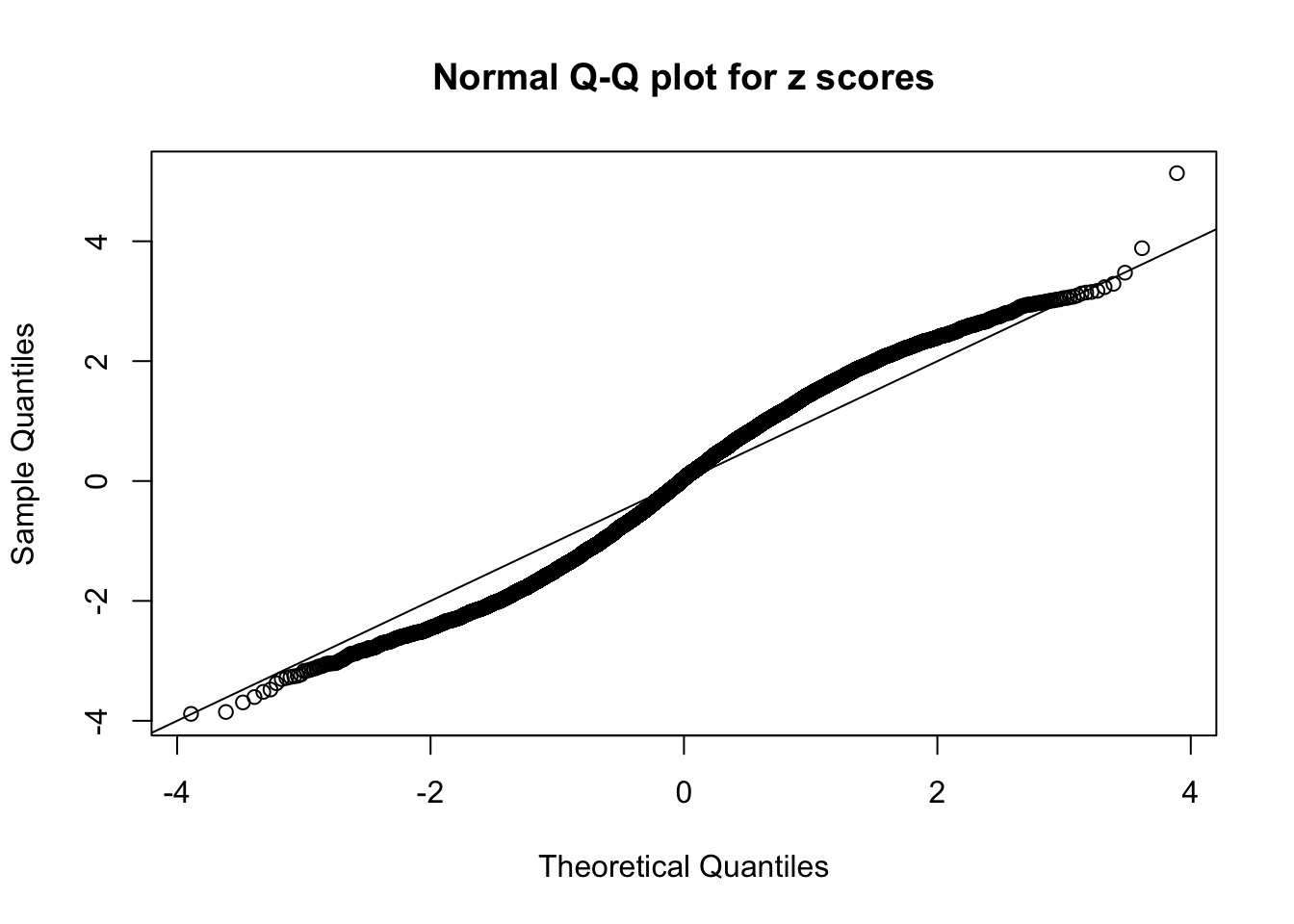
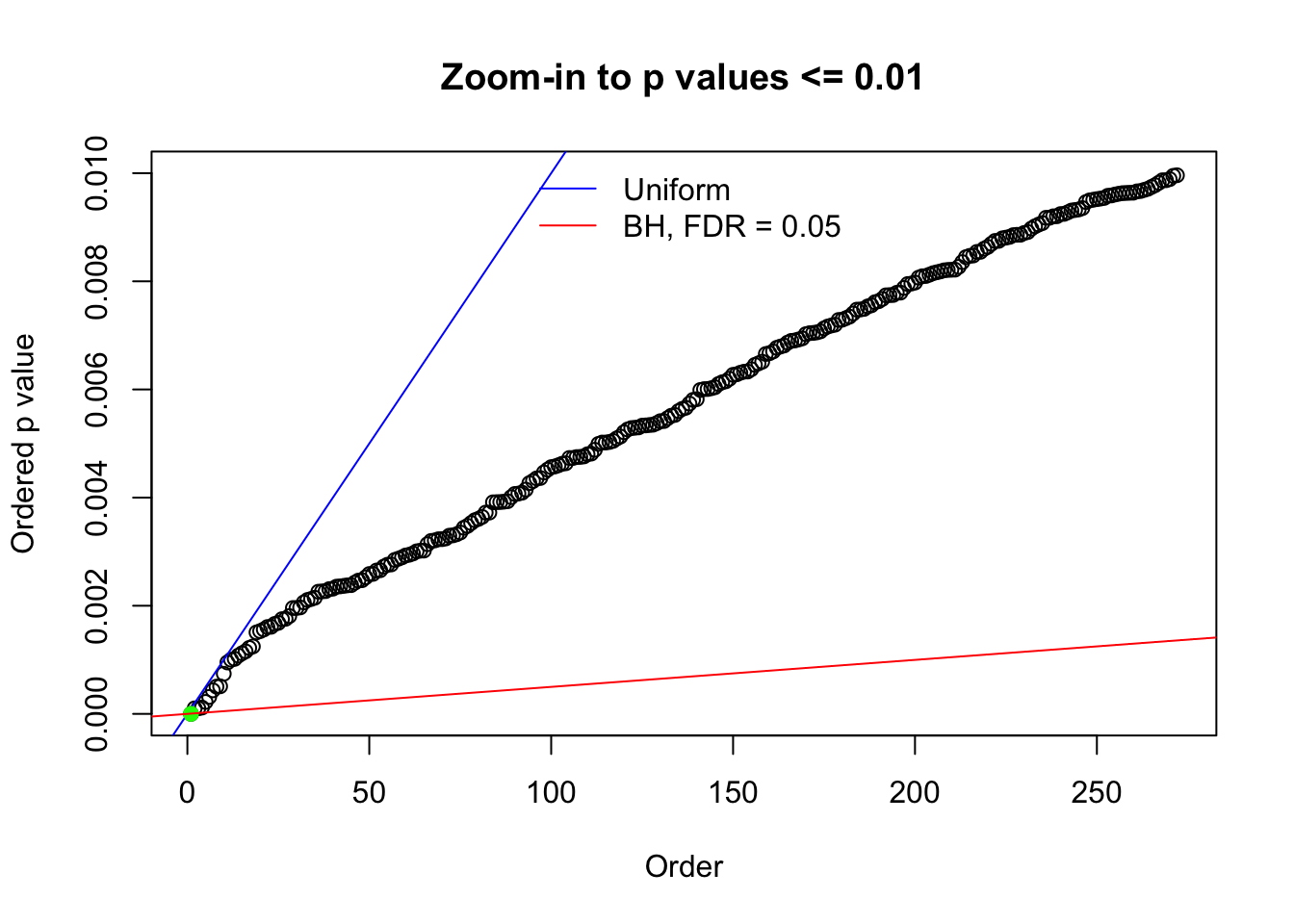
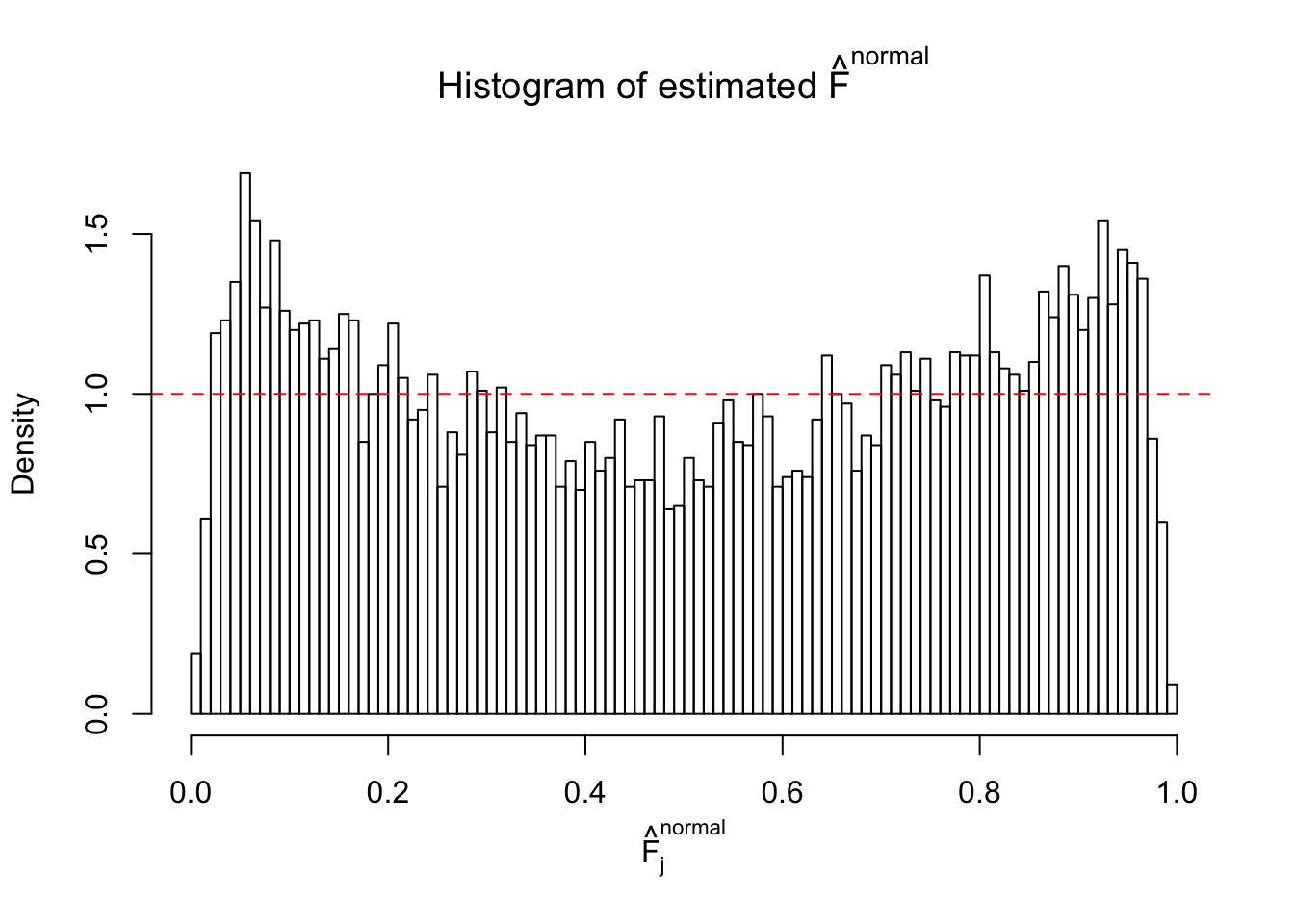
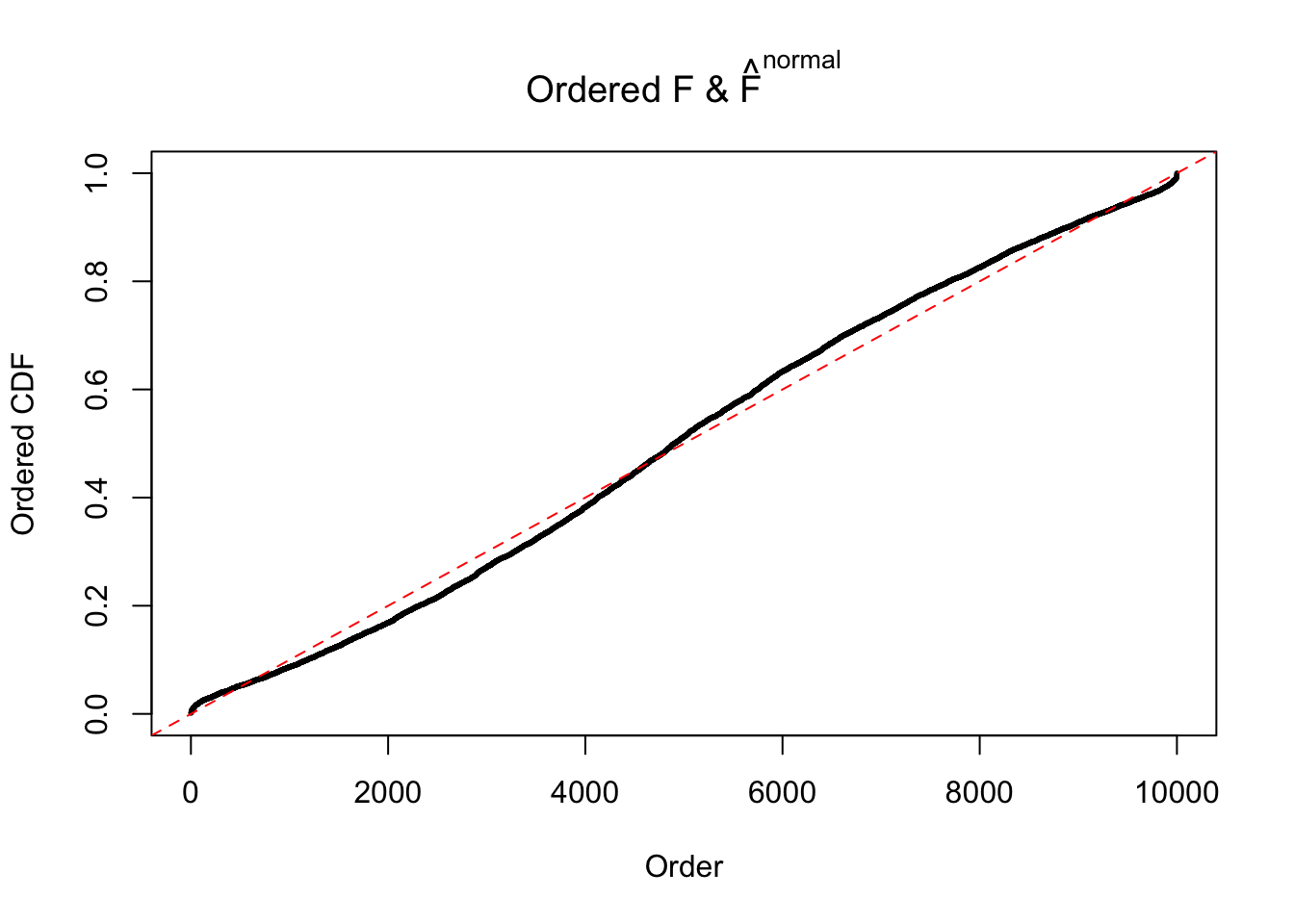
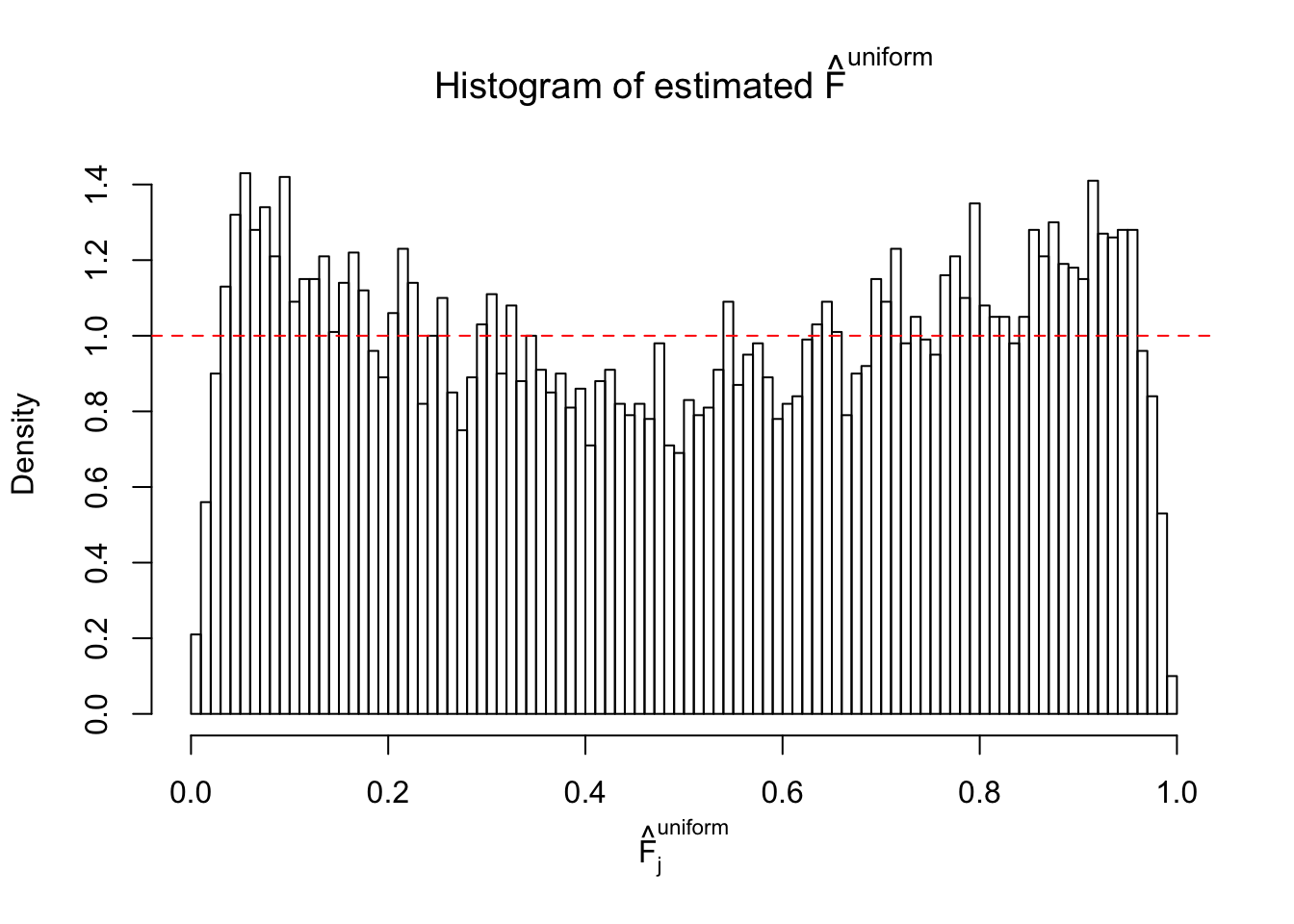
N0. 32 : Data Set 483 ; Number of False Discoveries: 1 ; pihat0 = 0.9998828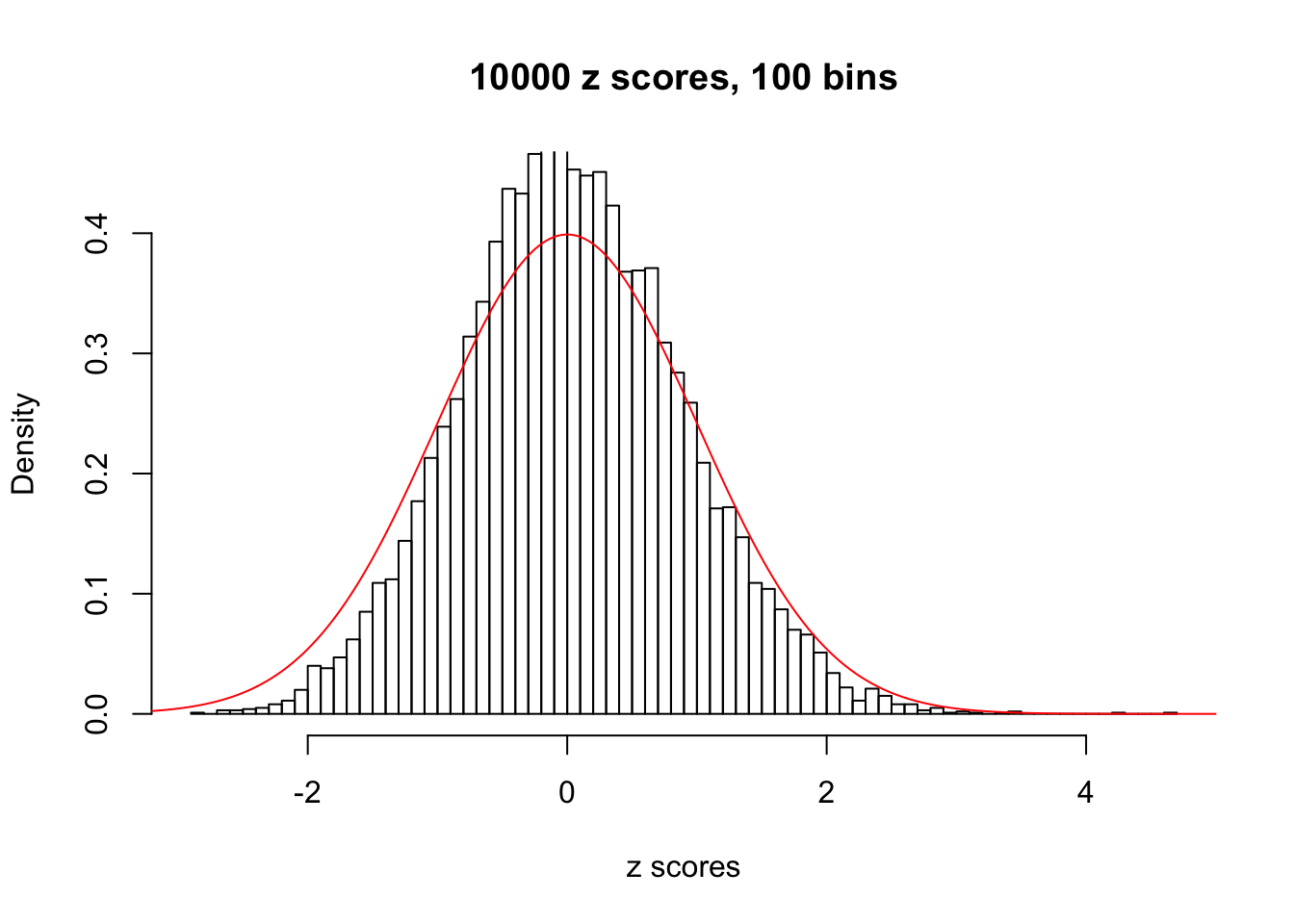
N0. 33 : Data Set 501 ; Number of False Discoveries: 1 ; pihat0 = 0.09362328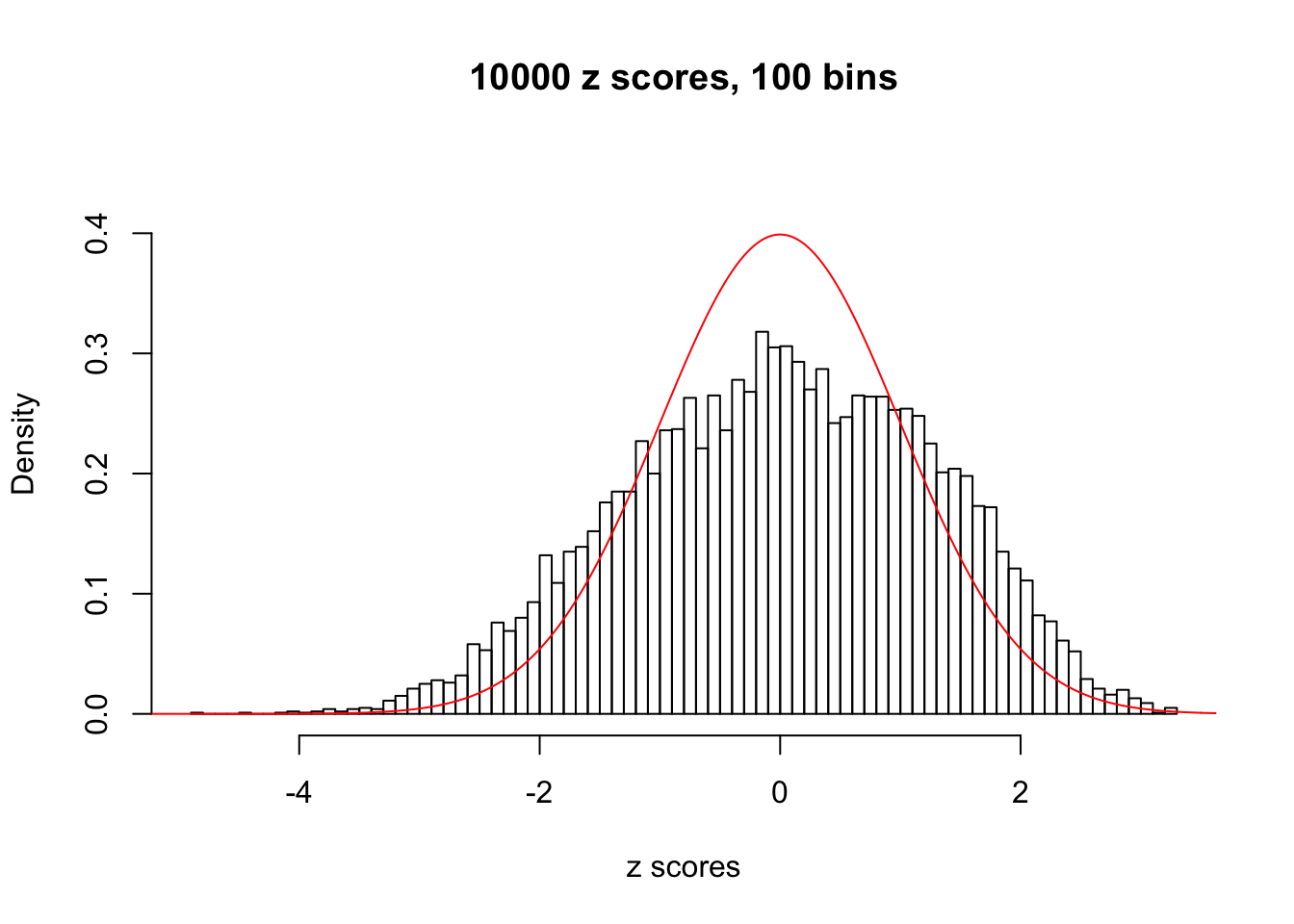
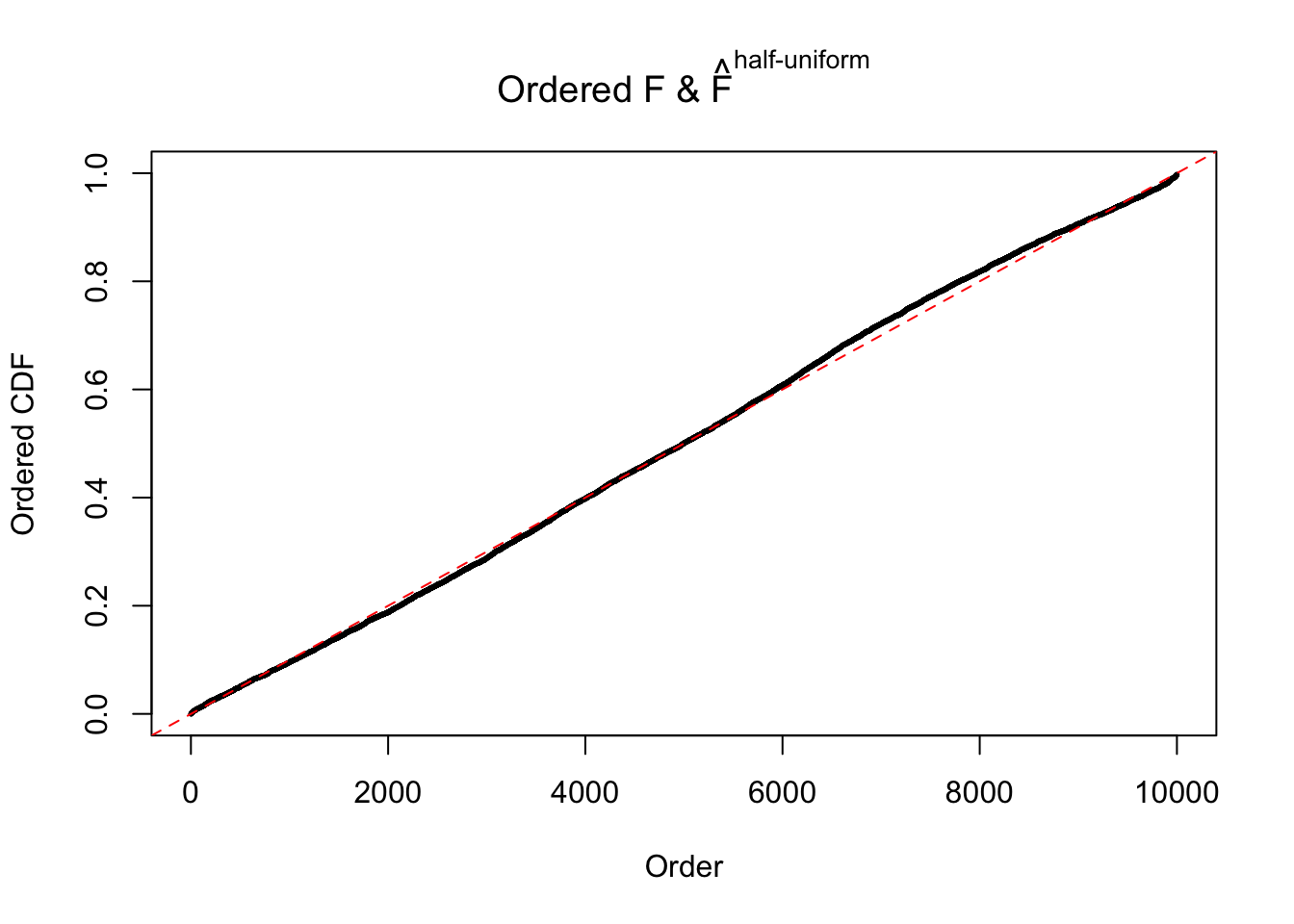
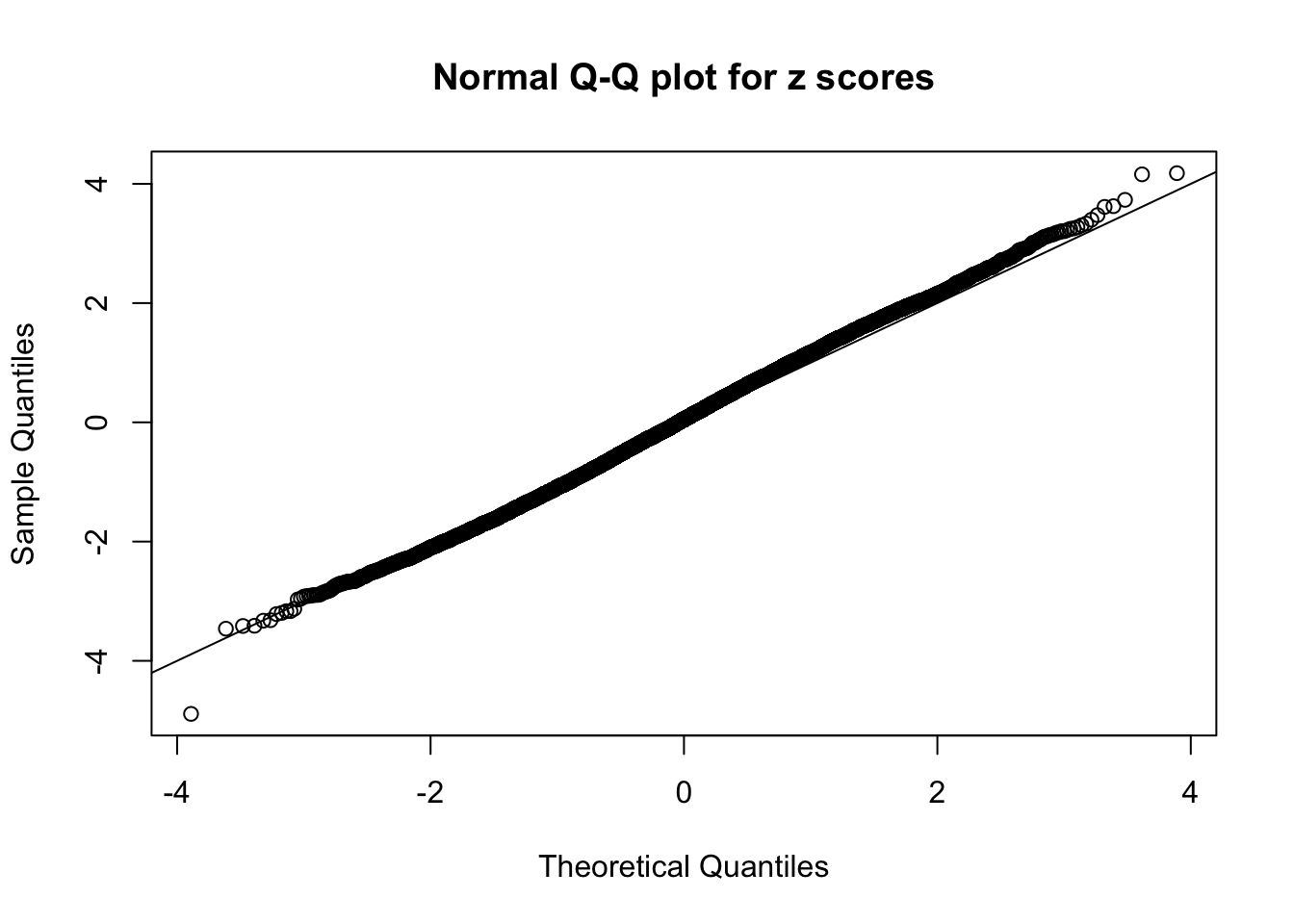
N0. 34 : Data Set 530 ; Number of False Discoveries: 1 ; pihat0 = 0.4320548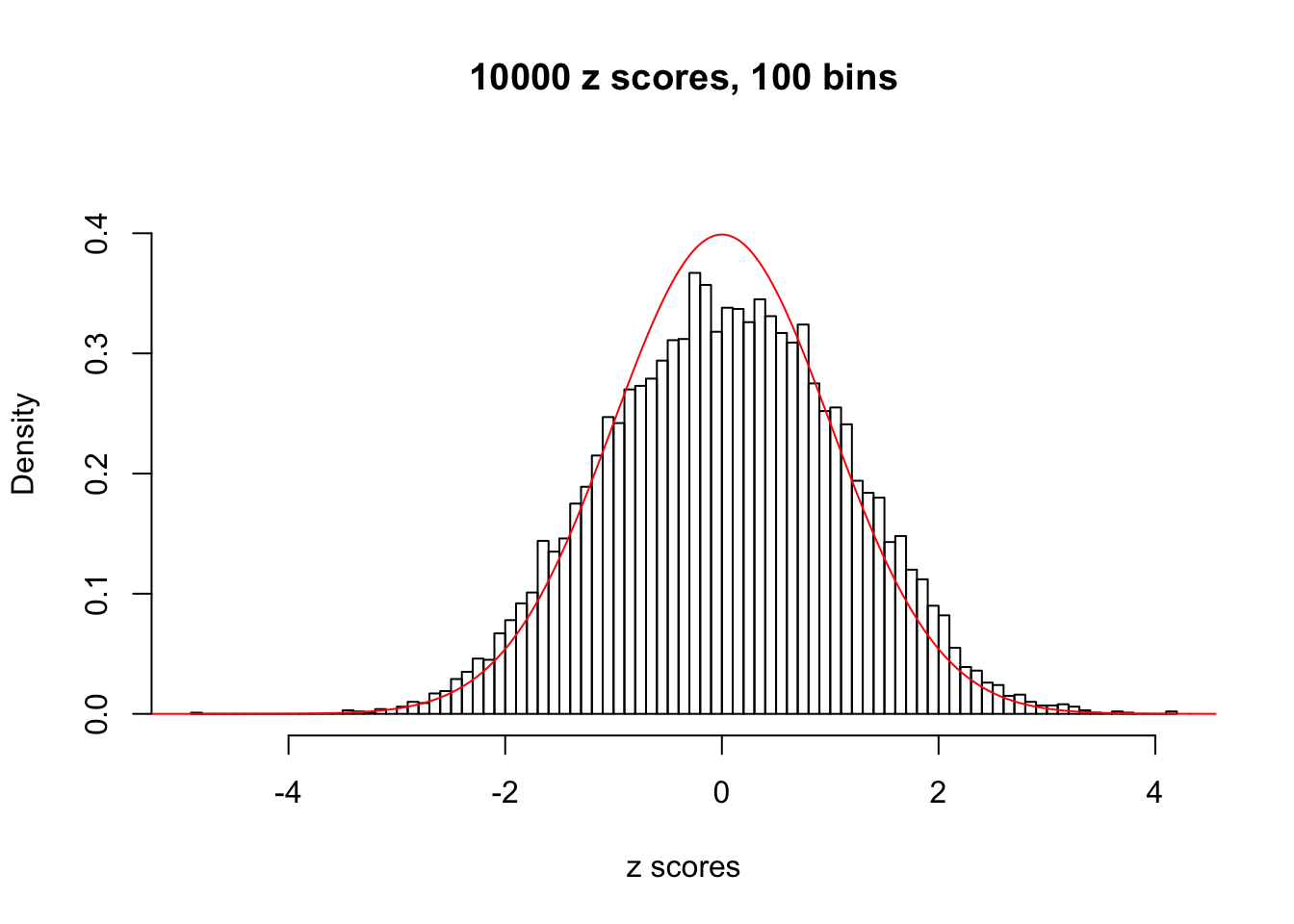
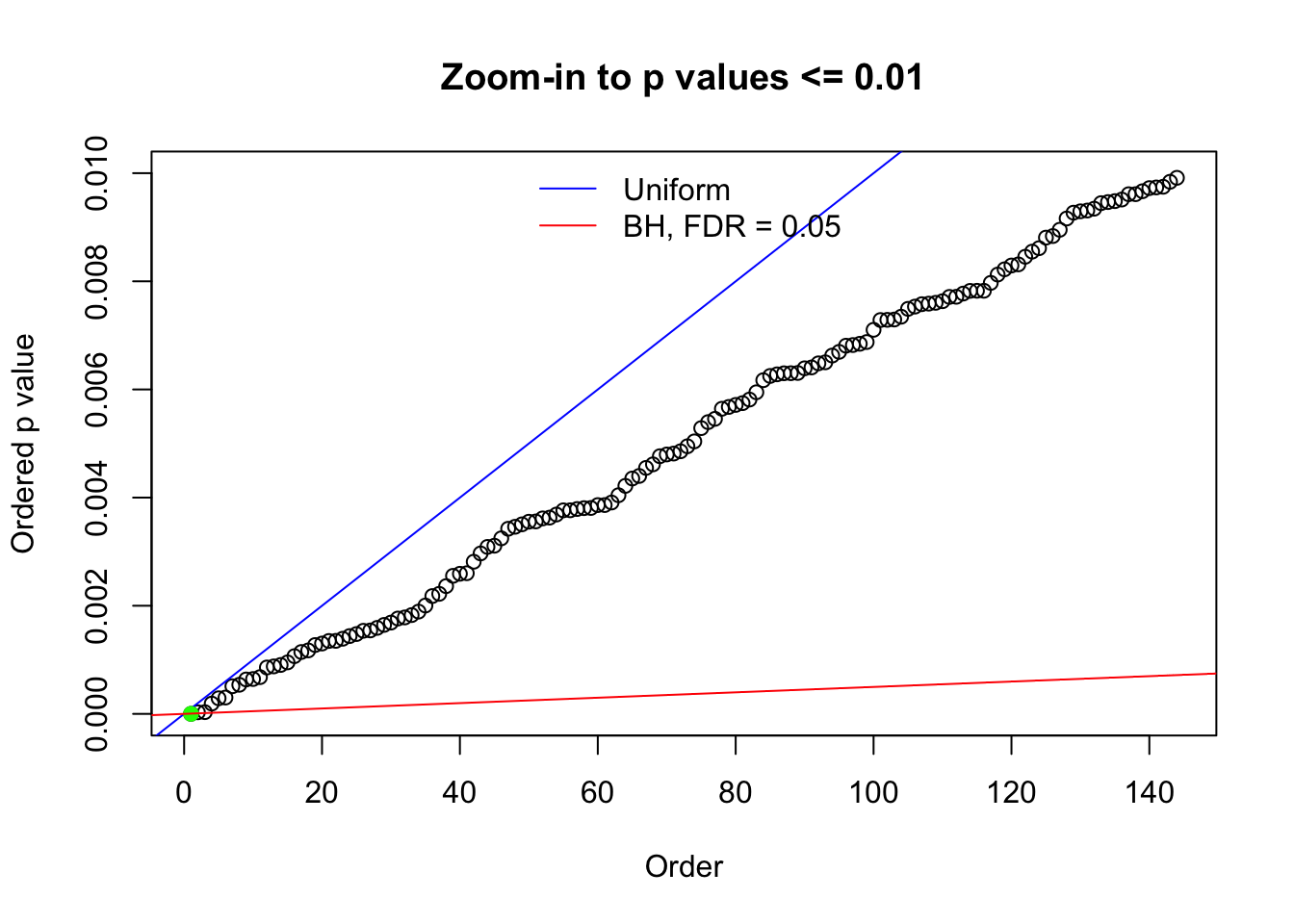
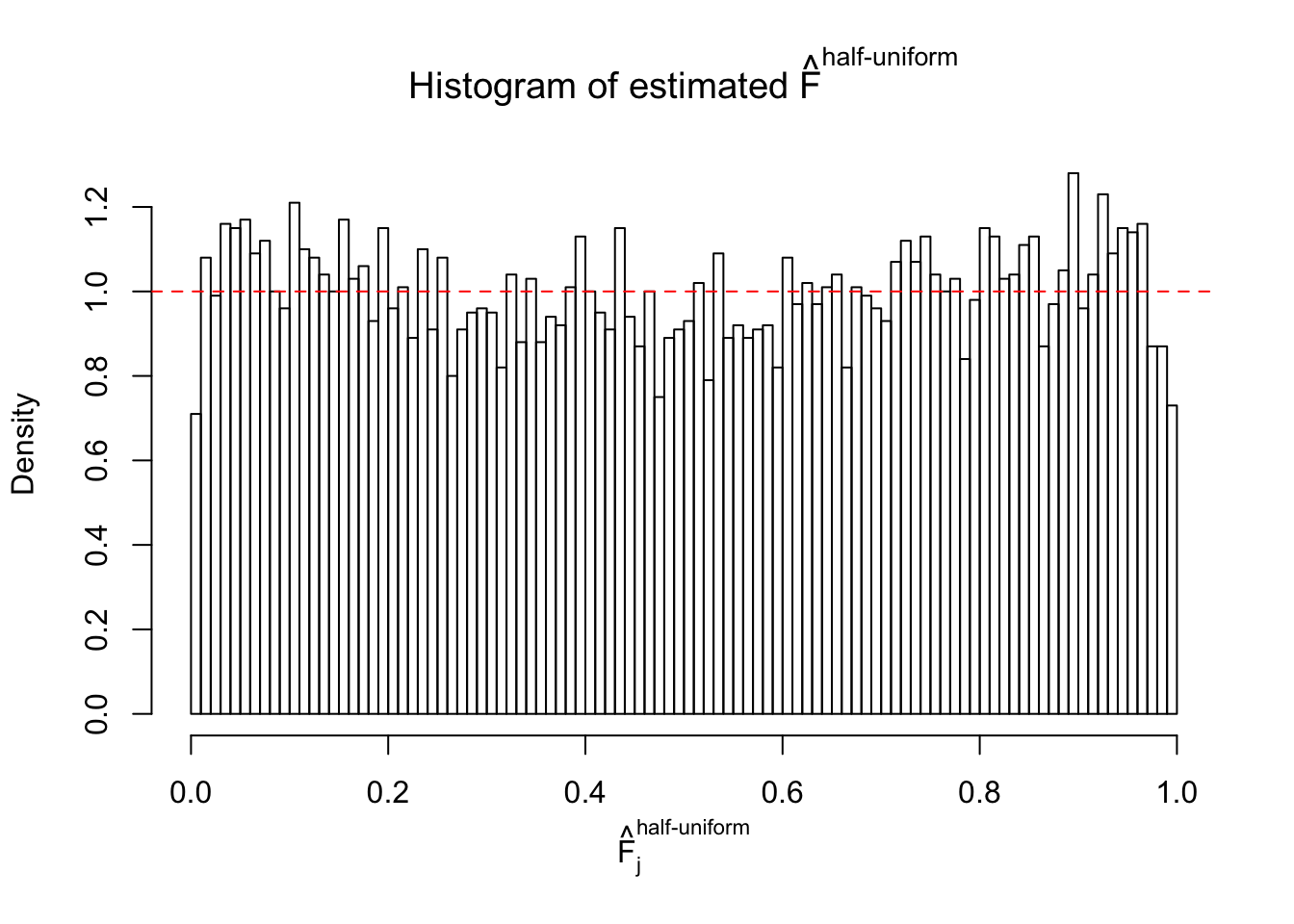
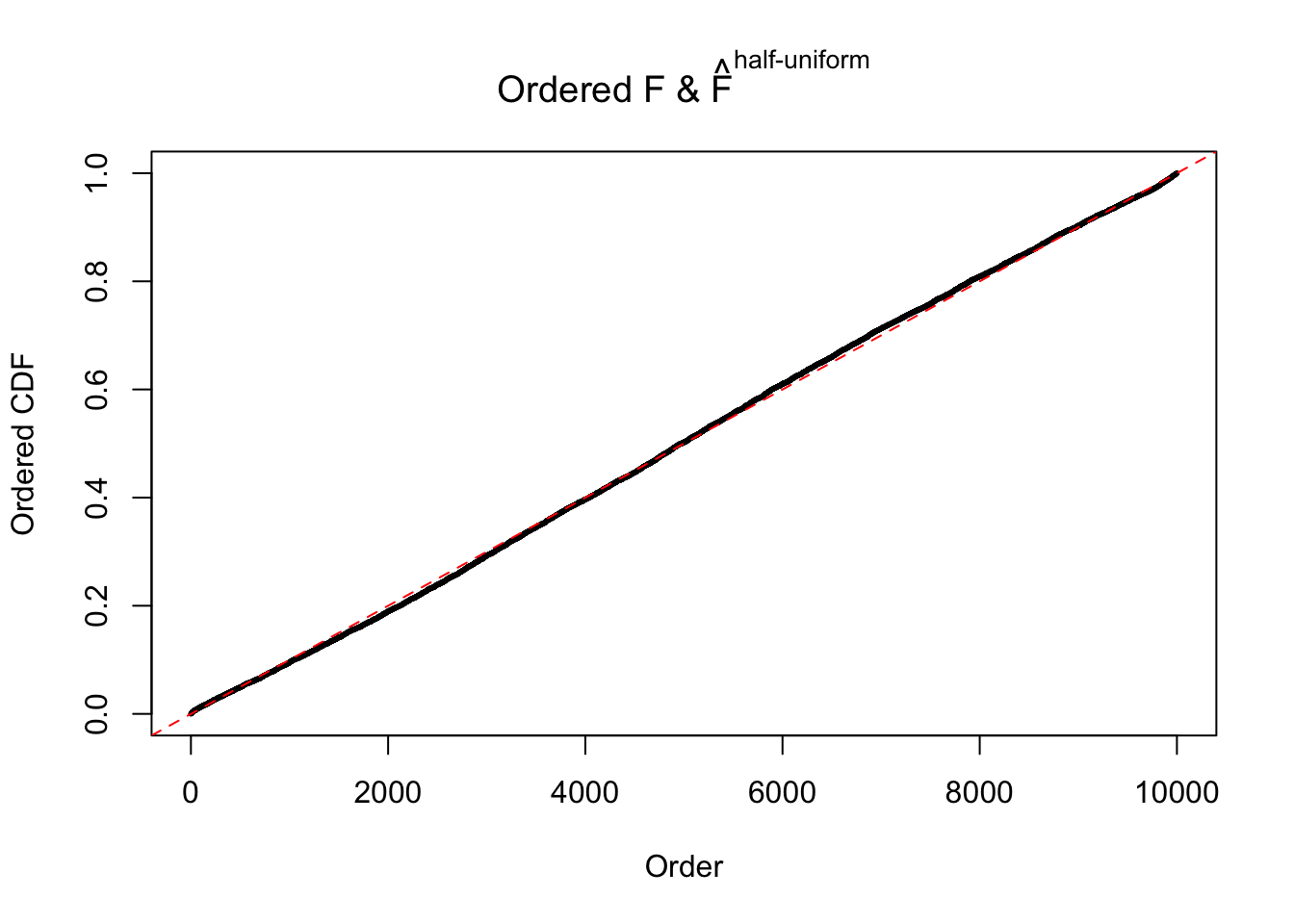
N0. 35 : Data Set 574 ; Number of False Discoveries: 1 ; pihat0 = 0.3723755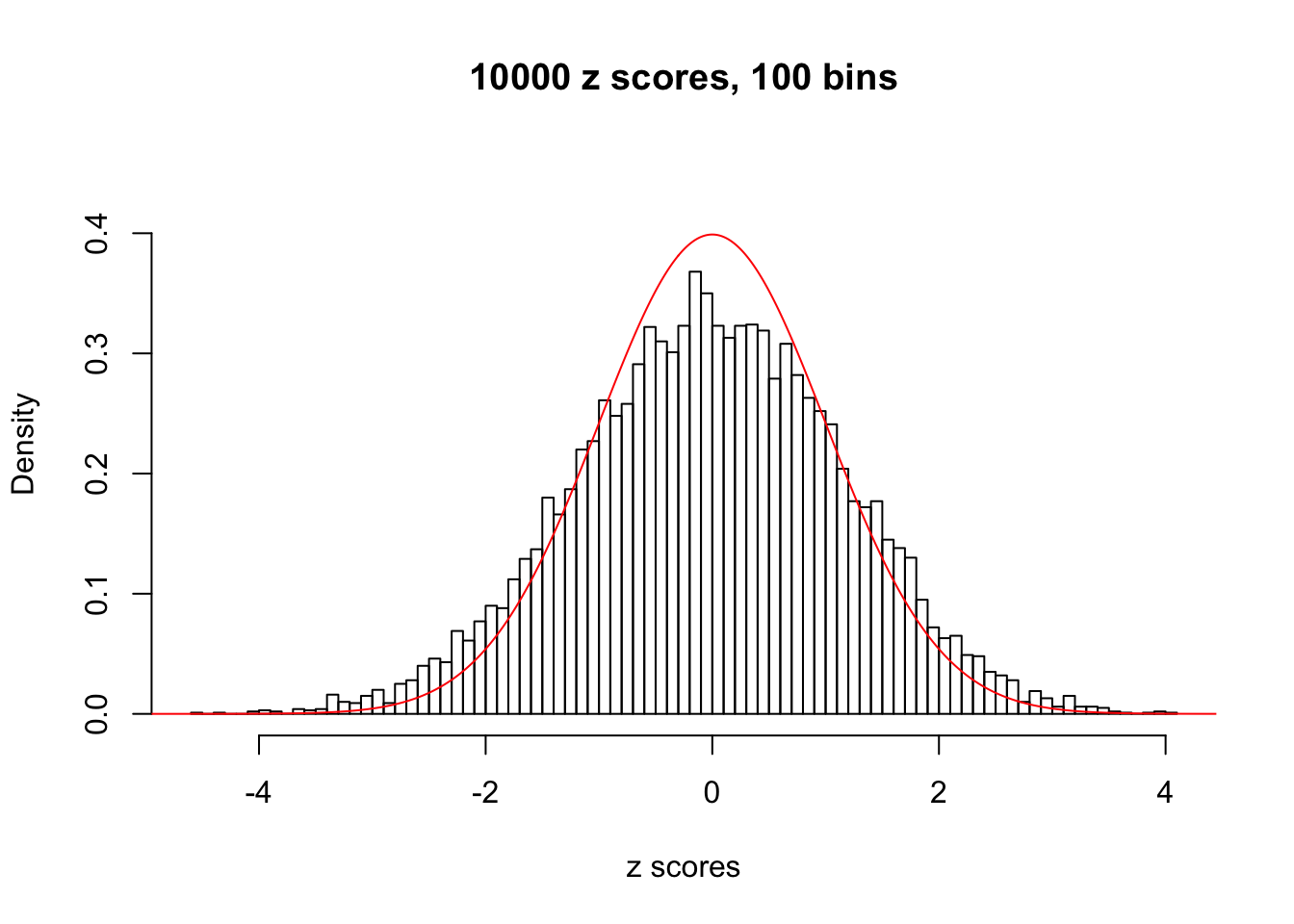
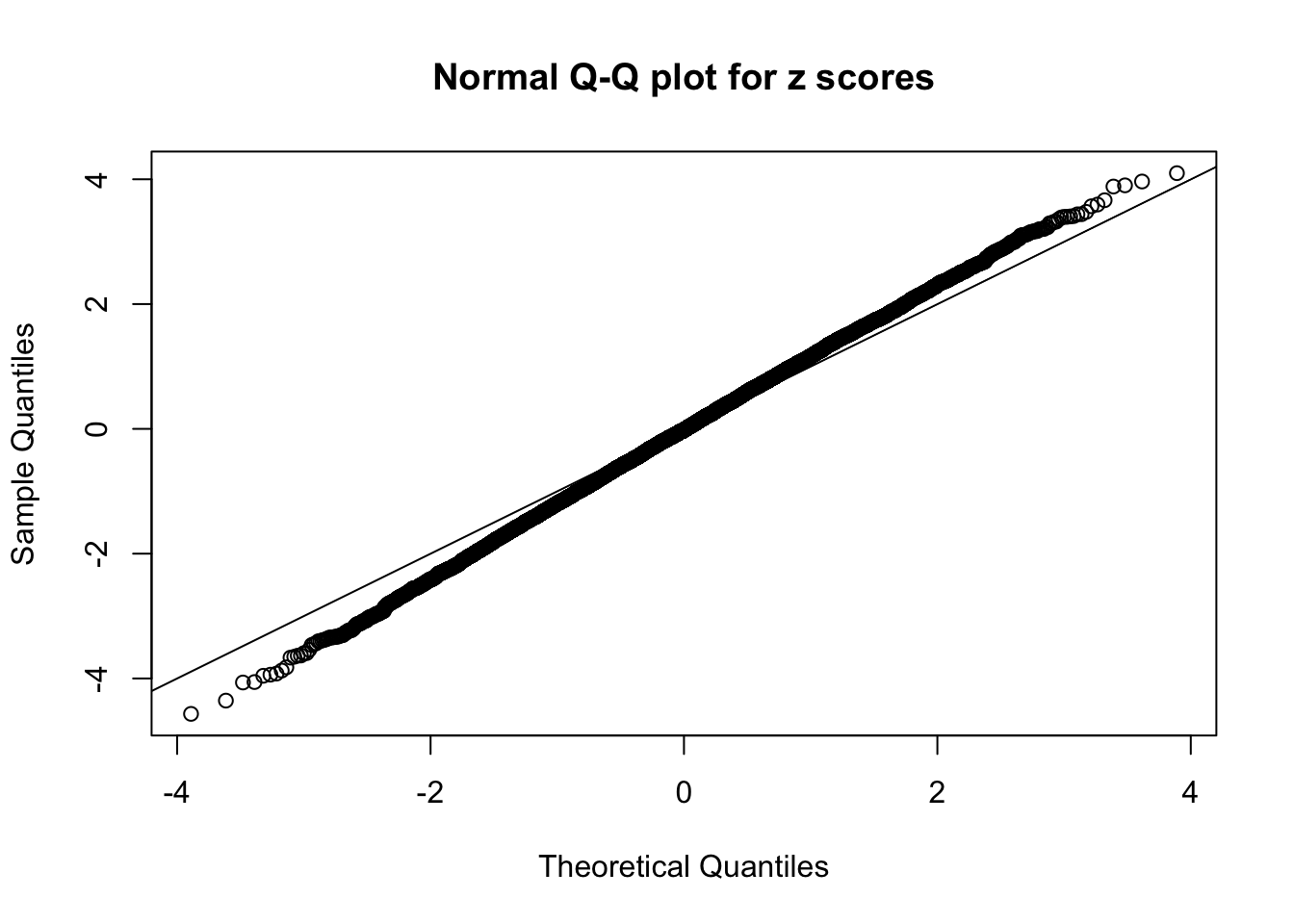
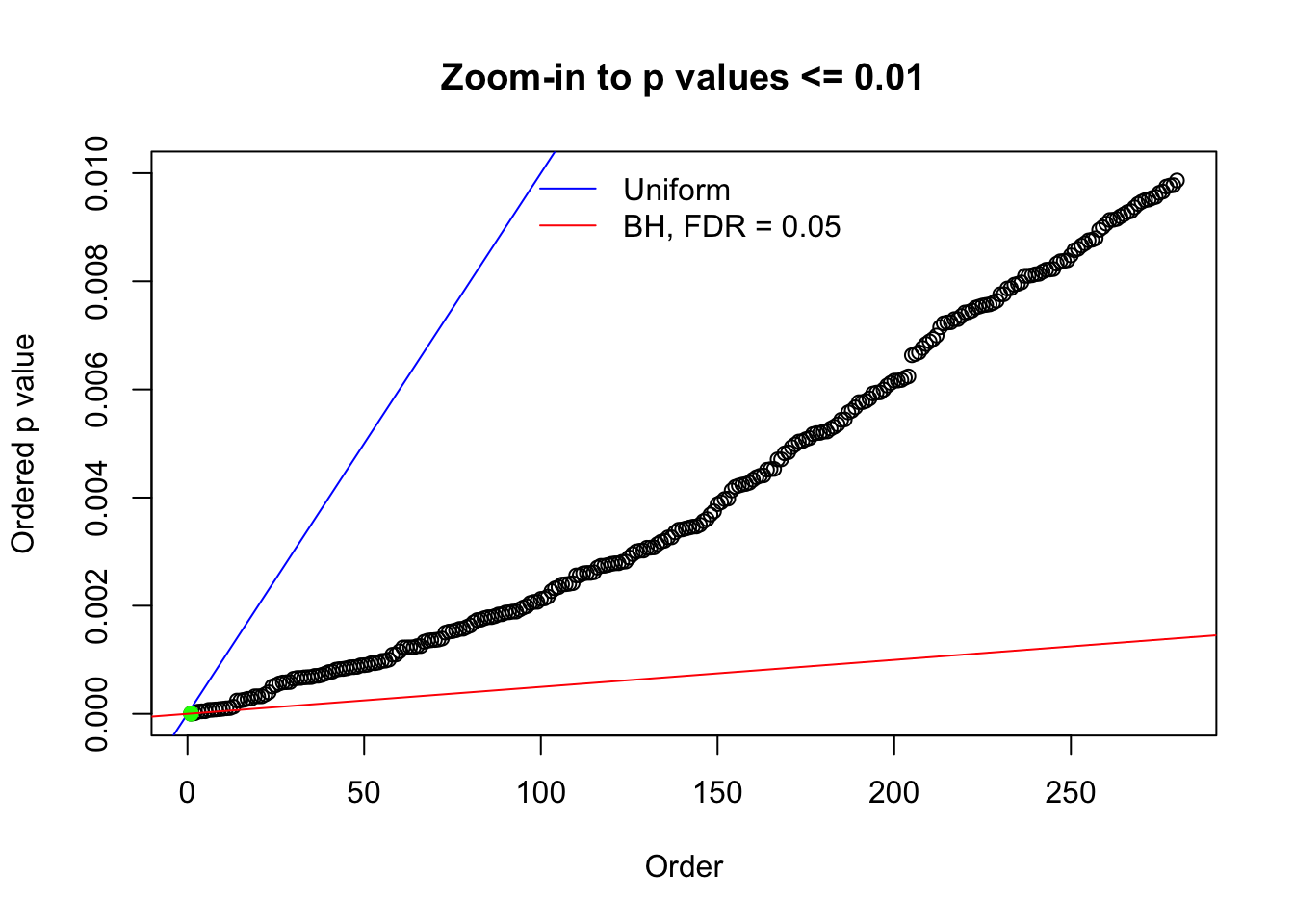
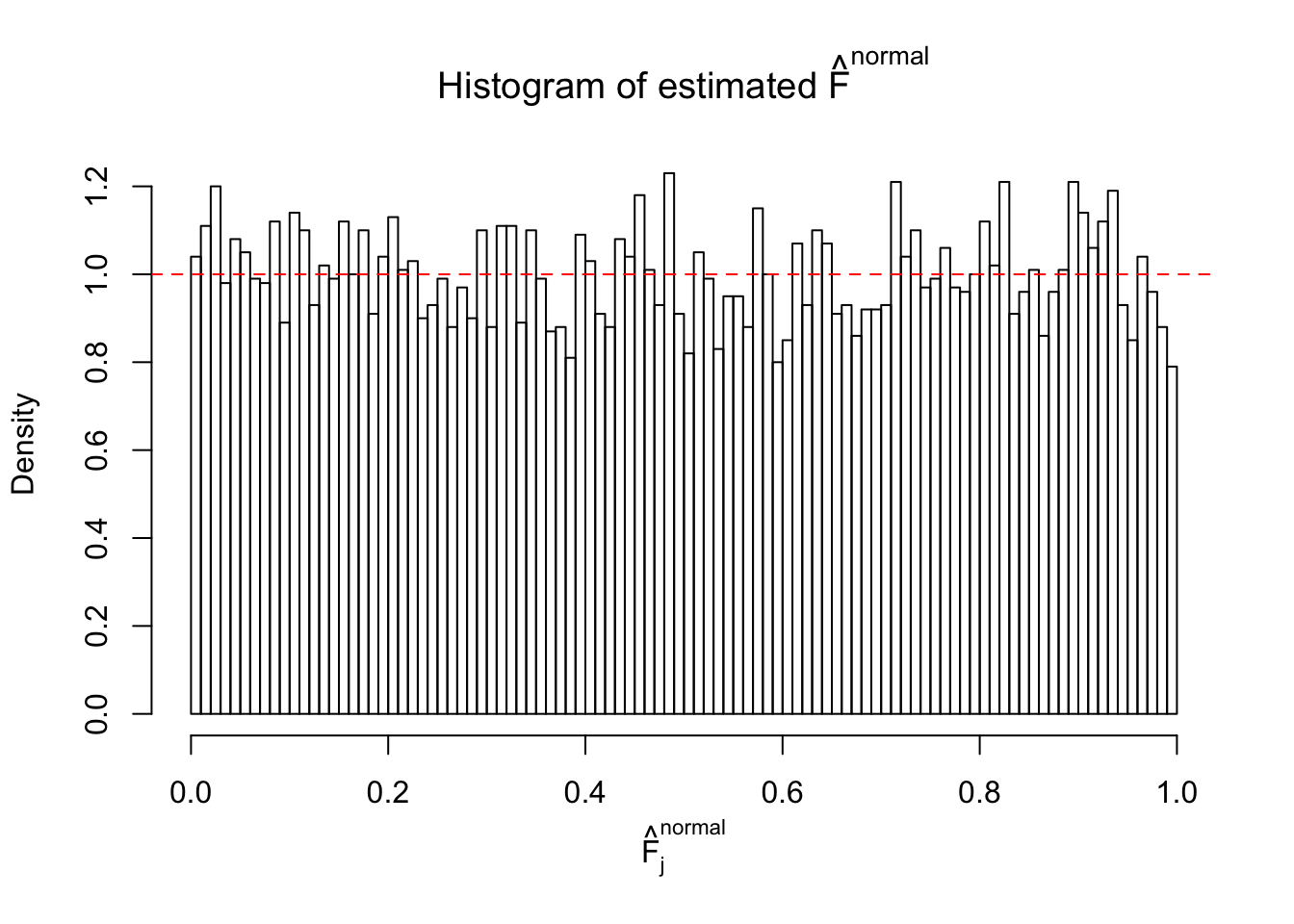
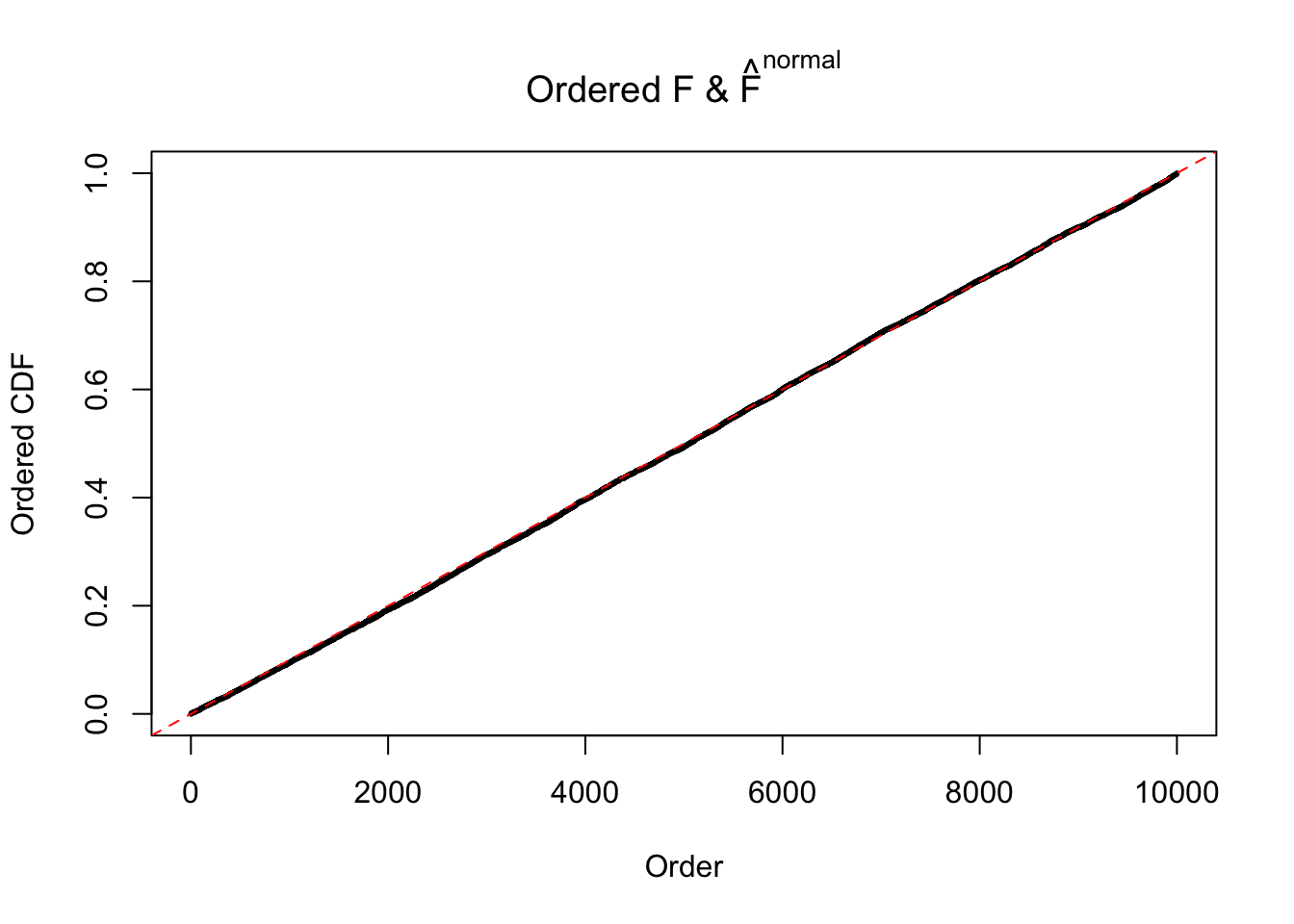
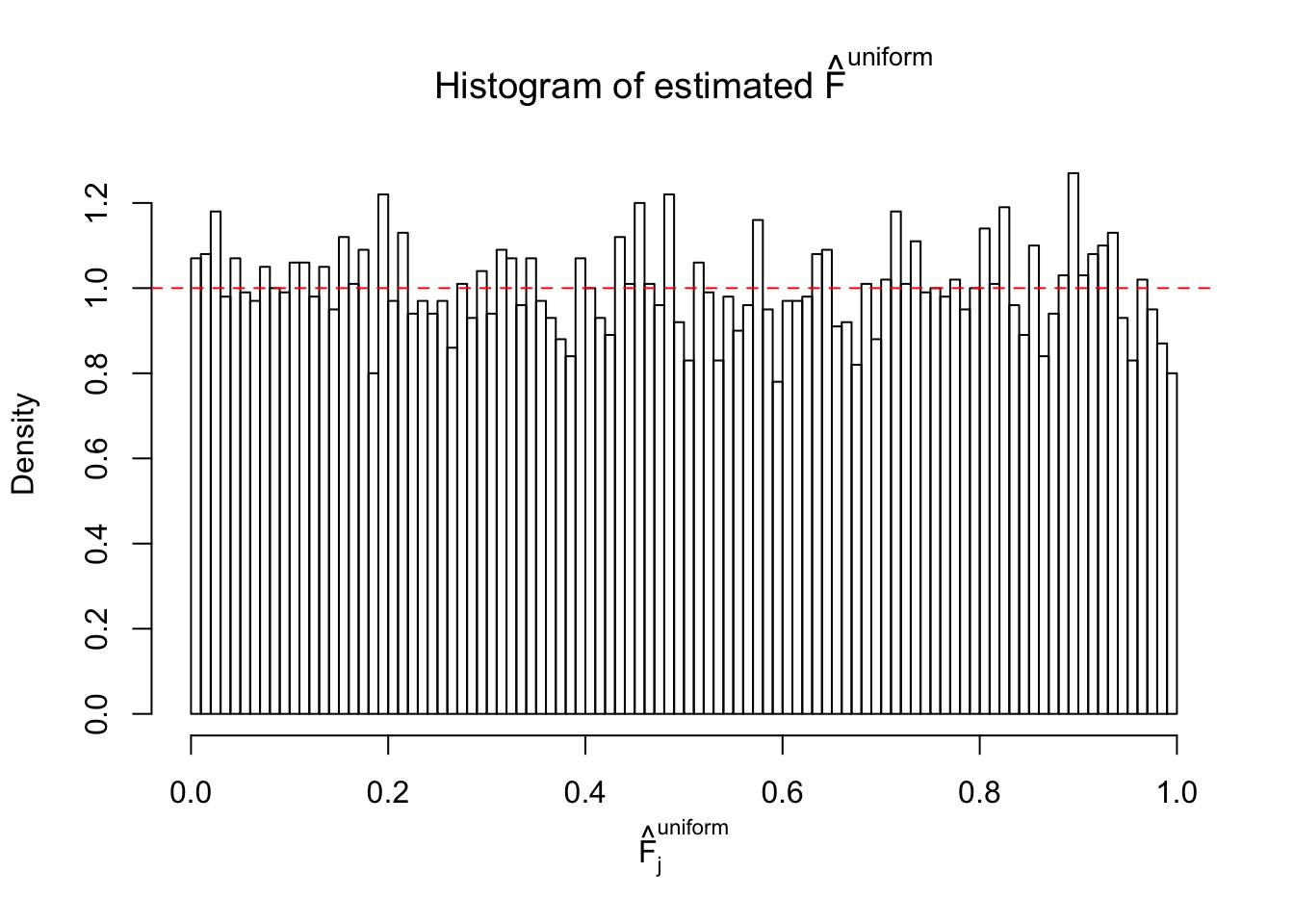
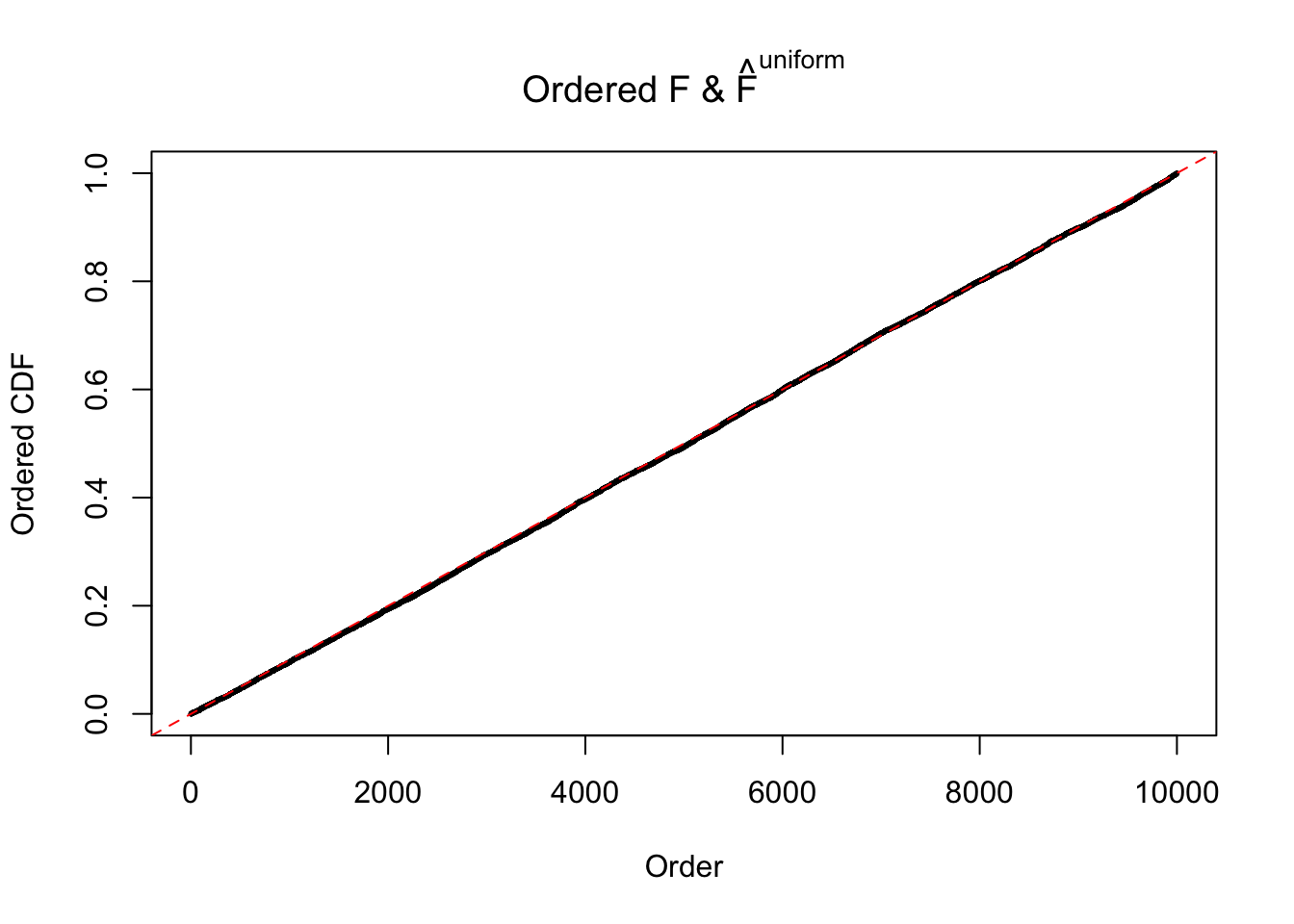
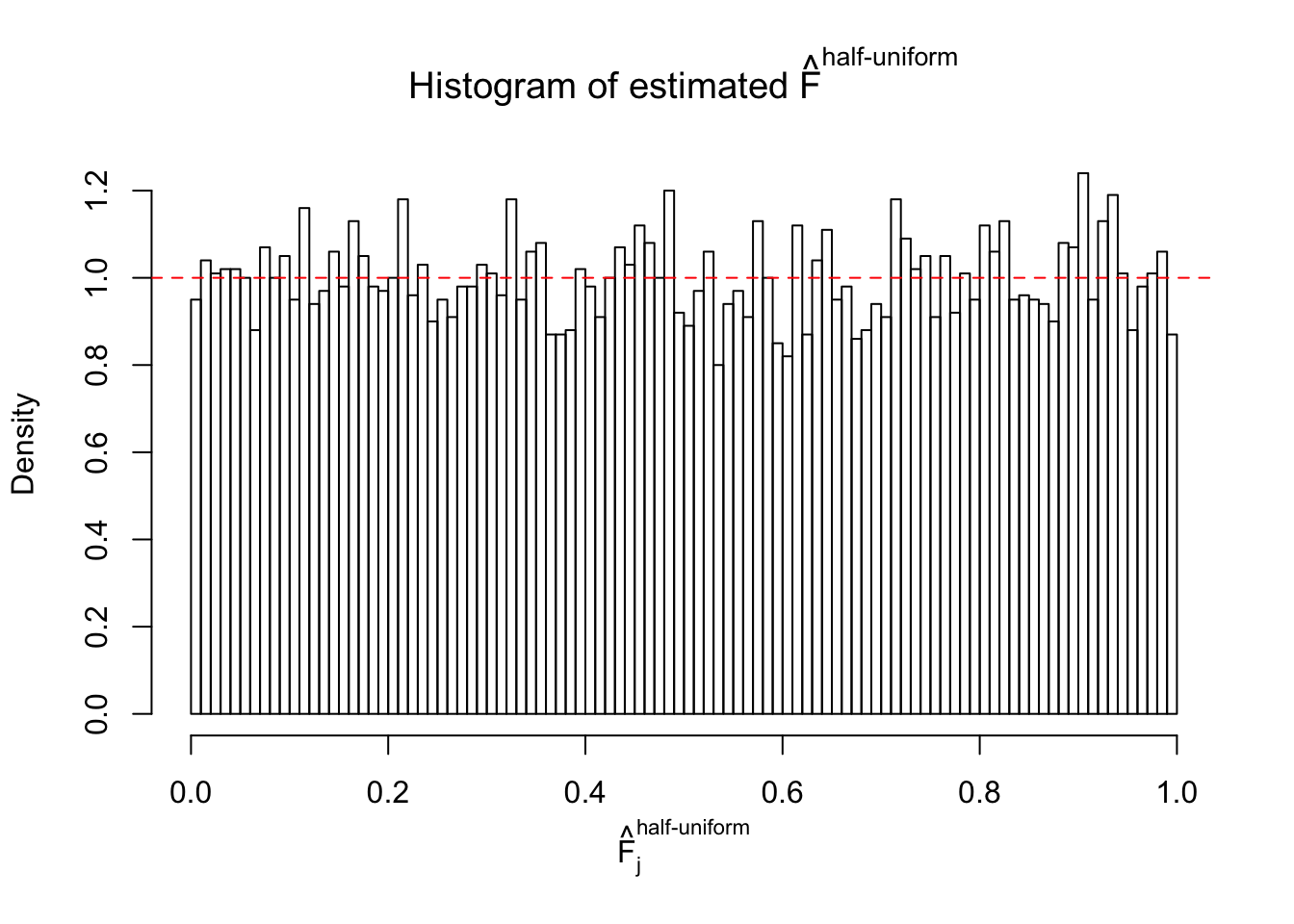
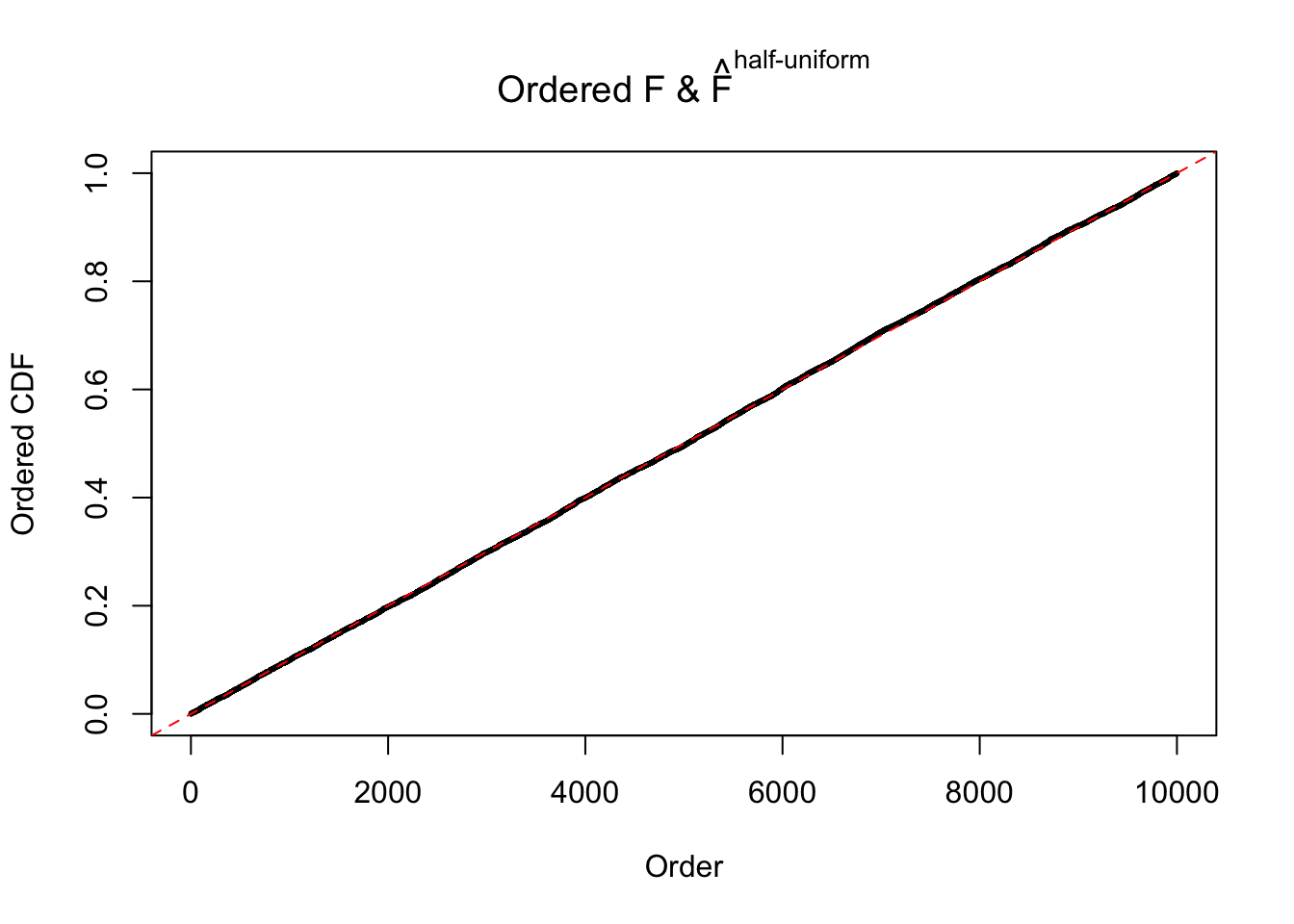
N0. 36 : Data Set 575 ; Number of False Discoveries: 1 ; pihat0 = 0.03307994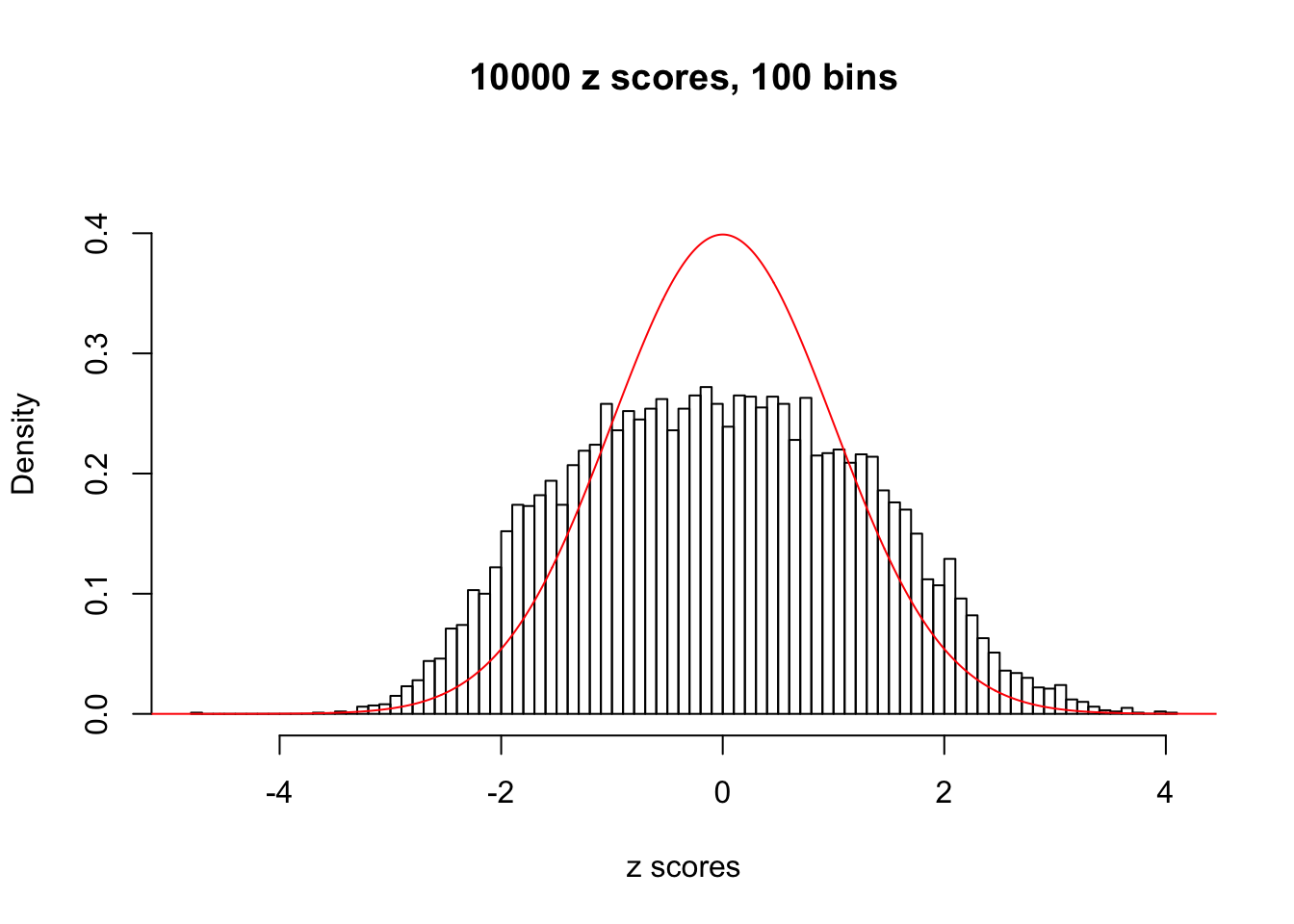
N0. 37 : Data Set 643 ; Number of False Discoveries: 1 ; pihat0 = 0.160838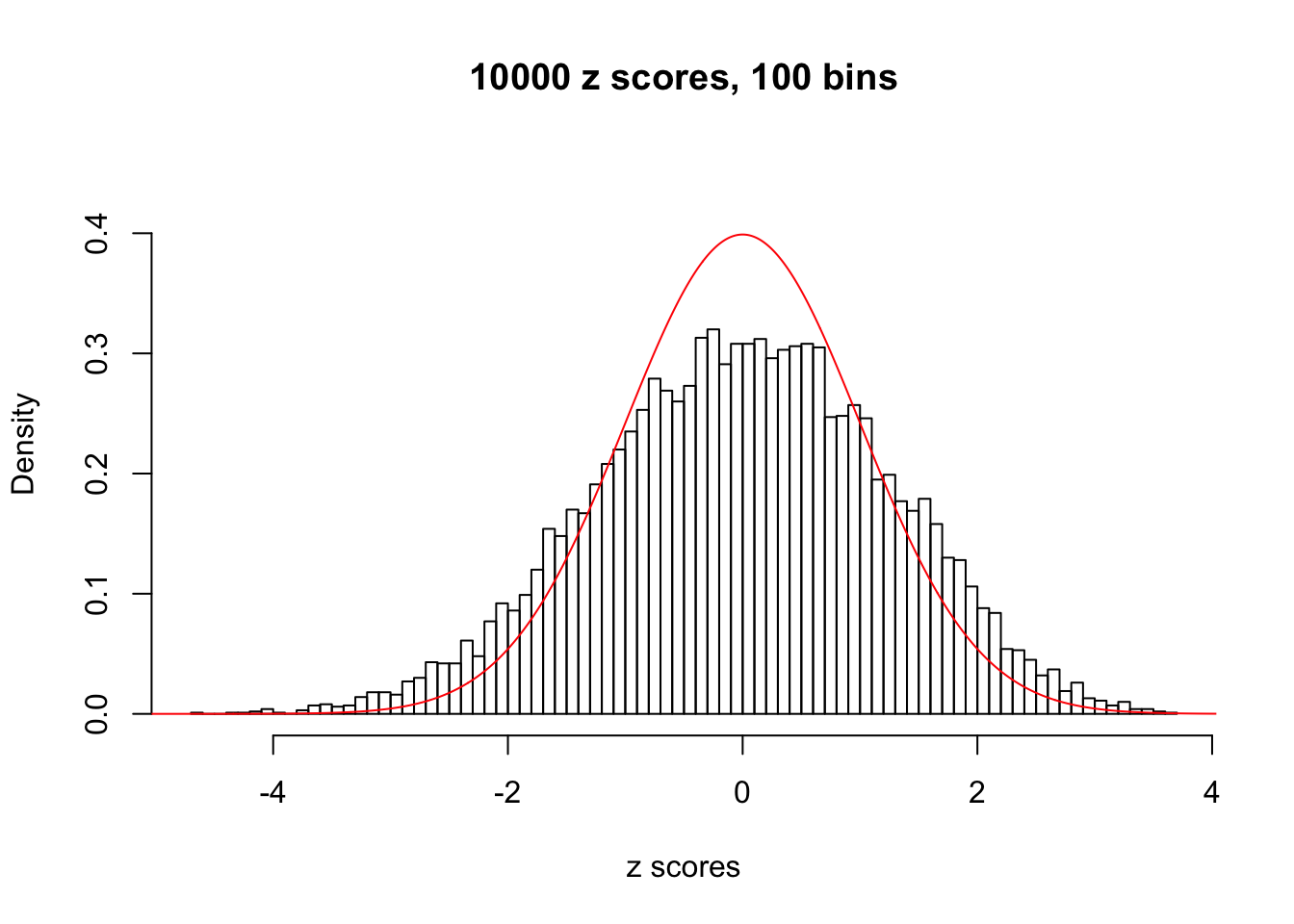
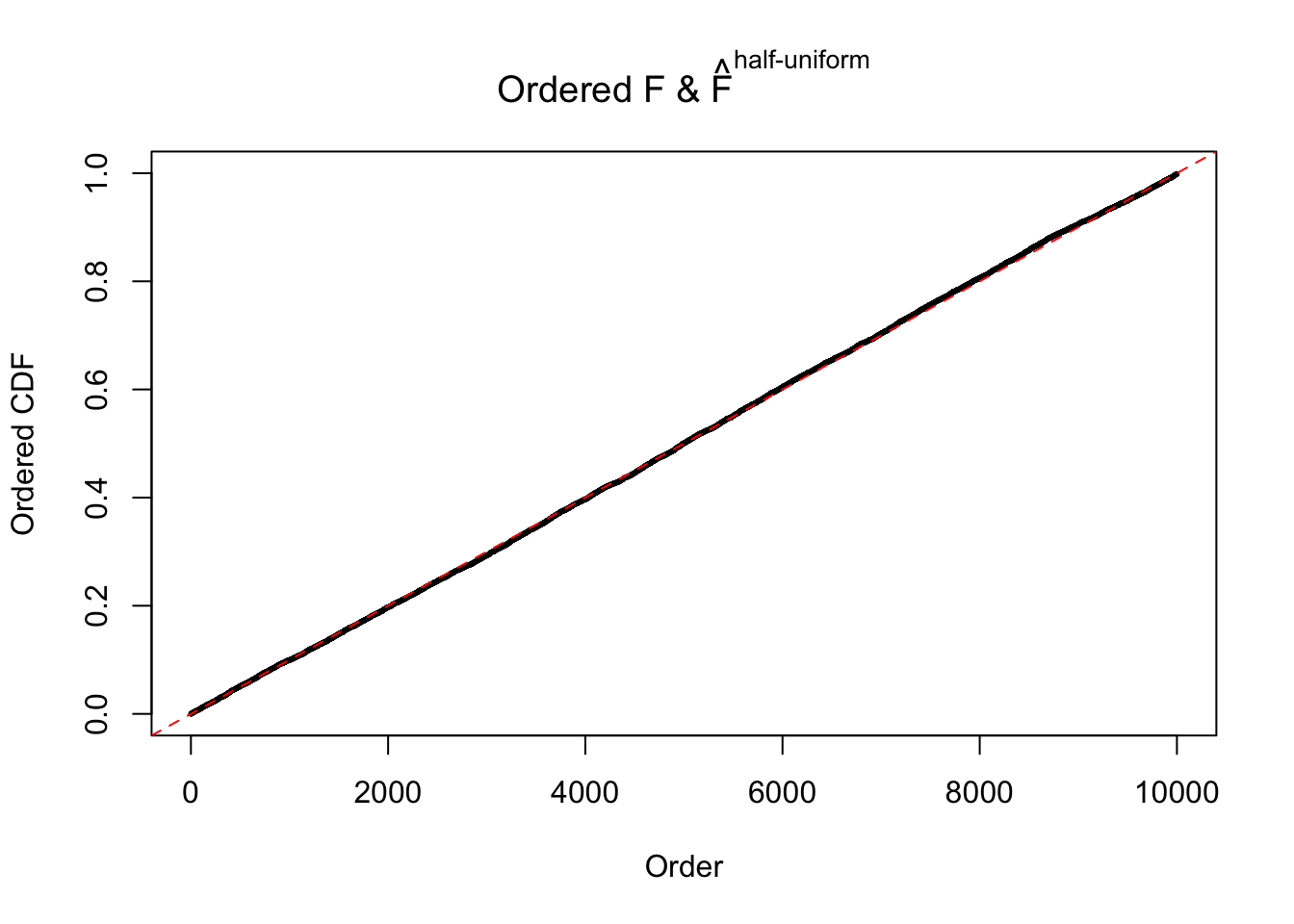
N0. 38 : Data Set 769 ; Number of False Discoveries: 1 ; pihat0 = 0.1227421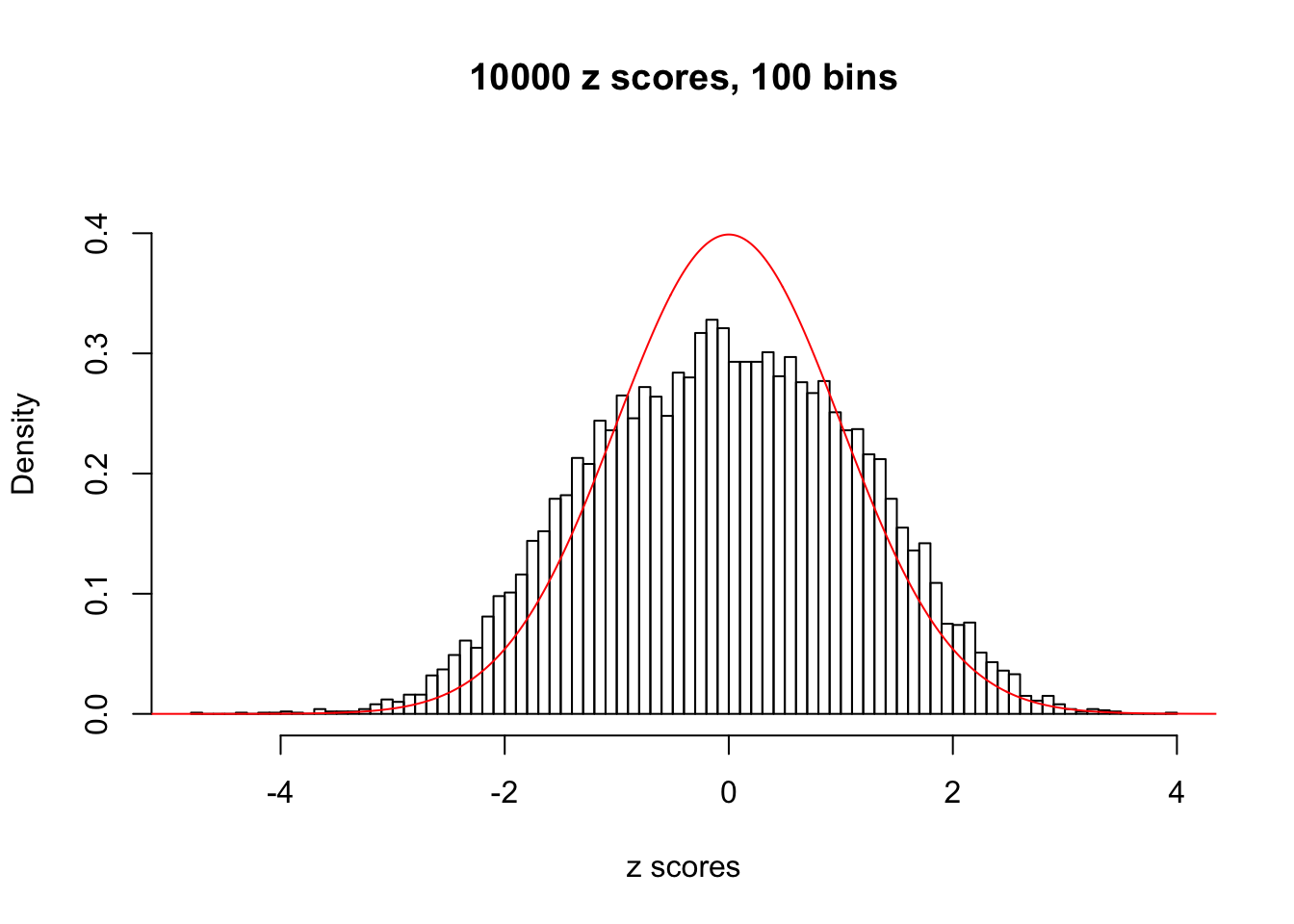
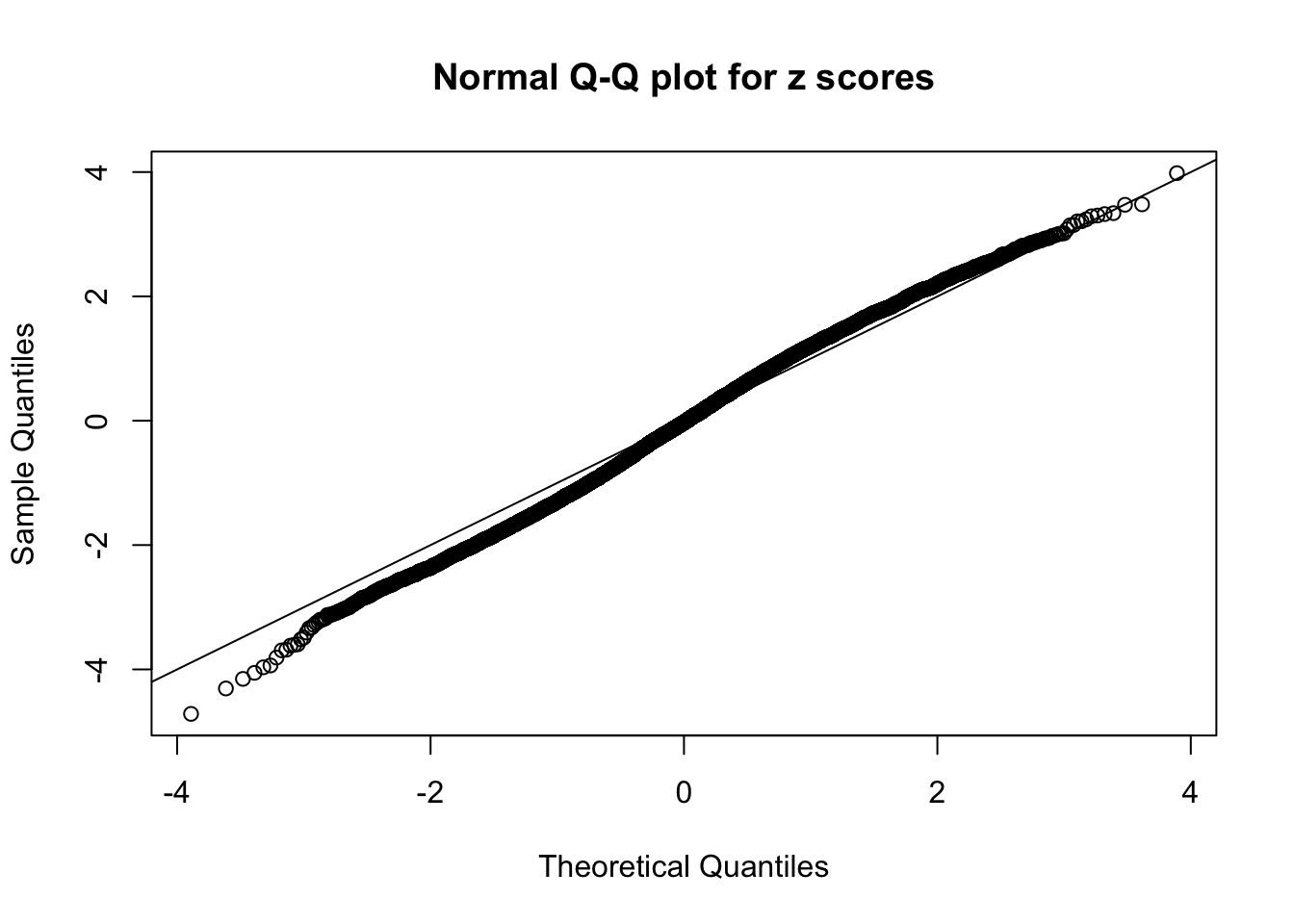
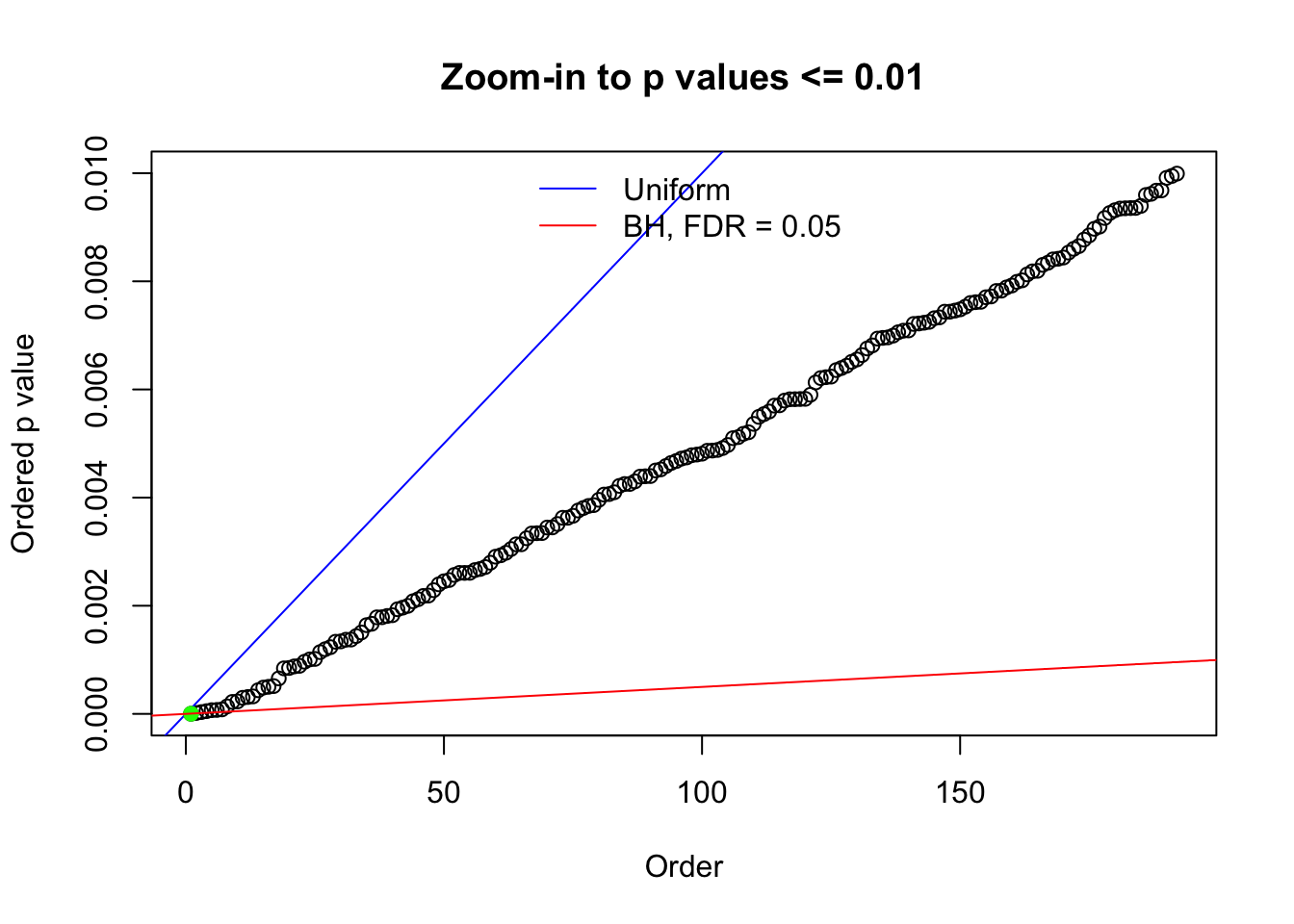
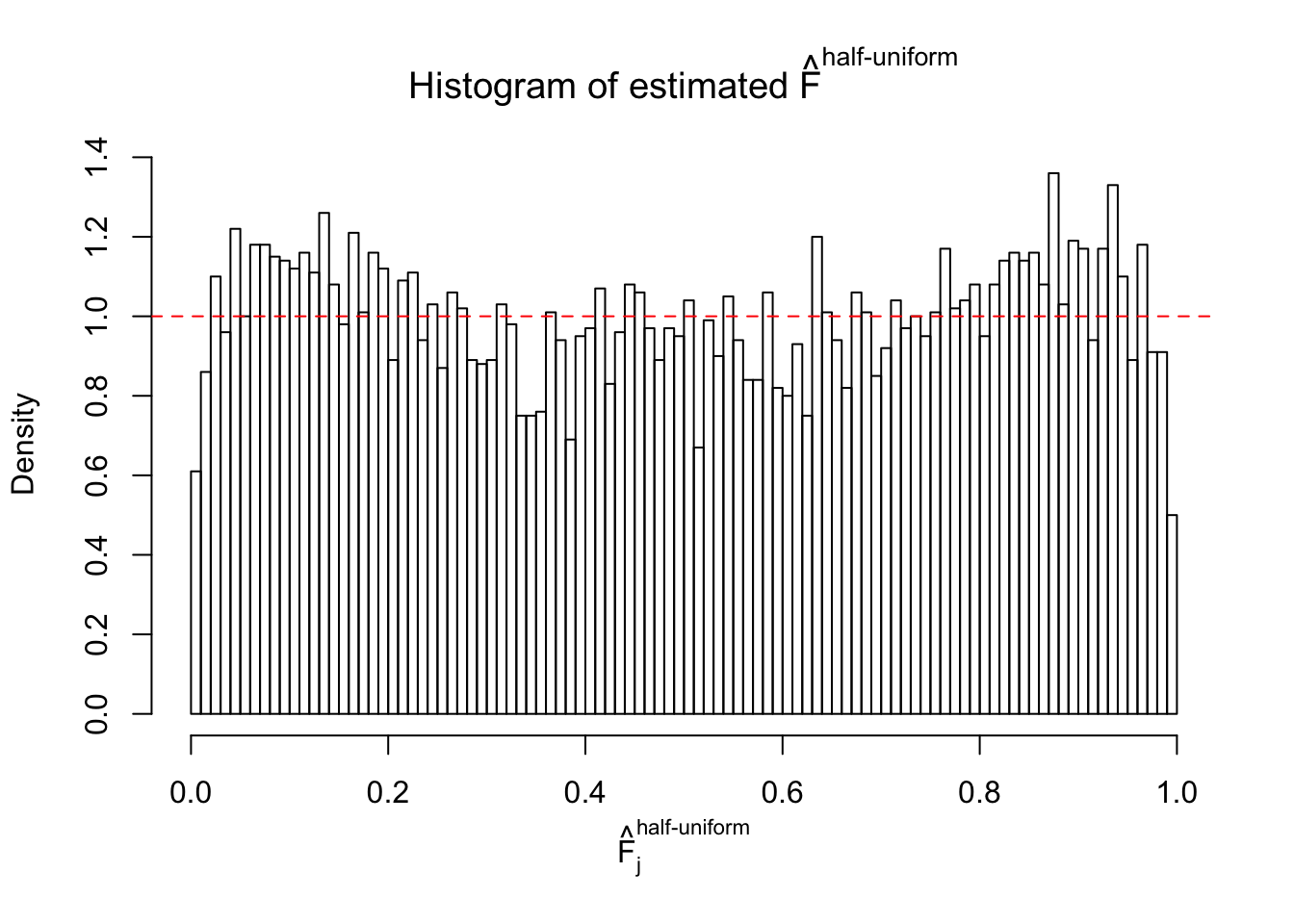
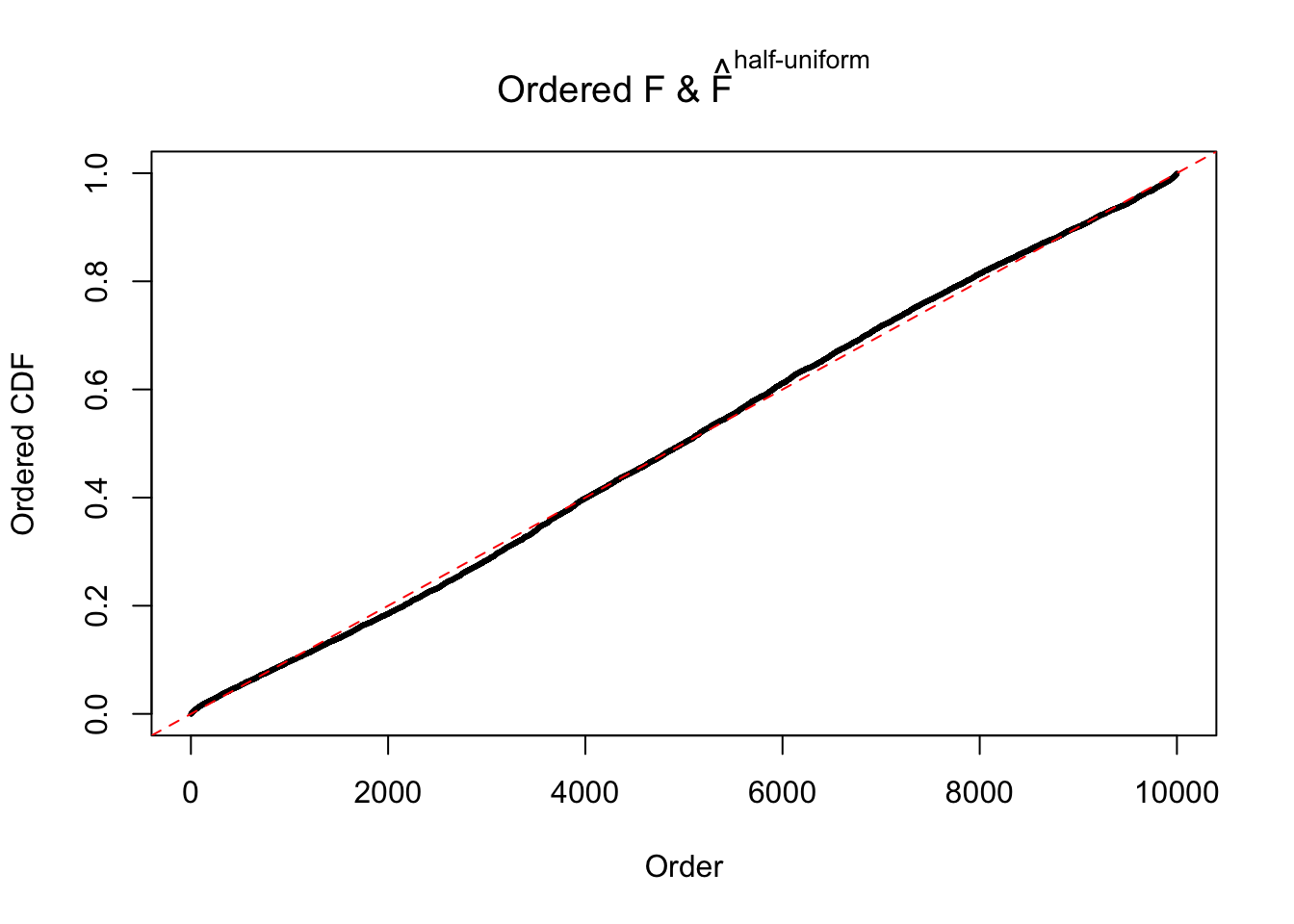
N0. 39 : Data Set 778 ; Number of False Discoveries: 1 ; pihat0 = 0.05117821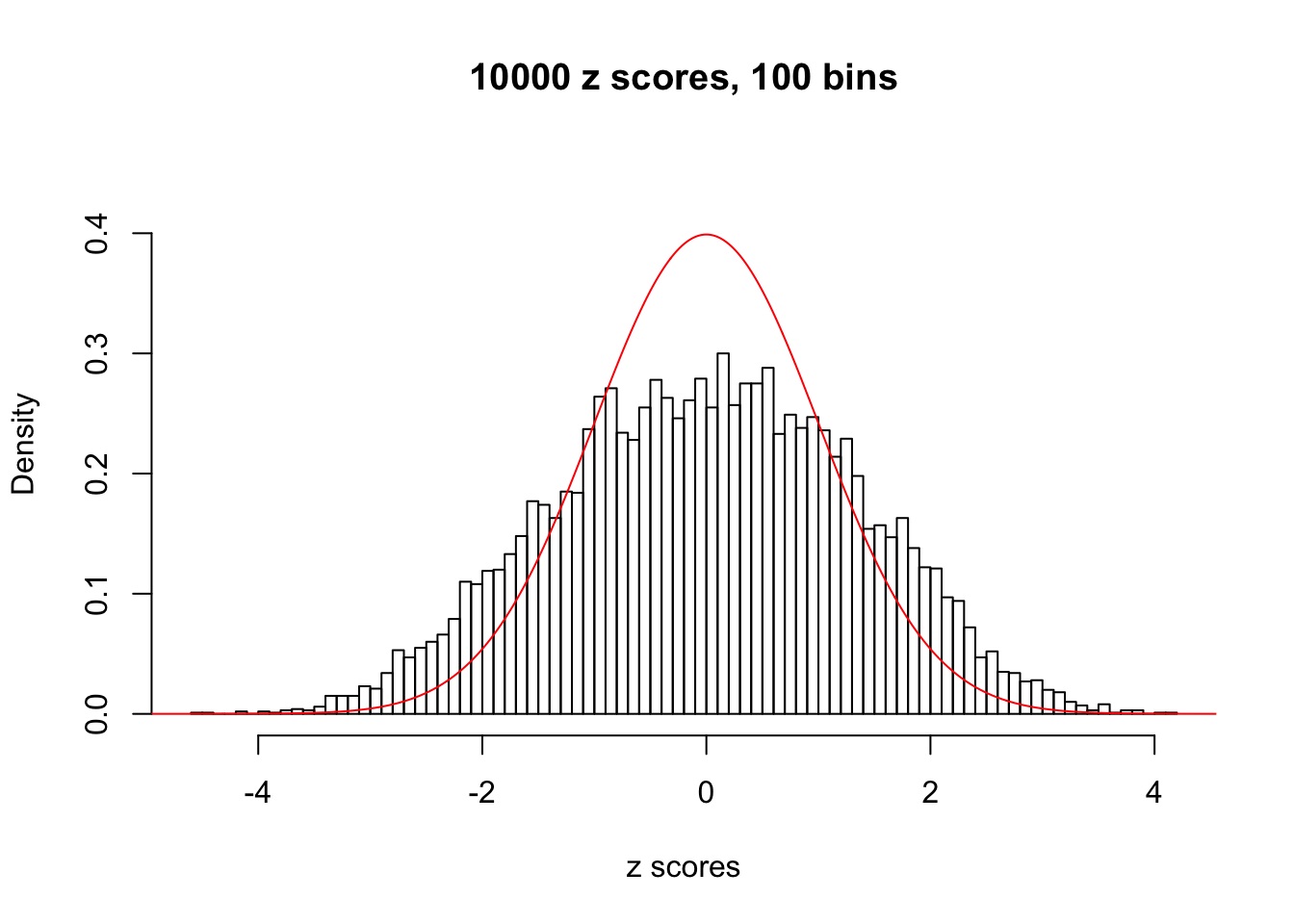
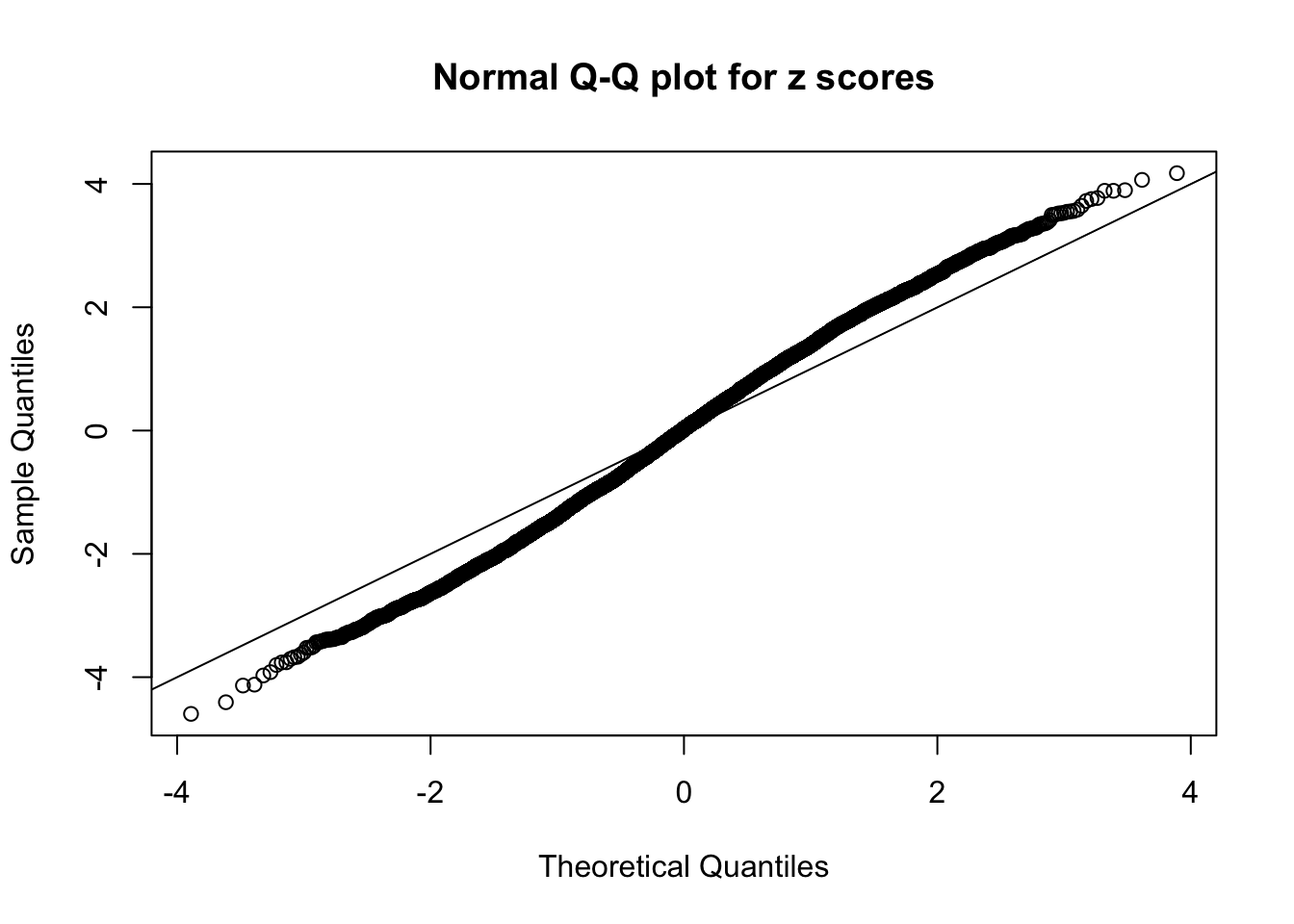
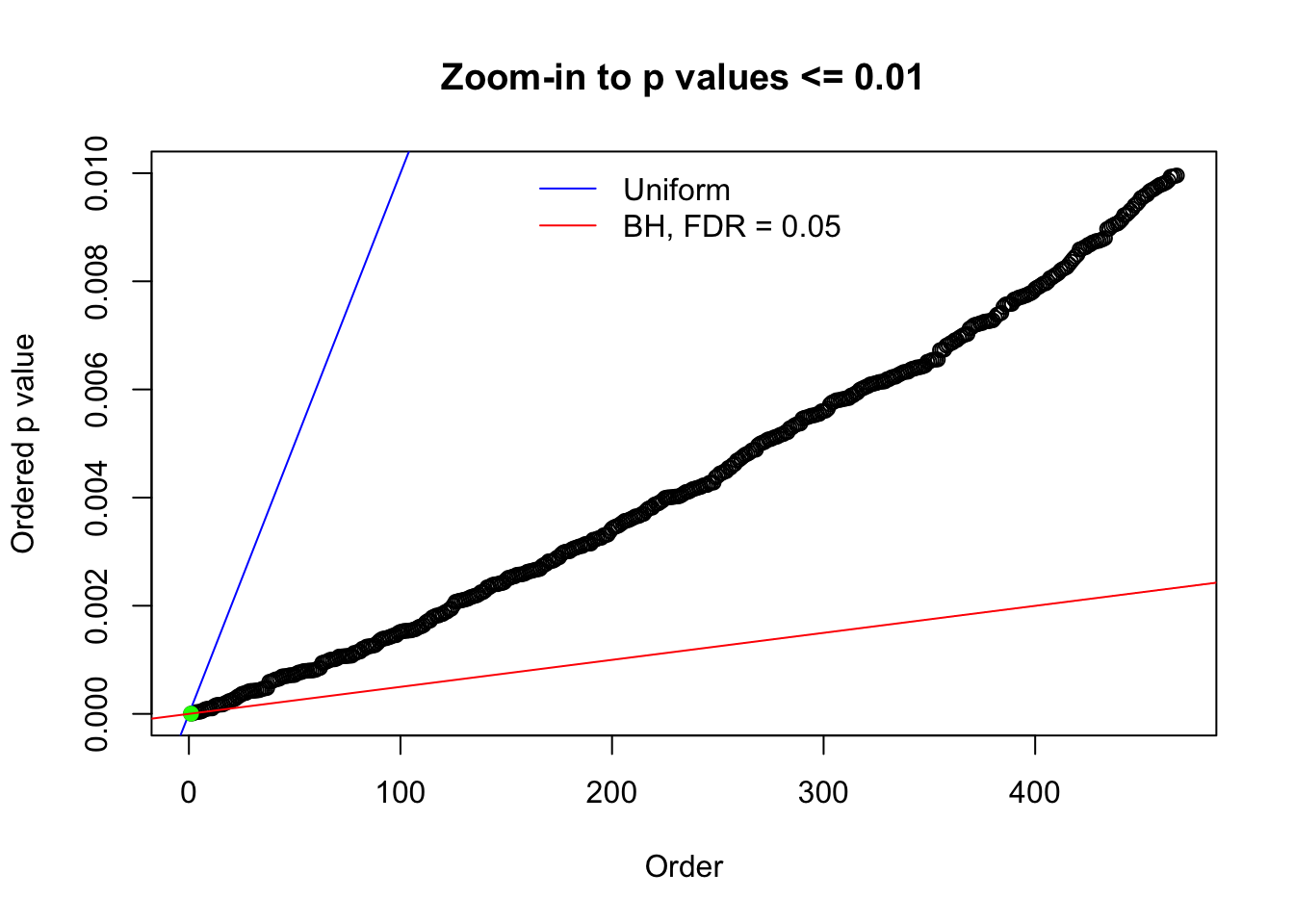
N0. 40 : Data Set 817 ; Number of False Discoveries: 1 ; pihat0 = 1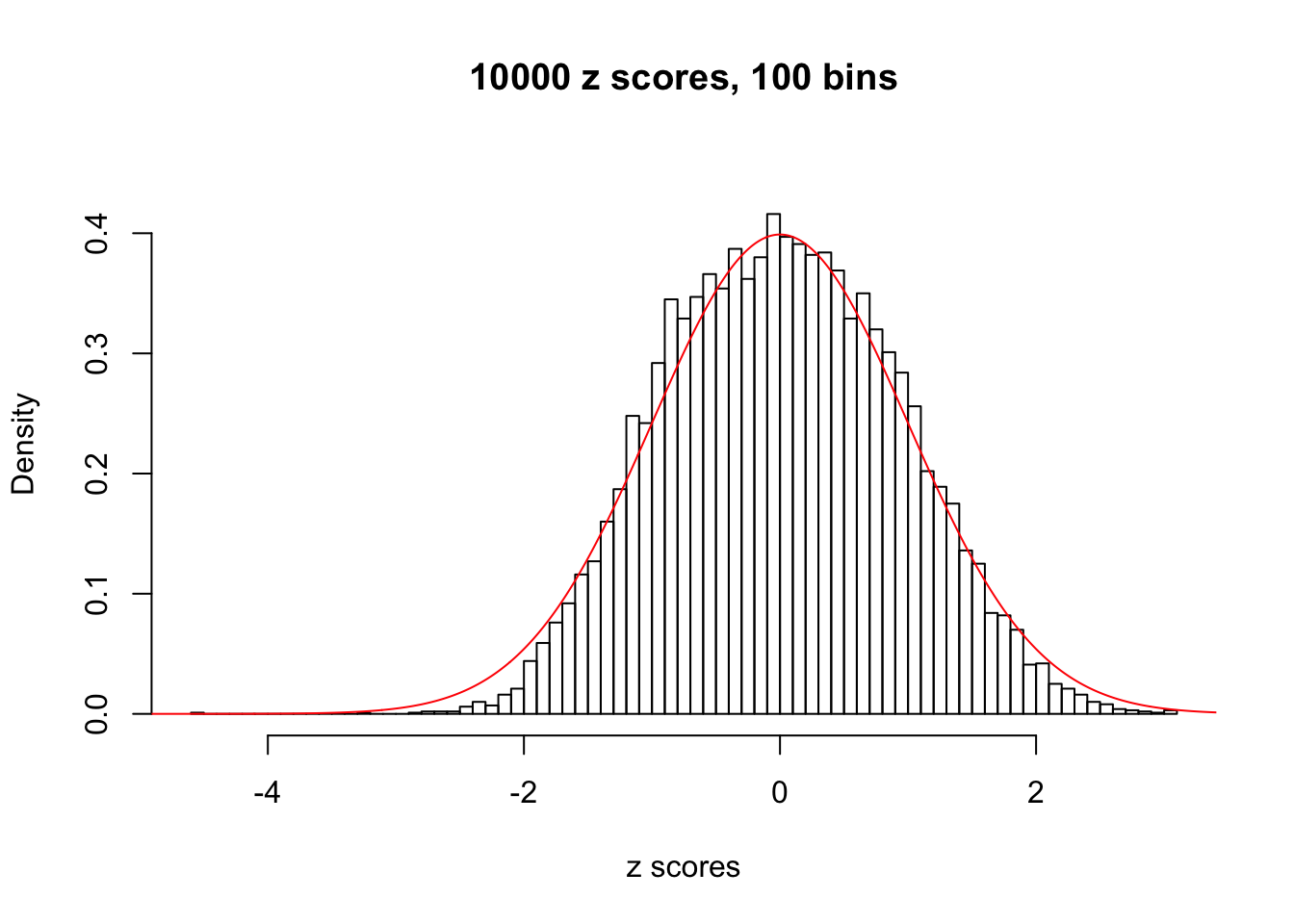
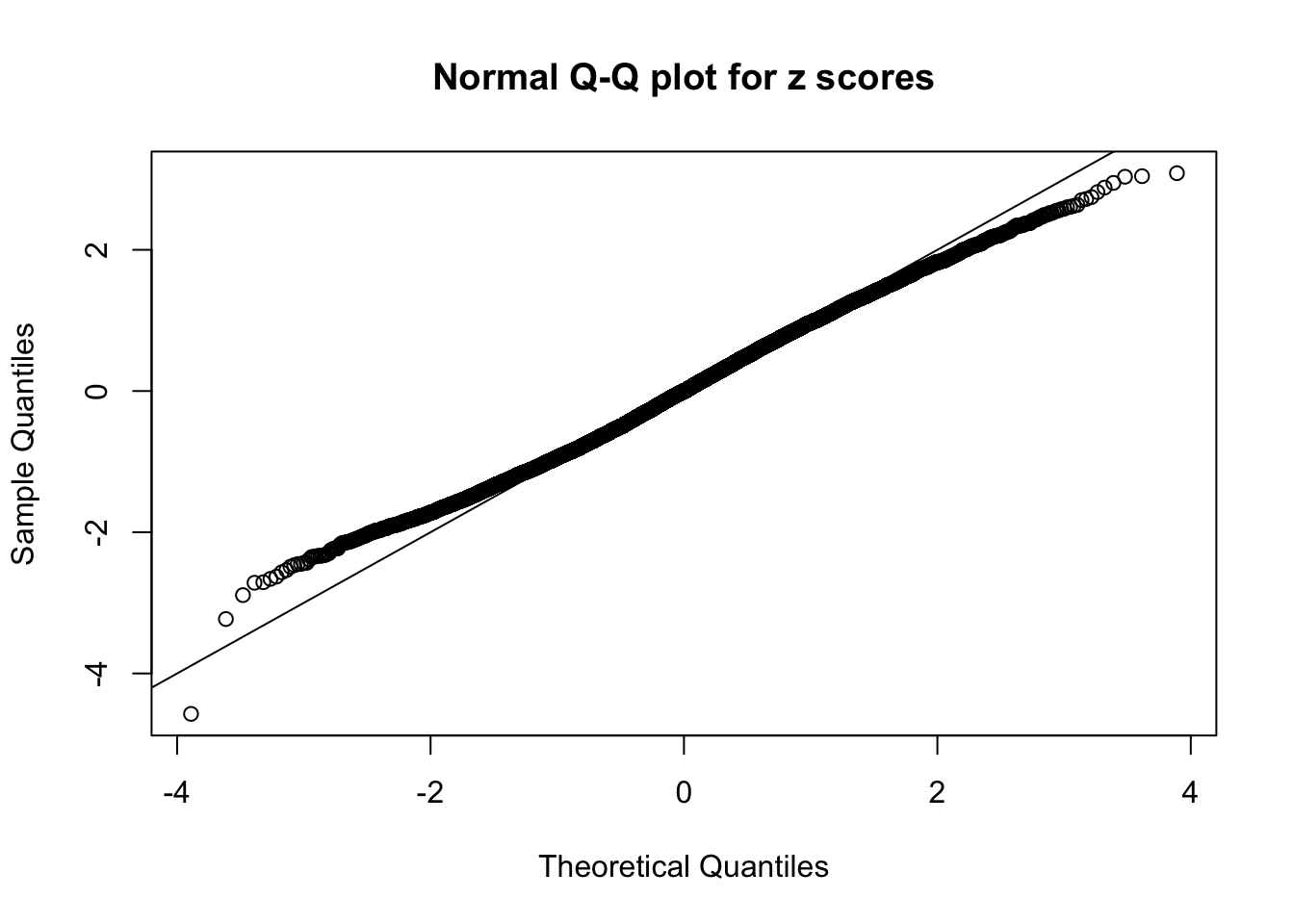
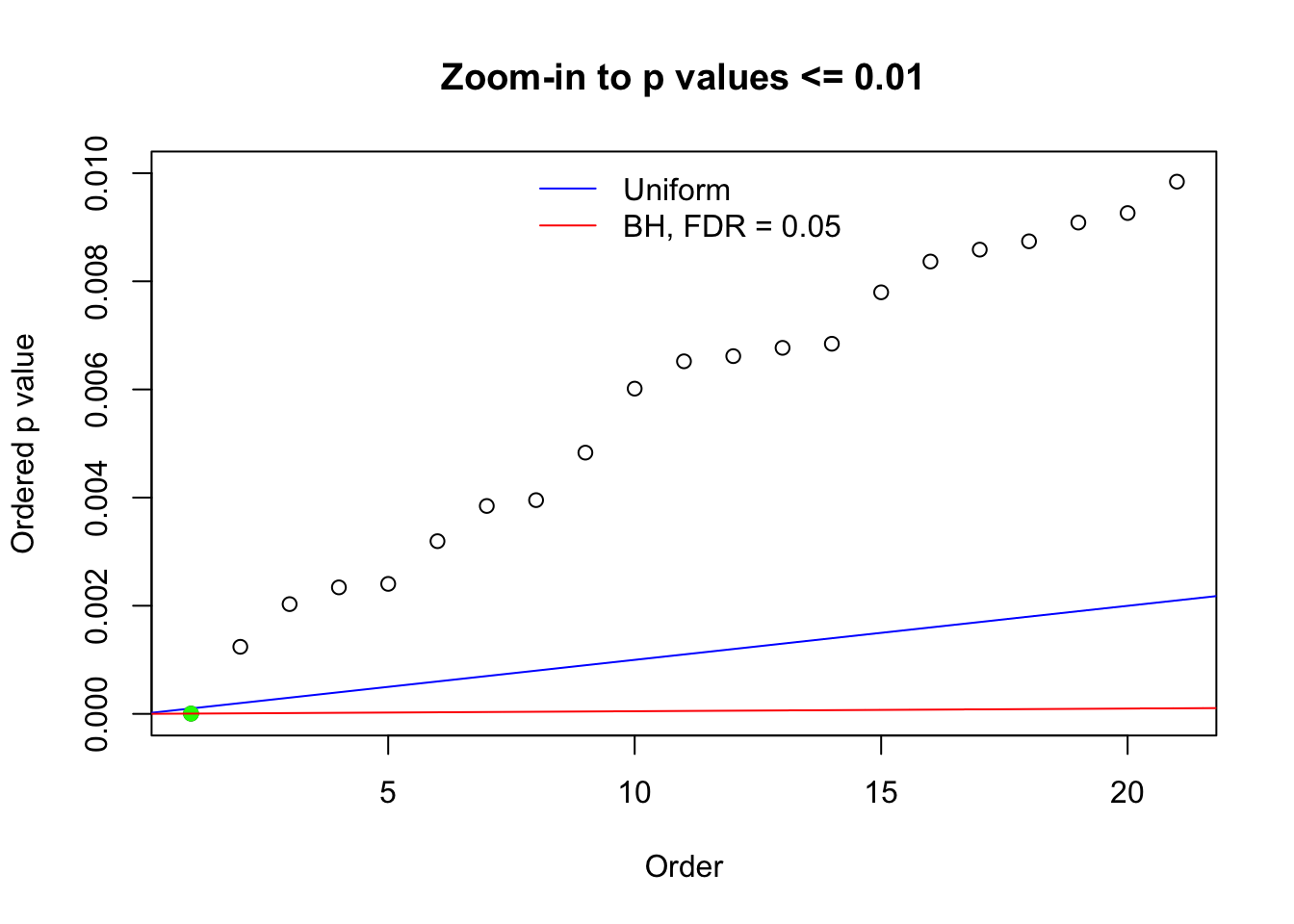
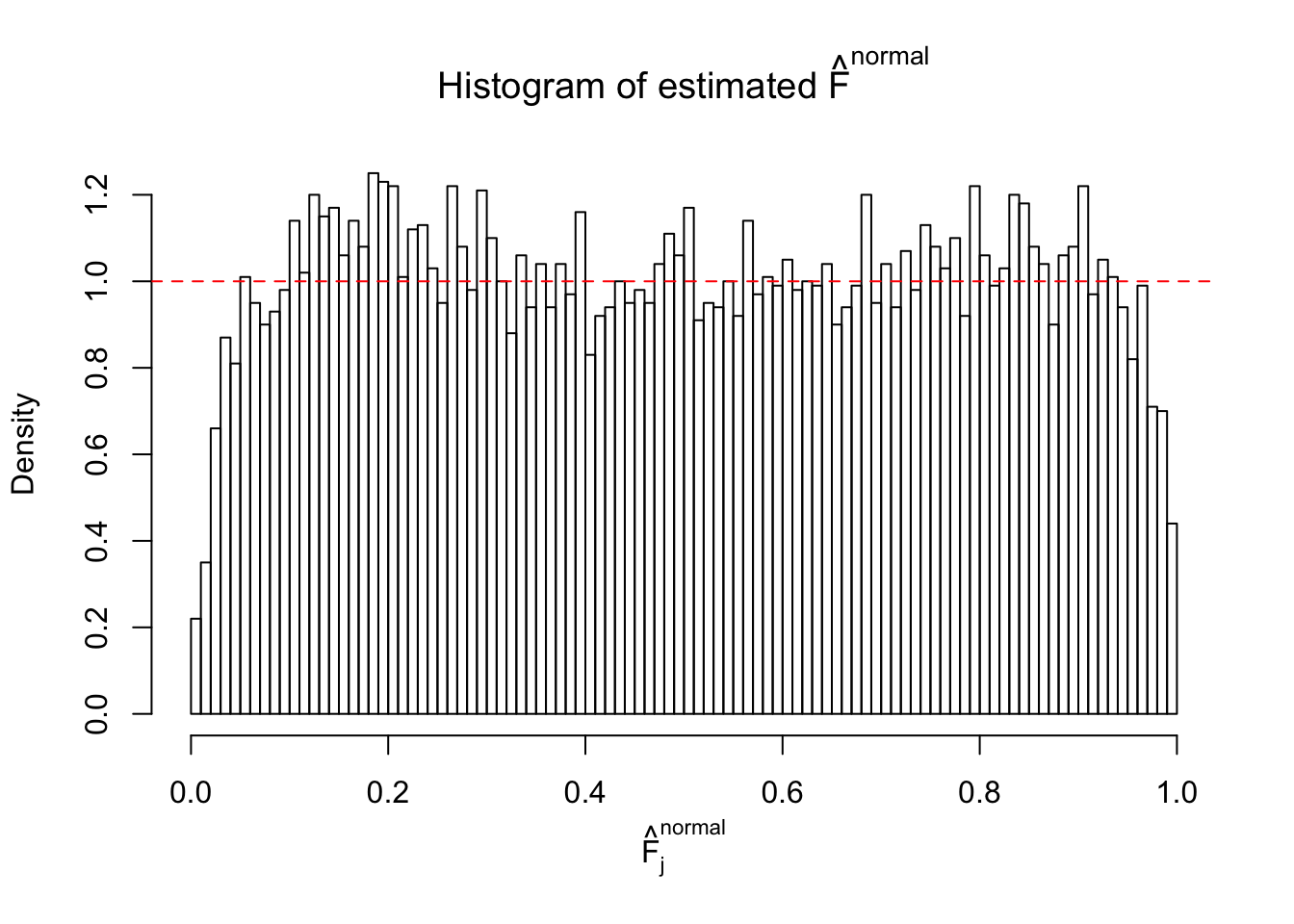
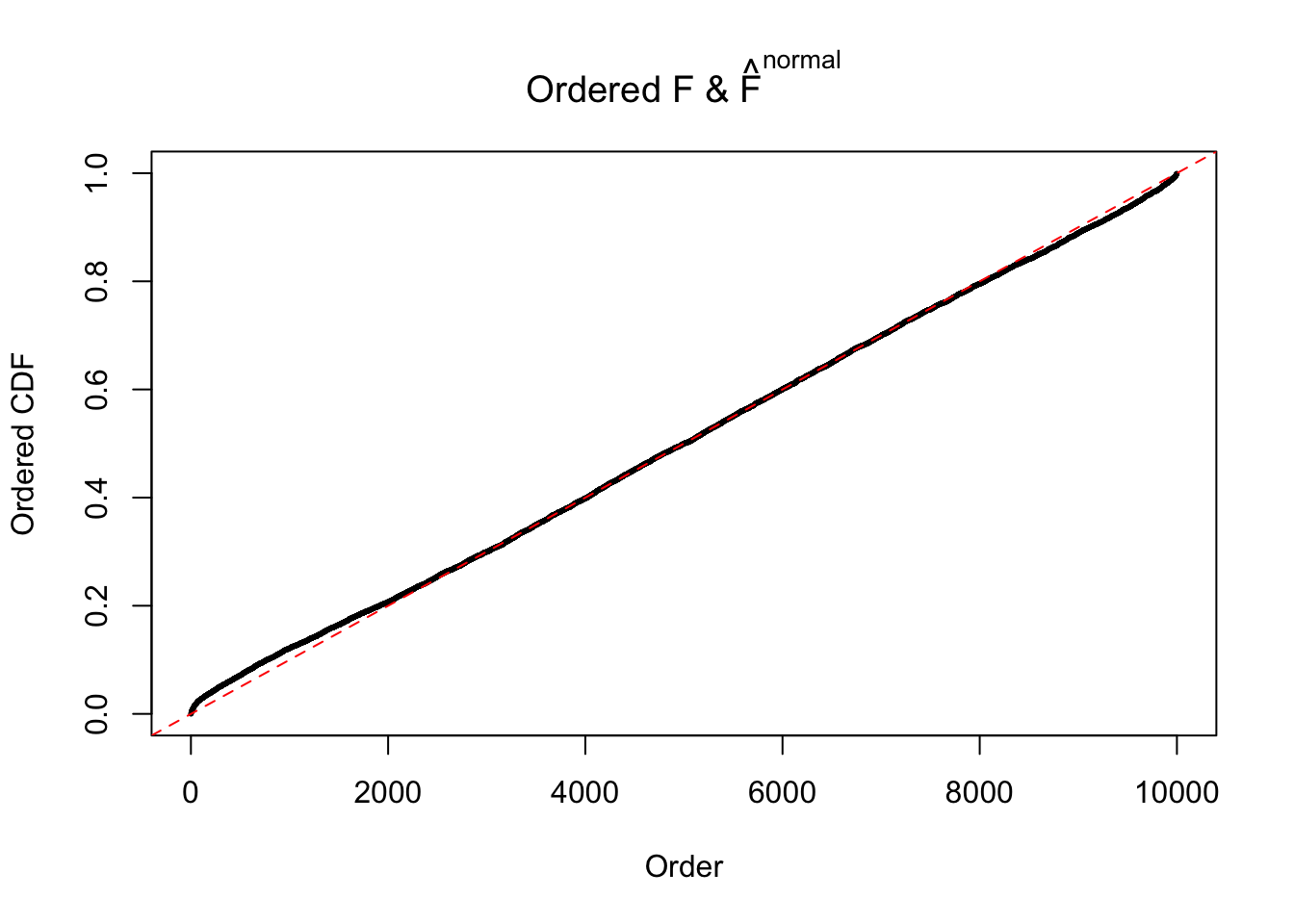
N0. 41 : Data Set 837 ; Number of False Discoveries: 1 ; pihat0 = 0.828704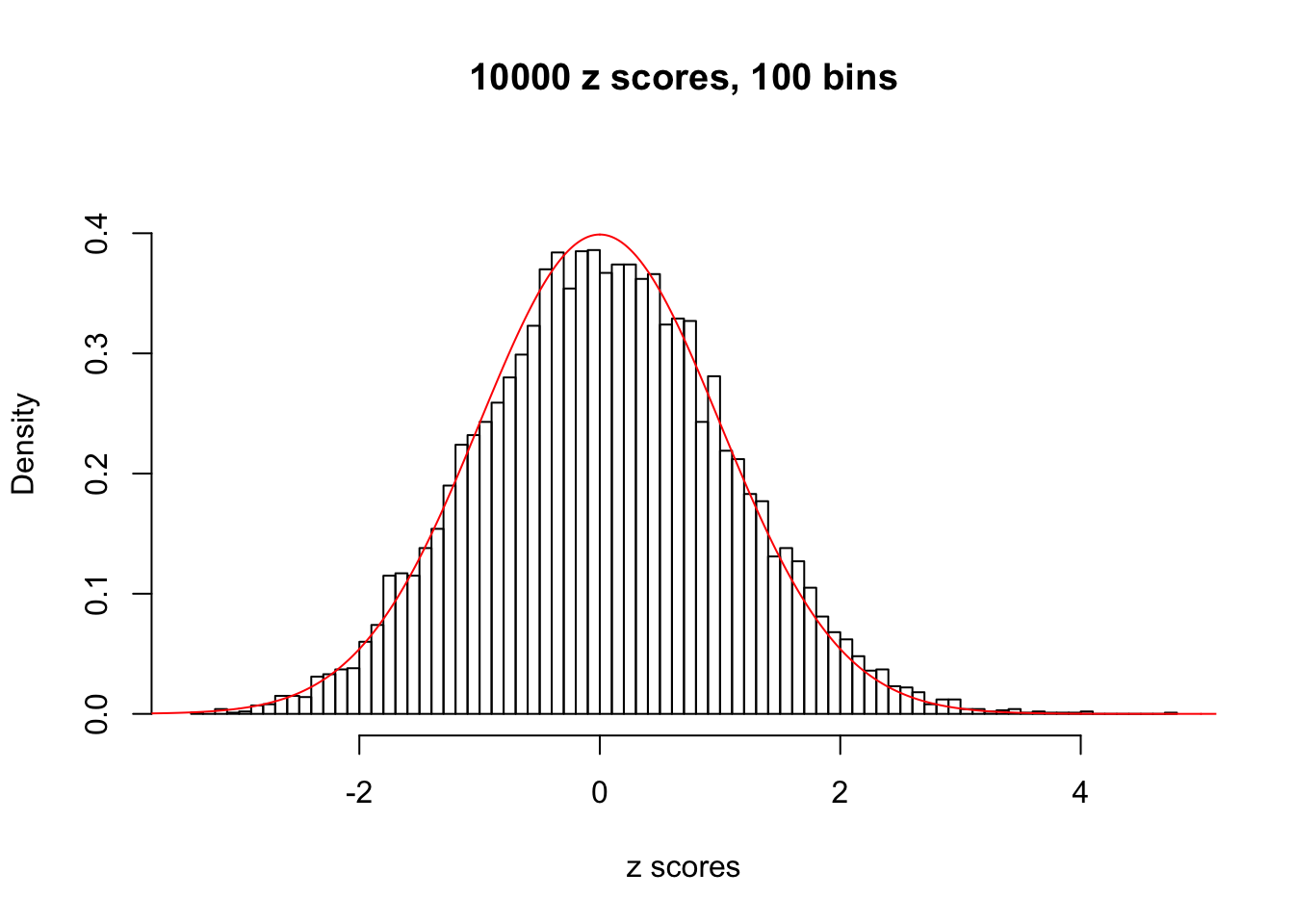
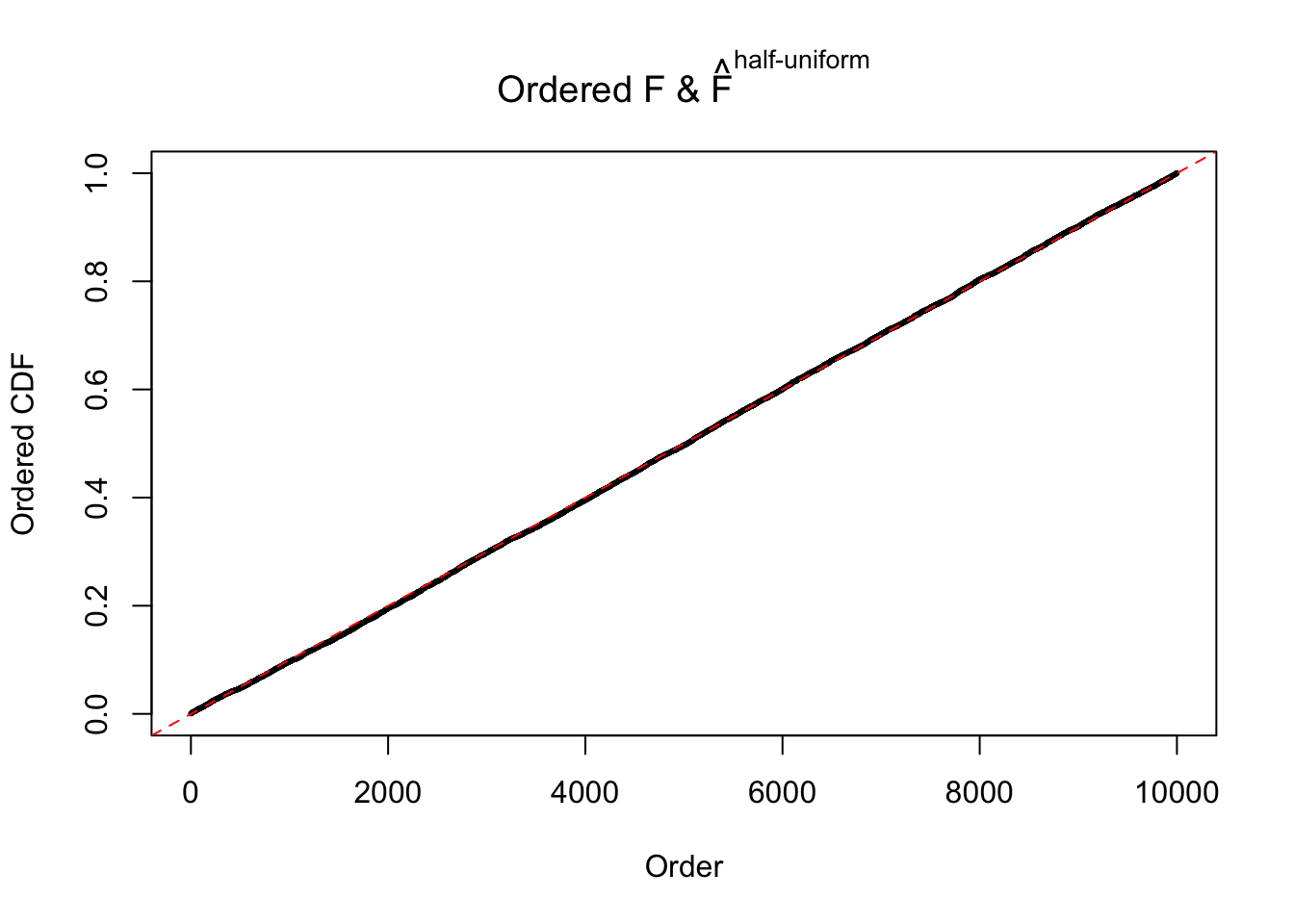
N0. 42 : Data Set 897 ; Number of False Discoveries: 1 ; pihat0 = 0.7555982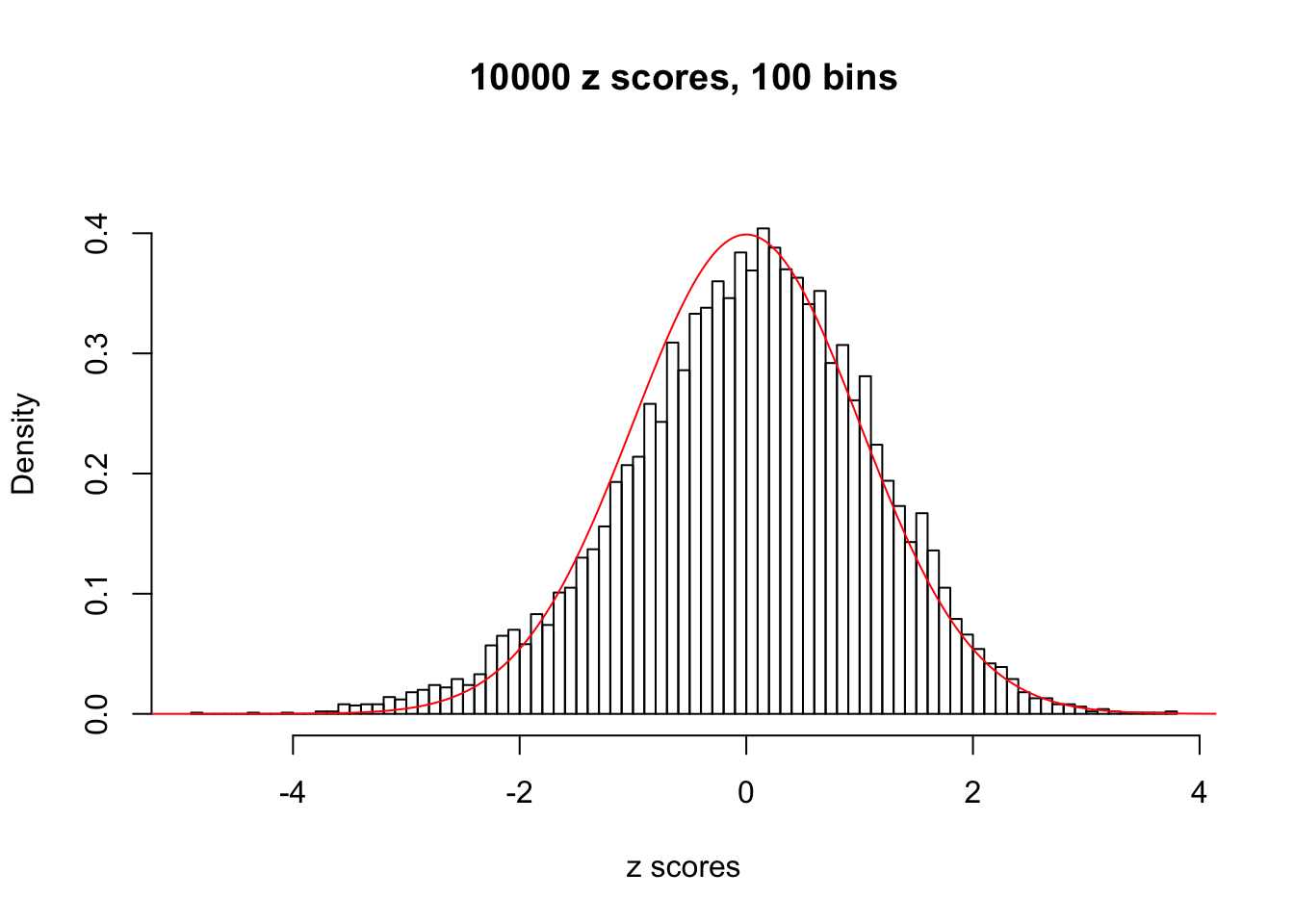
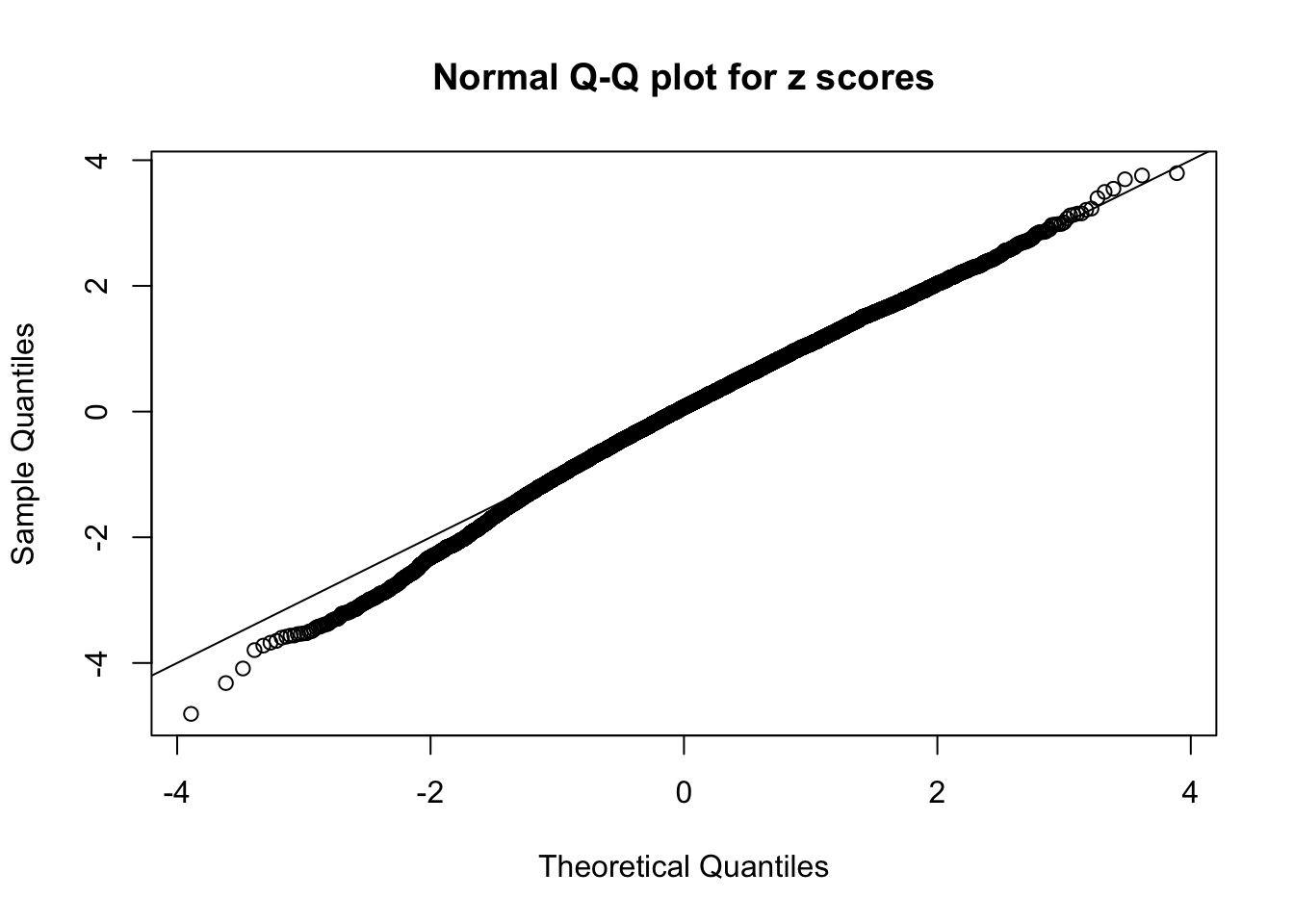
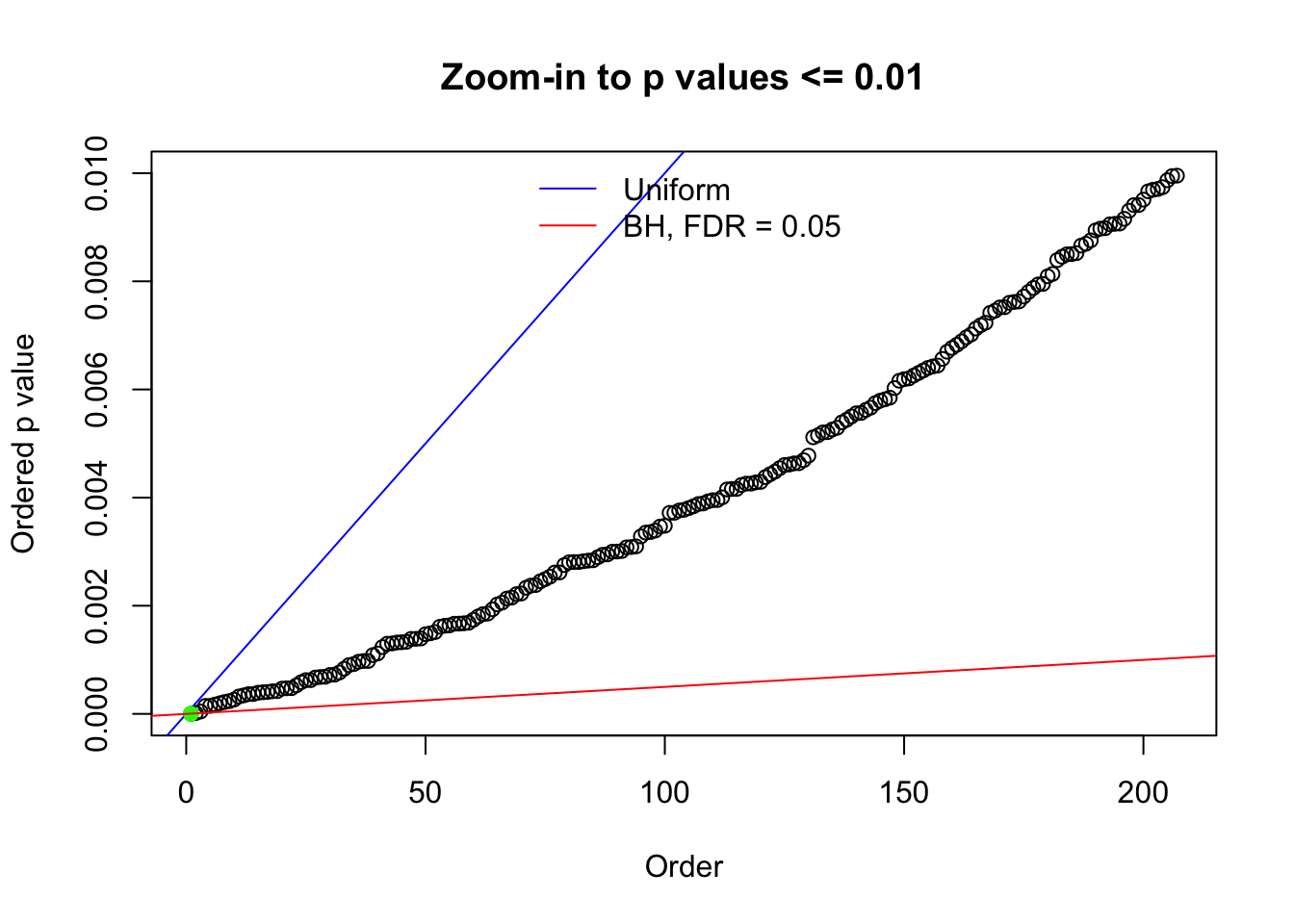
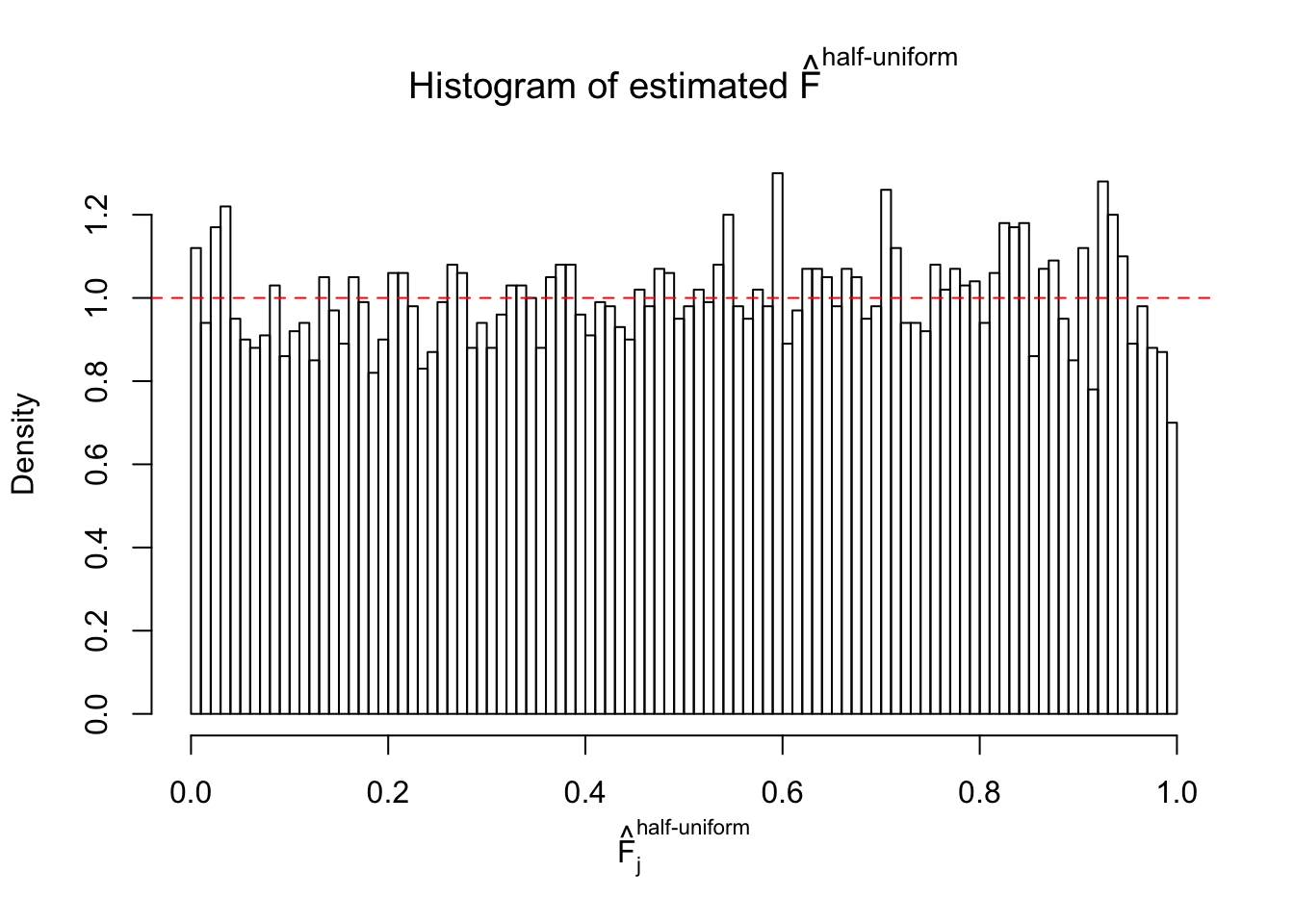
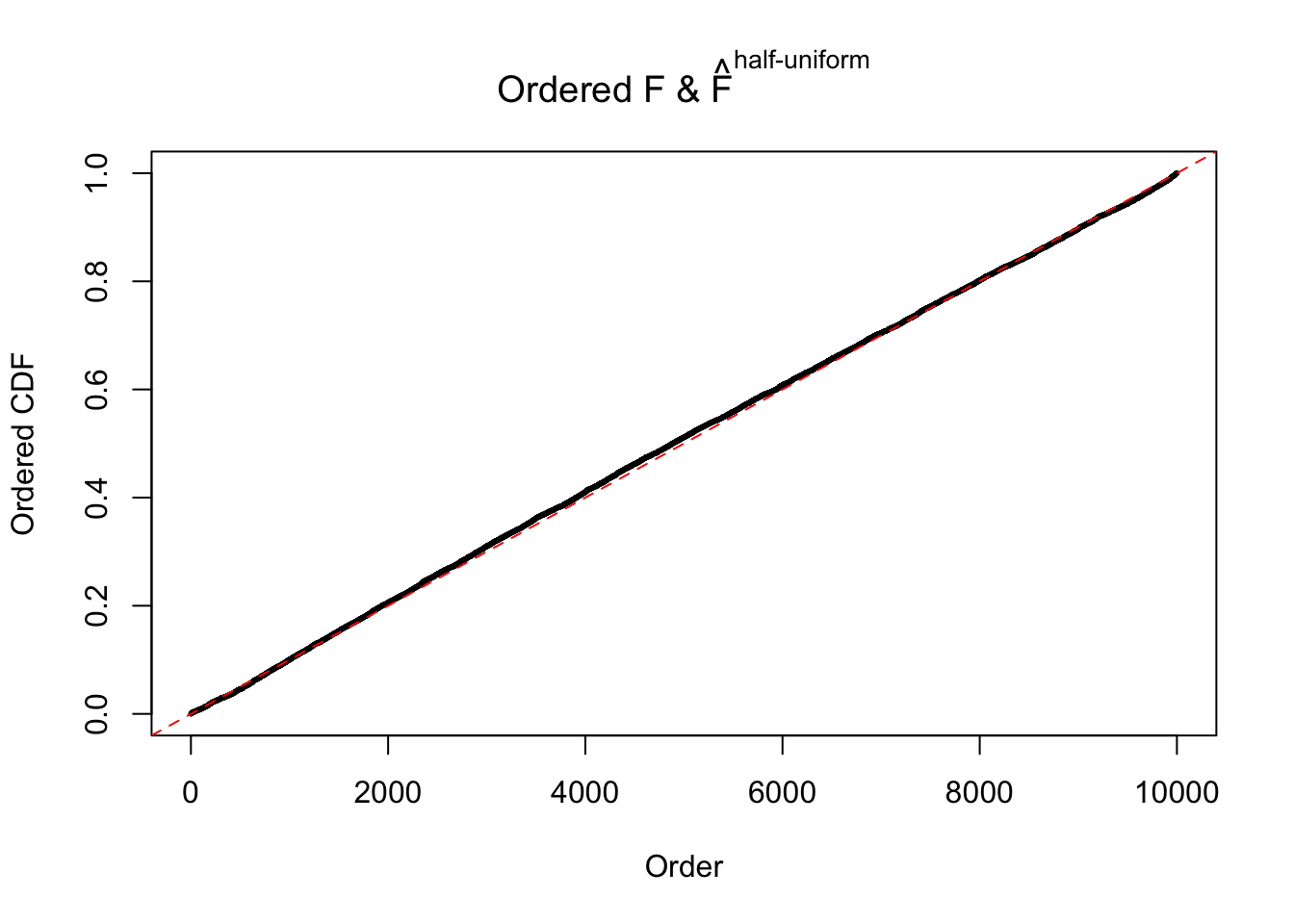
N0. 43 : Data Set 923 ; Number of False Discoveries: 1 ; pihat0 = 0.01590919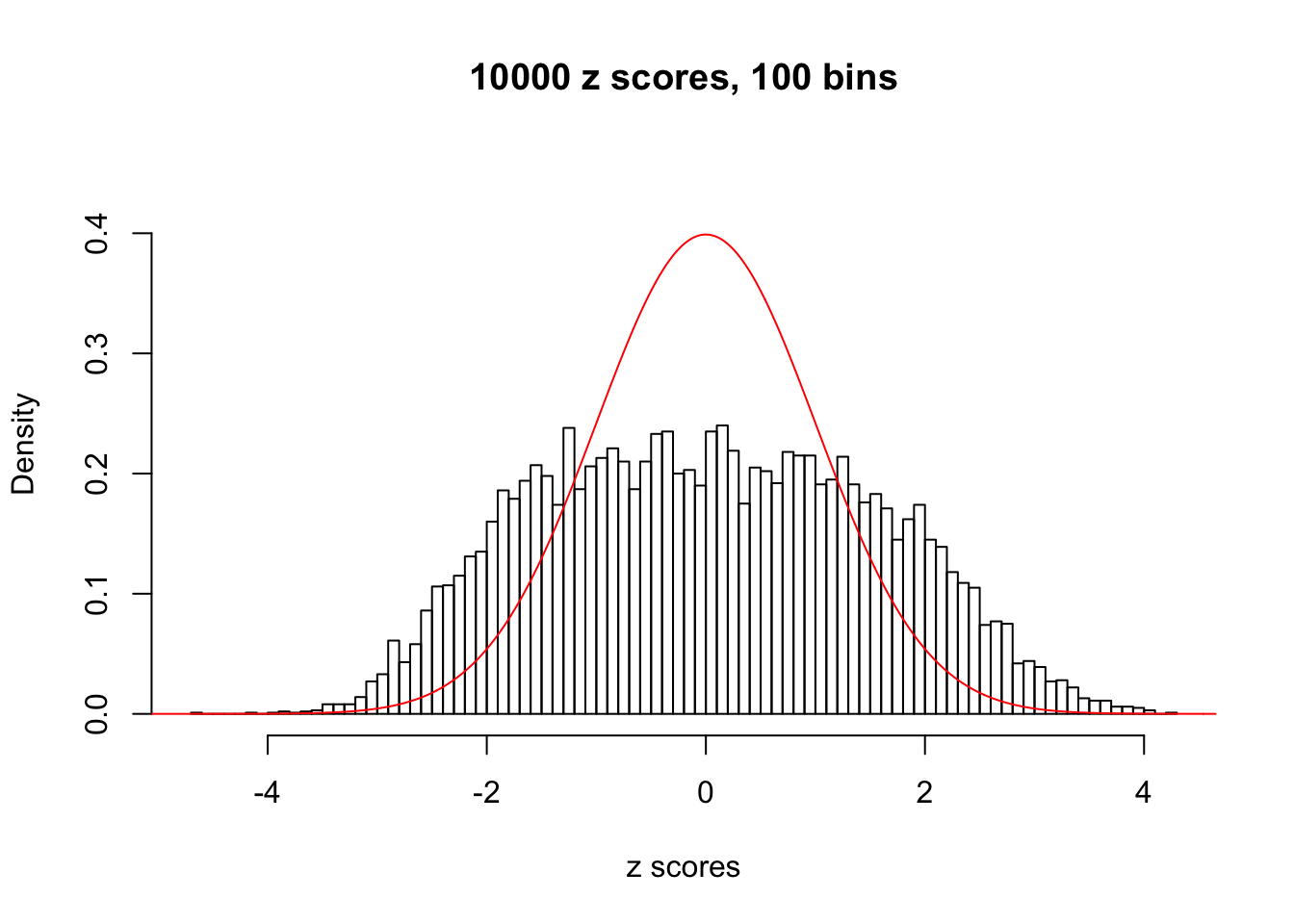
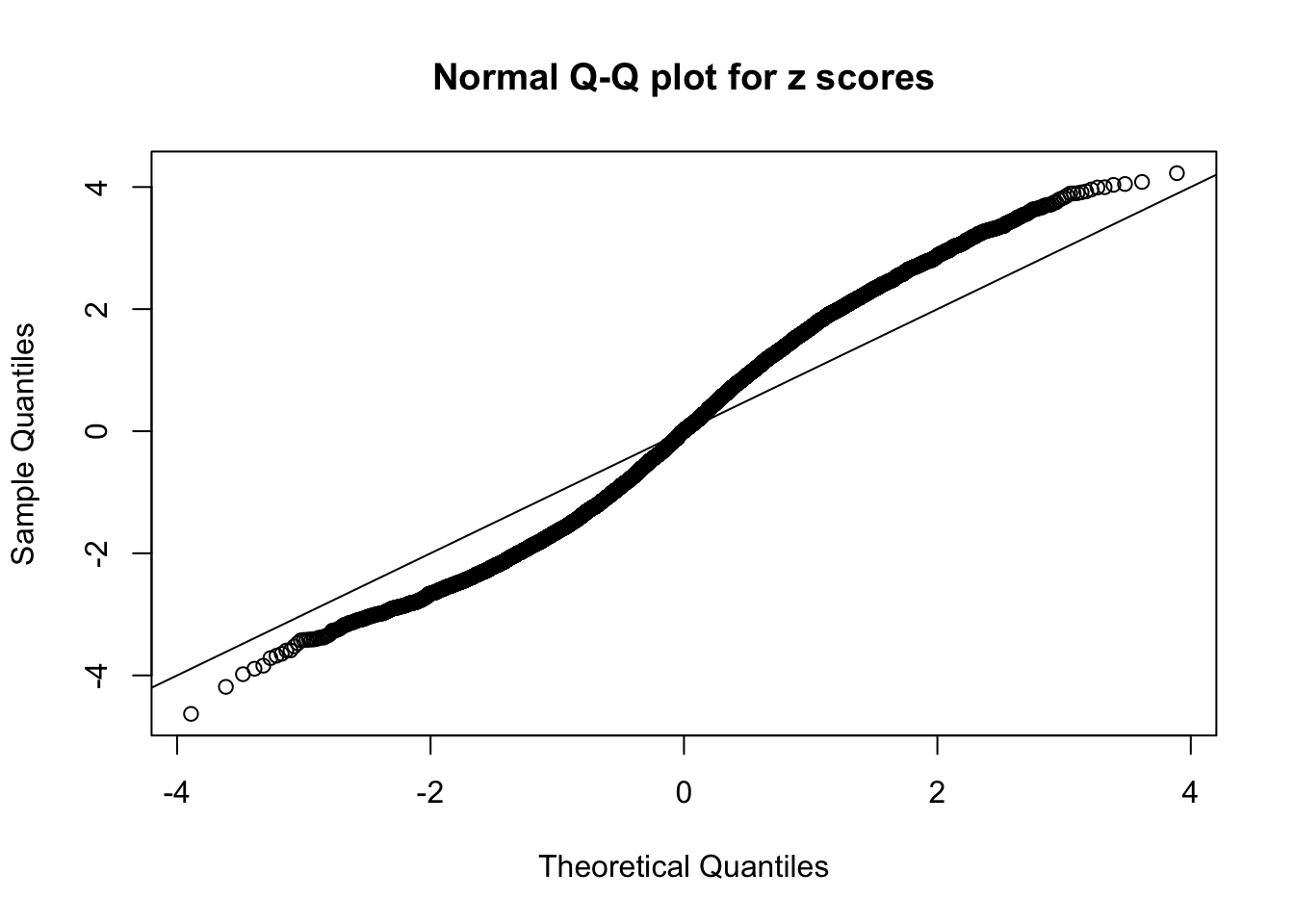
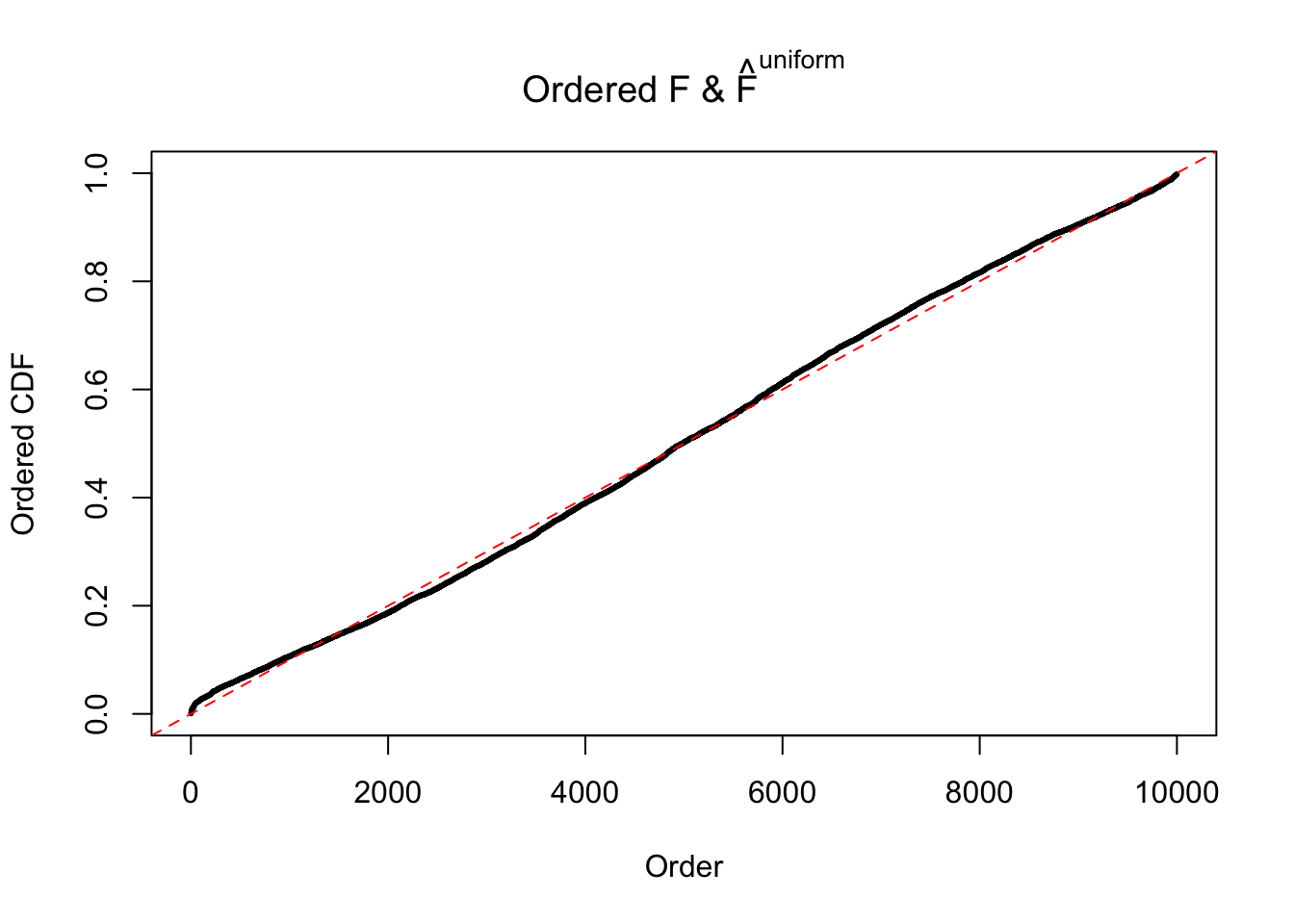
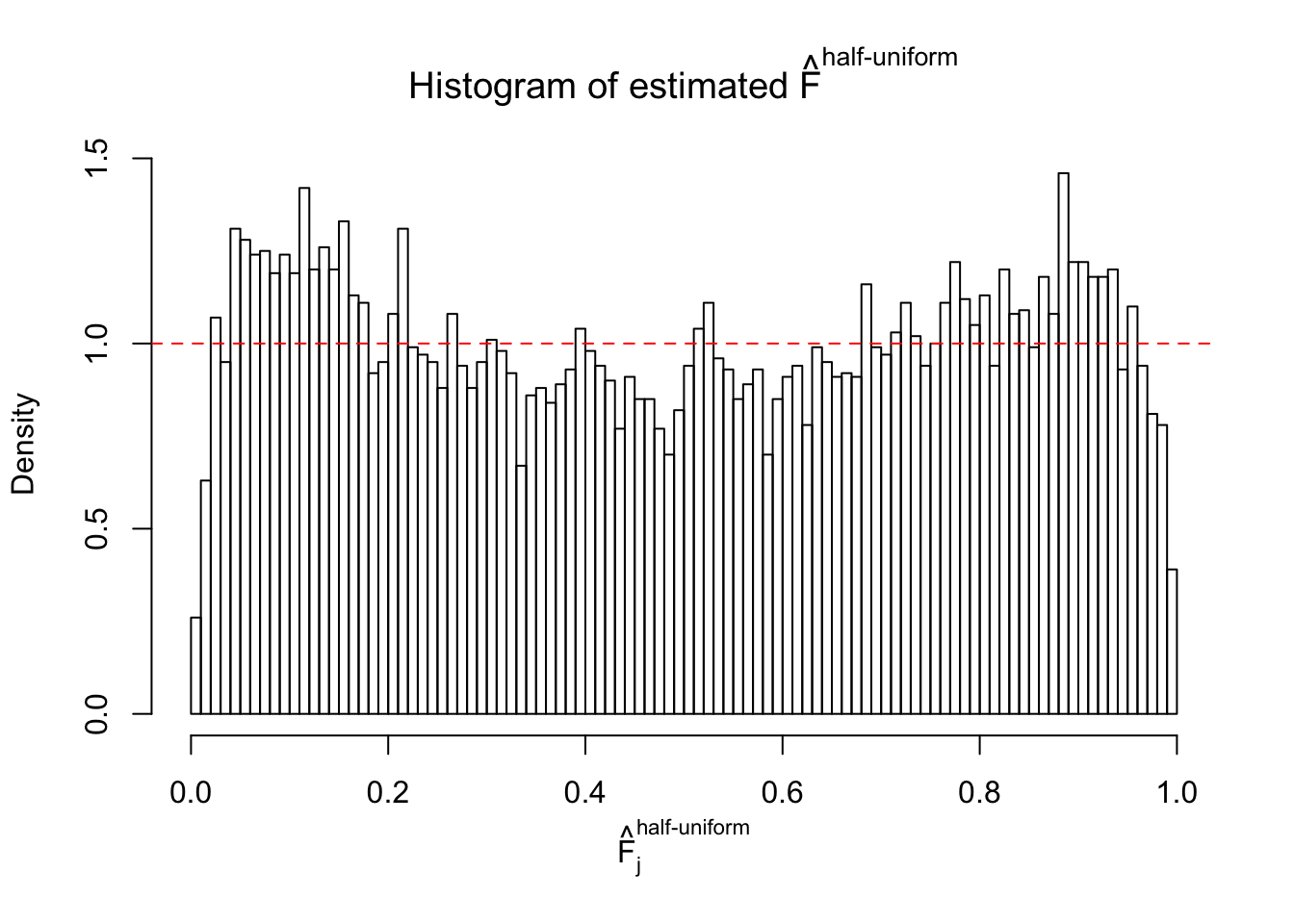
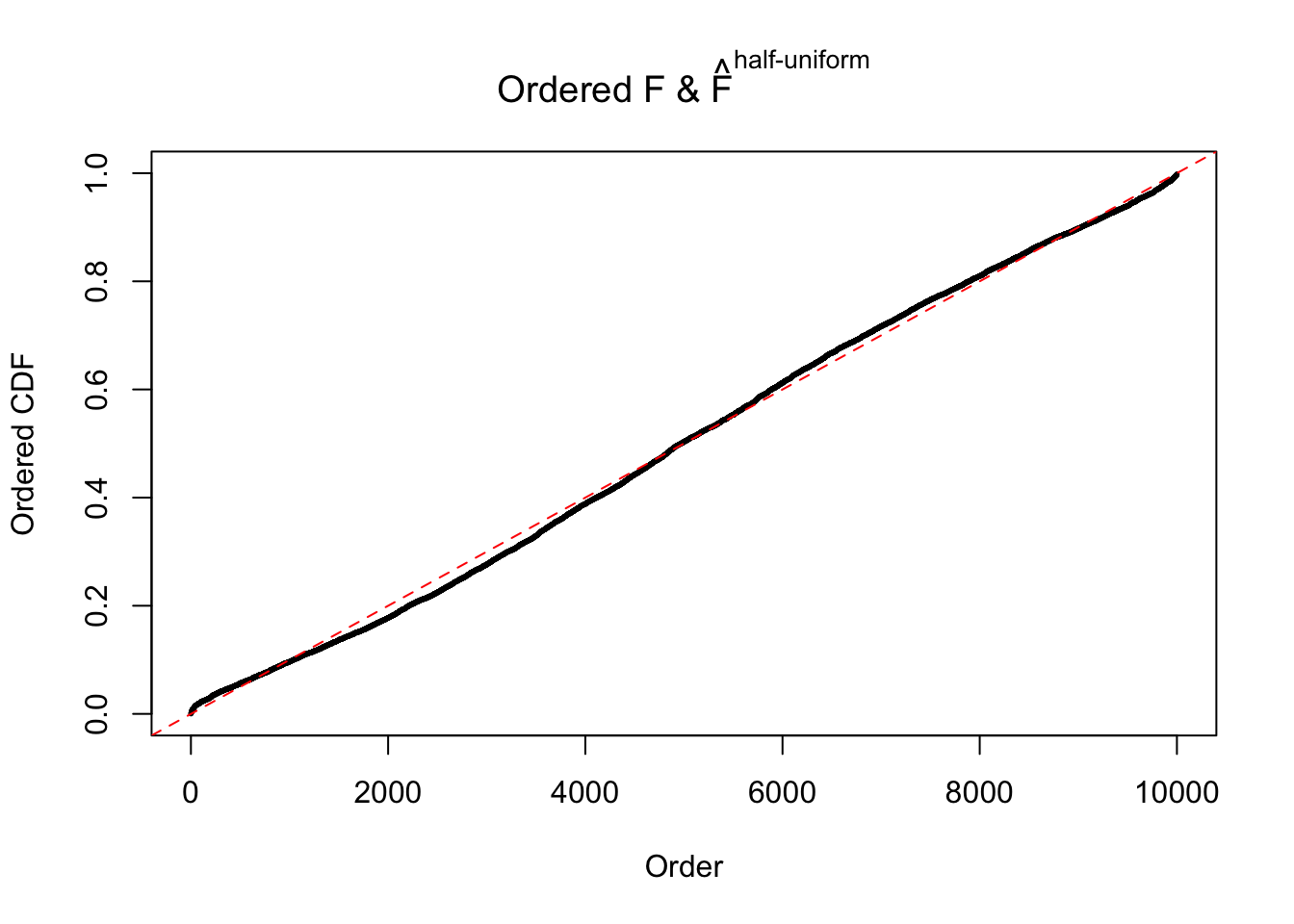
N0. 44 : Data Set 955 ; Number of False Discoveries: 1 ; pihat0 = 0.9998902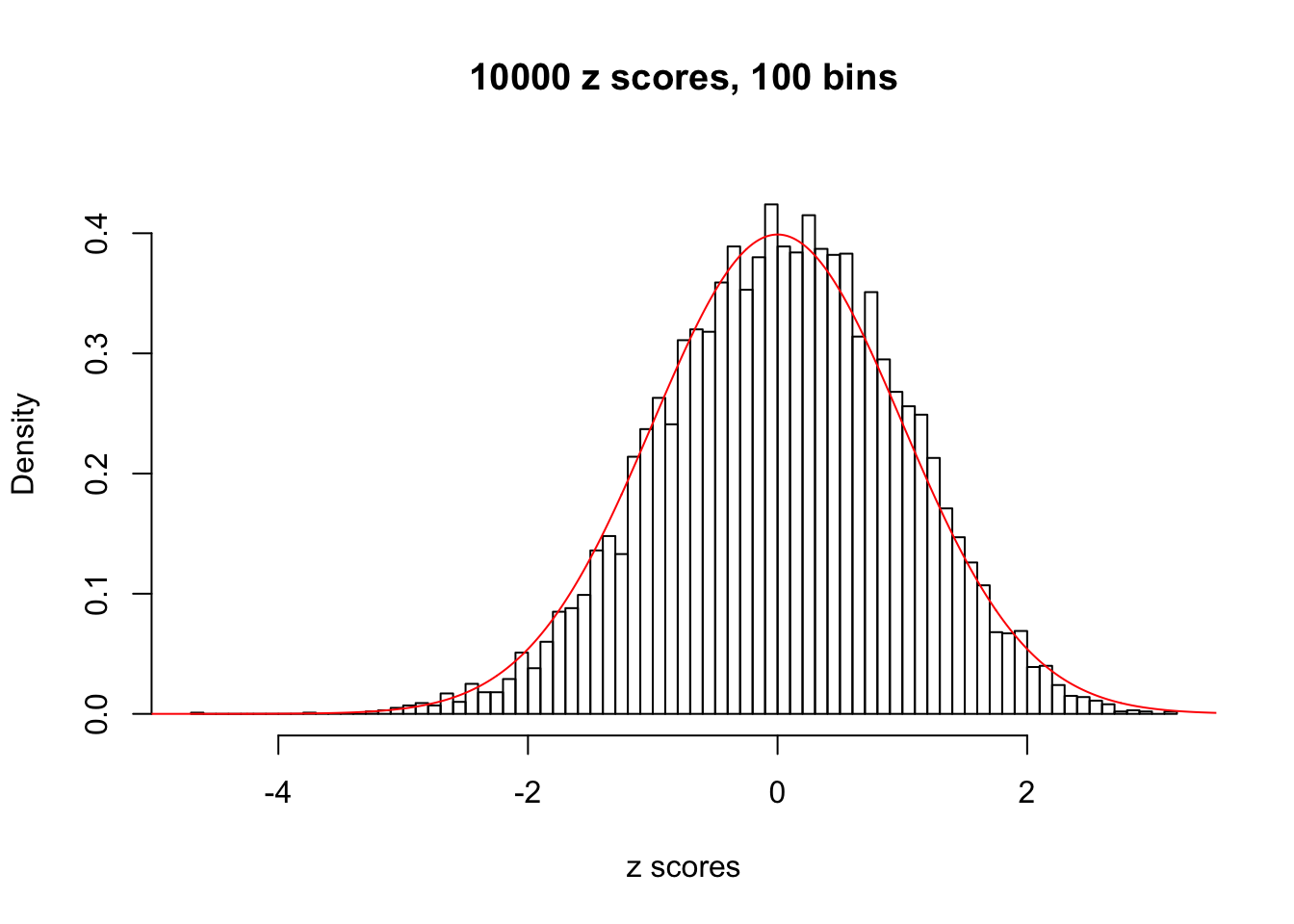
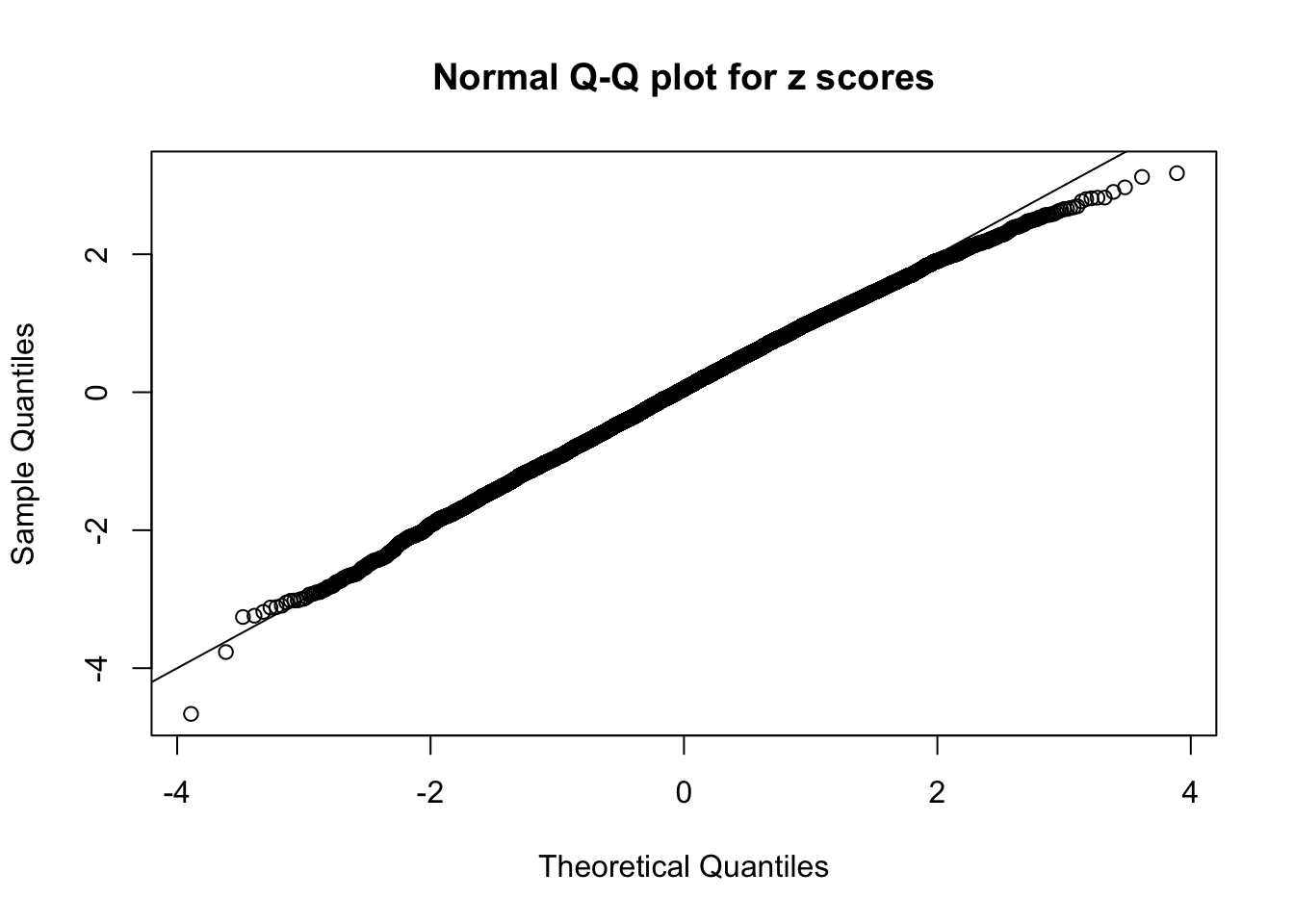
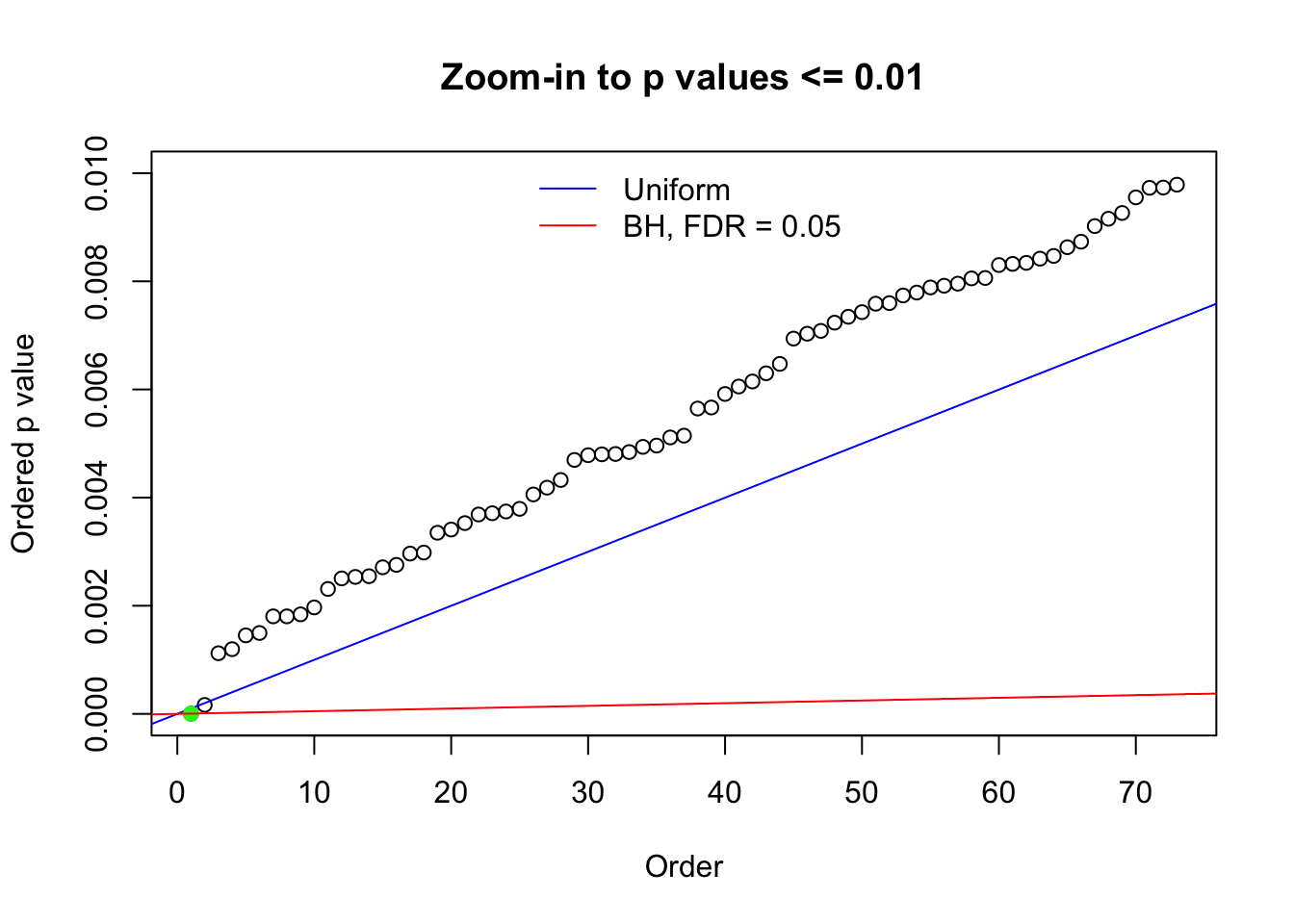
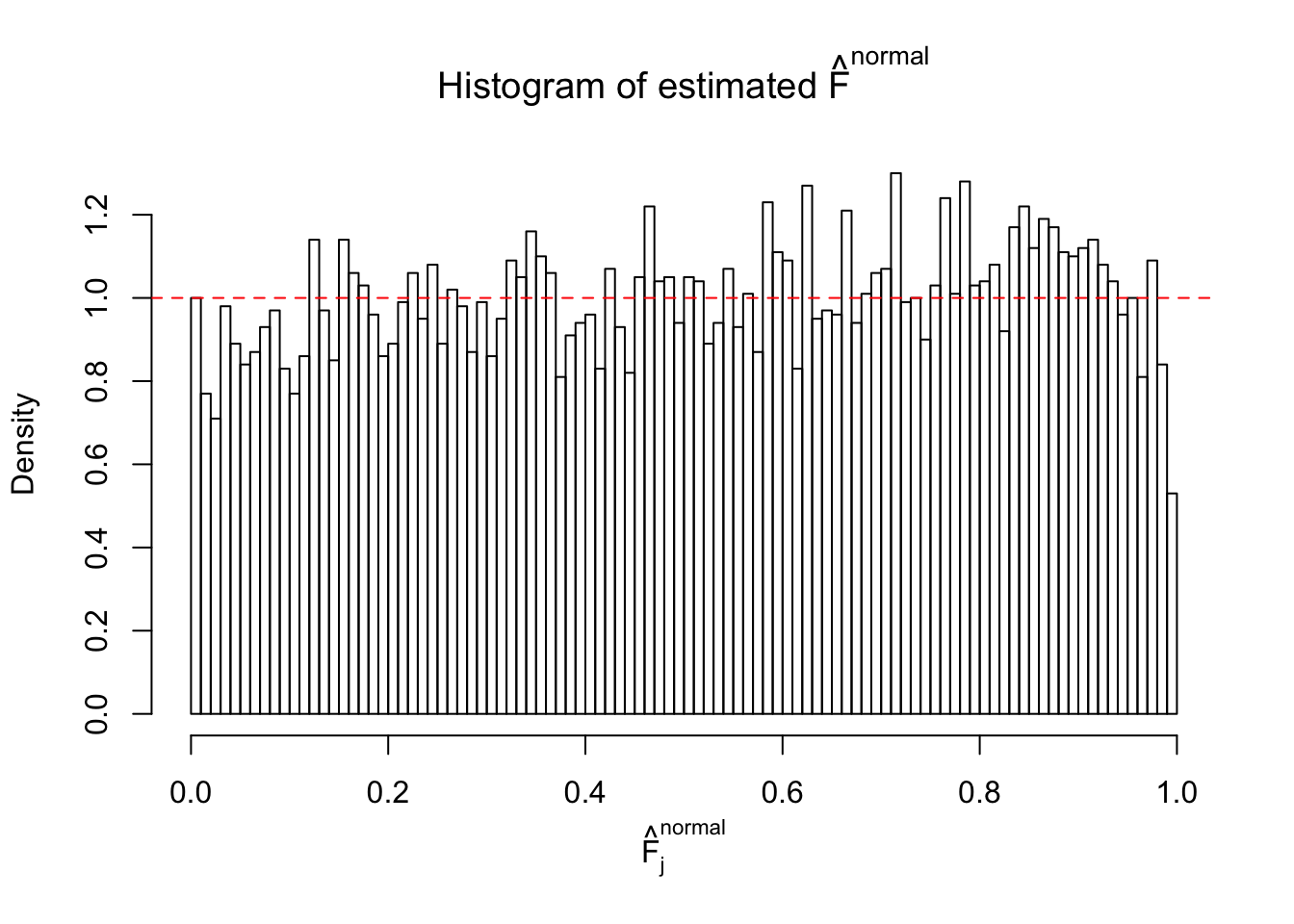
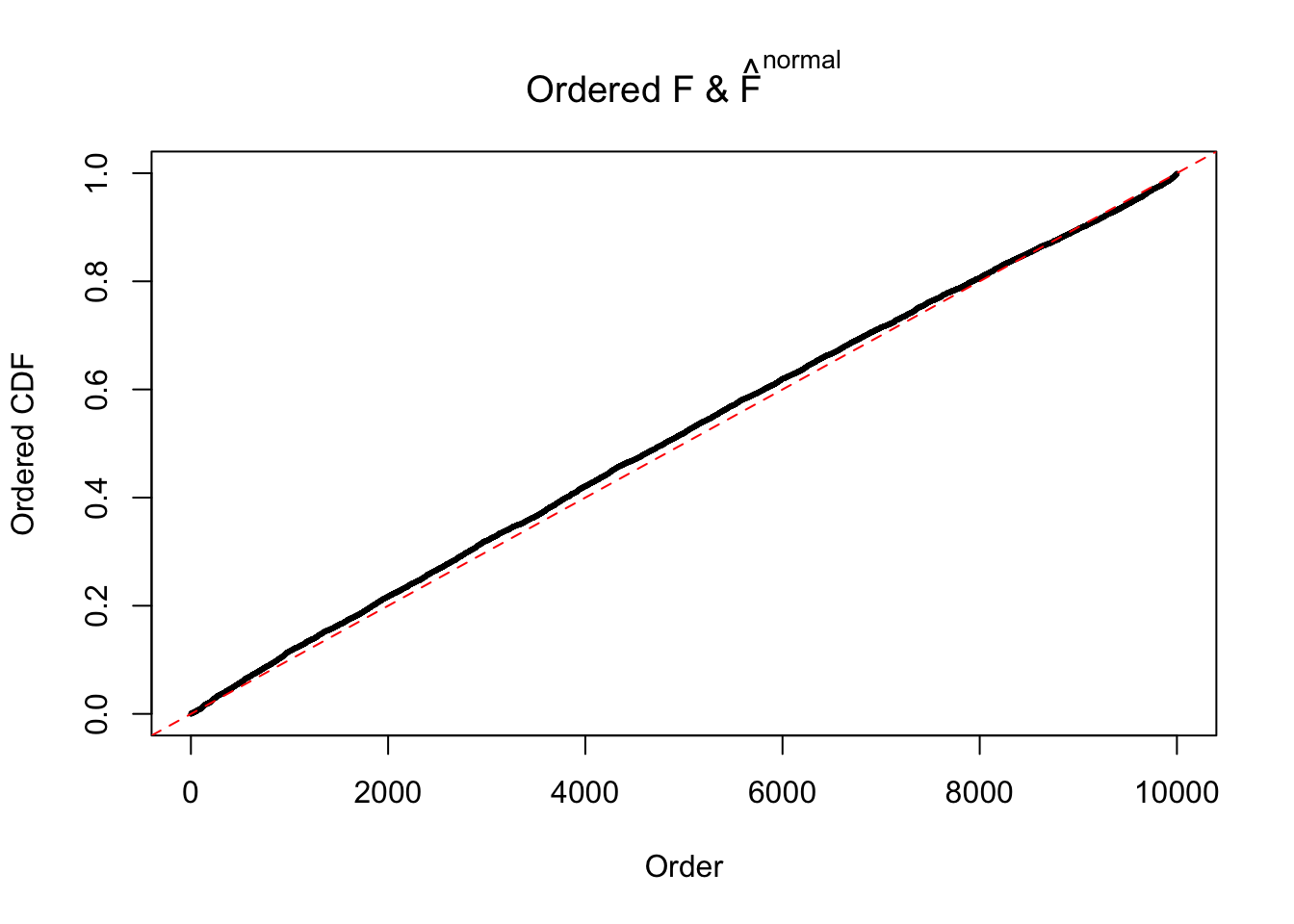
N0. 45 : Data Set 971 ; Number of False Discoveries: 1 ; pihat0 = 0.1368012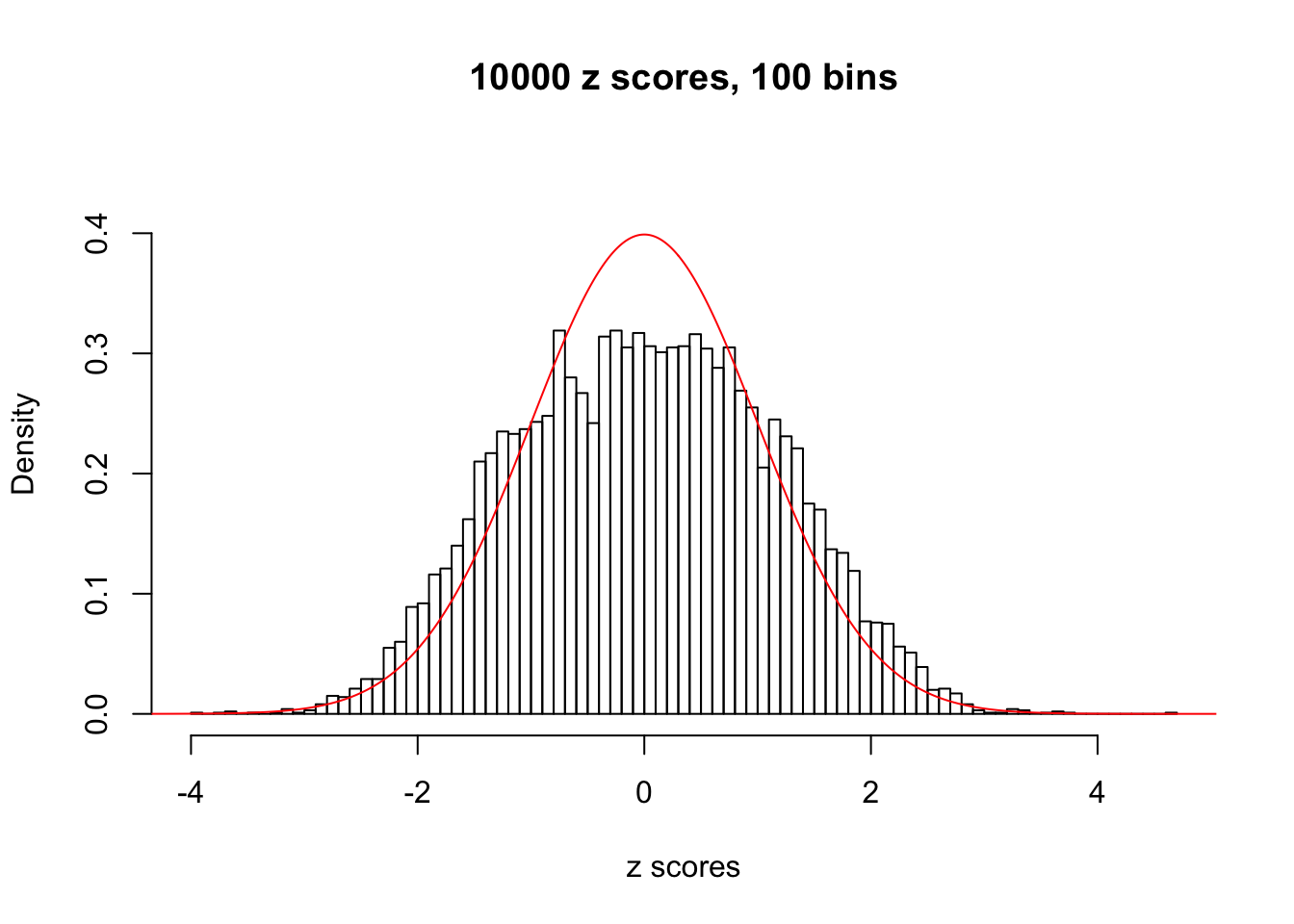
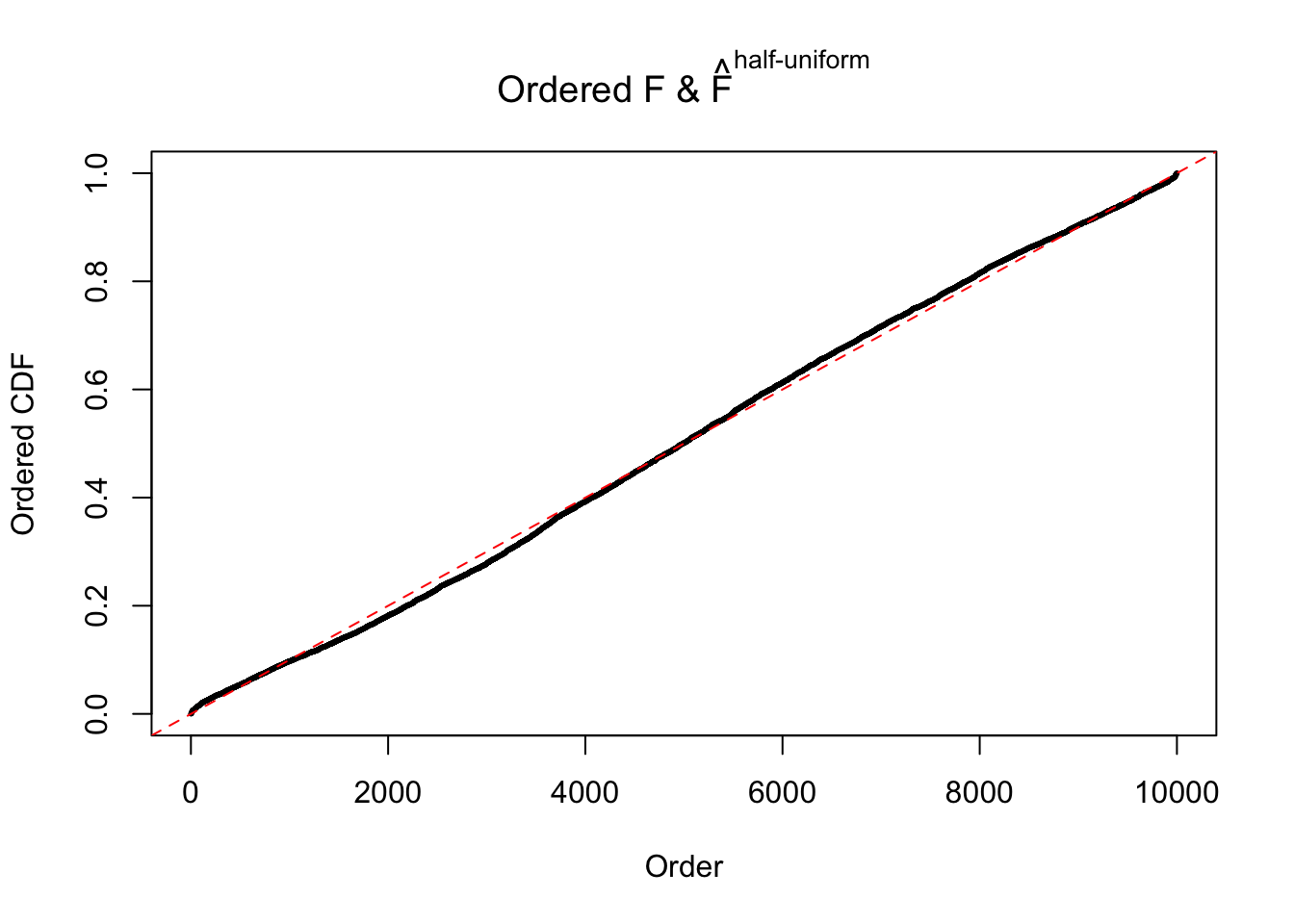
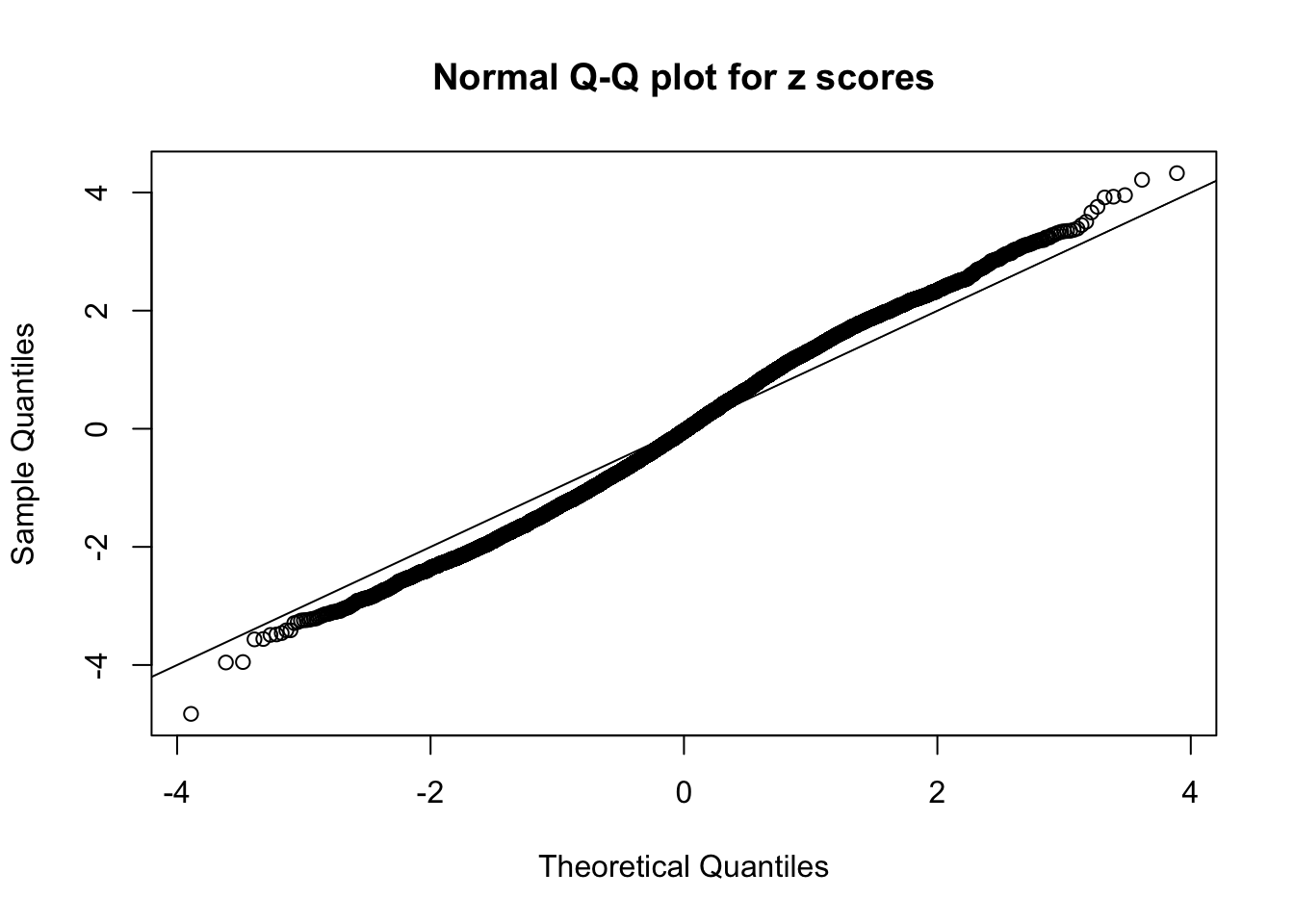
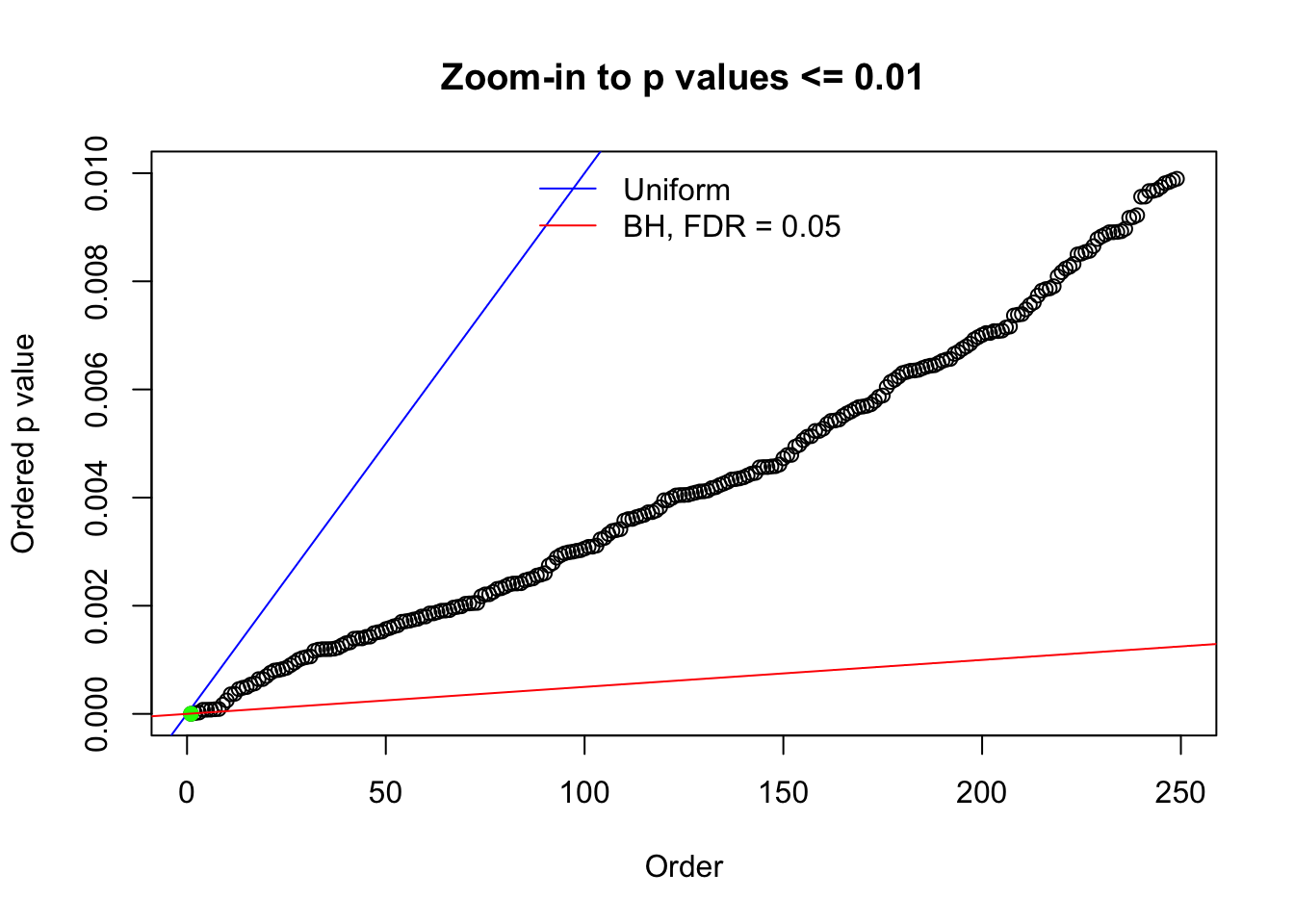
N0. 46 : Data Set 997 ; Number of False Discoveries: 1 ; pihat0 = 0.1018171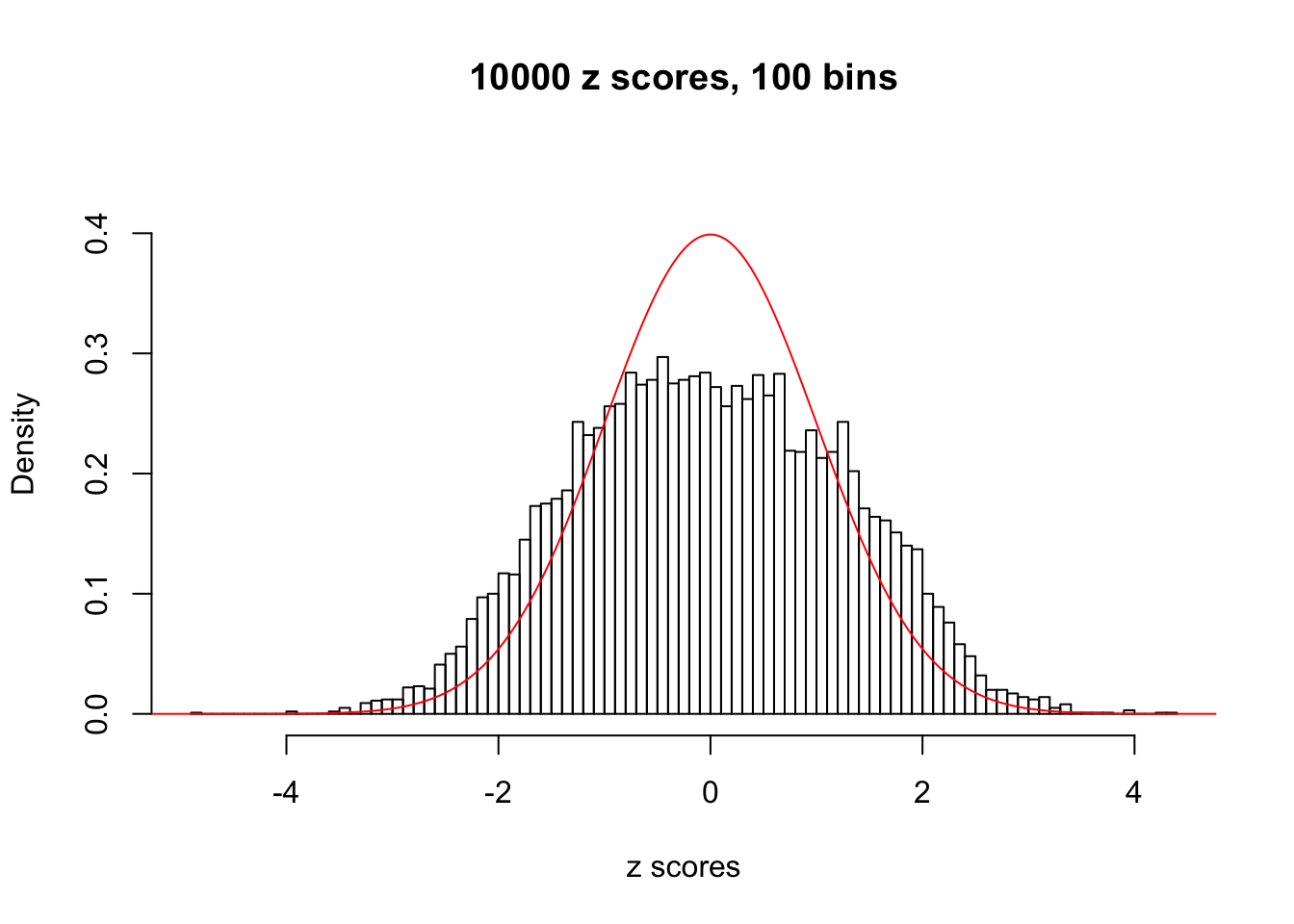
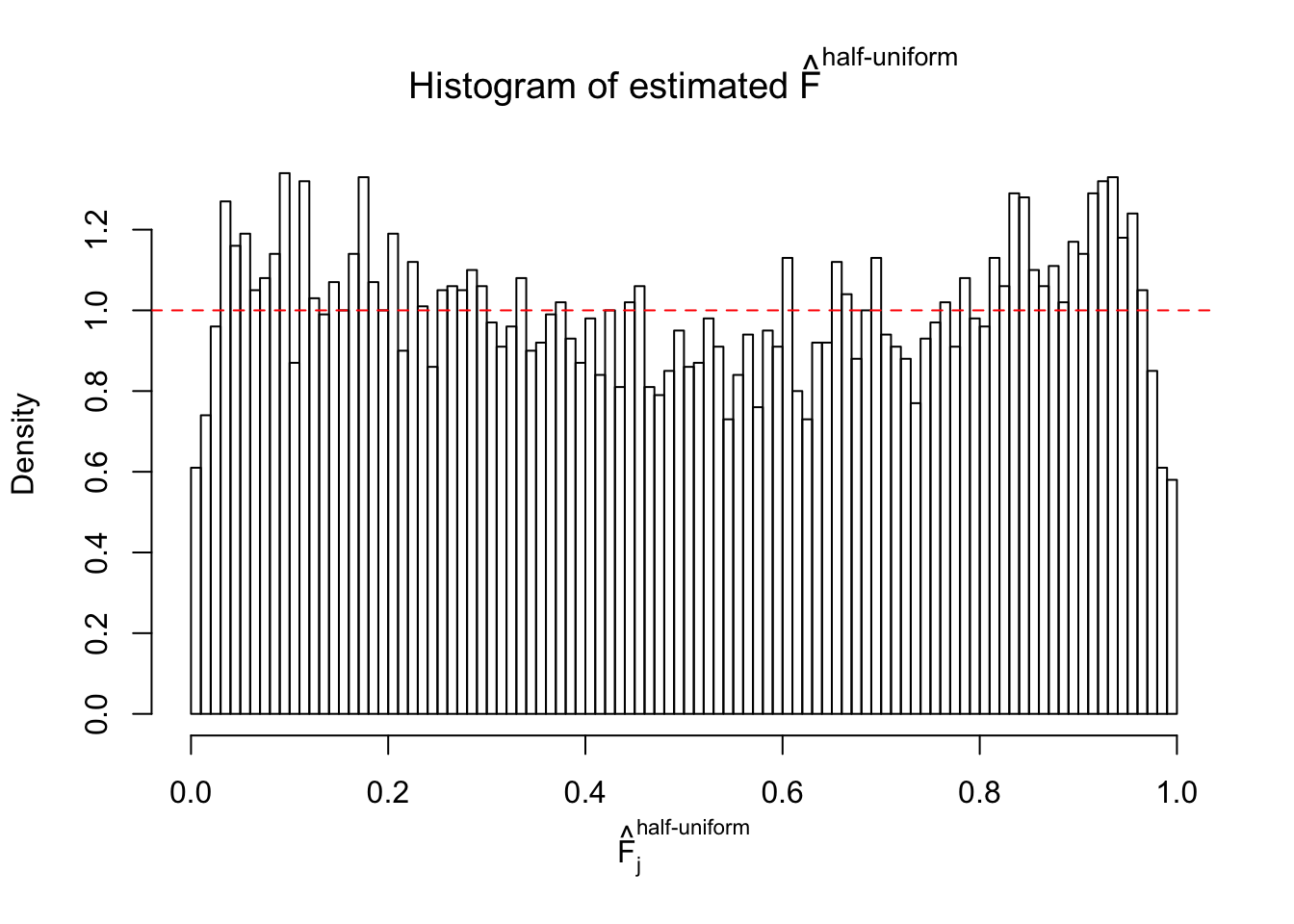
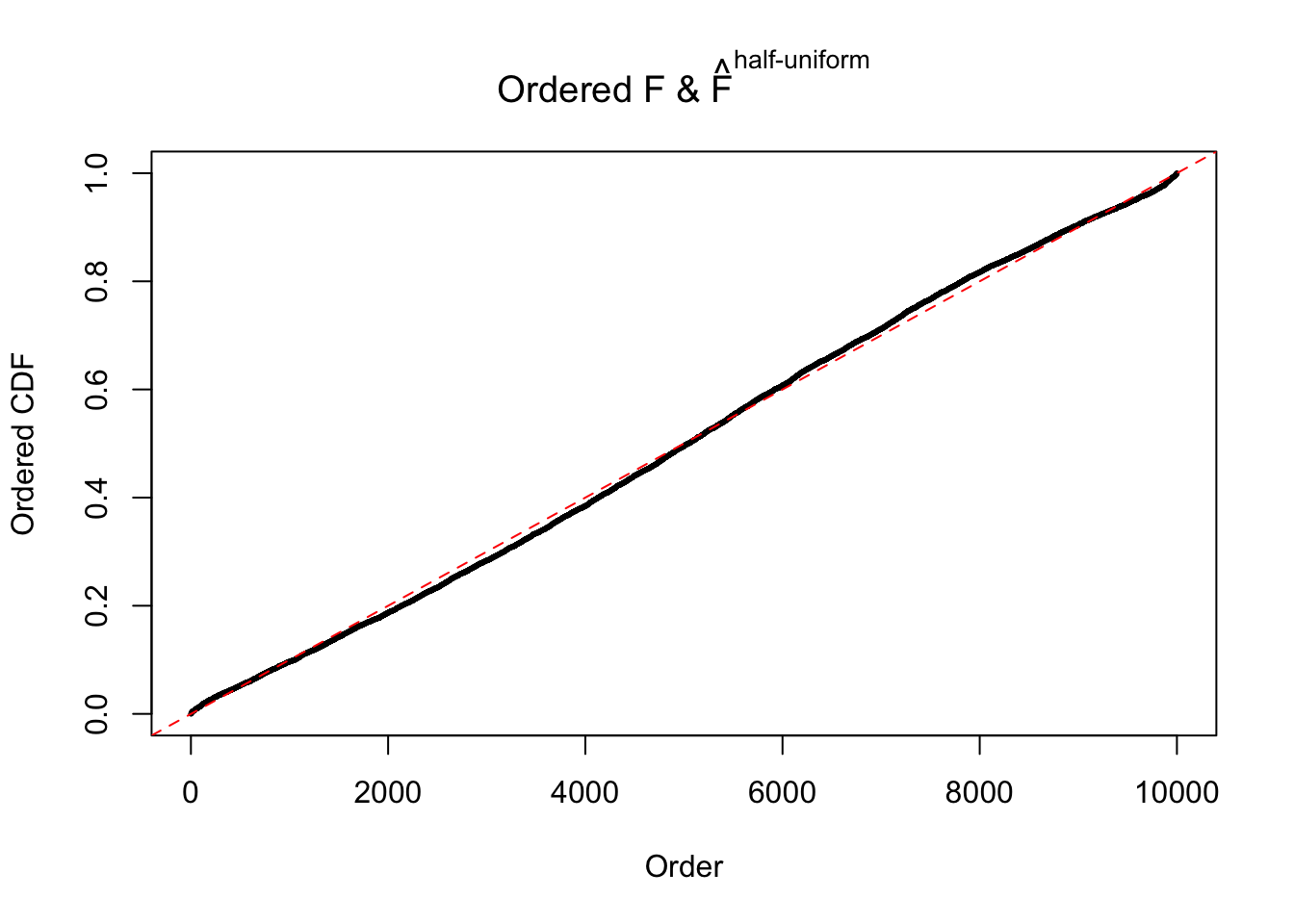
Remarks on goodness of fit
The simulation shows that oftentimes, ASH, no matter what kind of mixture prior is used, would only be able to produce a bad fit for the pseudo-effects due to correlation-induced inflation. However, occasionally, if uniform or halfuniform is used as the mixture component for the prior, the model may have a good fit, as indicated by the uniformness of \(\left\{\hat F_j\right\}\).
Session information
sessionInfo()R version 3.4.2 (2017-09-28)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Sierra 10.12.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.2 backports_1.1.1 magrittr_1.5 rprojroot_1.2
[5] tools_3.4.2 htmltools_0.3.6 yaml_2.1.14 Rcpp_0.12.13
[9] stringi_1.1.5 rmarkdown_1.6 knitr_1.17 git2r_0.19.0
[13] stringr_1.2.0 digest_0.6.12 evaluate_0.10.1This R Markdown site was created with workflowr