Rmosek: Primal vs Dual with \(l_1\) regularization
Lei Sun
2017-06-23
Last updated: 2017-06-23
Code version: b9c4ac9
Introduction
Following previous simulation, we are adding \(l_1\) regularization to the primal form such that
\[ \begin{array}{rl} \min\limits_{f \in \mathbb{R}^m, \ \ g \in \mathbb{R}^n} & -\sum\limits_{i = 1}^n\log\left(g_i\right) + \sum\limits_{j = 1}^m\lambda_j\left|f_j\right| \\ \text{s.t.} & Af + a = g\\ & g \geq 0 \ . \end{array} \]
Its dual form is
\[ \begin{array}{rl} \min\limits_{\nu \in \mathbb{R}^n} & a^T\nu-\sum\limits_{i = 1}^n\log\left(\nu_i\right) \\ \text{s.t.} & \left|A^T\nu\right| \leq \lambda\\ & \nu\geq0 \ . \end{array} \]
Right now we haven’t figured out how to program the \(l_1\) regularized primal form in Rmosek, so here we are only comparing the dual form with or without regularization.
Simulation
Let \(\lambda\) be
\[ \lambda_i = \begin{cases} 0 & i \text{ odd ;}\\ a / \rho^{i/2} & i \text{ even .}\\ \end{cases} \] with \(a = 10\), \(\rho = 0.5\). \(n = 10^4\), \(m = 10\), \(A\) and \(a\) are generated in the same way.
The dual optimization in all \(1000\) simulation trials reaches the optimal solution both with and without regularization.
Total time cost
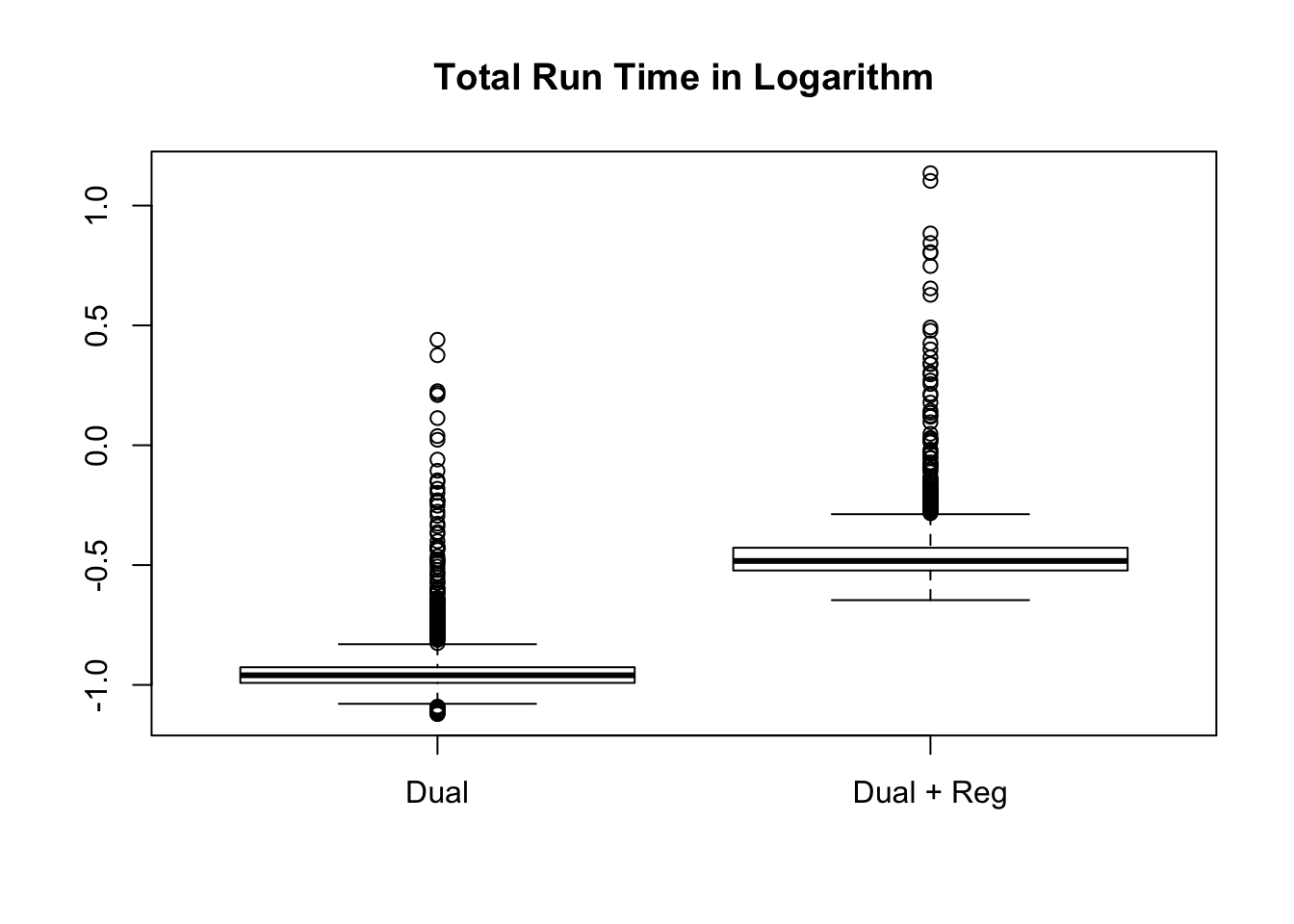
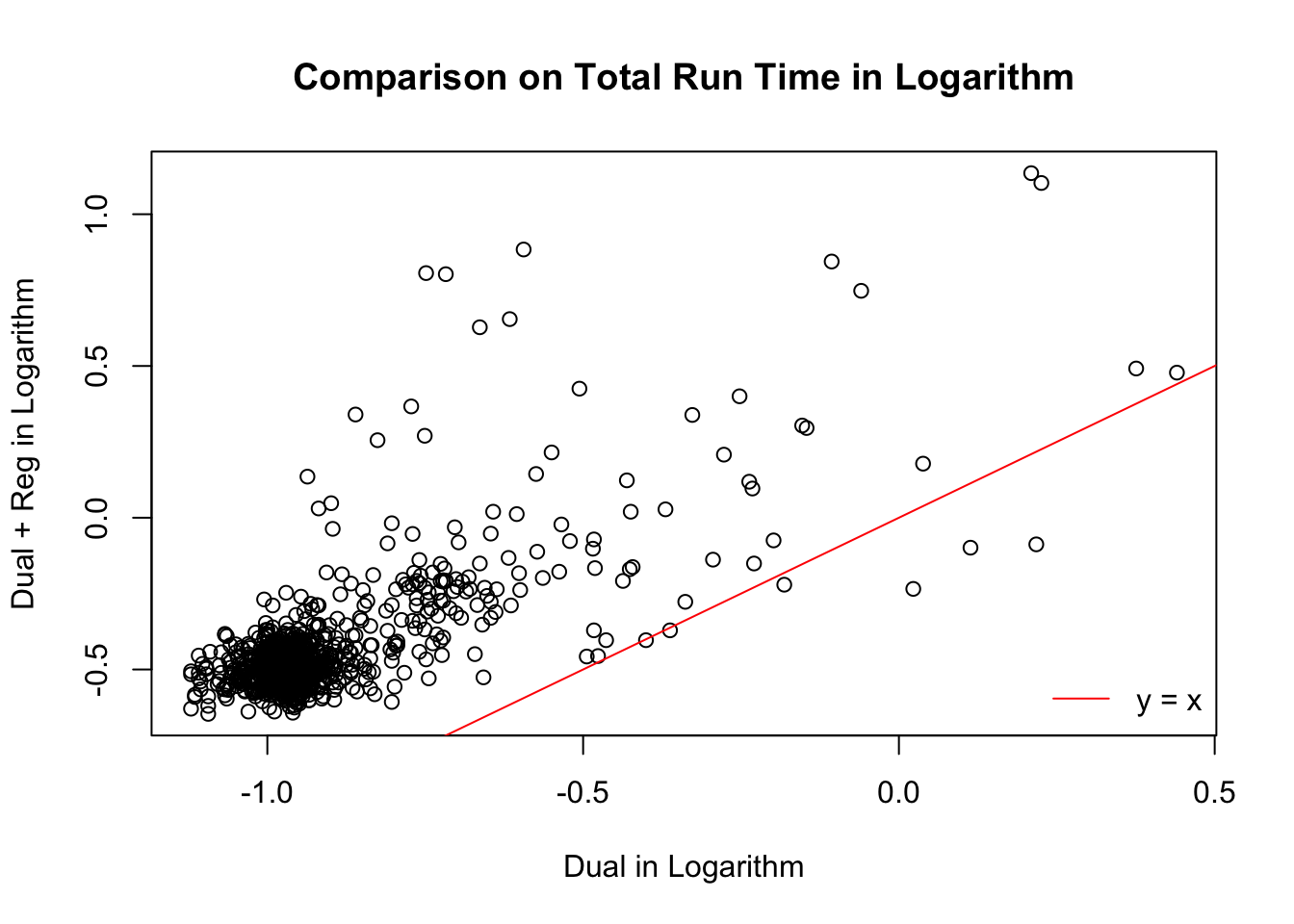
Number of iterations
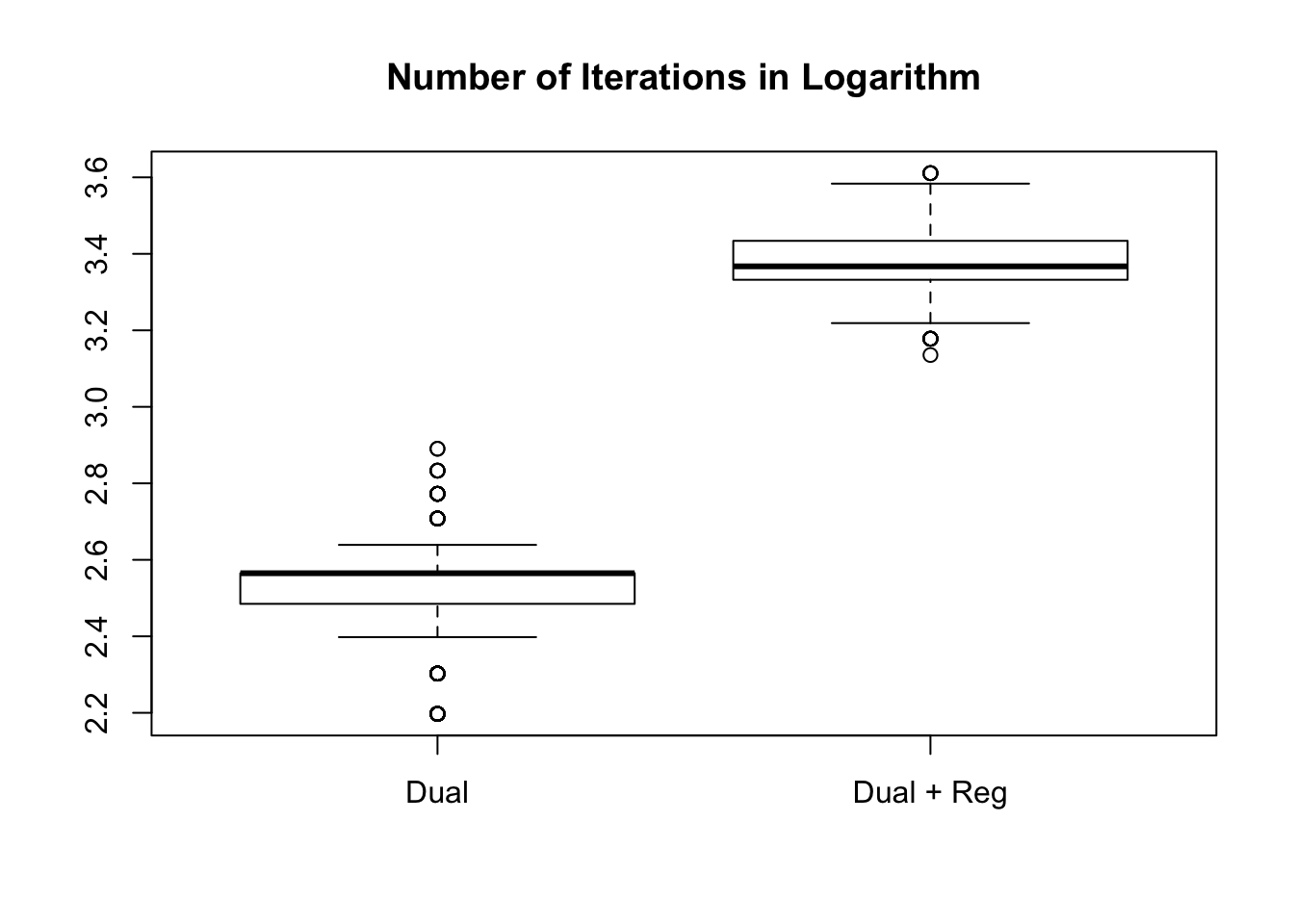
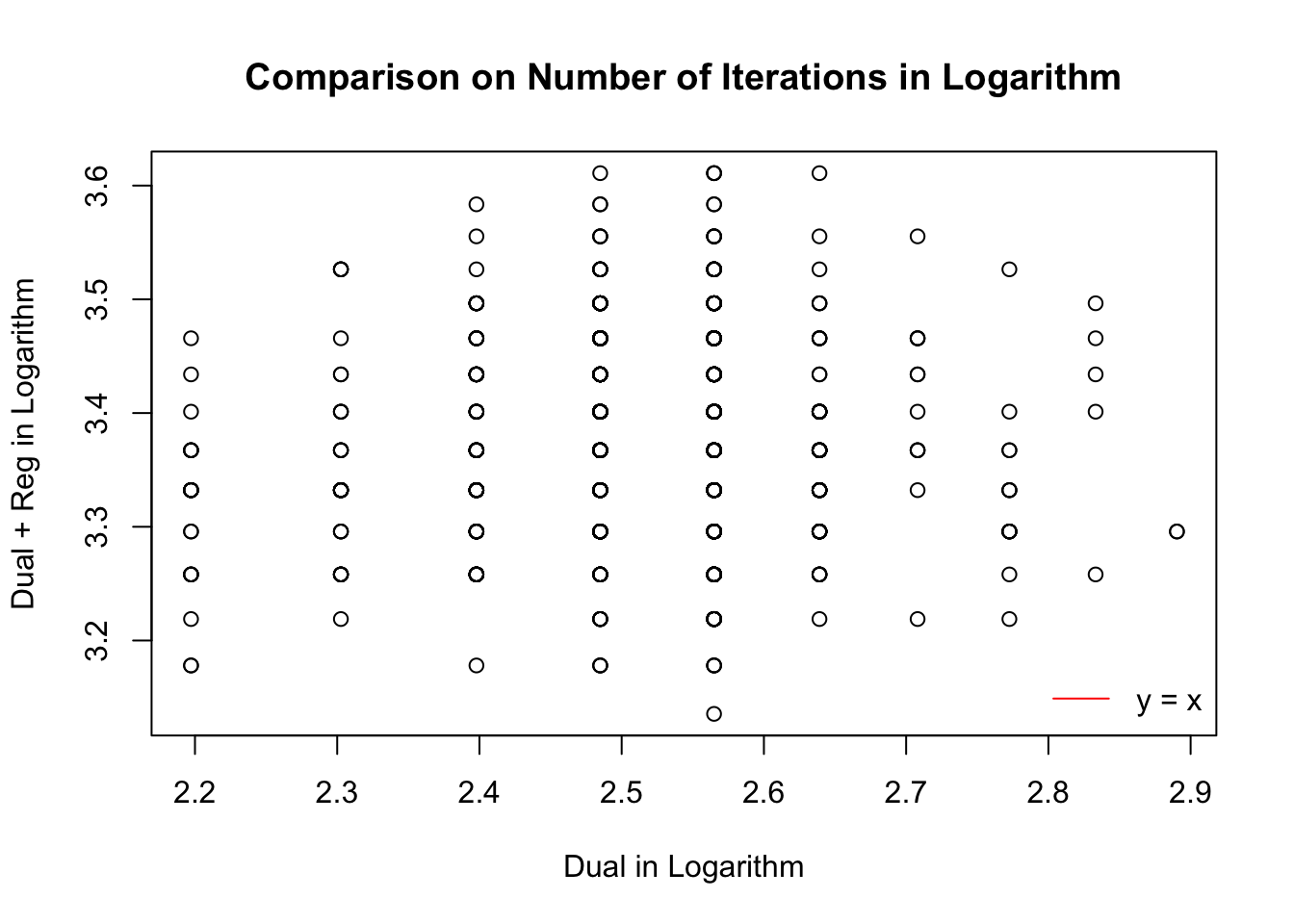
Time per iteration
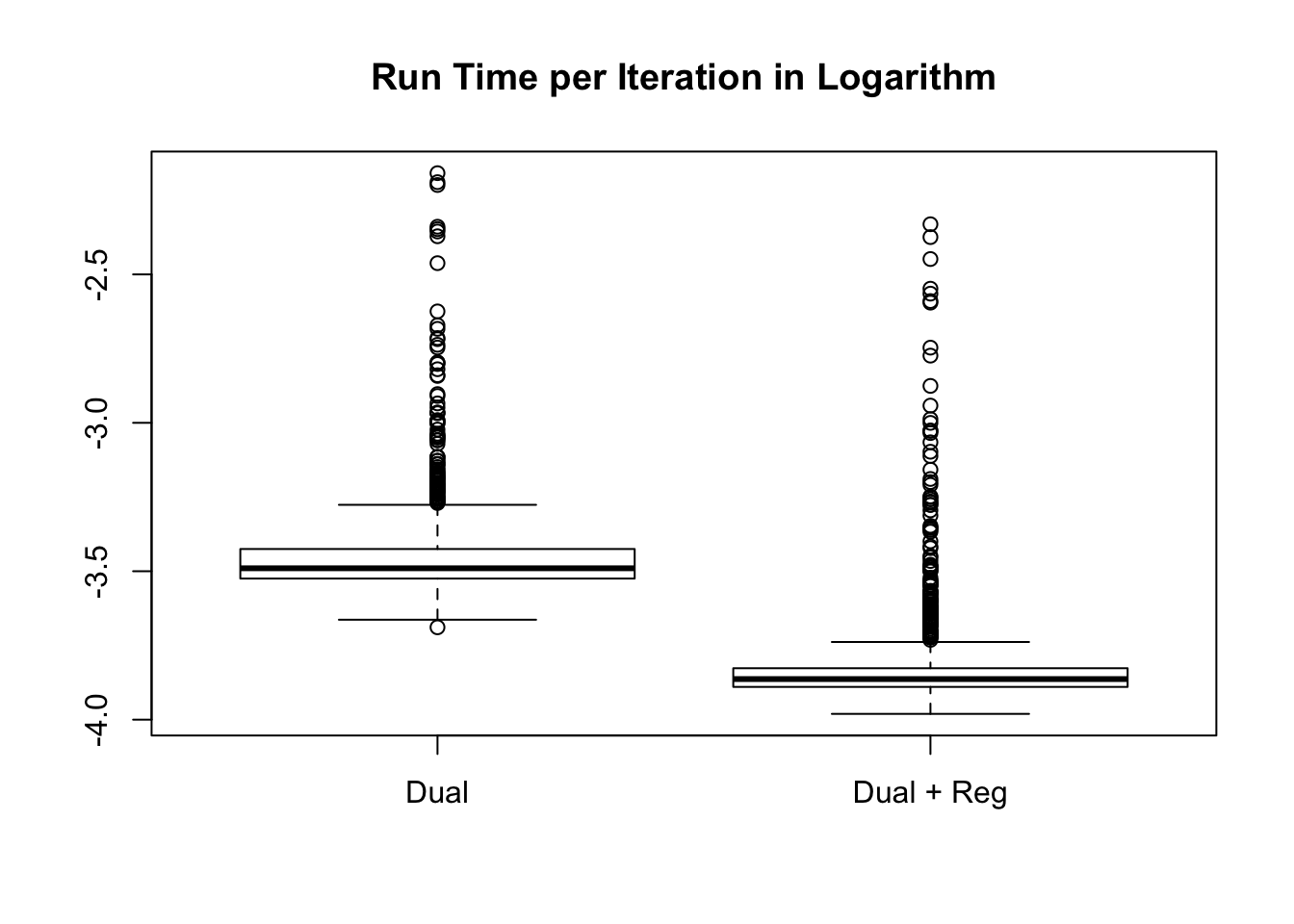
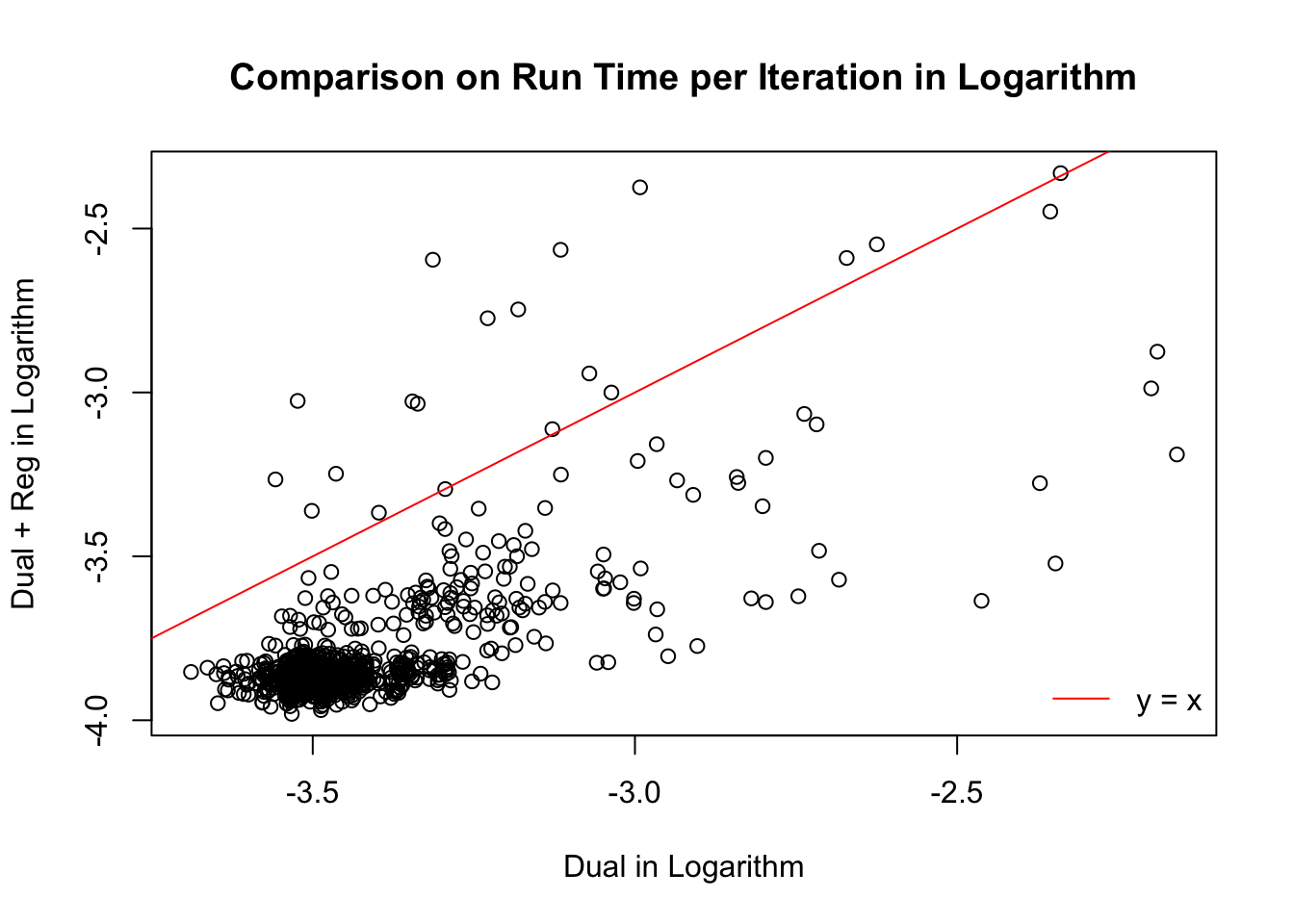
Session information
sessionInfo()R version 3.3.3 (2017-03-06)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.5
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] backports_1.0.5 magrittr_1.5 rprojroot_1.2 tools_3.3.3
[5] htmltools_0.3.6 yaml_2.1.14 Rcpp_0.12.11 stringi_1.1.2
[9] rmarkdown_1.6 knitr_1.16 git2r_0.18.0 stringr_1.2.0
[13] digest_0.6.12 evaluate_0.10 This R Markdown site was created with workflowr