Simulating Design Matrix \(X\)
Lei Sun
2018-01-25
Last updated: 2018-01-30
Code version: 5442ab8
Introduction
In order to investigate and compare linear regression variable selection methods, we need to construct design matrices \(X\). Here we take a look at multiple methods to simulate \(X\).
The design matrix \(X\) is simulated so that the columns have noticeable correlation structures. In our simulation, each row of \(X\) is independently drawn from a \(N(0, \Sigma)\) distribution.
Simulation Setting
Data are generated in a global null setting by \[ y_n = X_{n \times p}\beta_p + e_n \] where \[ \begin{array}{c} n = 2000 \\ p = 1000 \\ e_n \sim N(0, 1) \\ \end{array} \] and \[ \beta_p \equiv 0 \]
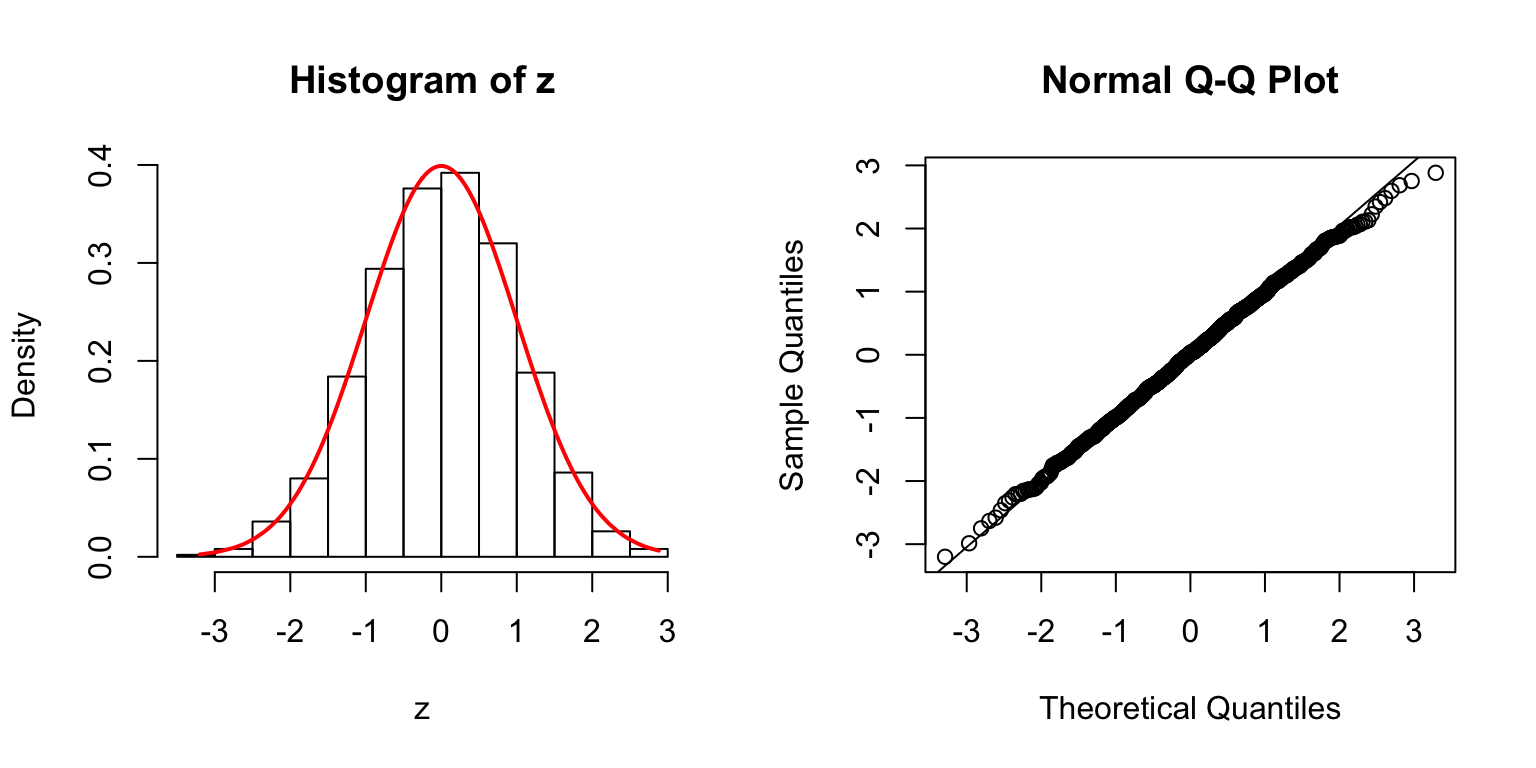
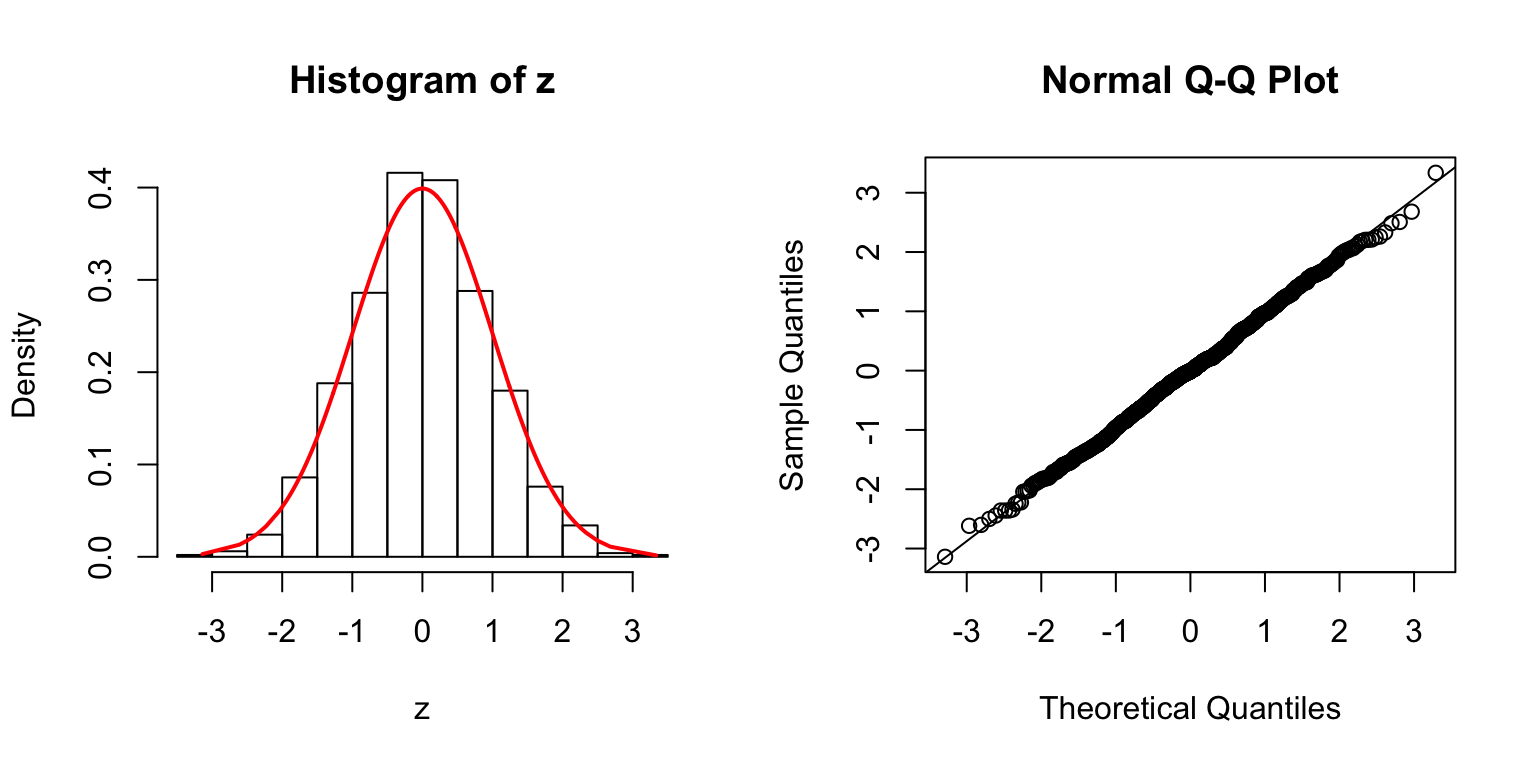
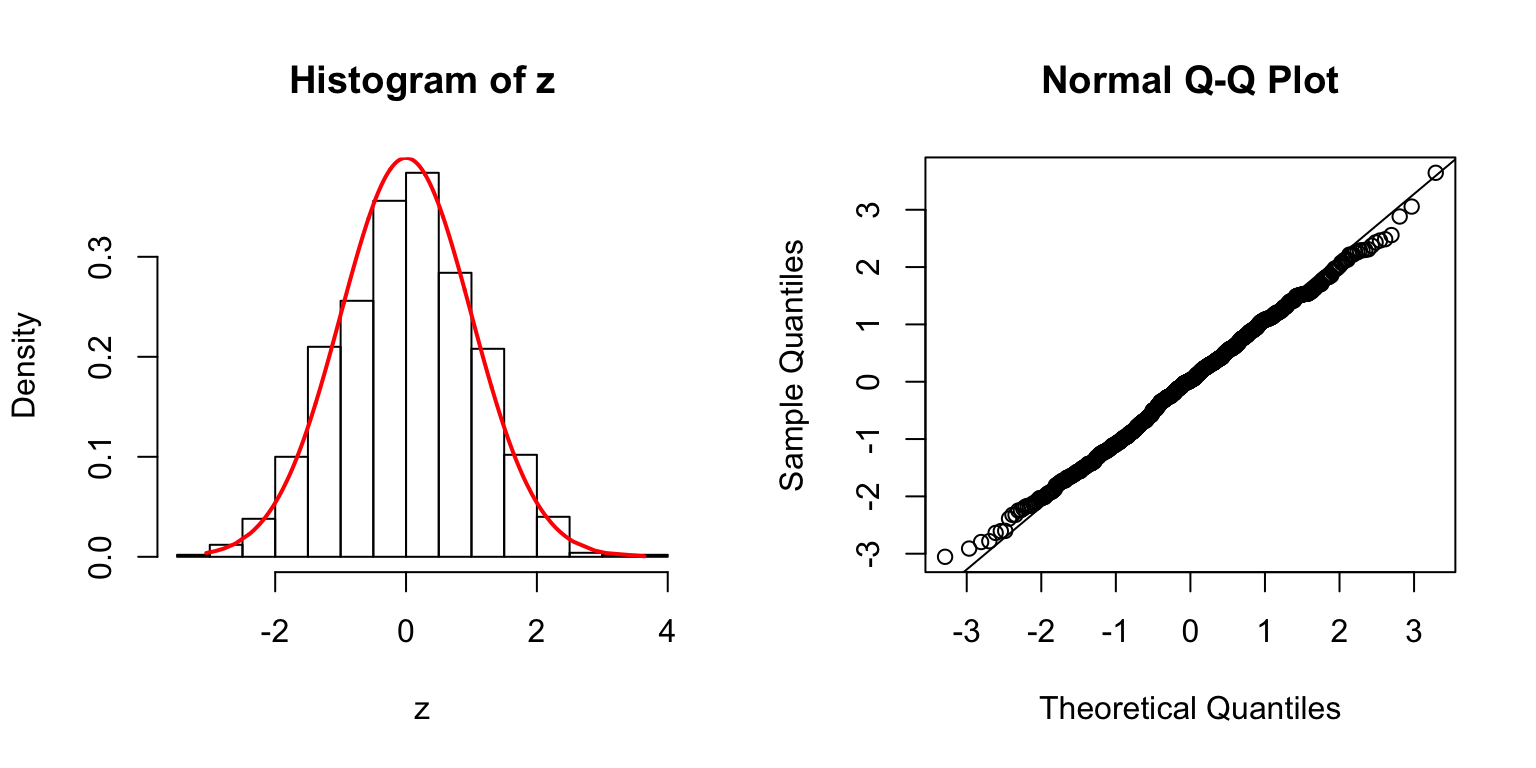
\(\Sigma = I\)
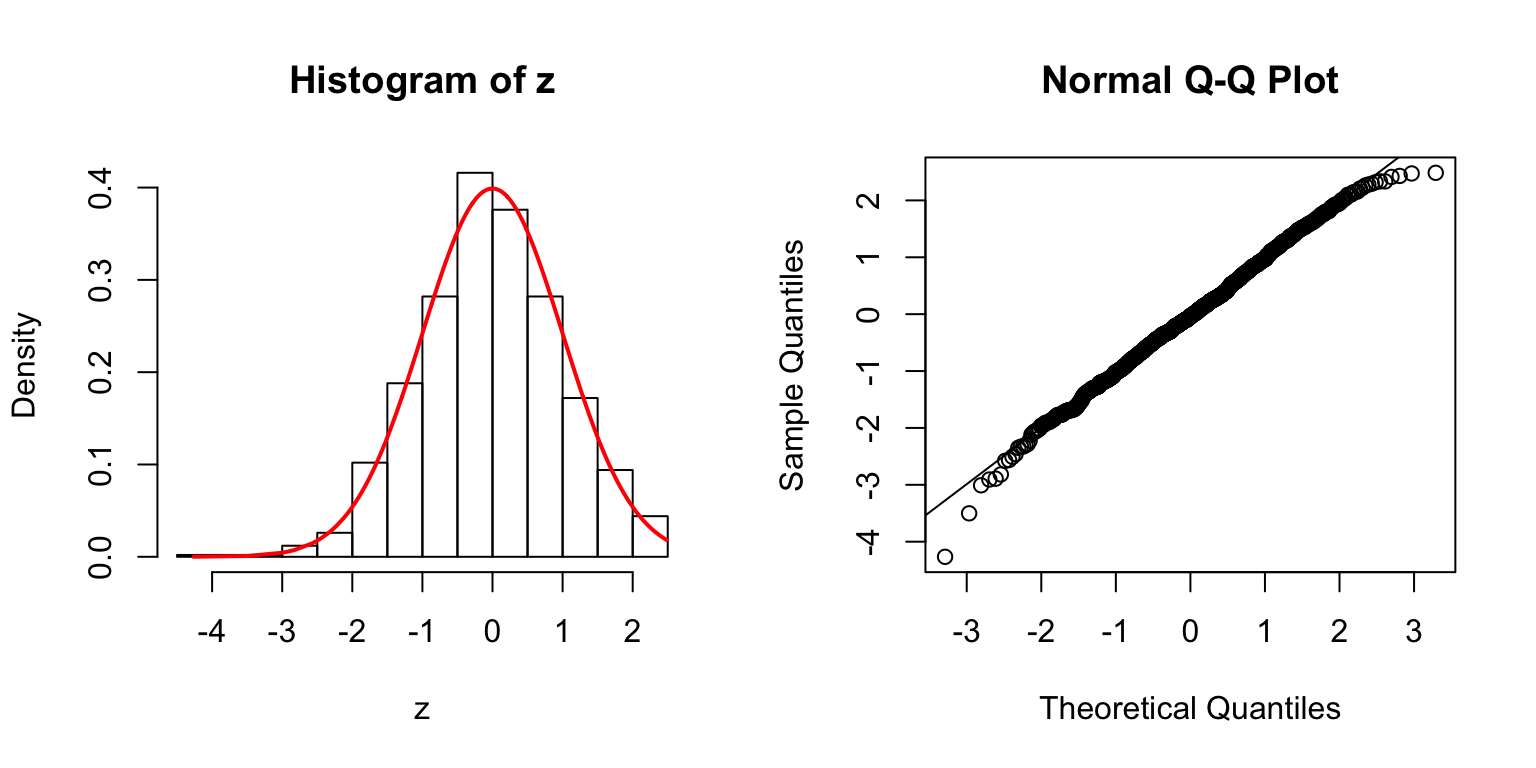
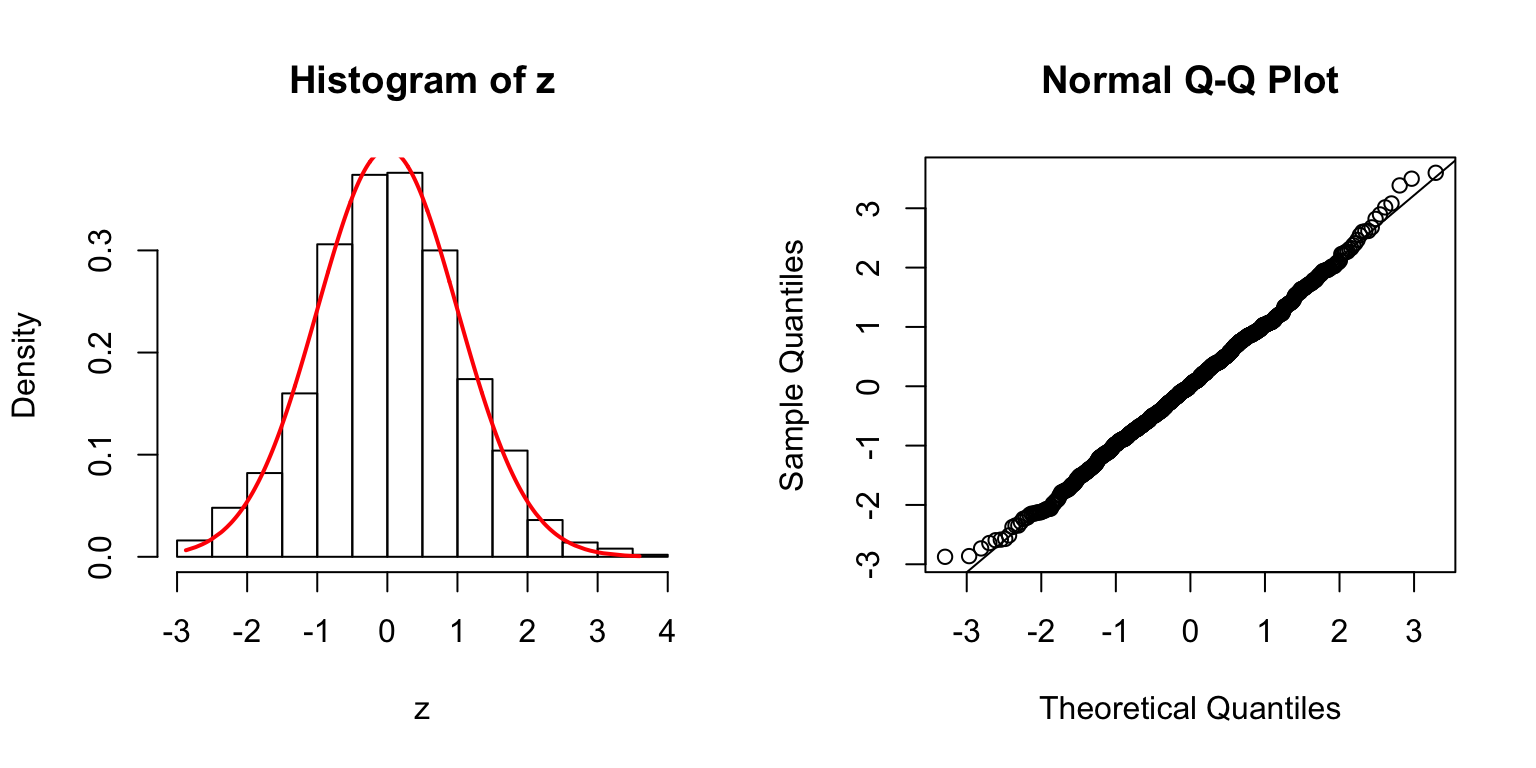
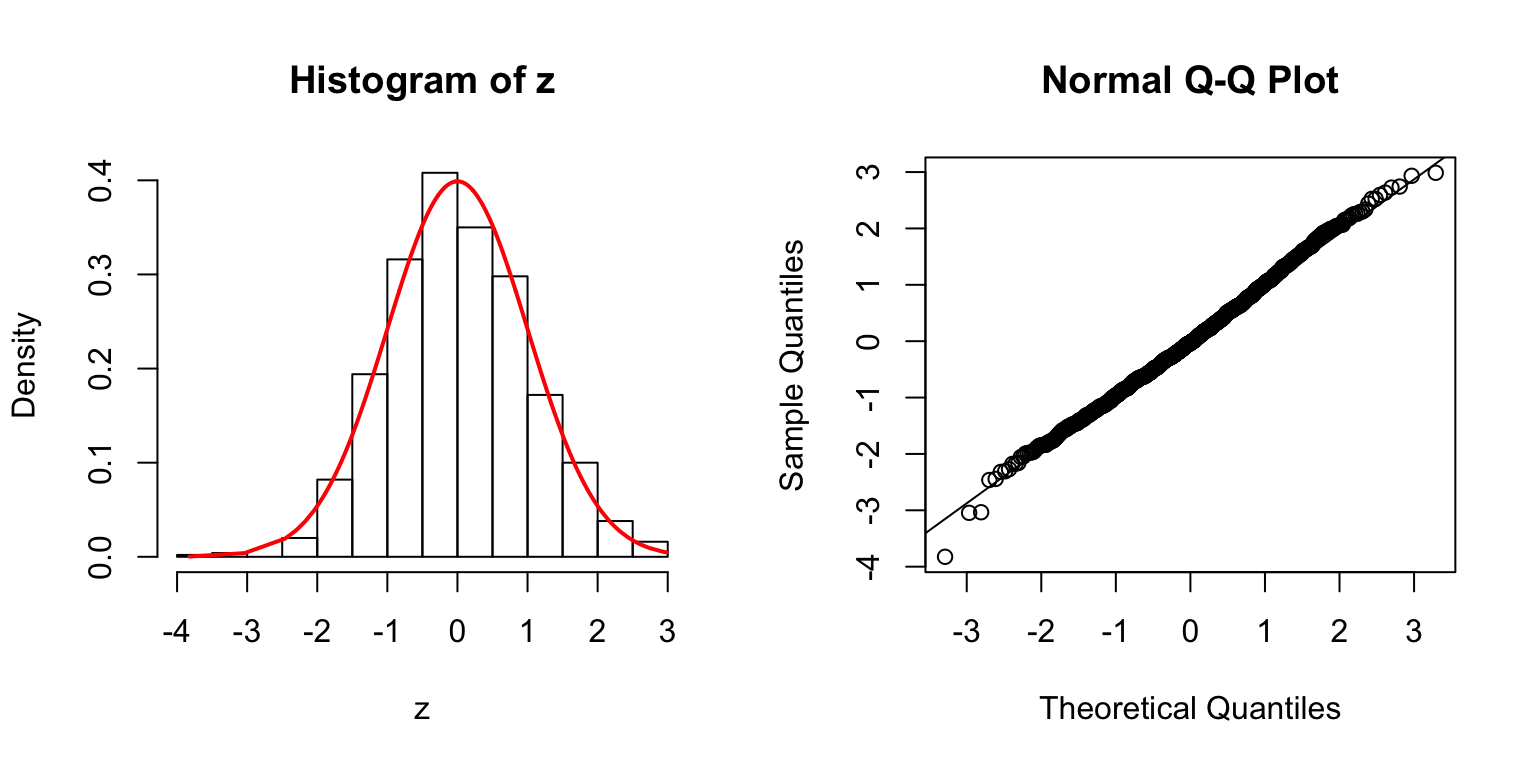
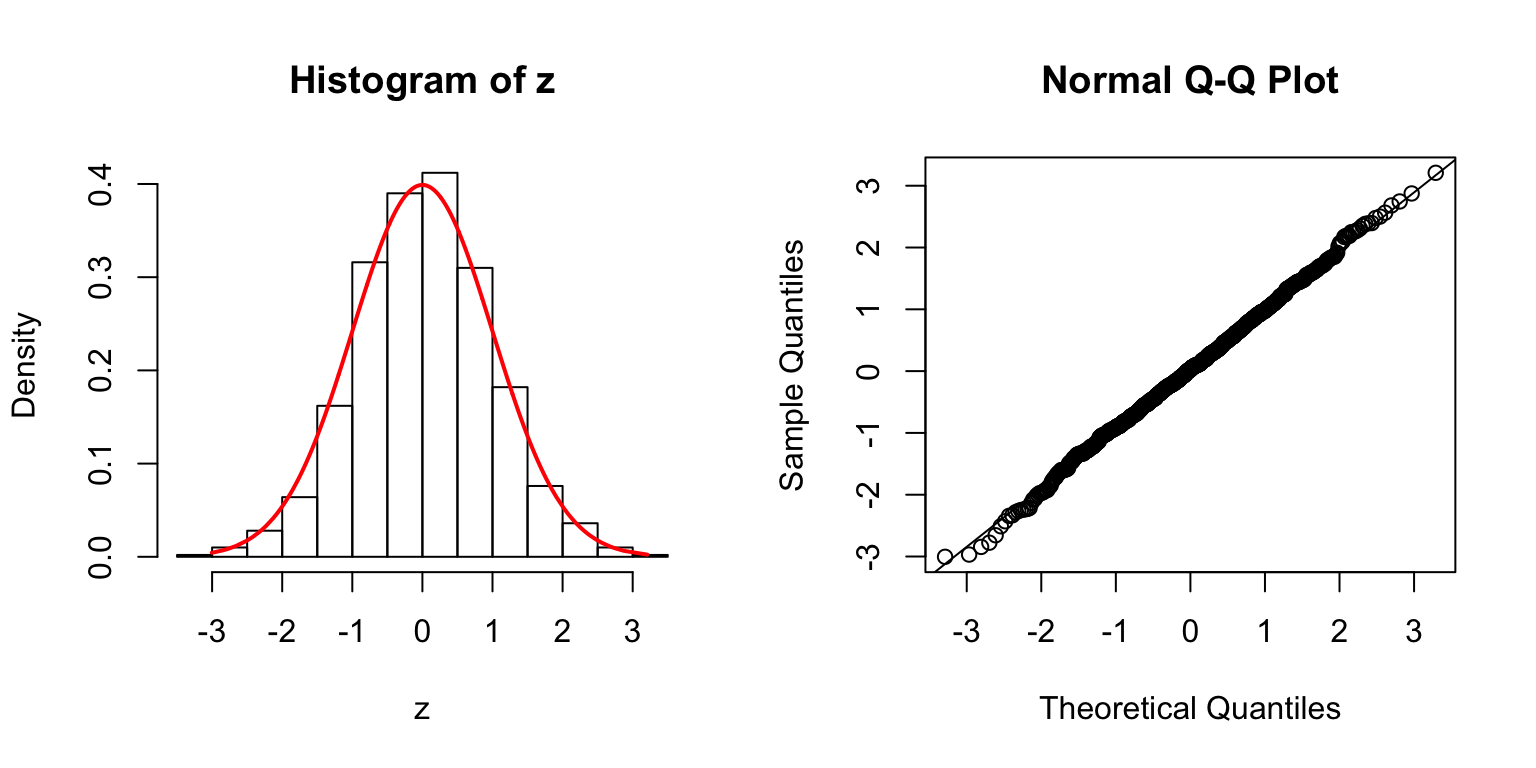
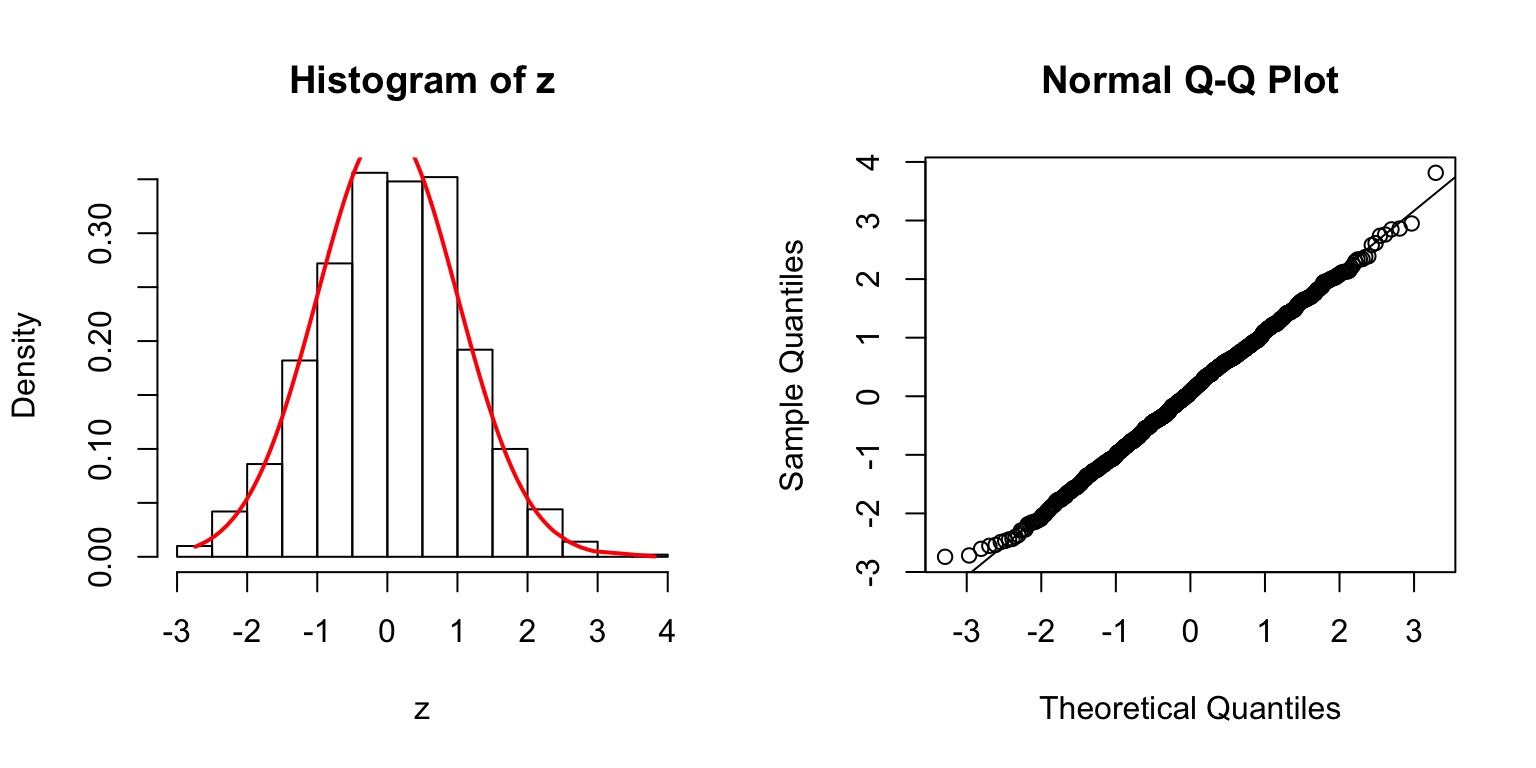
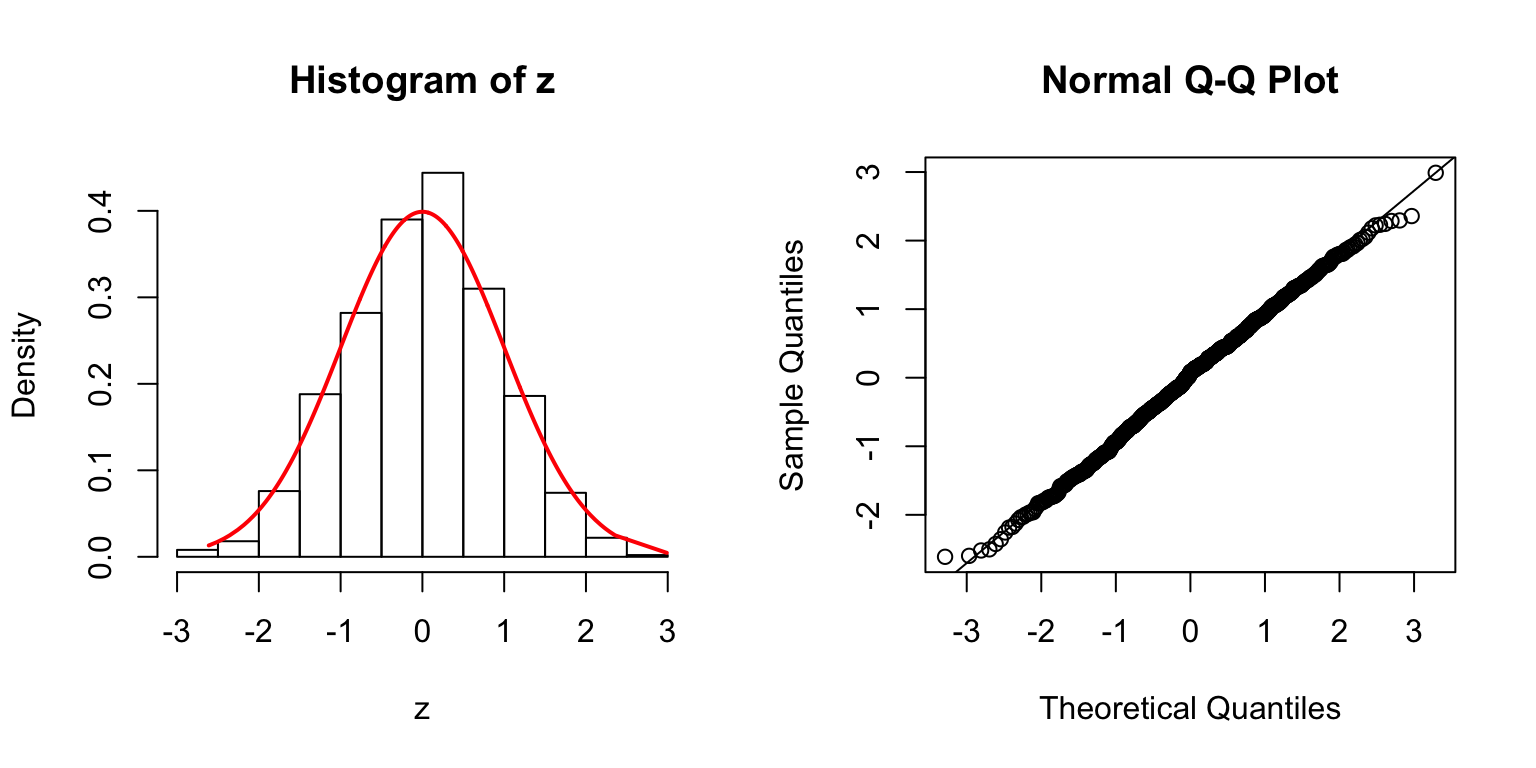
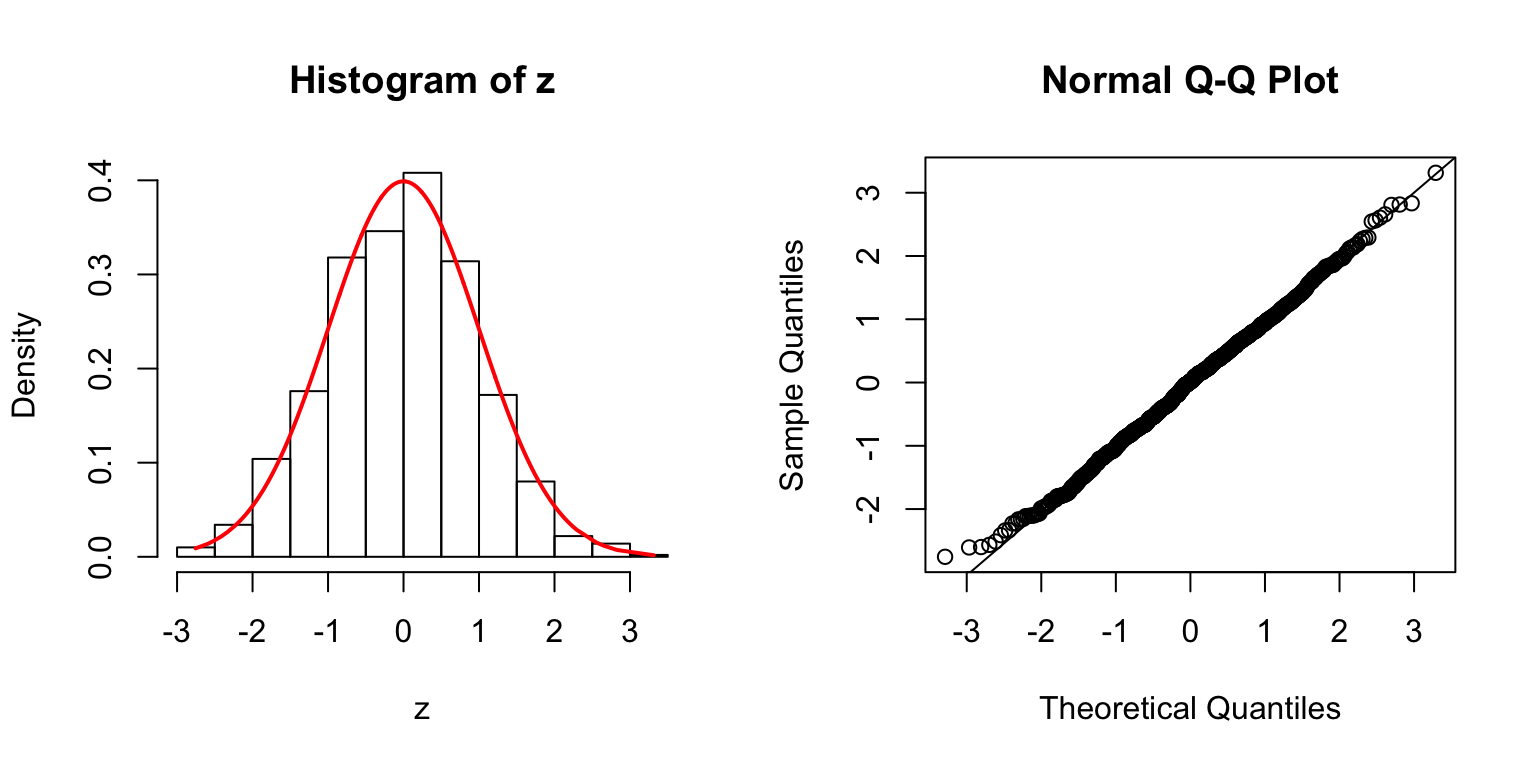
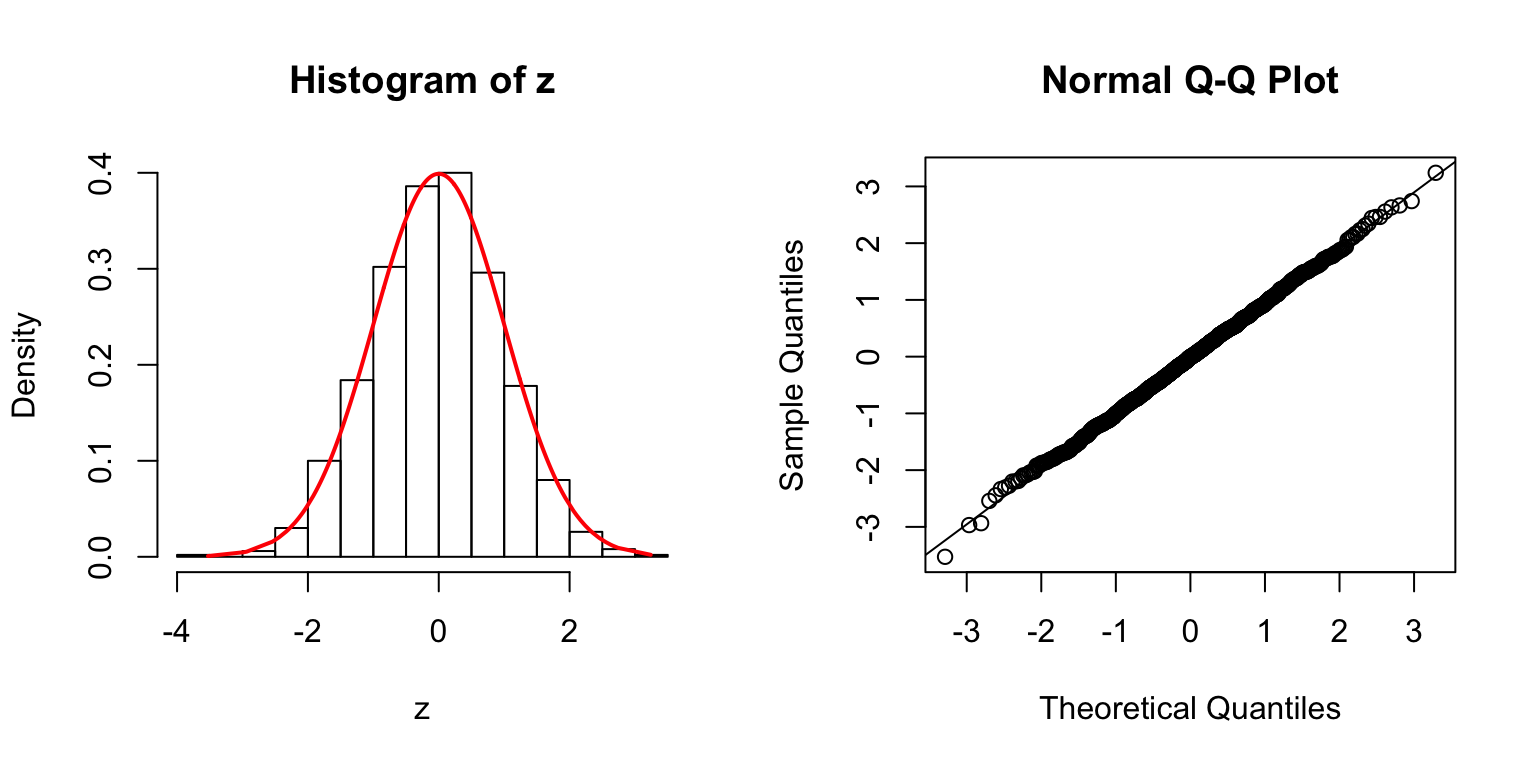
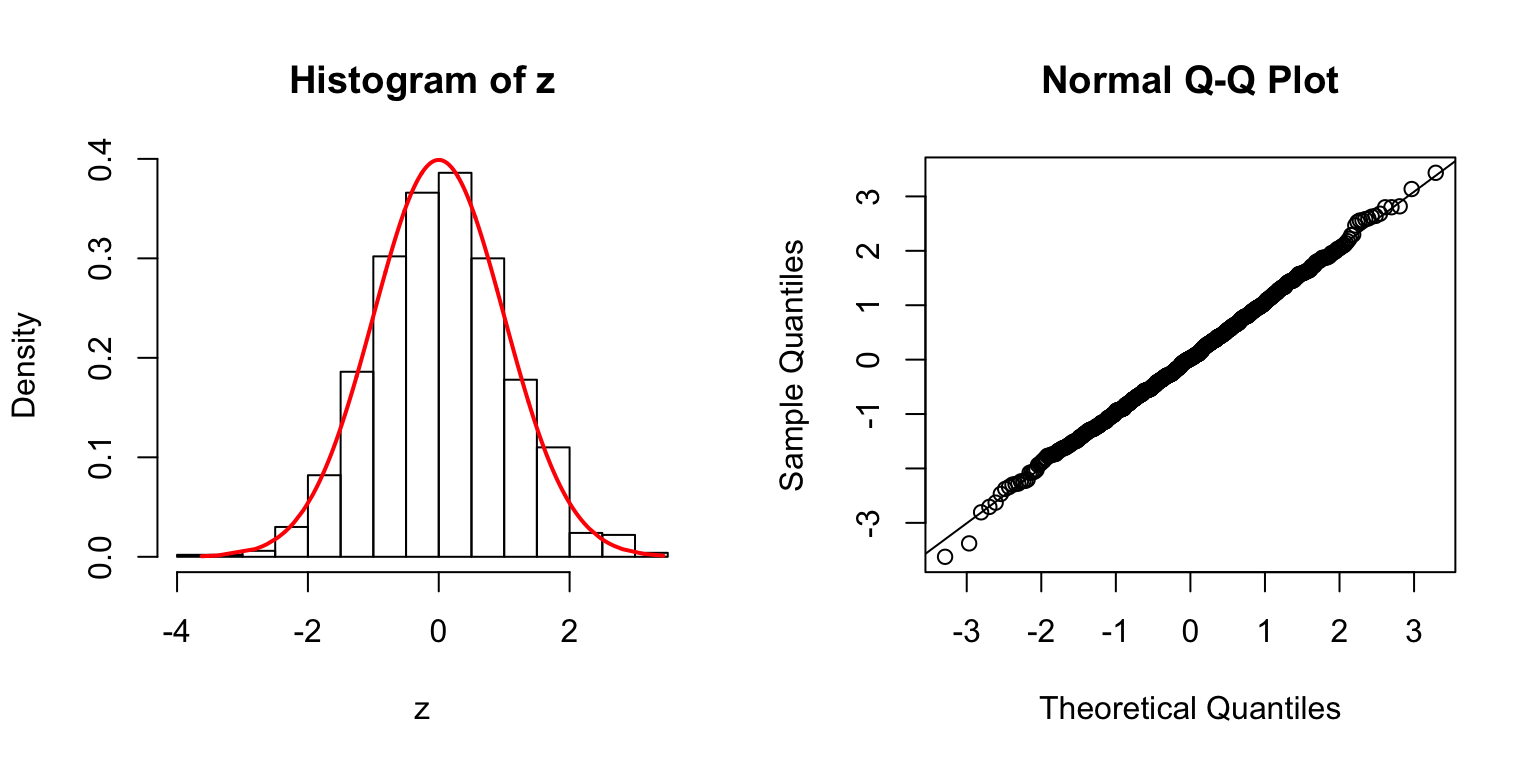
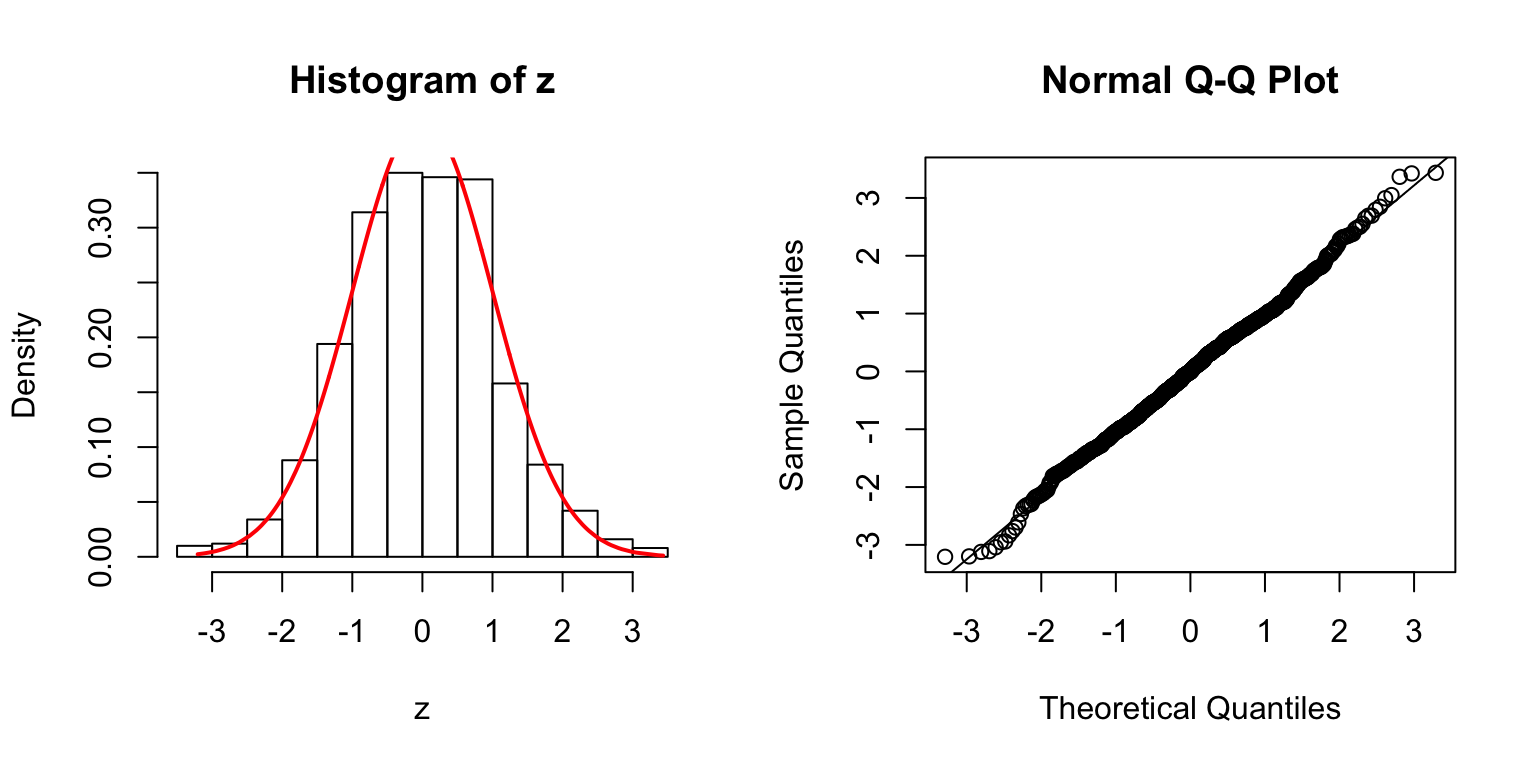
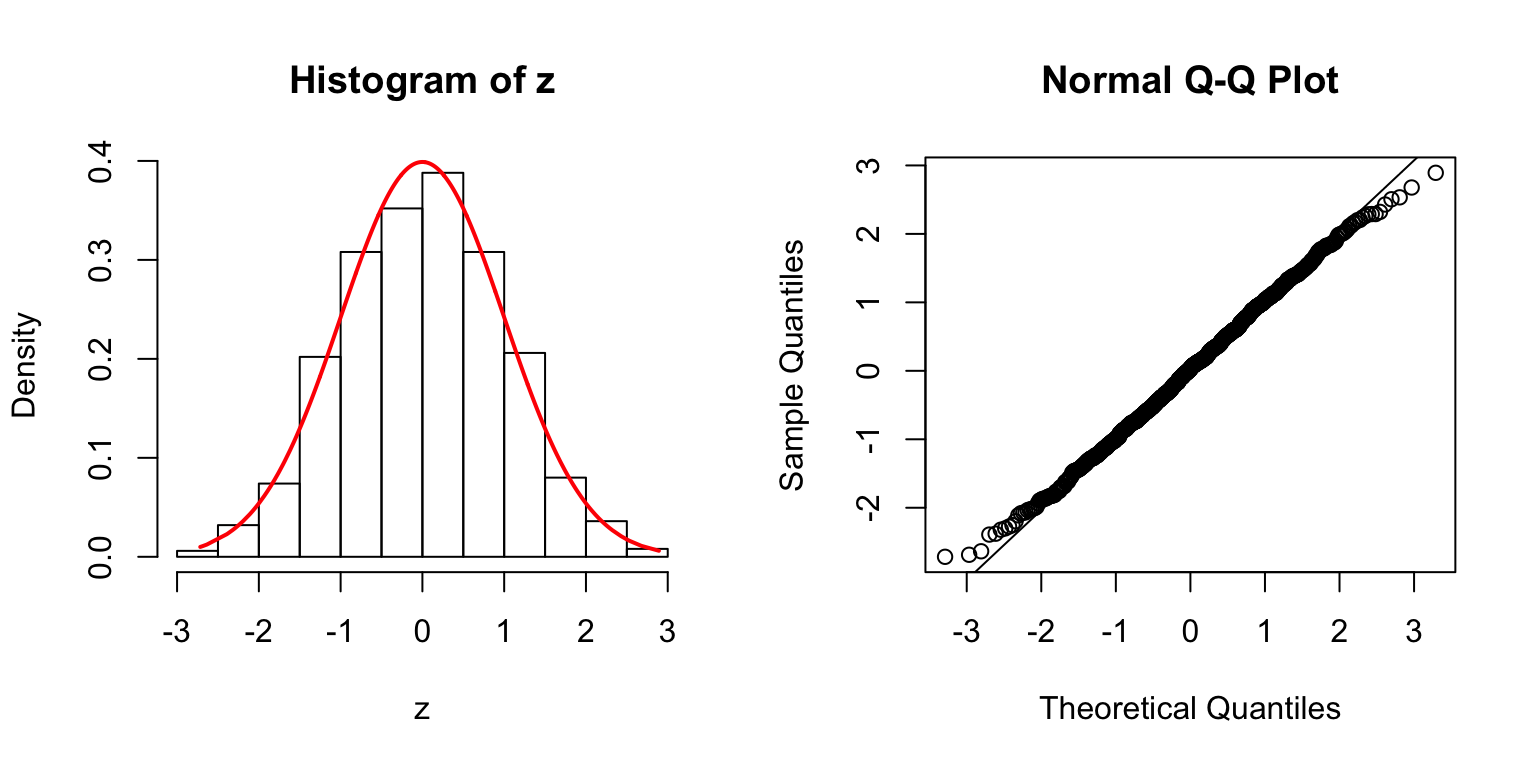
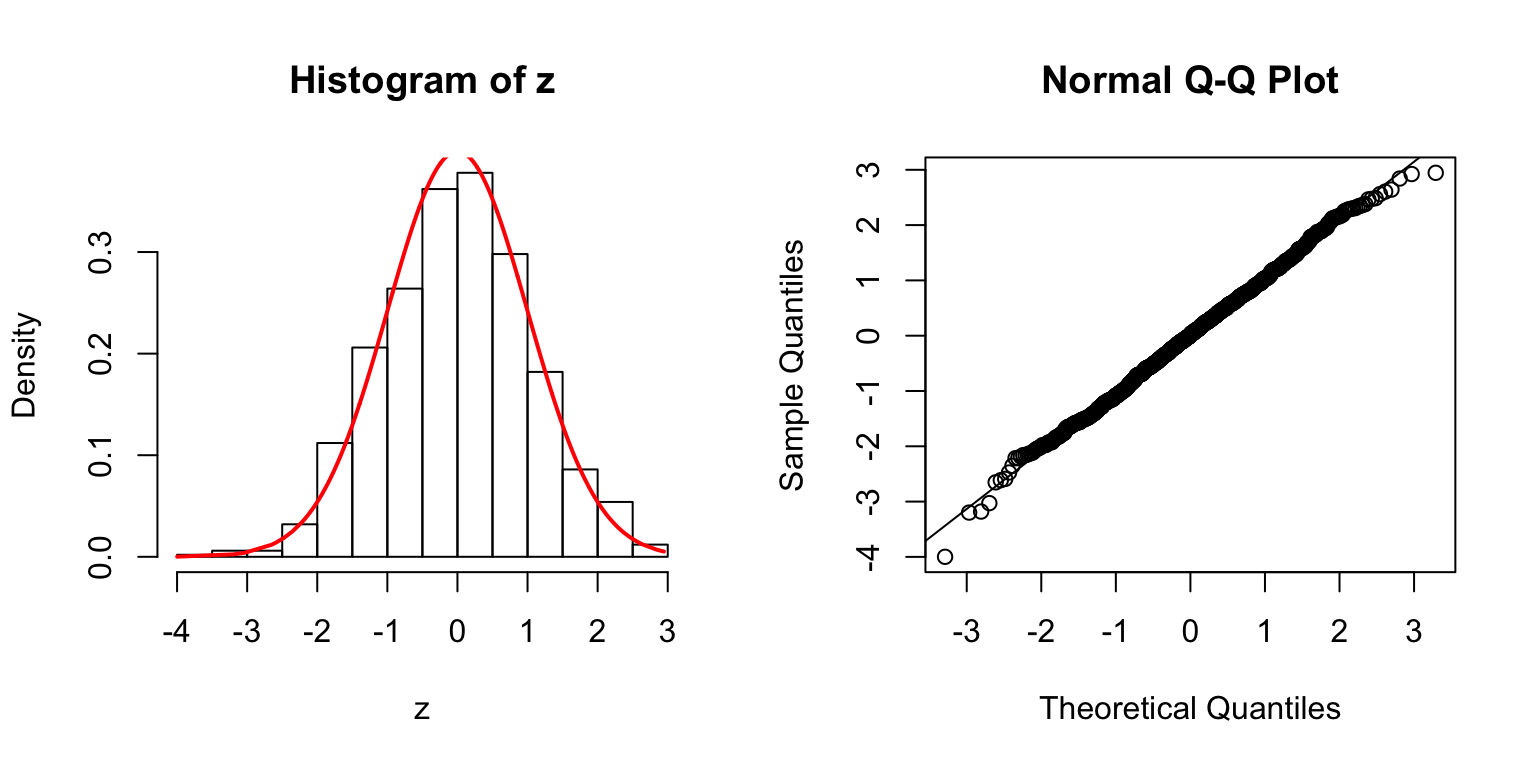
\(\Sigma\): Toeplitz
\(\Sigma_{j,k} = \rho^{|j - k|}\).
\(\rho = 0.2\)
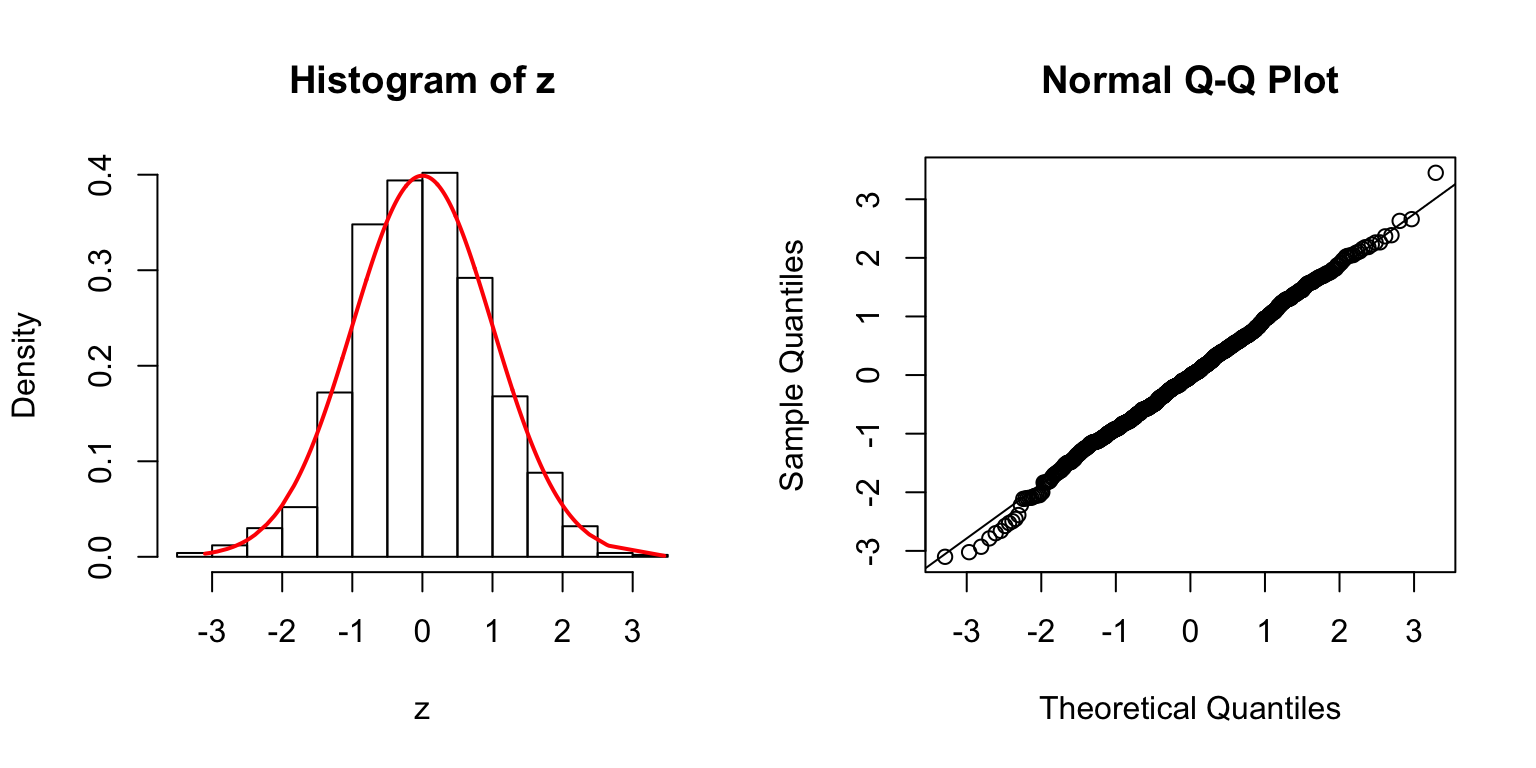
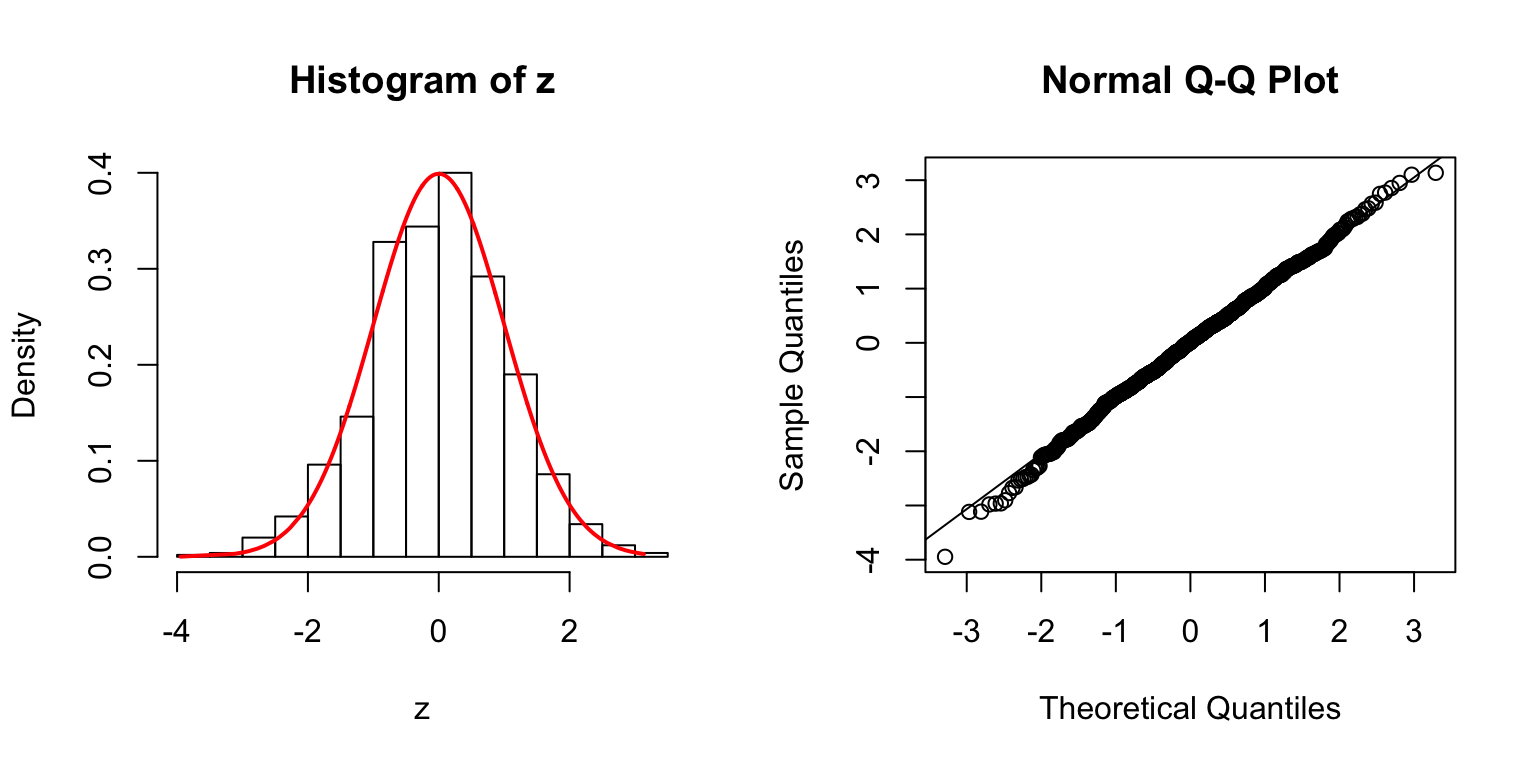
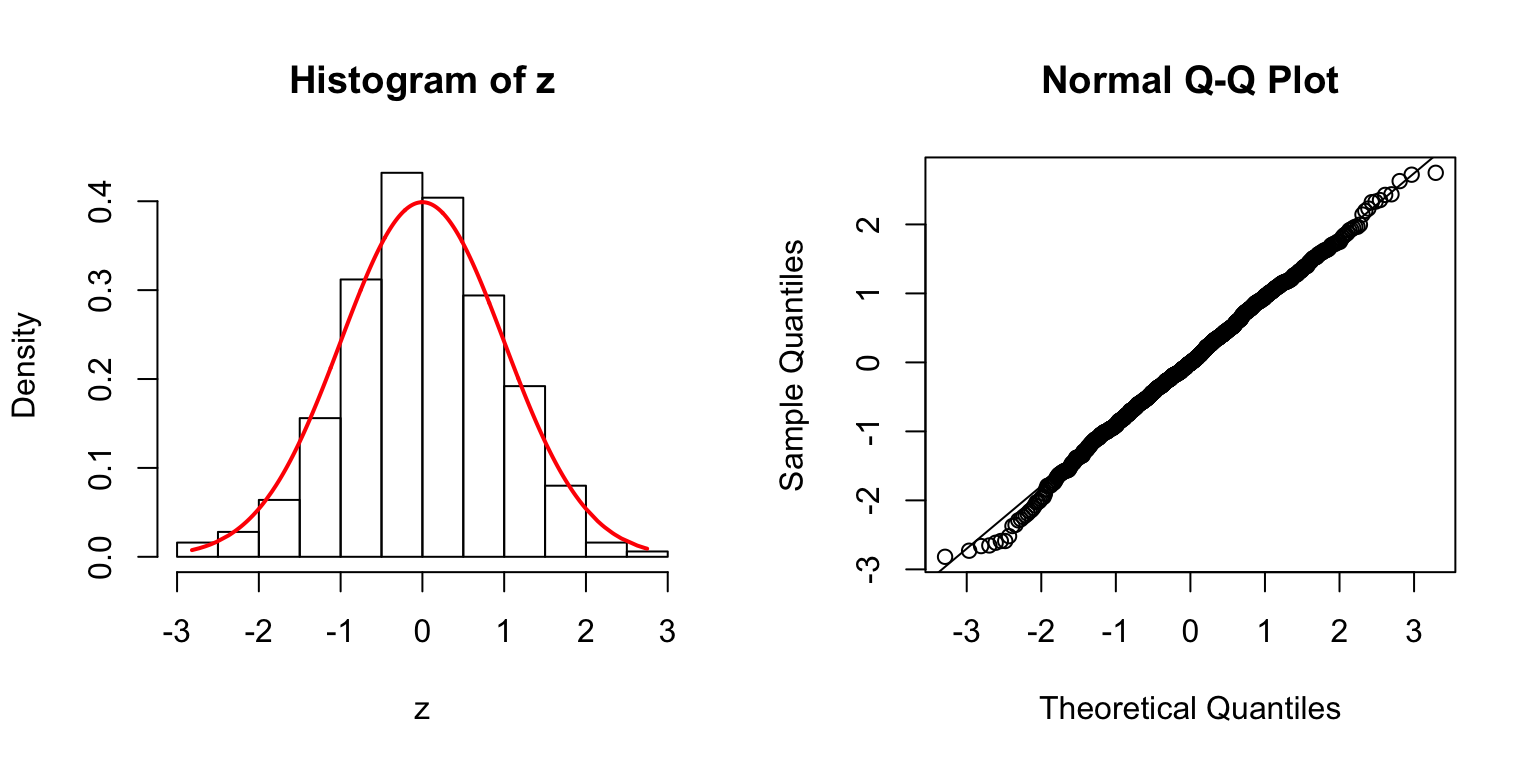
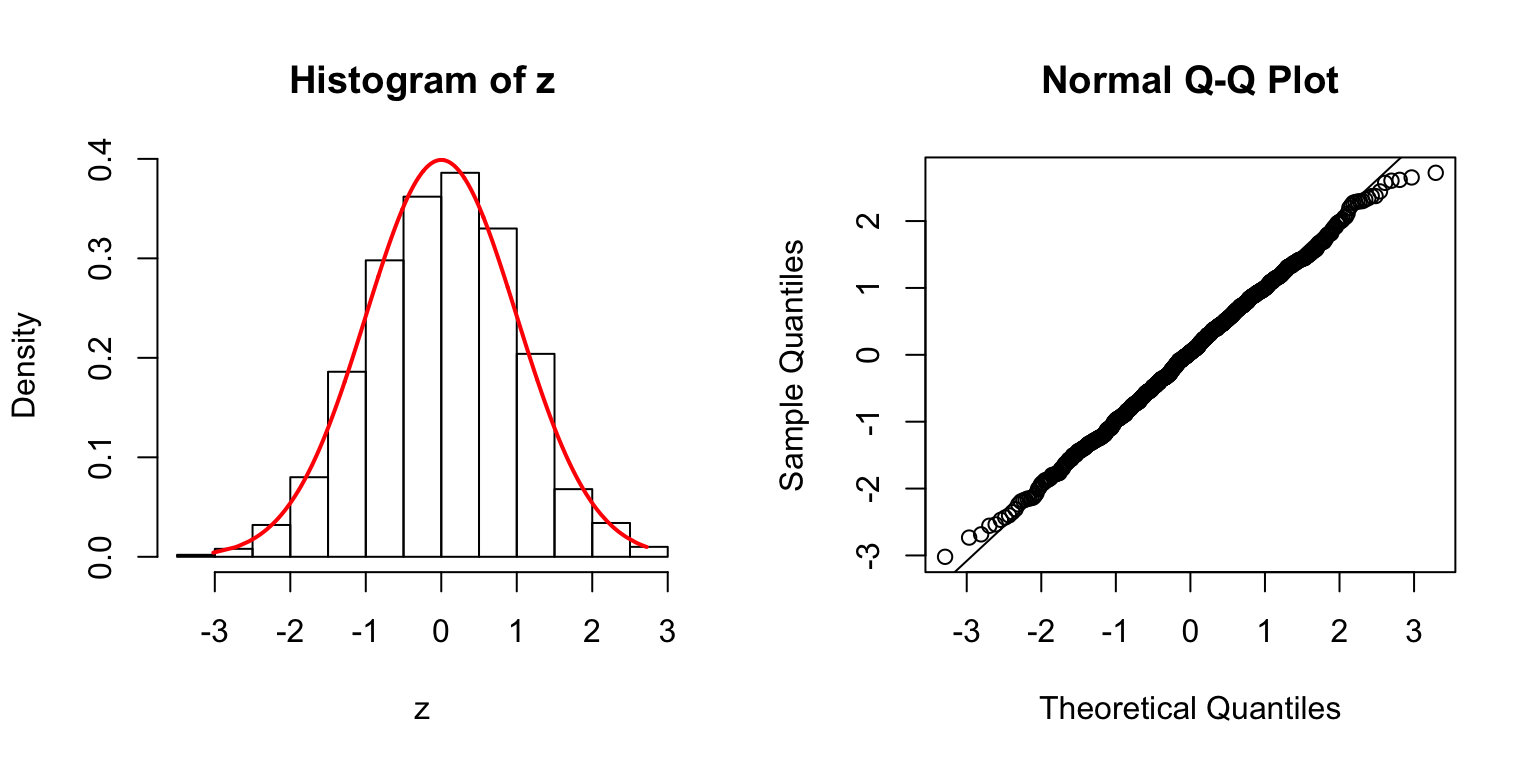
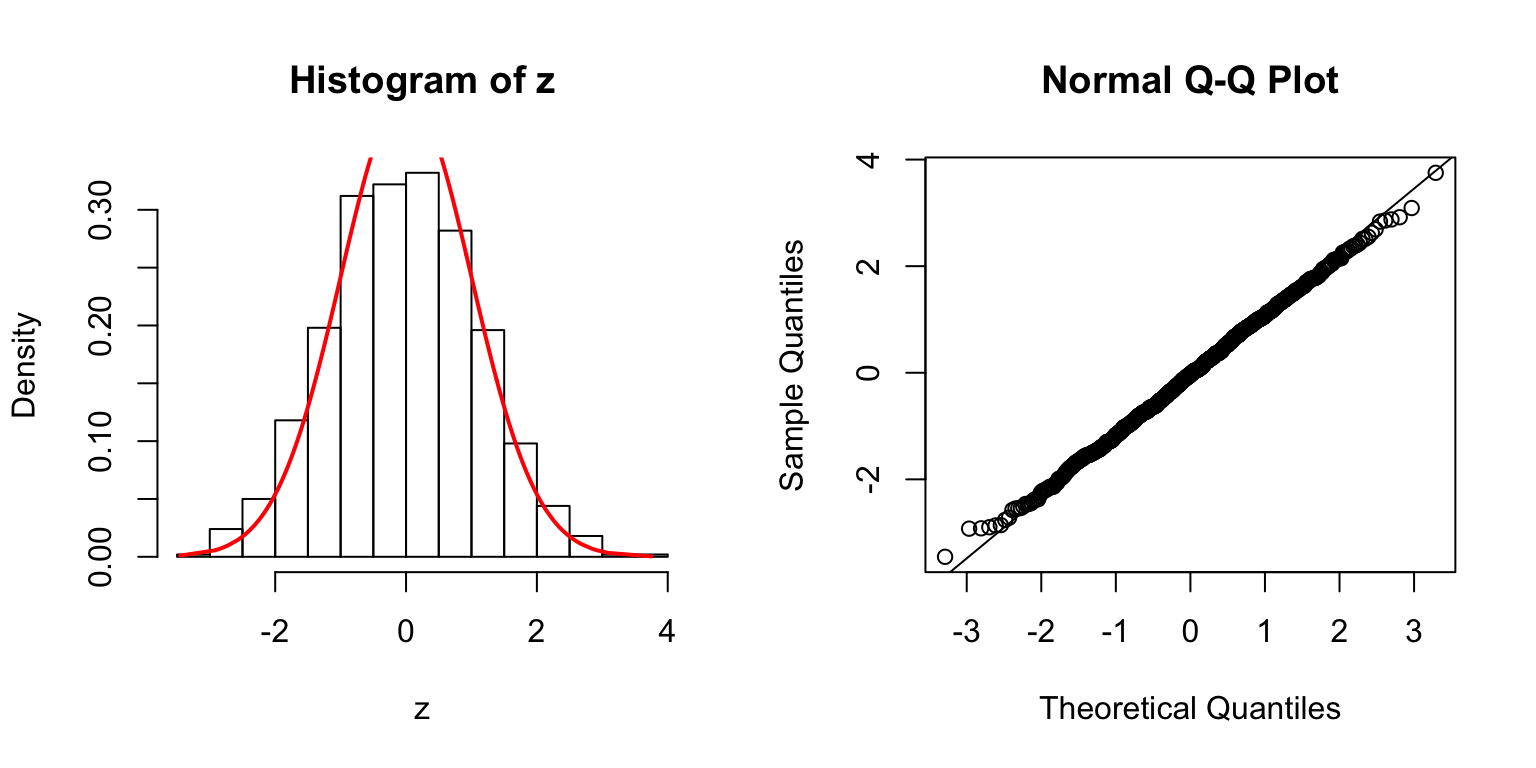
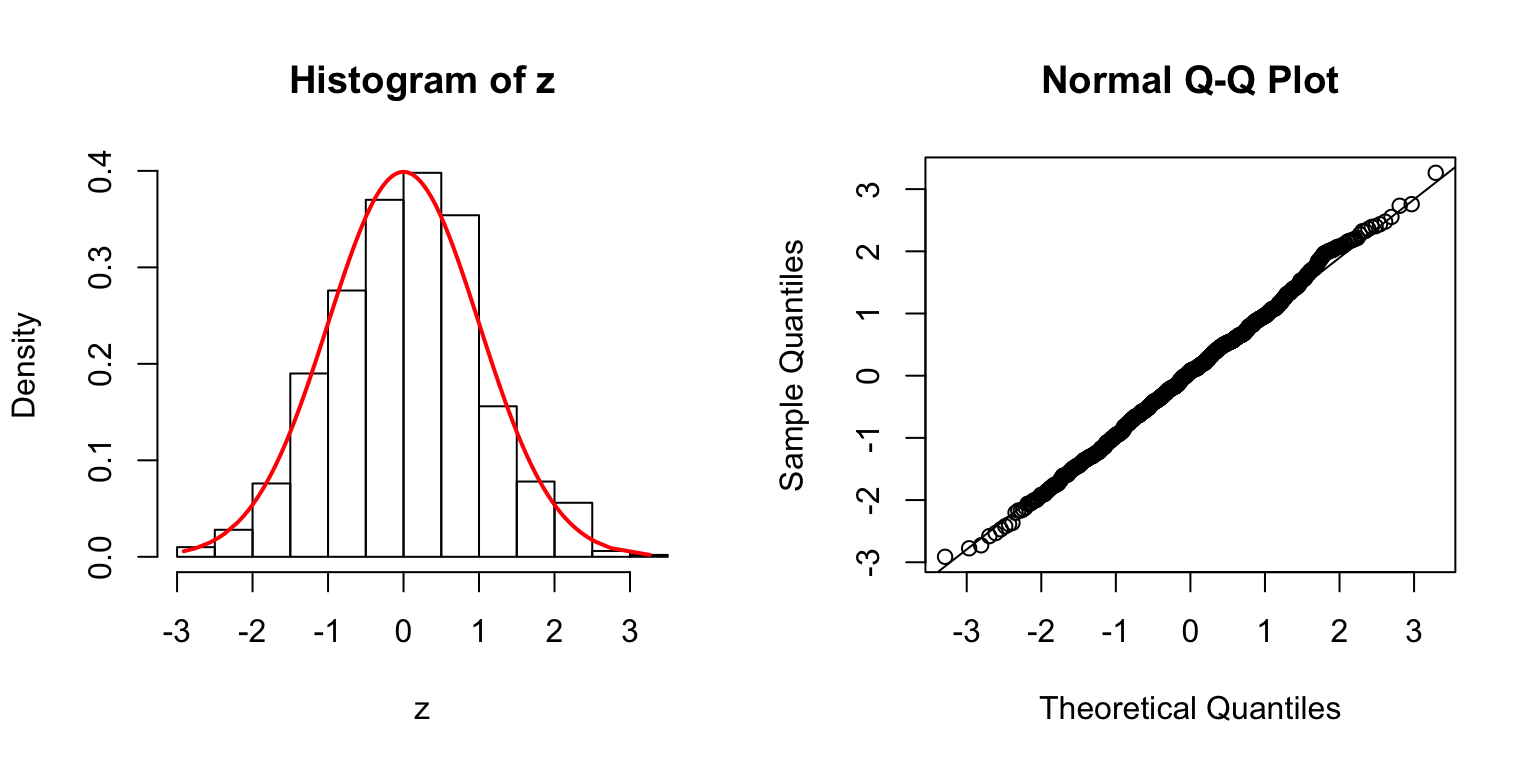
\(\rho = 0.5\)
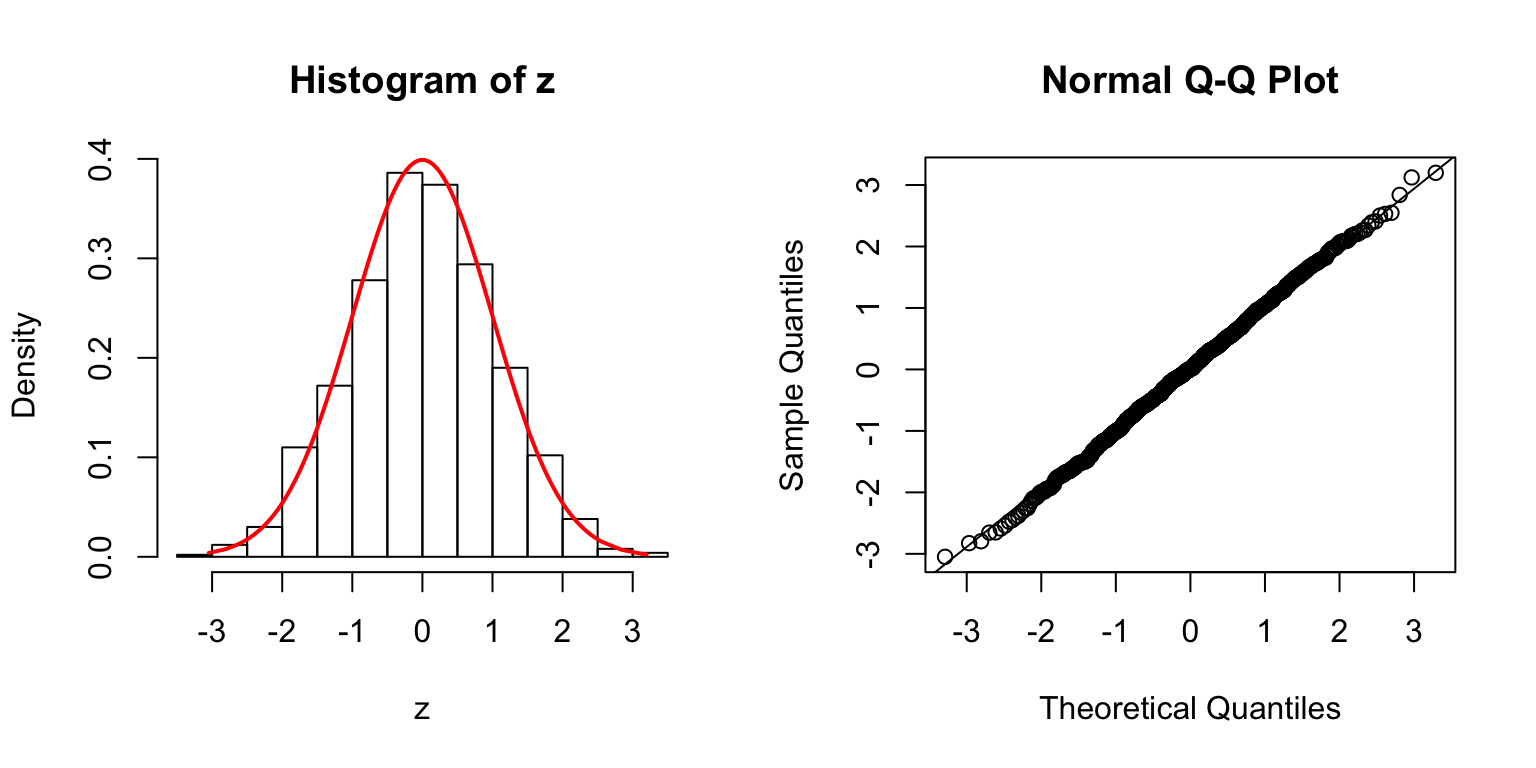
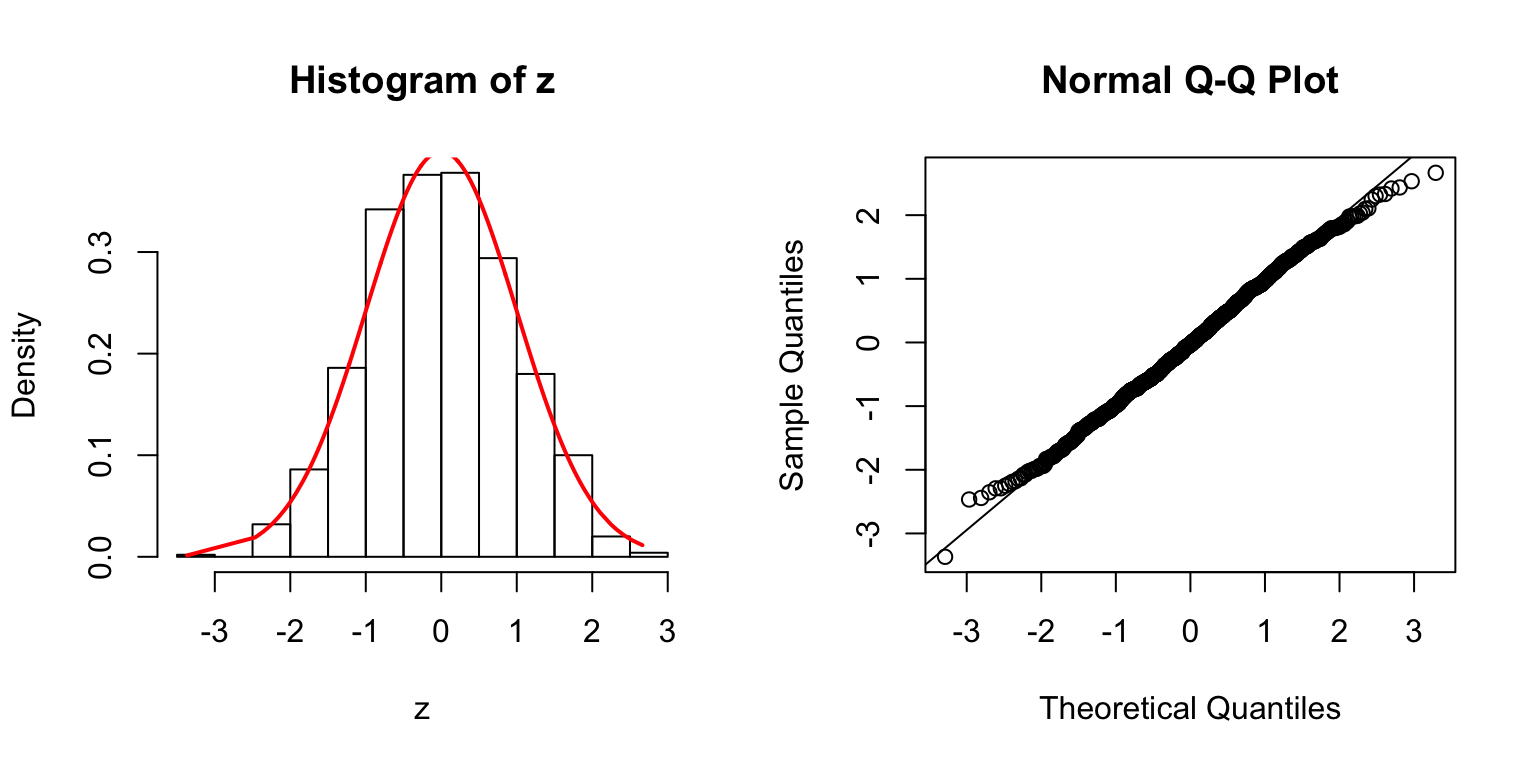
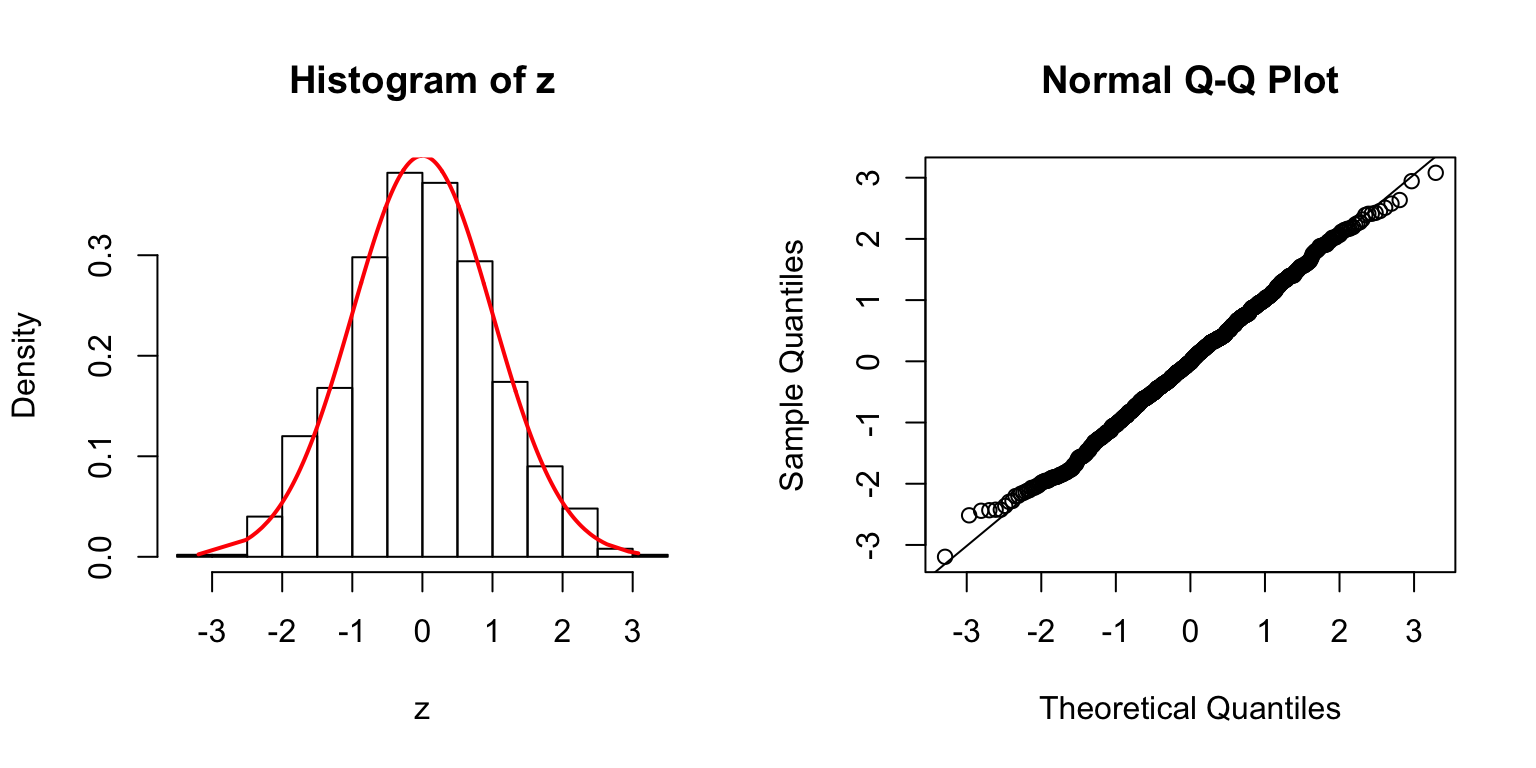
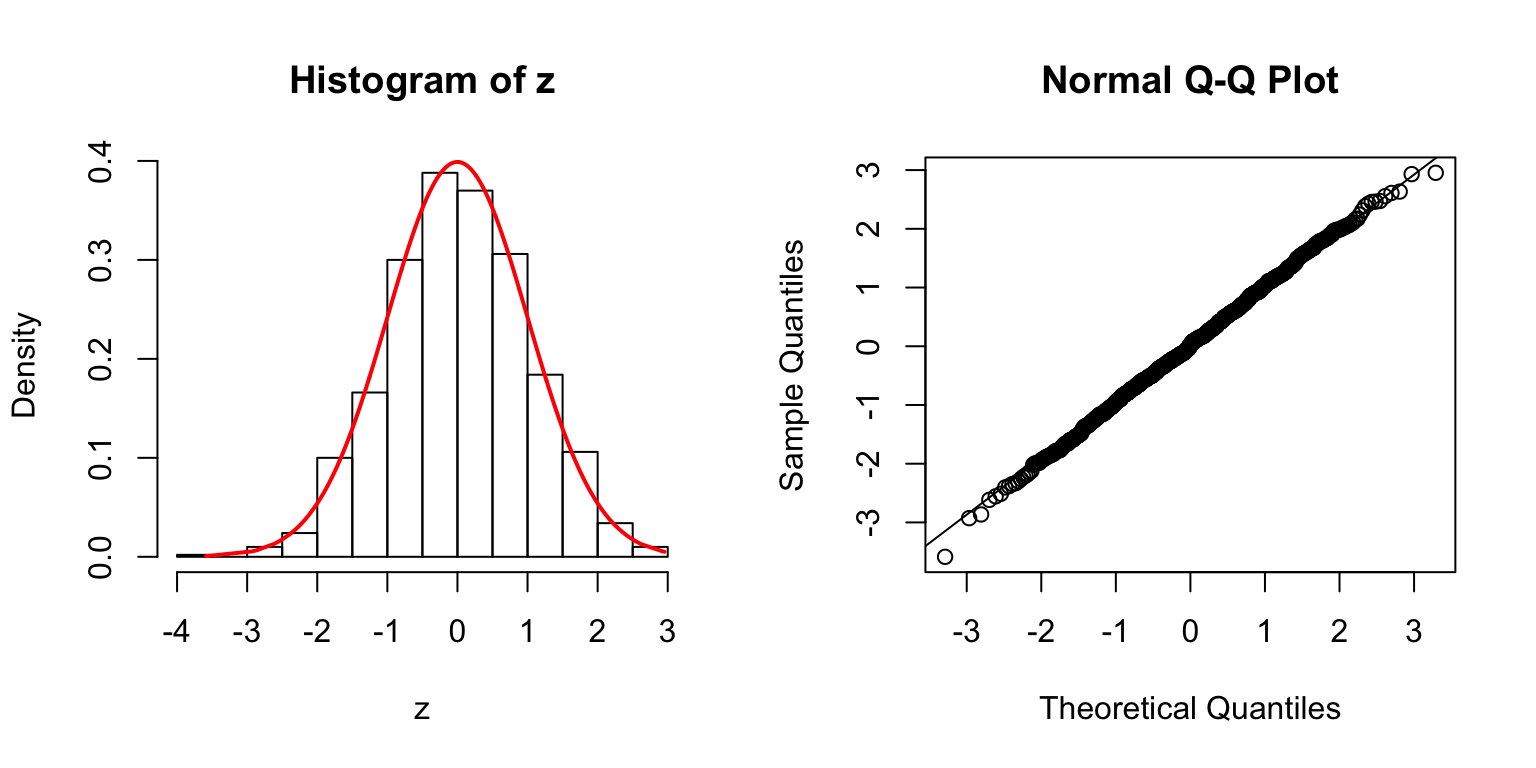
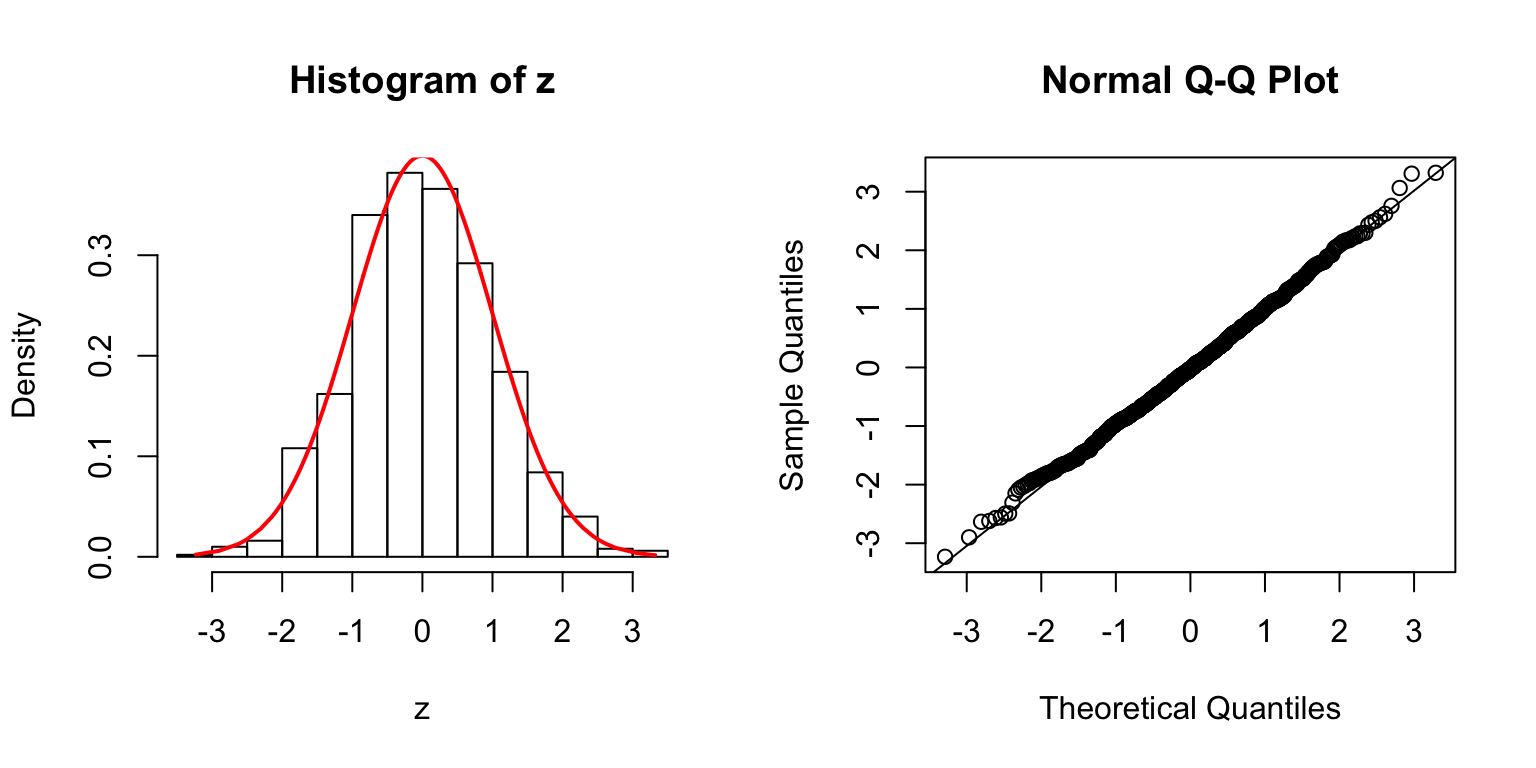
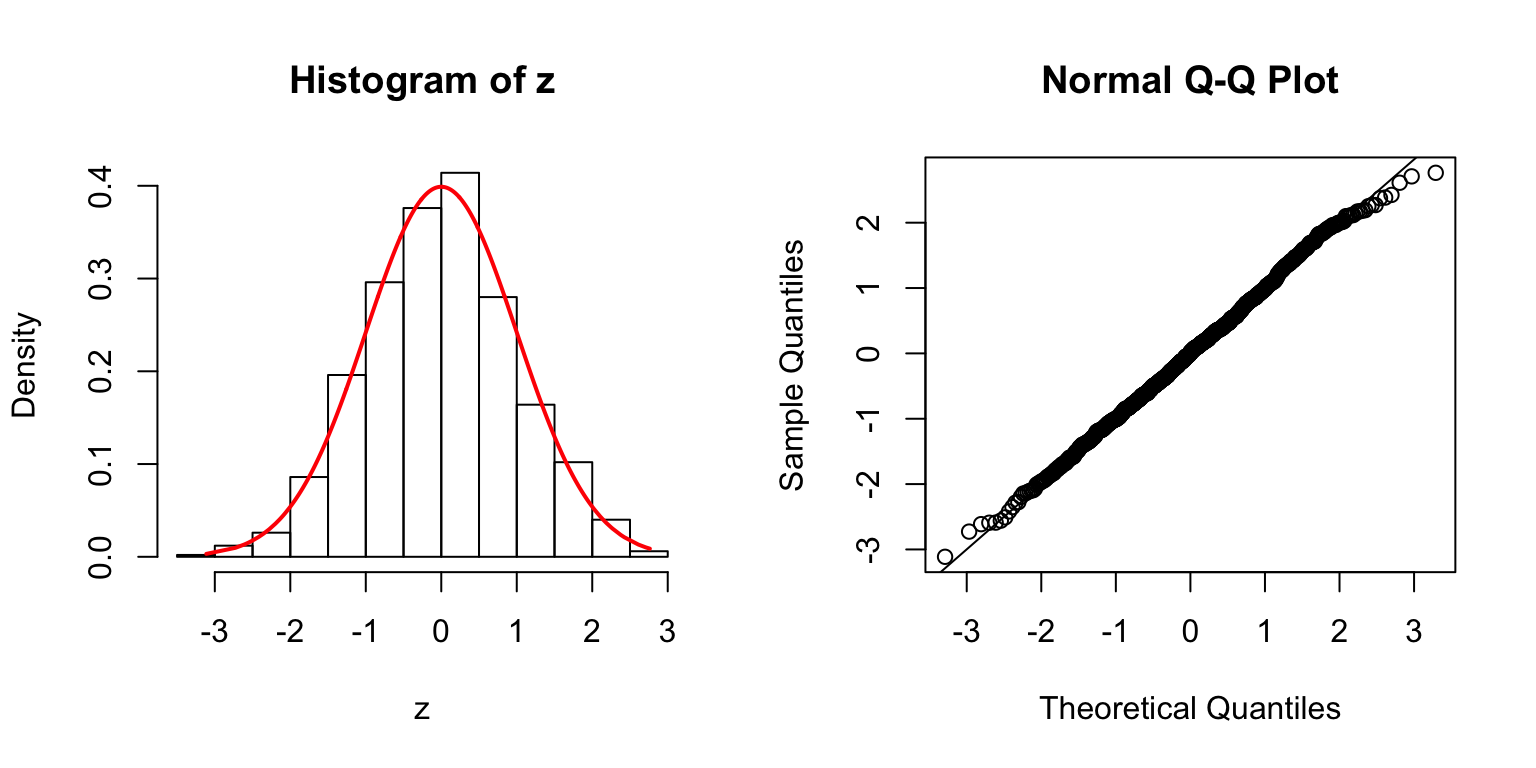
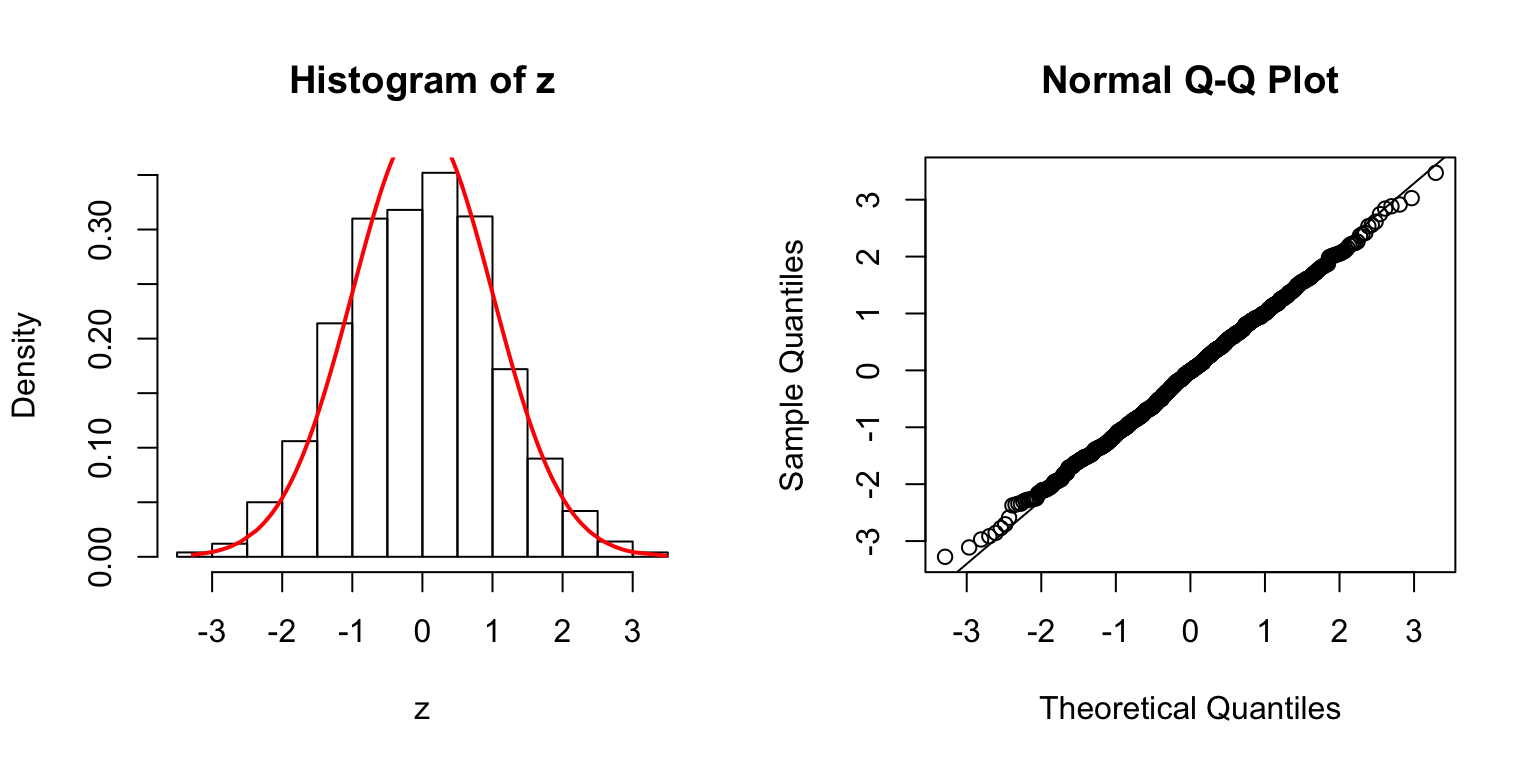
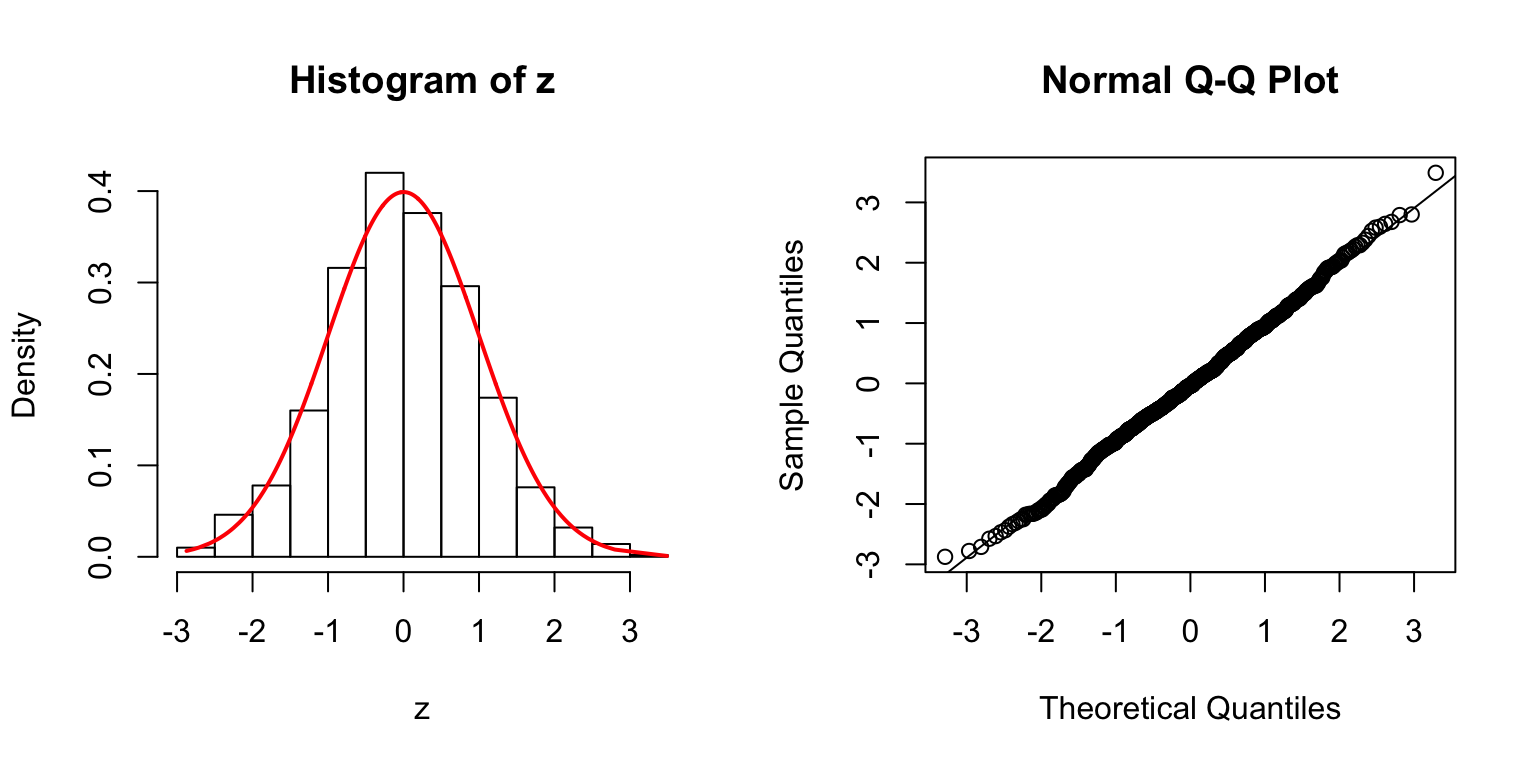
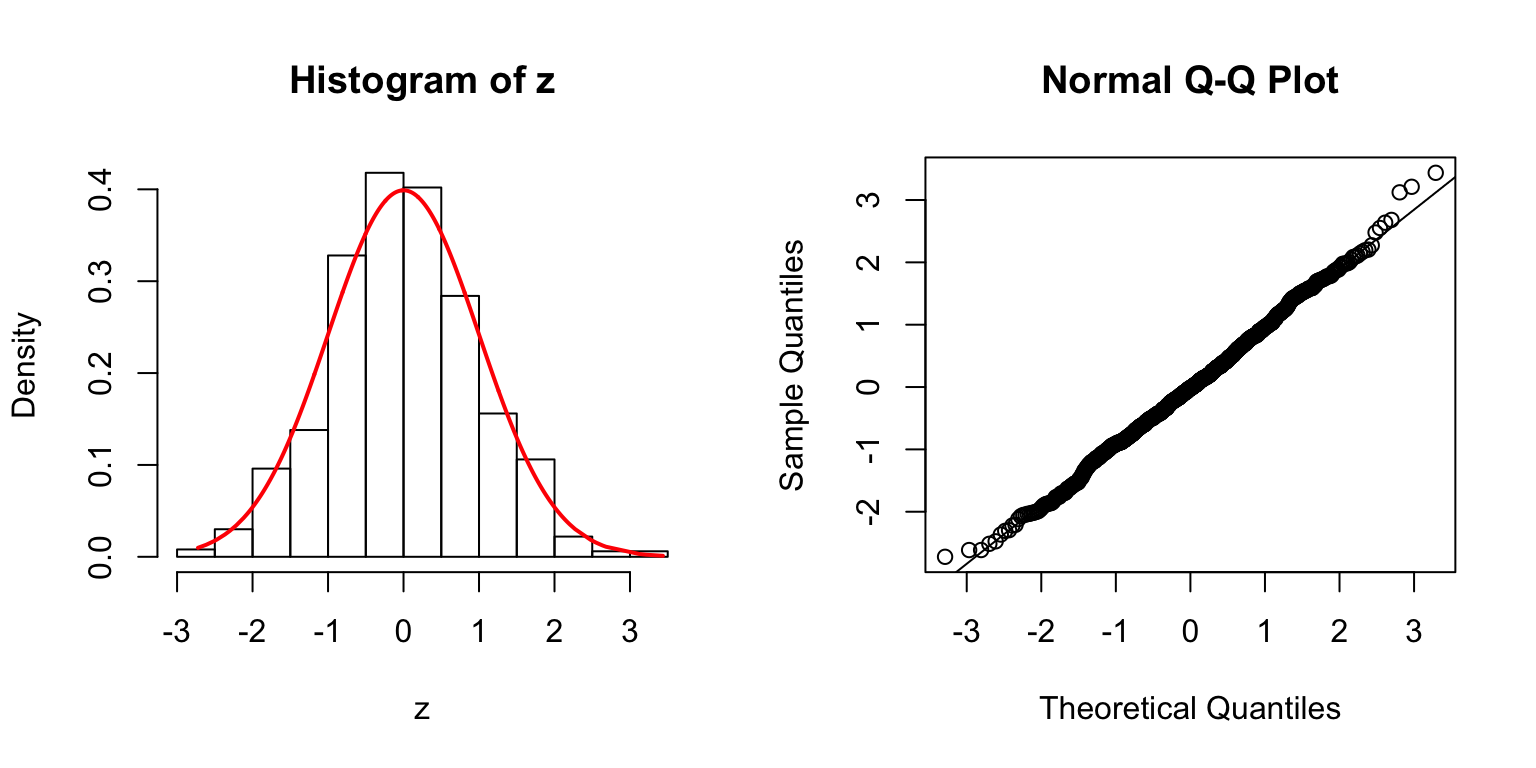
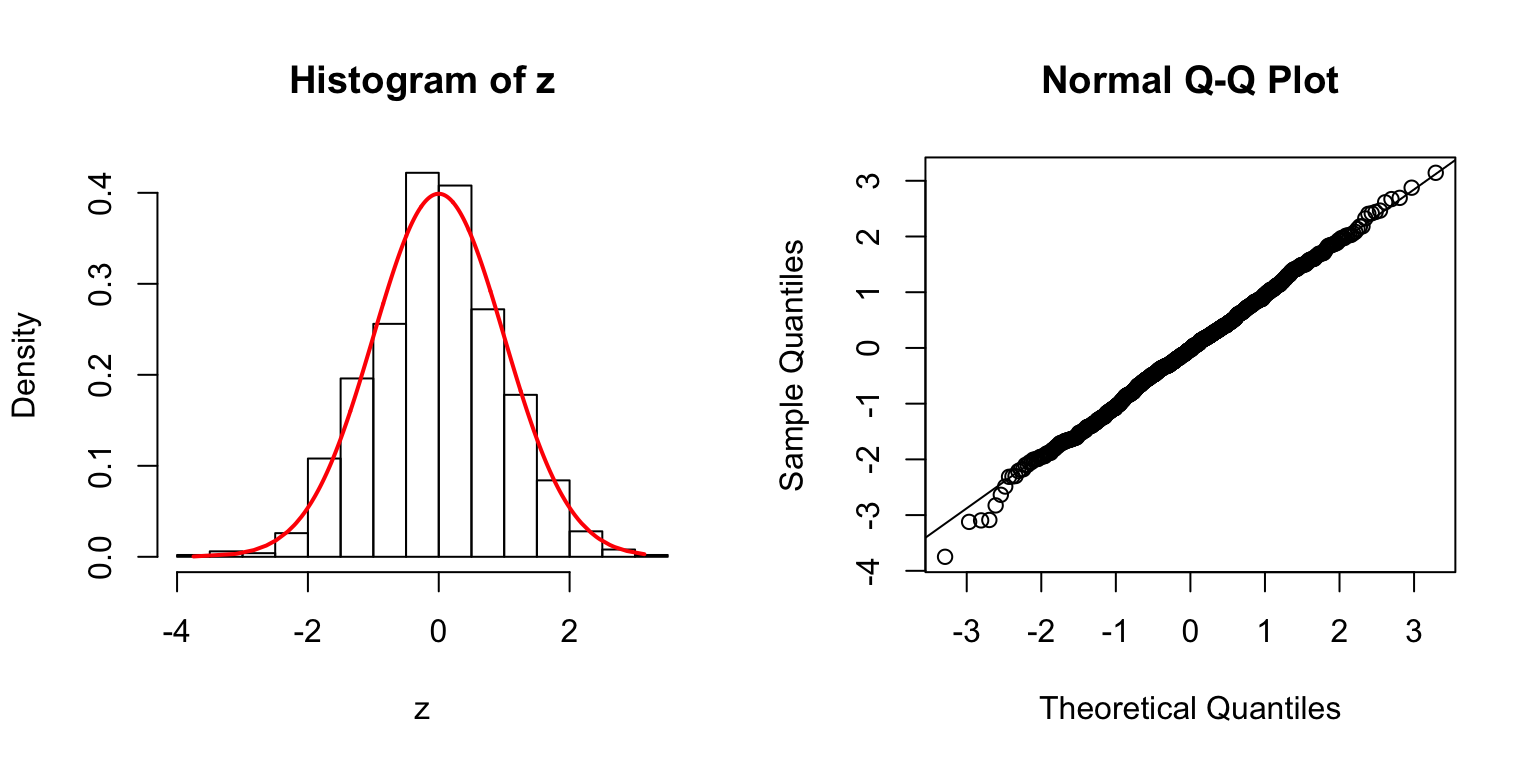
\(\rho = 0.8\)
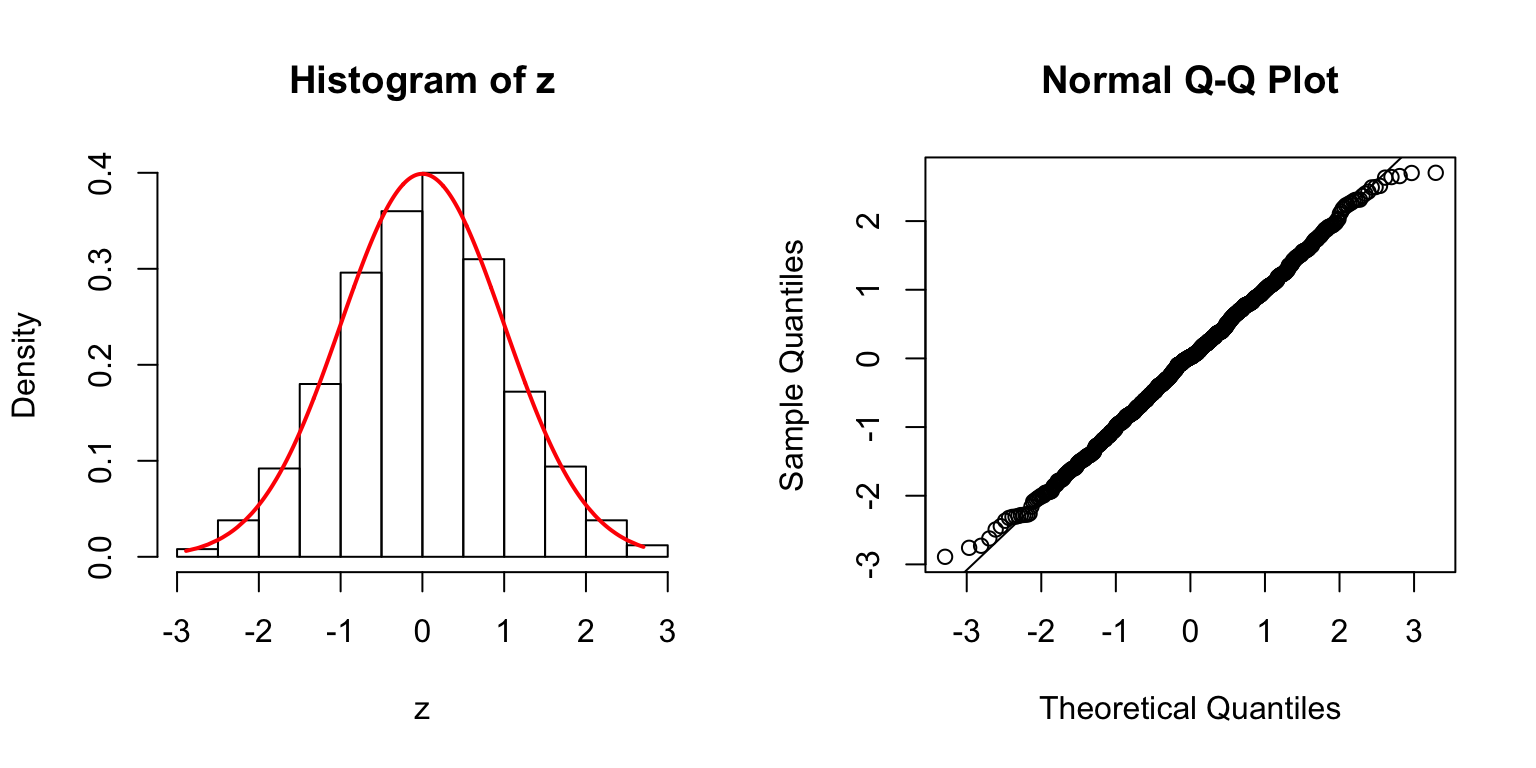
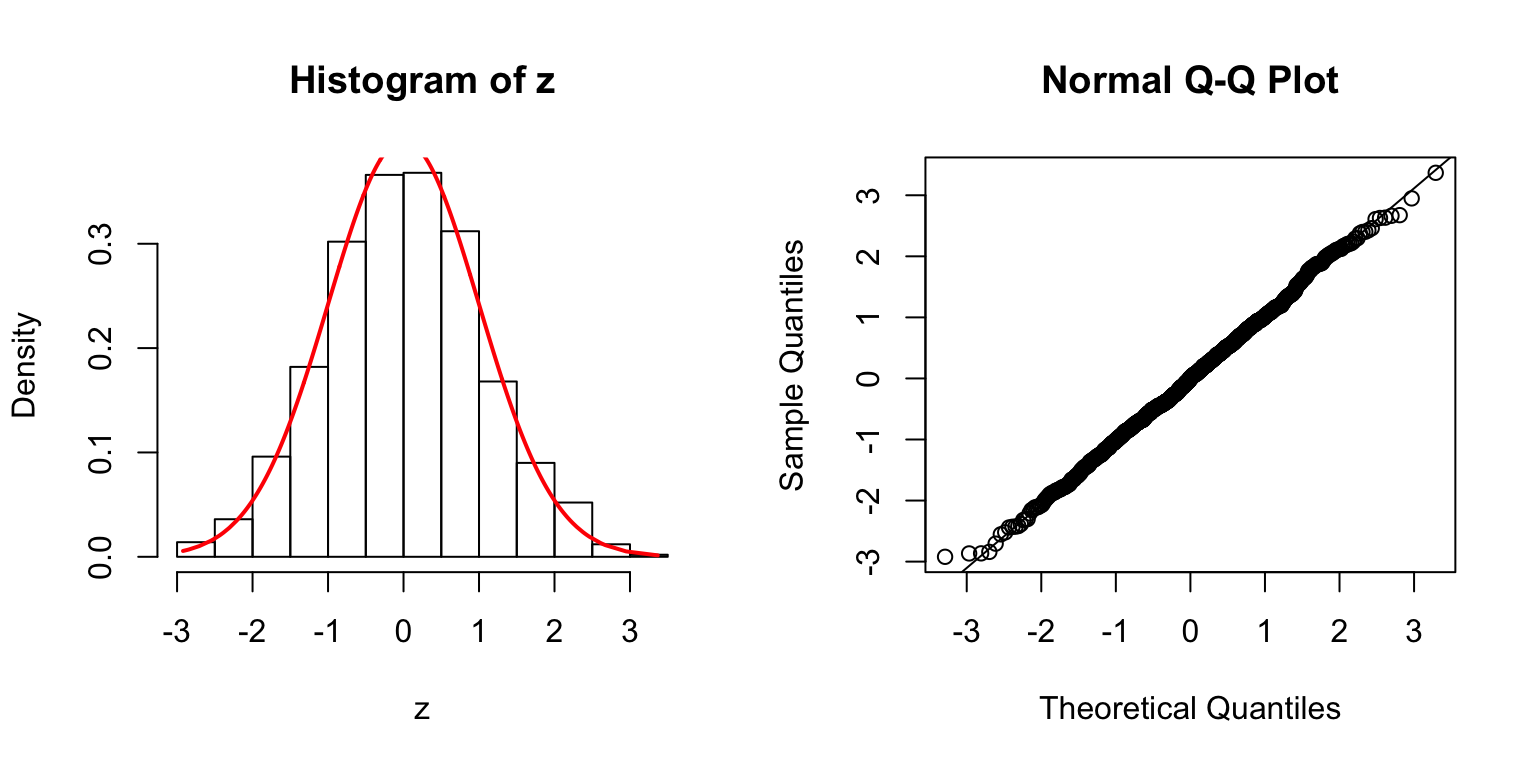
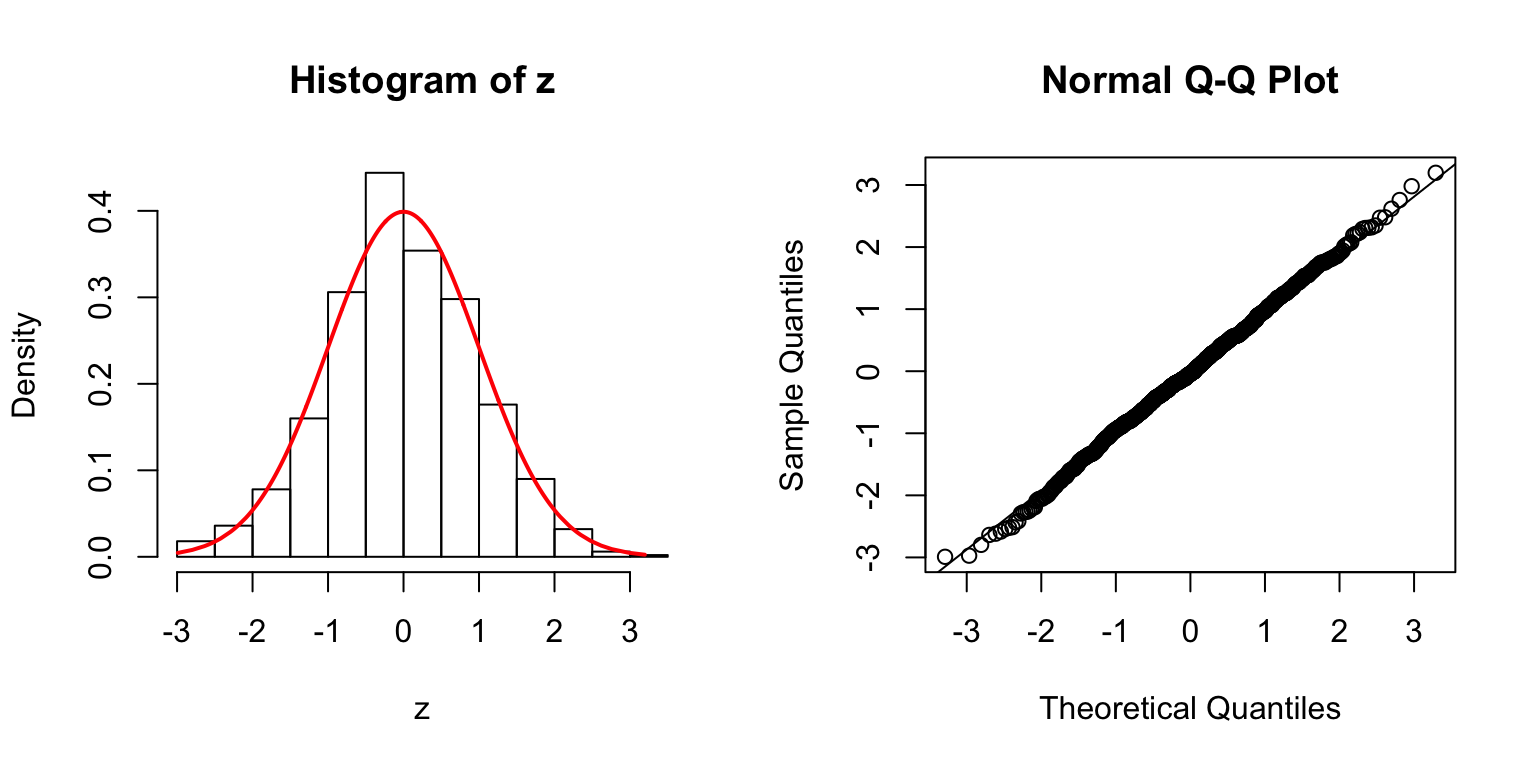
\(\Sigma\): high collinearity
\(\Sigma = B_{p \times d} \cdot B_{p \times d}^T + I\), where \(B_{i, j} \stackrel{\text{iid}}{\sim} N(0, 1)\). Then transform \(\Sigma\) to a correlation matrix.
\(d = 5\)
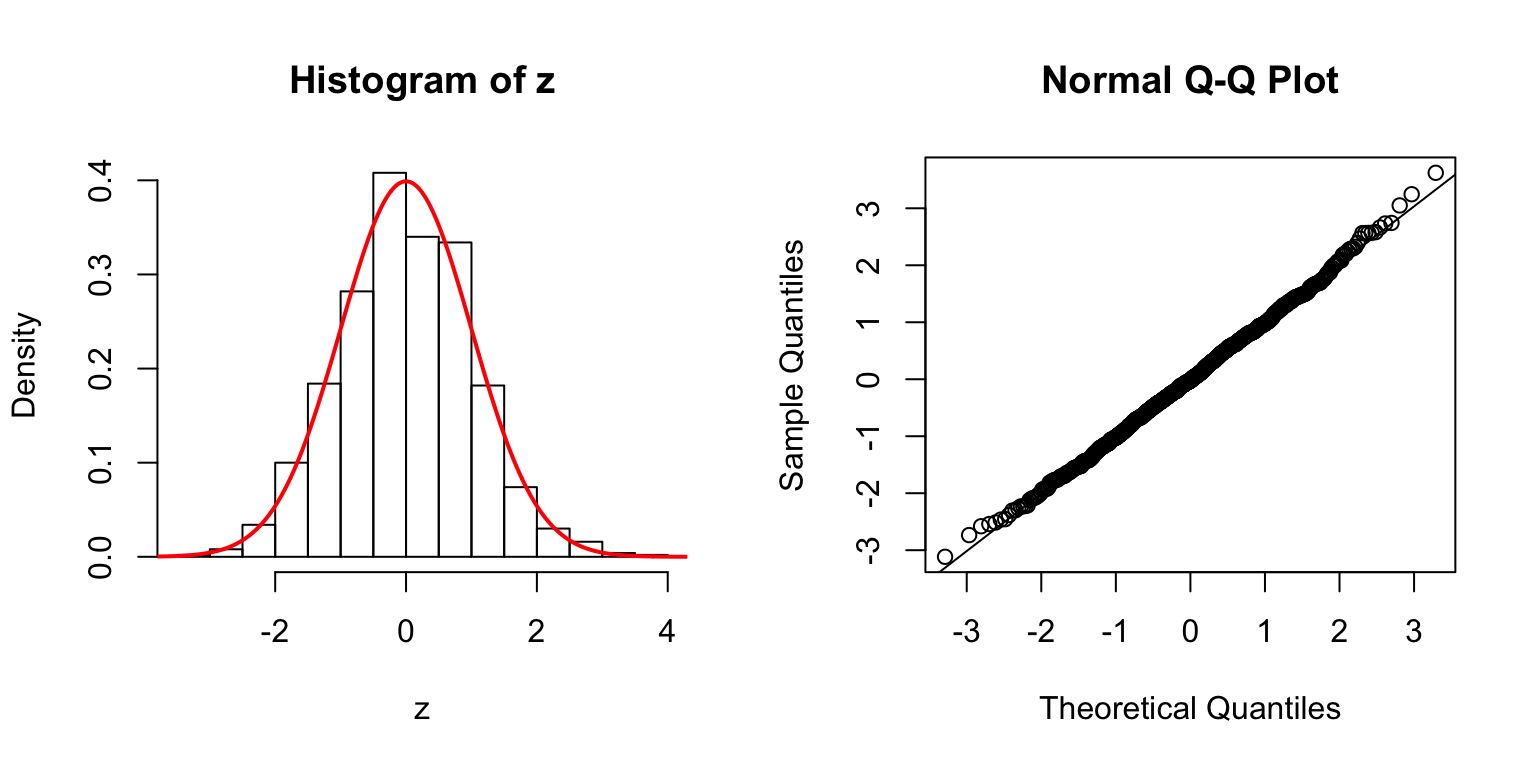
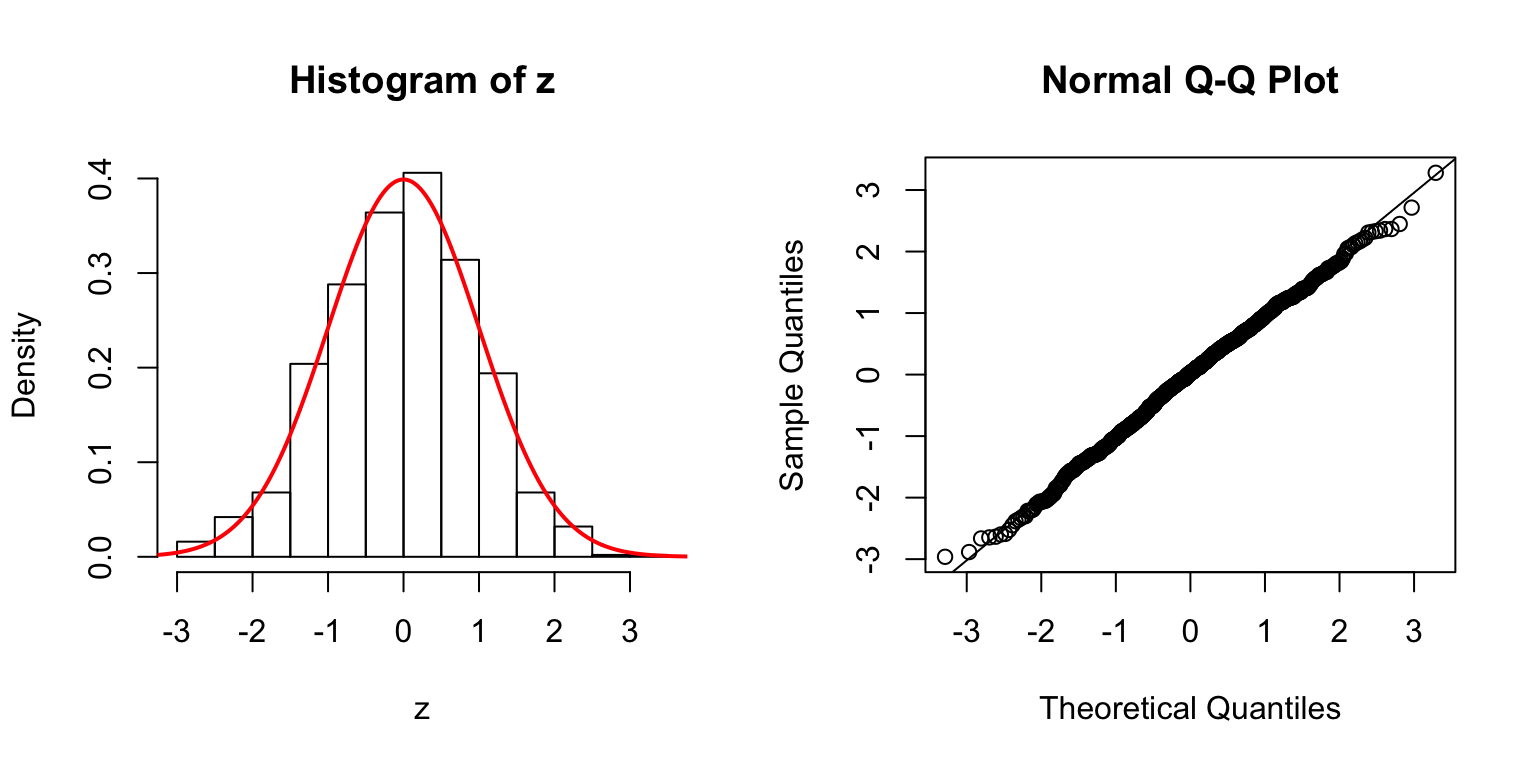
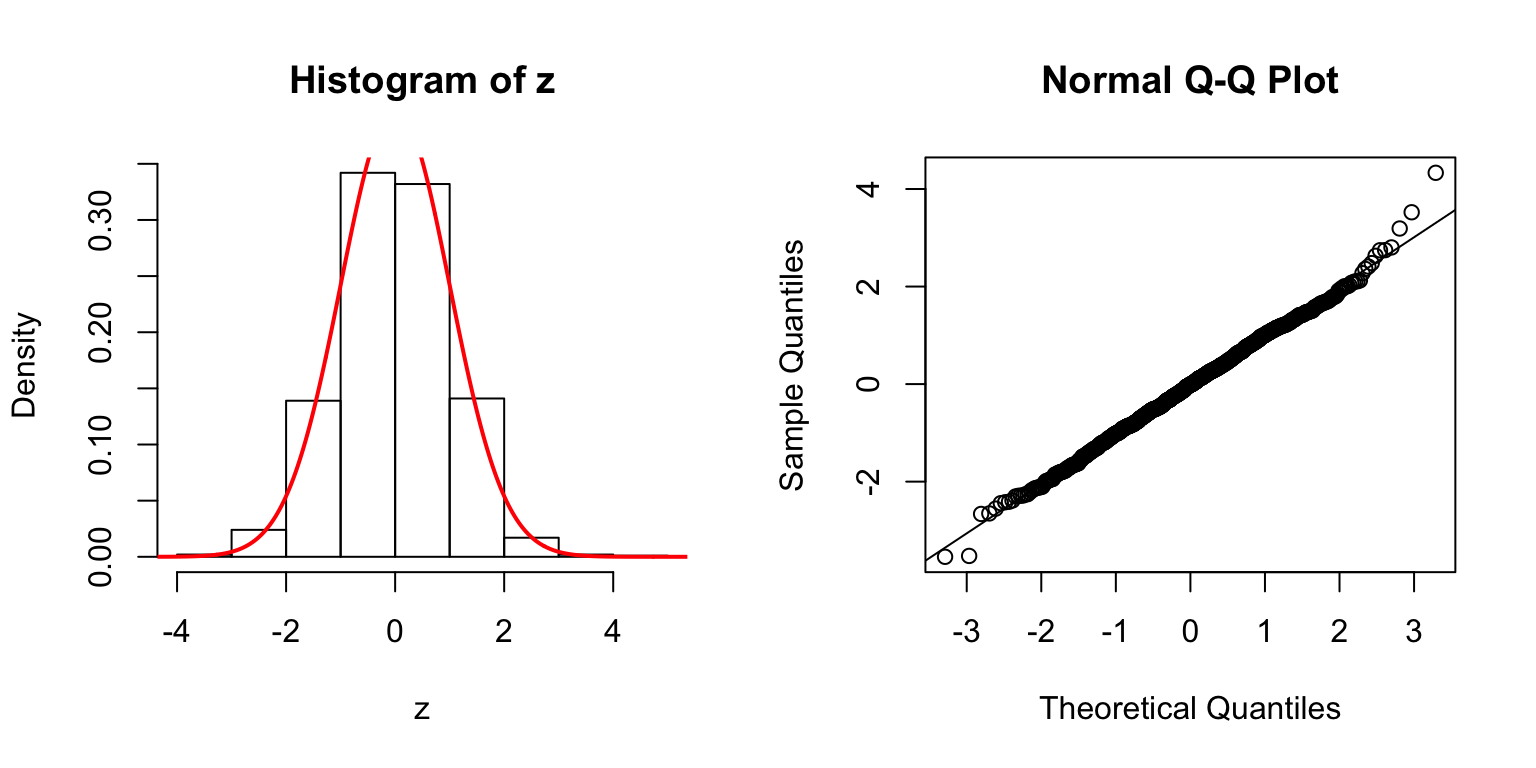
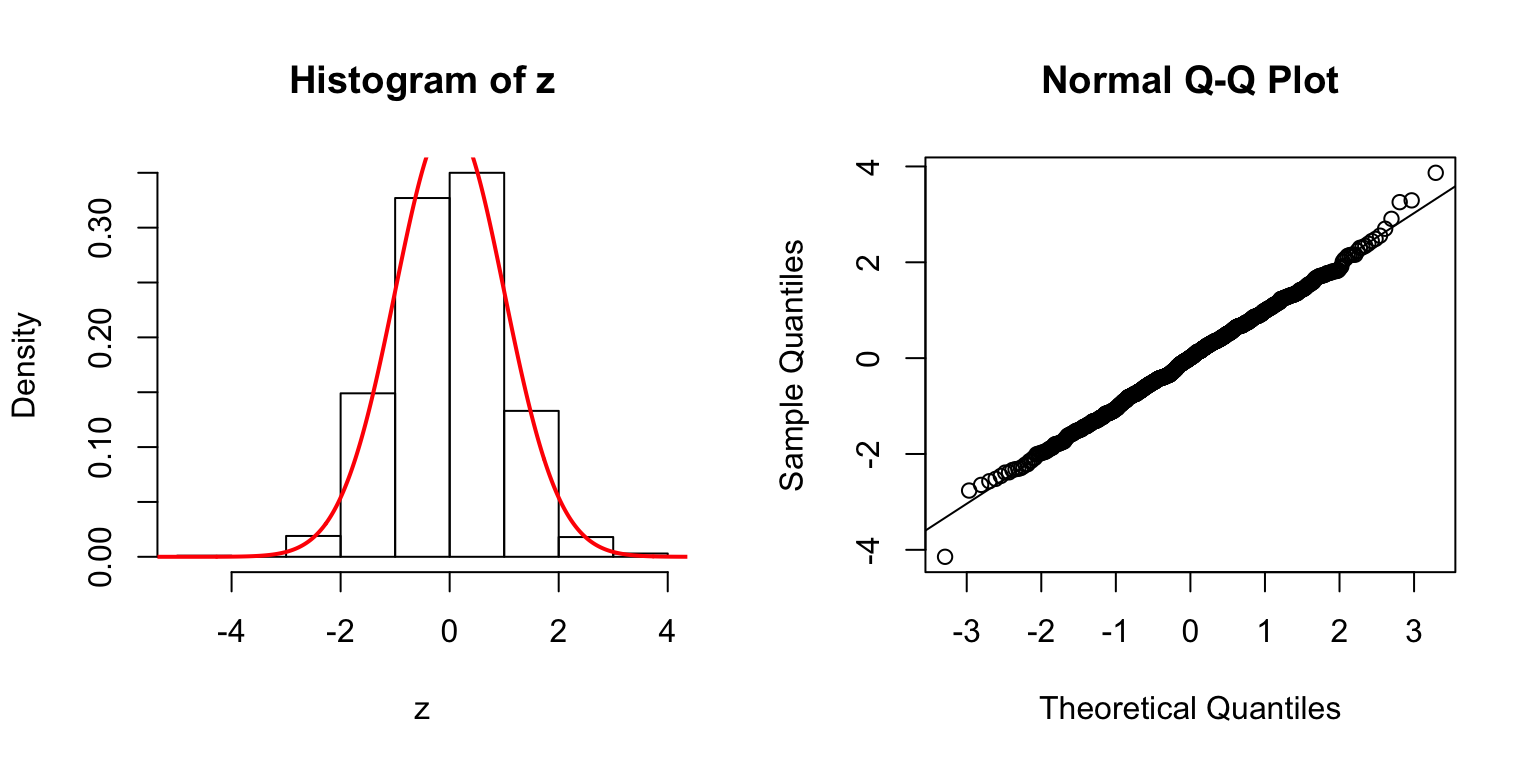
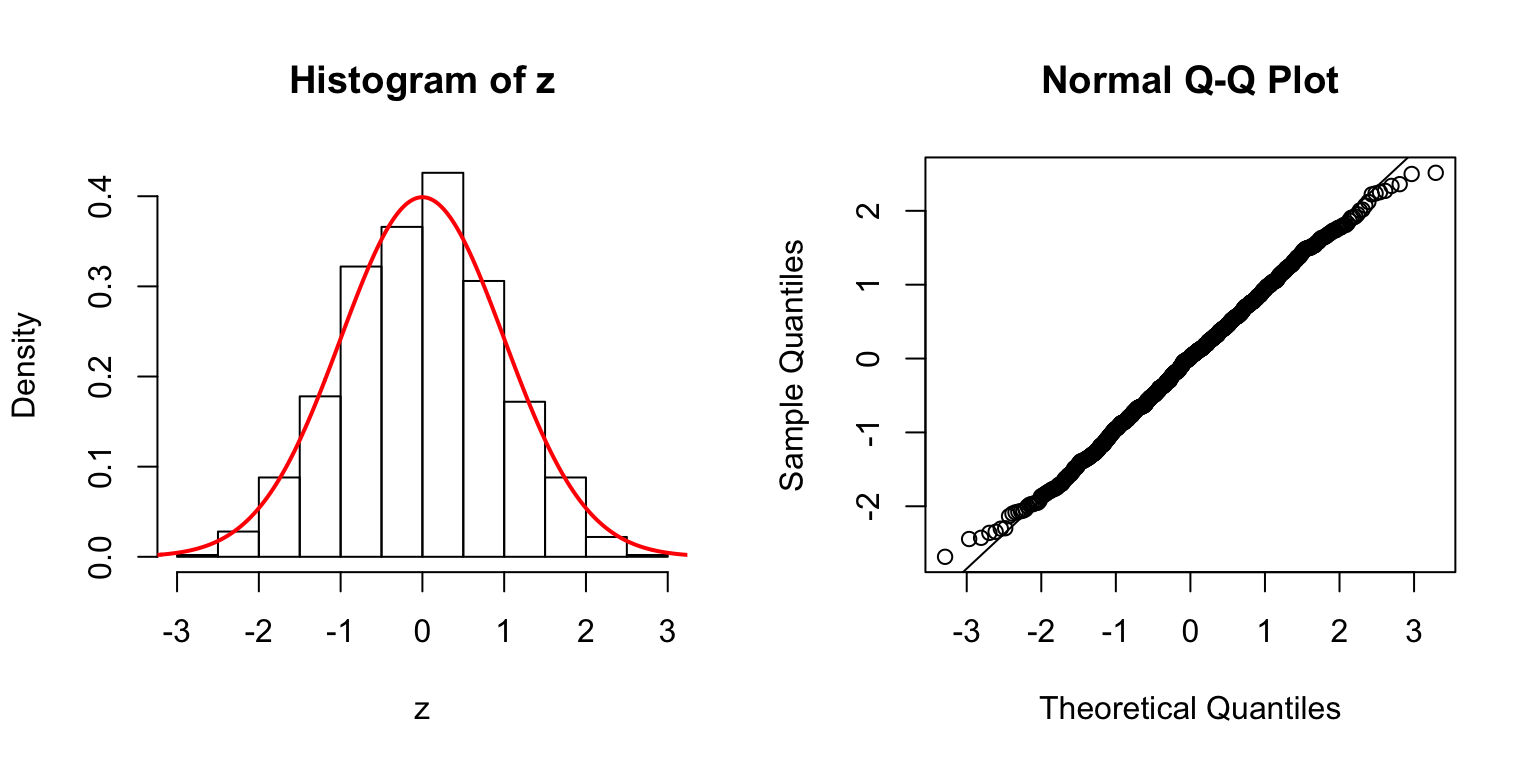
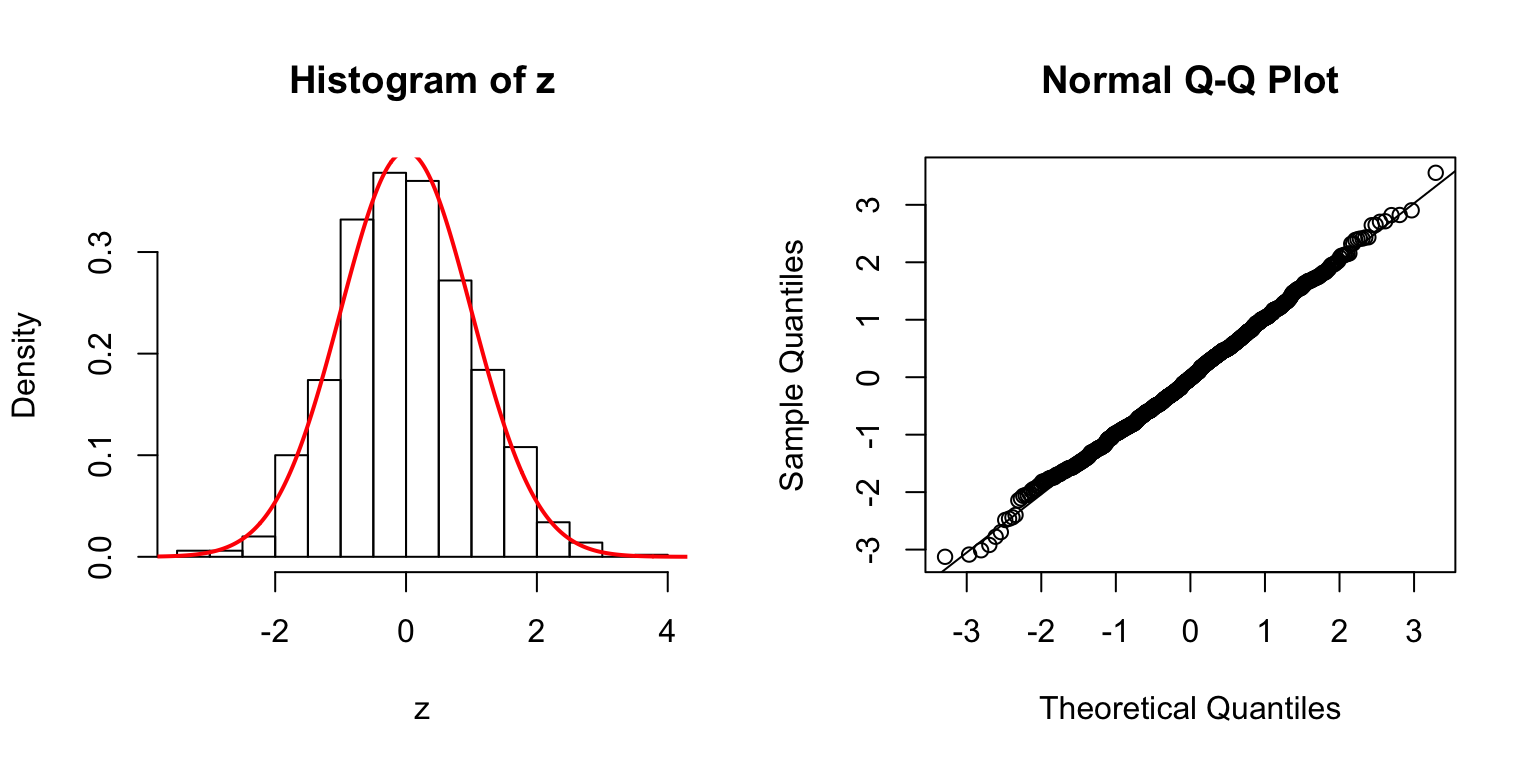
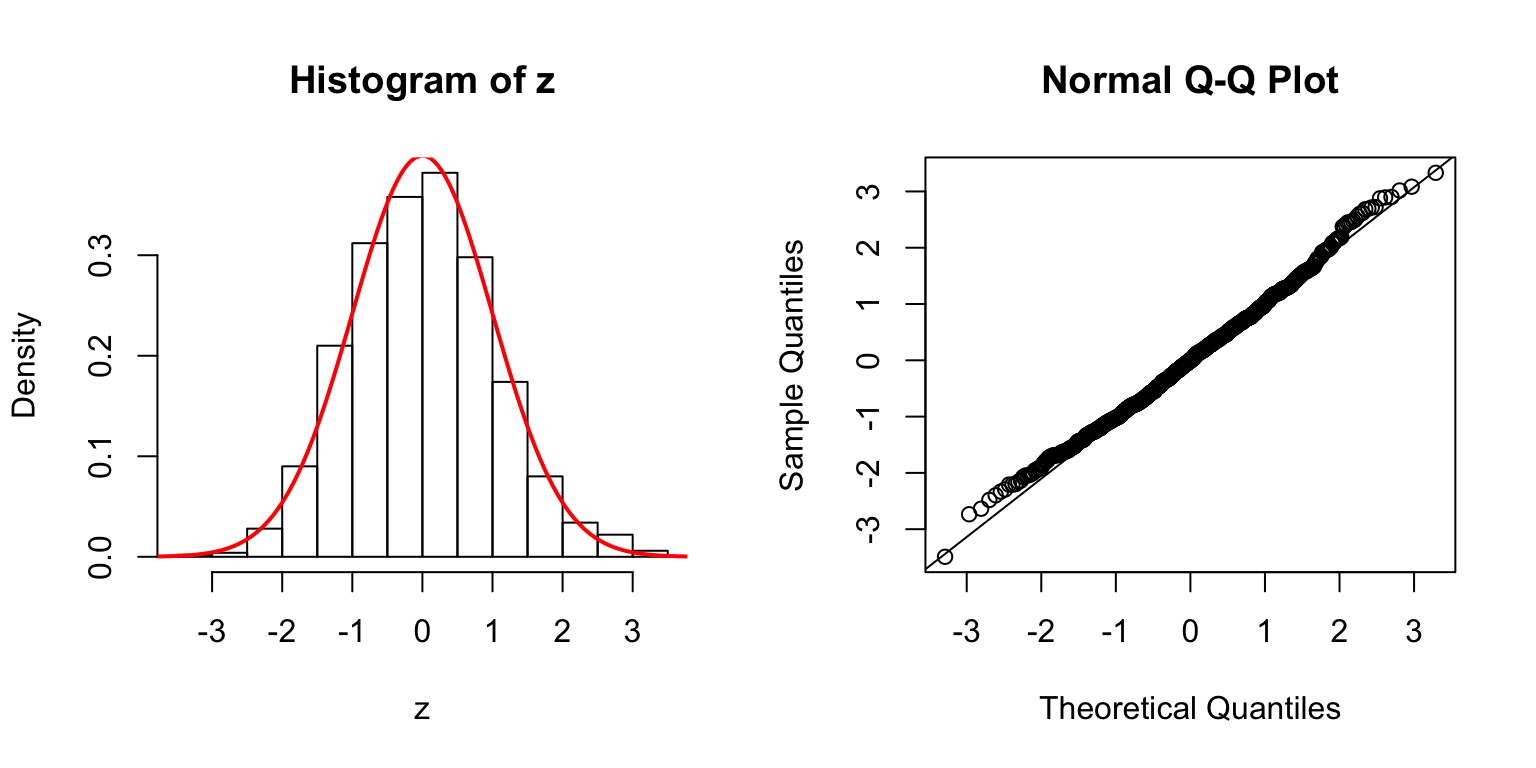
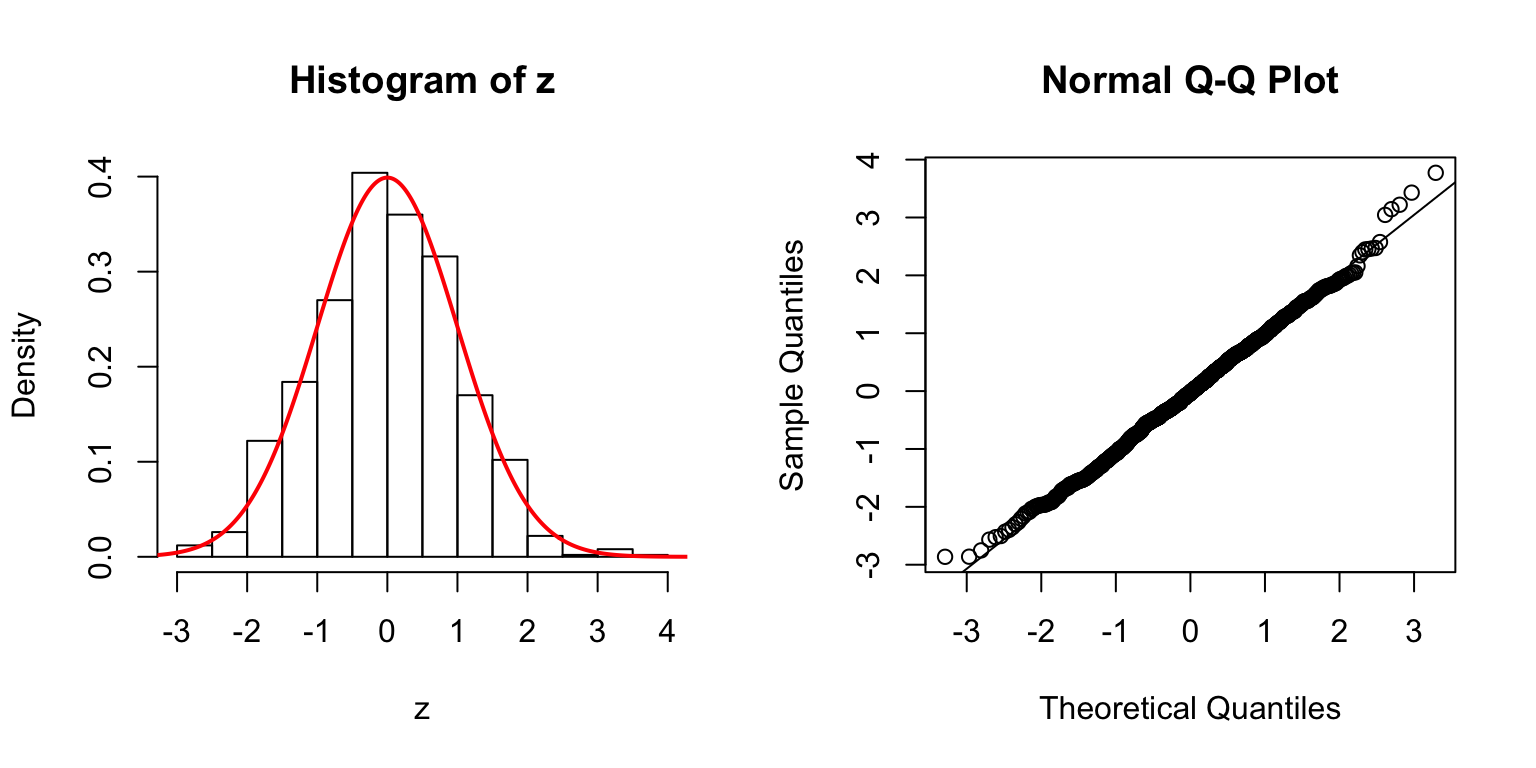
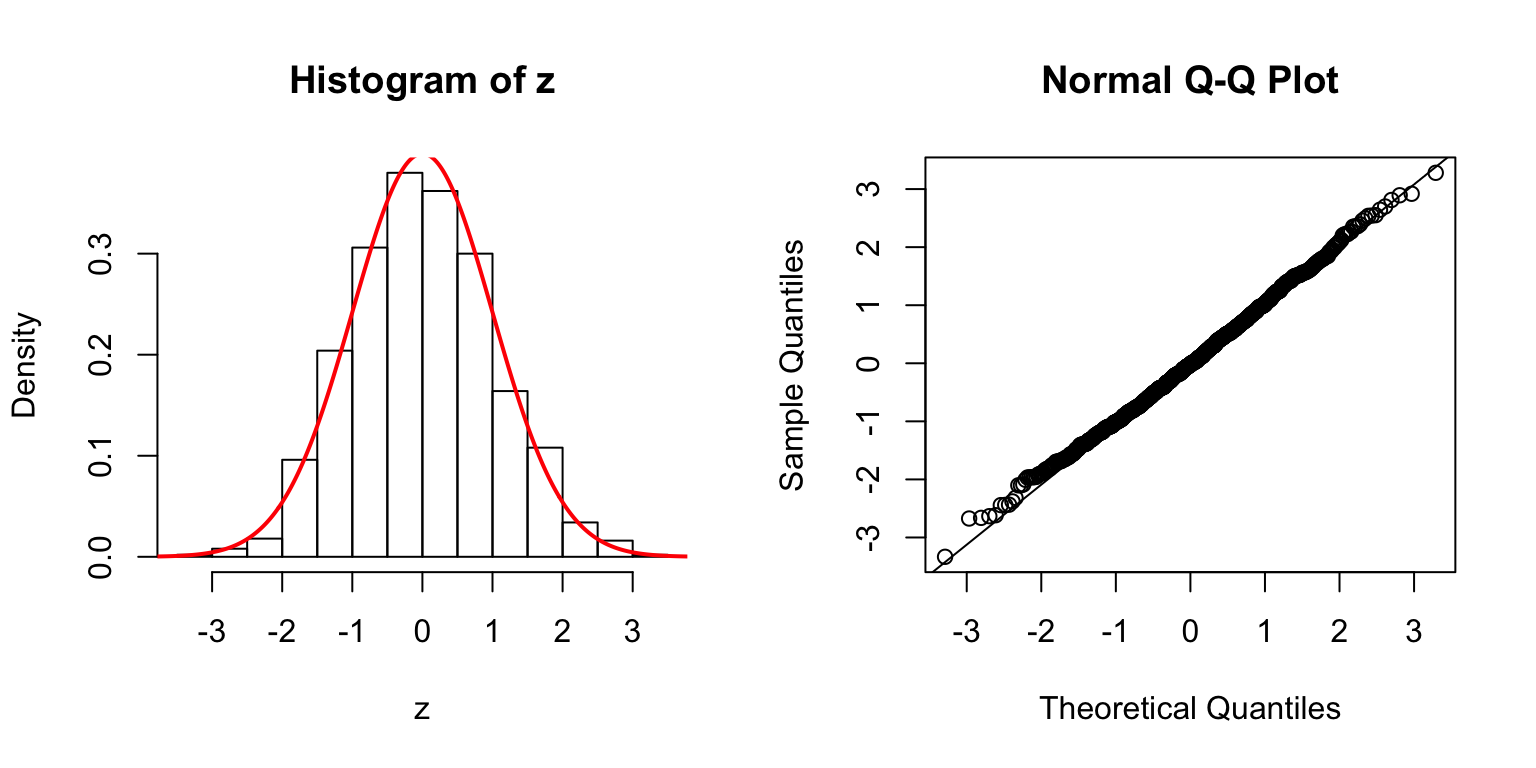
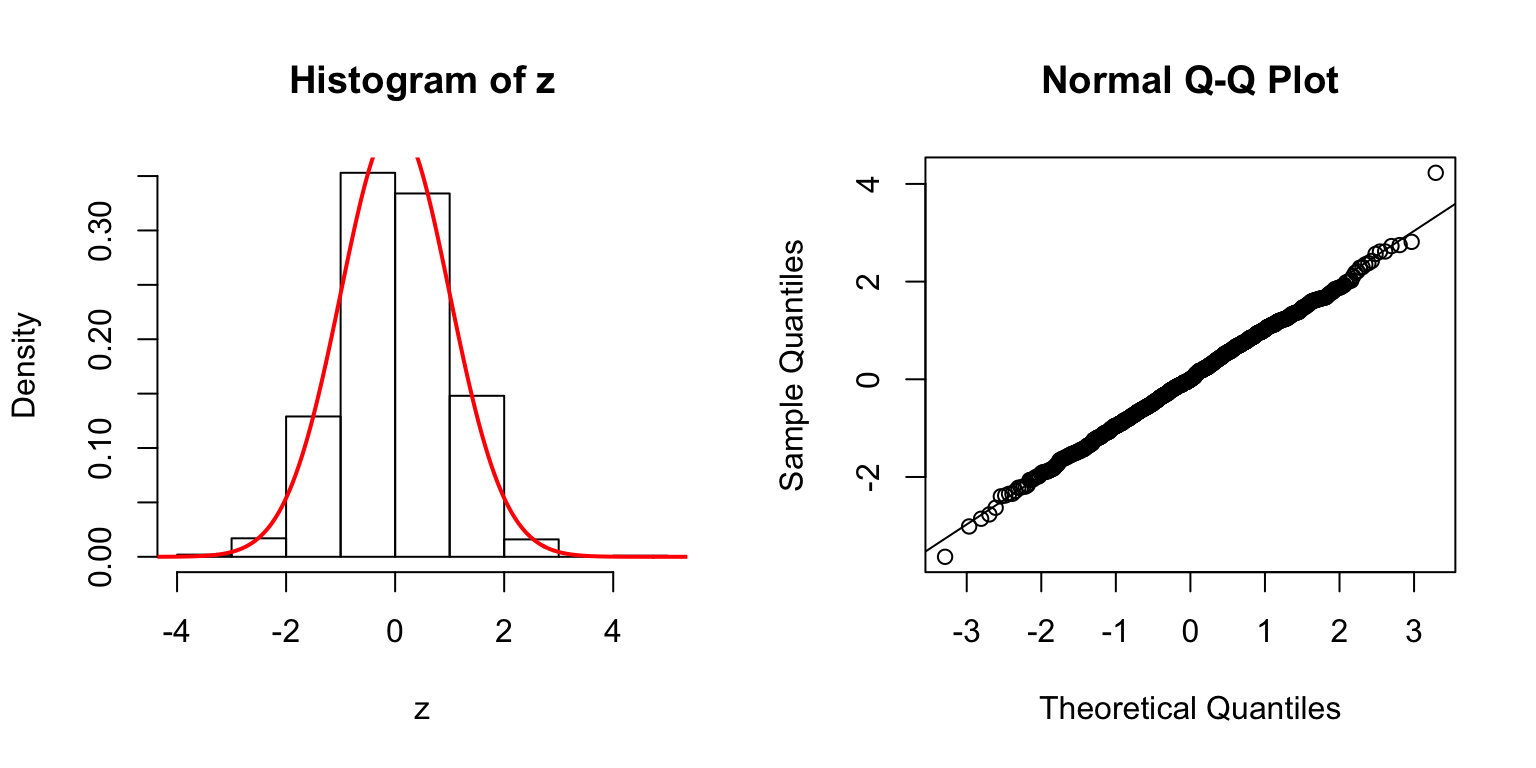
Start from \(\Sigma_{\hat\beta}\)
In the \(n > p\) setting, \(\hat\beta \sim N\left(\beta, \Sigma_{\hat\beta} = \sigma_e^2\left(X^TX\right)^{-1}\right)\). In simulation, we can first construct a desirable \(\Sigma_{\hat\beta}\), and build an \(X\) from that.
One way is to let \(\Sigma_{\hat\beta} / \sigma_e^2 = B_{p \times d} \cdot B_{p \times d}^T + I\), where \(B_{i, j} \stackrel{\text{iid}}{\sim} N(0, 1)\). Then rescale the matrix such that the mean of its diagnal \(= 1\). Generate \(X_{n \times p}\) such that \((X^TX)^{-1} = \Sigma_{\hat\beta} / \sigma_e^2\).
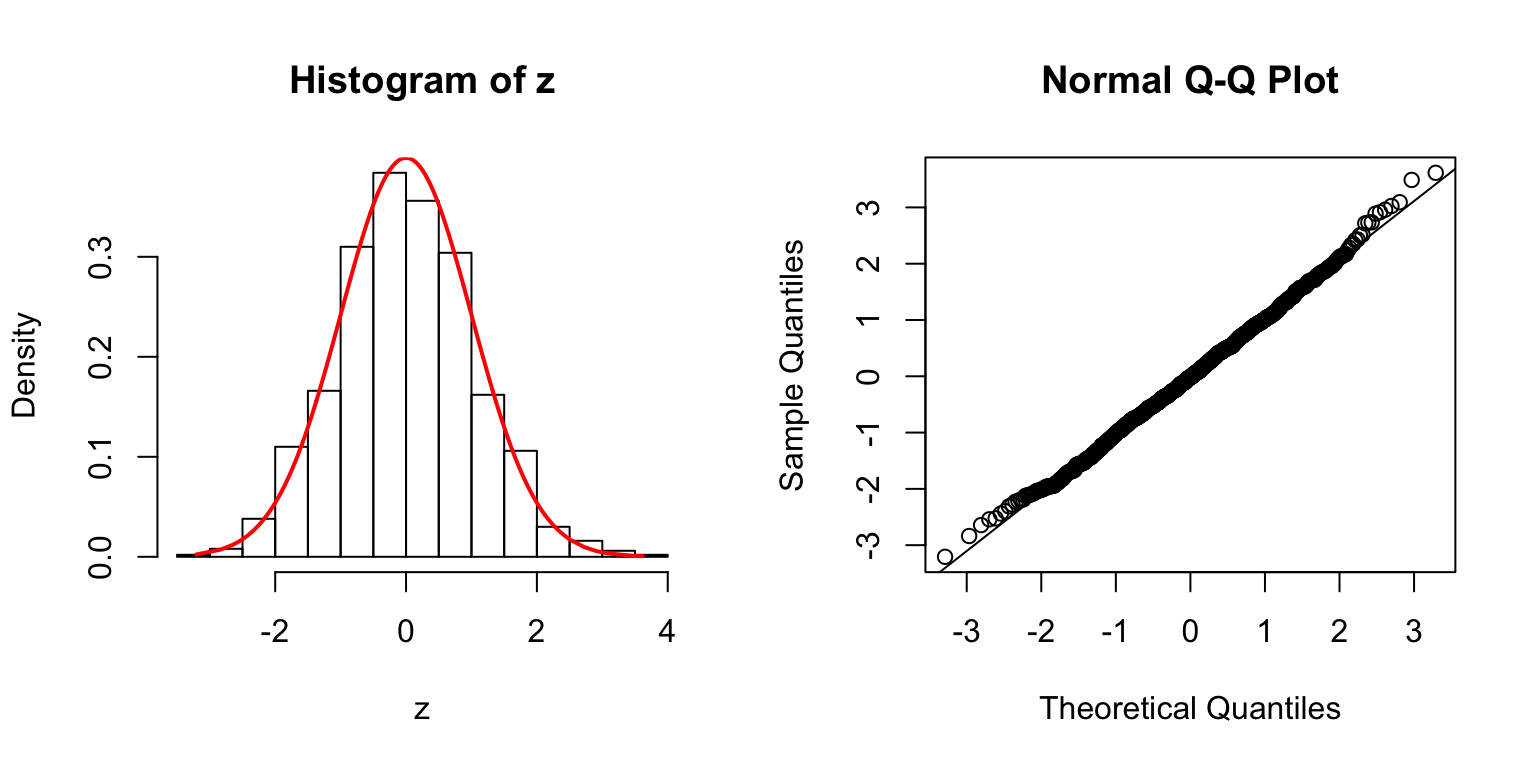
\(d = 1\)
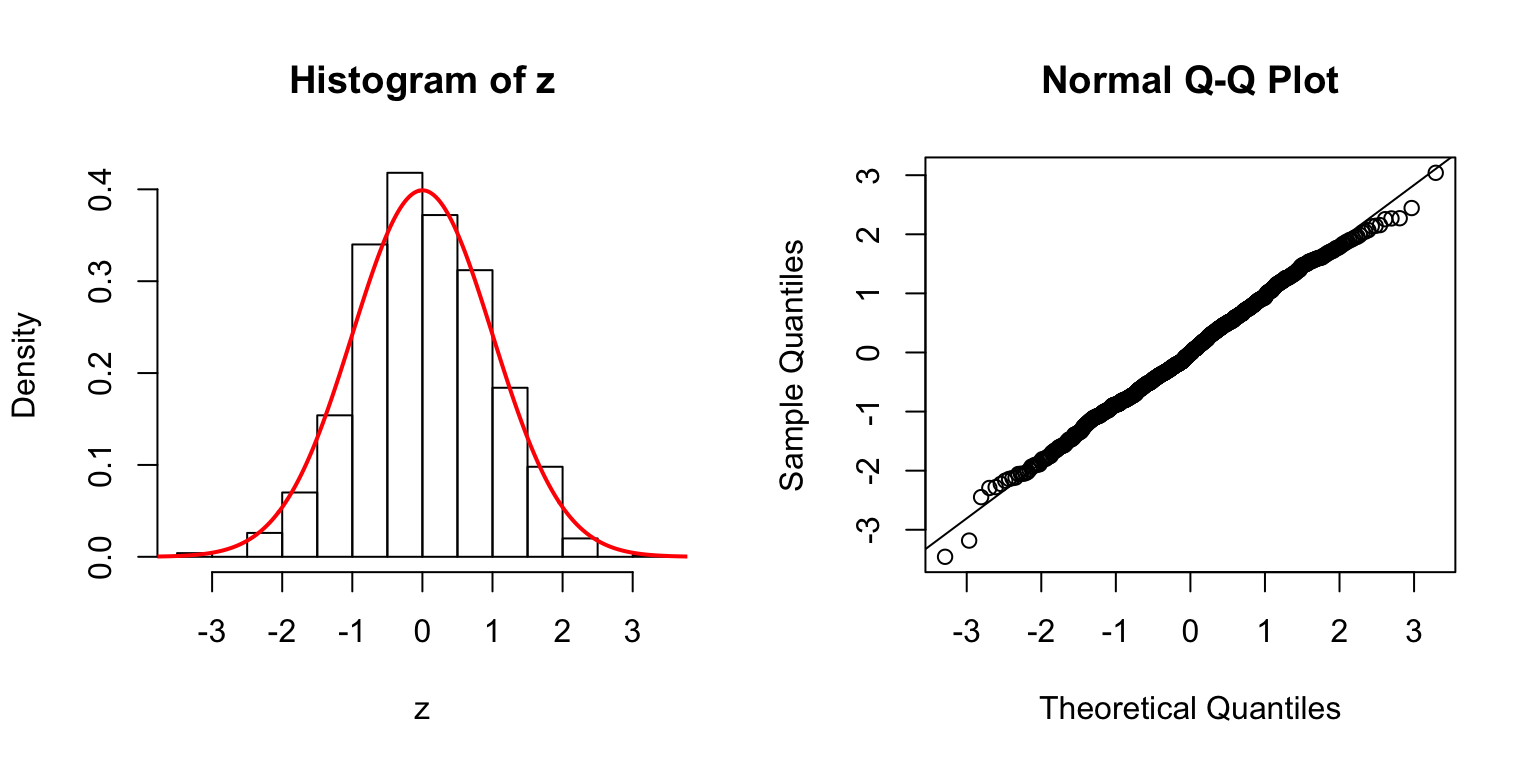
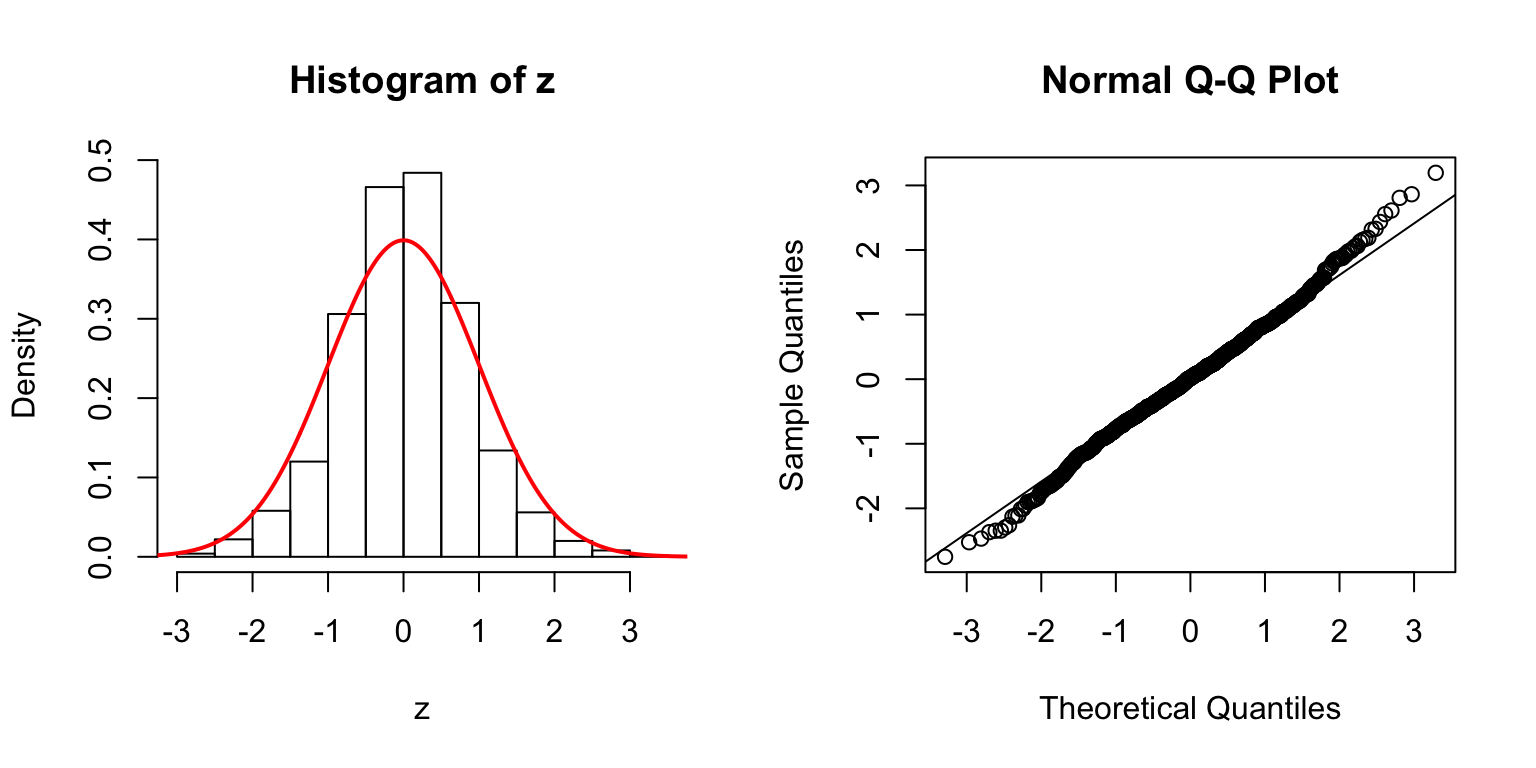
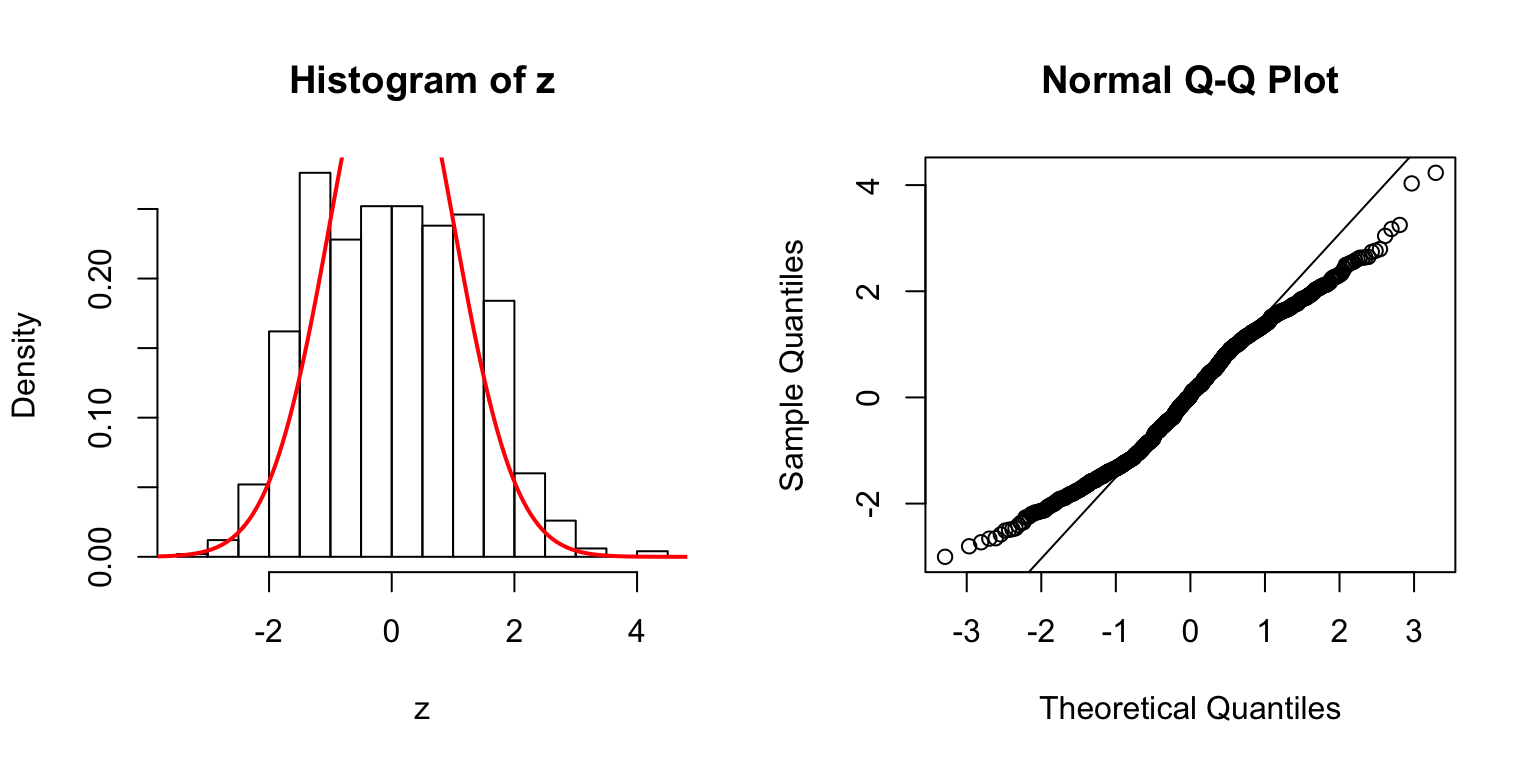
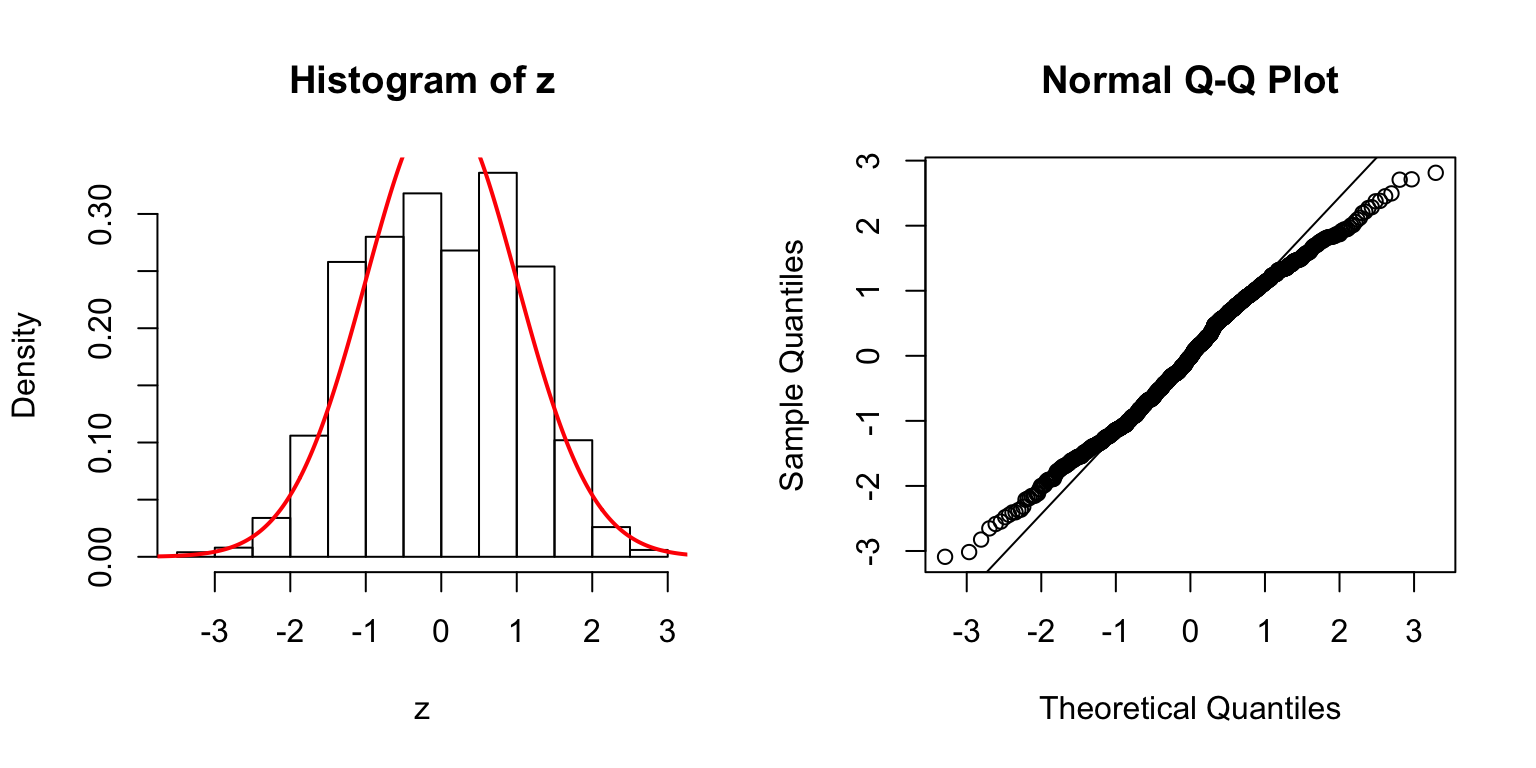
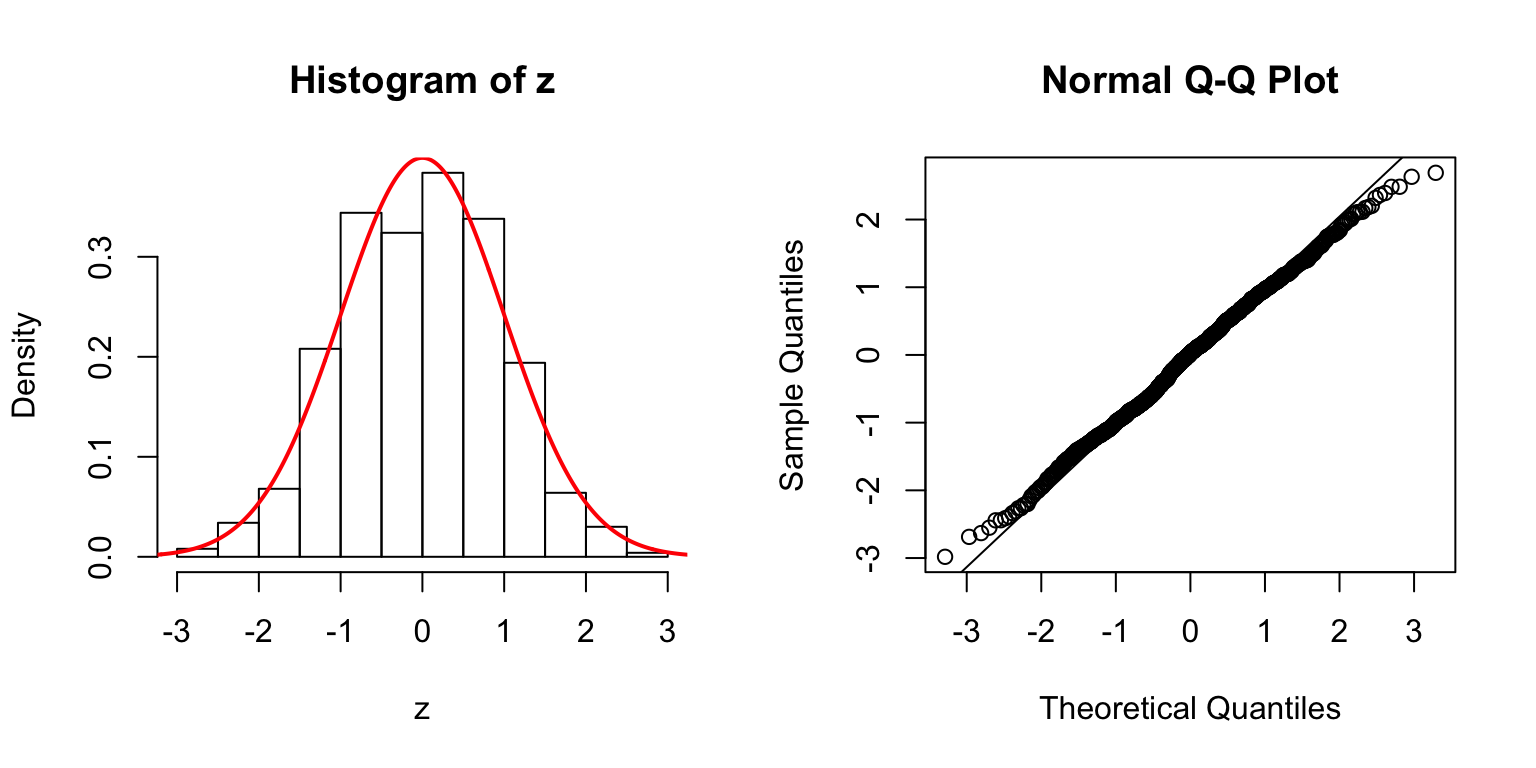
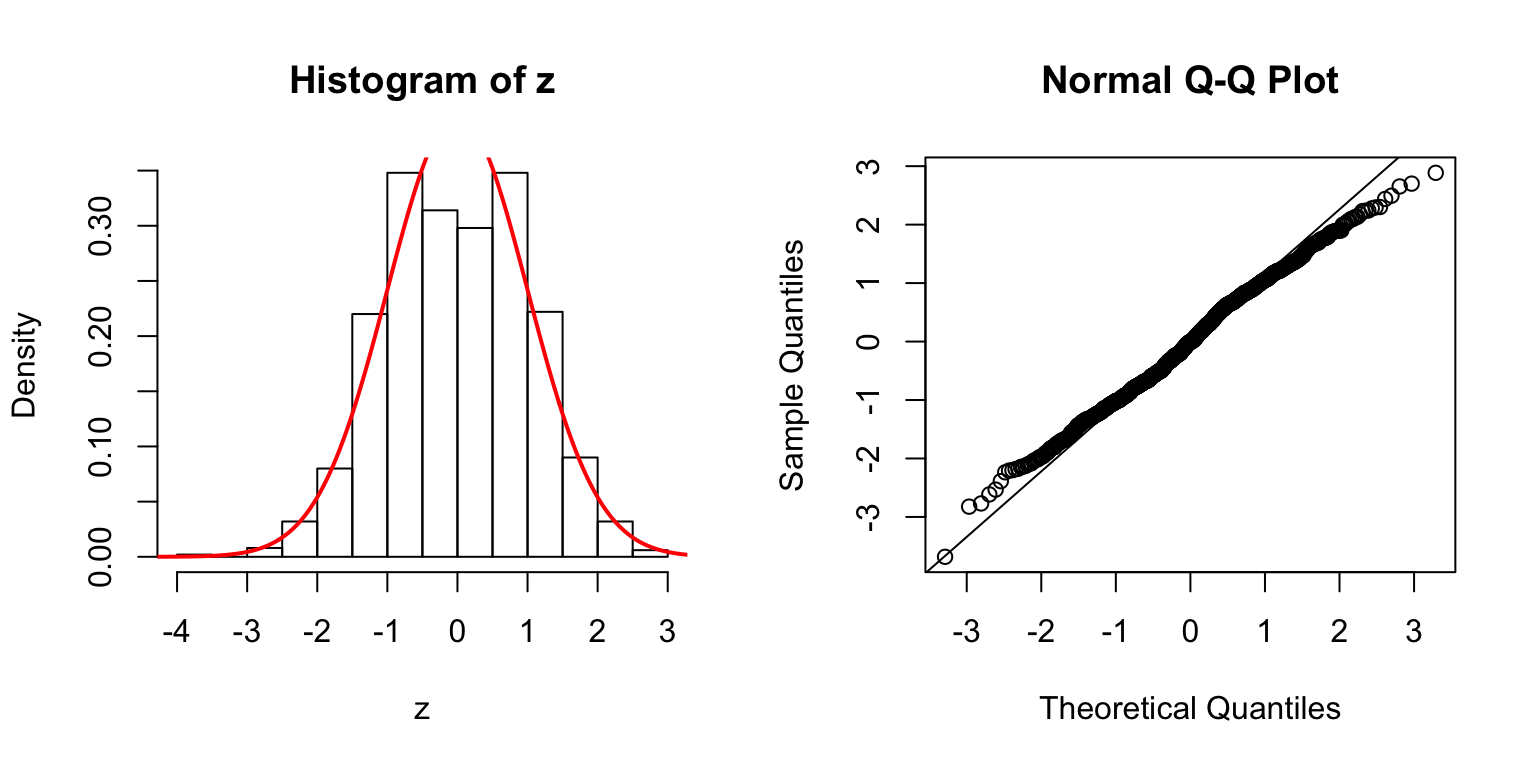
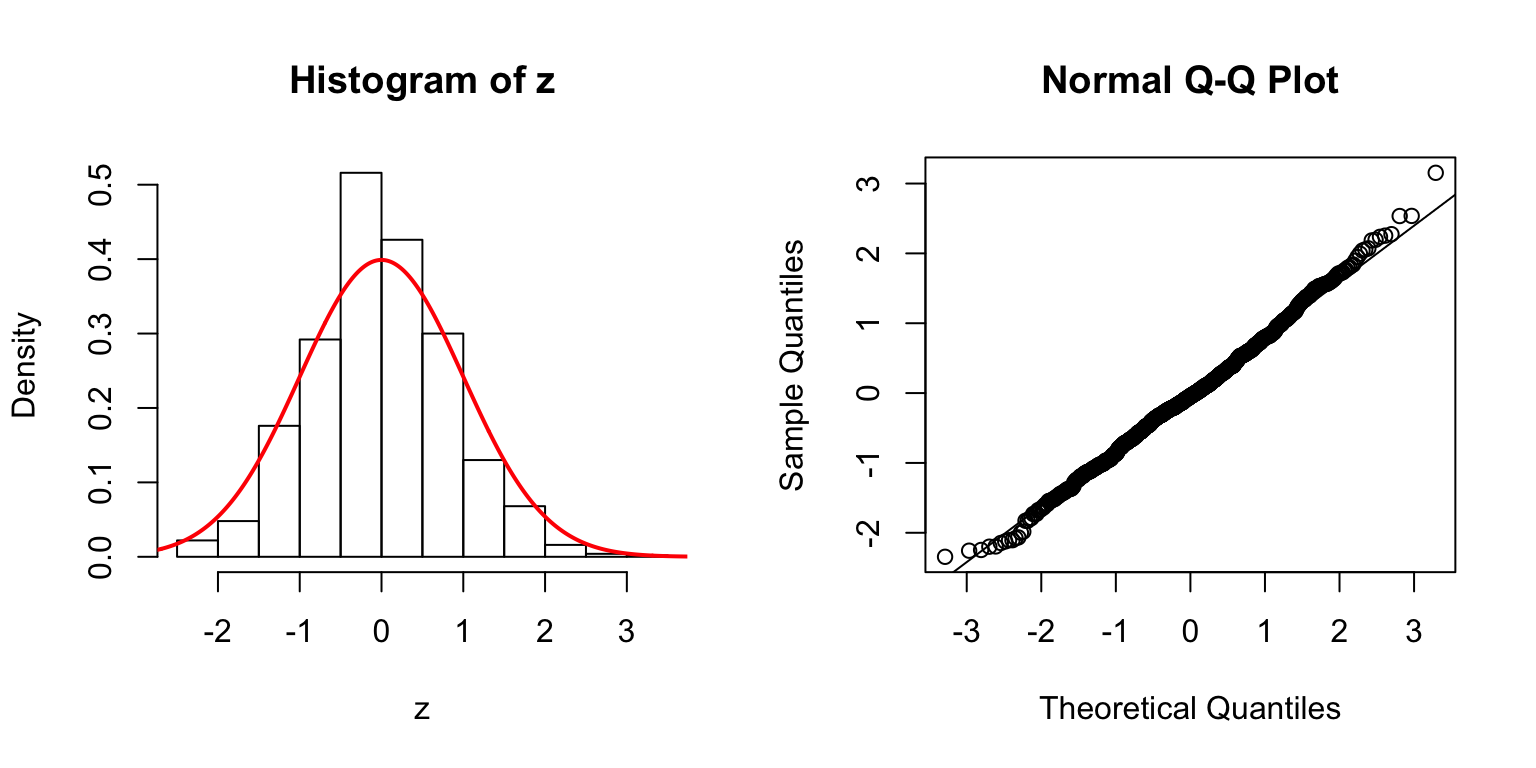
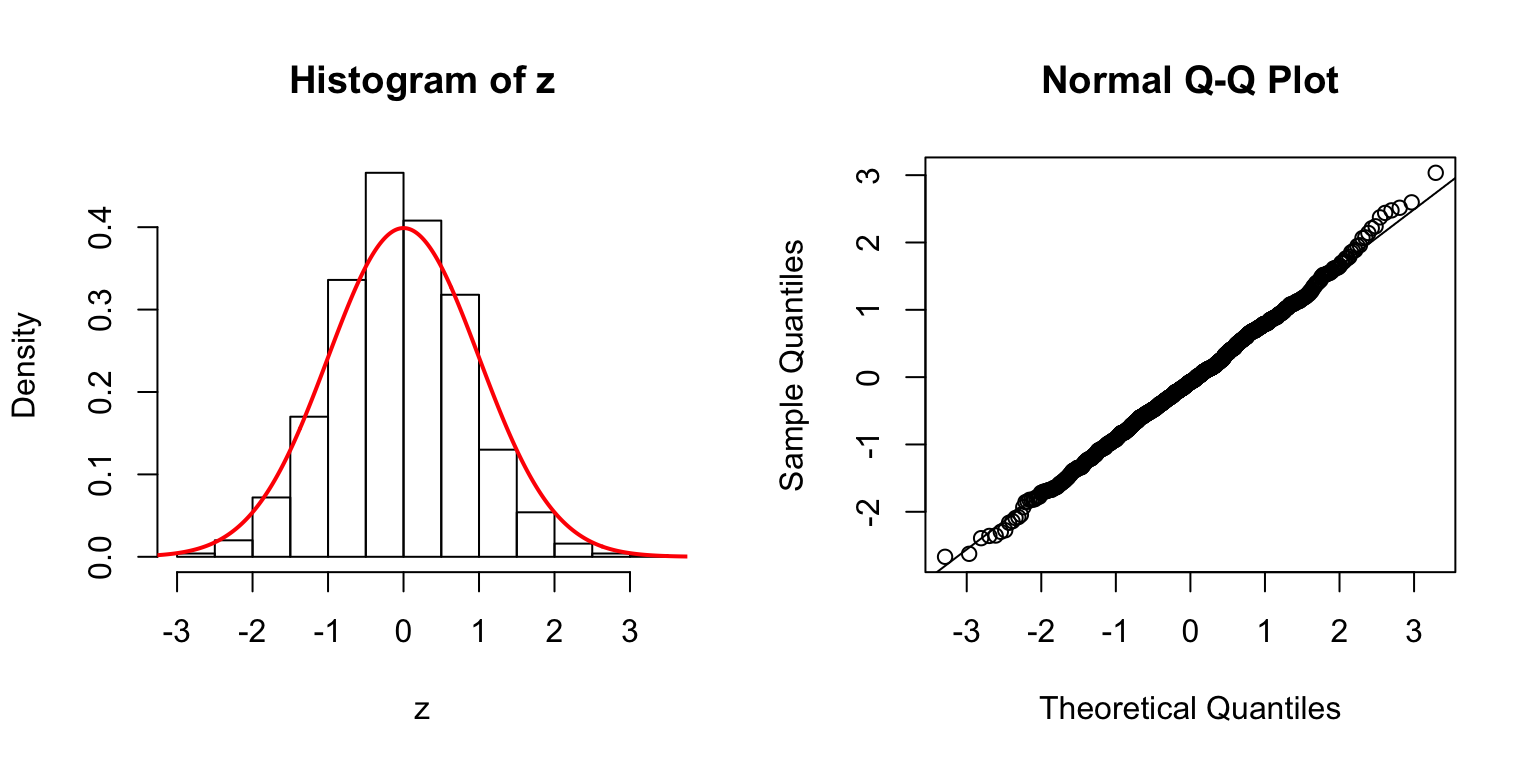
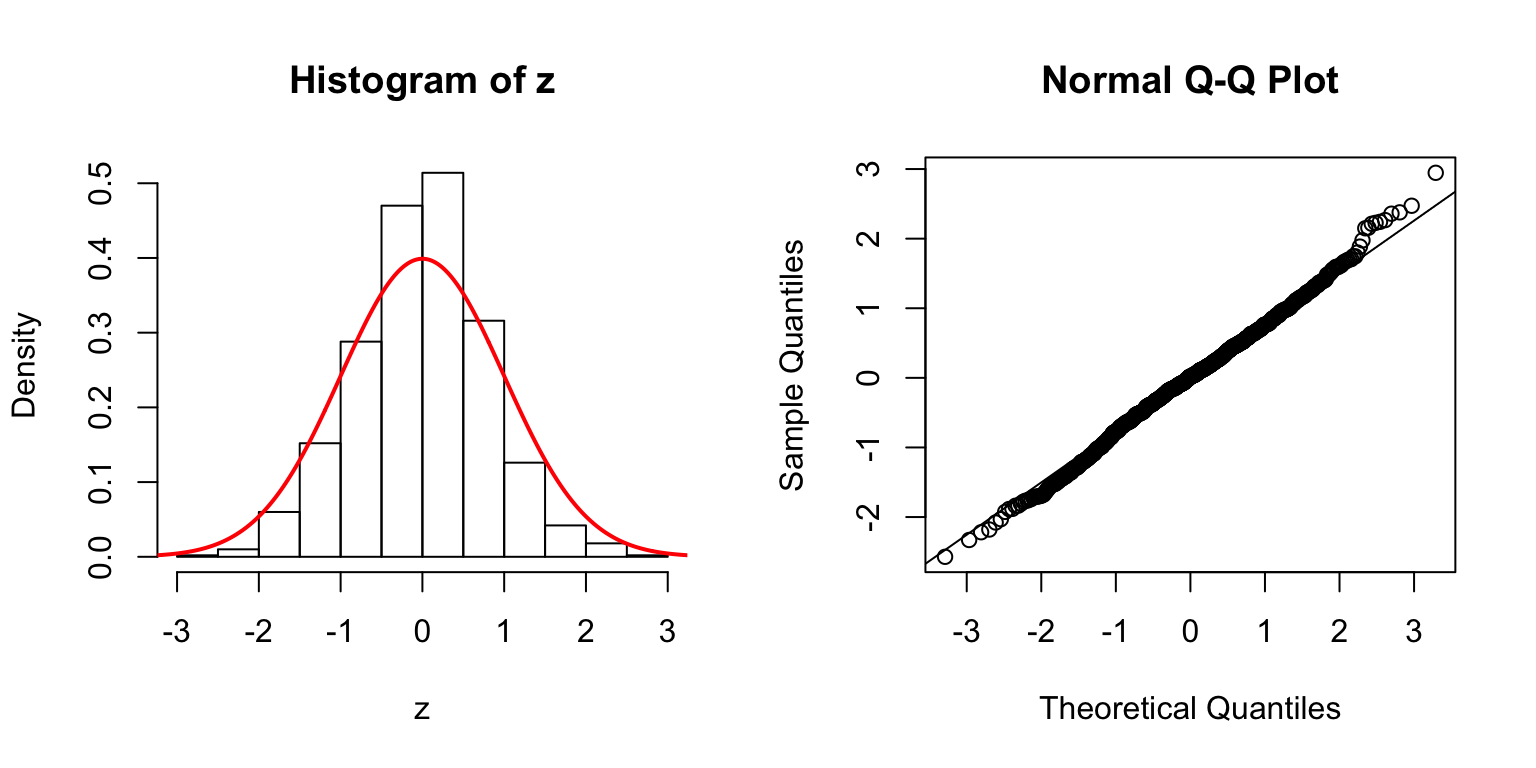
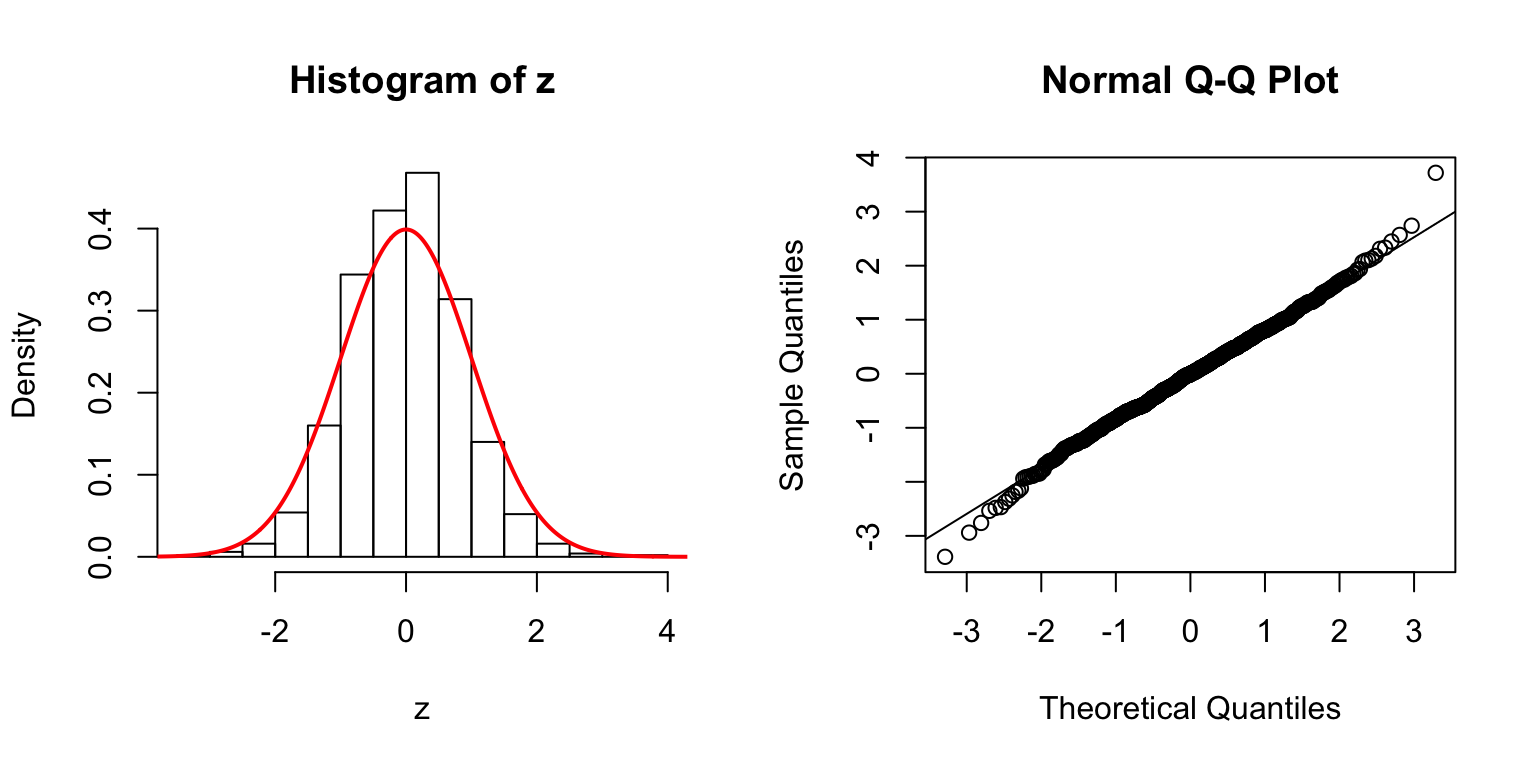
\(d = 5\)
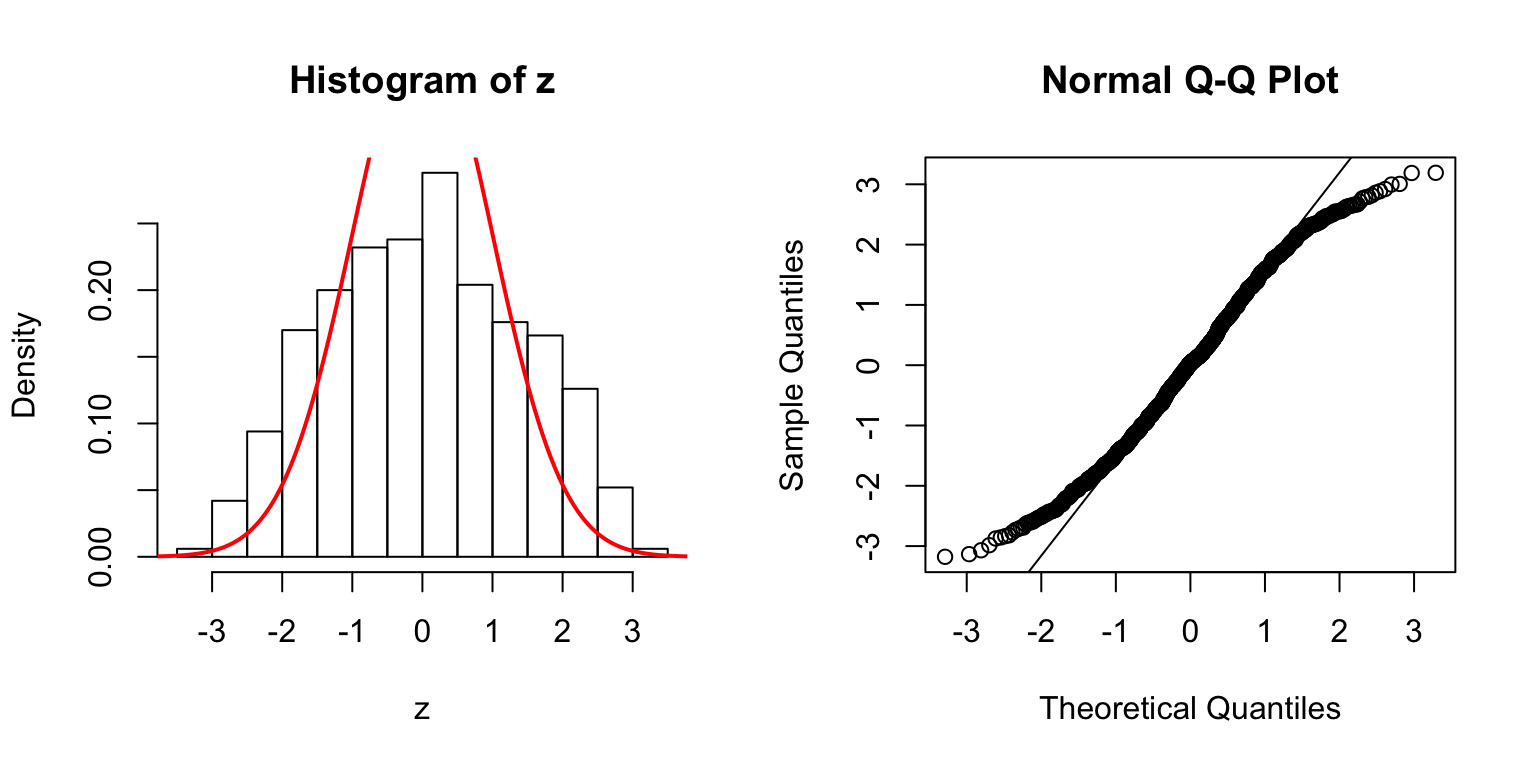
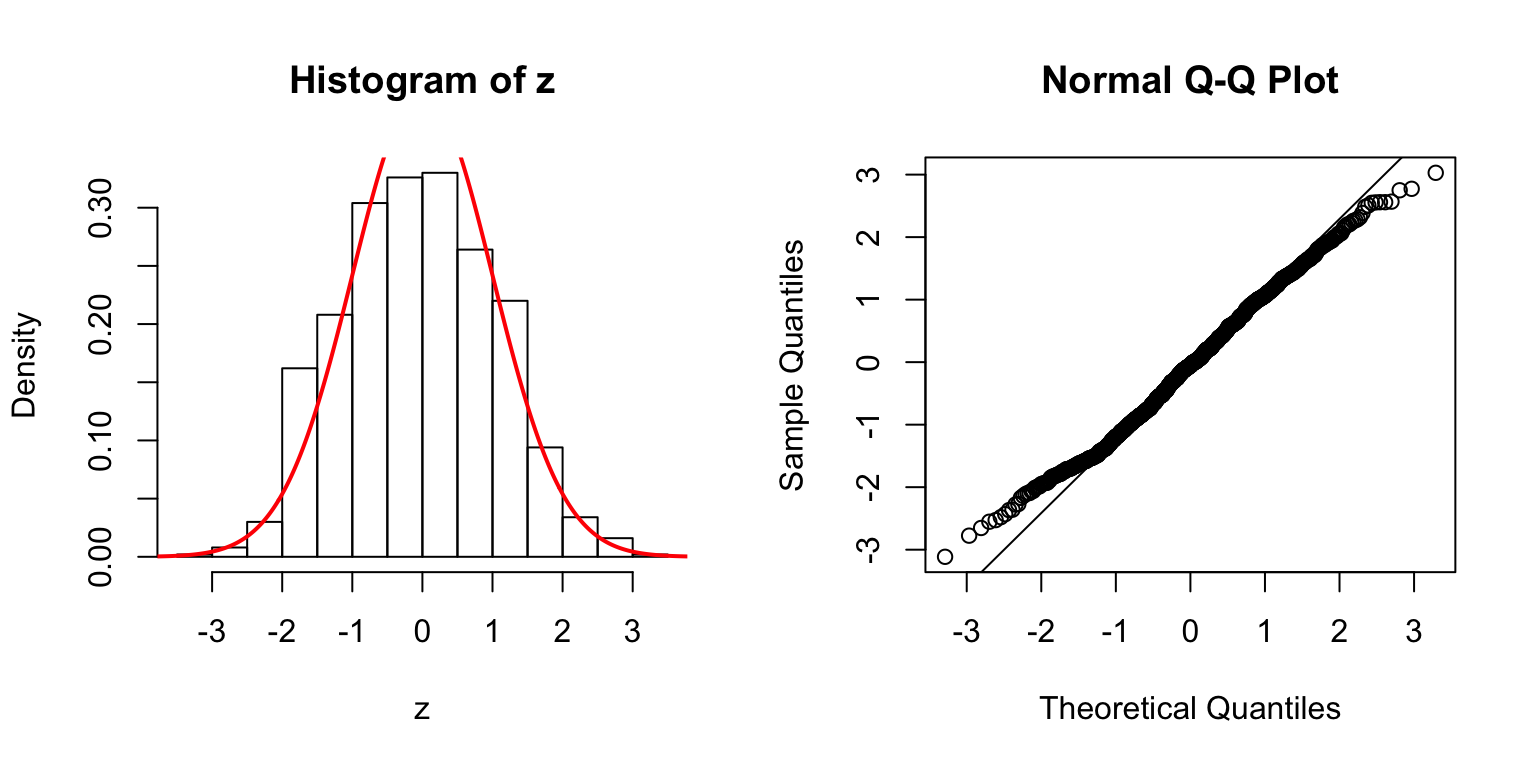
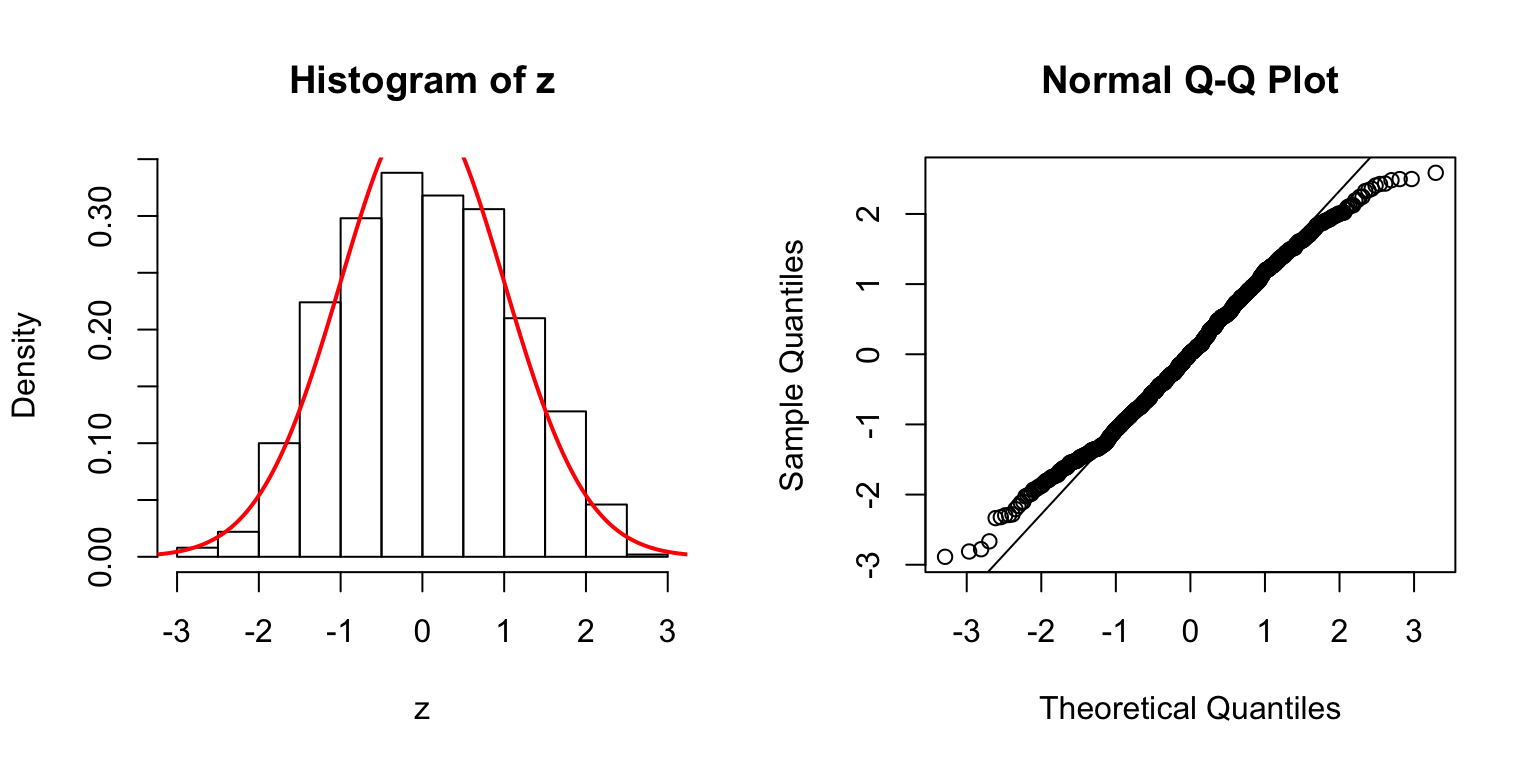
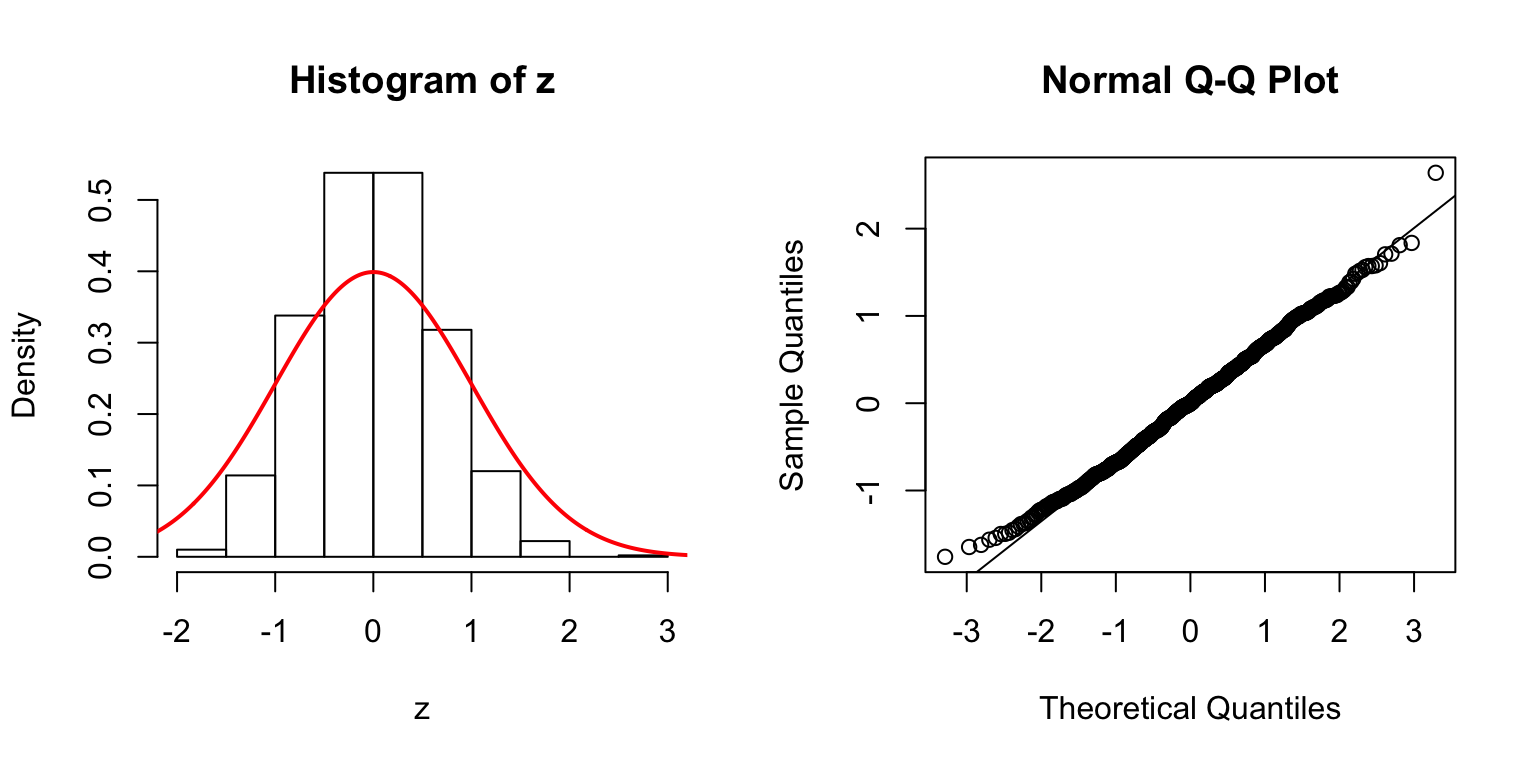
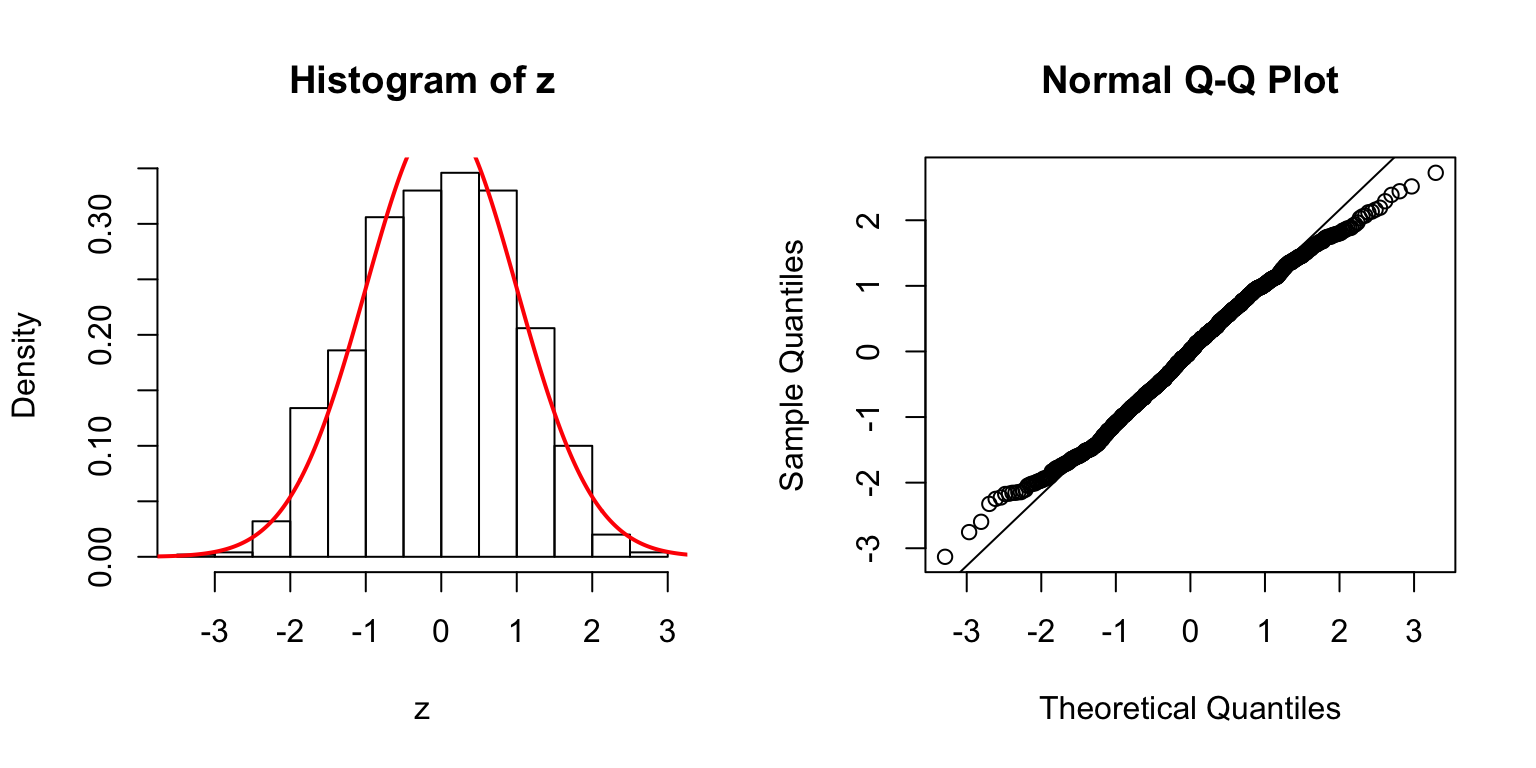
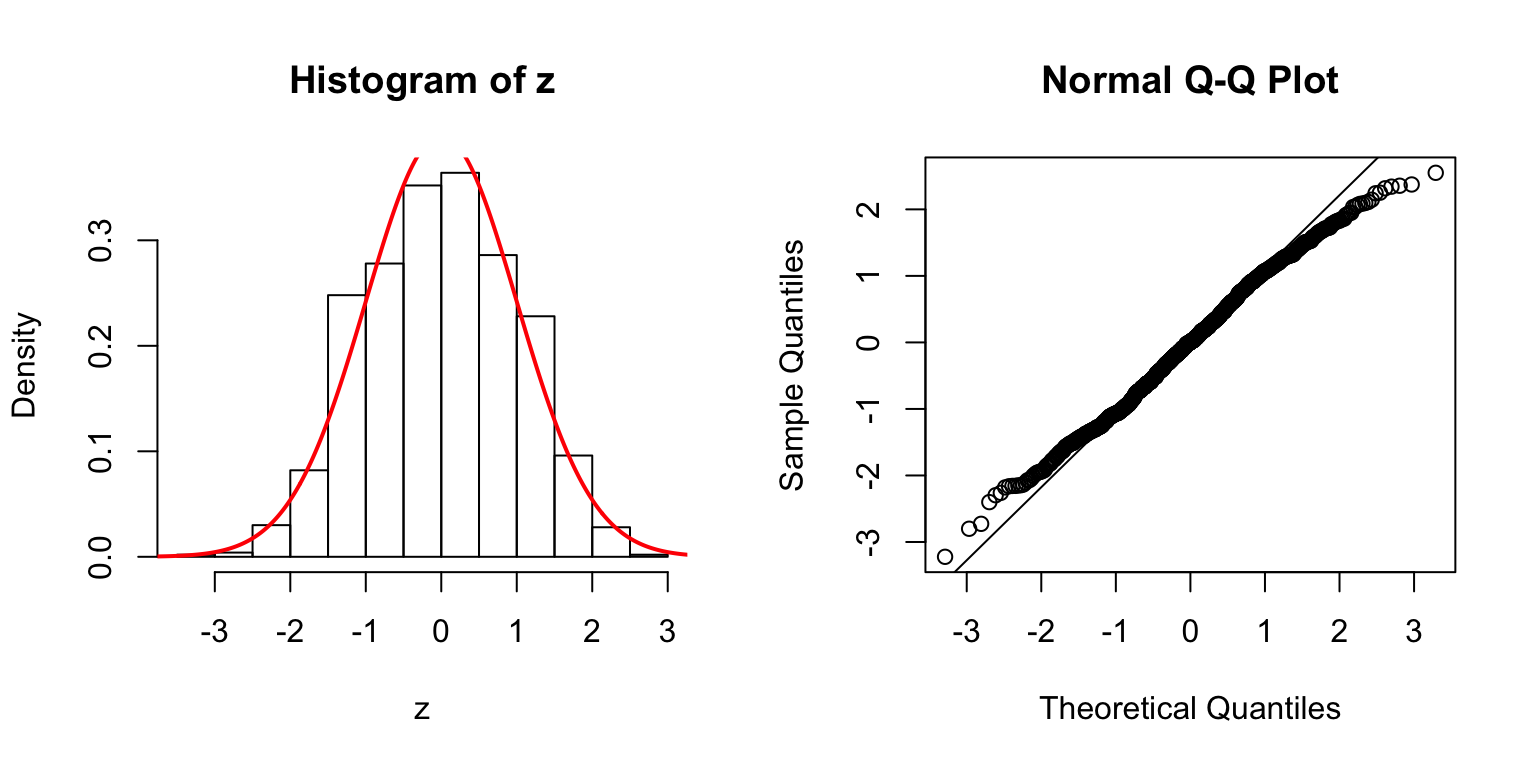
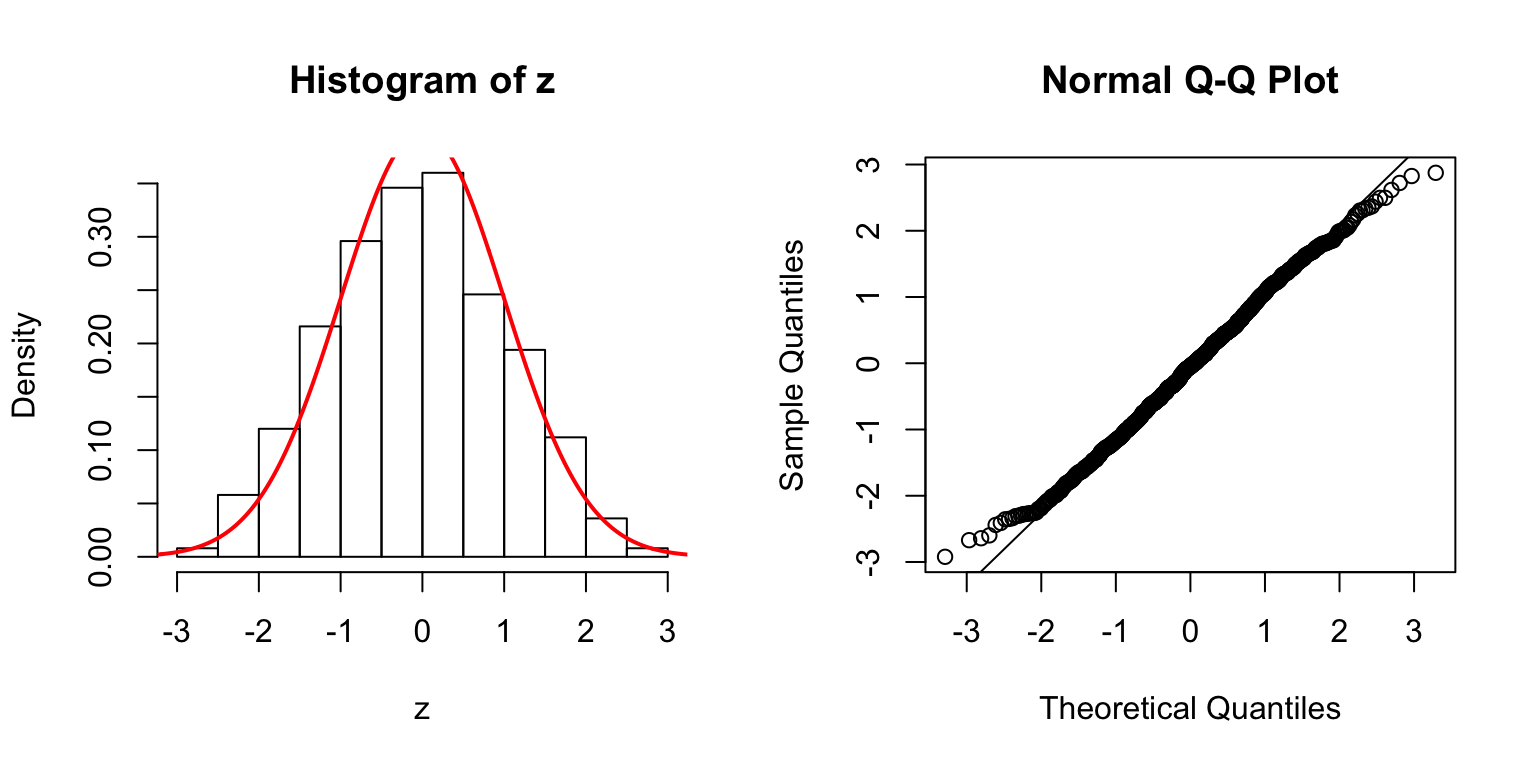
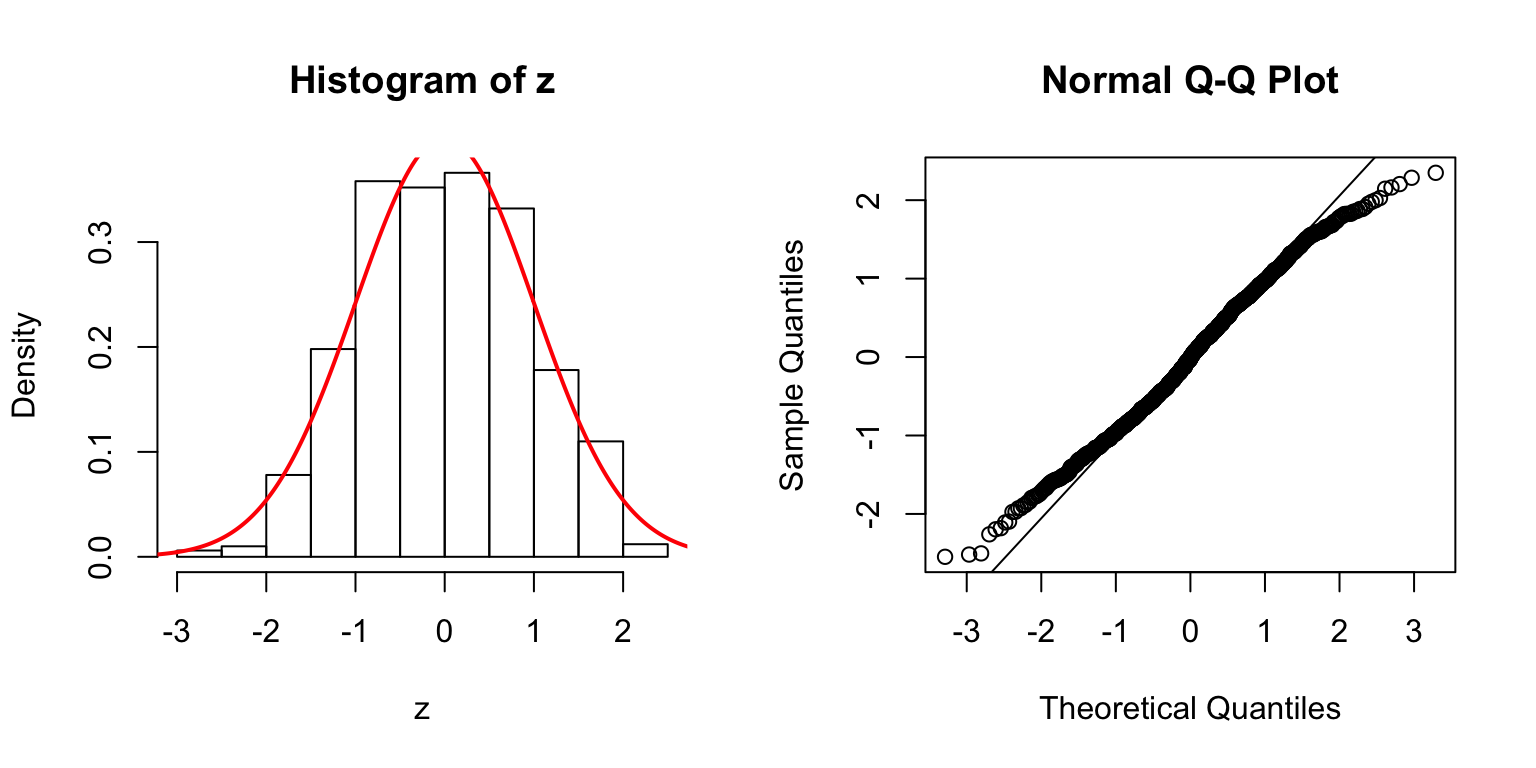
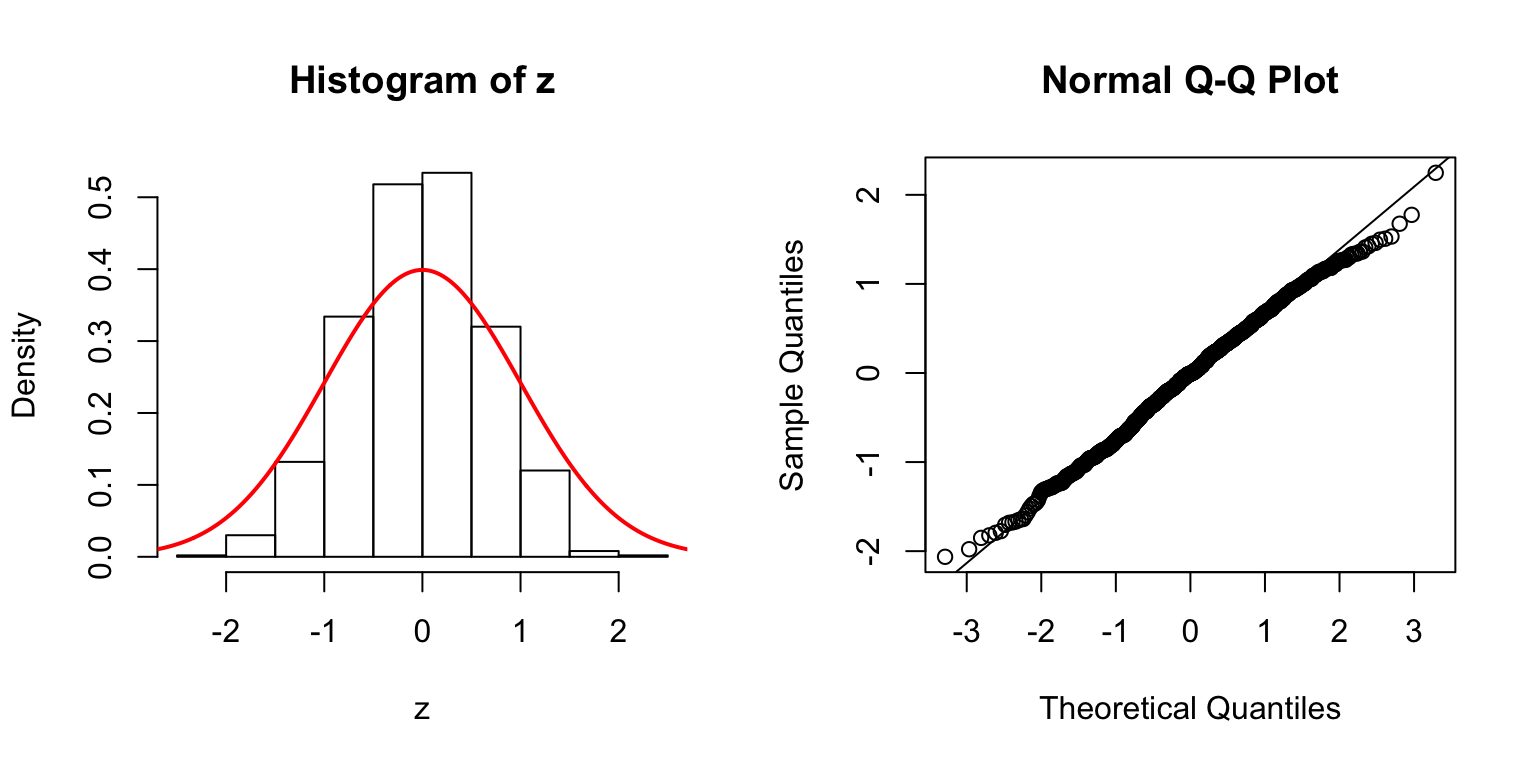
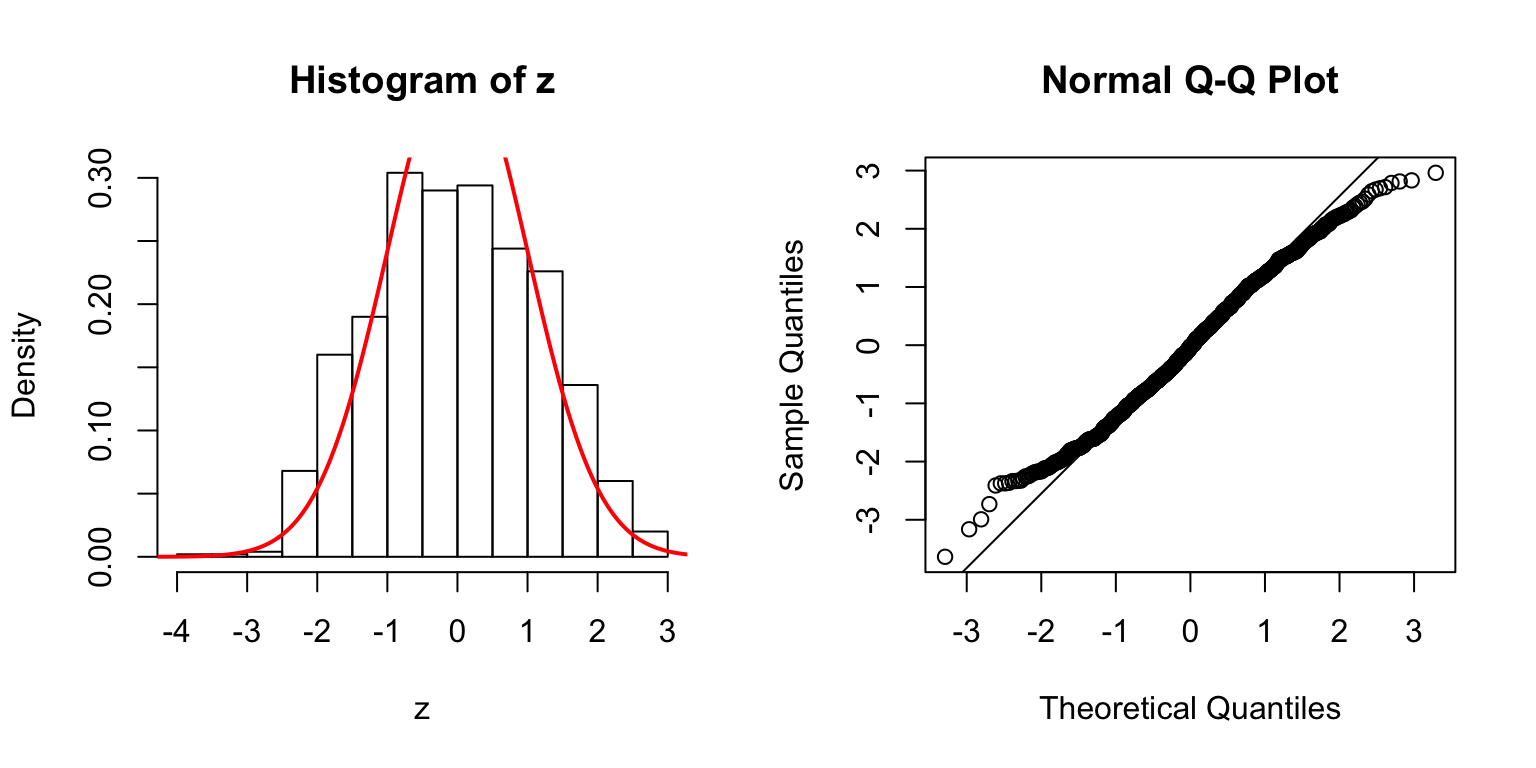
\(d = 20\)
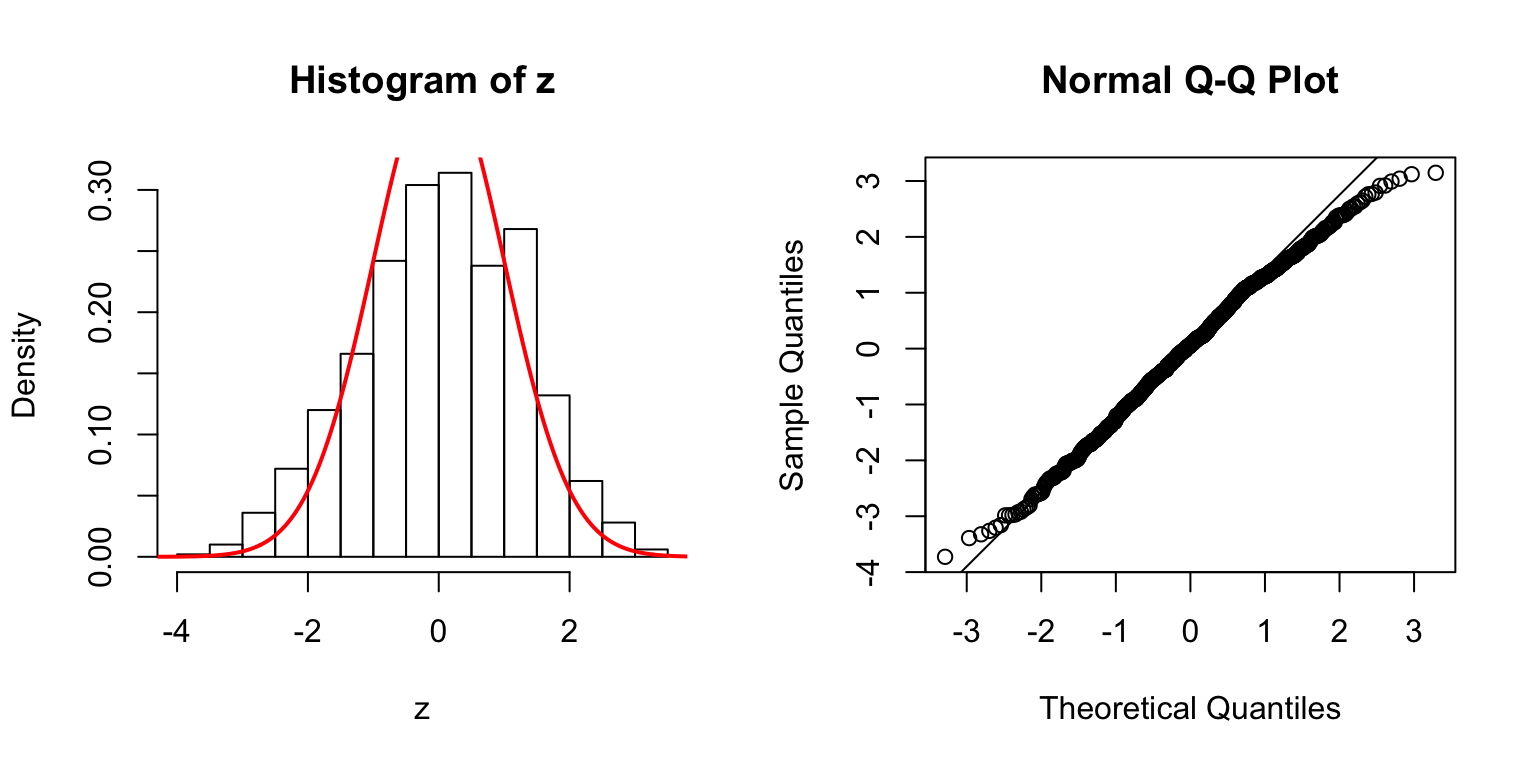
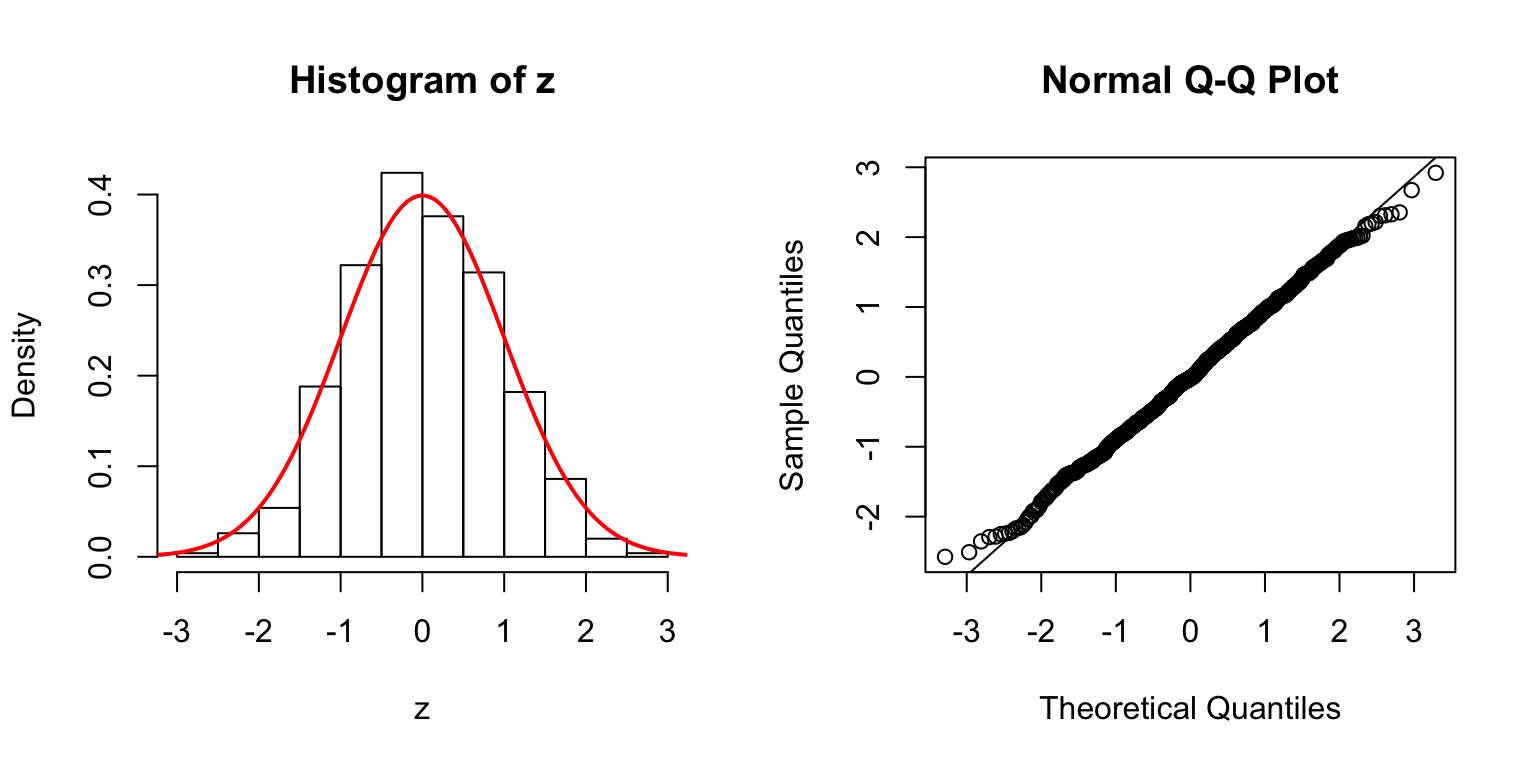
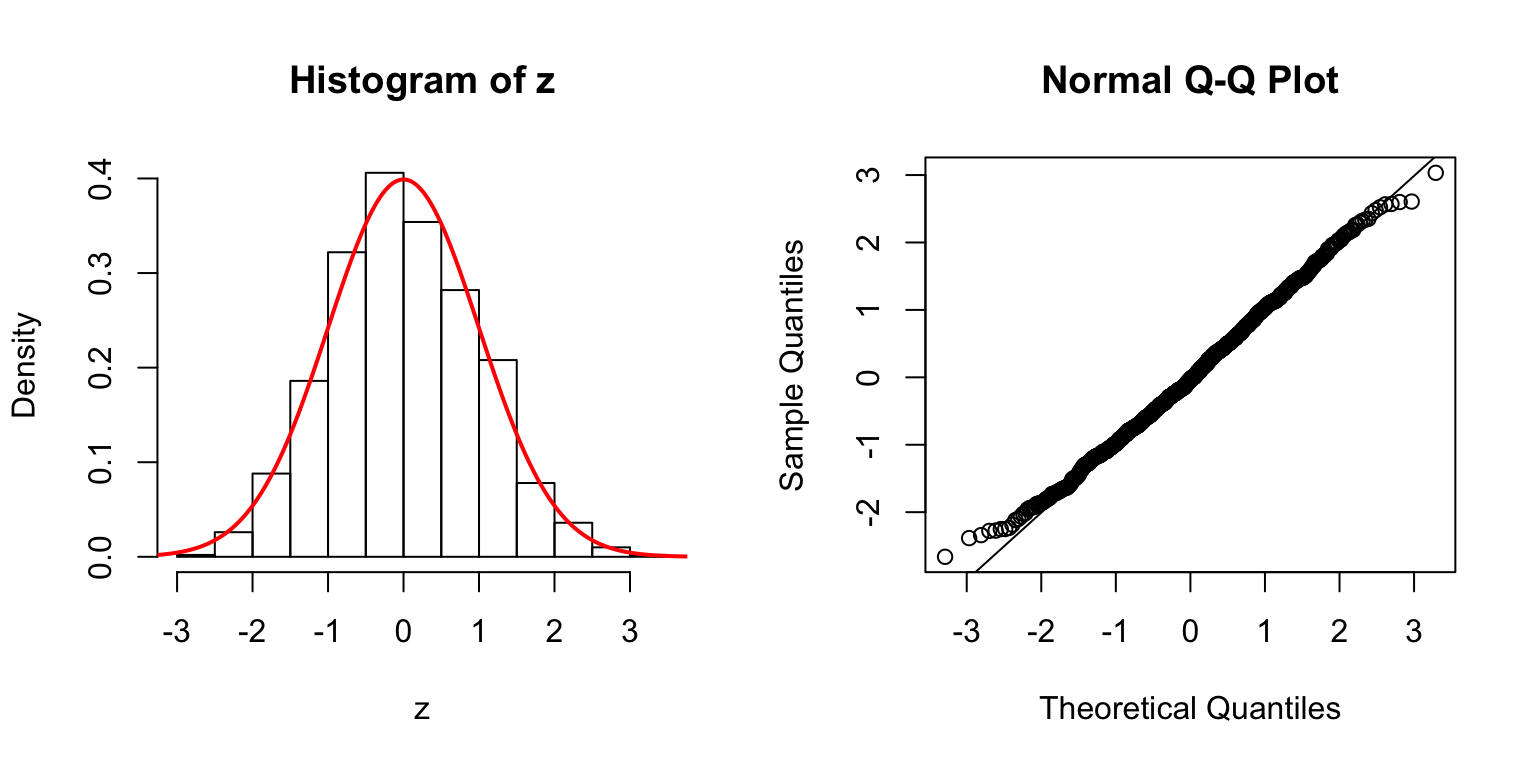
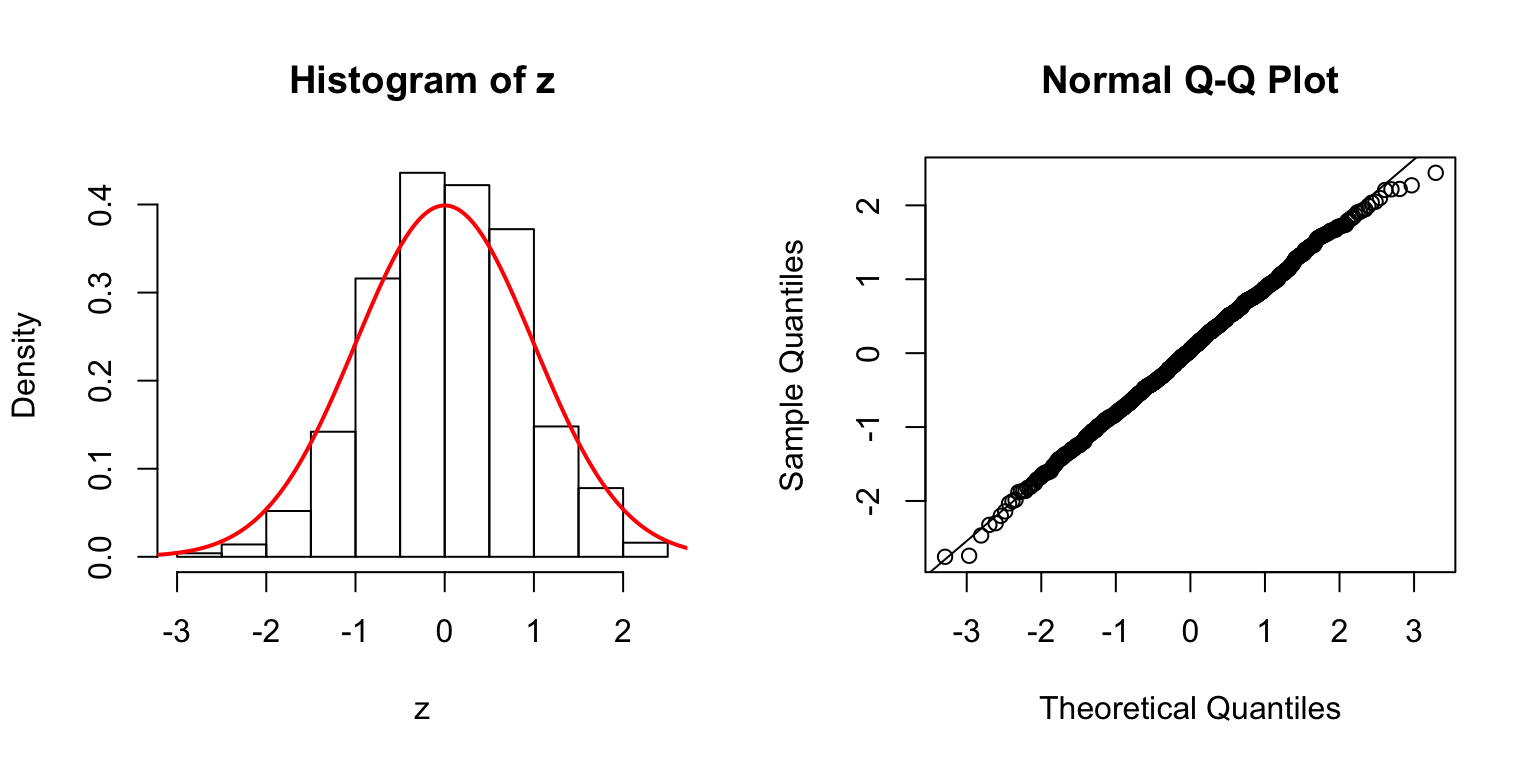
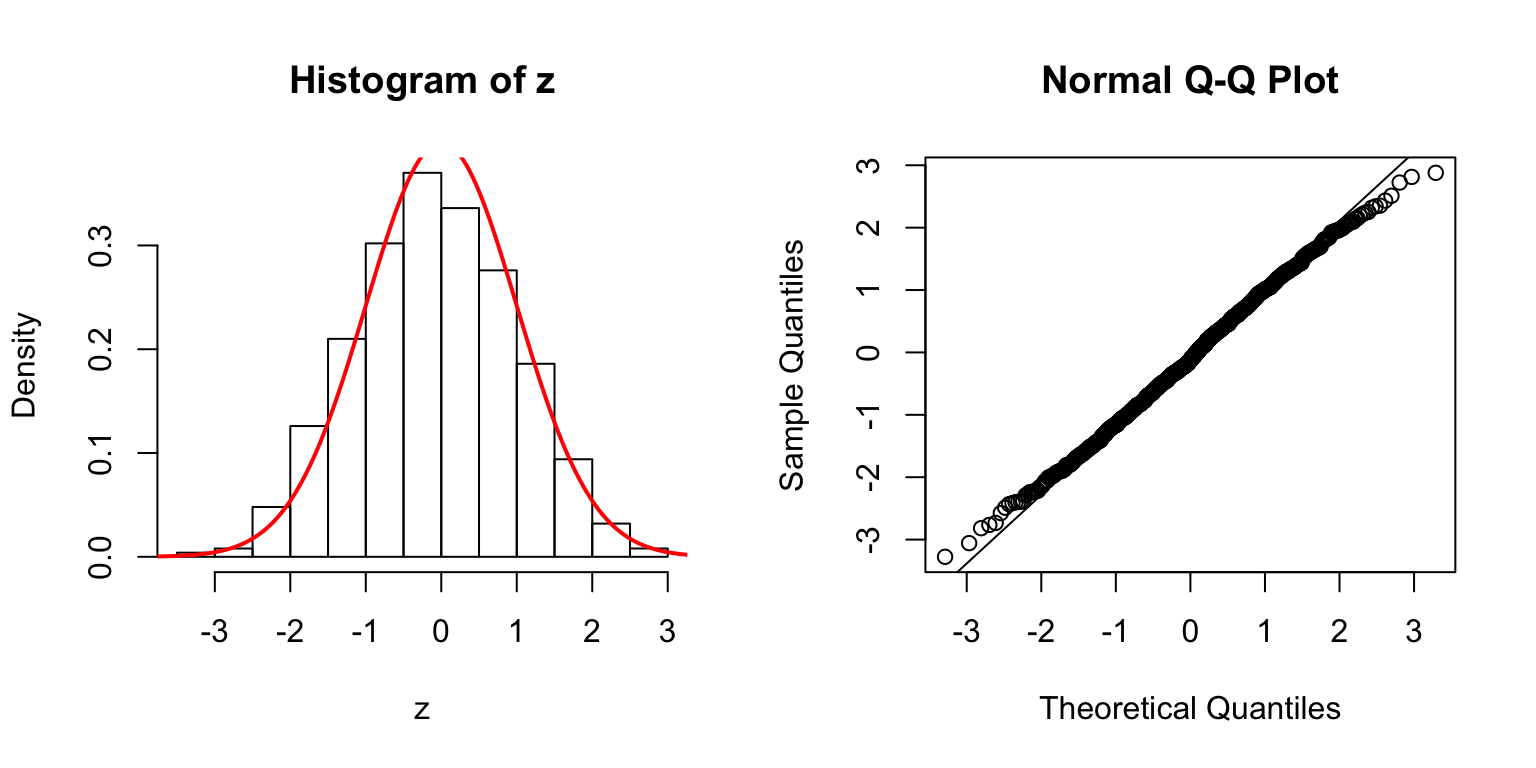
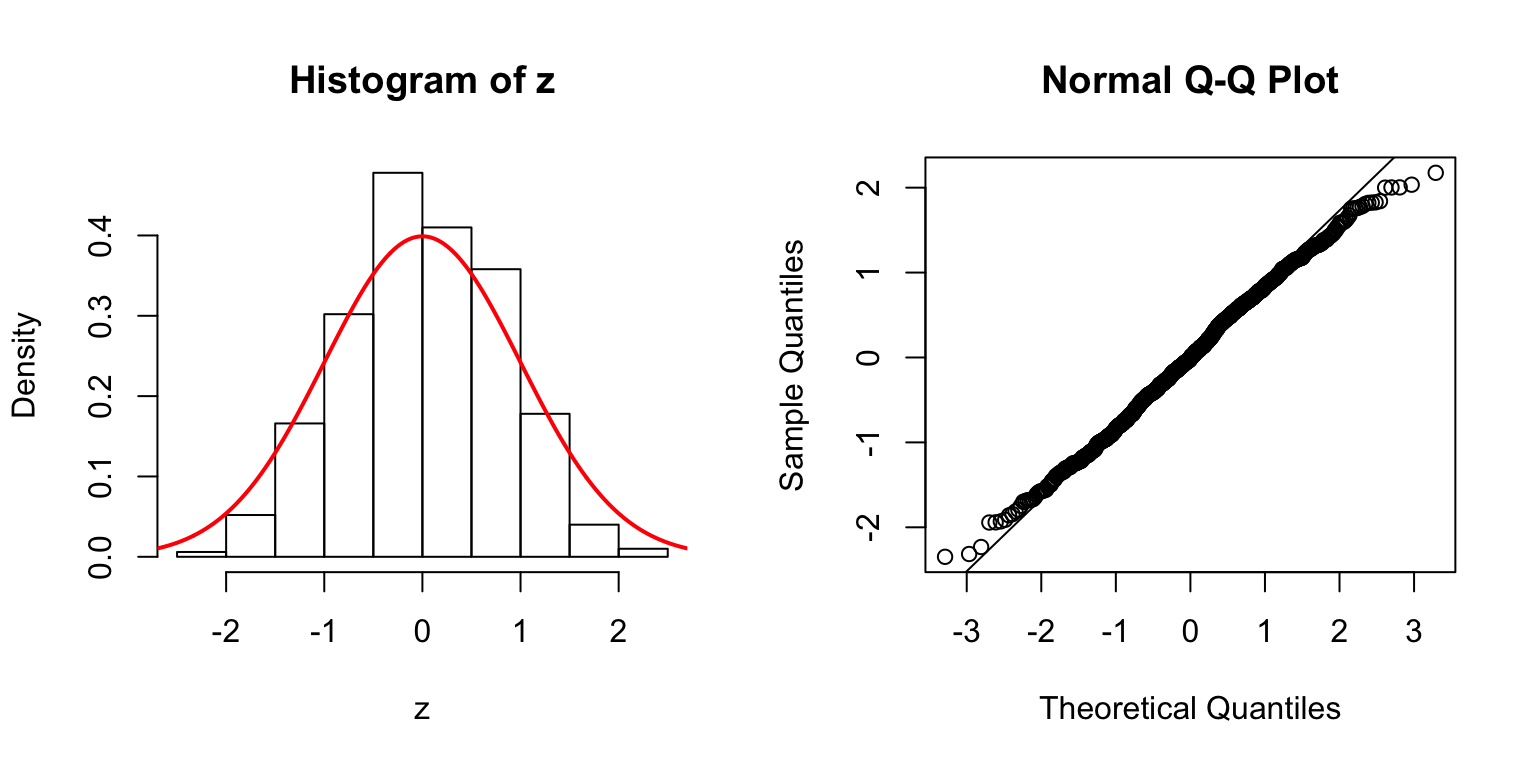
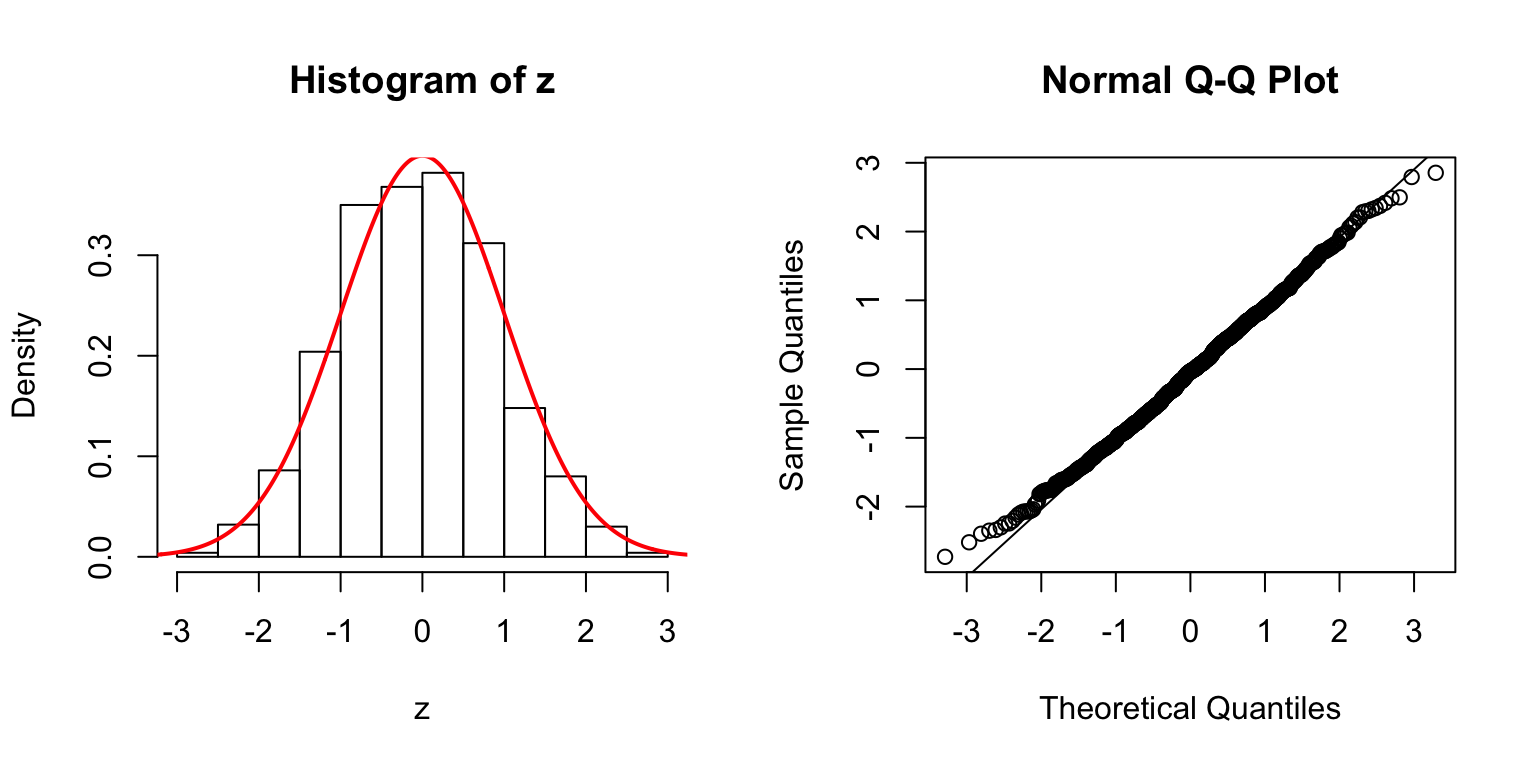
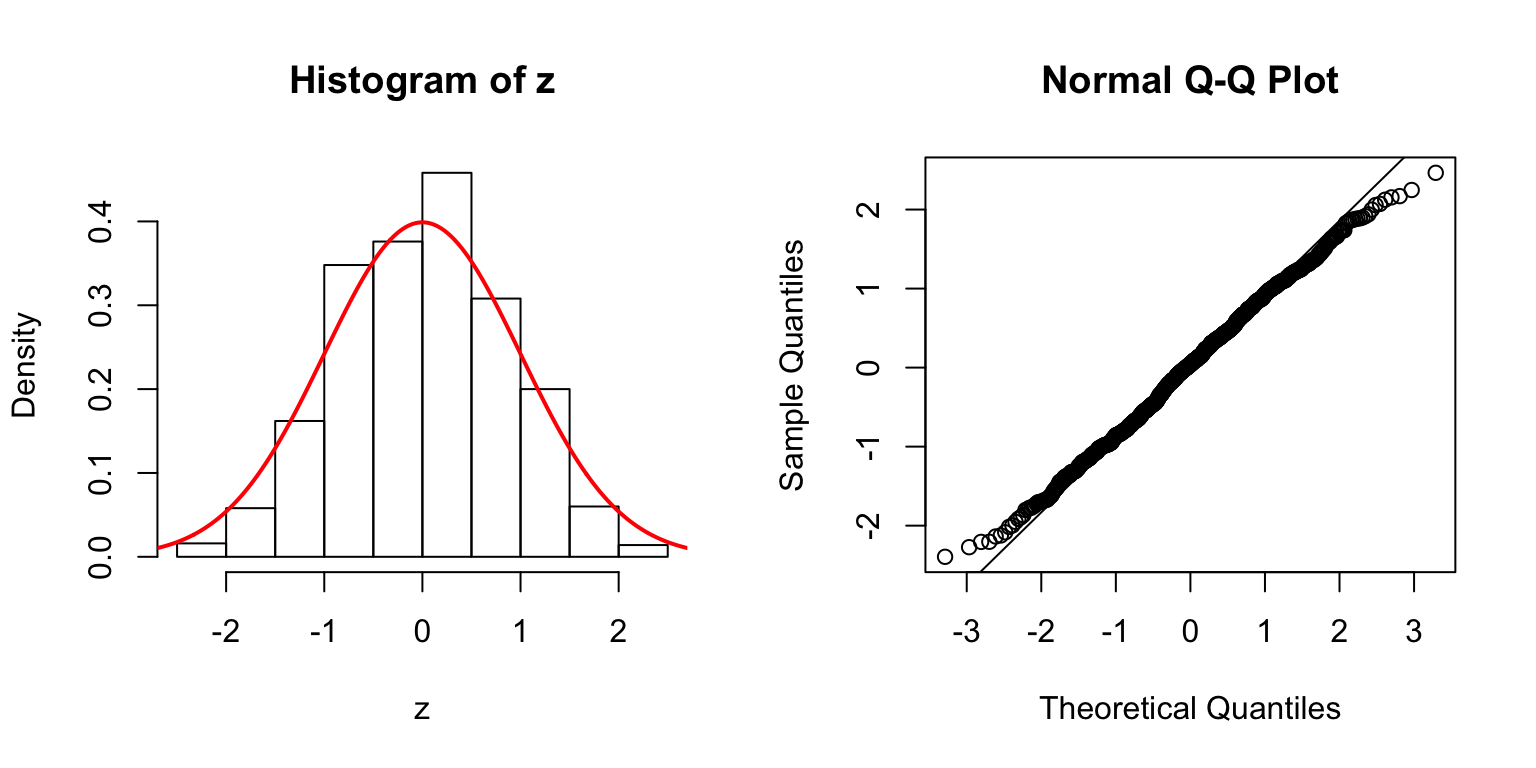
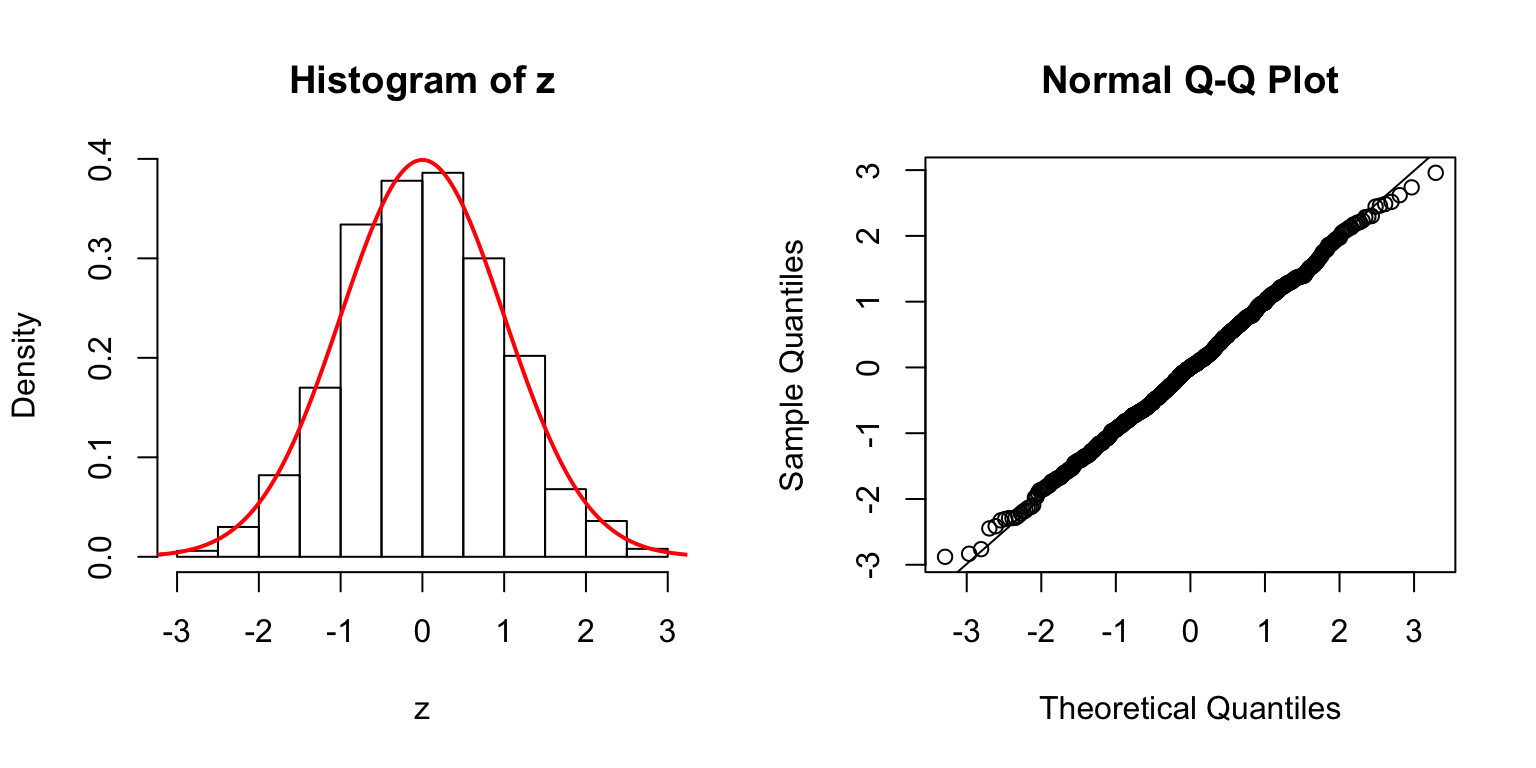
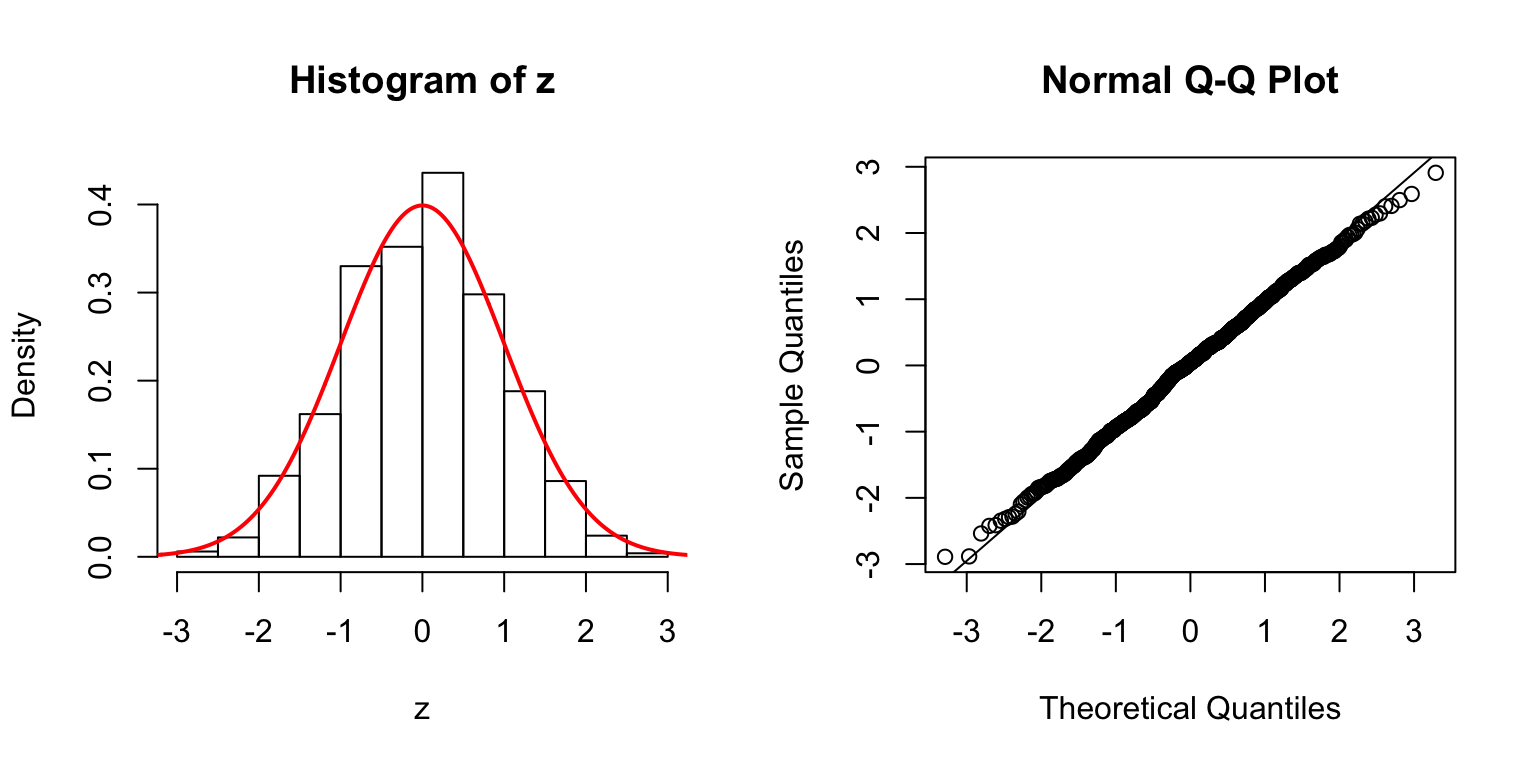
\(d = 50\)
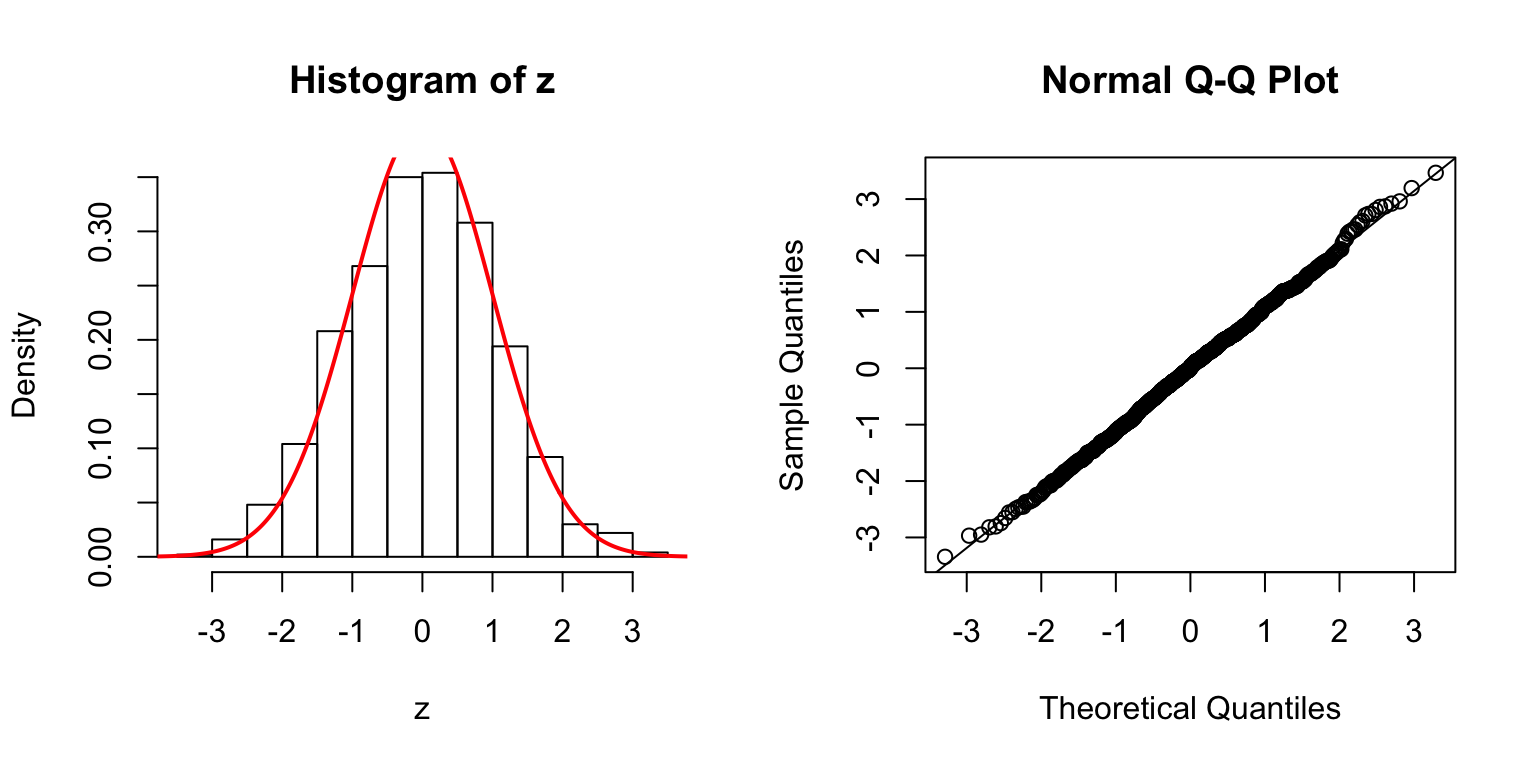
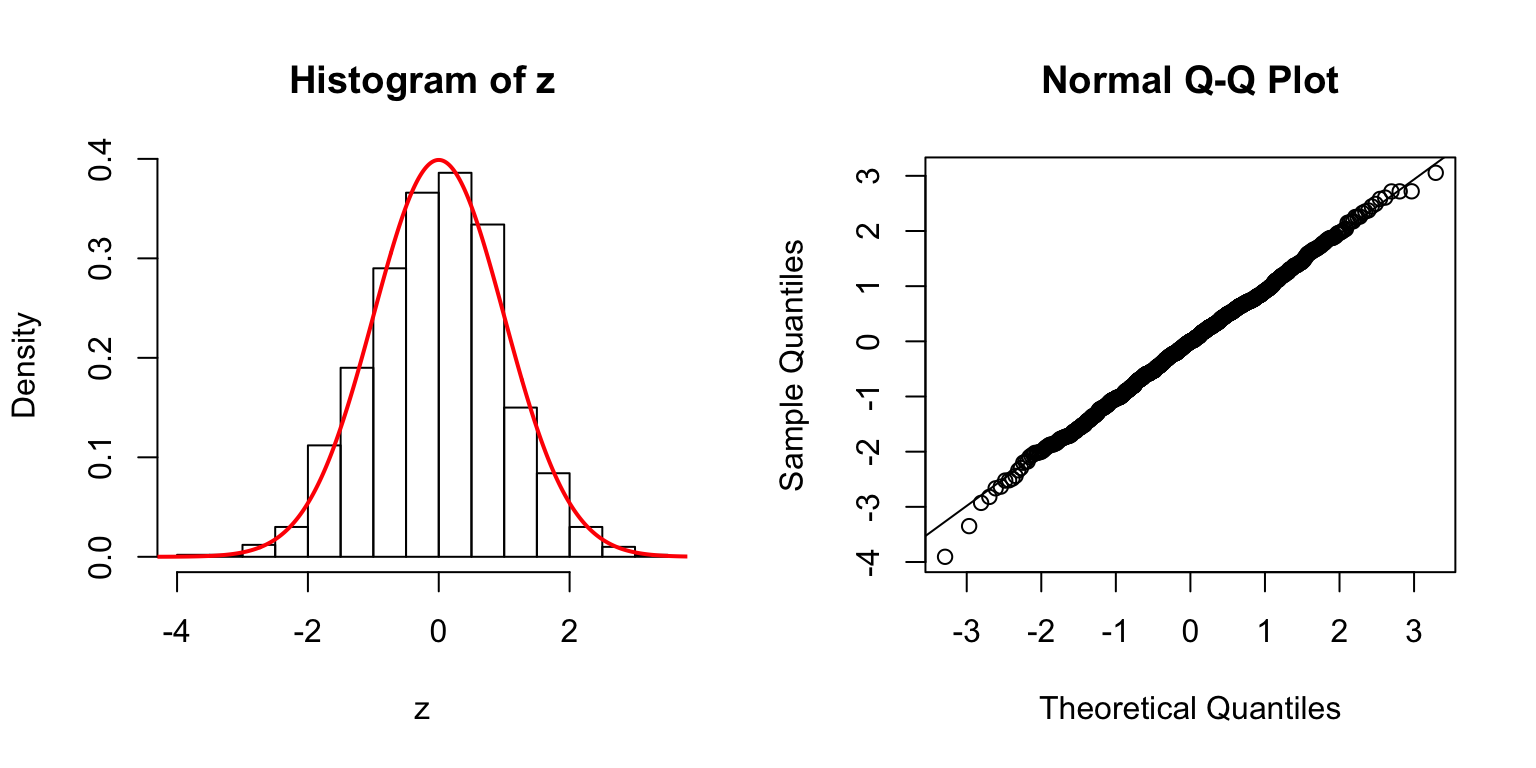
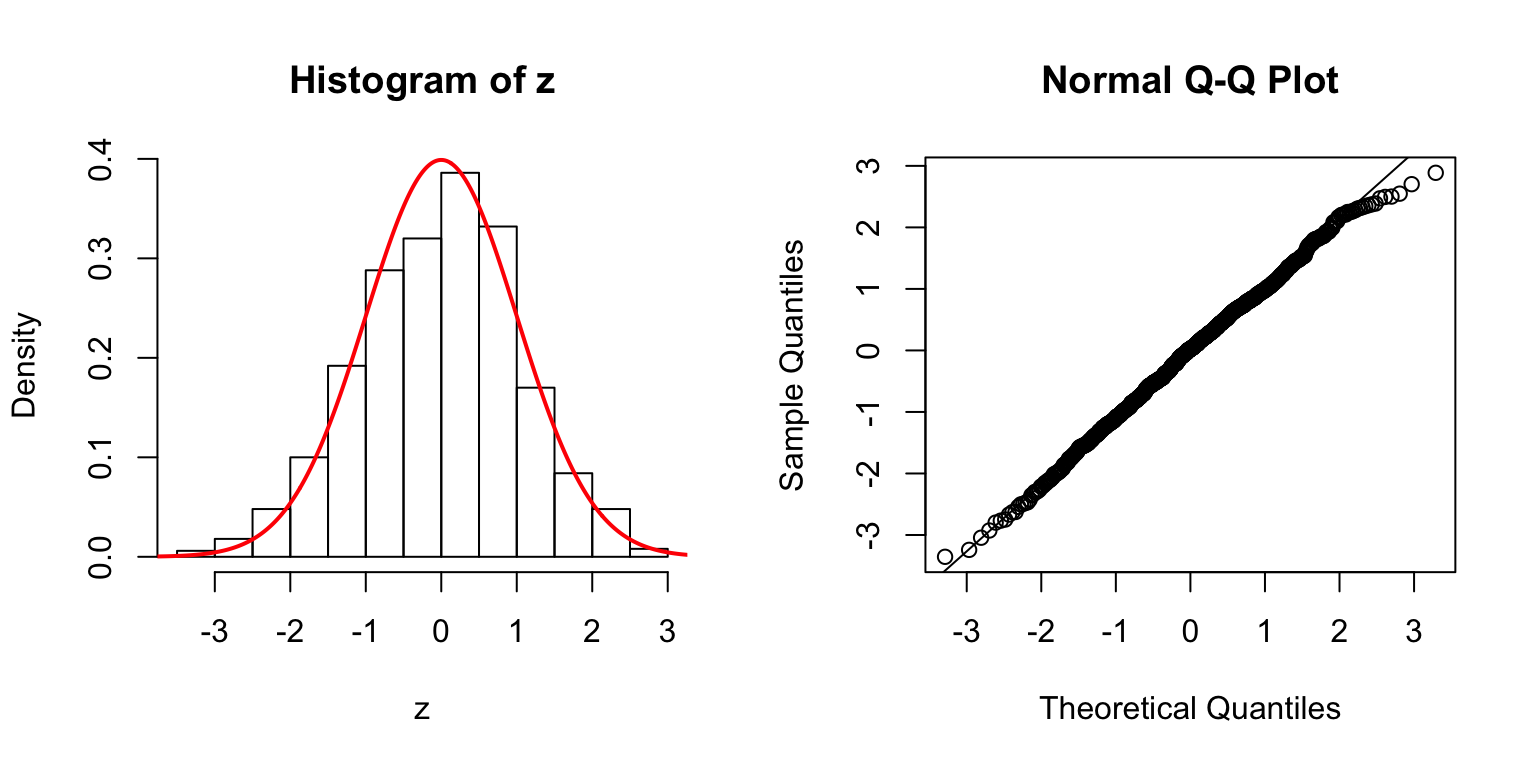
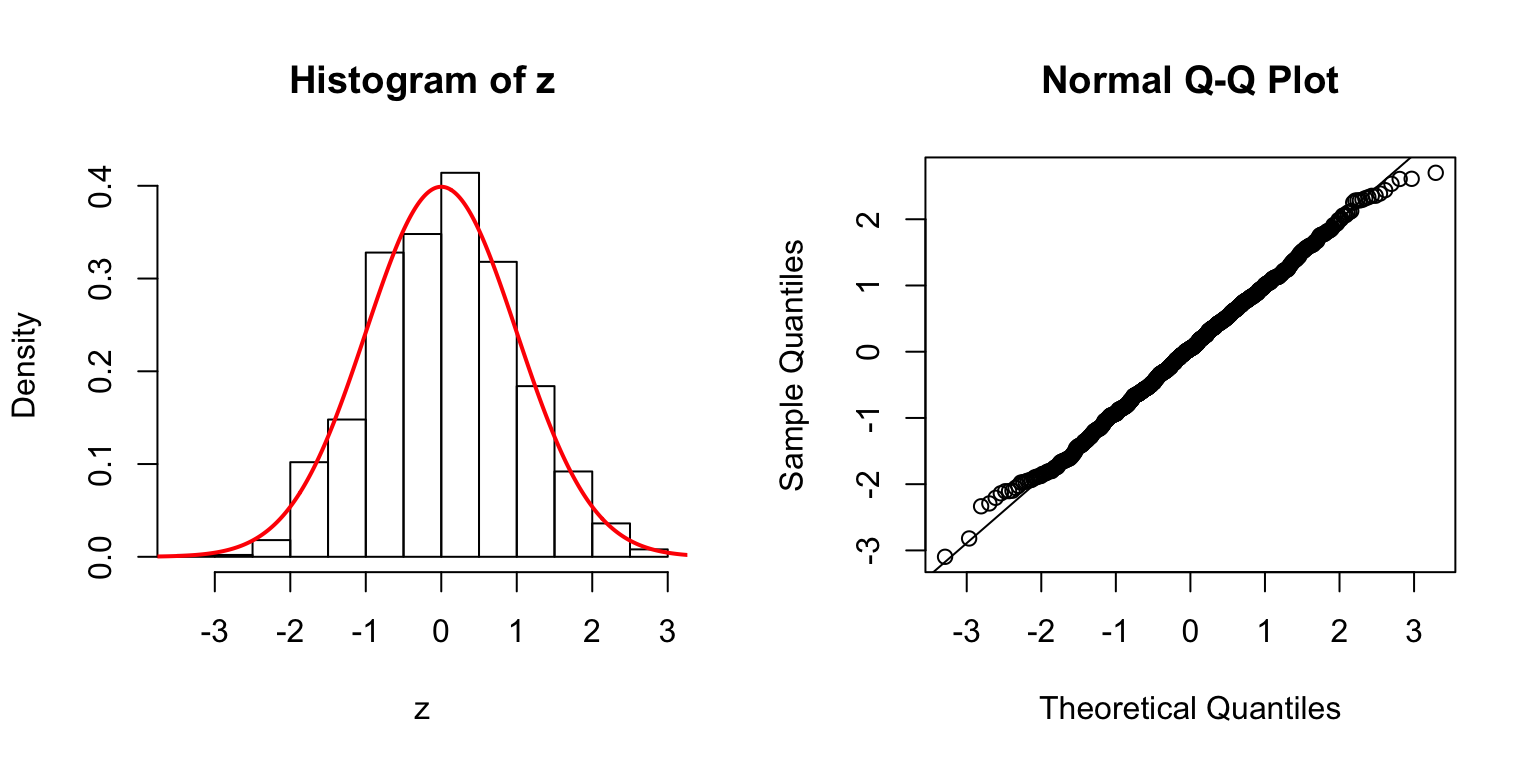
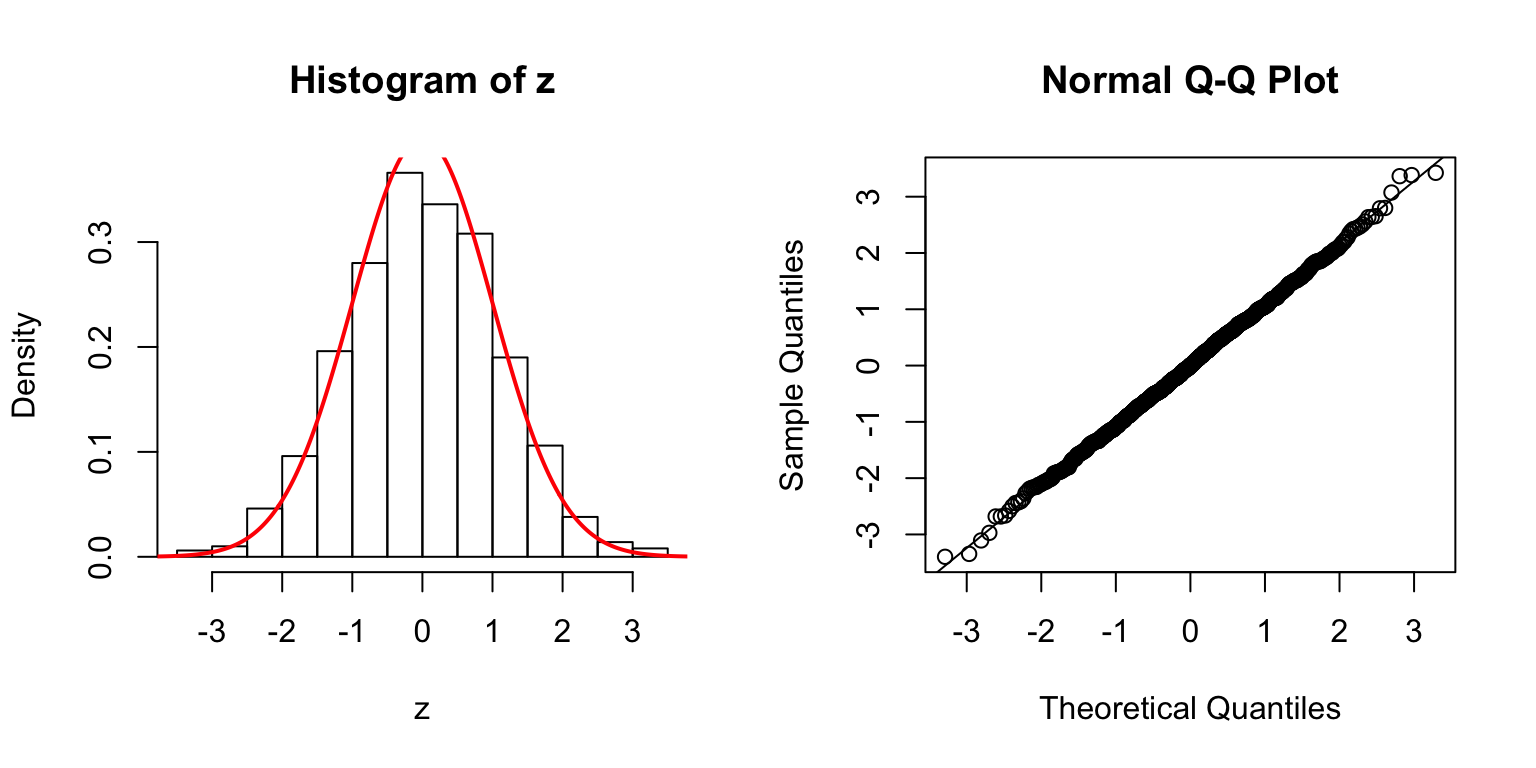
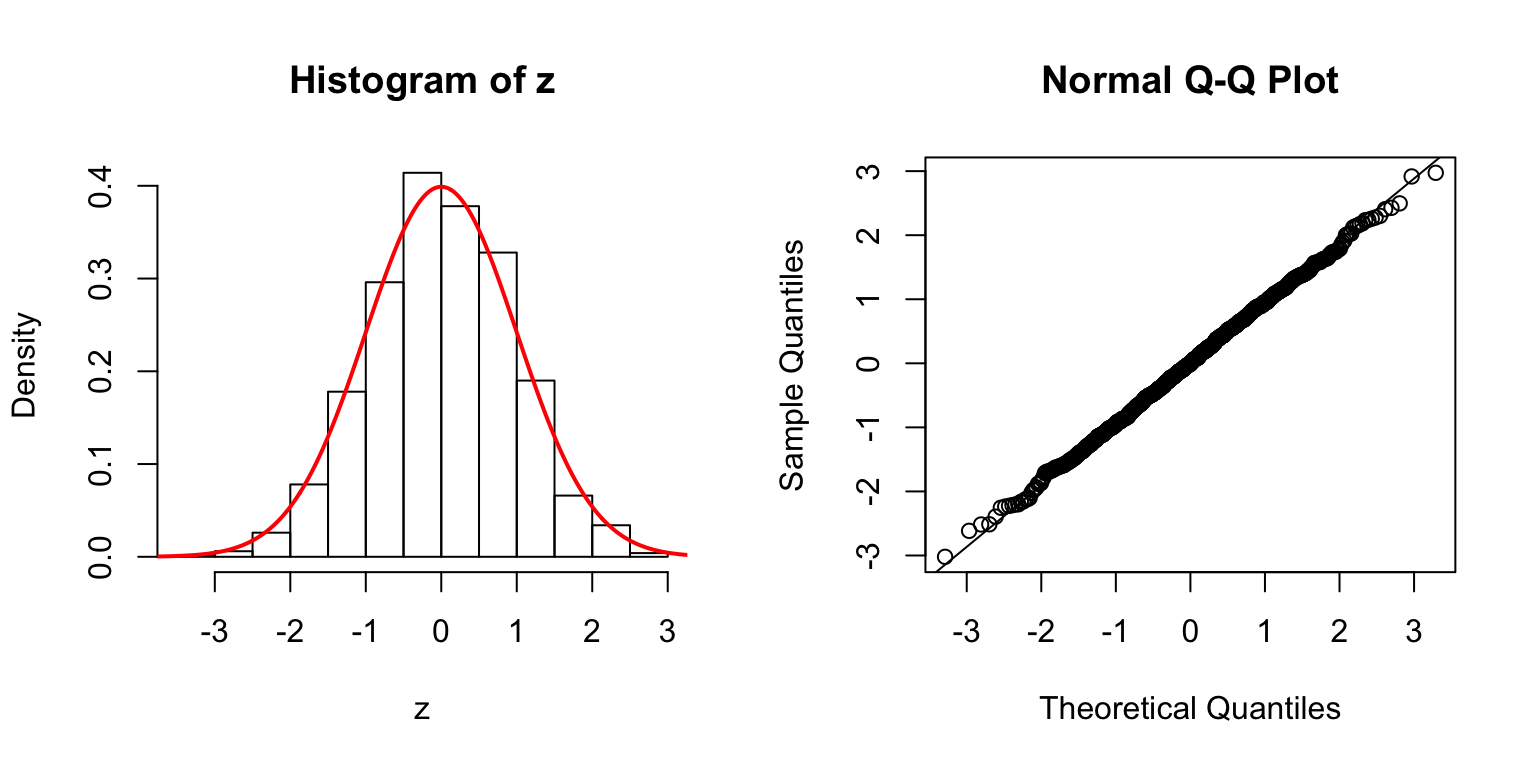
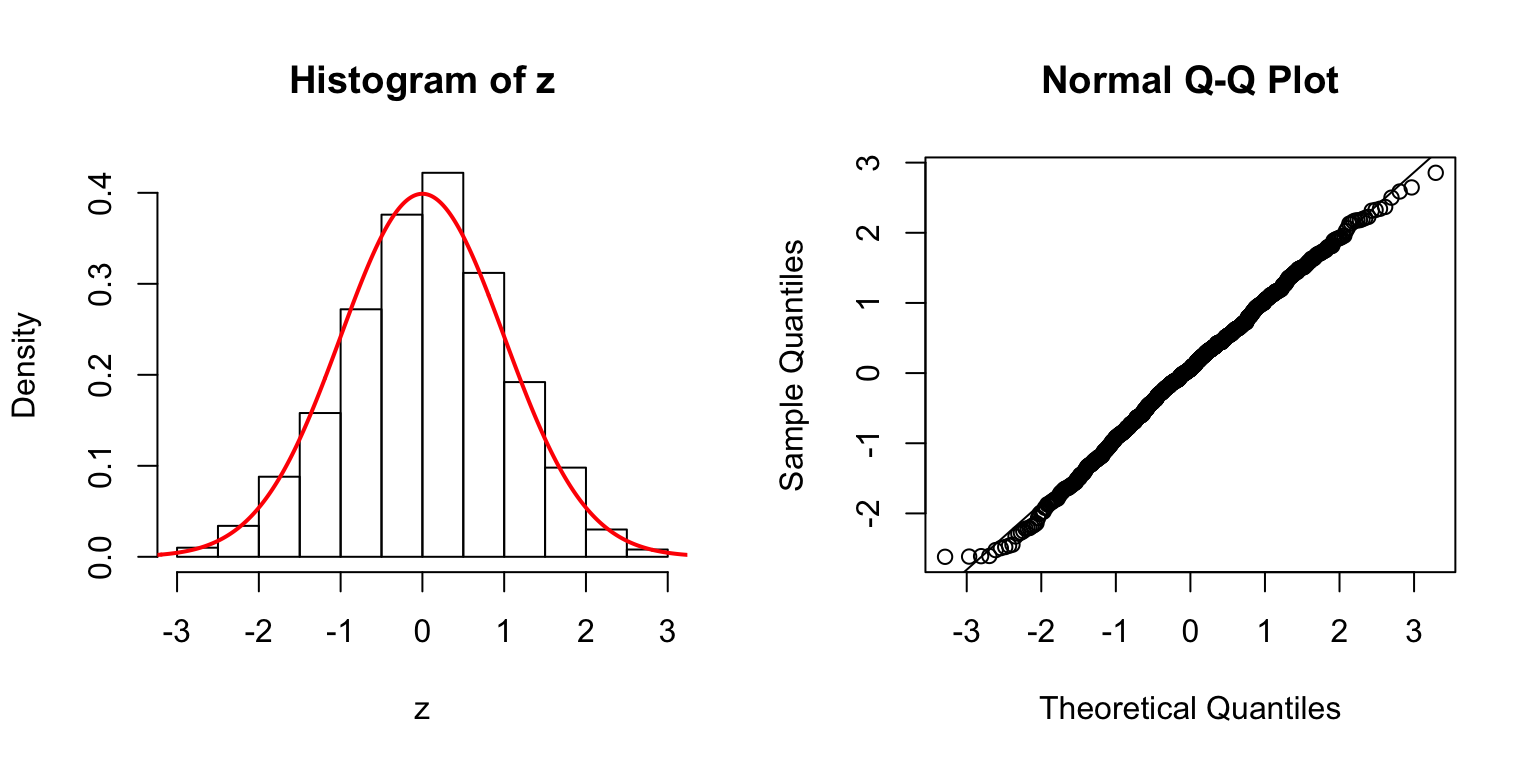
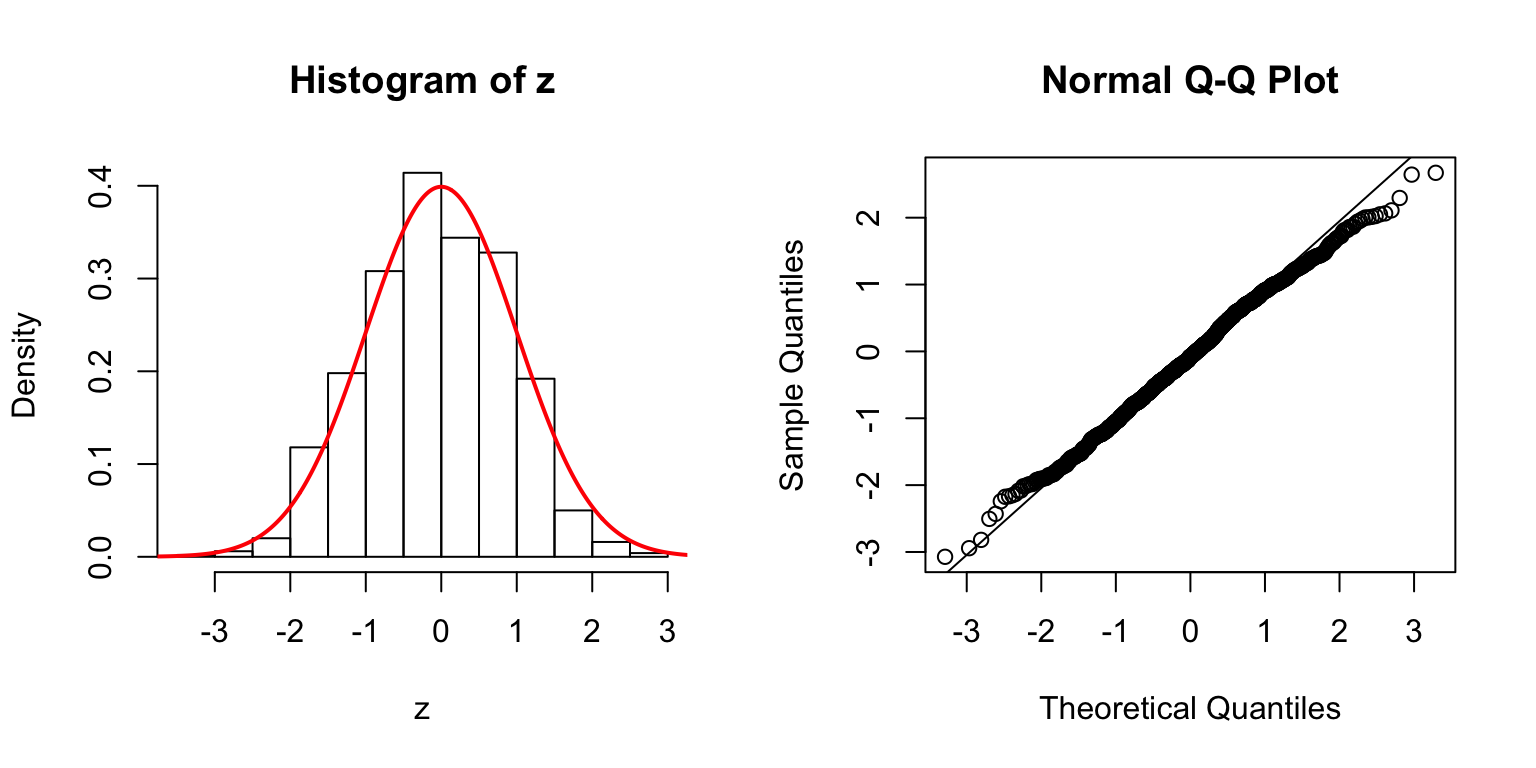
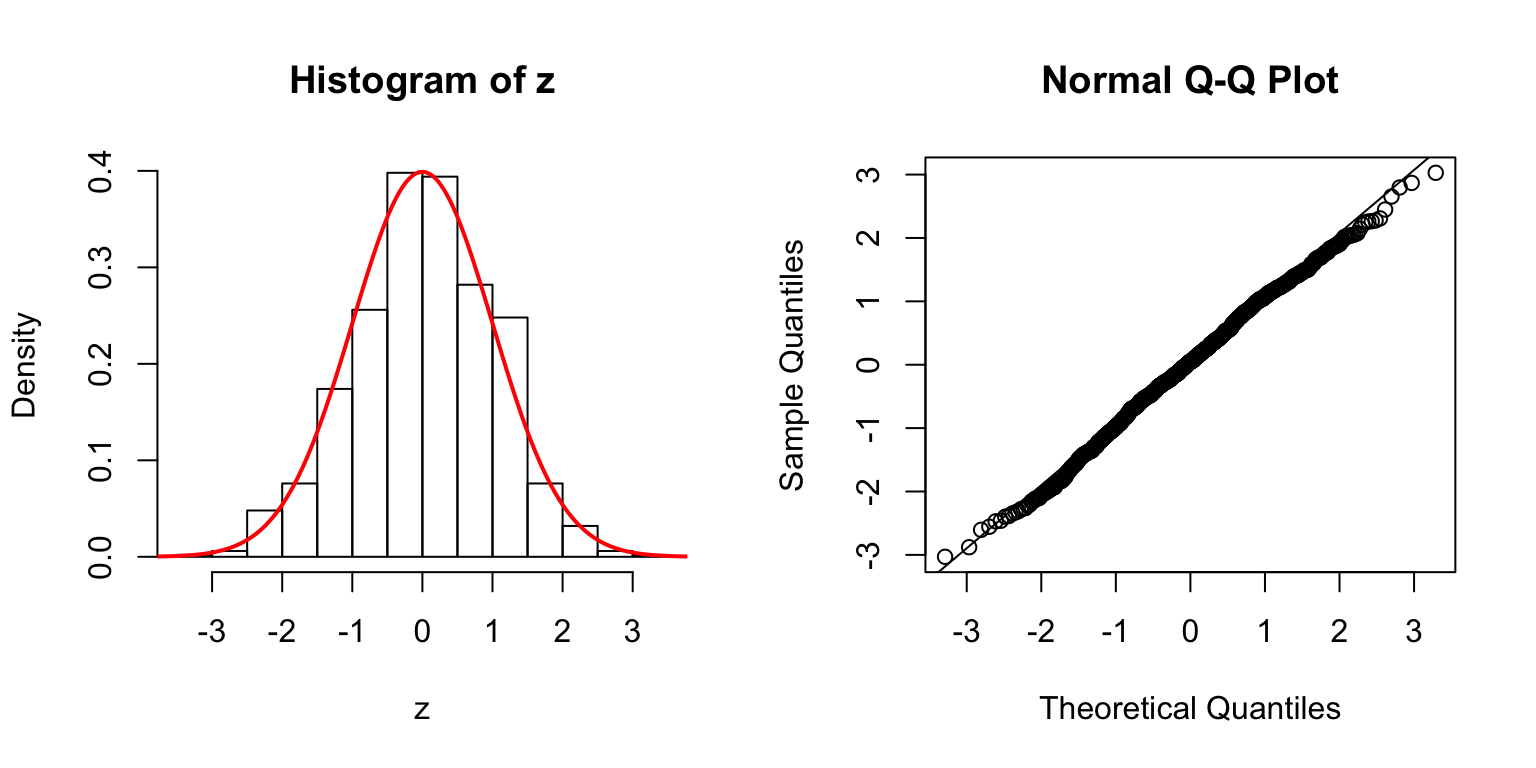
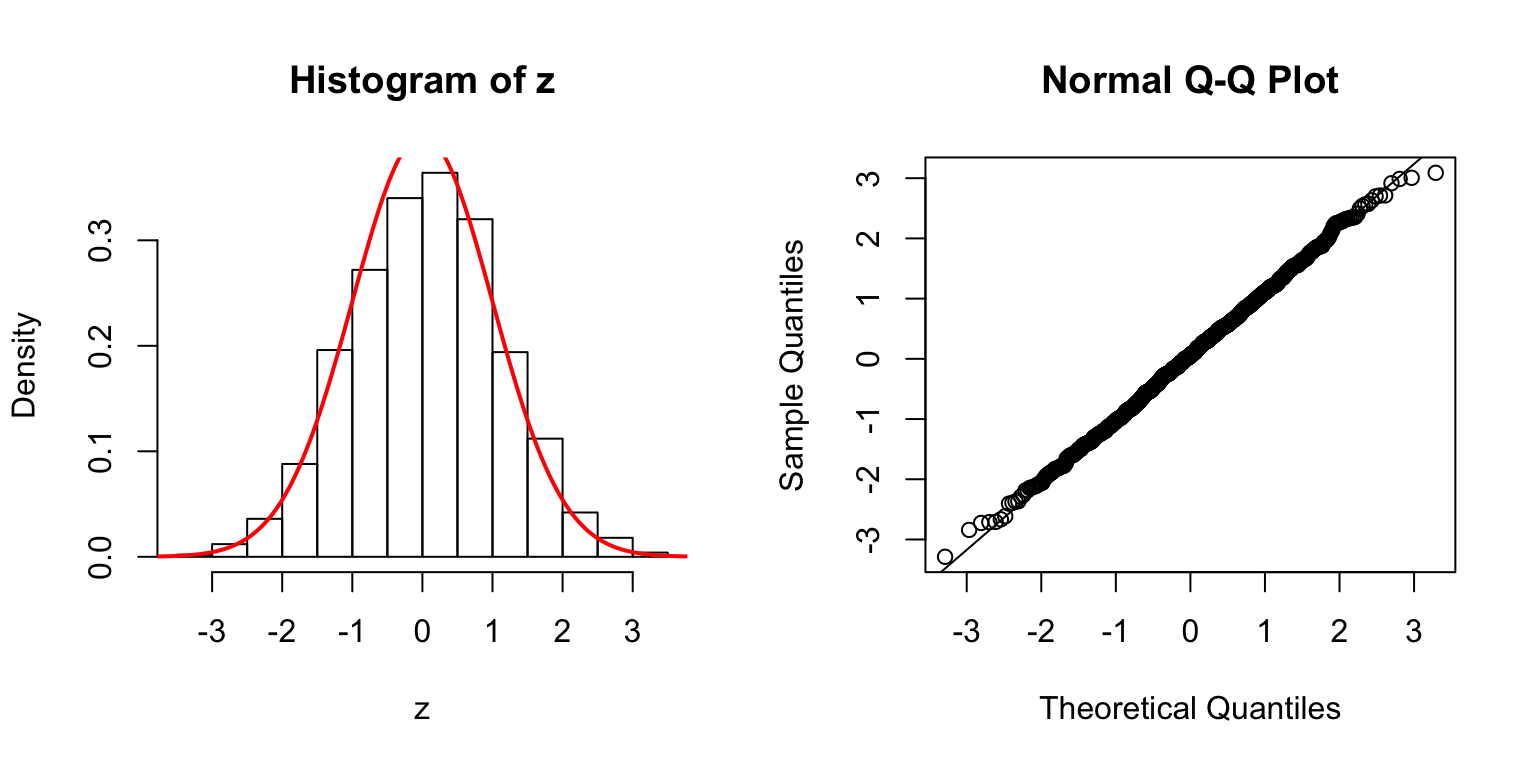
\(d = 100\)
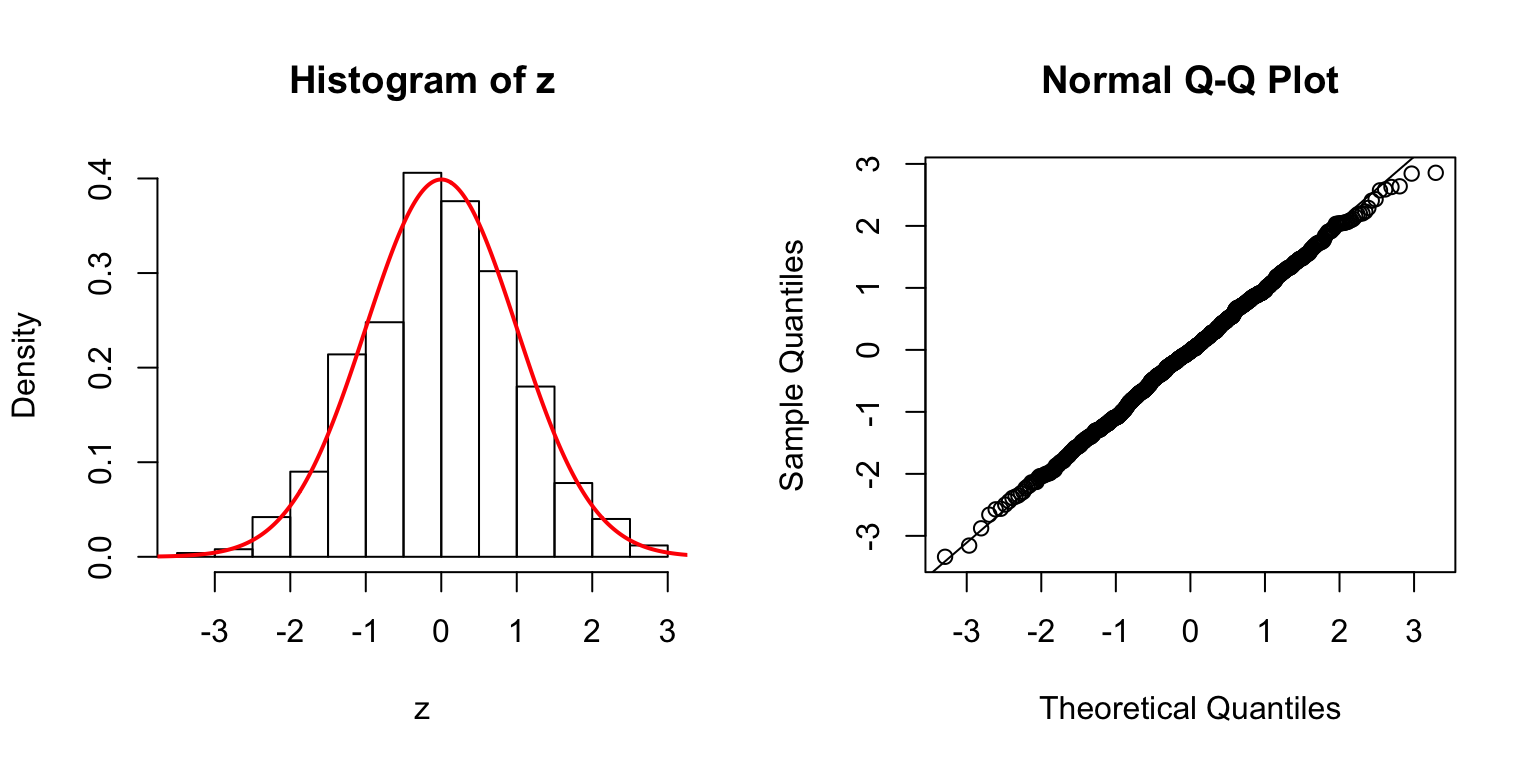
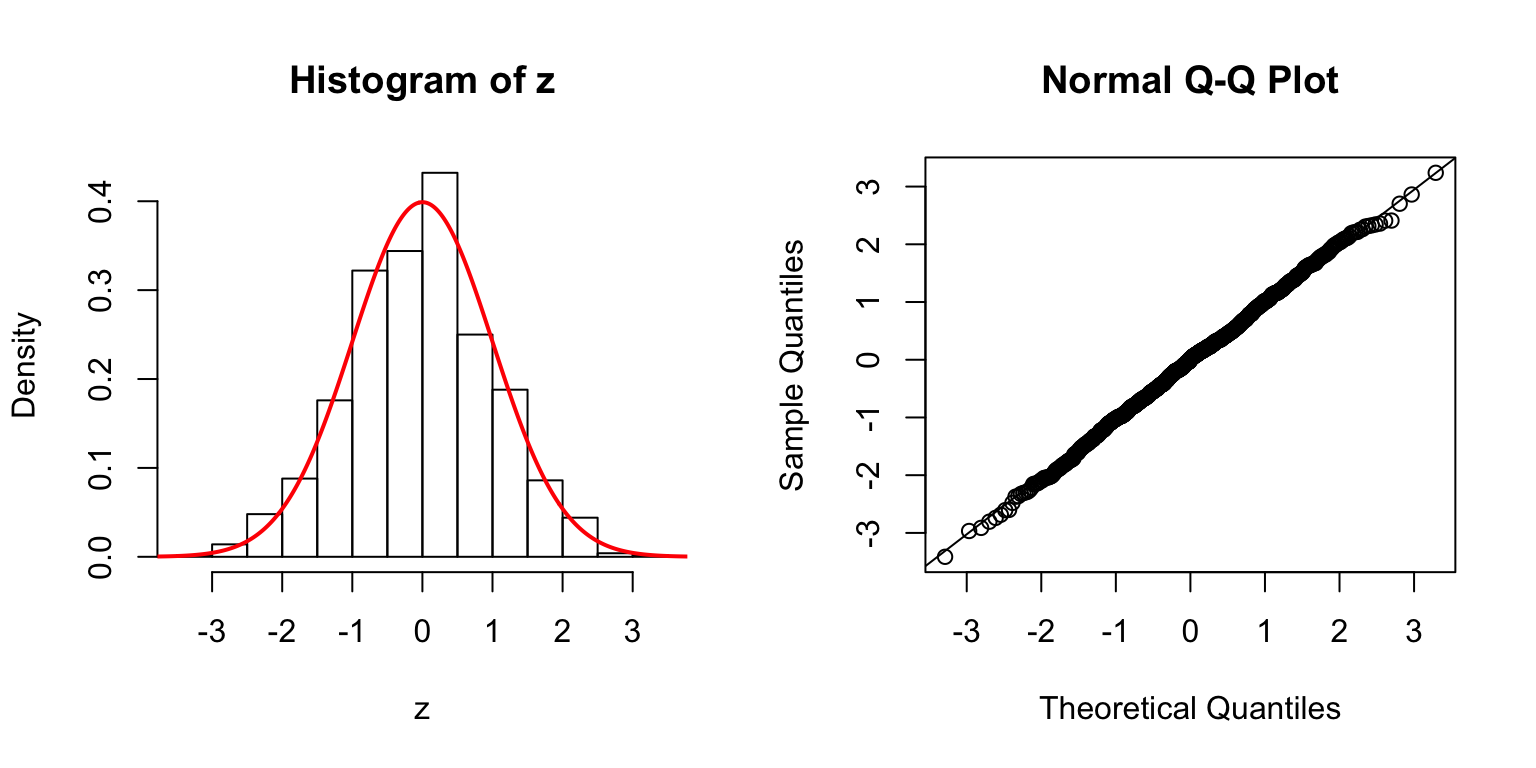
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.3 backports_1.1.2 magrittr_1.5 rprojroot_1.3-2
[5] tools_3.4.3 htmltools_0.3.6 yaml_2.1.16 Rcpp_0.12.14
[9] stringi_1.1.6 rmarkdown_1.8 knitr_1.18 git2r_0.21.0
[13] stringr_1.2.0 digest_0.6.14 evaluate_0.10.1This R Markdown site was created with workflowr