True Signal vs Correlated Null

Introduction

We’ve shown that in many real data sets when we have correlated null \(z\) scores, we can fit their empirical distribution with Gaussian and its derivatives.

But what if we have real signals instead of the global null? Can we fit real signals with Gaussian derivatives with reasonable weights? Let’s start with the most basic case: \(z \sim N(0, \sqrt{2}^2)\) independently. This data set can be seen as generated as follows.

\[ \begin{array}{c} \beta_j \sim N(0, 1)\\ z_j \sim N(\beta_j, 1) \end{array} \]

Illustration

Let normalized weights \(W_k^s = W_k\sqrt{k!}\) with variance \(\text{var}(W_k^s) = \alpha_k = \bar{\rho_{ij}^k}\).

n = 1e4
m = 5
set.seed(777)
zmat = matrix(rnorm(n * m, 0, sd = sqrt(2)), nrow = m)

library(ashr)
source("../code/ecdfz.R")
res = list()
for (i in 1:3) {
  z = zmat[i, ]
  p = (1 - pnorm(abs(z))) * 2
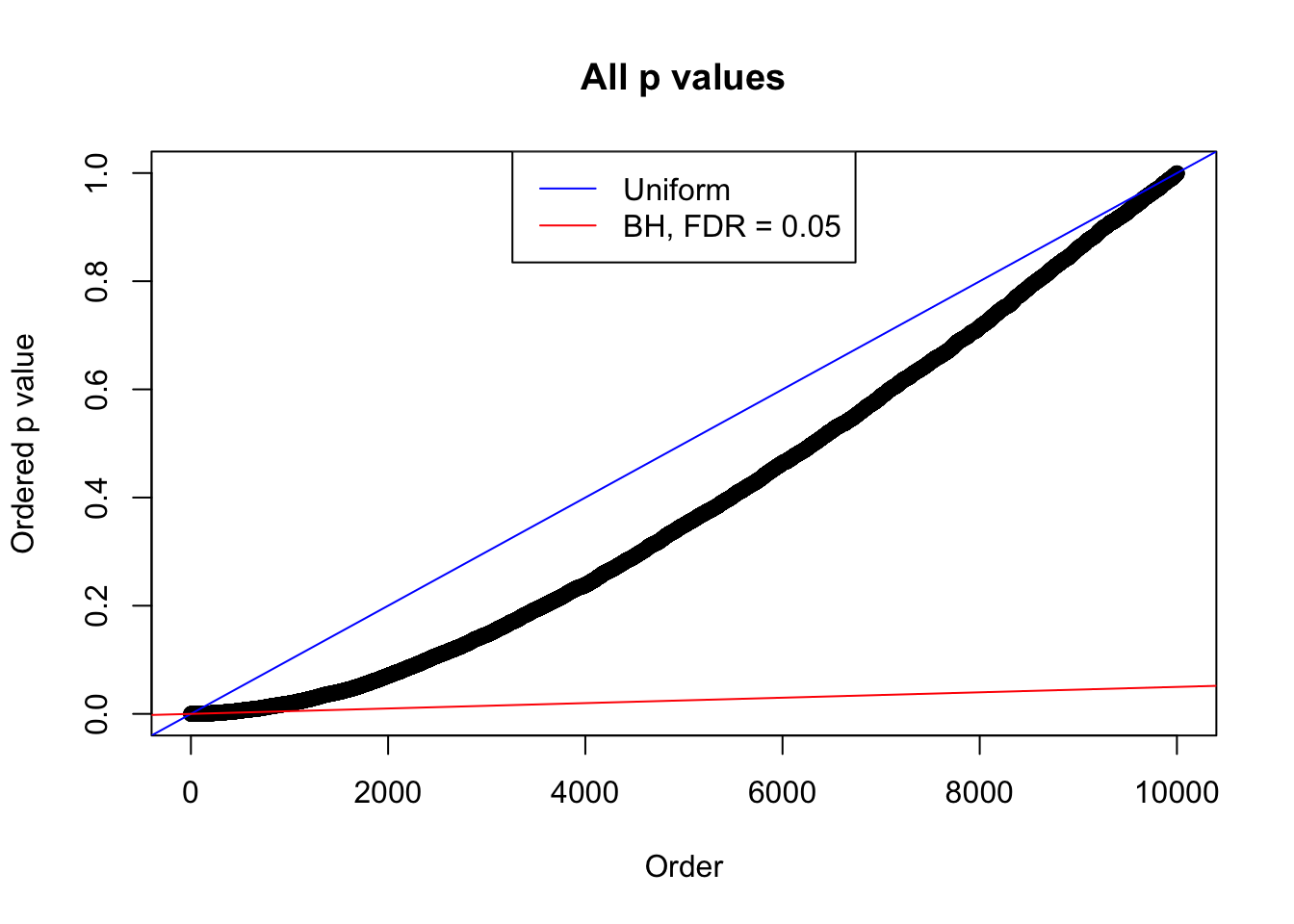
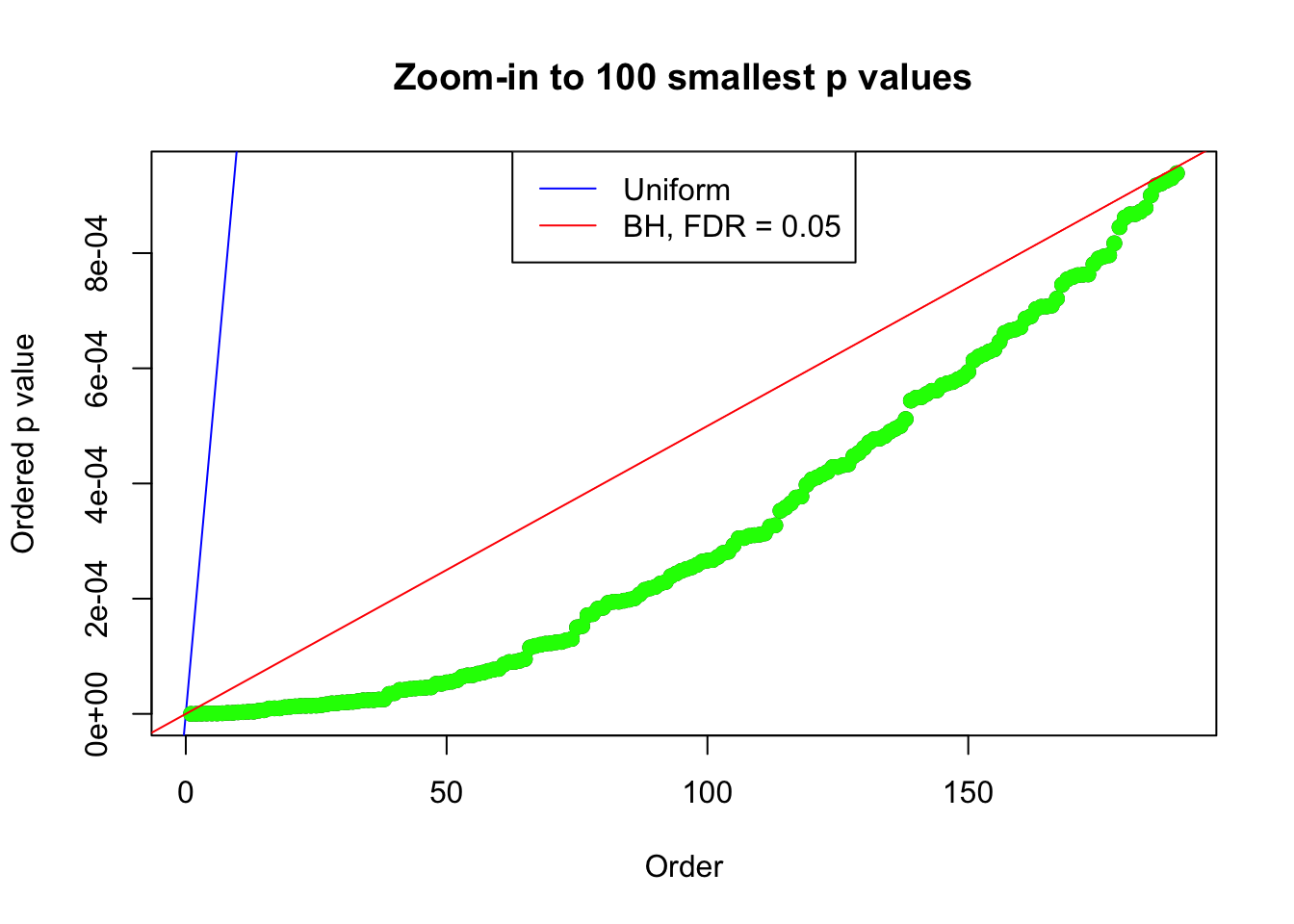
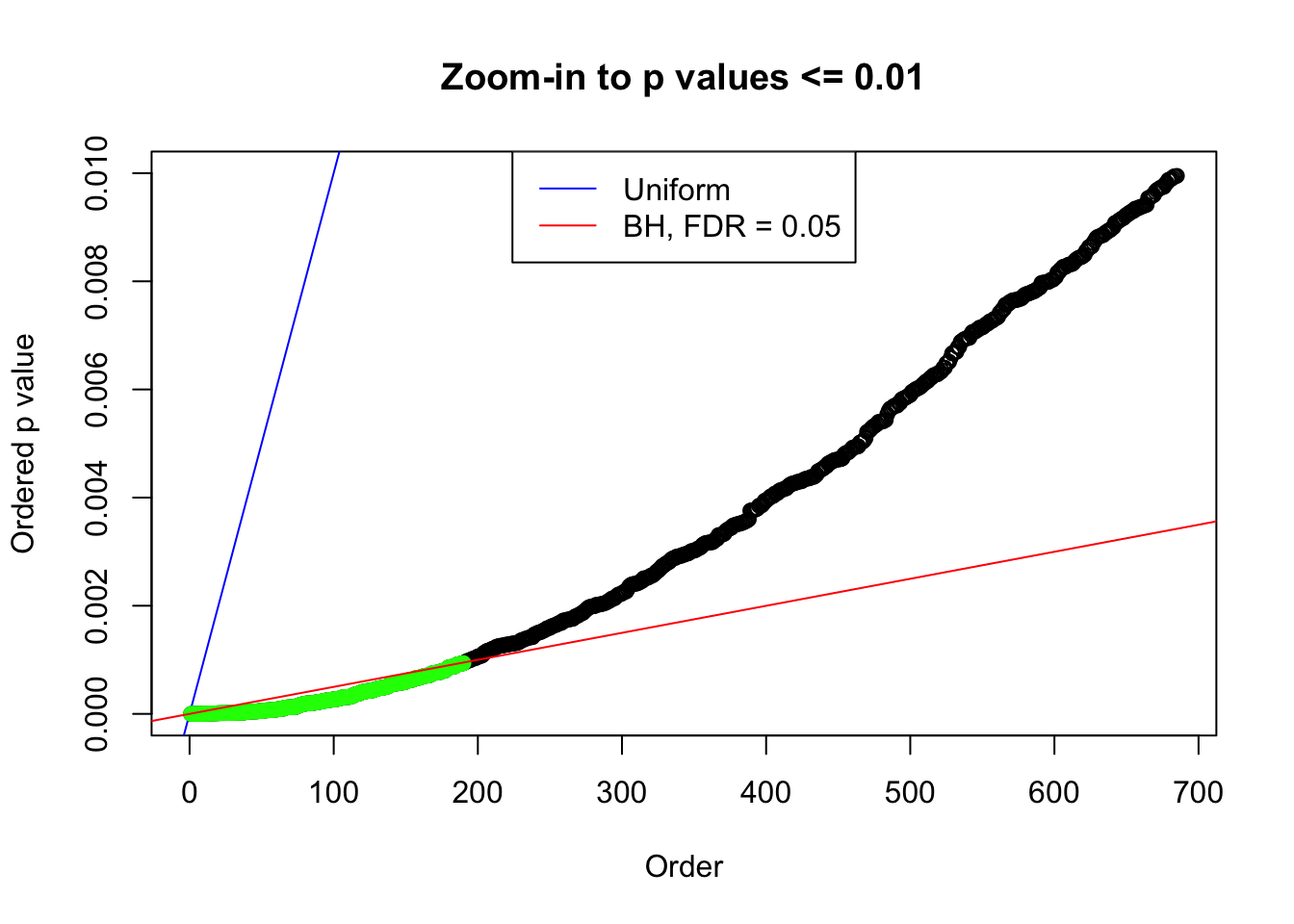
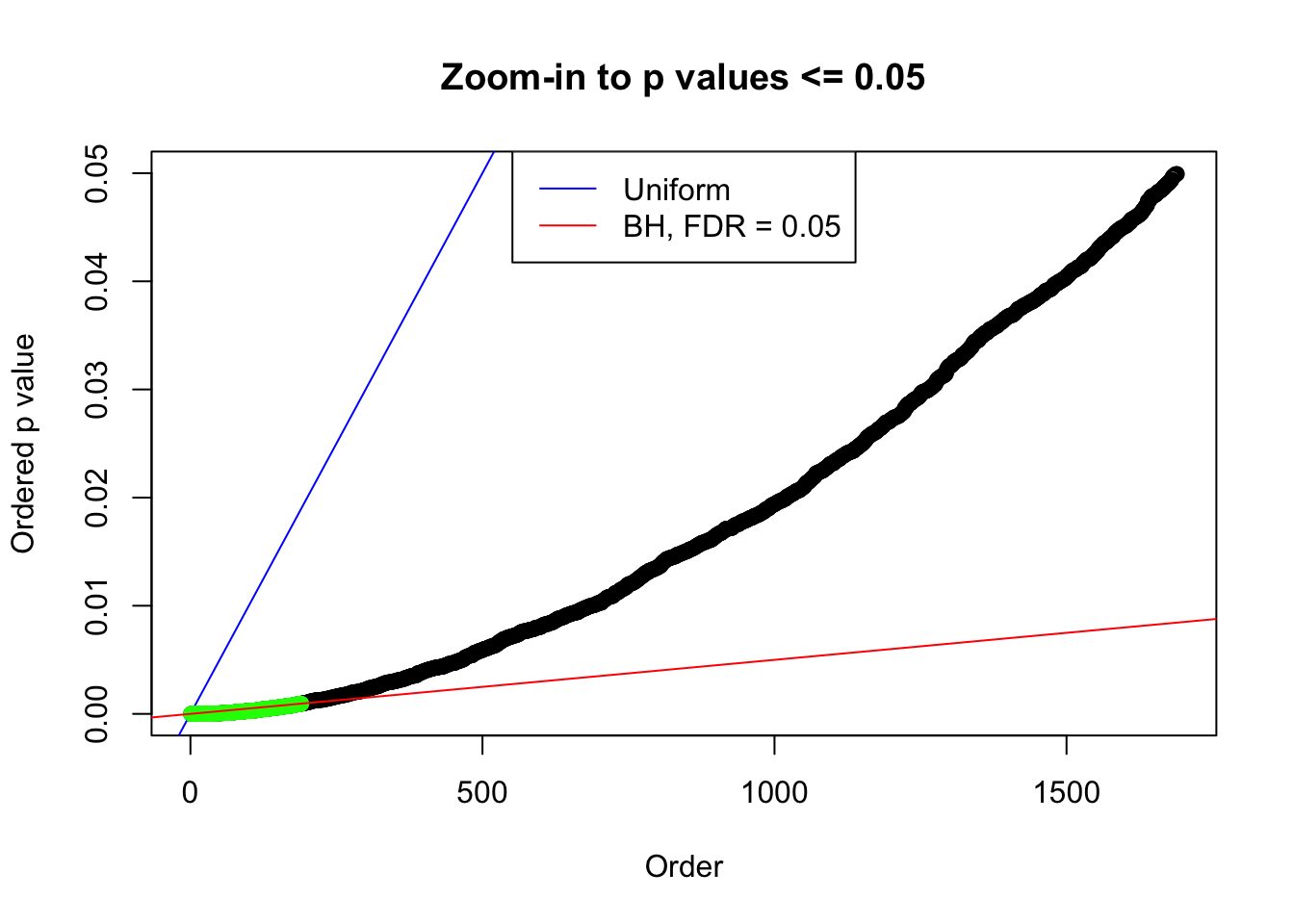
  bh.fd = sum(p.adjust(p, method = "BH") <= 0.05)
  pihat0.ash = get_pi0(ash(z, 1, method = "fdr"))
  ecdfz.fit = ecdfz.optimal(z)
  res[[i]] = list(z = z, p = p, bh.fd = bh.fd, pihat0.ash = pihat0.ash, ecdfz.fit = ecdfz.fit)
}

Number of Discoveries: 207 ; pihat0 = 0.3309512 
Log-likelihood with N(0, 2): -17629.27 
Log-likelihood with Gaussian Derivatives: -17634.06 
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 4.790331 
Normalized weights:
1 : -0.0177035771860527 ; 2 : 0.689887136368602 ; 3 : -0.0509478089605657 ; 4 : 0.474815572091947 ; 5 : -0.0255292356243276 ; 6 : 0.197260355735445 ; 7 : 0.0209642526780779 ;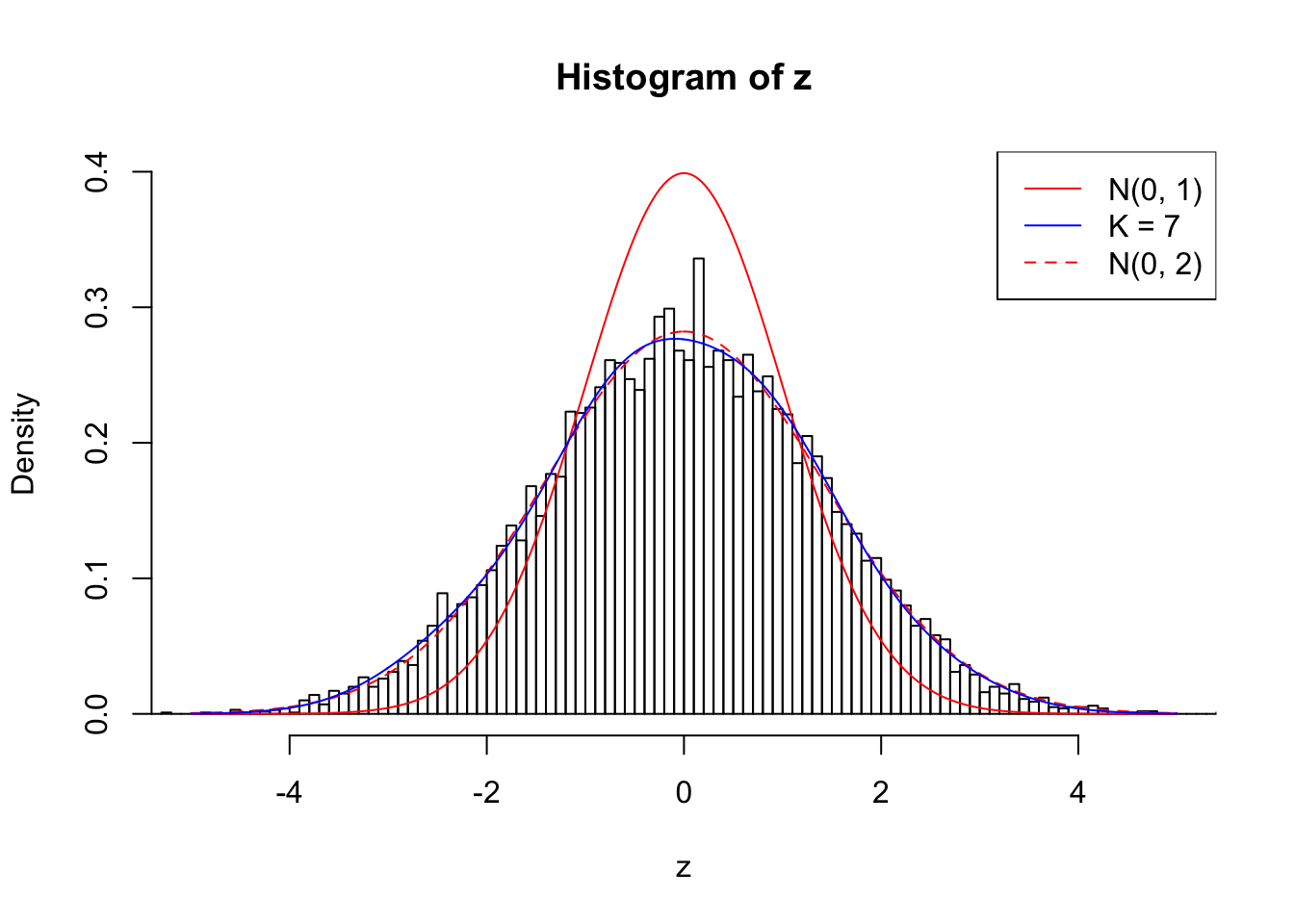

Zoom in to the right tails: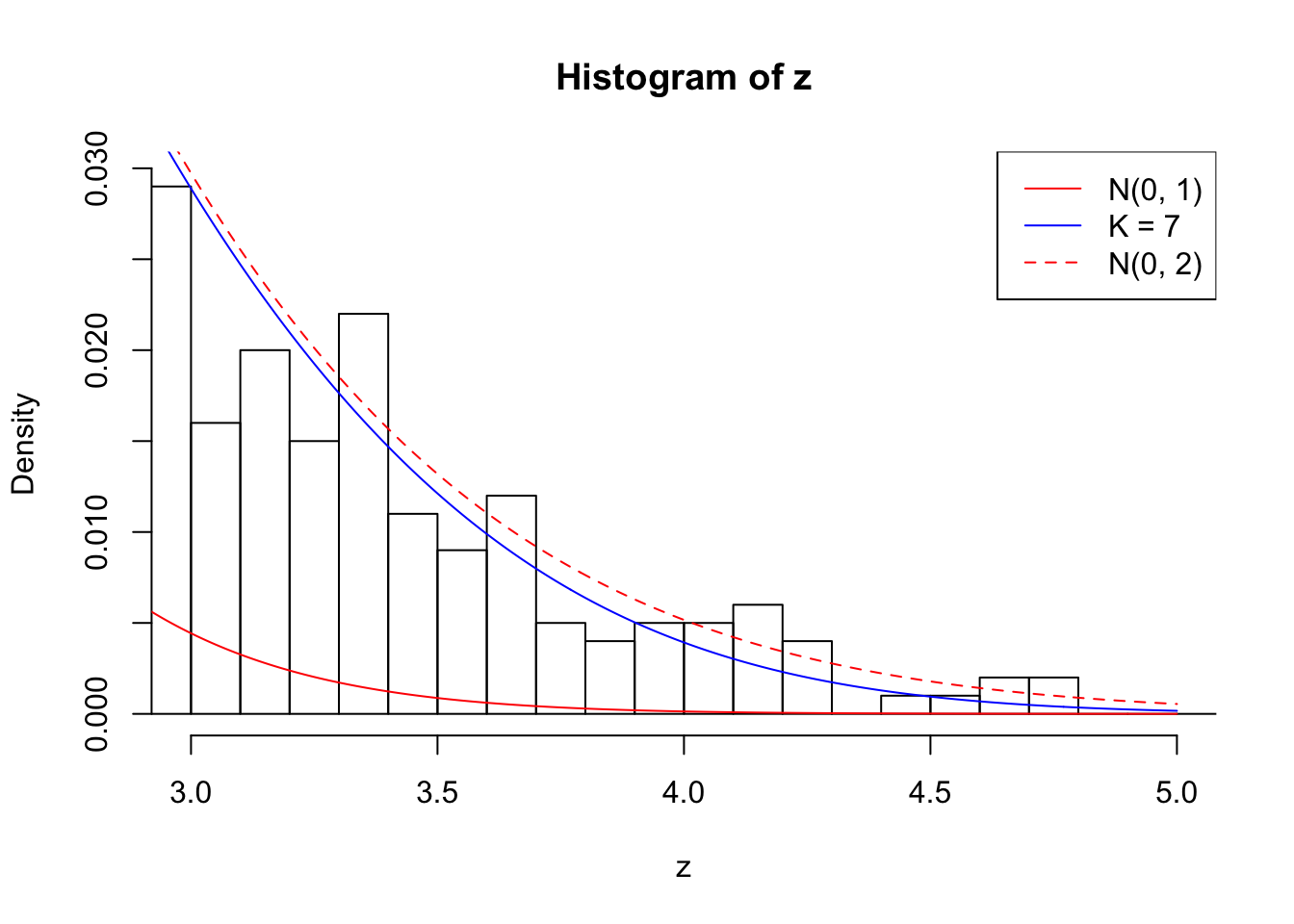

Zoom in to the left tails: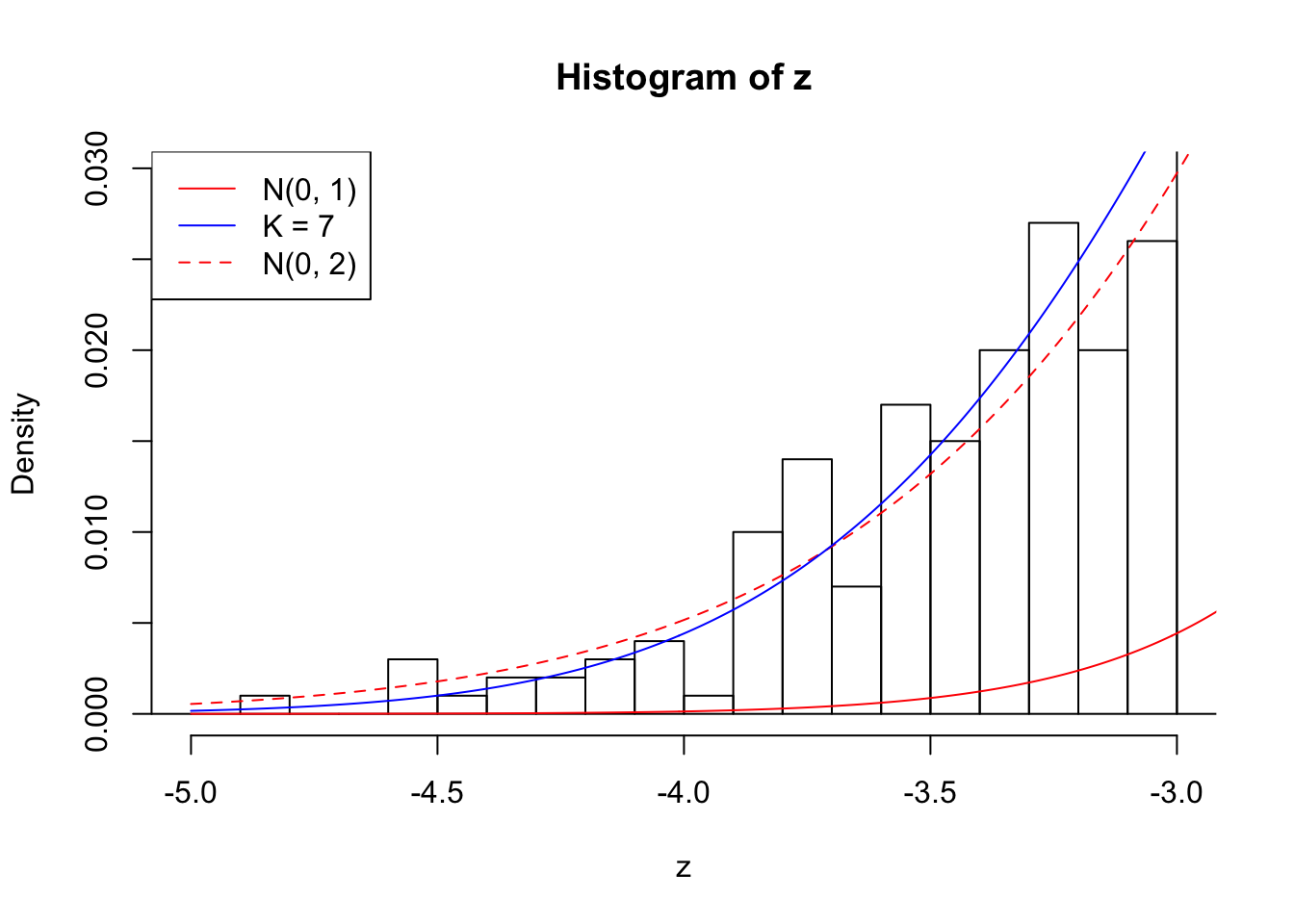

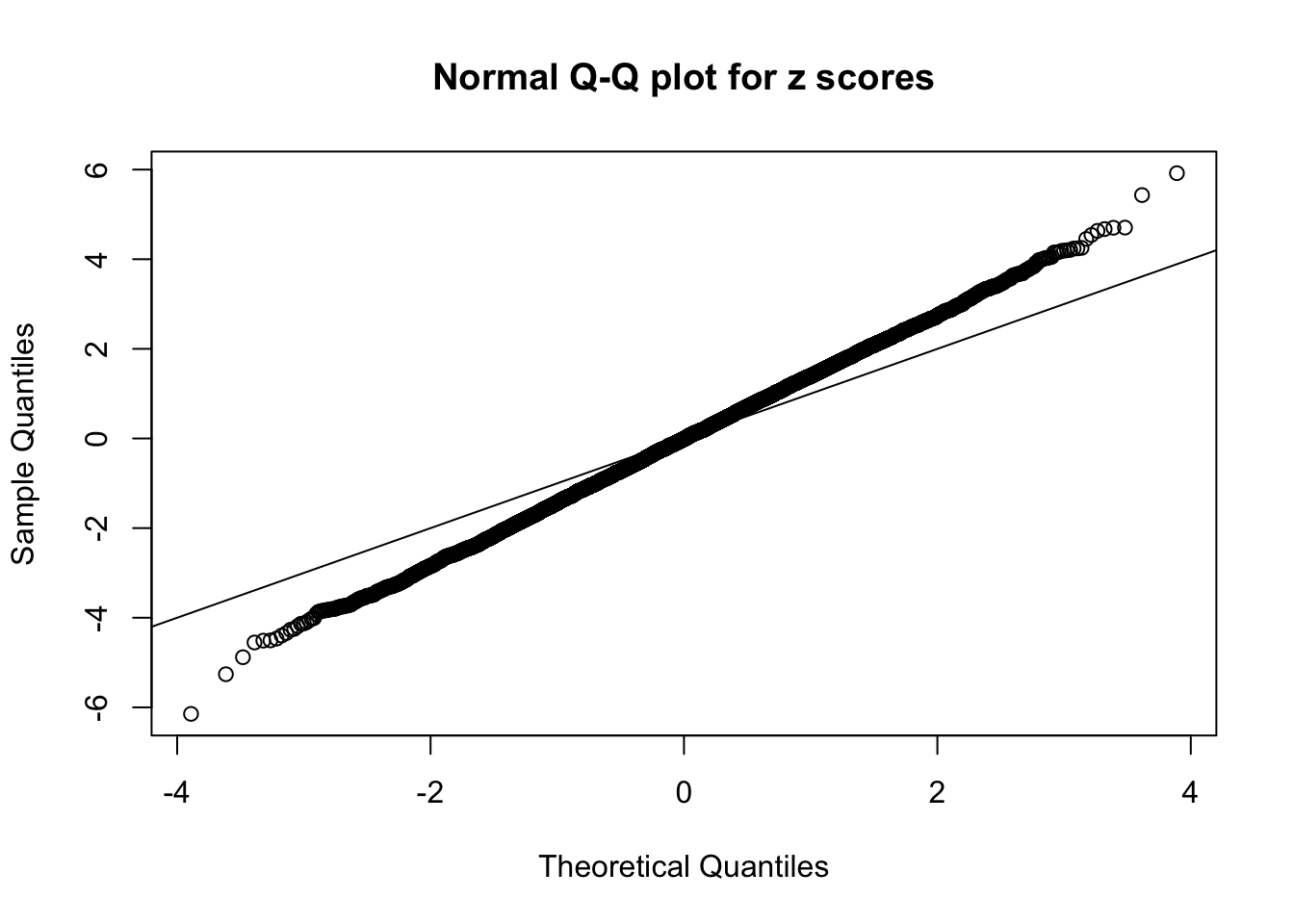
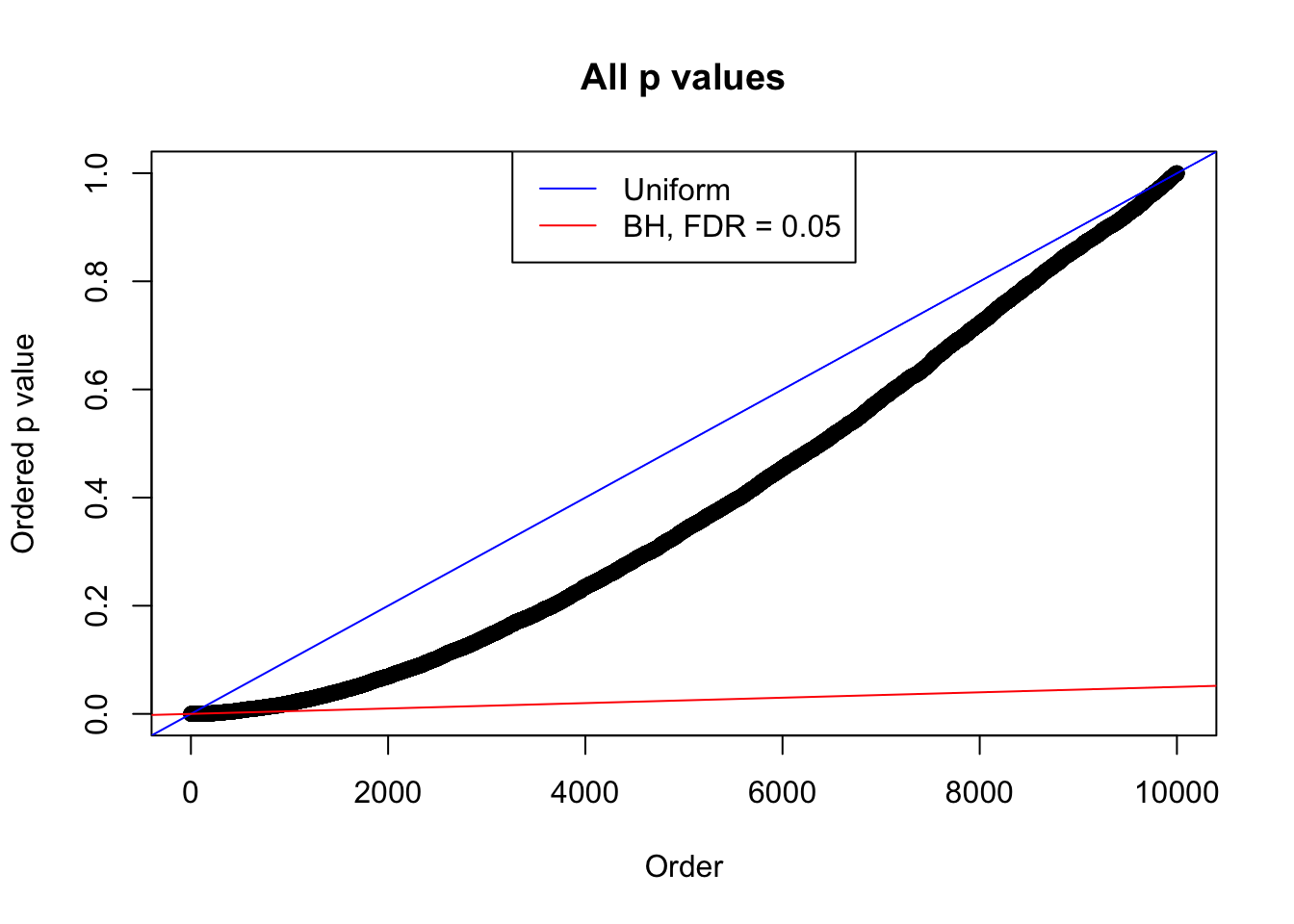
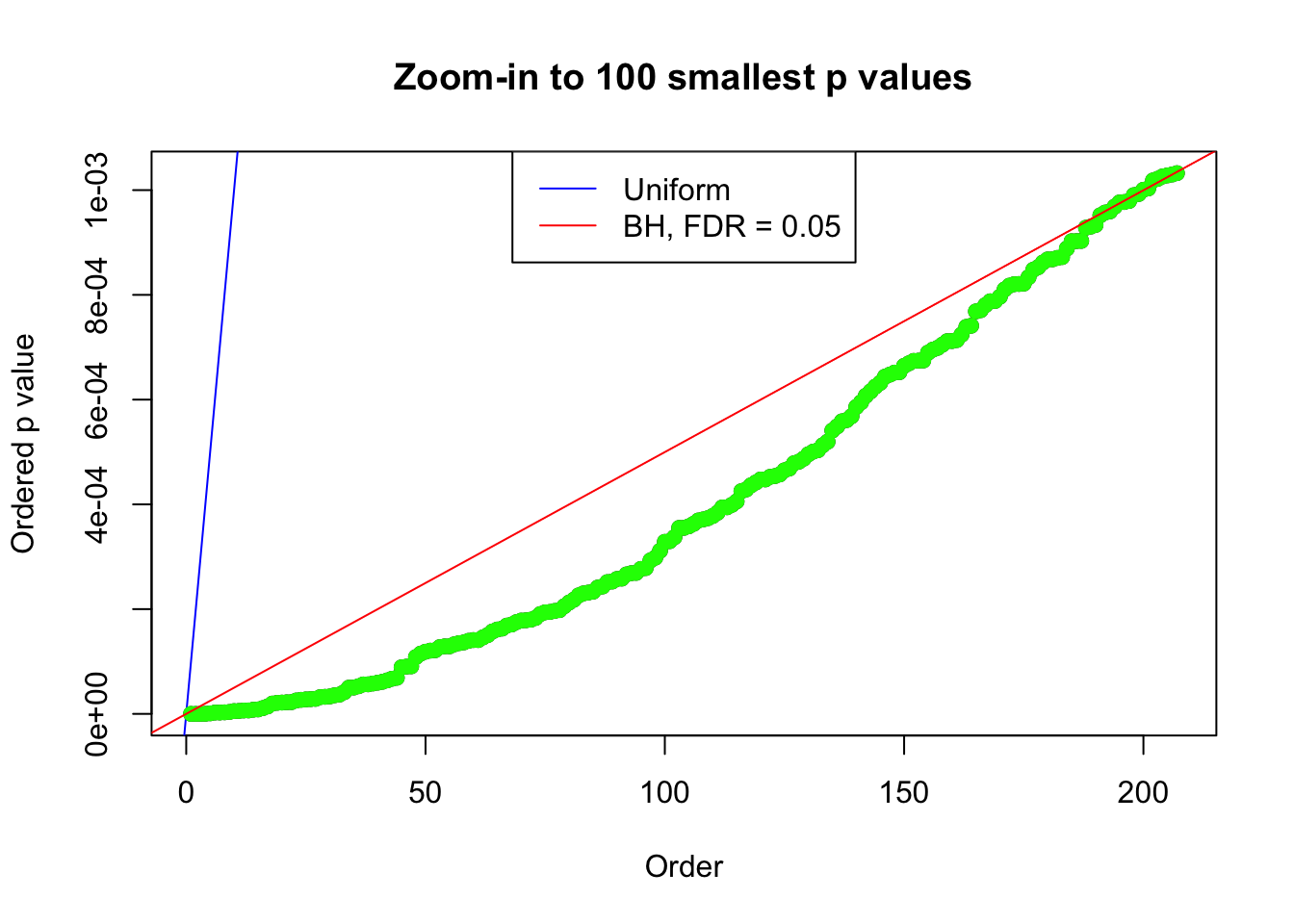
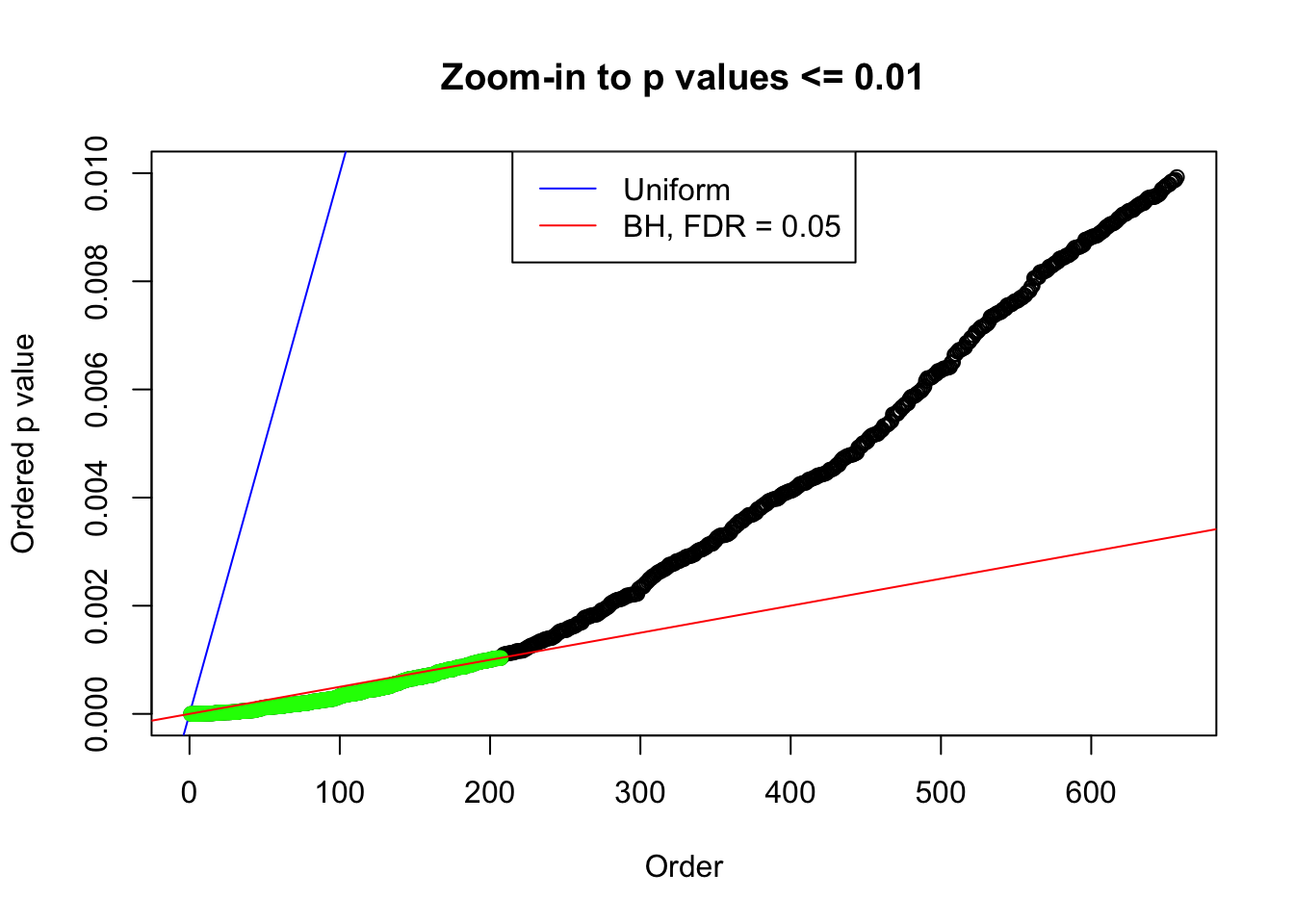
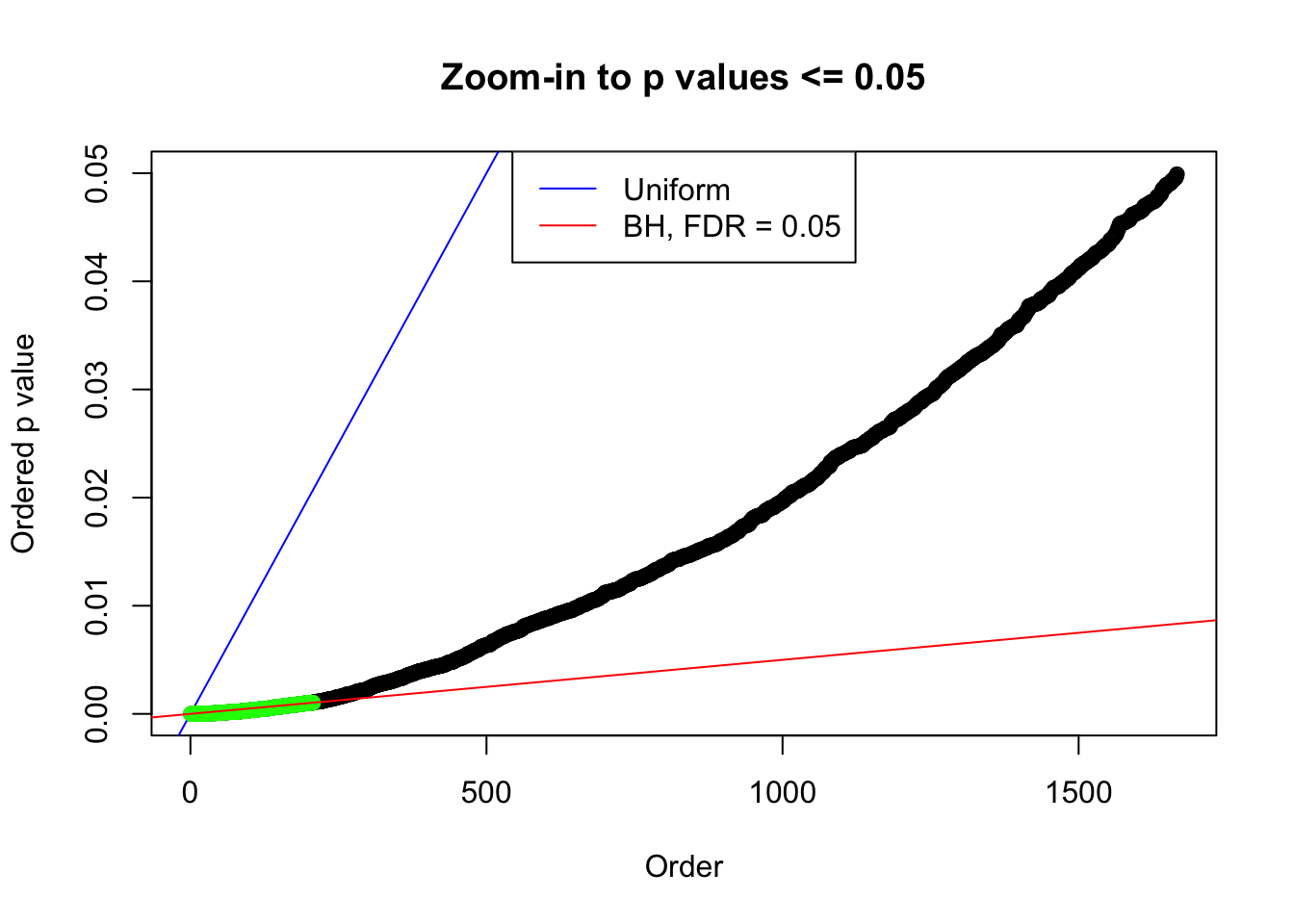
Number of Discoveries: 210 ; pihat0 = 0.3484933 
Log-likelihood with N(0, 2): -17695.54 
Log-likelihood with Gaussian Derivatives: -17691.84 
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: -3.698983 
Normalized weights:
1 : -0.00662167797406594 ; 2 : 0.716277504382886 ; 3 : -0.0310338589748257 ; 4 : 0.594319021051848 ; 5 : -0.00405607696274195 ; 6 : 0.364148970093227 ; 7 : 0.0347791611900783 ; 8 : 0.0862488827136366 ;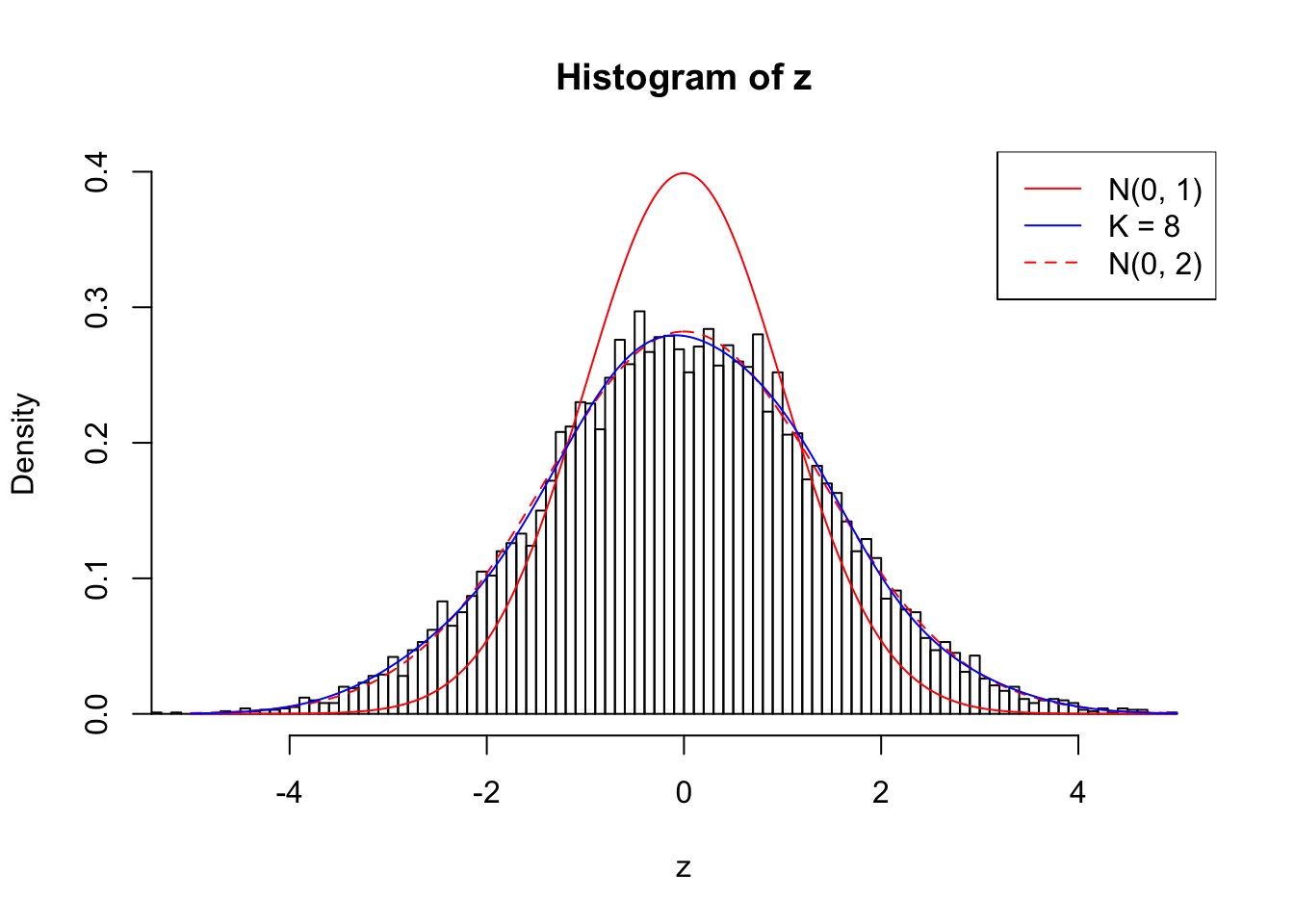

Zoom in to the right tails: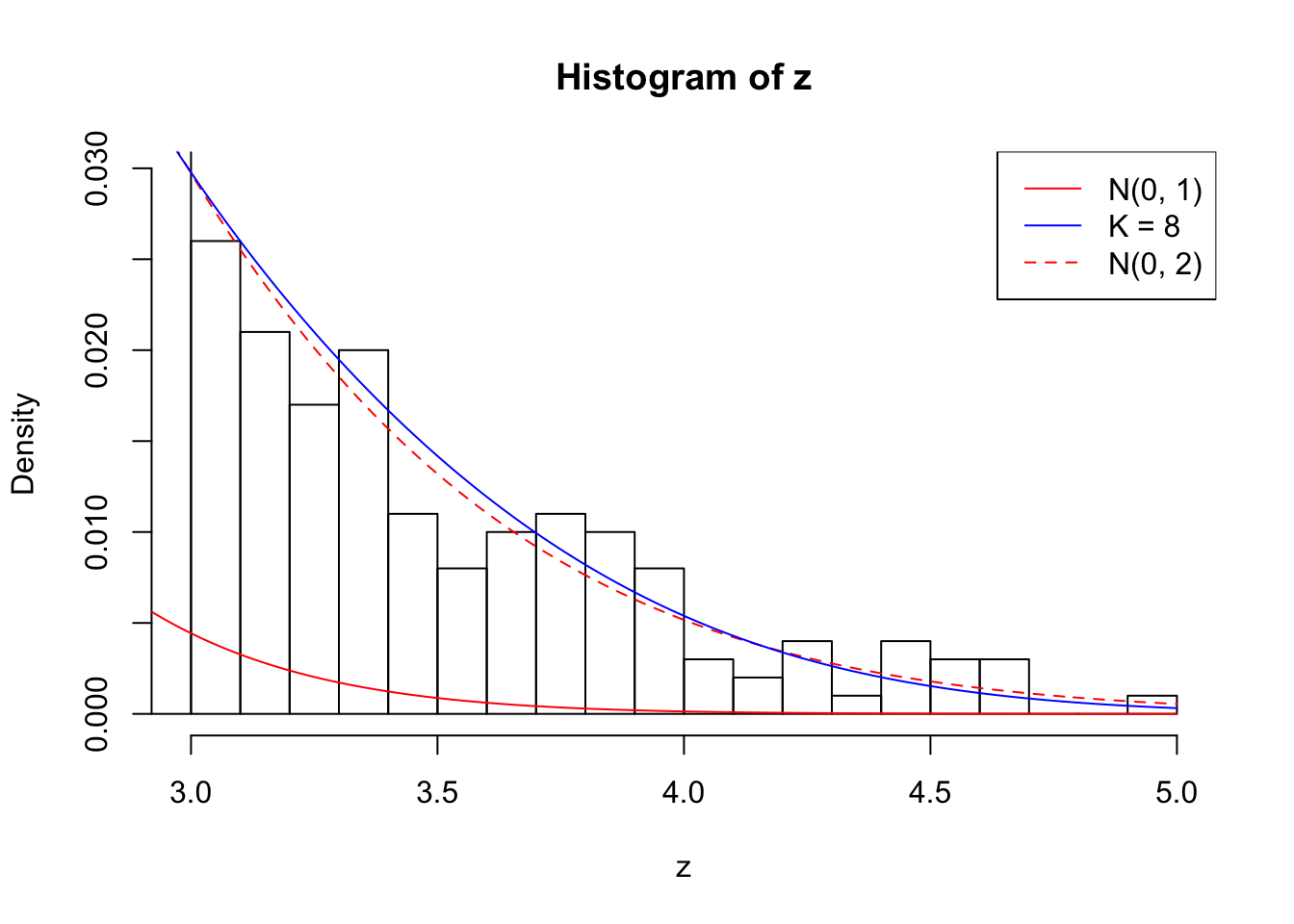

Zoom in to the left tails: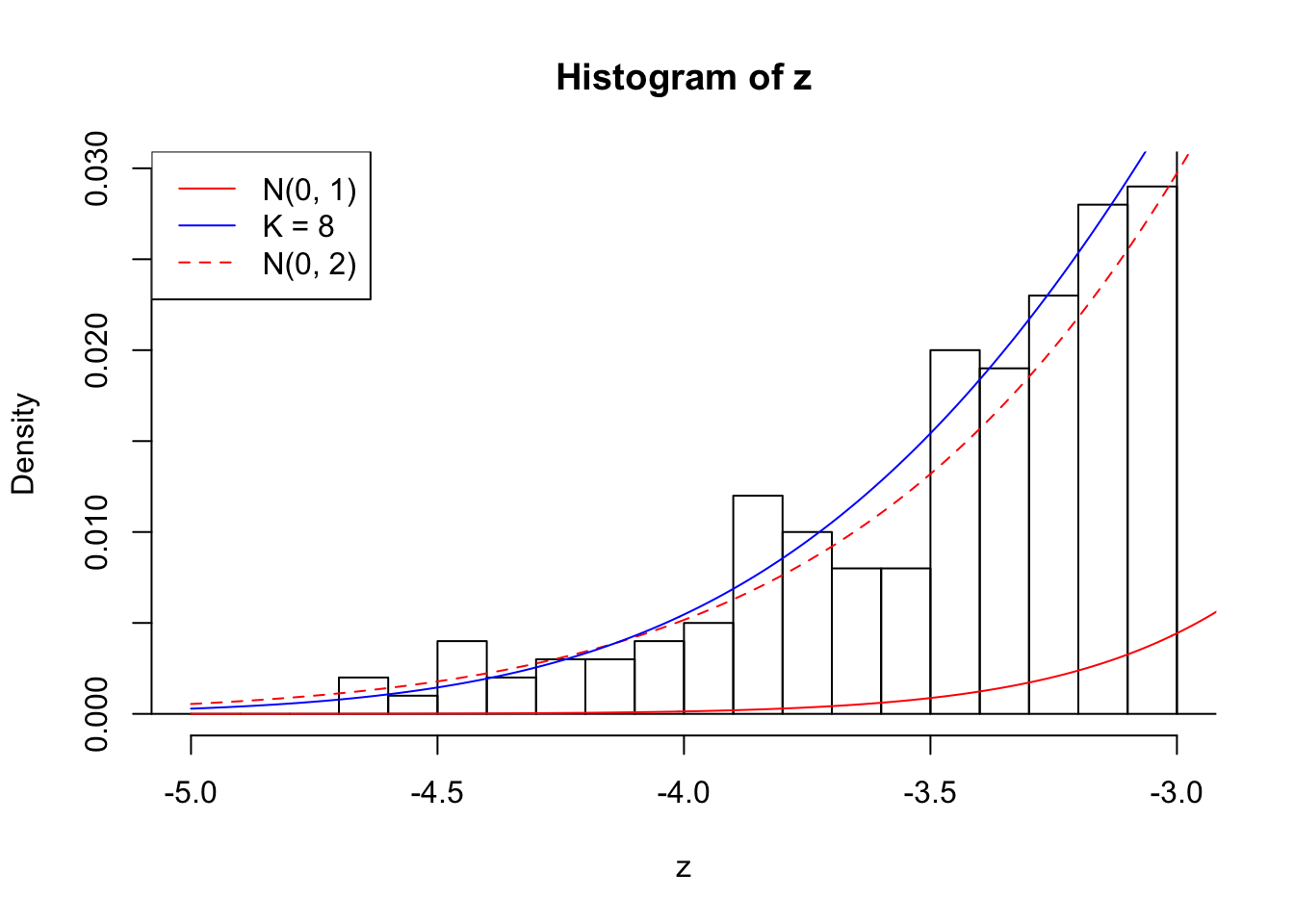

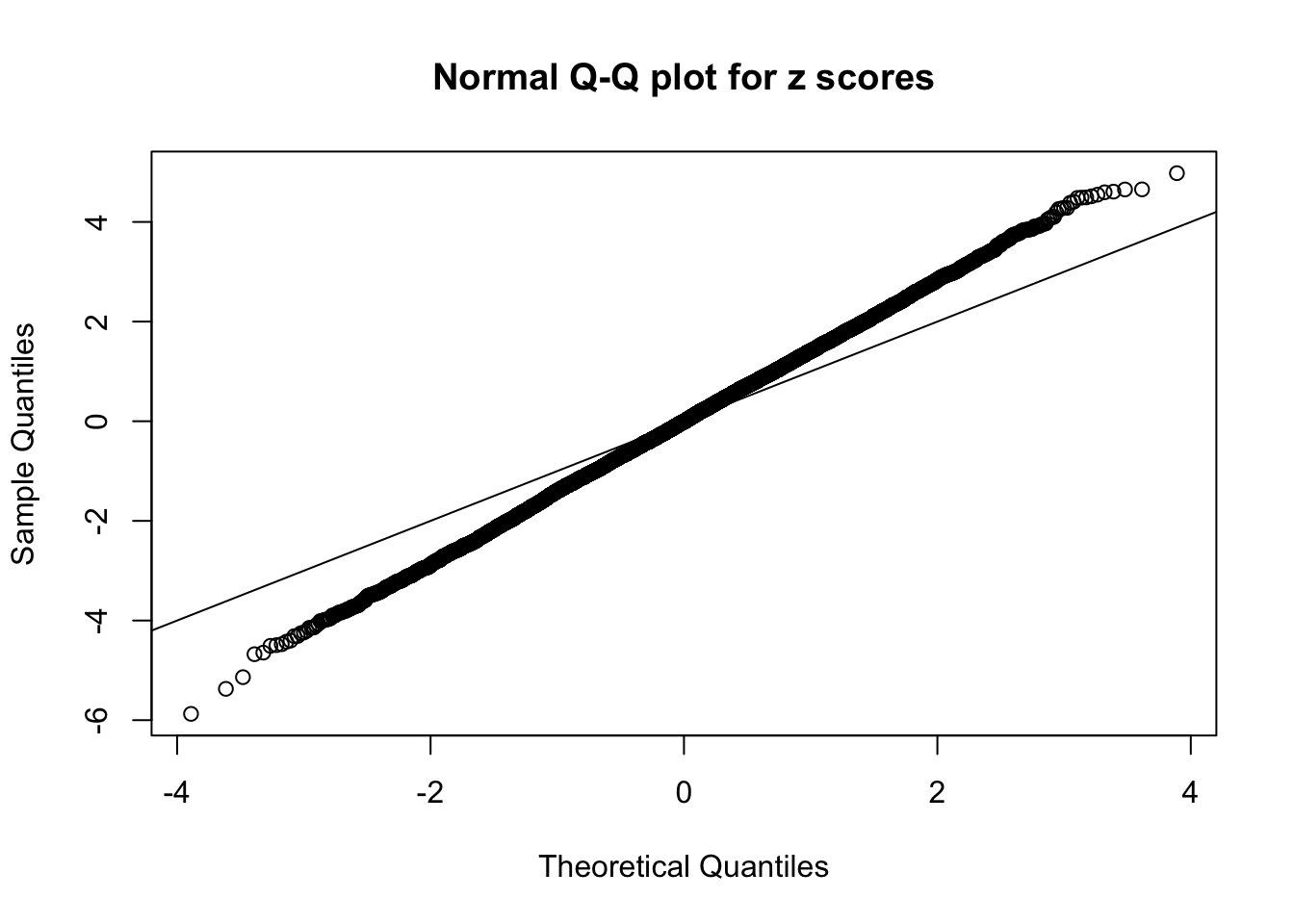
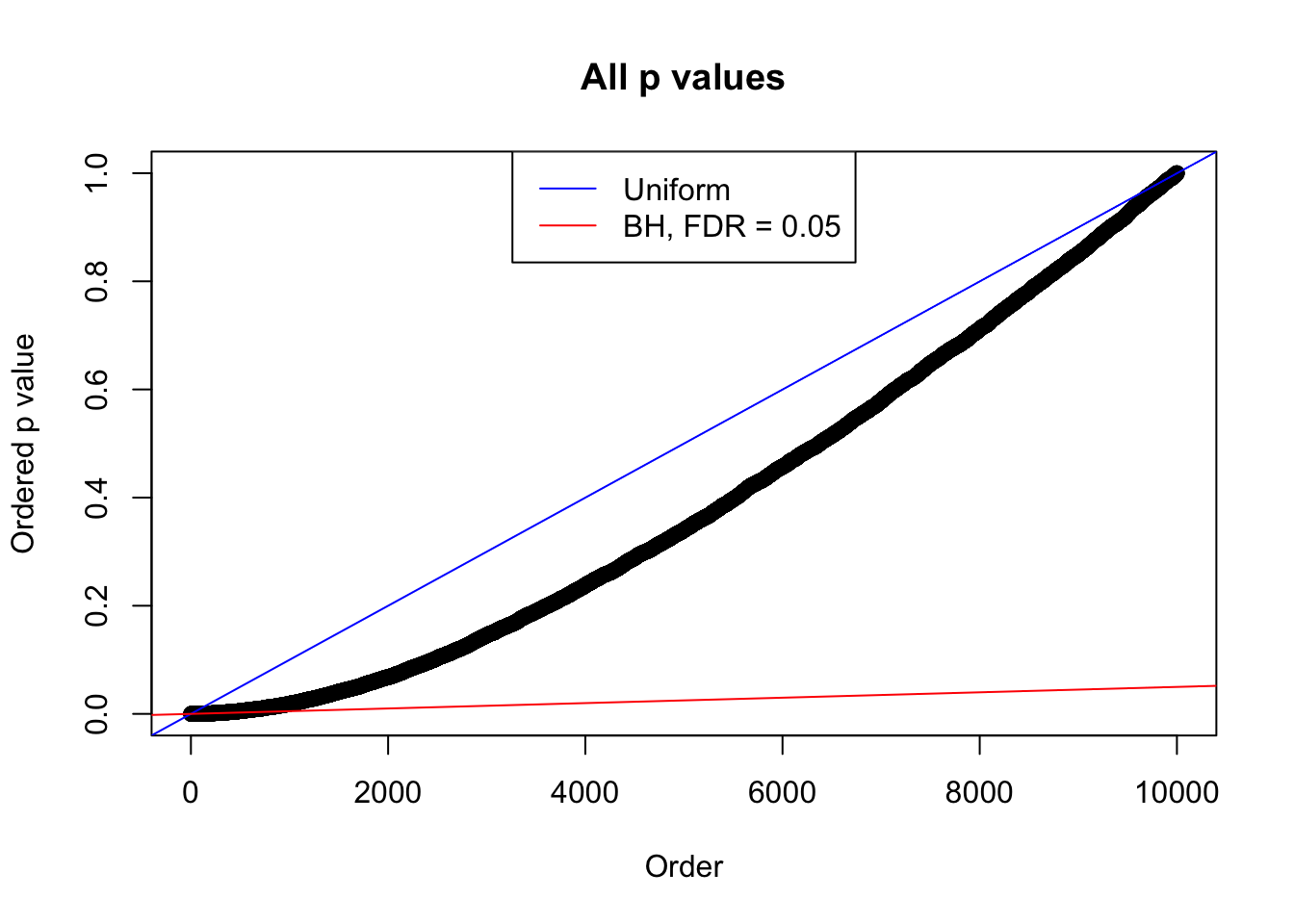
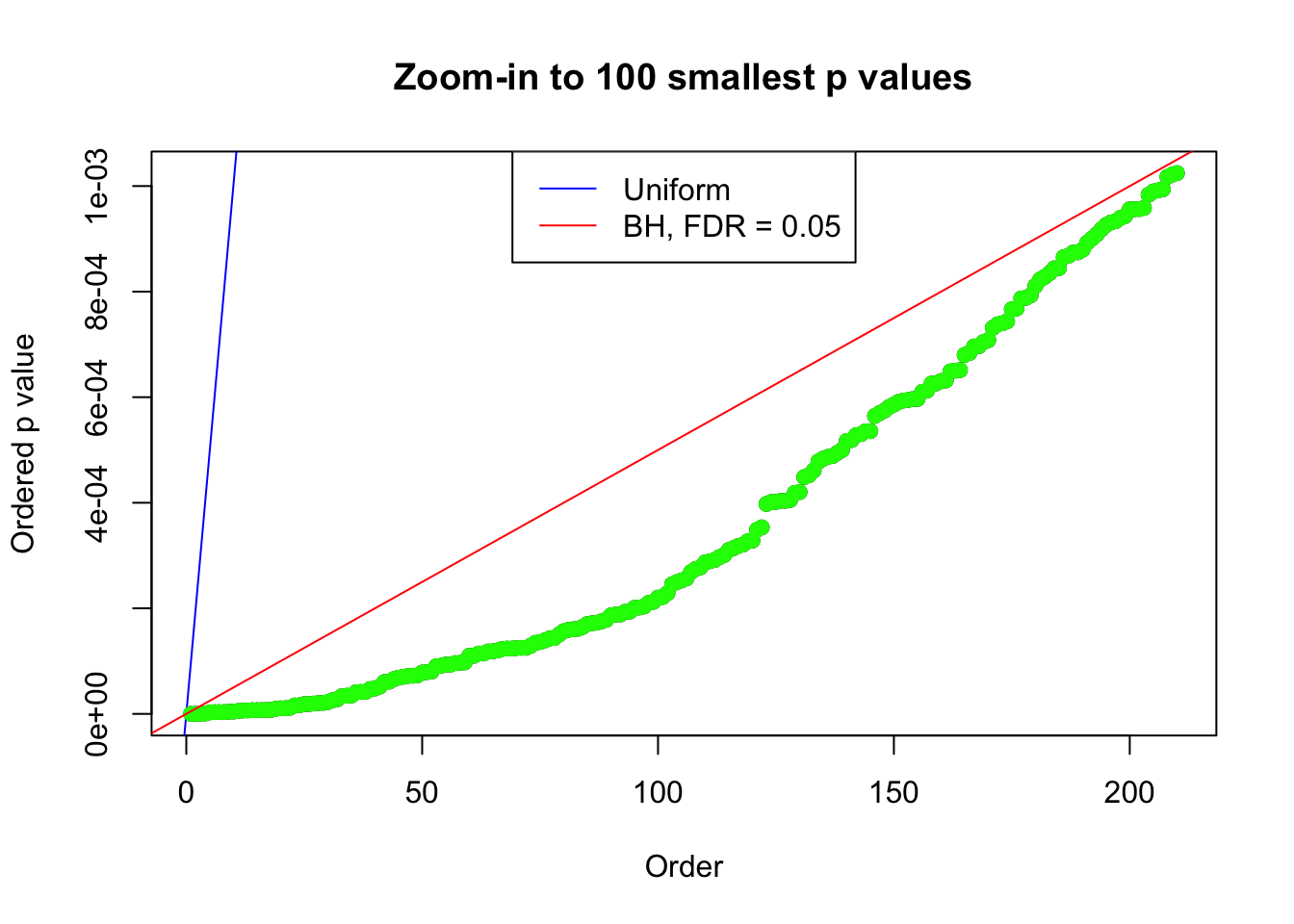
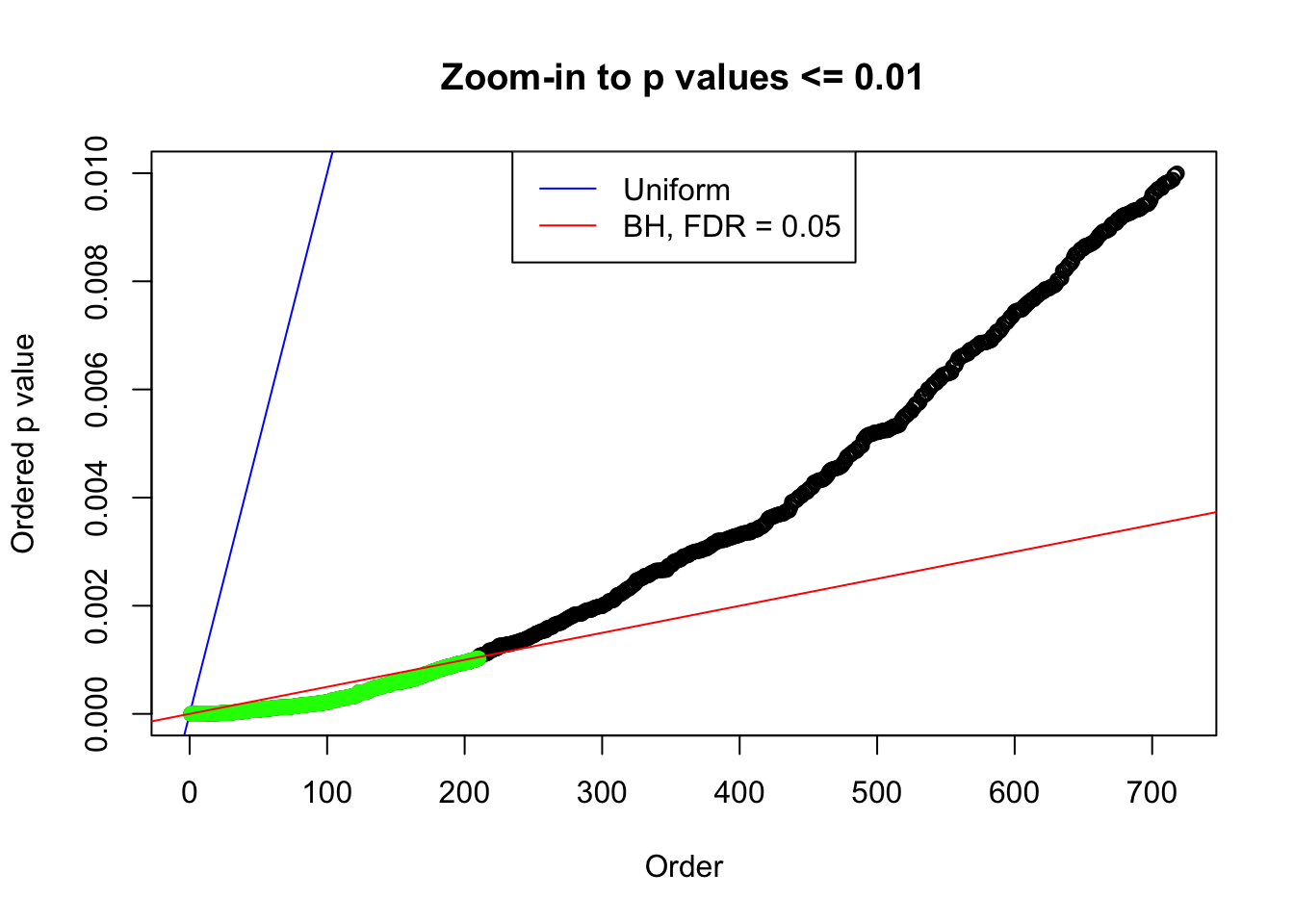
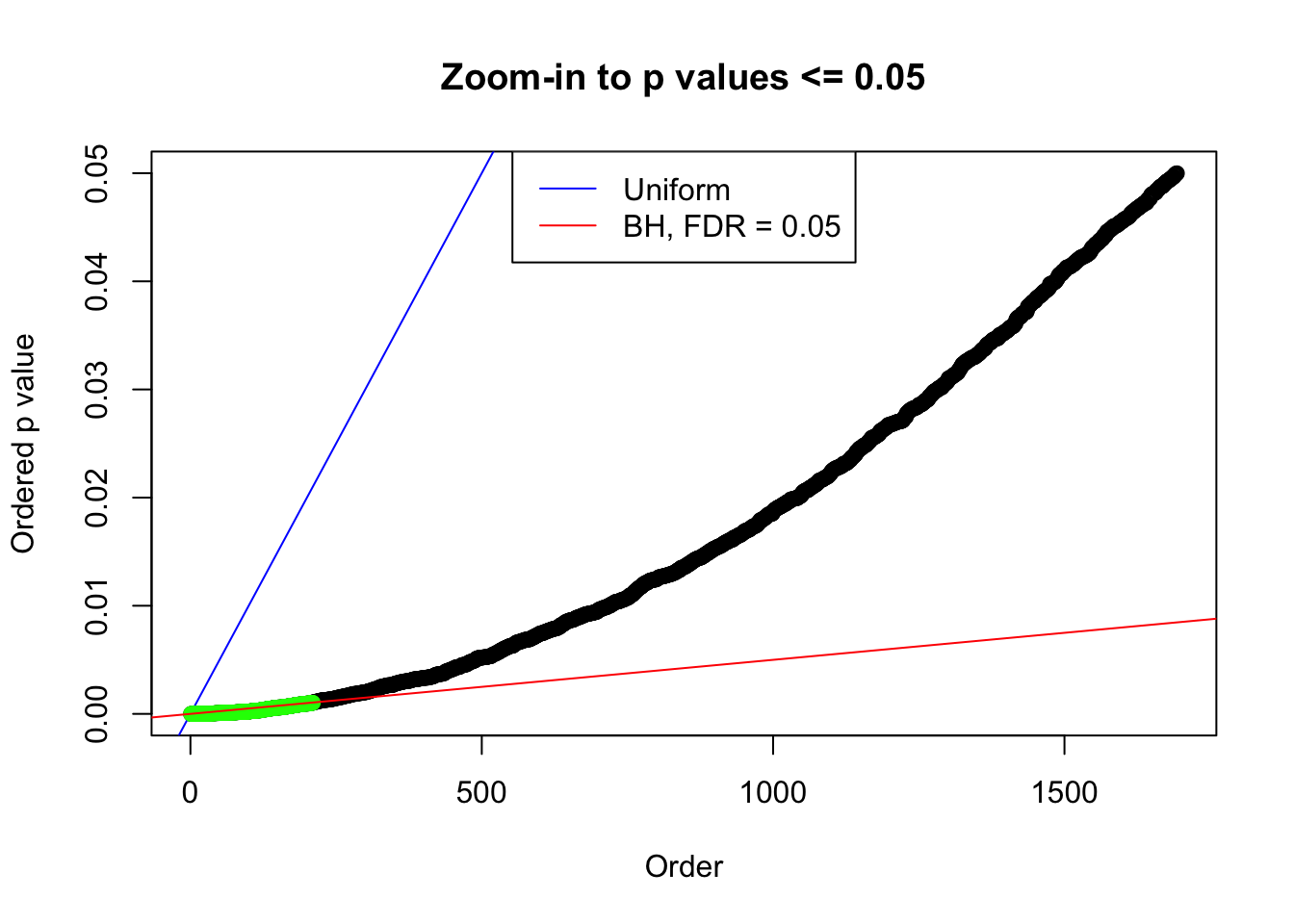
Number of Discoveries: 190 ; pihat0 = 0.3438938 
Log-likelihood with N(0, 2): -17620.41 
Log-likelihood with Gaussian Derivatives: -17620.47 
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 0.05853415 
Normalized weights:
1 : 0.00412988146644346 ; 2 : 0.691757356275142 ; 3 : 0.0624186506260473 ; 4 : 0.566017599686127 ; 5 : 0.0720236790272216 ; 6 : 0.359005476183793 ; 7 : 0.0491535934289797 ; 8 : 0.11765212650001 ;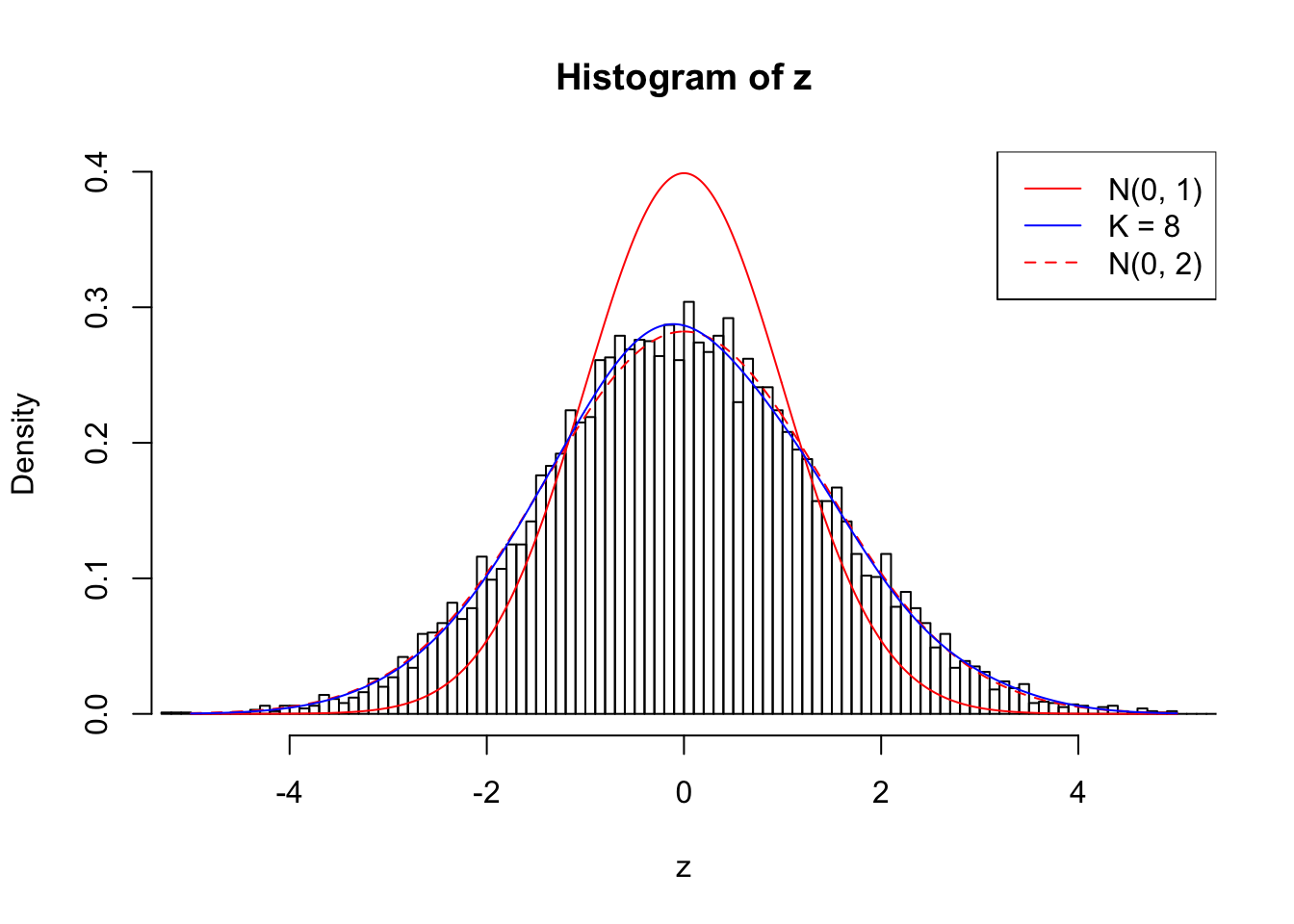

Zoom in to the right tails: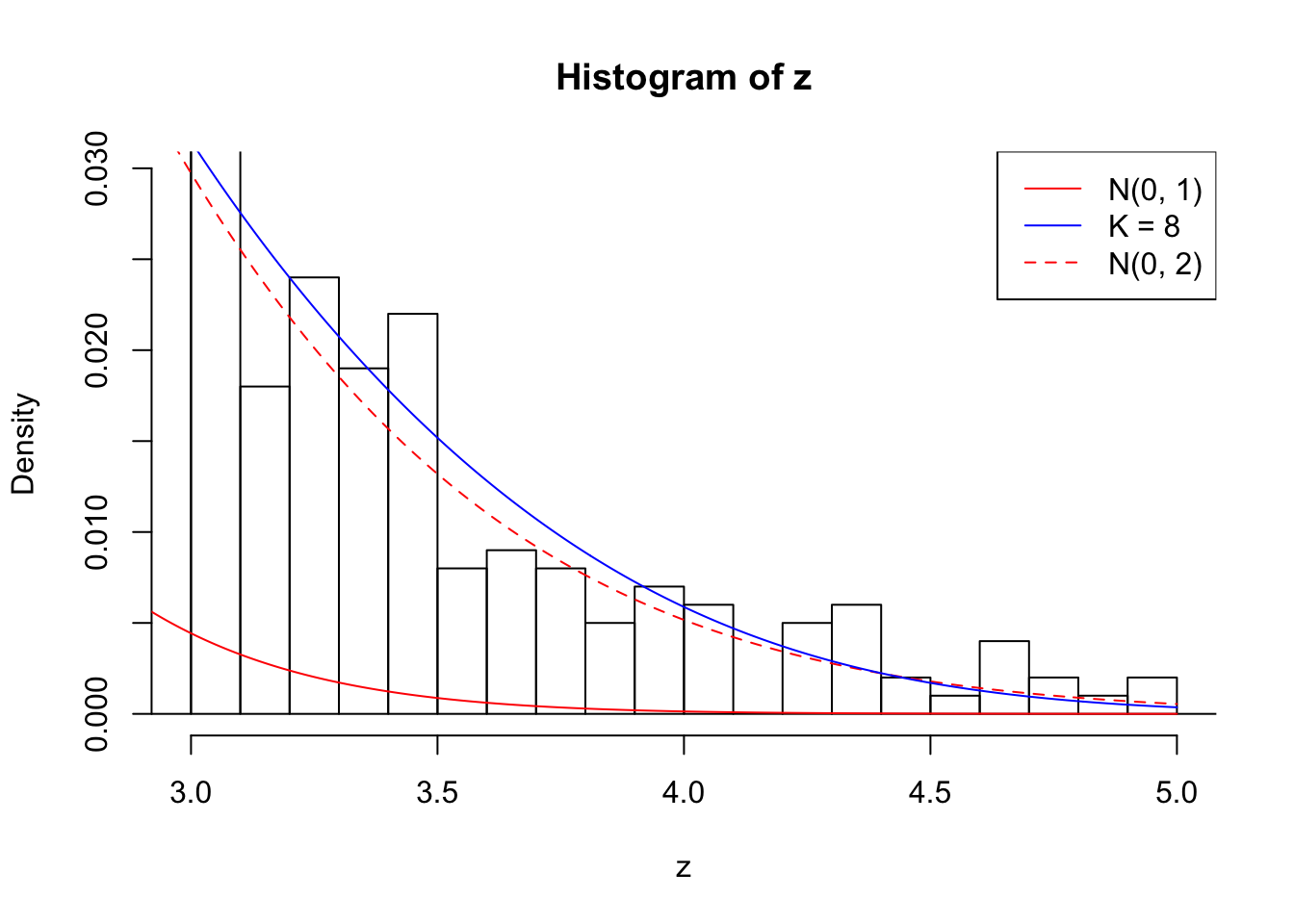

Zoom in to the left tails: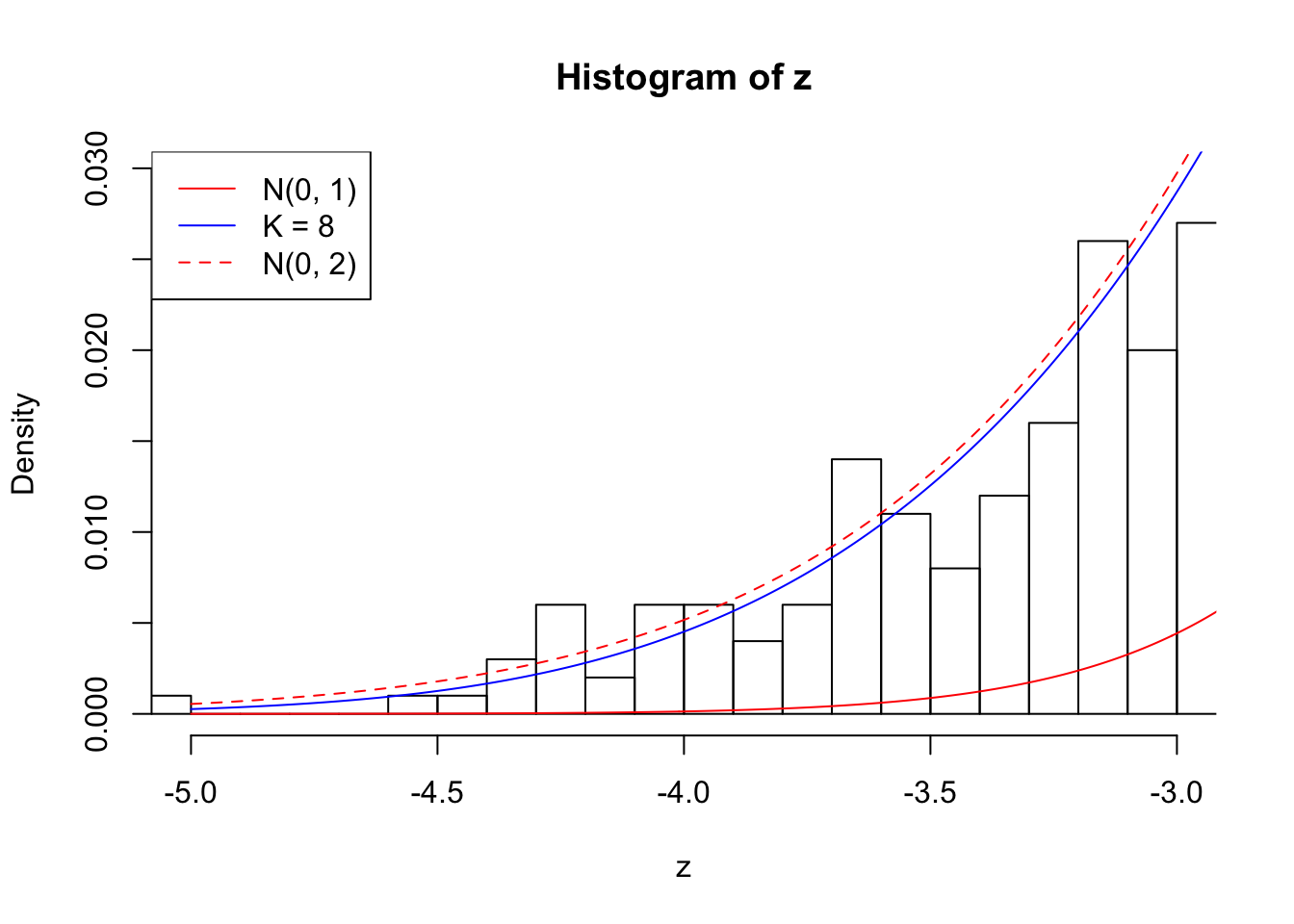

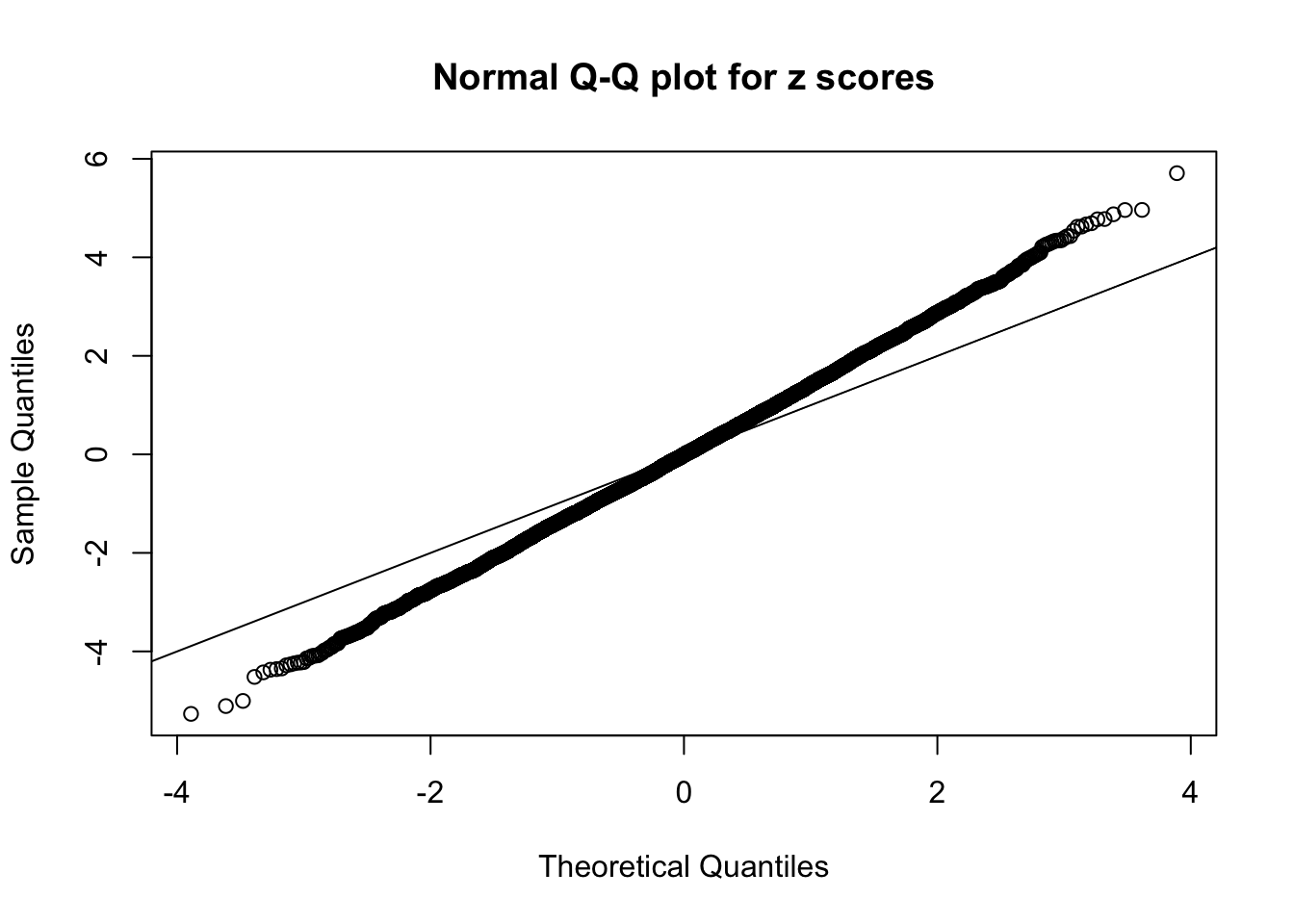
Session information

sessionInfo()

R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.3

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] cvxr_0.0.0.9009 EQL_1.0-0       ttutils_1.0-1   ashr_2.1.5     

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.10      knitr_1.15.1      magrittr_1.5     
 [4] MASS_7.3-45       doParallel_1.0.10 pscl_1.4.9       
 [7] SQUAREM_2016.10-1 lattice_0.20-34   foreach_1.4.3    
[10] stringr_1.1.0     tools_3.3.2       parallel_3.3.2   
[13] grid_3.3.2        htmltools_0.3.5   iterators_1.0.8  
[16] yaml_2.1.14       rprojroot_1.2     digest_0.6.9     
[19] Matrix_1.2-7.1    codetools_0.2-15  evaluate_0.10    
[22] rmarkdown_1.3     stringi_1.1.2     backports_1.0.5  
[25] truncnorm_1.0-7