True Signal vs Correlated Null: Larger Effects
Lei Sun
2017-03-30
Last updated: 2017-03-31
Code version: 6675cff
n = 1e4
m = 5
set.seed(777)
SNR = 10
z.sd = sqrt(10^(SNR / 10) + 1)
zmat = matrix(rnorm(n * m, 0, sd = z.sd), nrow = m, byrow = TRUE)library(ashr)
source("../code/ecdfz.R")
res = list()
for (i in 1:m) {
z = zmat[i, ]
p = (1 - pnorm(abs(z))) * 2
bh.fd = sum(p.adjust(p, method = "BH") <= 0.05)
pihat0.ash = get_pi0(ash(z, 1, method = "fdr"))
ecdfz.fit = ecdfz.optimal(z)
res[[i]] = list(z = z, p = p, bh.fd = bh.fd, pihat0.ash = pihat0.ash, ecdfz.fit = ecdfz.fit)
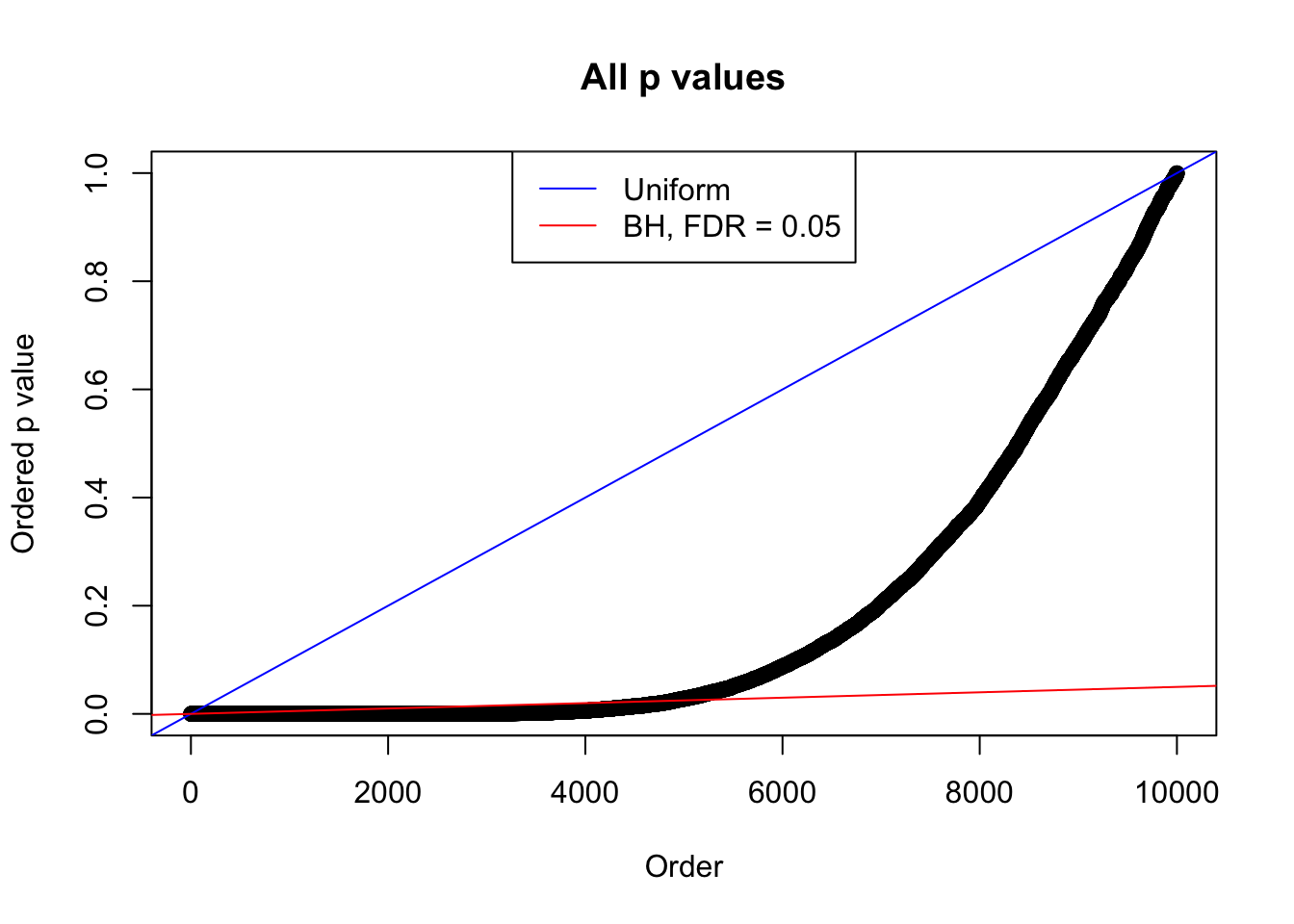
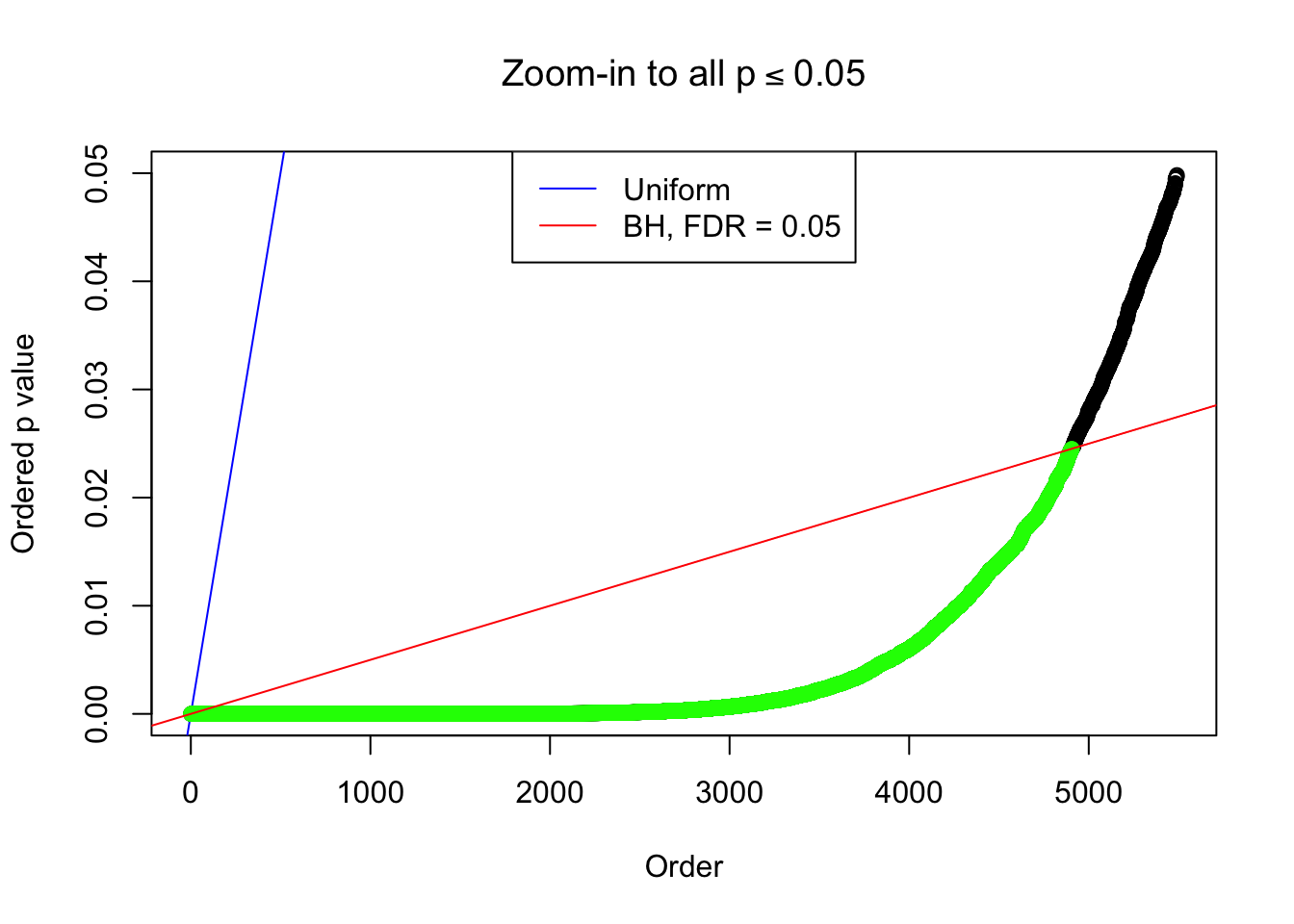
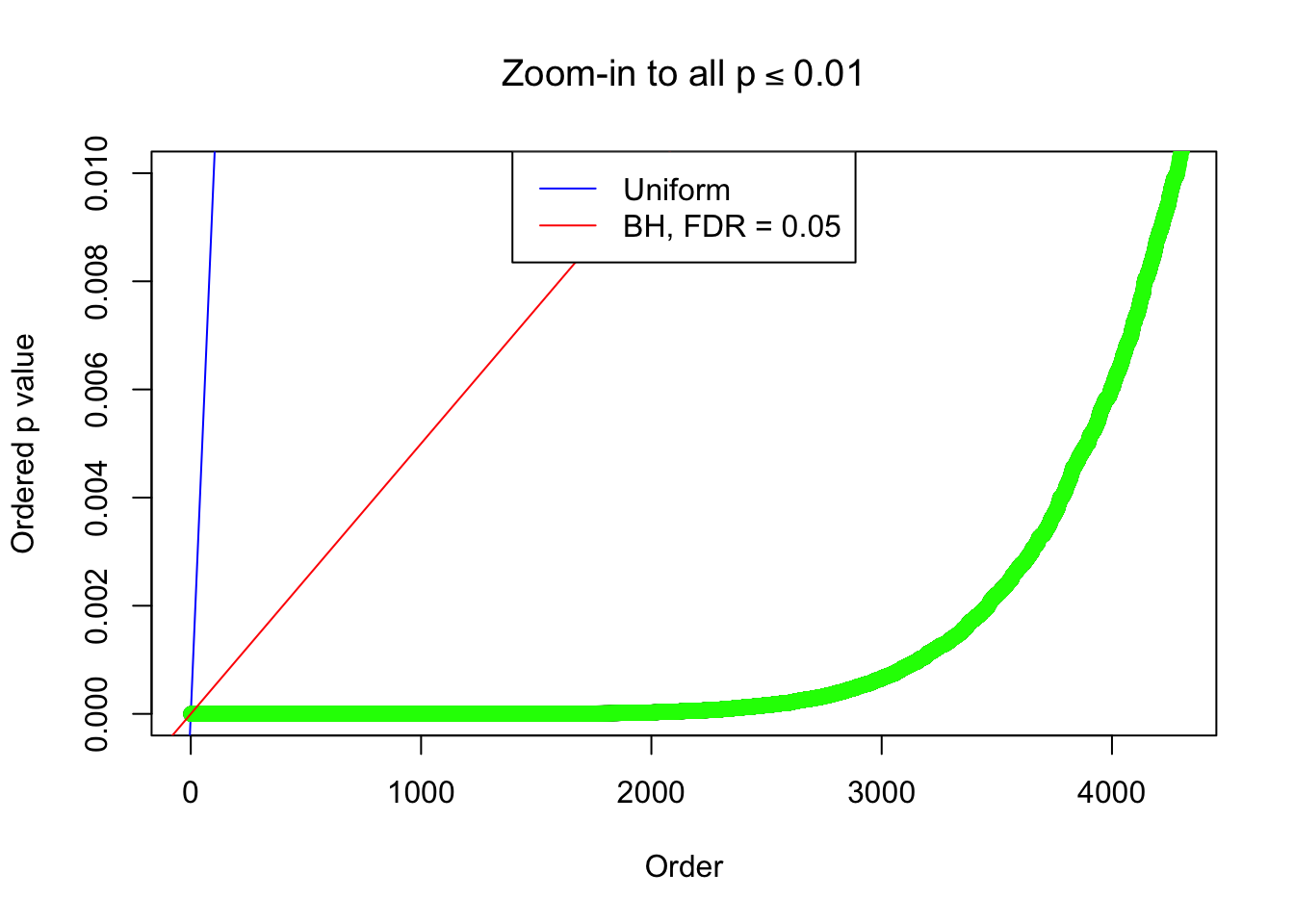
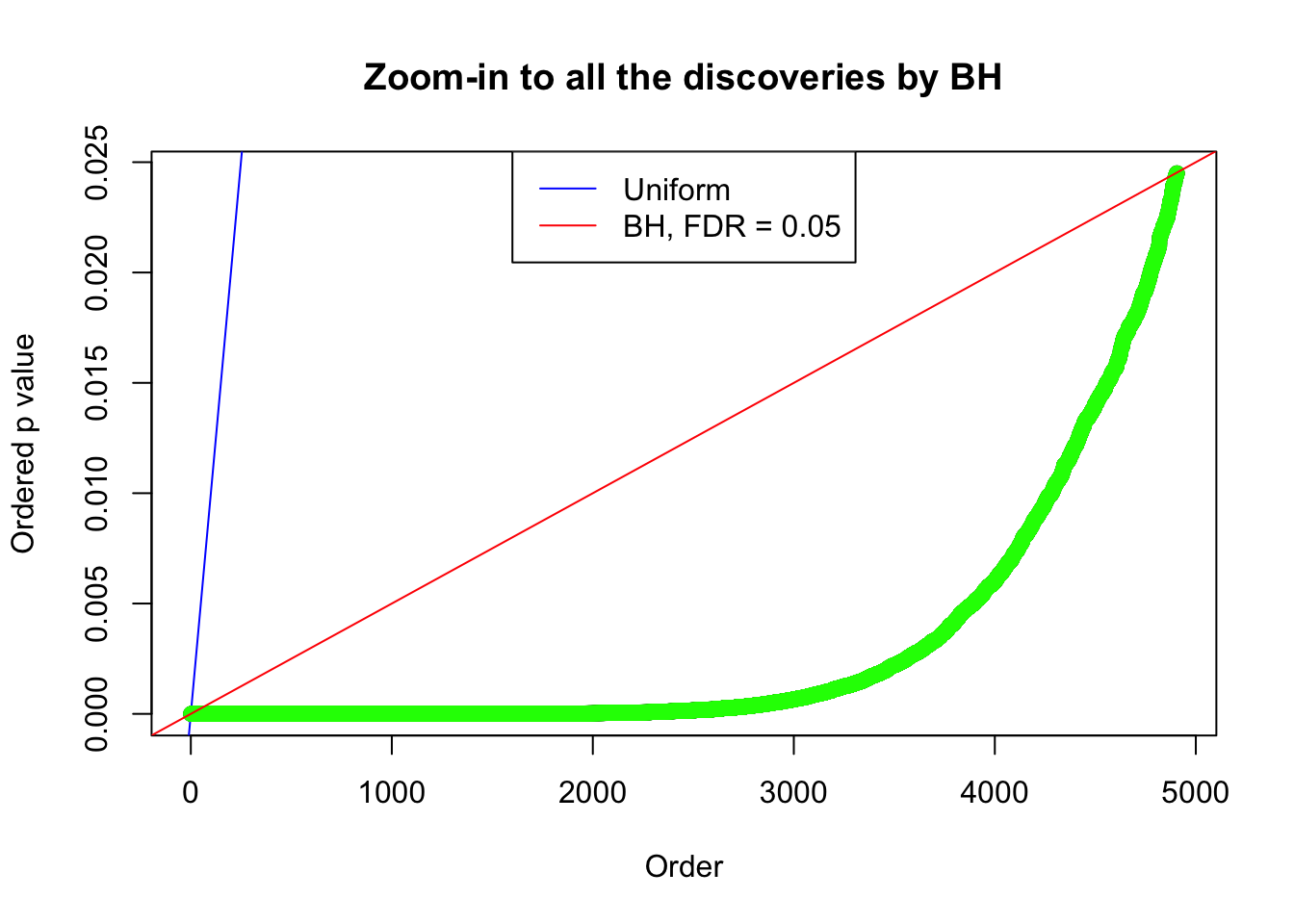
}Example 1 : True Distribution: N(0, 11 ); Number of Discoveries: 4977 ; pihat0 = 0.06823293
Log-likelihood with N(0, 2): -40427.36
Log-likelihood with Gaussian Derivatives: -44630.56
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 4203.197
Normalized weights:
1 : -0.00382730748165912 ; 2 : 2.22406852311656 ; 3 : -0.00951101006644363 ; 4 : 1.8299655755807 ; 5 : -0.015346138215793 ;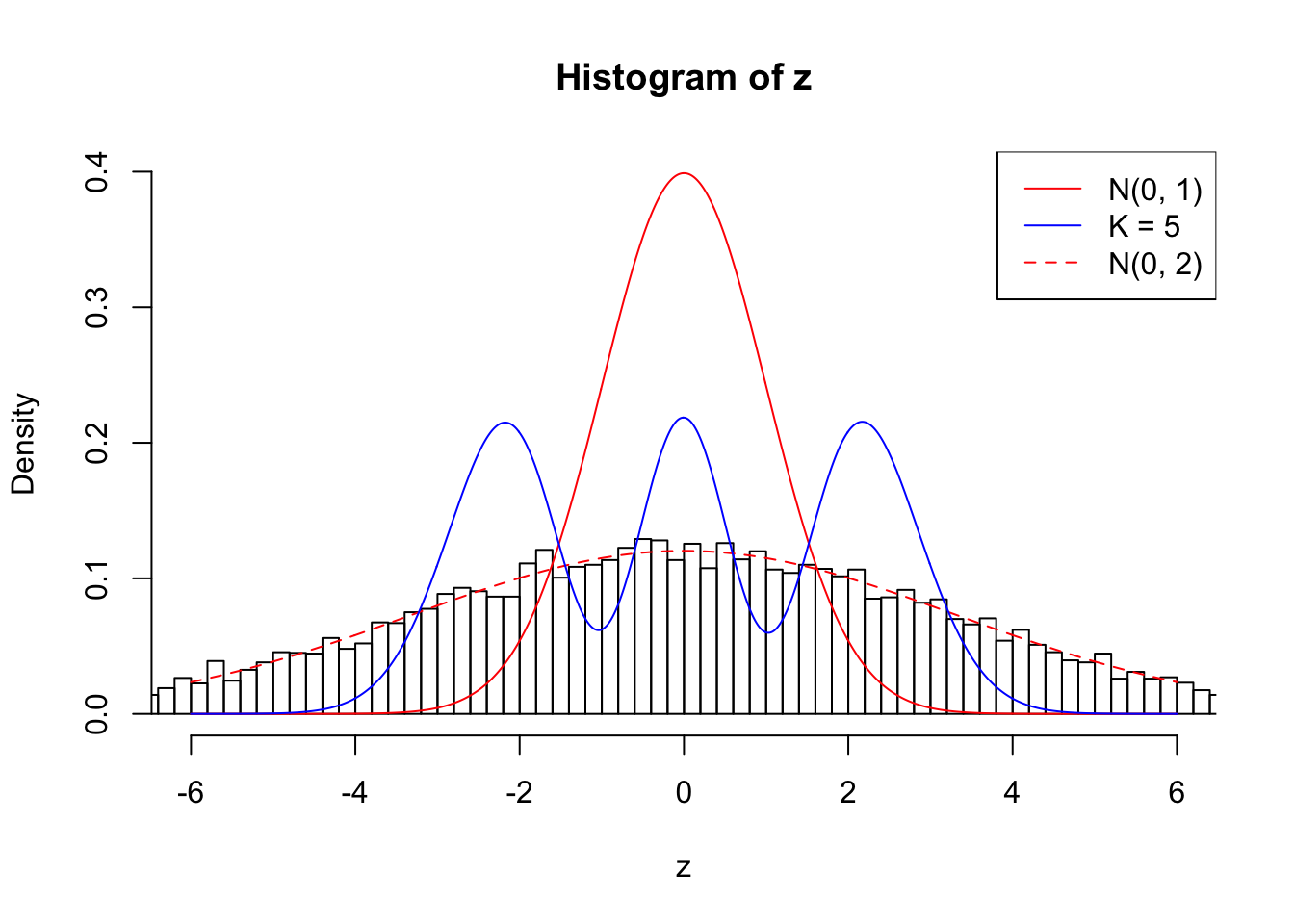
Zoom in to the left tail: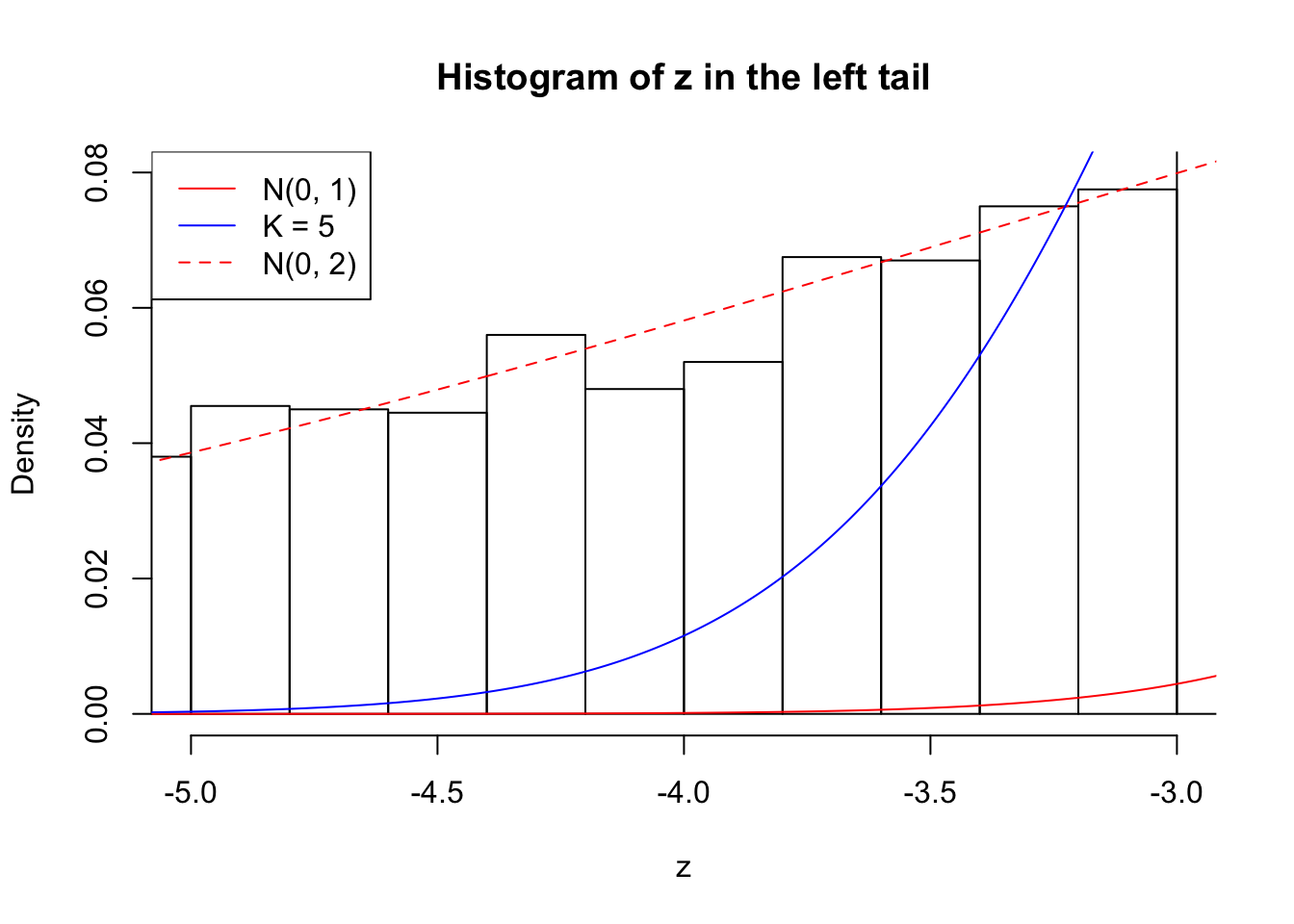
Zoom in to the right tail: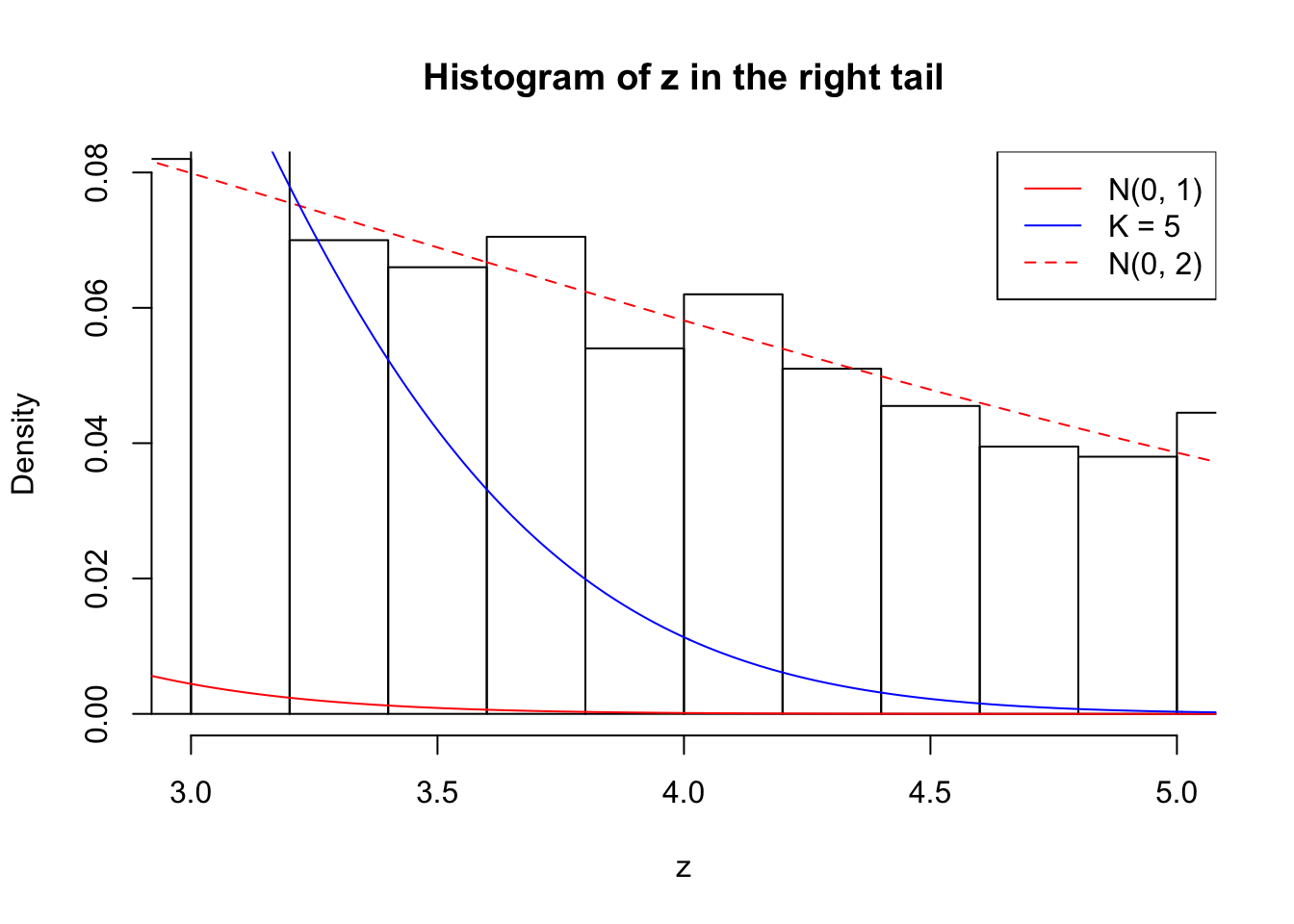
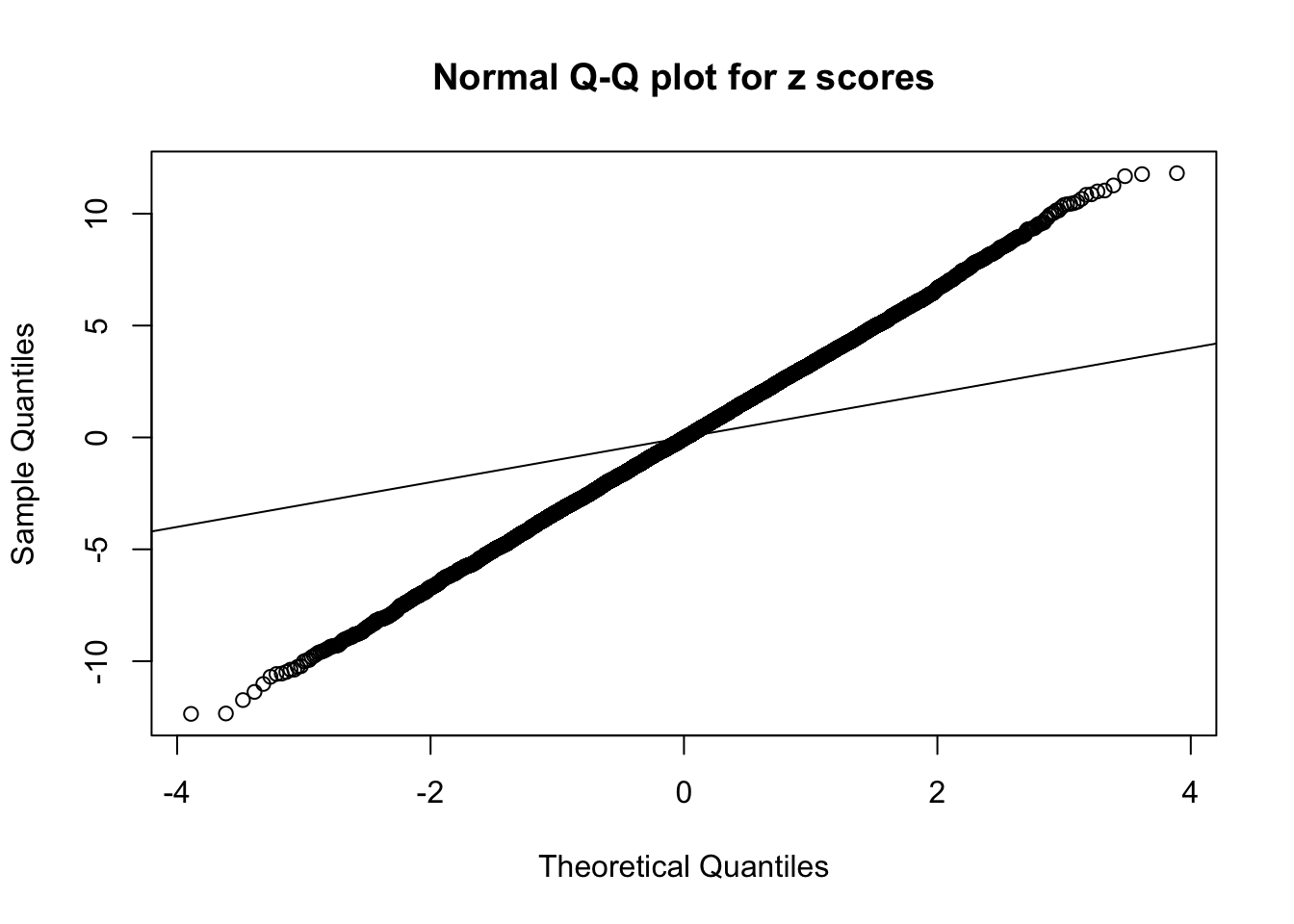
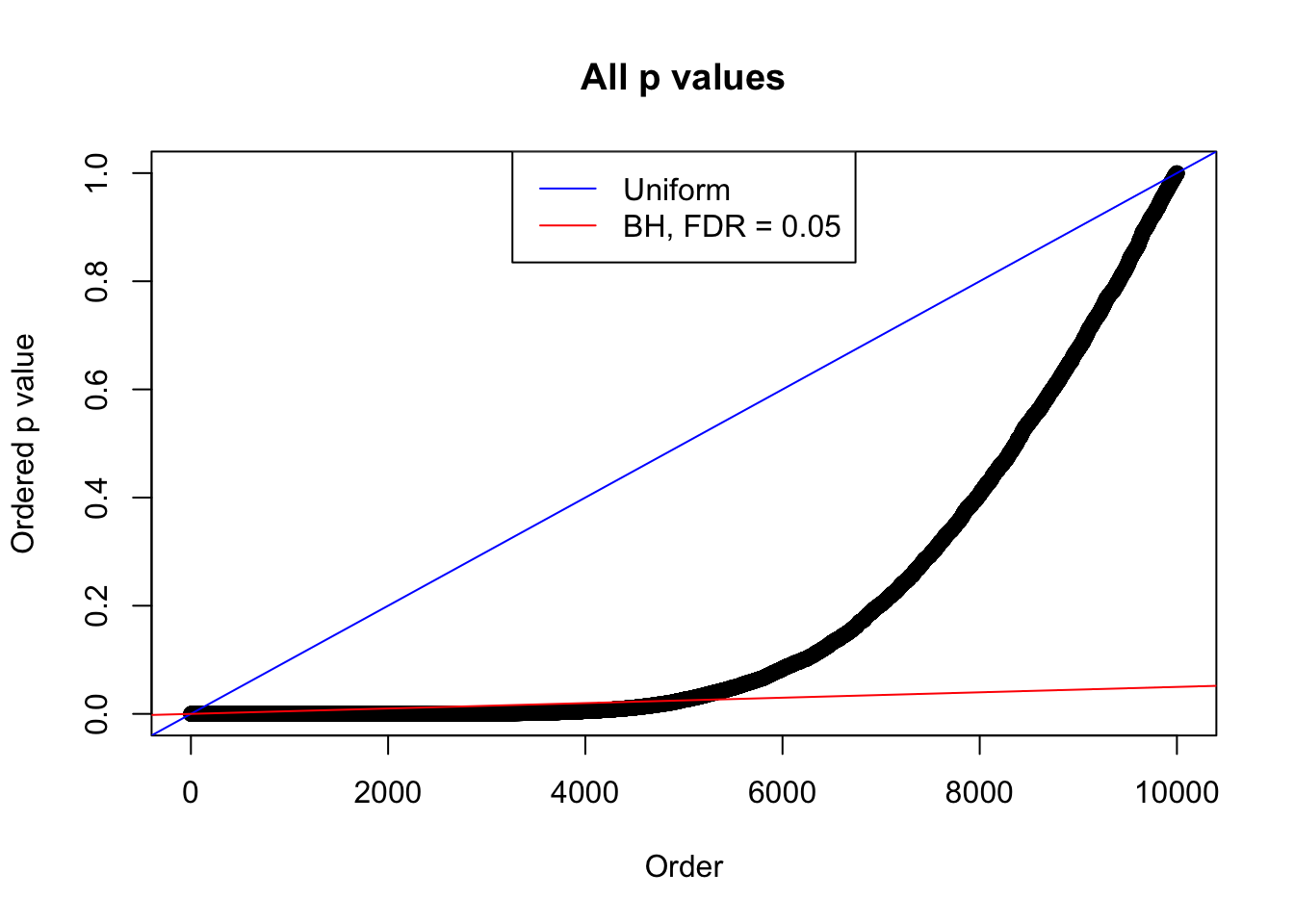
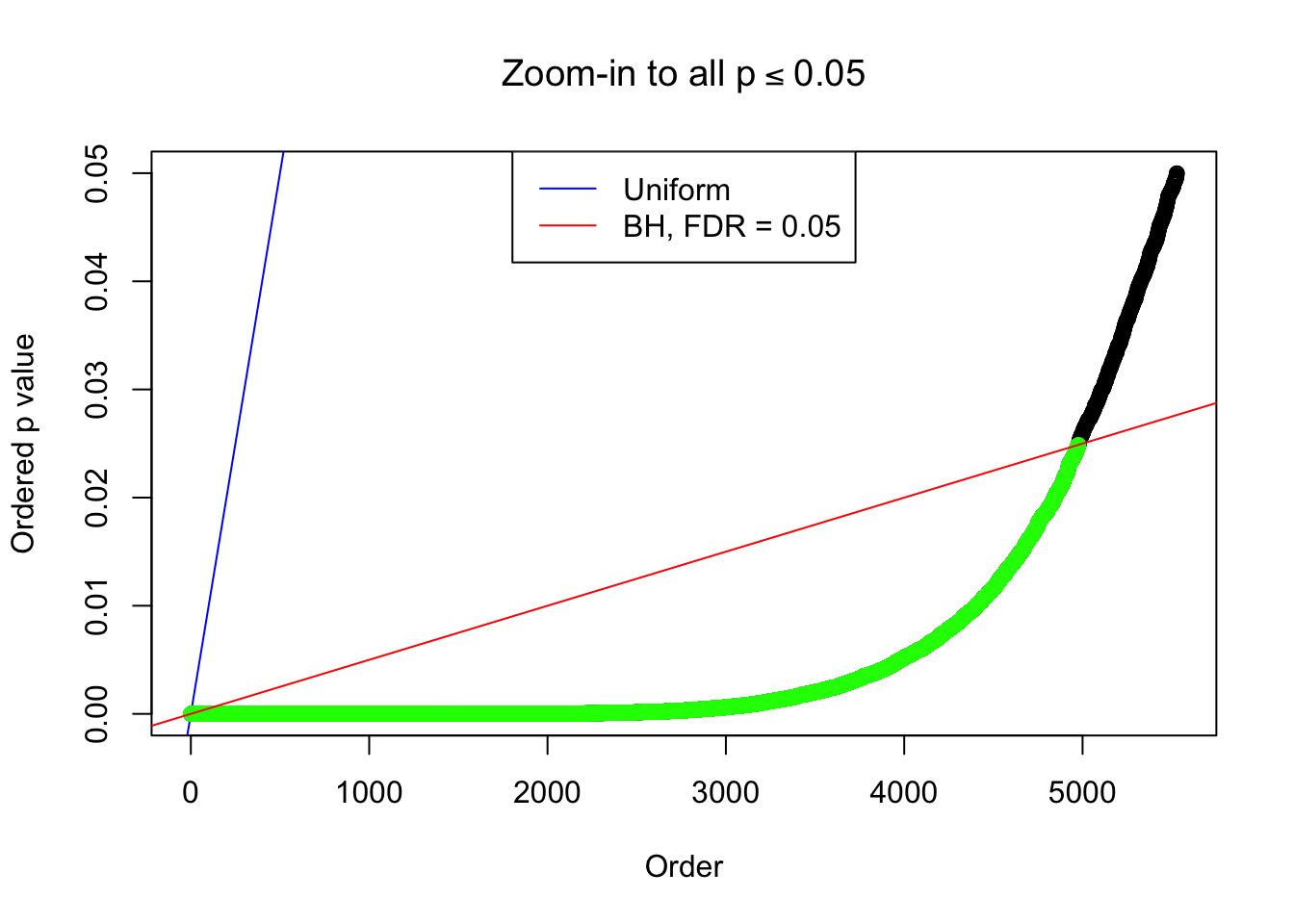
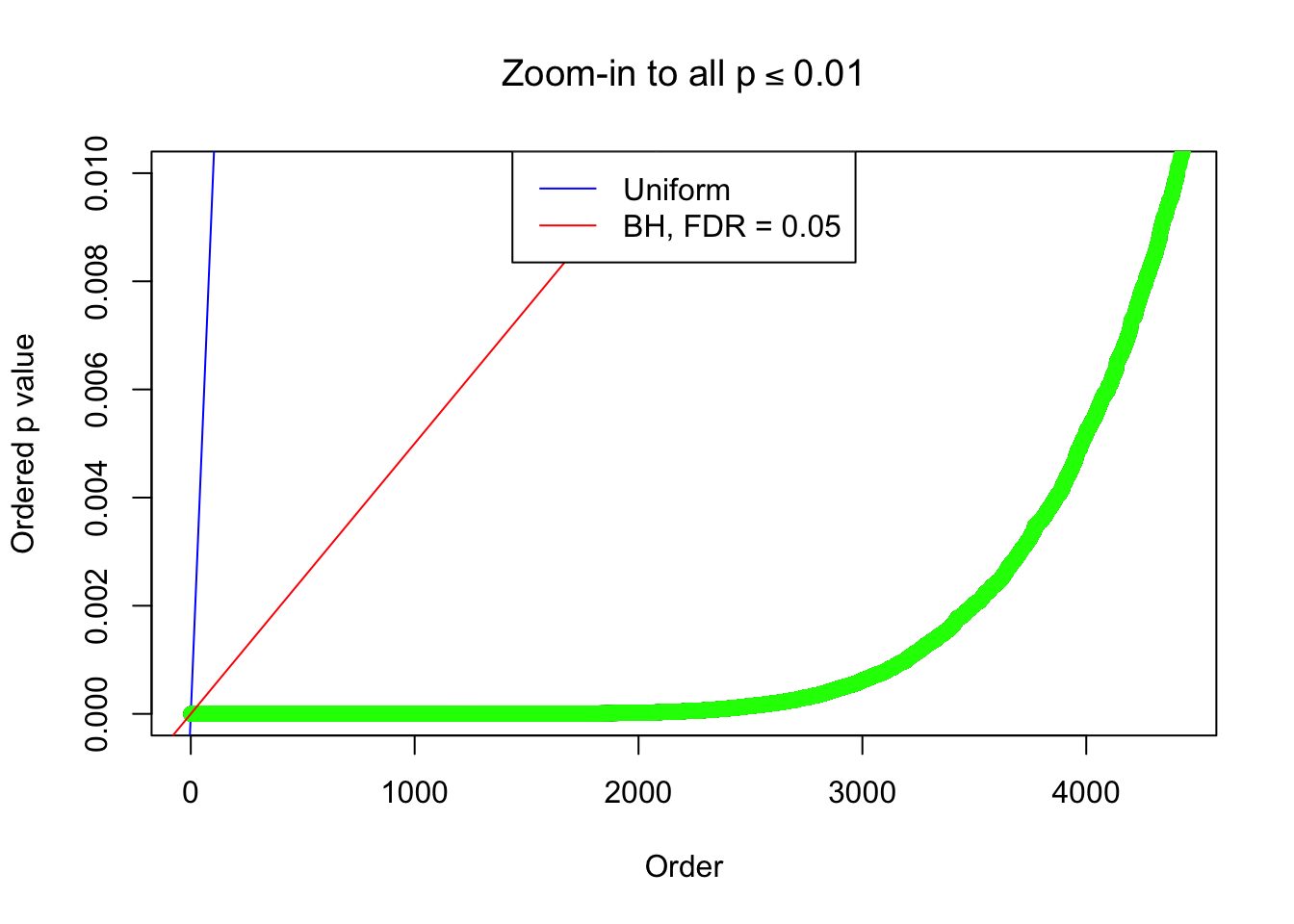
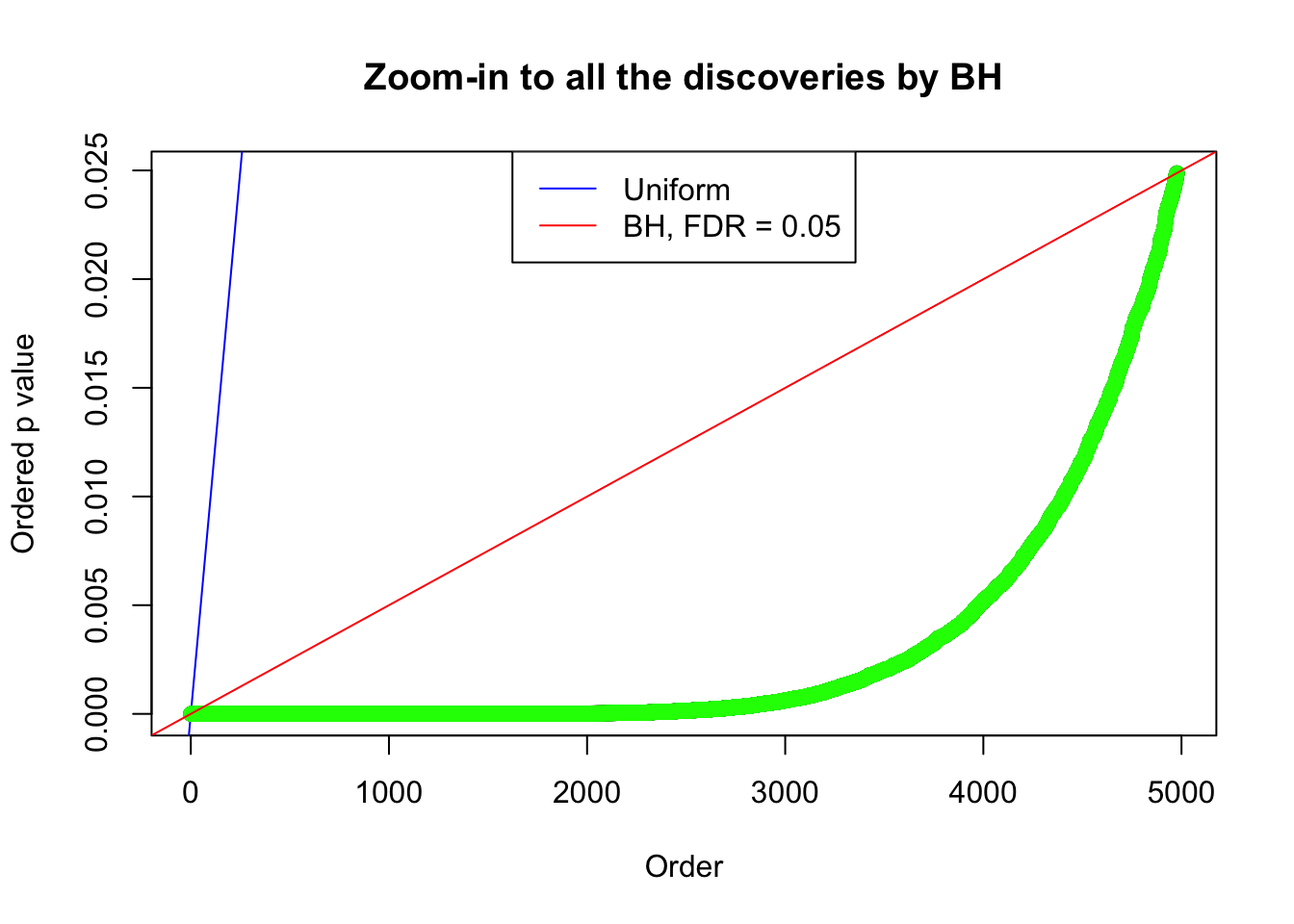
Example 2 : True Distribution: N(0, 11 ); Number of Discoveries: 5020 ; pihat0 = 0.06017972
Log-likelihood with N(0, 2): -39966.98
Log-likelihood with Gaussian Derivatives: -43703.65
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 3736.67
Normalized weights:
1 : 0.00100643048290564 ; 2 : 2.24334837780945 ; 3 : 0.0220715785973863 ; 4 : 1.84039616975457 ; 5 : 0.0142926191586435 ;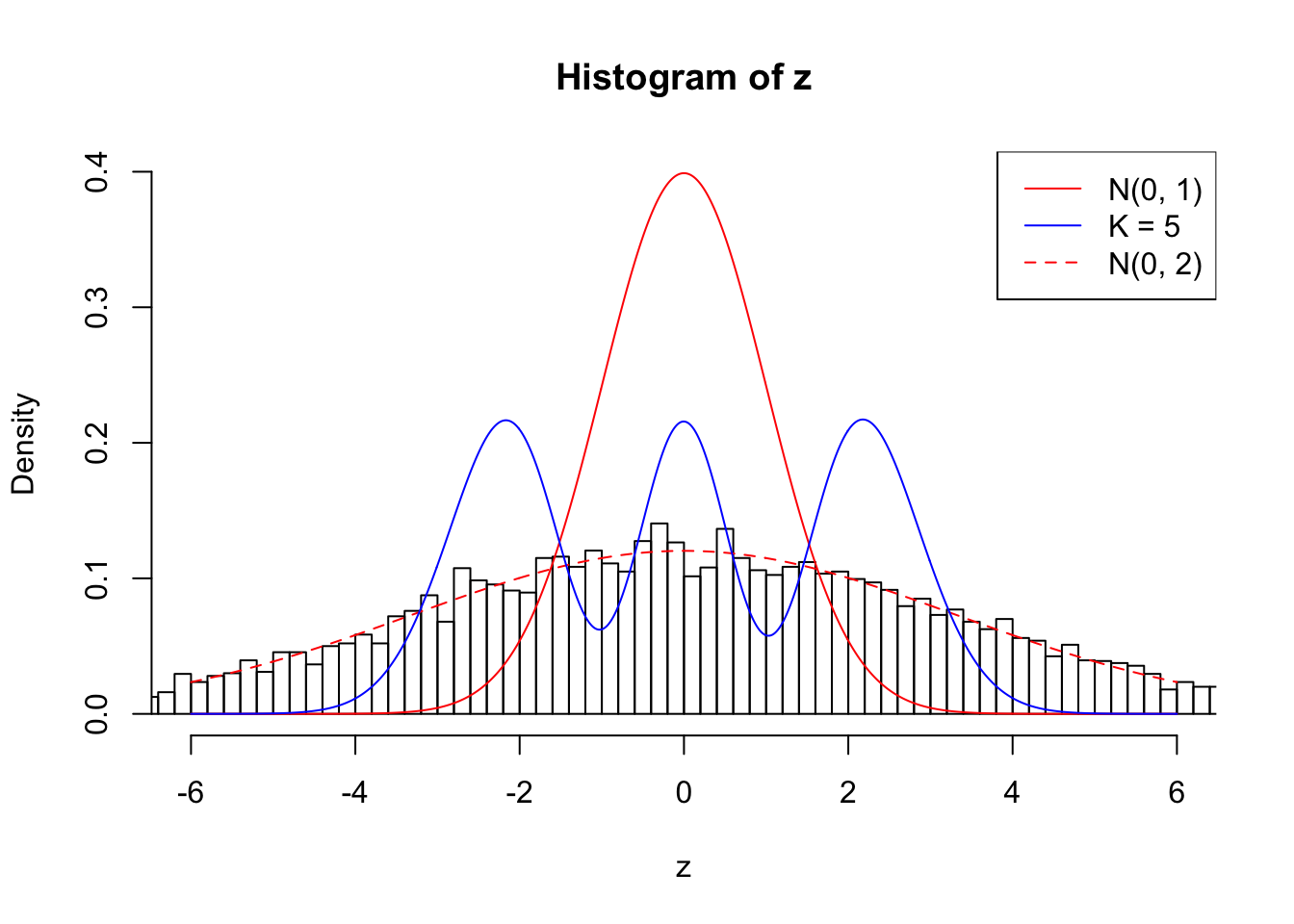
Zoom in to the left tail: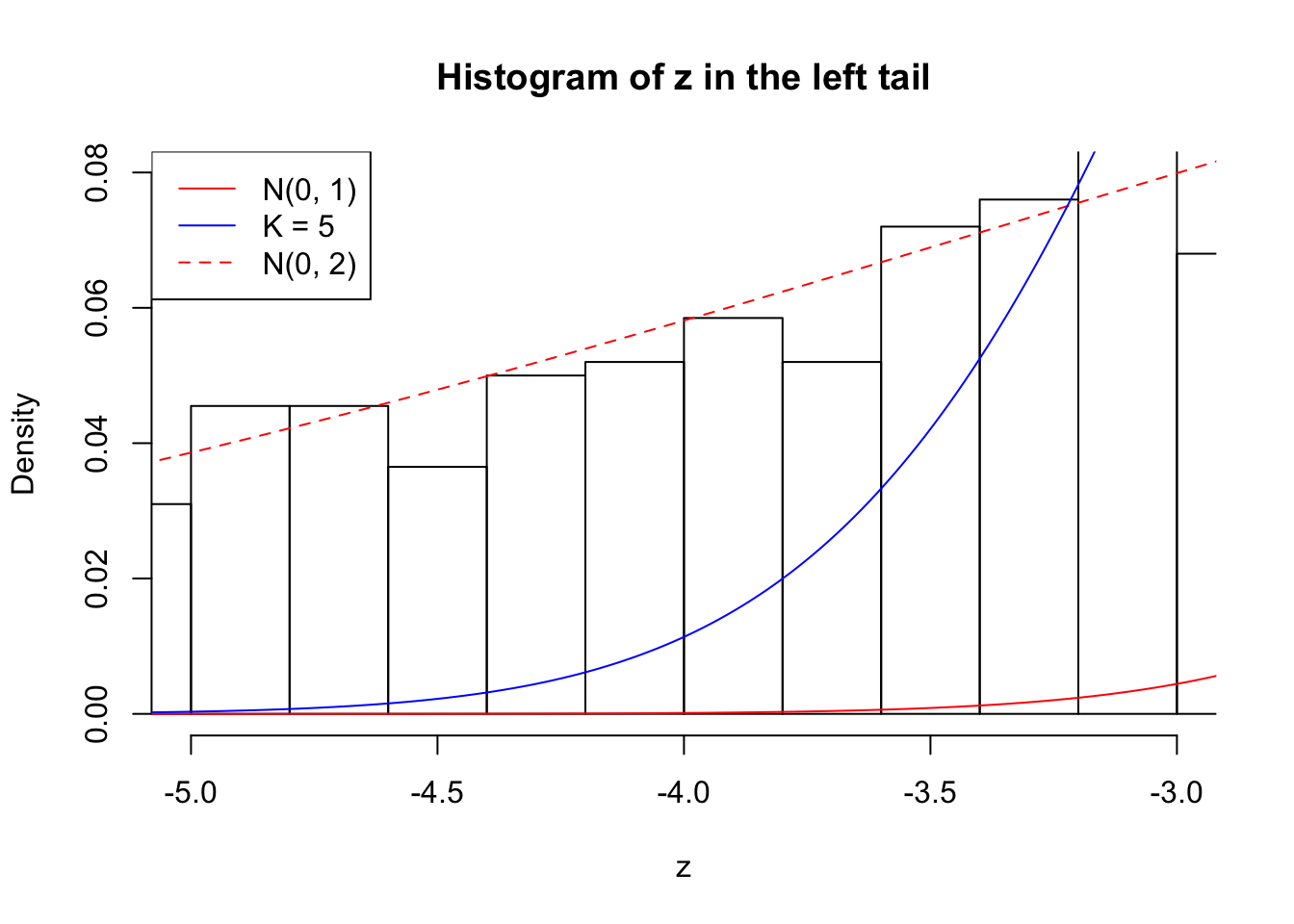
Zoom in to the right tail: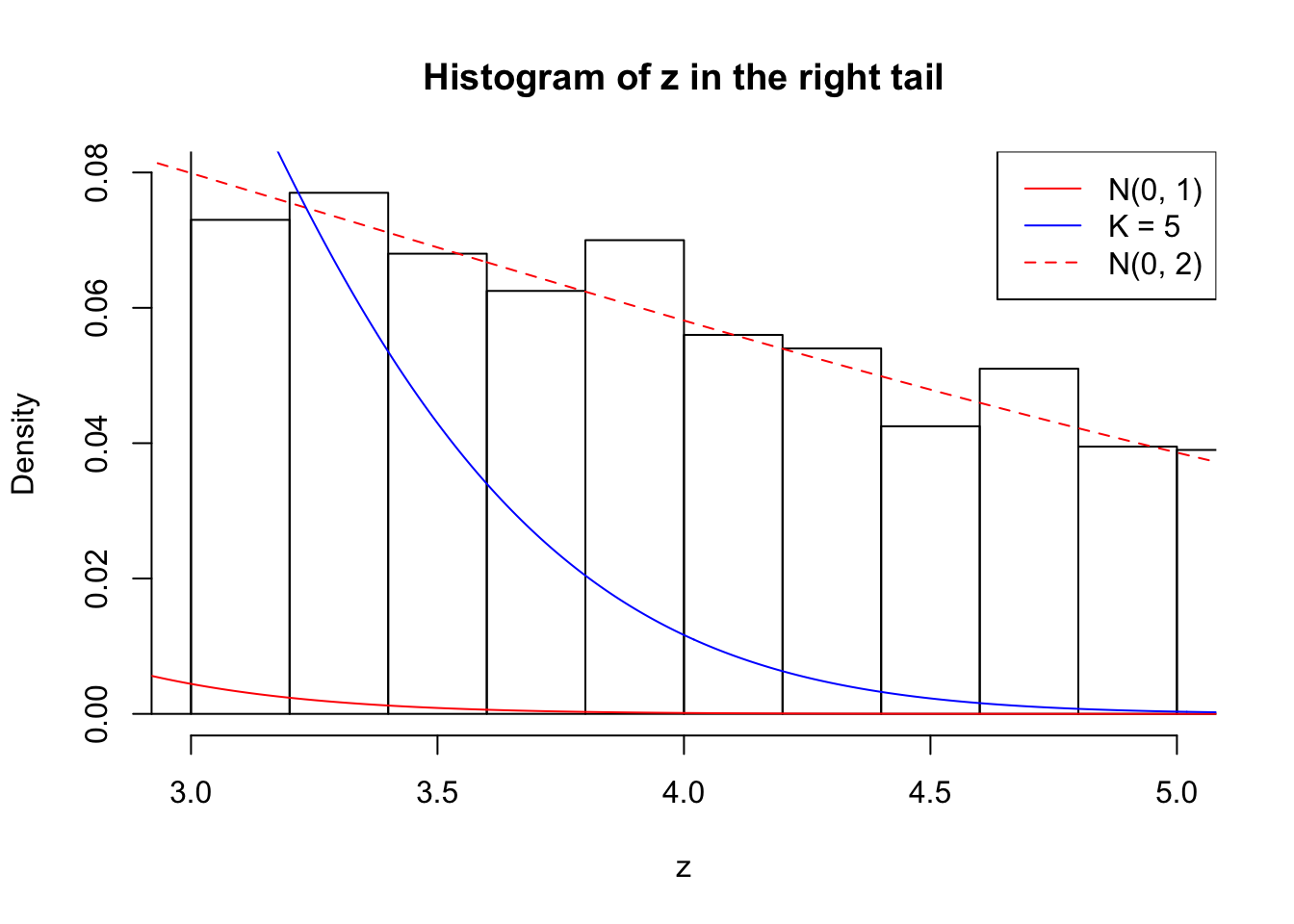
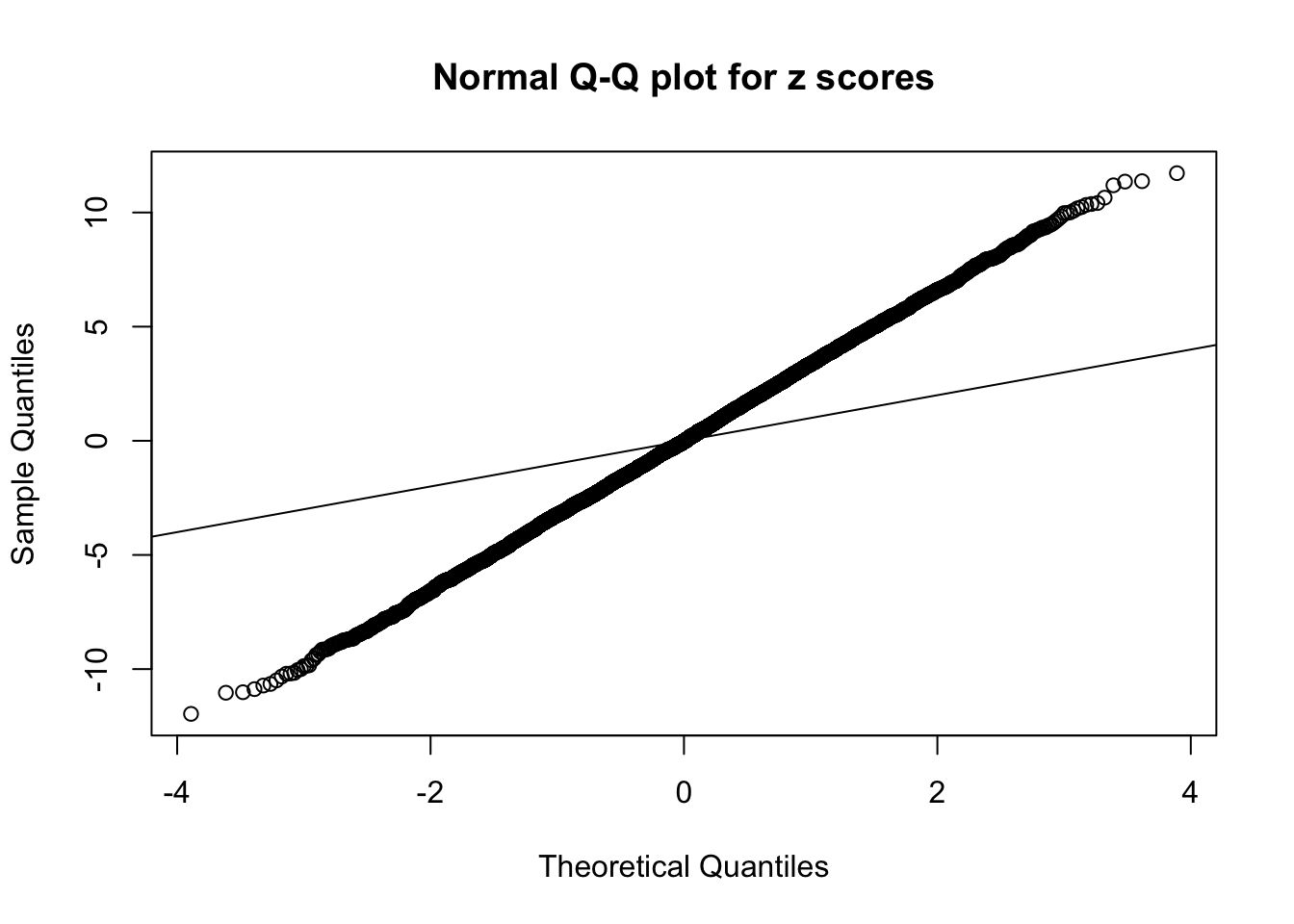
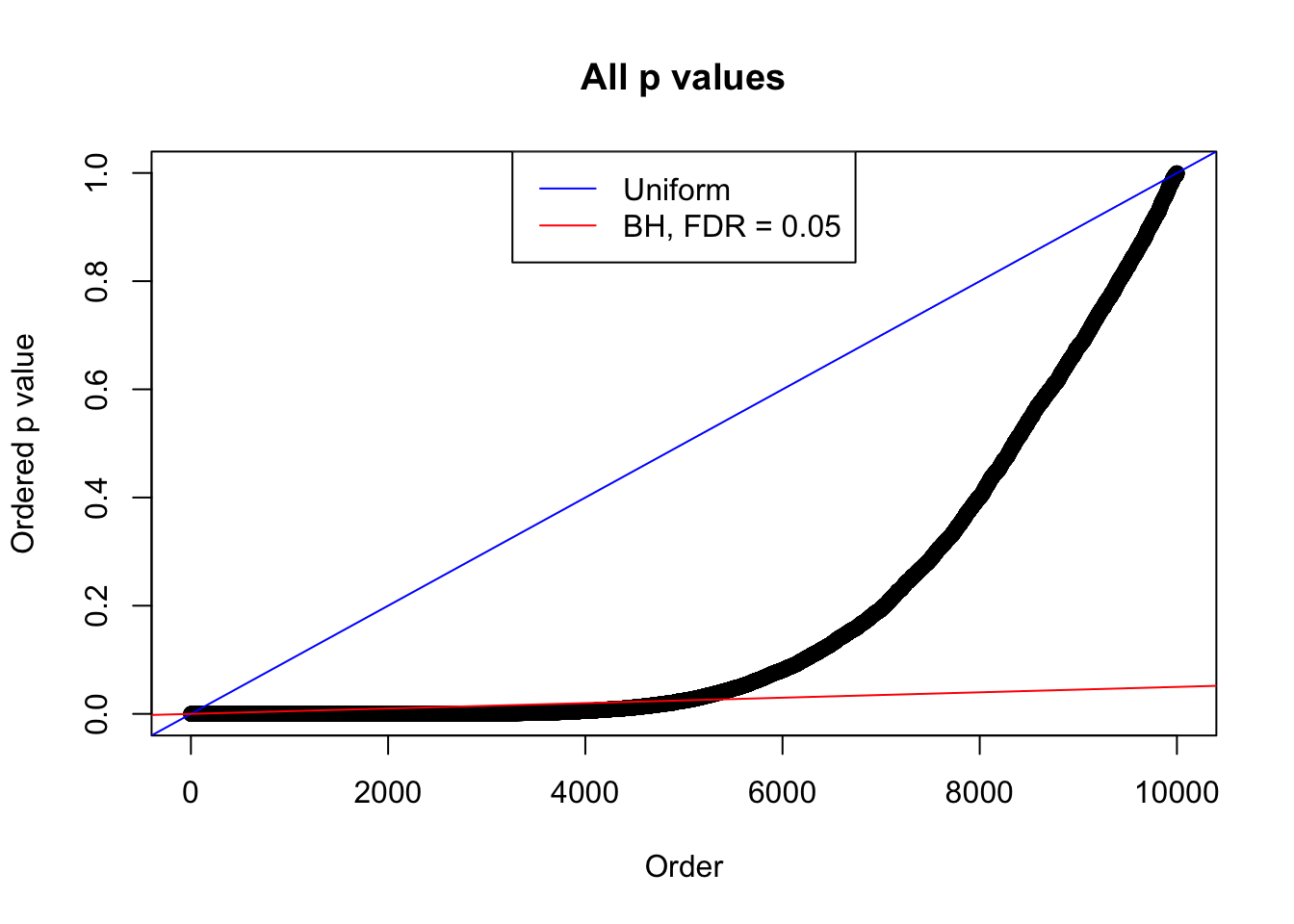
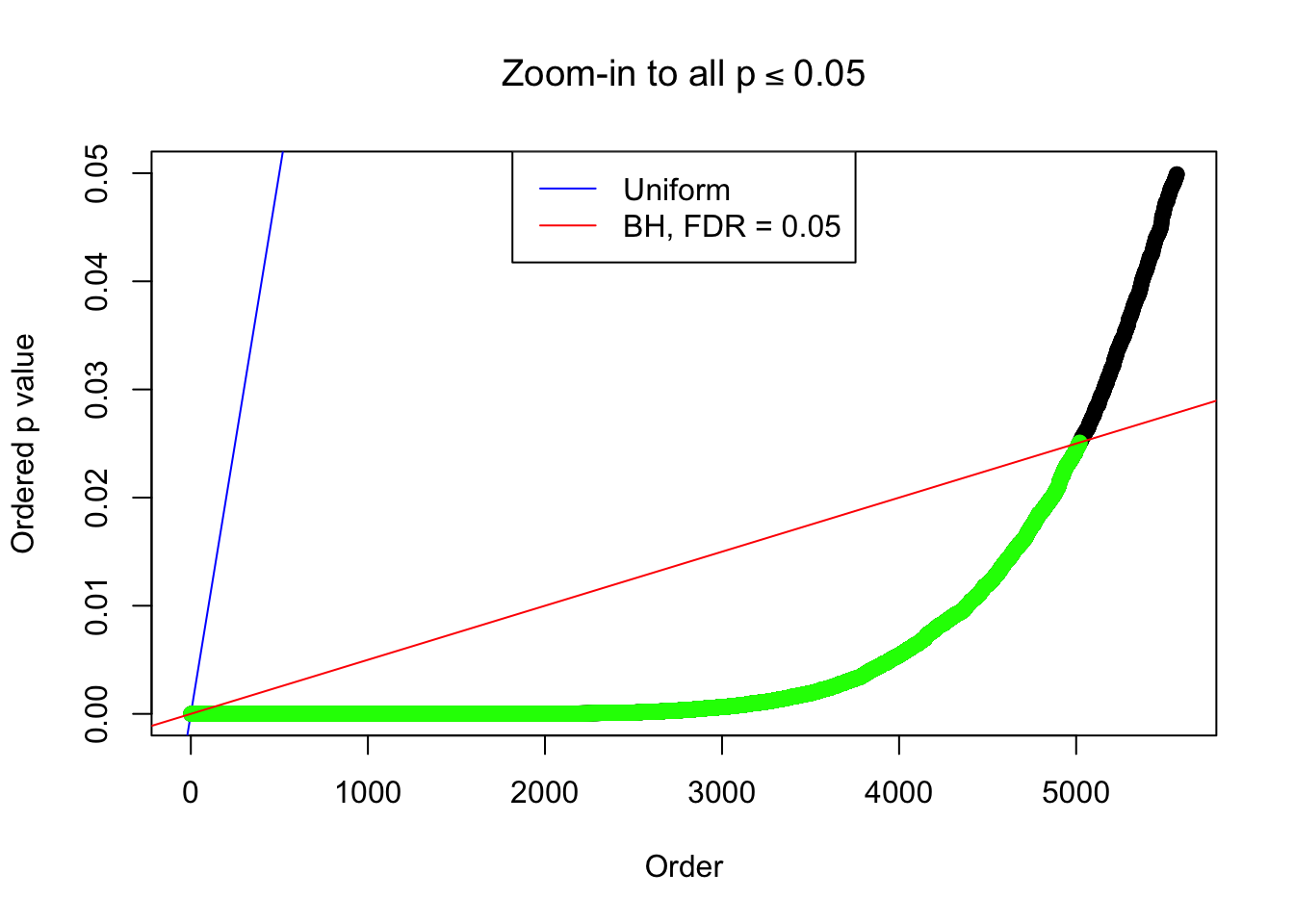
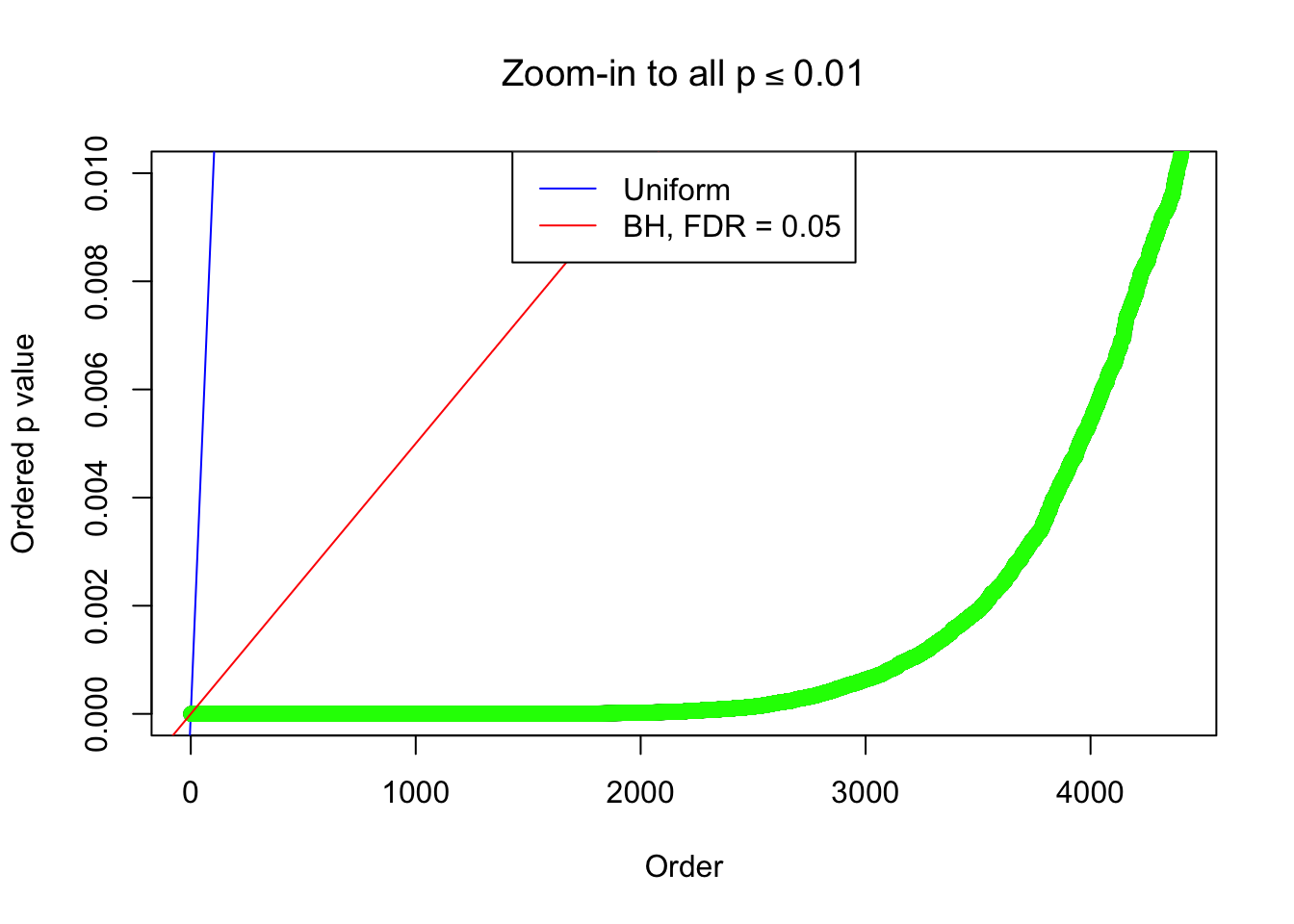
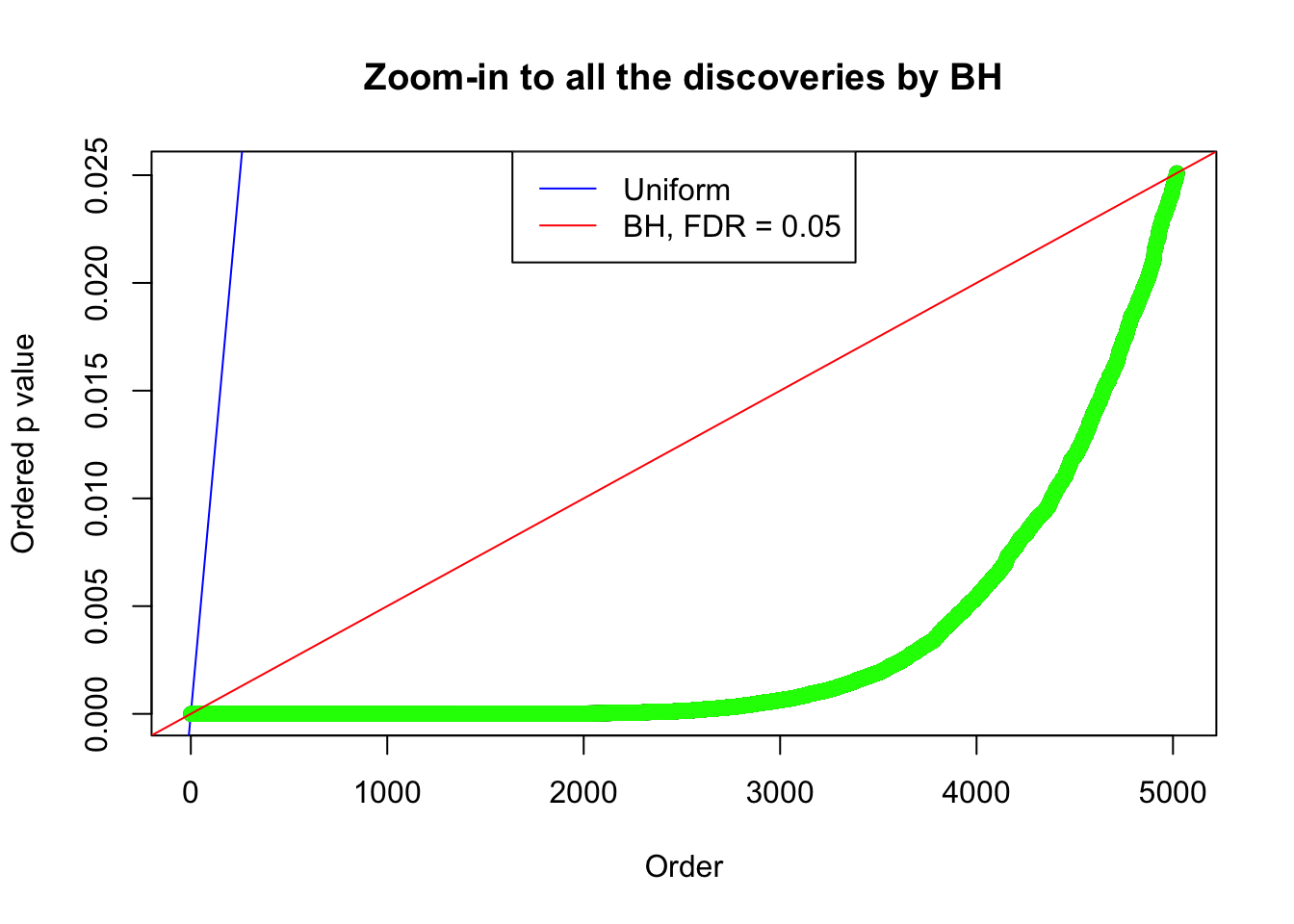
Example 3 : True Distribution: N(0, 11 ); Number of Discoveries: 4925 ; pihat0 = 0.06355277
Log-likelihood with N(0, 2): -40004.09
Log-likelihood with Gaussian Derivatives: -44023.88
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 4019.787
Normalized weights:
1 : -0.00289551549367048 ; 2 : 2.22475240252674 ; 3 : 0.00281874593524768 ; 4 : 1.81006740776991 ; 5 : 0.0021288830629003 ;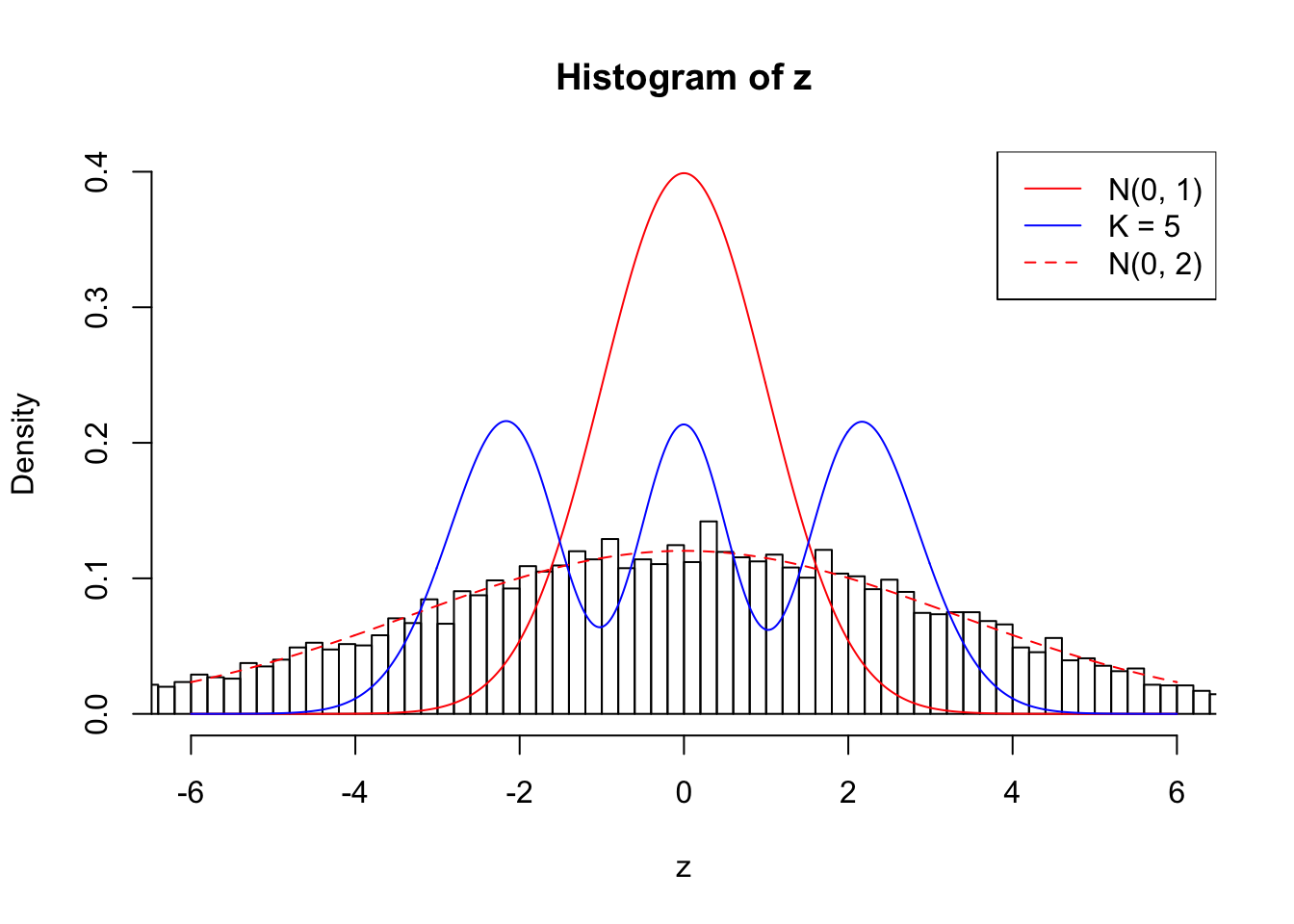
Zoom in to the left tail: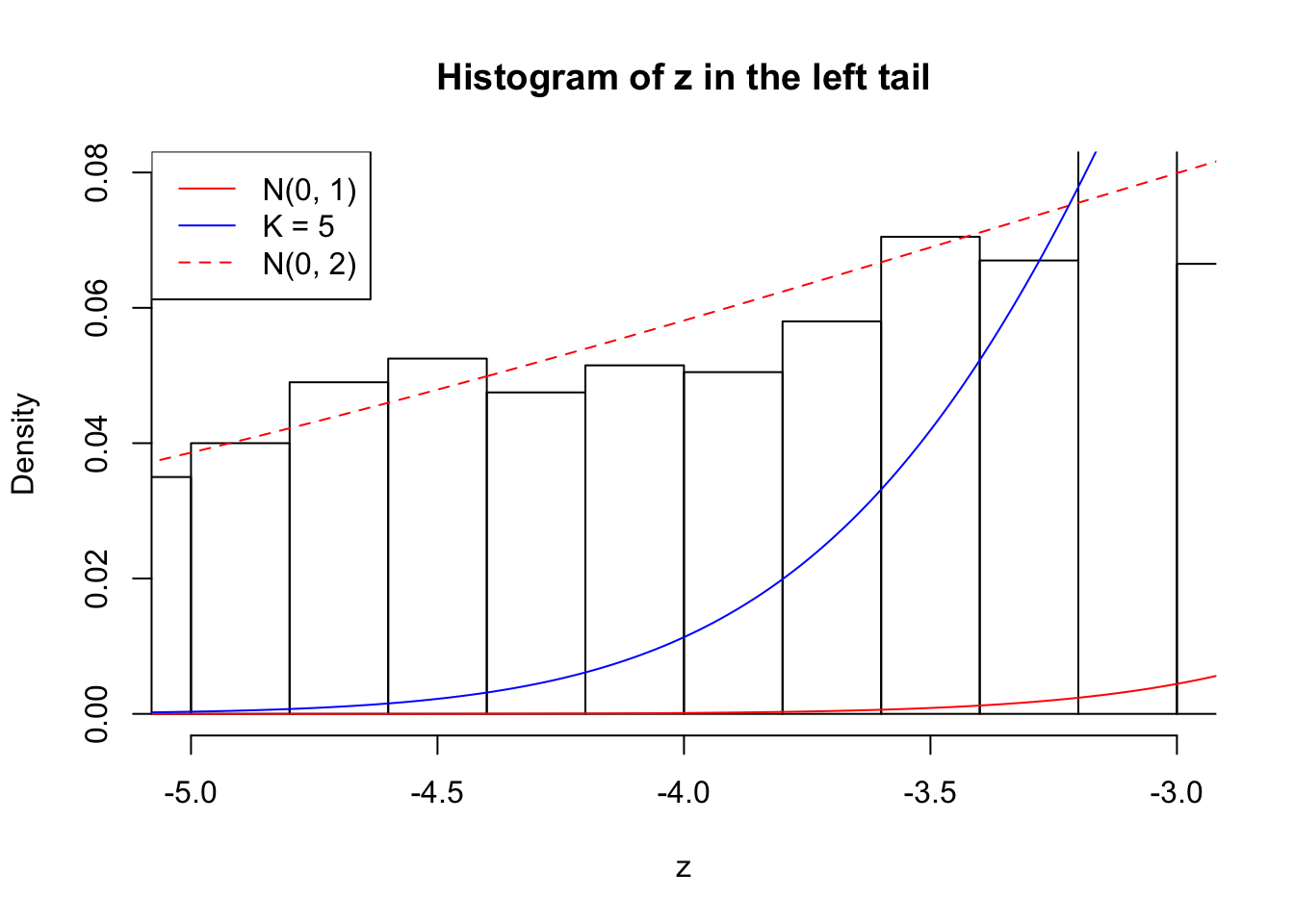
Zoom in to the right tail: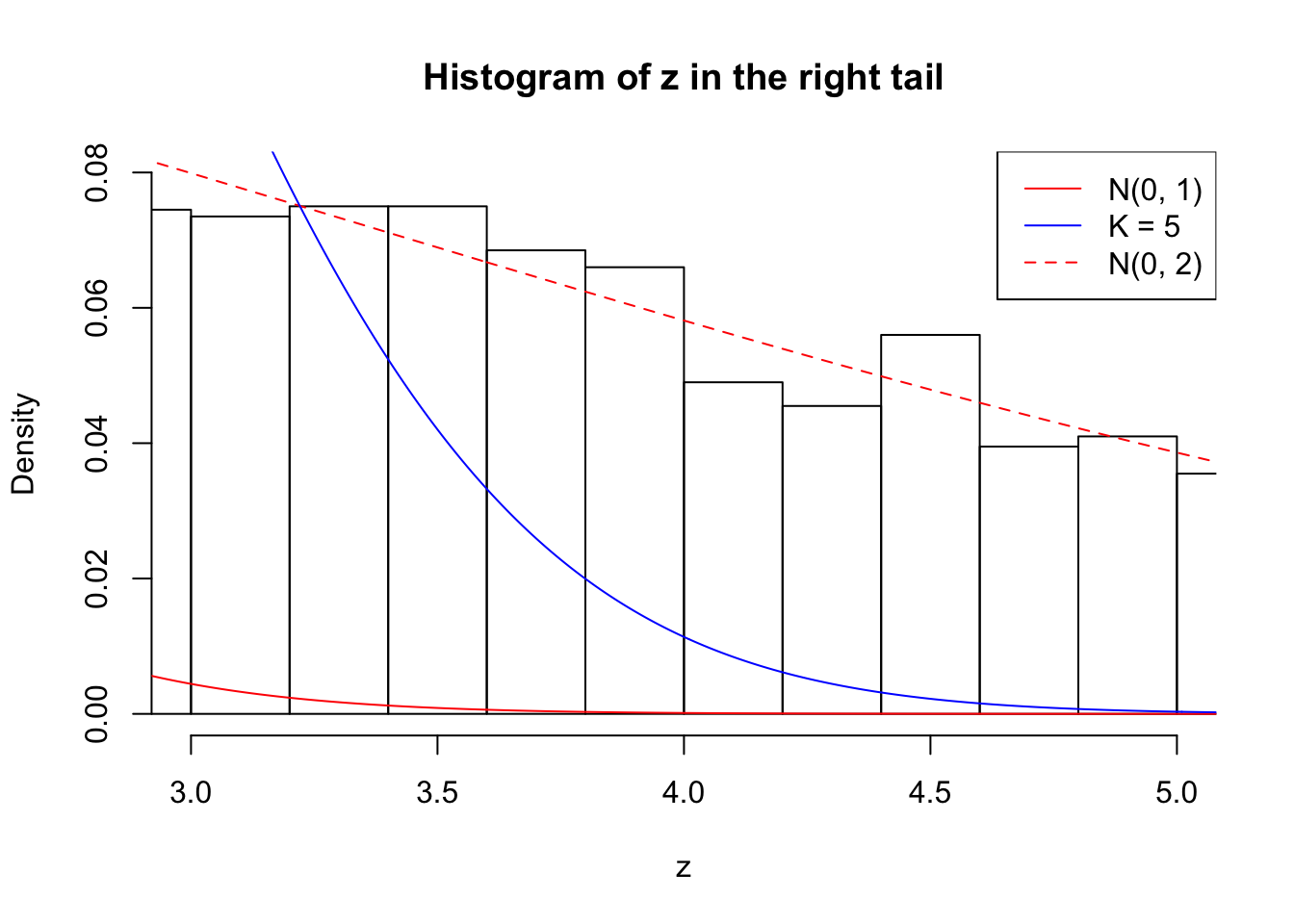
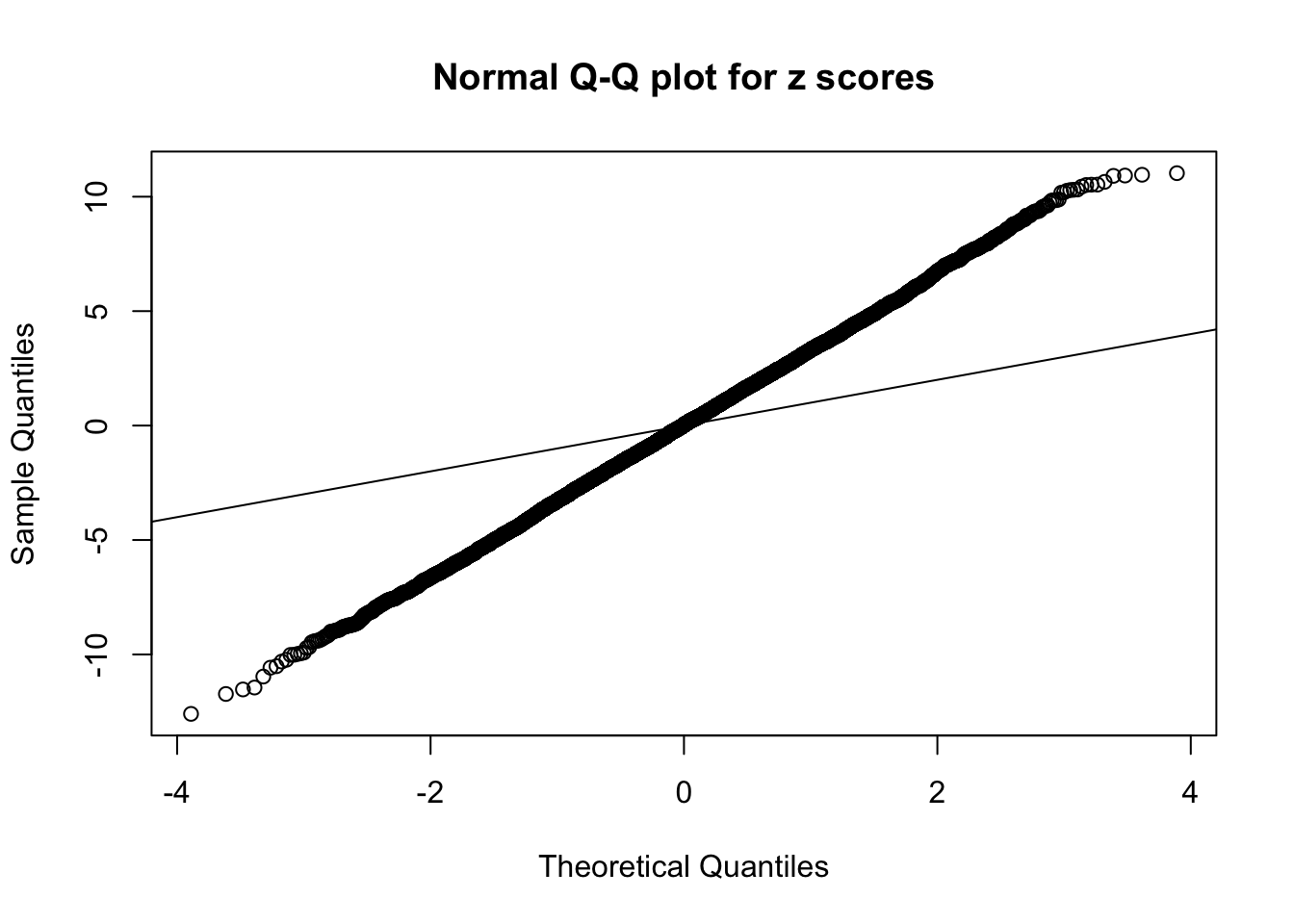
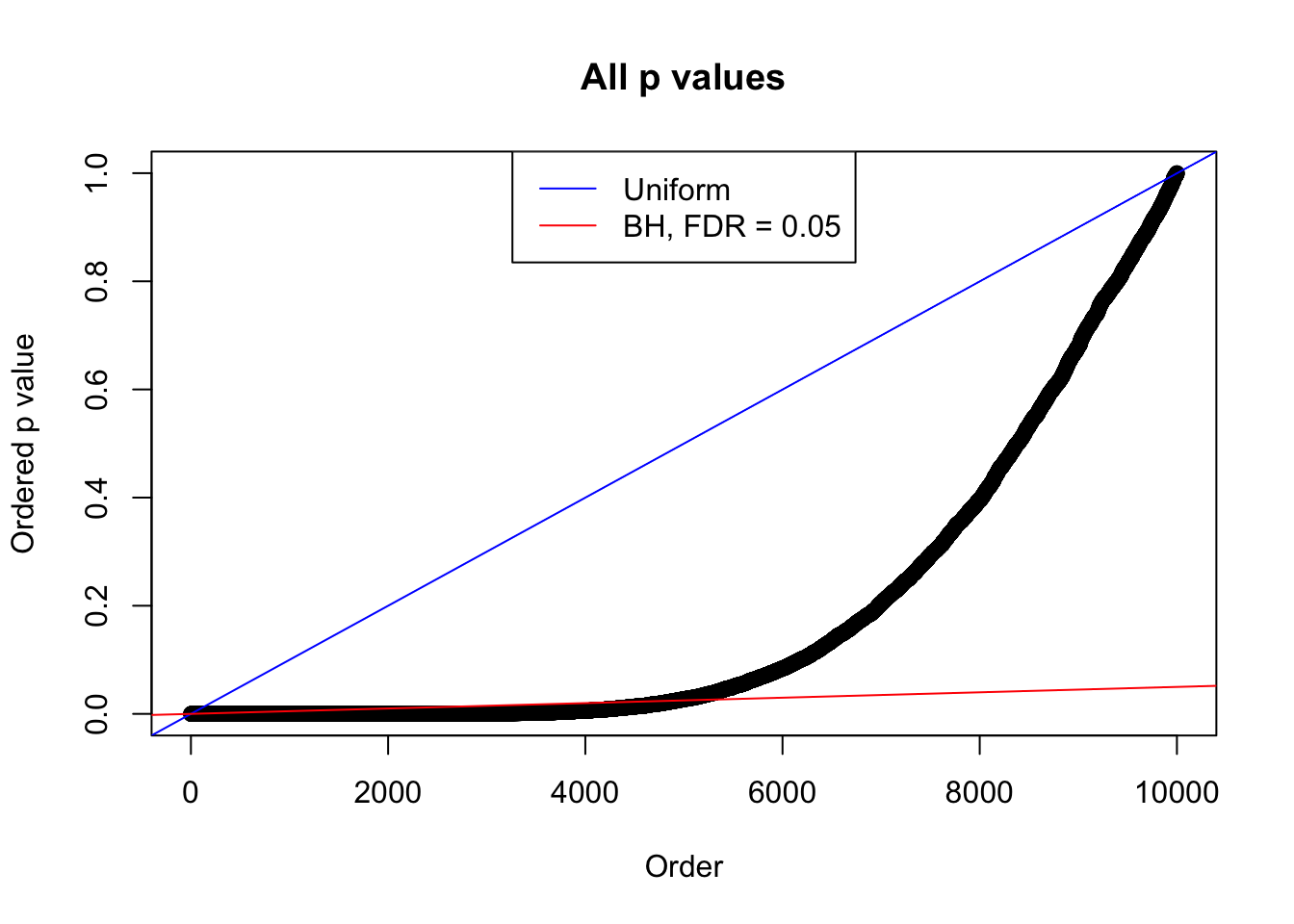
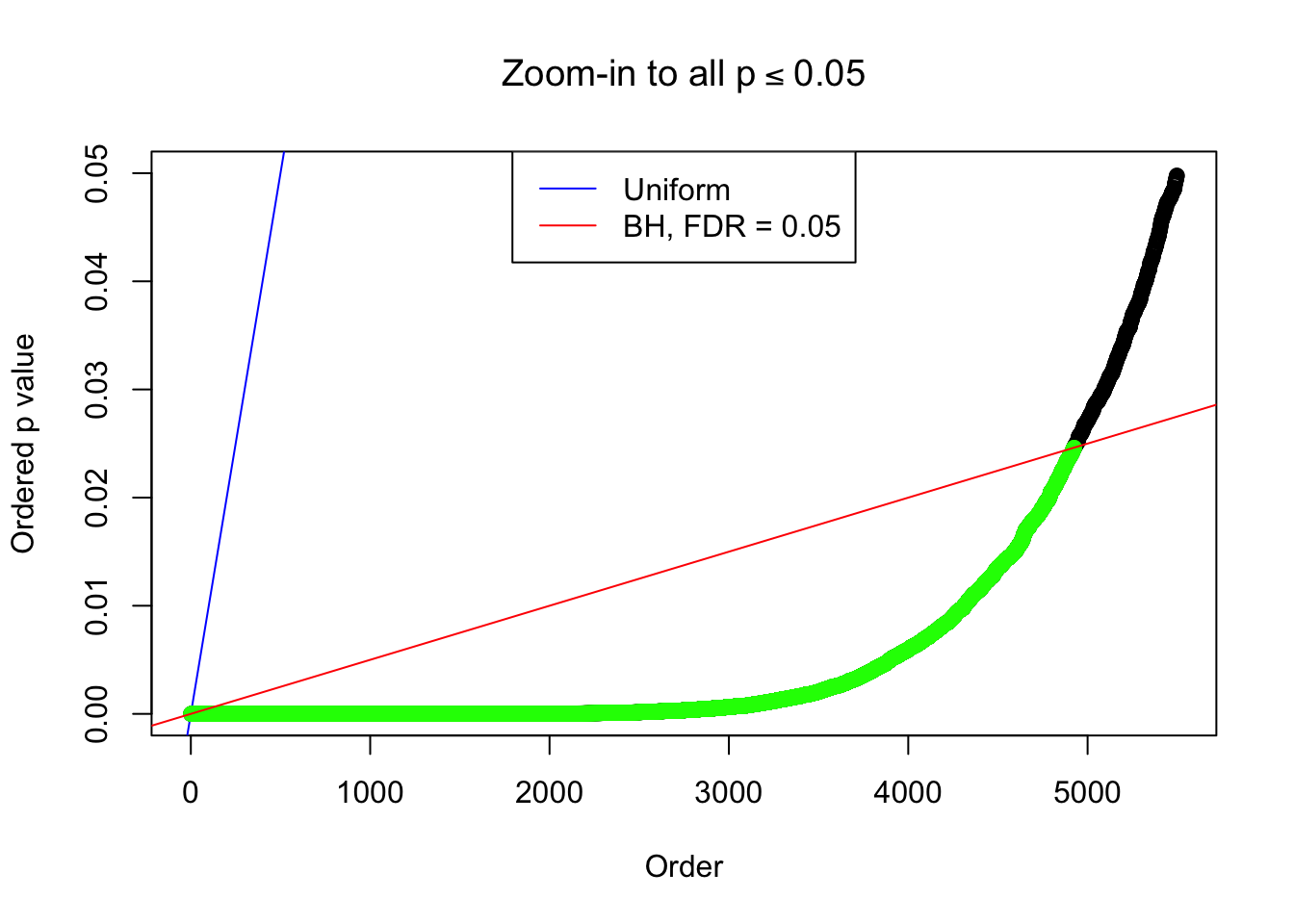
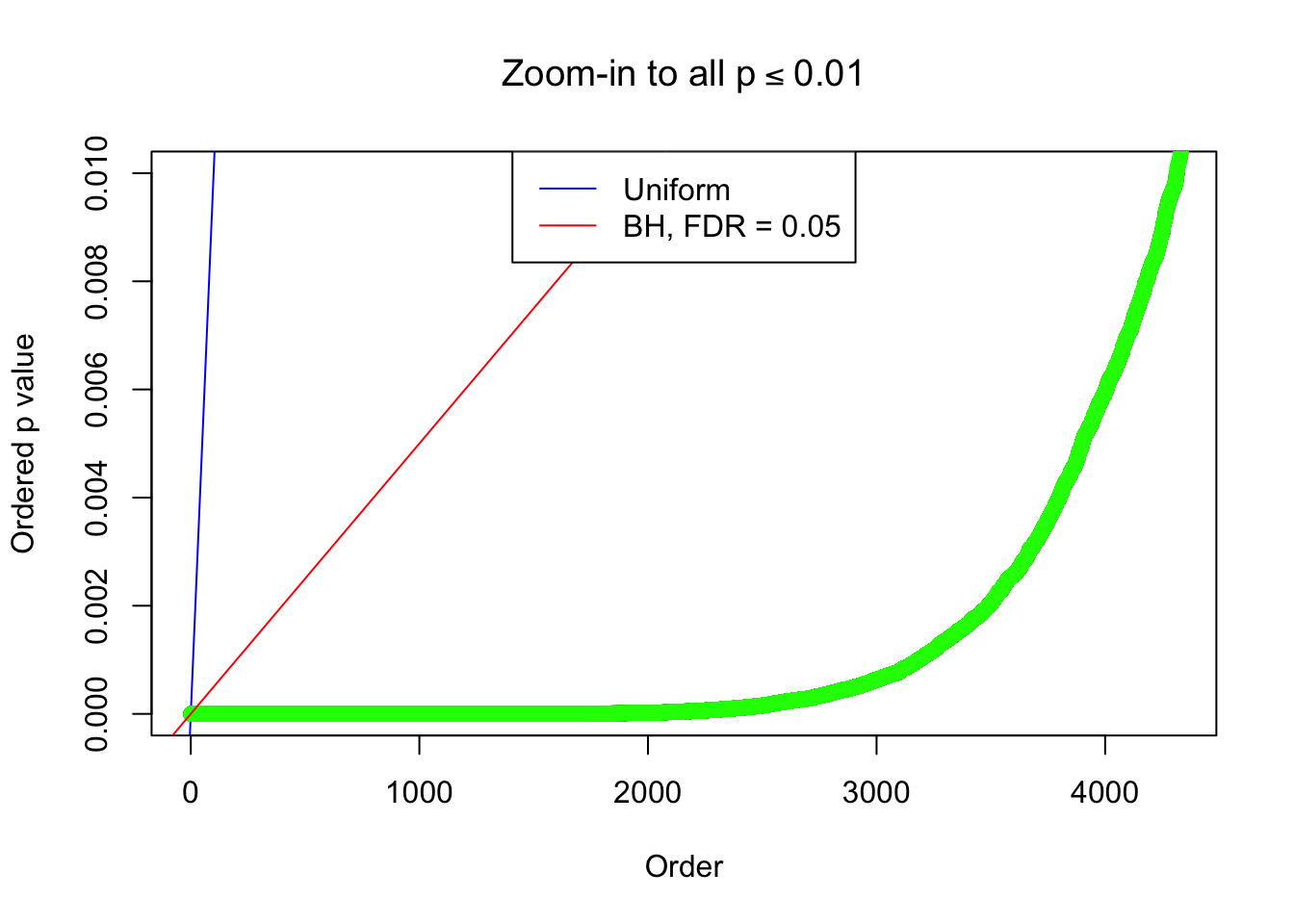
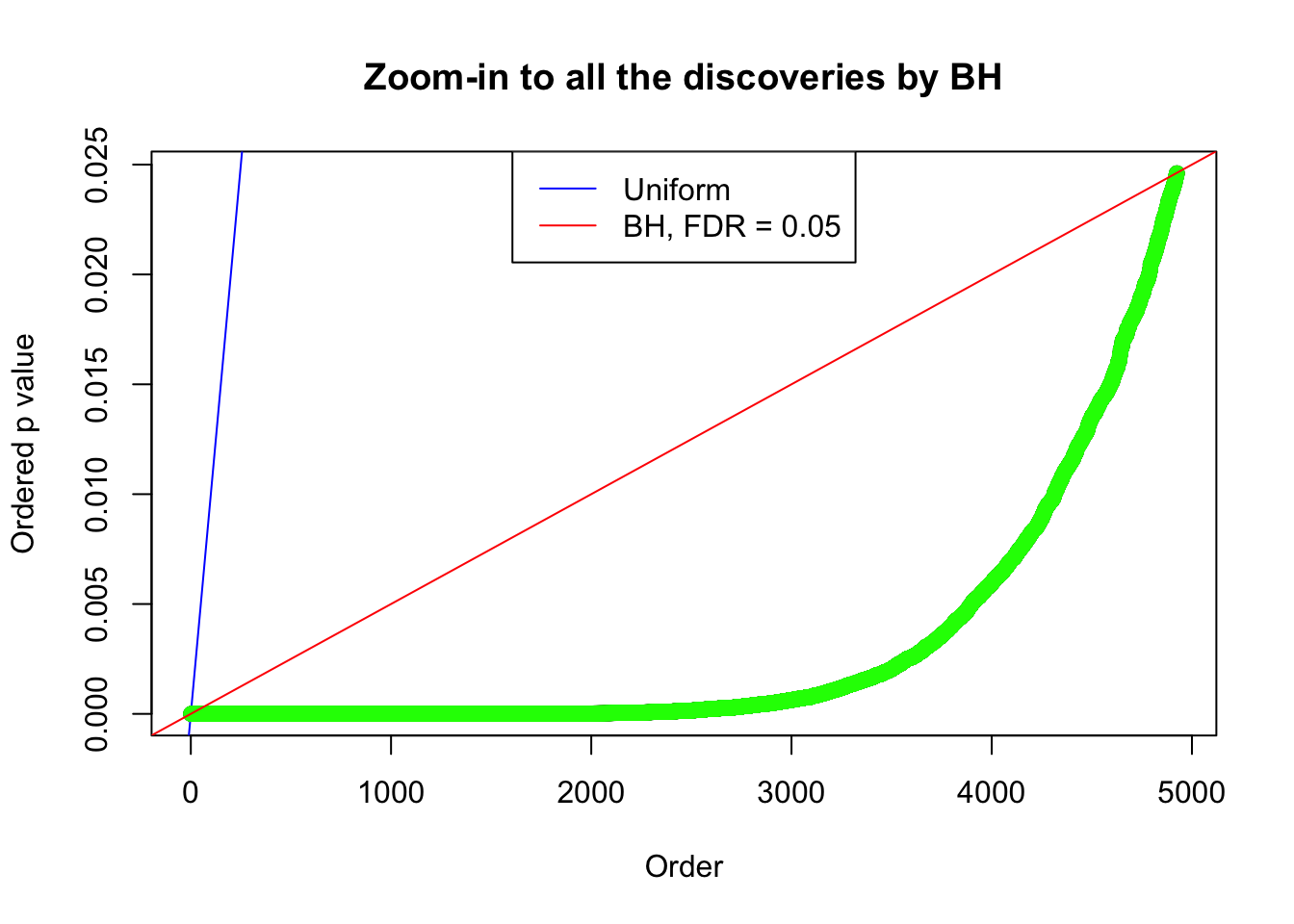
Example 4 : True Distribution: N(0, 11 ); Number of Discoveries: 4965 ; pihat0 = 0.06219233
Log-likelihood with N(0, 2): -39699.49
Log-likelihood with Gaussian Derivatives: -43405.06
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 3705.569
Normalized weights:
1 : -0.000357052297026235 ; 2 : 2.22689809003591 ; 3 : 0.0101246626391944 ; 4 : 1.81512653998256 ; 5 : -0.000994344669459804 ;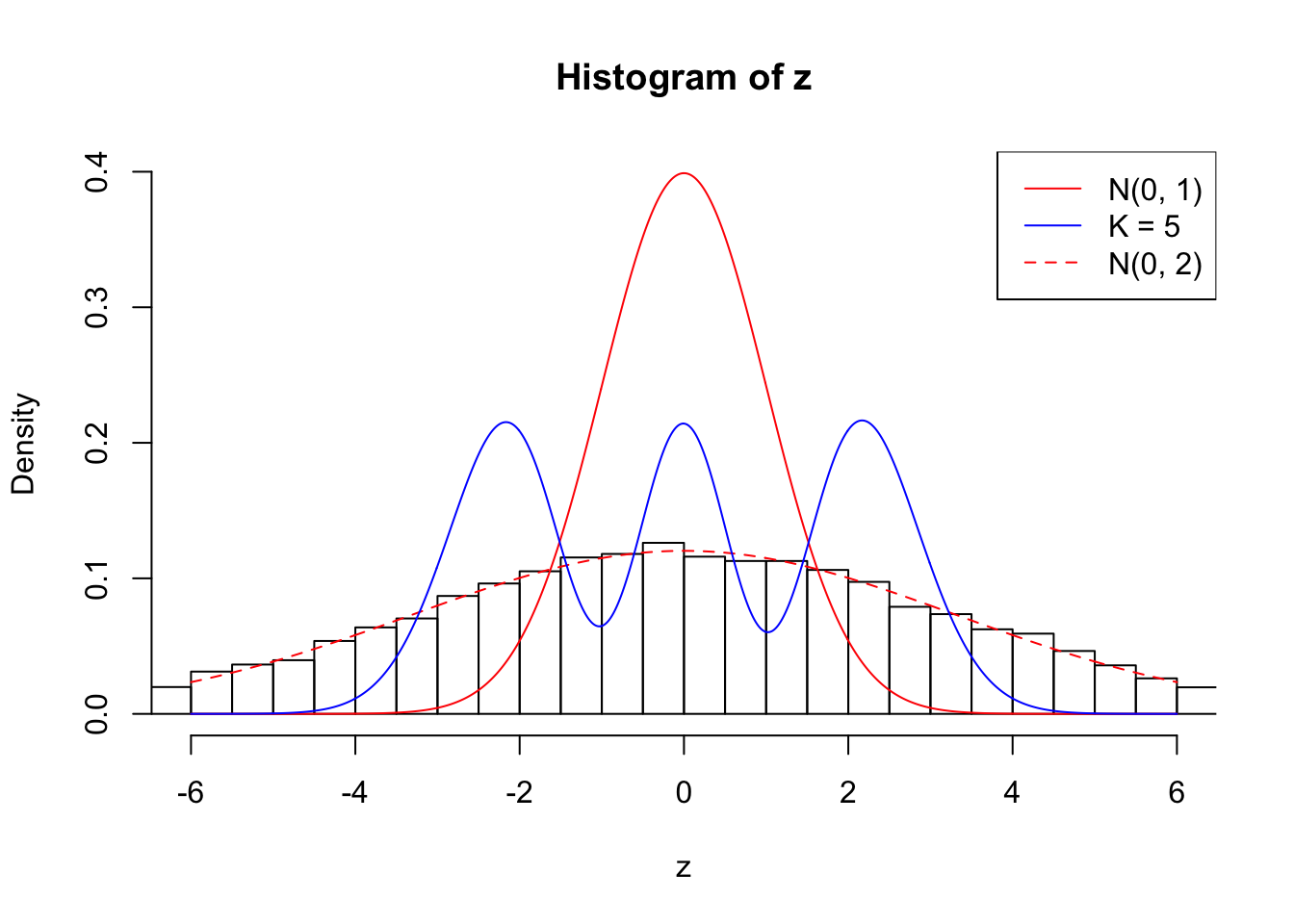
Zoom in to the left tail: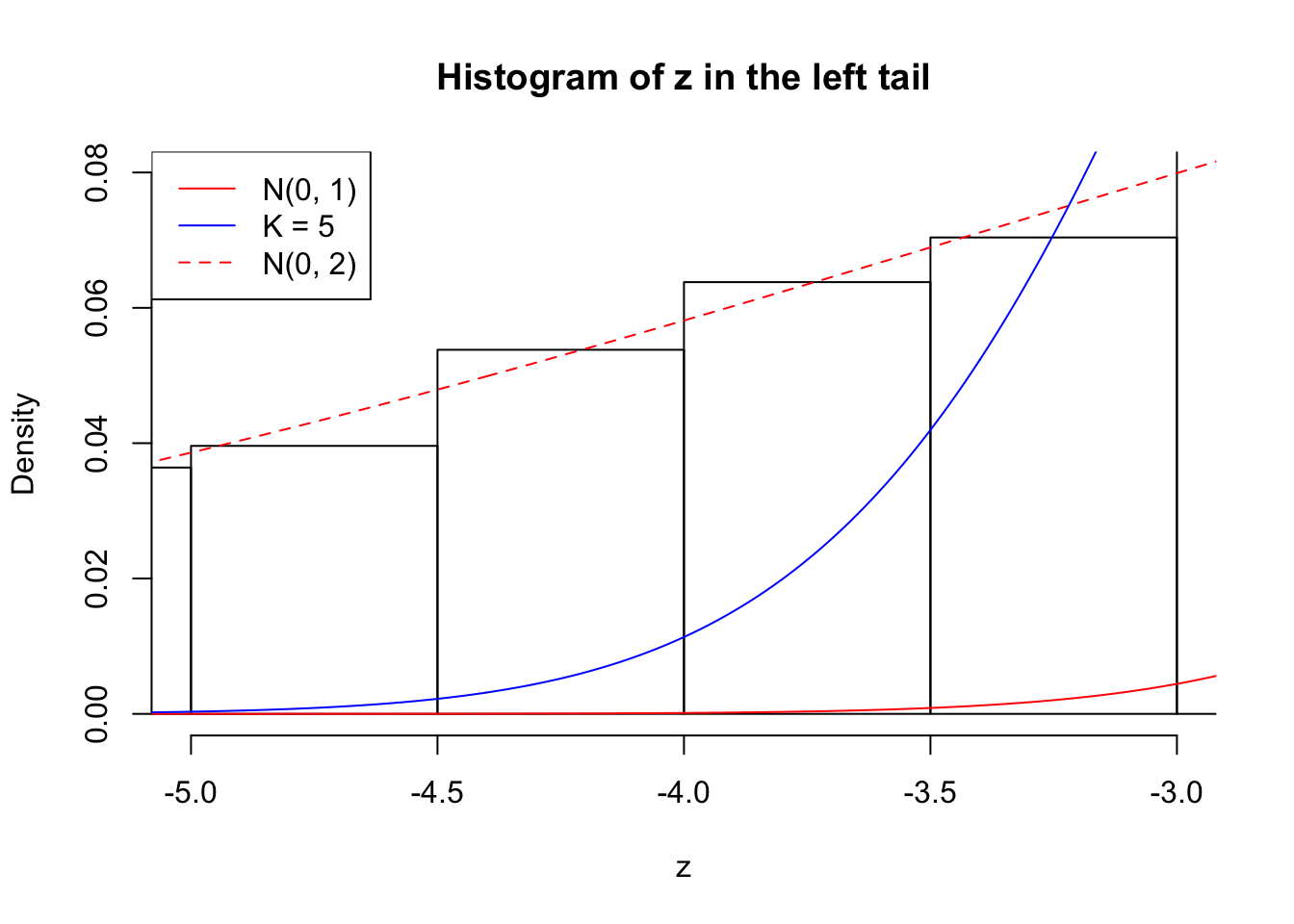
Zoom in to the right tail: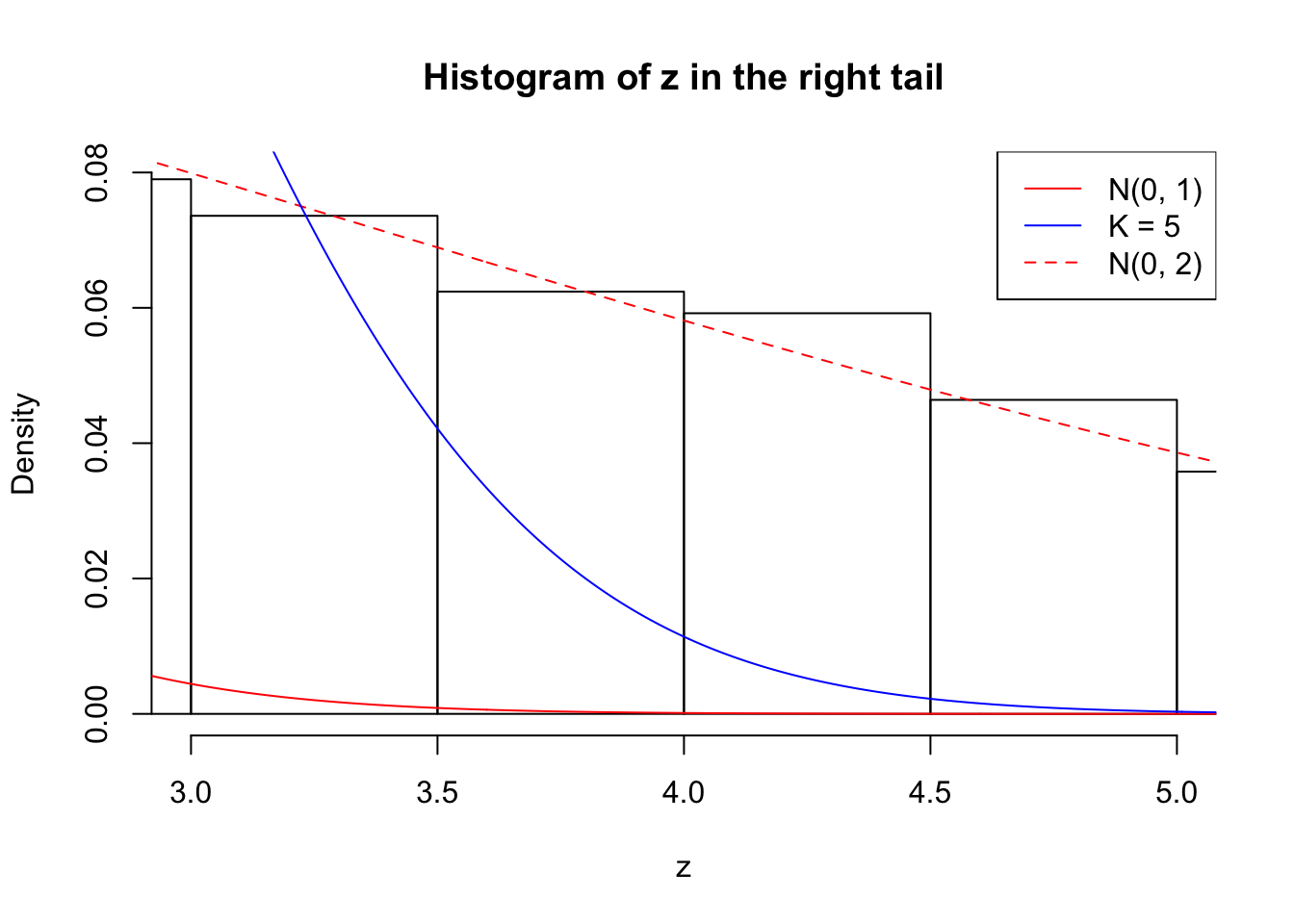
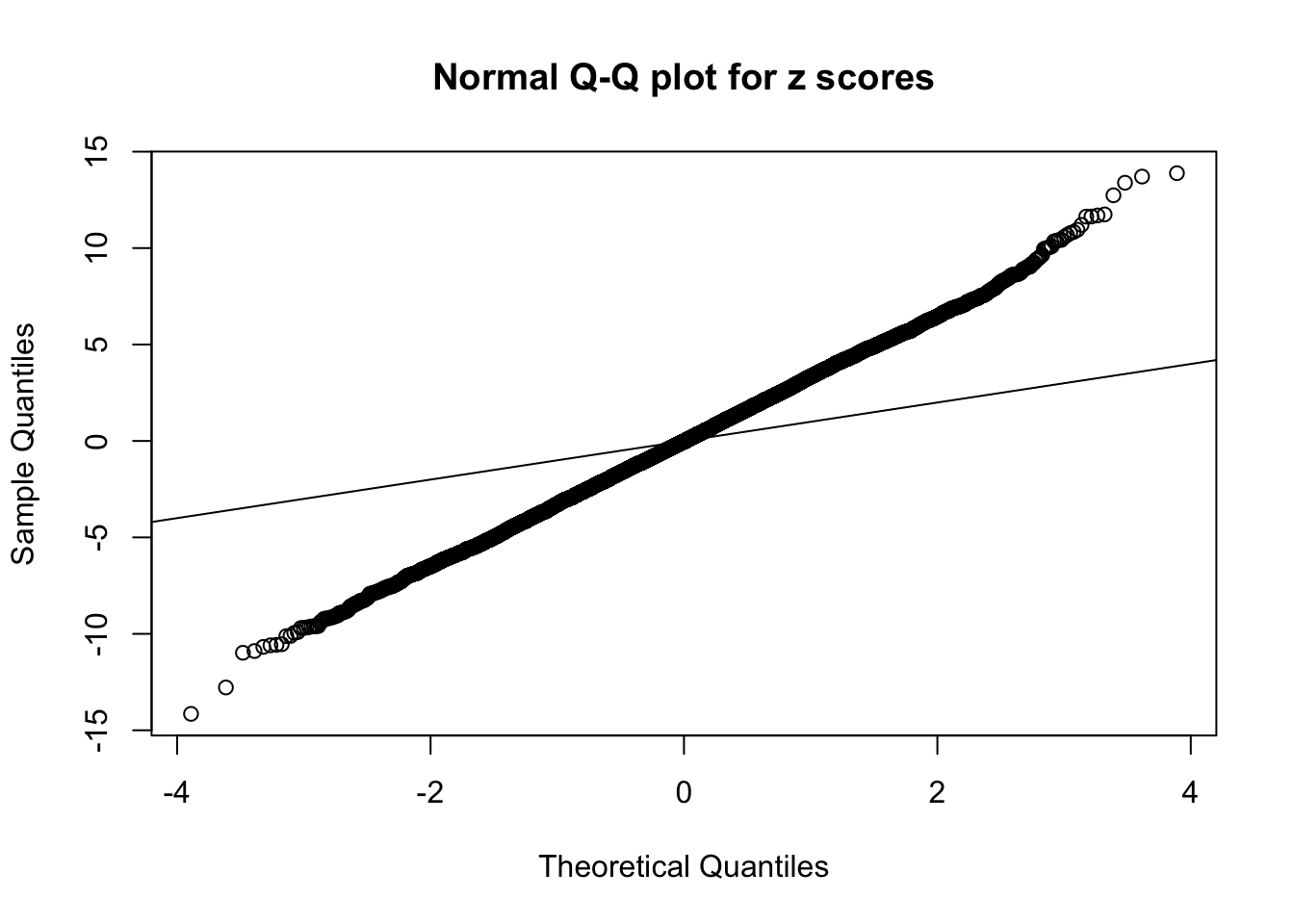
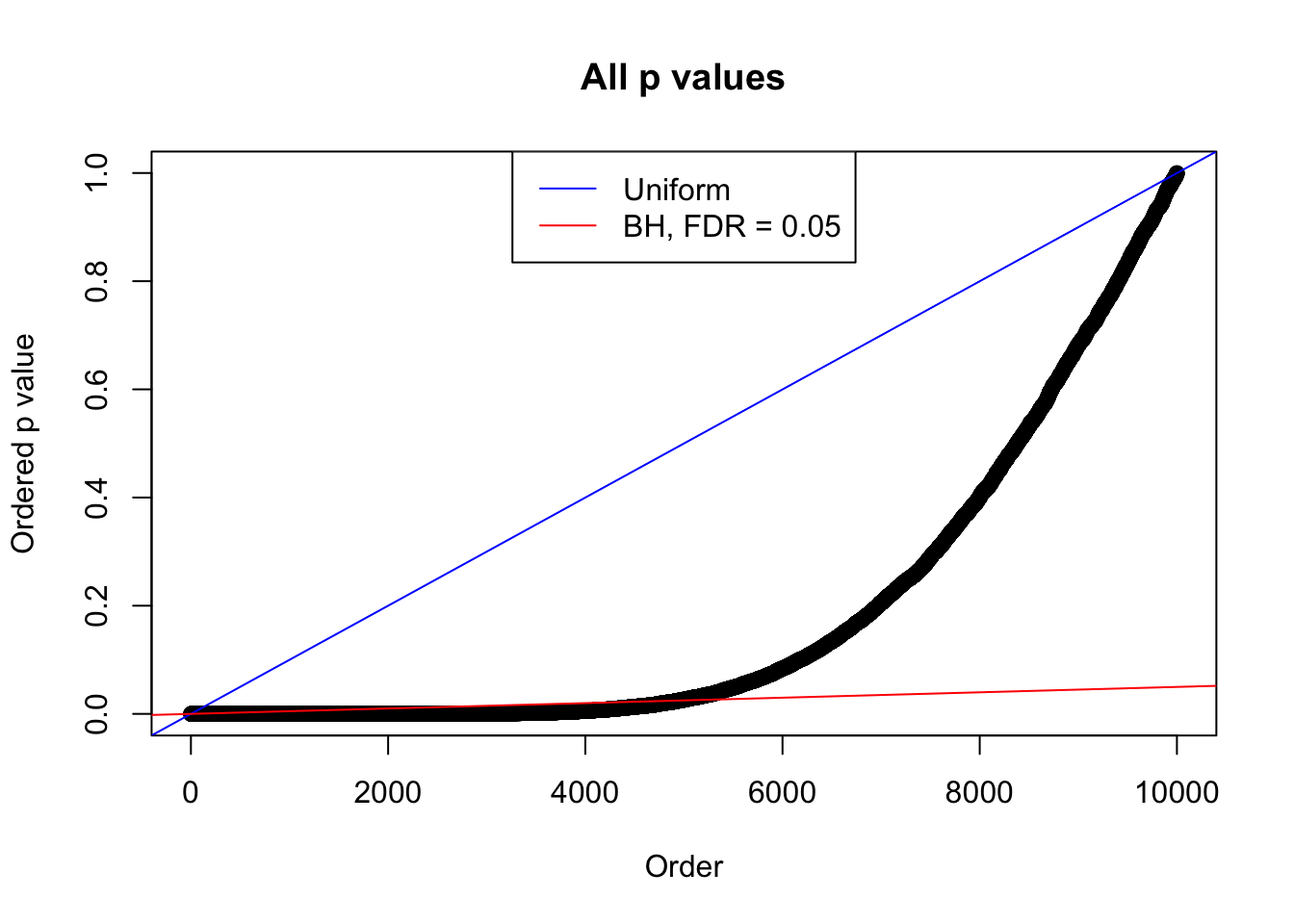
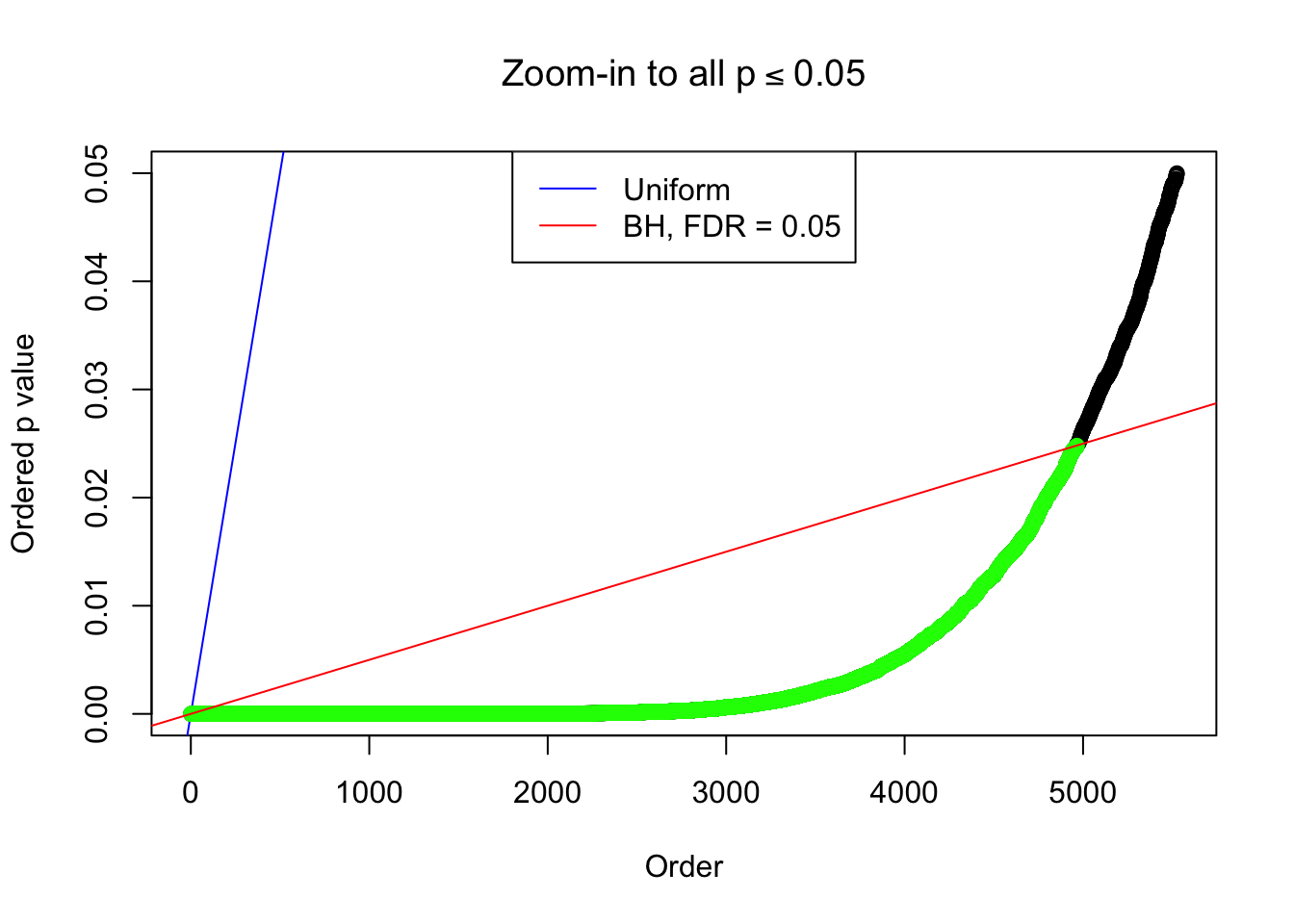
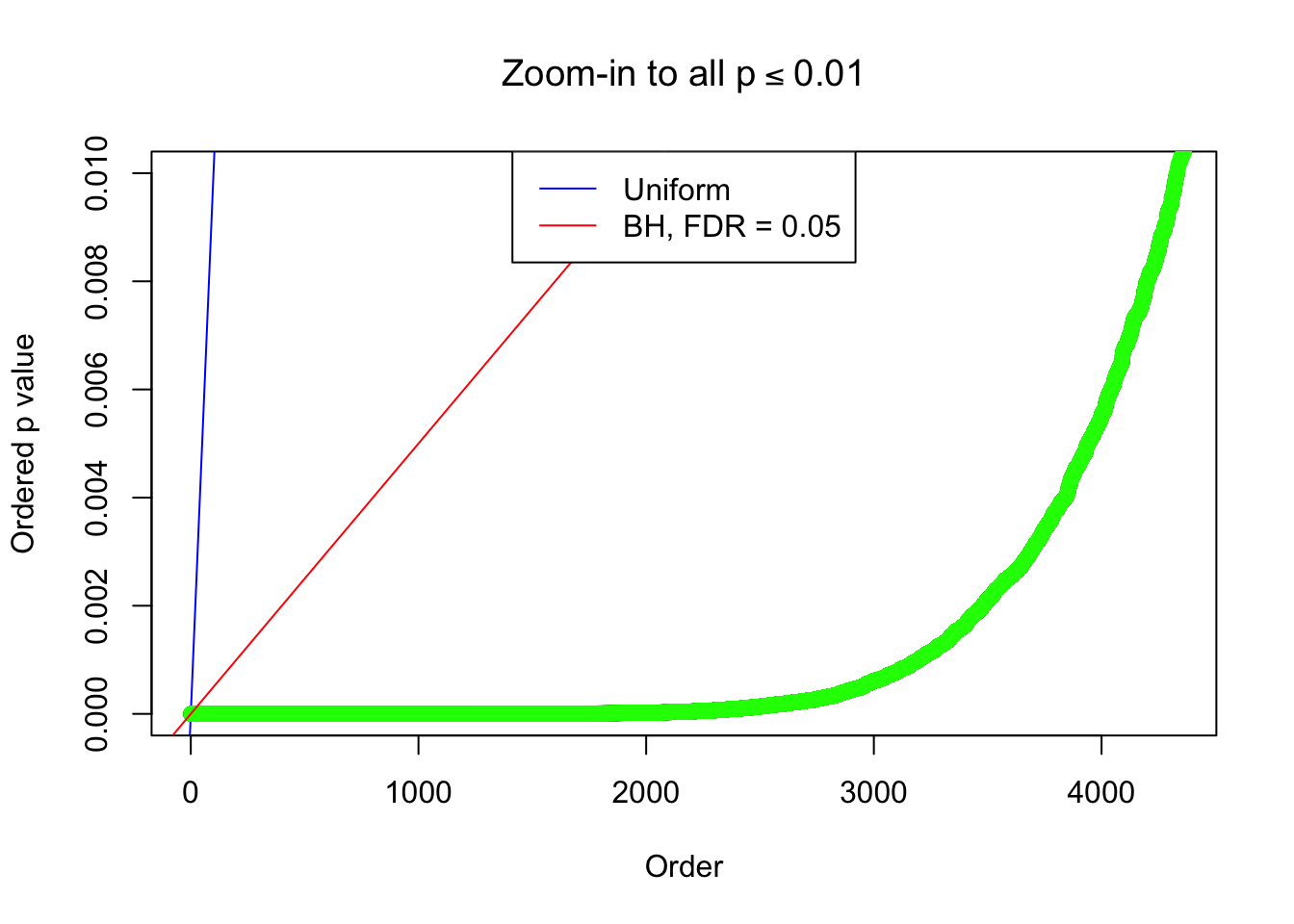
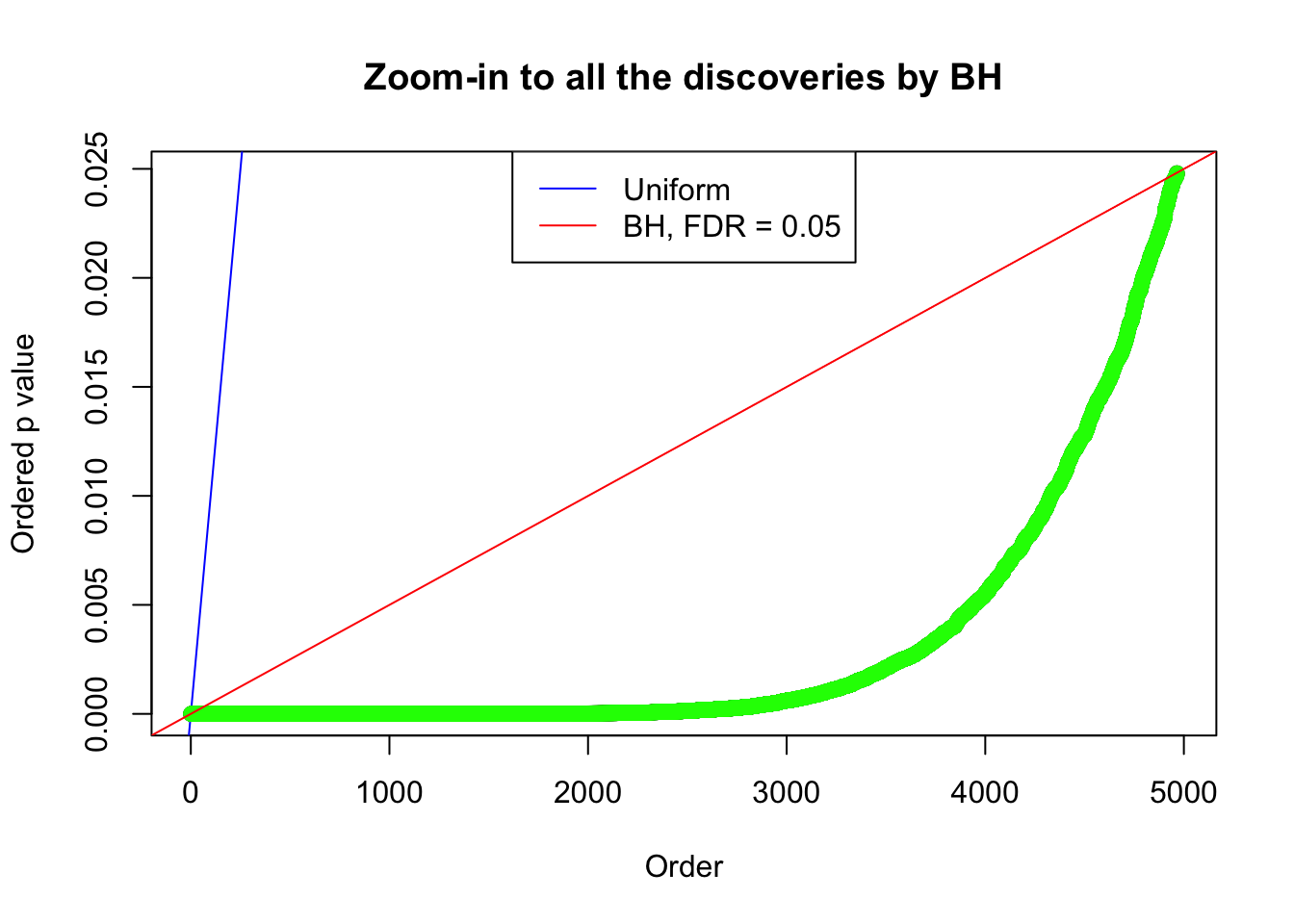
Example 5 : True Distribution: N(0, 11 ); Number of Discoveries: 4906 ; pihat0 = 0.06347912
Log-likelihood with N(0, 2): -39867.33
Log-likelihood with Gaussian Derivatives: -43879.25
Log-likelihood ratio between true N(0, 2) and fitted Gaussian derivatives: 4011.923
Normalized weights:
1 : -0.0276238416835523 ; 2 : 2.22721330383646 ; 3 : -0.0594743974219201 ; 4 : 1.80111999596238 ; 5 : -0.00705084272022214 ;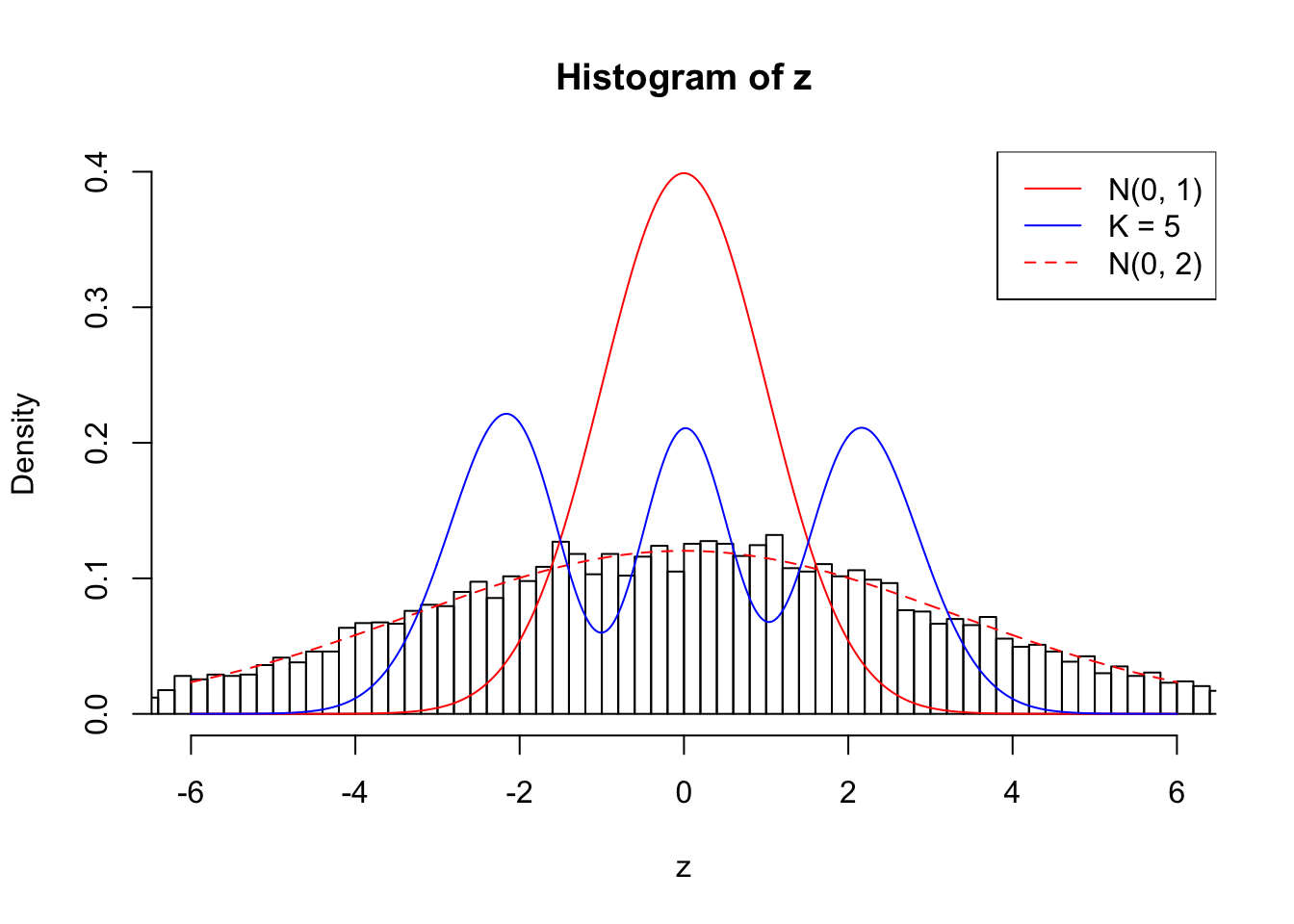
Zoom in to the left tail: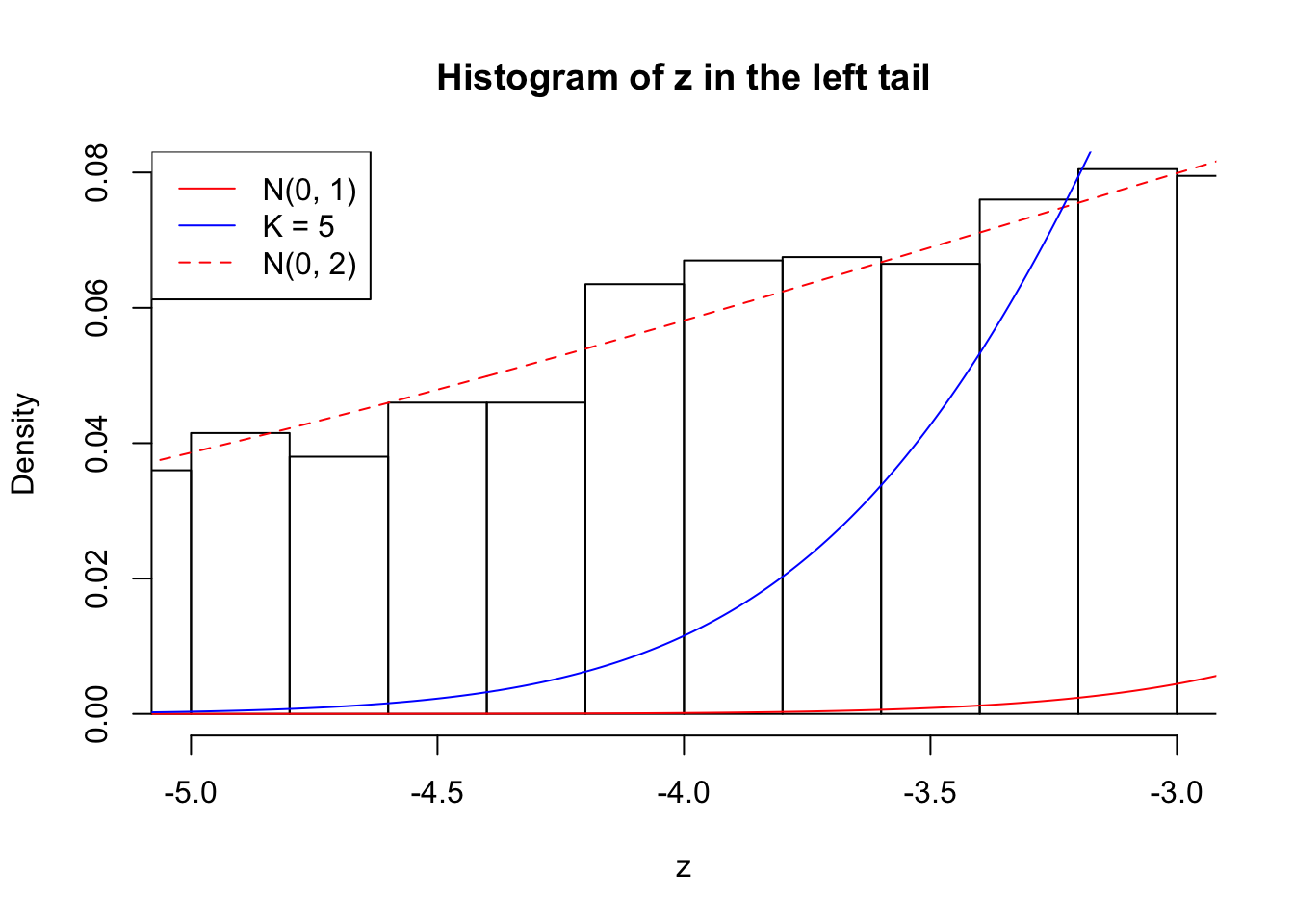
Zoom in to the right tail: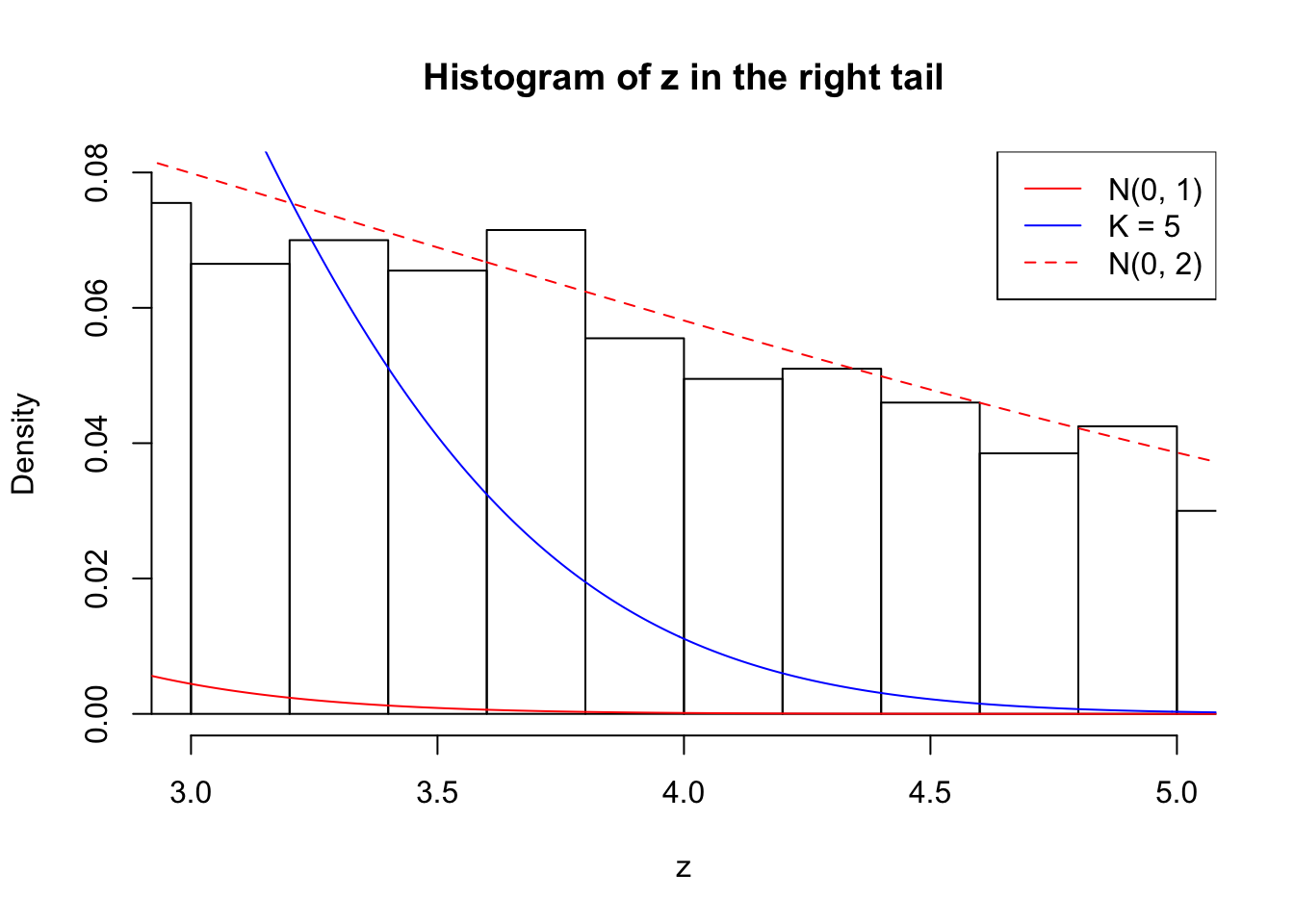
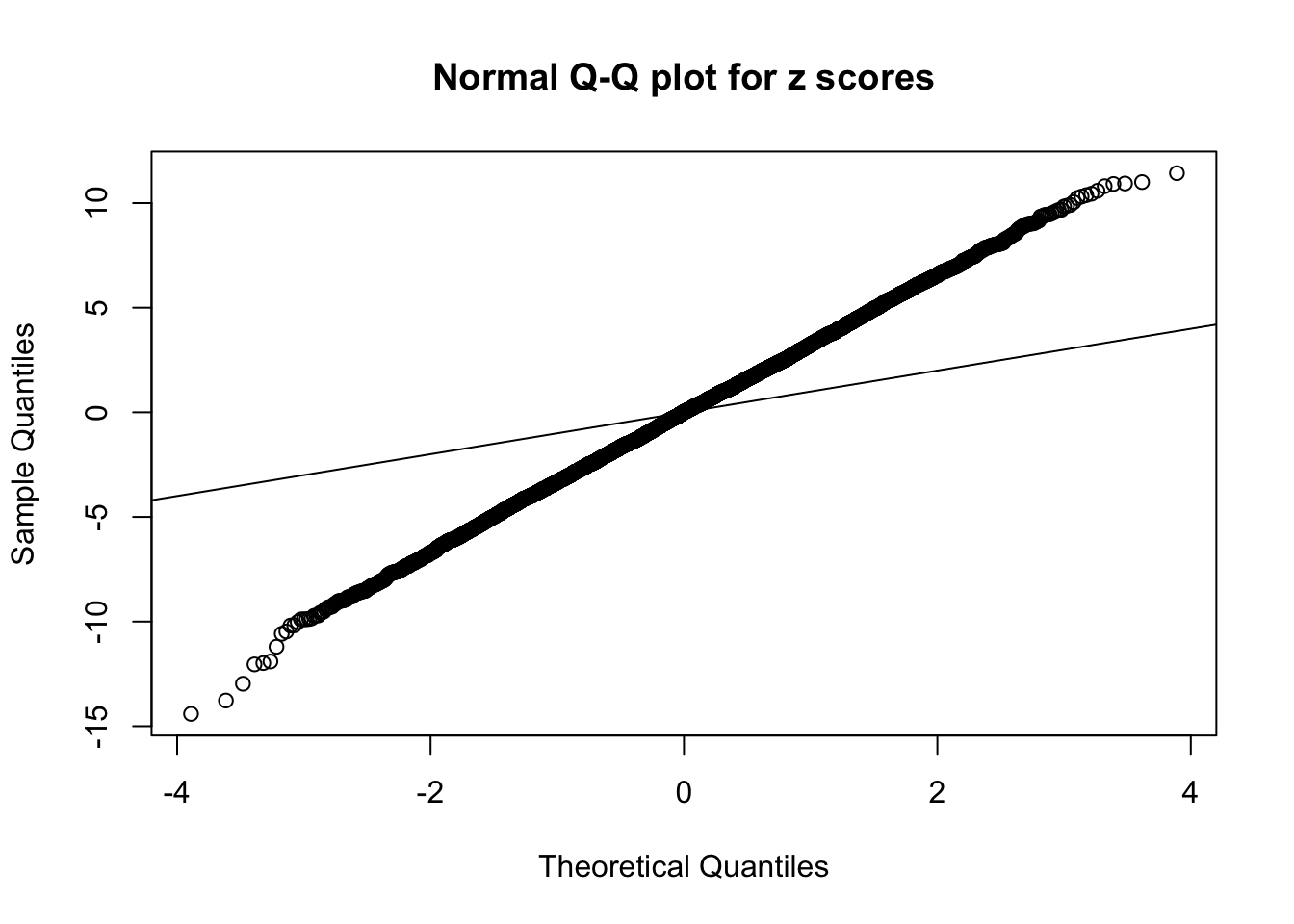
Session information
sessionInfo()R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.4
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] cvxr_0.0.0.9009 EQL_1.0-0 ttutils_1.0-1 ashr_2.1.5
loaded via a namespace (and not attached):
[1] Rcpp_0.12.10 knitr_1.15.1 magrittr_1.5
[4] MASS_7.3-45 doParallel_1.0.10 pscl_1.4.9
[7] SQUAREM_2016.10-1 lattice_0.20-34 foreach_1.4.3
[10] stringr_1.2.0 tools_3.3.2 parallel_3.3.2
[13] grid_3.3.2 git2r_0.18.0 htmltools_0.3.5
[16] iterators_1.0.8 yaml_2.1.14 rprojroot_1.2
[19] digest_0.6.11 Matrix_1.2-7.1 codetools_0.2-15
[22] evaluate_0.10 rmarkdown_1.3 stringi_1.1.2
[25] backports_1.0.5 truncnorm_1.0-7 This R Markdown site was created with workflowr