Last updated: 2018-05-28

workflowr checks: (Click a bullet for more information)

  • ✔ R Markdown file: up-to-date

    Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

  • ✔ Environment: empty

    Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

  • ✔ Seed: set.seed(20180501)

    The command set.seed(20180501) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

  • ✔ Session information: recorded

    Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

  • ✔ Repository version: d0a7fde

    Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

    Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 
    
Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    log/

Untracked files:
    Untracked:  analysis/binom.Rmd
    Untracked:  analysis/glm.Rmd
    Untracked:  analysis/overdis.Rmd
    Untracked:  analysis/smashtutorial.Rmd
    Untracked:  analysis/test.Rmd
    Untracked:  data/treas_bill.csv
    Untracked:  docs/figure/smashtutorial.Rmd/
    Untracked:  docs/figure/test.Rmd/

Unstaged changes:
    Modified:   analysis/ashpmean.Rmd
    Modified:   analysis/nugget.Rmd
    Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
Expand here to see past versions:
    File Version Author Date Message
    Rmd d0a7fde Dongyue 2018-05-28 glm covariate
    Rmd 4d531f1 Dongyue 2018-05-28 glm covariate

Introduction

Consider estimating spatially-structured \(\mu_t\) from Poisson sequence: \[Y_t\sim Poisson(\lambda_t).\] We assume that \(\lambda_t\) satisfies \[\log(\lambda_t)=X_t'\beta+\mu_t\], where \(X_t\) are \(p-\)dimensional covaraites and \(\beta\) is unknown coefficients.

For Bionomial sequence: \[Y_t\sim Binomial(n_t,p_t).\] Assume that \[logit(p_t)=X_t'\beta+\mu_t\], where \(\mu_t\) has smooth structure.

Method

Apply ash to \(Y_t\) and let the posterior mean be \(\tilde\lambda_t\). Define \(\tilde Y_t=\log(\tilde\lambda_t)+\frac{Y_t-\tilde\lambda_t}{\tilde\lambda_t}\) and apply smash.gaus allowing covariates method to \(\tilde Y_t\), which gives \(\hat\mu_t\) and \(\hat\beta\). The recovered smooth mean structure is given by \(\exp(\hat\mu_t)\).

Similarly to Binomial data, \(\tilde Y_t=logit(\tilde p_t)+\frac{Y_t/n_t-\tilde p_t}{\tilde p_t(1-\tilde p_t)}\).

Simulations

Data generation

Poisson sequence: Given \(\mu_t, t=1,2,\dots,T\), \(\lambda_t=\exp(\mu_t+X_t'\beta+N(0,\sigma^2))\), generate \(Y_t\sim Poisson(\lambda_t)\).

Bionimial sequence(\(p\)): Given \(\mu_t, t=1,2,\dots,T\),\(p_t=logit(\mu_t+X_t'\beta+N(0,\sigma^2))\), generate \(Y_t\sim Binomial(n_t,p_t)\), where \(n_t\) is given.

For each case, we run 3 times of simulation and plot the fitted curve.

Poisson Seq

The length of sequence \(T\) is set to be 256, covariates \(X_t\) are generate from \(N(0,I_{p\times p})\), and \(\beta\) is chosen to be \((1,2,-3,-4,5)\) then normalized to have unit norm.

simu_study_poix=function(mu,beta,sigma=1,snr=2,nsimu=3,filter.number=1,family='DaubExPhase',seed=1234){
  set.seed(1234)
  n=length(mu)
  p=length(beta)
  X=matrix(rnorm(n*p,0,1),nrow=n,byrow = T)
  Xbeta=X%*%beta
  mu.est=c()
  beta.est=c()
  y.data=c()
  #lambda.null=exp(mu+Xbeta)
  #var.st=1/mean(lambda.null)
  #var.mu=var(mu)
  #sigma=sqrt(max(var.mu/(snr^2)-var.st,0))
  for(s in 1:nsimu){
    lambda=exp(mu+Xbeta+rnorm(n,0,sigma))
    yt=rpois(n,lambda)
    fit=smash_gen_x_lite(yt,X,wave_family = family,filter.number = filter.number,dist_family = 'poisson')
    mu.est=rbind(mu.est,fit$mu.est)
    beta.est=rbind(beta.est,fit$beta.est)
    y.data=rbind(y.data,yt)
  }
  return(list(mu.est=mu.est,beta.est=beta.est,y=y.data,X=X,sigma=sigma))
}
beta=c(1,2,-3,-4,5)
beta=beta/norm(beta,'2')

Step

mu=c(rep(2,128), rep(5, 128), rep(6, 128), rep(2, 128))
result=simu_study_poix(mu,beta)
plot(result$mu.est[1,],type='l',col=2,ylab = '',main='Estimated mean function(mu), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(exp(mu),lty=2)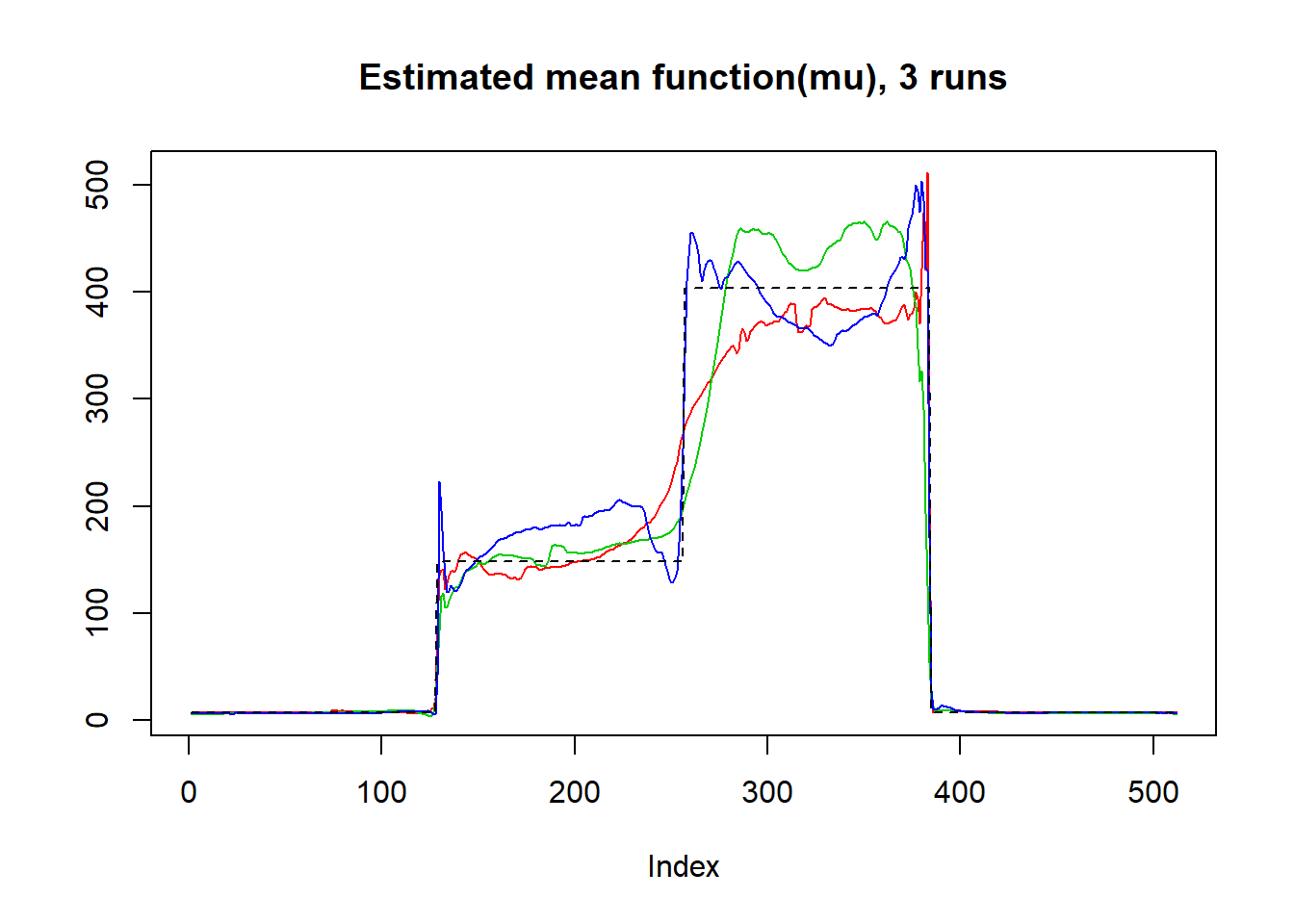

plot(log(result$mu.est[1,]),type='l',col=2,ylab = '',main='Estimated mean function(log mu), 3 runs')
lines(log(result$mu.est[2,]),col=3)
lines(log(result$mu.est[3,]),col=4)
lines(mu,lty=2)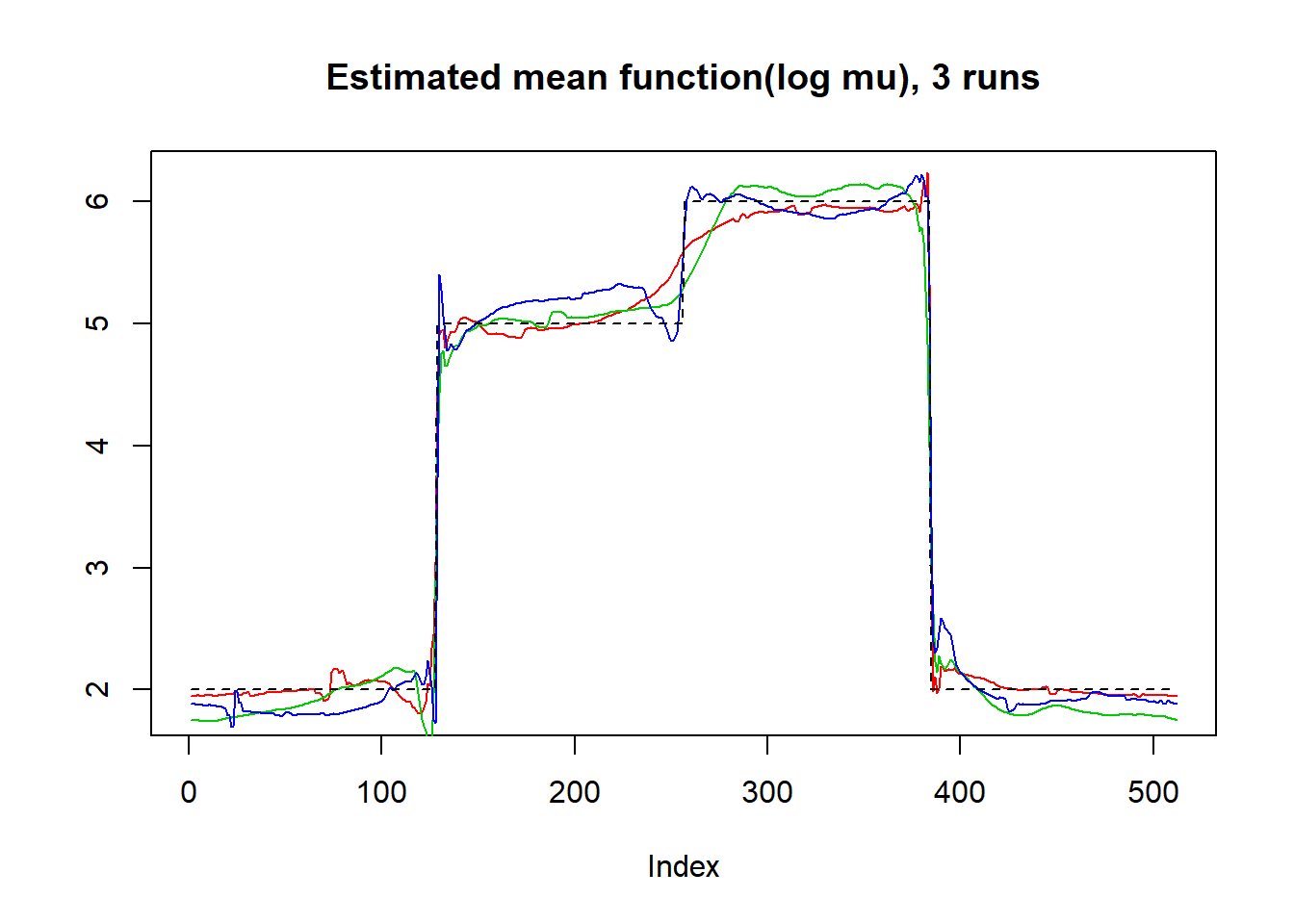

plot(beta,result$beta.est[1,],col=2,pch=1,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[3,],col=4,pch=3,type='p')
abline(0,1,lty=2)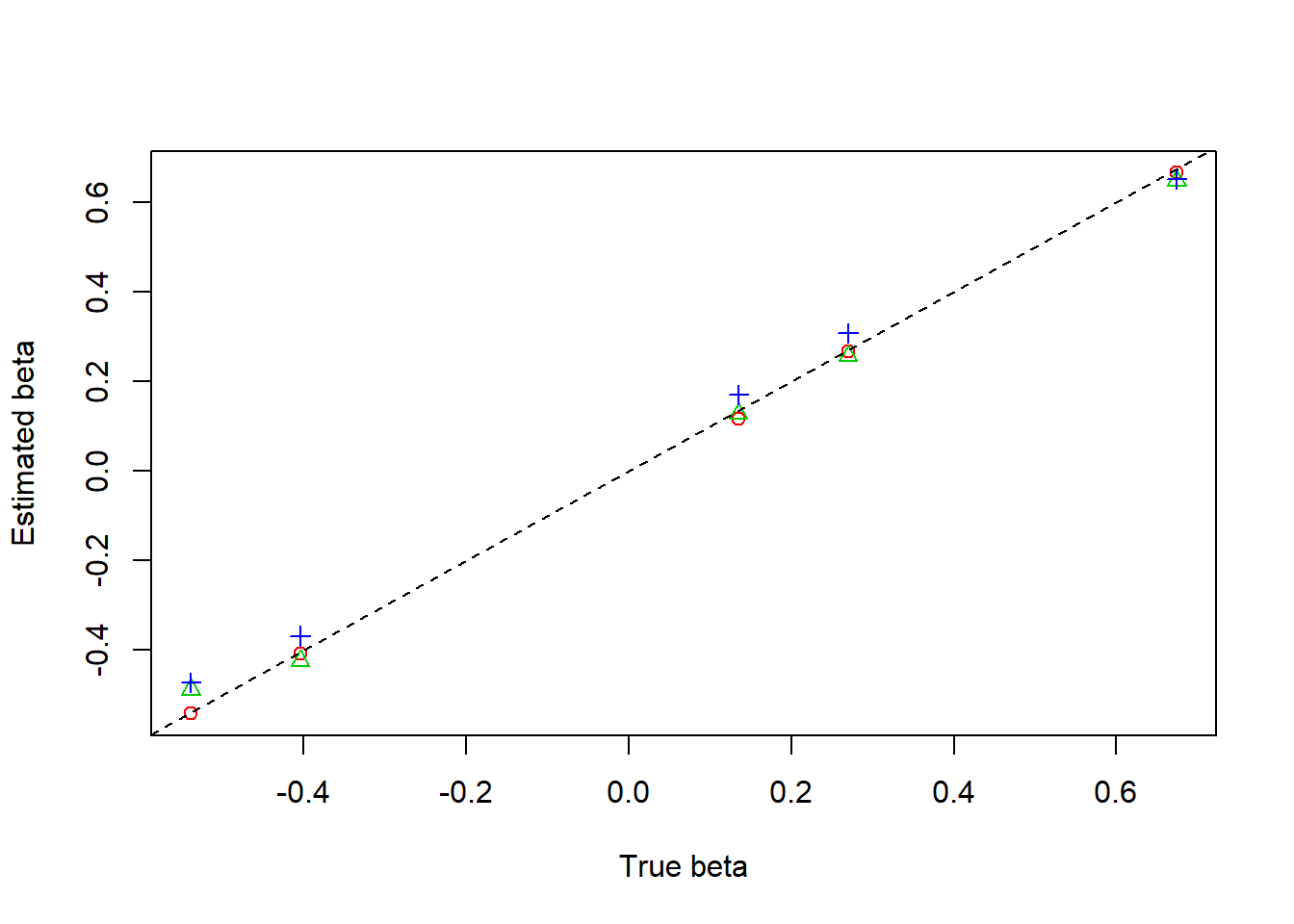

Bumps

m=seq(0,1,length.out = 256)
h = c(4, 5, 3, 4, 5, 4.2, 2.1, 4.3, 3.1, 5.1, 4.2)
w = c(0.005, 0.005, 0.006, 0.01, 0.01, 0.03, 0.01, 0.01, 0.005,0.008,0.005)
t=c(.1,.13,.15,.23,.25,.4,.44,.65,.76,.78,.81)
f = c()
for(i in 1:length(m)){
  f[i]=sum(h*(1+((m[i]-t)/w)^4)^(-1))
}
mu=f*1.2

result=simu_study_poix(mu,beta)
plot(exp(mu),lty=2,ylab = '',main='Estimated mean function(mu), 3 runs',type = 'l')
lines(result$mu.est[1,],type='l',col=2)
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)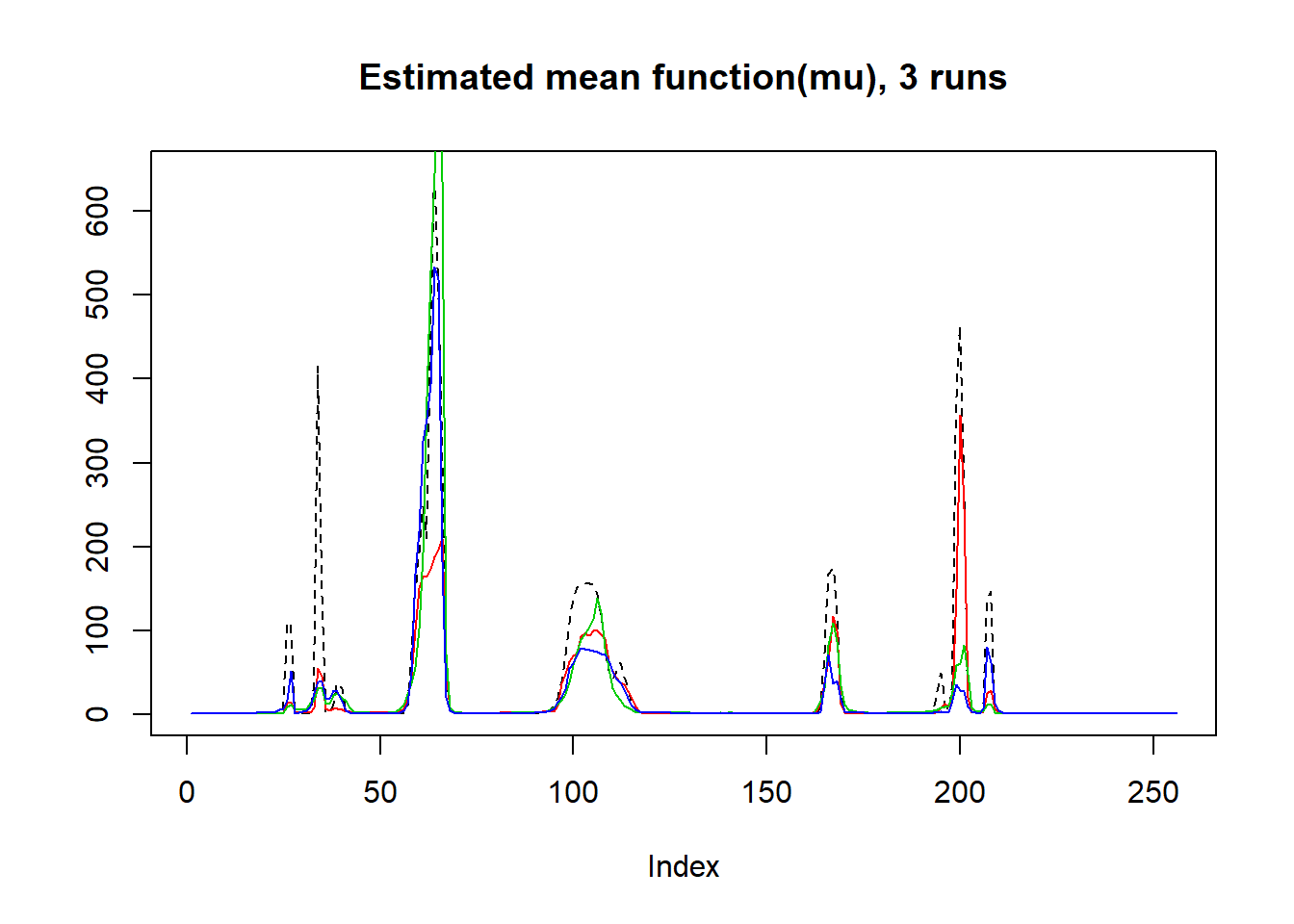

plot(mu,lty=2,ylab = '',main='Estimated mean function(log mu), 3 runs',type = 'l')
lines(log(result$mu.est[1,]),type='l',col=2)
lines(log(result$mu.est[2,]),col=3)
lines(log(result$mu.est[3,]),col=4)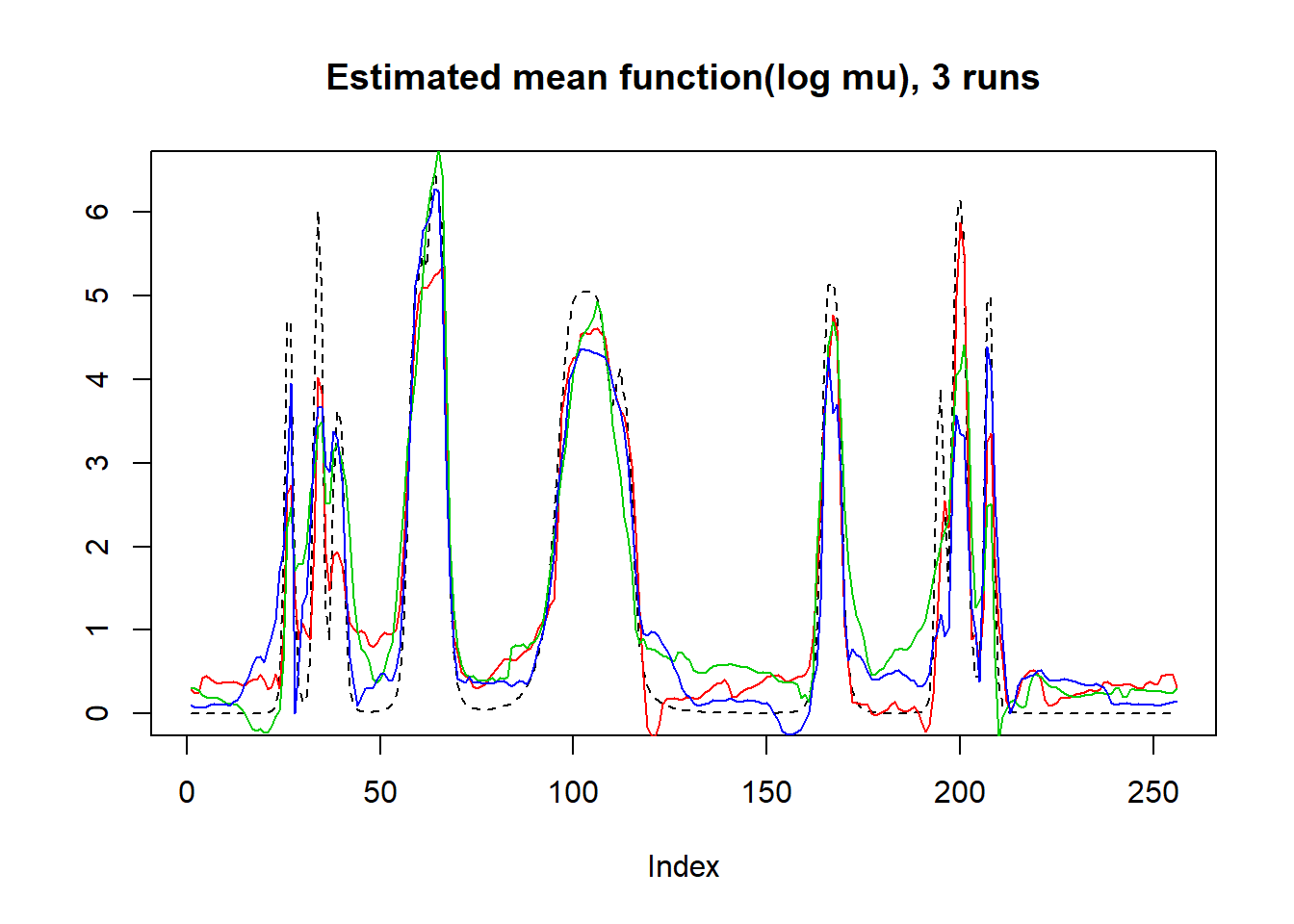

plot(beta,result$beta.est[3,],col=4,pch=3,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[1,],col=2,pch=1,type='p')
abline(0,1,lty=2)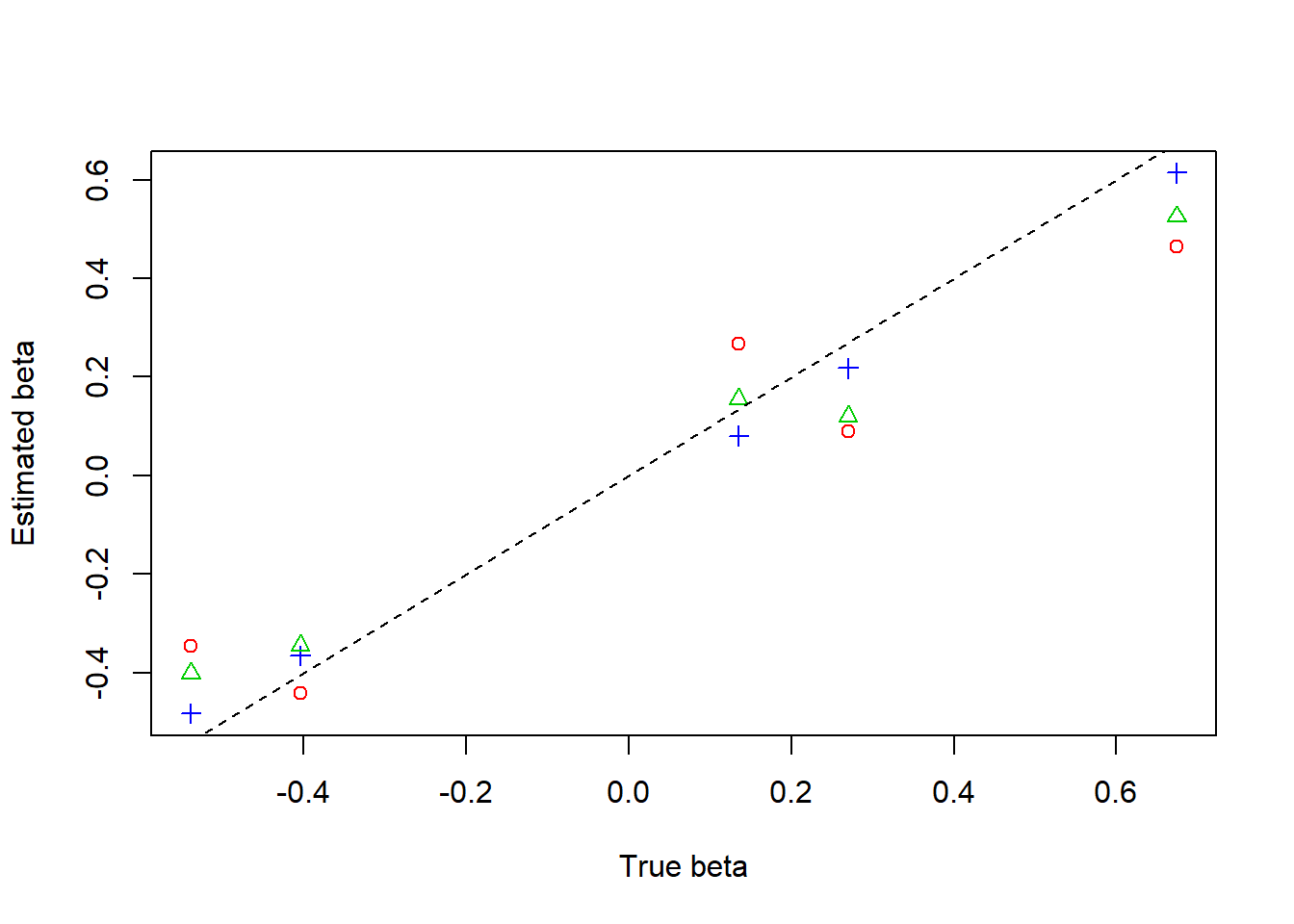

Parabola

r=function(x,c){return((x-c)^2*(x>c)*(x<=1))}
f=function(x){return(0.8 − 30*r(x,0.1) + 60*r(x, 0.2) − 30*r(x, 0.3) +
500*r(x, 0.35) − 1000*r(x, 0.37) + 1000*r(x, 0.41) − 500*r(x, 0.43) +
7.5*r(x, 0.5) − 15*r(x, 0.7) + 7.5*r(x, 0.9))}
mu=f(1:256/256)
mu=mu*7

result=simu_study_poix(mu,beta,filter.number = 8,family = 'DaubLeAsymm')
plot(result$mu.est[1,],type='l',col=2,ylab = '',main='Estimated mean function(mu), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(exp(mu),lty=2)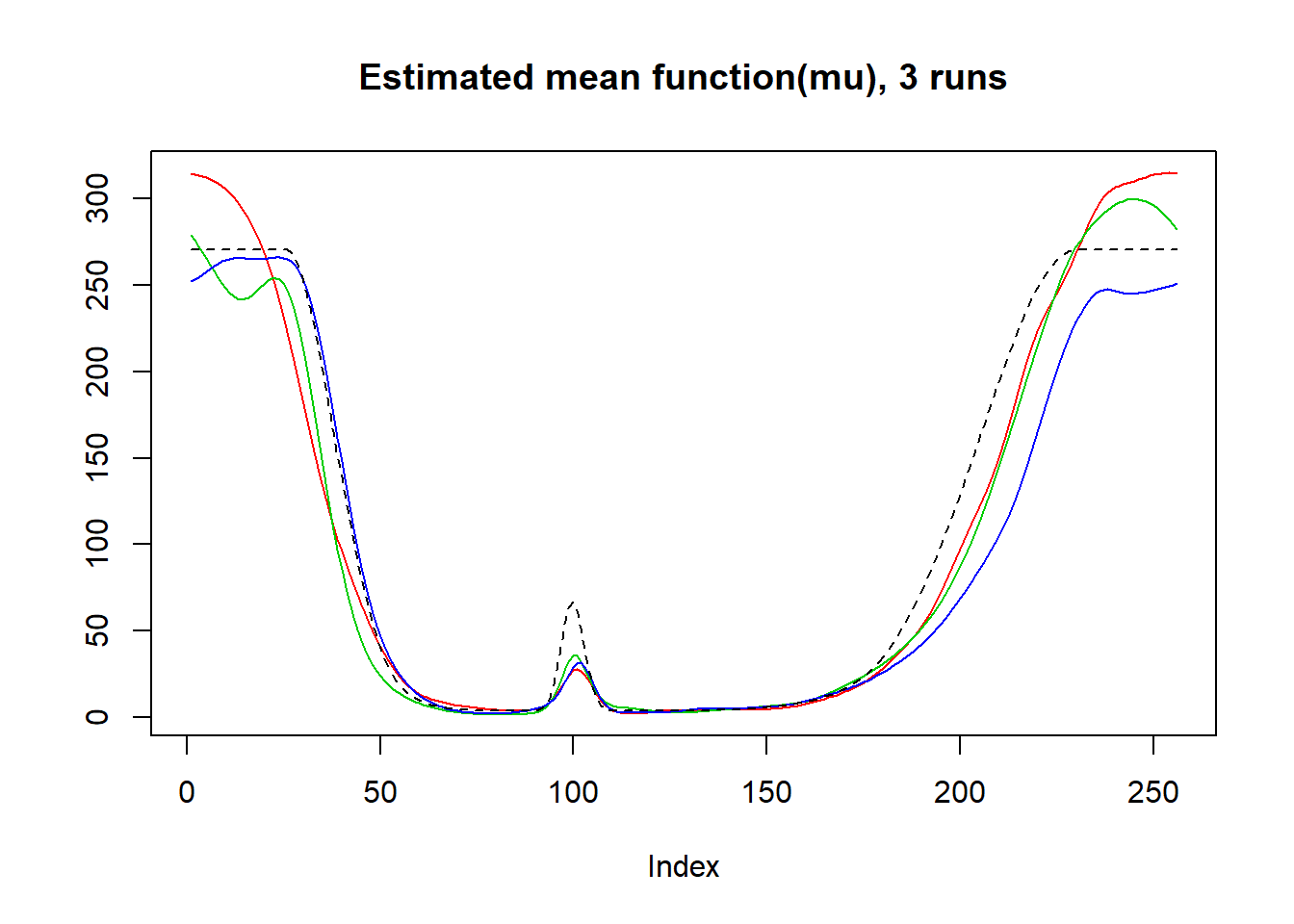

plot(log(result$mu.est[1,]),type='l',col=2,ylab = '',main='Estimated mean function(log mu), 3 runs')
lines(log(result$mu.est[2,]),col=3)
lines(log(result$mu.est[3,]),col=4)
lines(mu,lty=2)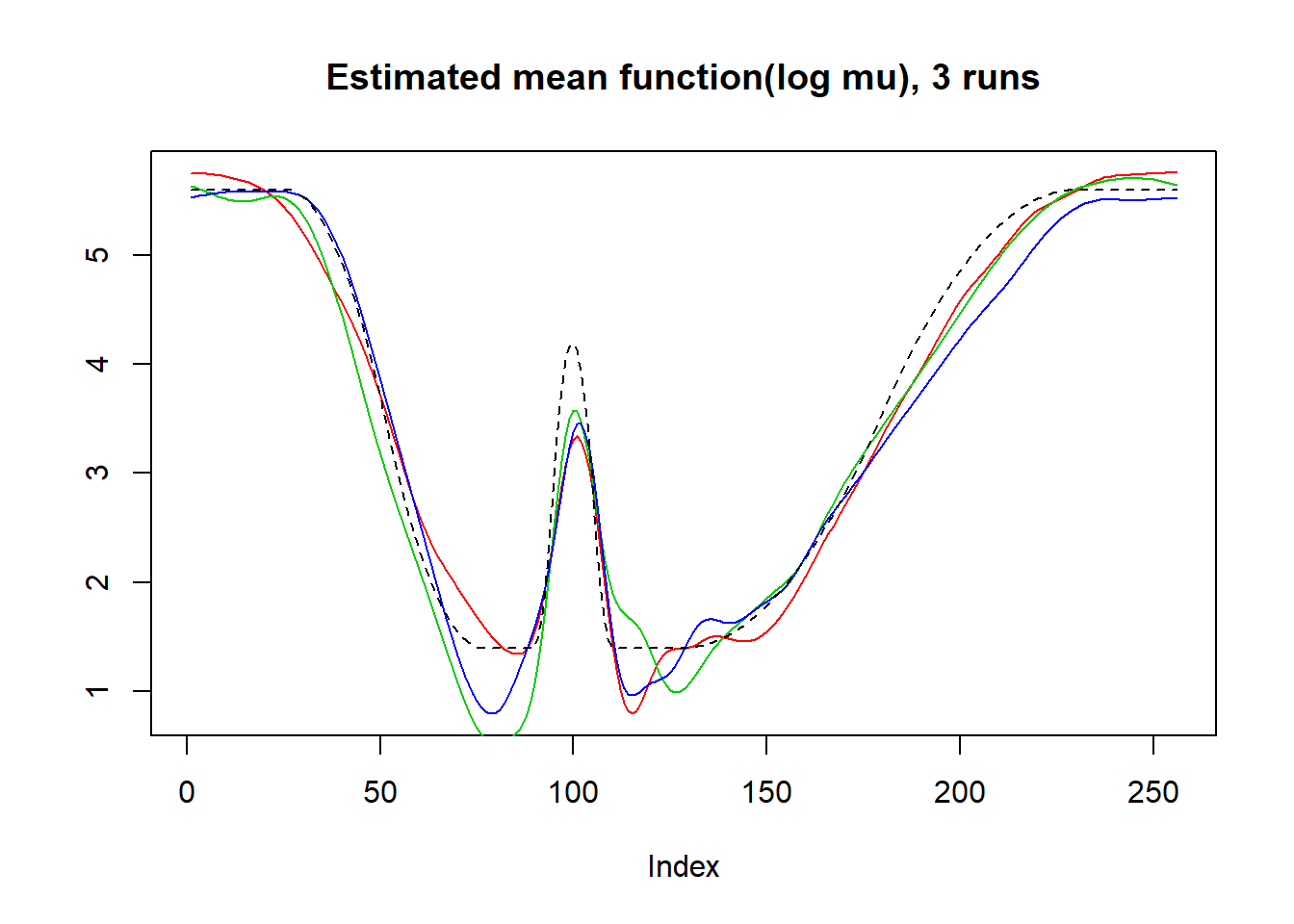

plot(beta,result$beta.est[1,],col=2,pch=1,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[3,],col=4,pch=3,type='p')
abline(0,1,lty=2)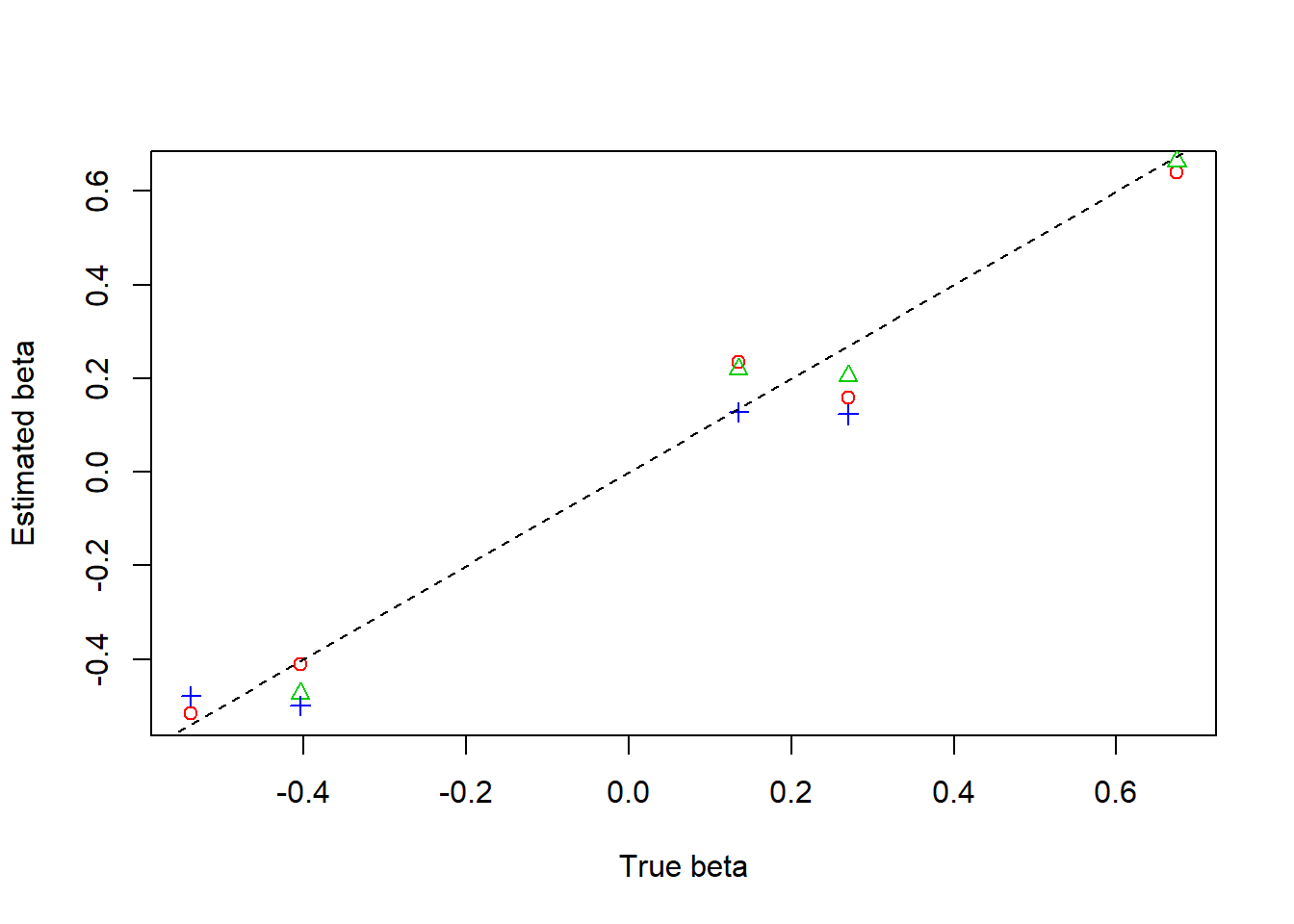

wave

f=function(x){return(0.5 + 2*cos(4*pi*x) + 2*cos(24*pi*x))}
mu=f(1:256/256)
mu=mu-min(mu)

result=simu_study_poix(mu,beta,filter.number = 8,family = 'DaubLeAsymm')
plot(exp(mu),lty=2,ylab = '',main='Estimated mean function(mu), 3 runs',type = 'l')
lines(result$mu.est[1,],type='l',col=2)
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)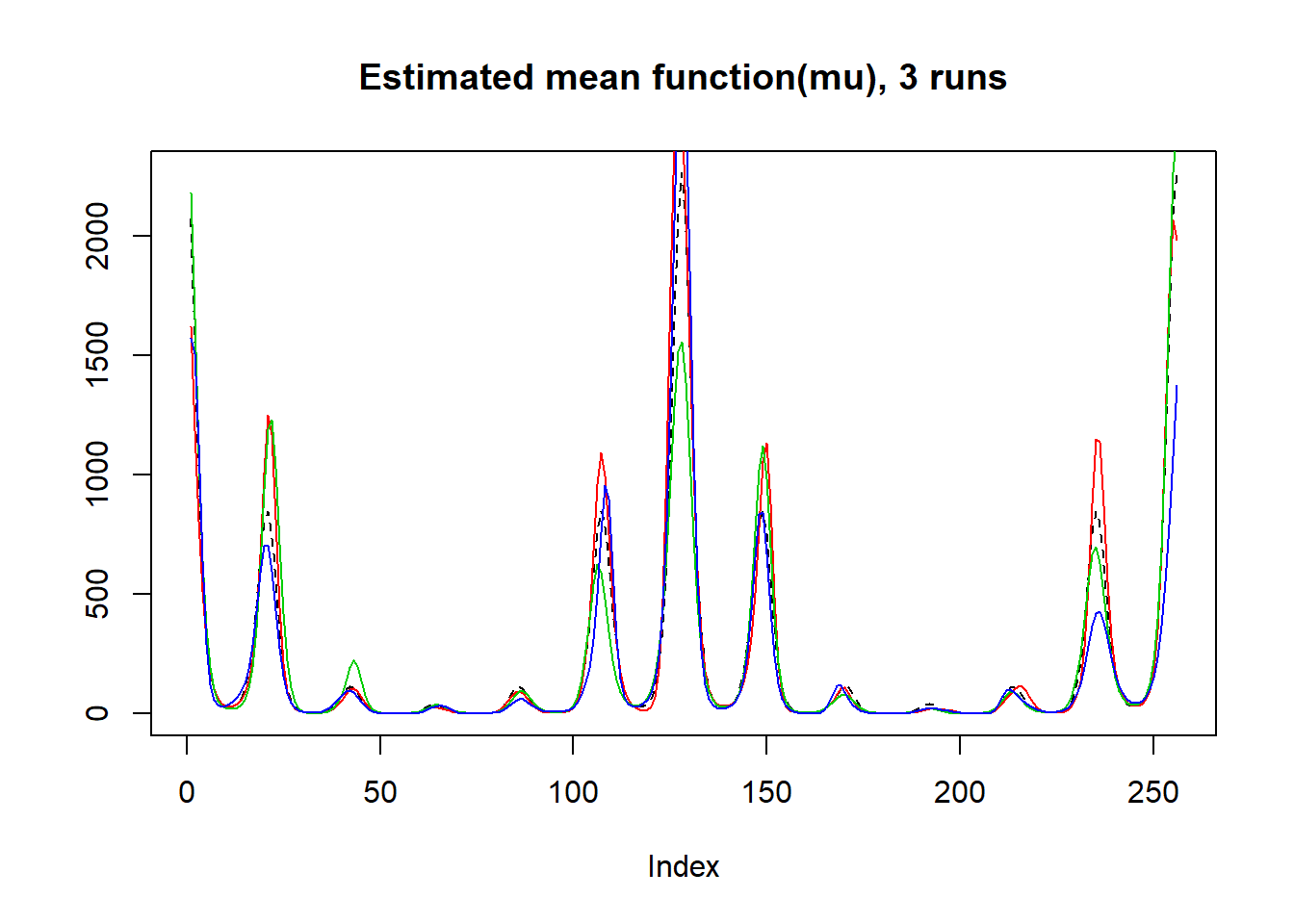

plot(mu,lty=2,ylab = '',main='Estimated mean function(log mu), 3 runs',type = 'l')
lines(log(result$mu.est[1,]),type='l',col=2)
lines(log(result$mu.est[2,]),col=3)
lines(log(result$mu.est[3,]),col=4)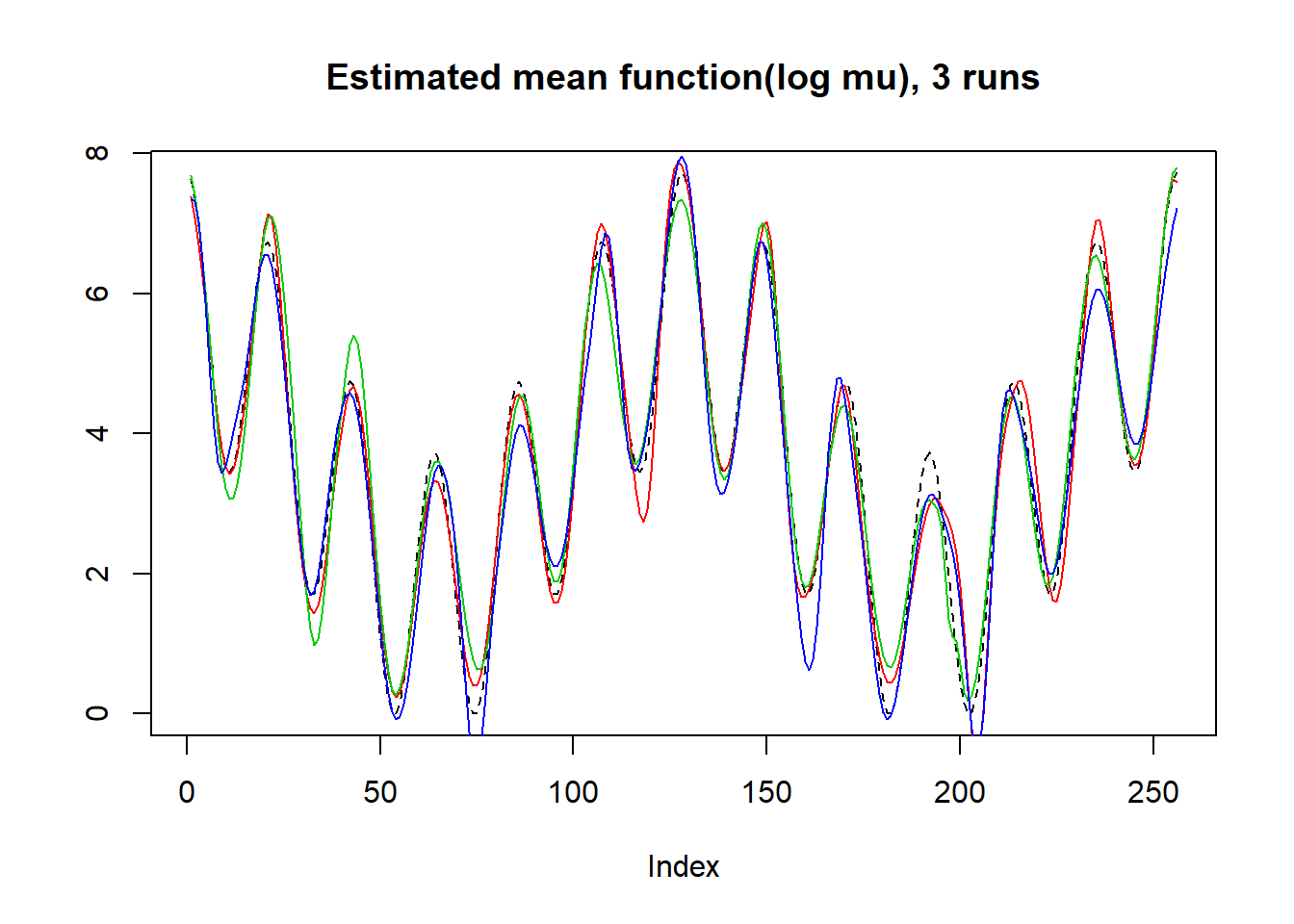

plot(beta,result$beta.est[1,],col=2,pch=1,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[3,],col=4,pch=3,type='p')
abline(0,1,lty=2)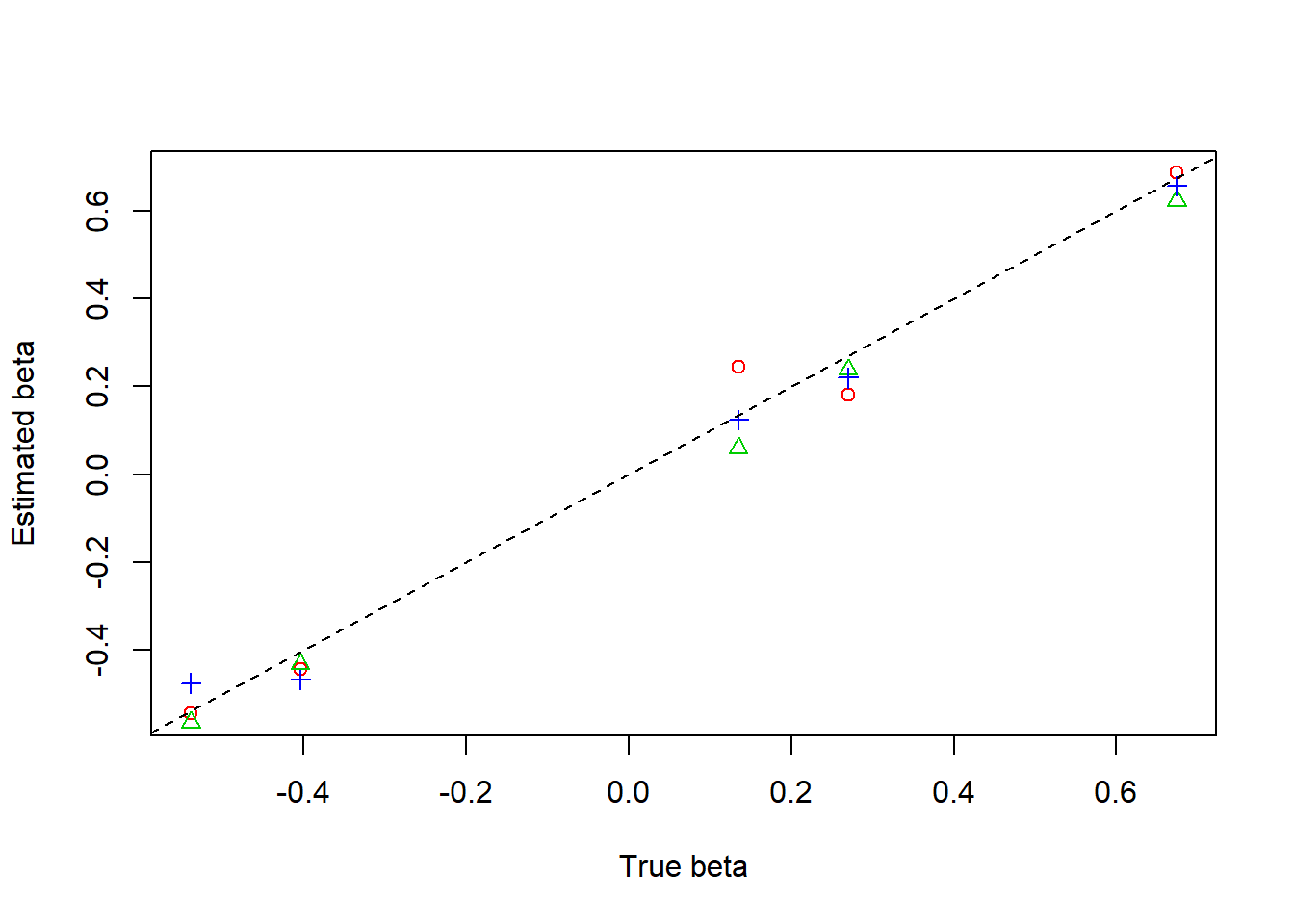

Binomial Seq

The length of sequence \(T\) is set to be 256, covariates \(X_t\) are generate from \(N(0,I_{p\times p})\), and \(\beta\) is chosen to be \((1,2,-3,-4,5)\) then normalized to have unit norm. \(n_t\) is from Poisson(50).

Step

mu=c(rep(-3,128), rep(0, 128), rep(3, 128), rep(-3, 128))
result=simu_study_binomx(mu,beta,ntri)
plot(result$mu.est[1,],type='l',col=2,ylab = '',main='Estimated mean function(p), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(logistic(mu),lty=2)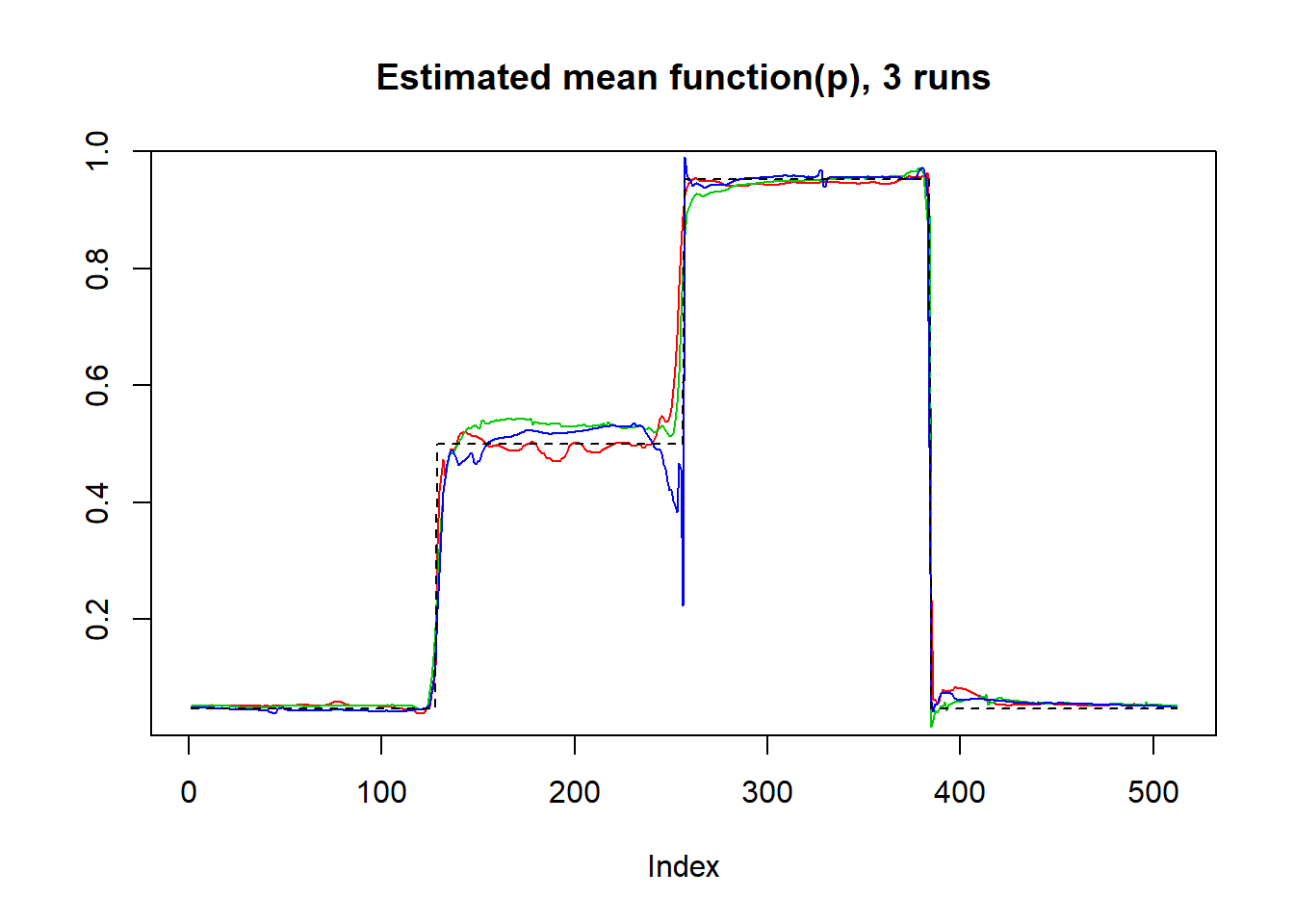

plot(logit(result$mu.est[1,]),type='l',col=2,ylab = '',main='Estimated mean function(logit p), 3 runs')
lines(logit(result$mu.est[2,]),col=3)
lines(logit(result$mu.est[3,]),col=4)
lines(mu,lty=2)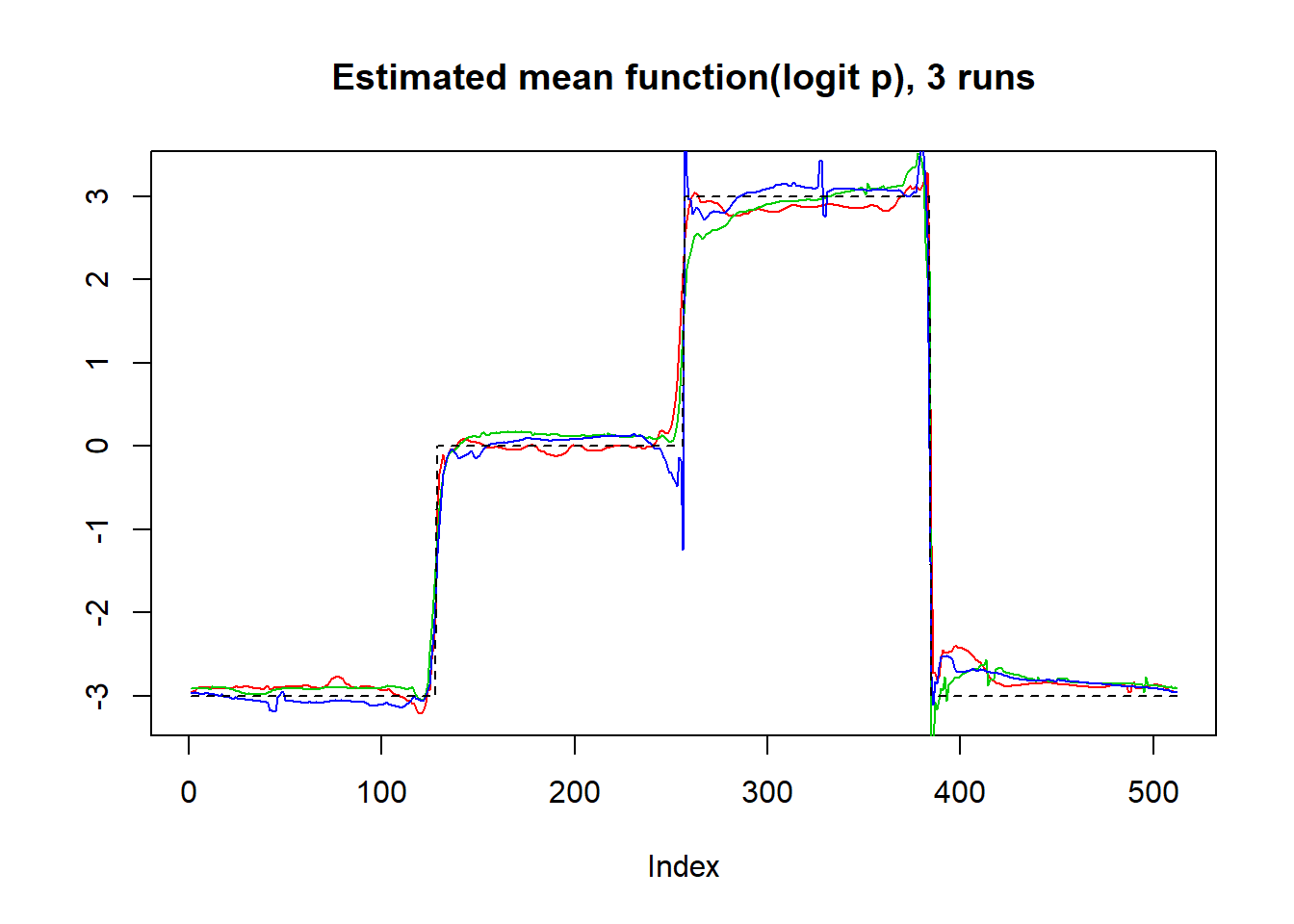

plot(beta,result$beta.est[3,],col=4,pch=3,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[1,],col=2,pch=1,type='p')
abline(0,1,lty=2)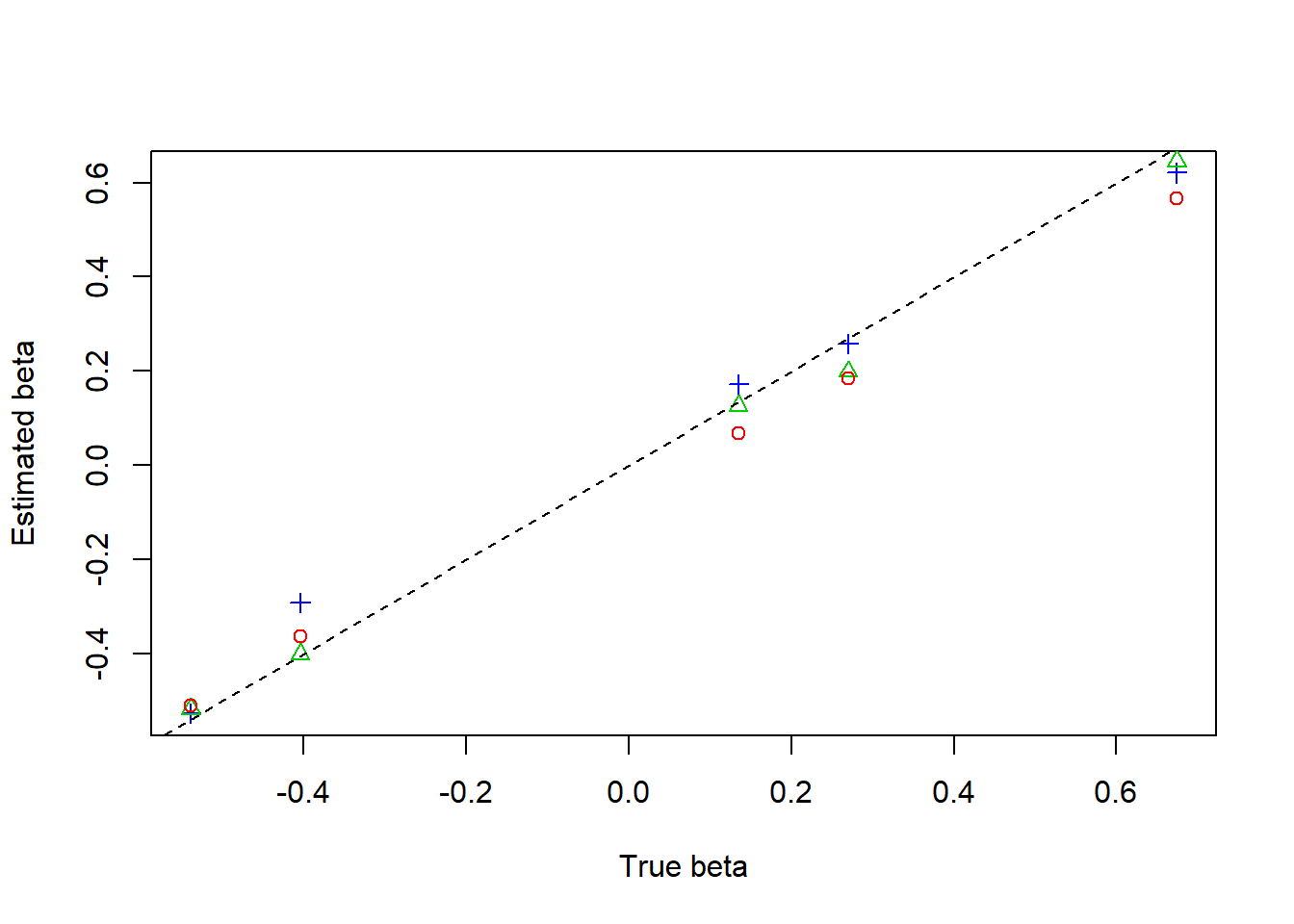

Bumps

m=seq(0,1,length.out = 256)
h = c(4, 5, 3, 4, 5, 4.2, 2.1, 4.3, 3.1, 5.1, 4.2)
w = c(0.005, 0.005, 0.006, 0.01, 0.01, 0.03, 0.01, 0.01, 0.005,0.008,0.005)
t=c(.1,.13,.15,.23,.25,.4,.44,.65,.76,.78,.81)
f = c()
for(i in 1:length(m)){
  f[i]=sum(h*(1+((m[i]-t)/w)^4)^(-1))
}
mu=f-3

result=simu_study_binomx(mu,beta,ntri)
plot(logistic(mu),lty=2,type='l',ylab = '',main='Estimated mean function(p), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(result$mu.est[1,],col=2)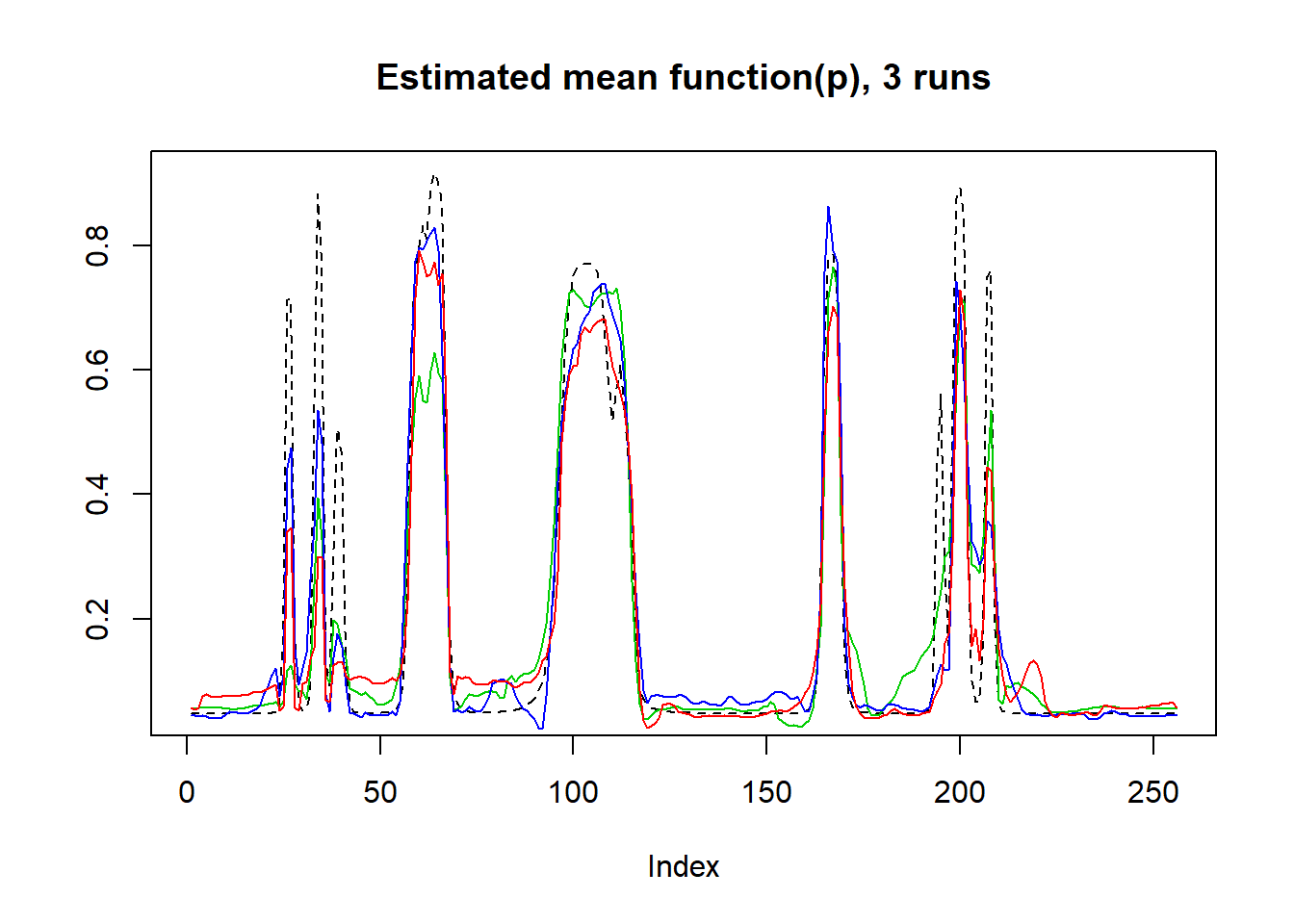

plot(mu,lty=2,type='l',ylab = '',main='Estimated mean function(logit p), 3 runs',ylim=c(-4,3))
lines(logit(result$mu.est[2,]),col=3)
lines(logit(result$mu.est[3,]),col=4)
lines(logit(result$mu.est[1,]),col=2)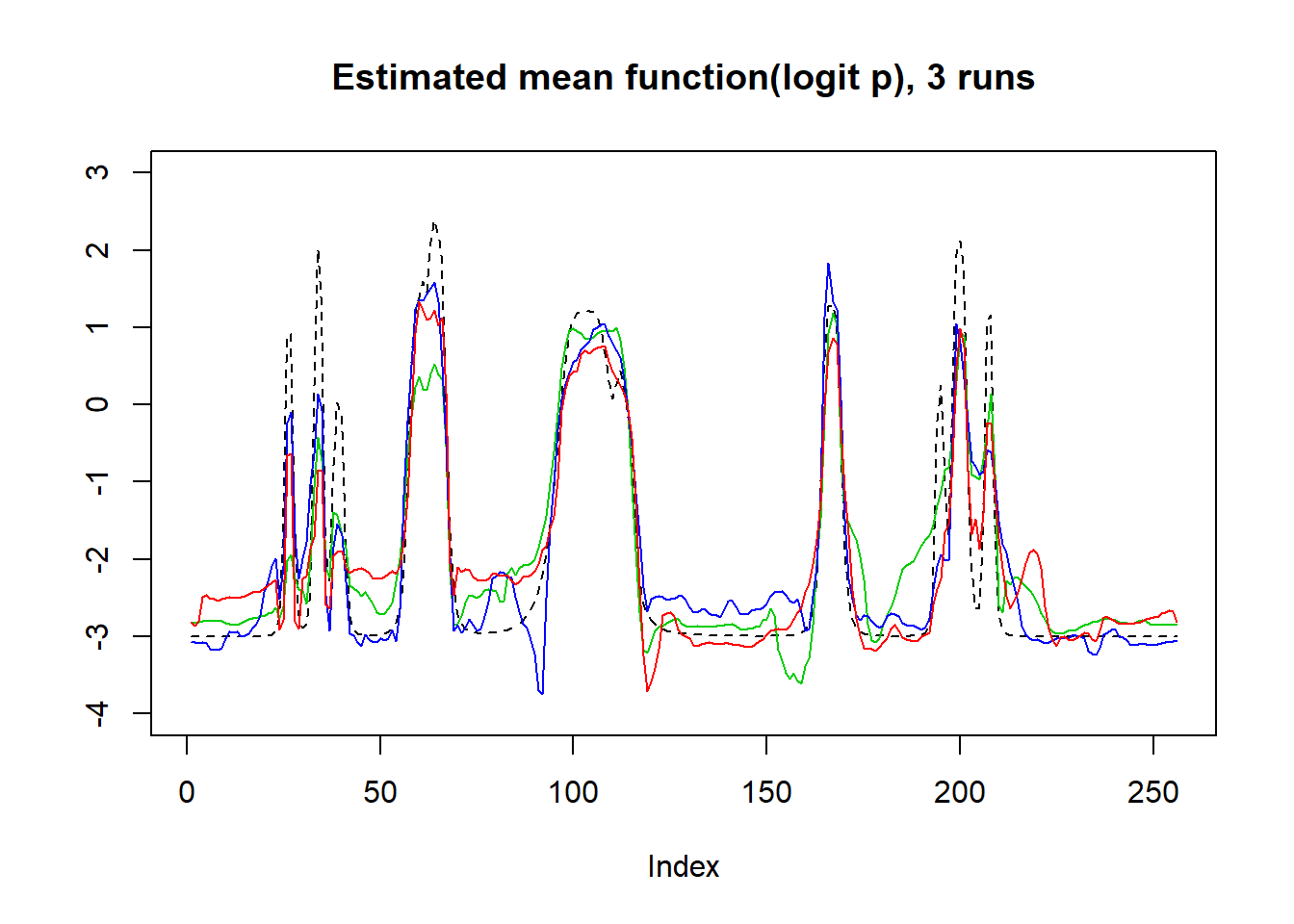

plot(beta,result$beta.est[2,],col=3,pch=2,xlab = 'True beta',ylab = 'Estimated beta')
lines(beta,result$beta.est[3,],col=4,pch=3,type='p')
lines(beta,result$beta.est[1,],col=2,pch=1,type='p')
abline(0,1,lty=2)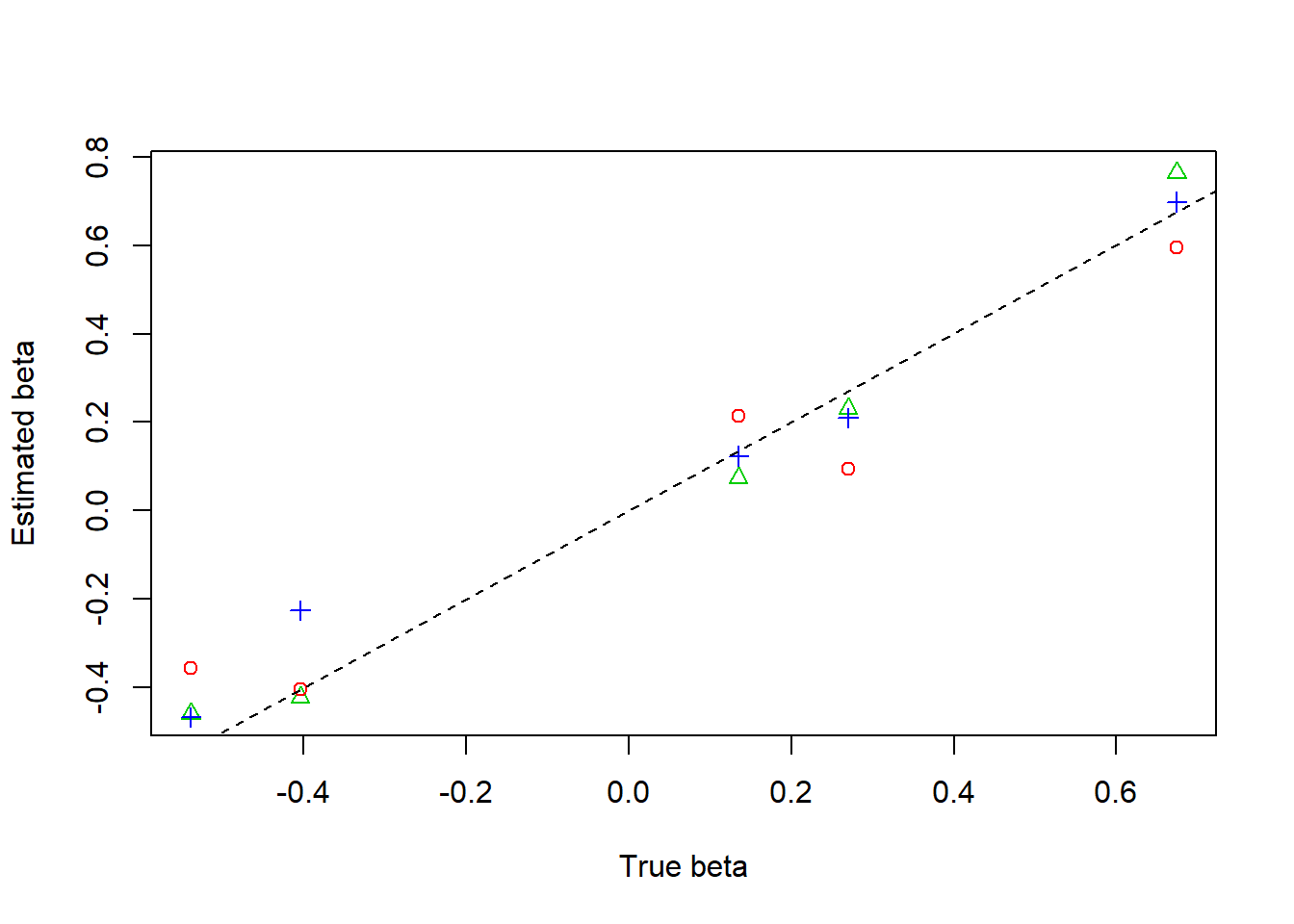

Parabola

r=function(x,c){return((x-c)^2*(x>c)*(x<=1))}
f=function(x){return(0.8 − 30*r(x,0.1) + 60*r(x, 0.2) − 30*r(x, 0.3) +
500*r(x, 0.35) − 1000*r(x, 0.37) + 1000*r(x, 0.41) − 500*r(x, 0.43) +
7.5*r(x, 0.5) − 15*r(x, 0.7) + 7.5*r(x, 0.9))}
mu=f(1:256/256)
mu=(mu-min(mu))*10-3

result=simu_study_binomx(mu,beta,ntri,filter.number = 8,family = 'DaubLeAsymm')
plot(result$mu.est[1,],type='l',col=2,ylab = '',main='Estimated mean function(p), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(logistic(mu),lty=2)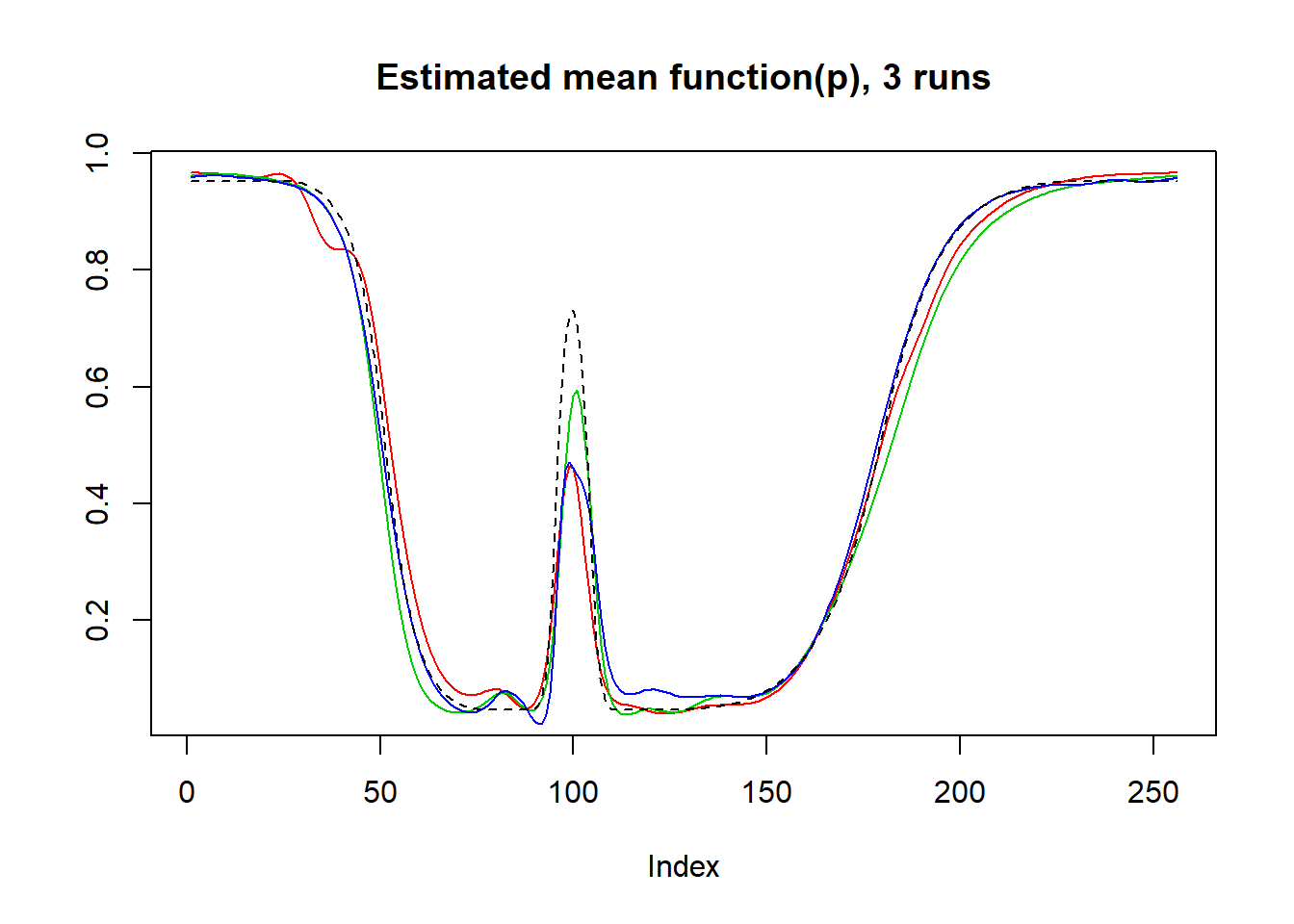

plot(logit(result$mu.est[1,]),type='l',col=2,ylab = '',main='Estimated mean function(logit p), 3 runs')
lines(logit(result$mu.est[2,]),col=3)
lines(logit(result$mu.est[3,]),col=4)
lines(mu,lty=2)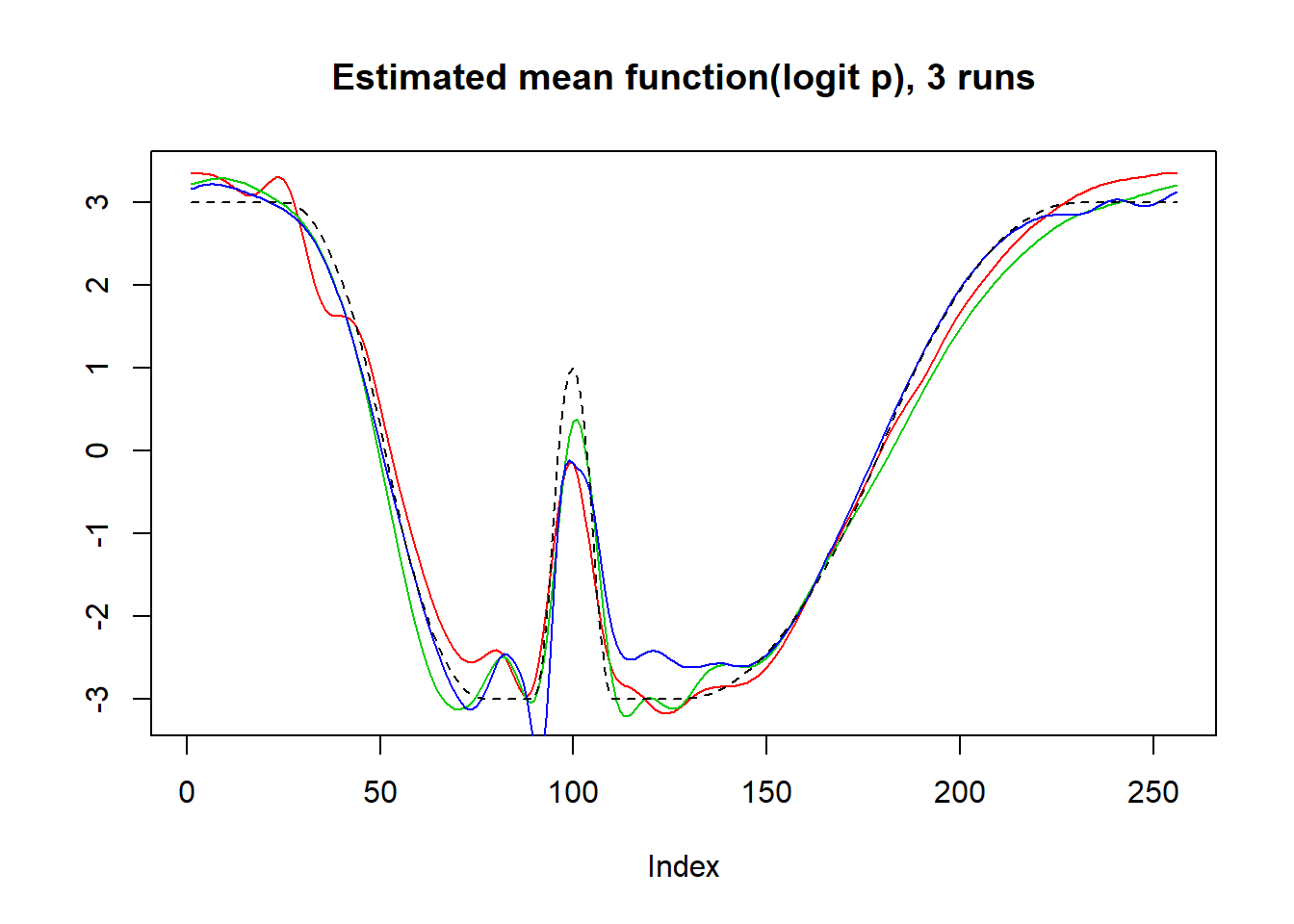

plot(beta,result$beta.est[3,],col=4,pch=3,xlab = 'True beta',ylab = 'Estimated beta',ylim=c(-0.5,0.85))
lines(beta,result$beta.est[2,],col=3,pch=2,type='p')
lines(beta,result$beta.est[1,],col=2,pch=1,type='p')
abline(0,1,lty=2)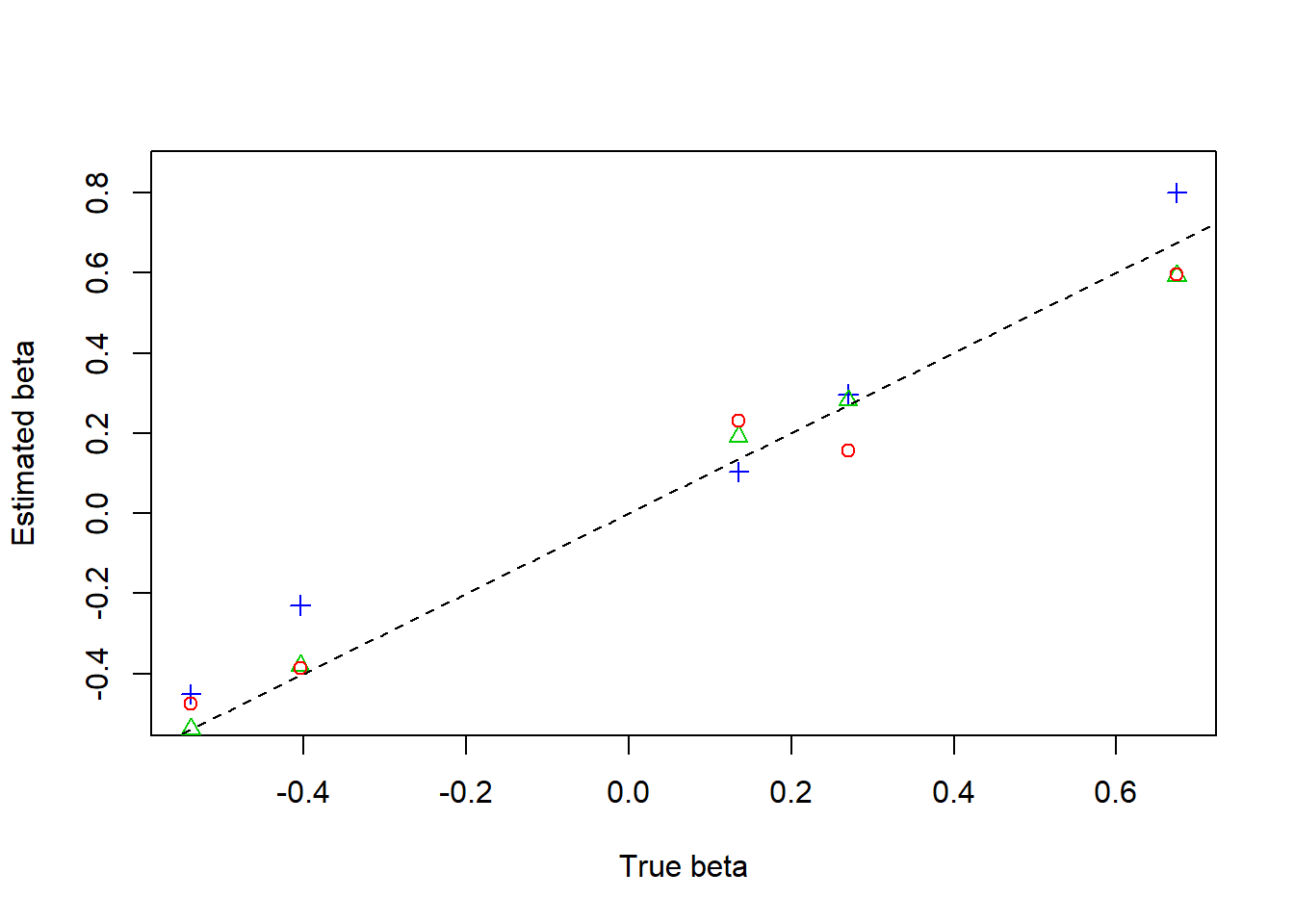

wave

f=function(x){return(0.5 + 2*cos(4*pi*x) + 2*cos(24*pi*x))}
mu=f(1:256/256)

result=simu_study_binomx(mu,beta,ntri,filter.number = 8,family = 'DaubLeAsymm')
plot(logistic(mu),lty=2,type='l',ylab = '',main='Estimated mean function(p), 3 runs')
lines(result$mu.est[2,],col=3)
lines(result$mu.est[3,],col=4)
lines(result$mu.est[1,],col=2)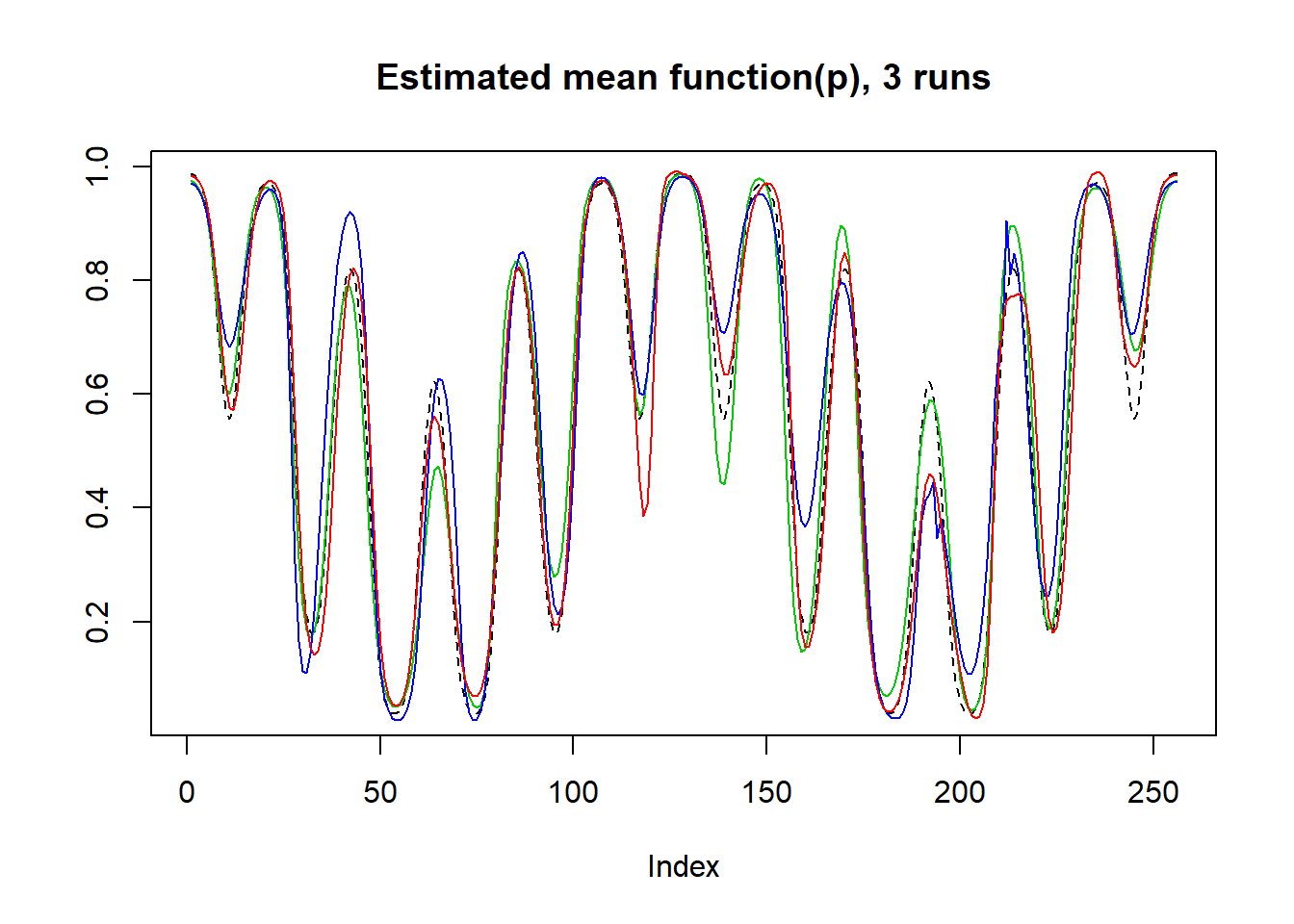

plot(mu,lty=2,type='l',ylab = '',main='Estimated mean function(logit p), 3 runs')
lines(logit(result$mu.est[2,]),col=3)
lines(logit(result$mu.est[3,]),col=4)
lines(logit(result$mu.est[1,]),col=2)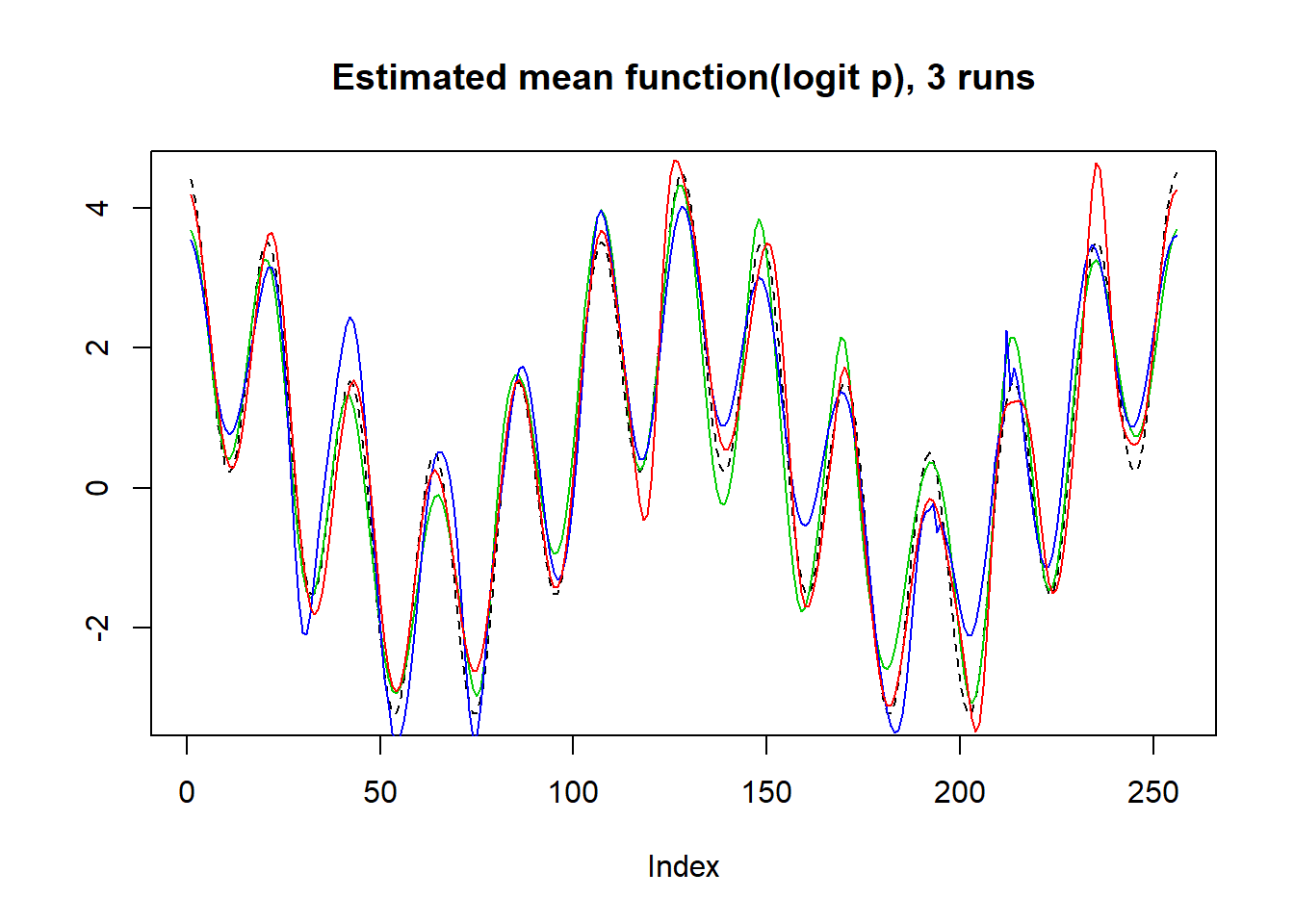

plot(beta,result$beta.est[2,],col=3,pch=2,xlab = 'True beta',ylab = 'Estimated beta',ylim=c(-0.7,0.6))
lines(beta,result$beta.est[3,],col=4,pch=3,type='p')
lines(beta,result$beta.est[1,],col=2,pch=1,type='p')
abline(0,1,lty=2)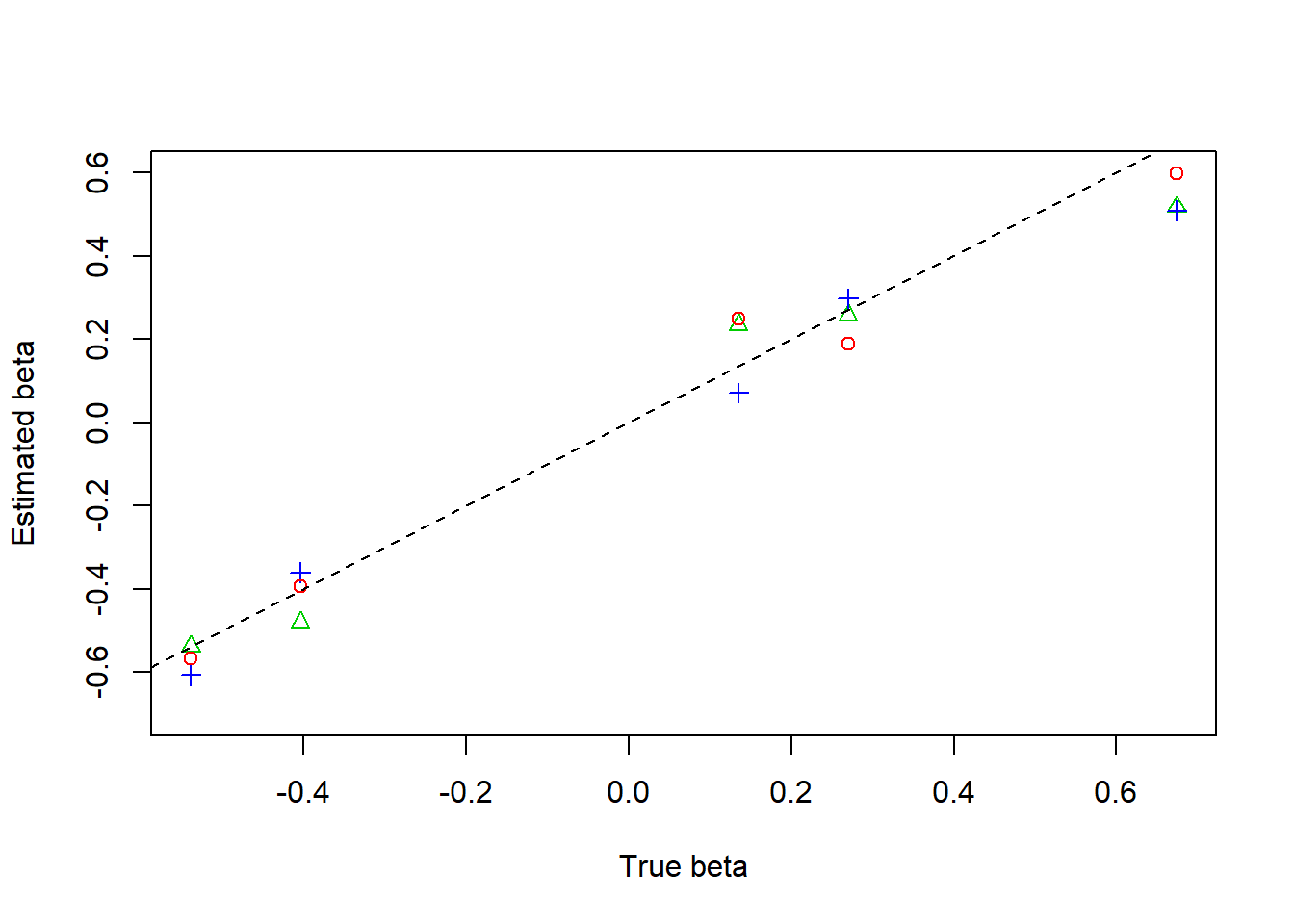

Session information

sessionInfo()
R version 3.4.0 (2017-04-21)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 16299)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.1252 
[2] LC_CTYPE=English_United States.1252   
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.1252    

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] smashrgen_0.1.0  wavethresh_4.6.8 MASS_7.3-47      caTools_1.17.1  
[5] ashr_2.2-7       smashr_1.1-5    

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.16        compiler_3.4.0      git2r_0.21.0       
 [4] workflowr_1.0.1     R.methodsS3_1.7.1   R.utils_2.6.0      
 [7] bitops_1.0-6        iterators_1.0.8     tools_3.4.0        
[10] digest_0.6.13       evaluate_0.10       lattice_0.20-35    
[13] Matrix_1.2-9        foreach_1.4.3       yaml_2.1.19        
[16] parallel_3.4.0      stringr_1.3.0       knitr_1.20         
[19] REBayes_1.3         rprojroot_1.3-2     grid_3.4.0         
[22] data.table_1.10.4-3 rmarkdown_1.8       magrittr_1.5       
[25] whisker_0.3-2       backports_1.0.5     codetools_0.2-15   
[28] htmltools_0.3.5     assertthat_0.2.0    stringi_1.1.6      
[31] Rmosek_8.0.69       doParallel_1.0.11   pscl_1.4.9         
[34] truncnorm_1.0-7     SQUAREM_2017.10-1   R.oo_1.21.0

This reproducible R Markdown analysis was created with workflowr 1.0.1