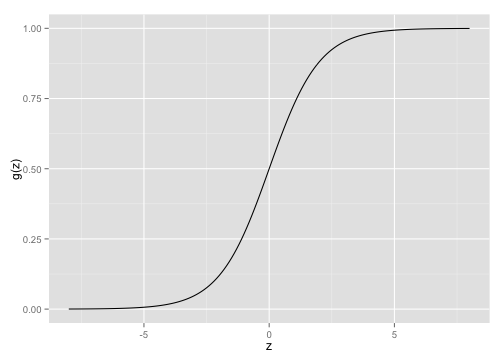
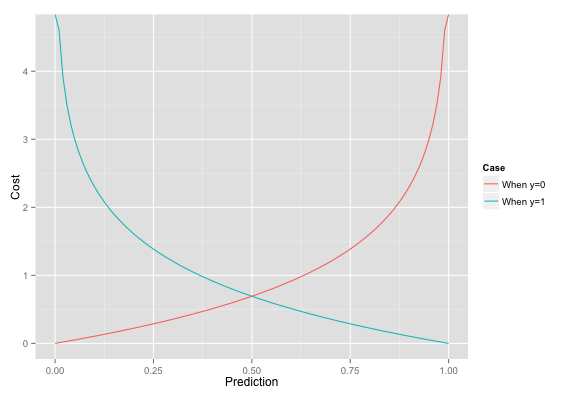
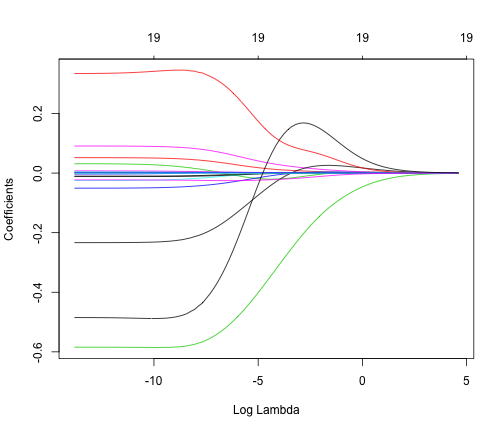
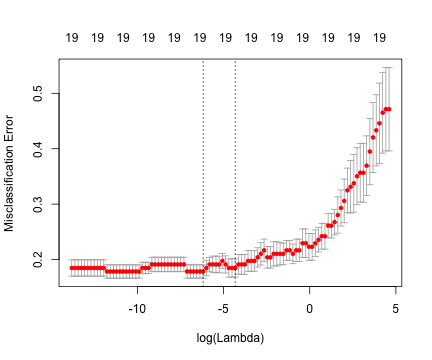
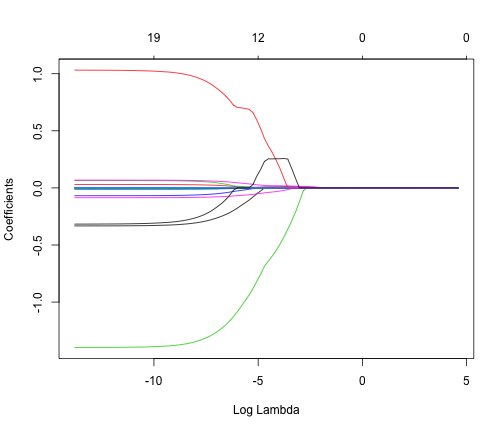
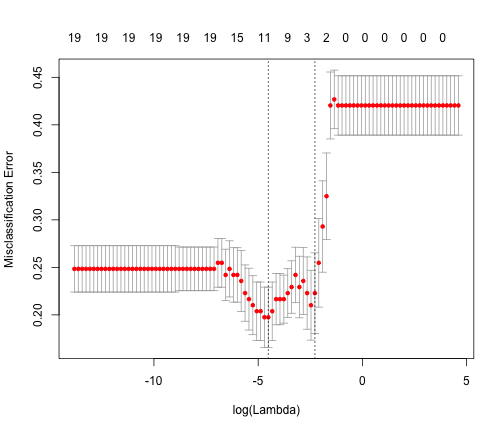
- Brief intro to logistic regression
- Motivation for regularization techniques
- Explanation of the most common regularization techniques:
- Ridge regression
- Lasso regression
- An example of each on a sample dataset
R packages to install if you want to follow along:
pkgs <- c('glmnet', 'ISLR')
install.packages(pkgs)